Heavy Rainfall Probabilistic Model for Zielona Góra in Poland
Abstract
1. Introduction
| Class | Description Due to Land Use | Frequency of Design Rainfall Occurrence [1 per C Years] | Probability p [%] | Frequency of Outflow Occurrence [1 per C Years] | Probability p [%] |
|---|---|---|---|---|---|
| I | Non-urban (rural) areas | 1 per 1 | 1 | 1 per 10 | 10 |
| II | Residential areas | 1 per 2 | 50 | 1 per 20 | 5 |
| III | City centers and service and industrial areas | 1 per 5 | 20 | 1 per 30 | 3.33 |
| IV | Underground communication facilities, passages and crossings under streets, etc. | 1 per 10 | 10 | 1 per 50 | 2 |
2. Materials and Methods
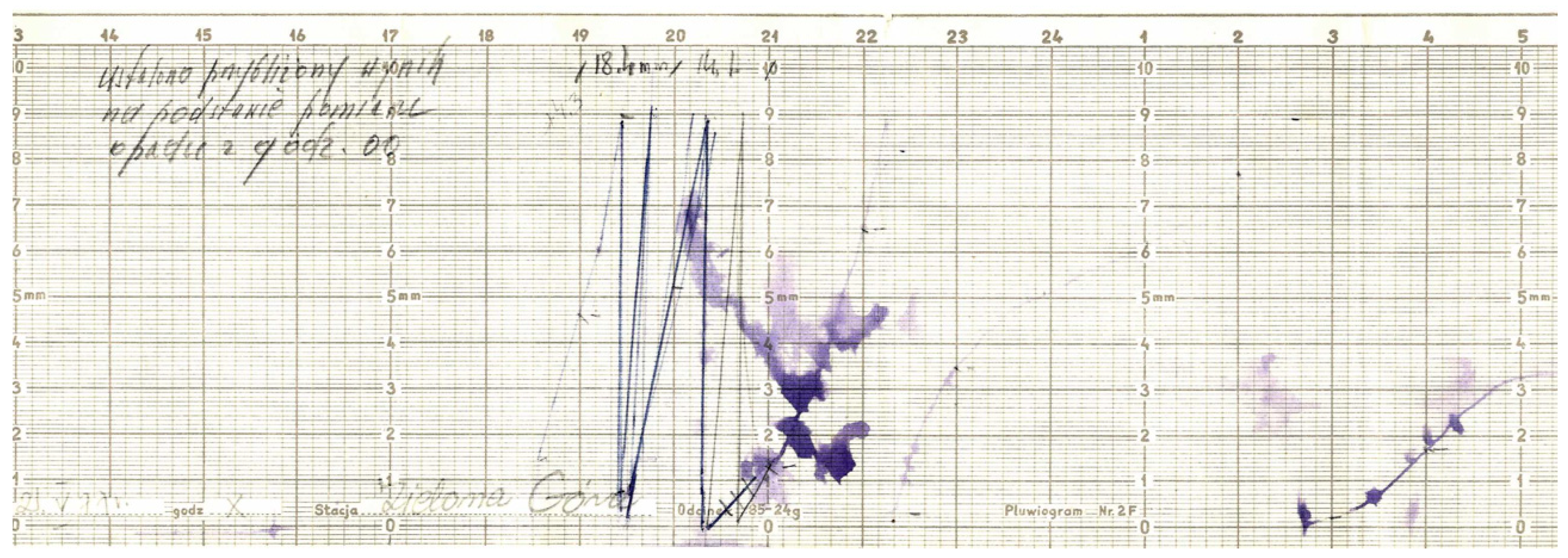
2.1. Heavy Rainfall Records
2.2. Probabilistic Models
- Minutes: 5, 10, 20, 30, 40, and 50;
- Hours: 1, 1.5, 2, 3, 6, 12, and 18;
- Days: 1, 1.5, 2, 3, 4, 5, and 6.
3. Results
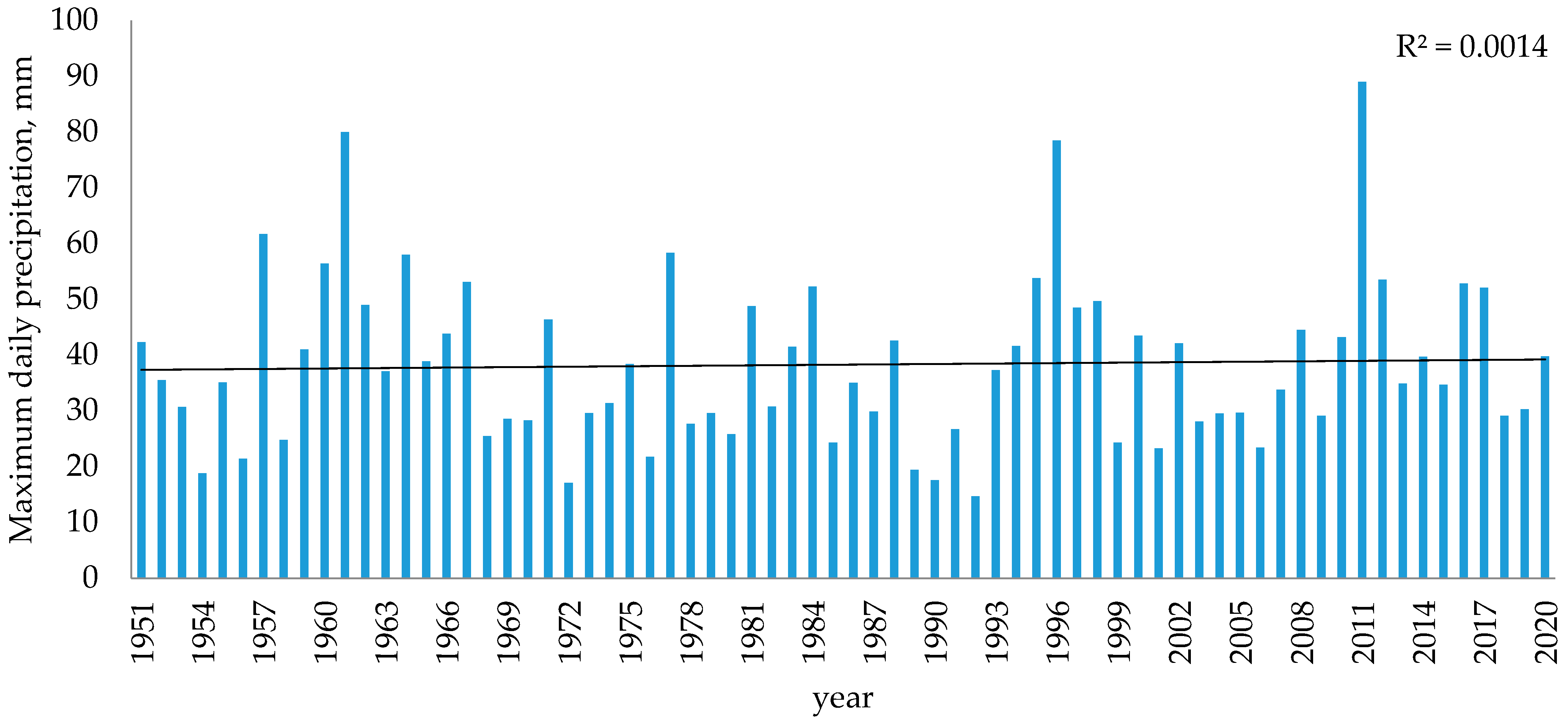
3.1. Climatological Background
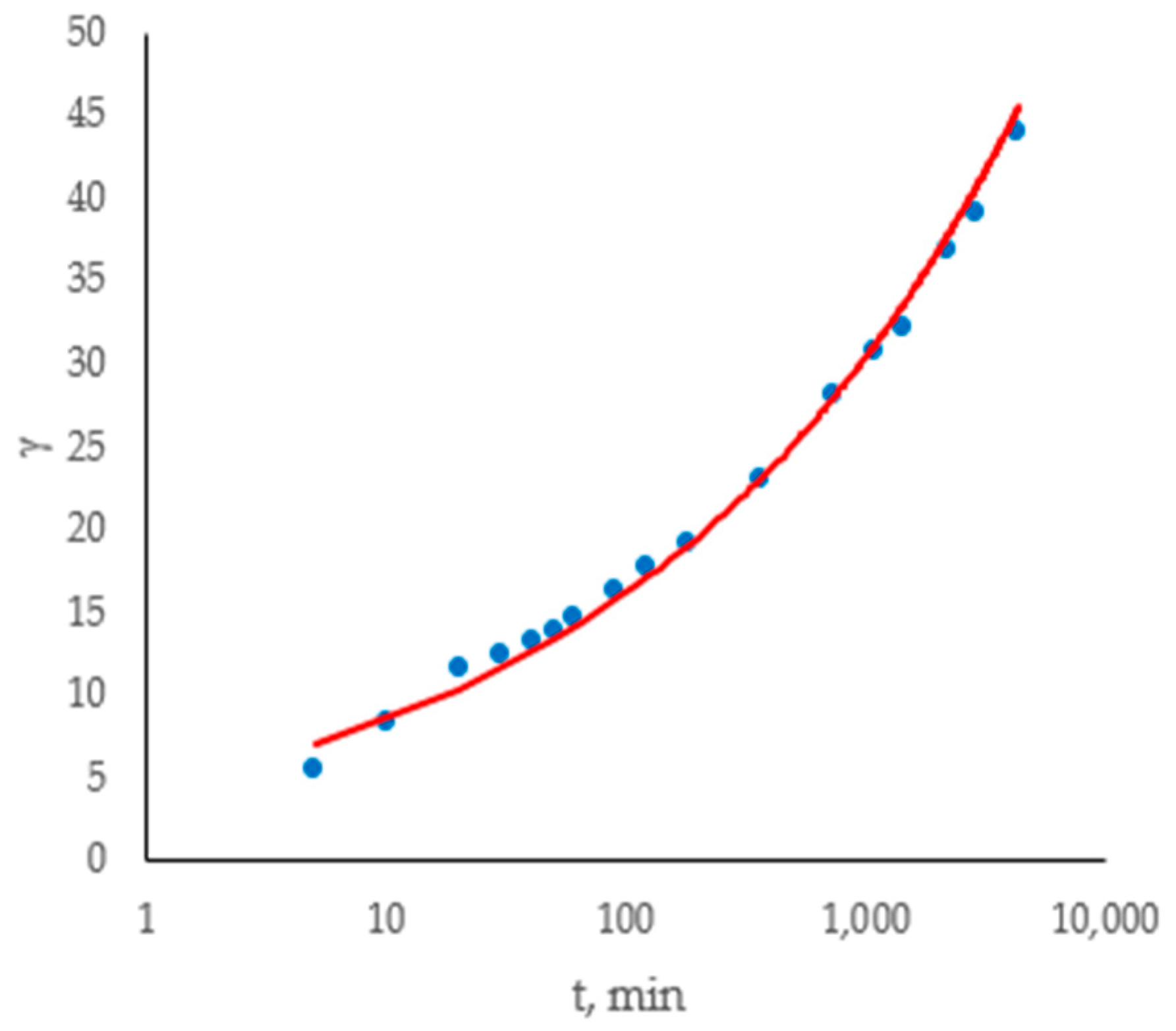
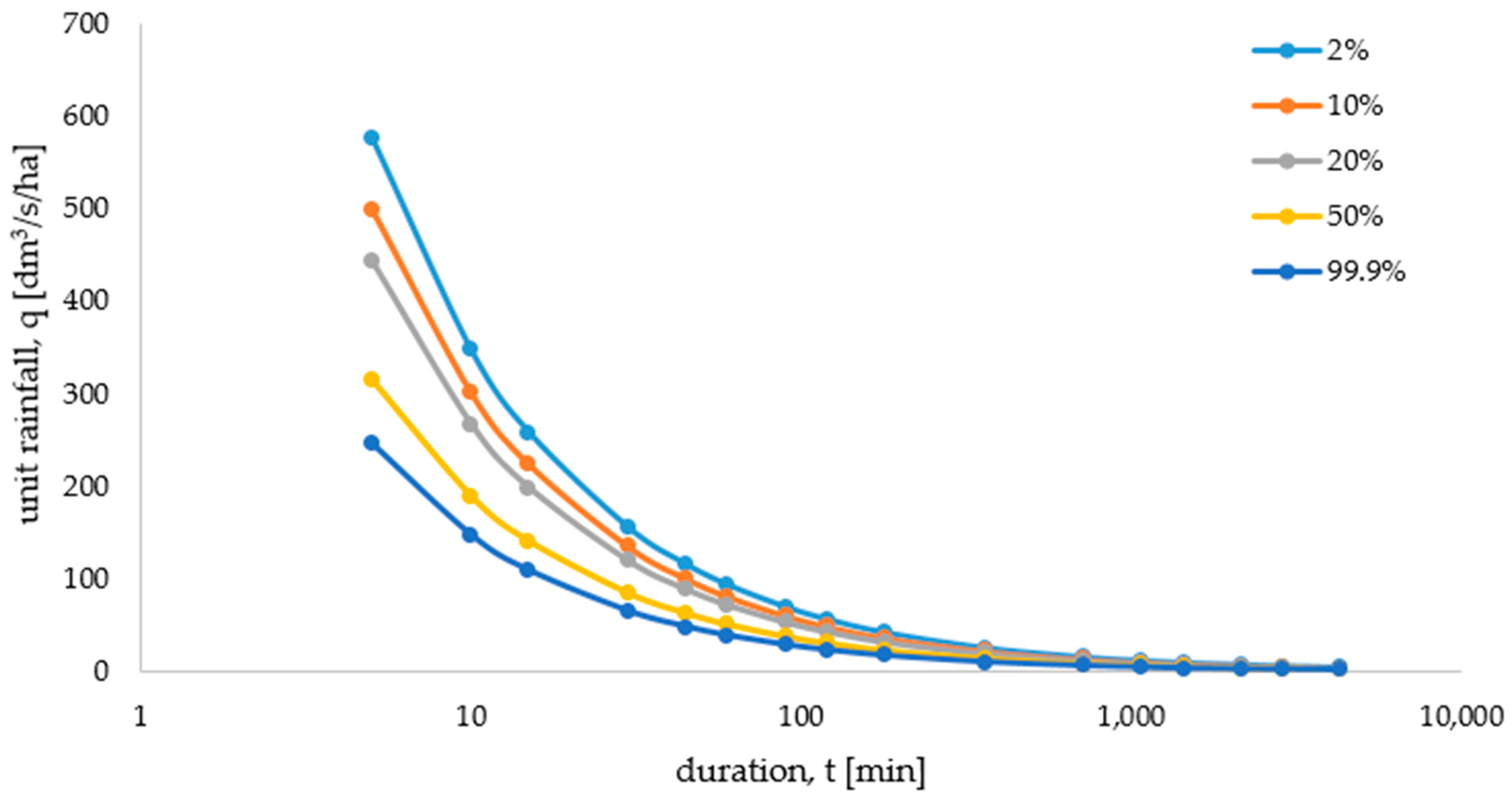
3.2. Zielona Góra Maximum Precipitation Probabilistic Model
4. Comparison of the Regional Model with the PMAXTP Atlas
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kotowski, A.; Kaźmierczak, B.; Dancewicz, A. The Modelling of Precipitations for the Dimensioning of Sewage Systems. Stud. Z Zakr. Inżynierii 2010, 68, 170. [Google Scholar]
- Kotowski, A. Basics of Safe Dimensioning of Drainage Areas [Podstawy Bezpiecznego Wymiarowania Odwodnień Terenów]; Seidel-Przywecki: Warszawa, Poland, 2015. [Google Scholar]
- EN 752:2008; Drain and Sewer Systems Outside Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2008.
- Schmitt, T.G. Kommentar Zum Arbeitsblatt A 118 “Hydraulische Bemessung Und Nachweis von Entwässerungssystemen”; DWA: Hennef, Germany, 2000. [Google Scholar]
- Schmitt, T.G.; Thomas, M. Rechnerischer Nachweis der Uberstauhaufigkeit Auf der Basis von Modellregen und Starkregenserien. Korresp. Abwasser 2000, 47, 63–69. [Google Scholar]
- Kubiszyn, K.; Łochańska, D. Do Changes of Rainfall Trends Affect Choice of Drainage Systems? Civ. Environ. Eng. Rep. 2022, 32, 389–409. [Google Scholar] [CrossRef]
- Kotowski, A.; Worrowicz, P. The New Method for Limiting Outflow from Storm Overflows. Environ. Prot. Eng. 2007, 33, 41. [Google Scholar]
- Kotowski, A.; Wójtowicz, P. Analysis of Hydraulic Parameters of Conical Vortex Regulators. Pol. J. Environ. Stud. 2010, 19, 749–756. [Google Scholar]
- Barszcz, M.P.; Kaznowska, E.; Wasilewicz, M. Analiza Wysokości Opadów Maksymalnych z Modelu PMAXTP i Ich Zastosowanie Do Weryfikacji Działania Miejskiego Systemu Odwodnienia Analysis of Maximum Rainfall Amounts from the PMAXTP Model, and Their Application in Verifying the Performance. Przegląd Geogr. 2024, 96, 473–494. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; National Risk Management Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2010; Volume 276.
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and Modeling of Flooding in Urban Drainage Systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Słyś, D.; Stec, A. Hydrodynamic Modelling of the Combined Sewage System for the City of Przemyśl. Environ. Prot. Eng. 2012, 38, 99–112. [Google Scholar]
- Büchele, B.; Kreibich, H.; Kron, A.; Thieken, A.; Ihringer, J.; Oberle, P.; Merz, B.; Nestmann, F. Flood-Risk Mapping: Contributions towards an Enhanced Assessment of Extreme Events and Associated Risks. Nat. Hazards Earth Syst. Sci. 2006, 6, 485–503. [Google Scholar] [CrossRef]
- Jha, A.K.; Bloch, R.; Lamond, J. Cities and Flooding: A Guide to Integrated Urban Flood Risk Management for the 21st Century; World Bank Publications: Washington, DC, USA, 2012; ISBN 0821388665. [Google Scholar]
- Kubal, C.; Haase, D.; Meyer, V.; Scheuer, S. Integrated Urban Flood Risk Assessment–Adapting a Multicriteria Approach to a City. Nat. Hazards Earth Syst. Sci. 2009, 9, 1881–1895. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B. Water Supply System Reliability Management. Environ. Prot. Eng. 2009, 35, 29–35. [Google Scholar]
- Tchorzewska-Cieslak, B. Matrix Method for Estimating the Risk of Failure in the Collective Water Supply System Using Fuzzy Logic. Environ. Prot. Eng. 2011, 37, 111–118. [Google Scholar]
- Zevenbergen, C.; Veerbeek, W.; Gersonius, B.; Van Herk, S. Challenges in Urban Flood Management: Travelling across Spatial and Temporal Scales. J. Flood Risk Manag. 2008, 1, 81–88. [Google Scholar] [CrossRef]
- Kaźmierczak, B.; Kotowski, A. The Influence of Precipitation Intensity Growth on the Urban Drainage Systems Designing. Theor. Appl. Climatol. 2014, 118, 285–296. [Google Scholar] [CrossRef]
- Konishi, S.; Kitagawa, G. Information Criteria and Statistical Modeling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 0387718869. [Google Scholar]
- Larsen, A.N.; Gregersen, I.B.; Christensen, O.B.; Linde, J.J.; Mikkelsen, P.S. Potential Future Increase in Extreme One-Hour Precipitation Events over Europe Due to Climate Change. Water Sci. Technol. 2009, 60, 2205–2216. [Google Scholar] [CrossRef]
- Olsson, J.; Berggren, K.; Olofsson, M.; Viklander, M. Applying Climate Model Precipitation Scenarios for Urban Hydrological Assessment: A Case Study in Kalmar City, Sweden. Atmos. Res. 2009, 92, 364–375. [Google Scholar] [CrossRef]
- Onof, C.; Arnbjerg-Nielsen, K. Quantification of Anticipated Future Changes in High Resolution Design Rainfall for Urban Areas. Atmos. Res. 2009, 92, 350–363. [Google Scholar] [CrossRef]
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.; Tignor, M.; Miller, H. IPCC Fourth Assessment Report (AR4). Climate Change. 2007. Available online: https://www.ipcc.ch/assessment-report/ar4/ (accessed on 27 May 2025).
- Kyselý, J.; Gaál, L.; Picek, J.; Schindler, M. Return Periods of the August 2010 Heavy Precipitation in Northern Bohemia (Czech Republic) in the Present Climate and under Climate Change. J. Water Clim. Change 2013, 4, 265–286. [Google Scholar] [CrossRef]
- Kubiszyn, K. Analysis of the Local Precipitation Trends in the Podkarpackie and Lubuskie Voivodeships. Civ. Environ. Eng. Rep. 2023, 33, 122–138. [Google Scholar] [CrossRef]
- PN-EN 752:2017; Drain and Sewer Systems Outside Buildings—Sewer System Management. British Standards Institution: London, UK, 2017.
- Hershfield, D.M. Rainfall Frequency Atlas of the United States; Technical paper No. 40; U.S. Government Printing Office: Washington, DC, USA, 1961; pp. 1–61.
- Kaźmierczak, B.; Kotowski, A. Depth-Duration-Frequency Rainfall Model for Dimensioning and Modelling of Wrocław Drainage Systems. Environ. Prot. Eng. 2012, 38, 127–138. [Google Scholar] [CrossRef]
- Suligowski, R. Maksymalne Wysokości Opadów o Określonym Czasie Trwania i Prawdopodobieństwie Przewyższenia w Kielcach. In Woda w Mieście; Monografie Komisji Hydrologicznej PTG: Kracow, Poland, 2014; Volume 2, pp. 271–280. [Google Scholar]
- Twardosz, R.; Niedźwiedź, T.; Łupikasza, E. The Influence of Atmospheric Circulation on the Type of Precipitation (Kraków, Southern Poland). Theor. Appl. Climatol. 2011, 104, 233–250. [Google Scholar] [CrossRef]
- Twardosz, R.; Łupikasza, E.; Niedźwiedź, T.; Walanus, A. Long-Term Variability of Occurrence of Precipitation Forms in Winter in Kraków, Poland. Clim. Change 2012, 113, 623–638. [Google Scholar] [CrossRef]
- Mrowiec, M. Wpływ Nierównomierności Przestrzennej Opadów na Obliczanie Pojemności Kanalizacyjnych Zbiorników Retencyjnych; Gaz, Woda i Technika Sanitarna: Warsaw, Poland, 2014; pp. 259–263. [Google Scholar]
- Zawilski, M.; Brzezińska, A. Areal Rainfall Intensity Distribution over an Urban Area and Its Effect on a Combined Sewerage System. Urban Water J. 2014, 11, 532–542. [Google Scholar] [CrossRef]
- Bogdanowicz, E.; Stachý, J. Maximum Rainfall in Poland. Design Characteristics. Res. Mater 1998, 23, 98. [Google Scholar]
- Kruszewski, A.; Buczek, T.; Kruczek, P.; Skąpski, K. Rola Systemu Telemetrii w czasie zdarzeń ekstremalnych na przykładzie powodzi w maju i czerwcu 2010 roku. In Wybrane Problemy Sterowania i Zarządzania Zasobami Wodnymi na tle Zadań Gospodarki Wodnej; IMGW-PIB: Warszawa, Poland, 2013. [Google Scholar]
- Licznar, P.; Zaleski, J. Metodyka Opracowania Polskiego Atlasu Natężenia Deszczów (PANDa); Instytut Meteorologii i Gospodarki Wodnej-Państwowy Instytut Badawczy: Warszawa, Poland, 2020; ISBN 8364979353. [Google Scholar]
- Ozga-Zieliński, B. Modele Probabilistyczne Opadów Maksymalnych o Określonym Czasie Trwania i Prawdopodobieństwie Przewyższenia: Projekt PMAXTP; Instytut Meteorologii i Gospodarki Wodnej Państwowy Instytut Badawczy: Warszawa, Poland, 2022. [Google Scholar]
- Wdowikowski, M.; Wartalska, K.; Kaźmierczak, B.; Kotowski, A. Zasady Formułowania Probabilistycznych Modeli Deszczów Maksymalnych; Gaz, Woda i Technika Sanitarna: Warsaw, Poland, 2023; Volume 1, pp. 22–29. [Google Scholar]
- Montes-Pajuelo, R.; Rodríguez-Pérez, Á.M.; López, R.; Rodríguez, C.A. Analysis of Probability Distributions for Modelling Extreme Rainfall Events and Detecting Climate Change: Insights from Mathematical and Statistical Methods. Mathematics 2024, 12, 1093. [Google Scholar] [CrossRef]
- Strong, R.; Borgstroem, O.; Nathan, R.; Wasko, C.; O’Shea, D. Global Applicability of the Kappa Distribution for Rainfall Frequency Analysis. Water Resour. Res. 2025, 61, e2024WR039035. [Google Scholar] [CrossRef]
- Ahn, M.S.; Ullrich, P.A.; Gleckler, P.J.; Lee, J.; Ordonez, A.C.; Pendergrass, A.G. Evaluating Precipitation Distributions at Regional Scales: A Benchmarking Framework and Application to CMIP5 and 6 Models. Geosci. Model Dev. 2023, 16, 3927–3951. [Google Scholar] [CrossRef]
- Abbas, A.; Ahmad, T.; Ahmad, I. Modeling Zero-Inflated Precipitation Extremes. arXiv 2025, arXiv:2504.11058. [Google Scholar]
- Wdowikowski, M.; Kaźmierczak, B.; Kotowski, A. Probabilistyczne Modelowanie Deszczów Maksymalnych na Przykładzie Dorzecza Górnej i Środkowej Odry; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2021; ISBN 8374931639. [Google Scholar]
- Maciążek, A. Modernizacja Wyposażenia Technicznego i Pomiarowego Służby Obserwacyjno-Pomiarowej. Gaz. Obs. IMGW 2005, 54, 34–40. [Google Scholar]
- Urban, G. Climate of Zielona Góra; Institute of Meteorology and Water Management: Warszawa, Poland, 2020. [Google Scholar]
- Filipiak, J. Problem Dokładności Serii Opadowych w Aspekcie Instalacji Cyfrowych Deszczomierzy Rejestrujących. Ann. Univ. Mariae Curie-Skłodowska. Sect. B Geogr. Geol. Mineral. Et Petrographia 2001, 55, 145–152. [Google Scholar]
- Licznar, P. Generatory Syntetycznych Szeregów Opadowych do Modelowania Sieci Kanalizacji Deszczowych i Ogólnospławnych; Wydawnictwo Uniwersytetu Przyrodniczego we Wrocławiu: Wrocław, Poland, 2009. [Google Scholar]
- Kaźmierczak, B. Prognozy Zmian Maksymalnych Wysokości Opadów Deszczowych We Wrocławiu; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2019. [Google Scholar]
- Ben-Zvi, A. Rainfall Intensity–Duration–Frequency Relationships Derived from Large Partial Duration Series. J. Hydrol. 2009, 367, 104–114. [Google Scholar] [CrossRef]
- Brath, A.; Castellarin, A.; Montanari, A. Assessing the Reliability of Regional Depth-duration-frequency Equations for Gaged and Ungaged Sites. Water Resour. Res. 2003, 39, 1367. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Castellarin, A.; Brath, A. Relationships between Statistics of Rainfall Extremes and Mean Annual Precipitation: An Application for Design-Storm Estimation in Northern Central Italy. Hydrol. Earth Syst. Sci. 2006, 10, 589–601. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Theory & Methods: Generalized Exponential Distributions. Aust. N. Z. J. Stat. 1999, 41, 173–188. [Google Scholar]
- Gupta, R.D.; Kundu, D. Generalized Exponential Distribution: Different Method of Estimations. J. Stat. Comput. Simul. 2001, 69, 315–337. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized Exponential Distribution: Existing Results and Some Recent Developments. J. Stat. Plan. Inference 2007, 137, 3537–3547. [Google Scholar] [CrossRef]
- Kotowski, A.; Kaźmierczak, B. Probabilistic Models of Maximum Precipitation for Designing Sewerage. J. Hydrometeorol. 2013, 14, 1958–1965. [Google Scholar] [CrossRef]
- Kottegoda, N.T.; Natale, L.; Raiteri, E. Statistical Modelling of Daily Streamflows Using Rainfall Input and Curve Number Technique. J. Hydrol. 2000, 234, 170–186. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, A.; Holleman, I. Rainfall Depth-Duration-Frequency Curves and Their Uncertainties. J. Hydrol. 2008, 348, 124–134. [Google Scholar] [CrossRef]
- Shinyie, W.L.; Ismail, N.; Jemain, A.A. Semi-Parametric Estimation Based on Second Order Parameter for Selecting Optimal Threshold of Extreme Rainfall Events. Water Resour. Manag. 2014, 28, 3489–3514. [Google Scholar] [CrossRef]
- D’Agostino, R.B. Goodness-of-Fit-Techniques; CRC Press: Boca Raton, FL, USA, 1986; Volume 68, ISBN 0824774876. [Google Scholar]
- Shin, H.; Jung, Y.; Jeong, C.; Heo, J.-H. Assessment of Modified Anderson–Darling Test Statistics for the Generalized Extreme Value and Generalized Logistic Distributions. Stoch. Environ. Res. Risk Assess. 2012, 26, 105–114. [Google Scholar] [CrossRef]
- Haan, L.; Ferreira, A. Extreme Value Theory: An Introduction; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3. [Google Scholar]
- Zucchini, W. An Introduction to Model Selection. J. Math. Psychol. 2000, 44, 41–61. [Google Scholar] [CrossRef] [PubMed]
- Laio, F.; Di Baldassarre, G.; Montanari, A. Model Selection Techniques for the Frequency Analysis of Hydrological Extremes. Water Resour. Res. 2009, 45, W07416. [Google Scholar] [CrossRef]
- Lee, S.H.; Maeng, S.J. Frequency Analysis of Extreme Rainfall Using L-moment. Irrig. Drain. J. Int. Comm. Irrig. Drain. 2003, 52, 219–230. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; U.S. Geological Survey: Reston, VA, USA, 2002.
- Pruchnicki, J. Metody Opracowań Klimatologicznych; Wydawnictwa Politechniki Warszawskiej: Warsaw, Poland, 1987. [Google Scholar]
- Von Storch, H.; Navarra, A. Analysis of Climate Variability: Applications of Statistical Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999; ISBN 3540663150. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100, ISBN 0123850231. [Google Scholar]
- Węglarczyk, S. Opad Miarodajny, Przeszłość i Teraźniejszość, Teoria i Praktyka; KGW-PAN Monograph: Warsaw, Poland, 2014; Available online: https://www.dropbox.com/sh/0wthyz1sy59pvg8/AAAXvW3ZQQLpEPxjjWkDYN9Ua/Monografie%20Komitetu%20Gospodarki%20Wodnej%20PAN?dl=0 (accessed on 27 May 2025).
- Kaźmierczak, B.; Wartalska, K.; Wdowikowski, M.; Ozga-Zieliński, B.; Sidorczyk, M.; Kotowski, A. Reliable Precipitation Data for Dimensioning Drainage of Areas and Buildings. Rocz. Ochr. Sr. 2025, 27, 13–19. [Google Scholar] [CrossRef]
- Kaźmierczak, B.; Wdowikowski, M. Maximum Rainfall Model Based on Archival Pluviographic Records—Case Study for Legnica (Poland). Period. Polytech. Civ. Eng. 2016, 60, 305–312. [Google Scholar] [CrossRef]
- Anghel, C.G. Revisiting the Use of the Gumbel Distribution: A Comprehensive Statistical Analysis Regarding Modeling Extremes and Rare Events. Mathematics 2024, 12, 2466. [Google Scholar] [CrossRef]
- Shamkhi, M.S.; Azeez, M.K.; Obeid, Z.H. Deriving Rainfall Intensity-Duration-Frequency (IDF) Curves and Testing the Best Distribution Using EasyFit Software 5.5 for Kut City, Iraq. Open Eng. 2022, 12, 834–843. [Google Scholar] [CrossRef]






| Distribution (Number of Parameters) | Likelihood Function |
|---|---|
| Fréchet (3) | |
| Gamma (3) | |
| GED (3) | |
| Gumbel (2) | |
| Log-normal (3) | |
| Weibull (3) |
| Month | Maximum Monthly Rainfall, mm | Minimum Monthly Rainfall, mm | Average Monthly Rainfall, mm |
|---|---|---|---|
| I | 107.2 | 2.0 | 40.3 |
| II | 93.0 | 2.4 | 33.3 |
| III | 129.9 | 8.1 | 38.2 |
| IV | 81.4 | 1.7 | 37.7 |
| V | 132.8 | 8.7 | 55.0 |
| VI | 143.5 | 8.5 | 59.4 |
| VII | 219.3 | 6.0 | 80.9 |
| VIII | 196.4 | 6.9 | 68.4 |
| IX | 144.4 | 1.1 | 46.3 |
| X | 162.4 | 2.9 | 41.5 |
| XI | 123.3 | 0.8 | 41.7 |
| XII | 114.8 | 5.0 | 43.9 |
| t, min | m = 1 p = 0.020 | m = 5 p = 0.098 | m = 10 p = 0.196 | m = 25 p = 0.490 | m = 50 p = 0.980 |
|---|---|---|---|---|---|
| mm | mm | mm | mm | mm | |
| 5 | 13.6 | 10.1 | 8.9 | 7.1 | 5.6 |
| 10 | 19.2 | 14.4 | 12.3 | 10.5 | 8.5 |
| 20 | 30.1 | 23.3 | 17.4 | 13.9 | 11.6 |
| 30 | 37.9 | 25.2 | 19.6 | 15.6 | 12.5 |
| 40 | 39.9 | 27.7 | 22.0 | 16.5 | 13.3 |
| 50 | 40.6 | 27.7 | 22.7 | 17.6 | 13.9 |
| 60 | 41.8 | 33.0 | 26.3 | 18.5 | 14.8 |
| 90 | 45.1 | 38.0 | 26.3 | 19.8 | 16.3 |
| 120 | 45.9 | 38.0 | 28.1 | 22.4 | 17.8 |
| 180 | 51.9 | 38.9 | 33.4 | 24.7 | 19.2 |
| 360 | 55.0 | 43.8 | 37.7 | 27.6 | 23.1 |
| 720 | 56.9 | 49.7 | 41.1 | 35.7 | 28.1 |
| 1080 | 73.6 | 55.7 | 49.3 | 39.7 | 30.9 |
| 1440 | 89.1 | 60.6 | 55.0 | 41.1 | 32.3 |
| 2160 | 96.0 | 68.8 | 61.0 | 46.6 | 36.9 |
| 2880 | 103.5 | 72.1 | 63.3 | 51.6 | 39.2 |
| 4320 | 109.6 | 77.1 | 68.0 | 57.0 | 44.1 |
| t, min | GED | Weibull | LogN | Fréchet | Gumbel | Gamma | |
|---|---|---|---|---|---|---|---|
| 5 | α | 1.2073 | 1.2218 | 0.8047 | 1.1158 | 2.8022 | 1.1974 |
| β | 0.5373 | 6.9021 | 0.5524 | 2.1726 | 2.8019 | 1.7482 | |
| γ | 5.588 | 5.336 | 5.593 | 3.887 | 5.589 | ||
| 10 | α | 0.934 | 1.4506 | 0.7255 | 1.1155 | 3.6127 | 1.1751 |
| β | 0.3835 | 10.0798 | 0.8429 | 2.6083 | 4.5195 | 2.1422 | |
| γ | 8.499 | 8.014 | 8.485 | 5.357 | 8.479 | ||
| 20 | α | 0.8478 | 2.4935 | 1.0529 | 0.898 | 1.5692 | 0.8506 |
| β | 0.2291 | 13.7787 | 0.8868 | 3.71 | 2.4516 | 4.5979 | |
| γ | 11.599 | 11.432 | 11.599 | 10.667 | 11.599 | ||
| 30 | α | 0.828 | 3.0051 | 1.0079 | 0.8971 | 1.9607 | 0.8329 |
| β | 0.1833 | 15.2481 | 1.1671 | 4.5722 | 4.179 | 5.7783 | |
| γ | 12.499 | 12.172 | 12.499 | 10.378 | 12.499 | ||
| 40 | α | 0.6898 | 3.4532 | 1.0405 | 0.8176 | 1.8469 | 0.6995 |
| β | 0.1445 | 16.3324 | 1.2689 | 4.8956 | 4.4391 | 7.7066 | |
| γ | 13.299 | 12.897 | 13.299 | 11.065 | 13.299 | ||
| 50 | α | 0.6259 | 3.8474 | 1.0765 | 0.7734 | 1.6968 | 0.6359 |
| β | 0.1232 | 17.209 | 1.3334 | 5.2324 | 4.4171 | 9.302 | |
| γ | 13.899 | 13.497 | 13.899 | 11.805 | 13.899 | ||
| 60 | α | 0.7971 | 4.0984 | 1.1353 | 0.8748 | 1.379 | 0.8045 |
| β | 0.1373 | 18.2752 | 1.3024 | 5.8697 | 3.4332 | 7.7877 | |
| γ | 14.799 | 14.594 | 14.799 | 13.63 | 14.799 | ||
| 90 | α | 0.508 | 4.302 | 1.3958 | 0.6597 | 1.2201 | 0.516 |
| β | 0.1005 | 19.5611 | 1.1018 | 4.9403 | 2.9965 | 12.0712 | |
| γ | 16.299 | 16.131 | 16.299 | 15.181 | 16.299 | ||
| 120 | α | 0.678 | 4.441 | 1.1378 | 0.8105 | 1.5574 | 0.6887 |
| β | 0.1142 | 21.5927 | 1.4142 | 6.117 | 4.5909 | 9.8078 | |
| γ | 17.799 | 17.454 | 17.799 | 15.775 | 17.799 | ||
| 180 | α | 0.7391 | 4.871 | 1.1002 | 0.8511 | 1.7216 | 0.7496 |
| β | 0.1092 | 23.4419 | 1.5583 | 6.947 | 5.8069 | 9.991 | |
| γ | 19.199 | 18.754 | 19.199 | 16.39 | 19.199 | ||
| 360 | α | 0.7853 | 4.8504 | 0.981 | 0.884 | 1.9674 | 0.7949 |
| β | 0.1106 | 27.5004 | 1.6845 | 7.2844 | 6.8062 | 9.6907 | |
| γ | 23.099 | 22.438 | 23.099 | 19.605 | 23.099 | ||
| 720 | α | 0.9482 | 5.1145 | 0.7429 | 1.0834 | 3.5905 | 0.9625 |
| β | 0.1116 | 33.5368 | 2.0793 | 8.9322 | 15.8564 | 9.0007 | |
| γ | 28.099 | 26.407 | 28.079 | 16.966 | 28.099 | ||
| 1080 | α | 1.2541 | 6.1379 | 0.6378 | 1.1797 | 4.9274 | 1.2749 |
| β | 0.1061 | 37.7856 | 2.426 | 11.3887 | 27.3413 | 8.5104 | |
| γ | 30.752 | 27.841 | 30.783 | 9.801 | 30.732 | ||
| 1440 | α | 1.1821 | 7.0333 | 0.7759 | 1.1033 | 3.0399 | 1.1734 |
| β | 0.0916 | 39.8475 | 2.3453 | 12.5417 | 17.7746 | 10.3342 | |
| γ | 32.239 | 30.489 | 32.266 | 20.934 | 32.242 | ||
| 2160 | α | 0.7879 | 8.751 | 1.0153 | 0.8997 | 1.9386 | 0.8 |
| β | 0.0625 | 44.9462 | 2.2479 | 13.0911 | 12.4994 | 17.1124 | |
| γ | 36.899 | 35.843 | 36.899 | 30.372 | 36.899 | ||
| 2880 | α | 0.8456 | 9.5142 | 0.8784 | 0.9531 | 3.0244 | 0.859 |
| β | 0.0585 | 48.5409 | 2.5137 | 15.0585 | 24.0482 | 17.8585 | |
| γ | 39.199 | 37.16 | 39.199 | 22.938 | 39.199 | ||
| 4320 | α | 0.9199 | 9.0368 | 0.694 | 1.0791 | 3.8322 | 0.9335 |
| β | 0.0606 | 53.9953 | 2.7247 | 16.1135 | 30.142 | 16.7588 | |
| γ | 44.099 | 40.491 | 44.06 | 22.648 | 44.099 | ||
| t, min | Fréchet | Gamma | GED | Gumbel | Log-Normal | Weibull |
|---|---|---|---|---|---|---|
| 5 | 0.287 | 0.114 | 0.115 | 0.695 | 0.201 | 0.120 |
| 10 | 0.398 | 0.383 | 0.951 | 0.592 | 0.350 | 0.368 |
| 20 | 0.254 | 0.503 | 0.514 | 2.169 | 0.207 | 0.458 |
| 30 | 0.308 | 0.423 | 0.427 | 1.524 | 0.313 | 0.401 |
| 40 | 0.207 | 0.541 | 0.538 | 1.448 | 0.206 | 0.525 |
| 50 | 0.293 | 0.835 | 0.828 | 1.601 | 0.243 | 0.845 |
| 60 | 0.431 | 0.352 | 0.359 | 2.032 | 0.272 | 0.319 |
| 90 | 0.541 | 0.759 | 0.743 | 2.113 | 0.537 | 0.964 |
| 120 | 0.426 | 0.392 | 0.392 | 1.573 | 0.320 | 0.388 |
| 180 | 0.422 | 0.285 | 0.285 | 1.556 | 0.383 | 0.291 |
| 360 | 0.392 | 0.688 | 0.693 | 2.182 | 0.444 | 0.660 |
| 720 | 0.344 | 0.587 | 0.611 | 0.631 | 0.318 | 0.315 |
| 1080 | 0.239 | 0.314 | 0.699 | 0.445 | 0.213 | 0.275 |
| 1440 | 0.284 | 0.266 | 0.268 | 0.861 | 0.258 | 0.273 |
| 2160 | 0.514 | 0.292 | 0.295 | 1.101 | 0.406 | 0.272 |
| 2880 | 0.545 | 0.508 | 0.515 | 0.628 | 0.575 | 0.449 |
| 4320 | 0.287 | 0.959 | 0.985 | 0.579 | 0.279 | 0.521 |
| A2crit | 0.757 | 0.762 | 0.723 | 0.757 | 0.752 | 0.757 |
| t, min | Fréchet | Gamma | GED | Log-Normal | Weibull |
|---|---|---|---|---|---|
| 5 | 203.02 | 199.40 | 199.36 | 201.54 | 199.38 |
| 10 | 240.50 | 228.44 | 228.28 | 237.28 | 229.66 |
| 20 | 276.14 | 251.04 | 250.58 | 271.24 | 255.42 |
| 30 | 287.38 | 272.58 | 272.34 | 282.98 | 274.20 |
| 40 | 299.92 | 289.36 | 289.24 | 296.18 | 289.86 |
| 50 | 303.58 | 295.20 | 295.14 | 300.38 | 295.38 |
| 60 | 309.08 | 303.02 | 303.00 | 307.08 | 302.60 |
| 90 | 312.30 | 303.32 | 303.16 | 309.62 | 304.38 |
| 120 | 312.44 | 306.56 | 306.50 | 309.80 | 306.80 |
| 180 | 327.50 | 316.30 | 316.20 | 323.58 | 316.88 |
| 360 | 339.42 | 329.12 | 329.00 | 351.54 | 329.68 |
| 720 | 348.72 | 340.70 | 340.62 | 361.34 | 341.20 |
| 1080 | 355.64 | 346.66 | 346.58 | 367.32 | 346.98 |
| 1440 | 375.40 | 368.20 | 368.08 | 373.66 | 368.52 |
| 2160 | 390.50 | 378.82 | 378.70 | 386.38 | 379.60 |
| 2880 | 404.30 | 393.42 | 393.30 | 400.72 | 394.20 |
| 4320 | 433.02 | 404.46 | 404.46 | 410.28 | 8.4031 |
| t, min | Gamma | GED | Weibull |
|---|---|---|---|
| 5 | 1.87 | 1.83 | 2.00 |
| 10 | 2.41 | 2.88 | 2.50 |
| 20 | 3.94 | 4.01 | 3.67 |
| 30 | 4.23 | 4.30 | 4.00 |
| 40 | 3.02 | 3.11 | 2.63 |
| 50 | 3.44 | 3.45 | 3.36 |
| 60 | 3.69 | 3.72 | 3.60 |
| 90 | 3.61 | 3.56 | 4.47 |
| 120 | 2.96 | 2.93 | 3.10 |
| 180 | 3.02 | 3.02 | 3.03 |
| 360 | 3.86 | 3.87 | 3.83 |
| 720 | 2.89 | 2.93 | 2.50 |
| 1080 | 2.26 | 2.34 | 2.23 |
| 1440 | 3.25 | 3.24 | 3.30 |
| 2160 | 2.39 | 2.38 | 2.34 |
| 2880 | 3.33 | 3.35 | 3.02 |
| 4320 | 3.50 | 3.55 | 3.11 |
| t, min | α | λ | γ |
|---|---|---|---|
| 5 | 0.947 | 0.2766 | 4.59 |
| 10 | 0.2766 | 8.29 | |
| 20 | 0.1980 | 11.29 | |
| 30 | 0.1753 | 12.49 | |
| 40 | 0.1531 | 12.99 | |
| 50 | 0.1454 | 13.69 | |
| 60 | 0.1454 | 13.69 | |
| 90 | 0.1323 | 16.49 | |
| 120 | 0.1294 | 18.19 | |
| 180 | 0.1165 | 19.99 | |
| 360 | 0.1036 | 23.89 | |
| 720 | 0.0924 | 28.59 | |
| 1080 | 0.0872 | 32.39 | |
| 1440 | 0.0746 | 35.69 | |
| 2160 | 0.0628 | 38.69 | |
| 2880 | 0.0491 | 41.29 | |
| 4320 | 0.0447 | 41.29 |
| t, Duration | Probability of Occurrence, p | |||||||
|---|---|---|---|---|---|---|---|---|
| 1% | 2% | 5% | 10% | 20% | 33% | 50% | 99.9% | |
| 5 | 19.14 | 17.29 | 14.94 | 13.25 | 11.60 | 10.45 | 9.44 | 7.35 |
| 10 | 22.99 | 20.80 | 18.01 | 15.97 | 13.98 | 12.57 | 11.34 | 8.78 |
| 15 | 25.59 | 23.17 | 20.08 | 17.82 | 15.59 | 14.01 | 12.62 | 9.75 |
| 30 | 30.73 | 27.87 | 24.20 | 21.48 | 18.79 | 16.87 | 15.17 | 11.65 |
| 45 | 34.20 | 31.06 | 26.99 | 23.97 | 20.96 | 18.80 | 16.88 | 12.93 |
| 60 | 36.90 | 33.53 | 29.17 | 25.90 | 22.64 | 20.30 | 18.22 | 13.93 |
| 90 | 41.07 | 37.36 | 32.53 | 28.90 | 25.26 | 22.62 | 20.28 | 15.46 |
| 120 | 44.32 | 40.34 | 35.15 | 31.23 | 27.29 | 24.43 | 21.89 | 16.65 |
| 180 | 49.32 | 44.95 | 39.20 | 34.84 | 30.44 | 27.23 | 24.37 | 18.48 |
| 360 | 59.23 | 54.07 | 47.24 | 42.01 | 36.68 | 32.78 | 29.27 | 22.09 |
| 720 | 71.13 | 65.05 | 56.92 | 50.65 | 44.21 | 39.45 | 35.16 | 26.40 |
| 1080 | 79.17 | 72.48 | 63.48 | 56.51 | 49.30 | 43.97 | 39.15 | 29.30 |
| 1440 | 85.42 | 78.26 | 68.59 | 61.07 | 53.27 | 47.48 | 42.24 | 31.55 |
| 2160 | 95.07 | 87.20 | 76.50 | 68.13 | 59.42 | 52.92 | 47.03 | 35.02 |
| 2880 | 102.58 | 94.15 | 82.66 | 73.63 | 64.20 | 57.15 | 50.75 | 37.71 |
| 4320 | 114.17 | 104.90 | 92.19 | 82.14 | 71.61 | 63.70 | 56.49 | 41.86 |
| t, Duration | Probability of Occurrence, p | |||||||
|---|---|---|---|---|---|---|---|---|
| 1% | 2% | 5% | 10% | 20% | 33% | 50% | 99.9% | |
| 5 | −0.84 | −0.69 | −0.83 | −0.54 | −0.55 | −0.60 | −0.74 | −0.25 |
| 10 | −0.79 | −0.60 | −0.85 | −0.61 | −0.57 | −0.68 | −0.74 | −0.18 |
| 15 | −0.69 | −0.57 | −0.89 | −0.58 | −0.62 | −0.69 | −0.82 | −0.05 |
| 30 | −0.53 | −0.47 | −0.94 | −0.60 | −0.68 | −0.79 | −0.87 | 0.05 |
| 45 | −0.40 | −0.46 | −0.95 | −0.49 | −0.67 | −0.86 | −0.88 | 0.07 |
| 60 | −0.30 | −0.33 | −0.89 | −0.47 | −0.70 | −0.84 | −0.92 | 0.17 |
| 90 | −0.07 | −0.26 | −0.82 | −0.43 | −0.70 | −0.86 | −0.88 | 0.34 |
| 120 | 0.08 | −0.14 | −0.84 | −0.45 | −0.63 | −0.89 | −0.89 | 0.45 |
| 180 | 0.38 | 0.05 | −0.70 | −0.30 | −0.64 | −0.84 | −0.87 | 0.62 |
| 360 | 1.07 | 0.53 | −0.55 | −0.14 | −0.61 | −0.88 | −0.87 | 1.01 |
| 720 | 1.97 | 1.15 | −0.27 | 0.18 | −0.45 | −0.81 | −0.76 | 1.50 |
| 1080 | 2.63 | 1.62 | −0.03 | 0.42 | −0.31 | −0.80 | −0.75 | 1.90 |
| 1440 | 3.28 | 2.04 | 0.18 | 0.61 | −0.17 | −0.77 | −0.64 | 2.15 |
| 2160 | 4.23 | 2.70 | 0.59 | 1.00 | −0.03 | −0.72 | −0.53 | 2.68 |
| 2880 | 4.92 | 3.25 | 0.88 | 1.24 | 0.07 | −0.60 | −0.45 | 3.09 |
| 4320 | 6.23 | 4.10 | 1.35 | 1.71 | 0.36 | −0.41 | −0.19 | 3.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wdowikowski, M.; Nowakowska, M.; Bełcik, M.; Galiniak, G. Heavy Rainfall Probabilistic Model for Zielona Góra in Poland. Water 2025, 17, 1673. https://doi.org/10.3390/w17111673
Wdowikowski M, Nowakowska M, Bełcik M, Galiniak G. Heavy Rainfall Probabilistic Model for Zielona Góra in Poland. Water. 2025; 17(11):1673. https://doi.org/10.3390/w17111673
Chicago/Turabian StyleWdowikowski, Marcin, Monika Nowakowska, Maciej Bełcik, and Grzegorz Galiniak. 2025. "Heavy Rainfall Probabilistic Model for Zielona Góra in Poland" Water 17, no. 11: 1673. https://doi.org/10.3390/w17111673
APA StyleWdowikowski, M., Nowakowska, M., Bełcik, M., & Galiniak, G. (2025). Heavy Rainfall Probabilistic Model for Zielona Góra in Poland. Water, 17(11), 1673. https://doi.org/10.3390/w17111673








