Abstract
In this paper, we investigated how the added mass, the hydrodynamic damping and the drag coefficient of a Wave Energy Converter (WEC) can be calculated using DualSPHysics. DualSPHysics is a software application that applies the Smoothed Particle Hydrodynamics (SPH) method, a Lagrangian meshless method used in a growing range of applications within the field of Computational Fluid Dynamics (CFD). Furthermore, the effect of the drag force on the WEC’s motion and average absorbed power is analyzed. Particularly under controlled conditions and in the resonance region, the drag force becomes significant and can greatly reduce the average absorbed power of a heaving point absorber. Once the drag coefficient has been determined, it is used in a modified equation of motion in the frequency domain, taking into account the effect of the drag force. Three different methods were compared for the calculation of the average absorbed power: linear potential flow theory, linear potential flow theory modified to take the drag force into account and DualSPHysics. This comparison showed the considerable effect of the drag force in the resonance region. Calculations of the drag coefficient were carried out for three point absorber WECs: one spherical WEC and two cylindrical WECs. Simulations in regular waves were performed for one cylindrical WEC with two different power take-off (PTO) systems: a linear damping and a Coulomb damping PTO system. The Coulomb damping PTO system was added in the numerical coupling between DualSPHysics and Project Chrono. Furthermore, we considered the optimal PTO system damping coefficient taking the effect of the drag force into account.
Keywords:
SPH; WEC; drag force; power take-off (PTO) system; DualSPHysics; numerical coupling; multiphysics 1. Introduction
Wave energy is a potential source of clean electricity that can make a significant contribution to the de-carbonization of the world’s electricity supply. A wide variety of devices to harvest wave energy, known as wave energy converters (WECs), have been designed over recent decades [1]. However, none of them have yet achieved the level of technological development needed to be economically viable [2]. The type of WEC studied in the current research is the heaving point absorber, one of the most investigated types of WECs [3]. These devices typically consist of a floating buoy moved by the waves and connected to a PTO system, which converts the float’s movement into electricity. In order to assess the performance and survivability of wave energy converters, which are necessary for exploiting wave energy, the related wave-induced hydrodynamic forces and WEC motions have to be investigated. Physical experiments are widely used; nevertheless, they have very high costs and require a high level of expertise, and scaling may become an important issue in some cases. On the other hand, numerical methods have become very popular in recent years [4], mainly due to the unprecedented growth of the computational resources available. A complete review on the numerical methods used to simulate the hydrodynamic response of point absorbers can be found in [5].
Most studies concerning WECs employ potential flow theory based on the linearized form of the Navier–Stokes equations. Applying linear potential flow theory allows the numerical modeling of WECs in the time or frequency domain [6], enabling fast calculations of the WEC’s motion. In this research, the open-source linear potential flow software NEMOH [7] is used for the calculation of the hydrodynamic coefficients and the motion of the WEC. Furthermore, this method needs to assume small amplitude oscillations of the WEC and the fluid to be incompressible and inviscid and have an irrotational motion. This results in an underestimation of the wave-induced forces on WECs under highly-nonlinear sea states [8]. Previous simplifications are too restrictive when modeling WECs; therefore, it may be more appropriate to employ higher fidelity models, generally known as CFD (Computational Fluid Dynamics) methods. The most commonly used CFD methods in hydrodynamics are mesh-based. Different point absorbers have been studied numerically using these methods in [9,10]. Despite being very robust mathematically and computationally, mesh-based methods face important challenges when capturing the free surface and the rapidly-evolving nonlinearities. Due to their ability to overcome these drawbacks, meshless CFD methods have gained attention in recent years, with the Smoothed Particle Hydrodynamics (SPH) method being the most widely used [11,12,13]. In contrast with the mesh-based methods, in SPH, the fluid is discretized in a series of points, named particles, that move with the velocity calculated from the Navier–Stokes equations carrying all physical properties with them [14]. The meshless Lagrangian formulation makes the SPH method a very interesting alternative when simulating free-surface flows with a wave–structure interaction, such as the case investigated in this work. In [15], the hydrodynamic response of a point absorber was computed using SPH and a finite volume solver. In [16,17], the authors exploited the capabilities of the SPH to model nonlinearities to study the interaction between a point absorber and extreme waves. In this research, the open-source software DualSPHysics [18] (available at www.dual.sphysics.org) is employed to obtain the hydrodynamic and drag coefficients of different point absorbers. Furthermore, DualSPHysics has been recently coupled [19] with Project Chrono [20], enabling the effect of the PTO system to be included in the simulations. This software has proven to be a valuable tool in the modeling of the wave–structure interaction in general and of floating WECs in particular (see [17,21,22,23,24]).
Estimating the hydrodynamic coefficients of floating bodies has been done before with CFD [25,26,27] and with SPH [28]. The drag coefficient has also been estimated using SPH in [29,30,31], but these studies were limited only to a fixed body in a current. In this research, three point absorbers with different float geometries are considered: one spherical and two cylindrical. The drag coefficient for each is calculated with DualSPHysics and validated with results from previous CFD simulations in the case of the sphere [32] or with experimental data in the cylindrical cases [33,34]. The linear model (in the frequency domain) has also been extended in order to take into account the effect of the drag force by writing the drag force term from the Morison equation in its Fourier series. Finally, the motion and absorbed power of a cylindrical heaving WEC are calculated using the original linear model, the extended linear model and the SPH method. These results are obtained considering two different kinds of PTO systems: a linear damper and a Coulomb damper. In order to model the Coulomb damper PTO system with DualSPHysics, the DualSPHysics–Project Chrono coupling was extended.
The paper is organized as follows: Section 2 describes the basic theoretical principles of SPH and its implementation in DualSPHysics; Section 3 provides a description of the methodology followed to obtain the hydrodynamic and drag coefficients and the modified equation of motion that includes the effect of the drag force; Section 4 outlines the numerical setup employed and the different test cases; Section 5 discusses the main results obtained using the original linear theory, the extended linear theory and DualSPHysics; finally, Section 6 presents an overview of the conclusions.
2. Smoothed Particle Hydrodynamics—DualSPHysics
DualSPHysics applies the SPH method, which is a meshless Lagrangian method used in a growing range of applications within the field of CFD. In SPH, the fluid is discretized in a set of particles for which the position, velocity, density and pressure are computed by solving the Navier–Stokes equations and by the interpolation of the values of neighboring particles. The contribution of each of the neighboring particles depends on the inter-particle distance and on the kernel function W, which has an area of influence defined by the smoothing length h (see [14,18,23,35]).
2.1. Governing Equations
The Navier–Stokes equations written in their SPH notation are solved each timestep for each of the particles. The momentum and continuity equations are given in Equations (1) and (2), respectively. In the following equations, the physical properties of particle a are calculated, with b representing each of its neighboring particles:
where m is mass, is velocity, P is pressure, is density and is the gravity acceleration. represents the kernel function and depends on the distance between particles a and b. In this work, a Quintic kernel [36] is applied, since this type of kernel is well suited for general free-surface problems (see [19]). One of the main advantages of the Quintic kernel is that the tensile instability that appears using other kernels, such as the Cubic Spline, is avoided using the kernel adopted in this work. More information can be found in [37]. The diffusion term introduced on the right-hand side of the continuity equation (Equation (2)) acts as a numerical noise filter, thereby improving the numerical stability and smoothing the density and pressure field (see [38,39,40]). In this paper, the recently proposed density diffusion term of [41] is applied, since it has been proven to produce more accurate results for the pressure field near boundaries while keeping the computational cost limited. The term takes the following form:
where with being the position of particle k and being the dynamic density, equal to the difference of the total () and hydrostatic () density: .
represents the artificial viscosity term, proposed in [14]:
where , is the velocity of particle k, , is the mean speed of sound, and is a coefficient tuned for proper dissipation (see [18]). The artificial viscosity term, , is added in the momentum equation based on the Neumann–Richtmeyer artificial viscosity with the aim of reducing oscillations and stabilizing the SPH scheme, following the work in [14]. DualSPHysics code uses this numerical viscosity; however, more physical treatments need to be implemented in the future in order to properly identify the turbulence by using the K-Epsilon model or Sub-Particle Scale model. Throughout this paper, is set to be equal to 0.01 (as in [21,42]) or 0.00 (in the case of inviscid simulations). Since the fluid is weakly-compressible in DualSPHysics, an equation of state is used to calculate the fluid pressure as a function of the density instead of solving a Poisson-like equation. The speed of sound is artificially lowered such that a reasonable time step can be employed while ensuring that density variations are kept lower than 1% during the simulation.
where is the polytropic constant and is the reference fluid density.
2.2. Boundary Conditions
In DualSPHysics, the boundaries are described by a set of particles for which the same equations (Equations (1) and (2)) as used for fluid particles are solved. However, the particles belonging to the boundary do not move according to the forces acting on them: boundary particles remain either fixed or move according to a predefined movement. These boundary conditions are called Dynamic Boundary Conditions (DBC) and have the advantage of being able to deal with complex geometries and being computationally efficient. However, due to excessive repulsive forces near the boundary between a structure and the fluid, a gap appears of the order of magnitude of the smoothing length h (see [43]). Furthermore, at this same boundary, unphysical values of pressure are observed. These issues are dealt with in the modified DBC (mDBC) implementation recently added to DualSPHysics, as described in [43]. For each boundary particle of mDBC, a ghost node is mirrored into the fluid. Boundary particles then receive the properties of the fluid at the position of the ghost node. The density is calculated using a first-order consistent SPH interpolation, as proposed in [44]. The mDBC method has proven to show results with more realistic physical values for pressure at the boundaries and a significant reduction in the size of the gap between the fluid and boundary without a significant extra computational cost.
2.3. Floating Bodies
DualSPHyics has the capability to accurately simulate fluid-driven objects, as described and validated in [23,45], and is used extensively in this paper. The force per unit mass acting on one boundary particle k of the floating body is calculated by summing the contributing forces exerted on this boundary particle k by fluid particles a within the compact support of the kernel:
where is the force per unit mass acting on boundary particle k of the floating body and is the force per unit mass acting on boundary particle k exerted by fluid particle a, calculated with Equation (1) [46]. Once the force acting on the floating body is computed, the body’s motion can be determined, assuming it is rigid:
where M is the body’s total mass, I is the moment of inertia, is the velocity, is the rotational velocity, is the centre of mass, is the mass of floating boundary particle k and is the position of floating particle k. Equations (7) and (8) are integrated over time in order to compute the velocity of the floating particle:
2.4. Coupling Dualsphysics—Project Chrono
Project Chrono is an open-source software package that enables the numerical modeling of mechanical constraints and collisions between objects [20]. It has recently been successfully coupled to DualSPHysics [19,47] and is used in this case for the modeling of the PTO system of a WEC.
Linear damping was already implemented in the coupling, which is applied here for the simulation with a linear damping PTO system (see Equation (10)).
where is the linear PTO system damping coefficient and is the WEC’s heave velocity. The DualSPHysics–Project Chrono model is here extended with the Coulomb damping model, applying the force described in Equation (11), where is the PTO damping coefficient for a Coulomb damping PTO system.
where is the Coulomb damping coefficient.
3. Methodology
In this study, both linear potential flow theory as well as the SPH method are applied. Therefore, this section begins with a brief overview of the linear potential flow theory. Next, we describe how the hydrodynamic coefficients can be computed using DualSPHysics. Finally, we describe how the equation of motion based on linear potential flow theory was modified to take into account the effect of the drag force. A schematic overview of the applied theories and equations used in the current study for the calculation of the motion and the average absorbed power of the studied WECs is given in Figure 1.
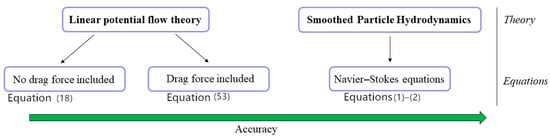
Figure 1.
Schematic overview of the applied theories and equations in the current study.
In the calculation of the hydrodynamic coefficients and the equation of motion in the present study, we assume linear potential flow theory [6], which is a subset of linear wave theory that allows the fluid velocity, , to be expressed as the gradient of the time dependent velocity potential (Equation (12)).
Potential flow theory makes some essential assumptions: (i) the fluid is inviscid, (ii) the fluid is incompressible and (iii) the flow is irrotational [3]. Furthermore, it is assumed that the motion amplitude of the WEC is much smaller than the wavelength. It is assumed that all time-dependent variables oscillate with the same wave angular frequency , enabling the separation of the time dependence from the time-independent velocity potential ,
where is the complex amplitude of the velocity potential. Due to application of the principle of superposition, linear potential flow theory allows the separation of the total velocity potential into the following components (Equation (14)):
where is the total velocity potential, is the incident wave velocity potential, is the diffracted wave velocity potential and is the sum of the radiated wave velocity potentials for each degree of freedom (DoF) of the WEC. In the current study, only one DoF for each WEC is modeled: namely the heave motion. Since the oscillatory motion of the waves and the WEC is considered to be harmonic, all forces and displacements can be decomposed into their spatial and temporal dependencies [6]. Therefore, the WEC’s heave displacement can be written as
where is the complex amplitude of the WEC’s heave displacement. Applying Newton’s second law of motion and writing all terms in its complex amplitudes results in the following equation (see [6]):
where is the complex amplitude of the excitation force, is the complex amplitude of the radiation force, is the complex amplitude of the hydrostatic force and is the complex amplitude of the PTO system force. It is here assumed that the PTO system is a linear damping PTO system, following Equation (10). Equation (16) can be further rewritten, following the same approach as in [6]:
where is the heave component of the hydrodynamic damping, is the heave component of the added mass, is the hydrostatic spring stiffness or hydrostatic coefficient equal to with being the cross-sectional area at the undisturbed sea level, and is the PTO system damping coefficient for a linear PTO system without a spring coefficient. From Equation (17), the complex amplitude of the device’s heave motion can be obtained,
Equation (18) is further extended to include the effect of the drag force in Section 3.2. Equation (18) can be used to calculate the average absorbed power [6]:
An optimal value for can be calculated, leading to the maximal average absorbed power [48]:
3.1. Determination of Hydrodynamic Coefficients Using DualSPHysics
The added mass, hydrodynamic damping and drag coefficient are estimated in DualSPHysics by running a forced motion test. The test consists of the WEC heaving according to a fixed sinusoidal motion in still water. The heave motion and heave velocity of the WEC can be described as follows:
where a is the heave amplitude of the WEC with a forced heave motion.
Following potential flow theory, the total vertical force acting on the heaving WEC, as the sum of the hydrodynamic, hydrostatic, drag and PTO system force, is expressed as
where is the viscous force, written as the semi-empirical Morison equation [49,50]:
where is the drag coefficient. The viscous force can be approximated by writing out its Fourier series and retaining only the first term: Equation (25). It is preferred to retain only the first term since this allows the modification of the equation of motion depending on only one single frequency. This is justified since the second appearing term of the drag force’s Fourier series has a magnitude five times lower than the first frequency component. The same approach was used in [51].
Now, the force from Equation (23) can be written as a sum of a sine and a cosine, containing only one frequency component:
One way of estimating the hydrodynamic coefficients is to apply the least-square method when comparing the theoretical total force with Equation (23) with the total force acting on the WEC, calculated with DualSPHysics, . However, since multiple coefficients have to be estimated, we chose to apply Fourier analysis. A similar approach was followed in [25,26,28,52]. The coefficients of the Fourier series of the force (Equation (26)) acting on the heaving WEC can be used to calculate the hydrodynamic coefficients.
Equation (28) assumes that the cross-sectional area of the WEC, , is constant. This is true for a cylinder, but not for, e.g., a sphere, where the varying cross-sectional area causes non-linear static Froude–Krylov forces (see [32,53]). The two main non-linearities affecting point absorber WECs in the resonance region are the drag forces and the non-linear Froude–Krylov forces, the latter being a purely geometrical effect [32,53,54]. Therefore, the heave amplitude of the spherical WEC was kept low in order to limit these non-linear Froude–Krylov forces.
Equation (30) is only applicable when the fluid is inviscid. The first simulations were performed in an inviscid fluid by setting the artificial viscosity coefficient in DualSPHysics equal to zero: . This does not lead to numerical instabilities of the water particles at the water surface since the density-diffusion term is applied [41]. Once the inviscid simulations are finished, the derived hydrodynamic damping coefficient can be used in viscous simulations to estimate the drag coefficient :
The test cases discussed in this paper all have a high Reynolds number (), meaning that the drag coefficient mainly depends on the pressure distribution surrounding the WEC and not on the distribution of the wall shear stresses (see [55] (Chapter 9)). In order to obtain an accurate pressure distribution, it is essential to apply the mDBC method instead of DBC. It is described in [53] that the total drag can be separated into a scale-independent and a scale-dependent (or viscous) drag component. Viscous effects depend on the Reynolds number and do not scale with Froude scaling. On the other hand, there is form drag and vortex-induced drag, which is independent of scale (Figure 2). Since artificial viscosity is used in the DualSPHysics simulations throughout this paper, it is expected that the viscous drag component is not modeled correctly. However, it follows from [53] that the viscous drag term only covers a small part of the total drag (1–4%), whereas the vortex-induced drag covers 18–19% of the total drag. Vortex shedding is generated by high pressure and velocity gradients close to regions of high wall curvature [53]. Vorticity is modeled in DualSPHysics since the software supports flow rotationality and there is numerical (artificial) viscosity. The presence of these vortices is proven later in the present study (see Figure 3). Vortices surrounding the heaving WEC disrupt the dynamic pressure field, causing a loss in heave amplitude. Furthermore, in [4], it was concluded that pressure or form drag is the main contributor of drag forces, caused by flow separation and vortex shedding, whereas skin friction drag was considered negligible.
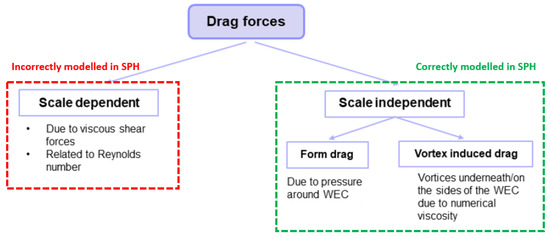
Figure 2.
Schematic overview of different drag forces acting on the Wave Energy Converter (WEC).
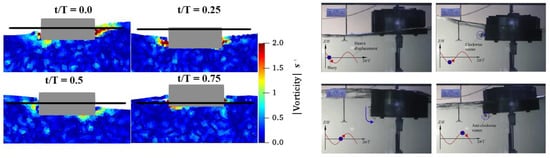
Figure 3.
Vorticity in DualSPHysics surrounding a heaving cylindrical WEC in regular waves with m, s, Ns/m (left), compared to experimental measurements of the heaving WEC, as performed in [56] (right).
3.2. Derivation of the Equation of Motion and the Optimal Damping Coefficient Including the Effect of Drag Forces
After the drag coefficient has been determined with DualSPHysics, it can be used in potential flow theory. The aim of this section is to derive a modified equation of motion including the effect of the drag force. Furthermore, a modified equation for the value of is derived, since it has been proven that the drag coefficient has an influence on the optimal linear PTO damping coefficient of a heaving WEC (see [34,56]).
3.2.1. Linear Damping PTO System
The PTO force from a linear damping PTO system is written as follows in the time domain:
The complex amplitude of the linear damping PTO system force is given by
In order to obtain a modified equation of motion and a new estimate for the optimal damping coefficient taking into account the effect of the drag force, defined in Equation (24), this force has to be written in the frequency domain. In a first step, it is assumed the WEC is oscillating in still water. The drag force contains a quadratic term, which can be approximated as follows by calculating its Fourier series and retaining only the first frequency component (see also [51]):
In this case, is a real number; this will not be the case when the fluid is no longer still. Equation (41) can now used in the equation of motion:
Equation (38) is, however, only true if the water surrounding the WEC is standing still, which is no longer the case when the WEC is moving in waves. In the formula of the drag force, the relative velocity difference has to be used, which is the difference between the WEC’s velocity and the vertical velocity of the surrounding water particles (see Equation (45)).
where H is the wave height, k is the wave number and is the depth at which the vertical fluid particle velocity is calculated, taken as half of the draft in current research.
The relative velocity difference is written as a function of the WEC’s velocity in order to simplify further results:
where is the ratio of the amplitude of to the amplitude of and is the phaseshift between and . Harmonic decomposition is applied in a similar manner as in Equation (36):
Equation (50) is the complex amplitude of the viscous force written as a function of the complex amplitude of the WEC’s heave motion . This force can be introduced in the equation of motion of the WEC:
Note that and are not known in advance since they depend on , so an iterative procedure has to be followed to solve Equation (53).
Once a solution for is found, can be calculated from Equation (52), and an updated value of the optimal damping coefficient of the heaving WEC can be calculated:
3.2.2. Coulomb Damping PTO System
In case a hydraulic PTO system is applied, the PTO system force can be approximated as a Coulomb damping system [48]:
where is the Coulomb damping coefficient. The first frequency component of the Fourier series of this PTO system force can be used as approximation in the frequency domain (see Equation (56)). is written in such a way that it resembles the complex amplitude of the linear PTO system force (see Equation (33)):
The second frequency component, at , has an amplitude of one-third of the first frequency component. However, it can be proven that this second-frequency component (and all other higher-order frequency components) does not change the average absorbed power of the WEC (see also later in Section 5). Therefore, only the first frequency component of is retained below. This now means that can be written as the linear damping PTO system force with an equivalent damping coefficient :
4. Test Cases and Numerical Setup
The methods used to determine described in Section 3.1 are applied to three different WECs:
- A heaving sphere with a diameter of 5 m, as studied in [32]. For this WEC, the added mass and hydrodynamic damping were also estimated wtih DualSPHysics.
- A cylindrical WEC with a diameter of 0.5 m and draft of 0.11 m, as studied in [17,56], hereafter referred to as “cylinder1”.
- A cylindrical WEC with a diameter of 0.3 m and draft of 0.28 m, as studied in [34,57], hereafter referred to as ’cylinder2’. This WEC is studied in more detail by analyzing its response amplitude operator (RAO) and comparing it with the experimental results found in [57]. The WEC is also simulated with two kinds of PTO systems (a linear damping and a Coulomb damping PTO system) and the average absorbed power is compared for a range of damping coefficients.
Spherical and cylindrical shapes of the WECs were chosen since these are the shapes that are regularly used for heaving point absorbers. A spherical WEC was chosen since this shape induces extra non-linear forces, named non-linear Froude—Krylov forces, due to their non-uniform cross-sectional area [54]. Two cylindrical shapes were chosen since a flat cylinder provides a balance between the power absorption, WEC bandwidth and material cost considerations (see [58]), whereas for a slender cylinder, the drag force is expected to be more significant [34].
An overview of important settings and parameters applied during the DualSPHysics simulations is listed below.
- Simulations were carried out with two different types of boundary conditions: Dynamic Boundary Conditions (DBC) and modified Dynamic Boundary Conditions (mDBC), as described in Section 2.2. Both SPH results were compared to the theoretical force calculated with Equation (23), with the hydrodynamic coefficients from NEMOH and as in [32]. It is clear from Figure 4 that mDBC gave significantly better results compared to DBC. When mDBC was applied, the repulsive forces exerted by the boundary particles of the sphere were much smaller than when applying DBC, resulting in a smaller gap between the sphere and the fluid.
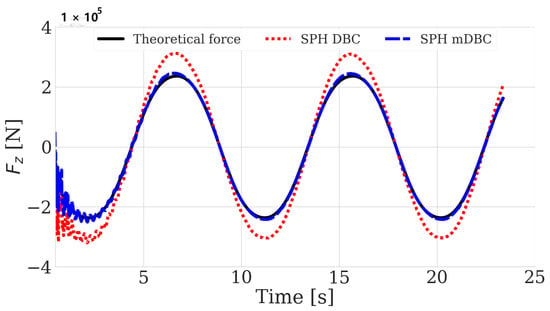 Figure 4. Vertical force acting on a sphere with prescribed heave motion, m s.
Figure 4. Vertical force acting on a sphere with prescribed heave motion, m s. - Artificial viscosity was applied with an artificial viscosity coefficient . Artificial viscosity was introduced into SPH in [14] and was used primarily due to its simplicity [18]. It was stated in [59] that this artificial viscosity corresponds to an equivalent kinematic viscosity of (in 2D), which is generally much higher than the real kinematic viscosity of water = 1 × 10 m²/s. Therefore, one way of reducing the numerical dissipation caused by artificial viscosity is by lowering ; however, this was not preferred since the value of has been proven to give the best results in the validation of wave flumes to study the wave propagation and wave loadings exerted onto coastal structures [21,42] and is also the value used when simulating the WEC in regular waves. Only in the case where the hydrodynamic coefficients and are computed is set to be equal to zero, as described in Section 3.1.
- The initial speed of sound was set to , with d being the depth of the numerical wave basin. It was found that convergence was reached with a lower resolution when the speed of sound was decreased. This can be related to the influence of on the viscosity: it is stated in [59] that the equivalent kinematic viscosity associated with the artificial viscous term has the form . Further decreasing leads to overly large timesteps and therefore less accurate results.
- A convergence test was done by varying the interparticle distance and studying the resulting hydrodynamic coefficients , and the drag coefficient , calculated with Equations (28), (30) and (31), respectively. The hydrodynamic coefficients were compared to results from potential flow theory obtained with NEMOH and the drag coefficient was compared to results from previous experimental or numerical tests from [32,33,34]. The results of these convergence tests are described in Section 5.
- The domain size of the basin was set to be large enough to avoid interaction with side walls (see Figure 5). Sloped sidewalls were provided as well as numerical damping layers, with the aim of reducing side wall reflection.
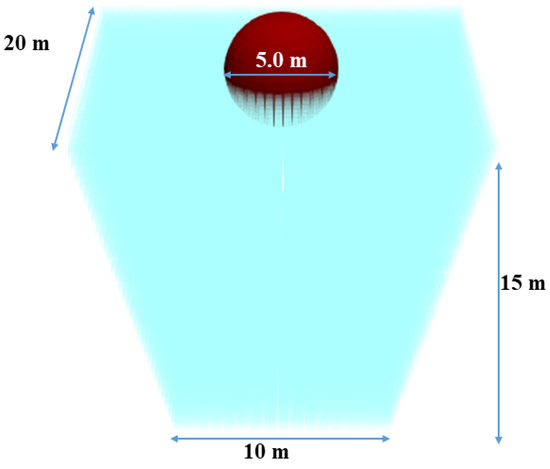 Figure 5. Dimensions of the numerical wave basin for hydrodynamic coefficients and drag coefficient test for a heaving sphere.
Figure 5. Dimensions of the numerical wave basin for hydrodynamic coefficients and drag coefficient test for a heaving sphere.
5. Results and Discussion
5.1. Estimation of the Hydrodynamic Coefficients and of the Drag Coefficient
Before calculating the drag coefficient , wer briefly checked whether DualSPHysics was able to accurately compute the hydrodynamic coefficients corresponding to the added mass and the hydrodynamic damping . This computation was carried out for the heaving sphere described in Section 4 by simulating this heaving sphere in an inviscid fluid () in DualSPHysics. Equations (28) and (30) were applied in order to calculate and . The obtained values were compared to the values found by NEMOH, which applies linear potential flow theory. In order to obtain results comparable to linear theory, the heave amplitude a of the sphere was kept rather low, at m. Finally, the results of and are displayed in Figure 6, showing that DualSPHysics was able to accurately compute and , apart from some discrepancies in the low-frequency region.
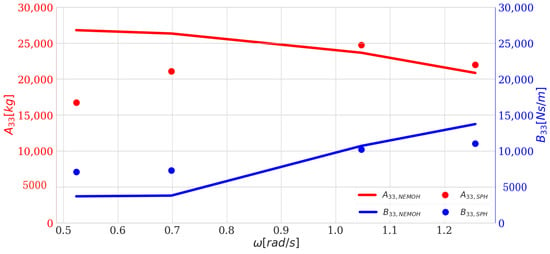
Figure 6.
Hydrodynamic coefficients and calculated with NEMOH and with Smoothed Particle Hydrodynamics (SPH)–DualSPHysics for a sphere with a diameter of 5 m.
In the following simulations, carried out to compute the drag coefficient , was set to be equal to 0.01 as suggested in [21]. As discussed in Section 3.1, DualSPHysics supports flow rotationality and adds artificial viscosity, resulting in vortex shedding. Vortex shedding is expected to be present in regions with a high wall curvature, such as the corners of a heaving cylindrical WEC, and results in a significant part of the total drag force. Therefore, a brief qualitative analysis was carried out to investigate the presence of vorticity in DualSPHysics simulations. The cylindrical WEC with a diameter if 0.5 m and draft of 0.11 m—cylinder1—was simulated in DualSPHysics in regular waves with m, s and Ns/m, in a similar way as was done in an experimental study in [56]. The high value of was chosen in order to induce a large phase difference and thus high relative velocities and high vortex-induced drag. A qualitative comparison between the numerical and experimental model is displayed in Figure 3, showing the magnitude of vorticity calculated in DualSPHysics and the flow patterns surrounding the WEC during experiments. It is clear that DualSPHysics shows high vorticity at the sides and corners of the heaving WEC, similar to the results in the experimental case studied in [56].
The presence of vortex shedding around the heaving cylindrical WEC in DualSPHysics simulations implied that there was a drag force acting on the WEC. In the remainder of this section, we determine whether this drag force was accurately modeled in DualSPHysics by calculating the drag coefficient , applying Equation (31). This was calculated for the three WECs described in Section 4: one spherical WEC and two cylindrical WECs. In all cases, the values of and used in Equation (31) were those obtained from NEMOH, which is the same approach as followed in [32]. This means that does not only account for the viscous non-linear effects, but also for other non-linear effects, as also described in [29]. Figure 7 shows the results for the calculation of using the approach described in Section 3.1, for different ratios of , with D being the WEC’s diameter and the interparticle distance. The convergence analyses are performed for the sphere studied in [32] with m and s, the cylinder studied in [17,56], with m and s (cylinder1 in Figure 7) and the cylinder studied in [34,60], with m and s (cylinder2 in Figure 7). The value obtained from previous numerical tests or experiments performed in [32,33,34] is displayed as well; it is clear that the result of DualSPHysics converges towards a slightly higher value of than obtained in previous numerical or experimental tests. One possible explanation for why the DualSPHysics simulations slightly overestimate the value of is the use of the artificial viscosity value with , resulting in excessive equivalent kinematic viscosity as described in Section 4. In future work, a more physical viscosity and turbulence model will be implemented in DualSPHysics. The value obtained for cylinder1 simulated in DualSPHysics was compared to the obtained from the results described in [33]; i.e., . In [33,61], experimental and numerical tests were carried out for a heaving vertical cylinder with similar values for the Keulegan–Carpenter number and the Reynolds number . The value obtained for cylinder2 in DualSPHysics was compared to the value determined experimentally in [34]; i.e., . In [34,60], the drag coefficient was determined by performing one or multiple heave decay tests for the cylinder. However, this approach was not followed here since decay tests in DualSPHysics require a very high resolution for decent accuracy (see [62]). The test for cylinder2 performed in DualSPHysics was carried out at a period of s and a heave amplitude m, resulting in values for and of the same order of magnitude as those in the free decay tests, which is important since depends on both and [63].
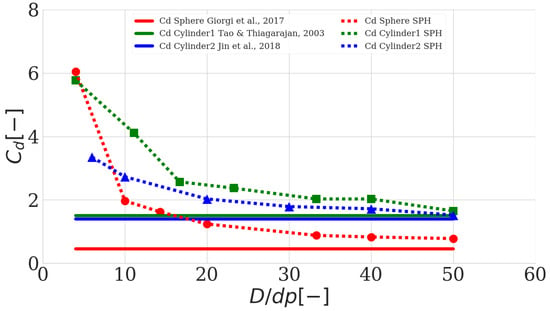
Figure 7.
Convergence test for drag coefficient using a varying resolution for (i) a sphere with m, s [32], (ii) a cylinder with m, s (cylinder1, [56]) and a cylinder with m, s (cylinder2, [34]).
An overview of the heave amplitude a and the heave period T applied during the DualSPHysics tests is displayed in Table 1, as well as the obtained value of .

Table 1.
Heave amplitude a and heave period T applied during the forced oscillation with DualSPHysics of a spherical WEC and two cylindrical WECs, as well as the obtained drag coefficient .
5.2. Cylindrical WEC in Regular Waves
Once the values were determined, a study was carried out on the WEC’s behavior in regular waves. This study was carried out only for cylinder2, since experimental validation for this WEC was available from [34]. The modified equation of motion including the effect of the drag force, Equation (53), was used for the calculation of the heave motion and the average absorbed power. The used in Equation (53) equalled 1.5, determined with DualSPHysics (see Table 1). The results of the heave motion and average absorbed power were then compared with the results obtained from simulations in DualSPHysics.
5.2.1. Undamped Heaving WEC
Before studying the heaving WEC with a PTO system, the response amplitude operator (RAO) of the undamped heaving WEC was calculated. This RAO could be calculated by comparing different modeling techniques: (i) linear potential flow theory—Equation (18), (ii) linear potential flow theory with a correction term taking into account the effect of the drag force—Equation (53), (iii) SPH simulations using DualSPHysics and (iv) experimental results using data from [34,57]. This RAO was calculated for the undamped case ( Ns/m) with m as was done in the experiments. The dimensions of the numerical wave basin modeled in DualSPHysics differed for each wave frequency, since the WEC should be placed at least one wavelength away from the piston [17]. An example of the numerical wave basin for a specific wave frequency is given in Figure 8. This numerical wave basin was provided with a beach and numerical damping (introduced in [21]) in order to reduce wave reflection. Furthermore, periodic boundaries were provided at the sides, reducing reflection from the side walls. Figure 9 shows that the SPH simulations fit well with the experimental results and that the linear theory with a correction term for the drag force significantly increased accuracy compared to the conventional linear potential flow theory. It is clear that applying linear potential flow theory without the inclusion of the drag force greatly overestimates the RAO, at least for the WEC analyzed in the present study.
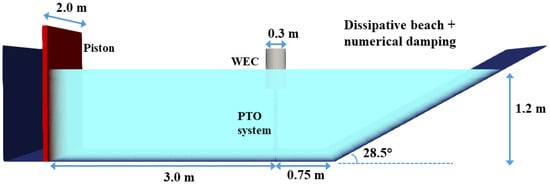
Figure 8.
Dimensions of a basin for a heaving cylindrical WEC in waves with s in DualSPHysics.
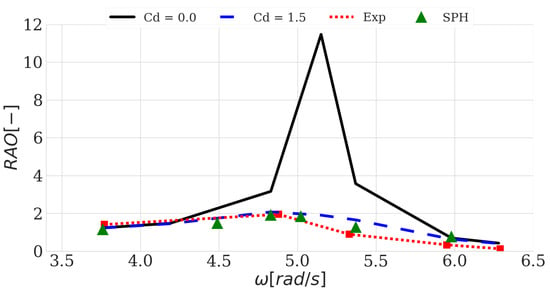
Figure 9.
Response amplitude operator (RAO) for the cylindrical WEC cylinder2 without a power take-off (PTO) system, calculated with (i) linear potential flow theory with = 0.0, (ii) linear potential flow theory with = 1.5, (iii) SPH–DualSPHysics and (iv) obtained from experiments [34], H = 0.08 m.
5.2.2. Linear Damping PTO System
In the next step, simulations with cylinder2 were carried out with a linear damping PTO system and the average absorbed power was calculated in three different ways: (i) linear potential flow theory, (ii) linear potential flow theory with = 1.5 in Equation (53) and (iii) with DualSPHysics. The results are displayed in Figure 10. Similar to the results was found in [34], the optimal PTO system damping coefficient was significantly larger than (). The average absorbed power was significantly lower when including the drag force, due to the high relative velocities in the resonance region leading to considerable drag forces. It is clear from Figure 10 that the average absorbed power calculated with DualSPHysics lay close to the results obtained from the modified equation of motion with = 1.5. The lower values for average absorbed power obtained with DualSPHysics could be due to the use of only one constant value for in the equation of motion and thus in the calculation of the average absorbed power, while actually increased with decreasing amplitude [32]. At Ns/m, the WEC’s heave amplitude was approximately m whereas at Ns/m the WEC’s heave amplitude was only m.
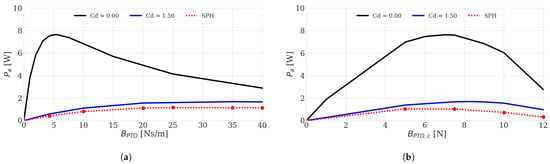
Figure 10.
Average absorbed power of cylinder2 with (a) a linear damping PTO system and (b) a Coulomb damping PTO system for a range of PTO system damping coefficients, calculated with linear potential flow theory with (i) = 0.00, (ii) = 1.50 and (iii) with DualSPHysics— m, s.
From Figure 10, the optimal linear PTO damping coefficient can be found. This value was then used to compute the velocity of the WEC in regular waves with m, s and compare the different modeling techniques—see Figure 11. Figure 11 shows that the velocity calculated with linear potential flow theory with lay close to the velocity calculated with DualSPHysics, while linear potential flow theory with overestimates the velocity.
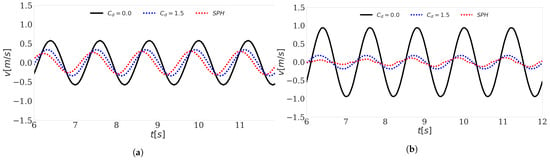
Figure 11.
Velocity of cylinder2 with (a) a linear damping PTO system, Ns/m and (b) a Coulomb damping PTO system, calculated with linear potential flow theory with (i) = 0.00, (ii) = 1.50 and (iii) with DualSPHysics— m, s.
5.2.3. Coulomb Damping PTO System
The same procedure was repeated with a Coulomb damping PTO system: the average absorbed power was calculated with (i) linear potential flow theory, (ii) linear potential flow theory with = 1.5 and (iii) with DualSPHysics. In the case in which linear potential flow theory was applied, Equation (56) was applied for the PTO system force in the frequency domain. For the DualSPHysics calculation, the PTO system force with Coulomb damping, expressed in Equation (55), was implemented in Project Chrono and applied in the DualSPHysics–Project Chrono coupling. The results are displayed in Figure 10. From Figure 10, it is clear that the calculations using Equation (56) gave results close to the DualSPHysics results, meaning that the approximation of the Coulomb damping PTO system force as its first frequency component is valid.
From Figure 10, the optimal Coulomb damping coefficient could be found. This value was then used to compute the velocity of the WEC in regular waves with m, s and compare the different modeling techniques (see Figure 11). Figure 11 shows that the velocity calculated with linear potential flow theory with lay close to the velocity calculated with DualSPHysics, while linear potential flow theory with overestimated the velocity. Figure 11 also shows that the velocity computed with DualSPHysics was no longer a sine wave since the WEC was latched briefly when its velocity reaches zero. This is an inherent property of the Coulomb damping PTO system force which is a square wave and latches the WEC shortly when it reaches its maximum or minimum displacement [48,64]. This behavior was not visible in the linear potential flow theory, with or , since these theories simplify as a sine wave.
6. Conclusions
In this study, we investigated how the hydrodynamic coefficients of a floating body (added mass and hydrodynamic damping) can be determined with DualSPHysics when using appropriate settings (see Section 4). The artificial viscosity coefficient should be set to be equal to zero and the heave amplitude of the moving WEC should be kept sufficiently low in order to allow a fair comparison with hydrodynamic coefficients calculated with NEMOH. It was found that the phenomenon of vortex shedding, responsible for causing a significant part of the drag force, is present in DualSPHysics simulations of a cylindrical WEC (see Figure 3). A significant and novel result of the current study is that the drag coefficient of heaving WECs can be determined with DualSPHysics. This is not only useful for WECs but for floating offshore structures in general. For the test cases studied in this research, the interparticle distance was found to be required to be lower than with D being the WEC’s diameter in order to obtain accurate results. mDBC should be applied a boundary condition in order to achieve accurate results with reasonable resolution. The results were validated with experimental data obtained from [33,34].
Once an accurate value of is found, the effect of the drag force can be included in the equation of motion of the WEC (Equation (53)) in the frequency domain. In the current study, it was shown that this Equation (53) allowed accurate calculation of the WEC’s heave motion, with results similar to those calculated with DualSPHysics, validated with experimental data from [34]. Furthermore, an updated value of the optimal linear PTO system damping coefficient can be calculated with Equation (54). The average absorbed power taking into account the effect of the drag force was calculated and compared to results from DualSPHysics simulations. The results show that the average absorbed power near resonance is significantly lower when including the drag force and that the obtained from the modified equation of motion taking into account the drag force lies significantly higher than the obtained from the equation of motion without the inclusion of the drag force. These findings are confirmed by simulations of the heaving WECs in DualSPHysics. Future research could further extend the modified equation of motion by applying it to WECs that oscillate with one or more than one degree of freedom, such as pitching or surging WECs.
Besides a linear damping PTO system, a Coulomb damping PTO system has been included in the DualSPHysics–Project Chrono coupling. An approximation of the Coulomb damping PTO system force has also been included in the equation of motion, and the results are compared with DualSPHysics. A major outcome of the current study is that the modified equation of motion including the effect of the drag force gives results similar to those obtained from DualSPHysics for heaving WECs with a linear damping or Coulomb damping PTO system.
Author Contributions
N.Q. conceptualized the investigation, ran the numerical simulations, developed the new analytical model and wrote the manuscript. P.R.-G. assisted in writing the manuscript and in developing the numerical simulations. J.M.D. assisted in setting up the numerical model in DualSPHysics and in developing the numerical model of the Coulomb damping with the DualSPHysics–Project Chrono coupling. V.S. and P.T. proofread the text and helped in structuring the publication. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Research Foundation Flanders (FWO), Belgium—FWO research project No.1SC5421N. In addition, Vasiliki Stratigaki is a postdoctoral researcher (fellowship 1267321N) of the FWO, Belgium. This research was partially funded by the Ministry of Economy and Competitiveness of the Government of Spain under the project “WELCOME ENE2016-75074-C2-1-R” and by Xunta de Galicia (Spain) under the project ED431C 2017/64 “Programa de Consolidación e Estructuración de Unidades de Investigación Competitivas (Grupos de Referencia Competitiva)” cofunded by European Regional Development Fund (ERDF). J. M. Domínguez acknowledges funding from the Spanish government under the program “Juan de la Ciervaincorporación 2017” (IJCI-2017-32592).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study was supported by experimental data published in [34]. Furthermore, the authors of [34] provided additional experimental data for the RAO, displayed in Figure 9 in the current study.
Acknowledgments
This work was supported by experimental results provided by Siya Jin and the research group led by Ron Patton, University of Hull; see also [34,57]. Furthermore, this study has been supported by the research group EPhysLab of the University of Vigo, led by Moncho Gómez-Gesteira.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations and symbols are used in this manuscript:
| a | Heave amplitude of the WEC (m) |
| Cross-sectional area of the heaving WEC (m²) | |
| Added mass (kg) | |
| Hydrodynamic damping in heave (Ns/m) | |
| Linear PTO system damping coefficient (Ns/m) | |
| Coulomb damping PTO system damping coefficient (N) | |
| Drag coefficient (-) | |
| Speed of sound in DualSPHysics (m/s) | |
| D | WEC diameter (m) |
| d | Depth of the numerical basin (m) |
| Interparticle distance in DualSPHysics (m) | |
| Excitation force (N) | |
| Hydrostatic force (N) | |
| Radiation force (N) | |
| PTO system force (N) | |
| Coulomb damping PTO system force (N) | |
| Rotal vertical force acting on the heaving WEC (N) | |
| Force per unit mass acting on boundary particle k (N/kg) | |
| g | Gravitational acceleration (m/s²) |
| H | Wave height (m) |
| h | Smoothing length in DualSPHysics (m) |
| Hydrostatic spring stiffness (N/m) | |
| k | Wave number (1/m) |
| m | WEC’s mass (kg) |
| P | Fluid pressure (Pa) |
| Average absorbed power (W) | |
| Position of particle k in DualSPHysics (m) | |
| T | Wave period (s) |
| t | Time (s) |
| Vertical fluid velocity (m/s) | |
| v | WEC’s heave velocity (m/s) |
| WEC’s relative velocity, equal to , (m/s) | |
| W | Kernel function |
| Half of the WEC’s draft (m) | |
| Artificial viscosity coefficient applied in DualSPHysics | |
| Ratio of the WEC’s relative velocity amplitude to the WEC’s velocity amplitude | |
| Artificial viscosity term in DualSPHysics (m²/s) | |
| Fluid density (kg/m³) | |
| Velocity potential | |
| Phaseshift between and v (rad) | |
| Rotational velocity (rad/s) | |
| Angular wave frequency (rad/s) | |
| Complex amplitude | |
| CFD | Computational Fluid Dynamics |
| DBC | Dynamic Boundary Condition |
| mDBC | Modified DBC |
| PTO | Power take-off |
| SPH | Smoothed Particle Hydrodynamics |
| WEC | Wave Energy Converter |
References
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Fernandez, G.V.; Balitsky, P.; Stratigaki, V.; Troch, P. Coupling methodology for studying the far field effects of wave energy converter arrays over a varying bathymetry. Energies 2018, 11, 2899. [Google Scholar] [CrossRef]
- Balitsky, P.; Verao Fernandez, G.; Stratigaki, V.; Troch, P. Assessing the Impact on Power Production of WEC array separation distance in a wave farm using one-way coupling of a BEM solver and a wave propagation model. In Proceedings of the Twelfth European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; pp. 1176-1–1176-10. [Google Scholar]
- Josh, D.; Ronan, C. Efficient nonlinear hydrodynamic models for wave energy converter design—A scoping study. J. Mar. Sci. Eng. 2020, 8, 35. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Y.H. A synthesis of numerical methods for modeling wave energy converter-point absorbers. Renew. Sustain. Energy Rev. 2012, 16, 4352–4364. [Google Scholar] [CrossRef]
- Folley, M. (Ed.) Numerical Modelling of Wave Energy Converters; Academic Press, School of Planning, Architecture and Civil Engineering, Queen’s University Belfast: Belfast, UK, 2016. [Google Scholar]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–12. [Google Scholar]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef]
- Yu, Y.H.; Li, Y. Reynolds-Averaged Navier-Stokes simulation of the heave performance of a two-body floating-point absorber wave energy system. Comput. Fluids 2013, 73, 104–114. [Google Scholar] [CrossRef]
- Reabroy, R.; Zheng, X.; Zhang, L.; Zang, J.; Yuan, Z.; Liu, M.; Sun, K.; Tiaple, Y. Hydrodynamic response and power efficiency analysis of heaving wave energy converter integrated with breakwater. Energy Convers. Manag. 2019, 195, 1174–1186. [Google Scholar] [CrossRef]
- Gotoh, H.; Khayyer, A. On the state-of-the-art of particle methods for coastal and ocean engineering. Coast. Eng. J. 2018, 60, 79–103. [Google Scholar] [CrossRef]
- Manenti, S.; Wang, D.; Domínguez, J.M.; Li, S.; Amicarelli, A.; Albano, R. SPH modeling of water-related natural hazards. Water 2019, 11, 1875. [Google Scholar] [CrossRef]
- Violeau, D.; Rogers, B.D. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2016, 54, 1–26. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Westphalen, J.; Greaves, D.; Raby, A.; Hu, Z.; Causon, D.; Mingham, C.; Omidvar, P.; Stansby, P.; Rogers, B. Investigation of Wave-Structure Interaction Using State of the Art CFD Techniques. Open J. Fluid Dyn. 2013, 4. [Google Scholar] [CrossRef]
- Omidvar, P.; Stansby, P.K.; Rogers, B.D. SPH for 3D floating bodies using variable mass particle distribution. Int. J. Numer. Methods Fluids 2013, 72, 427–452. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.; Tagliafierro, B.; Altomare, C.; Domínguez, J.M.; Gómez-Gesteira, M.; Viccione, G. Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics. Renew. Energy 2020, 162, 1763–1776. [Google Scholar] [CrossRef]
- Crespo, A.J.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Canelas, R.B.; Brito, M.; Feal, O.G.; Domínguez, J.M.; Crespo, A.J. Extending DualSPHysics with a Differential Variational Inequality: Modeling fluid-mechanism interaction. Appl. Ocean Res. 2018, 76, 88–97. [Google Scholar] [CrossRef]
- Tasora, A.; Anitescu, M. A matrix-free cone complementarity approach for solving large-scale, nonsmooth, rigid body dynamics. Comput. Methods Appl. Mech. Eng. 2011, 200, 439–453. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Domínguez, J.M.; Crespo, A.J.; Altomare, C.; Stratigaki, V.; Troch, P.; Kortenhaus, A. Coupling methodology for smoothed particle hydrodynamics modelling of non-linear wave-structure interactions. Coast. Eng. 2018, 138, 184–198. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Crespo, A.J.C.; Domínguez, J.M.; Feal, O.G.; Gesteira, G.; Canelas, R.B.; Coe, R.G.; Bacelli, G.; Cho, H.; Spencer, S.J. Numerical Modelling of a Point—Absorbing WEC Model Using DualSPHysics Coupled with a Multiphysics Library. In Proceedings of the Thirteenth European Wave and Tidal Energy Conference, Naples, Italy, 1–6 September 2019; pp. 1172-1–1176-8. [Google Scholar]
- Zoontjes, R.; Siegersma, H.; Ottens, H. Using CFD to determine heave added mass and damping of a suction pile. Proc. Int. Conf. Offshore Mech. Arct. Eng. OMAE 2009, 5, 407–416. [Google Scholar] [CrossRef]
- Kim, J.H.; Lakshmynarayanana, P.; Temarel, P. Added mass and damping coefficients for a uniform flexible barge using VOF. In Proceedings of the 11th International Conference on Hydrodynamics, Singapore, 19–24 October 2014. [Google Scholar]
- Bonfiglio, L. Added mass and damping of oscillating bodies: A fully viscous numerical approach. Recent Adv. Fluid Mech. Heat Mass Transf. Biol. 2011, 1, 210–215. [Google Scholar]
- Ramli, M.Z.; Temarel, P.; Tan, M. Hydrodynamic Coefficients for a 3-D Uniform Flexible Barge Using Weakly Compressible Smoothed Particle Hydrodynamics. J. Mar. Sci. Appl. 2018, 17, 330–340. [Google Scholar] [CrossRef]
- Gholami Korzani, M.; Galindo-Torres, S.A.; Scheuermann, A.; Williams, D.J. Parametric study on smoothed particle hydrodynamics for accurate determination of drag coefficient for a circular cylinder. Water Sci. Eng. 2017, 10, 143–153. [Google Scholar] [CrossRef]
- Tafuni, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A.J. A versatile algorithm for the treatment of open boundary conditions in Smoothed particle hydrodynamics GPU models. Comput. Methods Appl. Mech. Eng. 2018, 342, 604–624. [Google Scholar] [CrossRef]
- Novak, G.; Domínguez, J.M.; Tafuni, A.; Četina, M.; Žagar, D. Evaluation of the drag coefficient of a fully submerged body using SPH. Acta Hydrotech. 2019, 32, 107–119. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Consistency of viscous drag identification tests for wave energy applications. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork Cork, Ireland, 27 August–2 September 2017; pp. 643-1–643-8. [Google Scholar]
- Tao, L.; Thiagarajan, K. Low KC flow regimes of oscillating sharp edges. II. Hydrodynamic forces. Appl. Ocean Res. 2003, 25, 53–62. [Google Scholar] [CrossRef]
- Jin, S.; Patton, R.J.; Guo, B. Viscosity effect on a point absorber wave energy converter hydrodynamics validated by simulation and experiment. Renew. Energy 2018, 129, 500–512. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Stratigaki, V.; Altomare, C.; Domínguez, J.M.; Troch, P.; Kortenhaus, A. Implementation of open boundaries within a two-way coupled SPH model to simulate nonlinear wave-structure interactions. Energies 2019, 12, 697. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Dehnen, W.; Aly, H. Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon. Not. R. Astron. Soc. 2012, 425, 1068–1082. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Fourtakas, G.; Dominguez, J.M.; Vacondio, R.; Rogers, B.D. Local uniform stencil (LUST) boundary condition for arbitrary 3-D boundaries in parallel smoothed particle hydrodynamics (SPH) models. Comput. Fluids 2019, 190, 346–361. [Google Scholar] [CrossRef]
- Rota Roselli, R.A.; Vernengo, G.; Altomare, C.; Brizzolara, S.; Bonfiglio, L.; Guercio, R. Ensuring numerical stability of wave propagation by tuning model parameters using genetic algorithms and response surface methods. Environ. Model. Softw. 2018, 103, 62–73. [Google Scholar] [CrossRef]
- English, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A.J.C.; Stansby, P.K.; Lind, S.J.; Gomez-Gesteira, M. Correction for Dynamic Boundary Conditions. In Proceedings of the 2019 International SPHERIC Workshop, Exeter, UK, 25–27 June 2019; pp. 128–134. [Google Scholar]
- Liu, M.B.; Liu, G.R. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Ren, B.; He, M.; Dong, P.; Wen, H. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method. Appl. Ocean Res. 2015, 50, 1–12. [Google Scholar] [CrossRef]
- Canelas, R.B.; Domínguez, J.M.; Crespo, A.J.; Gómez-Gesteira, M.; Ferreira, R.M. A Smooth Particle Hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 2015, 78, 581–593. [Google Scholar] [CrossRef]
- Brito, M.; Canelas, R.B.; García-Feal, O.; Domínguez, J.M.; Crespo, A.J.; Ferreira, R.M.; Neves, M.G.; Teixeira, L. A numerical tool for modelling oscillating wave surge converter with nonlinear mechanical constraints. Renew. Energy 2020, 146, 2024–2043. [Google Scholar] [CrossRef]
- Cargo, C.J.; Plummer, A.R.; Hillis, A.J.; Schlotter, M. Determination of optimal parameters for a hydraulic power take-off unit of a wave energy converter in regular waves. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 98–111. [Google Scholar] [CrossRef]
- Retes, M.P.; Giorgi, G.; Ringwood, J.V. A Review of Non-Linear Approaches for Wave Energy Converter Modelling. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 08C1-3-1–08C1-3-10. [Google Scholar]
- Morison, J.R.; O’Brien, M.P.; Johnson, J.W.; Schaaf, S. Experimental Studies of Forces on Piles. Petroleum Trans. AIME 1950, 189, 149–157. [Google Scholar] [CrossRef]
- Kaneko, S.; Nakamura, T.; Inada, F.; Kato, M.; Ishihara, K.; Nishihara, T. (Eds.) Vibrations in Fluid-Structure Interaction Systems. In Flow-induced Vibrations, 2nd ed.; Academic Press: Cambridge, MA, USA, 2014; Chapter 8; pp. 359–401. [Google Scholar] [CrossRef]
- Bonfiglio, L. A hybrid RANSE—Strip theory method for prediction of ship motions. In Proceedings of the 3rd International Conference on Maritime Technology and Engineering (MARTECH 2016), Lisbon, Portugal, 4–6 July 2016. [Google Scholar]
- Palm, J.; Eskilsson, C.; Bergdahl, L.; Bensow, R.E. Assessment of scale effects, viscous forces and induced drag on a point-absorbing wave energy converter by CFD simulations. J. Mar. Sci. Eng. 2018, 6, 124. [Google Scholar] [CrossRef]
- Giorgi, G.; Penalba, M.; Ringwood, J.V. Nonlinear Hydrodynamic Models for Heaving Buoy Wave Energy Converters. In Proceedings of the 3rd Asian Wave and Tidal Energy Conference, Singapore, 24–28 October 2016. [Google Scholar]
- Munson, B.R.; Young, D.F.; Okiishi, T.H.; Huebsch, W.W. Fundamentals of Fluid Dynamics; Fowley, D., Ed.; Wiley: Hoboken, NJ, USA, 2009; pp. 93–146. [Google Scholar]
- Zang, Z.; Zhang, Q.; Qi, Y.; Fu, X. Hydrodynamic responses and efficiency analyses of a heaving-buoy wave energy converter with PTO damping in regular and irregular waves. Renew. Energy 2018, 116, 527–542. [Google Scholar] [CrossRef]
- Jin, S.; Patton, R.J.; Guo, B. Enhancement of wave energy absorption efficiency via geometry and power take-off damping tuning. Energy 2019, 169, 819–832. [Google Scholar] [CrossRef]
- Balitsky, P.; Quartier, N.; Fernandez, G.V.; Stratigaki, V.; Troch, P. Analyzing the Near-Field Effects and the Power Production of an Array of Heaving Cylindrical WECS and OSWECs Using a Coupled Hydrodynamic-PTO Model. Energies 2018, 11, 3489. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Guo, B.; Patton, R.; Jin, S.; Gilbert, J.; Parsons, D. Nonlinear modeling and verification of a heaving point absorber for wave energy conversion. IEEE Trans. Sustain. Energy 2018, 9, 453–461. [Google Scholar] [CrossRef]
- Tao, L.; Thiagarajan, K. Low KC flow regimes of oscillating sharp edges I. Vortex shedding observation. Appl. Ocean Res. 2003, 25, 21–35. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Devolder, B.; Kortenhaus, A.; Troch, P. Feasibility study of applying SPH in a coupled simulation tool for wave energy converter arrays. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC2017), Cork, Ireland, 27 August–1 September 2017; pp. 739-1–739-10. [Google Scholar]
- Rafiee, A.; Fiévez, J. Numerical Prediction of Extreme Loads on the CETO Wave Energy Converter. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Balitsky, P.; Fernandez, G.V.; Stratigaki, V.; Troch, P. Assessment of the power output of a two-array clustered WEC farm using a bem solver coupling and a wave-propagation model. Energies 2018, 11, 2907. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).