Abstract
This study focuses on the reliable parametrization of the full Soil Water Retention Curve (SWRC) from saturation to oven-dryness using high resolution but limited range measured water retention data by the Hydraulic Property Analyzer (HYPROP) system. We studied the performance of five unimodal water retention models including the Brooks and Corey model (BC model), the Fredlund and Xing model (FX model), the Kosugi model (K model), the van Genuchten constrained model with four free parameters (VG model), and the van Genuchten unconstrained model with five free parameters (VGm model). In addition, eleven alternative expressions including Peters–Durner–Iden (PDI), bimodal, and bimodal-PDI variants of the original models were evaluated. We used a data set consisting of 94 soil samples from Turkey and the United States with high-resolution measured data (a total of 9264 measured water retention data pairs) mainly via the HYPROP system and supplemented for some samples with measured dry-end data using the WP4C instrument. Among unimodal expressions, the FX and the K models with the Mean Absolute Error (MAE) values equal to 0.005 cm3 cm−3 and 0.015 cm3 cm−3 have the highest and the lowest accuracy, respectively. Overall, the alternative variants provided a better fit than the unimodal expressions. The unimodal models, except for the FX model, fail to provide reliable dry-end estimations using HYPROP data (average MAE: 0.041 cm3 cm−3, average r: 0.52). Our results suggested that only models that account for the zero water content at the oven dryness and properly shift from the middle range to dry-end (i.e., the FX model and PDI variants) can adequately represent the full SWRC using typical data obtained via the HYPROP system.
1. Introduction
The soil water retention curve (SWRC) is considered the most critical curve in soil physics and has numerous applications in the agro-hydrological areas. A considerable number of studies have been conducted on SWRC’s related research topics including in situ and laboratory measurement techniques [1,2,3,4,5], mathematical parametrization [6,7,8,9,10,11,12,13,14,15], and indirect estimation via pedotransfer function (PTF) [1,16,17,18,19,20,21,22,23]. The SWRC is often used to determine the soil hydraulic conductivity curve via capillary bundle models [24,25]. When applying Richards’ equation [26] to study the unsaturated water flow, these two curves together are used as the controlling components.
Various models have been developed over the years to parametrize the SWRC. These models provide a continuous representation of the water content and soil tension relationship over the wet, intermediate and dry parts of the curve where typically sparse or even no measured data are available. Moreover, the soil hydraulic equations are often implemented in hydrologic models to characterize saturated/unsaturated water flow of different soil types and soil horizons and to describe the spatiotemporal heterogeneity of soil hydraulic properties across the scales from subfields, to fields, up to the landscape and beyond. However, the most widely used SWRC models such as models developed by Brooks and Corey [7] and van Genuchten [15] may not adequately describe the complete SWRC for all soils since they are unimodal and assume a residual water content for high dry-end tensions.
Undisturbed soils may have pore systems that are different from the approximately normally distributed unimodal type, which makes widely used unimodal water retention models inadequate for these heterogeneous pore systems. For such soils, multimodal retention functions can provide a better description of the SWRC. To address this shortcoming, Durner [27] suggested superimposing unimodal SWRCs of the van Genuchten model [15]. Later, Romano et al. [28] proposed a bimodal water retention function by conceptually dividing the pore domain into textural and structural parts. They assumed a lognormal pore size distribution function for each component and formulated the bimodal function as the weighted sums of the two components.
The widely used SWRC models typically consider residual water content for very high tensions. The residual water content has been assumed as the water held by adsorptive forces [29], the air dry water content [30], the water content at which water movement stops [31] and the water content at a very large tension head such as the permanent wilting point [15]. In practice, generally, the residual water content simply acts as a fitting parameter at which the slope of the SWRC becomes zero toward the SWRC dry-end. However, this assumption is incorrect because for the very dry part of the SWRC water content eventually becomes zero [14]. To overcome this issue, the Peters–Durner–Iden (PDI) SWRC model variant [10,14] was proposed which reaches zero water content at oven dryness through a linear water content reduction in the dry range of the SWRC against the logarithmic transformation of the soil tension, pF [10]. The main advantages of PDI variants are that they do not require more parameters than the original SWRCs and showed a great match to experimental data [32].
The parameters of SWRC’s models are obtained by fitting the equations to the measured water retention data or are estimated via PTFs. The performance evaluation of the soil hydraulic models is typically done using data sets with a limited number of measured data points per sample and often sparse or no data on the SWRC dry-end [33,34] due to the difficulties in measuring the SWRC at matric suctions larger than 1500 kPa. This shortcoming exists mainly because the traditional standard equilibrium approach (i.e., the sandbox apparatus, the sand/kaolin box, and the pressure plate extractor) typically produces a few discrete measured water retention data pairs per soil sample. Consequently, much attention has been paid to extending the predictive capability of the existing SWRC models to the dry region from limited measurements in the wet region [35,36].
An alternative laboratory approach for measurement of the soil water retention is the extended evaporation method [2,3]. The HYPROP system (Hydraulic Property Analyzer, METER Group, Inc., Pullman, WA, USA) is a commercial laboratory instrument that works based on the extended evaporation method. HYPROP generates high-resolution data typically close to 100 water retention data points in the 0 to 100 kPa soil tension range plus an extra point close to the wilting point by considering the air-entry value as an additional measurement [37]. In recent years, the HYPROP system has been increasingly used and evaluated around the world [4,38,39,40,41,42,43,44] and promising results have been reported. For instance, Bezerra-Coelho et al. [38] evaluated the HYPROP system as applied to the van Genuchten [15] soil hydraulic functions for a wide range of soil textures using the HYDRUS-1D software package [45]. They reported an extremely well HYPROP performance, especially for the SWRC. In another study, Zhuang et al. [44] reported an excellent agreement between the soil hydraulic properties measured by multistep flux and the hanging water column experiments against the HYPROP system.
While this paper focuses on the direct-fit of soil water retention data to SWRC models, the second part of this study [17] concentrates on the performance of the respective parametric PTFs and summarizes the overall result. HYPROP data, although high resolution, are almost entirely in the wet-end and the middle part of the SWRC since HYPROP cannot generate dry-end data. It is crucial for the soil hydraulic models to provide an accurate estimation of soil water content for the entire range of the SWRC from saturation to over dryness in particular in arid regions. Accurate estimation of water content on the dry part of the curve is essential for understanding many critical processes related to soil including wind erosion, plant growth, methane oxidation, water conservation, biological and microbial activities, and nitrogen mineralization [8,46,47,48,49]. Consequently, it is crucial to determine how HYPROP limited range of measurement impacts the performance of the soil water retention models describing the entire SWRC from saturation to over-dryness, the main objective of this study. The specific objectives of this study were to: (i) investigate the performance of 16 unimodal, bimodal, PDI-unimodal and Bimodal-PDI SWRC models at different parts of the SWRC and (ii) investigate the extrapolation ability of the models beyond the HYPROP measurement range using additional dry-end measured data via the WP4C instrument (METER Group, Inc., Pullman, WA, USA).
2. Materials and Methods
2.1. Extended Evaporation Approach Using the HYPROP System
Figure 1 illustrates the main parts of the HYPROP system (accuracy: 0.15 kPa (0 to 82 kPa); resolution: 0.001 kPa) as well as four typical phases of an optimum measurement campaign.
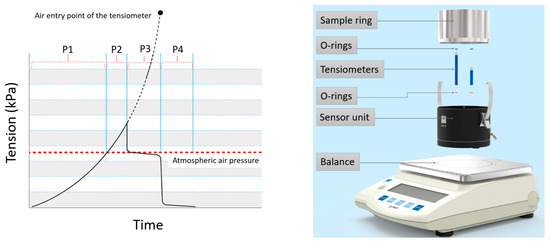
Figure 1.
Hydraulic Property Analyzer (HYPROP) system components (right) and the four typical phases (P1 to P4) of a measurement campaign (left) for the optimal measuring curve including the regular measurement range phase (P1), the boiling delay phase (P2), the cavitation phase (P3) and the air entry phase (P4), adapted from HYPROP user manual [50].
During phase one, the tensiometers are in the regular measurement range wherein the tension values increase steadily until the boiling point of the water is reached. If the system is filled completely air-free (an ideal case) the boiling delay phase (phase two) will occur in which the tension increases to above the ambient air pressure (up to the boiling delay area). During phases one and two, the measured soil tension reflects the real soil matric potential of the soil surrounding tensiometers. Phase three, the “Cavitation phase”, happens when water vapor is generated in the tensiometers, which causes a sharp reduction in the tension value down to the boiling point. During this phase, the tensiometers no longer provide readings that are representative of the real soil tension. After this phase, the tension value decreases only slightly until a second sharp reduction in tension values occurs, this time down to zero, as air enters the ceramic tip of the tensiometer because the tension in the soil surrounding tensiometers becomes greater than the air-entry pressure of the ceramic material (phase four). The air entry point depends on the material characteristic of the ceramic tip and equals to approximately 880 kPa for the HYPROP system’s tensiometers. HYPROP works based on the extended evaporation method, meaning the initiation of the air-entry phase can be used as an extra soil matric potential measurement point which further extends the range of the readings to the dry part of the SWRC.
2.2. Dew Point Technique Using WP4C System
WP4C uses the chilled-mirror dew-point technique to measure the tension of a soil sample. Figure 2 illustrates the main parts of the WP4C system. Inside the chamber, a 15 mL sample cup is sealed against a sensor block containing an internal fan, a dew-point sensor, a temperature sensor, and an infrared thermometer. The air within the sample chamber is circulated by the fan, which helps to speed up the equilibrium time and to also control the conductance of the dew-point sensor’s boundary layer. The dew-point and the infrared thermometer sensors simultaneously measure the dew-point temperature of the air and the sample temperature, respectively. The sample block temperature is monitored and stabilized using an internal thermo-electrical module. The equilibrium of the liquid phase water of the sample with the vapor phase water in the headspace of the sealed chamber is reached when the water potential of the sample becomes the same as the water potential of the air. WP4C directs a beam of light onto the mirror and uses the photoelectric cell to precisely determine the change in reflectance when condensation occurs on the mirror. At the condensation point, the temperature is recorded using the thermocouple attached to the mirror. At equilibrium, the vapor pressure of the air in the headspace is determined as the saturation vapor pressure at dew-point temperature and the saturation vapor pressure is computed from sample temperature. Finally, the water potential of the sample is calculated using the headspace and saturation vapor pressure values.
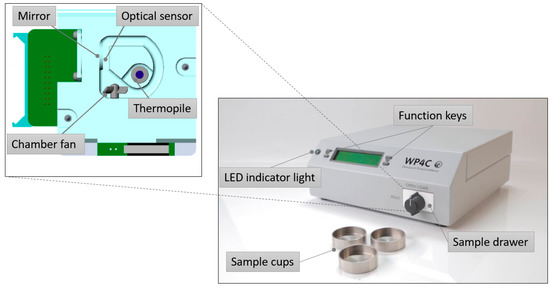
Figure 2.
WP4C components: Views of the front and inside of the soil chamber block adapted from WP4C Dew Point PotentioMeter Operator’s Manual [51].
2.3. Data Collection and Laboratory Analyses
A total of 94 soil samples were used in this study including 15 samples collected from multiple irrigation experimental sites in southern and central California, USA and 79 samples collected from the areas surrounding cities of Ankara and Anamur located in central and southern Turkey, respectively. HYPROP measurement campaigns were completed at the Technical University of Braunschweig in Germany and the University of California, Riverside for the soils from Turkey and the United States, respectively. The soil texture was determined by the hydrometer method [52] and the PARIO soil particle analyzer (METER Group, Inc., Pullman, WA, USA) for the Turkish and Unites States samples, respectively. More details about the soil data set and the laboratory procedures are outlined in Haghverdi et al. [1,16]. Table 1 summarizes the characteristics of the soils used in this study.

Table 1.
Characteristics of the soils used in this study.
For the United States samples, 250 cm3 stainless-steel cylinders (inside diameter: 8 cm, height: 5 cm) were used to collect undisturbed samples. All samples were brought up to saturation and then two vertically aligned tensiometers were installed in two holes made via a small auger, such that the tensiometers’ tips were positioned 1.25 cm below and above the center of the cylinder (2.5 cm). For the Turkish samples, the air-dried disturbed sieved samples (10 mesh sieve; <2.0 mm) were packed and brought up to saturation under vacuum in the same size cylinders to dry BDs close to the field condition (repacking was done in multiple steps to ensure consistent BD of the repacked samples). Only the upper part of the samples was open to the atmosphere for evaporation. For each sample, depending on the soil type, the measurement campaign lasted between 4 and 14 days (on average, ten days per sample for the entire data set). Throughout the measurement campaign, the soil tensions were automatically monitored using HYPROP-VIEW software at the two depths using the tensiometers. The integral of the water content distribution over the entire column divided by the height of the sample was considered by HYPROP as the mean water content of the sample. The measurement frequencies of the tensiometers were set to be higher at the beginning of the experiment (approximately once a minute for the first hour) and further apart afterward (every ten minutes). The weights of the United States samples were continuously recorded, while the Turkish samples were weighed only twice a day following the single balance approach as outlined in the HYPROP operation manual [50].
Immediately after the HYPROP measurement campaign was finished, the WP4C Dew Point PotentioMeter instrument (METER Group, Inc., Pullman, WA, USA) was used to get data at the SWRC dry-end for the US samples. A total of 4–5 subsamples (each roughly 7 cm3) were sliced off the original undisturbed sample and stored in caped small sample cups (15 cm3 capacity). The subsamples were taken from the top, middle and bottom of the original sample with different water contents. The soil tension of each subsample was measured using WP4C and the weight of the sample was immediately recorded afterward. Finally, the subsamples and the remaining soil material from HYPROP were put in the oven to get the oven-dry weight of the sample. The water retention data measured by the HYPROP and WP4C are shown in Figure 3. The HYPROP measurement campaign yielded high-resolution data (on average, 98 data points per soil sample) between saturation and up close to the wilting point with an average pF of 1.76. On average WP4C measurements had a pF value of 4.68.
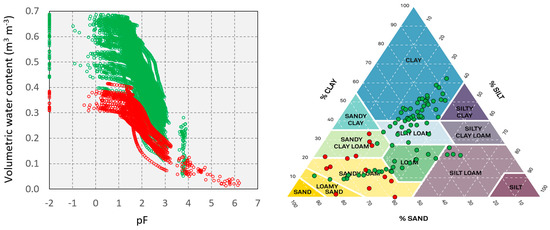
Figure 3.
Soil water retention data pairs measured by the HYPROP and WP4C (left) and soil textural classes (right) where green and red represent Turkish and USA samples, respectively.
2.4. Soil Hydraulic Models
A total of 16 models were evaluated in this study. In the following, the models are grouped into four categories including original unimodal expressions, PDI variants, bimodal variants, and bimodal-PDI variants. The unimodal variants were fitted to all the data. The bimodal variants were only fitted to the 15 samples from the United States as these were undisturbed cores and therefore retained structural and textural pores while disturbed samples from Turkey likely mainly reflect textural pores.
2.4.1. Original Unimodal Expressions
Five original unimodal water retention models were evaluated in this study including the Brooks and Corey model (BC model; [7]), the Fredlund and Xing model (FX model; [9]), the Kosugi model (K model; [12]), the van Genuchten constrained model with four free parameters (VG model; [15]), and the van Genuchten unconstrained model with five free parameters (VGm model; [15]).
The BC model is one of the first models developed to parametrize the SWRC consisting of a constant straight line and a power function joining around the bubbling pressure. The BC model is represented as:
where θ(h) is the volumetric water content at soil tension h, α (1/cm) is the inverse of the air entry value (the bubbling pressure), λ (−) is the pore size distribution index (which affects the slope of the curve) and θr and θs are the residual and saturated soil water contents, respectively.
The FX model assumes that the shape of the SWRC is dependent upon the pore size distribution of the soil and is given by:
with
and
where α, n, and m are the SWRC shape parameters, hr is the tension corresponding to θr and h0 is the soil tension at zero water content (in this study was set to 106.8 cm which is the suction at oven dryness for 105 °C, [53]) and e is the Euler number.
The K model is a modified version of the Kosugi [11] model that is derived by applying a three-parameter lognormal distribution law to the soil pore radius distribution function:
where “erfc” is the complementary error function, σ is the standard deviation of the log-transformed pore-size distribution density function, and hm is the suction corresponding to the median pore radius.
The VG model is considered to be the most widely used parameterization of the SWRC. It is represented as:
where α and n are the curve shape parameters and other parameters as previously defined. The VGm model with m as an additional shape parameter has five free parameters:
2.4.2. PDI Expressions
The PDI variants were derived for all the unimodal original expressions except for the BC model. The general form of the PDI model [10,14] consists of a capillary retention term, θcap(h) and an adsorptive retention term, θad(h), and is given as:
where Scap and Sad are the capillary and the water adsorption saturation functions and θr is the maximum water content for the water adsorption.
To guarantee that the water content reaches zero at h = h0, the Scap is substituted by scaled versions of the original functions:
where represents basic saturation functions and is the basic function at h = h0.
The basic classic saturation functions for the abovementioned unimodal expressions are:
The water adsorption saturation function is given as [10]:
where xa and x0 are pF values at suctions equal to ha and h0, respectively, ha is the suction at air entry for the adsorptive retention and b is the shape parameter which is given by:
2.4.3. Bimodal Expressions
The bimodal expressions for each unimodal model were the unscaled weighted sum of the two unimodal subfunctions without adsorption (Sad = 1):
where wi is the weighting factor for the subfunction i, subject to 0 < wi < 1 and Σ wi = 1. The is calculated using Equations (10)–(13).
2.4.4. Bimodal-PDI Expressions
The bimodal-PDI expression for each model was the scaled weighted sum of the two unimodal subfunctions with adsorption considered:
The is calculated using Equations (10)–(13). The Sad is calculated using Equation (14) for which the shape parameter b is calculated using Equations (15) and (16). The shape parameter is calculated only for the “coarsest” subfunction which is the subfunction with the lowest hm value for the K model or the highest α value for the FX, the VG and the VGm models.
2.5. Model Parametrization
HYPROP-FIT software was used to fit the soil hydraulic models to the measured water retention data. HYPROP-FIT works based on a revised version of SHYPFIT2.0 (Soil Hydraulic Properties Fitting, [54]). The fitting was simultaneously accomplished for both water retention and hydraulic conductivity models through minimizing the sum of weighted squared residuals between model estimations and measured data pairs (this study only focuses on the SWRC). The shuffled complex evolution algorithm [55] is used for parameters estimation, which guarantees that the best parameter combination (i.e., global minimum in the multidimensional parameter space) for the appropriate model combination is found. Table 2 summarizes the default bounds for the model parameters imposed during the fitting process by the HYPROP-FIT software. The bounds are chosen to provide a high degree of flexibility as well as physical consistency.

Table 2.
Default parameter bounds imposed during the fitting process by the HYPROP-FIT software.
2.6. Evaluation Statistics
The mean absolute error (MAE, Equation (19)), the root mean square error (RMSE, Equation (20)) and the correlation coefficient (r, Equation (21)) were used as the main statistics to assess the performance of the models. In addition, Mean Bias Error (MBE, Equation (22)) was calculated to determine the degree of systematic model bias, with positive and negative values indicating net over- and under-estimate of the data by the fitted model.
where E and M are the fitted and the measured soil water content values (cm3 cm−3), and are the mean fitted and the mean measured water content values and n is the number of the measured water retention points for all samples considered in each analysis.
3. Results
3.1. Overall Performance of the Models
Table 3 summarizes the overall performance of the unimodal and PDI models for the entire data set. Figure 4 shows the scatter plots of measured versus fitted water retention data for all the models and both datasets. The correlation coefficient values are close to 1 for all models, while the RMSE values vary between 0.007 cm3 cm−3 and 0.020 cm3 cm−3. The MBE values are close to zero indicating systematic bias for none of the models. Among unimodal expressions, the FX and the K models with the MAE values equal to 0.005 cm3 cm−3 and 0.015 cm3 cm−3 have the highest and the lowest accuracy, respectively. The PDI variants outperformed the unimodal expressions for VG, VGm and K models. This improvement was more pronounced for clay and clay loam samples compared to loam and sandy loam samples when performance statistics were separately calculated (data not shown here) for the textures with highest number of samples (i.e., clay, clay loam, loam, sandy loam). When MAE for each sample is separately calculated (data not shown here), the FX, FX-PDI and VGm-PDI model exhibit the best fit to the measured data for 47%, 23% and 22% of our soil samples, respectively. The K model followed by the BC model show the worst fit (highest MAE values) for 73% and 26% of the samples, respectively. The lower performance of the K and BC models were observed across clay, clay loam, loam, and sandy loam textures (data not shown here).

Table 3.
Overall performance of the unimodal and PDI models for the entire data set.
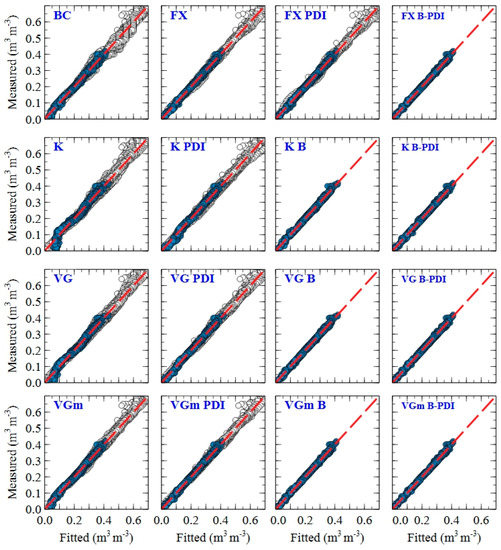
Figure 4.
Scatter plots of fitted versus measured soil water content for all 16 models. The while and blue circles depict Turkish and USA data, respectively. BC: Brooks and Corey [7], FX: Fredlund and Xing [9], K: Kosugi [12], VG and VGm: van Genuchten [15] constrained and unconstrained unimodal soil water retention models. PDI and B denote Peters–Durner–Iden [10,14] and bimodal variants of the models, respectively.
Table 4 summarizes the overall performance of all 16 models for the USA soils. The bimodal and the bimodal-PDI variants show similar statistics. For all models, the ranking of the variants from the highest to the lowest performance is: (i) bimodal-PDI, (ii) bimodal, (iii) PDI and (iv) unimodal. No systematic bias is observed since the MBE values are close to zero for all models. Among all 16 models, the K model shows the lowest accuracy with the MAE and RMSE values of 0.009 cm3 cm−3 and 0.012 cm3 cm−3, respectively. When MAE values for individual US soil samples are considered (data not shown here), the VGm-b-PDI and K model exhibit the best and worst fit for 47% and 93% of the samples, respectively.

Table 4.
Overall performance of the 16 models evaluated in this study for the USA soils.
3.2. Extrapolation Capability beyond HYPROP Range
Table 5 shows the dry-end performance of the 16 models for the US samples with and without the additional WP4C data included in the fitting process. With the dry-end WP4C data included, the MAE range between 0.005 cm3 cm−3 and 0.023 cm3 cm−3 and r values vary between 0.57 and 0.97. Without the dry-end data, the MAE values vary from 0.008 cm3 cm−3 to 0.078 cm3 cm−3 and the correlation coefficients range between 0.42 and 0.96. The MBE values range from −0.001 to 0.018 with WP4C data and from 0.001 to 0.078 without WP4C data included in the fitting process.

Table 5.
Performance of the 16 models at the Soil Water Retention Curve (SWRC) dry-end (pF range: 3.86–6.20, pF average: 4.68) with and without WP4C measurements included in the fitting process.
Without the dry-end data, there is a noticeable increase in the MAE and MBE values for the unimodal expressions except FX (more pronounced for the K, the VG and the VGm models), indicating a low performance mainly due to overestimation of the dry-end data. The FX model shows comparable performance with and without the dry-end data included in the fitting process with the MAE values equal to 0.009 cm3 cm−3 and 0.011 cm3 cm−3, respectively. All variants of the FX model show similar performance. Without dry-end data, for the K, the VG and the VGm models, the MAE values of the PDI, the bimodal, and the bimodal-PDI variants were substantially lower than that of the unimodal expressions. The performance improvement of these alternative variants over the original models is less pronounced with the dry-end data included in the fitting process. Except for the FX model, the none-PDI variants of the other models (i.e., the original expression as well as the bimodal variants) have an average r value of 0.56 showing a lower performance than the PDI variants with an average r value of 0.92.
3.3. Performance Across Tension Classes
Figure 5 illustrates the performance of the models at different parts of the SWRC divided into ten tension classes with 100 cm increments from saturation to 1000 cm (i.e., pF 0 to 3) and one extra class for pF values greater than 3. Except for the FX model, other unimodal models show relatively high MAE values for the first two classes near saturation (pF values 2–2.3). The MAE values continuously diminish from the wet-end to the middle part of the curve (pF values 2.48–2.9) for most models, yet start to increase again toward the dry-end (pF higher than 2.9–3). The bimodal and the PDI variants show a substantially lower error at the wet- and the dry-ends compared to the unimodal expression. The MAE values of the bimodal-PDI variants show little to no fluctuations across the tension classes.

Figure 5.
Performance of the 16 models at different suctions. BC: Brooks and Corey [7], FX: Fredlund and Xing [9], K: Kosugi [12], VG and VGm: van Genuchten [15] constrained and unconstrained unimodal models. PDI and b denote Peters–Durner–Iden [10,14] and bimodal variants, respectively. pF classes (C) tensions (cm of water): C1 (<100), C2 (100–200), C3 (200–300), C4 (300–400), C5 (400–500), C6 (500–600), C7 (600–700), C8 (700–800), C9 (800–900), C10 (900–1000) and C11 (>1000).
4. Discussion
4.1. Unimodal Expressions
Cornelis et al. [33] evaluated the performance of ten closed-form unimodal SWRC models including BC, VG, VGm, and K models and equations developed by Tani [56], Russo [57], Rossi and Nimmo [58], Kosugi [12,13], and Assouline et al. [6]. They found that the VGm model with a mean RMSE value of 0.008 cm3 cm−3 showed the highest match with the measured water retention data providing the best fit for 67% of the soil samples. The BC, the VG and the K models in their study showed lower performance with mean RMSE values of 0.014 cm3 cm−3, 0.010 cm3 cm−3 and 0.009 cm3 cm−3, respectively. Among unimodal expressions in our study, the VGm model (RMSE: 0.011 cm3 cm−3, MAE: 0.008 cm3 cm−3) ranked as the second-best model after the FX model (RMSE: 0.007 cm3 cm−3, MAE: 0.005 cm3 cm−3). The K (RMSE: 0.020 cm3 cm−3, MAE: 0.015 cm3 cm−3) and the BC (RMSE: 0.016 cm3 cm−3, MAE: 0.011 cm3 cm−3) models showed the lowest overall performance in our study and the lowest performance for most of the soil textures (data not shown).
The higher error near saturation for the BC model (MAE: 0.012 cm3 cm−3 for pF < 2) is attributed to its discontinuous form, which causes a sharp corner where its two parts meet near saturation. The poor match of the BC model near-saturation was also reported by Cornelis et al. [33]. Our results also showed relatively high wet-end MAE values for the K model (MAE: 0.016 cm3 cm−3 for pF < 2), the VG model (MAE: 0.012 cm3 cm−3 for pF < 2) and less pronounced for the VGm model (MAE: 0.008 cm3 cm−3 for pF < 2), a trend that was not reported by Cornelis et al. [33]. The differences between the results of the two studies might be related to the limited number of measured data near saturation in the data set used by Cornelis et al. [33] as opposed to the high-resolution wet-end data that was utilized in this study.
We realized when no dry-end data is included in the fitting process, except for the FX model, the unimodal models fail to provide reliable dry-end estimations (average MAE: 0.041 cm3 cm−3, average r: 0.52), a drawback also highlighted by Cornelis et al. [33], hence their extrapolation beyond the driest measured water retention point is not suggested (Table 5). Our results show that when additional dry-end measurements are included in the fitting process, the unimodal models perform better in the SWRC dry-end (average dry-end MAE improved from 0.041 cm3 cm−3 to 0.014 cm3 cm−3). We tested the feasibility of setting the residual water content to zero in the model data fitting scheme as a possible strategy to improve the dry-end estimation by the unimodal VG and VGm models. This strategy was ineffective, however, and caused a decrease in the overall performance of both models. For instance, the MAE values increased from 0.007 to 0.009 cm3 cm−3 for the VG model and from 0.005 to 0.006 cm3 cm−3 for the VGm model when the residual water content was set to zero. The FX model was the only unimodal expression that accounted for the zero water content at the oven dryness and accurately transitioned from the middle range to dry-end. A similar result was reported by Lu et al. [36] who studied the extrapolative capability of the FX model to estimate the complete SWRC for soils with various textures. They reported that when measured data pairs in the tension range of 0 to 1500 kPa are available, the fitted FX model provided a good agreement with experimental data from the complete SWRC. They, therefore, concluded that the need for the dry-end measurement can be eliminated with the FX model.
4.2. Bimodal and PDI Variants
The PDI and bimodal-PDI variants showed the best fit to the samples collected from Turkey (repacked) and the USA (undisturbed), respectively. The bimodal-PDI variants maintained high accuracy across a wide range from the saturation to the oven dryness with little to no fluctuations in their performances (Figure 5). The higher performance of bimodal variants compared to original unimodal models for undisturbed USA samples can be partially attributed to their ability to account for both structural and textural pore domains. This improvement is also attributed to the fact that free fitting parameters of the bimodal variants are twice more than unimodal expressions.
The low correlation coefficients of K-b, VG-b, and VGm-b models (Table 5) reveal that despite their high number of free parameters, bimodal variants fail to accurately estimate the dry-end data using HYPROP data. The PDI variants, on the other hand, outperformed unimodal and bimodal variants in estimating the SWRC dry-end with average dry-end MAE values of 0.008 cm3 cm−3 (WP4C included in the fitting process) and 0.014 cm3 cm−3 (WP4C not included in the fitting process). Lu et al. [17] evaluated the performance of three models (developed by Fayer and Simmons, [59]; Webb [60]; Khlosi et al., [61]) describing the complete SWRC using data points in the pressure plate measurement range (i.e., tension less than 1500 kPa) on eight soils. The results of their study illustrated that when measured data pairs are available in the 0 to 1500-kPa range, all three models could provide a reliable fit to the complete SWRC range. Our results suggested that typical HYPROP data (i.e., high-resolution data from saturation to 100 kPa soil tension range and an additional point close to the wilting point) are sufficient for an accurate representation of the full SWRC (from saturation to oven-dryness) when PDI variants are fitted to the experimental data. Since all of our undisturbed samples were coarse-textured and the number of soil samples was relatively limited, we recommend further investigations to determine whether the same result holds for other soil types.
5. Conclusions
This study focused on the full parametrization of the SWRC using high resolution but limited range measured soil water retention data generated by the HYPROP system. A total of sixteen soil water retention models were evaluated in this study using a high-resolution data set (a total of 9264 measured water retention data pairs) obtained via the extended evaporation method (the HYPROP system) and supplemental WP4C data covering the SWRC dry-end (available for some samples). The data set contained soil samples from Turkey and the United States, representing multiple soil textural classes. The models studied included five original widely used unimodal expressions and eleven additional PDI, bimodal, and bimodal-PDI variants. Table A1 summarizes the average values of the fitted model parameters for the 16 models across textural classes. Overall, the alternative variants (i.e., PDI and bimodal expressions) outperformed the original unimodal expressions. In the absence of additional dry-end measured data by the WP4C instrument, most of the original unimodal expressions provided undefined and unreliable water content estimations at the SWRC dry-end hence should not be used for parametrization of the full SWRC using HYPROP system. Our result only recommends the application of the PDI variants and FX model for complete SWRC estimation using the HYPROP system since these models account for zero water content at oven dryness and accurately model the SWRC dry-end.
Author Contributions
Conceptualization, A.H.; methodology, A.H., H.S.Ö., W.D.; software, A.H.; validation, A.H.; formal analysis, A.H., H.S.Ö., W.D., M.N.; investigation, A.H.; resources, A.H., H.S.Ö., W.D.; data curation, A.H., H.S.Ö., W.D., M.N.; writing—original draft preparation, A.H.; writing—review and editing, A.H., H.S.Ö., W.D.; visualization, A.H.; supervision, A.H., H.S.Ö., W.D.; project administration, A.H., H.S.Ö., W.D.; funding acquisition, A.H., H.S.Ö., W.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the USDA National Institute of Food and Agriculture Hatch/Multistate W3188 project CA-R-ENS-5170-RR.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Since the data set used in this study was relatively small, further application of these parameters is only suggested for similar soil types and only to provide general guidelines on how the models evaluated in this study perform.

Table A1.
Average values of the fitted model parameters for the 16 models across textural classes.
Table A1.
Average values of the fitted model parameters for the 16 models across textural classes.
| Model 1 | Par | C 2 | CL | L | LS | SCL | SL | SiL |
|---|---|---|---|---|---|---|---|---|
| BC | α | 0.051 | 0.045 | 0.015 | 0.060 | 0.040 | 0.026 | 0.006 |
| λ | 0.309 | 0.252 | 0.329 | 0.704 | 0.287 | 0.352 | 0.385 | |
| θr | 0.117 | 0.053 | 0.001 | 0.069 | 0.016 | 0.009 | 0.000 | |
| θs | 0.651 | 0.603 | 0.523 | 0.418 | 0.373 | 0.428 | 0.533 | |
| FX | α | 0.030 | 0.024 | 0.006 | 0.042 | 0.024 | 0.014 | 0.002 |
| n | 4.571 | 3.517 | 1.509 | 5.818 | 2.970 | 2.373 | 1.926 | |
| hr | 3135 | 465 | 1228 | 5238 | 359 | 606 | 25045 | |
| θs | 0.654 | 0.607 | 0.532 | 0.422 | 0.381 | 0.435 | 0.549 | |
| m | 0.244 | 0.244 | 0.782 | 0.443 | 0.332 | 0.625 | 0.752 | |
| FX-PDI | α | 0.032 | 0.029 | 0.008 | 0.039 | 0.031 | 0.015 | 0.003 |
| n | 3.233 | 2.552 | 1.317 | 4.899 | 2.580 | 1.904 | 1.327 | |
| θr | 0.301 | 0.189 | 0.012 | 0.100 | 0.060 | 0.054 | 0.036 | |
| θs | 0.651 | 0.604 | 0.530 | 0.420 | 0.378 | 0.433 | 0.543 | |
| m | 0.453 | 0.237 | 0.798 | 0.703 | 0.183 | 0.697 | 1.000 | |
| FX-b-PDI | α1 | 0.033 | 0.021 | 0.027 | 0.023 | 0.024 | 0.032 | 0.005 |
| n1 | 5.014 | 4.845 | 4.269 | 3.995 | 5.225 | 3.917 | 3.491 | |
| θr | 0.285 | 0.156 | 0.049 | 0.105 | 0.082 | 0.046 | 0.000 | |
| θs | 0.652 | 0.605 | 0.531 | 0.421 | 0.380 | 0.435 | 0.547 | |
| α2 | 0.031 | 0.023 | 0.009 | 0.043 | 0.014 | 0.013 | 0.010 | |
| n2 | 4.896 | 1.671 | 4.758 | 5.997 | 2.550 | 6.159 | 1.668 | |
| w2 | 0.469 | 0.671 | 0.602 | 0.717 | 0.549 | 0.325 | 0.420 | |
| m1 | 0.370 | 0.665 | 0.789 | 0.774 | 0.701 | 0.610 | 0.469 | |
| m2 | 0.490 | 0.369 | 0.657 | 0.789 | 0.758 | 0.808 | 0.787 | |
| K | hm | 141.8 | 200.7 | 508.7 | 47.5 | 236.8 | 293.8 | 958.8 |
| σ | 1.795 | 1.918 | 1.660 | 1.022 | 1.804 | 1.647 | 1.727 | |
| θr | 0.227 | 0.183 | 0.086 | 0.096 | 0.084 | 0.070 | 0.058 | |
| θs | 0.667 | 0.616 | 0.536 | 0.424 | 0.391 | 0.439 | 0.548 | |
| K-PDI | hm | 77 | 105 | 428 | 40 | 90 | 219 | 846 |
| σ | 0.971 | 1.232 | 1.517 | 0.678 | 1.083 | 1.260 | 1.504 | |
| θr | 0.376 | 0.326 | 0.140 | 0.150 | 0.189 | 0.137 | 0.107 | |
| θs | 0.653 | 0.608 | 0.532 | 0.426 | 0.382 | 0.434 | 0.544 | |
| K-b | hm1 | 2386 | 2789 | 2105 | 40 | 947 | 453 | 1055 |
| σ1 | 1.723 | 1.643 | 1.354 | 0.617 | 1.904 | 1.403 | 1.783 | |
| θr | 0.039 | 0.025 | 0.051 | 0.018 | 0.039 | 0.042 | 0.034 | |
| θs | 0.655 | 0.607 | 0.532 | 0.428 | 0.383 | 0.436 | 0.549 | |
| hm2 | 3720 | 3447 | 440 | 5178 | 641 | 1462 | 859 | |
| σ2 | 1.941 | 1.819 | 1.291 | 1.876 | 1.190 | 1.351 | 0.690 | |
| w2 | 0.522 | 0.525 | 0.486 | 0.387 | 0.419 | 0.493 | 0.371 | |
| K-b-PDI | hm1 | 371 | 1053 | 833 | 58 | 553 | 264 | 586 |
| σ1 | 1.290 | 1.144 | 1.298 | 0.652 | 1.264 | 1.352 | 1.265 | |
| θr | 0.346 | 0.248 | 0.144 | 0.143 | 0.153 | 0.121 | 0.145 | |
| θs | 0.653 | 0.606 | 0.531 | 0.421 | 0.383 | 0.437 | 0.547 | |
| hm2 | 300 | 629 | 269 | 41 | 104 | 392 | 695 | |
| σ2 | 1.362 | 1.738 | 1.040 | 0.566 | 1.457 | 1.298 | 0.868 | |
| w2 | 0.519 | 0.501 | 0.478 | 0.696 | 0.385 | 0.527 | 0.439 | |
| VG | α | 0.030 | 0.026 | 0.008 | 0.047 | 0.023 | 0.015 | 0.004 |
| n | 1.519 | 1.397 | 1.459 | 2.292 | 1.469 | 1.515 | 1.486 | |
| θr | 0.182 | 0.124 | 0.025 | 0.084 | 0.051 | 0.035 | 0.009 | |
| θs | 0.660 | 0.611 | 0.531 | 0.448 | 0.387 | 0.436 | 0.543 | |
| VG-PDI | α | 0.025 | 0.022 | 0.008 | 0.033 | 0.023 | 0.014 | 0.003 |
| n | 2.152 | 1.813 | 1.492 | 3.174 | 1.872 | 1.776 | 1.561 | |
| θr | 0.377 | 0.322 | 0.062 | 0.150 | 0.175 | 0.100 | 0.048 | |
| θs | 0.653 | 0.607 | 0.530 | 0.425 | 0.382 | 0.433 | 0.542 | |
| VG-b | α1 | 0.012 | 0.010 | 0.012 | 0.026 | 0.013 | 0.010 | 0.135 |
| n1 | 2.118 | 1.806 | 3.164 | 2.038 | 3.461 | 2.939 | 2.157 | |
| θr | 0.010 | 0.000 | 0.040 | 0.007 | 0.004 | 0.018 | 0.039 | |
| θs | 0.653 | 0.607 | 0.532 | 0.433 | 0.380 | 0.434 | 0.552 | |
| α2 | 0.014 | 0.018 | 0.013 | 0.125 | 0.016 | 0.026 | 0.005 | |
| n2 | 2.364 | 2.112 | 5.743 | 3.642 | 2.534 | 3.095 | 2.056 | |
| w2 | 0.512 | 0.515 | 0.486 | 0.471 | 0.471 | 0.440 | 0.557 | |
| VG-b-PDI | α1 | 0.016 | 0.015 | 0.023 | 0.036 | 0.015 | 0.025 | 0.014 |
| n1 | 2.619 | 2.158 | 4.393 | 3.181 | 4.170 | 4.183 | 1.642 | |
| θr | 0.218 | 0.070 | 0.107 | 0.137 | 0.097 | 0.079 | 0.158 | |
| θs | 0.652 | 0.605 | 0.531 | 0.420 | 0.382 | 0.435 | 0.547 | |
| α2 | 0.020 | 0.014 | 0.009 | 0.023 | 0.025 | 0.042 | 0.006 | |
| n2 | 1.954 | 2.005 | 3.127 | 4.892 | 2.078 | 2.518 | 2.842 | |
| w2 | 0.547 | 0.472 | 0.609 | 0.541 | 0.552 | 0.613 | 0.514 | |
| VGm | α | 0.048 | 0.041 | 0.004 | 0.053 | 0.038 | 0.021 | 0.001 |
| n | 4.549 | 3.300 | 1.278 | 8.287 | 4.354 | 2.814 | 1.036 | |
| θr | 0.136 | 0.086 | 0.039 | 0.073 | 0.024 | 0.028 | 0.058 | |
| θs | 0.653 | 0.625 | 0.524 | 0.445 | 0.377 | 0.433 | 0.549 | |
| m | 0.095 | 0.089 | 0.596 | 0.246 | 0.086 | 0.309 | 0.917 | |
| VGm-PDI | α | 0.036 | 0.033 | 0.007 | 0.036 | 0.030 | 0.016 | 0.001 |
| n | 4.596 | 3.480 | 1.379 | 5.768 | 3.019 | 2.563 | 1.139 | |
| θr | 0.371 | 0.296 | 0.083 | 0.145 | 0.135 | 0.095 | 0.102 | |
| θs | 0.651 | 0.604 | 0.530 | 0.422 | 0.379 | 0.433 | 0.546 | |
| m | 0.248 | 0.187 | 0.655 | 0.421 | 0.316 | 0.450 | 0.994 | |
| VGm-b | α1 | 0.009 | 0.004 | 0.017 | 0.031 | 0.014 | 0.008 | 0.004 |
| n1 | 3.705 | 2.504 | 7.352 | 1.985 | 4.525 | 4.815 | 8.349 | |
| θr | 0.009 | 0.009 | 0.050 | 0.000 | 0.011 | 0.027 | 0.002 | |
| θs | 0.651 | 0.605 | 0.532 | 0.441 | 0.380 | 0.435 | 0.548 | |
| α2 | 0.021 | 0.019 | 0.010 | 0.266 | 0.028 | 0.010 | 0.008 | |
| n2 | 2.896 | 2.378 | 2.869 | 6.018 | 4.969 | 4.374 | 4.742 | |
| w2 | 0.537 | 0.523 | 0.586 | 0.487 | 0.400 | 0.554 | 0.517 | |
| m1 | 0.712 | 0.756 | 0.536 | 0.568 | 0.467 | 0.571 | 0.330 | |
| m2 | 0.485 | 0.535 | 0.590 | 0.167 | 0.447 | 0.600 | 0.446 | |
| VGm-b-PDI | α1 | 0.014 | 0.018 | 0.015 | 0.023 | 0.016 | 0.012 | 0.005 |
| n1 | 2.403 | 2.701 | 6.140 | 1.725 | 1.256 | 2.969 | 8.223 | |
| θr | 0.195 | 0.131 | 0.112 | 0.129 | 0.128 | 0.090 | 0.051 | |
| θs | 0.652 | 0.605 | 0.531 | 0.422 | 0.382 | 0.436 | 0.546 | |
| α2 | 0.019 | 0.021 | 0.059 | 0.043 | 0.020 | 0.063 | 0.006 | |
| n2 | 3.252 | 3.705 | 3.788 | 9.167 | 7.448 | 8.085 | 6.824 | |
| w2 | 0.504 | 0.445 | 0.507 | 0.381 | 0.321 | 0.393 | 0.516 | |
| m1 | 0.389 | 0.236 | 0.639 | 0.671 | 0.583 | 0.596 | 0.400 | |
| m2 | 0.591 | 0.556 | 0.500 | 0.567 | 0.713 | 0.459 | 0.334 |
1 BC: Brooks and Corey [7], FX: Fredlund and Xing [9], K: Kosugi [12], VG: Van Genuchten [15] constrained and VGm: Van Genuchten [15] unconstrained unimodal soil water retention models. PDI and b denote Peters–Durner–Iden [10,14] and bimodal variants of the models, respectively; 2 C: Clay, CL: Clay loam, SCL: Sandy clay loam, L: Loam, LS: Loamy sand, SL: Sandy loam, Sil: Silt loam.
References
- Haghverdi, A.; Ozturk, H.S.; Durner, W. Measurement and estimation of the soil water retention curve using the evaporation method and the pseudo continuous pedotransfer function. J. Hydrol. 2018, 563, 251–259. [Google Scholar] [CrossRef]
- Schindler, U.; Durner, W.; Von Unold, G.; Mueller, L.; Wieland, R. The evaporation method: Extending the measurement range of soil hydraulic properties using the air-entry pressure of the ceramic cup. J. Plant Nutr. Soil Sci. 2010, 173, 563–572. [Google Scholar] [CrossRef]
- Schindler, U.; Durner, W.; Von Unold, G.; Müller, L. Evaporation Method for Measuring Unsaturated Hydraulic Properties of Soils: Extending the Measurement Range. Soil Sci. Soc. Am. J. 2010, 74, 1071–1083. [Google Scholar] [CrossRef]
- Schindler, U.; Mueller, L.; Da Veiga, M.; Zhang, Y.; Schlindwein, S.L.; Hu, C. Comparison of water-retention functions obtained from the extended evaporation method and the standard methods sand/kaolin boxes and pressure plate extractor. J. Plant Nutr. Soil Sci. 2012, 175, 527–534. [Google Scholar] [CrossRef]
- Ishimwe, E.; Blanchard, J.; Coffman, R.A. Field-Obtained Soil Water Characteristic Curves and Hydraulic Conductivity Functions. J. Irrig. Drain. Eng. 2018, 144, 04017056. [Google Scholar] [CrossRef]
- Assouline, S.; Tessier, D.; Bruand, A. A conceptual model of the soil water retention curve. Water Resour. Res. 1998, 34, 223–231. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. Hydraulic Properties of Porous Media and Their Relation to Drainage Design. Trans. ASAE 1964, 7, 26–28. [Google Scholar]
- Cornelis, W.; Gabriels, D.; Hartmann, R. A Conceptual Model to Predict the Deflation Threshold Shear Velocity as Affected by Near-Surface Soil Water. Soil Sci. Soc. Am. J. 2004, 68, 1154–1161. [Google Scholar] [CrossRef]
- Fredlund, D.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Iden, S.; Durner, W. Comment on “Simple consistent models for water retention and hydraulic conductivity in the complete moisture range” by A. Peters. Water Resour. Res. 2014, 50, 7530–7534. [Google Scholar] [CrossRef]
- Kosugi, K. Three-parameter lognormal distribution model for soil water retention. Water Resour. Res. 1994, 30, 891–901. [Google Scholar] [CrossRef]
- Kosugi, K. Lognormal Distribution Model for Unsaturated Soil Hydraulic Properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Kosugi, K. A new model to analyze water retention characteristics of forest soils based on soil pore radius distribution. J. For. Res. 1997, 2, 1–8. [Google Scholar] [CrossRef]
- Peters, A. Simple consistent models for water retention and hydraulic conductivity in the complete moisture range. Water Resour. Res. 2013, 49, 6765–6780. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.; Cornelis, W. Revisiting the pseudo continuous pedotransfer function concept: Impact of data quality and data mining method. Geoderma 2014, 226, 31–38. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.S.; Durner, W. Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: II. Evaluation of Parametric Pedotransfer Functions Against Direct Fits. Water 2020, 12, 896. [Google Scholar]
- Cornelis, W.M.; Ronsyn, J.; Van Meirvenne, M.; Hartmann, R. Evaluation of Pedotransfer Functions for Predicting the Soil Moisture Retention Curve. Soil Sci. Soc. Am. J. 2001, 65, 638–648. [Google Scholar] [CrossRef]
- Haghverdi, A.; Cornelis, W.; Ghahraman, B. A pseudo-continuous neural network approach for developing water retention pedotransfer functions with limited data. J. Hydrol. 2012, 442, 46–54. [Google Scholar] [CrossRef]
- Haghverdi, A.; Leib, B.G.; Cornelis, W. A Simple Nearest-Neighbor Technique to Predict the Soil Water Retention Curve. Trans. ASABE 2015, 58, 697–705. [Google Scholar]
- Minasny, B.; McBratney, A.B. The neuro-m method for fitting neural network parametric pedotransfer functions. Soil Sci. Soc. Am. J. 2002, 66, 352–361. [Google Scholar] [CrossRef]
- Nemes, A.; Rawls, W.J.; Pachepsky, Y. Use of the Nonparametric Nearest Neighbor Approach to Estimate Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 2006, 70, 327–336. [Google Scholar] [CrossRef]
- Schaap, M. Using neural networks to predict soil water retention and soil hydraulic conductivity. Soil Tillage Res. 1998, 47, 37–42. [Google Scholar] [CrossRef]
- Burdine, N. Relative Permeability Calculations from Pore Size Distribution Data. J. Pet. Technol. 1953, 5, 71–78. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]
- Romano, N.; Nasta, P.; Severino, G.; Hopmans, J.W. Using Bimodal Lognormal Functions to Describe Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 2011, 75, 468–480. [Google Scholar] [CrossRef]
- Corey, A. The Brooks-Corey relationships. In Proceedings of the International Workshop on Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media, Riverside CA, USA, 22–24 October 1997. [Google Scholar]
- Shao, Y. Physics and Modelling of Wind Erosion; Springer Science & Business Media. 2008. Available online: https://www.springer.com/gp/book/9781402088940 (accessed on 20 March 2020).
- Nitao, J.J.; Bear, J. Potentials and Their Role in Transport in Porous Media. Water Resour. Res. 1996, 32, 225–250. [Google Scholar] [CrossRef]
- Schneider, M.; Goss, K.-U. Prediction of water retention curves for dry soils from an established pedotransfer function: Evaluation of the Webb model. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Cornelis, W.; Khlosi, M.; Hartmann, R.; Van Meirvenne, M.; De Vos, B. Comparison of Unimodal Analytical Expressions for the Soil-Water Retention Curve. Soil Sci. Soc. Am. J. 2005, 69, 1902–1911. [Google Scholar] [CrossRef]
- Khlosi, M.; Cornelis, W.; Douaik, A.; Van Genuchten, M.T.; Gabriels, D. Performance Evaluation of Models That Describe the Soil Water Retention Curve between Saturation and Oven Dryness. Vadose Zone J. 2008, 7, 87–96. [Google Scholar] [CrossRef]
- Lu, S.; Ren, T.; Gong, Y.; Horton, R. Evaluation of Three Models that Describe Soil Water Retention Curves from Saturation to Oven Dryness. Soil Sci. Soc. Am. J. 2008, 72, 1542–1546. [Google Scholar] [CrossRef]
- Lu, S.; Ren, T.; Lu, Y.; Meng, P.; Sun, S. Extrapolative Capability of Two Models That Estimating Soil Water Retention Curve between Saturation and Oven Dryness. PLoS ONE 2014, 9, e113518. [Google Scholar] [CrossRef]
- Schindler, U.; Mueller, L.; von Unold, G.; Durner, W.; Fank, J. Emerging measurement methods for soil hydrological studies. In Novel Methods for Monitoring and Managing Land and Water Resources in Siberia; Springer: Cham, Switzerland, 2016; pp. 345–363. [Google Scholar]
- Bezerra-Coelho, C.R.; Zhuang, L.; Barbosa, M.C.; Soto, M.A.; Van Genuchten, M.T. Further tests of the HYPROP evaporation method for estimating the unsaturated soil hydraulic properties. J. Hydrol. Hydromech. 2018, 66, 161–169. [Google Scholar] [CrossRef]
- Fields, J.S.; Owen, J.S.; Zhang, L.; Fonteno, W.C. Use of the evaporative method for determination of soilless substrate moisture characteristic curves. Sci. Hortic. 2016, 211, 102–109. [Google Scholar] [CrossRef]
- Mc Grath, S.; Ratej, J.; Jovičić, V.; Curk, B. Čenčur Hydraulic Characteristics of Alluvial Gravels for Different Particle Sizes and Pressure Heads. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef]
- Herbrich, M.; Gerke, H.H. Scales of Water Retention Dynamics Observed in Eroded Luvisols from an Arable Postglacial Soil Landscape. Vadose Zone J. 2017, 16. [Google Scholar] [CrossRef]
- Naseri, M.; Iden, S.; Richter, N.; Durner, W. Influence of Stone Content on Soil Hydraulic Properties: Experimental Investigation and Test of Existing Model Concepts. Vadose Zone J. 2019, 18. [Google Scholar] [CrossRef]
- Schwen, A.; Zimmermann, M.; Bodner, G. Vertical variations of soil hydraulic properties within two soil profiles and its relevance for soil water simulations. J. Hydrol. 2014, 516, 169–181. [Google Scholar] [CrossRef]
- Zhuang, L.; Coelho, C.B.; Hassanizadeh, S.M.; Van Genuchten, M.T. Analysis of the Hysteretic Hydraulic Properties of Unsaturated Soil. Vadose Zone J. 2017, 16. [Google Scholar] [CrossRef]
- Šimunek, J.; Van Genuchten, M.T.; Šejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- De Neve, S.; Hofman, G. Quantifying soil water effects on nitrogen mineralization from soil organic matter and from fresh crop residues. Biol. Fertil. Soils 2002, 35, 379–386. [Google Scholar] [CrossRef]
- De Visscher, A.; Van Cleemput, O. Simulation model for gas diffusion and methane oxidation in landfill cover soils. Waste Manag. 2003, 23, 581–591. [Google Scholar] [CrossRef]
- Ryel, R.; Caldwell, M.; Yoder, C.; Or, D.; Leffler, A. Hydraulic redistribution in a stand of Artemisia tridentata: Evaluation of benefits to transpiration assessed with a simulation model. Oecologia 2002, 130, 173–184. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ma, J.; Guan, H.; Zhu, G. Determination of the saturated film conductivity to improve the EMFX model in describing the soil hydraulic properties over the entire moisture range. J. Hydrol. 2017, 549, 38–49. [Google Scholar] [CrossRef]
- METER Group. Operation Manual HYPROP. Available online: http://library.metergroup.com/Manuals/UMS/Hyprop_Manual.pdf (accessed on 20 March 2020).
- METER Group. WP4C Dew Point Potentio Meter Operator’s Manual. Available online: http://library.metergroup.com/Manuals/20588_WP4C_Manual_Web.pdf (accessed on 20 March 2020).
- Gee, G.W.; Bauder, J.W. Particle-Size Analysis, Methods of Soil Analysis: Part 1 Physical and Mineralogical Methods; Soil Science Society of America: Madison, WI, USA, 1986; Volume 5, pp. 383–411. [Google Scholar]
- Schneider, M.; Goss, K.-U. Prediction of the water sorption isotherm in air dry soils. Geoderma 2012, 170, 64–69. [Google Scholar] [CrossRef]
- Peters, A.; Durner, W. SHYPFIT 2.0 User’s Manual; Inst. Ökologie, Technische University: Berlin, Germany, 2015. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Tani, M. The properties of a water-table rise produced by a one-dimen-sional, vertical, unsaturated flow. J. Jpn. For. Soc. 1982, 64, 409–418. [Google Scholar]
- Russo, D. Determining soil hydraulic properties by parameter estimation: On the selection of a model for the hydraulic properties. Water Resour. Res. 1988, 24, 453–459. [Google Scholar] [CrossRef]
- Rossi, C.; Nimmo, J.R. Modeling of soil water retention from saturation to oven dryness. Water Resour. Res. 1994, 30, 701–708. [Google Scholar] [CrossRef]
- Fayer, M.J.; Simmons, C.S. Modified Soil Water Retention Functions for All Matric Suctions. Water Resour. Res. 1995, 31, 1233–1238. [Google Scholar] [CrossRef]
- Webb, S.W. A simple extension of two-phase characteristic curves to include the dry region. Water Resour. Res. 2000, 36, 1425–1430. [Google Scholar] [CrossRef]
- Khlosi, M.; Cornelis, W.; Gabriels, D.; Sin, G. Simple modification to describe the soil water retention curve between saturation and oven dryness. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).