Urban Flood Prediction Using Deep Neural Network with Data Augmentation
Abstract
1. Introduction
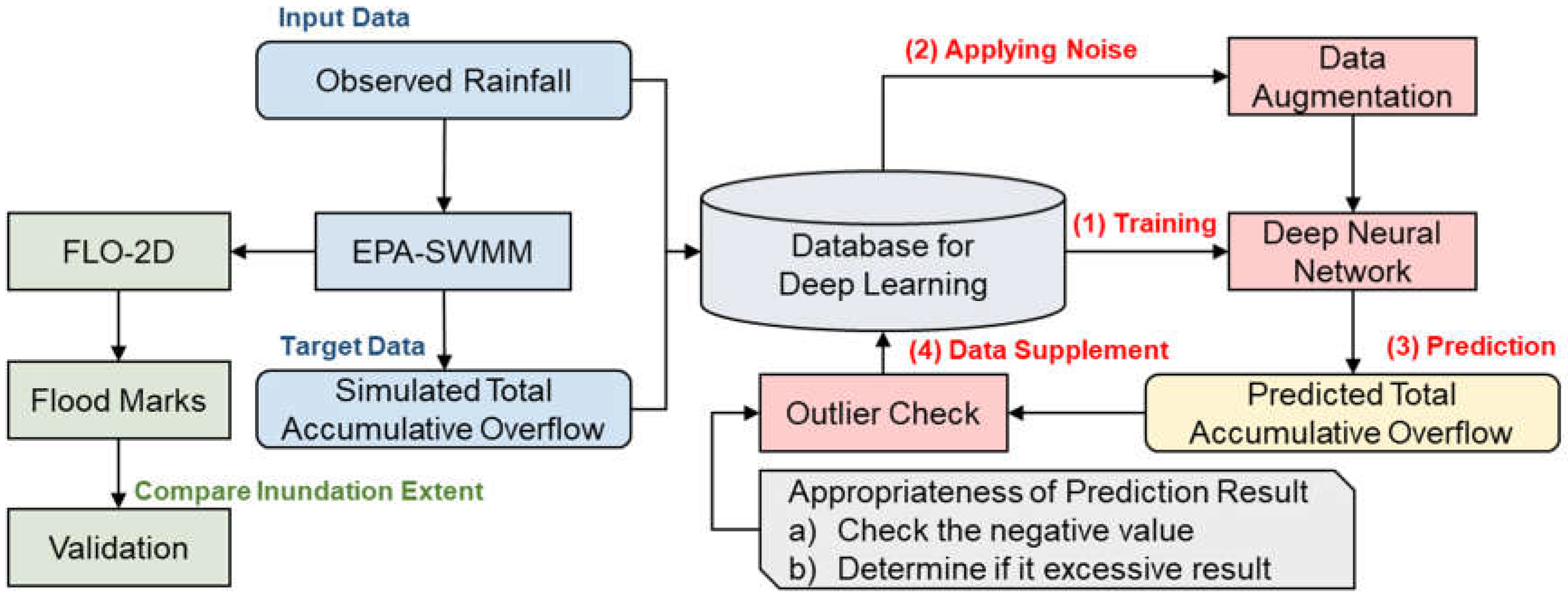
2. Methodology
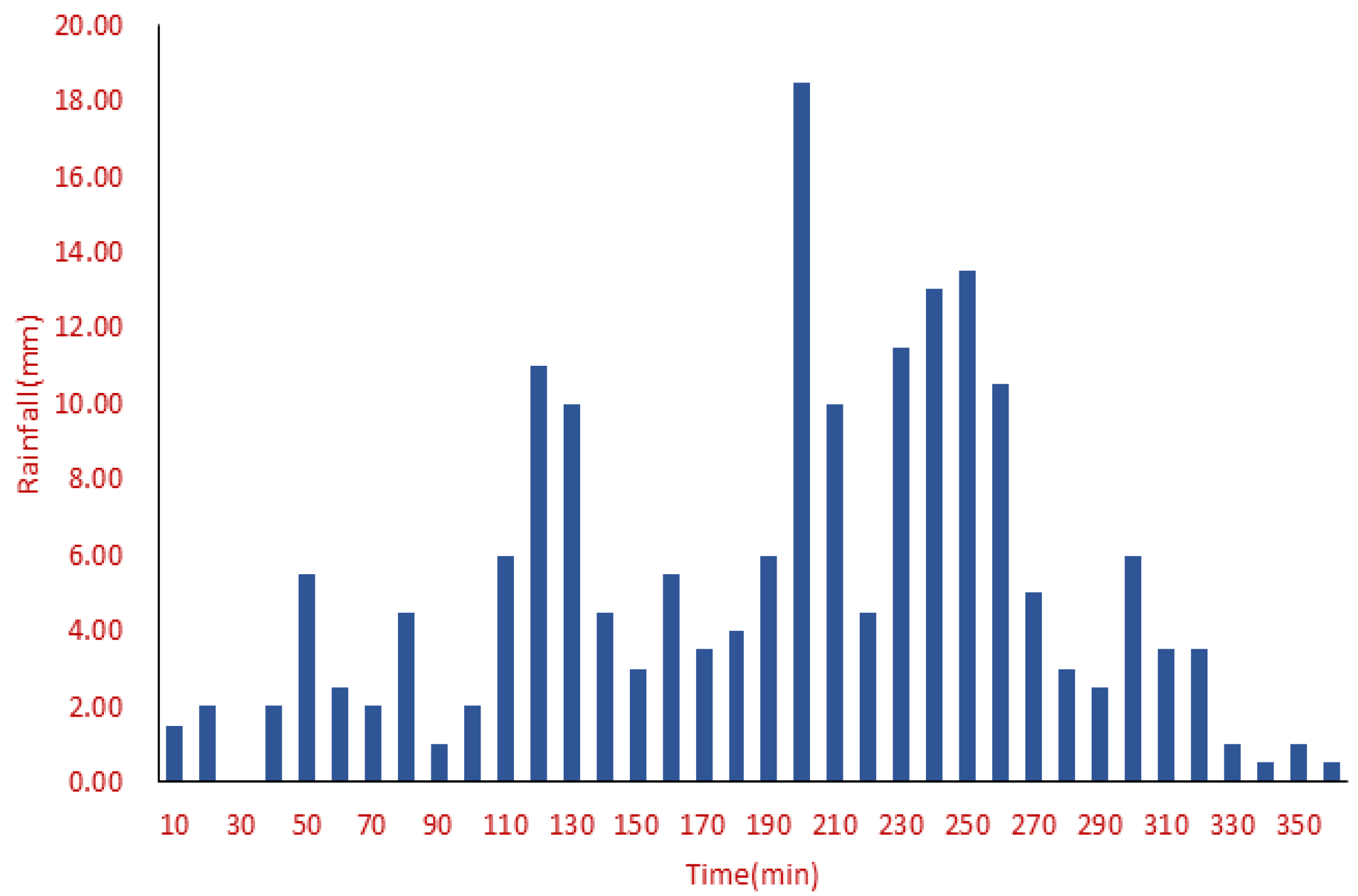
2.1. Observed Rainfall
2.2. Urban Runoff Simulation
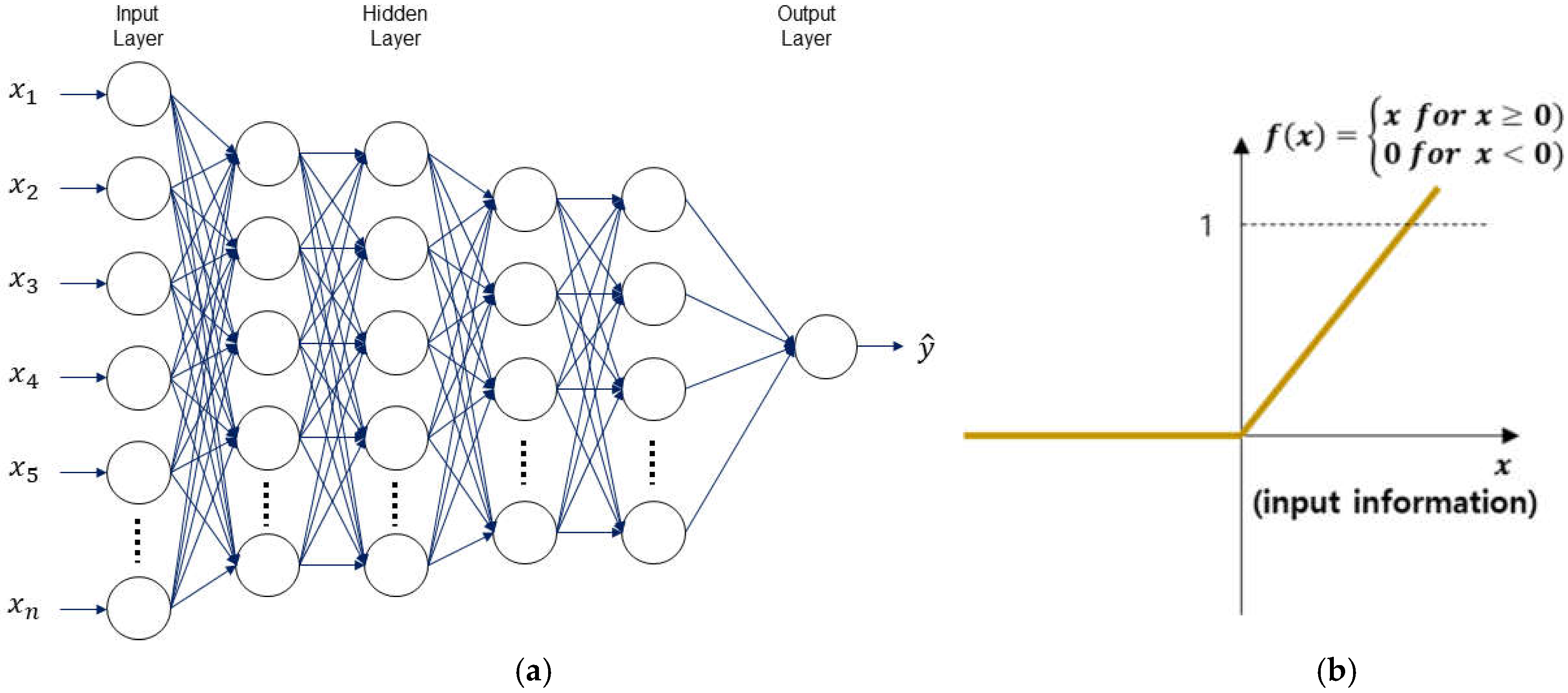
2.3. Deep Neural Network
2.4. Data Augmentation
3. Application
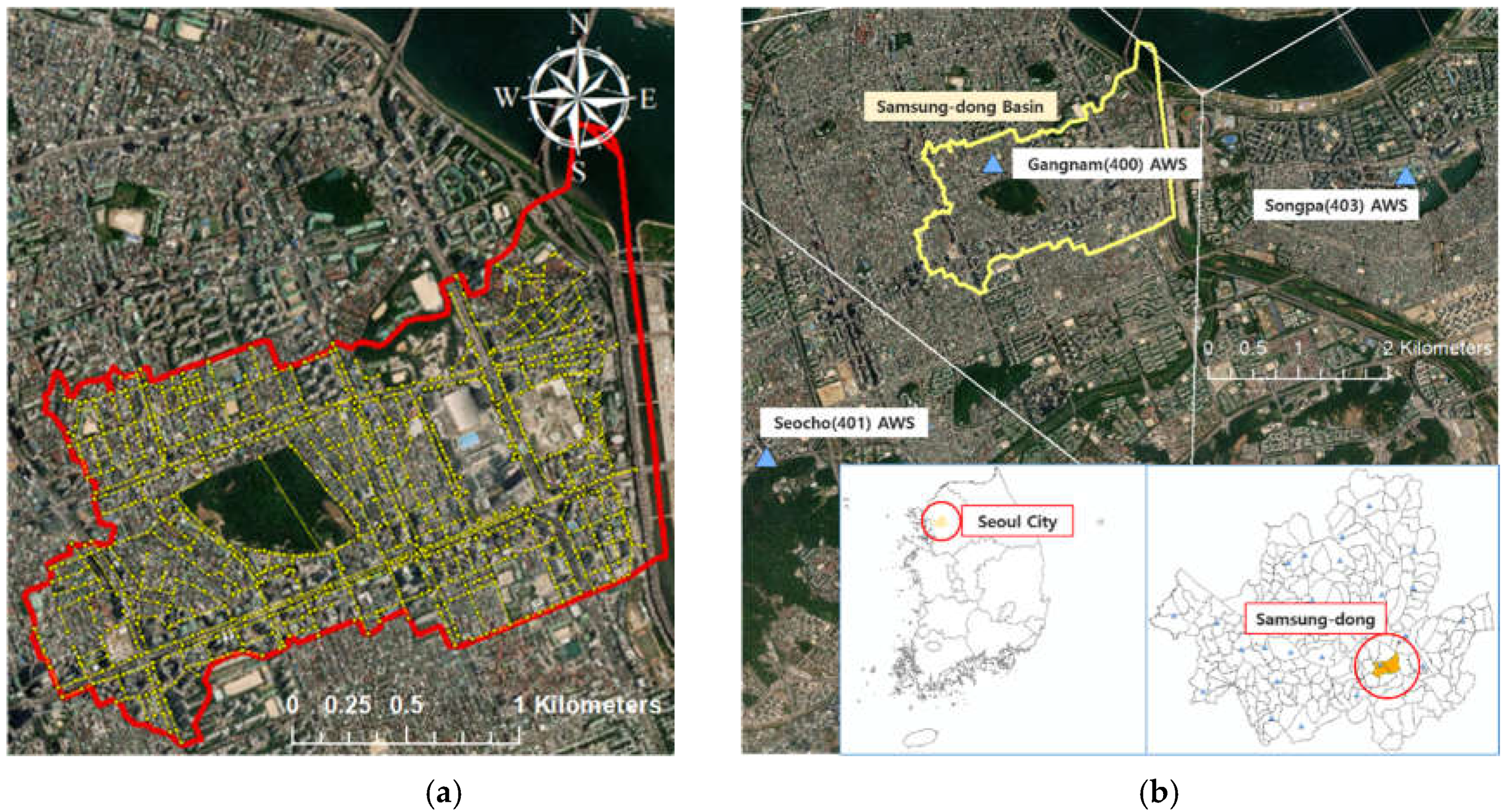
3.1. Study Area
3.2. SWMM Validation with Flood Trace Mark
3.3. Input Data
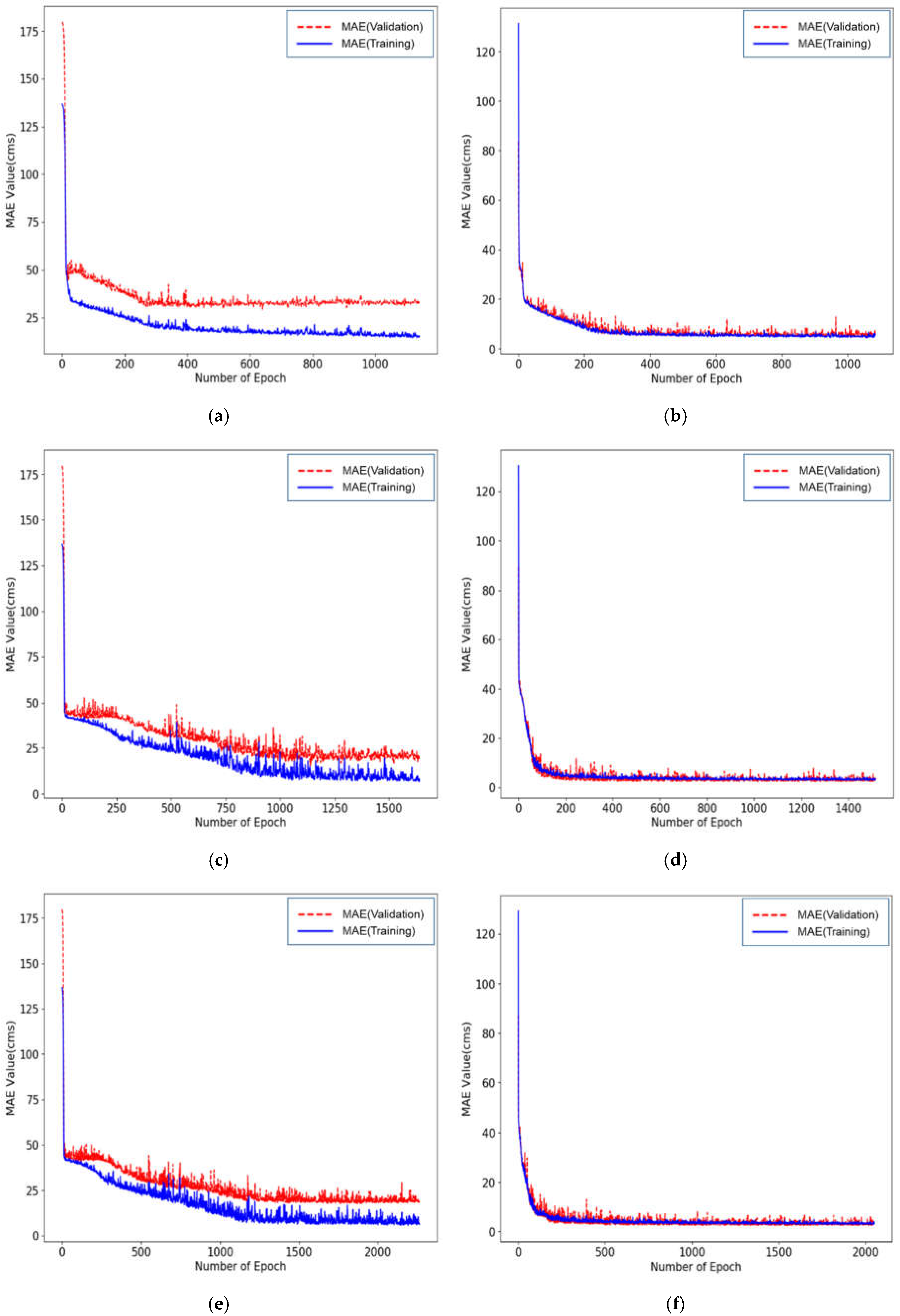
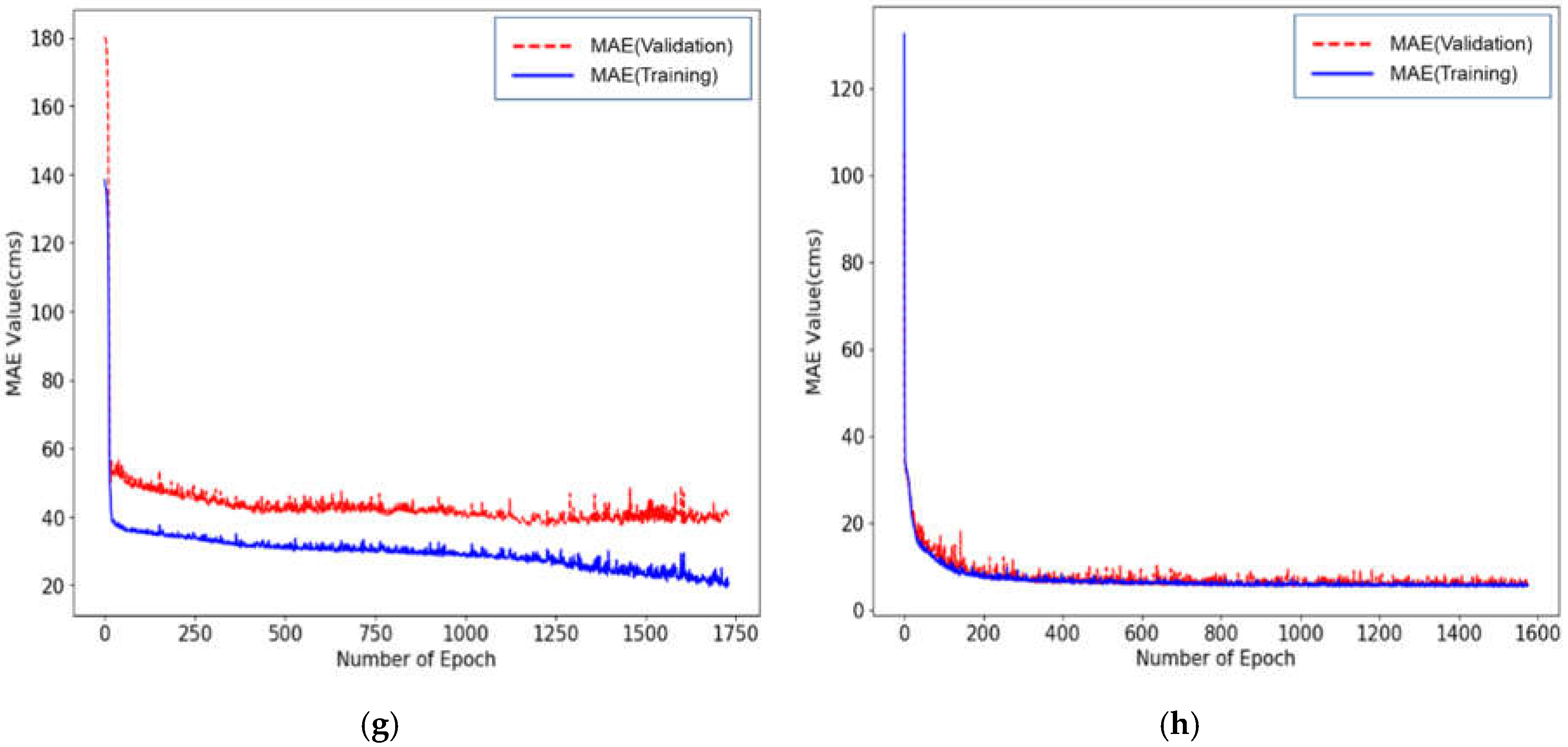
3.4. Prediction Model and Data Augmentation
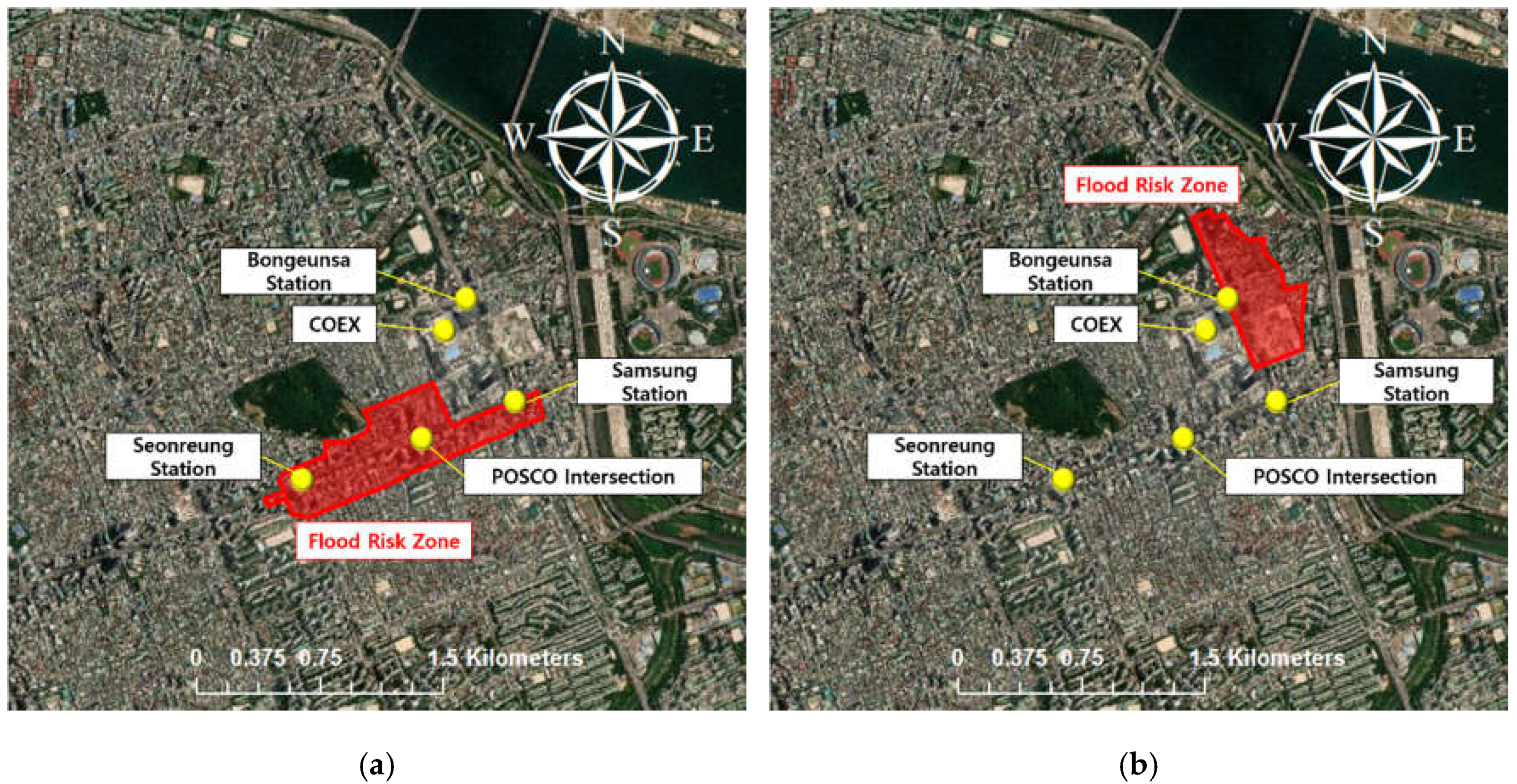
3.5. Prediction Results
4. Conclusions
- (1)
- Flood analysis was performed on the drainage basin of Samseong-dong, Seoul. The total accumulative overflow results for each heavy rainfall event were calculated using 70 observed rainfall events and EPA-SWMM. The characteristics of each rainfall event were analyzed and the correlation with the total accumulative overflow was calculated. As a result, rainfall characteristics that had a high correlation with urban outflow phenomena were identified. Although the highest correlation was found for the total rainfall and rainfall intensity, it was also found that maximum rainfall in 1- to 3-hour units during 6 hours of heavy rainfall was also highly correlated. It was found that the peak rainfall location did not have significant influence during rainfall events and that kurtosis, skewness, and rainfall time for rainfall events had a negative correlation with urban runoff.
- (2)
- As data augmentation was applied, it was found that the mean absolute error (MAE) and mean absolute percentage error (MAPE) values of the predictive results for testing data decreased for all input data combinations, which verified that prediction performance for data that were not applied to the training can be sufficiently improved using data augmentation. The largest difference of error analysis between the initial input condition (predicted with original DNN, Table 6) and after applying the 10th data augmentation was indicated at the CASE 4-based DNN model. Although input data with low correlation was used in CASE 4, it was judged that data augmentation could be helpful to partially overcome the poor predictive power.
- (3)
- The total accumulative overflow for the rainfall event on 27 July 2011, was predicted using the DNN constructed according to input data combinations. Predictions were made according to the data augmentation method, and the predictions of CASE 3 using a highly correlated input data combination were the closest to the results of SWMM. In the case of CASE 4, which used the least correlated input data, as more data augmentations were applied, the poorer the predictive results were. Although data augmentation can be used to make up for the lack of input data and reduce errors in learning, it is necessary to conduct proper correlation analysis between the input data and the target value data beforehand. It took 14 minutes for the one-dimensional urban runoff analysis of the SWMM model to be completed; however, predictions using the DNN took 2–3 seconds. In an event of heavy rainfall causing actual flooding, it is likely to save a lot of time in estimating the degree of urban flooding.
- (4)
- By successfully performing predictions using observed rainfall data and applying data augmentation, basic research on data supplementation techniques in the data-based analysis could be performed. The result of the proposed DNN model is expected to be used as basic data for the real-time flood response in urban areas. If a predictive model is constructed not only for the drainage basin in Samseong-dong but also for all drainage basins in Seoul, it seems that it would be possible to use practically for the entire flood forecasting and warning system in Seoul. Furthermore, if the predicted total accumulative overflow is linked with the expected inundation map, the rapid-simulation of a two-dimensional flood map could be possible. This methodology would be helpful to identify the flood risk area in an urban watershed.
Author Contributions
Funding
Conflicts of Interest
References
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; Marinis, G. Support Vector Regression for Rainfall-Runoff Modeling in Urban Drainage: A Comparison with the EPA’s Storm Water Management Model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H.C.; Wong, T.S.W. Evaluation of Rainfall and Discharge Inputs used by Adaptive Network-based Fuzzy Inference Systems (ANFIS) in rainfall-runoff modeling. J. Hydrol. 2010, 391, 248–262. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Li, X.; Willems, P. A Data-Driven Hybrid Urban Flood Modeling Approach. In EPiC Series in Engineering, HIC 2018, Proceedings of the 13th International Conference on Hydroinformatics, Palermo, Italy, 1–6 July 2018; Loggia, G.L., Freni, G., Puleo, V., Marchis, M.D., Eds.; EasyChair: Manchester, UK, 2018; Volume 3, pp. 1193–1200. [Google Scholar]
- Nikhil, B.C.; Arjun, N.; Keerthi, C.; Sreerag, S.; Ashwin, H.N. Flood Prediction using Flow and Depth Measurement with Artificial Neural Network in Canals. In Proceedings of the Third International Conference on Computing Methodologies and Communication (ICCMC 2019), Erode, India, 27–29 March 2019; pp. 798–801. [Google Scholar]
- Korea Meteorological Agency Meteorological Database. 2020. Available online: https://data.kma.go.kr (accessed on 2 September 2019).
- Yoon, S.S.; Bae, D.H.; Choi, Y.J. Urban Inundation Forecasting Using Predicted Radar Rainfall: Case Study. J. Korean Soc. Hazard Mitig. 2014, 14, 117–126. [Google Scholar] [CrossRef][Green Version]
- Huber, W.C.; Dickson, R.E. Storm Water Management Model. User’s Manual Version 4; Environmental Protection Agency: Washington, DC, USA, 1988.
- United States Environmental Protection Agency (EPA). Storm Water Management Model User’s Manual Version 5.0; Environmental Protection Agency: Washington, DC, USA, 2010.
- Park, J.H.; Kim, S.H.; Bae, D.H. Evaluating Appropriateness of the Design Methodology for Urban Sewer System. J. Korea Water Resour. Assoc. 2019, 52, 411–420. [Google Scholar]
- Mark, O.; Weesakul, S.; Apirumanekul, C.; Arronnet, S.B.; Djordjevic, S. Potential and Limitations of 1D Modeling of Urban Flooding. J. Hydrol. 2004, 299, 284–299. [Google Scholar] [CrossRef]
- Izumi, T.; Miyoshi, M.; Kobayashi, N. Runoff Analysis Using a Deep Neural Network. In Proceedings of the 12th International Conference on Hydroscience & Engineering, Hydro-Science & Engineering for Environmental Resilience, Taiwan, China, 6–10 November 2016. [Google Scholar]
- Agarap, A.F. Deep Learning using Rectified Linear Units (ReLU). arXiv 2019, arXiv:1803.08375v2. [Google Scholar]
- Kingma, D.P.; Ba, J.L. ADAM: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Cui, X.; Goel, V.; Kingsbury, B. Data Augmentation for Deep Neural Network Acoustic Modeling. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 1469–1477. [Google Scholar]
- Xu, Y.; Jia, R.; Mou, L.; Li, G.; Chen, Y.; Lu, Y.; Jin, Z. Improved Relation Classification by Deep Recurrent Neural Networks with Data Augmentation. arXiv 2016, arXiv:1601.03651v2. [Google Scholar]
- Seoul Metropolitan City. Comprehensive Plan for Storm and Flood Damage Reduction; Seoul Metropolitan City: Seoul, Korea, 2015; Volume 1, pp. 374–375. [Google Scholar]
- Risi, R.D.; Jalayer, F.; Paola, F.D. Meso-scale hazard zoning of potentially flood prone areas. J. Hydrol. 2015, 527, 316–325. [Google Scholar] [CrossRef]
- Moore, M.R. Development of a High-Resolution 1D/2D Coupled Flood Simulation of Charles City, Iowa. Master’s Thesis, University of Iowa, Iowa City, IA, USA, 2011. [Google Scholar]
- Son, A.L.; Kim, B.H.; Han, K.Y. A study on prediction of inundation area considering road network in urban area. J. Korean Soc. Civ. Eng. 2015, 35, 307–318. [Google Scholar] [CrossRef]
- Korea Institute of Civil Engineering and Building Technology. Road Design Manual; KICT: Korea, Seoul, 2001. [Google Scholar]

| Rainfall Station | Days of Observation | ||
|---|---|---|---|
| Seoul Area | Seoul (108) ASOS | 21 September 2010, 27 July 2011 | 267.5, 116.5 |
| Gangnam (400) AWS | 21 September 2010, 27 July 2011, 15 August 2012, 22 July 2013 | 253.5, 184.5, 131.5, 140.5 | |
| Kwanak Mountain (116) Weather Radar | 21 September 2010, 27 July 2011 | 110.0, 184.5 | |
| Seocho (401) AWS | 21 September 2010, 27 July 2011, 15 August 2012, 22 July 2013 | 258.0, 201.0, 129.5, 128.0 | |
| Gangdong (402) AWS | 21 September 2010, 27 July 2011 | 275.5, 111.5 | |
| Songpa (403) AWS | 21 September 2010, 27 July 2011 | 252.0, 194.5 | |
| Gangseo (404) AWS | 21 September 2010, 27 July 2011 | 70.0, 178.5 | |
| Yangchoen (405) AWS | 21 September 2010, 27 July 2011 | 52.0, 180.5 | |
| Dobong (406) AWS | 21 September 2010 | 166.5 | |
| Nowon (407) AWS | 21 September 2010, 27 July 2011 | 57.5, 88.5 | |
| Dongdaemun (408) AWS | 21 September 2010, 27 July 2011 | 232.5, 127.5 | |
| Jungrang (409) AWS | 21 September 2010, 27 July 2011 | 267.5, 112.0 | |
| KMA (410) AWS | 21 September 2010, 27 July 2011 | 251.5, 164.5 | |
| Mapo (411) AWS | 21 September 2010, 27 July 2011 | 241.5, 177.5 | |
| Seodaemun (412) AWS | 21 September 2010, 27 July 2011 | 154.5, 121.5 | |
| Gwangjin (413) AWS | 21 September 2010, 27 July 2011 | 249.0, 117.0 | |
| Seongbuk (414) AWS | 21 September 2010, 27 July 2011 | 160.0, 106.5 | |
| Yongsan (415) AWS | 21 September 2010, 27 July 2011 | 180.0, 136.5 | |
| Eunpyeong (416) AWS | 21 September 2010, 27 July 2011 | 238.5, 25.5 | |
| Geumcheon (417) AWS | 21 September 2010, 27 July 2011 | 160.0, 47.0 | |
| Hangang (418) AWS | 21 September 2010, 27 July 2011 | 240.5, 150.0 | |
| Seongdong (421) AWS | 21 September 2010, 27 July 2011 | 216.5, 118.0 | |
| Bukak Mountain (422) AWS | 27 July 2011 | 125.0 | |
| Gangbuk (424) AWS | 21 September 2010, 27 July 2011 | 119.5, 81.0 | |
| Namhyeon (425) AWS | 27 July 2011 | 248.0 | |
| Kwanak (509) AWS | 21 September 2010, 27 July 2011 | 91.0, 245.0 | |
| Yeongdeungpo (510) AWS | 21 September 2010, 27 July 2011 | 260.0, 181.0 | |
| Gwacheon (590) AWS | 21 September 2010, 27 July 2011 | 63.5, 140.0 | |
| Other Areas | Incheon (112) ASOS | 23 July 2017 | 69.3 |
| Cheonan (232) ASOS | 16 July 2017 | 223.6 | |
| Chungju (127) ASOS | 16 July 2017 | 284.4 | |
| Busan (159) ASOS | 16 July 2009, 27 July 2011, 15 July 2012, 25 August 2014, 11 September 2017 | 243.0, 229.5, 114.0, 91.0, 254.1, | |
| Ulsan (152) ASOS | 5 October 2016, 11 September 2017 | 91.2 | |
| Changwon (155) ASOS | 25 August 2014, 5 October 2016 | 209.5, 116.7 | |
| Statistical Characteristic | Gangnam Station | Gangnam Station | Dobong Station | Gangbuk Station |
|---|---|---|---|---|
| Observation Date | 21 September 2010 | 27 July 2011 | 21 September 2010 | 27 July 2011 |
| Total Rainfall (mm) | 253.50 | 184.50 | 166.50 | 81.00 |
| Max. Rainfall in 1 h (mm) | 78.00 | 71.00 | 57.00 | 25.00 |
| Max. Rainfall in 2 h (mm) | 136.50 | 105.50 | 106.00 | 38.00 |
| Max. Rainfall in 3 h (mm) | 181.50 | 143.00 | 136.00 | 41.00 |
| Rainfall Intensity (mm/h) | 42.25 | 30.75 | 27.75 | 13.35 |
| Peak Rainfall Location (%) | 25.00 | 55.56 | 66.67 | 77.78 |
| Standard Deviation (mm) | 5.17 | 4.38 | 4.68 | 2.49 |
| Skewness | 0.39 | 1.28 | 0.40 | 1.05 |
| Inter-event Time (min) | 60 | 10 | 100 | 130 |
| Kurtosis | −0.4973 | 1.2289 | −1.4715 | 0.3522 |
| Statistical Characteristic | Busan Station | Ulsan Station | Changwon Station | Cheonan Station |
|---|---|---|---|---|
| Observation Date | 11 September 2017 | 5 October 2016 | 5 October 2016 | 16 July 2017 |
| Total Rainfall (mm) | 254.10 | 233.80 | 116.70 | 223.60 |
| Max. Rainfall in 1 h (mm) | 84.90 | 103.10 | 74.90 | 69.30 |
| Max. Rainfall in 2 h (mm) | 144.90 | 166.40 | 97.10 | 118.50 |
| Max. Rainfall in 3 h (mm) | 176.20 | 203.30 | 107.20 | 142.50 |
| Rainfall Intensity (mm/h) | 42.35 | 38.97 | 19.45 | 37.27 |
| Peak Rainfall Location (%) | 36.11 | 77.78 | 75.00 | 75.00 |
| Standard Deviation (mm) | 5.15 | 6.06 | 4.96 | 4.05 |
| Skewness | 1.05 | 0.89 | 2.25 | 0.33 |
| Inter-event Time (min) | 0 | 0 | 20 | 0 |
| Kurtosis | 0.6922 | −0.4508 | 4.7215 | −0.8722 |
| CASE 1 (9 Inputs) | CASE 2 (6 Inputs) | CASE 3 (5 Inputs) | CASE 4 (4 Inputs) | Total Accumulative Overflow |
|---|---|---|---|---|
| Total Rainfall | Total Rainfall | Total Rainfall | Total Rainfall | 0.8144 |
| Max. Rainfall in 1 h | Max. Rainfall in 1 h | Max. Rainfall in 1 h | - | 0.5698 |
| Max. Rainfall in 2 h | Max. Rainfall in 2 h | Max. Rainfall in 2 h | - | 0.5114 |
| Max. Rainfall in 3 h | Max. Rainfall in 3 h | Max. Rainfall in 3 h | - | 0.3957 |
| Rainfall Intensity | Rainfall Intensity | Rainfall Intensity | - | 0.566 |
| Standard Deviation | Standard Deviation | - | - | 0.3623 |
| Skewness | - | - | Skewness | (−) 0.3778 |
| Kurtosis | - | - | Kurtosis | (−) 0.2499 |
| Inter-event Time | - | - | Inter-event Time | (−) 0.1087 |
| No. | MAE (Testing) | Number of Batches | Structure |
|---|---|---|---|
| 1 | 19.63 | 4 | 4/9/18/12/10 |
| 2 | 21.02 | 4 | 4/9/18/18/12/12/10 |
| 3 | 23.2 | 4 | 4/9/18/18/12/10 |
| 4 | 20.84 | 4 | 4/18/18/12/12/12/10/10 |
| 5 | 19.81 | 8 | 8/18/18/12/12/12/10/10 |
| 6 | 19.64 | 8 | 8/18/18/12/12/12/10/10 |
| 7(Selected) | 17.51 | 8 | 18/18/12/12/12/10/10/8 |
| 8 | 18.28 | 10 | 18/18/12/12/12/10/10/8 |
| 9 | 19.05 | 8 | 18/18/18/12/12/12/10/10/8 |
| Training and Validation Result | Input Criterion | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CASE 1 (MAE) | CASE 2 (MAE) | CASE 3 (MAE) | CASE 4 (MAE) | ||||||
| Train. | Val. | Train. | Val | Train. | Val | Train. | Val | ||
| Original DNN | 17.13 | 25.24 | 10.79 | 14.80 | 8.42 | 11.28 | 25.18 | 18.32 | |
| Number of Data Augmentations Applied | 1 | 10.40 | 15.04 | 4.01 | 10.27 | 6.68 | 9.83 | 9.80 | 21.71 |
| 2 | 7.45 | 11.17 | 5.09 | 7.69 | 3.81 | 5.65 | 10.37 | 13.52 | |
| 3 | 5.88 | 6.81 | 5.43 | 5.29 | 3.84 | 4.70 | 8.63 | 11.79 | |
| 4 | 6.69 | 7.25 | 4.30 | 5.33 | 3.98 | 4.48 | 7.98 | 11.25 | |
| 5 | 5.33 | 5.01 | 4.91 | 4.23 | 3.82 | 3.25 | 7.24 | 6.08 | |
| 6 | 5.06 | 4.71 | 3.16 | 3.28 | 3.11 | 3.08 | 7.40 | 7.77 | |
| 7 | 5.1 | 7.74 | 3.06 | 4.62 | 3.02 | 4.88 | 6.43 | 8.83 | |
| 8 | 4.92 | 3.94 | 3.24 | 2.42 | 2.95 | 2.70 | 7.15 | 6.04 | |
| 9 | 5.12 | 6.15 | 2.82 | 3.09 | 3.6 | 2.94 | 5.60 | 5.80 | |
| 10 | 4.17 | 4.71 | 3.43 | 3.74 | 3.31 | 3.97 | 6.04 | 5.78 | |
| Testing Result | Input Criterion | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CASE 1 | CASE 2 | CASE 3 | CASE 4 | ||||||
| MAE | MAPE | MAE | MAPE | MAE | MAPE | MAE | MAPE | ||
| Original DNN | 23.87 | 61.75 | 13.02 | 37.83 | 11.11 | 36.89 | 23.77 | 49.30 | |
| Number of Data Augmentations Applied | 1 | 13.91 | 46.94 | 7.92 | 48.75 | 5.90 | 21.31 | 27.32 | 71.77 |
| 2 | 10.06 | 11.04 | 5.41 | 6.18 | 4.75 | 6.46 | 12.75 | 14.28 | |
| 3 | 10.6 | 9.48 | 7.12 | 7.13 | 5.99 | 5.46 | 14.74 | 14.72 | |
| 4 | 8.33 | 12.62 | 4.20 | 6.73 | 3.92 | 6.76 | 11.80 | 22.24 | |
| 5 | 9.17 | 16.29 | 4.44 | 18.99 | 5.46 | 35.13 | 8.40 | 27.83 | |
| 6 | 6.23 | 57.27 | 3.39 | 6.96 | 6.21 | 14.34 | 7.96 | 12.97 | |
| 7 | 5.13 | 15.91 | 4.12 | 11.19 | 2.77 | 8.07 | 6.54 | 8.93 | |
| 8 | 1.96 | 11.56 | 3.77 | 27.99 | 3.77 | 7.24 | 7.27 | 42.32 | |
| 9 | 6.14 | 13.56 | 3.07 | 21.74 | 3.15 | 22.83 | 6.44 | 32.0 | |
| 10 | 4.46 | 34.42 | 3.38 | 11.49 | 4.22 | 7.83 | 4.15 | 7.02 | |
| Input Criterion | |||||
|---|---|---|---|---|---|
| CASE 1 | CASE 2 | CASE 3 | CASE 4 | ||
| Average of Absolute R-square (refer to in Table 4) | 0.4395 | 0.5366 | 0.5715 | 0.3877 | |
| Simulated with SWMM | 144.7 | ||||
| Prediction with Original DNN | 168.66 | 159.10 | 142.15 | 149.90 | |
| Predict with Data Augmentation | 1 | 174.92 | 147.67 | 143.36 | 145.61 * |
| 2 | 149.27 | 160.80 | 152.75 | 140.37 | |
| 3 | 130.88 | 166.44 | 149.01 | 134.75 | |
| 4 | 146.63 * | 148.31 | 150.18 | 132.25 | |
| 5 | 152.48 | 147.14 | 146.77 | 119.99 | |
| 6 | 154.49 | 148.82 | 160.14 | 142.34 | |
| 7 | 162.85 | 143.57 * | 147.71 | 136.49 | |
| 8 | 129.85 | 160.21 | 160.21 | 136.32 | |
| 9 | 151.82 | 149.65 | 162.69 | 137.04 | |
| 10 | 147.39 | 142.69 | 144.51 * | 138.47 | |
| Standard Deviation | 13.21 | 7.58 | 6.32 | 6.47 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.I.; Han, K.Y. Urban Flood Prediction Using Deep Neural Network with Data Augmentation. Water 2020, 12, 899. https://doi.org/10.3390/w12030899
Kim HI, Han KY. Urban Flood Prediction Using Deep Neural Network with Data Augmentation. Water. 2020; 12(3):899. https://doi.org/10.3390/w12030899
Chicago/Turabian StyleKim, Hyun Il, and Kun Yeun Han. 2020. "Urban Flood Prediction Using Deep Neural Network with Data Augmentation" Water 12, no. 3: 899. https://doi.org/10.3390/w12030899
APA StyleKim, H. I., & Han, K. Y. (2020). Urban Flood Prediction Using Deep Neural Network with Data Augmentation. Water, 12(3), 899. https://doi.org/10.3390/w12030899





