Abstract
Utilizing floodwater resources is important in relieving water shortages, and dynamic control of the flood limited water level (FLWL) for reservoir operation in a flood season is an effective method to achieve this objective. Based on the capacity-constrained pre-release method, this study proposed an improved dynamic control method that considered the duration of dry periods and the lead time of flood forecasts. The pre-release process was divided into two periods: water use and flood control. Taking Xianghongdian Reservoir in the Huai River Basin of China as an example, this study analyzed the statistical laws of continuous dry periods and effective flood forecast lead times and compared the effects of the negative exponential and asymptotic regression models in fitting the dry period distribution. We also calculated the floodwater volume over the FLWL in different situations and evaluated the flood control risks in a worst-case scenario. Statistical law of the dry period duration showed obvious negative index distribution characteristics; the relationship between increased water storage, dry period, and lead time can provide support for the operation decisions of the reservoir. The method did not increase the flood control risk under worst-case scenarios, and it can be used to effectively utilize reservoir floodwater resources.
1. Introduction
With the development of the economy and the increase in population, the demand for water resources is increasing. Together with the unreasonable exploitation and utilization of water resources, many countries and regions suffer from water shortage in varying degrees, which may substantially restrict their economic and social development. The utilization of floodwater resources in the flood season is an important way to alleviate regional water resource shortages [1,2,3]. As a common component of a watershed system, reservoirs play an important role in utilizing floodwater resources. The flood limited water level (FLWL) is the maximum allowed reservoir water level during the flood season. The traditional FLWL is usually set as a fixed value during an entire flood season, which is determined based on the design rainstorm or design flood. However, this method ignores the annual and seasonal variation of inflows and gives excessive priority to low probability floods. This usually results in water being spilled during the flood season and, consequently, no water can be stored after the flood season, especially in arid and semiarid areas [4]. Therefore, to ensure the safety of flood control in a basin, effective utilization of floodwater resources can be achieved through the dynamic control of reservoir FLWLs [5,6,7,8]. Many scholars have carried out in-depth studies and proposed a variety of dynamic control methods for FLWL during reservoir operation.
Dynamic control of the flood limited water level (DC-FLWL) means that the FLWL is allowed to fluctuate within specified bounds based on real-time forecast information [9]. At present, the dynamic control methods of FLWL for reservoirs can mainly be divided into three types: capacity-constrained pre-release, forecasting operation, and reservoir storage compensation. The capacity-constrained pre-release method, also known as the pre-store and pre-release method, implies that the reservoir uses the short-term hydrological and meteorological forecast information of the flood season to pre-store the amount of water over the FLWL, and it releases all the floodwater over the FLWL before the next flood occurs. This method can lead to the water level decreasing rapidly to the original FLWL, thereby ensuring the flood control safety of the basin. Wang et al. [10] gave a detailed mathematical description of the pre-store and pre-release method for the planning and construction stage as well as the real-time application stage and applied it to the Biliuhe Reservoir. Chou et al. [11] utilized real-time forecast information to alleviate flood severity by releasing the water stored in the reservoir before the arrival of a large flood; this method also ensured the water supply rate after the flood season. The forecasting operation method uses real-time flood forecasting information and selects that information as the index to determine the magnitude of the incoming flood, formulate the corresponding reservoir operation rules, increase the outflow during the operation period, and raise the FLWL under flood control security. Zhao et al. [12] set up a real-time flood control operation model with the maximum peak clipping rate, proposed the method of dynamic use of flood control storage by stages and determined the upper bound of DC-FLWL. The reservoir storage compensation method refers to the reservoir group with the same flood control target, which uses the differences in reservoir flood storage to transform the surplus storage of one reservoir into the upper bound of the FLWL of the other reservoir. There is a complex hydraulic connection between the cascade reservoirs, and the reservoir storage compensation method is mostly combined with the capacity-constrained pre-release method. Guo et al. [13,14] proposed a joint operation and dynamic control model of FLWLs for the optimization of cascade reservoirs based on the "large-scale system decomposition and coordination theory", which was applied to the Qingjiang cascade reservoirs to obtain the optimal combination of the FLWL. The water quality issue is an integral part of the post-flood scenario. However, while attempting to address the problem of water shortage through non-structural measures, the importance of water quality management in natural resource governance is neglected. Withanachchi et al. [15] provided a framework for an analytical review of the existing institutions and regulation system, as well as the prospective water policy system; this is important in identifying the obstacles to water quality governance under the existing regulations and governance system that hinder effective water resource management.
The capacity-constrained pre-release method has been widely used in many previous studies. Its basic idea is to determine the upper bound of DC-FLWL according to the amount of water that can be released within the forecast lead time. However, there is considerable error in the forecasting process due to many factors, such as the forecast model structure and inadequate real-time information [16,17]. Therefore, scholars have paid considerable attention to the availability of the forecasting information and the risk control considering the forecasting uncertainty [18,19,20,21]. Li et al. [22] analyzed the flood forecast error and uncertainty of the flood hydrograph shape, established the dynamic control model considering the inflow uncertainty, and applied it to the Three Gorges Reservoir, which increased the benefits in terms of power generation and floodwater utilization rate without increasing the flood control risk. Hui et al. [23] considered the uncertainty of flood forecasting as well as engineering uncertainty and determined the minimum risk to derive the optimal condition for releases where the current marginal damage from the hedging release equaled the future expected marginal damage from storm releases. Based on the analysis of the uncertainty of inflow forecast and the accepted flood control risk, Ding et al. [24,25] established a two-stage optimal operation model that proposed two objectives: the conservation benefits in the current stage and flood risk in a later stage. They derived hedging rules from the analytical framework and systematically analyzed the effects of the preferences of decision makers for water utilization and reservoir inflow forecast uncertainty on the DC-FLWL; then, they proposed availability criterion and a subsequent method for applying forecast information to DC-FLWL.
In addition to flood forecasting information, with the improvement of meteorological forecasting levels in recent years, rainfall forecasting information has also been applied to hydrological events and reservoir operations [26]. For example, Ren et al. [27] comprehensively considered rainfall and flood forecasting information and proposed an improved capacity-constrained pre-release method that had been successfully applied to a reservoir with short confluence time and low accuracy of flood forecasting. Zhong et al. [28] established a probabilistic inflow forecasting scheme based on the numerical weather prediction (NWP) data by applying the Bayesian model averaging (BMA) method, which provided the basis for its application in reservoir operation. Cai et al. [29,30] established an uncertainty analysis model under the Bayesian theory with a generalized probability density function and adopted the fuzzy probability to describe the fuzziness of the system. The new model can obtain the conditional probability distribution of the precipitation with high accuracy and reliability by the NWP as well as account for the fuzzy events in real-world flood control.
Assuming that the reservoir water level maintains the upper bound at the recession flood stage, and that there is a long period without rain (i.e., a dry period) before the next flood occurs, then generally the inflow is less than the floodwater utilization discharge at that time. If the reservoir releases as floodwater utilization discharge, the reservoir water level will drop slowly, and the water level will not reach the upper bound of FLWL when the forecasted large inflow arrives; the traditional capacity-constrained pre-release method does not consider this potential scenario. We consider that the release time does not begin at the large forecasted inflow; instead, when the reservoir inflow is less than its utilization discharge, the reservoir begins the pre-release process, and only the part of floodwater that is released as utilization discharge on dry days is truly transformed into a conservation source.
Based on the above scenario, this study proposed a two-period capacity-constrained pre-release method. The determination of the duration of the dry period is the key element of this method. According to the short-term rainfall forecast and flood forecast information, the pre-release process was divided into two periods: a water use pre-release period and a flood control pre-release period. The reservoir was used for hydropower generation when dry periods were forecasted. However, when a large inflow was forecasted, the reservoir utilized the flood control pre-release process. However, when the current rainfall forecast had a high degree of uncertainty, the forecast interval time was usually a fixed value (such as 24 h), and the lack of forecasting information for the duration of the dry period made it difficult to directly guide the DC-FLWL for the reservoir. Therefore, based on the historical rainfall and runoff data, this study analyzed the statistical laws of the continuous dry period duration and flood forecasting lead time of the basin, constructed different floodwater resource utilization scenarios, estimated the floodwater volume over the reservoir FLWL by using the proposed method, discussed the operation conditions of the reservoir under the worst-case scenario (zero rainfall forecast), and proposed corresponding solutions to ensure that the reservoir flood control risk was not increased. This study took Xianghongdian Reservoir in the Huai River Basin as an example to verify the effectiveness of the proposed method.
2. Materials and Methods
In real-time reservoir operation, the water use pre-release was based on the short-term meteorological forecast, and the reservoir was released according to the floodwater utilization discharge in the forecasted days without rain. When a long period without rain was forecasted, the reservoir had enough time to release all the floodwater over the FLWL through water use pre-release, and then the reservoir water level could be safely reduced to the FLWL. If the water use pre-release was not timely, and a large inflow was forecasted to arrive, then the flood control pre-release would be utilized instead to ensure the safety of the basin. Then, the floodwater over the FLWL would be released within the effective lead time, and the reservoir water level could therefore decrease to the original FLWL. Figure 1 shows the schematic diagram of the two-period capacity-constrained pre-release method. Lin et al. [31] proposed a method to determine the pre-store timing . The reservoir started to store the flood tail at time until the water level was stored to the planned upper bound of the FLWL at time . Then, the reservoir started to pre-release according to the floodwater utilization discharge at time . When a large inflow was forecasted, the reservoir began flood control pre-release to ensure that the water level of the reservoir could fall to the original FLWL at time .
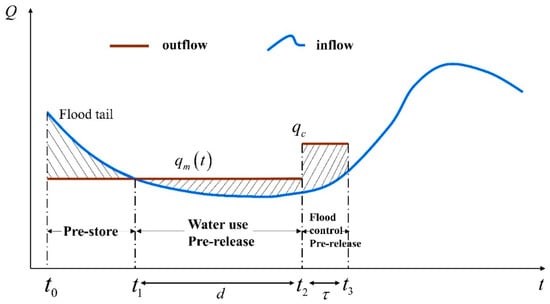
Figure 1.
Two-period capacity-constrained pre-release method. Note: outflow is the drainage process of the reservoir; inflow is the reservoir inflow process; flood tail is the recession flood stage of the last flood; is the pre-store time; is the water use pre-release time; is the flood control pre-release time; is the continuous dry period duration, is the flood forecast lead time, is the daily average utilization discharge (mainly for power generation and various types of water supply) in the dry period, and is the average flood outflow in the flood forecast period.
2.1. Statistical Analysis of Dry Period Durations
In the two-period capacity-constrained pre-release method, the duration of the dry period is the key to determine the floodwater volume over the FLWL in the water use pre-release period [32]. Since there was no corresponding short-term meteorological forecast data, this study followed the continuous dry period duration statistical law by analyzing historical rainfall data. A previous study [33] used the maximum entropy principle to study the distribution law of dry period duration and found that the latter conformed to the negative exponential distribution. The probability density function is as follows:
where is the dry period duration in a certain region, is the average dry period duration, and is the shortest dry period duration.
The distribution function of dry period duration can be further deduced as follows:
Based on the above theories, the specific steps to deduce the probability distribution of dry period duration are as follows:
- Step 1: Collect actual rainfall data series from recent years;
- Step 2: Count the series of dry period duration , ; is the number of times that a continuous dry period duration has occurred in the actual rainfall data series;
- Step 3: Determine the shortest dry period duration and calculate the average dry period duration .
By substituting and into Equations (1) and (2), the probability distribution of dry period duration can be obtained.
To test whether the dry period duration accorded with the negative exponential distribution and whether the probability distribution results were reasonable, this study used the asymptotic regression model to simulate the rule of continuous dry period duration through comparing the results of the two methods to analyze their rationality. The model formula is as follows:
where is an asymptote, is the response range, and is the rate.
2.2. Analysis of Flood Forecast Lead Time
The forecast lead time of a flood is the interval between the forecast time and the occurrence time of the flood. The current flood forecast model is generally based on the measured rainfall data as the input (known conditions) to forecast future floods, so its lead time refers to the average confluence time of floods. In practice, the specific method to determine the valid forecast lead time is generally to designate the time difference between the end time of the main rainfall and the occurrence time of the flood peak flow as the natural forecast lead time of the flood, as shown in Figure 2.
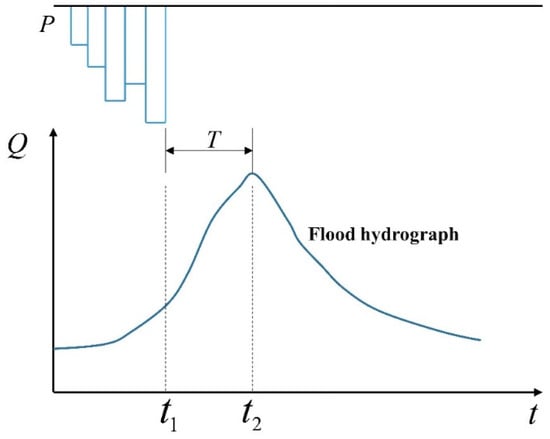
Figure 2.
Natural forecast lead time of a flood. Note: is the precipitation; is the flood forecast lead time; is the end time of the main rainfall; and is the occurrence time of the flood peak flow.
In a specific basin, the natural forecast lead time of a flood is related to the rainfall intensity, spatial and temporal distribution of the rainfall, location of the storm center, and trend and velocity of the water flow. Therefore, the natural forecast lead time of each flood is different; for example, the lead time will be longer if the storm center is in the upstream area, while the lead time will be shorter if the storm center is in the downstream area. In addition, the combination of storm intensity and rainfall time will also affect the length of the forecast lead time to an extent.
Based on the historical rainfall and flood data, this paper analyzed the law of the reservoir flood natural forecast lead time. The specific steps are as follows:
- Step 1: For each flood, the natural forecast lead time was determined according to the measured rainfall and flow process of the basin, as shown in Figure 2.
- Step 2: For a series of historical floods in the basin, step 1 was repeated to obtain a set of forecast lead time data. The statistical characteristic parameters of the series of lead time were calculated using Equations (5) and (6).
- Step 3: The normal distribution was used to fit the probability distribution density of the flood forecast lead time.
2.3. Calculation of Floodwater Volume Over FLWL
Since the flood control situation is different in each flood event, the amount of allowable floodwater over the FLWL is also different. The key problem of reservoir floodwater resource utilization is to analyze the real-time floodwater volume over the FLWL. Suppose that the days without rain are , the effective lead time of real-time flood forecast is , and the amount of floodwater over the FLWL can be determined according to Equations (7)–(10).
where is the floodwater volume over the FLWL in the water use pre-release period, is the daily average utilization discharge (mainly for power generation and various types of water supply) in the dry period, is the daily average inflow in the dry period, is the floodwater volume over the FLWL in the flood control pre-release period, is the average outflow in the flood forecast period, is the average inflow in the flood forecast period, is the interval time of the flood forecast period, is the safety discharge of the downstream flood protection point, is the discount coefficient ( ≤ 1) that reflects the margin of the pre-release process to the downstream flood control safety, is the reservoir discharge capacity function, is the water level at time ; and is the total planned floodwater volume over the FLWL.
2.4. Analysis of the Worst-Case Scenario
Considering the worst-case scenario, after the implementation of the pre-store period, the meteorological forecast will experience a complete failure, and the next flood will immediately reach the reservoir; at that time, the main task of the flood control system is to release all the floodwater stored over the FLWL in a timely manner to reduce the water level to the original FLWL within the flood forecast lead time. By comparing the release time and effective forecast lead time to analyze whether there is a risk, if the release time is shorter than the effective forecast lead time, then the former does not add the original reservoir flood control risk. When the meteorological forecast fails, the release time can be determined according to Equation (11):
If the reservoir water level still exceeds the original FLWL after the implementation of pre-release in accordance with Equation (11), the amount of the part of water that failed to be released in time shall be analyzed. The amount of water that failed to be released in time shall be deducted on the basis of the total floodwater volume over the FLWL; then, it is considered as the safe floodwater volume over the FLWL. This volume can be determined according to Equations (12) and (13):
where refers to the amount of water not released in time, and refers to the safe floodwater volume over the FLWL.
2.5. Case Study Area
This study undertook the Xianghongdian Reservoir in the Huai River Basin of China as an example. Xianghongdian Reservoir [34] is located in Jinzhai County, Anhui Province. The reservoir watershed is shown in Figure 3. The main tributaries in the upper reaches are the Yanzi River, Songjia River, and Jiangjia River. The reservoir basin covers a drainage area of 1400 km2, the average annual rainfall in the reservoir area is 1497 mm, the average annual runoff depth is 777 mm, and the annual runoff volume is 1.088 billion m3, approximately 20% of which occurs in July. Xianghongdian Reservoir suffered 30 large and small floods from 1998 to 2006; the statistics are shown in Table 1.
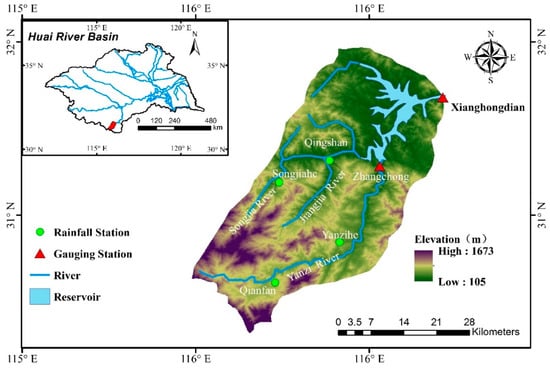
Figure 3.
Xianghongdian Reservoir watershed.

Table 1.
Historical floods of Xianghongdian Reservoir.
The reservoir was built in 1958 as a multipurpose, multi-year regulating storage reservoir used mainly for flood control and irrigation; however, it is also utilized for hydropower generation and other uses. The design flood water level is 140.98 m, the flood water check level is 143.37 m, the FLWL is 125 m, the normal pool level is 128.0 m, and the total storage capacity is 2.613 billion m3. The FLWL of the Xianghongdian Reservoir is 125 m (with a 1227.1 million m3 storage capacity), at 3 m lower than the normal pool level of 128 m (a 1413 million m3 storage capacity), with a total storage capacity difference of 185.9 million m3. However, since the 1990s, Xianghongdian Reservoir has experienced few floods and many droughts; aside from 1991, 1994, and 2003–2005, where its level was at the FLWL or above, the reservoir level has been under 125 m. In addition, the Xianghongdian Reservoir together with the Foziling Reservoir must provide 440,000 hm2 of irrigation water to fertile fields downstream. Thus, while ensuring the safety of the basin, it is necessary to implement real-time DC-FLWL in the flood season to reasonably adjust its flood storage and conservation storage, increase the refilling rate at the end of the flood season, and make full use of floodwater resources.
The floodwater utilization discharge of Xianghongdian Reservoir is mainly used for power generation, and the total flow discharge release capacity of the power station is 200 m3/s, so the floodwater utilization discharge is 200 m3/s. The level of safe downstream discharge is 2500 m3/s, and to leave a sufficient safety margin for the downstream area, the discount coefficient was set to 0.5. In this study, the floodwater resource utilization of Xianghongdian Reservoir was analyzed based on the frequent flood process (10-year flood).
3. Results
Following the methodology described in Section 2, we analyzed the statistical law of dry period duration and the effective forecast lead time of floods to determine the floodwater volume over the FLWL; we also analyzed the worst-case scenario to clarify the flood control risk.
3.1. Dry Period Duration
Considering that the runoff coefficient of Xianghongdian Reservoir is 0.3, and its rainfall patterns vary both spatially and temporally during the flood season, the rainfall–runoff situation is relatively complex; therefore, days with historical rainfall less than or equal to 3 mm are counted as dry in this study. According to the actual rainfall data of the basin from 1956 to 2015 (flood season: May to September), a total of 7284 of the 9180 daily rainfall data had rainfall less than or equal to 3 mm. The number of times that a continuous dry period duration has occurred is 1200. We counted the number of consecutive days without rain. In order to know whether the distribution law of dry periods is consistent with the distribution law both on a long time scale and short time scale, we divided the 60-year time series into independent continuous 10-year series and determined the statistics for each time scale; the results are shown in Figure 4. It can be seen from the figure that the statistical indicators of the dry period duration in each 10-year series show moderate change; the median is 4 days, with the mean of all the years being about 6 days, and the fluctuation range is within 1 day.
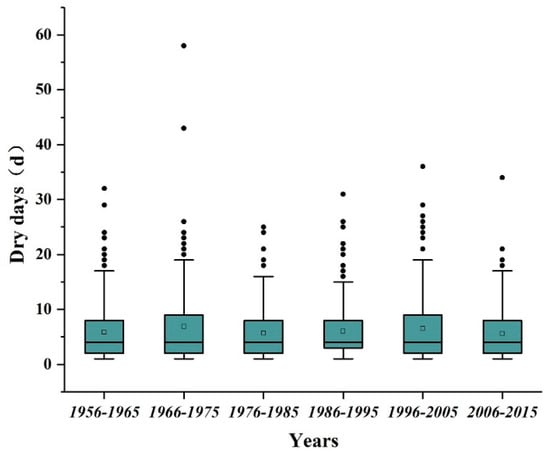
Figure 4.
Box and whisker plots of dry period in the basin during 1956–2015. The horizontal line in the box represents the median of the distribution (50% of the data are greater than this value), and the upper and lower box limits represent the upper and lower quartiles (25% of data greater/lower than the value), respectively. Maximum and minimum values are indicated by the top and bottom horizontal lines. The outlier points show values of more than two-thirds of the quantile.
Furthermore, we calculated the frequency of the duration of each dry period. The results are shown in Figure 5 and Figure 6.
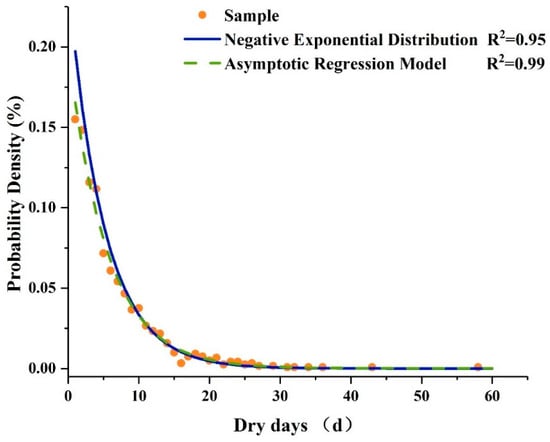
Figure 5.
Probability density function of dry days.
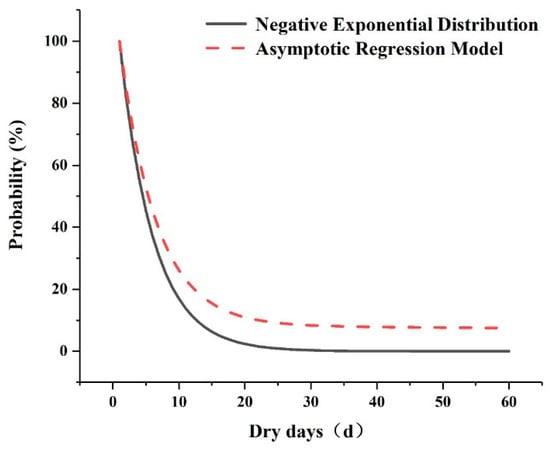
Figure 6.
Probability function of dry days.
According to the fitting results of the two methods, the distribution function of the dry period duration was obtained and the statistical parameters of duration in dry period were extracted, as shown in Table 2.

Table 2.
Statistical parameters from dry periods.
Table 2 shows that in the case of P > 50%, the difference between the two simulation results is within 1 day, but when P < 50%, the difference is more than 1 day; the smaller the probability, the greater the gap in duration of the dry days. Hence, the median P = 50% was taken as the basis for comprehensively choosing the duration of a dry period. The probability of a continuous dry period exceeding 5 days was approximately 50%. In this study, the maximum period of water use for the pre-release of the reservoir was 5 days.
3.2. Flood Forecast Lead Time
According to the 10 floods and corresponding rainfall data of Xianghongdian Reservoir from 2008 to 2016, the natural forecast lead time series of floods can be obtained according to the method described in Section 2.2, and the results are shown in Table 3.

Table 3.
Statistical value of the forecast lead time of historical floods.
Assuming that the natural forecast lead time of a flood follows a normal distribution X-N (, ), we can assume that the mean is 9.90 h and the mean variance is 5.30 h.
3.3. Increased Water Storage
Based on the analysis of the statistical law of the continuous dry period in Section 3.1, 5 days is taken as the upper bound of dry period duration for the water use pre-release period in Xianghongdian Reservoir, and is taken as 1, 2, 3, 4, and 5 days in different scenarios. Considering the information transmission, pre-release decision, order transmission and implementation time, and gate operation time amongst others, we took 10 h as the upper bound of effective lead time and analyzed the scenarios of 1–10 h.
According to the calculation steps introduced in Section 2, the analysis results of dry period duration, and the flood forecast lead time, we constructed different floodwater resource utilization scenarios. The results of 50 scenarios of floodwater utilization were calculated according to Equations (7)–(10), as shown in Table 4 and Figure 7. It was observed that with the increase in the number of dry days and forecast lead time, the excess water volume of the reservoir over the FLWL also increased.

Table 4.
Increased water storage in different scenarios.
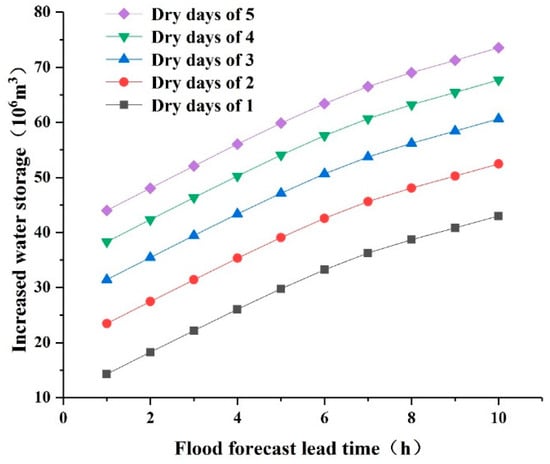
Figure 7.
Statistical chart of floodwater volume over the flood limited water level (FLWL) in different scenarios.
3.4. Worst-Case Scenario Analysis
After the implementation of overstoring water in the reservoir, we simulated the worst-case scenario where a dry period was predicted but the next flood would occur immediately. At that point, the water level of the reservoir was faced with the risk of exceeding the original FLWL. To ensure the safety of flood control in the downstream area, the simulated reservoir was released according to the maximized discharge capacity (less than or equal to the safety discharge of the downstream area ); we then estimated the release time and the amount of safe floodwater volume over the FLWL, as shown in Table 5 and Table 6 and Figure 8.

Table 5.
Release times in different scenarios.

Table 6.
Safe level of increased water storage in different scenarios.
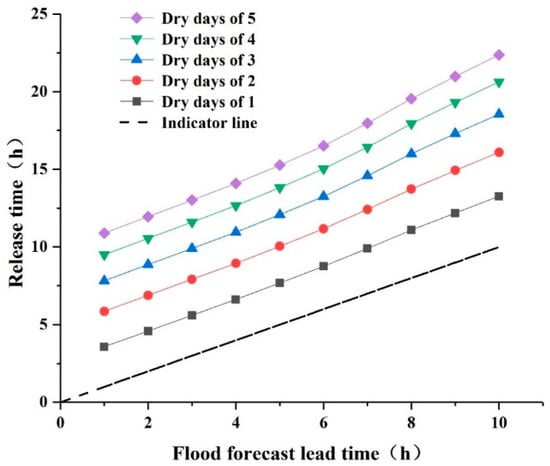
Figure 8.
Relationships between the release time and flood forecast lead time in different scenarios. Note: the top left of the indicator line shows that floodwater stored over the FLWL cannot be released completely within the lead time.
Table 5 and Figure 8 show that in the worst-case scenario, Xianghongdian Reservoir cannot fully release all the floodwater stored over the FLWL within the flood forecasting lead time; specifically, the water level of the reservoir cannot be reduced to the original FLWL in time, which will increase the flood control risk of the reservoir. To ensure the safety of the reservoir and downstream area, the part of floodwater stored over the FLWL that could not be released in time was deducted from the total floodwater volume over the FLWL; then, the safe floodwater volume over the FLWL (i.e., a safe level of increased water storage) was obtained. The results are shown in Table 6.
Table 4 and Table 6, respectively, show the total increased water storage and safe increased water storage level of Xianghongdian Reservoir in different dry duration periods and different flood forecast lead times. For example, in the scenario where the dry period is 5 days, the flood forecast lead time is 6 h, and the discount coefficient is 0.5, the floodwater volume over the FLWL (i.e., increased water storage) is , the corresponding water level is 126 m, representing a 1 m increase compared to the original FLWL. In the worst-case scenario, the safe floodwater volume over the FLWL (i.e., safe increased water storage level) is , and the corresponding water level is 125.4 m.
4. Discussion
4.1. Analysis of Real-Time Increased Water Storage
The benefit of the dynamic control of the flood limited water level in the flood season is obtained by reducing the abandoned water and increasing the storage capacity of the reservoir. As there may be many floods in a year, and the actual rising water level of each flood is different, the real-time increased water storage of DC-FLWL is also different. In order to better evaluate the actual benefits of DC-FLWL, six historical floods were selected in this study, and the real-time increased water storage was calculated; the results are shown in Table 7. Four floods produced over-storage benefits, retaining a certain amount of water, and two floods showed negative over-storage. This is because in the case of some small floods, the reservoir released water for power generation, causing the actual outflow volume to be more than the inflow volume during the entire flood period. It can be seen from the real-time water level of the reservoir that the water level of Xianghongdian Reservoir was low all year round; therefore, it is necessary to retain the flood in the flood season to improve the storage capacity of the reservoir.

Table 7.
Real-time increased water storage of flood events.
4.2. Application of Dry Period Duration Infromation in DC-FLWL
For the rainfall forecasting information, the existing dynamic control methods of FLWL for the reservoir operation mainly considered the rainfall forecast information: the NWP data. This approach [28,35,36] could lengthen the lead time of the flood forecasting, while the traditional flood forecast method takes precipitation from ground as the input. However, the method proposed in this study focused on the historical continuous dry period duration and forecasting information. Actually, it also lengthens the pre-release time to a certain extent in a different way. Different pre-release methods are adopted by our proposed approach for when the basin is forecasted to have rain or will be dry. The total planned floodwater volume over the FLWL consists of two parts: the water use floodwater volume over the FLWL and the flood control floodwater volume over the FLWL. The water was converted for conservation uses by the water use pre-release process. In the real-time reservoir operation, if the real-time dry days in the basin are longer than the predicted continuous dry days, the reservoir can release part of the flood control floodwater volume over the FLWL through the water use pre-release process to provide continuous water conservation.
Differing from other research, this study introduced the dry period duration into the capacity-constrained pre-release method. Our study provided a new approach on how to calculate the dry period duration and apply the information on dry days to the utilization of reservoir floodwater resources. An asymptotic regression model was used to verify the negative exponential distribution of dry period durations proposed by some scholars. According to the historical measured rainfall data, we obtained the statistical parameters of the dry period duration (Table 2). Compared with the two methods, the simulation results of negative exponential distribution were more conservative than the simulation results of the asymptotic regression model. The fitness of the two methods was similar in the high-frequency band, but the difference was large in the low-frequency band. The probability of the continuous dry period duration of Xianghongdian Reservoir exceeding 5 days was approximately 50%. In addition, Figure 7 shows that when the lengths of the dry periods increased, the floodwater volumes over the FLWL of the reservoir also increased; however, the floodwater volume differences between adjacent durations became smaller, which was related to the flood tail and inflow process of the reservoir before the arrival of the next forecasted flood.
4.3. Floodwater Utilization in the Worst-Case Scenario
Table 5 and Figure 8 show that the reservoir failed to reduce the water level to the original FLWL within the flood forecast lead time in all 50 scenarios. The reason for this failure was that with an extreme failure in rainfall forecasting, the reservoir should pre-release both the flood control floodwater volume over the FLWL within the forecast lead time as well as the water use floodwater volume over the FLWL that was supposed to be released during dry days. In addition, Xianghongdian Reservoir has a relatively small discharge capacity. Although this water is released according to the maximum discharge capacity on the premise of ensuring the safety of the downstream area, the release time still exceeds the flood forecast lead time. This increases the flood control risk of the reservoir; however, it does not mean that the reservoir cannot carry out the DC-FLWL. This study simulates the reservoir fully meeting the original design flood control risk by deducting the amount of water that cannot be released in time based on the total floodwater volume over the FLWL. This approach ensures the safety of flood control in the reservoir and has not been reported in other studies. Table 6 shows the safe increased water storage; it can be noted that the volume difference is very small between the scenarios that have same flood forecast lead time but different dry days. This is because when the number of dry days is zero, the amount of increased water volume is mainly dependent on the flood forecast lead time and the upper bound of FLWL difference results in the reservoir discharge capacity difference. Thus, the volume difference is small; however, it still exists. Actually, the principle of this part corresponds to the original capacity-constrained pre-release method.
Ultimately, the DC-FLWL of reservoirs is actually a problem of balancing flood control and water conservation, and its goal is to pursue risk minimization and benefit maximization. In real-time operation, we used meteorological forecast information, but we analyzed the historical rainfall data to choose the dry period duration in this study. The longer the time of pre-release, the higher the risk of flood control. While determining the upper bound of FLWL, we laid the foundation for the next step of risk and benefit analysis.
5. Conclusions
Making full use of floodwater resources in the flood season can improve their utilization rate; however, it is associated with some additional risks. Based on this background, this study attempts to determine an optimal solution by studying the dynamic control scheme of FLWL of the Xianghongdian Reservoir. Our overall results can be summarized as follows:
- (1)
- The two-period capacity-constrained pre-release method proposed in this study divided the pre-release process into the water use pre-release period and flood control pre-release period. The method has a clear concept, simple principle, and simple calculation procedure. The research example showed that the method is feasible.
- (2)
- According to the historical rainfall data of the Xianghongdian Reservoir basin, the statistical parameters for the dry period duration have obvious negative index distribution characteristics. Compared with the asymptotic regression model, it is safer to use the negative exponential model to describe the distribution law of the dry period duration.
- (3)
- According to the dry period duration and flood forecast lead time, different floodwater resource utilization scenarios were simulated to establish the relationship between the floodwater volume over the FLWL (i.e., increased water storage), dry period duration, and flood forecast lead time, which can provide support for real-world operation decisions of the reservoir. When Xianghongdian Reservoir had a simulated dry period of 5 days and a flood forecast lead time of 6 h, the reservoir’s floodwater volume over the FLWL was , and the corresponding water level was 126 m, which was 1.0 m higher than the original FLWL.
- (4)
- Through the analysis of reservoir operations under the worst-case scenario, the flood control burden of the reservoir was quantified, which was helpful in proposing solutions and ensuring the flood control safety of the basin. When the dry period duration of Xianghongdian Reservoir was 5 days and the flood forecast lead time was 6 h, considering the worst-case scenario, the water capacity that could not be released in time was deducted from the original total floodwater volume over the FLWL; a of safe floodwater volume over the FLWL was still available.
This presented study only focused on a single reservoir. However, this method proposed herein can and should be applied to the DC-FLWL of multiple reservoirs in the future. In addition, it is necessary to further build the risk evaluation index system in reservoir operation decision-making and put forward more effective compensation measures considering forecast uncertainty.
Author Contributions
Conceptualization, L.H. and X.W. (Xinyu Wan); formal analysis, X.W. (Xianhui Wang) and F.Z.; funding acquisition, L.H. and X.W. (Xinyu Wan); investigation, X.W. (Xianhui Wang) and Q.Y.; Methodology, X.W. (Xinyu Wan), X.W (Xianhui Wang) and P.Z.; software, F.Z. and M.L.; supervision, X.W. (Xinyu Wan); validation, P.Z.; writing—original draft, L.H.; writing—review & editing, X.W. (Xinyu Wan), M.L. and Q.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (No. 2016YFC0400909), the Postgraduate Research and Practice Innovation Program of Jiangsu Province (No. SJKY19_0478) and the Fundamental Research Funds for the Central Universities (No. 2019B72314).
Acknowledgments
The authors would like to thank the anonymous reviewers and editors for their constructive comments that greatly improved the final version of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McFarlane, D.; Stone, R.; Martens, S.; Thomas, J.; Silberstein, R.; Ali, R.; Hodgson, G. Climate change impacts on water yields and demands in south-western Australia. J. Hydrol. 2012, 475, 488–498. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Ralph, F.M.; Das, T.; Neiman, P.J.; Cayan, D.R. Atmospheric rivers, floods and the water resources of California. Water 2011, 3, 445–478. [Google Scholar] [CrossRef]
- Zhai, M.; Lin, Q.; Huang, G.; Zhu, L.; An, K.; Li, G.; Huang, Y. Adaptation of cascade hydropower station scheduling on a headwater stream of the Yangtze River under changing climate conditions. Water 2017, 9, 293. [Google Scholar] [CrossRef]
- Windsor, J.S. Optimization model for the operation of flood control systems. Water Resour. Res. 1973, 9, 1219–1226. [Google Scholar] [CrossRef]
- Yun, R.; Singh, V.P. Multiple duration limited water level and dynamic limited water level for flood control, with implications on water supply. J. Hydrol. 2008, 354, 160–170. [Google Scholar] [CrossRef]
- Diao, Y.; Wang, B. Scheme optimum selection for dynamic control of reservoir limited water level. Sci. China Technol. Sci. 2011, 54, 2605–2610. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.; Liu, P.; Chen, A.B. Methodology that improves water utilization and hydropower generation without increasing flood risk in mega cascade reservoirs. Energy 2018, 143, 785–796. [Google Scholar] [CrossRef]
- Chang, J.; Guo, A.; Du, H.; Wang, Y. Floodwater utilization for cascade reservoirs based on dynamic control of seasonal flood control limit levels. Environ. Eeath Sci. 2017, 76, 1–12. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, H. Theory, Method and Application of Reservoir Dynamic of the Limited Water Level; Press of Hydraul. And Hydropower of China: Beijing, China, 2006; pp. 1–17. (In Chinese) [Google Scholar]
- Wang, G.; Liang, G.; Wang, B.; Bin, H.E. Dynamic operation of reservoir normal elevation based on rainfall forecast and constrained pre-discharge capacity and its application. J. Hydroelec. Eng. 2010, 4, 28–31. (In Chinese) [Google Scholar]
- Chou, F.N.F.; Wu, C. Expected shortage based pre-release strategy for reservoir flood control. J. Hydrol. 2013, 497, 1–14. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhong, P.; Liu, G.; Wan, X.; Wang, Y. Research on dynamic control domain of flood control level of Hekoucun Reservoir based on forecasting operation. Water Resour. Power 2019, 37, 56–59. (In Chinese) [Google Scholar]
- Zhou, Y.; Guo, S.; Liu, P.; Xu, C. Joint operation and dynamic control of flood limiting water levels for mixed cascade reservoir systems. J. Hydrol. 2014, 519, 248–257. [Google Scholar] [CrossRef]
- Chen, J.; Guo, S.; Li, Y.; Liu, P.; Zhou, Y. Joint operation and dynamic control of flood limiting water levels for cascade reservoirs. Water Resour. Manag. 2013, 27, 749–763. [Google Scholar] [CrossRef]
- Withanachchi, S.; Ghambashidze, G.; Kunchulia, I.; Urushadze, T.; Ploeger, A. A paradigm shift in water quality governance in a transitional context: A critical study about the empowerment of local governance in Georgia. Water 2018, 10, 98. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Mascaro, G.; Vivoni, E.R.; Deidda, R. Implications of ensemble quantitative precipitation forecast errors on distributed streamflow forecasting. J. Hydrometeorol. 2010, 11, 69–86. [Google Scholar] [CrossRef]
- Jain, S.K.; Yoganarasimhan, G.N.; Seth, S.M. A risk-based approach for flood control operation of a multipurpose reservoir. J. Am Water Resour. 1992, 28, 1037–1043. [Google Scholar] [CrossRef]
- Krzysztofowicz, R.; Duckstein, L. Preference criterion for flood control under uncertainty. Water Resour. Res. 1979, 15, 513–520. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.; Huang, Q.; Wang, J.; Yu, Z.; Zhang, J. Optimal hedging rules for water supply reservoir operations under forecast uncertainty and conditional value-at-risk criterion. Water 2017, 9, 568. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.; Peng, Y.; Zhou, H. Risk analysis of dynamic control of reservoir limited water level by considering flood forecast error. Sci. China Technol. Sci. 2011, 54, 1888–1893. [Google Scholar] [CrossRef]
- Li, X.; Guo, S.; Liu, P.; Chen, G. Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. J. Hydrol. 2010, 391, 124–132. [Google Scholar] [CrossRef]
- Hui, R.; Lund, J.; Zhao, J.; Zhao, T. Optimal pre-storm flood hedging releases for a single reservoir. Water Resour. Mang. 2016, 30, 5113–5129. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Cai, X.; Li, Y.; Zhou, H. Multiobjective hedging rules for flood water conservation. Water Resour. Res. 2017, 53, 1963–1981. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Peng, Y.; Zeng, R.; Zhou, H.; Cai, X. An analytical framework for flood water conservation considering forecast uncertainty and acceptable risk. Water Resour. Res. 2015, 51, 4702–4726. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Ren, M.; He, X.; Huang, J.; Li, H. Real-time dynamic control of reservoir waterlevel in flood season and its risk analysis based on short-term rainfall forecast information. J. Hydraul Eng. 2013, 43, 66–72. (In Chinese) [Google Scholar] [CrossRef]
- Zhong, Y.; Guo, S.; Ba, H.; Xiong, F.; Chang, F.; Lin, K. Evaluation of the BMA probabilistic inflow forecasts using TIGGE numeric precipitation predictions based on artificial neural network. Hydrol. Res. 2018, 49, 1417–1433. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J.; Li, Z. Assessment and modelling of uncertainty in precipitation forecasts from TIGGE using fuzzy probability and Bayesian theory. J. Hydrol. 2019, 577, 123995. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J.; Li, Z. Improving TIGGE Precipitation Forecasts Using an SVR ensemble approach in the Huaihe River Basin. Adv. Meteorol. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Lin, H.; Zhong, P.; Liu, G.; Wan, X.; Wang, Y.; Lu, L. A method of determining the timing of water storage during dynamic control of flood limited water level in the reservoir. China Rural Water Hydropower 2019, 9, 157–161. (In Chinese) [Google Scholar]
- Ding, W.; Zhou, H. Dynamic control of flood limited water level for reservoirs: Developments and trends. China Flood Drought Manag. 2018, 28, 6–10. (In Chinese) [Google Scholar] [CrossRef]
- Qu, Y.; Sun, G.; Li, Z. The maximum entropy principle and its applications. J. Qingdao Inst. Architect. Eng. 1996, 17, 94–100. (In Chinese) [Google Scholar]
- Wan, X.; Yang, Q.; Jiang, P.; Zhong, P.A. A hybrid model for real-time probabilistic flood forecasting using Elman Neural Network with heterogeneity of error distributions. Water Resour. Manag. 2019, 33, 4027–4050. [Google Scholar] [CrossRef]
- Bao, H.J.; Zhao, L.N.; He, Y.; Li, Z.J.; Manful, D. Coupling ensemble weather predictions based on TIGGE database with Grid-Xinanjiang model for flood forecast. Adv. Geosci. 2011, 29, 61–67. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).