1. Introduction
Fittings, including bends, elbows, T-junctions, diffusers, confusors, and cutting valves, are essential elements of any hydraulic system. The liquid flow through fittings connecting pipelines is more complicated than that through straight sections [
1]. The pressure losses associated with the fittings are caused by disturbances in liquid flow which occur during changes in its direction or sudden or gradual changes in the cross-section or shape of the pipeline. The prediction of the pressure losses in fittings is much more uncertain than in the case of straight pipes [
2], and the flow mechanisms of liquid inside such fittings is not clearly defined.
Pipeline fittings are the most important part of the system and installation of a water supply, heat distribution, or industrial network, as they allow flexibility in the route of the pipeline. Investigations of water flow through fittings have tremendous significance in understanding and improving their flow capacity and minimizing hydraulic losses. It is well known that viscous incompressible liquids [
3] and compressible gases [
4] moving through fittings are characterized by flow splitting [
5,
6,
7], occurrence of secondary flows [
1,
8,
9,
10], and Dean vortexes, and, in general, by high instability [
8,
9,
11,
12].
T-junction fittings have particularly wide application not only in the systems and installations of water supply and heat distribution networks, but also in industrial installations, where they can be used for mixing two or more fluids. In convergent or divergent T-junctions, turbulent flows occur and effectively mix various fluids flowing through the T-junction [
13]. T-junction systems are applied in industry to mix air and fuel in gas turbines or combustion engines [
11,
14], to mix hot and cold water in the pipelines in nuclear power plants [
8], or to mix various chemical compounds for which the mixing quality is an important factor affecting the chemical reaction rate. Multiphase (air–water) flow structures through a T-junction have also been investigated [
15,
16], and the blood flow through T-junctions with variously sloped arms has been modeled [
9,
17,
18,
19].
The fittings applied in the systems and installations of water supply and heat distribution networks should be tight at joints, not corrode, be resistant against mechanical and chemical action of liquids, and present the lowest possible hydraulic resistance (hydraulic losses). Nowadays, fittings made of various materials are accessible (steel, cast iron, copper, brass, poly(vinyl chloride)—PVC, polybutylene—PB, polyethylene—PE, polypropylene—PP), and they are joined with pipelines with use of various technologies. There are few items in the scientific and technical literature concerning problems connected to the determination of values of the local resistance coefficient ζ for the fittings during Newtonian liquid flow [
2,
20,
21,
22,
23,
24,
25,
26].
At present, researchers deal mainly with the mathematical modeling of flow structures in various liquids in elbows with various ratios of curvature radius to diameter (R/D), as well as in T-junctions, diffusers, and confusors [
4,
22,
24]. To make models of flow structures in Newtonian and non-Newtonian liquids, CFD (computational fluid dynamics) software is used, i.e., the so-called computational mechanics of fluids [
1,
12,
15,
16,
22,
27,
28]. The mathematical modeling of such flow structures is very hard because the multiphase flows depend on numerous factors and variables [
2,
5,
6,
29,
30].
Csizmadia and Hős [
22] presented results of investigations of local resistance coefficients in diffusers with angles 7.5°–40°, and in elbows with a curvature radius to diameter ratio R/D = 1–10. The investigations were performed with the use of water and two non-Newtonian liquids. The values of local resistance coefficients, determined experimentally in the diffusers and elbows, were compared to the results of calculations done with CFD software. It was stated that the values of local resistance coefficients calculated in the CFD were lower than those obtained in the experiment. On this basis, the researchers suggested that the lower values of local resistance coefficients calculated in the software probably resulted from the assumption that the internal surfaces of the walls of the diffusers and elbows were hydraulically smooth, which was, in fact, not the case.
Liu and Duan [
31] presented results of investigations of local resistance coefficients and hydraulic losses in elbows bent with a 90° angle as well as in conical diffusers and edge reducers. The scope of the investigations encompassed elbows with the diameters D = 25 mm, 40 mm, and 50 mm and the curvature radius to diameter ratios R/D = 1.5, 2.0, 4.0, and 6.0; conical diffusers with the inlet diameter D
1 = 50 mm and outlet diameter D
2 = 25 mm and cone convergence angles θ = 3°, 5°, 10°, 20°, and 90°; and two edge reducers with the inlet and outlet diameters D
1/D
2 = 50 mm/25 mm and D
1/D
2 = 68 mm/25 mm. The investigations were performed with use of a non-Newton liquid which was a coal–water mix with a mass concentration 57%–62%. The authors proved that during the flow of the coal–water mix with a given mass concentration through the tested fittings, the parameters of these fittings, i.e., R/D, θ, and β, had an insignificant impact on the values of the local resistance coefficient. As the Reynolds number increased to 1000 and the mass concentration of the coal–water mix increased, the values of the local resistance coefficient of the tested fittings decreased, whereas for higher values of the Reynolds number (Re > 1000), they presented various behaviors (trends) due to particular rheological properties of the coal–water mix, wherein shear stresses increased in line with the rise in the Reynolds number.
Costa et al. [
32] compared results of investigations of the local resistance coefficient in T-junctions with a 90° angle during water flow. The authors conducted tests for two types of T-junction. The first type had a joint with sharp edges, and the second one with rounded edges. The researchers proved that the T-junction joint with rounded edges, when compared to the T-junction joint with sharp edges, reduced the value of the local resistance coefficient by 10%–20% and increased the turbulence in the water flow.
Li et al. [
24] presented the results of investigations into the reduction of hydraulic resistance in joined elbows and T-junctions by application of wedge elements at the internal surface of the wall beyond the bend and T-junction outlet, with the aim to change the flow structure in the liquid stream and suppress the Dean vortexes that occur there, and to increase the hydraulic resistance. The authors investigated the effect of reduction of the hydraulic resistance in the joined elbows and T-junctions with use of experimental and numerical methods, by determining values of the local resistance coefficient ζ of the joined fittings. The results showed that wedge elements applied with an appropriate height indeed reduced the hydraulic resistance. The researchers proved that the height of the wedge element used to reduce the hydraulic resistance in joined elbows and T-junctions should not exceed 1/4 of the internal diameter of the pipeline.
In aiming to calculate installations of water supply and heat distribution networks, it is necessary to know a numerical value of the local resistance coefficient ζ, which can be determined with reference to the available literature [
2,
21,
22,
23,
24,
25,
26,
31,
33,
34,
35,
36]. Depending on which literature sources are used during selection of the local resistance coefficient value of fittings in calculations of hydraulic losses in installations of water supply and heat distribution networks, various results can be obtained. The increase of hydraulic resistance in a given fitting is affected by the internal surface roughness of its wall, bending angle, diameter, and type of joining with the pipeline. Accordingly, the installations of water supply and heat distribution networks where high hydraulic losses occur are characterized by higher investment and exploitation costs, as they require pumps with higher delivery head which, in turn, must be equipped with more powerful engines.
Currently, there is no information in the scientific and technical literature explaining how to calculate the values of the local resistance coefficient ζ in welded polypropylene T-junctions for design purposes. The present paper includes a comparative analysis of the results of investigations into the values of the local resistance coefficient ζ in welded polypropylene T-junctions, which were obtained experimentally on the test rig and calculated according to the directives [
26]. It also proposes equations and a nomogram for calculation of this coefficient for design purposes. The objects of the investigations were the welded polypropylene T-junctions with an internal diameter of 13.2 mm, which were (1) properly warmed up and properly pressed, (2) poorly warmed up and poorly pressed, or (3) excessively warmed up and excessively pressed.
3. Results and Discussion
Analysis of the individual T-junctions (
Figure 3) showed that their warming up and pressing to the pipe affected the local hydraulic resistance occurring during water flow. In case of the properly warmed up and properly pressed T-junction (
Figure 3a), as a result of pressing the T-junction to the pipe, two adjoining small fashes developed inside of it at both ends. In case of the poorly warmed up and poorly pressed T-junction (
Figure 3b), two small fashes developed as well; however, they did not adjoin but were far apart. In case of the excessively warmed up and excessively pressed T-junction (
Figure 3c), big fashes developed, which created a distinct orifice in the cross-section of the T-junction at both ends.
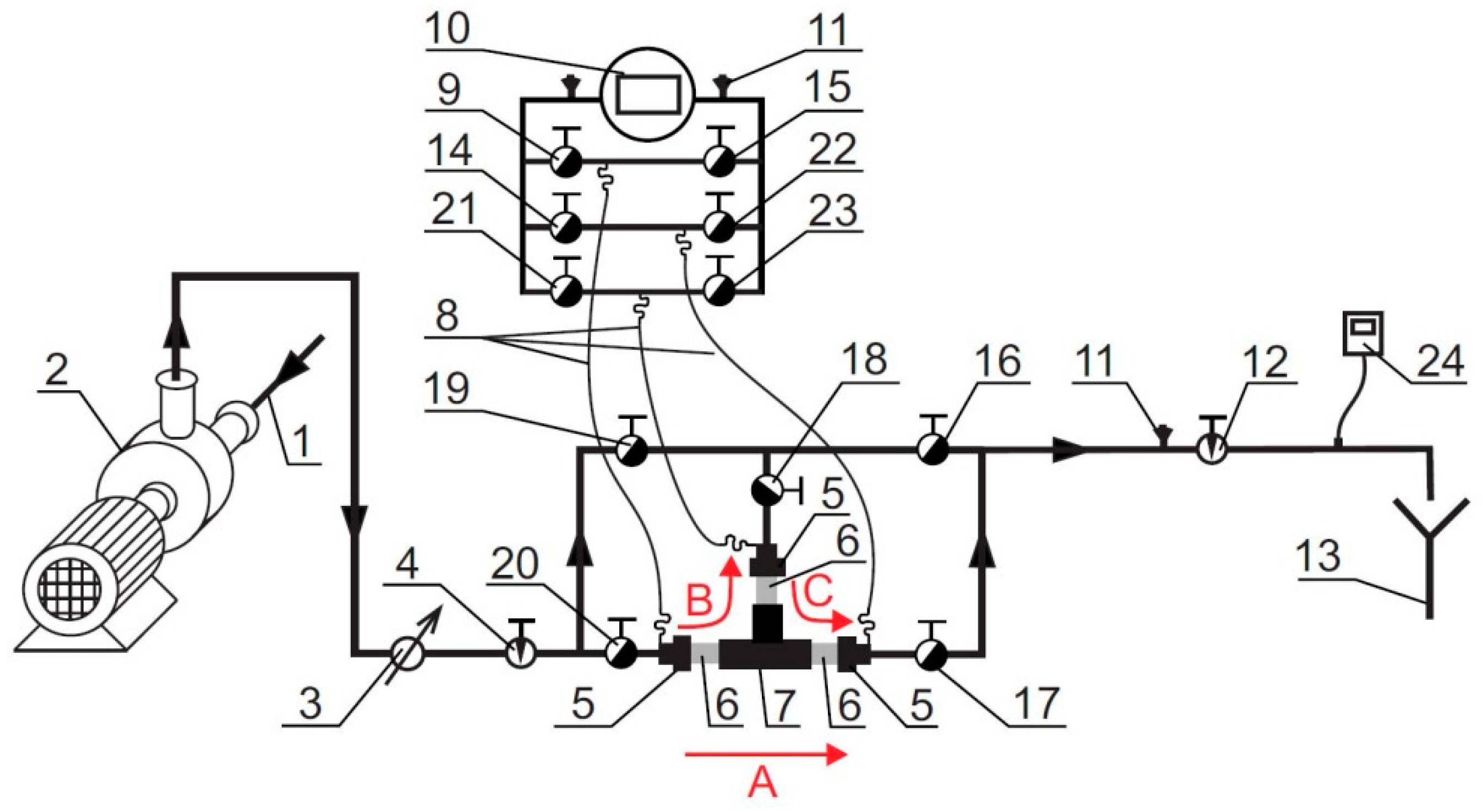
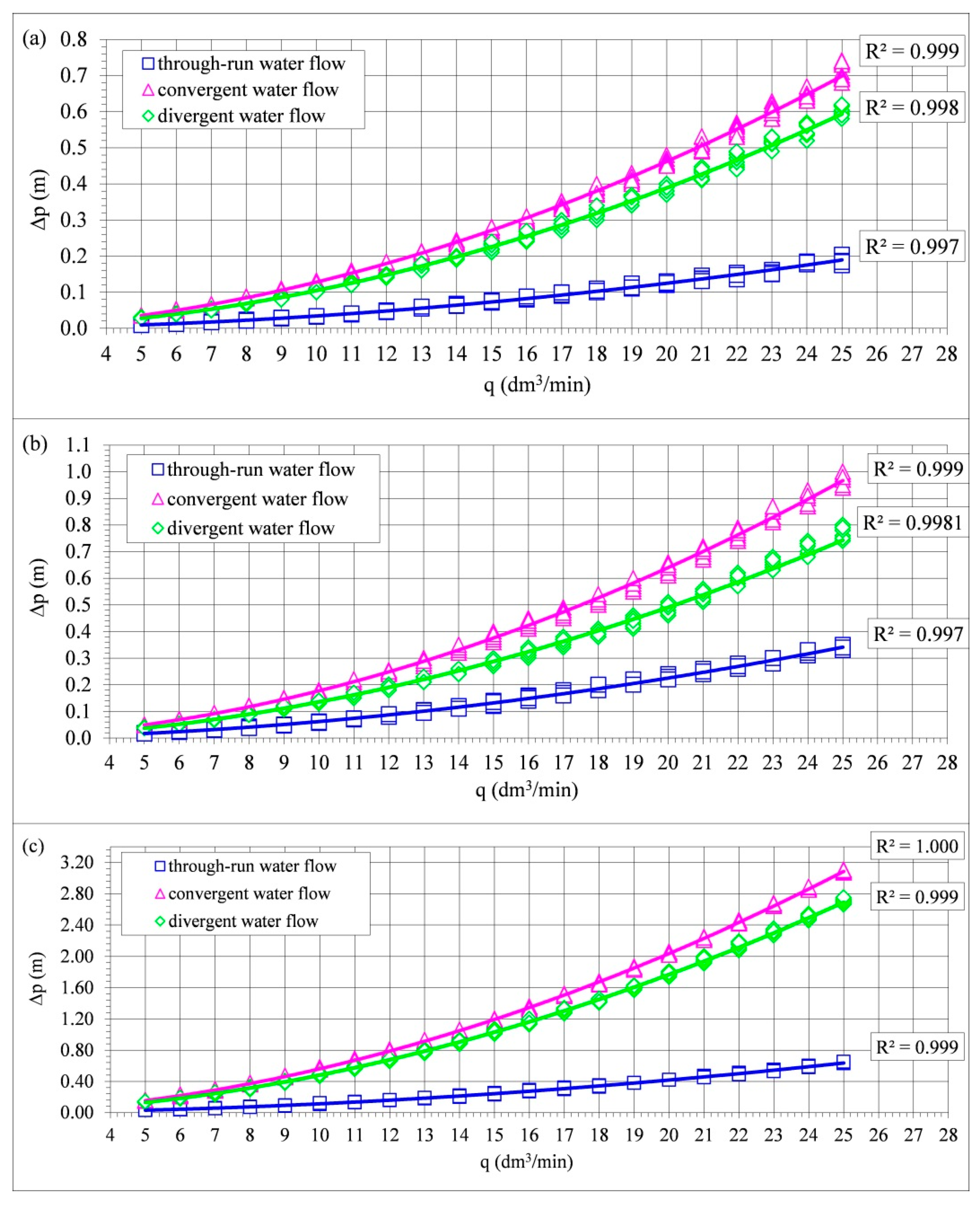
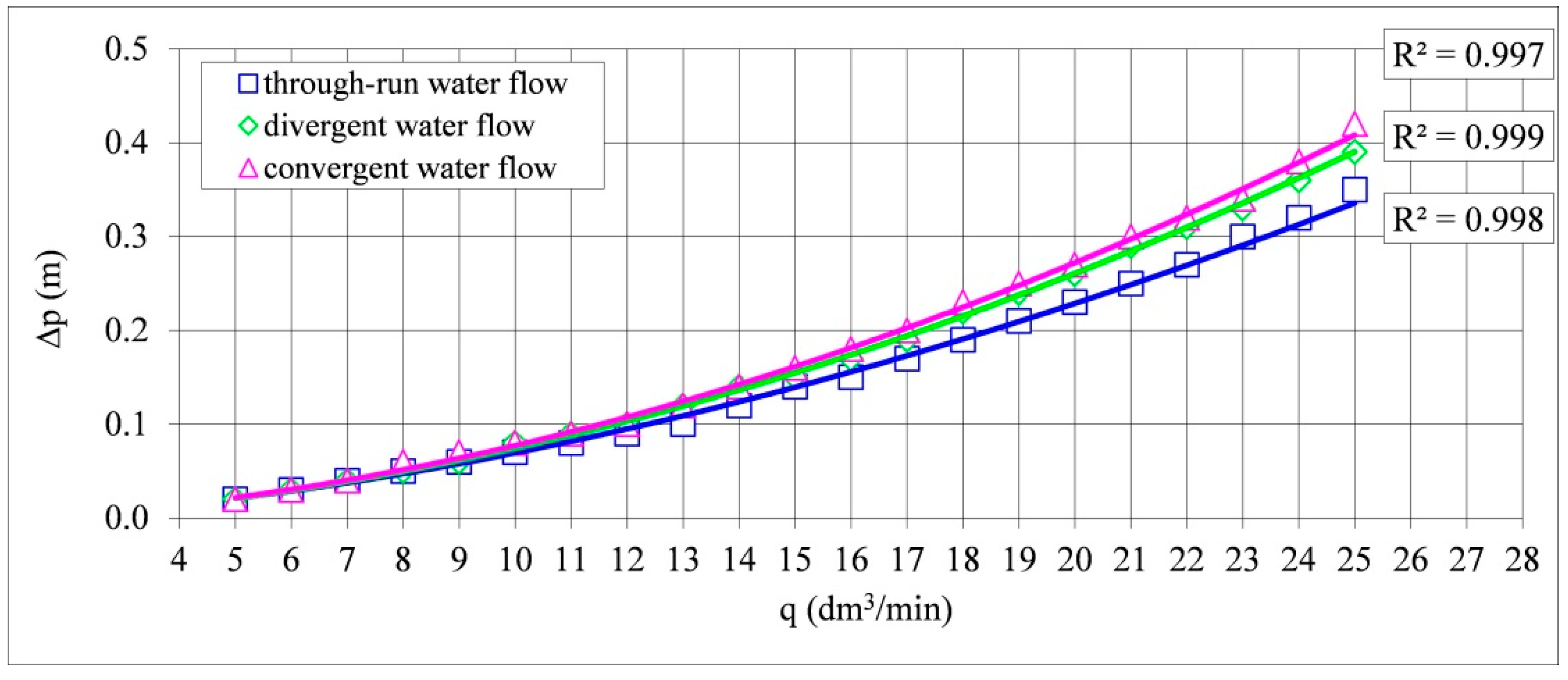
Figure 4 presents the results of measurements of the real pressure difference Δp, i.e., the hydraulic resistance of the T-junction after subtraction of the hydraulic resistances occurring in the screwed joints and the pipe section mounted between them, constituting the sum of the pipe sections used for the investigation of a given T-junction (
Figure 5). During the measurements, the hydraulic resistance in the T-junctions increased along with the increase of the value of the water flow rate (
Figure 4), which was a trend corresponding to the literature data [
21,
23,
34,
35,
36]. The lowest hydraulic resistance during the water flow occurred in case of the properly warmed up and properly pressed T-junctions (
Figure 3a), and the highest occurred in the case of the excessively warmed up and excessively pressed ones (
Figure 3c). The trend (regression) of the measured values of Δp was of an exponential type and the values of the determination coefficient R
2 from sample were over 0.98, indicating that the hydraulic resistance of the welded T-junctions depended at least 98% on the water flow rate and manufacturing precision of the T-junction joint, and only 2% on other factors like water temperature or gravitational acceleration.
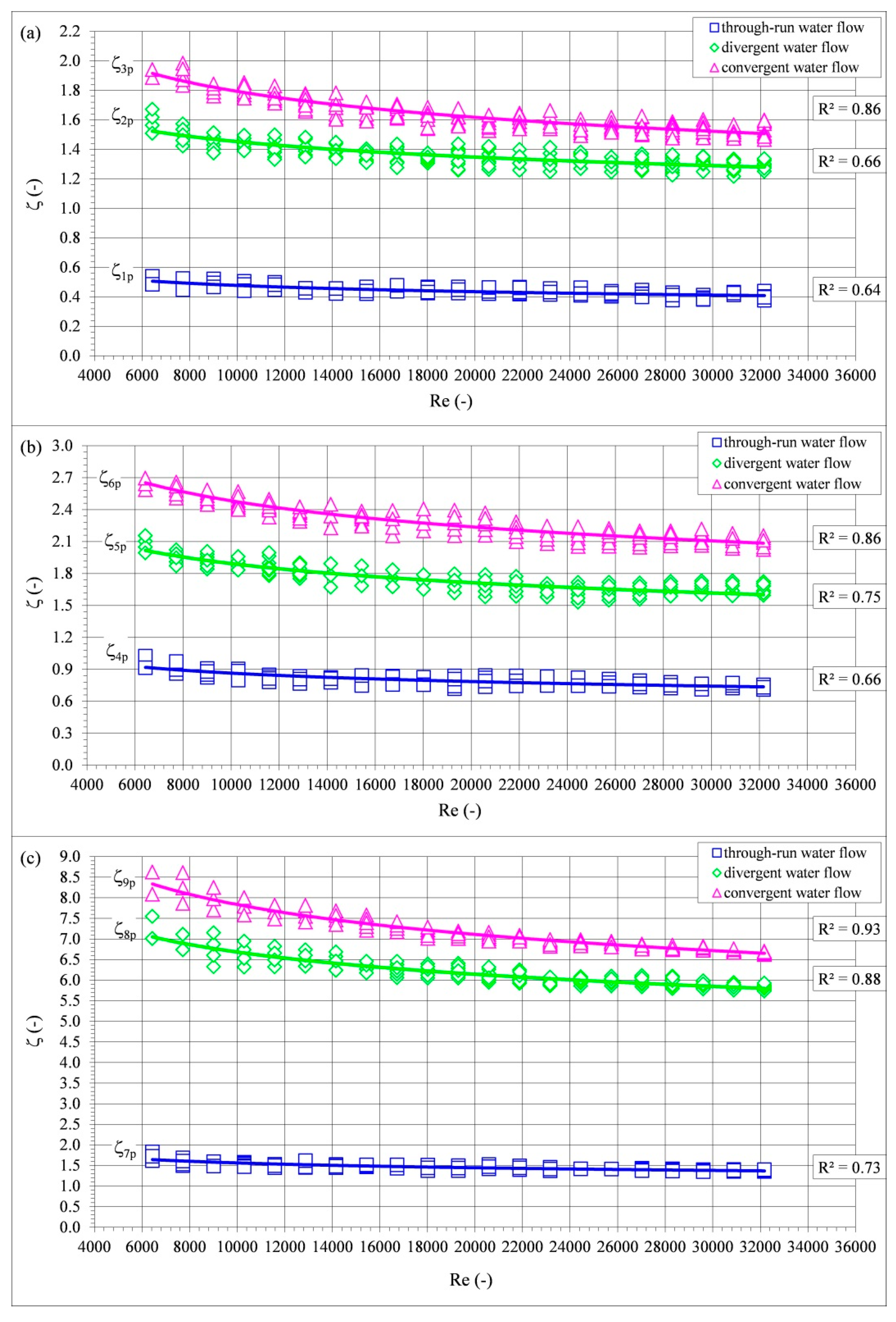
Using Equations (1) and (2) for assumed values of the water flow rate q and measured values of the real pressure difference Δp in the individual T-junctions (
Figure 4), local resistance coefficients ζ
1p, ζ
2p, ζ
3p, ζ
4p, ζ
5p, ζ
6p, ζ
7p, ζ
8p, and ζ
9p were determined and are presented in
Figure 6 as a function of the Reynolds number. The Reynolds number depends on the water flow velocity, internal diameter of a T-junction, and the water kinematic viscosity coefficient; hence, it described the hydraulic flow conditions of water in the tested T-junctions very well. Both the local resistance coefficient and the Reynolds number are dimensionless quantities; thus, researchers who determine local resistance coefficients ζ in fittings analyze them as a function of the Reynolds number [
2,
4,
11,
12,
21,
22,
23,
24,
25,
26,
31,
32,
33,
34,
35,
36]. The values of the local resistance coefficients decreased along with the increase of the Reynolds number (
Figure 6), which was the trend expected according to the literature data [
17,
32]. The lowest values of the local resistance coefficients occurred for the properly warmed up and properly pressed T-junctions, and the highest for the excessively warmed up and excessively pressed ones. The trend (regression) of the measured values of ζ was of an exponential type, and the values of the determination coefficient R
2 from sample were over 0.64, indicating that the local resistance coefficient depended at least 64% on the Reynolds number Re, i.e., on the water flow velocity V, the T-junction diameter d, the water kinematic viscosity coefficient ν, and manufacturing precision of the T-junction joint, and depended 36% on the pressure difference Δp occurring in the T-junction during the water flow.
Table 1 presents basic statistics of the value of the local resistance coefficient determined from the measurements. The mean value of the local resistance coefficient from the measurements made for the properly warmed up and properly pressed T-junctions with through-run water flow was equal to ζ
1p = 0.44, the divergent water flow ζ
2p = 1.37, and the convergent water flow ζ
3p = 1.65. The mean value of the local resistance coefficient from the measurements made for the too poorly warmed up and too poorly pressed T-junctions with the through-run water flow was equal to ζ
4p = 0.80, the divergent water flow ζ
5p = 1.75, and the convergent water flow ζ
6p = 2.29. The mean value of the local resistance coefficient from the measurements made for the excessively warmed up and excessively pressed T-junctions with the through-run water flow was equal to ζ
7p = 1.47, the divergent water flow ζ
8p = 6.26, and the convergent water flow ζ
9p = 7.26.
Table 2 presents the values determined from the nomograms proposed by Rennels and Hudson [
26] used to calculate values of the local resistance coefficient in T-junctions for engineering purposes, i.e., for designing systems and installations of water supply.
Comparison of the mean values of the local resistance coefficient determined from the measurements (
Table 1) with the values read from the nomograms recommended for design of systems and installations of water supply (
Table 2) allowed us to state that the real values of the local resistance coefficients in the polypropylene T-junctions were significantly higher than those read from the nomograms [
26].
The functional dependence between the values of the local resistance coefficient determined from the measurements and the Reynolds number Re for the tested T-junctions was best described by an exponential mathematical model in form of the following equations.
where ζ
1w: local resistance coefficient for the properly warmed up and properly pressed T-junctions with the through-run water flow; ζ
2w: local resistance coefficient for the properly warmed up and properly pressed T-junctions with the divergent water flow; ζ
3w: local resistance coefficient for the properly warmed up and properly pressed T-junctions with the convergent water flow; ζ
4w: local resistance coefficient for the poorly warmed up and poorly pressed T-junctions with the through-run water flow; ζ
5w: local resistance coefficient for the poorly warmed up and poorly pressed T-junctions with the divergent water flow; ζ
6w: local resistance coefficient for the poorly warmed up and poorly pressed T-junctions with the convergent water flow; ζ
7w: local resistance coefficient for the excessively warmed up and excessively pressed T-junctions with the through-run water flow; ζ
8w: local resistance coefficient for the excessively warmed up and excessively pressed T-junctions with the divergent water flow; ζ
9w: local resistance coefficient for the excessively warmed up and excessively pressed T-junctions with the convergent water flow; Re: Reynolds number.
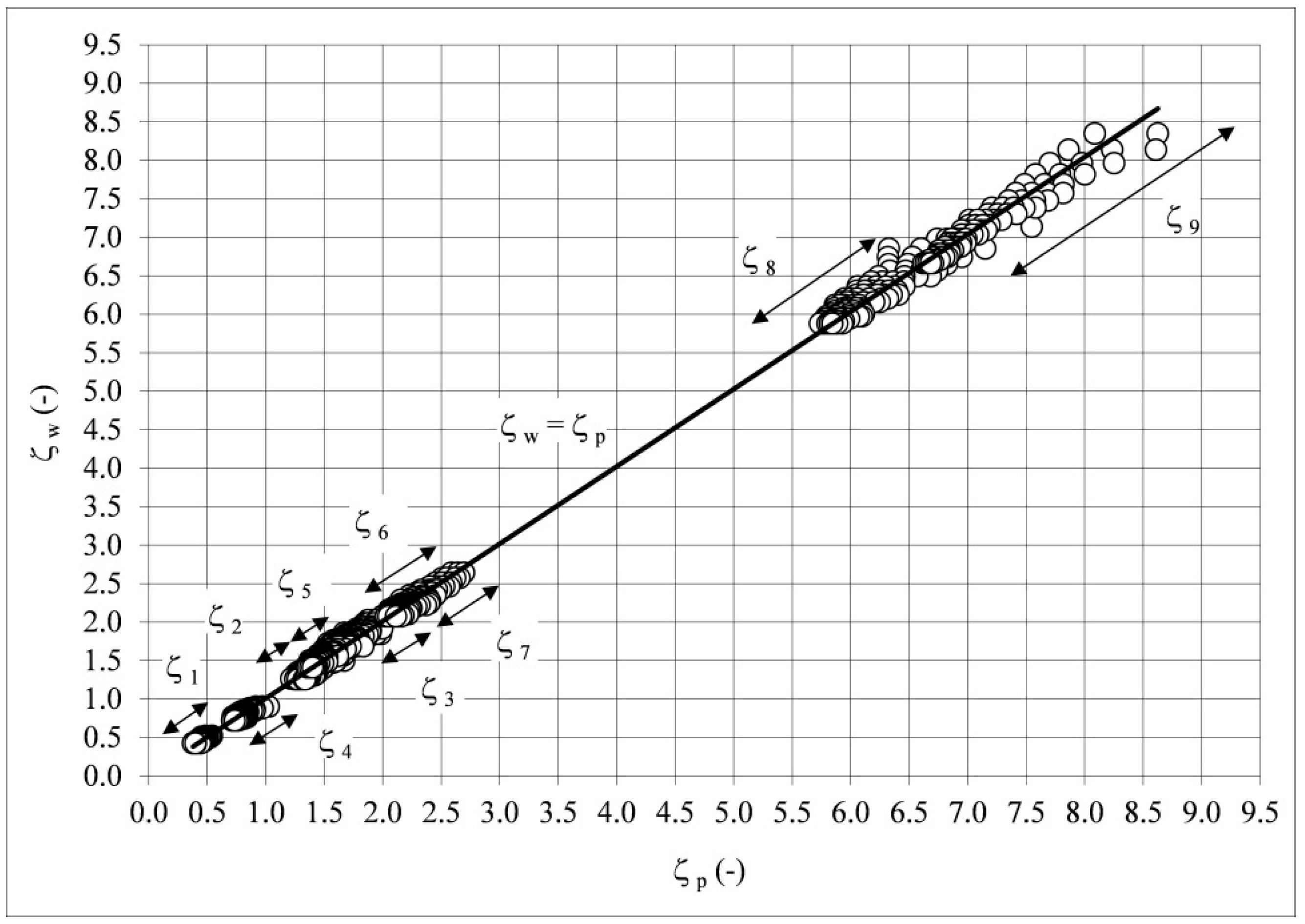
An evaluation of the adjustment of the exponential mathematical model for calculations of the local resistance coefficient ζ in polypropylene T-junctions was performed with use of a graph (
Figure 7), where the ordinates were the results of calculations from Equations (3)–(11), i.e., predicted values ζ
w, whereas the abscissae were the values obtained from the measurements ζ
p (
Figure 6). The obtained points were approximated by a linear function crossing the origin of coordinates; thus, the correctness of choice of the mathematical model was verified by the slope coefficient of the linear function. The analysis of the dependence presented in
Figure 7 allowed us to state that the exponential mathematical model described reality well, as the slope coefficient of the linear function was equal to 1.
In calculations of standpipes and pipe sections connecting the standpipe and tapping points, the minimum and maximum velocities of water flow were applied [
38]. If the Reynolds number is written in the form [
26]
then Equations (3)–(11) assume the following forms
where V is the water flow velocity in m⋅s
−1, ν is the kinematic viscosity coefficient of water in m
2⋅s
−1, and d is the internal diameter of the T-junction in m.
A statistical analysis was performed to check whether differences between the mean values of the local resistance coefficients obtained in measurements ζ
1p, ζ
2p, ζ
3p, ζ
4p, ζ
5p, ζ
6p, ζ
7p, ζ
8p, ζ
9p (
Figure 6) and calculated from Equations (13)–(21), ζ
1cal, ζ
2cal, ζ
3cal, ζ
4cal, ζ
5cal, ζ
6cal, ζ
7cal, ζ
8cal, and ζ
9cal, were indeed significant. First, the normality of distribution was checked using the Shapiro–Wilk test, and then the homogeneity of variance was tested using the Levene test. Calculations of normality of distribution and homogeneity of variance were done with STATISTICA software and the obtained results are presented in
Table 3. In both tests for individual groups, the values of calculated probability p
cal were greater than the assumed significance level α = 0.05 (
Table 3), meaning that the conditions of normal distribution and homogeneity of variance in the examined groups were satisfied. Student’s
t-test was then used for two populations; a zero hypothesis (H
0: n
1 = n
2) stated that the mean values were statistically equal, and an alternative hypothesis (H
1: n
1 ≠ n
2) stated that the mean values were statistically different. Calculations of the Student
t-statistic value |t
cal| were performed using the computer software STATISTICA (StatSoft Polska Sp. zo.o, Poland); the obtained results are gathered in
Table 4.
For the alternative hypothesis, it was determined that a critical region |t
cal| ≥ t
α = 0.05 and, for v = n
1 + n
2 – 2 = 40 degrees of freedom and α = 0.05, i.e., a selected 5% risk of error (significance level), the critical value t
α = 0.05 = 2.021 was read from the tables. Analysis of
Table 4 allowed us to state that |t
cal| ≤ t
α=0.05, i.e., the zero hypothesis could not be rejected; thus, the differences between the mean values of the results of the local resistance coefficients obtained from measurements, ζ
1p, ζ
2p, ζ
3p, ζ
4p, ζ
5p, ζ
6p, ζ
7p, ζ
8p, and ζ
9p (
Figure 6) and calculated from Equations (13)–(21), ζ
1cal, ζ
2cal, ζ
3cal, ζ
4cal, ζ
5cal, ζ
6cal, ζ
7cal, ζ
8cal, and ζ
9cal, were statistically insignificant, i.e., equal to each other. This is also confirmed by the fact that the calculated probability value, p
cal, was greater than 0.05 (assumed significance level).
Thus, Equations (13)–(21) can be used in the design of water supply installations made of polypropylene to determine real values of the local resistance coefficient ζ, with dependence on an assumed manufacturing precision of joints of the T-junctions with an internal diameter of 13.2 mm. Using these equations for design purposes according to the requirements of the standard PN-EN 806-3:2006 [
38], a nomogram was worked out to determine values of local resistance coefficients ζ depending on water flow velocity in polypropylene T-junctions with an internal diameter of 13.2 mm (
Figure 8).
Currently, designers of water supply networks apply simplified methods of estimation of the local resistance coefficient ζ in fittings; thus, the pressure losses in these water supply networks are calculated inaccurately. Until now, it has not been known how to determine the local resistance coefficient ζ of a welded polypropylene T-junction with a given internal diameter. Now, a designer of polypropylene water supply networks, using the nomogram (
Figure 8) and assuming a water flow velocity, can exactly determine the real value of the local resistance coefficient ζ in a welded polypropylene T-junction with the internal diameter of 13.2 mm, depending on water flow direction, and then exactly calculate the real value of the pressure losses that will occur in the designed water supply system.
Analysis of the results of the investigations allowed us to state that the local resistance coefficient ζ in a welded polypropylene T-junction significantly depends on the manufacturing precision of the T-junction joints. Many manufacturers and distributors of fittings do not submit the values of the local resistance coefficient ζ in technical catalogues; thus, it is not clear whether they correspond to reality, because the values of ζ for polypropylene fittings with the same diameter but from different manufacturers are not the same. The values of ζ for the fittings, calculated according to the recommended guidelines [
33], were significantly lower than the measured values [
21,
23,
25,
34,
36]. This was also confirmed by the present investigations, performed with use of the welded polypropylene T-junctions with an internal diameter of 13.2 mm. Accordingly, it must be stated that the values of the local resistance coefficient ζ for fittings should be determined by measurement. Analyzing the problem of local resistance coefficients ζ, one must also consider the hydraulic resistance resulting the joining of this fitting with a straight section of the pipeline. In fact, the straight sections between the fittings are a source of hydraulic resistances as well. In the technical and scientific literature, there is often no information on whether a determined local resistance coefficient ζ concerns the fitting itself or also includes the resistances occurring in the straight pipeline section between the fittings. According to the standard methodology of determination of local resistances [
37], the hydraulic resistance occurring in straight sections between fittings should also be considered. Due to this fact, the hydraulic resistance occurring in these sections of the pipeline should be measured, not calculated, because the accuracy of these calculations depends on the assumed or calculated value of the linear resistance coefficient λ as well as the assumed value of absolute roughness k.
4. Conclusions
The local resistance coefficient ζ of welded polypropylene T-junctions does not have a constant value, and depends on the water flow velocity and manufacturing precision of a given T-junction. An increase of the water flow velocity in a welded polypropylene T-junctions results in a fall in the value of the local resistance coefficient ζ. Equations (13)–(21) and the nomogram shown in
Figure 8 can be used to design of water supply installations made of polypropylene and to determine real values of the resistance coefficient ζ relative to the assumed manufacturing precision of a T-junction with an internal diameter 13.2 mm.
The comparison of the mean values of the local resistance coefficient ζ determined from the measurements of properly warmed up and properly pressed T-junctions with the respective values for poorly warmed up and poorly pressed T-junctions (ζ4p, ζ5p, ζ6p) and excessively warmed up and excessively pressed T-junctions (ζ7p, ζ8p, ζ9p) allowed us to state that for the through-run water flow, the value of ζ4p increased by 45%, ζ7p by 70.1%, in the divergent water flow ζ5p increased by 21.7% and ζ8p by 78.1%, and in the convergent water flow, ζ6p increased by 27.9% and ζ9p by 77.3%.
As the real value of the local resistance coefficient ζ in a welded polypropylene T-junction significantly depends on the welding time and pressing force applied to the elements being welded, it is necessary for fitting manufacturers to precisely determine the welding time and pressing force, as well as to equip welding sets with dynamometers measuring the pressing force during joining of the fittings being welded.
The comparison of the mean values of the local resistance coefficient ζ determined from the measurements with the values read from the nomograms recommended for designing water supply networks [
26] allowed us to state that for the properly warmed up and properly pressed T-junctions, in the through-run water flow, the value of ζ
1p increased by 88.6%, in the divergent water flow ζ
2p increased by 4.4%, and in the convergent water flow ζ
3p increased by 32.1%; for poorly warmed up and poorly pressed T-junctions, in the through-run water flow, the value of ζ
4p increased by 93.8%, in the divergent water flow, ζ
5p increased by 25.1%, and in the convergent water flow, ζ
6p increased by 51.1%; for the excessively warmed up and excessively pressed T-junctions, in the through-run water flow, the value of ζ
7p increased by 96.6%, in the divergent water flow, ζ
8p increased by 79.1%, and in the convergent water flow, ζ
9p increased by 84.6%.
In case of the welded polypropylene T-junctions, the methods of calculating the value of the local resistance coefficient outlined in Reference [
26] significantly underestimate the results as compared to the values obtained in measurements. The big difference between the values of the coefficient ζ obtained by measurement and the values determined according to the guidelines indicates that recommended methods of calculating the value of the local resistance coefficient for fittings should be specified.
The values of the local resistance coefficient ζ of welded polypropylene T-junctions published in the literature and catalogues significantly differ from the real values obtained by measurement. Due to this fact, it is necessary to perform further investigations of welded polypropylene fittings in a range of diameters, which will allow real values of the coefficient ζ to be determined and enable new guidelines for the determination of values of local resistance coefficients to be established.