A Simple Modelling Framework for Shallow Subsurface Water Storage and Flow
Abstract
1. Introduction
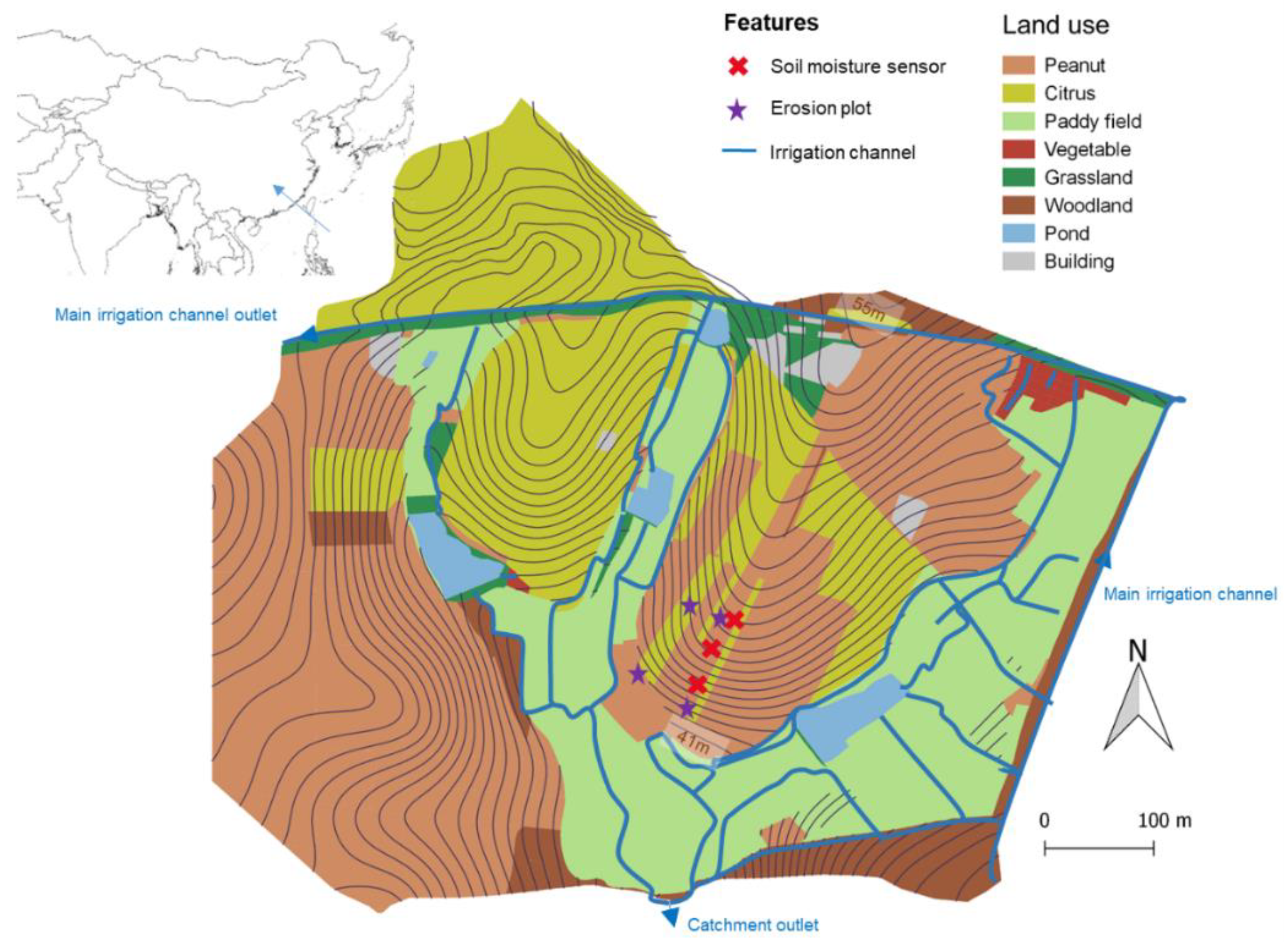
2. Site Description and Data
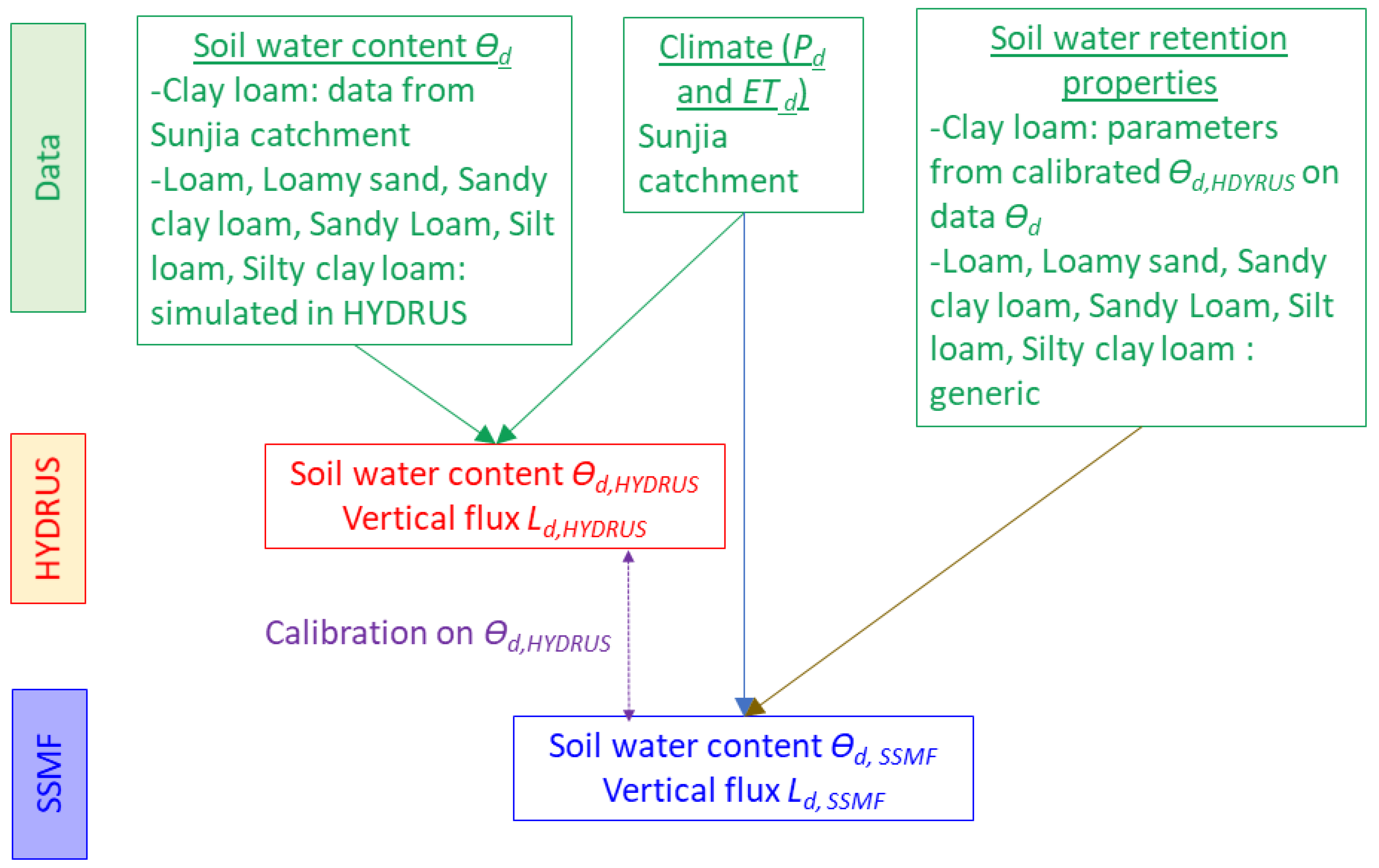
3. Development of the Shallow Subsurface Modelling Framework
3.1. Model Requirements
- Its results should be comparable to the Richards equation solution;
- It should be computationally simple and parsimonious, with a minimum number of calibrating parameters;
- It should be computationally flexible, allowing future accommodation of any type of soil or vegetation process, yet able to compute relatively short-term depth-averaged volumetric soil water content θd (m3/m3) as well as soil water flux Ld (e.g., m/d) across a shallow depth (m).
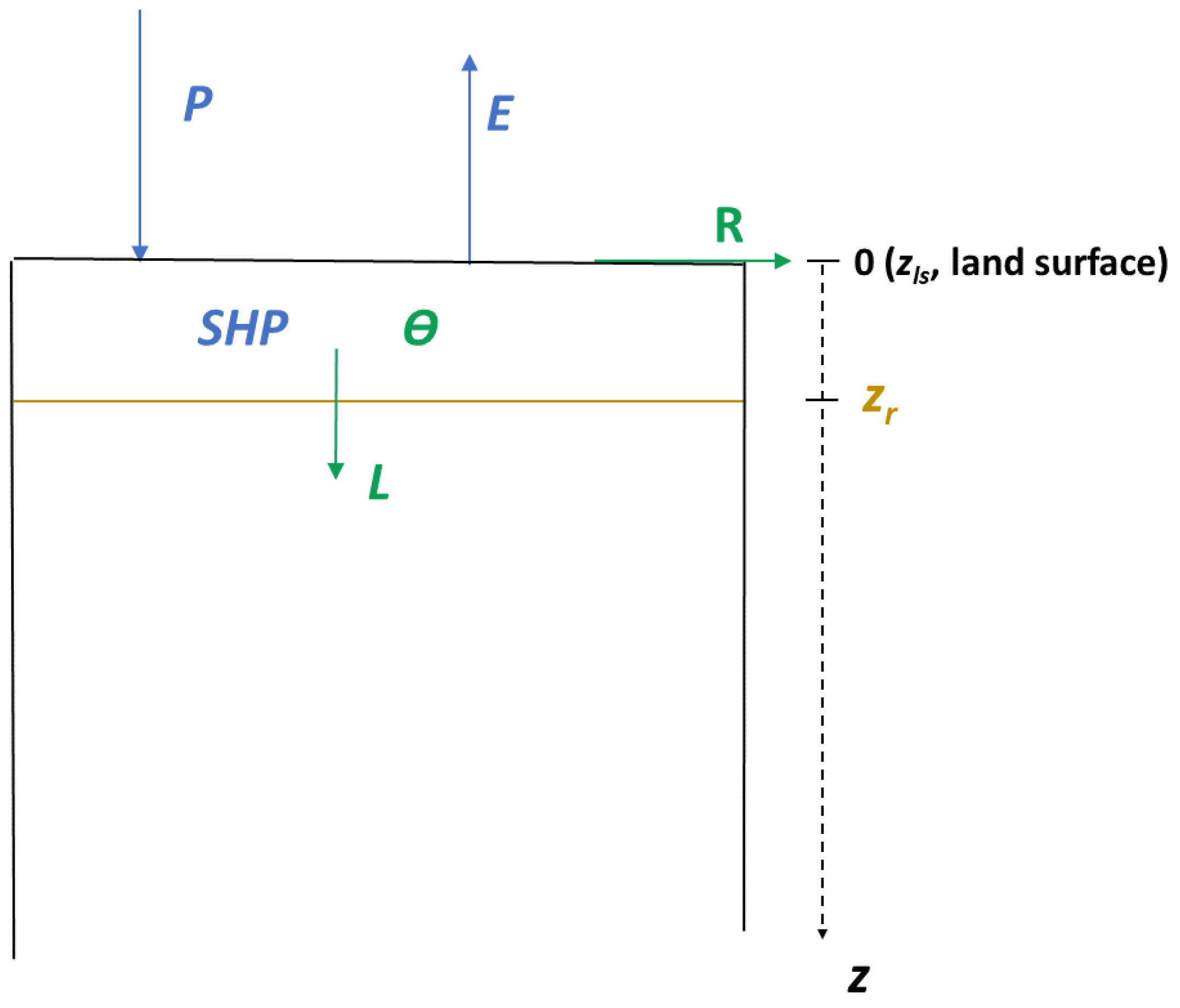
3.2. Model Conceptualization and Development
3.3. Model Evaluation
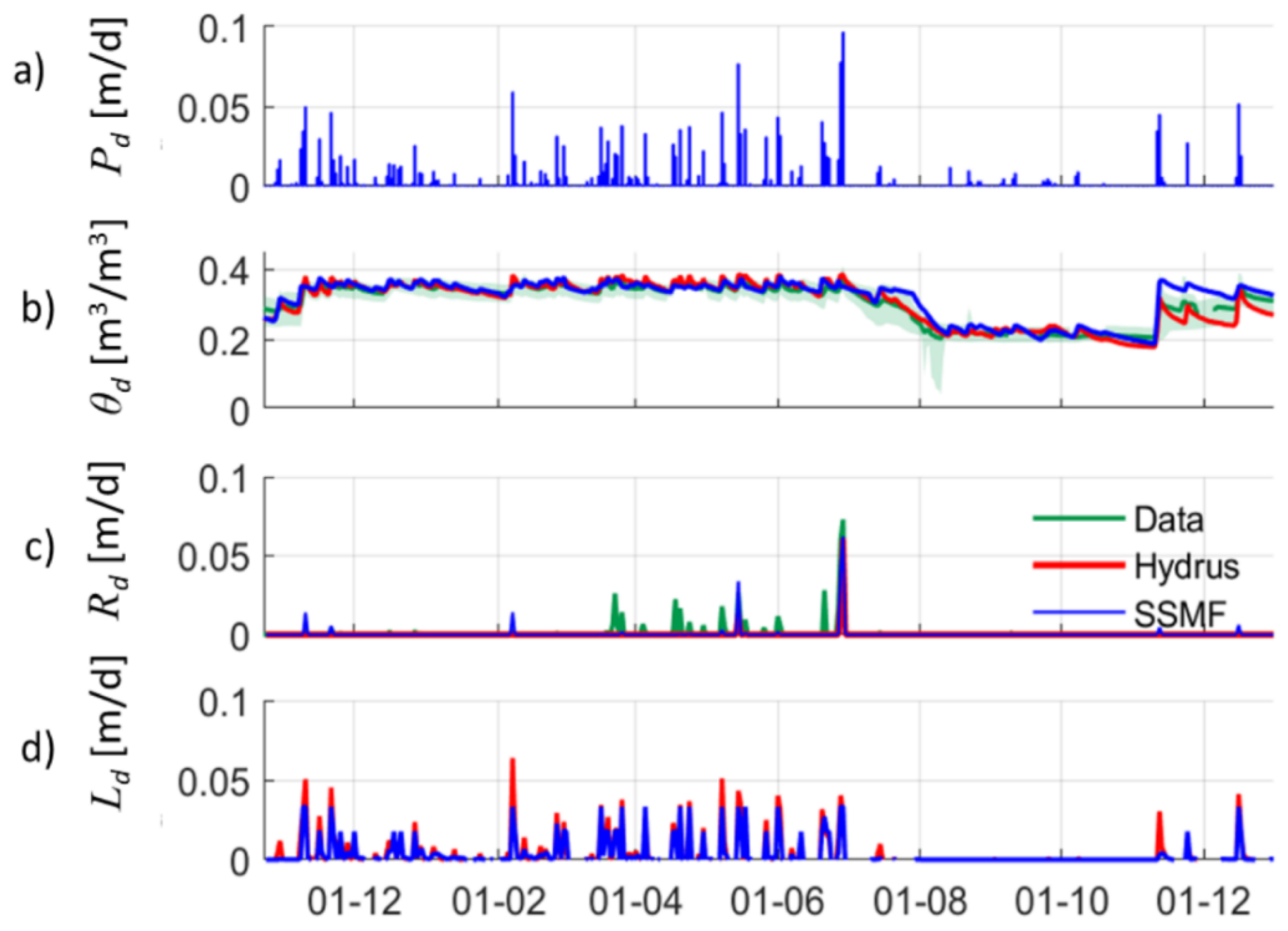
4. Results
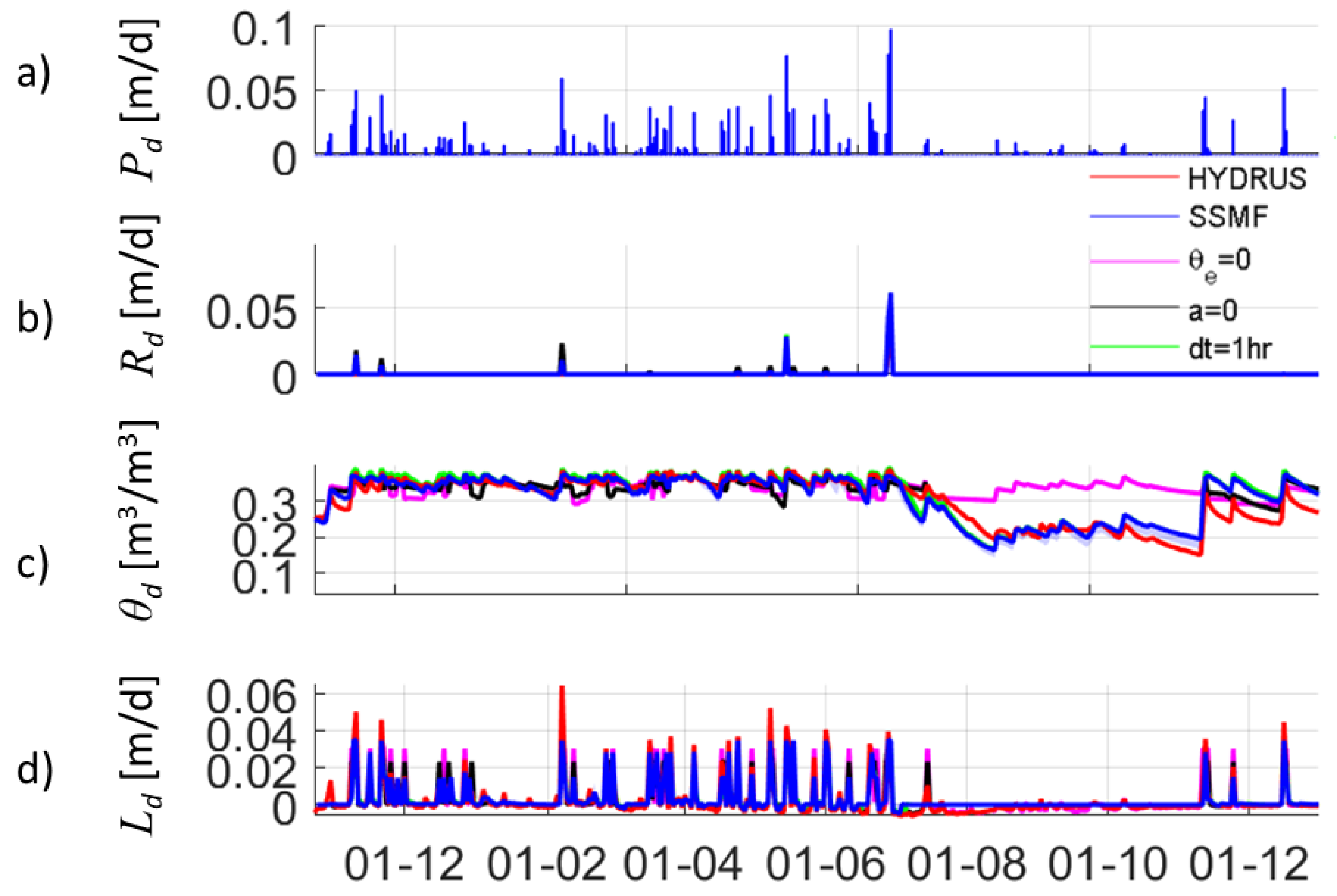
4.1. Evaluation of SSMF against Data and HYDRUS Simulations
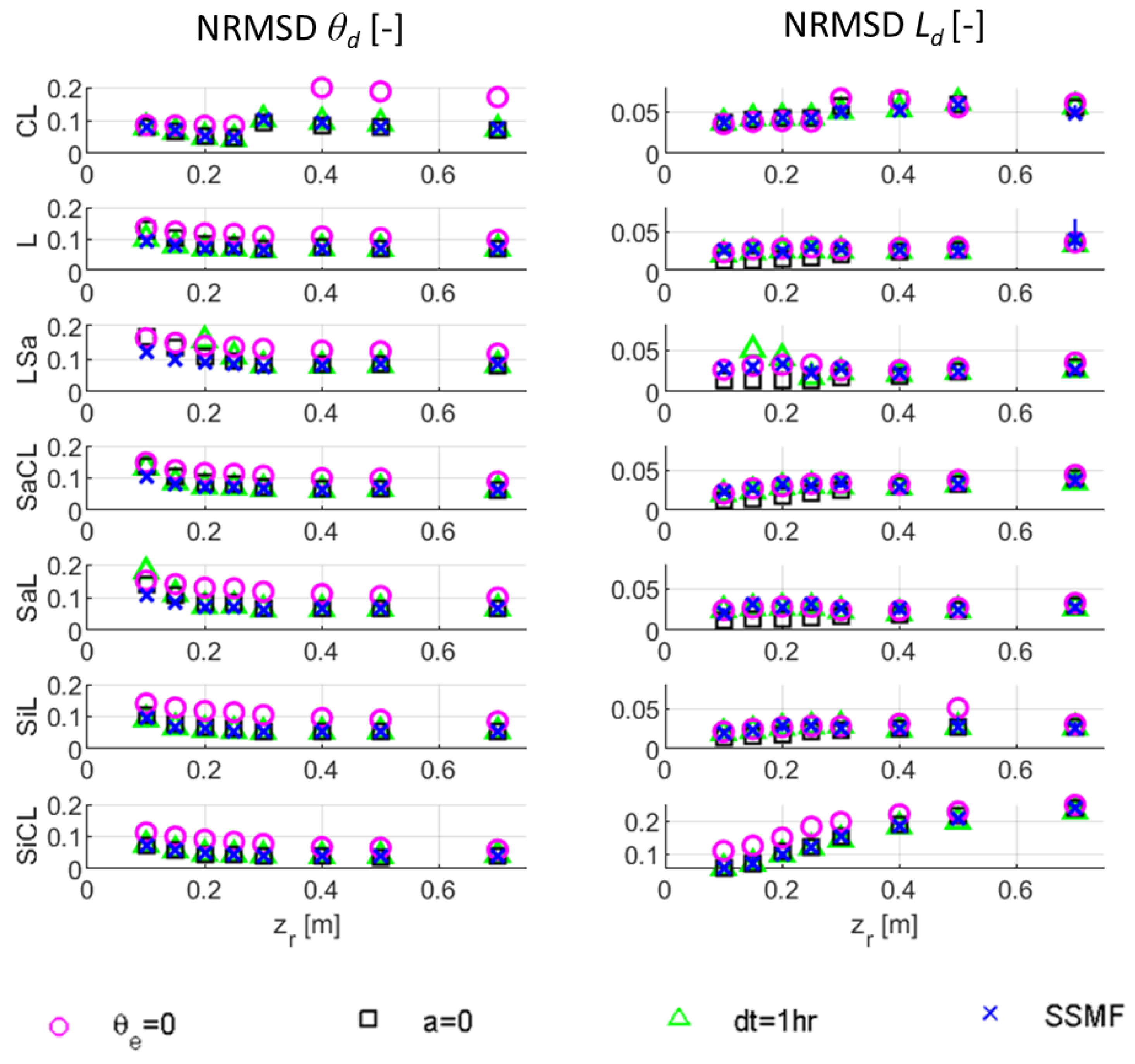
4.2. SSMF Parameters Influence
5. Discussion
5.1. General Performance of the SSMF
5.2. Evaluation of the Influence of the SSMF Parameters
5.3. Overland Flow
5.4. The SSMF Concept Application in the Context of Soil Hydraulics Modelling
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Augeard, B.; Bresson, L.M.; Assouline, S.; Kao, C.; Vauclin, M. Dynamics of soil surface bulk density: Role of water table elevation and rainfall duration. Soil Sci. Soc. Am. J. 2008, 72, 412–423. [Google Scholar] [CrossRef]
- Liu, H.; Lei, T.W.; Zhao, J.; Yuan, C.P.; Fan, Y.T.; Qu, L.Q. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. J. Hydrol. 2011, 396, 24–32. [Google Scholar] [CrossRef]
- Ahuja, L.R.; Ma, L.W.; Timlin, D.J. Trans-disciplinary soil physics research critical to synthesis and modeling of agricultural systems. Soil Sci. Soc. Am. J. 2006, 70, 311–326. [Google Scholar] [CrossRef]
- Schwen, A.; Zimmermann, M.; Bodner, G. Vertical variations of soil hydraulic properties within two soil profiles and its relevance for soil water simulations. J. Hydrol. 2014, 516, 169–181. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids in porous media. Jpn. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Using the Hydrus-1D and Hydrus-2D codes for estimating unsaturated soil hydraulic and solute transport parameters. In Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; van Genuchten, M.T., Leij, F.J., Wu, L., Eds.; University of California: Riverside, CA, USA, 1999; pp. 1523–1536. [Google Scholar]
- Buckingham, E. Studies on the Movement of Soil Moisture; Bull. USDA, Bureau of Soils: Washington, DC, USA, 1907; p. 38.
- Darcy, H. Détermination des lois d’écoulement de l’eau à travers le sable. In Les Fontaines Publiques de la Ville de Dijon; Victor Dalmont: Paris, France, 1856; pp. 590–594. [Google Scholar]
- Gandolfi, C.; Facchi, A.; Maggi, D. Comparison of 1D models of water flow in unsaturated soils. Environ. Model. Softw. 2006, 21, 1759–1764. [Google Scholar] [CrossRef]
- Verrot, L.; Destouni, G. Data-model comparison of temporal variability in long-term time series of large-scale soil moisture. J. Geophys. Res.-Atmos. 2016, 121. [Google Scholar] [CrossRef]
- Porporato, A.; D’odorico, P.; Laio, F.; Ridolfi, L.; Rodriguez-Iturbe, I. Ecohydrology of water-controlled ecosystems. Adv. Water Resour. 2002, 25, 1335–1348. [Google Scholar] [CrossRef]
- Bergström, S. The HBV model. In Computer Models of Catchment Hydrology; Singh, V.P., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 443–476. [Google Scholar]
- Santhi, C.; Srinivasan, R.; Arnold, J.G.; Williams, J.R. A modelling approach to evaluate the impacts of water quality management plans implemented in a catchment in Texas. Environ. Modell. Softw. 2006, 21, 1141–1157. [Google Scholar] [CrossRef]
- Deng, J.; Zhu, B.; Zhou, Z.; Zheng, X.; Li, C.; Wang, T.; Tang, J. Modeling nitrogen loadings from agricultural soils in southwest China with modified DNDC. J. Geophys. Res.-Biogeo. 2011, 116. [Google Scholar] [CrossRef]
- Dawson, J.J.C.; Smith, P. Carbon losses from soil and its consequences for land-use management. Sci. Total Environ. 2007, 382, 165–190. [Google Scholar] [CrossRef] [PubMed]
- Manzoni, S.; Taylor, P.; Richter, A.; Porporato, A.; Ågren, G.I. Environmental and stoichiometric controls on microbial carbon-use efficiency in soils. New Phytol. 2012, 196, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.L.; Wen, Q.X.; Freney, J. (Eds.) Nitrogen in Soils of China; Springer Science & Business Media: Berlin, Germany, 2012; Volume 74. [Google Scholar]
- Salvucci, G.D.; Entekhabi, D. Equivalent steady soil moisture profile and the time compression approximation in water balance modeling. Water. Resour. Res. 1994, 30, 2737–2749. [Google Scholar] [CrossRef]
- Brutsaert, W. The daily mean zero-flux plane during soil-controlled evaporation: A Green’s function approach. Water. Resour. Res. 2014, 50, 9405–9413. [Google Scholar] [CrossRef]
- Lehman, P.; Or, D. Evaporation and capillary coupling across vertical textural contrasts in porous media. Phys. Rev. E 2009, 80, 46318. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Horn, R.; Smucker, A. Pore shrinkage dependency of inorganic and organic soils on wetting and drying cycles. Soil. Sci. Soc. Am. J. 2007, 71, 1095–1104. [Google Scholar] [CrossRef]
- Or, D.; Ghezzehei, T.A. Modeling post-tillage soil structural dynamics: A review. Soil Till. Res. 2002, 64, 41–59. [Google Scholar] [CrossRef]
- Tahir, M.; Lv, Y.; Gao, L.; Hallett, P.D.; Peng, X. Soil water dynamics and availability for citrus and peanut along a hillslope at the Sunjia Red Soil Critical Zone Observatory (CZO). Soil Till. Res. 2016, 163, 110–118. [Google Scholar] [CrossRef]
- Lv, Y.; Gao, L.; Geris, J.; Verrot, L.; Peng, X. Assessment of water sources and their contributions to streamflow by endmember mixing analysis in a subtropical mixed agricultural catchment. Agr. Water. Manag. 2018, 203, 411–422. [Google Scholar] [CrossRef]
- He, Z.; Zhang, M.; Wilson, M.J. Distribution and classification of red soils in China. In The Red Soils of China; Wilson, M.J., He, Z., Yang, X., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 29–33. [Google Scholar]
- Ma, L.; Cheng, Y.; Wang, J.; Yan, X. Mechanical insights into the effect of fluctuation in soil moisture on nitrous oxide emissions from paddy soil. Paddy Water Environ. 2017, 2, 359–369. [Google Scholar] [CrossRef]
- Zhou, H.; Peng, X.; Peth, S.; Xiao, T.Q. Effects of vegetation restoration on soil aggregate microstructure quantified with synchrotron-based micro-computed tomography. Soil Tillage Res. 2012, 124, 17–23. [Google Scholar] [CrossRef]
- Soil Science Division Staff. Soil Survey Manual; Ditzler, C., Scheffe, K., Monger, H.C., Eds.; USDA Handbook 18; Government Printing Office: Washington, DC, USA, 2017.
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Salem, H.M.; Valero, C.; Muñoz, M.A.; Rodríguez, M.G.; Silva, L.L. Short-term effects of four tillage practices on soil physical properties, soil water potential, and maize yield. Geoderma 2015, 237, 60–70. [Google Scholar] [CrossRef]
- Laio, F.; D’Odorico, P.; Ridolfi, L. An analytical model to relate the vertical root distribution to climate and soil properties. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. Hydraulic properties of porous media. Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1964; 24p. [Google Scholar]
- Campbell, G.S. A simple method for determining unsaturated conductivity from moisture retention data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil. Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Beven, K.; Feyen, J. GLUE based assessment on the overall predictions of a MIKE SHE application. Water Resour. Manag. 2009, 23, 1325–1349. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress: II. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Vogel, T.; van Genuchten, M.T.; Cislerova, M. Effect of the shape of the soil hydraulic functions near saturation on variably-saturated flow predictions. Adv. Water Resour. 2001, 24, 133–144. [Google Scholar] [CrossRef]
- Destouni, G. Applicability of the steady state flow assumption for solute advection in field soils. Water Resour. Res. 1991, 27, 2129–2140. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop requirements. In Irrigation and Drainage Paper; No. 56; FAO: Rome, Italy, 1998; 300p. [Google Scholar]
- Zhang, M.K.; Xu, J.M. Restoration of surface soil fertility of an eroded red soil in southern China. Soil Tillage Res. 2005, 80, 13–21. [Google Scholar] [CrossRef]
- Zhang, W.L.; Wu, S.X.; Ji, H.J.; Kolbe, H. Estimation of agricultural non-point source pollution in China and the alleviating strategies I. Estimation of agricultural non-point source pollution in China in early 21 century. Sci. Agric. Sin. 2004, 37, 1008–1017. [Google Scholar]
- Wei, L.; Zhang, B.; Wang, M. Effects of antecedent soil moisture on runoff and soil erosion in alley cropping systems. Agr. Water. Manag. 2007, 94, 54–62. [Google Scholar] [CrossRef]
- Schmidt, J.; Werner, M.V.; Michael, A. Application of the EROSION 3D model to the CATSOP watershed, The Netherlands. Catena 1999, 37, 449–456. [Google Scholar] [CrossRef]
- Flanagan, D.C.; Nearing, M.A. USDA-Water Erosion Prediction Project: Hillslope profile and watershed model documentation. In Nserl Report; USDA-ARS National Soil Erosion Research Laboratory: West Lafayette, IN, USA, 1995. [Google Scholar]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth. Syst. Sci. Discuss. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Or, D.; Lehmann, P.; Assouline, S. Natural length scales define the range of applicability of the Richards’ equation for capillary flows. Water Resour. Res. 2015, 51, 7130–7144. [Google Scholar] [CrossRef]
- Vogel, H.-J.; Ippisch, O. Estimation of a critical spatial discretization limit for solving Richards’ equation at large scales. Vadose Zone J. 2008, 7, 112–114. [Google Scholar] [CrossRef]
- Bresler, E.; Dagan, G. Unsaturated flow in spatially variable fields. 2. Application of water flow models to various fields. Water Resour. Res. 1983, 19, 421–428. [Google Scholar] [CrossRef]
- Dagan, G.; Bresler, E. Unsaturated flow in spatially variable fields. 1. Derivation of models of infiltration and redistribution. Water Resour. Res. 1983, 19, 413–420. [Google Scholar] [CrossRef]

| (-) | (-) | α (1/m) | (-) | (-) | (-) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CZO clay loam 0–0.3 m | 0.050 | 0.390 | 1.256 | 0.5 | 0.035 | 0.05 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
| CZO clay loam 0.3–3 m | 0.050 | 0.385 | 1.438 | 0.5 | 0.029 | 0.086 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
| Loam 0–3 m | 0.078 | 0.430 | 1.56 | 0.5 | 0.250 | 3.6 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
| Loamy sand 0–3 m | 0.035 | 0.437 | 1.5 | 0.5 | 1.466 | 4.85 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
| Sandy clay loam 0–3 m | 0.1 | 0.39 | 1.48 | 0.5 | 0.314 | 5.9 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
| Sandy loam 0–3 m | 0.041 | 0.453 | 1.378 | 0.5 | 0.621 | 3 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
| Silt loam 0–3 m | 0.067 | 0.45 | 1.41 | 0.5 | 0.108 | 2 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
| Silty clay loam 0–3 m | 0.089 | 0.430 | 1.23 | 0.5 | 1.466 | 1 | [0;24] | [0;] | [0;100] | [0;10] | [0,1] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verrot, L.; Geris, J.; Gao, L.; Peng, X.; Oyesiku-Blakemore, J.; Smith, J.U.; Hodson, M.E.; Zhang, G.; Hallett, P.D. A Simple Modelling Framework for Shallow Subsurface Water Storage and Flow. Water 2019, 11, 1725. https://doi.org/10.3390/w11081725
Verrot L, Geris J, Gao L, Peng X, Oyesiku-Blakemore J, Smith JU, Hodson ME, Zhang G, Hallett PD. A Simple Modelling Framework for Shallow Subsurface Water Storage and Flow. Water. 2019; 11(8):1725. https://doi.org/10.3390/w11081725
Chicago/Turabian StyleVerrot, Lucile, Josie Geris, Lei Gao, Xinhua Peng, Joseph Oyesiku-Blakemore, Jo U. Smith, Mark E. Hodson, Ganlin Zhang, and Paul D. Hallett. 2019. "A Simple Modelling Framework for Shallow Subsurface Water Storage and Flow" Water 11, no. 8: 1725. https://doi.org/10.3390/w11081725
APA StyleVerrot, L., Geris, J., Gao, L., Peng, X., Oyesiku-Blakemore, J., Smith, J. U., Hodson, M. E., Zhang, G., & Hallett, P. D. (2019). A Simple Modelling Framework for Shallow Subsurface Water Storage and Flow. Water, 11(8), 1725. https://doi.org/10.3390/w11081725





