Abstract
Exchange processes of surface and groundwater are important for the management of water quantity and quality as well as for the ecological functioning. In contrast to most numerical simulations using coupled models to investigate these processes, we present a novel integral formulation for the sediment-water-interface. The computational fluid dynamics (CFD) model OpenFOAM was used to solve an extended version of the three-dimensional Navier–Stokes equations which is also applicable in non-Darcy-flow layers. Simulations were conducted to determine the influence of ripple morphologies and surface hydraulics on the flow processes within the hyporheic zone for a sandy and for a gravel sediment. In- and outflowing exchange fluxes along a ripple were determined for each case. The results indicate that larger grain size diameters, as well as ripple distances, increased hyporheic exchange fluxes significantly. For higher ripple dimensions, no clear relationship to hyporheic exchange was found. Larger ripple lengths decreased the hyporheic exchange fluxes due to less turbulence between the ripples. For all cases with sand, non-Darcy-flow was observed at an upper layer of the ripple, whereas for gravel non-Darcy-flow was recognized nearly down to the bottom boundary. Moreover, the sediment grain sizes influenced also the surface water flow significantly.
1. Introduction
Hyporheic exchange—the exchange of stream and shallow subsurface water—is controlled by pressure gradients along the streambed surface and subsurface groundwater gradients. Over multiple scales, the bedform induced hyporheic exchange was identified as a crucial process for the biogeochemistry and ecology of rivers [1,2,3,4,5,6,7,8,9,10]. On large and intermediate scales, stream stage differences, meander loops or bars can generate hyporheic exchange. Accordingly, it is possible to control surface water-groundwater exchange by river stage manipulation e.g., to manage the inflow of saline groundwater into a river [11]. A decrease of the groundwater level, in turn, impacts surface water infiltration up to a maximum where groundwater and surface water are disconnected. This condition is achieved when the clogging layer does not cross the top of the capillary zone above the water table [12]. On small scales, river sediments usually form topographic features such as dunes or ripples. The flowing fluid encounters an uneven surface on the permeable streambed, which results in an irregular pattern in the pressure along that surface and induces hyporheic exchange [11,12,13].
Within theoretical, experimental, and computational studies the general mechanics of the bedform induced hyporheic exchange were examined over the past decades. By manipulating streambed morphology, stream discharge, and groundwater flow, experiments have been used to study driving forces for the hyporheic exchange intensively [14,15,16,17]. At submerged structures such as pool-riffle sequences or ripples, turbulences, eddies or hydraulic jumps may occur. Packman et al. [15], Tonina and Buffington [18], Voermans et al. [19] and other studies showed, that turbulence influences hyporheic exchange and should not be ignored. Facing these complex three-dimensional flow dynamics at the sediment-water interface, it can be challenging to establish suitable flume experiments or field studies. Computational fluid dynamics has proven to be a viable alternative. The majority of these studies have focused on surface-subsurface coupled models. Reasons for the application of different models for the surface and the subsurface are for example the strong temporal variability in streams including relatively high velocities, whereas the velocities and temporal variabilities in the groundwater are usually several orders of magnitude smaller, leading to different applied equations for the stream and the subsurface. Often, the two computational domains are linked by pressure. Pressure distributions from a surface water model are consequently used for a coupled groundwater model [20,21,22,23,24,25,26]. However, also fully coupled models such as the Integrated Hydrology Model [27] or HydroGeoSphere have already been successfully applied [28,29,30]. Within these models, open channel flow is described by the two-dimensional diffusion-wave approximation of the St. Venant equations, whereas the three-dimensional Richards equation is used for the subsurface. Water and solute exchange flux terms enable to simultaneously solve one system of equations for both flow regimes.
For many coupled surface-subsurface models, the Darcy law is applied within the sediment. However, especially for coarse bed rivers, this law may cause errors in the presence of non-Darcy hyporheic flow [15]. Following Bear [31], the linear assumption of the Darcy law is only valid if the Reynolds number does not exceed a value between 1 and 10. Applying Darcy’s law in non-Darcy-flow areas leads to an overestimating of groundwater flow rates [32]. Packman et al. [15] investigated hyporheic exchange through gravel beds with dune-like morphologies and applied the modified Elliot and Brooks model [33]. They realized that the model did not perform well—among other reasons—due to non-Darcy flow in the near-surface sediment which was not considered in the model. One possible solution to model groundwater in non-Darcy-flow areas is e.g., to use the Darcy-Brinkmann equation instead of the Darcy law. However, there is an additional parameter—the effective viscosity—which has to be determined.
In the present study, an extended version of the three-dimensional Navier–Stokes equations after Oxtoby et al. [34] is used for the whole system comprising the stream as well as the subsurface. For the application in the groundwater, sediment porosity, as well as an additional drag term, are included into the Navier–Stokes equations. The model is consequently also applicable for high Reynolds numbers within the subsurface where the Darcy law cannot be applied. To our knowledge, this solver was never used for the hyporheic zone before. We apply the new integral solver to evaluate the effect of ripple geometries and surface hydraulics on hyporheic exchange processes, based on the study by Broecker et al. [35] who investigated free surface flow and tracer retention over streambeds and ripples without considering the subsurface. In Broecker et al. [35] the three-dimensional Navier–Stokes equations were solved in combination with an implemented transport equation. In that study, ripple sizes, spacing as well as flow velocities affected pressure gradients and tracer retention considerably. Seven simulation cases were examined varying ripple height, length, distance, and flow rate. The investigated ripple geometries and flow rates are mainly transferred to the present study. Only case 6 is not used for the present study, as the irregular distance between the ripples gave no significant new findings compared to equal distances [35]. In contrast to Broecker et al. [35], the present study examines both free surface flow and subsurface flow. The aim of the present study is to evaluate the impact of ripple dimensions, lengths, spacing and surface velocity on flow dynamics within the hyporheic zone using a new integral model.
2. Materials and Methods
2.1. Geometry and Mesh
The analyzed geometry consists of a prismatic domain with a length of 15 m, a width of 1 m and a height of 1.5 m at the inlet and 1 m at the outlet. A weir structure is included in front of the outlet to fix the water level. A rippled area of approximately 3 m is introduced 6 m downstream of the inlet. The model geometry of the reference case with the corresponding initial water depth can be seen in Figure 1.
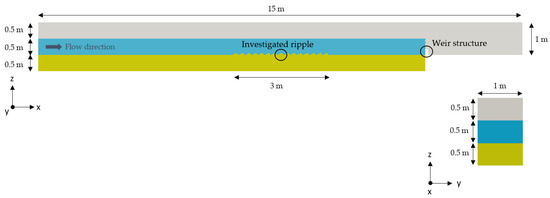
Figure 1.
Model geometry and initial condition for the water level (sediment: yellow, water: blue, air: gray); top: front view, bottom right: cross-section.
The mesh has been discretized using the three-dimensional finite element mesh generator gmsh. The ripple parameters are based on the approach of Broecker et al. [35]. Table 1 summarizes the most important ripple parameter values. Unstructured elements were chosen in the x-z-plane to depict the curved profile of the ripples. Thereafter the elements have been extruded with 10 layers in the y-direction to produce a three-dimensional mesh. Different meshes with similar mesh conditions have been created for the varying ripple geometries. Smaller element sizes were chosen for surface water and the subsurface, as detailed processes in the air phase are not of interest for the present study. The air phase was only included to account for water level fluctuations which showed to have a significant effect on the pressure distribution at the streambed [31]. The mesh resolution has been examined by calculating the fraction of the turbulent kinetic energy in the resolved motions after Pope [36], who suggest to resolve 80% of the turbulent kinetic energy for a well resolved large eddy simulation (LES). In our simulation we are around this range with 75–83% resolution for the water phase with the applied meshes using the LES turbulence model (see Section 2.3). Lower resolutions were observed for the air-phase, which is not of interest for our simulations.

Table 1.
Simulation cases including ripple geometries and flow rates.
2.2. Numerical Model
To simulate exchange processes of surface water and groundwater, the open source software Open Source Field Operation and Manipulation (OpenFOAM) version 2.4.0 has been used. A solver called “porousInter” has been applied. This solver was developed by Oxtoby et al. [34] and is based on the interFoam solver by OpenFOAM. PorousInter is a multiphase solver for immiscible fluids and extends the three-dimensional Navier–Stokes equations by the consideration of soil porosity and effective grain size diameter. For our simulations two phases—water and air—are considered to allow water level fluctuations. Since the porousInter–solver does not account for the solid fraction of the soil, values that are represented by [ ]f are averaged only over the pore space volume. The conservation of mass and momentum are defined after Oxtoby et al. [34] as:
Mass conservation equation
Momentum conservation equation
where φ is the soil porosity (-); is the velocity (m/s); ρ is the density (kg/m3); t is time (s); p is pressure (Pa); μ is the dynamic viscosity (Ns/m2), g is the gravitational acceleration (m/s2) and D an additional drag term (kg/(m2s2)). The drag term was developed by Ergun [37] and accounts for momentum loss by means of fluid friction with the porous medium and flow recirculation within the sediment. To consider flow recirculation, an effective added mass coefficient is included after van Gent [38]. The porous drag term is defined as:
with dp (m) as effective grain size diameter.
PorousInter uses the volume of fluid (VOF) approach. Consequently, multiple phases are treated as one fluid with changing properties [39]. The indicator fraction α (-) varies between zero for the air phase and one for the water phase. The water-air interface is captured by a convective transport equation:
The dynamic viscosity and the density of each fluid are calculated according to their fraction as:
The subscripts w and a denote the fluids water and air.
2.3. Turbulence
Turbulent properties have been captured by a large eddy simulation (LES) turbulence model (see also Section 3.1). Eddies up to a certain size were consequently directly resolved, whereas for small eddies a subgrid model is used. For the present study, the Smagorinski subgrid scale model [40] has been applied.
A measure M(,t) for the turbulence resolution was calculated after Pope [36]:
where defines the turbulent kinetic energy of the resolved motions by:
and defines the turbulent kinetic energy of the residual motions. The solver by Oxtoby et al. [34] had to be adjusted to write automatically. and were calculated and averaged for the whole running time. A measure M(,t) = 0.25 corresponds to a resolution of 75% of the turbulent kinetic energy.
2.4. Boundary and Initial Conditions
Figure 2 shows the most important boundary conditions. The inlet of the boundary is divided into two fractions: for the air and for the water phase. The parameter α is fixed accordingly at the inlet. For the water phase the discharge is set to 0.5 m3/s for case 1–5 and to 0.25 m3/s for case 6, whereas for the air phase a total pressure condition is defined with a total pressure of 0 Pa. The total pressure condition specifies the given total pressure for outflow and the dynamic pressure subtracted from the total pressure for inflow. Next to the air phase at the inlet, the total pressure definition is applied for the upper boundary and at the outlet. The streambed is surrounded by walls. Consequently, the velocity is set to 0 m/s with a no flow condition.
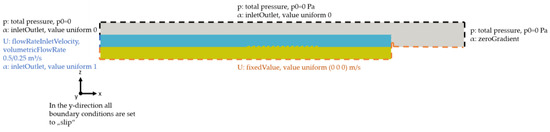
Figure 2.
Boundary conditions.
In OpenFOAM a definition of a constant water level at the outlet is challenging [41]. Therefore, a weir structure is established as a barrier to keep a constant water level for our model. The water flows freely over the weir top. Behind the weir, the water level decreases before it flows out of the model. This method is described e.g., in Bayon-Barrachina and Lopez-Jimenez [42]. For case 1–5 and case 6 different heights for the weir structure were chosen, since the water level is affected by the flow rate of the surface water. For the weir structure and at the whole bottom of the model, an impervious no slip condition is used. All boundary conditions in the third dimension contain slip conditions.
For the sediment, two materials are chosen: coarse sand with a grain size diameter of 2 mm and medium gravel with a grain size diameter of 1.5 cm. Both sediments have an effective porosity of 0.25 and are considered to be homogeneous. According to Freeze and Cherry [32] coarse sand has a hydraulic conductivity of about 10−2 m/s and medium gravel of about 10−1 m/s. These values are only estimations and are not considered in our simulations. An initial water level of 1 m is set from the inlet up to the weir structure (see Figure 1).
2.5. Validation
To ensure reliable behavior of the integral model concerning the hydraulics for the interaction of groundwater and surface water, the solver was tested based on two applications. The seepages through dams with different water levels and dam geometries were compared with numerical and analytical solutions.
First, flow through a rectangular dam with a constant water level at both sides was investigated. The dam width amounts to 16 m and the dam height to 24 m. The dam height is equal to the water level at the left side of the dam. A median grain size diameter of 2 mm and a porosity of 0.25 were defined which correspond to a sandy dam filling. At the right hand, the water level is fixed to 4 m. The seepage through the dam was compared with two numerical solutions after Westbrook [43] and Aitchison and Coulson [44] and with a one-dimensional [45] as well as with a two-dimensional analytical solution after Di Nucci [46] (see Figure 3). The seepage calculated with the integral solver was in between the two-dimensional analytical solution after Di Nucci and the numerical solutions after Westbrook and Aitchison and Coulson. A large deviation was recognized for the one-dimensional solution. Based on the two-dimensional velocities observed in the numerical simulation, an analytical one-dimensional solution is obviously not adequate.
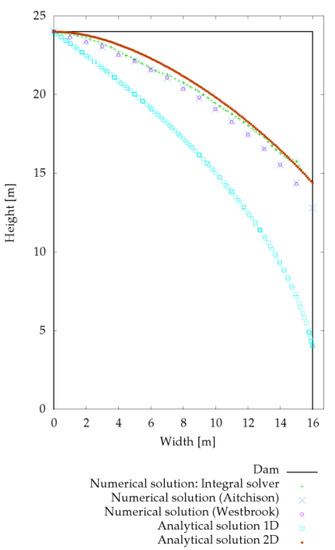
Figure 3.
Seepage calculated with 1D and 2D analytical and numerical solutions for a rectangular dam.
For the second validation case, the seepage through a homogeneous dam with a constant water level of 1.9 m on the left side was compared with an analytical solution by Kozeny [47] and an analytical solution by Casagrande [48]. The latter is an improvement of the solution by Kozeny. The dam has a height of 2.2 m and a width of 8.7 m. The two-dimensional mesh consists of 750,000 rectangular elements with a width of 0.02 m in x-and y-direction. The dam material properties were the same as in the first validation case. A good agreement can be recognized for the simulated water levels with the calculated analytical data (see Figure 4). At the entrance and at the outlet, the results gained with the integral model were closer to the solution after Casagrande compared to the solution after Kozeny.
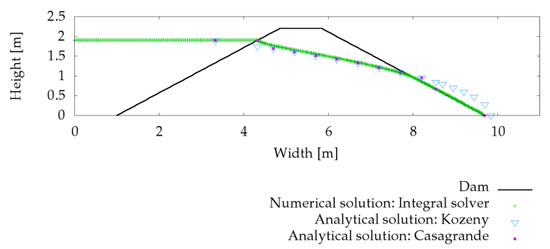
Figure 4.
Seepage through a homogeneous dam after Kozeny [45], Casagrande [48] and calculated with the integral solver.
Our test simulations showed that the integral flow model can predict the interaction of surface and groundwater with reasonable accuracy compared to analytical and numerical solutions.
3. Results and Discussion
In the following section, results for the reference case (see Table 1, case 1) will be presented for both sandy and gravel sediments. Based on these results, the influence of the different ripple parameters and surface water discharge on the flow field will be analyzed, including pressure and velocity distributions as well as hyporheic exchange fluxes after 5 min simulation time. For all cases we focused on a single ripple in the center of a series of ripples. For the quantification of the fluxes, fluxes through the cell faces at the investigated ripple are calculated at the intersections of surface water and sediment. The ripple is divided into an area left and right from the ripple crest (see Figure 5). In- as well as outflowing fluxes for both sides as well as the sum of these fluxes divided by the face area—defined as “total flux”—are determined. The fluxes are averaged for the time frame of 60–300 s due to non-steady flow conditions.
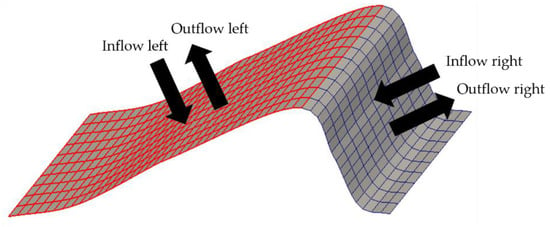
Figure 5.
In- and outflowing fluxes at the left and right side of the ripple crest.
3.1. Reference Case
For the reference case (see Table 1, case 1), the discharge amounts to 0.5 m3/s, the ripple length to 20 cm and the height to 5.6 cm. Figure 6 shows the pressure distribution and velocity vectors at the investigated ripple (see Figure 1) for case 1 with a sandy and a gravel sediment. The solver solves the pressure term p_rgh as the static pressure minus the hydrostatic pressure (ρgz with z as coordinate vector). The highest pressure is observed at the last third of the upstream face of the ripple. Low pressure is present at the ripple crest and the first two-thirds of the upstream face as well as downstream the crest. As these pressure differences lead to hyporheic exchange, flow occurs in downstream and upstream directions from high to low pressure. The described flow paths fit well to the results by Fox et al. [49], where the exchange of water between surface and subsurface was illustrated based on tracer experiments in the laboratory at a rippled sandy streambed. Also Thibodeaux and Boyle [50], Elliott and Brooks [14] and Janssen et al. [51] came to similar results from laboratory experiments with triangular bedforms. Fehlman [52] and Shen et al. [53] presented non-hydrostatic pressure distributions at triangular bed forms which were also similar to our results with pressure peaks at the middle of the stoss face, pressure minimum at the crest with low pressure remaining at the lee face until the pressure increases again at the stoss face of the following ripple. The description of the principal pressure pattern at the observed ripple in our simulations is valid for the sand as well as for the gravel, though the pressure values differ. Due to the higher resistance of the sand compared to gravel, higher pressure gradients are observed. Conversely, it behaves in terms of subsurface velocities: higher velocities are determined in the gravel sediment compared to the less permeable sand.
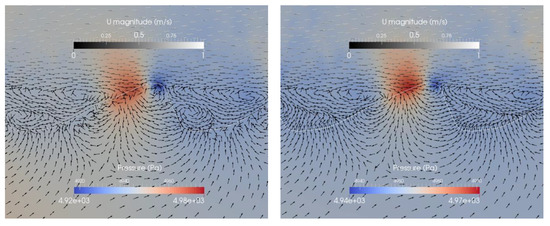
Figure 6.
Pressure distribution and velocity vectors at a sandy (left) and gravel (right) ripple for case 1 (Table 1). The white line indicates the sediment-water interface. The colors indicate the pressure distribution. Please note that the scaling is different in the right and the left panel. The arrows indicate flow directions of the surface and the subsurface flow. To visualize the intensity of the flow U a grey is used.
The applied LES turbulence model allows to resolve large parts of the turbulence at the streambed directly. Hence, between each ripple pair, eddies are identified. Comparing Figure 6 left and Figure 6 right, it is obvious, that the flow field in the surface water depends on the properties of the sediment: While in the sand, two eddies (clockwise as well as counterclockwise) can be recognized between the ripples, for the gravel only one eddy is apparent which flows in clockwise direction. This indicates, that a simple successively coupling via pressure distributions from surface water as a boundary condition for a groundwater model as for the example in [23,24] is not adequate, since not only the surface water influences the subsurface, but also the subsurface affects the surface flow conditions. The feedback from the subsurface to the surface is consequently also important. The clockwise eddies are located in the area where surface water introduces into the ripple, while the counterclockwise ripple is located in the area where the water within the ripple flows back to the surface water.
Table 2 and Table 3 show the in- and outflowing fluxes for all cases as well as the total fluxes per ripple area for gravel and sand according to Figure 5 As described already above, in- as well as outflow are observed at the ripple lee while at the ripple stoss the outflow is dominant. The total flux is much higher for the gravel with 1.8 × 10−2 m3/s/m2 than for the sand with 2.7 × 10−3 m3/s/m2. This fits to the flume experiment results by Tonina and Buffington [17], where larger hyporheic exchange was claimed for gravel compared to sandy sediments.

Table 2.
Hyporheic fluxes of a single ripple in the center of a series of ripples for case 1–6 (sand). Right and left indicate the part of the ripple right and left of the ripple crest (compare Figure 4).

Table 3.
Hyporheic fluxes of a single ripple in the center of a series of ripples for case 1–6 (gravel). Right and left indicate the part of the ripple right and left of the ripple crest (compare Figure 4).
Based on the overall high velocities within the sediment our simulations indicate, that non-Darcy-flow is present in the whole ripple nearly down to the bottom boundary for the gravel bed and to a part of the sandy bed (see Figure 7). At the near-surface area at the crest of the gravel ripple, Reynolds numbers up to 1770 were recognized, while for the sandy bed Reynolds numbers up to 330 were determined. For a better illustration of the non-Darcy-flow areas, Reynolds numbers up to 10 are illustrated in Figure 7. Consequently, dark red areas have a Reynolds number that equals or is higher than 10. Due to lower permeability, the flow velocities of the surface water influenced the sandy sediment less than the gravel bed with high permeability. The explicit modeling of the hyporheic zone with Darcy’s law is not possible in river beds with such coarse grain sizes since groundwater flow rates would be overestimated. Facing e.g., contaminant transport depending on residence time serious misperceptions could appear. The Reynolds number distribution of the following cases were similar to the reference case: for the whole gravel ripple down to the bottom non-Darcy-flow is apparent, while for the sand a small layer at the interface as well as the crest shows non-Darcy-flow areas. Only for case 5 with a distance of 20 cm between each ripple, there is even more non-Darcy-flow within the sandy ripple.
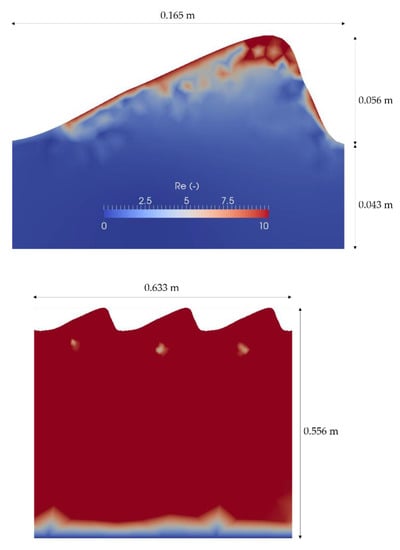
Figure 7.
Reynolds numbers at a sandy (top) and gravel (bottom) ripple for case 1 (Table 1).
Janssen et al. [51] stated that the largest discrepancies of most CFD simulations of flow over ripples and dunes occur in the eddy zone. Especially for Reynolds-averaged Navier–Stokes turbulence models this is a known weakness. Therefore, we have chosen a LES turbulence model. At the same time, we are aware of the computational limitation, which is additionally increased by the calculation of the three-dimensional Navier–Stokes equations in the sediment in contrast to the commonly applied Darcy law. However, facing the growing availability of computational sources and the observed non-Darcy-flow areas in the investigated cases, we apply a promising tool for analyzing integral surface-subsurface flow processes with high resolution.
3.2. Ripple Dimension
For cases 2 and 3 the ripple length to height ratio is the same as for the reference case (see Table 1), but the ripple height and length are quartered for case 2 and doubled for case 3. Figure 8 shows the velocity and pressure distributions for the investigated ripples in the middle for case 2 for sand and gravel. The general pressure pattern for case 2 for sand and gravel as well as for the reference case are similar: the lowest pressure occurs at the crest and the highest pressure upstream of the crest. But the high-pressure area related to the ripple size is much higher for case 2 than for the reference case. Related to the ripple face area at the interface, we consequently expect higher inflow rates compared to the reference case, which can be seen in Table 2 and Table 3. The total flux per area is higher for case 2 with 5.1 × 10−3 m3/s/m2 and 1.81 × 10−2 m3/s/m2 than for the reference case with 2.7 × 10−3 m3/s/m2 and 1.84 × 10−2 m3/s/m2.
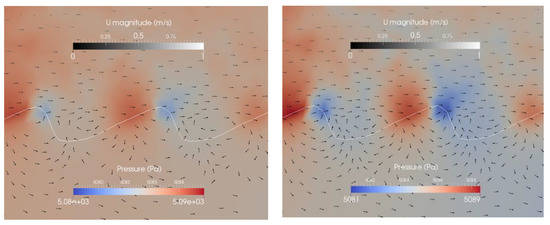
Figure 8.
Pressure distribution and velocity vectors at a sandy (left) and gravel (right) ripple for case 2 (Table 1). The white line indicates the sediment-water interface. The colors indicate the pressure distribution. Please note that the scaling is different in the right and the left panel. The arrows indicate flow directions of the surface and the subsurface flow. To visualize the intensity of the flow U a grey is used.
The flow field within the ripple is again directed upstream and downstream from the point of highest pressure. For both simulations (case 2 sand and gravel) only one eddy was recognized in a clockwise direction. For case 3 high turbulence was recognized between the ripples with up to five eddies (see Figure 9). Significantly high- and low-pressure areas are recognized in the turbulent phase of the surface area especially for the simulation with sandy sediment. For this simulation two instead of one inflow area can be recognized at the upstream face of the ripple. Between these inflow areas, there is an outflow area. Another outflow area is located upstream of the lower inflow area, but the main outflow occurs downstream of the ripple crest. In the simulation of the gravel ripple, less eddies are observed than for the simulation with the sand. For the gravel ripple only one inflow area is present. The outflow is located similar to case 1 and 2: upstream from the inflow area and downstream from the crest.
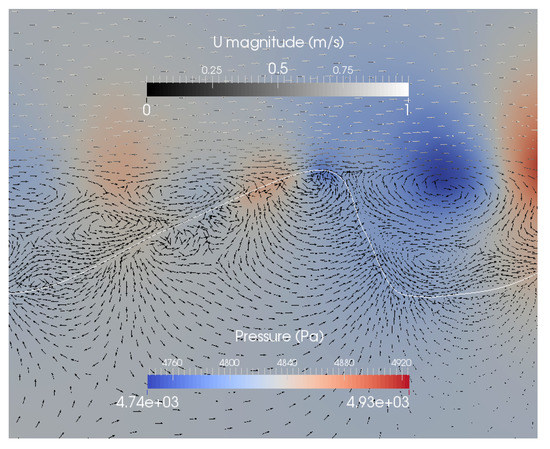
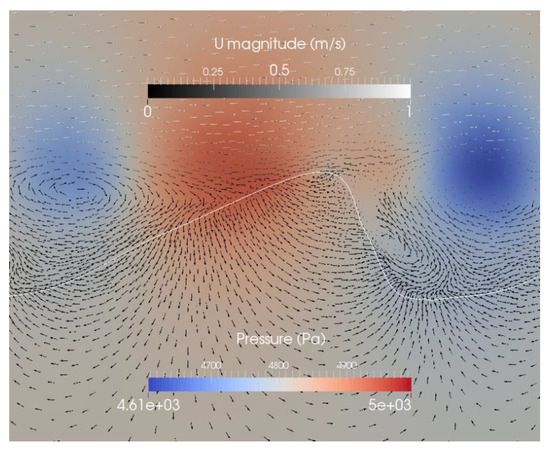
Figure 9.
Pressure distribution and velocity vectors at a sandy (top) and gravel (bottom) ripple for case 3 (Table 1). The white line indicates the sediment-water interface. The colors indicate the pressure distribution. Please note that the scaling is different in the right and the left panel. The arrows indicate flow directions of the surface and the subsurface flow. To visualize the intensity of the flow U a grey is used.
The total fluxes per area are bigger for case 3 with sand (3.0 × 10−3 m3/s/m2) compared to the reference case (case 1) with sand (2.7 × 10−3 m3/s/m2). For the gravel the opposite is true (case 3). 1.7 × 10−2 m3/s/m2 and case 1: 1.8 × 10−2 m3/s/m2). The extremely high turbulence between the ripples for the sand could be an explanation for that. The results for cases 2 and 3 with gravel and sand show, that a general statement about the influence of the ripple size is not possible, as there is a complex relation between the size and the material leading to different turbulence and pressure distributions, where also a threshold can be conceivable. Tonina and Buffington [16] presented results from a laboratory experiment with a pool-riffle channel and came to the same conclusion that hyporheic exchange does not necessarily decrease with lower bed form amplitudes. Closer investigations with more simulations including additional ripple size variations would be necessary for a more profound interpretation.
3.3. Ripple Length
For case 4 the ripple height equals the reference case, but the ripple length is doubled with 40 cm. This leads to less turbulence between the ripples (compare Figure 6 and Figure 10). The bigger area leads to higher fluxes per ripple, but the total flux per area is smaller compared to the reference case for sand as well as for gravel (case 4: 2.2 × 10−3 m3/s/m2 and 1.7 × 10−2 m3/s/m2, case 1: 2.7 × 10−3 m3/s/m2 and 1.8 × 10−2 m3/s/m2). The pressure distribution is very similar to the reference case (case 1). The decisive difference is probably again the turbulence, which is higher for large height-to-length-ratios as already described by Broecker et al. [31].
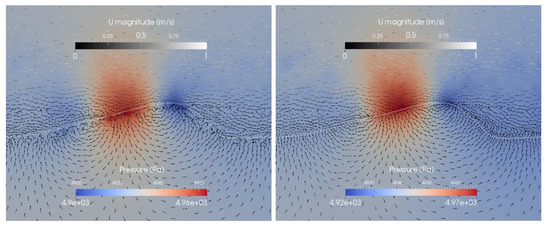
Figure 10.
Pressure distribution and velocity vectors at a sandy (left) and gravel (right) ripple for case 4 (Table 1). The white line indicates the sediment-water interface. The colors indicate the pressure distribution. Please note that the scaling is different in the right and the left panel. The arrows indicate flow directions of the surface and the subsurface flow. To visualize the intensity of the flow U a grey is used.
3.4. Ripple Distance
Figure 11 shows the velocity and pressure distributions for case 5 with the same ripple geometry as for the reference case, but with a distance between the ripples of 20 cm. This distance leads to higher pressure gradients for gravel and sand compared to the reference case. The flow fields within the ripples are similar to the reference case. But for this case there are also in- and outflow areas at the flat streambed between the ripples for both simulations. Eddies occur between the investigated ripples, but due to the distance, they are more elongated than for the reference case (case 1). Since the pressure gradients are higher for case 5 compared to the reference case and the area is the same for both cases, (the area is only the ripple area, not the flat part between the ripples) the total flux is higher for gravel as well as for sand compared to the reference case with both sediments (case 5: 3.9 × 10−3 m3/s/m2 and 2.7 × 10−2 m3/s/m2, case 1: 2.7 × 10−3 m3/s/m2 and 1.8 × 10−2 m3/s/m2). Broecker et al. [31] already presumed higher hyporheic exchange for this case compared to the reference case, based on the higher pressure gradients. To our knowledge, distances between the ripples were never investigated so far for hyporheic zone processes, apart from Broecker et al. [31] where only a surface water model was used.
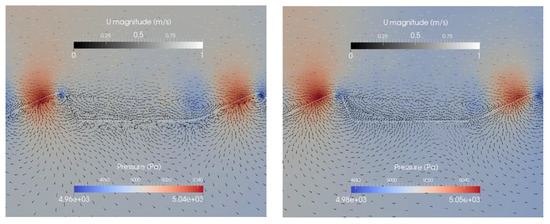
Figure 11.
Pressure distribution and velocity vectors at a sandy (left) and gravel (right) ripple for case 5 (Table 1). The white line indicates the sediment-water interface. The colors indicate the pressure distribution. Please note that the scaling is different in the right and the left panel. The arrows indicate flow directions of the surface and the subsurface flow. To visualize the intensity of the flow U a grey is used.
Compared to the investigated sandy ripples described above, the non-Darcy-flow areas of case 5 are significantly larger (compare Figure 7 and Figure 12). Due to the distance between the ripples, higher velocities reach the ripple stoss which influence the velocities within the ripple.
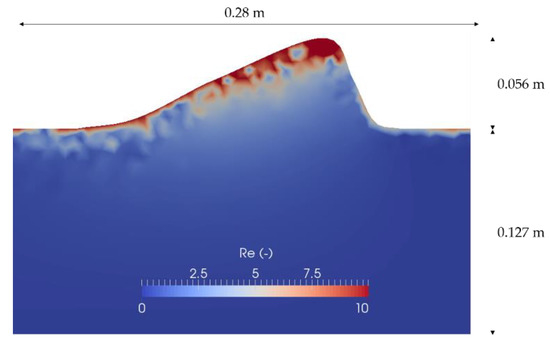
Figure 12.
Reynolds numbers at a sandy ripple for case 5
3.5. Flow Rate
For case 6 the discharge was set to 0.25 m3/s (for case 1–5 the discharge was 0.5 m3/s). The ripple geometry is the same as for the reference case (case 1). Comparing the reference case with case 6, it is obvious that both flow discharges show qualitatively similar flow fields. The flow velocities within the ripples decrease due to lower surface water velocities. Nevertheless, there is still a layer with Reynolds numbers higher than 10, which is slightly smaller than for the reference case (see Figure 13). The hyporheic fluxes are decreased compared to the reference case (case 6: 2.9 × 10−4 m3/s/m2 and 1.9 × 10−3 m3/s/m2, case 1: 2.7 × 10−3 m3/s/m2 and 1.8 × 10−2 m3/s/m2). This fits with laboratory observations e.g., by Marion et al. [54] and Elliott and Brooks [14].
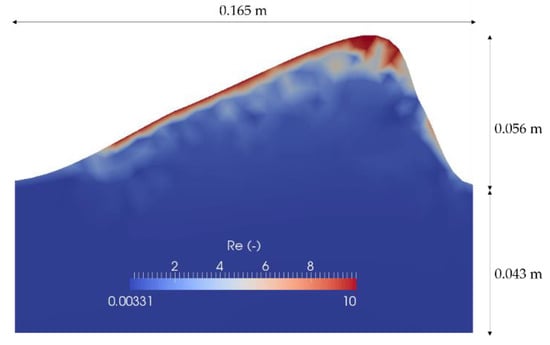
Figure 13.
Reynolds numbers at a sandy ripple for case 6.
4. Conclusions
CFD simulations were designed to simultaneously examine both surface and subsurface flow processes with an extended version of the three-dimensional Navier–Stokes equations. Based on two simulations for seepages through dams, it was shown that the applied model can describe the interaction of groundwater and surface water. The validated CFD model was applied to investigate the impact of bed form structures, grain sizes and surface flow discharges on hyporheic exchange processes. The examined ripple structures changed the streambed pressure and created in- and outflowing fluxes at the interface which were calculated for each case study for a representative ripple in the middle and play a significant role in biogeochemical processes within the hyporheic zone. It was shown that not only the surface water influences the flow within the sediment, but also the sediment properties lead to a change of the flow field within the surface water. Consequently, we claim, that a simple coupling of surface water with a closed boundary at the streambed, which is commonly used, is not appropriate at least for coarse sediments. Moreover, non-Darcy-flow areas were observed for all cases within the sediment. For the sandy sediment, the non-Darcy-flow areas are restricted to the upper layer and the crest of the investigated ripples. For the gravel non-Darcy-flow was observed almost down to the bottom of the model. The application of the Darcy law in these areas would lead to an overestimation of flow rates. For equations that can be applied in non-Darcy-flow areas in the subsurface such as the Darcy-Brinkmann-equation, additional parameters such as the effective viscosity have to be determined.
Comparing the extended Navier–Stokes equations with the commonly used coupling of surface water with a Darcy-law-model, the integral model is definitely more time consuming than the coupled models. The model shows direct feedbacks from surface to subsurface and vice versa, is applicable also in non-Darcy-flow areas and provides high resolution results. The applied LES turbulence model gives additional insights about the turbulence at the interface which has a high impact on hyporheic exchange.
The general flow paths were the same for almost all simulations. Upstream of the crest, in high pressure areas, surface water flows into the ripple. Subsurface water flows out of the ripple towards the crest as well as upstream of the inflow area. Only for the ripple with the highest dimension multiple inflow areas were recognized upstream of the crest. Higher turbulences were generally observed for sandy ripples compared to gravel ripples. Gravel ripples always showed higher hyporheic exchange fluxes compared to sand ripples. Three ripple dimensions with the same height to length ratios were examined, but no clear relationship to exchange fluxes was found. For longer ripples, the exchange was slightly smaller due to less turbulence, while distances between the ripples increased the hyporheic exchange fluxes drastically. Also, in the flat streambed sections exchange was observed. Decreasing flow rates lead to decreasing exchange fluxes.
Numerous of the observations of our simulations were already seen in laboratory experiments. Our simulations allowed to get a deeper understanding of the present velocity and pressure distribution at the interface and to determine in- and outflowing fluxes, which can be important for the understanding and prediction of hydrological, chemical, and biological processes. In contrast to other coupled models, it is applicable in non-Darcy-flow areas and allows to simultaneously simulate the surface and subsurface with one system of equation for surface and groundwater. We can develop upscaling approaches where we quantify the exchange rates depending on the ripple geometry and other variables with the high resolution three-dimensional integral model to serve as sink/source terms in one- or two-dimensional shallow water flow models. The shallow water equations are based on vertical averaged velocities (not discretizing the vertical dimension) and are generally applied on coarser scales. In a next step, also transport equations will be included in the presented integral model.
Author Contributions
Methodology, T.B. and K.T.; Software, T.B. and K.T.; Validation, T.B.; Investigation, T.B. and V.S.G.; Writing—original draft, T.B.; Writing—review and editing, T.B., R.H., G.N. and J.L.; Visualization, T.B.; Supervision, R.H. G.N. and J.L.
Funding
The funding provided by the German Research Foundation (DFG) within the Research Training Group ‘Urban Water Interfaces’ (GRK 2032) is gratefully acknowledged.
Acknowledgments
Parts of the simulations were computed on the supercomputers of Norddeutscher Verbund für Hoch- und Höchstleistungsrechnen in Berlin.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boulton, A.J.; Findlay, S.; Marmonier, P.; Stanley, E.H.; Valett, H.M. The functional significance of the hyporheic zone in streams and rivers. Annu. Rev. Ecol. Syst. 1998, 29, 59–81. [Google Scholar] [CrossRef]
- Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Cardenas, M.B. Hyporheic zone hydrologic science: A historical account of its emergence and a prospectus. Water Resour. Res. 2015, 51, 3601–3616. [Google Scholar] [CrossRef]
- Dahm, C.N.; Grimm, N.B.; Marmonier, P.; Valett, H.M.; Vervier, P. Nutrient dynamics at the interface between surface waters and groundwaters. Freshw. Biol. 1998, 40, 427–451. [Google Scholar] [CrossRef]
- Findlay, S. Importance of surface-subsurface exchange in stream ecosystems: The hyporheic zone. Limnol. Oceanogr. 1995, 40, 159–164. [Google Scholar] [CrossRef]
- Gomez-Velez, J.D.; Harvey, J.W.; Cardenas, M.B.; Kiel, B. Denitrification in the Mississippi River network controlled by flow through river bedforms. Nat. Geosci. 2015, 8, 941. [Google Scholar] [CrossRef]
- Harvey, J.; Gooseff, M. River corridor science: Hydrologic exchange and ecological consequences from bedforms to basins. Water Resour. Res. 2015, 51, 6893–6922. [Google Scholar] [CrossRef]
- Stonedahl, S.H.; Harvey, J.W.; Packman, A.I. Interactions between hyporheic flow produced by stream meanders, bars, and dunes. Water Resour. Res. 2013, 49, 5450–5461. [Google Scholar] [CrossRef]
- Stonedahl, S.H.; Harvey, J.W.; Wörman, A.; Salehin, M.; Packman, A.I. A multiscale model for integrating hyporheic exchange from ripples to meanders. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Schaper, J.L.; Posselt, M.; McCallum, J.L.; Banks, E.W.; Hoehne, A.; Meinikmann, K.; Shanafield, M.A.; Batelaan, O.; Lewandowski, J. Hyporheic Exchange Controls Fate of Trace Organic Compounds in an Urban Stream. Environ. Sci. Technol. 2018, 52, 12285–12294. [Google Scholar] [CrossRef]
- Harvey, J.W.; Bencala, K.E. The Effect of streambed topography on surface-subsurface water exchange in mountain catchments. Water Resour. Res. 1993, 29, 89–98. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water; a Single Resource; Diane Publishing Inc.: Darby, PA, USA, 1998; Volume 1139. [Google Scholar]
- Wondzell, S.M.; Gooseff, M. Geomorphic controls on hyporheic exchange across scales: Watersheds to particles. Treatise Geomorphol. 2013, 9, 203–218. [Google Scholar]
- Elliott, A.H.; Brooks, N.H. Transfer of nonsorbing solutes to a streambed with bed forms: Laboratory experiments. Water Resour. Res. 1997, 33, 137–151. [Google Scholar] [CrossRef]
- Packman, A.I.; Salehin, M.; Zaramella, M. Hyporheic Exchange with Gravel Beds: Basic Hydrodynamic Interactions and Bedform-Induced Advective Flows. J. Hydraul. Eng. 2004, 130, 647–656. [Google Scholar] [CrossRef]
- Mutz, M.; Kalbus, E.; Meinecke, S. Effect of instream wood on vertical water flux in low-energy sand bed flume experiments. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. Hyporheic exchange in gravel bed rivers with pool-riffle morphology: Laboratory experiments and three-dimensional modeling. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. A three-dimensional model for analyzing the effects of salmon redds on hyporheic exchange and egg pocket habitat. Can. J. Fish. Aquat. Sci. 2009, 66, 2157–2173. [Google Scholar] [CrossRef]
- Voermans, J.; Ghisalberti, M.; Ivey, G. The variation of flow and turbulence across the sediment–water interface. J. Fluid Mech. 2017, 824, 413–437. [Google Scholar] [CrossRef]
- Saenger, N.; Kitanidis, K.P.; Street, R. A numerical study of surface-subsurface exchange processes at a riffle-pool pair in the Lahn River, Germany. Water Resour. Res. 2005, 41, 12424. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Wilson, J.L. Dunes, turbulent eddies, and interfacial exchange with permeable sediments. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Bardini, L.; Boano, F.; Cardenas, M.B.; Revelli, R.; Ridolfi, L. Nutrient cycling in bedform induced hyporheic zones. Geochim. Cosmochim. Acta 2012, 84, 47–61. [Google Scholar] [CrossRef]
- Trauth, N.; Schmidt, C.; Maier, U.; Vieweg, M.; Fleckenstein, J.H. Coupled 3-D stream flow and hyporheic flow model under varying stream and ambient groundwater flow conditions in a pool-riffle system. Water Resour. Res. 2013, 49, 5834–5850. [Google Scholar] [CrossRef]
- Trauth, N.; Schmidt, C.; Vieweg, M.; Maier, U.; Fleckenstein, J.H. Hyporheic transport and biogeochemical reactions in pool-riffle systems under varying ambient groundwater flow conditions. J. Geophys. Res. Biogeosci. 2014, 119, 910–928. [Google Scholar] [CrossRef]
- Chen, X.; Cardenas, M.B.; Chen, L. Hyporheic Exchange Driven by Three-Dimensional Sandy Bed Forms: Sensitivity to and Prediction from Bed Form Geometry. Water Resour. Res. 2018, 54, 4131–4149. [Google Scholar] [CrossRef]
- Chen, X.; Cardenas, M.B.; Chen, L. Three-dimensional versus two-dimensional bed form-induced hyporheic exchange. Water Resour. Res. 2015, 51, 2923–2936. [Google Scholar] [CrossRef]
- VanderKwaak, J.E. Numerical Simulation of Flow and Chemical Transport in Integrated Surface-Subsurface Hydrologic Systems. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1999. [Google Scholar]
- Brunner, P.; Simmons, C. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Groundwater 2011, 50, 170–176. [Google Scholar] [CrossRef]
- Brunner, P.; Cook, P.G.; Simmons, C.T. Hydrogeologic controls on disconnection between surface water and groundwater. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Alaghmand, S.; Beecham, S.; Jolly, I.D.; Holland, K.L.; Woods, J.A.; Hassanli, A. Modelling the impacts of river stage manipulation on a complex river-floodplain system in a semi-arid region. Environ. Model. Softw. 2014, 59, 109–126. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Upper Saddle River, NJ, USA, 1979. [Google Scholar]
- Packman, A.I.; Brooks, N.H.; Morgan, J.J. A physicochemical model for colloid exchange between a stream and a sand streambed with bed forms. Water Resour. Res. 2000, 36, 2351–2361. [Google Scholar] [CrossRef]
- Oxtoby, O.; Heyns, J.; Suliman, R. A finite-volume solver for two-fluid flow in heterogeneous porous media based on OpenFOAM. In Proceedings of the 7th Open Source CFD International Conference, Hamburg, Germany, 24–25 October 2013. [Google Scholar] [CrossRef]
- Broecker, T.; Elsesser, W.; Teuber, K.; Özgen, I.; Nützmann, G.; Hinkelmann, R. High-resolution simulation of free-surface flow and tracer retention over streambeds with ripples. Limnologica 2018, 68, 46–58. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow Through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- van Gent, M. Wave Interaction with Permeable Coastal Structures; Elsevier Science: Amsterdam, The Netherlands, 1995; Volume 95. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Thorenz, C.; Strybny, J. On the numerical modelling of filling-emptying system for locks. In Proceedings of the 10th International Conference on Hydroinformatics, Hamburg, Germany, 14–18 July 2012. [Google Scholar]
- Bayon-Barrachina, A.; Lopez-Jimenez, P.A. Numerical analysis of hydraulic jumps using OpenFOAM. J. Hydroinform. 2015, 17, 662–678. [Google Scholar] [CrossRef]
- Westbrook, D.R. Analysis of inequality and residual flow procedures and an iterative scheme for free surface seepage. Int. J. Numer. Methods Eng. 1985, 21, 1791–1802. [Google Scholar] [CrossRef]
- Aitchison, J.; Coulson, C.A. Numerical treatment of a singularity in a free boundary problem. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 330, 573–580. [Google Scholar] [CrossRef]
- Kobus, H.; Keim, B. Grundwasser. Taschenbuch der Wasserwirtschaft; Blackwell Wissenschaftsverlag: Hoboken, NJ, USA, 2001; pp. 277–313. [Google Scholar]
- Di Nucci, C. A free boundary problem for fluid flow through porous media. arXiv 2015, arXiv:1507.05547. Available online: https://arxiv.org/abs/1507.05547 (accessed on 14 July 2015).
- Lattermann, E. Wasserbau-Praxis: Mit Berechnungsbeispielen Bauwerk-Basis-Bibliothek; Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- Casagrande, A. Seepage Through Dams; Harvard University Graduate School of Engineering: Cambridge, MA, USA, 1937. [Google Scholar]
- Fox, A.; Boano, F.; Arnon, S. Impact of losing and gaining streamflow conditions on hyporheic exchange fluxes induced by dune-shaped bed forms. Water Resour. Res. 2014, 50, 1895–1907. [Google Scholar] [CrossRef]
- Thibodeaux, L.J.; Boyle, J.D. Bedform-generated convective transport in bottom sediment. Nature 1987, 325, 341–343. [Google Scholar] [CrossRef]
- Janssen, F.; Cardenas, M.B.; Sawyer, A.H.; Dammrich, T.; Krietsch, J.; de Beer, D. A comparative experimental and multiphysics computational fluid dynamics study of coupled surface–subsurface flow in bed forms. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Fehlman, H.M. Resistance Components and Velocity Distributions of Open Channel Flows Over Bedforms; Colorado State University: Fort Collins, CO, USA, 1985. [Google Scholar]
- Shen, H.W.; Fehlman, H.M.; Mendoza, C. Bed Form Resistances in Open Channel Flows. J. Hydraul. Eng. 1990, 116, 799–815. [Google Scholar] [CrossRef]
- Marion, A.; Bellinello, M.; Guymer, I.; Packman, A. Effect of bed form geometry on the penetration of nonreactive solutes into a streambed. Water Resour. Res. 2002, 38, 27-1–27-12. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).