Rainfall-Runoff Modelling Using Hydrological Connectivity Index and Artificial Neural Network Approach
Abstract
1. Introduction
2. Study Area and Database
3. Methodology
3.1. Artificial Neural Networks (ANNs)
3.1.1. Determination of Input Structure
3.1.2. Data Pre-Processing
3.2. Hydrological Connectivity
3.3. Normalized Difference Vegetation Index
3.4. Evaluation of Results
4. Results and Discussion
4.1. Statistical Analysis of Data
4.2. Development and Application of ANN Model
4.2.1. Results of the Best Input Delay Values
4.2.2. ANN Models
Different Patterns of Hydro-Climate Data
Combination of Hydro-Climate, Hydro-Geomorphic and Biophysical Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Srinivasulu, S.; Jain, A. A comparative analysis of training methods for artificial neural network rainfall–runoff models. Appl. Soft Comput. 2006, 6, 295–306. [Google Scholar] [CrossRef]
- Porporato, A.; Ridolfi, L. Multivariate nonlinear prediction of river flows. J. Hydrol. 2001, 248, 109–122. [Google Scholar] [CrossRef]
- Pumo, D.; Viola, F.; Noto, L.V. Generation of natural runoff monthly series at ungauged sites using a regional regressive model. Water 2016, 8, 209. [Google Scholar] [CrossRef]
- Pumo, D.; Conti, F.L.; Viola, F.; Noto, L.V. An automatic tool for reconstructing monthly time-series of hydro-climatic variables at ungauged basins. Environ. Model. Softw. 2017, 95, 381–400. [Google Scholar] [CrossRef]
- Grayson, R.B.; Moore, I.D.; McMahon, T.A. Physically based hydrologic modeling: 1. A terrain-based model for investigative purposes. Water Resour. Res. 1992, 28, 2639–2658. [Google Scholar] [CrossRef]
- Tiwari, H.; Rai, S. Review of Information and soft computing techniques (ISCT) approaches in Water Resources Projects. In Managing Information Technology; DESIDOC: Delhi, India, 2015; pp. 89–94. [Google Scholar]
- Antar, M.A.; Elassiouti, I.; Allam, M.N. Rainfall-runoff modelling using artificial neural networks technique: A Blue Nile catchment case study. Hydrol. Process. 2006, 20, 1201–1216. [Google Scholar] [CrossRef]
- Jain, A.; Sudheer, K.; Srinivasulu, S. Identification of physical processes inherent in artificial neural network rainfall runoff models. Hydrol. Process. 2004, 18, 571–581. [Google Scholar] [CrossRef]
- Lallahem, S.; Mania, J. A nonlinear rainfall-runoff model using neural network technique: Example in fractured porous media. Math. Comput. Model. 2003, 37, 1047–1061. [Google Scholar] [CrossRef]
- Nourani, V. An emotional ANN (EANN) approach to modeling rainfall-runoff process. J. Hydrol. 2017, 544, 267–277. [Google Scholar] [CrossRef]
- Nourani, V.; Kalantari, O. Integrated artificial neural network for spatiotemporal modeling of rainfall–runoff–sediment processes. Environ. Eng. Sci. 2010, 27, 411–422. [Google Scholar] [CrossRef]
- Phukoetphim, P.; Shamseldin, A.Y.; Adams, K. Multimodel approach using neural networks and symbolic regression to combine the estimated discharges of rainfall-runoff models. J. Hydrol. Eng. 2016, 21, 04016022. [Google Scholar] [CrossRef]
- Tongal, H.; Booij, M.J. Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J. Hydrol. 2018, 564, 266–282. [Google Scholar] [CrossRef]
- Wilby, R.; Abrahart, R.; Dawson, C. Detection of conceptual model rainfall—Runoff processes inside an artificial neural network. Hydrol. Sci. J. 2003, 48, 163–181. [Google Scholar] [CrossRef]
- Wu, C.; Chau, K. Rainfall–runoff modeling using artificial neural network coupled with singular spectrum analysis. J. Hydrol. 2011, 399, 394–409. [Google Scholar] [CrossRef]
- Hsu, K.l.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Birikundavyi, S.; Labib, R.; Trung, H.T.; Rousselle, J. Performance of neural networks in daily streamflow forecasting. J. Hydrol. Eng. 2002, 7, 392–398. [Google Scholar] [CrossRef]
- Lin, J.-Y.; Cheng, C.-T.; Chau, K.-W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.; Bhatia, K. Comparative study of neural network, fuzzy logic and linear transfer function techniques in daily rainfall-runoff modelling under different input domains. Hydrol. Process. 2011, 25, 175–193. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Cheng, C.-T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.; Rangan, D.; Ramasastri, K. A neuro-fuzzy computing technique for modeling hydrological time series. J. Hydrol. 2004, 291, 52–66. [Google Scholar] [CrossRef]
- Chang, T.K.; Talei, A.; Quek, C.; Pauwels, V.R. Rainfall-runoff modelling using a self-reliant fuzzy inference network with flexible structure. J. Hydrol. 2018, 564, 1179–1193. [Google Scholar] [CrossRef]
- Firat, M.; Güngör, M. Hydrological time-series modelling using an adaptive neuro-fuzzy inference system. Hydrol. Process. 2008, 22, 2122–2132. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, Ö.; Komasi, M. Two hybrid artificial intelligence approaches for modeling rainfall–runoff process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Toth, E.; Brath, A. Multistep ahead streamflow forecasting: Role of calibration data in conceptual and neural network modeling. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Chua, L.H.; Wong, T.S.; Sriramula, L. Comparison between kinematic wave and artificial neural network models in event-based runoff simulation for an overland plane. J. Hydrol. 2008, 357, 337–348. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Mahjouri, N. Integrating support vector regression and a geomorphologic artificial neural network for daily rainfall-runoff modeling. Appl. Soft Comput. 2016, 38, 329–345. [Google Scholar] [CrossRef]
- Sajikumar, N.; Thandaveswara, B. A non-linear rainfall–runoff model using an artificial neural network. J. Hydrol. 1999, 216, 32–55. [Google Scholar] [CrossRef]
- Campolo, M.; Andreussi, P.; Soldati, A. River flood forecasting with a neural network model. Water Resour. Res. 1999, 35, 1191–1197. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R.L. An artificial neural network approach to rainfall-runoff modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Liong, S.Y.; Gautam, T.R.; Khu, S.T.; Babovic, V.; Keijzer, M.; Muttil, N. Genetic programming: A new paradigm in rainfall runoff modeling1. J. Am. Water Resour. Assoc. 2002, 38, 705–718. [Google Scholar] [CrossRef]
- Nayak, P.; Sudheer, K.; Ramasastri, K. Fuzzy computing based rainfall–runoff model for real time flood forecasting. Hydrol. Process. 2005, 19, 955–968. [Google Scholar] [CrossRef]
- Riad, S.; Mania, J.; Bouchaou, L.; Najjar, Y. Predicting catchment flow in a semi-arid region via an artificial neural network technique. Hydrol. Process. 2004, 18, 2387–2393. [Google Scholar] [CrossRef]
- Singh, A.; Malik, A.; Kumar, A.; Kisi, O. Rainfall-runoff modeling in hilly watershed using heuristic approaches with gamma test. Arab. J. Geosci. 2018, 11, 261. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Vincent, P.; Vasudevan, G. Genetic programming model for forecast of short and noisy data. Hydrol. Process. 2007, 21, 266–272. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H.C.; Quek, C.; Jansson, P.-E. Runoff forecasting using a Takagi–Sugeno neuro-fuzzy model with online learning. J. Hydrol. 2013, 488, 17–32. [Google Scholar] [CrossRef]
- Xu, Z.; Li, J. Short-term inflow forecasting using an artificial neural network model. Hydrol. Process. 2002, 16, 2423–2439. [Google Scholar] [CrossRef]
- Abebe, A.; Price, R. Managing uncertainty in hydrological models using complementary models. Hydrol. Sci. J. 2003, 48, 679–692. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Dulal, K.N. Model trees as an alternative to neural networks in rainfall—Runoff modelling. Hydrol. Sci. J. 2003, 48, 399–411. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Shrestha, D.L. A novel method to estimate model uncertainty using machine learning techniques. Water Resour. Res. 2009, 45, 1–16. [Google Scholar] [CrossRef]
- Tokar, A.S.; Johnson, P.A. Rainfall-runoff modeling using artificial neural networks. J. Hydrol. Eng. 1999, 4, 232–239. [Google Scholar] [CrossRef]
- Zhang, B.; Govindaraju, R.S. Geomorphology-based artificial neural networks (GANNs) for estimation of direct runoff over watersheds. J. Hydrol. 2003, 273, 18–34. [Google Scholar] [CrossRef]
- Young, C.-C.; Liu, W.-C. Prediction and modelling of rainfall–runoff during typhoon events using a physically-based and artificial neural network hybrid model. Hydrol. Sci. J. 2015, 60, 2102–2116. [Google Scholar] [CrossRef]
- Borselli, L.; Cassi, P.; Torri, D. Prolegomena to sediment and flow connectivity in the landscape: A GIS and field numerical assessment. Catena 2008, 75, 268–277. [Google Scholar] [CrossRef]
- Pringle, C.M. Hydrologic connectivity and the management of biological reserves: A global perspective. Ecol. Appl. 2001, 11, 981–998. [Google Scholar] [CrossRef]
- Sidle, R.C.; Gomi, T.; Usuga, J.C.L.; Jarihani, B. Hydrogeomorphic processes and scaling issues in the continuum from soil pedons to catchments. Earth Sci. Rev. 2017, 175, 75–96. [Google Scholar] [CrossRef]
- Sidle, R.C.; Tsuboyama, Y.; Noguchi, S.; Hosoda, I.; Fujieda, M.; Shimizu, T. Stormflow generation in steep forested headwaters: A linked hydrogeomorphic paradigm. Hydrol. Process. 2000, 14, 369–385. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Huo, Z.; Feng, S.; Kang, S.; Huang, G.; Wang, F.; Guo, P. Integrated neural networks for monthly river flow estimation in arid inland basin of Northwest China. J. Hydrol. 2012, 420, 159–170. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Kişi, Ö.; Adamowski, J.; Ramezani-Charmahineh, A. Evaluation of data driven models for river suspended sediment concentration modeling. J. Hydrol. 2016, 535, 457–472. [Google Scholar] [CrossRef]
- Pumo, D.; Francipane, A.; Lo Conti, F.; Arnone, E.; Bitonto, P.; Viola, F.; La Loggia, G.; Noto, L. The SESAMO early warning system for rainfall-triggered landslides. J. Hydroinform. 2016, 18, 256–276. [Google Scholar] [CrossRef]
- Goyal, M.K.; Bharti, B.; Quilty, J.; Adamowski, J.; Pandey, A. Modeling of daily pan evaporation in subtropical climates using ANN, LS-SVR, Fuzzy Logic, and ANFIS. Expert Syst. Appl. 2014, 41, 5267–5276. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, A.; Sharma, N.; Flügel, W.-A. Daily suspended sediment simulation using machine learning approach. Catena 2016, 138, 77–90. [Google Scholar] [CrossRef]
- Kim, T.-W.; Valdés, J.B. Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: New York, NY, USA, 1978; pp. 105–116. [Google Scholar]
- Chua, L.H.; Wong, T.S. Runoff forecasting for an asphalt plane by Artificial Neural Networks and comparisons with kinematic wave and autoregressive moving average models. J. Hydrol. 2011, 397, 191–201. [Google Scholar] [CrossRef]
- Chang, T.K.; Talei, A.; Alaghmand, S.; Ooi, M.P.-L. Choice of rainfall inputs for event-based rainfall-runoff modeling in a catchment with multiple rainfall stations using data-driven techniques. J. Hydrol. 2017, 545, 100–108. [Google Scholar] [CrossRef]
- Vafakhah, M. Comparison of cokriging and adaptive neuro-fuzzy inference system models for suspended sediment load forecasting. Arab. J. Geosci. 2013, 6, 3003–3018. [Google Scholar] [CrossRef]
- Croke, J.; Mockler, S.; Fogarty, P.; Takken, I. Sediment concentration changes in runoff pathways from a forest road network and the resultant spatial pattern of catchment connectivity. Geomorphology 2005, 68, 257–268. [Google Scholar] [CrossRef]
- Jarihani, A.A.; Callow, J.N.; McVicar, T.R.; Van Niel, T.G.; Larsen, J.R. Satellite-derived Digital Elevation Model (DEM) selection, preparation and correction for hydrodynamic modelling in large, low-gradient and data-sparse catchments. J. Hydrol. 2015, 524, 489–506. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.; McCool, D.; Yoder, D. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); United States Department of Agriculture: Washington, DC, USA, 1997; Volume 703.
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; Agriculture Handbook 537; U.S. Department of Agriculture: Washington, DC, USA, 1978.
- Cavalli, M.; Trevisani, S.; Comiti, F.; Marchi, L. Geomorphometric assessment of spatial sediment connectivity in small Alpine catchments. Geomorphology 2013, 188, 31–41. [Google Scholar] [CrossRef]
- Durigon, V.; Carvalho, D.; Antunes, M.; Oliveira, P.; Fernandes, M. NDVI time series for monitoring RUSLE cover management factor in a tropical watershed. Int. J. Remote Sens. 2014, 35, 441–453. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Photo Interpretation; John Wiley and Sons: New York, NY, USA, 1994. [Google Scholar]
- Jarihani, B.; Sidle, R.C.; Bartley, R.; Roth, C.H.; Wilkinson, S.N. Characterisation of hydrological response to rainfall at multi spatio-temporal scales in savannas of semi-arid Australia. Water 2017, 9, 540. [Google Scholar] [CrossRef]
- Trancoso, R.; Phinn, S.; McVicar, T.R.; Larsen, J.R.; McAlpine, C.A. Regional variation in streamflow drivers across a continental climatic gradient. Ecohydrology 2017, 10, e1816. [Google Scholar] [CrossRef]
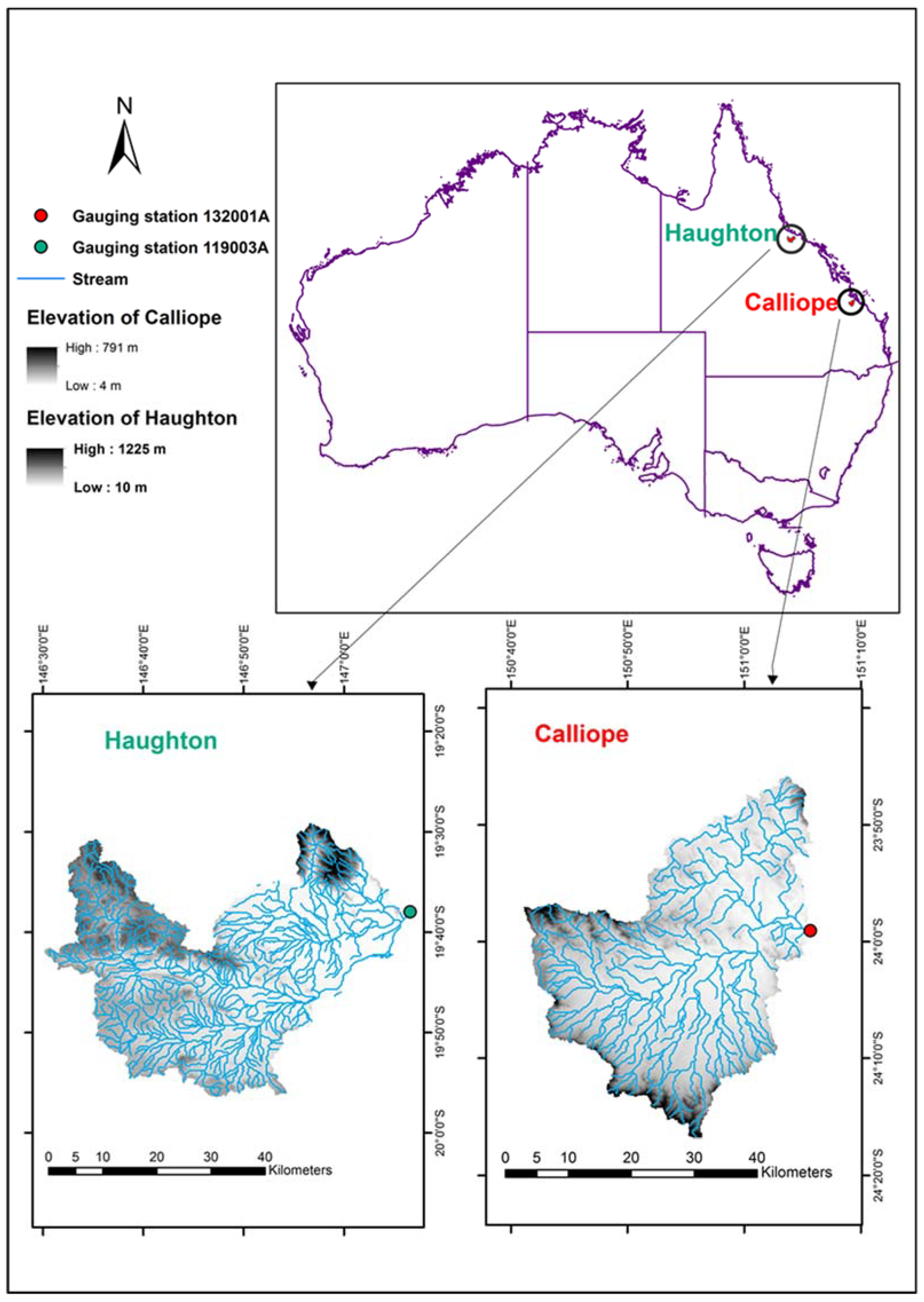

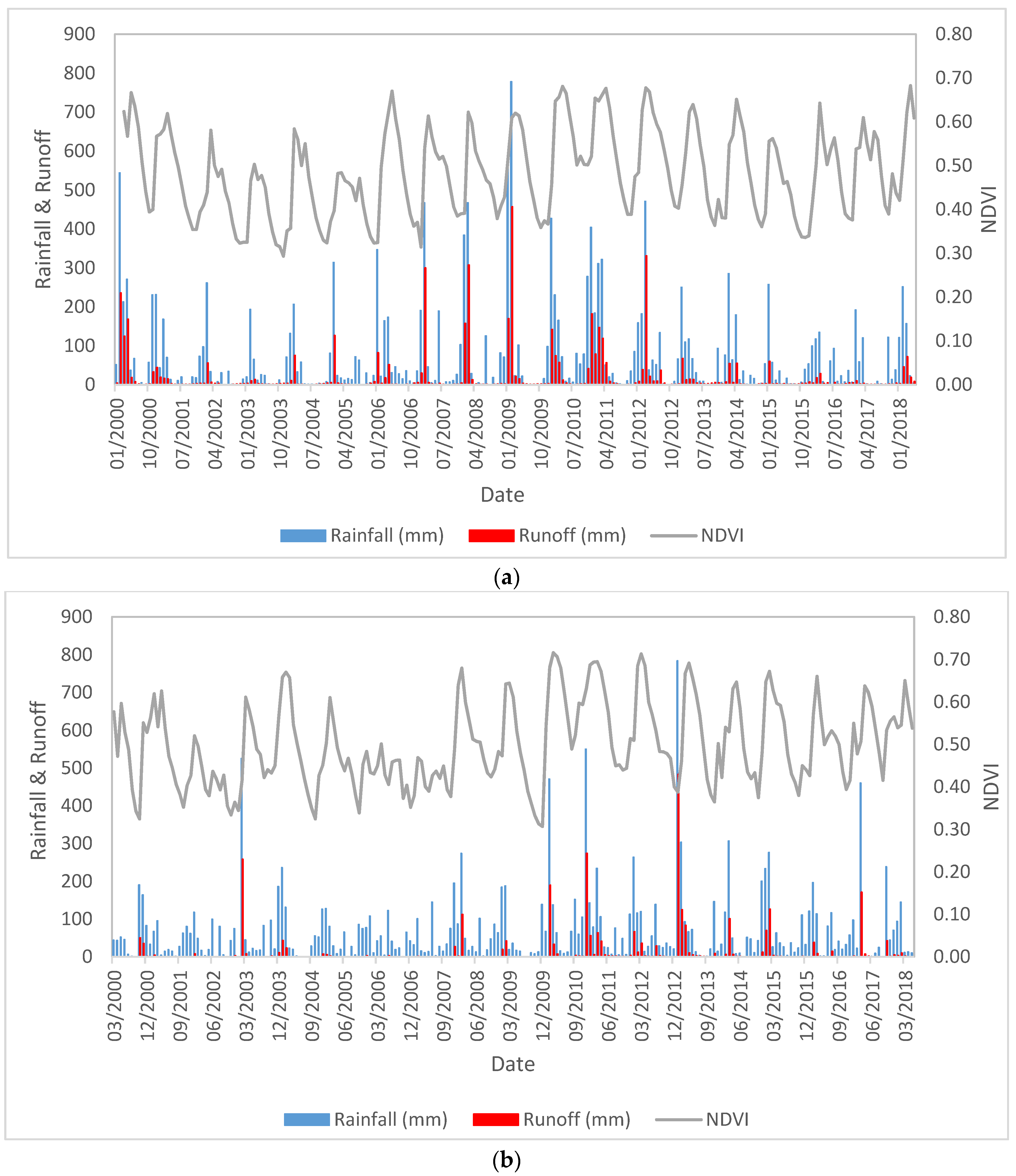
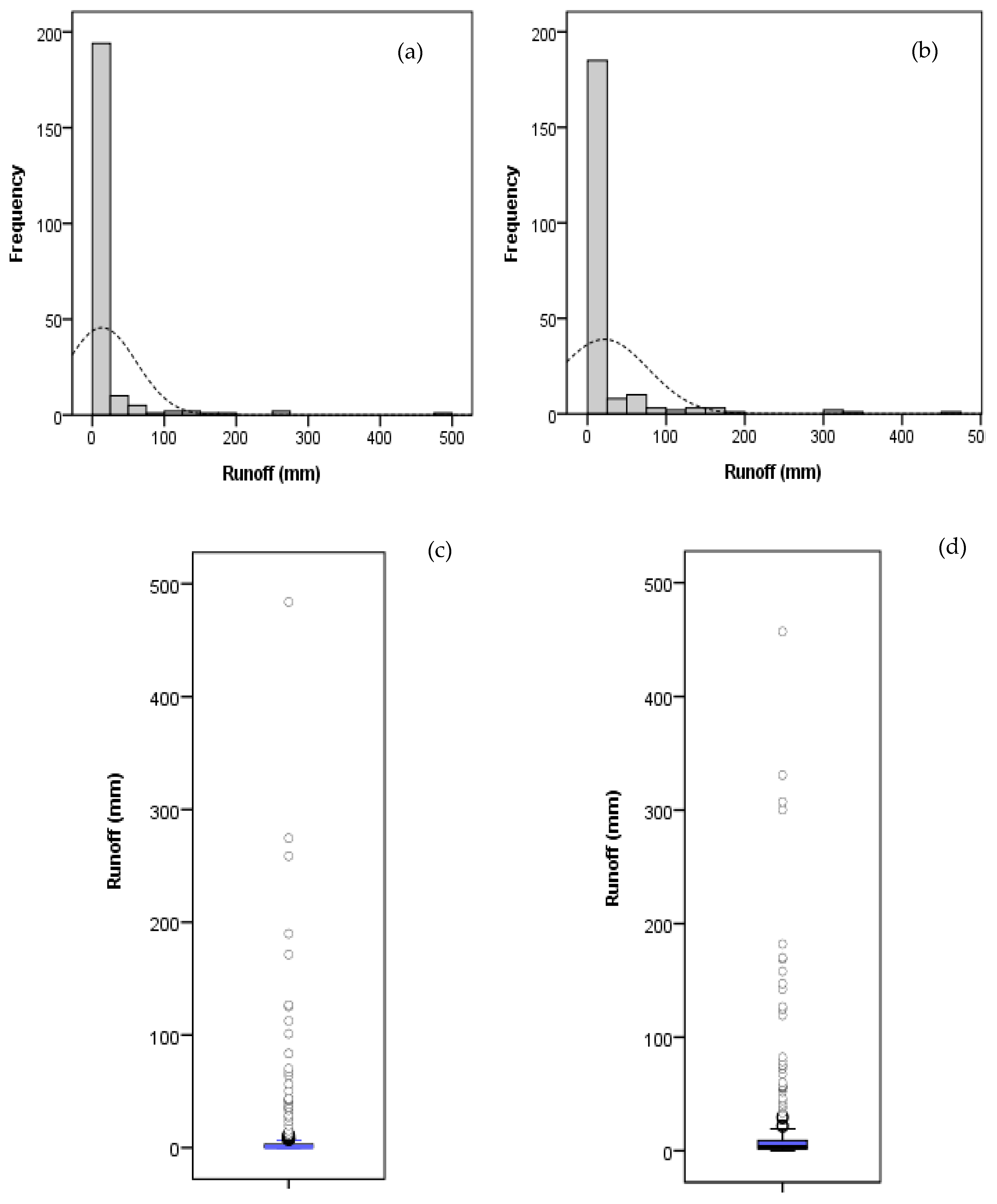

| Station Name | River | Latitude (N) | Longitude (E) | Datum of Gage (m) | Drainage Area (km2) |
|---|---|---|---|---|---|
| 119003A | Haughton River at Powerline | 19°37′59.3″ | 147°06′37.0″ | 8.875 | 1773 |
| 132001A | Calliope River at Castlehope | 23°59′05.9″ | 151°05′51.2″ | 2.439 | 1288 |
| Variable | Statistical Parameter | The Haughton River Catchment | The Calliope River Catchment | ||||
|---|---|---|---|---|---|---|---|
| Calibration (70%) | Validation (30%) | Total Data | Calibration (70%) | Validation (30%) | Total Data | ||
| Number of data | 153 | 66 | 219 | 153 | 66 | 219 | |
| Period (m/y) | March 2000–November 2012 | December 2012–May 2018 | March 2000–May 2018 | March 2000–November 2012 | December 2012–May 2018 | March 2000–May 2018 | |
| P (mm) | 0.01 | 0.27 | 0.01 | 0.00 | 0.00 | 0.00 | |
| 778.15 | 285.35 | 778.15 | 550.04 | 784.29 | 784.29 | ||
| 80.81 | 56.35 | 73.44 | 65.31 | 81.19 | 70.09 | ||
| 128.71 | 71.64 | 114.92 | 86.22 | 126.24 | 99.94 | ||
| 2.54 | 1.64 | 2.71 | 3.21 | 3.41 | 3.52 | ||
| 7.53 | 2.17 | 9.27 | 13.60 | 15.05 | 16.93 | ||
| 1.59 | 1.27 | 1.56 | 1.32 | 1.55 | 1.43 | ||
| R (mm) | 0.17 | 0.56 | 0.17 | 0.00 | 0.05 | 0.00 | |
| 457.22 | 72.33 | 457.22 | 274.59 | 483.84 | 483.84 | ||
| 26.13 | 9.19 | 21.03 | 10.16 | 21.04 | 13.44 | ||
| 65.48 | 15.67 | 55.89 | 36.44 | 67.07 | 47.88 | ||
| 4.00 | 2.87 | 4.73 | 5.69 | 5.54 | 6.38 | ||
| 18.35 | 7.70 | 26.48 | 35.32 | 35.78 | 50.22 | ||
| 2.51 | 1.70 | 2.66 | 3.59 | 3.19 | 3.56 | ||
| NDVI | 0.29 | 0.34 | 0.29 | 0.31 | 0.37 | 0.31 | |
| 0.68 | 0.68 | 0.68 | 0.72 | 0.69 | 0.72 | ||
| 0.48 | 0.49 | 0.48 | 0.49 | 0.52 | 0.50 | ||
| 0.10 | 0.09 | 0.10 | 0.10 | 0.09 | 0.10 | ||
| 0.18 | 0.13 | 0.16 | 0.47 | 0.09 | 0.34 | ||
| −1.00 | −1.09 | −1.01 | −0.57 | −1.05 | −0.74 | ||
| IC | 1.04 | 1.11 | 1.04 | 0.50 | 0.50 | 0.50 | |
| 1.84 | 1.76 | 1.84 | 1.17 | 1.12 | 1.17 | ||
| 1.33 | 1.38 | 1.34 | 0.88 | 0.88 | 0.88 | ||
| 0.19 | 0.17 | 0.19 | 0.17 | 0.16 | 0.17 | ||
| −0.84 | −0.37 | −0.69 | −0.40 | −0.35 | −0.39 | ||
| −0.12 | −0.84 | −0.38 | −0.84 | −0.81 | −0.83 | ||
| Catchment | Lag | Cross-Correlation | Partial-Autocorrelation |
|---|---|---|---|
| Haughton River | 0 | 0.88 | |
| 1 | 0.46 | 0.29 | |
| 2 | 0.11 | −0.07 | |
| 3 | 0.00 | −0.02 | |
| Calliope River | 0 | 0.89 | |
| 1 | 0.17 | 0.16 | |
| 2 | 0.08 | 0.02 | |
| 3 | 0.00 | −0.03 |
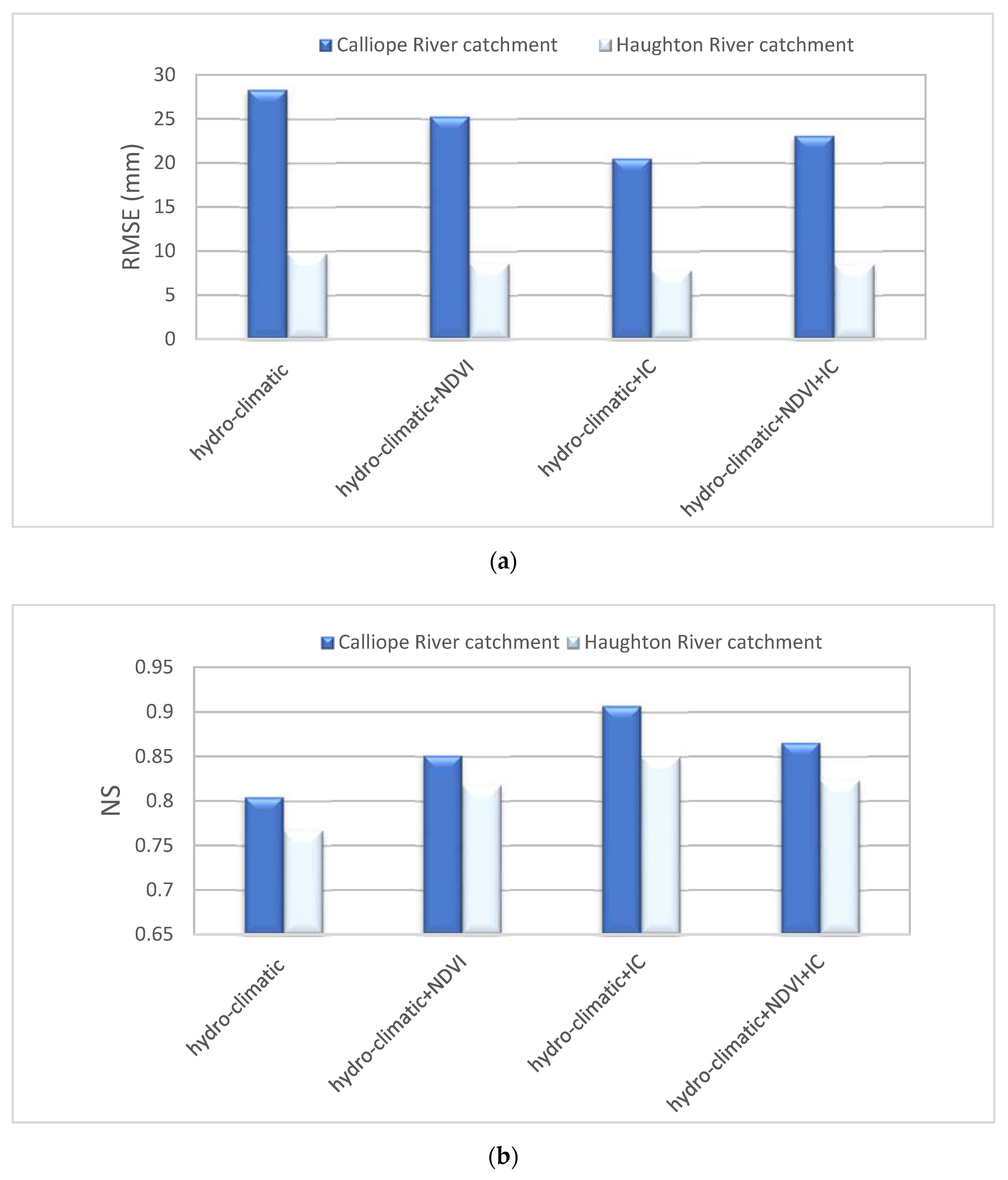
| Catchment | Inputs | Structure | Calibration | Validation | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE (mm) | NS | R2 | RMSE (mm) | NS | R2 | |||
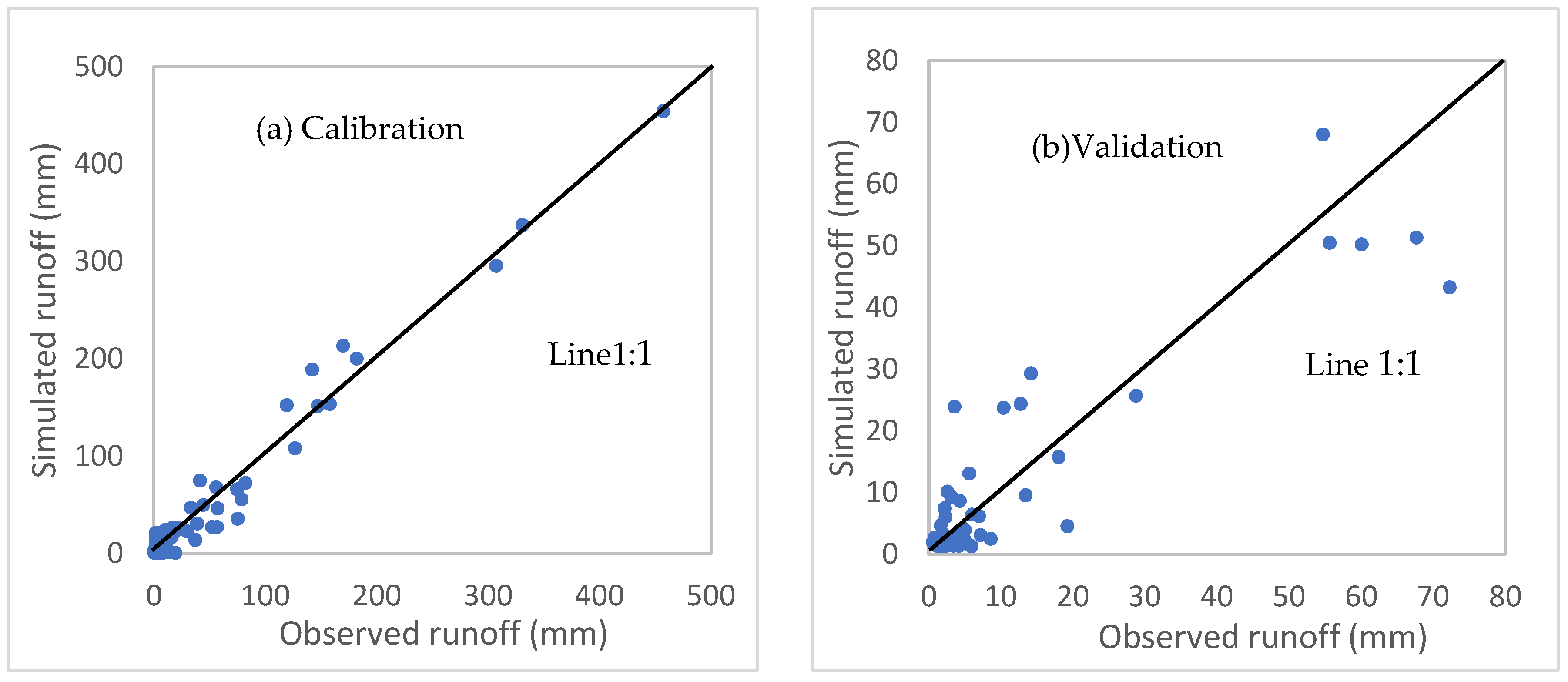
| Haughton River | 1-9-1 | 25.0 | 0.94 | 0.94 | 10.8 | 0.71 | 0.64 | |
| 2-9-1 | 22.2 | 0.95 | 0.95 | 10.4 | 0.73 | 0.74 | ||
| 2-10-1 | 21.9 | 0.96 | 0.96 | 9.4 | 0.79 | 0.69 | ||
| 2-6-1 | 16.5 | 0.94 | 0.93 | 9.3 | 0.79 | 0.73 | ||
| 3-9-1 | 17.6 | 0.90 | 0.89 | 9.4 | 0.78 | 0.68 | ||
| 3-6-1 | 15.1 | 0.97 | 0.96 | 9.1 | 0.80 | 0.76 | ||
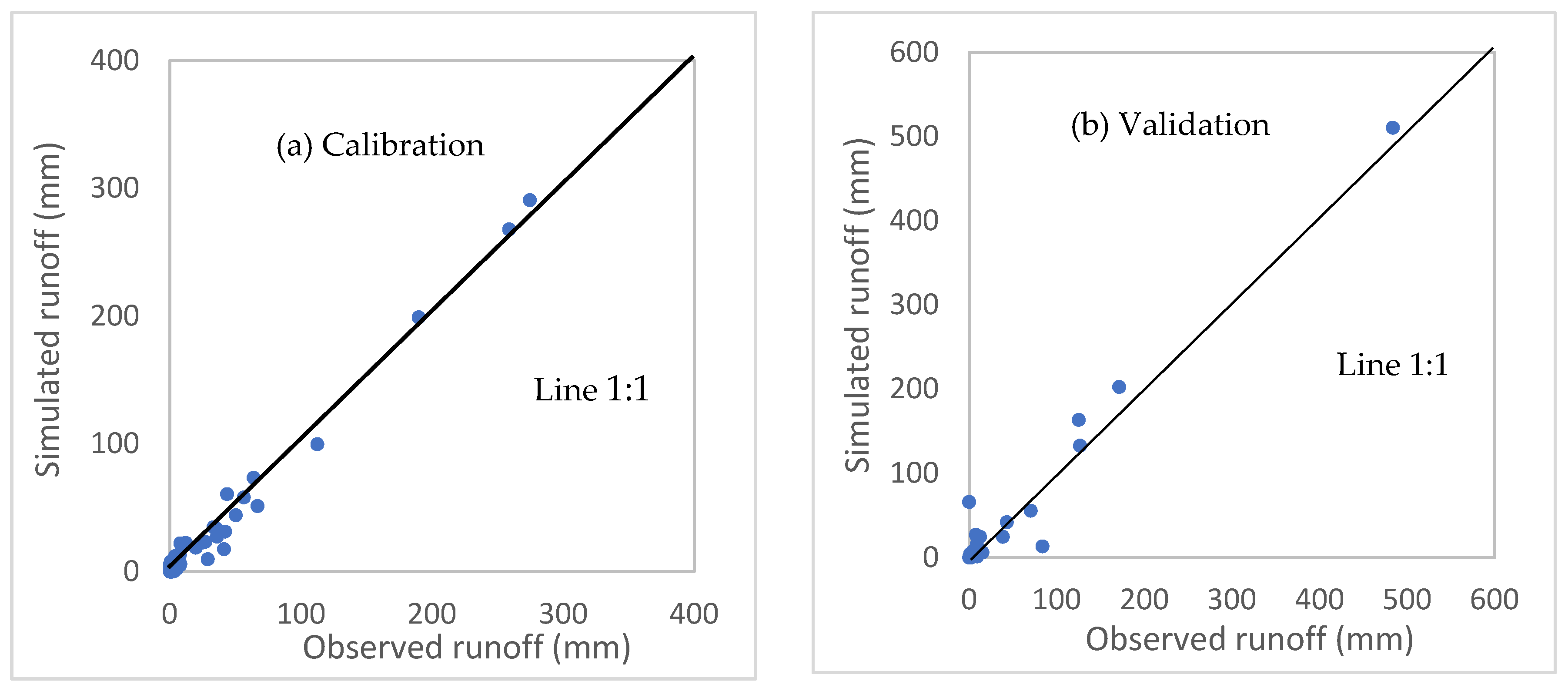
| Calliope River | 1-5-1 | 9.8 | 0.96 | 0.96 | 28.7 | 0.81 | 0.81 | |
| 2-6-1 | 9.5 | 0.95 | 0.96 | 28.5 | 0.83 | 0.82 | ||
| 2-6-1 | 10.5 | 0.95 | 0.94 | 29.8 | 0.73 | 0.74 | ||
| 2-10-1 | 9.6 | 0.95 | 0.96 | 28.0 | 0.81 | 0.81 | ||
| 3-6-1 | 8.1 | 0.97 | 0.97 | 25.7 | 0.85 | 0.85 | ||
| 3-6-1 | 9.8 | 0.93 | 0.96 | 29.3 | 0.80 | 0.80 | ||
| Inputs | Structure | Calibration | Validation | ||||
|---|---|---|---|---|---|---|---|
| RMSE (mm) | NS | R2 | RMSE (mm) | NS | R2 | ||
| 2-6-1 | 13.6 | 0.98 | 0.96 | 9.1 | 0.80 | 0.76 | |
| 3-10-1 | 8.3 | 0.99 | 0.99 | 7.7 | 0.85 | 0.79 | |
| 3-6-1 | 15.1 | 0.97 | 0.95 | 7.8 | 0.85 | 0.79 | |
| 2-10-1 | 12.5 | 0.98 | 0.96 | 7.2 | 0.87 | 0.82 | |
| 3-11-1 | 12.1 | 0.98 | 0.97 | 7.4 | 0.87 | 0.81 | |
| 3-5-1 | 14.8 | 0.97 | 0.95 | 7.4 | 0.87 | 0.81 | |
| 3-9-1 | 14.7 | 0.97 | 0.96 | 8.2 | 0.84 | 0.76 | |
| 4-10-1 | 14.2 | 0.97 | 0.97 | 8.4 | 0.83 | 0.75 | |
| 4-10-1 | 19.2 | 0.95 | 0.93 | 10.1 | 0.75 | 0.71 | |
| 3-6-1 | 14.8 | 0.97 | 0.96 | 8.4 | 0.83 | 0.79 | |
| 4-11-1 | 19.8 | 0.95 | 0.93 | 9.7 | 0.77 | 0.74 | |
| 4-11-1 | 14.4 | 0.97 | 0.95 | 8.9 | 0.81 | 0.73 | |
| 3-6-1 | 16.3 | 0.97 | 0.95 | 8.2 | 0.84 | 0.76 | |
| 4-6-1 | 15.7 | 0.97 | 0.97 | 8.5 | 0.82 | 0.79 | |
| 4-6-1 | 13.7 | 0.98 | 0.96 | 8.3 | 0.83 | 0.81 | |
| 4-6-1 | 19.7 | 0.95 | 0.93 | 7.5 | 0.86 | 0.80 | |
| 5-5-1 | 17.4 | 0.96 | 0.95 | 8.2 | 0.83 | 0.76 | |
| 5-6-1 | 14.4 | 0.97 | 0.95 | 8.3 | 0.83 | 0.77 | |
| Inputs | Structure | Calibration | Validation | ||||
|---|---|---|---|---|---|---|---|
| RMSE (mm) | NS | R2 | RMSE (mm) | NS | R2 | ||
| 2-10-1 | 9.3 | 0.96 | 0.92 | 19.0 | 0.92 | 0.93 | |
| 3-7-1 | 8.8 | 0.96 | 0.96 | 25.6 | 0.85 | 0.88 | |
| 3-6-1 | 7.8 | 0.969 | 0.95 | 29.0 | 0.81 | 0.89 | |
| 2-10-1 | 8.6 | 0.96 | 0.95 | 18.8 | 0.92 | 0.92 | |
| 3-9-1 | 6.2 | 0.98 | 0.97 | 20.9 | 0.90 | 0.92 | |
| 3-10-1 | 5.8 | 0.98 | 0.94 | 23.6 | 0.87 | 0.88 | |
| 3-11-1 | 8.2 | 0.97 | 0.97 | 18.5 | 0.94 | 0.96 | |
| 4-11-1 | 6.4 | 0.98 | 0.97 | 22.7 | 0.88 | 0.88 | |
| 4-7-1 | 13.5 | 0.91 | 0.94 | 19.0 | 0.92 | 0.92 | |
| 3-7-1 | 6.5 | 0.98 | 0.98 | 26.5 | 0.84 | 0.86 | |
| 4-11-1 | 6.4 | 0.98 | 0.95 | 27.6 | 0.83 | 0.83 | |
| 4-6-1 | 6.8 | 0.98 | 0.98 | 24.1 | 0.87 | 0.88 | |
| 3-11-1 | 6.1 | 0.98 | 0.99 | 18.0 | 0.95 | 0.96 | |
| 4-10-1 | 6.4 | 0.98 | 0.97 | 18.4 | 0.92 | 0.93 | |
| 4-7-1 | 9.5 | 0.95 | 0.96 | 23.6 | 0.87 | 0.87 | |
| 4-10-1 | 6.6 | 0.98 | 0.98 | 22.3 | 0.89 | 0.91 | |
| 5-6-1 | 10.5 | 0.94 | 0.95 | 27.9 | 0.82 | 0.86 | |
| 5-10-1 | 8.6 | 0.96 | 0.97 | 28.4 | 0.75 | 0.74 | |
| Input Pattern | Haughton River | Calliope River | ||
|---|---|---|---|---|
| The Best Model | %REp | The Best Model | %REp | |
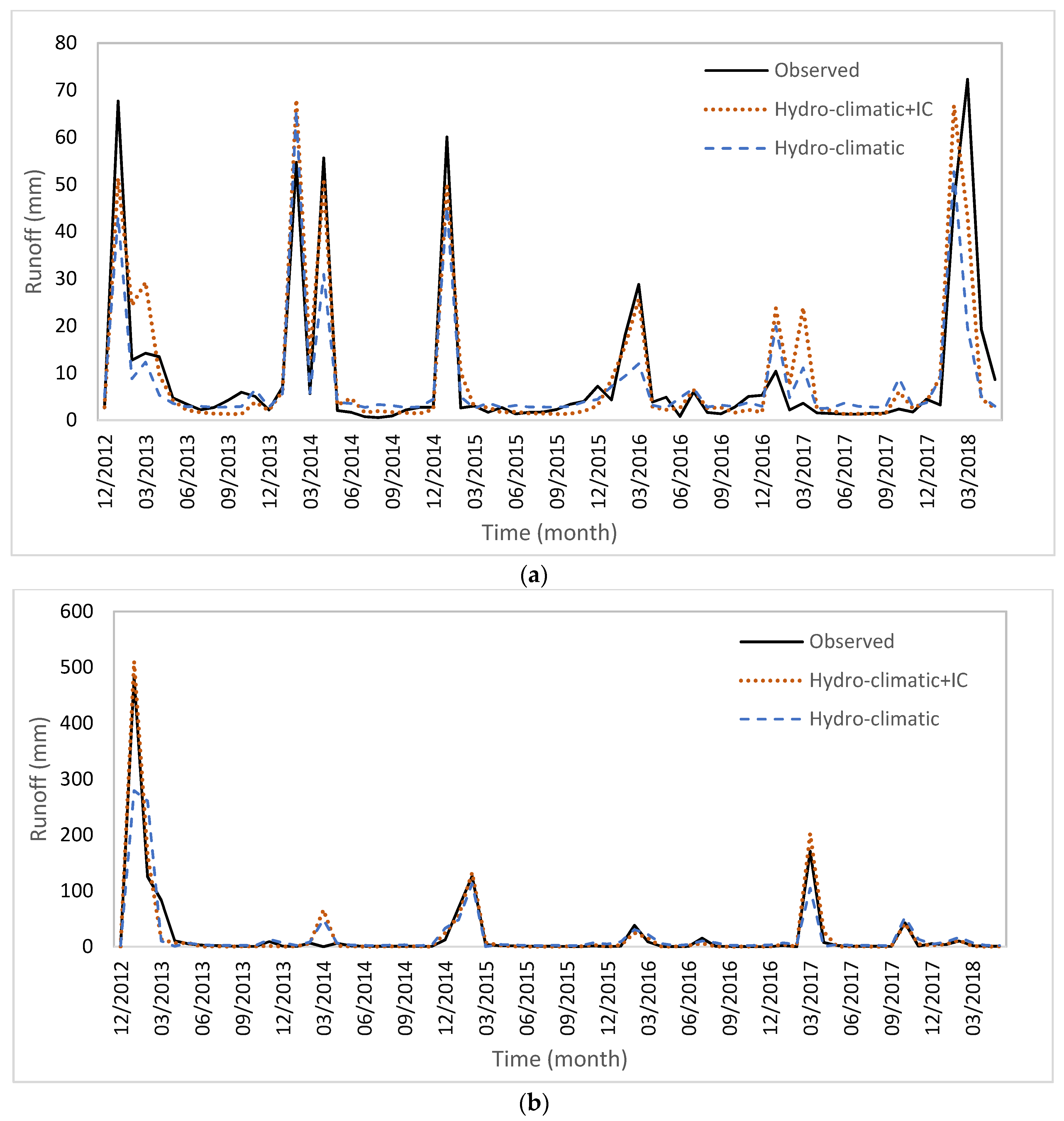
| Hydro-climatic | −36.1 | −17.9 | ||
| Hydro-climatic + IC | −12.8 | −3.9 | ||
| Hydro-climatic + NDVI | −14.0 | −16.4 | ||
| Hydro-climatic + NDVI+IC | –15.6 | −22.3 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asadi, H.; Shahedi, K.; Jarihani, B.; Sidle, R.C. Rainfall-Runoff Modelling Using Hydrological Connectivity Index and Artificial Neural Network Approach. Water 2019, 11, 212. https://doi.org/10.3390/w11020212
Asadi H, Shahedi K, Jarihani B, Sidle RC. Rainfall-Runoff Modelling Using Hydrological Connectivity Index and Artificial Neural Network Approach. Water. 2019; 11(2):212. https://doi.org/10.3390/w11020212
Chicago/Turabian StyleAsadi, Haniyeh, Kaka Shahedi, Ben Jarihani, and Roy C. Sidle. 2019. "Rainfall-Runoff Modelling Using Hydrological Connectivity Index and Artificial Neural Network Approach" Water 11, no. 2: 212. https://doi.org/10.3390/w11020212
APA StyleAsadi, H., Shahedi, K., Jarihani, B., & Sidle, R. C. (2019). Rainfall-Runoff Modelling Using Hydrological Connectivity Index and Artificial Neural Network Approach. Water, 11(2), 212. https://doi.org/10.3390/w11020212






