Advanced Soft Computing Techniques for Monthly Streamflow Prediction in Seasonal Rivers
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
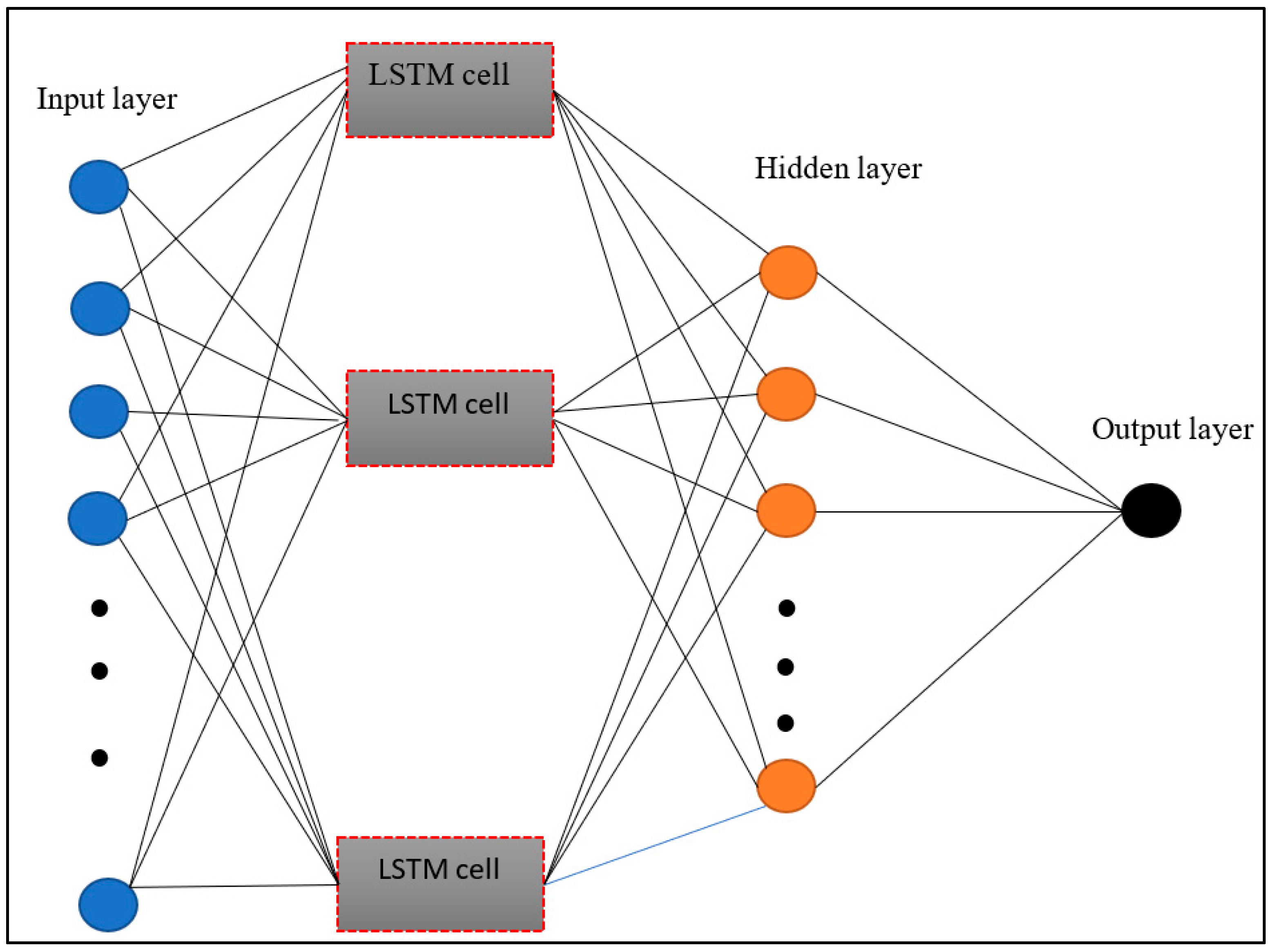
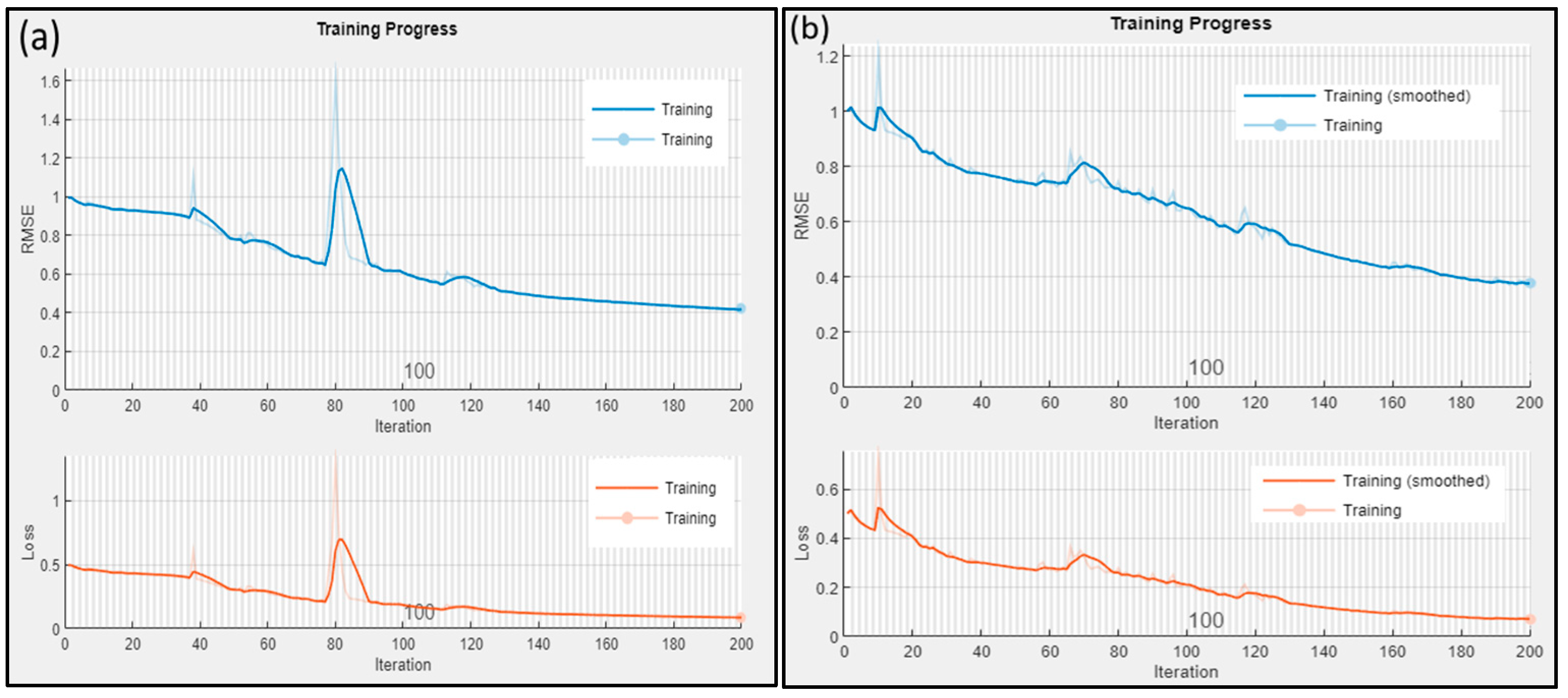
2.2. Long Short-Term Memory (LSTM)
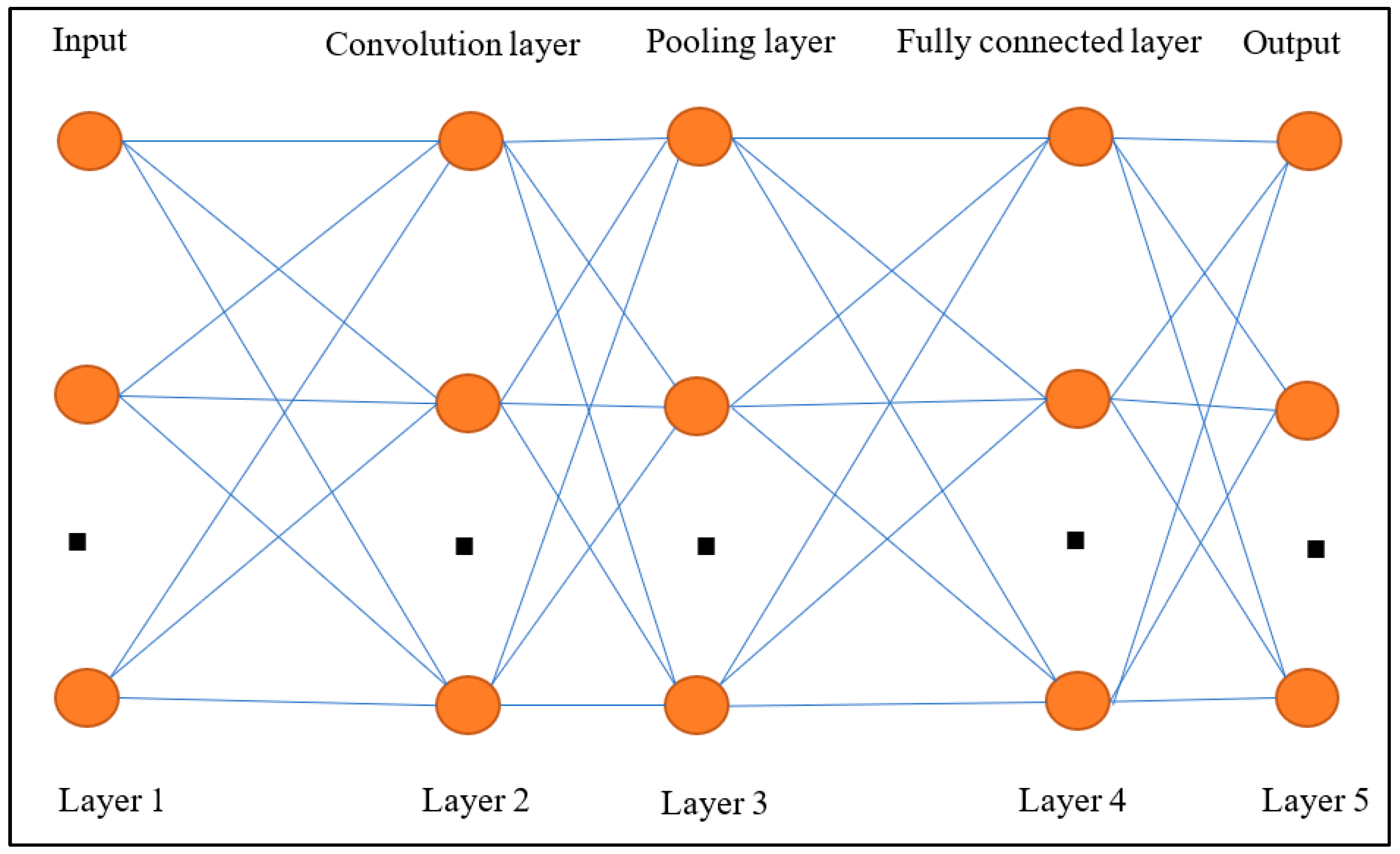
2.3. Convolutional Neural Network (CNN)
2.4. Recurrent Neural Network (RNN)
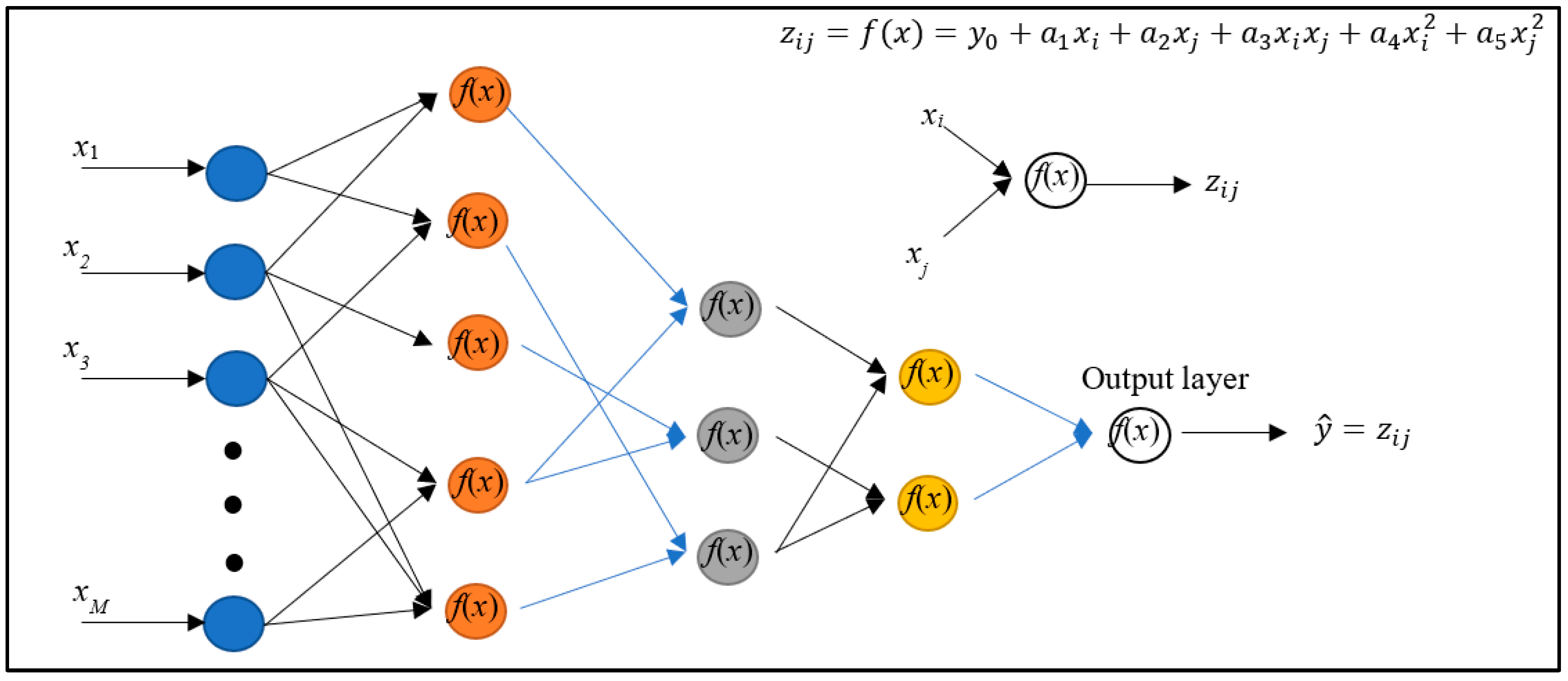
2.5. The Group Method of Data Handling Model (GMDH)
2.6. Selection of Model Input Combinations
2.7. Measurement of Model Prediction Success
3. Results
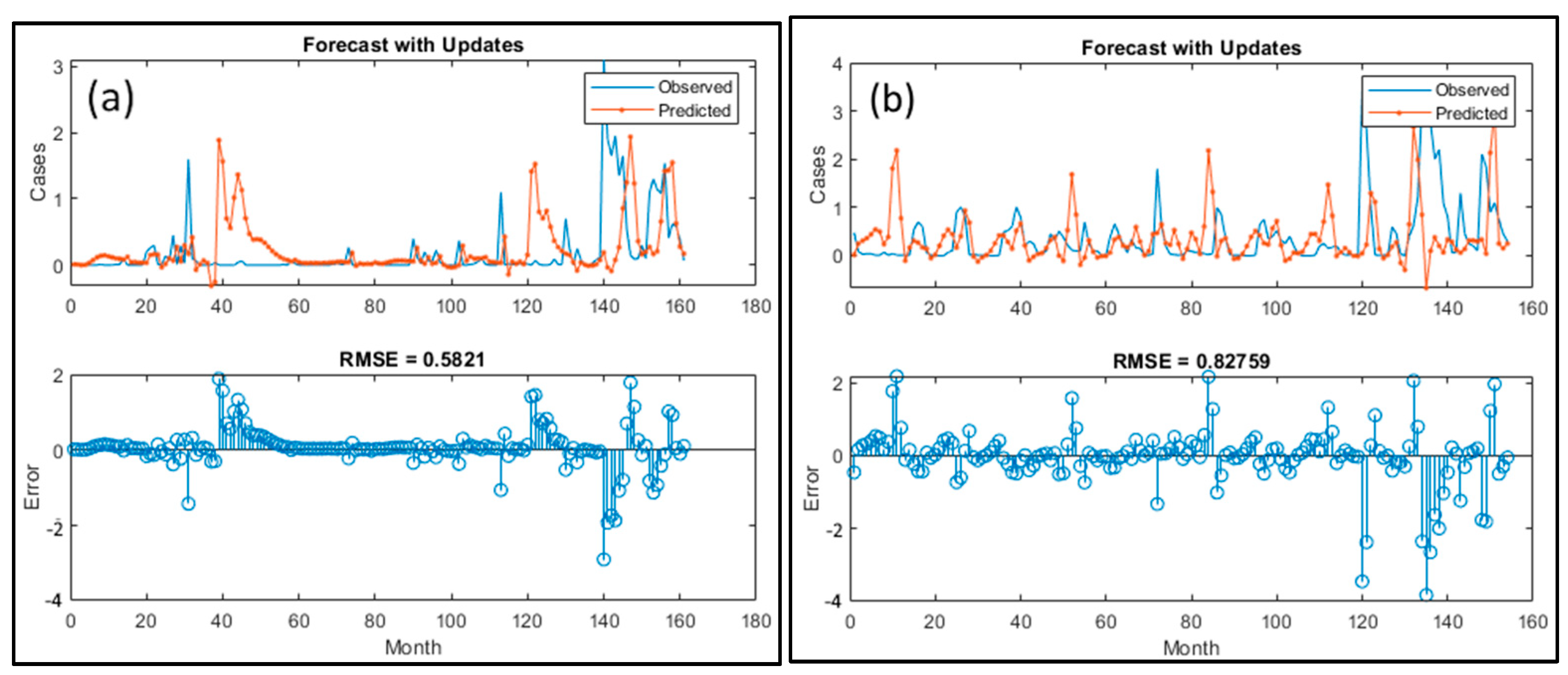
3.1. CNN-RNN Results
3.2. GMDH Results
3.3. LSTM Model Results
3.4. Evaluation of the Performance of Models
4. Discussion
5. Conclusions
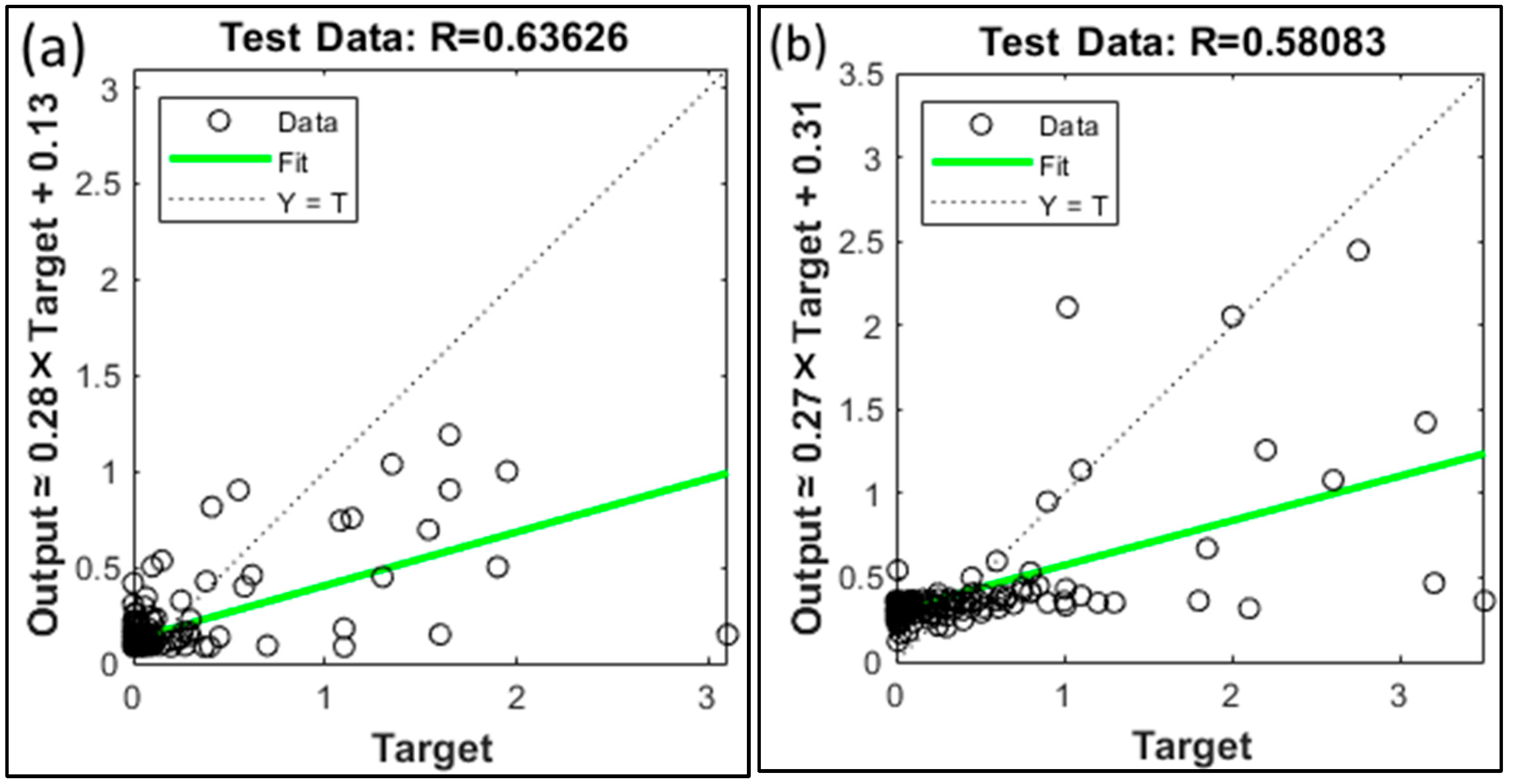
- At the Sidi AEK Djillali station, the GMDH model outperformed both the LSTM and CNN-RNN models across all four evaluation metrics.
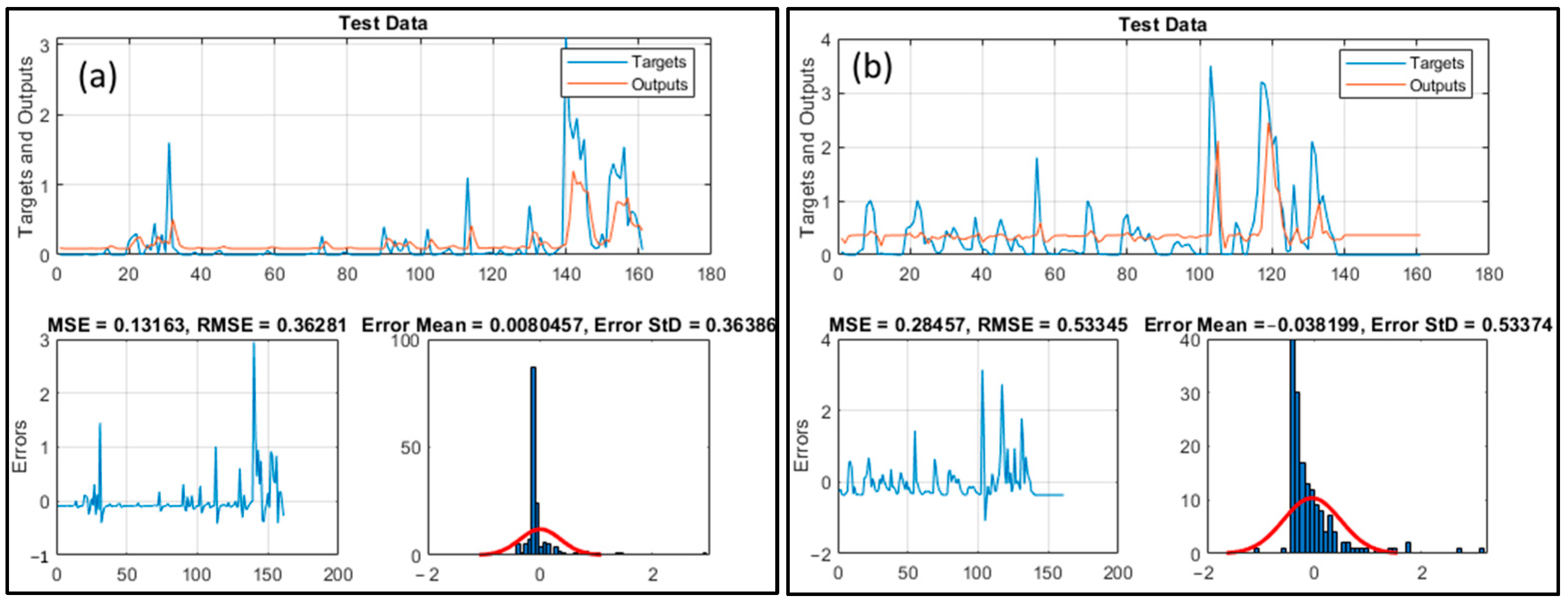
- The GMDH model registered MSE and MAE values of 0.132 and 0.185, respectively, highlighting its enhanced predictive accuracy. Its R value of 0.636 demonstrates strong alignment with observed data, and its minimal MBE of −0.008 indicates reduced bias.
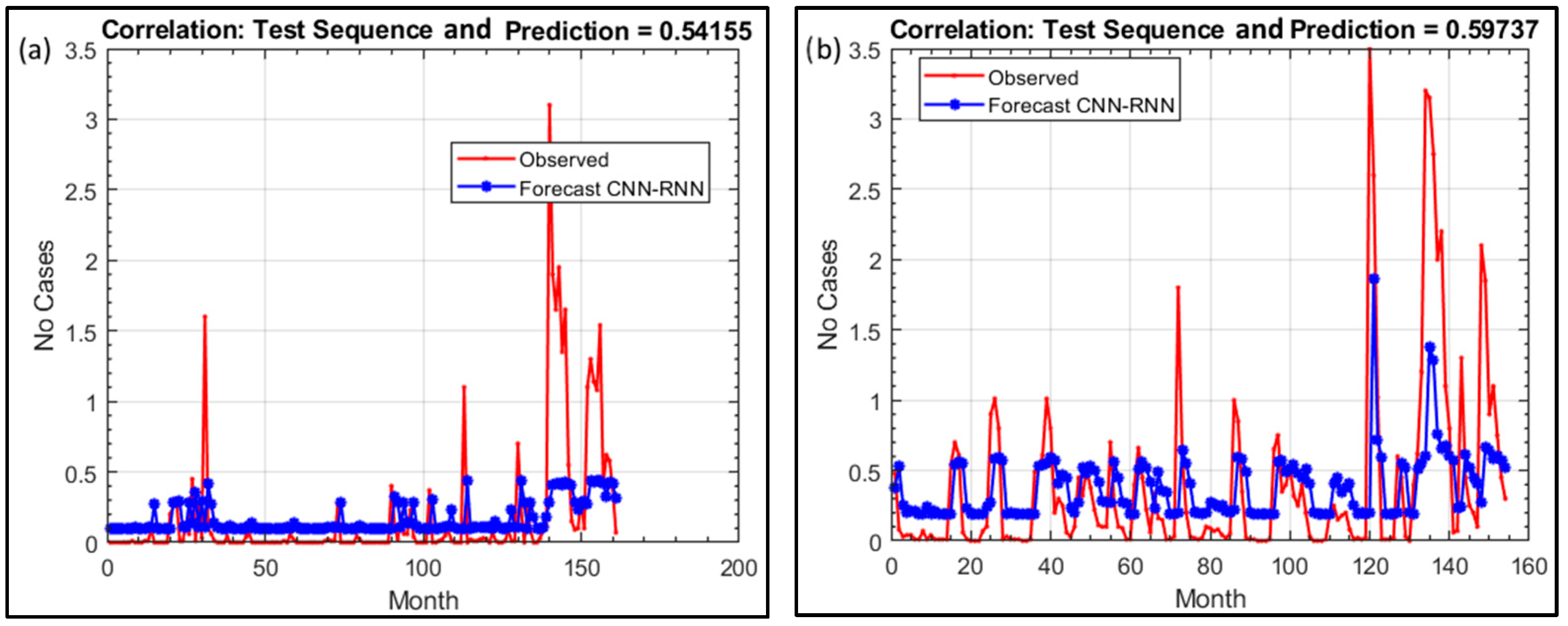
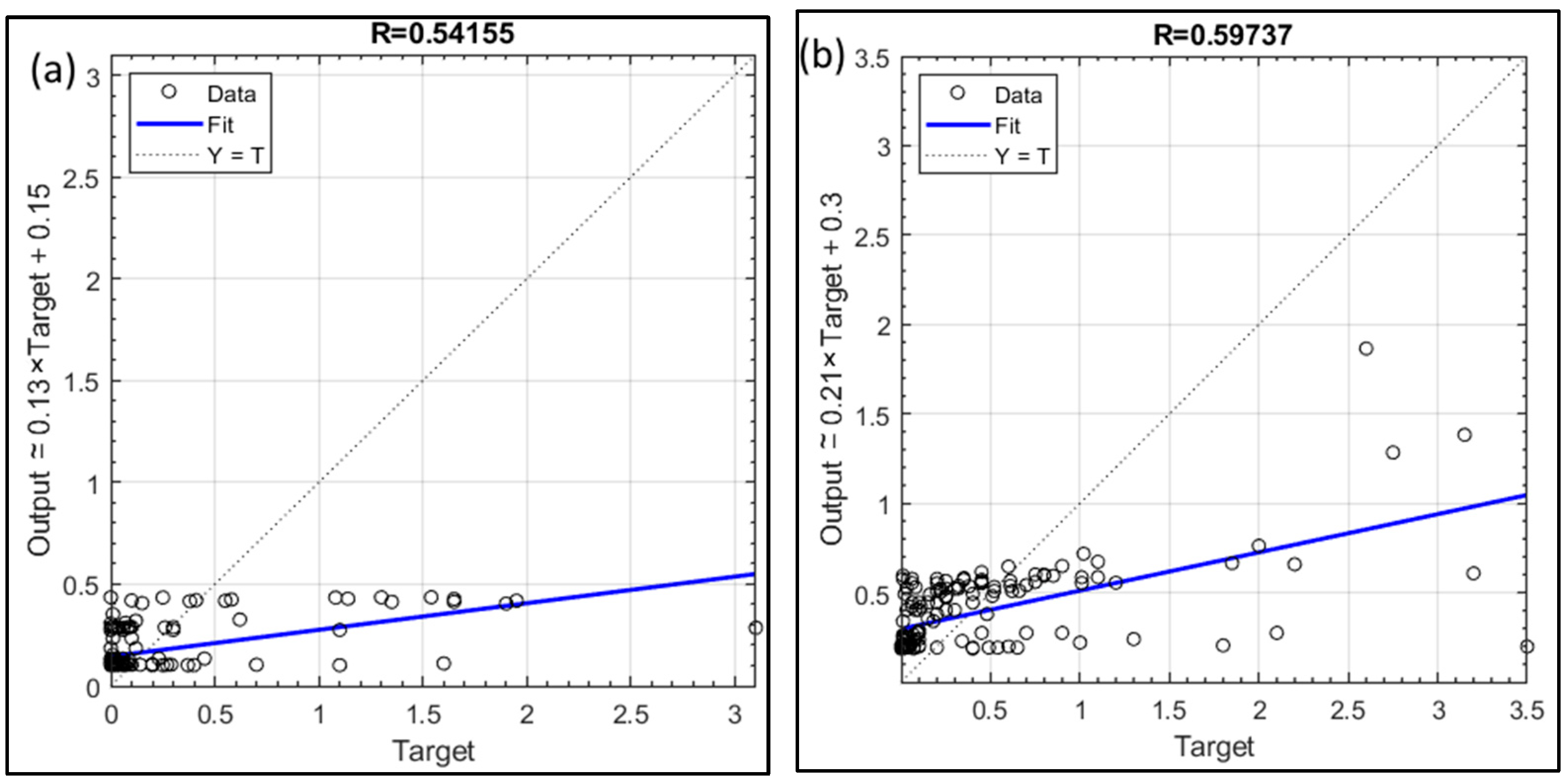
- At the Kef Mehboula station, the GMDH and CNN-RNN models outperformed the LSTM model. The CNN-RNN model had the most favorable MSE value of 0.285, while the GMDH model performed best in MAE, scoring 0.335. Both models exhibited strong correlation coefficients with observed data, with R values of 0.581 and 0.597, respectively.
- The GMDH model showed a modest overestimation with a positive MBE (0.038). Overall, the GMDH model performed best at both stations, but all three models demonstrated promise for predicting monthly streamflow time series.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ConvLSTM | Convolutional LSTM |
| CNN | Convolutional neural networks |
| LSTM | Long short-term memory |
| RNN | Recurrent neural network |
| MLR | Multiple linear regression |
| PSO | Particle swarm optimization |
| ANFIS | Adaptive neuro-fuzzy inference system |
| GMDH | Group method of data handling |
| MSE | Mean square error |
| MBE | Mean bias error |
| MAE | Mean absolute error |
| R | Correlation coefficient |
| ML | Machine learning |
| BN | Bayesian networks |
| GEP | Gene expression programming |
| AR | Autoregressive |
| ARMA | Autoregressive moving average |
| RT | Random tree |
| KNN | K-nearest neighbor |
| GP | Gaussian process |
| ANN | Artificial neural network |
| ELM | Extreme learning machine |
| MLP | Multilayer perceptron |
| RF | Random forest |
| DWT | Discrete wavelet transform |
| ABC | Artificial bee colony |
| LMD | Local mean decomposition |
| LWLR | Locally weighted linear regression |
| SARIMA | Seasonal autoregressive integrated moving average |
| LSSVM | Least squares support vector machine |
References
- Mehdizadeh, S.; Kozekalani Sales, A. A Comparative Study of Autoregressive, Autoregressive Moving Average, Gene Expression Programming and Bayesian Networks for Estimating Monthly Streamflow. Water Resour. Manag. 2018, 32, 3001–3022. [Google Scholar] [CrossRef]
- Al-Juboori, A.M. A Hybrid Model to Predict Monthly Streamflow Using Neighboring Rivers Annual Flows. Water Resour. Manag. 2021, 35, 729–743. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Yuan, X.; Xu, Z. An improved long short-term memory network for streamflow forecasting in the upper Yangtze River. Stoch. Environ. Res. Risk Assess. 2020, 34, 1313–1329. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Fu, M.; Wang, C.; Mohtar, W.H.M.W.; Deo, R.C.; El-Shafie, A. Application of the Hybrid Artificial Neural Network Coupled with Rolling Mechanism and Grey Model Algorithms for Streamflow Forecasting Over Multiple Time Horizons. Water Resour. Manag. 2018, 32, 1883–1899. [Google Scholar] [CrossRef]
- Samanataray, S.; Sahoo, A.A. Comparative Study on Prediction of Monthly Streamflow Using Hybrid ANFIS-PSO Approaches. KSCE J. Civ. Eng. 2021, 25, 4032–4043. [Google Scholar] [CrossRef]
- Shu, X.; Ding, W.; Peng, Y.; Wang, Z.; Wu, J.; Li, M. Monthly Streamflow Forecasting Using Convolutional Neural Network. Water Resour. Manag. 2021, 35, 5089–5104. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, D.; Wang, G.; Qiu, J.; Long, K.; Du, Y.; Dai, Y.; Xie, H.; Wei, Z.; Shangguan, W.; et al. A hybrid deep learning algorithm and its application to streamflow prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Tiefenbacher, J.P. Using Optimized Deep Learning to Predict Daily Streamflow: A Comparison to Common Machine Learning Algorithms. Water Resour. Manag. 2022, 36, 699–716. [Google Scholar] [CrossRef]
- Forghanparast, F.; Mohammadi, G. Using Deep Learning Algorithms for Intermittent Streamflow Prediction in the Headwaters of the Colorado River, Texas. Water 2022, 14, 2972. [Google Scholar] [CrossRef]
- Haznedar, B.; Kilinc, H.C.; Ozkan, F.; Yurtsever, A. Streamflow forecasting using a hybrid LSTM-PSO approach: The case of Seyhan Basin. Nat. Hazards 2023, 117, 681–701. [Google Scholar] [CrossRef]
- Katipoğlu, O.M. Monthly streamflow prediction in Amasya, Türkiye, using an integrated approach of a feedforward backpropagation neural network and discrete wavelet transform. Model. Earth Syst. Environ. 2023, 9, 2463–2475. [Google Scholar] [CrossRef]
- Katipoğlu, O.M.; Keblouti, M.; Mohammadi, B. Application of novel artificial bee colony optimized ANN and data preprocessing techniques for monthly streamflow estimation. Environ. Sci. Pollut. Res. 2023, 30, 89705–89725. [Google Scholar] [CrossRef]
- Abda, Z.; Zerouali, B.; Chettih, M.; Santos, C.A.G.; de Farias, C.A.S.; Elbeltagi, A. Assessing machine learning models for streamflow estimation: A case study in Oued Sebaou watershed (Northern Algeria). Hydrol. Sci. J. 2022, 67, 1328–1341. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Mellak, S. Stream flow prediction using a new approach of hybrid artificial neural network with discrete wavelet transform. A case study: The catchment of Seybouse in northeastern Algeria. Alger. J. Environ. Sci. Technol. 2022, 8, 2435–2439. [Google Scholar]
- Beddal, D.; Achite, M.; Baahmed, D. Streamflow prediction using data-driven models: Case study of Wadi Hounet, northwestern Algeria. J. Water Land Dev. 2020, 47, 16–24. [Google Scholar] [CrossRef]
- Karakoyun, E.; Kaya, N. Hydrological simulation and prediction of soil erosion using the SWAT model in a mountainous watershed: A case study of Murat River Basin, Turkey. J. Hydroinf. 2022, 24, 1175–1193. [Google Scholar] [CrossRef]
- Mehr, A.D.; Ghadimi, S.; Marttila, H.; Haghighi, A.T. A new evolutionary time series model for streamflow forecasting in boreal lake-river systems. Theor. Appl. Climatol. 2022, 148, 255–268. [Google Scholar] [CrossRef]
- Atashi, V.; Gorji, H.T.; Shahabi, S.M.; Kardan, R.; Lim, Y.H. Water level forecasting using deep learning time-series analysis: A case study of red river of the north. Water 2022, 14, 1971. [Google Scholar] [CrossRef]
- Kartal, V.; Karakoyun, E.; Akiner, M.E.; Katipoğlu, O.M.; Kuriqi, A. Optimizing river flow rate predictions: Integrating cognitive approaches and meteorological insights. Nat. Hazards 2024, 1–28. [Google Scholar] [CrossRef]
- Roniki, A.; Swain, R.; Behera, M.D. Future projections of worst floods and dam break analysis in Mahanadi River Basin under CMIP6 climate change scenarios. Environ. Monit. Assess. 2023, 195, 1173. [Google Scholar]
- Fatemeh, G.; Kang, D. Improving long-term streamflow prediction in a poorly gauged basin using geo-spatiotemporal mesoscale data and attention-based deep learning: A comparative study. J. Hydrol. 2022, 615, 128608. [Google Scholar]
- Achite, M.; Touaibia, B. Sécheresse et gestion des ressources en eau dans le bassin versant de la Mina. In Proceedings of the 2ème Colloque International Sur L’eau et L’Environnement, Sidi Fredj, Algérie, 30 January 2007. [Google Scholar]
- Achite, M.; Wałęga, A.; Toubal, A.K.; Mansour, H.; Krakauer, N. Spatiotemporal characteristics and trends of meteorological droughts in the wadi mina basin, northwest algeria. Water 2021, 13, 3103. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. Daily urban air quality index forecasting based on variational mode decomposition, sample entropy and LSTM neural network. Sustain. Cities Soc. 2019, 50, 101657. [Google Scholar] [CrossRef]
- Zuo, R.; Xiong, Y.; Wang, J.; Carranza, E.J.M. Deep learning and its application in geochemical mapping. Earth-Sci. Rev. 2019, 192, 1–14. [Google Scholar] [CrossRef]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional time series forecasting with convolutional neural networks. arXiv 2017, arXiv:1703.04691. [Google Scholar]
- Hoseinzade, E.; Haratizadeh, S. CNNpred: CNN-based stock market prediction using a diverse set of variables. Expert Syst. Appl. 2019, 129, 273–285. [Google Scholar] [CrossRef]
- Salman, A.G.; Kanigoro, B.; Heryadi, Y. Weather forecasting using deep learning techniques. In Proceedings of the International Conference on Advanced Computer Science and Information Systems (ICACSIS), Depok, Indonesia, 10–11 October 2015; pp. 281–285. [Google Scholar]
- Dikshit, A.; Pradhan, B.; Huete, A. An improved SPEI drought forecasting approach using the long short-term memory neural network. J. Environ. Manag. 2021, 283, 111979. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Cao, J.; Zhu, J. An LSTM Short-Term Solar Irradiance Forecasting under Complicated Weather Conditions. IEEE Access 2019, 7, 145651–145666. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R.; Xiang, Y.; Sankaran, A.; Deo, R.C.; Xiao, F.; Zhu, S. Advanced extreme learning machines vs. deep learning models for peak wave energy period forecasting: A case study in Queensland, Australia. Renew. Energy 2021, 177, 1031–1044. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Polynomial theory of complex systems. IEEE Trans. Syst. Man Cybern. 1971, SMC-1, 364–378. [Google Scholar] [CrossRef]
- Nariman-Zadeh, N.; Darvizeh, A.; Felezi, M.E.; Gharababaei, H. Polynomial modelling of explosive compaction process of metallic powders using GMDH-type neural networks and singular value decomposition. Model. Simul. Mater. Sci. Eng. 2002, 10, 727–744. [Google Scholar] [CrossRef]
- Samsudin, R.; Saad, P.; Shabri, A. A hybrid least squares support vector machines and GMDH approach for river flow forecasting. Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 3691–3731. [Google Scholar]
- Ghorbani, M.A.; Deo, R.C.; Karimi, V.; Yaseen, Z.M.; Terzi, O. Implementation of a hybrid MLP-FFA model for water level prediction of Lake Egirdir, Turkey. Stoch. Environ. Res. Risk Assess. 2018, 32, 1683–1697. [Google Scholar] [CrossRef]
- Dehghani, A.; Moazam, H.M.Z.H.; Mortazavizadeh, F.; Ranjbar, V.; Mirzaei, M.; Mortezavi, S.; Ng, J.L.; Dehghani, A. Comparative evaluation of LSTM, CNN, and ConvLSTM for hourly short-term streamflow forecasting using deep learning approaches. Ecol. Inform. 2023, 75, 102119. [Google Scholar] [CrossRef]
- Khodakhah, H.; Aghelpour, P.; Hamedi, Z. Comparing linear and non-linear data-driven approaches in monthly river flow prediction, based on the models SARIMA, LSSVM, ANFIS, and GMDH. Environ. Sci. Pollut. Res. 2022, 29, 21935–21954. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow prediction using an integrated methodology based on convolutional neural network and long short-term memory networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Fang, F.; Kinouchi, T.; Navon, I.M.; Pain, C.C. Long lead-time daily and monthly streamflow forecasting using machine learning methods. J. Hydrol. 2020, 590, 125376. [Google Scholar] [CrossRef]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019, 67, 1471–1481. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, Y.; Son, S.W.; Luo, J.J.; Oh, S.G.; Wang, Y. A deep-learning ensemble method to detect atmospheric rivers and its application to projected changes in precipitation regime. J. Geophys. Res. Atmos. 2023, 128, e2022JD037041. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, Y.; Li, J.; Chen, B.; Deng, L.; Wen, D. East Asia atmospheric river forecast with a deep learning method: GAN-UNet. J. Geophys. Res. Atmos. 2024, 129, e2023JD039311. [Google Scholar] [CrossRef]
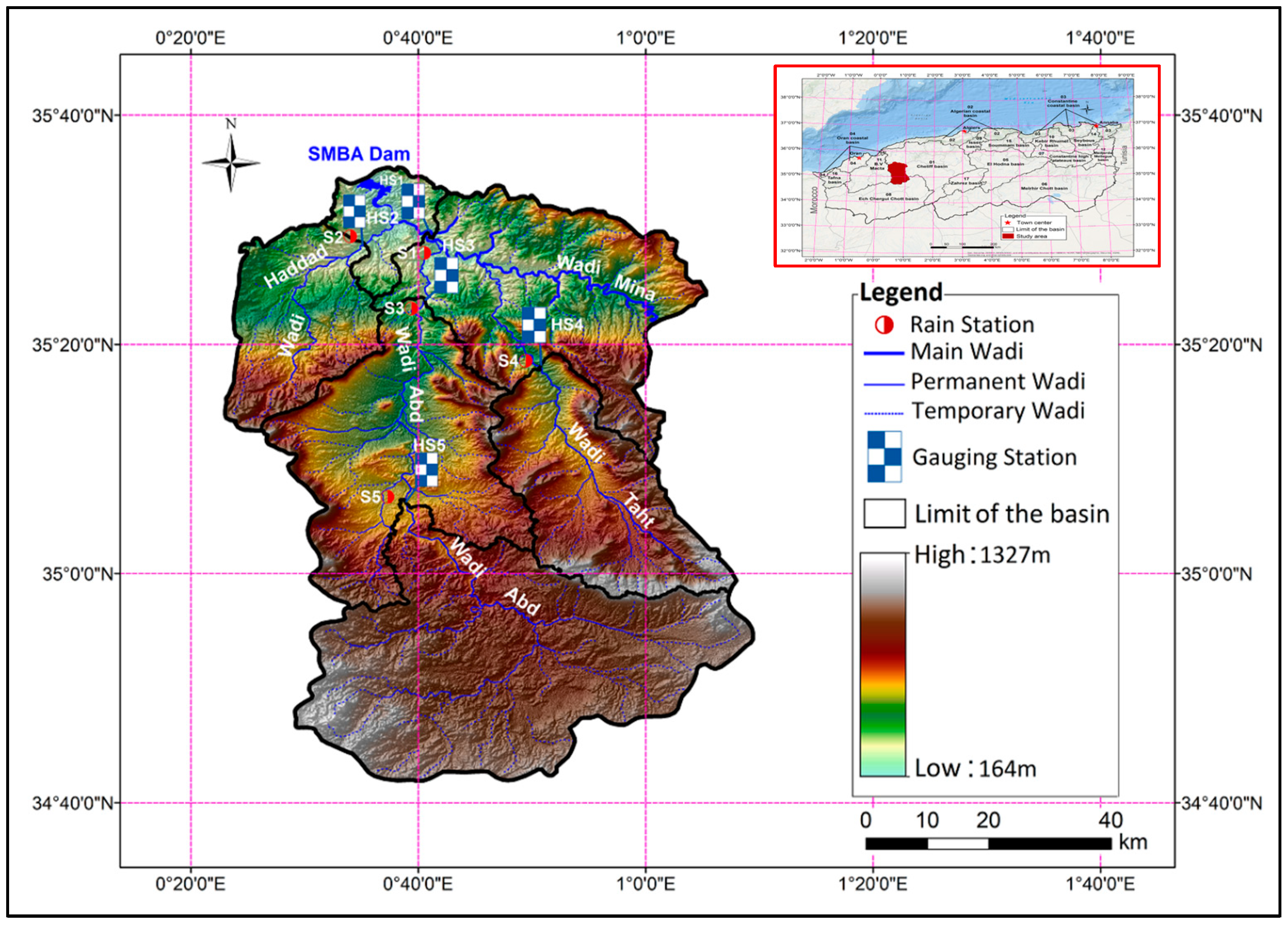
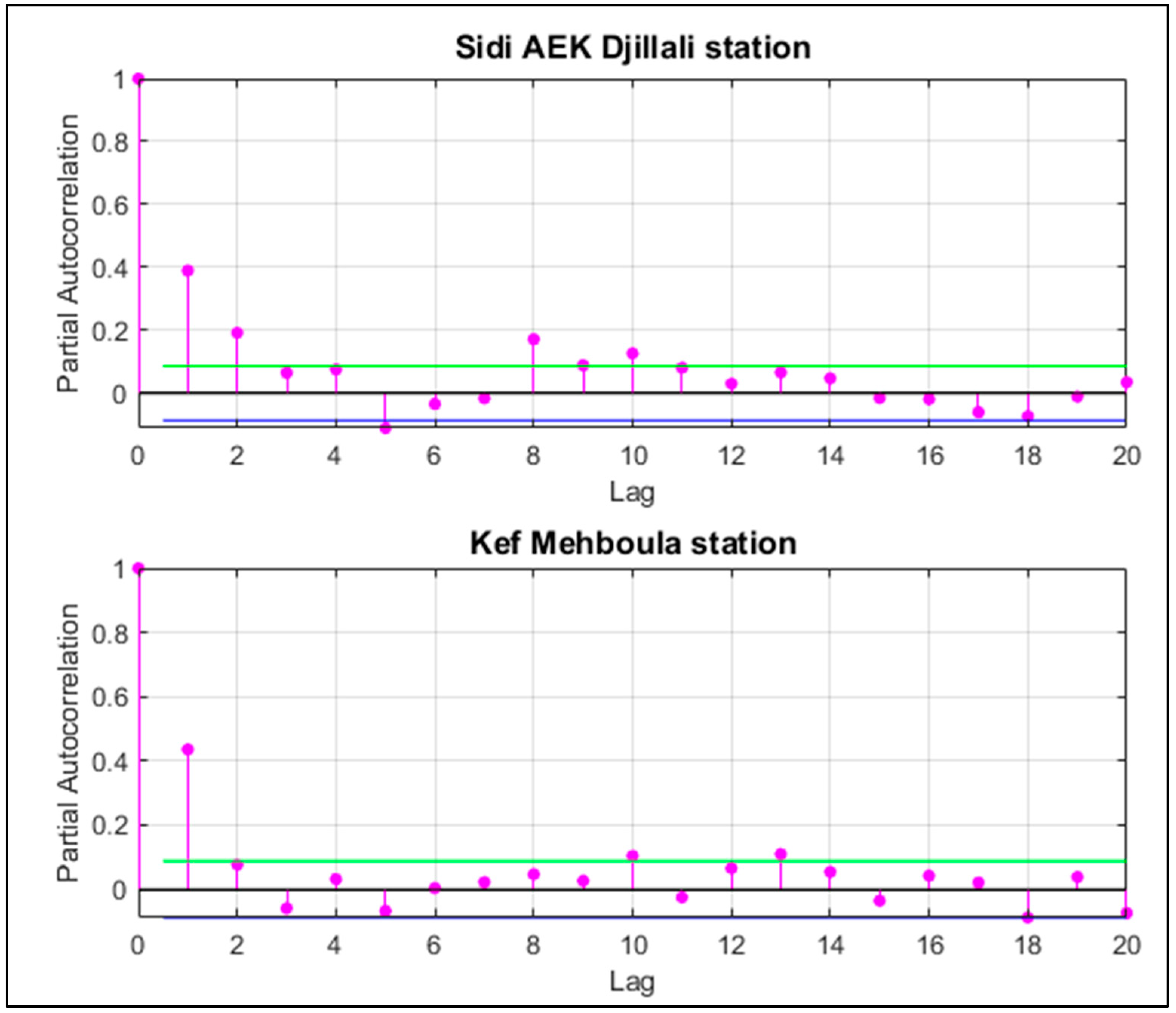
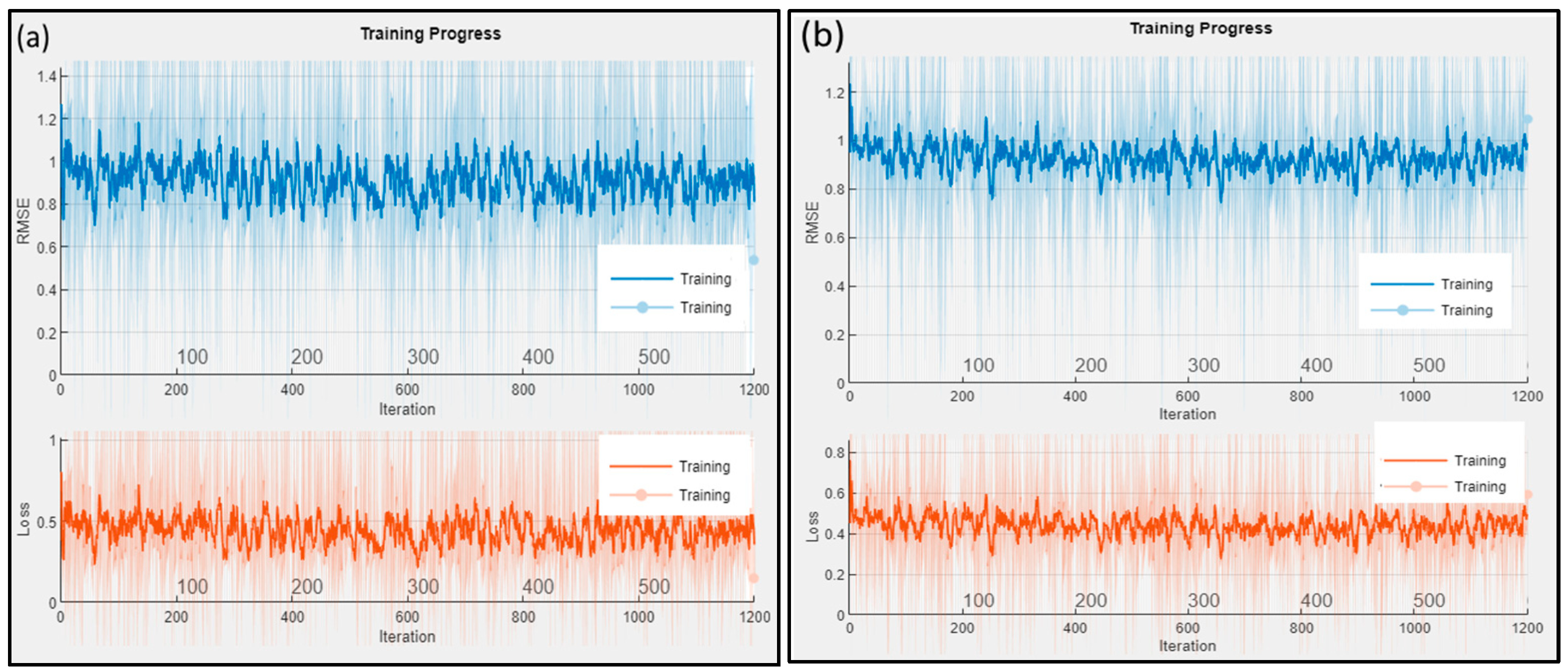
| ID | Name | Elevation (m) | Basin Area (km2) | Latitude | Longitude |
|---|---|---|---|---|---|
| 013401 | Sidi Abdelkader Djillali | 241 | 480 | 35°28′46.05″ N | 0°35′19.99″ E |
| 013001 | Kef Mehboula | 502 | 680 | 35°18′05.21″ N | 0°50′47.89″ E |
| Parameters of LSTM Model | ||
|---|---|---|
| Number of Features = 1 | Max. Epochs = 200 | Learning Rate Schedule = piecewise’ |
| Number of Responses = 1 | Gradient Threshold = 1 | Learn Rate Drop Period = 125 |
| Number of Hidden Units = 200 | Initial Learning Rate = 0.005 | Learn Rate Drop Factor = 0.2 |
| Train algorithm: Adam | Verbose = 0 | |
| Parameters of CNN-RNN Model | ||
|---|---|---|
| Network architecture: CNN-RNN | Horizon = 50 | Learning rate = 0.1 |
| Months to look back: 1, 2 | Mini Batch Size = 48 | Solver: Adam |
| Train Function = trainlm | Max. Epochs = 250 | Momentum constant = 0.25 |
| MSE | MAE | MBE | R | |
|---|---|---|---|---|
| Sidi AEK Djillali station | ||||
| LSTM | 0.339 | 0.317 | 0.053 | 0.102 |
| CNN-RNN | 0.166 | 0.217 | −0.017 | 0.542 |
| GMDH | 0.132 | 0.185 | −0.008 | 0.636 |
| Kef Mehboula station | ||||
| LSTM | 0.685 | 0.489 | −0.041 | 0.039 |
| CNN-RNN | 0.298 | 0.335 | −0.018 | 0.597 |
| GMDH | 0.285 | 0.349 | 0.038 | 0.581 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achite, M.; Katipoğlu, O.M.; Kartal, V.; Sarıgöl, M.; Jehanzaib, M.; Gül, E. Advanced Soft Computing Techniques for Monthly Streamflow Prediction in Seasonal Rivers. Atmosphere 2025, 16, 106. https://doi.org/10.3390/atmos16010106
Achite M, Katipoğlu OM, Kartal V, Sarıgöl M, Jehanzaib M, Gül E. Advanced Soft Computing Techniques for Monthly Streamflow Prediction in Seasonal Rivers. Atmosphere. 2025; 16(1):106. https://doi.org/10.3390/atmos16010106
Chicago/Turabian StyleAchite, Mohammed, Okan Mert Katipoğlu, Veysi Kartal, Metin Sarıgöl, Muhammad Jehanzaib, and Enes Gül. 2025. "Advanced Soft Computing Techniques for Monthly Streamflow Prediction in Seasonal Rivers" Atmosphere 16, no. 1: 106. https://doi.org/10.3390/atmos16010106
APA StyleAchite, M., Katipoğlu, O. M., Kartal, V., Sarıgöl, M., Jehanzaib, M., & Gül, E. (2025). Advanced Soft Computing Techniques for Monthly Streamflow Prediction in Seasonal Rivers. Atmosphere, 16(1), 106. https://doi.org/10.3390/atmos16010106








