Abstract
The radio-wave refraction error caused by the troposphere and ionosphere badly affects accuracy in terms of the navigation, positioning, measurement, and control of a target; it is the main source of errors in high-accuracy measurement and control systems. The high-accuracy technology needed for radio-wave refraction error correction (mainly in the troposphere and ionosphere) has been the focus of research for a long time. At present, the correction methods used for radio-wave refraction errors have a low accuracy. For an S-band radio-wave signal, the accuracy of refraction error correction can generally only reach m-level (elevation angle of 15° and above), and thus has difficulty meeting the requirements of dm-level accuracy refraction error correction for deep-space and high-orbit targets. To improve the accuracy of radio-wave refraction error correction for deep-space and high-orbit targets, a novel correction method for tropospheric and ionospheric range error due to refraction is proposed in this study, on the basis of the measured data from a water vapor radiometer and dual-frequency Global Navigation Satellite System (GNSS). The comprehensive calibration test is conducted in combination with the Chinese Area Positioning System (CAPS) in Kunming. Results show that this method can effectively correct the range error due to refraction that is caused by the troposphere and ionosphere. For an S-band radio-wave signal, the accuracy of refraction error correction can reach dm-level accuracy (elevation angle of 15° and above), which is 50% higher than that achieved with traditional methods. This work provides an effective support system for major projects, such as lunar exploration and Mars exploration.
1. Introduction
The evolution of science and technology has facilitated the rapid growth of China’s progress regarding space, such as lunar exploration, Mars exploration, and other major projects where the target orbit is higher than 2000 km [1]. This situation requires an increasingly accurate target measurement and control system that is developed to dm-level and even cm-level accuracy [2]. In terms of S-band deep-space/high-orbit measurement and control systems (such as in lunar exploration), the radio-wave signal passes through the troposphere and ionosphere [3,4,5]. The signals are refracted by different tropospheric and ionospheric layers. The precise determination of the ionospheric refractivity index is crucial for the evaluation of tropospheric and ionospheric delay, which depends on the refraction ratio [6]. The range error due to refraction caused by the troposphere and ionosphere reaches levels from several meters to more than 10 m. It is worth noting that solar activity is the driving force behind changes in the troposphere and ionosphere; it effectively influences radio wave propagation and satellite navigation systems [7]. Traditional ionospheric or tropospheric refraction correction methods have low accuracy or low efficiency at a low elevation angle [8]. While solar activity is intense and elevation is low, the range error due to refraction is great and becomes one of the largest error sources affecting measurement and control accuracy, especially in coastal areas. Geomagnetic storms are another important factor that disturbs the ionosphere significantly; in some cases, the ionospheric total electron content (TEC) on the dayside could increase by 250% [9], which significantly increases the difficulty of ionospheric parameter correction [10,11,12] and, finally, can cause obvious errors of refraction. This error needs to be taken into consideration and corrected with high accuracy; otherwise, satisfying the requirements of high-accuracy measurement and control systems in the abovementioned projects will be difficult [1,2].
In the literature [13], shipborne theodolite readings are given using meteorological sounding data. Using the sounding data, Wu et al. (2017) [14] exhibited a low angle of elevation based on the lattice atmospheric parameter profile model. This model can effectively eliminate the refraction error caused by the troposphere. However, meeting the requirements of real-time high-accuracy refraction correction is difficult, due to the limitations of the means of meteorological exploration. In addition, as meteorological sounding is complex, it is also difficult to meet the requirements of simple operation and all-weather observation. Mo et al. (2010) [15] provide a correction method for tropospheric radio-wave refraction error, based on the average piecewise model. Furthermore, the application of the tropospheric approximation model in aerospace and deep-space measurement and control are analyzed [16,17]. Chen et al. 2010 [18] calculate and compare the correction precision of the Klobuchar model, the international reference ionosphere model, and the China reference ionosphere model through an analysis of spacecraft exterior trajectory measurement. The US Kua Jialing Laboratory made a refraction error correction of P-ban radar, using dual-frequency GPS [19]. The abovementioned studies only show the troposphere and ionosphere correction method, which can correct the refraction errors caused by the troposphere or ionosphere to a certain extent and will effectively improve the detection accuracy of the equipment. However, the ionospheric observation data in different regions of China are not used or are less frequently used in model construction, and the tropospheric and ionospheric observation data are not integrated in real time [20]. Especially at a low angle of elevation, the range residual error is more than 10 m or is even larger in some cases. Therefore, the accuracy of the range data after refraction correction has difficulty meeting the practical requirements of its applications and urgently needs to be further improved.
In this study, real-time correction methods for tropospheric and ionospheric range errors are given on the basis of radiometer and GNSS measurement data; these methods are adopted to meet the needs of high-accuracy measurement and control systems for high-orbit targets at a height of more than 2000 km. Briefly, Marcor technology and the adaptive grid method are adopted to calculate the refraction error correction for the troposphere and ionosphere [21], respectively. In addition, a comprehensive calibration test of range error due to refraction is conducted using a combination of laser radar and the CAPS system in Kunming. The results show that this proposed error correction method can effectively correct range errors due to refraction, caused by the troposphere and ionosphere. The correction residual is at dm-level accuracy, which can greatly improve the accuracy of measurement and control systems of targets with an orbit higher than 2000 km. This work can provide support for many major projects in China, such as lunar exploration, Mars exploration and other major projects. As the number of satellites increases, the range and the angular diameter of a target will be greatly reduced, and the accuracy of ionospheric range refraction correction will be further improved.
Please note that the refraction error refers to the refraction error of range, angle of elevation, and velocity. In this study, only the correction method for range error due to refraction caused by the troposphere and ionosphere is analyzed, and correction methods for the angle of elevation and velocity refraction errors are not discussed.
2. High-Accuracy Correction Technology for Tropospheric Refraction Error
The tropospheric range error due to refraction mainly includes bending and delay errors. When the angle of elevation is more than 3°, the bending error can be ignored, while the tropospheric range error due to refraction mainly refers to the tropospheric delay error [2].
The tropospheric delay can be divided into dry and wet delays [22]:
dry delay (or static item delay) :
and wet delay :
where refers to a static item of the refractive index; refers to a wet item of the refractive index; s refers to the length of the delay path.
The research results show that the change in the tropospheric dry delay is small. The dry delay accuracy in the zenith direction reaches mm-level accuracy [2] and has a high calculation accuracy. However, the temporal and spatial change of wet delay is large, and the calculation accuracy is relatively low. Therefore, the key to the high-accuracy calculation of tropospheric range error due to refraction correction is to acquire high-accuracy tropospheric wet delay data in real time, and the dry delay is then calculated by means of a piecewise model and the Hopfield and Niell projection function [23]. The Niell projection function is currently considered to be the most accurate.
On the basis of the measured data by a dual-frequency water vapor radiometer, the tropospheric wet delay is calculated using Marcor technology as [24]:
where ; refers to the water vapor density profile, g/m3; refers to the atmospheric temperature profile, K; refers to the brightness temperature of cosmic microwave background radiation; , refer to the atmospheric radiation brightness temperature and the atmospheric mean radiation temperature measured by the microwave radiometer , along the radio-wave propagation’s oblique path; refers to weight function; , , refer to the total atmospheric absorption coefficient, oxygen absorption coefficient, and water vapor absorption coefficient. , refer to oxygen molecule absorption coefficient in the working frequencies and , respectively.
Figure 1 shows the all-around tropospheric wet delay at the angles of elevation of 5°, 10°, and 60° in Qingdao on 25 June 2017 (DOY 206). The geomagnetic condition was very quiet on this particular day. The solid line in the figure refers to the wet delay, as calculated by Marcor technology (hereafter referred to as the Marcor technology wet-delay value); the dotted line refers to the model value calculated by combining the Hopfield model with the Niell projection function (hereafter referred to as the projection function wet-delay value).
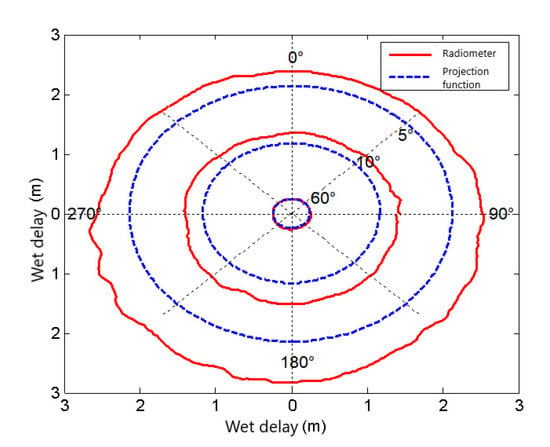
Figure 1.
Tropospheric wet delay at different angles of elevation.
As observed, the projection function is accurate regarding a high angle of elevation (60°). The wet delay calculated by the two methods above has a good consistency. Therefore, the wet delay calculated by means of Marcor technology is also accurate. As the angle of elevation decreases, the wet delay increases rapidly, and the difference between them also increases rapidly. At different azimuth angles, the Marcor technology wet-delay values are greater than the projection function wet-delay values. The non-uniformity of the troposphere in a horizontal direction is ignored in the calculation of the projection function wet-delay value. The differences in tropospheric wet delay at different azimuth angles cannot be reflected. The Marcor technology wet-delay value can fully reflect the environmental characteristics around the test site. A sea zone is observed in the range of 90°–270°, as shown in Figure 2 (the red star represents the test site). The wet delay is relatively large. The wet-delay value at an angle of elevation of 5° is 0.6 m larger than the projection function wet-delay value. In the northern region, the deviation between them is relatively small.
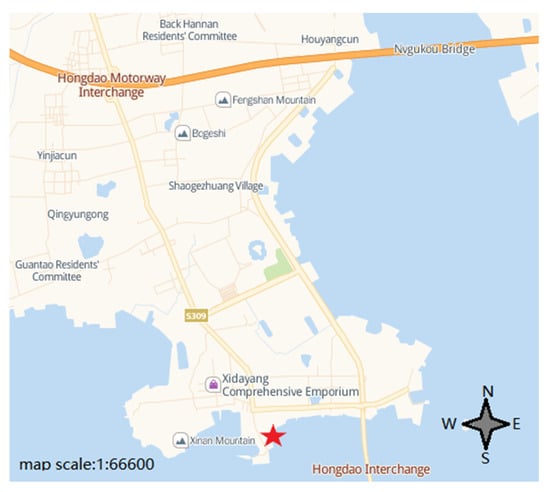
Figure 2.
The test site and its surrounding terrain.
3. High-Accuracy Correction Technology of Ionospheric Refraction Error
As is similar to the tropospheric refraction error, the ionospheric range error due to refraction mainly includes delay and bending effects. For the S-band radio wave, when the angle of elevation of the target is higher than 3°, the bending effect can be ignored, and the ionospheric refraction error is from the ionospheric delay [25,26]. A functional relationship exists between the ionospheric delay and electron content in the ionospheric path, :
For those targets with an orbit higher than 2000 km, the radio-wave signal nearly passes through the ionosphere area. The key to the ionospheric refraction error is the total electron content of the ionosphere in the target path . The calculation method can be found in the relevant literature and will not be repeated here [27].
The range error correction method is shown in Figure 3. This study assumes that when the range between Target O and the nearby satellite satisfies certain conditions in a period of time (~), the result of at from the target to the receiver (recorded as ) is equal in size to at from Satellite i to the receiver (recorded as ).
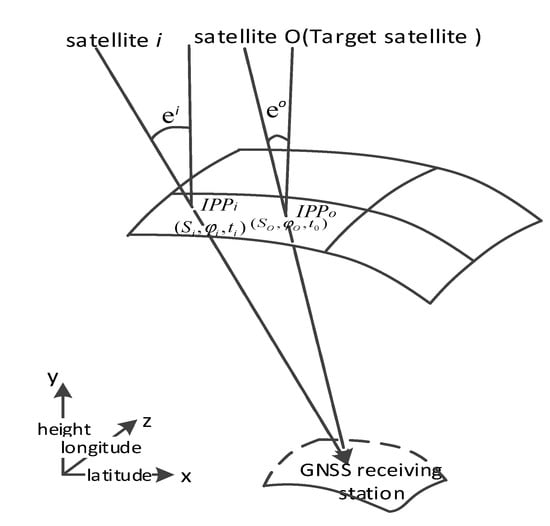
Figure 3.
Schematic of the self-adaptive grid method.
refer to the angle of the solar hour of the target and Satellite i; refer to the latitude of the target and Satellite i. If the zenith angles of the target and Satellite i are , respectively, then:
For easy description, the range between the satellite and its target is called the angular diameter: (). The angular diameter is integrated with time information but is not a fixed grid in the space. In the self-adaptive grid method, the satellite nearest to the target (that is, the satellite with the smallest angular diameter to the target ) is selected. The electron content in the path is calculated first, using , and the total electron content of the ionosphere in the target path is calculated based on Formula (13), where . Then, it is converted into the ionospheric range error due to refraction, based on Formula (11). The local time effect of the ionosphere is considered in the selection of available satellites and the division of the grid. The time is integrated with the latitude of point . The angle of solar time is also used instead of the longitude. The satellite with the smallest angular diameter in the temporal and spatial significance of the target is selected within a certain time range.
The GPS observation data on 25 June 2017 are used to analyze the correction effect of the self-adaptive grid method. With the No. 7 GPS satellite PRN7 as the target, the electron content in the target satellite path is first calculated and is then converted into a range error. In addition, it is used as the benchmark ∆R_0 (that is, the range error due to refraction before correction). As shown in Figure 4, the horizontal coordinate represents time, and the longitudinal coordinate represents ionospheric range error due to refraction. In range error correction using the self-adaptive grid method, a single satellite with the smallest angular diameter to the target satellite (PRN7) is selected to calculate the electron content in the path. Then, it is converted into an ionospheric range error due to refraction, based on Formulas (1)–(3), ∆R_iono (black dotted lines).
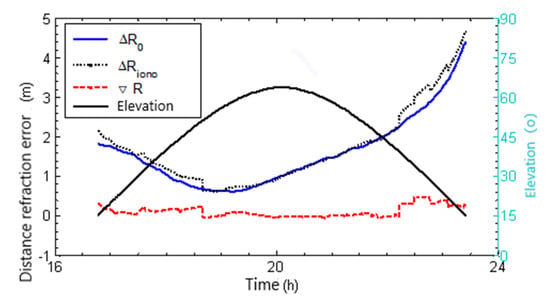
Figure 4.
Analysis of the correction effect by the self-adaptive grid method.
This study assumes that the working frequency of the radio-wave signal is 2.5 GHz. As observed, the range error due to refraction that is obtained by the self-adaptive grid method and the error before correction (true value) will increase rapidly with a reduction in the angle of elevation of the target (shown as the longitudinal coordinate on the right of Figure 3). A better consistency is obtained. The residual after the error correction is reduced greatly, and changes when it is near zero. The correction residual is generally less than 0.3 m, and the correction residual is nearly independent of the angle of elevation of the target. Therefore, the range error caused by the ionosphere can be effectively corrected.
Figure 4 shows an example of correction of the ionospheric range error due to refraction, based on the GPS data of PRN7. In fact, this method also has a good correction effect for other GPS satellites. In addition, the method is also applicable to all satellites of the Global Navigation Satellite System (GLONASS), Galileo and Beidou.
4. Calibration Test and Accuracy Analysis on Radio-Wave Refraction Error Correction
In this study, we mainly focus on calm geomagnetic conditions. From 25 August to 3 September 2017, the Chinese Institute of Radio-wave Propagation, in cooperation with the Yunnan Observatory and the Time Service Center of the Chinese Academy of Sciences, conducted a comprehensive test of tropospheric and ionospheric refraction error correction in the Yunnan Observatory. During the period from 25 August to 3 September 2017, the geomagnetic conditions were relatively quiet for most of that time. However, a very small geomagnetic storm occurred on 31 August 2017 and could have affected the results. The contribution made by the storm will be tested and investigated in the future.
The precise orbit provided by CAPS (the Chinese area positioning system) in the Yunnan station of the National Time Service Center of the Chinese Academy of Sciences reaches cm-level accuracy, and its working frequency is in the C-band. For this band, the refraction errors caused by the troposphere and ionosphere are at m-level accuracy, which should be considered. The high-accuracy ranging data based on the laser radar and CAPS system can be used to test the correction accuracy of the calculations of ionospheric range error due to refraction. Ultimately, the range error is converted into an S-band (2.5 GHz) correction residual error on the basis of the dispersion characteristics of the ionosphere (Formula (11)). CAPS data can be used in the ionospheric correction accuracy analysis and calibration.
Figure 5 shows the examples of the range error due to refraction of No. 7 satellite, before and after correction. The range error before correction ((∆R)_caps = R_caps-R_0) (blue line) increases rapidly with the decrease in the angle of elevation of the satellite. R_caps refers to the detection value of the target CAPS system (excluding systematic error); R_0 refers to the precise orbit of the target; blue lines show the refraction error correction residual (∇R)_caps, (∇R)_caps =(∆R)_caps-(∆R)_trop-(∆R)_iono; (∆R)_trop refers to the tropospheric range error correction as calculated with Marcor technology; (∆R)_iono refers to the ionospheric range error correction. As observed, the range error correction residual is greatly reduced to dm-level accuracy after the refraction error correction, and this reduction is unrelated to the angle of elevation. Therefore, the refraction errors caused by the troposphere and ionosphere are effectively corrected. The target measurement accuracy is also greatly improved.
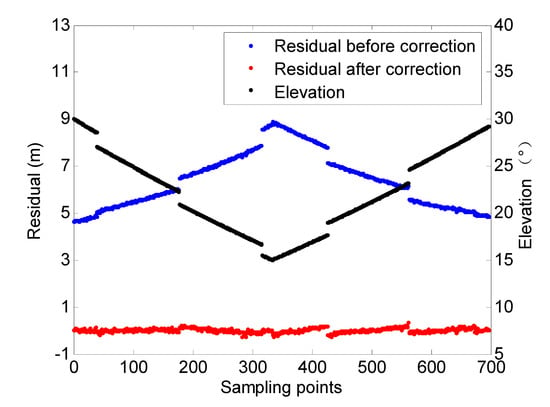
Figure 5.
Analysis of ionospheric range error correction accuracy.
Figure 5 shows the residual and the jump in the angle of elevation before correction. The reason is that this mechanism is more successful than that of the CAPS system. The CAPS system works for 1 h after a 1-hour interval.
The correction effects using the No. 1 and No. 4 satellites are similar to those in Figure 5. This similarity further indicates the effectiveness of the proposed range error correction method for the troposphere and ionosphere.
5. Discussion
The high-accuracy correction methods presented herein to ameliorate range error due to refraction caused by the troposphere and ionosphere are proposed to meet the requirements of the high-accuracy measurement and control systems of targets with an orbit higher than 2000 km, such as are needed for high-resolution, lunar exploration, Mars exploration and other high-orbit projects. The brightness temperature of the troposphere, measured based on water vapor radiation, is calculated by Marcor technology in real time to obtain the wet delay value in the target path. The real-time calculation of the tropospheric refraction error of the high-orbit target is realized in combination with the dry delay value, as calculated by the Hopfield model. The GPS satellite that is nearest to the target and with the smallest angular diameter is selected in the ionosphere. The electron content in the path is calculated first and is then converted into the ionospheric range refraction value. The real-time calculation of the ionospheric range error due to refraction correction is achieved.
A comprehensive calibration test of radio-wave refraction error correction accuracy is also conducted. The accuracy of real-time tropospheric and ionospheric refraction error correction is analyzed and verified, using the measured data provided by the CAPS system. The test results show that the proposed method can effectively correct range errors due to refraction caused by the troposphere and ionosphere for an S-band radio-wave signal. The correction residual is at dm-level accuracy, which greatly improves the measurement and control system accuracy for deep-space and high-orbit targets.
The Marcor technology is affected by the measurement accuracy of the brightness temperature of the atmosphere. The measurement accuracy of the brightness temperature of a water vapor radiometer should be guaranteed to ensure the accuracy of ionospheric range error correction. The water vapor radiometer used in this study is a self-made device in the China Radio Propagation Research Institute. If the angle of elevation is more than 10°, then the measurement accuracy of the brightness temperature is better than 1 K.
Only GPS satellite data during relatively quiet geomagnetic conditions are used in the ionospheric range error correction presented in this study. In addition, the satellite nearest to the target satellite with the smallest angular diameter is used to ensure that a GPS satellite is available near the target satellite. GPS satellite data are limited (only 32 are available at present). Therefore, the satellites that are selected are sometimes far from the target satellite and have a large angular diameter. This condition affects the accuracy of ionospheric refraction error correction, to a certain extent. When the selected satellite is nearer to the target satellite, the angular diameter is smaller, and the accuracy of calculating range error due to refraction correction by the self-adaptive grid method is greater.
6. Conclusions
In the paper, in order to improve the accuracy of radio-wave refraction error correction for deep-space and high-orbit targets, a correction method for tropospheric and ionospheric range error due to refraction is proposed, based on the measured data of a water vapor radiometer and dual-frequency GNSS. The main conclusions are as follows:
- The change in the tropospheric dry delay is small. The dry delay definition in the zenith direction reaches mm-level accuracy and has a high calculation accuracy.
- The given method is excellent for correcting range errors due to refraction caused by the troposphere and ionosphere.
- For an S-band radio-wave signal, the accuracy levels of refraction error correction can reach dm-level accuracy (elevation angle of 15° and above), which is 50% higher than can be achieved by the traditional method.
The GNSS system has been constructed, and it operates well. In addition, China’s Beidou system has been completely developed [28,29,30], and at least 30 satellites of the Beidou system can be simultaneously detected. Galileo, GLONASS, and the Beidou system can also be used for refraction error correction. The number of satellites will increase, and the range and the angular diameter to the target will thus be greatly reduced. Therefore, the accuracy of ionospheric range refraction correction will be further improved. Besides, the method provided in this paper is suitable for quiet geomagnetic time periods. The effectiveness of the system during intense geomagnetic storms needs to be further investigated.
Author Contributions
Developed the basic idea of the paper, K.L.; designed the experiments and analysis tools, performed the experiments, and analyzed the data, K.L. and Z.Y.; participated in discussion and interpretation of the data, C.Z., Q.Z., H.W., D.S. and X.D.; wrote the paper, K.L. and Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 61971385).
Acknowledgments
The authors would like to thank the Beijing Institute of Tracking and Telecommunications Technology for organizing and conducting experiments, and thank the Yunnan Observatory and the National Time Service Center of the Chinese Academy of Sciences in Yunnan for providing CAPS system data. This research was funded by the National Natural Science Foundation of China (grants no. 61971385).
Conflicts of Interest
The authors declare no conflict of interest.
References
- van’t Klooster, K.; Petelin, M.; Thumm, M.; Aloisio, M. Ka-band groundstation antenna aspects for deep space telecommunication and radar. In Proceedings of the 7th European Conference on Antennas and Propagation (EuCAP), Gothenburg, Sweden, 8–12 April 2013; pp. 242–246. [Google Scholar]
- Jiang, C.; Wang, B. Atmospheric refraction corrections of radiowave propagation for airborne and satellite-borne radars. Sci. China Ser. E Technol. Sci. 2001, 44, 280–290. [Google Scholar] [CrossRef]
- Feltens, J.; Bellei, G.; Springer, T.; Kints, M.V.; Zandbergen, R.; Budnik, F.; Schönemann, E. Tropospheric and ionospheric media calibrations based on global navigation satellite system observation data. J. Space Weather Space Clim. 2018, 8, A30. [Google Scholar] [CrossRef]
- Häusler, B.; Pätzold, M.; Tyler, G.L.; Barriot, J.P.; Bird, M.K.; Dehant, V.; Hinson, D.P.; Simpson, R.A.; Treumann, R.A.; Eidel, W.; et al. Venus atmospheric, ionospheric, surface and interplanetary radio-wave propagation studies with the VeRa radio-science experiment. ESA Publ. 2007, SP-1295, 30. [Google Scholar]
- Moshkov, A.V.; Pozhidaev, V.N. Features of radio wave refraction in the near-polar regions. J. Commun. Technol. Electron. 2014, 59, 1107–1111. [Google Scholar] [CrossRef]
- Unver, O.; Guyer, S.; Uzel, T.; Can, Z. The Ionospheric refractivity effects on the GPS signals. In Proceedings of the 6th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 12–14 June 2013; pp. 779–782. [Google Scholar]
- Bosy, J.; Figurski, M.; Wielgosz, P. A strategy for GPS data processing in a precise local network during high solar activity. GPS Solut. 2003, 7, 120–129. [Google Scholar] [CrossRef]
- Chenglin, D.; Chuanling, M.; Jianfeng, C.; Ying, H.; Jian, W. A new method on tropospheric refraction correction at low elevation. Infrared Laser Eng. 2012, 41, 1195–1199. [Google Scholar]
- Mannucci, A.J.; Tsurutani, B.T.; Iijima, B.A.; Komjathy, A.; Saito, A.; Gonzalez, W.D.; Guarnieri, F.L.; Kozyra, J.U.; Skoug, R. Dayside global ionospheric response to the major interplanetary events of October 29–30, 2003 “Halloween Storms”. Geophys. Res. Lett. 2005, 32, L12S02. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.; Deng, Y.; Huang, C.-M. Extraction of the geomagnetic activity effect from TEC data: A comparison between the spectral whitening method and 28 day running median. J. Geophys. Res. Space Phys. 2017, 122, 3632–3639. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, M.; Deng, Y.; Wang, J.; Huang, H.; Deng, X.; Huang, C. Improvement of a Deep Learning Algorithm for Total Electron Content Maps: Image Completion. J. Geophys. Res. Space Phys. 2019, 124, 790–800. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.-S.; Huang, C.-M.; Huang, L. A new pair of indices to describe the relationship between ionospheric disturbances and geomagnetic activity. J. Geophys. Res. Space Phys. 2014, 119, 10156–10163. [Google Scholar] [CrossRef]
- Han, X.P.; Unit, P.L.A. A Kind of New Carrier-Borne Theodolite Atmospheric Refraction Revises Method. Tech. Autom. Appl. 2016, 36, 1369. [Google Scholar]
- Wu, P.; Li, Y.; Shao, S.; Kang, D.; Chen, J.; Li, X.; Wei, H.; Rao, R. Low Elevation Atmospheric Refraction Correction Method Based on Gridding Atmospheric Parameter Profile Mode. Acta Optica Sinica 2017, 37, 0601004. [Google Scholar]
- Mo, J.; Zhong, R. A method for radio refraction error correction of troposphere. Fire Control Command Control 2010, 1, 164–165. [Google Scholar]
- Ni, X.; Mao, Y.; Chen, H.; Guo, C. Application of Approximate Formula on TT&C System. J. Ordnance Equip. Eng. 2016, 37, 174–176. [Google Scholar]
- Chang-Jiang, L.; Chao-Feng, W.; Dan, L. Influence of Correction for Atmospheric Refraction in passive TDOA location on system TDOA error. In Proceedings of the 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 24–27 October 2019; pp. 1–4. [Google Scholar]
- Chen, X.; Zhao, J.; Wang, X.; Chen, J.; Zhang, H.; Yang, H. Validating Effects of Ionospheric Delay Correction Models. J. Spacecr. TT&C Technol. 2016, 35, 182–187. [Google Scholar]
- Hunt, S.M.; Close, S.; Coster, A.J.; Stevens, E.; Schuett, L.M.; Vardaro, A. Equatorial atmospheric and ionospheric modeling at Kwajalein missile range. Linc. Lab. J. 2000, 12, 45–64. [Google Scholar]
- Luo, W.; Liu, Z.; Li, M. A preliminary evaluation of the performance of multiple ionospheric models in low- and mid-latitude regions of China in 2010–2011. GPS Solut. 2014, 18, 297–308. [Google Scholar] [CrossRef]
- Hu, G. Research on error analysis and correction technique of atmospheric refraction for InSAR measurement with distributed satellites. J. Comput. Commun. 2016, 4, 142. [Google Scholar] [CrossRef][Green Version]
- Shu, T.; Zhu, Q.; Liu, K.; Lin, L. Comparative study of wet delay models and model based on Marcor technology in Ji’nan area. Chin. J. Radio Sci. 2020, 35, 422–429. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Wang, G.; Zhong, H.; Tang, C. Evaluation of COMPASS ionospheric model in GNSS positioning. Adv. Space Res. 2013, 51, 959–968. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, X.; Cao, P. An improved algorithm for the integral vapor of atmosphere measurement using a microwave radiometer. Chin. J. Radio Sci. 2011, 5, 933–937. [Google Scholar]
- Zhao, Z.; Lin, L.; Lu, C.; Zhang, R.; Liu, K.; Zhang, X. Radiowave Propagation of Satellite Systems; National Defense Industry Press: Beijing, China, 2020. [Google Scholar]
- Liu, K.; Yuan, Z.; Zhou, C.; Zhao, J.; Zhu, Q.; Dong, X.; Wand, H.; Sheng, D. Study on Ionospheric Refraction Error Correction Method for High Orbit Target. Available online: http://www.cjors.cn/en/article/doi/10.12665/j.cjors.2020216 (accessed on 31 August 2021).
- Allen, R.S.; US Air Force Geophysics Laboratory. Considerations Relative to Adapting TRANSIT Observations to Predicting Radar Range Correction. Available online: https://catalog.hathitrust.org/Record/102325731 (accessed on 31 August 2021).
- Jin, S. Recent progresses on Beidou/COMPASS and other global navigation satellite systems (GNSS)–I. Adv. Space Res. 2013, 51, 941. [Google Scholar] [CrossRef]
- Hu, L.; Yue, X.; Ning, B. Development of the Beidou Ionospheric Observation Network in China for space weather monitoring. Space Weather 2017, 15, 974–984. [Google Scholar] [CrossRef]
- Li, B.; Qin, Y.; Li, Z.; Lou, L. Undifferenced cycle slip estimation of triple-frequency BeiDou signals with ionosphere prediction. Mar. Geod. 2016, 39, 348–365. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).