Abstract
Volcanic ash clouds often become multilayered and thin with distance from the vent. We explore one mechanism for the development of this layered structure. We review data on the characteristics of turbulence layering in the free atmosphere, as well as examples of observations of layered clouds both near-vent and distally. We then explore dispersion models that explicitly use the observed layered structure of atmospheric turbulence. The results suggest that the alternation of turbulent and quiescent atmospheric layers provides one mechanism for the development of multilayered ash clouds by modulating vertical particle motion. The largest particles, generally m, are little affected by turbulence. For particles in which both settling and turbulent diffusion are important to vertical motion, mostly in the range of 10–100 m, the greater turbulence intensity and more rapid turbulent diffusion in some layers causes these particles to spend greater time in the more turbulent layers, leading to a layering of concentration. The results may have important implications for ash cloud forecasting and aviation safety.
Keywords:
turbulence; eddy diffusivity; ash layer; volcanic cloud; ash cloud; Pinatubo; aviation safety 1. Introduction
Volcanic ash is a multi-billion dollar economic hazard to aviation, as shown during the 2010 eruptions of Eyjafjallajökull, Iceland [1,2]. It is also a risk to flight safety, with hundreds of encounters of varying severity recorded, and several instances of multiple engine flame-out in flight. The International Airways Volcano Watch (IAVW), which seeks to safely separate aircraft from volcanic ash in flight, relies on detecting areas of ash and forecasting its future movement [3]. The IAVW acts through nine Volcanic Ash Advisory Centers (VAACs). In case of eruption that potentially affects flight safety, the VAACs issue both a written Volcanic Ash Advisory (VAA) and a Volcanic Ash Graphic (VAG), which state and show the analysis of the current position of an ash cloud and the forecast position to 18 h from present. Ash cloud positions are rendered as polygons for separate aircraft flight levels or altitude ranges, and flight paths are adjusted accordingly.
However, the model forecasting of ash presence and concentration is generally poorly resolved vertically, although there is some progress in this direction, for example, Ref. [4,5]. Aircraft flying in a supposedly ash-contaminated region at a particular altitude may encounter no ash or significant and potentially damaging amounts, due to the high degree of ash stratification with altitude. The improved understanding and forecasting of stratification would assist enormously in managing the hazard and support the continuing development of the IAVW.
Photography and satellite imagery of numerous volcanic eruptions show that a single or multiple layered structure is a fundamental aspect of near-source volcanic cloud development [6,7], with a single, volcanic umbrella cloud layer being dominant in most of Figure 1. Aerial as well as ground-based photography have been particularly useful near the volcano to elucidate this layering. Lidar backscatter data have been key in defining the more complicated layered structure in distal regions, particularly those from the CALIOP (Cloud-Aerosol LIdar with Orthogonal Polarization) instrument (Figure 2). Volcanic layers can be stratospheric as well as tropospheric [8].
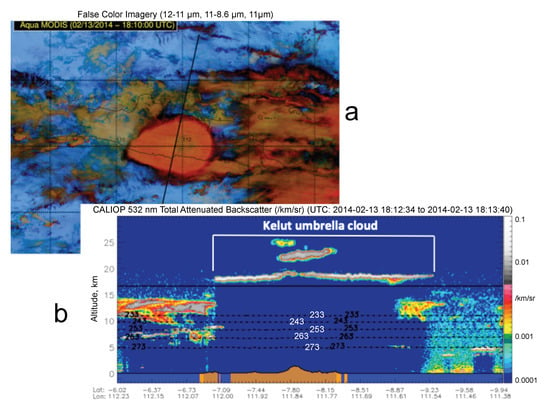
Figure 1.
(a) Aqua-MODIS RGB false color image of Java, Indonesia, capturing the Kelut umbrella cloud on 13 February 2014 (red hues). (b) CALIOP nadir lidar total attenuated backscatter (along the track shown in (a) with a solid line) showing isotherms (kelvin, black dotted lines) and tropopause (black solid line). Clouds between 10–15 km on the South (right) side under the umbrella cloud could be of volcanic origin. Near-source, volcanic clouds occur as thick, concentrated layers of ash (note the attenuation of the signal below the umbrella cap).
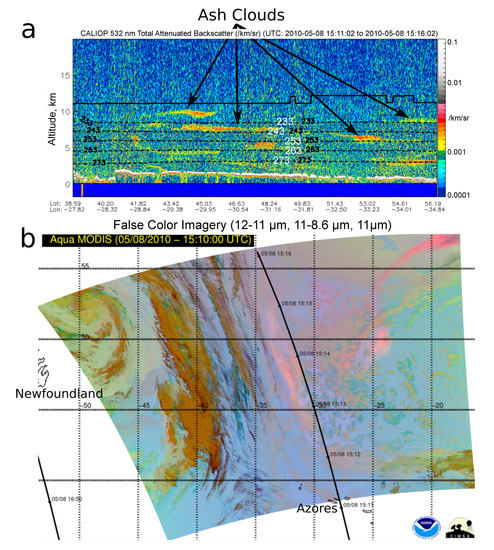
Figure 2.
(a) CALIOP nadir lidar total attenuated backscatter (along track shown in (b)) showing complex layering of Eyjafjallajökull ash cloud on 8 May 2010, isotherms (kelvins, black dotted lines) and tropopause (black solid line). (b) Aqua-MODIS RGB false color image [9] of North Atlantic capturing this ash cloud (pink hues). In distal regions, volcanic clouds tend to be thin, less concentrated, and often broken into multiple bodies.
Multiple layers are thought to form and separate by numerous processes, some of these unique to volcanic clouds. The primary volcanic cloud layer near the vent, such as the volcanic umbrella cloud or anvil cloud, arises from the driving of hot eruptive gas and ash parcels outward around their equilibrium level, or neutral buoyancy height [10]. As suggested by brightness temperatures over the surface of near-vent clouds and ground based photography, umbrella clouds can be solitary, accompanied by a single lower intrusion resulting from re-entrainment and column-edge downflow [11,12] or accompanied by lower level skirt clouds [13], which may or may not contain ash. Ash accretion, ash re-entrainment and source variability–injection of ash at different altitudes with changing eruption rate and wind fields, cause the development of multiple layers [7,14,15]. Gas-ash separation of particulate-laden and gaseous volcanic cloud components has been noted as a further cause of volcanic layer formation [16,17], perhaps enhanced by gravity current slumping of the particle laden component [18]. Double diffusion and convective sediment flux to a single [11,12,19,20,21] and multiple [6] levels by descending fingers that intrude below the level of a major volcanic cloud layer have been observed, and recreated in the laboratory.
Further from the vent, 500 km and hours in transport time, downward looking satellite sensors are used for cloud tracking, but these penetrate only partially into the highest layer of an optically thick cloud, and satellite remote sensing algorithms are most sensitive to the column integrated ash properties, even when multiple optically thin layers are present. Although horizontal, planview resolution can thus be good, satellite data and often volcanic ash transport and dispersal models (VATDs), used to forecast future position, have difficulty in reproducing the vertical structure of distal volcanic clouds [4,22,23]. Numerical inversion of VATDs has been used to map distal cloud positions seen in CALIOP and other data to time-varying release height from the source vent [5,24,25,26]. Dacre et al. [27] used a new scheme to calculate clear-air turbulence (CAT) in the NAME VATD model. Numerous distal clouds from the Eyjafjallajökull eruption were analyzed and thought to be controlled in thickness by an interaction between wind shear, which acted as thin layers, and turbulent diffusion, acting to thicken them [27].
Problem Statement
A correct understanding of layer formation and morphology is critical for any attempt to construct VATD models capable of producing output consistent with observations of vertical ash distribution, yet the formation mechanisms of atmospheric ash cloud layers are not fully understood. One potential mechanism for their formation and characteristics is the subject of the present contribution. Our working hypothesis is that, because particle settling and atmospheric turbulence act to varying degrees in a layered atmosphere, the turbulence structure of the atmosphere can cause ash layer formation, through the process of enhanced suspension in vertically restricted regions of high turbulence.
2. Materials and Methods
2.1. Background Materials
2.1.1. Atmosphere
Ash transport occurs in the large-scale structures of the wind field, while ash dispersion or spread is caused by the small-scale turbulence structures and eddies [12,28]. The free atmosphere itself, with or without volcanic clouds, generates small-scale turbulent eddies. Eddies are generally created in the troposphere by Rayleigh–Taylor (convective) instabilities associated with clouds, and can be found 33% of the time [29]. In the stratosphere, clear-air turbulence (CAT) is primarily thought to be generated by breaking of upward-propagated gravity waves from the troposphere or tropopause, i.e., the Kelvin–Helmholtz mechanism, acting during episodes of vertical wind shear in the horizontal wind components [30,31,32]. In volcanic clouds near the vent, turbulence is created by both the Rayleigh–Taylor and Kelvin–Helmholtz mechanisms, as ash clouds intrude into the atmosphere as gravity currents. Kelvin–Helmholtz instability is driven by the shear between the intruding cloud and the atmosphere [33]. Rayleigh–Taylor instability is driven by cloud top convective instabilities [29], convective sedimentation, fingering and local, eddy scale density reversal [11,16,34].
In the free atmosphere, parameters such as moisture content and temperature do not change monotonically with height; there are layers of relatively homogeneous air, separated by regions in which parameters vary rapidly [29,35]. Both the stratosphere and the troposphere are layered in this way on scales of [0.1–1 km] [36,37], although the layers in the troposphere tend to be more transient and discontinuous [38]. Information of sufficient resolution in the vertical direction to discern and characterize the turbulence layered structure is obtained from airborne measurement campaigns or rawinsonde balloon releases [39,40,41]. Several methods have been developed to derive turbulence from rawinsonde and other high-resolution data. Vasseur and Vanhoenacker [29] measured changes in the refractive index structure parameter for radio waves, as turbulence causes changes in the refractive index, based on rawinsonde pressure, temperature, humidity, wind speed and wind direction data. Clayson and Kantha [42] used variations in the potential temperature profile from an idealized profile to calculate the Thorpe scale, and derive turbulent dissipation and diffusivity. These estimates can be made for single rawinsonde profiles with simple calculations. Marlton et al. [43] have recently developed an accelerometer that can be added to the sonde instrument package and provide measures of instrument motion transformable into turbulence measures. In the troposphere, layers of constant relative humidity (RH) or mixing ratio, q, can act as tracers for high turbulence [40]. This is because as turbulence intensifies, mixing intensifies, and tracers become more evenly distributed throughout a layer. The macroscopic mixing caused by turbulence acts as a diffusive process, which is characterized by a (turbulent) eddy diffusivity, . (Atmospheric moisture is also important in aiding plume lift, especially in plumes from weak sources, or at low latitude, where the moisture content is high [10,44]. High RH layers might therefore indicate not only turbulence, but also particularly intense reservoirs of energy available for plume lift.) As a result of the layering, large-volume or bulk turbulence, and the eddy diffusivity, , that expresses its intensity, is highly anisotropic (), and only within thin, well-defined layers is it approximately isotropic () [38].
There are drawbacks to extrapolating high-resolution or point data to a regional scale because of spatial and temporal inhomogeneity; the troposphere is highly transient and spatially variable [42,45]; tropospheric isobaric surfaces are not necessarily parallel to the earth’s surface, especially at fronts and in mountain waves [35]. Fronts are associated with tropopause folds, non-horizontal isobaric surfaces separating cold from warm air, and turbulence in folds is generated by local dynamic and convective instabilities. Mountain waves form as the density stratified atmosphere flows past the lee side of a mountain or mountain range. These waves can break, resulting in local turbulence concentrated in non-horizontal layers.
We will use the high-resolution atmospheric data of Cho et al. [40] as the basis for testing a model of ash cloud layer development from the turbulence structure of the atmosphere. To explore a case study of the Pinatubo 1991 volcanic clouds, we will speculate on potential atmospheric layers based on the considerations outlined in this section.
2.1.2. Ash Clouds
Data are available from a number of sources on the shape and structure of both near-vent and distal ash clouds. In the near-vent region, data tend to be more limited, due to the lower optical depth. Nevertheless, cloud brightness temperature (BT) as measured from nadir-looking geostationary and low-earth orbiting satellites provides useful information, as the topography of the top of the near-vent clouds can be quite variable, with a distinct high point or swell above the central vent that might be many kilometers above the top of the main umbrella cloud [17]. In addition, airborne and ground-based photography and videography have provided extensive data on the features at the base of the main umbrella or anvil, and within the underlying cloud layers. Visible satellite imaging of the near vent cloud top consistently reveals strong, well-defined three-dimensional vortex structures above the vent, which evolve to smooth, somewhat more diffuse structures in the umbrella cloud [46].
Although the air can be choked with opaque, diffuse ash bodies that extend to ground level near vent, and although gravitational intrusions, such as umbrella clouds, are wedge-shaped by nature and therefore of variable depth, measurements have been made of the BT between the highest and lowest points on the cloud top, as indicated by the lowest and highest BT, respectively. The results suggest that umbrella clouds at the vent typically encompass depths of km (Table 1), which makes a large mass of ash available for transport at multiple levels. Some of the lower near-vent clouds also become distal clouds. In some cases, it might be possible to find the entire troposphere and even lower stratosphere charged with ash, or only a distinct layer or two of [1–10] km depth.

Table 1.
Examples of near-source, upper volcanic cloud depth from the top to lowest part near the cloud edge. Measured from geostationary imagery in first scene after eruption start (photography for Redoubt). Data from Bear-Crozier et al. [47]; and Pouget et al. [48] and Holasek et al. [7] (below divider).
In the distal region, airborne lidar, EARLINET-AERONET (European Aerosol Research LIdar NETtwork-AErosol RObotics NETwork) and CALIOP data typically show thinner, more discontinuous cloud structures (Figure 2) than is commonly seen near-source (Figure 1). Three separate tabulations of distal ash cloud layer data for the Eyjafjallajökull plume have been published [49,50,51], and the EARLINET data have been summarized and modeled [27]. The data suggest that distal clouds from this tropospheric eruption were typically 0.3–3 km thick, made up of 2–3 layers, with individual layers of 0.3–1.4 km depth, and maximum age of 129 h (<1 week) (Table 2). Dacre et al. [27] estimated a mean and standard deviation of the measured depths of km. The number density of particles in the clouds as they propagated over Europe generally peaked in the micron to submicron range, while the mass density peaked near 10 m [51], although the larger size modes may be underrepresented [52].

Table 2.
Measured distal Eyjafjallajökull cloud depths from CALIOP lidar. Data from Winker et al. [49] (top section), Marenco et al. [50] (middle) and Schumann et al. [51] (bottom). Note that the number of layers varies with spatial position.
Vernier et al. [53] using CALIOP data, discerned two or more well-defined layers in the cloud from Puyehue-Cordon Caulle three weeks after the eruption. Some of the layers showed fold or wrap-around structures (Figure 1a in Vernier et al. [53]), perhaps related to vertical-plane chaotic mixing [54]. Clouds were up to 3 km thick, with individual layers of 0.1–2 km depth, in the upper troposphere-lower stratosphere (UTLS), centered on the tropopause at 8–14 km altitude.
On 12–13 July 1991, 26 days after the last major eruption of Pinatubo, a lidar flight noted numerous stratospheric layers [8]. The data showed a number of well-defined layers of 0.5–1 km depth between about 14 and 25 km altitude (Figure 1 in Winker and Osborn [8]). Along much of the line of flight there were two layers (22 and 25 km), but in places there were up to five. Within the first day, modeling by Fero et al. [17] is consistent with a mean grain size of 90 m in the 22-km layer. Even after nearly a month, high backscatter lidar depolarization ratios at the base of the 22-km layer were still inexplicably consistent with particles in the 10–100 m range [8]. Although depolarization ratios in the 25-km layer were consistent with mostly sulfur aerosols, bothWinker and Osborn [8] and Fero et al. [17] mention that fine silicate particles occurred with the aerosols.
In all studies cited above, distal ash layers were horizontal or tilted relative to the horizon, and had extents in the cross-transport direction of hundreds of km in the troposphere (Eyjafjallajökull), to thousands of km in the stratosphere (Puyehue, Pinatubo). Other consistent features are thinning, more sharply defining, and breaking into multiple, more-distal clouds of near-vent volcanic clouds.
Back trajectories of distal ash clouds for Eyjafjallajökull and Puyehue-Cordon Caullé are generally consistent with theoretically possible cloud heights at the source [49,53]. However, it is not clear that ash was injected at these altitudes by the eruptions, given uncertainties in vertical parcel motion and settling speed, or lack of incorporation thereof in the models [53,55]. This observation suggests that settling might not be the sole, or even most important, factor in accounting for vertical positions of ash clouds in the distal region. Dacre et al. [27] suggested that an increase and decrease in ash cloud thickness are likely due to a balance between vertical wind shear and turbulent diffusion for distal clouds comprised of mostly micron and submicron particles.
2.2. Methods
The atmospheric observations summarized in Section 2.1.1 show that both the troposphere and stratosphere are layered in turbulence intensity on a scale of fractions of a kilometer to several kilometers, often due to both cloud top turbulence and vertical wind shear generation. The ash cloud observations summarized in Section 2.1.2 show that more distal, distinct ash clouds evolve from more proximal, diffuse and thicker clouds.
In many VATDs, sub-grid dispersal in the vertical direction is usually described by a single vertical diffusivity, , which may take on the same value as the horizontal diffusivity, ; the result is then uniform or isotropic ash dispersion. Our goal here is to contrast the physical behavior of an ash cloud under conditions of isotropic ( const.) or constant vertical turbulence (), and layered turbulence. We base our methodology on analytical and numerical models using synthetic atmospheres with and without multiple turbulent layers separated by relatively quiescent air.
2.2.1. Eulerian Analytical Formulation
In the case of isotropic turbulence, we begin by assuming Cartesian coordinates, , with velocity components, . The three components of the turbulent diffusivity, are the same, . The concentration of particles in the i-size fraction, , can be written for time, t and space as:
where represents the source/sink function, which in the case of ash clouds is mostly represented by aggregation and disaggregation of small particles. In the present case, such processes are set to zero. To derive an instructive solution, we assume a two-dimensional system in x and z (z upward, and motion in the y direction can be ignored) with a point-source in time and space, , the settling speed is negative, and that, following a streamtube, the motion of the volcanic cloud can be characterized by a single downwind coordinate direction s—for which the axis is everywhere tangent to the plume centerline, for example, Ref. [56,57]—and speed U in that direction. Under these assumptions, the advection-diffusion equation becomes:
with the well-known solution for the impulse initial condition [58,59]:
It is reasonably clear that the solution is a Gaussian in , in which ash in the mean is blown downwind at speed U and falls at speed , while spreading from the mean at rate .
The second case is for layered turbulence, in which , and generally . Since a 1D model is instructive in this system, we investigate vertical motions alone. In this system, there is a discontinuity in the diffusive flux at the lower boundary of a more turbulent layer because decreases suddenly, and in this case, the one-dimensional advection-diffusion equation:
becomes, in the region of the lower boundary of the upper layer:
for .
A step-like concentration gradient develops at the base of the upper layer, as some particles settle from the layer, while others are swept back into it by turbulence rather than settling through the boundary. The solution is well-known in volcanology and sedimentation research generally [21,60,61]:
where is some initial time at which sedimentation starts in a given control volume, and is negative or downward.
In a more quiescent layer below the boundary, particles only settle and are advected downwind, there is little turbulence to enhance persistence within the layer. Thus, for systems in which particle motion is controlled by both turbulent diffusion and settling, turbulent layers can retain particles longer than do quiescent layers because of continuing re-entrainment in eddies (Equation (6)). Particles fall relatively rapidly through the quiescent layers because of unhindered settling (Equation (3)), sometimes even enhanced by the effects of convective sedimentation [19], which is not included in the present model.
2.2.2. Lagrangian Formulation
We can gain additional insight by looking at the Lagrangian formulation of the problem. In a Lagrangian framework, common to many ash dispersion models, such as HYSPLIT, movement is given by:
where r is the position vector, v is the velocity vector and j is a time index, for which . For the vertical, z component of the position:
If turbulence is added, and assuming no mean vertical flow, this becomes:
where is the random vertical component of an instantaneous turbulence velocity. Note that the direction (up or down) and magnitude of change with time, and therefore the effective settling speed, , can be positive or negative (rising parcel) and of widely varying magnitude, depending on the ratio of to . Furthermore, can be related to the turbulent diffusion by:
where is the length scale of the largest eddies, the Ozmidov scale, which must be less than the layer thickness, i.e., , otherwise layers would be eroded by turbulence. One of the important features in a layered Lagrangian model is the treatment of the boundary between regions of different turbulence intensity [62] (cf. Equation (6)). For settling particles, Webster and Thomson [63] showed that, when particles are incident upon a thin region around the boundary, probabilities of transmission and reflection must be calculated. We have implemented the conceptualization of Thomson et al. [62] and Webster and Thomson [63] by numerical experimentation with heuristic, stochastic variation in thickness of a boundary region, wherein particles entering from the more turbulent side have a greater probability of being reflected back into the high-turbulence region. We chose outputs that conformed to the ideas and results of these previous workers, but detailed discussion of the different schemes is beyond the scope of the present contribution.
2.2.3. Similarity Theory
The velocity scales for turbulence in the z-direction and settling are, respectively, , the absolute value of the time-mean vertical turbulence velocity, and . The ratio of these forms the simple dimensionless group, :
Likewise, the timescales for the processes can be used to examine the conditions under which diffusion or settling dominates. From Equation (3), the timescale of vertical diffusion, , through a layer of depth, h, is given as . From Equation (6), the timescale of settling through the same layer, , is . The ratio of the two timescales indicates domination of particle transport through the layer by settling or turbulent diffusion in the vertical direction. The ratio is given by the dimensionless group, :
Potentially important or critical values of particle size and settling speed, , turbulence intensity, , and eddy diffusivity, are given in Table 3. In previous work describing the generation of ash cloud layering, values of have ranged from = 10,000 m/s and m/s [17] using the Puff VATD model, to , with a mean of 1 m/s, using the NAME model [27]. Note that in these models, larger-scale eddies are assumed to be characterized by the wind field as described in the NWP model, so that represents only the subgrid eddy diffusion. Thus, the effects of diffusion on eddies of the scale of the grid might be poorly resolved. Fero et al. [17] used NWP grids with a resolution of c. 200 km in the horizontal, and 1 km in the vertical, while Dacre et al. [27] used a grid with a resolution of c. 50 km in the horizontal, and 100 m in the vertical. In the Lagrangian model used in the present contribution, we have explored results for values of effective ranging from ∼3 to ∼6 m/s, in constructing a three-dimensional, unsteady velocity and diffusivity field following the spectral technique discussed in detail in Jenkins [64] and Bursik [12]. To obtain turbulence layering in this spectral model, the Fourier series describing the vertical dispersion is truncated at different wavenumbers [64] in different layers, resulting in an alternation of high- and low-eddy diffusivity or turbulence intensity (Table 3).

Table 3.
Values of dimensionless groups for different particle sizes and layer thicknesses. Note that the boundary between or and unity tends to fall in 10–250 m particle size range.
2.3. Numerical Analysis
To illustrate effects of turbulence layering on particle settling and motion, numerical experiments were performed using both the VATD model Ash3D [67] and a Lagrangian model (Section 2.2.2). For a thorough description of the Lagrangian model and the synthetic atmosphere in which it is run, see Jenkins [64] and Bursik [12]. Experimental parameter values of importance used in the models are shown in Table 4. In Section 3, we explore results from similarity analysis and numerical solutions based on the theoretical development. Numerical solutions are provided for atmospheres both layered and non-layered with respect to turbulence (Table 4).

Table 4.
Simulation parameters. Duration refers to emission from vent.
3. Results
In this section, we first investigate expected behavior of ash particles given a layering in atmospheric turbulence structure using similarity theory. We then look at numerical results showing what the typical particle vertical speed should be, given a synthetic atmospheric turbulence layering (Table 4). Output from several simulations for a synthetic, turbulence-layered atmosphere using different particle size and settling speed are then shown to investigate the potential effects of turbulence layering on particles of different sizes. We then discuss possible turbulence layering in the atmosphere associated with the climactic 1991 Pinatubo eruption, and run simulations in the resulting synthetic atmosphere.
We gain insight into expected behavior using results of the similarity analysis, and refer to Equations (11) and (12) to explore asymptotic behavior. In layers for which or , the mean turbulence speed is low relative to the settling speed, the timescale of diffusion is therefore long, hence motion is controlled by settling. In such a layer, mean concentration decreases linearly with time, as all particles exit the layer at approximately their settling speed. In layers for which or , diffusion is rapid relative to settling, i.e., the timescale of settling is long, hence motion is dominated by diffusion and continuous suspension. For layers in which or , Equation (6) holds, settling and turbulent transport are both important, and although particle concentration decreases exponentially, some particles persist in the layer a relatively long time due to turbulent suspension. Note that as layer thickness, h, increases, the timescale of diffusion increases faster than does that for settling, meaning it becomes more likely the particles will exit a layer by settling than by diffusion. For a typical diffusivity of m/s in the UTLS [68] at 10 km altitude, and layer of depth km, the critical settling speed, , dividing settling from diffusion dominated motion is c. 1 m/s, which would correspond to a pumice particle of diameter c. 100 m at about 2400 kg/cu m (e.g., [69]).
Numerical results for a layered system (Figure 3) are shown in Figure 4. Figure 3 is based on the observations of Cho et al. [40], who point out two layers of especially striking turbulence from 2–2.7 km and 3.8–4.2 km (Figure 3), but do not give specific values for turbulence intensity. We therefore apply high turbulence in these two layers through a simple Lagrangian random walk, and in other layers, low turbulence. The largest particles, in this case >1 mm, are dominated by settling and show little sensitivity to turbulence (Figure 4a). Intermediate sized particles, ∼10–250 m (Figure 4b,c), in the more turbulent layers initiate a random walk, being “stuck” within the eddies and subjected to turbulence-hindered settling. In these cases, consider the lower boundary of a layer with strong turbulence. All the particles there are subject to a random walk. They have a 50% percent probability of going up, and a 50% probability of going down. Those particles sent above the lower boundary due to turbulence are sent to a position higher above the boundary than their original position at the boundary. This will give them a greater chance to spend a longer time in the turbulent layer, whether or not one considers settling. Thus, for those layers dominated by the random walk and dispersion, , Equation (6) holds, and the behavior seen in Figure 4b,c occurs. The motion of the smallest particles, here c. 1 m, is dominated by turbulent diffusion. The particles spread slowly through the less turbulent layers, and rapidly in the more turbulent layers.
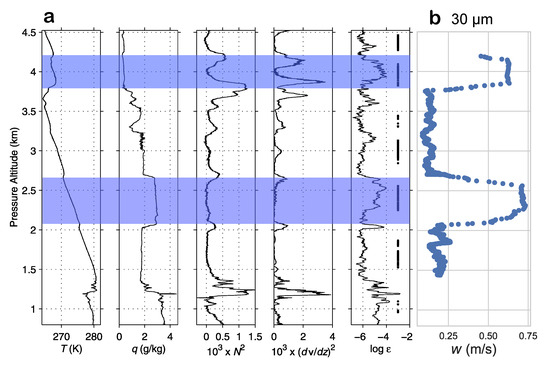
Figure 3.
(a) Turbulent tropospheric layers (shaded) indicated by constant mixing ratio (q), high turbulent energy dissipation rate (), and bounded by high total shear (). Modified from Cho et al. [40]. Shaded layers are high-diffusivity, unshaded are low-diffusivity, used in simplified layer model (Table 4). (b) Rolling mean of absolute value of instantaneous vertical speed for an example model 30 m particle (m/s). Note that speed tends to be higher in more turbulent layers (shaded in (a)).
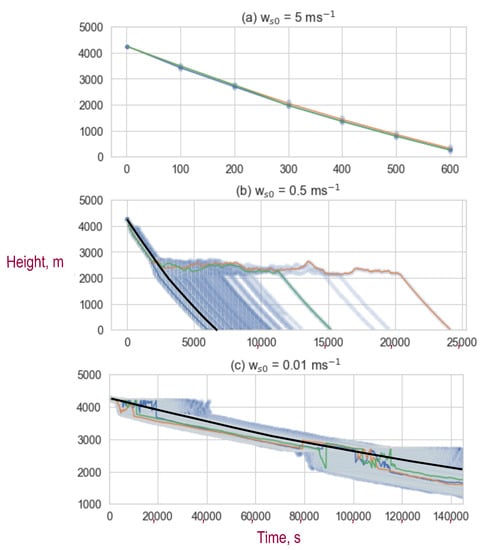
Figure 4.
Longitudinal time-section through Lagrangian dispersion model showing paths of volcanic particles settling through turbulent layers, in which suspension is enhanced. This output is based on layers in Figure 3. See Table 4. Most particles colored semitransparent blue, so deeper hue means more particles. A few separate particles are colored differently to show individual paths. In (b) and (c), the black particle path is for particle falling at effective settling speed. (a) 4 mm particles not affected by turbulence (Table 3). (b) 250 m particles are sometimes affected by turbulence, and can remain intermittently suspended in more turbulent layers. (c) 30 m particles are profoundly affected by variations in turbulence intensity.
In contrast, and following from Equation (3), spread from a point source in a VATD model, with isotropic turbulence and a wind of constant speed with height, is shown in Figure 5, together with spread in a layered atmosphere from the Lagrangian model. Ash diffuses and progressively spreads from the source as the center of mass descends at the settling speed. Using larger particles and a higher settling speed, the rate at which the center of mass descends would increase, but the rate at which the particles disperse from the center of mass would not be affected by particle size. Thus, at any one height below the source, particles with a higher settling speed would be spread less distance from the source.
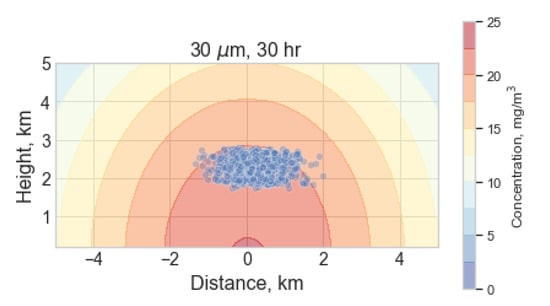
Figure 5.
Crosswind section through volcanic ash transport and dispersal (VATD) Ash3D (color contours) and Lagrangian model (separate particles) output for test case (Table 4). Instantaneous source and no wind shear, showing advection, settling and dispersal of m ash after 30 h. Note in the Lagrangian layered model, particles are concentrated in lower, high-turbulence layer.
Application to 1991 Pinatubo Eruption
There are no direct observations of turbulence values associated with the climactic 1991 eruption of Pinatubo. As noted in Section 2.2.3, Fero et al. [17] explored values of and m/s for the eruption. Given the understanding of turbulence generation, we can nevertheless speculate with some assurance that Rayleigh–Taylor cloud top turbulence generation was probably strong above the Pinatubo umbrella cloud [29], and that turbulence generation by both wind and umbrella flow near the tropopause at 16–17 km was probably strong due to the intrusion of the umbrella cloud and shift from southwesterly to northeasterly winds at that altitude [17]. This assessment is consistent with the general observation that the most intense level of clear-air turbulence development in the lower atmosphere is the tropopause [42]. We therefore construct a speculative turbulence layering for the eruption based on these considerations.
The main umbrella cloud of the climactic 1991 Pinatubo eruption was centered between 24 to 26 km height and ∼3–6 km thick, although ash was injected as low as 17 km and as high as 40 km [7,17]. The umbrella cloud acted as an intrusive gravity current for the first 4–5 h of eruption, and continued to be partly driven by buoyancy for an additional 5–6 h [7,17,46]. From the initial umbrella cloud, the development and separation of layers rapidly resulted in two main clouds, the first rich in larger particles (∼90 m; [17]) and centered at the tropopause (∼16–17 km); the second, a higher cloud rich in SO and fine particles that remained centered near the neutral buoyancy height of 25 km [17]. These two main ash transport regions persisted, centered around 14–16 and 22–25 km [8] until at least about a month after the eruption. Based on possible/likely generation of stronger turbulence by cloud-top convective and intrusion, and wind shear mechanisms, respectively, two regions centered around 17 and 25 km are given higher values of turbulence intensity in layered, Lagrangian model runs (Table 4).
With the atmosphere having these speculative intensely turbulent layers, we modeled the settling of 1 to 4000 m particles from the Pinatubo cloud for periods up to a week. Although particles as large as 1000 m were affected by the turbulence layering [70], we focus on the results for representative 10 and 30 m particles at 18 h, as these sizes were dominant in parts of the cloud for periods up to nearly a month (Section 2.1.2) [8], as their settling and dispersal behavior were similar to that for particles <10 and >30 m, respectively, and as the 18-h time window is particularly important to VAAC ash cloud forecasting. Eighteen hours is the length of the forecast window typically issued in volcanic ash advisories (VAA) and shown in volcanic ash graphics (VAG) issued by the VAACs. Also, by 18 h, the motion was dominated by the atmosphere [7,17]. The results for model 10 and 30 m particle sizes are consistent with observations of cloud heights, particle sizes (Section 2.1.2) and speculative layering within them (Figure 6). Given particles released from heights ranging from 23 to 27 km, after 18 h, 10 m particles are concentrated in and around the 24–25 km high-turbulence layers, whereas 30 m particles are mostly spread throughout the 14.5 to 19 km high-turbulence layer. This layer would not have persisted through time except for the continued suspension by the higher level of turbulence (Figure 7). In other numerical experiments, particles <10 m are distributed similarly to the 10 m particles, while particles up to ∼250 m are distributed similarly to the 30 m particles, so these two sizes give a generally good picture of fine and coarse particle distributions at this time.
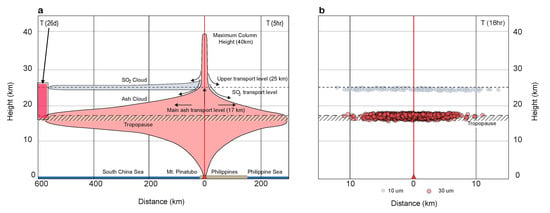
Figure 6.
(a) Schematic longitudinal section through Pinatubo ash cloud at 5hr, based on Fero et al. [17]. Semitransparent box on left labeled ’T(26d)’ shows range of volcanic cloud heights after 26 days according to Winker and Osborn [8]. (b) Cross section through Lagrangian dispersion model for 10 and 30 m particles (Table 4) with turbulence layered atmosphere, showing layered ash dispersal. In other experiments with particles 1–10 m and 30–100 m, output was similar to that for 10 and 30 m, respectively.
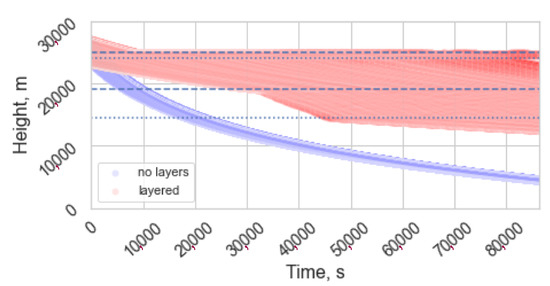
Figure 7.
Longitudinal time-section to one day (86,400 s) through Lagrangian dispersion model outputs showing paths of 30 m particles. Blue particles, weak homogeneous turbulence with high-turbulence layers removed, and turbulence diffusivity set to low value through depth of atmosphere; red particles, turbulence layering as in Table 4 and Figure 6 for Pinatubo. Note 18 h = 64,800 s. Existence of more turbulent layers enhances persistence of particles.
4. Discussion and Conclusions
In the present work, we have presented data and models on near-vent and distal volcanic cloud morphology and ash loading. We have performed numerical experiments comparing dispersal in an atmosphere with constant and variable with height. The observational data suggest that distal clouds of depth [0.1 to ∼5] km develop from near-vent clouds of [1–10] km depth. The downwind clouds occur at heights consistent with the original eruption column heights for both tropospheric and stratospheric eruptions. The depth range of the distal layers, being generally less than the near-vent depth range, and the common stacking of distal layers, suggest that their development is controlled by atmospheric processes. The observations from the numerical test case are consistent with the working hypothesis that the layering of the atmosphere in turbulence intensity, generally causing alternating suspension and settling dominated behavior of appropriately sized particles (in the present experiments and as observed, those of [10–100] m) is a cause of distal layer morphology. Particles larger than those in this size range are dominated by settling and show little sensitivity to variations in turbulence intensity. The results for the Pinatubo test case show that the turbulence structure of the atmosphere can cause ash layer formation or increase ash layer persistence, through the process of enhanced suspension in vertically restricted regions of high turbulence. The numerical results for both the test and Pinatubo cases are consistent with and explain in more detail those of Dacre et al. [27] that the motion and layering of [1–30] m particle clouds is driven by a balance between wind shear and turbulent diffusion.
Because of the complex interaction of the values of turbulence velocity, layer thickness, Ozmidov scale, treatment of the boundary between regions of different turbulence intensity, and settling speed or particle size, the modeling needs to be carefully constructed. Errors in the present work could have arisen especially due to poor characterization of the turbulence field and boundary effects between the different layers. The results suggest that the particle size affected by the processes explored here is not only sensitive to model conditions but also to the true physical state of the atmosphere, thus were one to measure turbulence intensity in detail, it might be possible to invert that information to obtain particle sizes persisting in more turbulent layers.
Thus, in addition to the near-vent volcanic processes modifying ash cloud layering, atmospheric processes can produce distal multilayered ash clouds, due to multiple, alternating layers of turbulent and quiescent air. The distal ash layers scale to the depth of the alternating turbulent and quiescent layers in the atmosphere, which are [0.1–1] km deep. The relevant model outputs (Figure 6 and Figure 7) are not inconsistent with those of VATD and backtrajectory models, in which homogeneous turbulence can be associated with layers, given pre-existing ash cloud layering at the source vent, or wind shear [4,22,23,49,53]. It is likely that shear together with layering in turbulent diffusivity controls the thickness of distal layers for periods of days to perhaps a month by hindering settling of particles in the 1–1000 m range [27]; note that the wind shear and turbulence layering processes are not mutually exclusive [40].
The results suggest that to better forecast the position and morphology of ash clouds for aviation safety and other purposes in VATDs, the vertical characteristics of the atmosphere need to be better resolved and characterized, particularly in the 18-h time window critical to forecasting in VAAs and VAGs. Because of the importance of turbulence and moisture to layer formation and detection, it is critical that these two parameters especially be estimated well, and at as high a vertical resolution as possible. Specifically, if appropriate sonde or other high-vertical resolution data are available, they should be used to measure heights of potentially elevated , to be used as input into high-resolution NWP models to provide better vertical turbulence parametrization for VATDs, and a better understanding of heights at which ash should occur in higher concentration. One perhaps important ramification of the present work is that it might be possible to determine a priori an ash-height injection time history, which should be critical to accurate forecasting of the height of ash, a priori, rather than find it a posteriori as currently done through inversion [5,24]. Being able to provide such information a priori could have a strong positive impact on forecasting the future heights and thicknesses of ash clouds for aviation using VATDs.
Author Contributions
Conceptualization, M.B.; methodology, M.B.; software, M.B. and Q.Y.; validation, M.B., M.P. and A.B.C.; formal analysis, M.B.; resources, M.B., M.P., A.B.-C., A.T.; data curation, M.B.; writing—original draft preparation, M.B., A.T.; writing—review and editing, M.B., Q.Y., A.B.-C., A.T., M.P.; visualization, M.B., Q.Y., M.P., A.B.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Available from the first author.
Acknowledgments
The helpful comments of two anonymous reviewers on an earlier ms, and four anonymous reviewers on the current ms are gratefully acknowledged. Simon Carn is thanked for initial interest and encouragement in this work. Bruce Pitman is thanked for useful conversation on this topic. Larry Mastin gave valuable feedback on an earlier version of the ms regarding related work. Q. Yang was funded by the Earth Observatory of Singapore. We thank the creators of Ash3D, Pandas, Matplotlib and Seaborn for excellent software tools enabling this research.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AERONET | AErosol RObotic NETwork |
| ASL | Above Sea Level |
| BT | Brightness Temperature |
| CALIOP | Cloud-Aerosol LIdar with Orthogonal Polarization |
| CAT | Clear-Air Turbulence |
| EARLINET | European Aerosol Research LIdar NETwork |
| HYSPLIT | Hybrid Single-Particle Lagrangian Integrated Trajectory |
| IAVW | International Airways Volcano Watch |
| MODIS | Moderate Resolution Imaging Spectrometer |
| NAME | Numerical Atmospheric dispersion Modeling Environment |
| NWP | Numerical Weather Prediction |
| RGB | Red-Green-Blue |
| RH | Relative Humidity |
| UTLS | Upper Troposphere - Lower Stratosphere |
| VATD | Volcanic Ash Transport and Dispersal |
| VAA | Volcanic Ash Advisory |
| VAAC | Volcanic Ash Advisory Center |
| VAG | Volcanic Ash Graphics |
References
- Casadevall, T.J. Volcanic Ash and Aviation Safety: Proceedings of the First International Symposium on Volcanic Ash and Aviation Safety. U.S. Geolog. Surv. Bull. 1994, 2047, 450. [Google Scholar]
- Mazzocchi, M.; Hansstein, F.; Ragona, M. The 2010 Volcanic Ash Cloud and Its Financial Impact on the European Airline Industry; CESifo Forum; ifo Institut für Wirtschaftsforschung an der Universität München: München, Germany, 2010; Volume 11, pp. 92–100. [Google Scholar]
- Tupper, A.; Itikarai, I.; Richards, M.; Prata, F.; Carn, S.; Rosenfeld, D. Facing the challenges of the international airways volcano watch: the 2004/05 eruptions of Manam, Papua New Guinea. Weather Forecast. 2007, 22, 175–191. [Google Scholar] [CrossRef]
- Heinold, B.; Tegen, I.; Wolke, R.; Ansmann, A.; Mattis, I.; Minikin, A.; Schumann, U.; Weinzierl, B. Simulations of the 2010 Eyjafjallajökull volcanic ash dispersal over Europe using COSMO–MUSCAT. Atmosp. Environ. 2012, 48, 195–204. [Google Scholar] [CrossRef]
- Kristiansen, N.I.; Prata, A.; Stohl, A.; Carn, S.A. Stratospheric volcanic ash emissions from the 13 February 2014 Kelut eruption. Geophys. Res. Lett. 2015, 42, 588–596. [Google Scholar] [CrossRef]
- Carazzo, G.; Jellinek, A.M. Particle sedimentation and diffusive convection in volcanic ash-clouds. J. Geophys. Res. 2013, 118, 1420–1437. [Google Scholar] [CrossRef]
- Holasek, R.E.; Self, S.; Woods, A.W. Satellite observations and interpretation of the 1991 Mount Pinatubo eruption plumes. J. Geophys. Res. 1996, 12, 635–27. [Google Scholar] [CrossRef]
- Winker, D.; Osborn, M. Preliminary analysis of observations of the Pinatubo volcanic plume with a polarization-sensitive lidar. Geophys. Res. Lett. 1992, 19, 171–174. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Heidinger, A.K.; Sieglaff, J. Automated retrievals of volcanic ash and dust cloud properties from upwelling infrared measurements. J. Geophys. Res. Atmosp. 2013, 118, 1436–1458. [Google Scholar] [CrossRef]
- Sparks, R.S.J.; Bursik, M.I.; Carey, S.N.; Gilbert, J.S.; Glaze, L.S.; Sigurdsson, H.; Woods, A.W. Volcanic Plumes; John Wiley & Sons: London, UK, 1997; 574p. [Google Scholar]
- Woods, A.W.; Kienle, J. The dynamics and thermodynamics of volcanic clouds: Theory and observations from the april 15 and april 21, 1990 eruptions of redoubt volcano, Alaska. J. Volcanol. Geotherm. Res. 1994, 62, 273–299. [Google Scholar] [CrossRef]
- Bursik, M. Tephra dispersal. In The Physics of Explosive Volcanic Eruptions; Gilbert, J.S., Sparks, R.S.J., Eds.; Geological Society of London, Special Publications: London, UK, 1998; Volume 145, pp. 117–146. [Google Scholar]
- Barr, S. Skirt clouds associated with the Soufriere eruption of 17 April 1979. Science 1982, 216, 1111–1112. [Google Scholar] [CrossRef] [PubMed]
- Tupper, A.; Carn, S.; Davey, J.; Kamada, Y.; Potts, R.; Prata, F.; Tokuno, M. An evaluation of volcanic cloud detection techniques during recent significant eruptions in the western ’Ring of Fire’. Remote Sens. Environ. 2004, 91, 27–46. [Google Scholar] [CrossRef]
- Thorsteinsson, T.; Jóhannsson, T.; Stohl, A.; Kristiansen, N.I. High levels of particulate matter in Iceland due to direct ash emissions by the Eyjafjallajökull eruption and resuspension of deposited ash. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Holasek, R.E.; Woods, A.W.; Self, S. Experiments on gas-ash separation processes in volcanic umbrella clouds. J. Volcanol. Geotherm. Res. 1996, 70, 169–181. [Google Scholar] [CrossRef]
- Fero, J.; Carey, S.N.; Merrill, J.T. Simulating the dispersal of tephra from the 1991 Pinatubo eruption: Implications for the formation of widespread ash layers. J. Volcanol. Geotherm. Res. 2009, 186, 120–131. [Google Scholar] [CrossRef]
- Prata, F.; Woodhouse, M.; Huppert, H.E.; Prata, A.; Thordarson, T.; Carn, S. Atmospheric processes affecting the separation of volcanic ash and SO2 in volcanic eruptions: inferences from the May 2011 Grímsvötn eruption. Atmosp. Chem. Phys. 2017, 17, 10709–10732. [Google Scholar] [CrossRef]
- Hoyal, D.C.J.D.; Bursik, M.I.; Atkinson, J.F. Setting-driven convection; a mechanism of sedimentation from stratified fluids. J. Geophys. Res. C Oceans 1999, 104, 7953–7966. [Google Scholar] [CrossRef]
- Hoyal, D.C.J.D.; Bursik, M.I.; Atkinson, J.F. The influence of diffusive convection on sedimentation from buoyant plumes. Mar. Geol. 1999, 159, 205–220. [Google Scholar] [CrossRef]
- Carazzo, G.; Jellinek, A.M. A new view of the dynamics, stability and longevity of volcanic clouds. Earth Planet. Sci. Lett. 2012, 325, 39–51. [Google Scholar] [CrossRef]
- Devenish, B.; Thomson, D.; Marenco, F.; Leadbetter, S.; Ricketts, H.; Dacre, H. A study of the arrival over the United Kingdom in April 2010 of the Eyjafjallajökull ash cloud using ground-based lidar and numerical simulations. Atmosp. Environ. 2012, 48, 152–164. [Google Scholar] [CrossRef]
- Folch, A.; Costa, A.; Basart, S. Validation of the FALL3D ash dispersion model using observations of the 2010 Eyjafjallajökull volcanic ash clouds. Atmosp. Environ. 2012, 48, 165–183. [Google Scholar] [CrossRef]
- Stohl, A.; Prata, A.; Eckhardt, S.; Clarisse, L.; Durant, A.; Henne, S.; Kristiansen, N.I.; Minikin, A.; Schumann, U.; Seibert, P.; et al. Determination of time-and height-resolved volcanic ash emissions and their use for quantitative ash dispersion modeling: The 2010 Eyjafjallajökull eruption. Atmosp. Chem. Phys. 2011, 11, 4333–4351. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C.; Potts, R.J. Estimation of optimal dispersion model source parameters using satellite detections of volcanic ash. J. Geophys. Res. Atmosp. 2017, 122, 8207–8232. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C.; Potts, R.J. Quantitative verification and calibration of volcanic ash ensemble forecasts using satellite data. J. Geophys. Res. Atmosp. 2018, 123, 4135–4156. [Google Scholar] [CrossRef]
- Dacre, H.; Grant, A.; Harvey, N.; Thomson, D.; Webster, H.; Marenco, F. Volcanic ash layer depth: Processes and mechanisms. Geophys. Res. Lett. 2015, 42, 637–645. [Google Scholar] [CrossRef]
- Harvey, N.J.; Huntley, N.; Dacre, H.F.; Goldstein, M.; Thomson, D.; Webster, H. Multi-level emulation of a volcanic ash transport and dispersion model to quantify sensitivity to uncertain parameters. Nat. Hazards Earth Syst. Sci. 2018, 18, 41–63. [Google Scholar] [CrossRef]
- Vasseur, H.; Vanhoenacker, D. Characteristics of tropospheric turbulent layers from radiosonde data. Electron. Lett. 1998, 34, 318–319. [Google Scholar] [CrossRef]
- Barat, J. Some characteristics of clear-air turbulence in the middle stratosphere. J. Atmosph. Sci. 1982, 39, 2553–2564. [Google Scholar] [CrossRef]
- Nastrom, G.; Eaton, F. The coupling of gravity waves and turbulence at White Sands, New Mexico, from VHF radar observations. J. Appl. Meteorol. 1993, 32, 81–87. [Google Scholar] [CrossRef]
- Sato, K.; Hashiguchi, H.; Fukao, S. Gravity waves and turbulence associated with cumulus convection observed with the UHF/VHF clear-air Doppler radars. J. Geophys. Res. Atmosp. 1995, 100, 7111–7119. [Google Scholar] [CrossRef]
- Britter, R.E.; Simpson, J.E. A note on the structure of the head of an intrusive gravity current. J. Fluid Mech. 1981, 112, 459–466. [Google Scholar] [CrossRef]
- Chakraborty, P.; Gioia, G.; Kieffer, S. Volcán Reventador’s unusual umbrella. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Sharman, R.D.; Trier, S.B.; Lane, T.P.; Doyle, J.D. Sources and dynamics of turbulence in the upper troposphere and lower stratosphere: A review. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Maekawa, Y.; Fukao, S.; Yamamoto, M.; Yamanaka, M.D.; Tsuda, T.; Kato, S.; Woodman, R.F. First observation of the upper stratospheric vertical wind velocities using the Jicamarca VHF radar. Geophys. Res. Lett. 1993, 20, 2235–2238. [Google Scholar] [CrossRef]
- Wilson, R.; Luce, H.; Hashiguchi, H.; Nishi, N.; Yabuki, Y. Energetics of persistent turbulent layers underneath mid-level clouds estimated from concurrent radar and radiosonde data. J. Atmosp. Sol. Terr. Phys. 2014, 118, 78–89. [Google Scholar] [CrossRef]
- Gage, K.; Green, J.; VanZandt, T. Use of Doppler radar for the measurement of atmospheric turbulence parameters from the intensity of clear-air echoes. Radio Sci. 1980, 15, 407–416. [Google Scholar] [CrossRef]
- Dehghan, A.; Hocking, W.K.; Srinivasan, R. Comparisons between multiple in-situ aircraft turbulence measurements and radar in the troposphere. J. Atmosp. Sol. Terr. Phys. 2014, 118, 64–77. [Google Scholar] [CrossRef]
- Cho, J.Y.; Newell, R.E.; Anderson, B.E.; Barrick, J.D.; Thornhill, K.L. Characterizations of tropospheric turbulence and stability layers from aircraft observations. J. Geophys. Res. Atmosp. 2003, 108. [Google Scholar] [CrossRef]
- Pavelin, E.; Whiteway, J.A.; Busen, R.; Hacker, J. Airborne observations of turbulence, mixing, and gravity waves in the tropopause region. J. Geophys. Res. Atmosp. 2002, 107, ACL–8. [Google Scholar] [CrossRef]
- Clayson, C.A.; Kantha, L. On turbulence and mixing in the free atmosphere inferred from high-resolution soundings. J. Atmosp. Ocean. Technol. 2008, 25, 833–852. [Google Scholar] [CrossRef]
- Marlton, G.J.; Giles Harrison, R.; Nicoll, K.A.; Williams, P.D. Note: A balloon-borne accelerometer technique for measuring atmospheric turbulence. Rev. Sci. Instrum. 2015, 86, 016109. [Google Scholar] [CrossRef]
- Tupper, A.; Textor, C.; Herzog, M.; Graf, H.F. Tall clouds from small eruptions: modelling the sensitivity of eruption height and fine ash fallout to tropospheric instability. Natl. Hazards 2009. [Google Scholar] [CrossRef]
- Thouret, V.; Cho, J.Y.; Newell, R.E.; Marenco, A.; Smit, H.G. General characteristics of tropospheric trace constituent layers observed in the MOZAIC program. J. Geophys. Res. Atmosp. 2000, 105, 17379–17392. [Google Scholar] [CrossRef]
- Pouget, S.; Bursik, M.; Johnson, C.G.; Hogg, A.J.; Phillips, J.C.; Sparks, R.S.J. Interpretation of umbrella cloud growth and morphology: implications for flow regimes of short-lived and long-lived eruptions. Bull. Volcanol. 2016, 78, 1–19. [Google Scholar] [CrossRef]
- Bear-Crozier, A.; Pouget, S.; Bursik, M.; Jansons, E.; Denman, J.; Tupper, A.; Rustowicz, R. Automated detection and measurement of volcanic cloud growth: towards a robust estimate of mass flux, mass loading and eruption duration. Nat. Hazards 2020, 101, 1–38. [Google Scholar] [CrossRef]
- Pouget, S.; Bursik, M.; Webley, P.; Dehn, J.; Pavolonis, M. Estimation of eruption source parameters from umbrella cloud or downwind plume growth rate. J. Volcanol. Geotherm. Res. 2013, 258, 100–112. [Google Scholar] [CrossRef]
- Winker, D.; Liu, Z.; Omar, A.; Tackett, J.; Fairlie, D. CALIOP observations of the transport of ash from the Eyjafjallajökull volcano in April 2010. J. Geophys. Res. Atmosp. 2012, 117. [Google Scholar] [CrossRef]
- Marenco, F.; Johnson, B.; Turnbull, K.; Newman, S.; Haywood, J.; Webster, H.; Ricketts, H. Airborne lidar observations of the 2010 Eyjafjallajökull volcanic ash plume. J. Geophys. Res. Atmosp. 2011, 116. [Google Scholar] [CrossRef]
- Schumann, U.; Weinzierl, B.; Reitebuch, O.; Schlager, H.; Minikin, A.; Forster, C.; Baumann, R.; Sailer, T.; Graf, K.; Mannstein, H.; et al. Airborne observations of the Eyjafjalla volcano ash cloud over Europe during air space closure in April and May 2010. Atmos. Chem. Phys. 2011, 11, 2245–2279. [Google Scholar] [CrossRef]
- Ansmann, A.; Tesche, M.; Seifert, P.; Groß, S.; Freudenthaler, V.; Apituley, A.; Wilson, K.M.; Serikov, I.; Linné, H.; Heinold, B.; et al. Ash and fine-mode particle mass profiles from EARLINET-AERONET observations over central Europe after the eruptions of the Eyjafjallajökull volcano in 2010. J. Geophys. Res. Atmosp. 2011, 116. [Google Scholar] [CrossRef]
- Vernier, J.P.; Fairlie, T.; Murray, J.; Tupper, A.; Trepte, C.; Winker, D.; Pelon, J.; Garnier, A.; Jumelet, J.; Pavolonis, M.; et al. An advanced system to monitor the 3D structure of diffuse volcanic ash clouds. J. Appl. Meteorol. Climatol. 2013, 52, 2125–2138. [Google Scholar] [CrossRef]
- Pierce, R.B.; Fairlie, T.D.A. Chaotic advection in the stratosphere: Implications for the dispersal of chemically perturbed air from the polar vortex. J. Geophys. Res. Atmosp. 1993, 98, 18589–18595. [Google Scholar] [CrossRef]
- Madankan, R.; Pouget, S.; Singla, P.; Bursik, M.; Dehn, J.; Jones, M.; Patra, A.; Pavolonis, M.; Pitman, E.; Singh, T.; Webley, P. Computation of probabilistic hazard maps and source parameter estimation for volcanic ash transport and dispersion. J. Comput. Phys. 2014, 271, 39–59. [Google Scholar] [CrossRef]
- Wright, S.J. Effects of Ambient Crossflows and Density Stratification on The Characteristic Behavior of Round Turbulent Buoyant Jets; Report KH-R-36 W.M. Keck Laboratory, Caltech: Pasadena, CA, USA, 1977. [Google Scholar]
- Hopkins, A.T.; Bridgman, C.J. A volcanic ash transport model and analysis of Mount St. Helens ashfall. J. Geophys. Res. 1985, 90, 10620–10630. [Google Scholar] [CrossRef]
- Csanady, D.T. Turbulent Diffusion in the Environment; D.Reidel Publishing Co.: Dordrecht, The Netherlands, 1980; 248p. [Google Scholar]
- Roberts, P.J.; Webster, D.R. Turbulent diffusion. In Environmental Fluid Mechanics: Theories and Applications; Shen, H.H., Cheng, A.H., Wang, K.H., Teng, M.H., Liu, C.C., Eds.; ASCE Press: Reston, VA, USA, 2002; pp. 7–45. [Google Scholar]
- Hazen, A. On sedimentation. Trans. Am. Soc. Civ. Eng. 1904, 53, 45–88. [Google Scholar] [CrossRef]
- Bursik, M.I.; Sparks, R.S.J.; Gilbert, J.S.; Carey, S.N. Sedimentation of tephra by volcanic plumes; I, Theory and its comparison with a study of the Fogo A plinian deposit, Sao Miguel (Azores). Bull.Volcanol. 1992, 54, 329–344. [Google Scholar] [CrossRef]
- Thomson, D.; Physick, W.; Maryon, R. Treatment of interfaces in random walk dispersion models. J. Appl. Meteorol. 1997, 36, 1284–1295. [Google Scholar] [CrossRef]
- Webster, H.N.; Thomson, D.J. Dry deposition modelling in a Lagrangian dispersion model. Int. J. Environ. Pollut. 2011, 47, 1–9. [Google Scholar] [CrossRef]
- Jenkins, A. Simulation of turbulent dispersion using a simple random model of the flow field. Appl. Math. Model. 1985, 9, 239–245. [Google Scholar] [CrossRef]
- Ganser, G. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Saxby, J.; Rust, A.; Cashman, K.; Beckett, F. The importance of grain size and shape in controlling the dispersion of the Vedde cryptotephra. J. Quat. Sci. 2020, 35, 175–185. [Google Scholar] [CrossRef]
- Schwaiger, H.F.; Denlinger, R.P.; Mastin, L.G. Ash3d: A finite-volume, conservative numerical model for ash transport and tephra deposition. J. Geophys. Res. Solid Earth 2012, 117, B4. [Google Scholar] [CrossRef]
- Wilson, R. Turbulent diffusivity in the free atmosphere inferred from MST radar measurements: A review. Ann. Geophys. 2004, 22, 3869–3887. [Google Scholar] [CrossRef]
- Scollo, S.; Coltelli, M.; Prodi, F.; Folegani, M.; Natali, S. Terminal settling velocity measurements of volcanic ash during the 2002–2003 Etna eruption by an X-band microwave rain gauge disdrometer. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Bursik, M.; Yang, Q.; Bear-Crozier, A.; Pavolonis, M.; Tupper, A. The development of volcanic ash cloud layers over hours to days due to turbulence layering. arXiv 2020, arXiv:physics.ao-ph/2012.14871, arXiv:physics.ao–ph/201214871. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).