Sensitivity of an Idealized Tropical Cyclone to the Configuration of the Global Forecast System–Eddy Diffusivity Mass Flux Planetary Boundary Layer Scheme
Abstract
1. Introduction
2. Background
3. Methods
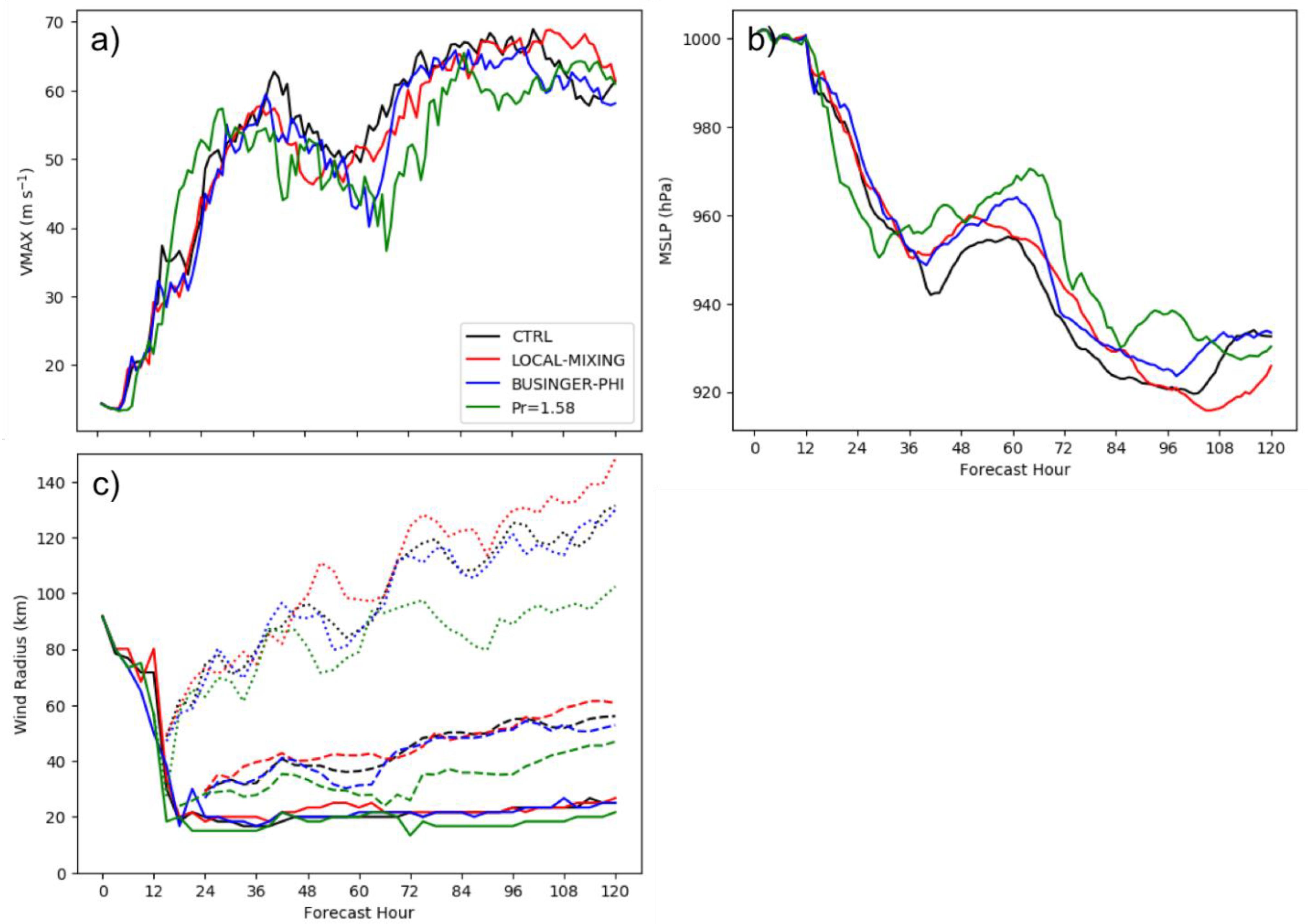
4. Results and Discussion
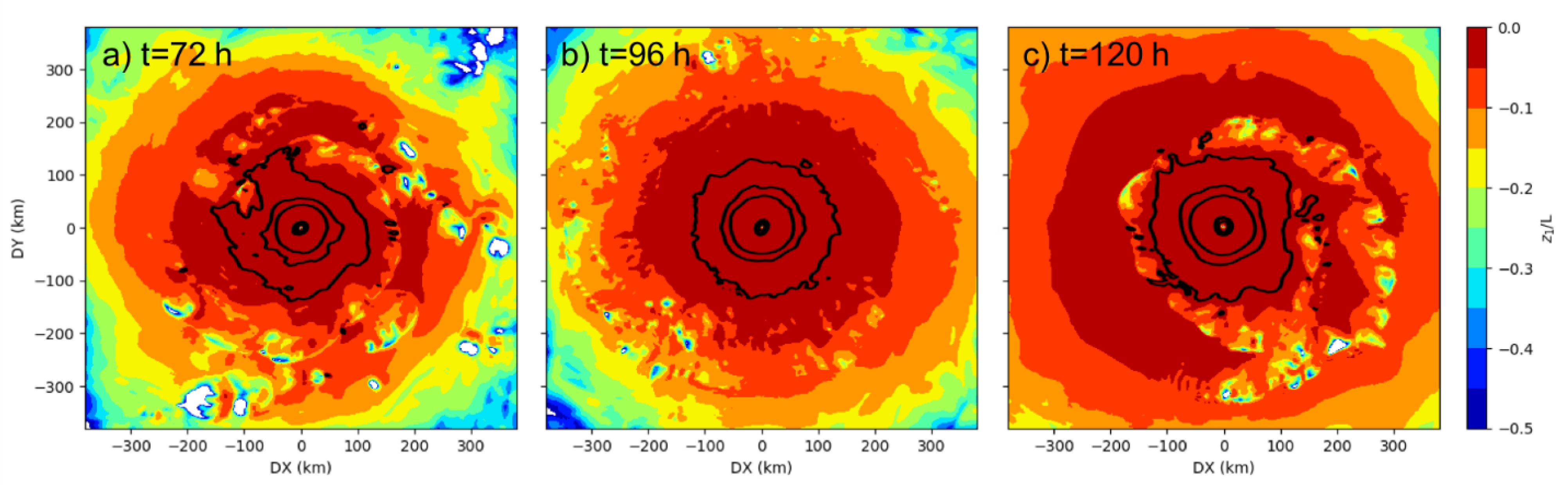
4.1. Characteristics of the CTRL Simulation
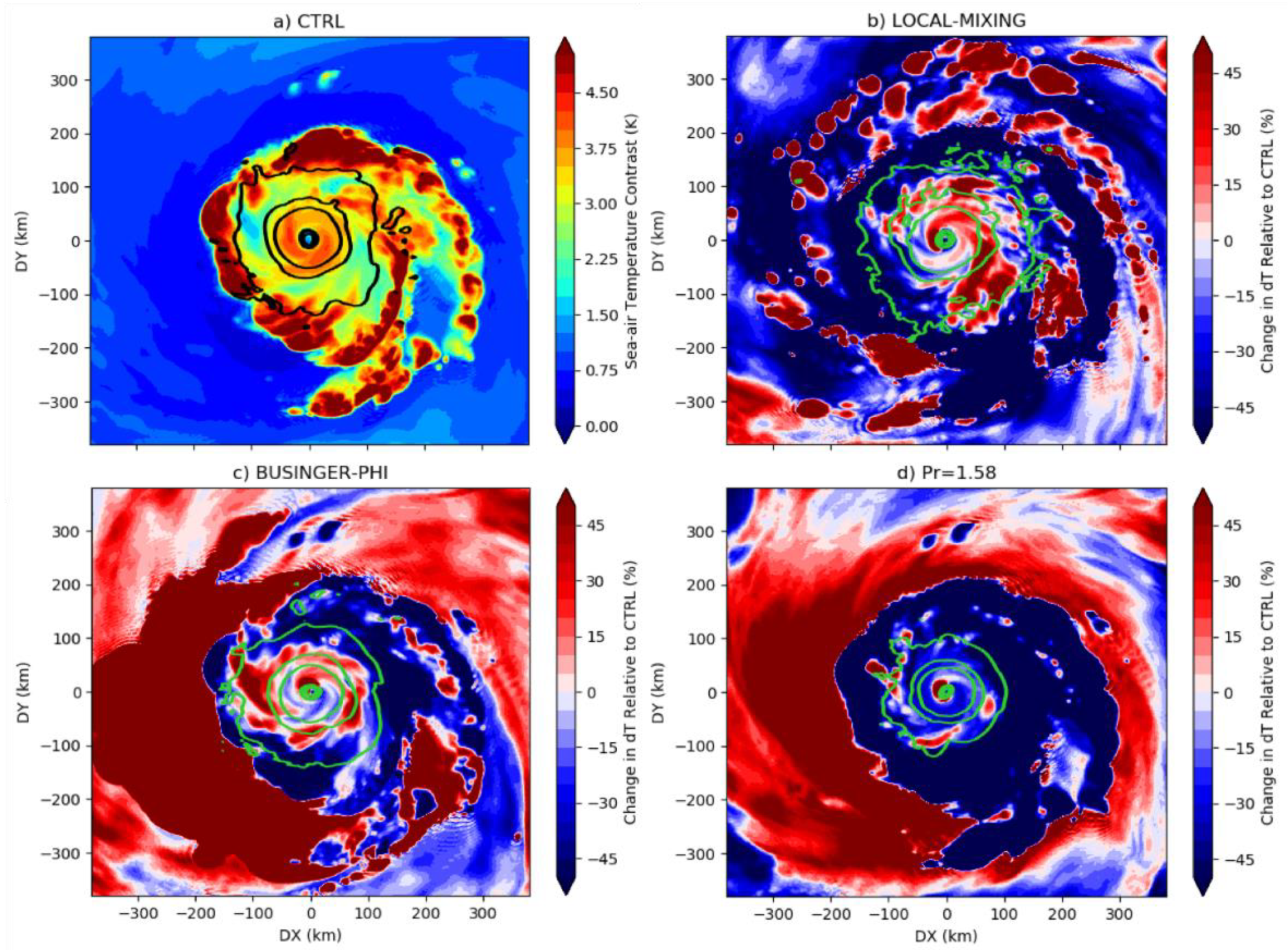
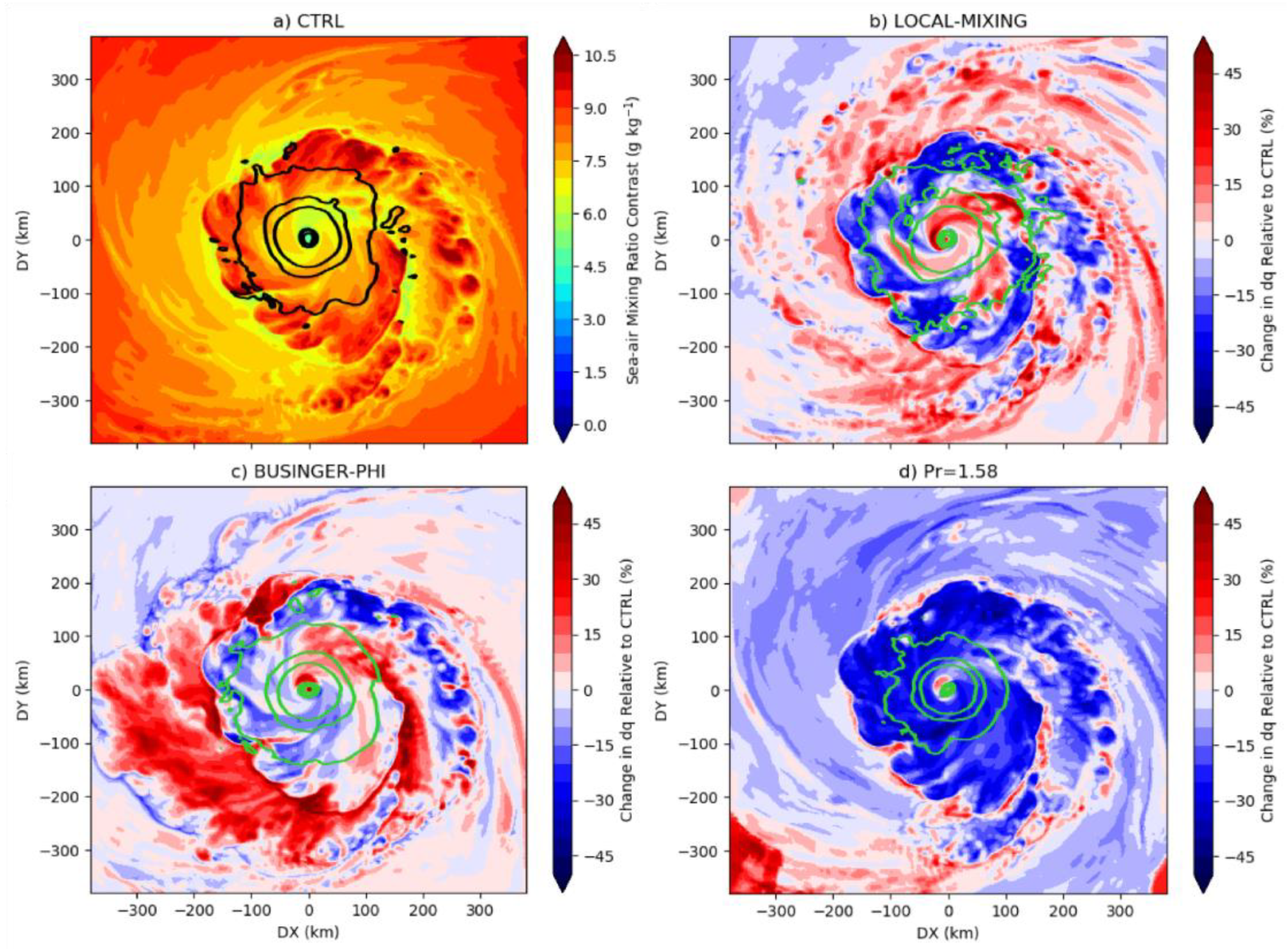
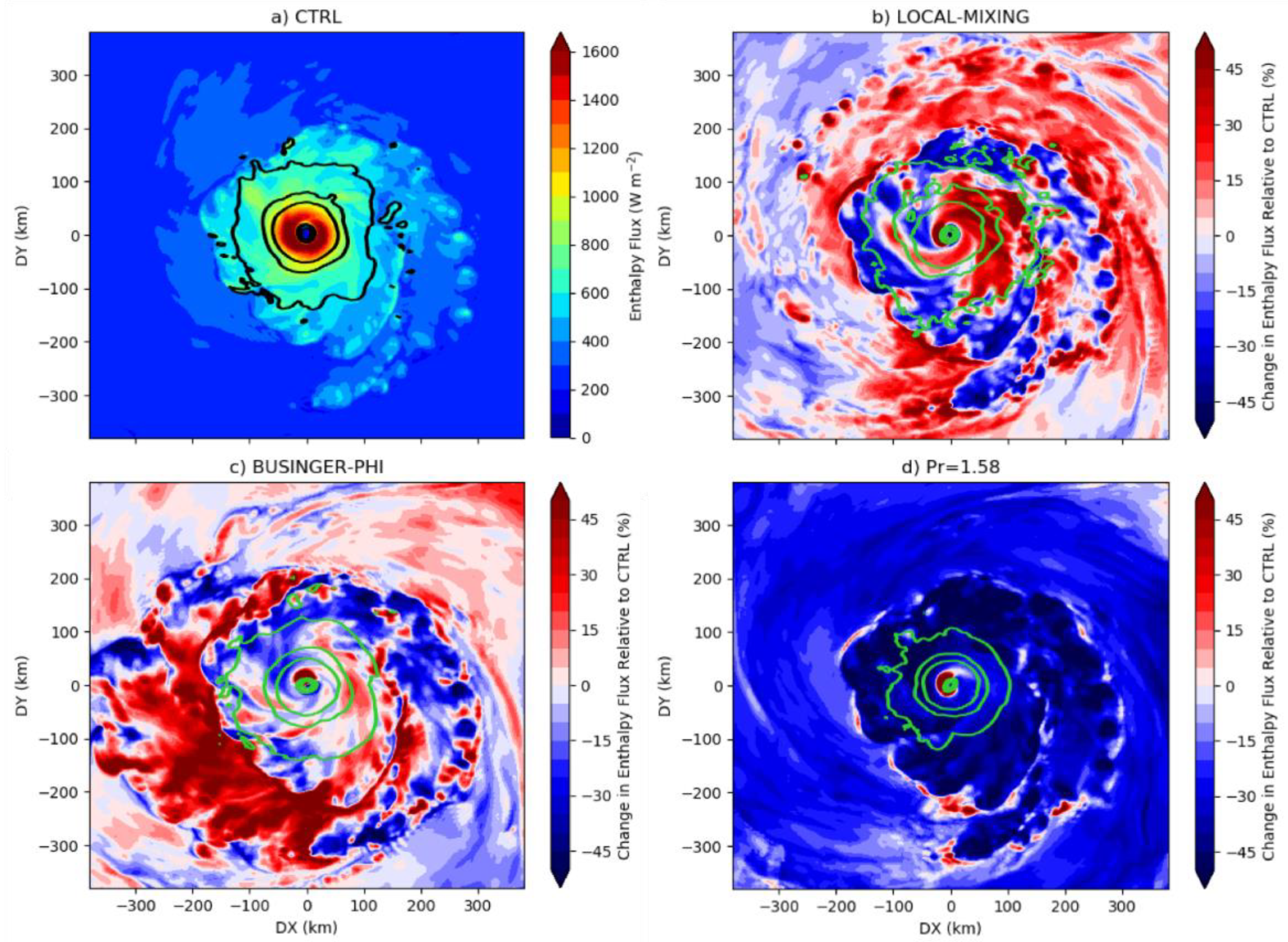
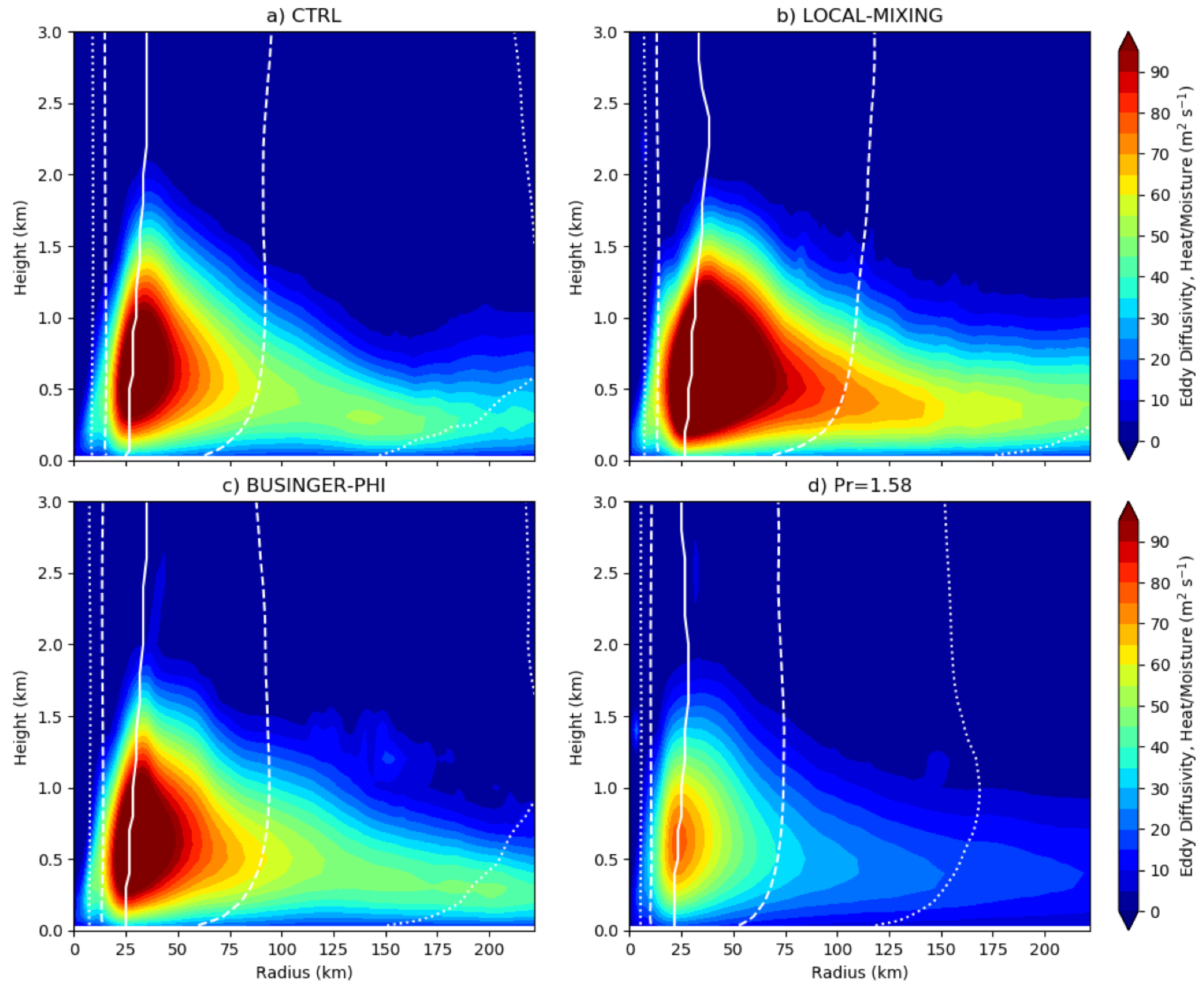
4.2. Non-local Mixing and Simulated Tropical Cyclones
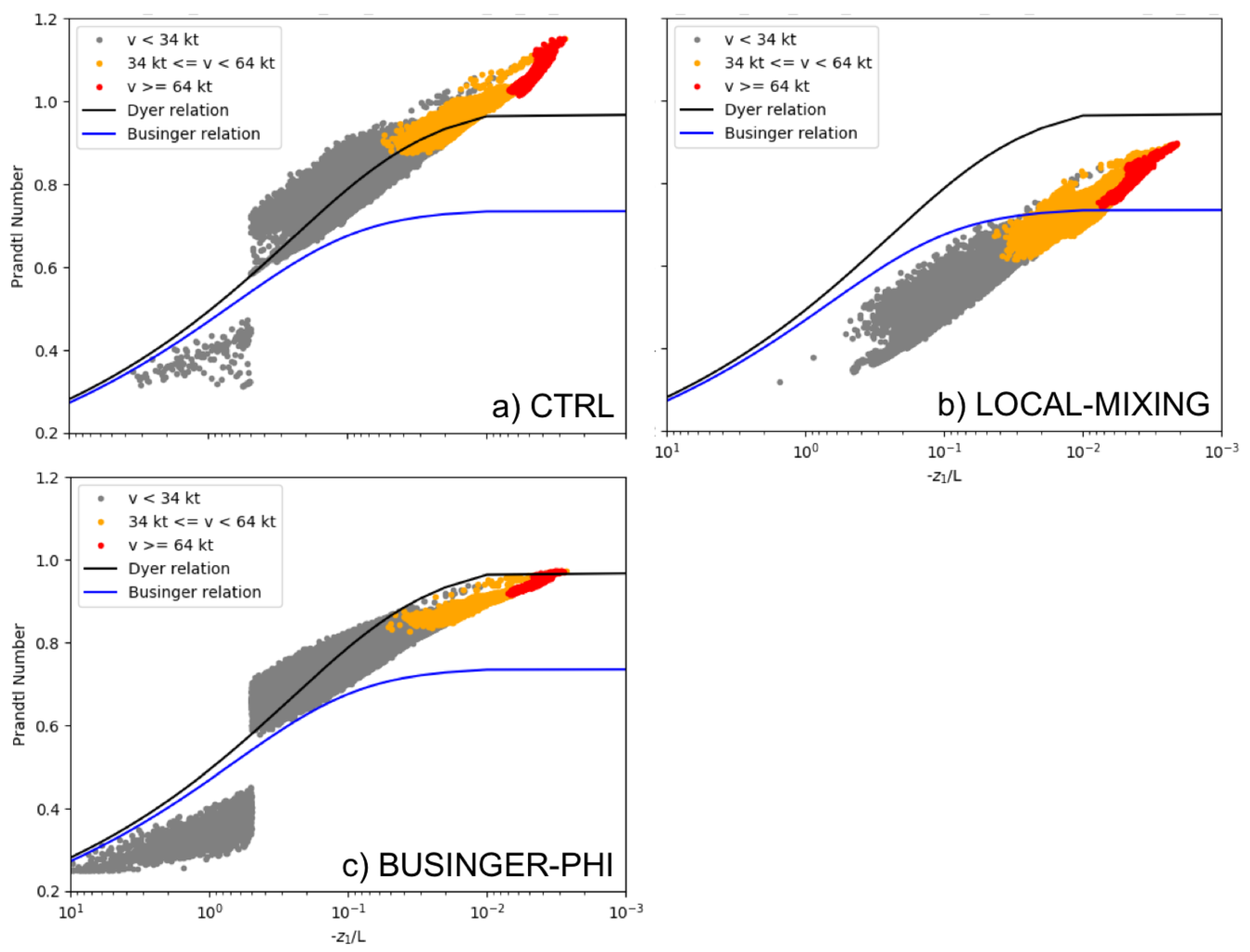
4.3. Stability Functions and Simulated Tropical Cyclones
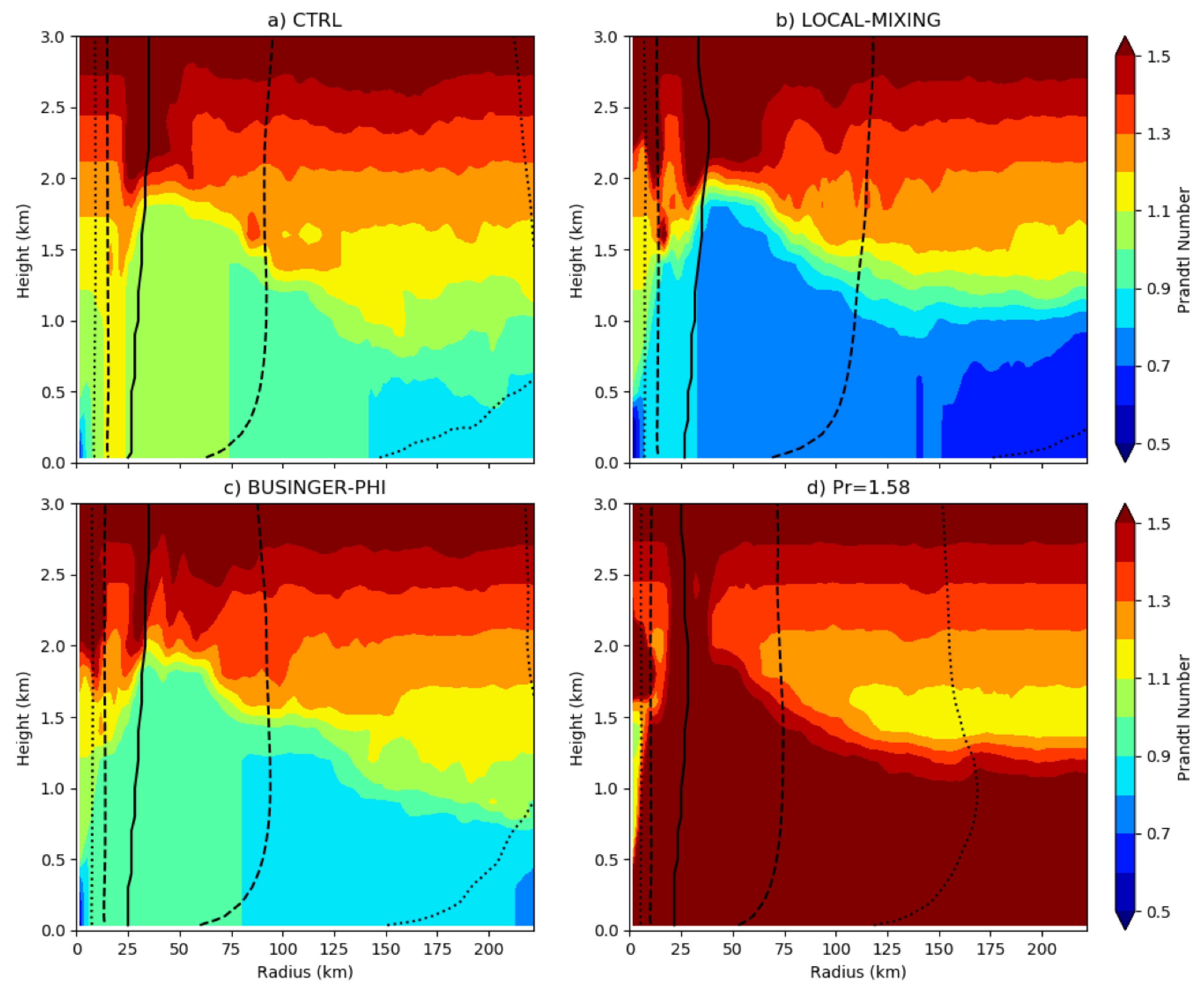
4.4. Tying the Results Together: Prandtl Number and Tropical Cyclones
5. Summary and Conclusions
- Has a smaller Kh and Kq for a given wind speed;
- Exhibits reduced enthalpy fluxes within its inner-core, even at similar wind speeds;
- Has smaller radii of maximum, 64-, and 34-kt winds, possibly due to the weaker enthalpy fluxes, with the largest impact on the 34-kt wind radius;
- Is more likely to undergo an initial period of rapid intensification, due to its smaller size;
- Reaches a weaker peak intensity due to the smaller enthalpy fluxes in the inner core.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stensrud, D.J. Parameterization Schemes: Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2007; ISBN 978-0-521-12676-2. [Google Scholar]
- Riehl, H. A Model of Hurricane Formation. J. Appl. Phys. 1950, 21, 917–925. [Google Scholar] [CrossRef]
- Kleinschmidt, E. Grundlagen einer Theorie der tropischen Zyklonen. Arch. Für Meteorol. Geophys. Bioklimatol. Ser. A 1951, 4, 53–72. [Google Scholar] [CrossRef]
- Malkus, J.S.; Riehl, H. On the Dynamics and Energy Transformations in Steady-State Hurricanes. Tellus 1960, 12, 1–20. [Google Scholar] [CrossRef]
- Emanuel, K. 100 Years of Progress in Tropical Cyclone Research. Meteorol. Monogr. 2018, 59, 15.1–15.68. [Google Scholar] [CrossRef]
- Bernardet, L.; Tallapragada, V.; Bao, S.; Trahan, S.; Kwon, Y.; Liu, Q.; Tong, M.; Biswas, M.; Brown, T.; Stark, D.; et al. Community Support and Transition of Research to Operations for the Hurricane Weather Research and Forecasting Model. Bull. Am. Meteorol. Soc. 2015, 96, 953–960. [Google Scholar] [CrossRef]
- Yablonsky, R.M.; Ginis, I.; Thomas, B.; Tallapragada, V.; Sheinin, D.; Bernardet, L. Description and Analysis of the Ocean Component of NOAA’s Operational Hurricane Weather Research and Forecasting Model (HWRF). J. Atmos. Ocean. Technol. 2015, 32, 144–163. [Google Scholar] [CrossRef]
- Biswas, M.K.; Bernardet, L.; Abarca, S.; Ginis, I.; Grell, E.; Kalina, E.; Kwon, Y.; Liu, B.; Liu, Q.; Marchok, T.; et al. Hurricane Weather Research and Forecasting (HWRF) Model: 2017 Scientific Documentation. Dev. Testbed Cent. 2018. [Google Scholar] [CrossRef]
- Mehra, A.; Tallapragada, V.; Zhang, Z.; Liu, B.; Zhu, L.; Wang, W.; Kim, H.-S. Advancing the State of the Art in Operational Tropical Cyclone Forecasting at Ncep. Trop. Cyclone Res. Rev. 2018, 7, 51–56. [Google Scholar] [CrossRef]
- Han, J.; Bretherton, C.S. TKE-Based Moist Eddy-Diffusivity Mass-Flux (EDMF) Parameterization for Vertical Turbulent Mixing. Weather Forecast. 2019, 34, 869–886. [Google Scholar] [CrossRef]
- Kepert, J.D. Choosing a Boundary Layer Parameterization for Tropical Cyclone Modeling. Mon. Weather Rev. 2012, 140, 1427–1445. [Google Scholar] [CrossRef]
- Zhang, J.A.; Drennan, W.M. An Observational Study of Vertical Eddy Diffusivity in the Hurricane Boundary Layer. J. Atmos. Sci. 2012, 69, 3223–3236. [Google Scholar] [CrossRef]
- Bu, Y.P.; Fovell, R.G.; Corbosiero, K.L. The Influences of Boundary Layer Mixing and Cloud-Radiative Forcing on Tropical Cyclone Size. J. Atmos. Sci. 2017, 74, 1273–1292. [Google Scholar] [CrossRef]
- Braun, S.A.; Tao, W.-K. Sensitivity of High-Resolution Simulations of Hurricane Bob (1991) to Planetary Boundary Layer Parameterizations. Mon. Weather Rev. 2000, 128, 3941–3961. [Google Scholar] [CrossRef]
- Smith, R.K.; Thomsen, G.L. Dependence of Tropical-Cyclone Intensification on the Boundary-Layer Representation in a Numerical Model. Q. J. R. Meteorol. Soc. 2010, 136, 1671–1685. [Google Scholar] [CrossRef]
- Zhang, J.A.; Marks, F.D.; Montgomery, M.T.; Lorsolo, S. An Estimation of Turbulent Characteristics in the Low-Level Region of Intense Hurricanes Allen (1980) and Hugo (1989). Mon. Weather Rev. 2011, 139, 1447–1462. [Google Scholar] [CrossRef]
- Zhang, J.A.; Gopalakrishnan, S.; Marks, F.D.; Rogers, R.F.; Tallapragada, V. A Developmental Framework for Improving Hurricane Model Physical Parameterizations Using Aircraft Observations. Trop. Cyclone Res. Rev. 2012, 1, 419–429. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.G.; Marks, F.; Zhang, J.A.; Zhang, X.; Bao, J.-W.; Tallapragada, V. A Study of the Impacts of Vertical Diffusion on the Structure and Intensity of the Tropical Cyclones Using the High-Resolution HWRF System. J. Atmos. Sci. 2013, 70, 524–541. [Google Scholar] [CrossRef]
- Zhang, J.A.; Nolan, D.S.; Rogers, R.F.; Tallapragada, V. Evaluating the Impact of Improvements in the Boundary Layer Parameterization on Hurricane Intensity and Structure Forecasts in HWRF. Mon. Weather Rev. 2015, 143, 3136–3155. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F.; Tallapragada, V. Impact of Parameterized Boundary Layer Structure on Tropical Cyclone Rapid Intensification Forecasts in HWRF. Mon. Weather Rev. 2017, 145, 1413–1426. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F. Effects of Parameterized Boundary Layer Structure on Hurricane Rapid Intensification in Shear. Mon. Weather Rev. 2019, 147, 853–871. [Google Scholar] [CrossRef]
- Tallapragada, V.; Kieu, C.; Kwon, Y.; Trahan, S.; Liu, Q.; Zhang, Z.; Kwon, I.-H. Evaluation of Storm Structure from the Operational HWRF during 2012 Implementation. Mon. Weather Rev. 2014, 142, 4308–4325. [Google Scholar] [CrossRef]
- Zhang, J.A.; Kalina, E.A.; Biswas, M.K.; Rogers, R.F.; Zhu, P.; Marks, F.D. A Review and Evaluation of Planetary Boundary Layer Parameterizations in Hurricane Weather Research and Forecasting Model Using Idealized Simulations and Observations. Atmosphere 2020, 11, 1091. [Google Scholar] [CrossRef]
- Wang, W.; Sippel, J.A.; Abarca, S.; Zhu, L.; Liu, B.; Zhang, Z.; Mehra, A.; Tallapragada, V. Improving NCEP HWRF Simulations of Surface Wind and Inflow Angle in the Eyewall Area. Weather Forecast. 2018, 33, 887–898. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Evaluating Formulations of Stable Boundary Layer Height. J. Appl. Meteorol. 2004, 43, 1736–1749. [Google Scholar] [CrossRef]
- Gall, R.; Franklin, J.; Marks, F.; Rappaport, E.N.; Toepfer, F. The Hurricane Forecast Improvement Project. Bull. Am. Meteorol. Soc. 2013, 94, 329–343. [Google Scholar] [CrossRef]
- Bao, J.-W.; Gopalakrishnan, S.G.; Michelson, S.A.; Marks, F.D.; Montgomery, M.T. Impact of Physics Representations in the HWRFX on Simulated Hurricane Structure and Pressure–Wind Relationships. Mon. Weather Rev. 2012, 140, 3278–3299. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, J.A.; Kieu, C.; Marks, F.D. Sensitivity of Hurricane Intensity and Structure to Two Types of Planetary Boundary Layer Parameterization Schemes in Idealized HWRF Simulations. Trop. Cyclone Res. Rev. 2018, 7, 201–211. [Google Scholar] [CrossRef]
- Troen, I.B.; Mahrt, L. A Simple Model of the Atmospheric Boundary Layer; Sensitivity to Surface Evaporation. Bound.-Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Pan, H.-L. Nonlocal Boundary Layer Vertical Diffusion in a Medium-Range Forecast Model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Han, J.; Witek, M.L.; Teixeira, J.; Sun, R.; Pan, H.-L.; Fletcher, J.K.; Bretherton, C.S. Implementation in the NCEP GFS of a Hybrid Eddy-Diffusivity Mass-Flux (EDMF) Boundary Layer Parameterization with Dissipative Heating and Modified Stable Boundary Layer Mixing. Weather Forecast. 2016, 31, 341–352. [Google Scholar] [CrossRef]
- Dyer, A.J.; Hicks, B.B. Flux-Gradient Relationships in the Constant Flux Layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Jordan, C.L. Mean Soundings for the West Indies Area. J. Meteorol. 1958, 15, 91–97. [Google Scholar] [CrossRef]
- Wang, Y. An Inverse Balance Equation in Sigma Coordinates for Model Initialization. Mon. Weather Rev. 1995, 123, 482–488. [Google Scholar] [CrossRef][Green Version]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile Relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Biswas, M.K.; Stark, D.; Carson, L. GFDL Vortex Tracker Users’ Guide V3.9a 2018.
- Kaplan, J.; DeMaria, M. Large-Scale Characteristics of Rapidly Intensifying Tropical Cyclones in the North Atlantic Basin. Weather Forecast. 2003, 18, 1093–1108. [Google Scholar] [CrossRef]
- Cione, J.J.; Kalina, E.A.; Zhang, J.A.; Uhlhorn, E.W. Observations of Air–Sea Interaction and Intensity Change in Hurricanes. Mon. Weather Rev. 2013, 141, 2368–2382. [Google Scholar] [CrossRef]
- Cione, J.J.; Bryan, G.H.; Dobosy, R.; Zhang, J.A.; de Boer, G.; Aksoy, A.; Wadler, J.B.; Kalina, E.A.; Dahl, B.A.; Ryan, K.; et al. Eye of the Storm: Observing Hurricanes with a Small Unmanned Aircraft System. Bull. Am. Meteorol. Soc. 2020, 101, E186–E205. [Google Scholar] [CrossRef]
- Hill, K.A.; Lackmann, G.M. Influence of Environmental Humidity on Tropical Cyclone Size. Mon. Weather Rev. 2009, 137, 3294–3315. [Google Scholar] [CrossRef]
- Sun, Y.; Zhong, Z.; Li, T.; Yi, L.; Hu, Y.; Wan, H.; Chen, H.; Liao, Q.; Ma, C.; Li, Q. Impact of Ocean Warming on Tropical Cyclone Size and Its Destructiveness. Sci. Rep. 2017, 7, 8154. [Google Scholar] [CrossRef]
- Emanuel, K.A. The Finite-Amplitude Nature of Tropical Cyclogenesis. J. Atmos. Sci. 1989, 46, 3431–3456. [Google Scholar] [CrossRef]
- Chen, D.Y.-C.; Cheung, K.K.W.; Lee, C.-S. Some Implications of Core Regime Wind Structures in Western North Pacific Tropical Cyclones. Weather Forecast. 2011, 26, 61–75. [Google Scholar] [CrossRef]
- Carrasco, C.A.; Landsea, C.W.; Lin, Y.-L. The Influence of Tropical Cyclone Size on Its Intensification. Weather Forecast. 2014, 29, 582–590. [Google Scholar] [CrossRef]
- Fudeyasu, H.; Ito, K.; Miyamoto, Y. Characteristics of Tropical Cyclone Rapid Intensification over the Western North Pacific. J. Clim. 2018, 31, 8917–8930. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, B.; Mehra, A.; Abdolali, A.; van der Westhuysen, A.; Moghimi, S.; Vinogradov, S.; Zhang, Z.; Zhu, L.; Wu, K.; et al. Investigating the Impact of High-Resolution Land–Sea Masks on Hurricane Forecasts in HWRF. Atmosphere 2020, 11, 888. [Google Scholar] [CrossRef]
- Liu, B.; Kim, H.-S.; Rosen, D.; Shin, J.; Thomas, B.; Sheinin, D.; Dong, J.; Zhu, L.; Zhang, C.; Wang, W.; et al. The HAFSv0.1A HFIP Real-Time Parallel Experiment: A Regional and Ocean-Coupled Configuration 2020. Available online: www.hfip.org/events/annual_meeting_nov_2020/index.php (accessed on 20 February 2021).
| Range of 𝛇 | Active Components |
|---|---|
| 𝛇 > 0.2 | Local mixing |
| −0.5 ≤ 𝛇 ≤ 0.2 | Local mixing; countergradient mixing |
| 𝛇 < −0.5 | Local mixing; mass-flux mixing |
| Type | Description |
|---|---|
| Shortwave, longwave radiation | Rapid Radiative Transfer Model for general circulation models (RRTMG) |
| Cumulus | scale-aware Simplified Arakawa-Schubert (scale-aware SAS) |
| Microphysics | modified tropical Ferrier-Aligo |
| Planetary boundary layer | GFS-EDMF |
| Surface layer | Geophysical Fluid Dynamics Laboratory (GFDL) |
| Land surface | None |
| Experiment | Description |
|---|---|
| CTRL | Default HWRF PBL configuration |
| LOCAL-MIXING | Non-local vertical mixing disabled |
| BUSINGER-PHI | Replace Dyer’s φm and φh with Businger’s |
| Pr = 1.58 | Set Pr to 1.58 in the PBL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalina, E.A.; Biswas, M.K.; Zhang, J.A.; Newman, K.M. Sensitivity of an Idealized Tropical Cyclone to the Configuration of the Global Forecast System–Eddy Diffusivity Mass Flux Planetary Boundary Layer Scheme. Atmosphere 2021, 12, 284. https://doi.org/10.3390/atmos12020284
Kalina EA, Biswas MK, Zhang JA, Newman KM. Sensitivity of an Idealized Tropical Cyclone to the Configuration of the Global Forecast System–Eddy Diffusivity Mass Flux Planetary Boundary Layer Scheme. Atmosphere. 2021; 12(2):284. https://doi.org/10.3390/atmos12020284
Chicago/Turabian StyleKalina, Evan A., Mrinal K. Biswas, Jun A. Zhang, and Kathryn M. Newman. 2021. "Sensitivity of an Idealized Tropical Cyclone to the Configuration of the Global Forecast System–Eddy Diffusivity Mass Flux Planetary Boundary Layer Scheme" Atmosphere 12, no. 2: 284. https://doi.org/10.3390/atmos12020284
APA StyleKalina, E. A., Biswas, M. K., Zhang, J. A., & Newman, K. M. (2021). Sensitivity of an Idealized Tropical Cyclone to the Configuration of the Global Forecast System–Eddy Diffusivity Mass Flux Planetary Boundary Layer Scheme. Atmosphere, 12(2), 284. https://doi.org/10.3390/atmos12020284








