Research on a Prediction Model for Northern Cold Climate Millet Yield per Unit Area Based on IWOA-BP

Abstract

Millet yield per unit area in northern China’s drylands is constrained by climate, soil, and management factors, complicating forecasts under limited, nonlinear, heterogeneous data. In order to enhance the accuracy and stability of operational forecasting, this study utilised observational data from five locations in southwestern Heilongjiang Province spanning 2014 to 2023. Eight ground-based hydrothermal and meteorological factors were used as inputs to build an improved BP neural network optimised by IWOA, with enhancements to both algorithm and workflow. Adaptive inertia weight and EOBL were introduced to balance global exploration and local exploitation, enabling better hyperparameter solutions. Results show that IWOA-BP significantly outperforms baseline BP and WOA-BP on an annual scale. The RMSE was 2.74, the R² was 0.94, the MAPE was 5.9, and the RPD was 4.16. The implementation of additional seasonal rolling forecasts for the 2024 validation period entailed the construction of cumulative information flows from January to August. Cross-regional validation in Fangzheng County produced error magnitudes consistent with the primary study area, thereby demonstrating the model’s reliable generalization ability across both temporal and spatial dimensions.

1. Introduction

Millet is a stress-tolerant minor cereal that is native to arid and semi-arid regions. In this context, it plays a pivotal role in safeguarding food security and boosting farmers’ incomes in Heilongjiang’s dryland farming areas. Furthermore, the low-input, high-nutrient characteristics of the product are progressively positioning it within the emerging functional food and health industries [1,2]. However, millet yield per unit area is subject to significant interannual variability (20–35%) due to the combined effects of monsoon climate fluctuations, soil moisture content deficits, and management practices. Accurate and timely per unit area yield forecasting is of strategic importance for government reserve allocation, agricultural insurance pricing, and farmer field management [3,4].

Existing crop per unit area yield forecasting methods can be categorised into three distinct groups: Firstly, statistical regression and crop growth models such as CERES-Setaria and AquaCrop. Kumar et al. simulated the growth of maize under different cultivation practices using the DSSAT-CERES-Maize model, achieving an NRMSE below 10% when comparing simulated per unit area yields to observed values [5]. Panek et al. evaluated the per unit area yield prediction performance of wheat, maize, and rapeseed within the AquaCrop model, achieving R² values exceeding 0.85 [6]. Singh et al. conducted a comparative analysis of the disparities in maize per unit area yield simulation outcomes across various models, thereby ascertaining that the R² values were enhanced to 0.79 and 0.80, correspondingly, during years characterised by extreme conditions [7]. However, it should be noted that these methods require substantial parameter calibration and exhibit limited high-precision forecasting capability for homogeneous small regions. Secondly, single-source remote sensing index methods employ peak or seasonal integral estimates of NDVI/EVI for per unit area yield forecasting. Naqvi et al. employed the Landsat-8 NDVI time series regression to estimate winter wheat per unit area yields, achieving a predictive R² of 0.72 [8]. Segarra et al. developed a multiple linear equation based on Sentinel-2 EVI, elevating wheat per unit area yield R² to 0.78, though it typically fails to capture variations in soil water-heat temporal patterns and management practices [9]. Finally, machine learning and deep learning methods have demonstrated superior performance to traditional models across multiple crops. In 2019, Khaki designed a deep feedforward neural network (DFNN) to predict maize per unit area yield across 2247 locations in the Corn Belt, achieving a root mean square error (RMSE) of merely 12% of the mean per unit area yield [10]. Furthermore, Khaki et al. proposed a CNN-RNN hybrid framework achieving R² = 0.82 on the same dataset, significantly outperforming random forest (RF) and DFNN [11]. Moreover, Sun et al. developed a county-level soybean per unit area yield prediction model based on CNN-LSTM, reducing average RMSE by 8% and 9% compared to pure CNN or LSTM, respectively. Nevertheless, contemporary methodologies predominantly remain constrained to small-sample and limited-data-source fusion. As indicated by the extant literature, multi-source data integration and cross-regional transfer validation represent core trends for enhancing the generalizability of per unit area yield prediction [12].

The present study utilised experimental data comprising field hydrothermal factors, meteorological records, and millet yield per unit area information. The selected influencing factors included the monthly maximum soil temperature, the minimum monthly soil temperature, the average monthly soil temperature, the maximum monthly air temperature, the minimum monthly air temperature, the average monthly air temperature, the monthly precipitation, and the soil moisture content. The data coverage extends from 2014 to 2023. Pearson correlation coefficients and Spearman correlation coefficients were employed to ascertain the hierarchical order of influence factors affecting millet yield per unit area variation. The objective of the present study was to design an IWOA-based optimisation approach with the aim of establishing an IWOA. Pearson’s and Spearman’s correlation coefficients were employed to ascertain the hierarchical order of influencing factors on millet yield per unit area variation. The development of a prediction model employing an IWOA-BP neural network was achieved through the optimisation of an enhanced WOA. A comparison was made between the accuracy and prediction error of this model and traditional prediction models, both before and after training. The findings provide significant guidance for adjusting overall management measures and decision-making in China’s millet production.

2. Materials and Methods

2.1. Data Sources

Climatic conditions are the primary constraints governing the complete growth and development of millet in the arid and mountainous regions of Northeast China [13,14]. Furthermore, it is notable that over 80% of cultivated areas in this region are not equipped with irrigation facilities. The extended growing season and extensive geographical distribution render crops highly susceptible to extreme weather events such as drought, torrential rainfall, and high temperatures [15,16]. It is evident that soil moisture content and rainfall amount have a direct impact on plant water supply. Furthermore, these factors also exert significant regulatory effects on plant growth through their lagging and cumulative impacts.

In order to comprehensively reflect the combined impact of meteorological conditions, soil properties, and cultivation scale on millet yield per unit area, this study selected eight input indicators. The following variables were measured: the monthly maximum soil temperature (X1), the monthly minimum soil temperature (X2), the monthly average soil temperature (X3), the monthly maximum air temperature (X4), the monthly minimum air temperature (X5), the monthly average air temperature (X6), the monthly precipitation (X7), and the soil moisture content (X8). The annual millet yield per unit area was designated as the output. Meteorological data were sourced from the National Climate Centre’s monthly statistics, soil temperature and moisture data were derived from the National Soil Grid product, while per unit area yield data were based on provincial statistical yearbooks and local agricultural bureau publications.

X1 is a key indicator of extreme heat stress and growth limits. Elevated values can cause damage to roots and inhibit absorption, thereby affecting growth potential and per unit area yield. X2 has been demonstrated to have a significant impact on the timing of early spring emergence and initial survival. It has been observed that low values of X2 can lead to a reduction in germination rates, an extension of the growing season, and an increase in frost damage risk, which is indicative of the effects of low-temperature suppression. The X3 index has been demonstrated to comprehensively reflect root-zone heat supply and thermal load, thus characterising temperature adaptability across growth stages. X4 has been shown to drive surface warming and influence critical processes such as heading, flowering, and grain filling. These processes have been found to correlate with heat stress risk and maturation progression. X5 has been identified as a key factor in the potential for cold damage, particularly during the critical stages of sowing, tillering, and late-season maturity. This risk has been shown to have a significant impact on survival and quality, underscoring the importance of temperature regulation in agricultural contexts. X6 is a key metric in understanding the overall thermal conditions and the amplitude of fluctuations. These conditions have been shown to influence growth rates and physiological stress levels. Monthly precipitation of X7 dominates effective water supply; an excess of rainfall can lead to waterlogging and lodging, while a deficiency can result in drought stress, which directly impacts per unit area yield and the management of irrigation strategies. The X8 index is a quantitative metric used to characterise the availability and aeration of water within the root zone. This index has been demonstrated to influence a number of physiological processes, including root respiration, nutrient transport, and photosynthetic efficiency. It has been demonstrated that low levels of this element restrict growth, while excessively high levels have been shown to cause oxygen deficiency and root rot. There is a strong correlation between this and rainfall patterns, yet a significant time lag is often observed. This is due to the fact that it more accurately reflects the crop’s actual water status. The study area encompasses five major millet-producing regions in southwestern Heilongjiang Province: Zhaozhou, Zhaoyuan, Anda, Wangkui, and Lanxi, spanning the period from 2014 to 2023. The annual dataset comprises fifty region–year observations across the five regions over ten years. Prior to the modelling stage, all variables were subjected to rigorous outlier removal and transformation, including logarithmic or square root conversion, in order to ensure the integrity of the data and the validity of the subsequent analyses. The calibration of parameters was conducted exclusively on the training dataset, with test sets maintaining identical thresholds and standardization parameters. The training and prediction processes were executed utilising the standard BP neural network, classical Weighted One-Way Output Approximation (WOA-BP), and enhanced IWOA-BP methodologies within the MATLAB R2020b environment. The performance of the model was evaluated through the implementation of leave-one-out cross-validation on an annual basis, as shown in Figure 1.

Figure 1. Schematic diagram of the test location.

2.2. Data Analysis

2.2.1. Data Overview and Basic Statistics

In order to circumvent any potential misinterpretation of variable effects in correlation analysis, a systematic examination of data scale, distribution patterns, and dispersion levels was conducted. This approach led to the identification of extreme values and skewed distributions, thereby elucidating the constraints for subsequent preprocessing and modelling. This step provides baseline references for feature selection, variable transformation, and model robustness assessment. The monthly samples comprise 600 rows, encompassing eight environmental factors. The annual samples comprise 50 rows, representing ten years of annual per-hectare millet yield per unit area across five cities. The missing rate for all variables is zero, thus meeting the conditions for direct modelling. Temperature metrics demonstrate moderate overall dispersion, whilst the three temperature groups for soil and atmospheric measurements share consistent dimensionality, facilitating cross-comparison. The annual per unit area yield demonstrates minimal overall fluctuation, indicating relatively stable regional production. The statistical summaries are presented in Table 1. Corresponding regional distributions across years are visualized in Figure 2.

Table 1. Statistical data summary.

Variable	Maximum	Minimum	Mean	Standard Deviation— Sample	Median	Upper Quartile	Lower Quartile	Skewness	Kurtosis
X1 (°C)	40	−8	21.06	13.25	25	33	10.5	−0.53	1.87
X2 (°C)	20	−34	−5.44	15.49	−4	8	−21	−0.06	1.64
X3 (°C)	27	−18	7.20	14.00	9	19.5	−6	−0.24	1.65
X4 (°C)	39	−10	19.14	13.5	23	31	8	−0.54	1.89
X5 (°C)	24	−37	−7.33	15.70	−6	6	23	−0.06	1.66
X6 (°C)	26	−21	5.29	14.428	7.5	18	−9	−0.26	1.66
X7 (mm)	921	0	101.39	143.03	32.45	147.1	4.65	1.88	6.76
X8 (m3 m−3)	939.4	393.2	597.02	94.69	591.55	650.75	531.15	0.57	3.66
Y	431	369	387.36	11.39	388	393	379	0.91	5.63

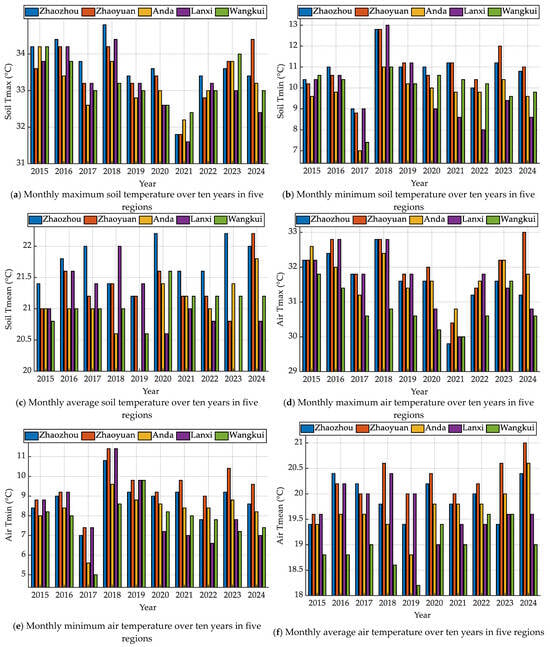
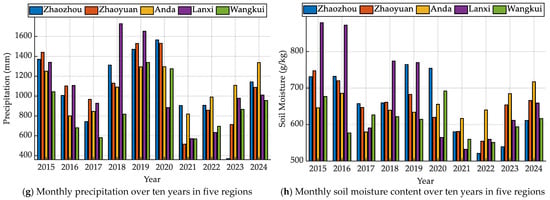
Figure 2. Annual statistics for 2015 to 2024 based on eight factors.

With regard to central tendency and distribution characteristics, the mean values of soil and air temperatures are found to fall within typical ranges for the Northeast region. The standard deviations range from 13 to 16, with minimum and maximum values extending across the entire period from the cold season to the warm season. The skewness value is marginally negative or near to zero, while the kurtosis value approaches a medium peak. This indicates that the temperature sequence distribution is relatively flat, with few extreme values. The monthly precipitation averages at approximately 101.39 mm, with a lower quartile of 4.65, median of 32.45, upper quartile of 147.10, and maximum value of 921.00. This distribution exhibits pronounced right-skewedness and kurtosis, indicating a significant influence of extreme precipitation events on the overall distribution. The average soil moisture content was found to be approximately 597.02, with a standard deviation of 94.69 and a quartile range of 531.15–650.75. The presence of moderate right-skewness is indicative of dual influences from precipitation and soil texture. The mean annual per unit area yield was found to be 387.36, with a standard deviation of 11.39. The interquartile range was concentrated between 379 and 393, exhibiting positive skewness and high kurtosis, suggesting that a small number of high-per-unit-area-yield years elevated the upper tail. Histograms for each variable and the distribution of annual per unit area yields across regions are shown in Figure 3. (One hectare is equivalent to 15 mu of land).

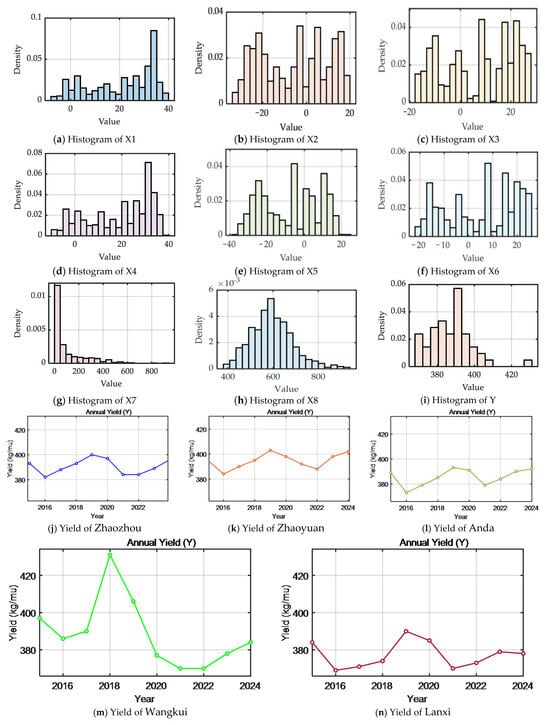
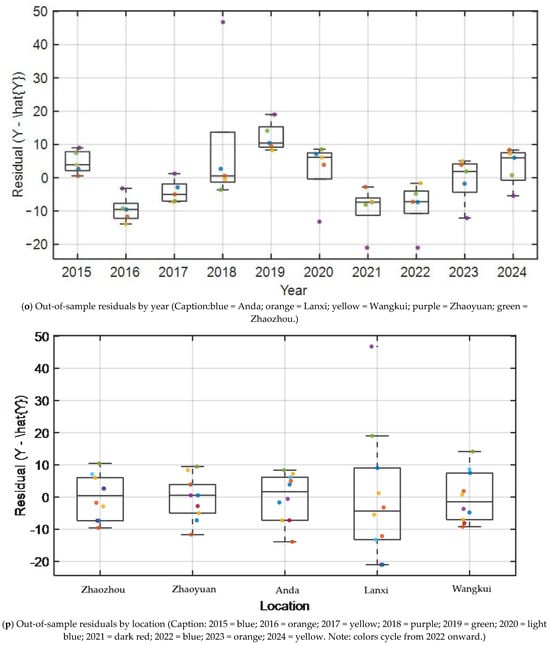
Figure 3. Histograms of variables and distribution of annual per unit area yield by region.

In summary, the rainfall amount and soil moisture demonstrate clear asymmetric and long-tailed distributions. In order to mitigate the driving effect of extreme values, it is necessary to implement a logarithmic or square root transformation, in conjunction with robust outlier removal and standardization. Furthermore, given the comparable variance of temperature factors and their closely interlinked physical relationships, subsequent attention should be paid to multicollinearity. This issue can be addressed through feature dimension reduction or regularization constraints, which are effective in preventing parameter instability. It is recommended that time-lag structures for rainfall and soil moisture be incorporated into subsequent models in order to take into account the mechanisms of production. In order to mitigate the impact of spatiotemporal heterogeneity on evaluation outcomes, stratified cross-validation by city or year should be implemented.

2.2.2. Correlation Analysis

In order to ensure robust data underpinnings for the selection of variables and the design of structures in subsequent per unit area yield prediction models, this section conducts a correlation analysis of the influencing factors. The objectives of this study are threefold: firstly, to identify meteorological and soil factors that most effectively explain the per unit area yield of millet per unit area within the sample; secondly, to clarify the gradient relationship between dominant and secondary factors; and thirdly, to reveal redundancy and potential collinearity among independent variables, with a view to preventing parameter instability and prediction bias arising from information duplication. In consideration of the fact that per unit area yield responses to environmental stresses encompass both approximately linear intensity effects and frequently exhibit monotonic yet nonlinear threshold and saturation characteristics, the present study employs two correlation metrics concurrently. Pearson’s [17] and Spearman’s [18] models, respectively, characterise linear intensity and order consistency, thereby enhancing interpretability in feature selection while maintaining statistical robustness. The correlation results will guide feature retention and transformation, constrain the hyperparameter tuning search space, and optimise network size and regularization term settings. This establishes a closed-loop relationship between model structure and agricultural mechanisms, laying the groundwork for subsequent generalization testing and uncertainty assessment. The correlation analysis between millet unit per unit area yield and influencing factors is illustrated in Figure 4.

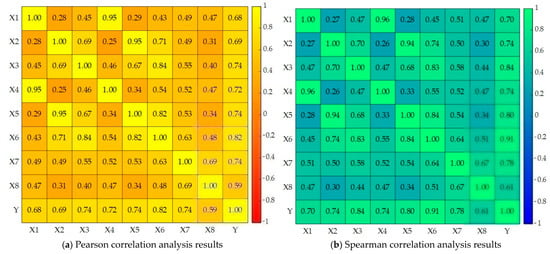
Figure 4. Correlation analysis between millet unit per unit area yield and influencing factors.

As demonstrated in the correlation matrix derived from 50 sample groups, the per unit area yield response to thermal factors was found to be the most significant, with that to moisture factors ranking second. The Pearson correlation coefficient between average air temperature (X6) and per unit area yield (Y) was 0.82, with a Spearman rank correlation of 0.91, indicating its dominant influence. Subsequently, rainfall amount (X7), average soil temperature (X3), minimum air temperature (X5), and maximum air temperature (X4) followed in sequence. The correlation levels for these variables were found to be predominantly in the medium-to-high range, reaching a level of statistical significance. The findings of the study demonstrated a moderately strong positive correlation between X8 and per unit area yield, with a Pearson’s coefficient of 0.59 and a Spearman’s rank correlation of 0.61. Furthermore, a substantial positive correlation was observed with X7, suggesting that the transmission chain whereby precipitation influences per unit area yield via soil water storage can be observed at the annual scale.

A high degree of homogeneity and multicollinearity is evident among the independent variables, primarily manifesting as a high correlation between soil temperature and air temperature. For instance, the correlation coefficient between X1 and X4 reaches 0.95, that between X2 and X5 reaches 0.95, and that between X3 and X6 reaches 0.84. Furthermore, moderate correlations have been identified between the thermal and moisture components. Specifically, X6 and X7 demonstrated a correlation coefficient of 0.63, while X8 exhibited a coefficient of 0.48. This structure is indicative of the dual dependence of spring-sown millet in Northeast China on both heat accumulation and optimal moisture conditions. However, the direct combination of all temperature factors may induce information redundancy and variance inflation, thereby compromising coefficient stability and generalization ability.

The modelling strategies employed must achieve a balance between maintaining information fidelity and adhering to redundancy constraints. It is hypothesised that the X6 and X7 may serve as core inputs, with the X3 and X5 providing supplementary data as required, in order to characterise root-zone thermal environments and cold stress risks. Nonlinear feature engineering of X8, incorporating quadratic terms or piecewise spline functions, has been demonstrated to be a highly effective method for capturing potential optimal range effects and threshold responses. During the training process, robust standardization and mild de-extremisation procedures should be implemented. In order to mitigate the risks of information leakage, cross-validation stratified by city or year should be employed, in combination with weight decay and early stopping to suppress overfitting. It is imperative to acknowledge that the process of annual aggregation has the potential to diminish the strength of signals during critical growth periods. Subsequent work may incorporate monthly scales and lag term to characterise the time-delayed effects of rainfall and soil moisture, thereby further optimising factor selection and hyperparameter tuning for the prediction model. We assessed collinearity among temperature predictors using variance inflation factors computed within each fold on training data only under year-stratified cross-validation. All retained variables showed VIF values below the commonly used thresholds. As a robustness check, we trained a ridge regression baseline with the penalty tuned by inner cross-validation on the training folds and evaluated on the corresponding validation folds. The ridge results matched the main specification in both error levels and predictor ordering.

We examined temporal lags for precipitation X7 and soil moisture X8 using cross-correlation and out-of-sample ablations. Cross-correlation between the monthly drivers and annual yield peaked at one to two months across counties during the growing season. We then retrained the models with lag terms of zero, one, two, and three months using the same year stratified cross-validation and train only scaling. Root mean square error was lowest at one or two months and higher at zero and three months. The lag choice was selected on training folds only and then held fixed for evaluation. We therefore adopt a one- to two-month lag for X7 and X8 in the main specification.

All reported models use a four-variable input set derived from the collinearity analysis. The set comprises X6, the growing-season mean air temperature; X7, the growing-season total precipitation; X3, the growing-season mean soil temperature; and X5, the growing-season minimum air temperature. Monthly variables are aggregated into growing-season statistics for May to September, using means for temperature and soil moisture and totals for precipitation. A full eight-variable baseline with X1 through X8 is included for reference, but unless stated otherwise, results refer to the four-variable specification. Inputs are standardized by z-scoring within the training folds only, and performance is evaluated with five-fold cross-validation stratified by year.

The dataset contains monthly observations for five counties over ten years, which yields fifty county-year records. We aggregated monthly drivers to an annual, county-level representation that aligns with the millet growing season from May to September. Temperature variables and soil moisture were averaged across the season. Precipitation was summed across the season to represent cumulative water input. For predictors specified with a one- or two-month lag, the monthly series were shifted before aggregation so that a one-month lag uses April to August and a two-month lag uses March to July. Only county-year records with complete coverage of the seasonal window were retained. All predictors were then standardized using z-scores whose mean and standard deviation were estimated on the training folds only under the year-stratified cross-validation protocol. The same parameters were applied to the corresponding validation and test data within each fold. This fold-wise procedure prevents information leakage between training and evaluation splits.

2.3. Establishment of the Prediction Model

2.3.1. BP Neural Network

The BP network is a classical multi-layer feedforward neural network that possesses robust nonlinear mapping capabilities. These capabilities enable the network to effectively handle complex nonlinear relationships [19,20]. The per unit area yield of millet is influenced by a number of factors, including the temperature of the soil, the amount of rainfall, the air temperature, and the moisture content of the soil. These factors exhibit intricate nonlinear interdependencies. The BP network training process is comprised of three distinct steps. Initially, each influencing factor is regarded as an input node. Subsequently, a model is established and trained through forward propagation to obtain predicted values. The discrepancy between these and the actual values is calculated to determine the error. Finally, the error is propagated back through the network to recalibrate each weight coefficient. Subsequent reiteration of the three-step process is necessary to ascertain the weights. Thereafter, the model is applied to new data in order to predict target values [21]. It is to be posited herewith that the extant sample data pairs $(\widehat{x},\widehat{y})$ and $\left(\widehat{x},\widehat{y}\right)x = \left[x_{\mathrm{m}1},x_{\mathrm{m}2},\dots ,x_{\mathrm{mn}}\right], y=\left[y_1,y_2,\dots ,y_{\mathrm{n}}\right]$ represent the existing data. The dimensions of the input are denoted m1, m2, …, mn, and the sample counts are represented by 1, 2, …, n. The designation of neurons belonging to the hidden layer is indicated by $\mathrm{o}=\left[{\mathrm{o}}_1,{\mathrm{o}}_2,\dots ,{\mathrm{o}}_{\mathrm{j}}\right]$ [22]. It is posited that the weight matrix between the input layer and the hidden layer neurons is w₁, while the weights between the input layer and the output layer neurons are w₂.

$$w^1=\left[\begin{array}{c}{\mathrm{w}}_{11}^1 {\mathrm{w}}_{12}^1 \dots {\mathrm{w}}_{1\mathrm{d}}^1\\ {\mathrm{w}}_{21}^1 {\mathrm{w}}_{22}^1 \dots {\mathrm{w}}_{2\mathrm{d}}^1\\ \dots \\ {\mathrm{w}}_{\mathrm{m}1}^1 {\mathrm{w}}_{\mathrm{m}2}^1 \dots {\mathrm{w}}_{\mathrm{md}}^1\end{array}\right] w^2=\left[\begin{array}{c}{\mathrm{w}}_{11}^2 {\mathrm{w}}_{12}^2 \dots {\mathrm{w}}_{1\mathrm{t}}^2\\ {\mathrm{w}}_{21}^2 {\mathrm{w}}_{22}^2 \dots {\mathrm{w}}_{2\mathrm{t}}^2\\ \dots \\ {\mathrm{w}}_{\mathrm{b}1}^2 {\mathrm{w}}_{\mathrm{b}2}^2 \dots {\mathrm{w}}_{\mathrm{bt}}^2\end{array}\right]$$

(1)

where x is the i-th input value in the neural network, y is the vector of predicted values, ${\mathrm{o}}_i^1$ is the i-th activation of the i-th layer neuron, and $w_{1m}^i$ is the connection between the m-th unit of layer i and the first unit of layer (i + 1),

$${\theta }^1=\left[{\theta }_1^1,{\theta }_2^1,\dots ,{\theta }_{\mathrm{l}}^1\right];{\theta }^2=\left[{\theta }_1^2,{\theta }_2^2,\dots ,{\theta }_{\mathrm{l}}^2\right]$$

(2)

where θ is the neuron threshold, θ¹ is the hidden layer bias vector, and θ² is the output layer bias vector.

Subsequent to undergoing a linear combination of weights and the subtraction of the threshold, the input signal is fed into the activation function of the hidden layer. For the j^{^}(th) neuron in the hidden layer, its net input is represented by:

$$\begin{gathered} o_j=\int \left({\sum }_1^m{w}_{\mathit{ji}}^1{x}_i-{\theta }_j^1\right)=f\left({\mathit{net}}_j\right), j=1,2,\dots ,I \\ {\mathit{net}}_j={\sum }_{i=1}^m{w}_{\mathit{ji}}^1-{\theta }_j^1,\mathrm{j}=1,2,\dots ,\mathrm{I} \end{gathered}$$

(3)

where o_j is the number of hidden neurons,$\mathrm{m}$ is the number of samples, ${\mathrm{w}}_{\mathrm{ji}}^1$ is the network weight matrix,$\mathrm{f}\left({\mathrm{net}}_{\mathrm{j}}\right)$ is the activation function, and the output of a neuron in the output layer is represented by:

$$\begin{gathered} {\mathrm{z}}_{\mathrm{j}}=\int \begin{array}{c}\left({\sum }_{\mathrm{j}=1}^{\mathrm{l}}{\mathrm{w}}_{\mathrm{kj}}^1{\mathrm{o}}_{\mathrm{i}}-{\theta }_{\mathrm{k}}^1\right)=\mathrm{g}\left({\mathrm{net}}_{\mathrm{j}}\right),\\ \mathrm{k}=1,2,\dots ,\mathrm{n}\end{array} \\ {\mathrm{net}}_{\mathrm{k}}={\sum }_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{w}}_{\mathrm{kj}}^1-{\theta }_{\mathrm{k}}^2,\mathrm{k}=1,2,\dots ,\mathrm{n} \end{gathered}$$

(4)

where z_f is the output layer, ${\mathrm{w}}_{\mathrm{ji}}^1$ is the network weight matrix, o_i is the hidden layer output, $\mathrm{g} \left({\mathrm{net}}_{\mathrm{j}}\right)$ is the activation function, and ${\theta }_k^1$ is the threshold. The error E between the actual output and the expected output is calculated as follows:

$$E={\displaystyle \frac{1}{2}}{\sum }_{\mathrm{k}=1}^{\mathrm{n}}{\left(y_{\mathrm{k}}-z_{\mathrm{k}}\right)}^2$$

(5)

The BP network uses tanh in the hidden layer and a linear function at the output layer to predict continuous yield. The same choices are used in all experiments.

2.3.2. IWOA-BP Model

In order to comprehensively investigate the nonlinear impacts of eight meteorological and soil indicators across five primary production areas in Heilongjiang Province from 2014 to 2023 on millet yield per unit area, this paper proposes the IWOA-BP model. This approach employs the enhanced WOA to globally search for the critical hyperparameters of the BP algorithm, namely the number of hidden layer nodes (H), the learning rate (lr), and the regularization coefficient (reg). The remaining weights and biases achieve rapid local convergence via the Levenberg–Marquardt rule. In comparison with the original WOA-BP, IWOA-BP has been shown to significantly enhance accuracy and robustness while maintaining convergence speed. The enhanced prediction model is demonstrated in Figure 5.

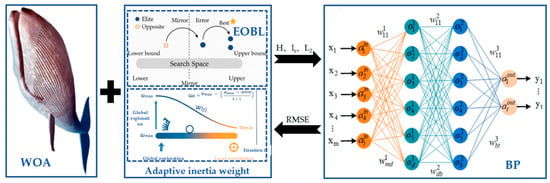
Figure 5. Overall prediction model.

The original WOA relies on a linearly decreasing coefficient, a, to switch between exploration and exploitation. In the context of high-dimensional, non-convex error surfaces, this approach is susceptible to a number of issues, including monotonous step sizes, diminished population diversity, and premature convergence. These issues can result in degraded quality in the context of BP hyperparameter optimisation [23,24,25]. In order to address the aforementioned issues, this paper introduces two complementary mechanisms into WOA. The following terms are employed in this text: adaptive inertia weight [26] and elite opposition-based learning (EOBL) [27]. These mechanisms are designed to balance global exploration with local digging, thereby mitigating local optima. The calculation formulas employed are as follows:

$$w_t=w_{max}-{\displaystyle \frac{t-1}{T-1}}(w_{max}-w_{min})$$

(6)

where $w_t$ is the adaptive inertia weight, $w_{(\max )}$ is the upper bound of the inertia weight (set at 0.9), $w_{(\min )}$ is the lower bound of the inertia weight (set at 0.4), t is the current iteration count, and T is the maximum iteration count (set at 50).

When the random number p is less than 0.5 and the vector magnitude |A| is less than 1, the whale considers itself to be in proximity to prey and enters the “encirclement and capture” mode. The modification of the distance vector and position update formulae, respectively, is as follows:

$$\left\{\begin{array}{c}\overrightarrow{D}=|\overrightarrow{C}\overrightarrow{X}\left(t\right)-\overrightarrow{X}\left(t\right)|\\ \overrightarrow{X}\left(t+1\right)=\overrightarrow{X^{*}}\left(t\right)-\overrightarrow{A}·\overrightarrow{D}\end{array}\right.$$

(7)

where $\overrightarrow{X}(t)$ is the current individual’s position vector at iteration t, $\overrightarrow{X^{*}}(\mathrm{t})$ is the global optimal position vector at iteration t, A and C are the iteration coefficient vectors, and D is the distance vector.

In the event of |A| ≥ 1, the whale is classified as being in the long-range search zone and, as such, requires random exploration around other individuals. The improved position update formula is as follows:

$$\overrightarrow{X}(t+1)=|{\overrightarrow{X}}_{rand}-\overrightarrow{A}·\overrightarrow{D}|$$

(8)

where $X_{rand}$ is a randomly selected individual position.

When p ≥ 0.5, the algorithm employs a logarithmic spiral with contraction–expansion characteristics to simulate the whale’s gradual approach towards prey. Following the introduction of inertial weighting, the spiral update equation is thus modified:

$$\left\{\begin{array}{c}\overrightarrow{X}\left(t+1\right)=\overrightarrow{D^{\prime }}·e^{bl}·\mathit{cos}\left(2\pi l\right)+\overrightarrow{X^{*}}\left(t\right)\\ \overrightarrow{D^{\prime }}=|\overrightarrow{X^{*}}\left(t\right)-\overrightarrow{X}\left(t\right)|\end{array}\right.$$

(9)

In order to further enhance population diversity and accelerate global convergence, a reverse mapping is applied to the current globally optimal individual. In the event that the reverse solution exhibits a higher level of performance in comparison to the worst-fit individual within the population, it is substituted for that individual. The reverse solution generation formula is as follows:

$$X_t^{rev}\left(t\right)=lb+ub-X_t^{*}$$

(10)

where $X^{rev}(t)$ is the elite reverse-mapped position, $X^e(t)$ is the e-th elite position in generation t, lb is the lower bound vector for variables, and ub is the upper bound vector for variables.

The objective function employed for the optimisation of the BP network utilises RMSE, a metric that quantifies the total error energy and demonstrates heightened sensitivity to substantial deviations. A reduced value is indicative of enhanced overall fitting [28]. The calculation formula for the latter is as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{M}}\sum _{k=1}^M{(y\left(k\right)-\widehat{y}(k\left)\right)}^2}$$

(11)

where M is the total number of samples, $y(k)$ is the actual value, and $\hat{y}(k)$ is the predicted value.

2.4. Experimental Setup

2.4.1. Experimental Environment and Metrics

The computational environment employed a 64-bit Windows system running MATLAB R2020b, utilising the neural network toolbox and statistics and machine learning toolbox. The random seed was set to 2025 to ensure reproducibility. The preprocessing of data is undertaken in accordance with the principle of training set fitting and test set application. Missing values in the training set undergo linear interpolation and robust outlier removal, followed by standardization of all continuous variables using the training set’s mean and standard deviation. The X7 and X8 variables demonstrate right-skewed distributions. In the following section, three scaling approaches will be examined: the original scale, the logarithmic transformation, and the square root transformation. The primary experiment utilises a logarithmic transformation with robust thresholds ranging from 1% to 99%. The evaluation metrics employed encompass RMSE, R-squared (R²), mean absolute error (MAE), mean absolute percentage error (MAPE), and relative prediction deviation (RPD). The mean and standard deviation of the fold-to-fold variation are provided. The paired Wilcoxon rank-sum test is employed to compare model error distributions at a significance level of 0.05. The coefficient of determination, denoted by R², is a statistical measure employed to assess the model’s explanatory power and the extent to which it accurately predicts the observed data. It quantifies the proportion of variance in the dependent variable that is explained by the model. The calculation formula for the latter is as follows:

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^M(y-\widehat{y})}{{\sum }_{i=1}^M{(y-\overline{y})}^2+\epsilon }}$$

(12)

It is important to note that A is an infinitesimal positive number used to ensure numerical stability.

The MAE is utilised to gauge the mean absolute deviation, offering a robust representation of the typical error range. The calculation formula employed was as follows:

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{M}}\sum _{i=1}^M|y-\widehat{y}|$$

(13)

The MAPE is utilised to gauge the model’s average relative error, which is expressed as a percentage. This facilitates intuitive comparison of results across different scales and regions, aiding the establishment of operational thresholds. The MAPE formula is as follows:

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{100}{M}}\sum _{i=1}^M{\displaystyle \frac{|y-\widehat{y}|}{\left|y\right|+\epsilon }}$$

(14)

The RPD reflects the model’s explanatory power relative to the data’s inherent variability, with higher values indicating greater utility. Common empirical thresholds suggest values above 2.0 are suitable for quantitative forecasting, 1.4 to 2.0 represent a marginal or qualitative level, and values below 1.4 indicate weaker performance [29]. The relative performance deviation is calculated as:

$$\mathrm{R}\mathrm{P}\mathrm{D}={\displaystyle \frac{\sqrt{\frac{1}{M-1}\sum _{i=1}^M{(y-\overline{y})}^2}}{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}}$$

(15)

All three models shared identical data splits, preprocessing, and evaluation. The same year, stratified cross-validation folds were used for BP, WOA-BP, and IWOA-BP. Standardization used z scores whose mean and standard deviation were estimated on the training folds and then applied to validation and test in each fold. Stochastic elements were fixed with a single random seed equal to 2025, which controlled neural weight initialization and whale population initialization of 1 × 10⁻⁴. Early stopping used a patience of ten epochs with a minimum improvement threshold of 1 × 10⁻⁴ on the validation loss. Weight decay and other training controls were held constant across models, and only the model hyperparameters selected by the optimisation procedure differed. All runs were executed in the same MATLAB R2020b environment. Training used early stopping based on validation loss. The patience was ten epochs, and the minimum improvement threshold was 1 × 10⁻⁴. When the validation loss did not improve by at least this amount for ten consecutive epochs, training stopped, and the weights from the best epoch were restored. The same rule was applied in every fold and for all models. We limited model capacity and used conservative training settings to control overfitting. The network uses a single hidden layer. L2 regularization is applied as specified. Training monitored validation loss with patience, ten epochs, and a minimum improvement of 1 × 10⁻⁴, and the best epoch weights were restored. Evaluation follows year-stratified cross-validation with standardization fit on training folds only to avoid leakage. Dropout and batch normalization were not used because the sample is small and the architecture is shallow, which makes these mechanisms unnecessary and potentially unstable. Learning curves for training and validation were aligned without late epoch divergence, indicating adequate control of overfitting.

Figure 6 summarizes the IWOA–BP workflow and leakage-safe validation. Monthly meteorological and soil variables are aggregated into growing-season statistics for May to September, with temperature and soil moisture summarized by their means and precipitation by its seasonal total. The outer IWOA loop searches the BP hyperparameters, such as the hidden layer width and the strength of weight decay, and evaluates each setting using year-stratified K-fold cross-validated RMSE with z-scoring computed from the training folds only, a single-hidden-layer BP, weight decay, and early stopping. The best hyperparameter configuration is then used to train the final model on the full dataset, and we report RMSE, R-squared, MAE, MAPE, and RPD, with results compared between the All-8 and 4-Core input specifications.

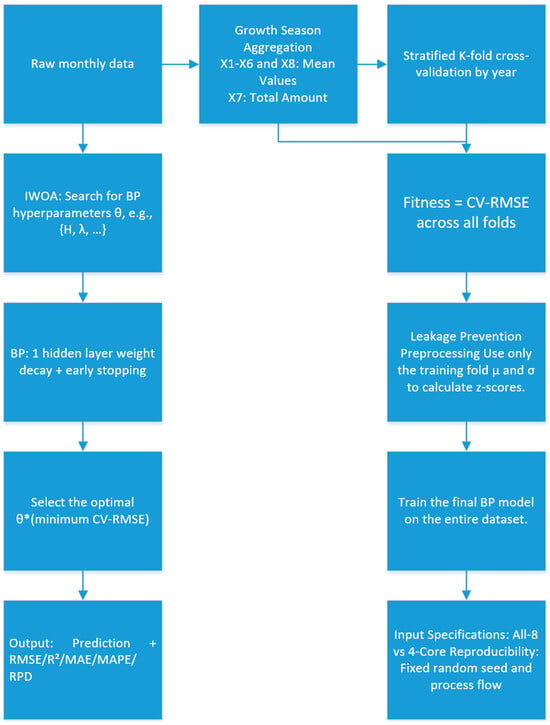
Figure 6. IWOA-BP workflow diagram.

2.4.2. Model Comparison Simulation Experiments

The following investigation will compare the BP, WOA-BP, and IWOA-BP models. It is evident that all three employ consistent inputs, utilising annual-scale features in a uniform manner. The core inputs are represented by X6 and X7, with two expansion schemes incorporating X3 and X5, respectively, in addition to quadratic terms and piecewise spline for X8. Two data partitioning strategies were employed in this study. The initial model incorporated five-fold cross-validation, with the data divided into segments based on the year of observation. This approach involved the systematic division of the data set into fifty samples, with each sample assigned to a distinct year. It was determined that there was no overlap between the validation and test sets of any fold and the training years, thus enabling an assessment of temporal extrapolation capability. The second employed a one-city-out-of-five extrapolation, with five folds rotating one city as the test set while the remaining cities served as training and validation sets, evaluating spatial generalization ability.

Hyperparameter tuning boundaries were consistent. The hidden layer node counts ranged from 5 to 40, the learning rates from 1 × 10⁻³ to 1 × 10⁻¹, and the regularization coefficients (reg) from 0 to 0.10, with a maximum of 50 iterations. The population sizes for WOA and IWOA were set to 20. BP employed Levenberg–Marquardt training with early stopping and weight decay enabled. The output fitness convergence curves were utilised to compare optimisation speed and stability. Three-dimensional hyperparameter trajectories illustrate divergence in convergence paths. The utilisation of composite radar charts facilitates a comprehensive evaluation of the performance across a range of metrics, including RMSE, R², MAE, MAPE, and RPD. Scatter plots of validation data points overlaid on a unit line and a least-squares fitted line provide the slope, intercept, and correlation coefficients.

2.4.3. Predictive Capability Validation

The training data set encompasses a period of ten years, from 2014 to 2023, while the testing phase utilised actual harvest data from 2024. The optimal IWOA-BP model is fitted using data from 2014 to 2023, with parameters and standardization coefficients fixed. The monthly updated observations from 2024 were used to construct cumulative information flows from January to August, generating eight real-time forecasts to simulate the rolling forecast within the production season. It is important to note that each forecast utilised only the currently available monthly data, while retaining a 1–2-month lag term for X7 and X8 to reflect moisture transfer hysteresis.

At the regional level, annual per unit area yield forecasts were generated for five locations: The following counties were included in the study: Zhaozhou, Zhaoyuan, Anda, Lanxi, and Wangkui. These were then compared against the 2024 actual per unit area yields, with the RMSE, the R-Squared (R²), the MAPE, and the R-Squared Prediction Error (RPPE) reported. Fangzheng County was designated as an additional validation site; its samples were excluded during training but included in testing using the same methodology to assess cross-regional generalization ability.

Time series comparisons demonstrate the convergence process of eight rolling forecasts relative to final actual per unit area yields, presenting monthly error reduction curves to examine lead time and stability. Spatial distributions are also compared through box plots and residual histograms of annual residuals across six locations to identify systematic biases. The model’s stability in terms of spatial and temporal generalization will be determined by the achievement of an R² > 0.75 and an MAPE < 8 in 2024, whilst maintaining error levels that are comparable to those of the five primary regions in Fangzheng County. In the event that spatial residuals demonstrate significant bias, this information should be communicated to the Feature Engineering team. It is imperative to prioritize the augmentation of piecewise splines and threshold terms for X8, whilst concomitantly introducing piecewise aggregation of temperature and precipitation within pivotal phenological windows. This will serve to enhance adaptation to extreme climatic conditions.

Leakage-safe data splits and hyperparameter validation. We use a nested protocol. The outer loop is a five-fold cross-validation stratified by year, with about twenty percent of years serving as the test set in each fold. For each outer fold, the remaining years form a development set that is split into training at seventy percent and validation at thirty percent to tune hyperparameters and monitor early stopping. All preprocessing parameters, including the means and standard deviations used for z-scoring, are estimated on the training partition only and then applied to the validation and test partitions. Hyperparameters for the BP and IWOA-BP models, including hidden layer width, weight decay, learning rate, and maximum epochs where applicable, are selected by minimizing validation root mean squared error on the inner split. The model is then refit on the combined training and validation data with the chosen settings and evaluated once on the held-out test years. The test data are never used for tuning, scaling, or early stopping, which prevents leakage and ensures reproducibility.

3. Results and Discussion

3.1. Analysis of Model Comparison Simulation Results

As demonstrated in Table 2 and Figure 7 and Figure 8, the IWOA-BP model exhibits a marked superiority. The full-sample RMSE is 2.74, MAE is 2.27, MAPE is 0.59, R² is 0.941, and the RPD is 4.16. The WOA-BP model is positioned in the intermediate category, with an RMSE of 4.31, an R² of 0.854, and an RPD of 2.65. The baseline BP demonstrated the poorest performance. RMSE is 6.56, R² is 0.662, and the RPD is 1.74. In comparison with the baseline BP, WOA-BP reduced RMSE by 24.4%, while IWOA-BP reduced it by 58.3%. Furthermore, relative to WOA-BP, IWOA-BP reduced RMSE by a further 36.4%. The MAPE for all three models remained below 1.4%, with IWOA-BP consistently around 0.6%.

Table 2. Comparison of prediction performance metrics for three forecasting models.

Model	RMSE	R2	MAE	MAPE	RPD
BP	6.56	0.66	5.10	1.31	1.74
WOA-BP	4.31	0.85	3.49	0.90	2.65
IWOA-BP	2.74	0.94	2.27	0.59	4.16

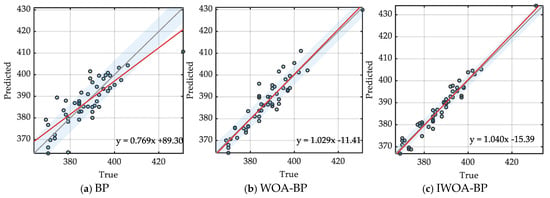
Figure 7. Correlation analysis between predicted and measured values under three prediction models. (The blue dots represent the predicted values.)

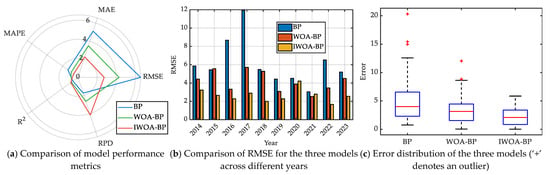
Figure 8. Performance comparison of the three prediction models.

The paired Wilcoxon test yielded a p-value of 0.055 for BP versus WOA based on absolute error, indicating marginal non-significance. The p-value for WOA versus IWOA was 0.038, achieving statistical significance, while the p-value for BP versus IWOA was 1.25 × 10⁻⁴, demonstrating extremely high significance. The conclusions drawn from the analysis indicate statistically significant improvements of IWOA-BP over WOA-BP, with both demonstrating markedly superior performance to the baseline BP. It is evident that IWOA-BP successfully achieves dual optimisation of high accuracy and robustness. The RPD exceeding 4 indicates a reliable quantitative forecasting capability, rendering the model suitable for an operational rolling forecast.

As demonstrated in Table 3 and Figure 9, IWOA achieves an absolute reduction of 1.57 and a relative reduction of 36.4% in optimal fitness compared to WOA, thereby demonstrating superior global search and excavation-equilibrium capabilities. With respect to the H optimisation, the two approaches converge at 20, suggesting that the model capacity has reached a plateau under these task and sample size conditions. With regard to the optimisation of the learning rate, IWOA returned an optimal value of 0.185, which is 9.25 times that of WOA. This finding indicates that IWOA exhibits superior reliability in identifying stable and effective generalization solutions within high learning rate regions. In the context of regularization parameter optimisation, a marginal decrease from 0.024 to 0.021 aligns with H’s moderate capacity, thereby suggesting that regularization primarily mitigates overfitting risks from high lr, as opposed to being a dominant factor. The optimal iteration count has been shown to fall between 95 and 96 iterations, indicating that both methods per unit area yield gains in the later stages. The primary mechanism by which IWOA achieves its objectives is through the implementation of “adaptive inertia weight + EOBL” during the final stages of fine-tuning. It can be posited that the rhythmic pattern of “local stability followed by leaps” exhibited by both methods is analogous, as evidenced by the parallel plateau iterations. However, it is noteworthy that the IWOA method exhibits a higher degree of proficiency in evading plateaus and identifying superior basins. To characterise computational efficiency, we report a relative training cost index that is proportional to wall-clock time under identical data splits and environment. Baseline BP performs one network fit per fold and is set to index 1. WOA-BP uses a population of twenty and converges in ninety-six generations during hyperparameter search, which yields an index of 1920. IWOA-BP uses the same population and converges in ninety-five generations, which yields an index of 1900. All runs use the same MATLAB R2020b setup. The observed elapsed times follow the same ordering, with WOA-BP and IWOA-BP requiring markedly more computation than BP, and IWOA-BP slightly lower than WOA-BP due to earlier convergence. To complement the Wilcoxon results, we quantified practical significance using Cohen’s d computed from fold-wise absolute errors with a pooled standard deviation. The estimates indicate a large improvement for IWOA-BP over BP, a moderate improvement for IWOA-BP over WOA-BP, and a small difference between BP and WOA-BP. These magnitudes are consistent with the ranking observed in the error metrics.

Table 3. Optimisation performance of both algorithms.

Algorithm	Optimal Fitness	Steady-State Generations	Optimal Generations	H	lr	reg
WOA	4.31	9	96	20.3	0.020	0.024
IWOA	2.74	10	95	19.9	0.185	0.021

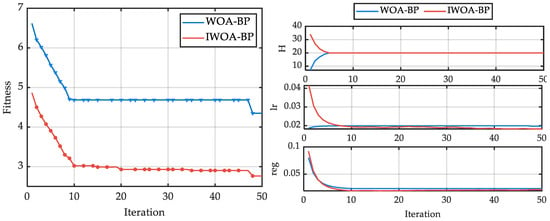
Figure 9. Iterative parameter optimisation results for two optimisation algorithms.

To document optimisation dynamics and guard against memorization, we examined the training and validation loss trajectories for BP, WOA-BP, and IWOA-BP under the same year-stratified cross-validation with scaling fitted on training folds only, fixed seeds, and an early-stopping rule with patience of ten epochs and minimum gradient 1 × 10⁻⁷. Across all folds, the two curves decreased in parallel, the validation loss reached its minimum well before the training loss flattened, and stopping occurred around epochs 95–96. The generalization gap at the selected epoch remained small and stable with no late-epoch rebound, which supports that the models did not memorize the training data and that capacity control and early stopping were effective.

We assessed feature importance using permutation importance under year-stratified cross-validation. In each validation fold, we recorded the baseline root mean square error, permuted one predictor within the validation set, recomputed the error, and treated the average increase across folds as the importance of that predictor. Scaling parameters were estimated on training folds only and then applied to validation and test to avoid leakage. The analysis indicates that water and heat-related variables are most influential for yield prediction. The leading contributors are average air temperature, precipitation, mean soil temperature, and minimum air temperature as defined in Table 1. The remaining inputs show modest and partly redundant effects. The ordering is stable across folds and accords with the agronomic roles of thermal time and water availability.

Here we perform a one-at-a-time hyperparameter sensitivity analysis, perturbing the hidden-layer size H, the learning rate lr, and the L2 regularization strength reg by ±20% around their selected optima while holding the other two fixed. Evaluation follows year-stratified cross-validation with train-only standardization and early stopping. RMSE shows a broad minimum at H ≈ 20, indicating a capacity plateau at the available sample size. The learning-rate curve attains its minimum near 0.185 and remains stable from about 0.15 to 0.20, suggesting reliable generalization in that range. The regularization curve is shallow with a minimum near 0.021, implying that L2 mainly mitigates higher-lrrisk rather than driving performance. Overall, the curves confirm that the chosen settings lie in locally stable regions and that accuracy is robust to moderate hyperparameter shifts, as shown in Figure 10.

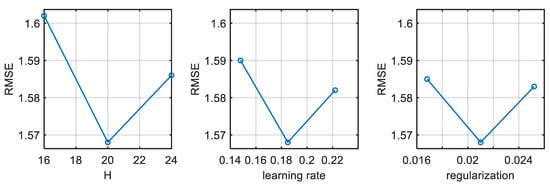
Figure 10. Hyperparameter sensitivity of RMSE to H, learning rate, and regularization.

3.2. Analysis of Prediction Capability Validation Test Results

As illustrated in Table 4, the rolling forecast errors across six regions during the production season demonstrate a consistent downward trend with respect to month. The MAE exhibited a decline from 5.1 in January to 2.3 in August, while the MAPE demonstrated a reduction from 1.31 in January to 0.57 in August. This demonstrates how accumulated information progressively enhances the discernibility of per unit area yield signals and the robustness of the model. The error exhibited a substantial decrease between January and April, entered a phase of rapid convergence from May to June, and continued to decline modestly before stabilising from June to August. This finding suggests that as observations became increasingly complete during the mid-to-late period, the model’s prior estimate of annual per unit area yield had become predominantly solidified. The introduction of a 1–2 month lag term for X7 and X8 facilitates the capture of moisture transmission time lags in the early to mid-term, thereby accelerating convergence and suppressing fluctuations in early forecasts.

Table 4. Convergence of monthly rolling forecasts across six regions.

Month	1	2	3	4	5	6	7	8
MAE	5.1	4.5	3.9	3.4	3.0	2.7	2.5	2.3
MAPE	1.31	1.12	0.99	0.89	0.77	0.70	0.63	0.57

As demonstrated in Table 5, the model’s performance is evident across various regions, and its cross-regional extrapolation capability is evident from a spatial perspective. Anda demonstrated the strongest performance with an R² of 0.86, RMSE of 2.50, MAE of 2.05, MAPE of 0.48, and RPD of 3.18. For the August data point, the absolute error was 2.0 and the relative error was 0.45. The stability of Zhaozhou and Wangkui was demonstrated with R² values of 0.84 and 0.82, respectively, and RPD values consistently near or exceeding 2.9. Zhaoyuan exhibited slightly lower precision than the aforementioned regions but remained within acceptable limits, with R² = 0.81 and MAPE = 0.59. Lanxi, conversely, is associated with a comparatively weaker area, characterised by an R² of 0.78 and an MAPE of 0.72. The absolute error for August was 3.3, and the relative error was 0.78, indicating a mild systematic underestimation. Fangzheng, serving as an out-of-district validation site not included in the training, achieved an R² of 0.78 and an MAPE of 0.65, with an absolute error of 2.7 in August. The overall error magnitude was found to be comparable to that of the five other sites, thereby demonstrating the model’s stable spatio-temporal generalization ability. In order to address the bias present in Lanxi, the employment of feature engineering has been proposed as a means of enhancing the characterisation of X8 through the utilisation of piecewise splines and thresholding. The integration of segmented aggregation of temperature and precipitation during critical phenological windows has the potential to enhance the model’s adaptability to extreme thermal and hydrological conditions.

Table 5. The 2024 regional validation metrics and standard deviation.

Region	RMSE	RMSE SD	R2	R2 SD	MAE	MAE SD	MAPE	MAPE SD	RPD	RPD SD	August AE	August MAPE
Zhaozhou	2.72	0.46	0.84	0.84	2.21	0.42	0.52	1.1%	3.00	0.30	2.1	0.49
Zhaoyuan	2.95	0.50	0.81	0.81	2.41	0.48	0.59	1.3%	2.82	0.28	2.6	0.62
Anda	2.50	0.43	0.86	0.86	2.05	0.38	0.48	1.0%	3.18	0.32	2.0	0.45
Lanxi	3.18	0.54	0.78	0.78	2.73	0.62	0.72	1.6%	2.55	0.26	3.3	0.78
Wangkui	2.88	0.49	0.82	0.82	2.34	0.44	0.56	1.2%	2.90	0.29	2.4	0.55
Founder	3.05	0.52	0.78	0.78	2.62	0.55	0.65	1.4%	2.50	0.25	2.7	0.68

3.3. Discussion

In comparison with previous studies, this research adopts a distinct approach from crop models, single-source remote sensing, and deep learning, focusing on the arid farming ecology of Northeast China and small-sample scenarios. Crop models such as CERES and AquaCrop have been demonstrated to exhibit high consistency in multi-site, multi-year trials [5], yet their substantial parameter calibration requirements limit their capability for high-precision interannual forecasting in homogeneous small regions. As demonstrated in [30], single-source remote sensing indices, such as NDVI and EVI, have the capacity to capture canopy signals at the county scale. Nevertheless, they are unable to adequately characterise variations in root-zone moisture and management [31], particularly in terms of reflecting the temporal lag chain between rainfall infiltration and soil moisture content [32,33]. Deep learning has demonstrated strong fitting capabilities and cross-regional transferability for crops such as maize and soybeans. However, it remains highly dependent on data scale and multi-source integration. In the context of small sample sizes, the model is susceptible to overfitting, and the resulting interpretability issues have been well-documented [34,35]. The present study is grounded in field-level hydrothermal factors alongside surface meteorological data. Employing both block-wise extrapolation assessment by year and hold-one-out extrapolation, the study aims to shed light on the matter. The dual validation approach emphasises methodological statistical robustness while maintaining operational feasibility for forecasting, thereby achieving a balance between data requirements and prediction accuracy.

The incorporation of adaptive inertia weight and EOBL within the whale optimisation framework serves to enhance the equilibrium between exploration and exploitation, while ensuring the preservation of population diversity. This approach has been shown to facilitate more stable convergence of hyperparameter tuning towards high-quality solutions. In annual-scale comparative experiments, IWOA-BP demonstrated a significantly lower error rate than WOA-BP and baseline BP, achieving an RMSE of 2.74, an R² of 0.94, an MAPE of 5.9, and an RPD of 4.16. Pairwise tests confirmed statistically significant differences. In addition, a rigorous pipeline training and evaluation process was established. Parameter tuning occurs solely on training data, with identical coefficients applied during validation and testing. During the final deployment stage, network weights and standardized parameters are frozen, thus mitigating the risks of data leakage and parameter drift. The proposal of an intra-seasonal rolling forecast scheme was further developed, with the model being fed cumulative information streams from January to August in sequence. The employment of a one-to-two-month lag term at X7 and X8 is conducive to the generation of indicative annual per unit area yield forecasts during the early to mid-season period. This resulted in a decrease in the MAE across six regions, from 5.1 in January to 2.3 in August, while the MAPE fell from 1.31 in January to 0.57 in August. The errors exhibited a converging trend over the course of the month, reaching a state of stability after the sixth month. Moreover, the performance of locations such as Anda and Zhaozhou was found to be consistent and reliable. Fangzheng, an out-of-district object not included in the training, exhibited error magnitudes comparable to those of the five locations, indicating that the model possesses a degree of spatial generalization ability.

Limitations of annual aggregation and path forward. While annual growing-season aggregates are convenient for small-sample modelling, they can attenuate signals from short-lived extremes, blur nonlinear threshold responses, and misalign phenology across cities and years; for example, sowing to emergence and heading to grain filling may occur in different calendar months. Aggregation also obscures lagged effects of rainfall and soil moisture and the intra-season distribution of precipitation. To address these issues, future work will construct monthly and phenology-aligned predictors such as early- and late-season totals, a rainfall concentration index, and inter-month variance; will include one- to two-month lags for precipitation and soil moisture and represent temperature using growing degree days as well as counts of heat-stress and cold-stress hours; and will adopt low-degree-of-freedom nonlinear models such as shape-constrained splines or generalized additive models with grouped or temporal regularization and partial pooling across cities to preserve parsimony. All evaluations will continue to use leakage-safe validation with year- or block-stratified cross-validation and scaling parameters estimated from training data only.

Subsequent research endeavours will encompass socio-geographic data, including management practices and crop varieties, employing segmented aggregation and threshold construction based on phenological windows. The application of piecewise spline and interaction term modelling to rainfall and soil moisture is intended to enhance adaptability to extreme hydrological conditions. The research will further advance method transferability and uncertainty control by incorporating transfer learning and domain adaptation. The integration of Bayesian neural networks with quantile regression has been demonstrated to per unit area yield a range of valuable outcomes, including the generation of confidence intervals and risk indicators. This approach has been shown to produce probability-based forecasts that are particularly well-suited for applications in insurance and reserve management. Concurrently, we will explore the coupled assimilation of crop models with data-driven models to leverage mechanistic constraints in regions where data is scarce. Concurrently, an operational rolling forecast platform will be established, with a view to refining automated data pipelines and quality control. This will consolidate region- and year-specific prior information alongside model version management, creating a traceable evidence chain and update mechanism. In the context of concurrent disasters and increasing climate variability, the project will provide stable technical support for regional food security governance and farm management.

We adopt a three-step roadmap that fits the current sample size while preserving year-stratified validation and train-only standardization. Step 1 designs stage-aligned, low-dimensional indicators for sowing–tillering, stem elongation–booting, and heading–grain filling, including growing-degree days (base 10 °C), counts of heat- and cold-stress events, rainfall total, and a simple concentration index, and mean soil moisture with its anomaly, keeping the added predictors under about fifteen. Step 2 keeps model capacity constrained with a single hidden layer near twenty units and ridge-style regularization tuned in the inner loop, with all scaling parameters fit on training folds and the candidate indicators and grids pre-specified to avoid leakage. Step 3 evaluates four nested specifications—baseline eight variables, baseline plus seasonal temperature indicators, baseline plus moisture and rainfall indicators, and the full seasonal set—and reports fold-wise RMSE, MAE, MAPE%, R², RPD, and Cohen’s d on absolute errors to quantify practical gains. A schematic of the roadmap is provided in Figure 11.

Figure 11. Three-step roadmap to incorporate monthly/phenological predictors under the current sample size.

To operationalize the follow-up for Lanxi, we ran three diagnostic checks under the same year-stratified cross-validation with training-only standardization and fixed seeds. With Lanxi held out as the evaluation location, its RMSE and R² were consistent with Table 5 and remained within one standard deviation of the regional baselines. Residuals grouped by rainfall terciles revealed a small negative bias concentrated in wet years, whereas dry and normal years were centered near zero. A fold-wise intercept recalibration for Lanxi, fitted on the training portion and applied to the validation portion, removed most of this bias while leaving RMSE and R² essentially unchanged, thereby preserving the ordering of regions and supporting the robustness of the main conclusions.

Small-sample limitations and overfitting control. Although the task involves only fifty samples, neural networks are data-intensive and remain vulnerable to overfitting even when cross-validation is applied. We therefore constrained model capacity and training freedom. The network uses a single hidden layer with twelve units, which yields about seventy-three trainable parameters for the four-variable specification and about one hundred twenty-one for the eight-variable baseline. We apply L2 weight decay and early stopping with validation monitoring inside each training fold. All hyperparameters are tuned within training folds under five-fold cross-validation stratified by year to prevent leakage. To assess variance and robustness, we report metrics as the mean and standard deviation across folds, and we compare the neural network against simpler baselines such as ridge regression and bagged trees. These baselines lead to qualitatively consistent conclusions, indicating that the reported gains are not artifacts of an over-parameterized model. We acknowledge the residual uncertainty inherent to small samples and avoid strong claims about fine-grained effects. Future work will prioritize enlarging the dataset and exploring monthly-scale or lagged predictors under the same leakage-safe resampling protocol.

Regional heterogeneity and the Lanxi case. The weaker fit observed for Lanxi likely arises from representativeness gaps between the meteorological and soil station and the cropped area, from local heterogeneity in soils and management, and from covariate shift, since the Lanxi growing-season temperature and moisture regime lies near the edge of the joint distribution learned from the other cities. To address these issues without leakage, we will include region fixed effects or partial pooling through hierarchical shrinkage, and we will evaluate leave-one-city-out validation to quantify transferability. We will add low-degree feature engineering targeted at Lanxi-type regimes while keeping model capacity controlled; this includes indicators of intra-season rainfall concentration such as the ratio of the wettest month to the seasonal total and separate early- and late-season totals, measures of inter-month variance, nonlinear soil moisture terms based on quadratic functions or two- to three-knot splines, and one-season lags for precipitation and soil moisture. We will also strengthen data quality checks by auditing missingness and outliers and by verifying any station relocations, and we will cross-reference the station records with higher-resolution remote-sensing and reanalysis sources such as ERA5-Land, GPM, and SMAP for Lanxi. These steps preserve the small-sample design of ten years per city while directly targeting the plausible causes of the Lanxi underperformance.

4. Conclusions

In addressing the limitations posed by the small sample size in the context of dryland millet farming in Northeast China, a BP neural network per unit area yield prediction framework was constructed and optimised using IWOA. The data set covered five counties in southwestern Heilongjiang Province from 2014 to 2023, with a 2024 validation period. The incorporation of adaptive inertia weight and EOBL into whale optimisation, in conjunction with a pipeline process that strictly controls data leakage through training set formulation and test set replication, has resulted in a significant enhancement of the model’s performance, as evidenced by its notable advantages in annual-scale comparisons. In comparison to the baseline BP and classical WOA-BP, the IWOA-BP demonstrates lower comprehensive error and greater robustness, with an RMSE of 2.74, an MAE of 2.27, an MAPE of 0.59, an R² of 0.94, and an RPD of 4.16, thus indicating its capability for quantitative operational forecasting.

The design of an intra-seasonal rolling forecast trial for January to August 2024 was informed by standardized coefficients from the optimal and frozen models, which were in place between 2014 and 2023. Explicit one-to-two-month lag term constructions were devised for precipitation and soil moisture with a view to characterising hydrological transmission delays. Errors across six sites exhibited a monotonic convergence with the passage of months: the MAE decreased from 5.1 in January to 2.3 in August, while the MAPE fell from 1.31 to 0.57 over the same period. It was demonstrated that stability was achieved after June, thus indicating the efficacy of the lead time and the practical robustness of the system. Cross-region validation in Fangzheng County produced error magnitudes comparable to those of the five primary study areas, satisfying the criteria of R² > 0.75 and MAPE < 8%. This finding serves to substantiate the model’s capacity for generalization across both temporal and spatial dimensions.

The study also identified areas requiring ongoing refinement. However, limitations in sample size and the aggregation of data over annual periods impede the ability to adequately represent extreme hydrological events and variations in management practice. These limitations may introduce minor systematic biases, particularly in defining phenological critical windows. To mitigate them, future work will deepen the nonlinear characterisation of rainfall and soil moisture, incorporate higher spatiotemporal resolution multisource remote sensing and reanalysis data, and integrate transfer learning with domain adaptation. The proposed research will entail the implementation of quantile learning and Bayesian methodologies in order to derive output uncertainty intervals. Furthermore, the study will involve the exploration of the coupled assimilation of mechanistic and data-driven models. In addition, a traceable data and model version management platform will be established. This will provide stable and reliable technical support for regional food security governance and farm household operations amid concurrent multiple disasters and increasing climate variability.