An Ensemble Learning Model for Aging Assessment of Silicone Rubber Considering Multifunctional Group Comprehensive Analysis
Abstract
1. Introduction
2. Experimental Data
2.1. Data Sources
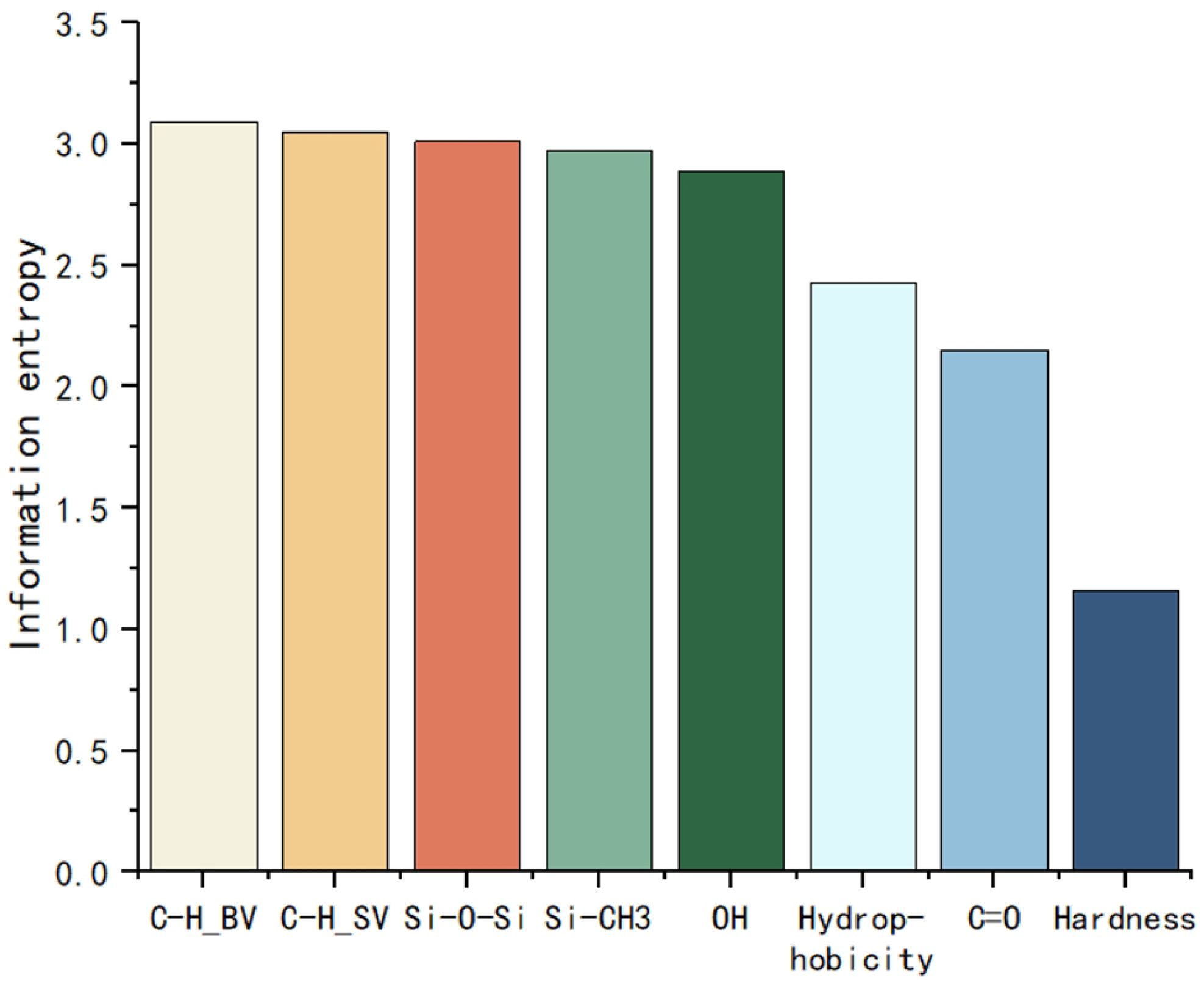
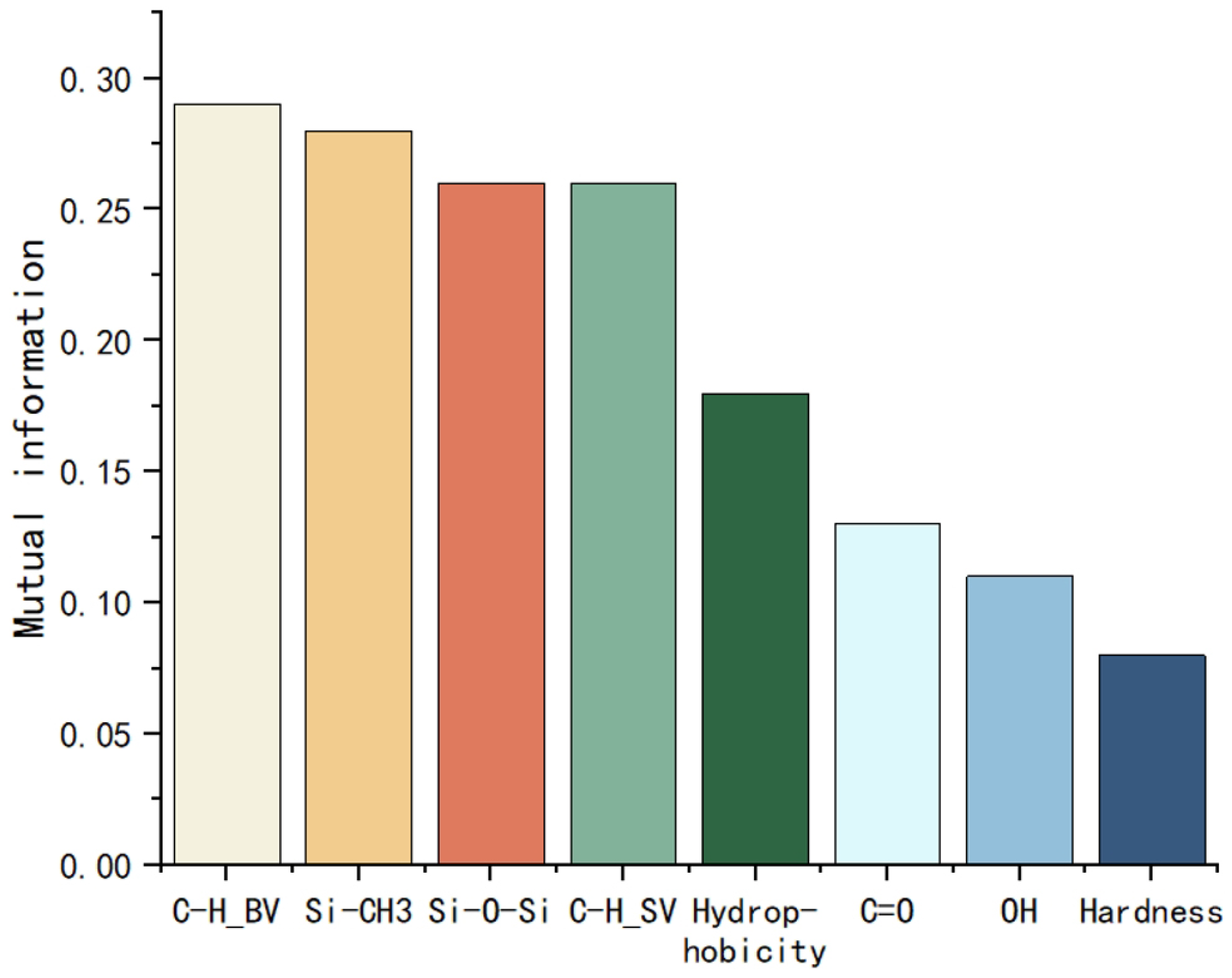
2.2. Selection of Characteristic Functional Groups
2.3. Selection of Aging Characteristics
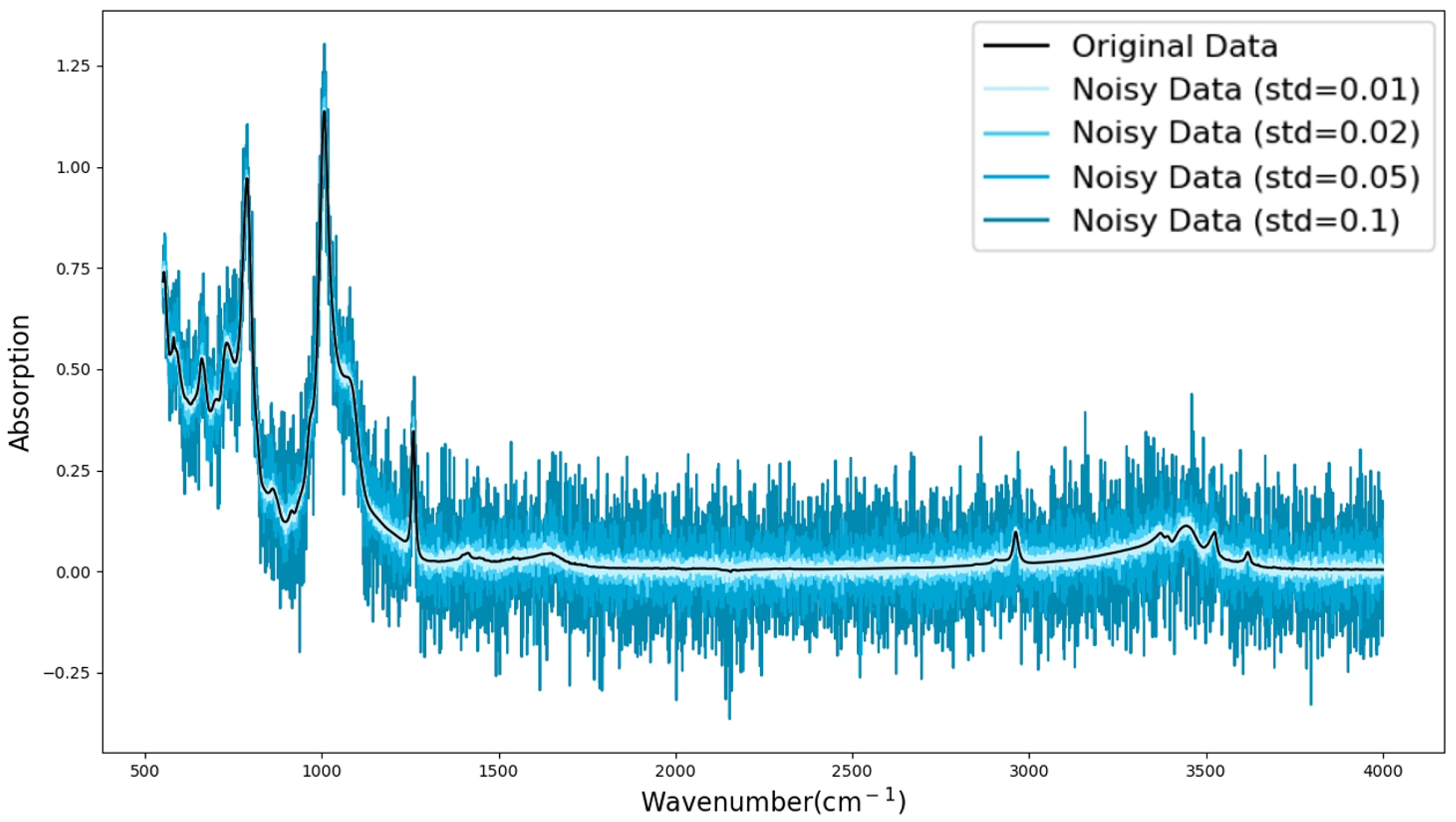
2.4. Data Augmentation
3. Model Architecture Design
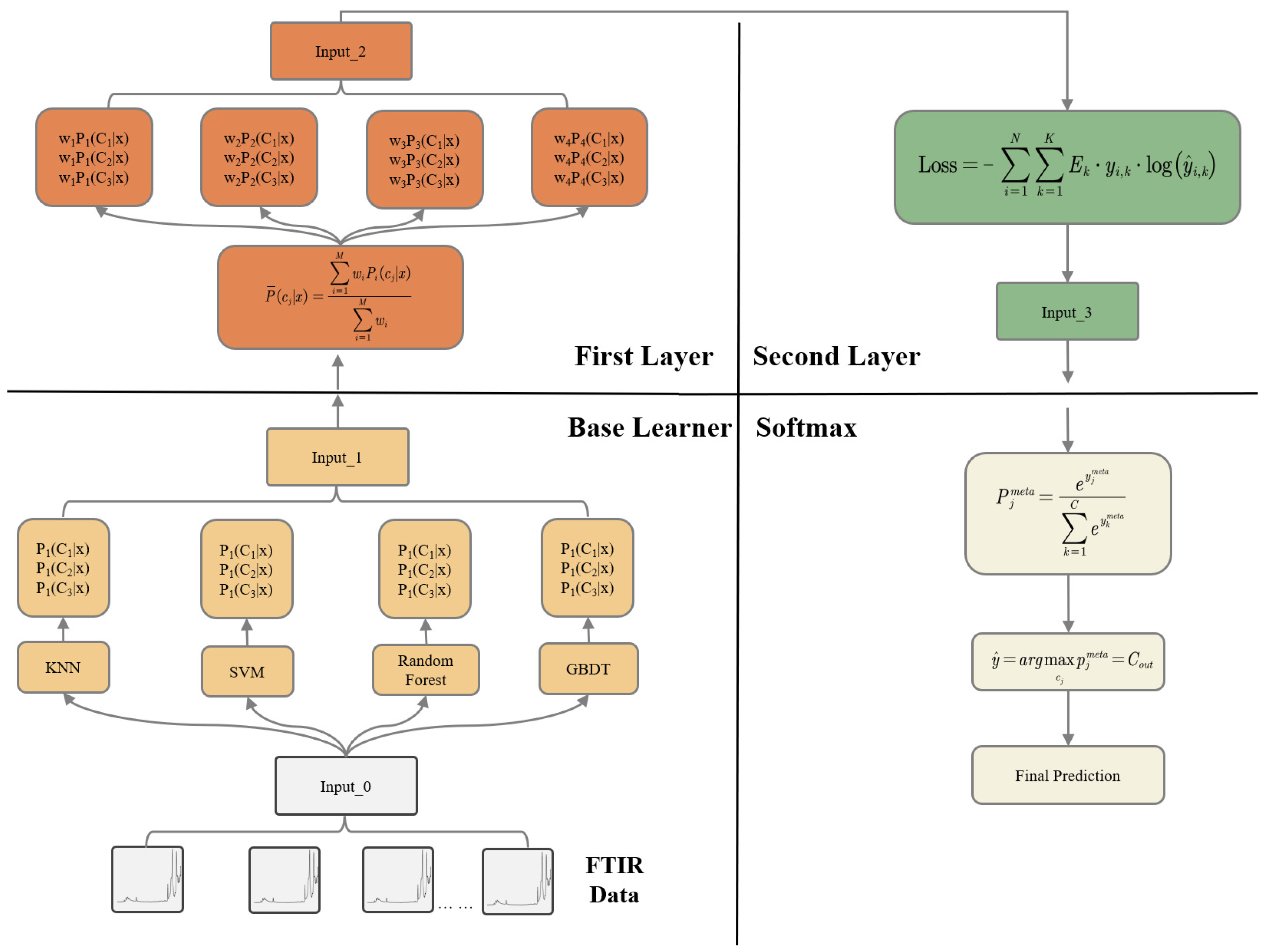
3.1. Model Introduction
3.2. Base Learners
3.3. First Layer
3.4. Second Layer
3.5. Model Output
4. Training and Testing
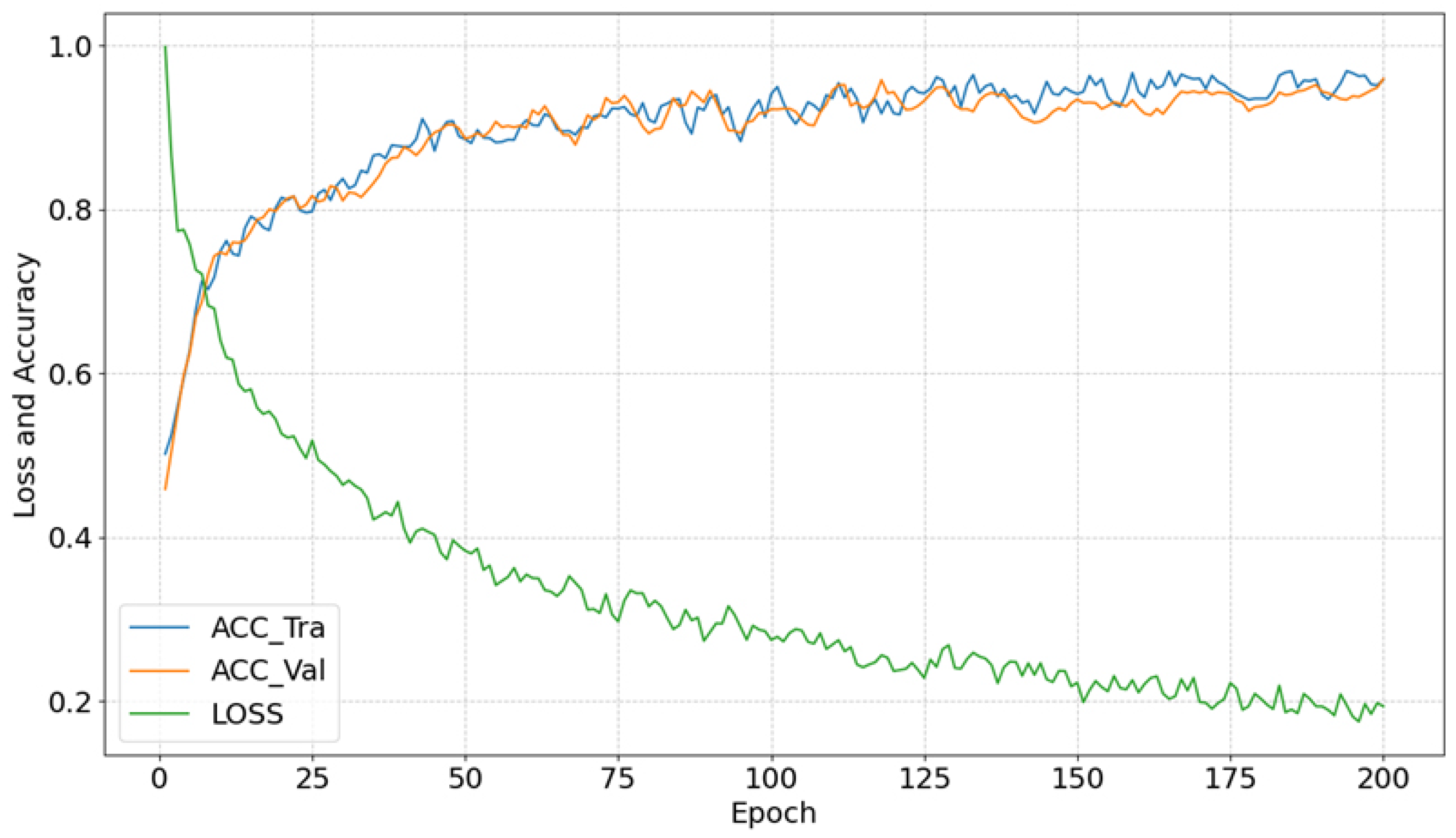
4.1. Model Training
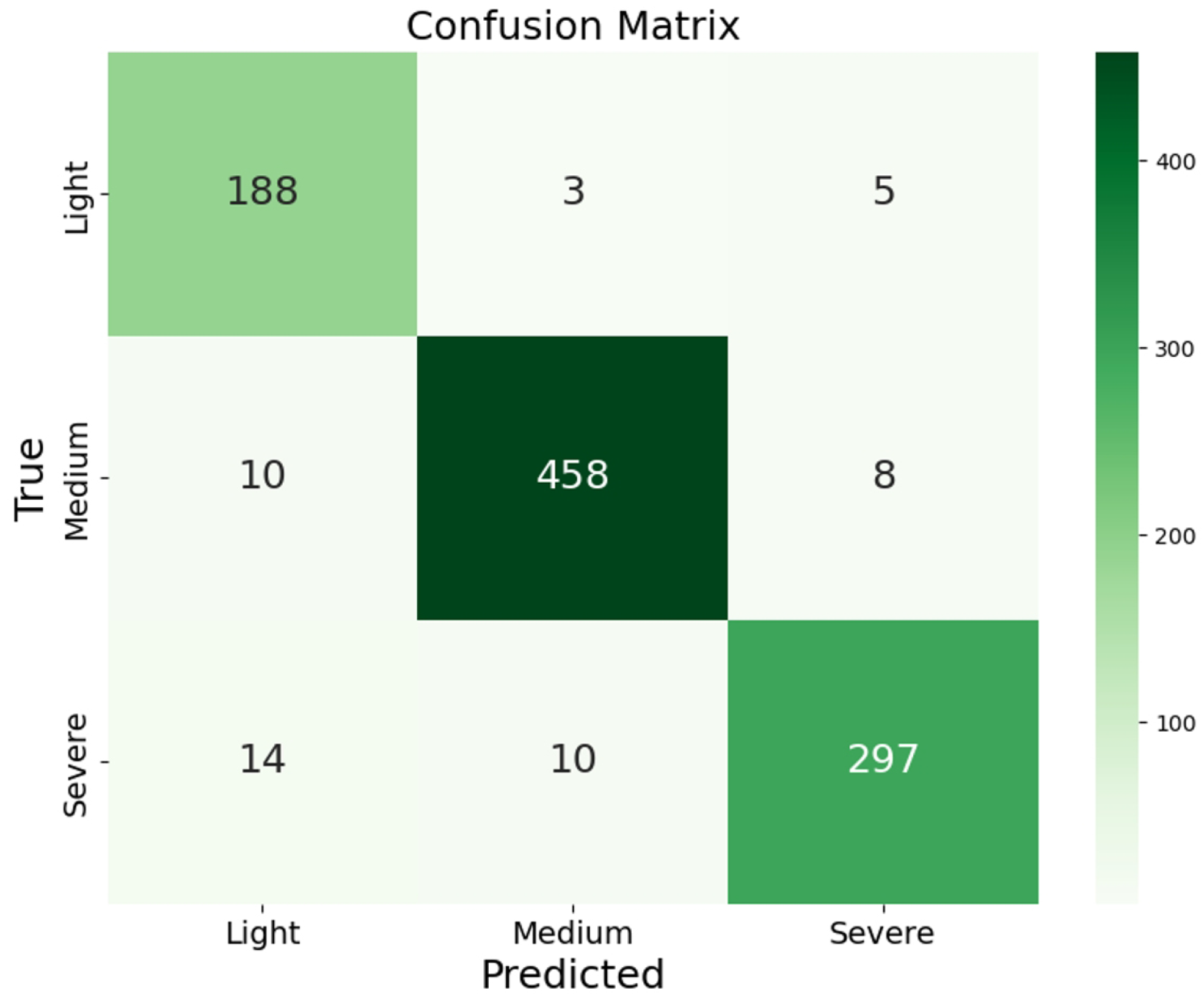
4.2. Model Performance
5. Model Evaluation
5.1. Generalization Capability Evaluation
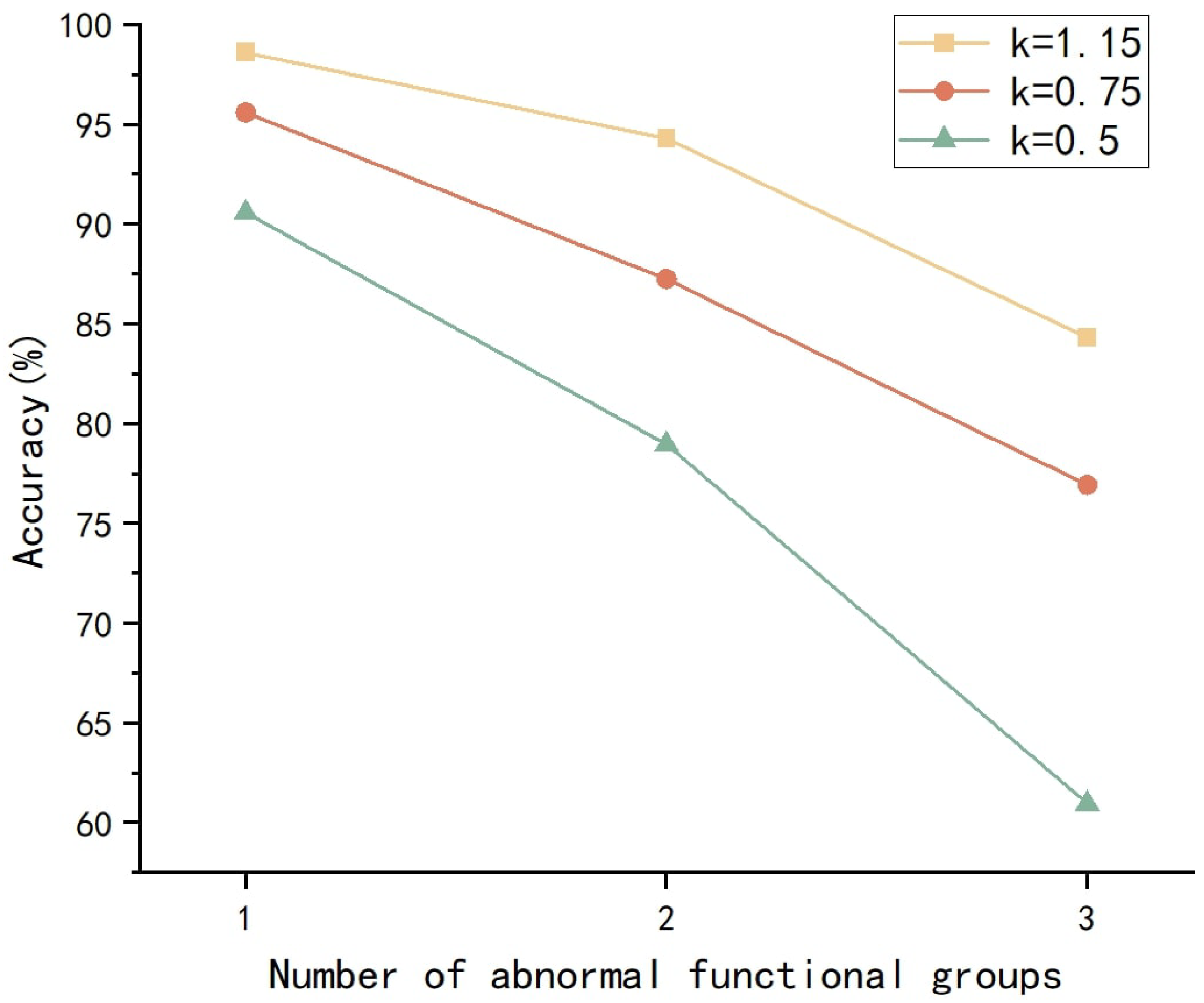
5.2. Robustness Testing
5.3. Ablation Experiments
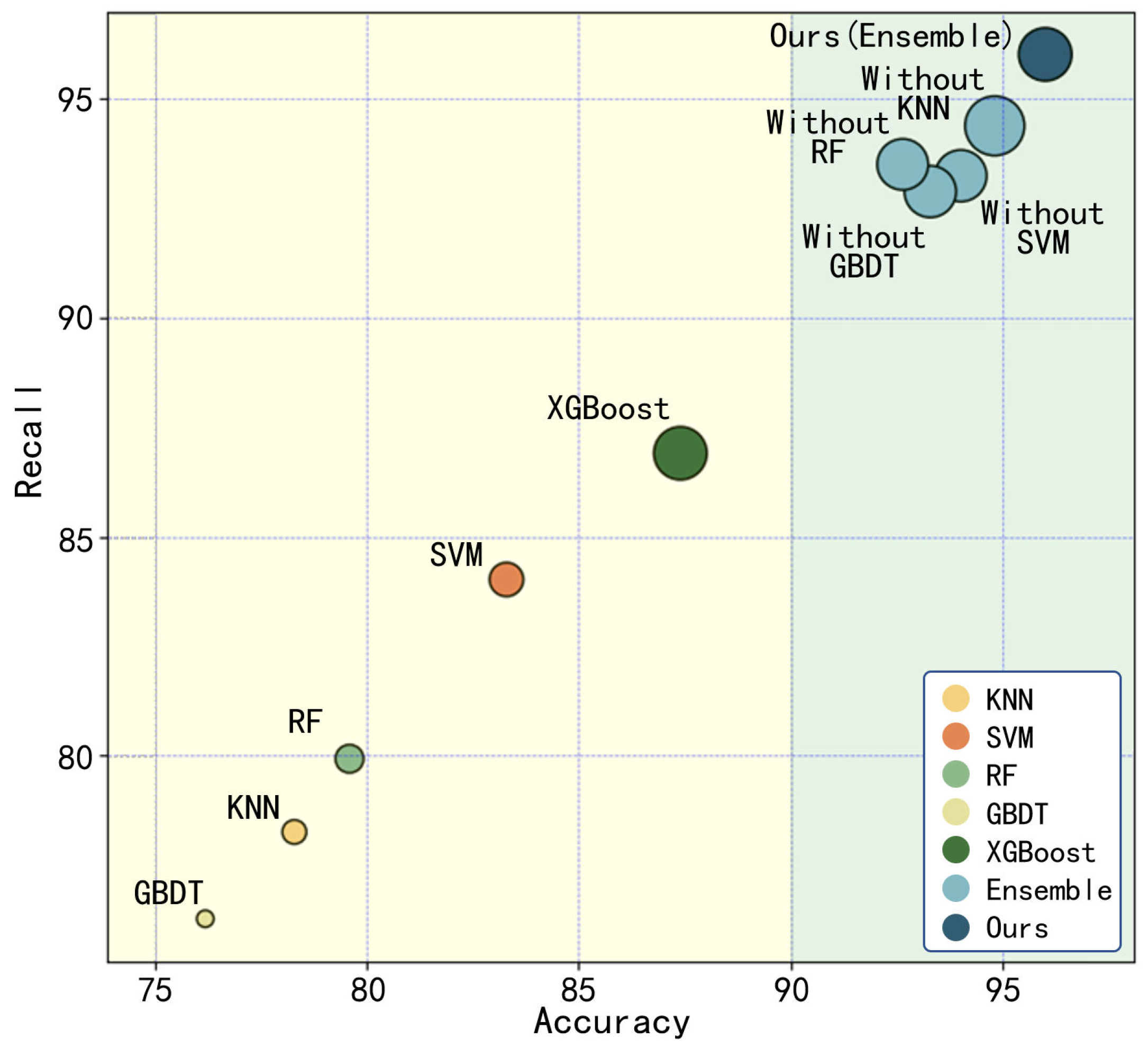
5.4. Performance Comparison
5.4.1. Comparison of Different Machine Learning Models
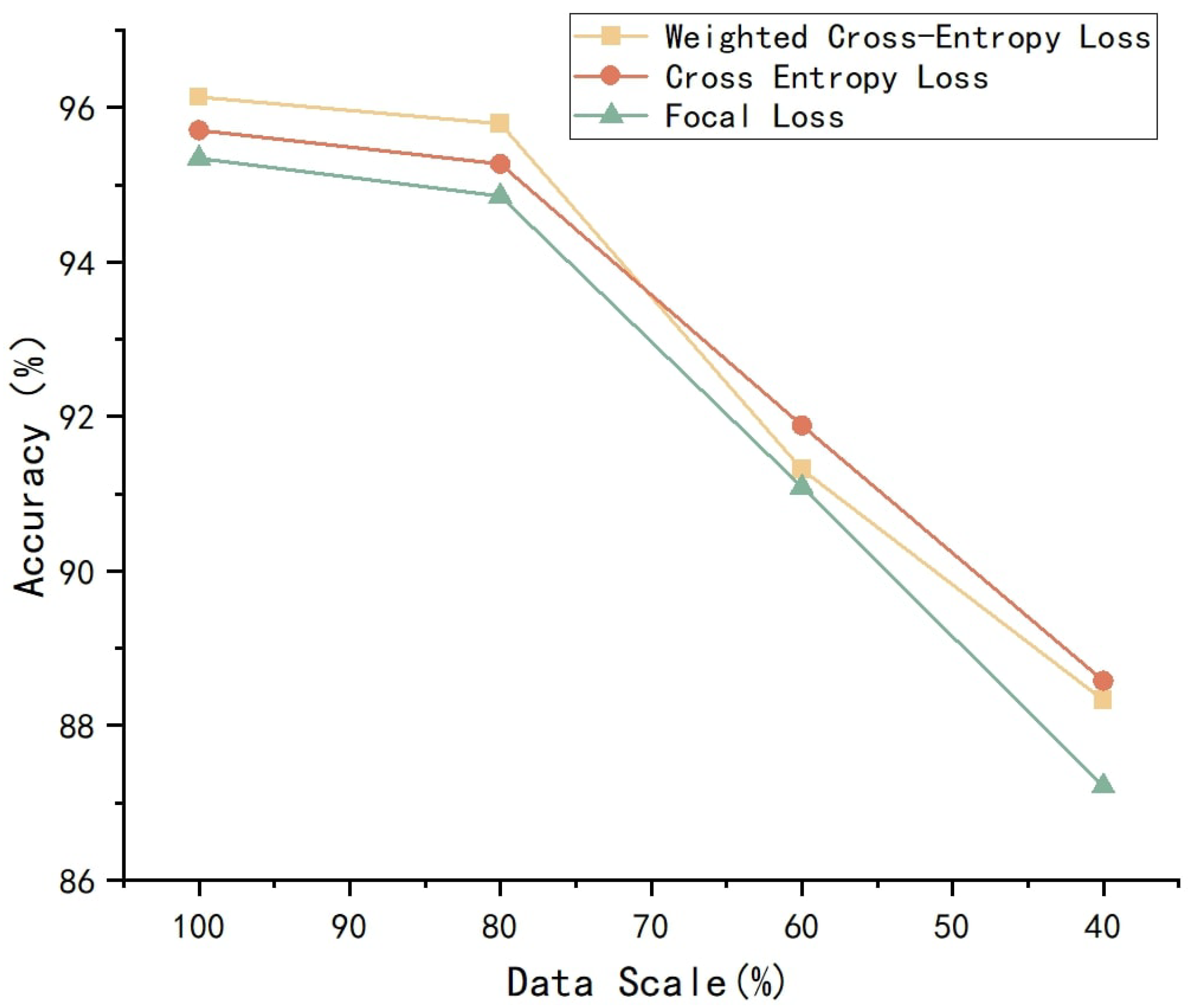
5.4.2. Comparison of Different Loss Functions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, X.D.; Wu, C.; Zuo, Z.; Deng, Y.; Gao, Y.F. Review and Prospects for Development of High Voltage Outdoor Organic Insulation. Proc. Csee 2024, 44, 7412–7426. [Google Scholar]
- Guan, Z.C.; Peng, G.M.; Wang, L.M.; Jia, Z.D.; Zhang, R.B. Application and key technical study of composite insulators. High Volt. Eng. 2011, 37, 513–519. [Google Scholar]
- Zeng, S.; Li, W.; Peng, Y.; Zhang, Y.; Zhang, G. Mechanism of accelerated deterioration of high-temperature vulcanized silicone rubber under multi-factor aging tests considering temperature cycling. Polymers 2023, 15, 3210. [Google Scholar] [CrossRef]
- Bi, M.; Deng, R.; Jiang, T.; Chen, X.; Pan, A.; Zhu, L. Study on corona aging characteristics of silicone rubber material under different environmental conditions. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 534–542. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, L.; Guan, Z.; Zhang, F. Aging characterization and lifespan prediction of silicone rubber material utilized for composite insulators in areas of atypical warmth and humidity. IEEE Trans. Dielectr. Electr. Insul. 2017, 23, 3547–3555. [Google Scholar] [CrossRef]
- Xiong, Y.; Rowland, S.M.; Robertson, J.; Day, R.J. Surface analysis of asymmetrically aged 400 kV silicone rubber composite insulators. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 763–770. [Google Scholar] [CrossRef]
- Amin, M.; Salman, M. Aging of polymeric insulators (an overview). Rev. Adv. Mater. Sci. 2006, 13, 93–116. [Google Scholar]
- Mavrikakis, N.; Siderakis, K.; Pylarinos, D.; Koudoumas, E. Assessment of field aged composite insulators condition in Crete. In Proceedings of the 9th International Conference on Deregulated Electricity Market Issues in South Eastern Europe, Nicosia, Cyprus, 25–26 September 2014. [Google Scholar]
- Liang, X.; Wang, S.; Fan, J.; Guan, Z. Development of composite insulators in China. IEEE Trans. Dielectr. Electr. Insul. 2020, 6, 586–594. [Google Scholar] [CrossRef]
- El-Hag, A.H.; Jayaram, S.H.; Cherney, E.A. Effect of insulator profile on aging performance of silicone rubber insulators in salt-fog. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 352–359. [Google Scholar] [CrossRef]
- Song, W.; Shen, W.W.; Zhang, G.J.; Song, B.P.; Lang, Y.; Su, G.Q.; Mu, H.B.; Deng, J.B. Aging characterization of high temperature vulcanized silicone rubber housing material used for outdoor insulation. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 961–969. [Google Scholar] [CrossRef]
- Chen, C.; Jia, Z.; Wang, X.; Lu, H.; Guan, Z.; Yang, C. Micro characterization and degradation mechanism of liquid silicone rubber used for external insulation. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 313–321. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, J. A portable unilateral nuclear magnetic resonance sensor used for detecting the aging status of composite insulator. Trans. China Electrotech. Soc. 2015, 31, 118–125. [Google Scholar]
- Chughtai, A.R.; Smith, D.M.; Kumosa, L.S.; Kumosa, M. FTIR analysis of non-ceramic composite insulators. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 585–596. [Google Scholar] [CrossRef]
- Akbari, M.; Shayegani-Akmal, A.A. Experimental investigation on the accelerated aging of silicone rubber insulators based on thermal stress. Int. J. Electr. Power Energy Syst. 2023, 149, 109049. [Google Scholar] [CrossRef]
- Zhang, Z.; Pang, G.; Lu, M.; Gao, C.; Jiang, X. Research on silicone rubber sheds of decay-like fractured composite insulators based on hardness, hydrophobicity, NMR, and FTIR. Polymers 2022, 14, 3424. [Google Scholar] [CrossRef]
- Gao, Y.; Liang, X.; Bao, W.; Li, S.; Wu, C. Failure analysis of a field brittle fracture composite insulator: Characterization by FTIR analysis and fractography. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 919–927. [Google Scholar] [CrossRef]
- Ji, H.; Zhang, X.; Guo, Y.; Xiao, S.; Wu, G. Evaluation method for the UV aging state of composite insulators based on hyperspectral characteristic. IEEE Trans. Instrum. Meas. 2023, 72, 2507509. [Google Scholar] [CrossRef]
- El-Hag, A. Application of machine learning in outdoor insulators condition monitoring and diagnostics. IEEE Instrum. Meas. Mag. 2021, 24, 101–108. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, T.; Li, M.; Zhou, Y. Deep-learning-based detection of transmission line insulators. Energies 2023, 16, 5560. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, Y.; Lv, L.; Zeng, X.; Xia, L.; Li, S.; Liu, J.; Kong, J.; Shao, T. Evaluation of aging and degradation for silicone rubber composite insulator based on machine learning. Energies 2023, 56, 424001. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, C.; Xie, M.; Cao, B. Classification method of composite insulator surface image based on GAN and CNN. Energies 2024, 31, 2242–2251. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, G.; Guo, Y.; Xiao, S.; Fan, Y.; Gao, G.; Zhang, X. A new noncontact detection method for assessing the aging state of composite insulators. IEEE Trans. Ind. Inform. 2024, 20, 6802–6813. [Google Scholar] [CrossRef]
- Kaneko, T.; Ito, S.; Minakawa, T.; Hirai, N.; Ohki, Y. Degradation mechanisms of silicone rubber under different aging conditions. Polym. Degrad. Stab. 2019, 168, 108936. [Google Scholar] [CrossRef]
- Gustavsson, T.G.; Gubanski, S.M.; Hillborg, H.; Karlsson, S.; Gedde, U.W. Aging of silicone rubber under ac or dc voltages in a coastal environment. IEEE Trans. Dielectr. Electr. Insul. 2002, 8, 1029–1039. [Google Scholar] [CrossRef]
- Hexuan, Z.; Shurong, Z.; Lianzhang, W.; Lianxuan, Z.; Yongpeng, Y. Influence of UV-irradiation on degradation of silicone rubber composite insulators in high-altitude regions. North China Electr. Power 2009, 3, 10–13. [Google Scholar]
- Gao, Y.; Li, S.; He, S.; Gu, X.; Yue, Y.; Chen, Y.; Liu, Q. Molecular dynamics supported thermal-moisture aging effects on properties of silicone rubber. Prog. Org. Coatings 2024, 192, 108503. [Google Scholar] [CrossRef]
- Lou, W.; Xie, C.; Guan, X. Understanding radiation-thermal aging of polydimethylsiloxane rubber through molecular dynamics simulation. NPJ Mater. Degrad. 2022, 6, 84. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Chen, J.; Song, L.; Wainwright, M.; Jordan, M. Learning to explain: An information-theoretic perspective on model interpretation. Int. Conf. Mach. Learn. 2018, 80, 883–892. [Google Scholar]
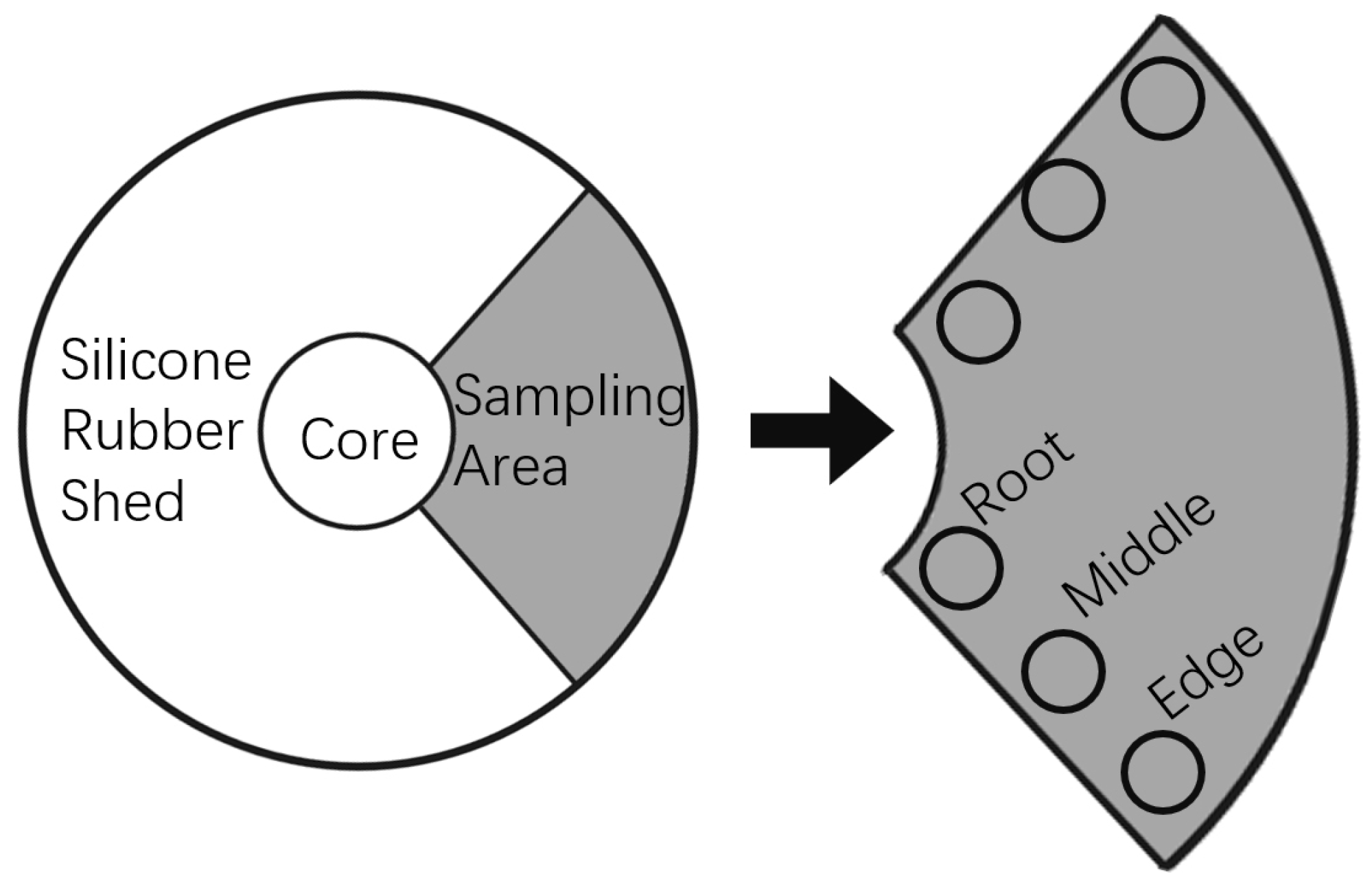


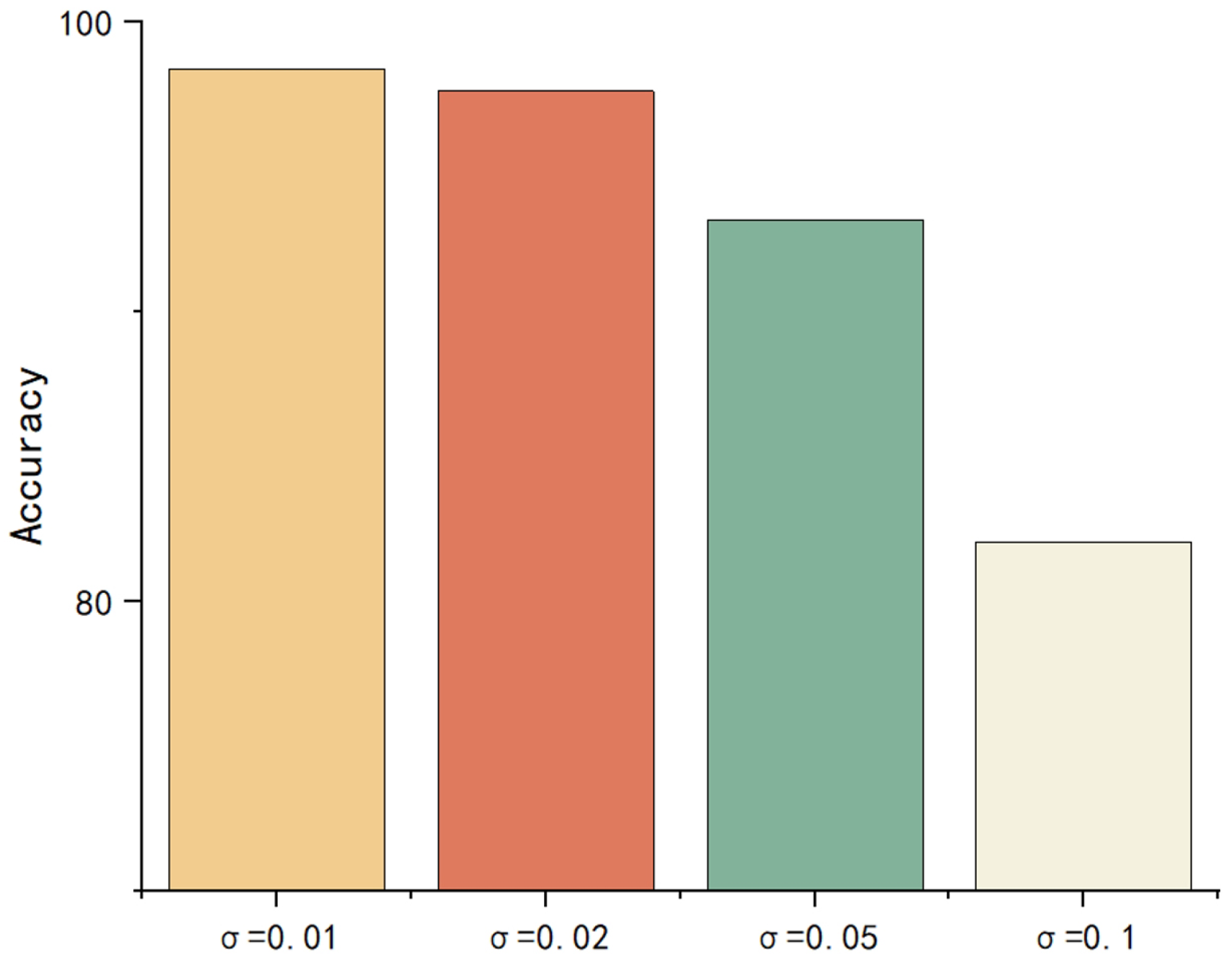
| Aging Class | Composite Characteristics | Number of Samples |
|---|---|---|
| Light Aging (0) | Water-repellent grades HC1-HC3, high elasticity, glossy surface, hardness below 70 Shore A, no visible roughness or chalking (Overall performance close to that of new silicone rubber products) | 225 |
| Medium Aging (1) | Water-repellent grades HC4-HC7 with reduced gloss, hardness 70-80 Shore A, increased roughness or water-repellent grades HC4-HC5 with complete loss of gloss. | 290 |
| Severe Aging (2) | Water repellent grades HC6-HC7 with complete loss of surface gloss, hardness above 80 Shore A and high roughness or significant chalking of the silicone rubber surface. | 225 |
| Functional Group | Wave Number () |
|---|---|
| -OH | 3200–3700 |
| C-H_SV | 2950–2975 |
| C-H_BV | 1200–1270 |
| Si-O-Si | 900–1168 |
| Si-CH3 | 765–870 |
| Models | Hyperparameters |
|---|---|
| KNN | ’n_neighbors’: 1, ’weights’: ’distance’, ’metric’: ’minkowski’, ’leaf_size’: 47, ’algorithm’: ’brute’, ’p’: 4 |
| SVM | ’C’: 10.659, ’kernel’: ’rbf’, ’gamma’: 4.052 |
| RF | ’max_depth’: 10, ’max_features’: 1, ’min_samples_leaf’: 1, ’min_samples_split’: 4, ’n_estimators’: 80 |
| GBDT | ’n_estimators’: 83, ’learning_rate’: 0.096, ’max_depth’: 7, ’min_samples_split’: 15 |
| Class | Precision | Recall | F1 Score | Accuracy |
|---|---|---|---|---|
| Light | 0.96 | 0.92 | 0.96 | 0.9617 |
| Medium | 0.96 | 0.96 | 0.93 | |
| Severe | 0.96 | 0.94 | 0.94 |
| Model | SSE |
|---|---|
| Without RF, SVM | 0.2253 |
| SVM | 0.0538 |
| Ensemble | 0.00148 |
| Removed Items | Accuracy (%) | Performance Changes (%) |
|---|---|---|
| Data Enhancement | 83.10 | −13.07 |
| KNN | 94.81 | −1.36 |
| SVM | 94.01 | −2.16 |
| RF | 93.29 | −2.88 |
| GBDT | 92.64 | −3.53 |
| KNN, SVM | 86.43 | −9.74 |
| KNN, RF | 87.38 | −8.79 |
| KNN, GBDT | 88.62 | −7.55 |
| SVM, RF | 82.74 | −13.43 |
| SVM, GBDT | 84.34 | −11.83 |
| RF, GBDT | 87.94 | −8.23 |
| Weighting analysis | 87.75 | −8.42 |
| Weighting analysis, loss function | 85.88 | −10.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Zhang, C.; Zhou, Z.; Liu, Z.; Deng, Y.; Gu, C.; Zhou, S.; Sun, D.; Liu, H.; Yu, X. An Ensemble Learning Model for Aging Assessment of Silicone Rubber Considering Multifunctional Group Comprehensive Analysis. Polymers 2025, 17, 2988. https://doi.org/10.3390/polym17222988
Zhang K, Zhang C, Zhou Z, Liu Z, Deng Y, Gu C, Zhou S, Sun D, Liu H, Yu X. An Ensemble Learning Model for Aging Assessment of Silicone Rubber Considering Multifunctional Group Comprehensive Analysis. Polymers. 2025; 17(22):2988. https://doi.org/10.3390/polym17222988
Chicago/Turabian StyleZhang, Kun, Chuyan Zhang, Zhenan Zhou, Zheyuan Liu, Yu Deng, Chen Gu, Songsong Zhou, Dongxu Sun, Hongli Liu, and Xinzhe Yu. 2025. "An Ensemble Learning Model for Aging Assessment of Silicone Rubber Considering Multifunctional Group Comprehensive Analysis" Polymers 17, no. 22: 2988. https://doi.org/10.3390/polym17222988
APA StyleZhang, K., Zhang, C., Zhou, Z., Liu, Z., Deng, Y., Gu, C., Zhou, S., Sun, D., Liu, H., & Yu, X. (2025). An Ensemble Learning Model for Aging Assessment of Silicone Rubber Considering Multifunctional Group Comprehensive Analysis. Polymers, 17(22), 2988. https://doi.org/10.3390/polym17222988









