Abstract
Novel high-entropy perovskite oxide powders were synthesized using a sol-gel process. The B-site contained five cations: chromium, cobalt, iron, manganese, and nickel. The B-site cations were present on an equiatomic basis. The A-site cation was lanthanum, with calcium doping. The amount of A-site doping varied from 0 to 30 at%, yielding a composition of La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ. The resulting perovskite powders were pressurelessly sintered in air at 1400 °C for 2 h. Sintered densities were measured, and the grain structure was imaged via scanning electron microscopy to investigate the effect of doping. Samples were cut and polished, and their resistance was measured at varying temperatures in air to obtain the electrical conductivity and the mechanism that governs it. Plots of electrical conductivity as a function of composition and temperature indicate that the increased configurational entropy of the perovskite materials has a demonstrable effect.
1. Introduction
Solid oxide fuel cell (SOFC) components (specifically cathodes and interconnects) have long made use of perovskite oxides [1]. Perovskite oxides (e.g., ABO3) can be modified by substituting B-site atoms and/or doping atoms on the A-site. When these compositional modifications increase the number of cations, the configurational entropy of the resulting oxide is also affected [2,3]. The more cations there are, the higher the configurational entropy. This greater entropy affects the crystallographic properties [4], the electrical properties [5,6,7], the densification behavior [1,6,7,8], and possibly more. Perovskites with cobalt on the B-site, especially LaCoO3, possess relatively high electrical conductivity [9], but the coefficient of thermal expansion is also large, which requires careful selection of other components to match the thermal expansion [10]. Alternative materials, especially those with less (or no) cobalt present, would alleviate this issue and possibly also reduce the cost of relying on larger quantities of cobalt. Of great interest for SOFC applications is increased electrical conductivity at low temperatures for potential alternative perovskites, as this would improve the utility of SOFCs, since they require high temperatures for efficient operation [11]. Thus, it is critical to evaluate the effect on electrical conductivity for high-entropy perovskite oxides.
Calcium doping has been previously investigated for lanthanum-based perovskite oxides [6,7,12,13]. The sintering properties and electrical conductivity were significantly affected, even for oxides with low configurational entropy. The electrical conductivity in lanthanum-based perovskites is known to be governed by small polaron hopping [14]. If the polaron concentration does not depend on temperature, the electrical conductivity has an Arrhenius-type relationship with temperature, as a function of the activation energy (Ec), as shown in Equation (1) [5].
where A is a constant, T is absolute temperature, Ec is the activation energy, and k is Boltzmann’s constant (8.617 × 10−5 eV K−1). Equation (1) has two cases, adiabatic and non-adiabatic. For the former, the exponent s = 1, while for the latter s = . When Equation (1) is plotted on a semi-log basis, e.g., for s = 1, if the data are linear, then (in this case) the conductivity is adiabatic.
The first materials identified with high configurational entropy were alloys [15]. In 2015, it was found that non-metals can also be prepared with high configurational entropy [3,16,17,18]. For both material types, the number of elements present determines the entropy. Equation (2) gives the configurational entropy S in terms of the universal gas constant (R), and the mole fractions (xi for cations, xj for anions) of each element present.
For clarity, Equation (2) may be rewritten for perovskite materials, which have two different crystallographic lattice sites for cations, A and B. Equation (3) shows the configurational entropy for perovskite materials [7].
When the cations in the perovskite are made to vary via doping or substitution, the unit cell of the perovskite will be affected. Different cations have different sizes, which will cause the lattice parameter to change. These ionic radii are not in themselves constant for a given species, as ambient conditions can affect them, as well as the oxidation state of the ion [19,20,21,22,23]. For perovskites with more than four B-site cations, the unit cell will vary from one cell to the next, since the eight lattice positions are insufficient to accommodate uniformity when five or more cations are available. That is, if each of the five cations are present in the unit cell, then at most three of them should be expected to have two atoms present in that cell. Thus, for the five B-site cations of the present perovskite oxide materials, the unit cell should be considered to be non-uniform throughout the bulk of the material. This effect will be compounded by doping on the A-site, as will the configurational entropy. Oxide materials with high configurational entropy have drawn interest for increased electrical conductivity [24] and ionic conductivity [17], improved dielectric constants [16], and decreased thermal conductivity [18].
This article gives data for the electrical conductivity at multiple temperatures of perovskite oxides with six or seven cations total: five B-site and one or two A-site. Calcium doping provided the second A-site cation, while the five B-site cations remained constant in both amount and composition. The amount of calcium doping varied from 0 to 30 at%.
2. Materials and Methods
2.1. Material Preparation
La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ powders [25,26] were prepared via a sol-gel method. The value of x was 0–0.3. Each B-site cation amounted to one-fifth of the total (on an atomic basis). They were chromium, cobalt, iron, manganese, and nickel. These were chosen because each of their end-member compositions is well-known and would allow for comparison with the properties of the high-entropy materials. Table 1 lists the starting materials used for preparing the high-entropy powders. The preparation began with weighing each starting powder, then mixing them with solvents (citric acid, C6H8O7, and ethylene glycol (CH2OH)2) for 4 h at 60 °C, before heating to 90 °C for 3 h. Citric acid (C6H8O7) and ethylene glycol ((CH2OH)2) were added in a 1:2 molar ratio, with the total moles of citric acid matched to the total moles of metal cations to ensure complete chelation and polymeric gel formation. See Table S1 in the Supplementary Material for an example recipe for producing the powder precursor.

Table 1.
Starting materials used for high-entropy perovskite powder synthesis. All materials were Alfa Aesar powders. For La2(CO3)3·XH2O, X was gravimetrically determined by drying at 400 °C for 1 h before each batch of material was weighed.
Once the powders were thoroughly mixed, the solvents were driven off by heating to 450 °C on a hot plate. This resulted in a dark gray-to-black powder, which was calcined in a muffle furnace for 8 h at 950 °C to ensure that no liquids remained. X-ray diffraction (XRD) determined whether a single-phase perovskite had been produced. A diffractometer (Rigaku D/Max-B Diffractometer, Rigaku Corp., Tokyo, Japan) with X-rays of wavelength 1.54056 Å (copper) was used for this characterization.
The synthesized perovskite powders were formed into pellets using a uniaxial pressing method. To facilitate green body formation, two drops of a 5 wt% aqueous polyvinyl alcohol (PVA) binder solution were added per gram of powder. PVA was selected due to its volatility, ensuring that it would decompose and be removed during sintering without leaving residue in the final product. The powder–binder mixture was placed in a stainless-steel die and pressed at 14 MPa for 2 min. The resulting green pellets were subsequently sintered in air at 1400 °C for 2 h.
2.2. Microstructure
Sintered perovskite pellets were polished to a mirror finish (using successively finer polishing compounds from 45 to 1 μm). Polished pellets were thermally etched for 2 h at 1200 °C. A scanning electron microscope (SEM) imaged etched pellets (FEI Quanta, FEG450, Thermo Fisher Scientific, Hillsboro, OR, USA). Sintered density was measured by the Archimedes method with distilled water.
2.3. Electrical Conductivity Measurements
The four-wire method was used to measure the resistance of each sintered perovskite pellet on an LR-700 AC resistance bridge (Linear Research, Inc., San Diego, CA, USA). Each pellet was cut into a rectangular block, and four coats of platinum paint were applied to both ends. The leads from the resistance bridge were connected to the painted ends of each sintered sample. The sample was then heated, and the resistance was measured at each temperature from 300 to 900 °C in 100 °C steps. These measured resistance values, R (in Ω), were used to obtain the electrical conductivity via Equation (4).
where A is the sample’s cross-sectional area, and l is the sample’s length.
The electrical conductivity values as a function of temperature were used with Equation (1) to plot the conductivity versus temperature. This allowed determination of the activation energy for electrical conduction, as well as showing the temperature-dependent behavior of the high-entropy perovskite materials.
3. Results
3.1. Configurational Entropy
Equation (3) was used to calculate the configurational entropy of the six- and seven-cation perovskite oxide materials prepared as described in Section 2.1. Table 2 presents the calculated configurational entropy for the four perovskite oxides prepared for this study.

Table 2.
Configurational entropy for La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ materials as a function of calcium doping. Configurational entropy calculated using Equation (3). R is the universal gas constant.
The results for configurational entropy in Table 2 indicate that all four perovskite oxide compositions prepared for this study satisfy the requirement for high entropy, as they are all greater than 1.5R [27]. As the configurational entropy values were derived directly from Equation (3) using nominal compositional ratios, they represent theoretical estimates and are not subject to experimental error.
3.2. X-Ray Diffraction
XRD patterns for all powders produced according to Section 2.1 are shown in Figure 1 (a larger version of Figure 1 appears in the Supplementary Material as Figure S1). For all four La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ materials (x varying from 0 to 0.3), the peaks present match those expected for perovskite oxides. All patterns were well indexed based on orthorhombic perovskite structures, using reference patterns from the Crystallography Open Database: LaCrO3 (Pnma, space group 62, ID# 1526176) and La0.8Ca0.2CrO3 (Pnma, space group 62, ID# 1531964). The observed reflections align with characteristic peaks for orthorhombic symmetry, including (002), (112), (202), (004), (024), (025), and (116). No secondary phases were detected, indicating that all samples were single-phase within the detection limits of the instrument (approximately 5 wt%). SEM imaging (see Section 3.3) further verified the absence of minor impurity phases not visible in the XRD patterns.
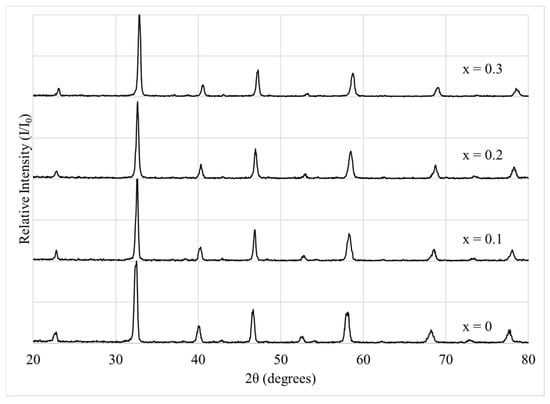
Figure 1.
XRD patterns for La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ. Calcium doping, x, varied from 0 to 0.3. All four patterns possess peaks from perovskite only. No other phases are apparent.
All sintered perovskite pellets remained visually and structurally stable under laboratory ambient conditions (∼22 °C, 40–60% RH) for over six months. While dedicated long-term environmental stability tests were not performed in this study, no degradation was observed during repeated characterization or storage.
3.3. Grain Structure
SEM images of the surfaces of thermally etched, sintered pellets of La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ are shown in Figure 2. Figure 2a, for the x = 0 material, shows significant porosity, both in size and frequency (a larger version of Figure 2a appears in the Supplementary Material as Figure S2). The grains also have irregular shape and varying size. The grain structure stands in stark contrast to that of Figure 2b, the x = 0.1 material (a larger version of Figure 2b appears in the Supplementary Material as Figure S3). The grains are still irregular in shape and vary in size, but they nonetheless possess a rounder character than in Figure 2a. Also, the amount of porosity has greatly decreased. Figure 2c shows that the x = 0.2 material has smaller grains with a more uniform size and round shape than the materials with less calcium content (a larger version of Figure 2c appears in the Supplementary Material as Figure S4). Figure 2d shows the x = 0.3 material, which has the smallest grains, and they have the most uniform size and shape (a larger version of Figure 2d appears in the Supplementary Material as Figure S5). None of the calcium-doped materials (Figure 2b–d) display a second, grain boundary phase. This, combined with improved density (inferred from reduced porosity) and more rounded grains, indicates that any calcium that might have aided sintering as a liquid phase was transient and absorbed back into the perovskite structure rather than precipitating along grain boundaries [10,28]. In addition, the presence of calcium increased the average grain size compared to the calcium-free material. These results were expected based on results of similar perovskite oxides [6,7].

Figure 2.
Grain structure of sintered La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ with varying calcium content: (a) x = 0, average grain size is 1.2 μm. Large pores are present, in relatively significant amount. (b) x = 0.1, average grain size is 1.8 μm. Fewer pores are present than in (a). No grain boundary phase observed. (c) x = 0.2, grains are finer, and pores are both smaller and less frequent than for materials with x = 0 or 0.1. Surface particles are remnants from the polishing operation. No grain boundary phase was observed. Average grain size is 1.5 μm. (d) x = 0.3, particles are fine and round, and pores are insignificant. Some surface particles are observed. These are from polishing. No grain boundary phase was observed. Average grain size was 1.5 μm.
The observed transition from angular grains in the undoped sample to more rounded grains in the calcium-doped compositions can be attributed to the formation of a transient liquid phase during sintering. Calcium is known to form low-melting eutectic mixtures with lanthanum- and B-site-containing oxides, which can temporarily exist as a liquid at the sintering temperature of 1400 °C. This transient liquid phase enhances mass transport through solution–reprecipitation mechanisms and reduces interfacial energy at grain boundaries, resulting in more isotropic grain growth and a rounded morphology. The absence of secondary phases at grain boundaries in the SEM images suggests that this liquid phase was reabsorbed into the perovskite lattice during cooling, consistent with previous reports on Ca-doped LaCrO3 systems [10,28]. The absence of a grain boundary phase was confirmed by EDS mapping (see Figure S6 in the Supplementary Material for EDS maps). The improved relative density and reduced porosity in the doped samples further support the presence of a transient liquid phase that promotes enhanced densification and grain coalescence.
The average grain size for x = 0 was 1.2 μm. Grain size increased from to 1.8 μm for x = 0.1, to 1.5 μm for x = 0.2, and to 1.5 μm for x = 0.3. SEM images show that the angular grains of the undoped material are replaced with more rounded grains (and higher density) in the Ca-doped materials. The imaged grains structures, and the average grain sizes measured from them, indicate that sintering of the calcium-doped samples benefited from a transient liquid phase [10,28]. The absence of a calcium-rich phase at the grain boundaries supports this conclusion, though there are other possible influences of the sintering behavior, such as anion vacancy formation [29], Schottky defect formation [30,31], unit cell distortion due to increased entropy [6], and intermediate phase kinetics [10,32,33,34,35].
3.4. Relative Density
Table 3 gives the relative density of the sintered La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ materials. Measured density was divided by a rule-of-mixtures theoretical density of the various end-member perovskites, using the percentage of each that is present in the novel six- and seven-cation materials. The percentages are notably lower than those obtained for similar perovskite oxides, but containing fewer cations [6,7]. It is possible that six or seven cations in these perovskite oxides distorted the unit cells sufficiently to reduce the density below the rule-of-mixtures estimate.

Table 3.
Relative density (%) for La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ sintered in air at 1400 °C for 2 h. The Archimedes immersion method was used to obtain the density of each sintered pellet and then compared to the theoretical density (obtained via the rule of mixtures of the end-member densities). The Archimedes method has inherent error, perhaps exceeding 1%.
3.5. Electrical Conductivity
Electrical conductivity of sintered La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ from 300–900 °C is plotted on a semi-log basis versus inverse temperature in Figure 3 (a larger version of Figure 3 appears in the Supplementary Material as Figure S7). The undoped material (x = 0) delivered the lowest electrical conductivity of the four sintered samples. All of the calcium-doped materials exhibited a significantly greater electrical conductivity compared to the calcium-free material. The variation among the doped materials was less significant. Table 4 gives the slope of linear fits to the data in Figure 3, along with the R2 value of each fit. The slopes of the three doped samples are all similar to one another, as were the magnitudes of their conductivity (as shown in Figure 3). For these high-entropy perovskite oxides, even minimal calcium doping increases the electrical conductivity, though further research is required to determine the underlying and as-yet unknown mechanism for this improvement. This nearly uniform behavior is distinct from similar materials but with fewer cations, and is possibly another effect of the increased configurational entropy of the present materials. Note that the electrical conductivity could be affected by the density [2,8,33,34] of the sintered pellets (Table 3), as the undoped material had a markedly lower density.
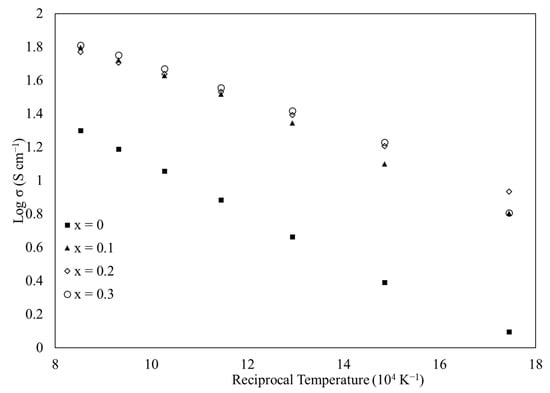
Figure 3.
Semi-log plot of electrical conductivity, σ, versus reciprocal temperature (104 K−1) for sintered La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ.

Table 4.
Slopes of the electrical conductivity versus temperature data from Figure 3. The R2 values indicate that the linear fits were of high quality.
Table 5 compares the electrical conductivity of the present high-entropy perovskite cations to the end-member constituents at 800 °C, where available (the LaCrO3 conductivity is for 700 °C). For all values of x > 0, the electrical conductivity is more than three times the x = 0 value. The variation between the values for the doped materials is small, with the x = 0.2 material having the lowest conductivity of the three at 800 °C. Note that the measured resistance values differed by more than the 0.1% tolerance of the LR-700, and these values are thus considered accurate.

Table 5.
Electrical conductivity values (in S cm−1) for La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ at 800 °C, compared to monolithic perovskites.
3.6. Electrical Conduction Activation Energy
Figure 4 is a semi-log plot of the adiabatic case (s = 1) of Equation (1) (a larger version of Figure 4 appears in the Supplementary Material as Figure S8). Linear fits were applied to the data to obtain the slope. These results are shown in Table 6, along with the R2 value of the linear fits. Because the R2 values were so close to 1 (which would indicate a perfect fit), the fits indicate that the conduction obeys the adiabatic case. Thus, the non-adiabatic case (s = ) was not plotted. In the same way that the 800 °C conductivity varied the calcium-doped materials, the activation energy of doped materials also fluctuated. The x = 0.2 material activation energy has a lower magnitude than the x = 0.1 and 0.3 materials. This is likely due to the high configurational entropy, since the measured resistance values from which these activation energies were derived varied by more than the 0.1% tolerance of the LR-700 AC resistance bridge. All three doped materials have lower activation energies compared to the undoped material, which correlates with the increased electrical conductivity at lower temperatures. This reduced barrier to conduction stands in contrast to results for similar medium- and high-entropy perovskite oxides [7]. Those materials possessed a greater activation energy when doped with calcium than when undoped. The behavior of the current materials may indicate that the effectively random arrangement of cations on the B-site, coupled with calcium doping, distorts the unit cell in such a way that electron flow is not impeded but encouraged. The adiabatic nature of the electrical conductivity supports the small polaron hopping model [5].
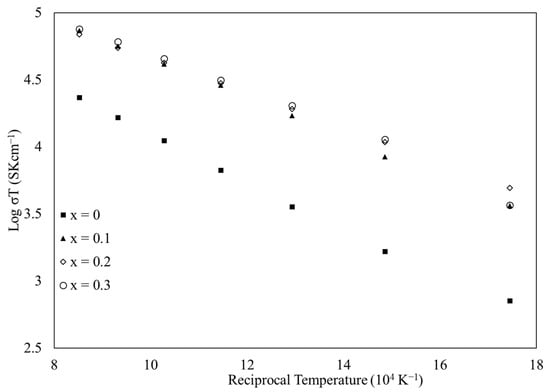
Figure 4.
Semi-log plot of σT versus reciprocal temperature (104 K−1) for sintered La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ.

Table 6.
Slopes and activation energies (in eV) for electrical conduction of sintered La1−xCax(Co0.25Cr0.25Fe0.25Ni0.25)O3−δ, determined from Figure 4.
It must be noted that the electrical conductivity of LaCoO3 remains the highest of such materials. While the high-entropy perovskites studied in this research exhibit lower conductivity, they should also be free of the large coefficient of thermal expansion that plagues LaCoO3. The thermal expansion behavior of the high-entropy oxides of this research have not been evaluated to confirm this, but reduced cobalt content should correlate with less thermal expansion.
3.7. Effect of Configurational Entropy
Decreased activation energies (Table 6) for calcium-doped materials indicate that electrical conductivity is increased for the seven-cation materials (x > 0) compared to the six-cation material (x = 0). However, the activation energy does not decrease linearly as calcium content increases, as seen by the greater activation energy when x = 0.2 compared to x = 0.1 and 0.3. For five- and six-cation materials with four B-site cations, activation energies increased with calcium doping, though the values also were not linear with calcium content. Increased calcium doping may in some way stabilize the unit cell distortion caused by the five B-site cations. When only lanthanum is present on the A-site, the cell may be unable to distort as well as when the calcium replaces some of the lanthanum. Because the calcium ions will have a different size, the unit cell may be able to distort more readily to accommodate the randomness of the B-site cations in that particular cell. Thus, even though the configurational entropy is higher, the unit cell may be more compliant, leading to decreased activation energy. The arrangement of cations in these high-entropy materials is yet to be determined. This would require high-quality crystallographic data, such as from synchrotron X-ray diffraction analyzed with Rietveld refinement.
While the electrical conductivity for the six- and seven-cation materials is greater than that previously reported for similar perovskite oxides with four B-site cations [7], the activation energy for the current materials is also greater. This is likely due to the increased configurational entropy of the six- and seven-cation perovskites. That is, the inconsistent arrangement of species inhibits electrical conduction to a greater degree as the entropy is increased. Again, this may correlate with unit cell distortion, which cannot be verified at this time. Furthermore, the high-entropy perovskites were not fully dense (see Table 3). Since higher porosity reduces electrical conductivity, fully dense high-entropy perovskites should have higher conductivity, though it is not expected to rival that of LaCoO3.
4. Conclusions
Novel high-entropy perovskite oxide powders were synthesized and sintered. The B-site contained five substituted cations in equal amounts: chromium, cobalt, iron, manganese, and nickel. Lanthanum was the A-site cation, doped with calcium from 0 to 30 at%, yielding La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ. The density of the sintered perovskites was measured and seen to increase significantly with calcium doping. The grain structure observed with SEM showed decreased pore size and frequency, and smaller, rounder grains for the compositions doped with calcium. Electrical conductivity was measured up to 900 °C, with the calcium-doped materials exhibiting significantly higher conductivity than the undoped material. The mechanism that governs this conduction was found to be adiabatic small polaron hopping. Increased configurational entropy of the perovskite materials has a demonstrable effect on electrical conductivity, with calcium doping delivering greater conductivity. The effect is inconsistent and does not vary linearly with calcium content. This may be due to crystal lattice distortion.
To elucidate the role of individual cations and defect interactions in the conduction mechanism, advanced techniques such as Seebeck measurements and variable oxygen partial pressure conductivity measurements could be highly informative and are recommended for future investigation, especially as needed to identify the mechanism of improved electrical conduction for calcium-doped La1−xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3−δ materials.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15080686/s1, Figure S1: XRD patterns for La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ. Calcium doping, x, varied from 0 to 0.3; Figure S2: Grain structure of undoped La(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ. Large pores are present, in relatively significant amount. Average grain size was 1.2 μm; Figure S3: Sintered microstructure for Ca-doped (x = 0.1) La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ. Fewer pores are present than for the material with x = 0. No grain boundary phase was observed. Average grain size was 1.8 μm; Figure S4: Sintered microstructure for Ca-doped (x = 0.2) La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ. Grains are finer and pores are smaller and less frequent than for materials with x = 0 or 0.1. Surface particles are remnants from the polishing operation. No grain boundary phase was observed. Average grain size was 1.5 μm; Figure S5: Sintered microstructure for Ca-doped (x = 0.3) La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ. Particles are fine and round, and pores are insignificant. Surface particles are remnants from the polishing operation. No grain boundary phase was observed. Average grain size was 1.5 μm; Figure S6: EDS mapping of La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ materials: (a) x = 0; (b) x = 0.1; (c) x = 0.2; (d) x = 0.3; Figure S7: Semi-log plot of electrical conductivity, σ, versus reciprocal temperature (10,000 K-1) for sintered La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ; Figure S8: Semi-log plot of σT versus reciprocal temperature (10,000 K-1) for sintered La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ; Table S1: Precursor recipe to produce 10 g of La1-xCax(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3-δ.
Author Contributions
Conceptualization, S.R.G. and R.K.; resources, R.K.; data curation, S.R.G. and G.S.; writing—original draft preparation, G.S.; writing—review and editing, G.S., S.R.G. and R.K.; visualization, G.S. and S.R.G.; supervision, R.K.; project administration, R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors acknowledge equipment and facility support from the School of Mechanical, Aerospace, and Materials Engineering and the IMAGE facility at SIUC.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Anderson, H.U. Fabrication and Property Control of LaCrO3 Based Oxides. In Processing of Crystalline Ceramics; Palmour, H., Davis, R.F., Hare, T.M., Eds.; Springer: Boston, MA, USA, 1978. [Google Scholar]
- Kolisetty, A.; Fu, Z.; Koc, R. Development of La(CrCoFeNi)O3 System Perovskites as Interconnect and Cathode Materials for Solid Oxide Fuel Cells. Ceram. Int. 2017, 43, 7647–7652. [Google Scholar] [CrossRef]
- Rost, C.; Sachet, E.; Borman, T.; Moballegh, A.; Dickey, E.; Hou, D.; Jones, J.; Curtarolo, S.; Maria, J. Entropy-Stabilized Oxides. Nat. Commun. 2015, 6, 8485. [Google Scholar] [CrossRef]
- Anand, G.; Wynn, A.P.; Handley, C.M.; Freeman, C.L. Phase stability and distortion in high-entropy oxides. Acta Mater. 2018, 146, 119–125. [Google Scholar] [CrossRef]
- Sehlin, S.; Anderson, H.; Koc, R.; Sparlin, D. Evidence for 2+-4+ Pairing in the (La,Ca)(Cr,Co)O3 Series. Ceram. Trans. 1991, 24, 249–256. [Google Scholar]
- Gajjala, S.R.; Swift, G.; Koc, R. Sintering and Electrical Conductivity of Calcium-Doped Three-Cation Perovskite Materials. J. Mater. Sci. Mater. Eng. 2024, 19, 3. [Google Scholar] [CrossRef]
- Swift, G.; Gajjala, S.R.; Koc, R. Sintering and Electrical Conductivity of Medium-and High-Entropy Calcium-Doped Four B-Site Cation Perovskite Materials. Crystals 2025, 15, 524. [Google Scholar] [CrossRef]
- Koc, R.; Anderson, H. Investigation of Strontium-doped La(Cr,Mn)O3 for Solid Oxide Fuel Cells. J. Mater. Sci. 1992, 27, 5837–5843. [Google Scholar] [CrossRef]
- Dudnikov, V.A.; Orlov, Y.S.; Solovyov, L.A.; Vereshchagin, S.N.; Ustyuzhanin, Y.N.; Zharkov, S.M.; Zeer, G.M.; Borus, A.A.; Bondarev, V.S.; Ovchinnikov, S.G. Crystal Structure and Thermoelectric Properties of Mechanically Activated LaCoO3. J. Taiwan Inst. Chem. Eng. 2024, 162, 105560. [Google Scholar] [CrossRef]
- Chick, L.A.; Liu, J.; Stevenson, J.W.; Armstrong, T.R.; McCready, D.E.; Maupin, G.D.; Coffey, G.W.; Coyle, C.A. Phase Transitions and Transient Liquid-Phase Sintering in Calcium-Substituted Lanthanum Chromite. J. Am. Ceram. Soc. 1997, 80, 2109–2120. [Google Scholar] [CrossRef]
- Talukdar, A.; Chakrovorty, A.; Sarmah, P.; Paramasivam, P.; Kumar, V.; Yadav, S.K.; Manickkam, S.; Ahmed, M. A Review on Solid Oxide Fuel Cell Technology: An Efficient Energy Conversion System. Int. J. Energy Res. 2024, 2024, 6443247. [Google Scholar] [CrossRef]
- Sun, X.; Pei, Z.; Guo, X.; Ye, X.; Wang, L.; Zhang, Y.; Dong, S. Impact of Ca Ions Substitution at A-site on LaCoO3 Perovskite Energy Applications. Mater. Sci. Eng. B. 2025, 319, 118343. [Google Scholar] [CrossRef]
- Bai, F.; Schulwitz, J.; Priamushko, T.; Hagemann, U.; Kostka, A.; Heidelmann, M.; Cherevko, S.; Muhler, M.; Li, T. Correlating Atomic-Scale Structural and Compositional Details of Ca-doped LaCoO3 Perovskite Nanoparticles with Activity and Stability Towards the Oxygen Evolution Reaction. J. Catal. 2024, 438, 115697. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, P.-Y.; Wang, F.; Wuliji, H.; Zhu, H.; Wang, J. Enhancing Strategy of the Small-Polaron Conductivity in LaCrO3: First-Principles Calculations and Experimental Validation. ACS Appl. Mater. Interfaces 2024, 16, 15073–15083. [Google Scholar] [CrossRef] [PubMed]
- Yeh, J.; Chen, S.; Lin, S.; Gan, J.; Chin, T.; Shun, T.; Tsau, C.; Chang, S. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Bérardan, D.; Franger, S.; Dragoe, D.; Meena, A.; Dragoe, N. Colossal Dielectric Constant in High Entropy Oxides. Phys. Status Solidi Rapid Res. Lett. 2016, 10, 328–333. [Google Scholar] [CrossRef]
- Bérardan, D.; Franger, S.; Meena, A.; Dragoe, N. Room Temperature Lithium Superionic Conductivity in High Entropy Oxides. J. Mater. Chem. A 2016, 4, 9536–9541. [Google Scholar] [CrossRef]
- Zhao, Z.; Xiang, H.; Dai, F.; Peng, Z.; Zhou, Y. (La0.2Ce0.2Nd0.2Sm0.2Eu0.2)2Zr2O7: A Novel High-Entropy Ceramic with Low Thermal Conductivity and Sluggish Grain Growth Rate. J. Mater. Sci. Technol. 2019, 35, 2647–2651. [Google Scholar] [CrossRef]
- Takaba, H.; Kimura, S.; Alam, M. Crystal and Electronic Structures of Substituted Halide Perovskites Based on Density Functional Calculation and Molecular Dynamics. Chem. Phys. 2017, 485, 22–28. [Google Scholar] [CrossRef]
- Lufaso, M.; Woodward, P. Prediction of the Crystal Structures of Perovskites Using the Software Program SPuDS. Acta Cryst. B 2001, 57, 725–738. [Google Scholar] [CrossRef]
- Jarin, S.; Yuan, Y.; Zhang, M.; Hu, M.; Rana, M.; Wang, S.; Knibbe, R. Predicting the Crystal Structure and Lattice Parameters of the Perovskite Materials via Different Machine Learning Models Based on Basic Atom Properties. Crystals 2022, 12, 1570–1590. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiaojie, X. Modeling of Lattice Parameters of Cubic Perovskite Oxides and Halides. Heliyon 2021, 7, e07601. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Y.; Liang, Z.; Ning, H.; Fu, X.; Xu, Z.; Qiu, T.; Xu, W.; Yao, R.; Peng, J. High-Entropy Oxides: Advanced Research on Electrical Properties. Coatings 2021, 11, 628–644. [Google Scholar] [CrossRef]
- Pechini, M.P. Method of Preparing Lead and Alkaline Earth Titanates and Niobates and Coating Method Using the Same to Form a Capacitor. U.S. Patent 3,330,697, 11 July 1967. [Google Scholar]
- Gajjala, S.R.; Fu, Z.; Koc, R. Investigation of (La1-X,CaX)(Ni0.25Fe0.25Cr0.25Co0.25)O3 for Solid Oxide Fuel Cells Cathode Materials. Ceram. Eng. Sci. Proc. 2019, 39, 85–97. [Google Scholar]
- Anandkumar, M.; Trofimov, E. Synthesis, Properties, and Applications of High-Entropy Oxide Ceramics: Current Progress and Future Perspectives. J. Alloy. Compd. 2023, 960, 170690. [Google Scholar] [CrossRef]
- Kiebach, R.; Pirou, S.; Aguilera, L.M. A Review on Dual-Phase Oxygen Transport membranes: From Fundamentals to Commercial Deployment. J. Mater. Chem. A 2022, 10, 2152–2195. [Google Scholar] [CrossRef]
- Li, X.; Hao, S.; Chen, Z.; Huang, T.; Fu, S.; Zhao, F.; You, K.; Luo, H. Roles of the A-Site Ca Dopant in Modifying Surface Properties of a Co-Based Perovskite Catalyst for Selective Oxidation of Cyclohexane. Am. Chem. Soc. 2024, 63, 6087–6099. [Google Scholar] [CrossRef]
- Ulyanova, A.V.; Senina, M.O.; Lemeshev, D.O. Dense ceramics based on solid solutions. J. Phys. Conf. Ser. 2021, 1942, 012049. [Google Scholar] [CrossRef]
- Halabi, R.; Simotko, S.; Tsur, Y. The influence of point defects on the sintering of magnesium oxide. J. Am. Ceram. Soc. 2024, 107, 8023–8035. [Google Scholar] [CrossRef]
- Koc, R.; Anderson, H.U. Liquid Phase Sintering of LaCrO3. J. Eur. Ceram. Soc. 1992, 9, 285–292. [Google Scholar] [CrossRef]
- Yokokawa, H.; Sakai, N.; Kawada, T.; Dokiya, M. Thermodynamic Stabilities of Perovskite Oxides for Electrodes and Other Electrochemical Materials. Solid State Ion. 1992, 52, 43–56. [Google Scholar] [CrossRef]
- Mori, M.; Hiei, Y.; Sammes, N.M. Sintering Behavior of Ca- or Sr-Doped LaCrO3 Perovskites Including Second Phase of AECrO4 (AE=Sr, Ca) in Air. Solid State Ion. 2000, 135, 743–748. [Google Scholar] [CrossRef]
- German, R.M.; Suri, P.; Park, S.J. Review: Liquid Phase Sintering. J. Mater. Sci. 2009, 44, 1–39. [Google Scholar] [CrossRef]
- Misusaki, J.; Yoshiro, M.; Yamauchi, S.; Fueki, K. Electrical Conductivity and Seebeck Coefficient of Nonstoichiometric La1-xSrxCoO3-δ. J. Electrochem. Soc. 1989, 136, 2082–2088. [Google Scholar] [CrossRef]
- Kharton, V.; Yaremchenko, A.; Naumovich, E. Research on the Electrochemistry of Oxygen Ion Conductors in the Former Soviet Union. II. Perovskite-Related Oxides. J. Solid State Electrochem. 1999, 3, 303–326. [Google Scholar] [CrossRef]
- Chiba, R.; Yoshimura, F.; Sakurai, Y. An Investigation of LaNi1−xFexO3 as a Cathode Material for Solid Oxide Fuel Cells. Solid State Ion. 1999, 124, 281–288. [Google Scholar] [CrossRef]
- He, Q.; Zhang, X.; Hao, H.; Hu, X. High-Temperature Electronic Transport Properties of La1−xCaxMnO3+δ (0.0≤x≤1.0). Phys. B 2008, 403, 2867–2871. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).