On Σ-Classes in E⁸. I. The Neighborhood of E₈

Abstract

In the cone of positive quadratic forms ${\mathcal{C}}^{8\times 8}$, it is shown that there exists in the neighborhood the quadratic form ${\mathsf{Q}}_{E_8}$ , a large cluster of non-equivalent S0-subcones of positive volume.

1. Introduction

Quadratic forms, translation lattices, and parallelohedra play a predominant role not only in the geometry of numbers but also in crystallography, where the lattice-like arrangement of atomic building blocks is a fundamental property of regular crystals. In crystallography, the discovery of quasicrystals, the structure of which can be viewed as projected from higher dimensional translation lattices, has greatly stimulated the investigation of lattices and parallelohedra in arbitrary dimensions. A reduction in quadratic forms and classification of parallelohedra requires, with increasing complexity, a partition of the cone of positive-definite quadratic forms.

In higher dimensions, quadratic forms corresponding to special lattices of densest packings of balls were widely investigated. In a more general approach, the collective of all lattices in the open cone ${\mathcal{C}}^{d\times d+}$ of positive-definite quadratic forms is considered by studying its subdivision into $\Phi$- and $\Sigma$-subcones.

In order to find ${\Sigma }_0$-classes in ${\mathbf{C}}^{8\times 8}$ it is worth looking at the parallelohedra of the maximal finite irreducible subgroups of $G{L}_8\left(ZZ\right)$ given by Plesken and Pohst [1]. In Table 1, the subgroups $F_1$ to $F_{26}$ are listed, each given by its order, its combinatorial type and its number of zones, whereof the number of closed zones is stated within brackets, as well as its number of belts. It becomes evident that many of these parallelohedra are minimal, having only open zones, whereof five types viz.: $F_5$, $F_8$, $F_{15}$, $F_{22}$, and $F_{26}$ are as much minimal as maximal. Of those, the exceptional lattice $F_5\equiv E_8$ is well-known and was described in detail by Conway and Sloane [2]. The lattice $E_8$ takes a particular position as it is the first case of a non-trivial self-dual lattice in $E^d$, $d>1$. It also occurs in classifying Lie-algebras.

Table 1. The parallelohedra of the maximal finite irreducible subgroups of $G{L}_8\left(ZZ\right)$.

No.	Group	Order	Comb. Type	Zones	Belts
$F_1$	$B_8$	$2^{8}8!$	16.256	8(8)	$4_{28}$
$F_2$	$D_8$	$2^{8}8!$	112.272	136(0)	$6_{224}$
$F_3$		$2·{1152}^2$	48.576	24(0)	$4_{114}{6}_{32}$
$F_4$	$D_8^{*}$	$2^{8}8!$	272.1120	56(0)	$4_{28}{6}_{512}$
$F_5$	$E_8$	$2^{14}{3}^5{5}^{2}7$	240.19449	8760(0)	$6_{1120}$
$F_6$		$3!·1152$	264.5304	36(0)	$4_{108}{6}_{972}$
$F_7$		${12}^{4}4!$	24.1296	12(12)	$4_{54}{6}_4$
$F_8$		$2·6^{4}4!$	348.3588	93(0)	$6_{1386}$
$F_9$		$2·{144}^2$	60.10404	18(18)	$4_2{256}_{48}$
$F_{10}$	$A_8$	$2·9!$	72.510	9(9)	$6_{84}$
$F_{11}$		$2·6^{4}4!$	186.5940	174(0)	$4_{54}{6}_{544}$
$F_{12}$		$2·6^{3}3!$	402.94254	1497(0)	$6_{2259}$
$F_{13}$	$A_8^{*}$	$2·9!$	510.362880	36(36)	$6_{3025}$
$F_{14}$		$2·{240}^2$	40.900	10(10)	$4_{100}{6}_{20}$
$F_{15}$		$4·{60}^2$	360.3840	180(0)	$6_{1700}$
$F_{16}$		$2·{240}^2$	60.14400	20(20)	$4_{225}{6}_{50}$
$F_{17}$		${(2·5!)}^2$	290.43310	1195(0)	$6_{1370}$
$F_{18}$		$2·3!·5!$	390.106200	450(0)	$6_{2160}$
$F_{19}$		$2·3!·5!$	180.6510	15(15)	$4_{90}{6}_{400}$
$F_{20}$		1152	296.13696	580(0)	$4_{66}{6}_{1168}$
$F_{21}$		1152	200.2992	304(0)	$4_{48}{6}_{564}$
$F_{22}$		$3·1152$	456.28632	264(0)	$6_{2260}$
$F_{23}$		672	398.90384	297(0)	$6_{2192}$
$F_{24}$		673	426.37638	21(21)	$4_{24}{6}_{1428}$
$F_{25}$		672	308.8028	1011(0)	$4_{21}{6}_{1386}$
$F_{26}$		24	398.127848	1036(0)	$6_{2227}$

In Section 2, the necessary definitions and notations are given. In Section 3, the parallelohedron belonging to the lattice $E_8$ is described, and its symmetry group is determined. In the following Section 4, the neighborhood of the lattice $E_8$ is investigated in order to find generic parallelohedra which are as much minimal as maximal. As a result, it is proven that in the neighborhood of $E_8$ there exists large clusters ${\mathsf{C}}_{E_8}$ of non-equivalent ${\Sigma }_0$-subcones which are as much minimal as maximal.

2. Basic Notations

The notations and methods developed in previous papers [3,4,5,6,7] will be applied. For convenience, the main definitions and tools will be summarized in this preliminary Section.

In Euclidean space $E^d$, a translation lattice is given by

$${\Lambda }^d:=\{\mathbf{t}\mid \mathbf{t}=t_1{\mathbf{a}}_1+\cdots +t_d{\mathbf{a}}_d,t_i\in ZZ\},$$

(1)

with lattice basis $\mathsf{B}$, ${\mathbf{a}}_1,\cdots ,{\mathbf{a}}_d$, and origin O.

The Gram matrix $\mathsf{Q}$ of ${\Lambda }^d$ is defined by the inner products

$$\mathsf{Q}:=\{q_{ij}\mid q_{ij}={\mathbf{a}}_i{\mathbf{a}}_j=|{\mathbf{a}}_i\left|\right|{\mathbf{a}}_j|cos{\alpha }_{ij},i,j=1,\cdots ,d\}.$$

(2)

Vice versa, $\mathsf{Q}$ determines ${\Lambda }^d$ up to an isometry in $E^d$.

The dual basis is given by

$${\mathbf{a}}_1^{*},\cdots ,{\mathbf{a}}_d^{*},$$

(3)

where ${\mathbf{a}}_i^{*}$, $i=1,\cdots ,d$, is the outer product of {${\mathbf{a}}_1,\cdots ,{\mathbf{a}}_d\}\backslash \left\{{\mathbf{a}}_i\right\}$. It holds that ${\mathbf{a}}_i{\mathbf{a}}_j^{*}={\delta }_{ij}$ and ${\mathsf{Q}}^{*}={\mathsf{Q}}^{-1}$.

The components of a lattice vector $\mathbf{t}$ depend on the choice of the lattice basis $\mathsf{B}$. For any $\mathsf{A}\in G{L}_d\left(ZZ\right)$, ${\mathsf{B}}^{\prime }:=\mathsf{A}\mathsf{B}$ is an equivalent lattice basis, and ${\mathsf{Q}}^{\prime }:=\mathsf{A}\mathsf{Q}{\mathsf{A}}^t$ is called arithmetically equivalent to $\mathsf{Q}$.

Within an infinite class of arithmetically equivalent Gram matrices, a Gram matrix ${\mathsf{Q}}_{opt}$ is referred to as being optimal if it minimizes the magnitudes of the components of all lattice vectors within a given ball of finite radius $\rho$. In [8], the concept of an optimal basis was introduced. It simultaneously reduces the Gram matrices $\mathsf{Q}$ and ${\mathsf{Q}}^{-1}$ such that ${\Delta }_{opt}:=tr{({\mathsf{Q}}_{opt}-{\mu }^2{\mathsf{Q}}_{opt}^{-1})}^2$ is minimal, where $\mu =\sqrt[d]{det\left(\mathsf{Q}\right)}$. We obtain

$${\Delta }_{opt}=\underset{\mathsf{A}\in G{L}_d\left(ZZ\right)}{min}tr{(\mathsf{A}\mathsf{Q}{\mathsf{A}}^t-{\mu }^2{\mathsf{A}}^{\circ }{\mathsf{Q}}^{-1}{\mathsf{A}}^{-1})}^2.$$

(4)

In low dimensions, reasonable results are obtained by successively applying only transpositions ${\mathbf{a}}_i^{\prime }={\mathbf{a}}_i\pm {\mathbf{a}}_j$, $1\le i\ne j\le d$, for $\mathsf{A}$. Note that for $d>3$, in general, $\Delta \left(\mathsf{A}\right)$ is not a steadily decreasing function of transpositions.

For a translation lattice ${\Lambda }^d$ having Gram matrix $\mathsf{Q}$, its Dirichlet parallelohedron $\mathsf{P}\left(\mathsf{Q}\right)$ at the origin O is obtained by intersections of closed half-spaces,

$${\mathsf{H}}_{\mathbf{t}}:=\{\mathbf{x}\in E^d\mid \mathbf{x}\mathbf{t}\le \frac{1}{2}{\left|\mathbf{t}\right|}^2\},$$

and thus,

$$\mathsf{P}\left(\mathsf{Q}\right):=\bigcap _{\forall \mathbf{t}\in {\Lambda }^d\backslash \left\{O\right\}}{\mathsf{H}}_{\mathbf{t}}.$$

(5)

It is sufficient to consider lattice vectors $\mathbf{t}$ only within a ball of radius 2R with center in O, where R is the radius of the largest interstitial ball that can be embedded into ${\Lambda }^d$.

A parallelohedron $\mathsf{P}$ in its face-to-face tiling of $E^d$ is denoted as being primitive or generic if in every vertex of $\mathsf{P}$ exactly $d+1$ adjacent parallelohedra meet. A primitve parallelohedron in $E^d$ has the maximal number $2(2^d-1)$ of facets. Voronoï [9] proved that every primitive parallelohedron $\mathsf{P}$ is affinely equivalent to a Dirichlet parallelohedron.

A polytope $\mathsf{P}$ consists of k-faces, $0\le k\le d$. The 0-faces are the vertices, the 1-faces are the edges, the $(d-2)$-faces are called ridges, and the $(d-1)$-faces are called facets. The number $N_{d-1}$ of facets and the number $N_0$ of vertices define the short symbol $N_{d-1}.N_0$ for $\mathsf{P}$. Among the k-faces of a polytope $\mathsf{P}$ exists a partial ordering with respect to the inclusion operation “⊂” which defines their hierarchical structure. The k-faces of $\mathsf{P}$ together with the empty set $\{\varnothing \}$ determine the face lattice $\mathcal{L}\left(\mathsf{P}\right)$. Polytopes that have isomorphic face lattices are denoted as being combinatorially equivalent.

Let ${\mathsf{P}}_0$ be the parallelohedron at the origin of ${\Lambda }^d$. If the lattice vector ${\mathbf{t}}_i$ carries ${\mathsf{P}}_0$ onto ${\mathsf{P}}_i$ such that ${\mathsf{F}}_i^{d-1}={\mathsf{P}}_0\cap {\mathsf{P}}_i$ is a common facet, then ${\mathbf{t}}_i$ is called a facet vector. The set of facet vectors is denoted by $\mathcal{F}$.

The face lattice $\mathcal{L}\left(\mathsf{P}\right)$ is used in order to determine the unified polytope scheme and the automorphism group $\mathcal{A}\left(\mathsf{P}\right)$.

The face lattice $\mathcal{L}\left(\mathsf{P}\right)$ guarantees the existence of subseries of mutually subordinated k-faces

$$\varnothing \subset {\mathsf{F}}_{i_0}^0\subset {\mathsf{F}}_{i_1}^1\subset {\mathsf{F}}_{i_2}^2\subset \cdots \subset {\mathsf{F}}_{i_{d-1}}^{d-1}\subset {\mathsf{F}}_{i_d}^d\equiv \mathsf{P},$$

(6)

denoted as d-flag. Each k-face ${\mathsf{F}}_{i_k}^k$, $0\le k\le d$, corresponds to a k-dimensional polytope ${\mathsf{P}}^{\prime }$. Its face lattice $\mathcal{L}\left({\mathsf{P}}^{\prime }\right)$ is given by the quotient $({\mathsf{F}}_{i_k}^k,\varnothing )$ of $\mathcal{L}\left(\mathsf{P}\right)$. (The quotient corresponds to the face lattice of the polytope ${\mathsf{F}}_{i_k}^k\equiv {\mathsf{P}}^{\prime }$.) Therefore, it is possible to number all k-faces of $\mathsf{P}$ in a systematic way, beginning at the bottom of the d-flag as shown in [10]. This is a highly time-consuming process. The polytope scheme is obtained by writing down for each facet ${\mathsf{F}}_{i_{d-1}}^{d-1}$, $i_{d-1}=1,2,\cdots ,N_{d-1}$, the numbers in increasing order of their subordinated vertices ${\mathsf{F}}_{i_0}^0$, $i_0\in \{1,2,\cdots ,N_0\}$. The scheme depends on the chosen d-flag. For all possible d-flags the corresponding scheme is determined and lexicographically ordered. In this lexicon, the first scheme is denoted as unified polytope scheme, There exists an isomorphism between the unified polytope scheme and the combinatorial type of the polytope $\mathsf{P}$.

The number of identical unified schemes corresponds to the order of the automorphism group $\mathcal{A}\left(\mathsf{P}\right)$. Each scheme in the class of identical unified schemes corresponds to a permutation $\mathsf{S}$ of the basis vectors. There exists an isomorphism between the class of identical unified schemes and the automorphisms of $\mathcal{A}\left(\mathsf{P}\right)$. Let $\mathsf{V}$ be a $(d\times d)$ matrix with columns given by the basis vectors (Note that this is only possible for irreducible groups.) Applying the permutation $\mathsf{S}$ to the basis vectors gives

$${\mathsf{V}}^{\prime }=\mathsf{S}\mathsf{V}.$$

(7)

(In the case that the group is reducible the process has to be repeated for each invariant subspace).

Zones and belts of a parallelohedron $\mathsf{P}$ are crucial for further operations on parallelohedra.

Definition 1. 

A belt B of a parallelohedron $\mathsf{P}$ is a complete set of parallel ridges of $\mathsf{P}$.

A belt contains either four or six ridges and thus four or six facets. Primitive parallelohedra contain 6-fold belts only which are determined by a triplet of facet vectors ${\mathbf{f}}_i,{\mathbf{f}}_j{\mathbf{f}}_k$ that fulfills the belt conditions,

$$\begin{array}{cc}\hfill \left(i\right)& {\mathbf{f}}_i,{\mathbf{f}}_j,{\mathbf{f}}_k\in \mathcal{F}\left(\mathsf{P}\right),\hfill \\ \hfill \left(ii\right)& {\mathbf{f}}_i+{\mathbf{f}}_j+{\mathbf{f}}_k=0,\hfill \\ \hfill \left(iii\right)& {\mathsf{F}}_i^{d-1}\cap {\mathsf{F}}_j^{d-1}={\mathsf{F}}_l^{d-2},{\mathsf{F}}_j^{d-1}\cap {\mathsf{F}}_k^{d-1}={\mathsf{F}}_m^{d-2},{\mathsf{F}}_k^{d-1}\cap {\mathsf{F}}_i^{d-1}={\mathsf{F}}_n^{d-2}.\hfill \end{array}$$

(8)

Definition 2. 

A zone Z of a parallelohedron $\mathsf{P}$ is a complete set of parallel edges of $\mathsf{P}$.

The edges of a zone Z are parallel to a dual zone vector ${\mathbf{z}}^{*}$. Referred to the dual basis (3), ${\mathbf{z}}^{*}$ has integer components,

$${\mathbf{z}}^{*}=z_1{\mathbf{a}}_1^{*}+\cdots +z_d{\mathbf{a}}_d^{*},z_i\in ZZ,gcd(z_1,\cdots ,z_d)=1.$$

(9)

With respect to any zone vector ${\mathbf{z}}^{*}$ the lattice vectors $\mathbf{t}$ may be classified into layers

$${\mathsf{L}}_i\left({\mathbf{z}}^{*}\right):=\{\mathbf{t}\in {\Lambda }^d\mid \mathbf{t}{\mathbf{z}}^{*}=i,i\in ZZ\}.$$

(10)

A zone Z is referred to as being closed if every 2-face of $\mathsf{P}$ contains either two edges of Z or else none. Otherwise, Z is denoted as being open.

Belts and zones of a parallelohedron $\mathsf{P}$ will prove to be of particular importance. In [4], the operation of a zone contraction ${\mathsf{P}}^{\downarrow }$, and its inverse operation, the zone extension ${\mathsf{P}}^{\uparrow }$, were introduced.

Let ${\mathsf{P}}_s$ be a parallelohedron with s closed zones. A zone contraction ${\mathsf{P}}_s^{\downarrow }$ is the process of contracting every edge of a closed zone $Z\subset {\mathsf{P}}_s$ by the amount of its shortest edge. and thus, the zone Z becomes open, or vanishes completely. If all zones of $\mathsf{P}$ are open, then ${\mathsf{P}}_0$ is denoted to be totally contracted, or minimal.

${\mathsf{P}}_s^{\uparrow }$, is a zone extension of ${\mathsf{P}}_s$ by ${\mathbf{z}}^{*}$ if

$${\mathsf{P}}_s^{\uparrow }={\mathsf{P}}_{(s+1)}^{\prime },\mathrm{a}nd{{\mathsf{P}}^{\prime }}_{(s+1)}^{\downarrow }={\mathsf{P}}_s.$$

Zone contractions and extensions are invariant under affine transformations.

In [3], it was proved:

Theorem 1. 

A zone $\mathsf{Z}$ with zone vector ${\mathbf{z}}^{*}$ is closed, or extendable if and only if all facet vectors of ${\mathsf{P}}_s$ lie in layers ${\mathit{L}}_i\left({\mathbf{z}}^{*}\right)$, $i\in \{-1,0,1\}$, only.

The zone vector ${\mathbf{z}}^{*}$ does not necessarily belong to the zones of ${\mathsf{P}}_s$. Let ${\mathsf{P}}_{s+1}^{\prime }$ be an extension of ${\mathsf{P}}_s$ by ${\mathbf{z}}^{*}$. The corresponding Gram matrix ${\mathsf{Q}}^{\prime }$ is given by

$${\mathsf{Q}}^{\prime }=\mathsf{Q}+\lambda ({\mathbf{z}}^{*}\otimes {\mathbf{z}}^{*}),\lambda >0\in IR.$$

(11)

If a parallelohedron ${\mathsf{P}}_s$ allows no extensions, then ${\mathsf{P}}_s$ is denoted to be maximal. Each maximal parallelohedron defines a zone-contraction lattice $\mathcal{L}\left({\mathsf{P}}_m\right)$ by contracting all combinations of closed zones. It is partially ordered by zone contraction. The least upper and greatest lower bounds are defined by the union and intersection of closed zones.

In $E^d$, a quadratic form is defined by

$$\phi \left(\mathbf{x}\right):={\mathbf{x}}^t\mathsf{Q}\mathbf{x}\equiv {(\mathbf{x}\otimes \mathbf{x})}^t\mathbf{q},\forall \mathbf{x}\in E^d,$$

(12)

where the tensor product $(\mathbf{x}\otimes \mathbf{x})$ and $\mathbf{q}$ are represented as vectors in $E^{d\times d}$.

The closed cone of positive-definite quadratic forms is the set

$${\mathcal{C}}^{d\times d}:=\{\mathsf{Q}\mid \phi \left(\mathbf{x}\right)\ge 0,\forall \mathbf{x}\in E^d\}.$$

(13)

Given a basis ${\mathbf{e}}_1,\cdots ,{\mathbf{e}}_d$ of $E^d$, a basis of $E^{d\times d}$ referred to the origin $\tilde{O}$ is obtained by the tensor products

$${\mathbf{e}}_{ij}:=({\mathbf{e}}_i\otimes {\mathbf{e}}_j),i,j=1,\cdots ,d,$$

(14)

with ${\mathbf{e}}_{ij}{\mathbf{e}}_{kl}={\delta }_{ik}{\delta }_{jl}$. Since $\mathsf{Q}$ is symmetric, $q_{ij}=q_{ji}$, it follows that the cone ${\mathcal{C}}^{d\times d}$ can be restricted to a subspace of dimension $\left(\genfrac{}{}{0pt}{}{d+1}{2}\right)$ defined by ${\mathbf{e}}_{ij}$, $1\le i\le j\le d$.

The cone ${\mathcal{C}}^{d\times d}$ is partitioned into open, connected subcones of positive volume. Basic is the subdivision into ${\Phi }^{+}$-subcones of equivalent combinatorial types of parallelohedra.

Definition 3. 

In the cone ${\mathcal{C}}^{d\times d}$, the domain of a combinatorial type of primitive parallelohedron $\mathsf{P}\left(\mathsf{Q}\right)$ is the open, connected subcone of Gram matrices

$${\Phi }^{+}\left[\mathsf{P}\left(\mathsf{Q}\right)\right]:=\{{\mathsf{Q}}^{\prime }\in {\mathcal{C}}^{d\times d+}\mid \mathsf{P}\left({\mathsf{Q}}^{\prime }\right){}_{\simeq }^{comb}\mathsf{P}\left(\mathsf{Q}\right)\}.$$

For a primitive parallelohedron $\mathsf{P}\left(\mathsf{Q}\right)$ a border wall $\mathsf{W}\subset \Phi$ is determined by contracting an edge $\mathsf{E}\subset \mathsf{P}$ such that $d+1$ facets, having facet vectors ${\mathbf{f}}_1,\cdots ,{\mathbf{f}}_{d+1}$, meet in some vertex $\mathbf{v}\subset \mathsf{P}$ with

$${\mathbf{f}}_{d+1}={\alpha }_1{\mathbf{f}}_1+\cdots +{\alpha }_d{\mathbf{f}}_d,{\alpha }_i\in QQ.$$

(15)

Given the facet vectors ${\mathbf{f}}_1,\cdots ,{\mathbf{f}}_{d+1}$, Equation (15) is solved for the ${\alpha }_i$, $i=1,\cdots ,d$ (see [3]). A necessary condition for $d+1$ facets to meet in $\mathbf{v}$ is given by

$${[\sum _{i=1}^d-{\alpha }_i({\mathbf{f}}_i\otimes {\mathbf{f}}_i)+\sum _{i=1}^d\sum _{j=1}^d{\alpha }_i{\alpha }_j({\mathbf{f}}_i\otimes {\mathbf{f}}_j)]}^t\mathbf{q}\equiv {\mathbf{n}}^t\mathbf{q}=0.$$

(16)

The wall normal $\mathbf{n}$ is normalized such that for $\mathbf{q}\in {\Phi }^{+}$, ${\mathbf{n}}^t\mathbf{q}>0$, and $gcd(n_{11},\cdots ,n_{dd})=1$.

By contracting an edge ${\mathsf{E}}_i\subset \mathsf{P}$, a closed half-space is obtained by

$${\mathsf{H}}_i:=\{{\mathbf{q}}^{\prime }\in {\mathcal{C}}^{d\times d}\mid {\mathbf{n}}_i^t{\mathbf{q}}^{\prime }\ge 0\}.$$

Let $N_1$ be the number of non-equivalent edges of $\mathsf{P}$. The closed subcone $\Phi$ with apex in $\tilde{O}$ becomes (see [5]):

$$\Phi :=\bigcap _{i=1}^{N_1}{\mathsf{H}}_i.$$

(17)

Not all $N_1$ half-spaces induce a wall of $\Phi$.

Next, the cone ${\mathcal{C}}^{d\times d}$ is partitioned into open, connected subcones ${\Sigma }^{+}$ of parallelohedra having the same set of facet vectors $\mathcal{F}$.

Definition 4. 

The connected open domain of all parallelohedra that have the same set of facet vectors is the domain

$${\Sigma }^{+}\left[\mathsf{P}\left(\mathsf{Q}\right)\right]:=\left\{{\mathsf{Q}}^{\prime }\in {\mathcal{C}}^{d\times d+}\mid \mathcal{F}\left[\mathsf{P}\left({\mathsf{Q}}^{\prime }\right)\right]=\mathcal{F}\left[\mathsf{P}\left(\mathsf{Q}\right)\right]\right\}.$$

For a primitive parallelohedron $\mathsf{P}\left(\mathsf{Q}\right)$, a border wall $\mathsf{W}\subset \Sigma$ is characterized by the loss of at least one pair of facet vectors $\pm \mathbf{f}\in \mathcal{F}$ transforming a 6-fold into a 4-fold belt. Each pair of facet vectors ${\mathbf{f}}_g$, ${\mathbf{f}}_h$, belonging to a triplet that fulfills the first two belt conditions (8), defines a closed half-space,

$${\mathsf{H}}_i:=\{{\mathsf{Q}}^{\prime }\in {\mathcal{C}}^{d\times d}\mid {\mathbf{f}}_g^t{\mathsf{Q}}^{\prime }{\mathbf{f}}_h\equiv {({\mathbf{f}}_g\otimes {\mathbf{f}}_h)}^t{\mathbf{q}}^{\prime }\equiv {\mathbf{n}}_i^t{\mathbf{q}}^{\prime }\ge 0\}.$$

(18)

The wall-normal $\mathbf{n}\equiv ({\mathbf{f}}_g\otimes {\mathbf{f}}_h)$ is normalized such that for ${\mathsf{Q}}^{\prime }\in {\Sigma }^{+}$, ${\mathbf{n}}^t{\mathbf{q}}^{\prime }>0$, and $gcd(n_{11},\cdots ,n_{dd})=1$. For each triplet, three combinations have to be considered in order to obtain all possible half-spaces.

The closed subcone $\Sigma$ with apex in $\tilde{O}$ becomes (see [3]):

$$\Sigma :=\bigcap _{i=1}^{3N_b}{\mathsf{H}}_i.$$

(19)

Not all $3N_b$ half-spaces induce a wall of $\Sigma$. The subcone $\Sigma$ is an aggregation of complete $\Phi$-subcones and contains at least one $\Phi$-subcone.

A Gram matrix $\mathsf{Q}$ is interior to ${\Sigma }^{+}$ if

$${\mathbf{n}}_i^t\mathbf{q}>0,i=1,\cdots ,3N_b.$$

(20)

Let s, $0\le s\le \left(\genfrac{}{}{0pt}{}{d+1}{2}\right)$, be the number of closed zones. The number s is an invariant of any primitive ${\Sigma }_s$-class in $E^d$. ${\Sigma }_0$-classes of positive volume occur in dimensions $d\ge 6$ only.

3. The Parallelohedron of the Lattice ${\mathit{E}}_{\mathbf{8}}$

Referred to an optimal basis the following Gram matrix is obtained.

$${\mathsf{Q}}_{E_8}:=\left(\begin{array}{cccccccc}\hfill 2& \hfill -1& \hfill -1& \hfill 0& \hfill -1& \hfill 1& \hfill -1& \hfill -1\\ \hfill -1& \hfill 2& \hfill 1& \hfill 0& \hfill 1& \hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 1& \hfill 2& \hfill -1& \hfill 1& \hfill 0& \hfill 1& \hfill 1\\ \hfill 0& \hfill 0& \hfill -1& \hfill 2& \hfill 0& \hfill -1& \hfill -1& \hfill -1\\ \hfill -1& \hfill 1& \hfill 1& \hfill 0& \hfill 2& \hfill -1& \hfill 0& \hfill 0\\ \hfill 1& \hfill -1& \hfill 0& \hfill -1& \hfill -1& \hfill 2& \hfill 0& \hfill 0\\ \hfill -1& \hfill 1& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 2& \hfill 1\\ \hfill -1& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 2\end{array}\right).$$

The corresponding parallelohedron is computed by half-space intersections (5).

$\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$ has 240 facets, 19,440 vertices, and 8760 zones all of which are open. Therefore, $\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$ is minimal. The 120 pairs of facet vectors $\pm {\mathbf{f}}_j$ are listed in Table 2. Applying Equation (10), it is readily verified that for all zone vectors ${\mathbf{z}}_k^{*}$ with components $\mid z_l\mid \le 4$, $l=1,2,\dots ,8$, the facet vectors ${\mathbf{f}}_j$, $j=1,\cdots ,240$, belong to layers ${\mathsf{L}}_i\left({\mathbf{z}}_k^{*}\right)$, $-n\le i\le n$, where $n\ge 2$. Therefore, by Theorem 1 $\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$ is as much minimal as maximal.

Table 2. The facet vectors $\pm {\mathbf{f}}_i$ of $\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$.

${\mathbf{f}}_1$	1 0 0 0 0 0 0 0	${\mathit{f}}_3$	0 1 0 0 0 0 0 0	${\mathbf{f}}_5$	1 1 0 0 0 0 0 0
${\mathbf{f}}_7$	0 0 1 0 0 0 0 0	${\mathbf{f}}_9$	1 0 1 0 0 0 0 0	${\mathbf{f}}_{11}$	0 1 −1 0 0 0 0 0
${\mathbf{f}}_{13}$	0 0 0 1 0 0 0 0	${\mathbf{f}}_{15}$	0 0 1 1 0 0 0 0	${\mathbf{f}}_{17}$	1 0 1 1 0 0 0 0
${\mathbf{f}}_{19}$	0 1 −1 −1 0 0 0 0	${\mathbf{f}}_{21}$	0 0 0 0 1 0 0 0	${\mathbf{f}}_{23}$	1 0 0 0 1 0 0 0
${\mathbf{f}}_{25}$	0 1 0 0 −1 0 0 0	${\mathbf{f}}_{27}$	0 0 1 0 −1 0 0 0	${\mathbf{f}}_{29}$	0 0 1 1 −1 0 0 0
${\mathbf{f}}_{31}$	0 0 0 0 0 1 0 0	${\mathbf{f}}_{33}$	0 1 0 0 0 1 0 0	${\mathbf{f}}_{35}$	0 1 −1 0 0 1 0 0
${\mathbf{f}}_{37}$	0 0 0 1 0 1 0 0	${\mathbf{f}}_{39}$	0 1 0 1 0 1 0 0	${\mathbf{f}}_{41}$	0 0 1 1 0 1 0 0
${\mathbf{f}}_{43}$	0 0 0 0 1 1 0 0	${\mathbf{f}}_{45}$	0 1 −1 0 1 1 0 0	${\mathbf{f}}_{47}$	0 0 0 1 1 1 0 0
${\mathbf{f}}_{49}$	1 0 0 0 0 −1 0 0	${\mathbf{f}}_{51}$	1 0 1 0 0 −1 0 0	${\mathbf{f}}_{53}$	1 −1 1 0 0 −1 0 0
${\mathbf{f}}_{55}$	1 0 0 −1 0 −1 0 0	${\mathbf{f}}_{57}$	0 0 1 0 −1 −1 0 0	${\mathbf{f}}_{59}$	1 0 1 0 −1 −1 0 0
${\mathbf{f}}_{61}$	0 0 0 0 0 0 1 0	${\mathbf{f}}_{63}$	1 0 0 0 0 0 1 0	${\mathbf{f}}_{65}$	0 0 0 1 0 0 1 0
${\mathbf{f}}_{67}$	1 0 0 1 0 0 1 0	${\mathbf{f}}_{69}$	1 0 1 1 0 0 1 0	${\mathbf{f}}_{71}$	1 −1 1 1 0 0 1 0
${\mathbf{f}}_{73}$	1 0 0 0 1 0 1 0	${\mathbf{f}}_{75}$	1 −1 0 0 1 0 1 0	${\mathbf{f}}_{77}$	1 0 −1 0 1 0 1 0
${\mathbf{f}}_{79}$	1 0 0 1 1 0 1 0	${\mathbf{f}}_{81}$	1 −1 0 1 1 0 1 0	${\mathbf{f}}_{83}$	1 −1 1 1 1 0 1 0
${\mathbf{f}}_{85}$	0 0 0 1 0 1 1 0	${\mathbf{f}}_{87}$	0 0 0 1 1 1 1 0	${\mathbf{f}}_{89}$	1 0 0 1 1 1 1 0
${\mathbf{f}}_{91}$	1 0 0 0 0 −1 1 0	${\mathbf{f}}_{93}$	1 −1 0 0 0 −1 1 0	${\mathbf{f}}_{95}$	1 −1 1 0 0 −1 1 0
${\mathbf{f}}_{97}$	1 −1 1 1 0 −1 1 0	${\mathbf{f}}_{99}$	1 −1 0 0 1 −1 1 0	${\mathbf{f}}_{101}$	0 1 0 0 0 0 −1 0
${\mathbf{f}}_{103}$	0 0 1 0 0 0 −1 0	${\mathbf{f}}_{105}$	0 1 0 −1 0 0 −1 0	${\mathbf{f}}_{107}$	0 1 −1 −1 0 0 −1 0
${\mathbf{f}}_{109}$	0 1 0 0 −1 0 −1 0	${\mathbf{f}}_{111}$	0 0 1 0 −1 0 −1 0	${\mathbf{f}}_{113}$	0 1 1 0 −1 0 −1 0
${\mathbf{f}}_{115}$	0 1 0 −1 −1 0 −1 0	${\mathbf{f}}_{117}$	0 1 0 0 0 1 −1 0	${\mathbf{f}}_{119}$	0 0 1 0 −1 −1 −1 0
${\mathbf{f}}_{121}$	0 1 0 −1 −1 −1 −1 0	${\mathbf{f}}_{123}$	0 0 1 −1 −1 −1 −1 0	${\mathbf{f}}_{125}$	1 −1 0 1 1 0 2 0
${\mathbf{f}}_{127}$	0 0 0 0 0 0 0 1	${\mathbf{f}}_{129}$	1 0 0 0 0 0 0 1	${\mathbf{f}}_{131}$	1 1 0 0 0 0 0 1
${\mathbf{f}}_{133}$	0 1 −1 0 0 0 0 1	${\mathbf{f}}_{135}$	1 1 −1 0 0 0 0 1	${\mathbf{f}}_{137}$	0 0 0 1 0 0 0 1
${\mathbf{f}}_{139}$	1 0 0 1 0 0 0 1	${\mathbf{f}}_{141}$	1 1 0 1 0 0 0 1	${\mathbf{f}}_{143}$	1 0 1 1 0 0 0 1
${\mathbf{f}}_{145}$	1 0 0 0 1 0 0 1	${\mathbf{f}}_{147}$	1 0 −1 0 1 0 0 1	${\mathbf{f}}_{149}$	1 1 −1 0 1 0 0 1
${\mathbf{f}}_{151}$	1 0 0 1 1 0 0 1	${\mathbf{f}}_{153}$	0 1 −1 0 0 1 0 1	${\mathbf{f}}_{155}$	0 0 0 1 0 1 0 1
${\mathbf{f}}_{157}$	0 1 0 1 0 1 0 1	${\mathbf{f}}_{159}$	1 1 0 1 0 1 0 1	${\mathbf{f}}_{161}$	0 1 −1 1 0 1 0 1
${\mathbf{f}}_{163}$	0 1 −1 0 1 1 0 1	${\mathbf{f}}_{165}$	1 1 −1 0 1 1 0 1	${\mathbf{f}}_{167}$	0 1 −2 0 1 1 0 1
${\mathbf{f}}_{169}$	0 0 0 1 1 1 0 1	${\mathbf{f}}_{171}$	1 0 0 1 1 1 0 1	${\mathbf{f}}_{173}$	1 1 0 1 1 1 0 1
${\mathbf{f}}_{175}$	0 1 −1 1 1 1 0 1	${\mathbf{f}}_{177}$	1 1 −1 1 1 1 0 1	${\mathbf{f}}_{179}$	1 0 0 0 0 −1 0 1
${\mathbf{f}}_{181}$	0 1 −1 1 1 2 0 1	${\mathbf{f}}_{183}$	1 0 0 1 0 0 1 1	${\mathbf{f}}_{185}$	1 0 −1 0 1 0 1 1
${\mathbf{f}}_{193}$	1 0 −1 1 1 0 1 1	${\mathbf{f}}_{195}$	1 0 0 1 1 1 1 1	${\mathbf{f}}_{197}$	1 0 −1 1 1 1 1 1
${\mathbf{f}}_{199}$	1 1 −1 1 1 1 1 1	${\mathbf{f}}_{201}$	1 0 0 2 1 1 1 1	${\mathbf{f}}_{203}$	1 0 −1 1 2 1 1 1
${\mathbf{f}}_{205}$	0 1 0 0 0 0 −1 1	${\mathbf{f}}_{207}$	1 1 0 0 0 0 −1 1	${\mathbf{f}}_{209}$	0 1 −1 0 0 0 −1 1
${\mathbf{f}}_{211}$	0 1 −1 −1 0 0 −1 1	${\mathbf{f}}_{213}$	0 1 0 0 −1 0 −1 1	${\mathbf{f}}_{215}$	0 1 0 0 0 1 −1 1
${\mathbf{f}}_{217}$	0 1 −1 0 0 1 −1 1	${\mathbf{f}}_{219}$	0 2 −1 0 0 1 −1 1	${\mathbf{f}}_{221}$	0 1 0 1 0 1 −1 1
${\mathbf{f}}_{223}$	0 1 −1 0 1 1 −1 1	${\mathbf{f}}_{225}$	0 0 1 0 0 0 0 −1	${\mathbf{f}}_{227}$	0 0 1 0 −1 0 0 −1
${\mathbf{f}}_{229}$	0 0 1 0 −1 −1 0 −1	${\mathbf{f}}_{231}$	0 0 1 −1 −1 −1 0 −1	${\mathbf{f}}_{233}$	0 0 0 0 0 0 1 −1
${\mathbf{f}}_{235}$	1 −1 1 0 0 −1 1 −1	${\mathbf{f}}_{237}$	0 0 1 −1 −1 −1 −1 −1	${\mathbf{f}}_{239}$	1 1 −1 1 1 1 0 2

The 240 facet vectors of $\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$ all belong to the same equivalence class of norm 2. The group ${\mathcal{G}}_{E_8}$ is of order $2^{14}{3}^5{5}^{2}7=240·2,903,040=696,729,600$. Because of the high order, the group ${\mathcal{G}}_{E_8}$ will be determined by a variant of the method described in Section 2. We note that perpendicular to every facet vector ${\mathbf{f}}_j$, $j=1,2,\cdots ,240$ there exist a sublattice ${\Lambda }_j^7$ which is equivalent to $\Lambda \left(E_7\right)$, and its group ${\mathcal{G}}_{{\Lambda }_i^7}$ is isomorphic to ${\mathcal{G}}_{E_7}$. (Note that ${\mathcal{G}}_{E_7}$ is not normal in ${\mathcal{G}}_{E_8}$.) The left coset decomposition of ${\mathcal{G}}_{E_8}$ with respect to ${\mathcal{G}}_{E_7}$ becomes

$${\mathcal{G}}_{E_8}={\mathsf{R}}_1{\mathcal{G}}_{E_7}\cup {\mathsf{R}}_2{\mathcal{G}}_{E_7}\cup \cdots \cup {\mathsf{R}}_{240}{\mathcal{G}}_{E_7},$$

The group ${\mathcal{G}}_{E_7}$ is determined following the procedure described in Section 2, taking into consideration d-flags that only contain the facet ${\mathsf{F}}_1^{d-1}$. Then, for the remaining facets ${\mathsf{F}}_j^{d-1}$, we determine the scheme only up to a unified scheme in order to obtain the coset representatives ${\mathsf{R}}_j$, $j=2,3,\cdots ,240$, and ${\mathsf{R}}_1$ is the identity $\mathsf{I}$.

Below are given generating rotations of order 7 (${\mathsf{S}}_1$), 10 (${\mathsf{S}}_2$), 12 (${\mathsf{S}}_3$), and 15 (${\mathsf{S}}_4$) which generate the group of pure rotations ${\mathcal{G}}_{E_{7}r}$.

$${\mathsf{S}}_1=\left(\begin{array}{cccccccc}\hfill 1& \hfill 0& \hfill -1& \hfill 1& \hfill -1& \hfill 0& \hfill -1& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill -1& \hfill 1& \hfill 1& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 1& \hfill -1& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill -1& \hfill -1& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0\end{array}\right),{\mathsf{S}}_2=\left(\begin{array}{cccccccc}\hfill 1& \hfill 0& \hfill -1& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 2& \hfill 0& \hfill -1& \hfill -1& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill 0\end{array}\right),$$

$${\mathsf{S}}_3=\left(\begin{array}{cccccccc}\hfill 1& \hfill 0& \hfill -1& \hfill 1& \hfill -1& \hfill 0& \hfill -1& \hfill -1\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill -1& \hfill -1& \hfill -1\end{array}\right),{\mathsf{S}}_4=\left(\begin{array}{cccccccc}\hfill 1& \hfill 0& \hfill -1& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill -1& \hfill 1& \hfill 1& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill -1& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill -1& \hfill 1& \hfill 1& \hfill 0\end{array}\right).$$

The full group is obtained by including the mirror reflection ${\mathsf{S}}_m$ of order 2,

$${\mathsf{S}}_m=\left(\begin{array}{cccccccc}\hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right).$$

It holds:

$${\mathsf{S}}_i^t{\mathsf{Q}}_{E_8}{\mathsf{S}}_i={\mathsf{Q}}_{E_8},\forall {\mathsf{S}}_i\in {\mathcal{G}}_{E_8}.$$

(21)

It is sufficient to verify Equation (21) for the generating operations only. The set of coset representatives ${\mathsf{R}}_j$, $j=1,\cdots ,240$, may be obtained as Supplementary Material.

4. The Neighborhood of ${\mathsf{Q}}_{{\mathit{E}}_{\mathbf{8}}}$

In the neighborhood of ${\mathsf{Q}}_{E_8}$, a form ${\mathsf{Q}}_1$ was found whose parallelohedron $\mathsf{P}\left({\mathsf{Q}}_1\right)$ is primitive and has the maximal number 510 of facets, 291,432 vertices, and 4881 zones all of which are open. Therefore, $\mathsf{P}\left({\mathsf{Q}}_1\right)$ is minimal.

$${\mathsf{Q}}_1=\left(\begin{array}{cccccccc}\hfill 2.00000& \hfill -1.01989& \hfill -1.03552& \hfill 0.04144& \hfill -1.11035& \hfill 1.05024& \hfill -1.04326& \hfill -1.05920\\ \hfill -1.01989& \hfill 2.00000& \hfill 1.01958& \hfill 0.05237& \hfill 1.02854& \hfill -1.05510& \hfill 1.03992& \hfill 0.12356\\ \hfill -1.03552& \hfill 1.01958& \hfill 2.00000& \hfill -1.06269& \hfill 1.02626& \hfill 0.05449& \hfill 1.02459& \hfill 1.09957\\ \hfill 0.04144& \hfill 0.05237& \hfill -1.06269& \hfill 2.00000& \hfill 0.02398& \hfill -1.07772& \hfill -1.09471& \hfill -1.03355\\ \hfill -1.11035& \hfill 1.02854& \hfill 1.02626& \hfill 0.02398& \hfill 2.00000& \hfill -1.05996& \hfill 0.03901& \hfill 0.02049\\ \hfill 1.05024& \hfill -1.05510& \hfill 0.05449& \hfill -1.07772& \hfill -1.05996& \hfill 2.00000& \hfill 0.02231& \hfill 0.02899\\ \hfill -1.04326& \hfill 1.03992& \hfill 1.02459& \hfill -1.09471& \hfill 0.03901& \hfill 0.02231& \hfill 2.00000& \hfill 1.03193\\ \hfill -1.05920& \hfill 0.12356& \hfill 1.09957& \hfill -1.03355& \hfill 0.02049& \hfill 0.02899& \hfill 1.03193& \hfill 2.00000\end{array}\right).$$

The Gram matrix ${\mathsf{Q}}_1$ defines the ${\Sigma }_0^1$-subcone. For each $\mathsf{Q}$ in the open ${\Sigma }_0^{1+}$-subcone, the set of facet vectors $\mathcal{F}\left[\mathsf{P}\right(\mathsf{Q}\left)\right]$ is an invariant of ${\Sigma }_0^1$ and we may denote it by $\mathcal{F}\left({\Sigma }_0^1\right)$. The facet vectors are given in Table 3.

Table 3. The facet vectors $\pm {\mathbf{f}}_i$ of $\mathsf{P}\left({\mathsf{Q}}_1\right)$.

${\mathbf{f}}_1$	1 0 0 0 0 0 0 0	${\mathbf{f}}_3$	0 1 0 0 0 0 0 0	${\mathbf{f}}_5$	1 1 0 0 0 0 0 0
${\mathbf{f}}_7$	0 0 1 0 0 0 0 0	${\mathbf{f}}_9$	1 0 1 0 0 0 0 0	${\mathbf{f}}_{11}$	0 1 −1 0 0 0 0 0
${\mathbf{f}}_{13}$	0 0 0 1 0 0 0 0	${\mathbf{f}}_{15}$	0 0 1 1 0 0 0 0	${\mathbf{f}}_{17}$	1 0 1 1 0 0 0 0
${\mathbf{f}}_{19}$	0 1 −1 −1 0 0 0 0	${\mathbf{f}}_{21}$	0 0 0 0 1 0 0 0	${\mathbf{f}}_{23}$	1 0 0 0 1 0 0 0
${\mathbf{f}}_{25}$	0 1 0 0 −1 0 0 0	${\mathbf{f}}_{27}$	0 0 1 0 −1 0 0 0	${\mathbf{f}}_{29}$	0 0 1 1 −1 0 0 0
${\mathbf{f}}_{31}$	0 0 0 0 0 1 0 0	${\mathbf{f}}_{33}$	0 1 0 0 0 1 0 0	${\mathbf{f}}_{35}$	0 1 −1 0 0 1 0 0
${\mathbf{f}}_{37}$	0 0 0 1 0 1 0 0	${\mathbf{f}}_{39}$	0 1 0 1 0 1 0 0	${\mathbf{f}}_{41}$	0 0 1 1 0 1 0 0
${\mathbf{f}}_{43}$	0 0 0 0 1 1 0 0	${\mathbf{f}}_{45}$	0 1 −1 0 1 1 0 0	${\mathbf{f}}_{47}$	0 0 0 1 1 1 0 0
${\mathbf{f}}_{49}$	1 0 0 0 0 −1 0 0	${\mathbf{f}}_{51}$	1 0 1 0 0 −1 0 0	${\mathbf{f}}_{53}$	1 −1 1 0 0 −1 0 0
${\mathbf{f}}_{55}$	1 0 0 −1 0 −1 0 0	${\mathbf{f}}_{57}$	0 0 1 0 −1 −1 0 0	${\mathbf{f}}_{59}$	1 0 1 0 −1 −1 0 0
${\mathbf{f}}_{61}$	0 0 0 0 0 0 1 0	${\mathbf{f}}_{63}$	1 0 0 0 0 0 1 0	${\mathbf{f}}_{65}$	0 0 0 1 0 0 1 0
${\mathbf{f}}_{67}$	1 0 0 1 0 0 1 0	${\mathbf{f}}_{69}$	1 0 1 1 0 0 1 0	${\mathbf{f}}_{71}$	1 −1 1 1 0 0 1 0
${\mathbf{f}}_{73}$	1 0 0 0 1 0 1 0	${\mathbf{f}}_{75}$	1 −1 0 0 1 0 1 0	${\mathbf{f}}_{77}$	1 0 −1 0 1 0 1 0
${\mathbf{f}}_{79}$	1 0 0 1 1 0 1 0	${\mathbf{f}}_{81}$	1 −1 0 1 1 0 1 0	${\mathbf{f}}_{83}$	1 −1 1 1 1 0 1 0
${\mathbf{f}}_{85}$	2 −1 1 1 1 0 1 0	${\mathbf{f}}_{87}$	1 −2 1 1 1 0 1 0	${\mathbf{f}}_{89}$	0 0 0 1 0 1 1 0
${\mathbf{f}}_{91}$	0 0 0 1 1 1 1 0	${\mathbf{f}}_{93}$	1 0 0 1 1 1 1 0	${\mathbf{f}}_{95}$	1 −1 1 2 1 1 1 0
${\mathbf{f}}_{97}$	1 0 0 0 0 −1 1 0	${\mathbf{f}}_{99}$	1 −1 0 0 0 −1 1 0	${\mathbf{f}}_{101}$	1 −1 1 0 0 −1 1 0
${\mathbf{f}}_{103}$	1 −1 1 1 0 −1 1 0	${\mathbf{f}}_{105}$	1 −1 2 1 0 −1 1 0	${\mathbf{f}}_{107}$	1 −1 0 0 1 −1 1 0
${\mathbf{f}}_{109}$	2 −1 1 0 1 −1 1 0	${\mathbf{f}}_{111}$	2 −1 1 1 1 −1 1 0	${\mathbf{f}}_{113}$	1 −2 1 1 1 −1 1 0
${\mathbf{f}}_{115}$	1 −1 1 1 −1 −1 1 0	${\mathbf{f}}_{117}$	1 −1 2 1 −1 −1 1 0	${\mathbf{f}}_{119}$	1 −1 1 0 −1 −2 1 0
${\mathbf{f}}_{121}$	0 1 0 0 0 0 −1 0	${\mathbf{f}}_{123}$	0 0 1 0 0 0 −1 0	${\mathbf{f}}_{125}$	0 1 0 −1 0 0 −1 0
${\mathbf{f}}_{127}$	0 1 −1 −1 0 0 −1 0	${\mathbf{f}}_{129}$	0 1 0 0 −1 0 −1 0	${\mathbf{f}}_{131}$	0 0 1 0 −1 0 −1 0
${\mathbf{f}}_{133}$	0 1 1 0 −1 0 −1 0	${\mathbf{f}}_{135}$	0 1 0 −1 −1 0 −1 0	${\mathbf{f}}_{137}$	0 1 0 0 0 1 −1 0
${\mathbf{f}}_{139}$	0 0 1 0 −1 −1 −1 0	${\mathbf{f}}_{141}$	0 1 0 −1 −1 −1 −1 0	${\mathbf{f}}_{143}$	0 0 1 −1 −1 −1 −1 0
${\mathbf{f}}_{145}$	1 −1 1 2 0 0 2 0	${\mathbf{f}}_{147}$	1 −1 0 1 1 0 2 0	${\mathbf{f}}_{149}$	1 −2 0 1 1 0 2 0
${\mathbf{f}}_{151}$	1 −1 1 1 1 0 2 0	${\mathbf{f}}_{153}$	2 −1 1 1 1 0 2 0	${\mathbf{f}}_{155}$	1 −2 1 1 1 0 2 0
${\mathbf{f}}_{163}$	1 −2 1 2 1 0 2 0	${\mathbf{f}}_{165}$	2 −1 0 1 2 0 2 0	${\mathbf{f}}_{167}$	1 −2 0 1 2 0 2 0
${\mathbf{f}}_{169}$	1 0 0 2 1 1 2 0	${\mathbf{f}}_{171}$	1 −1 0 2 1 1 2 0	${\mathbf{f}}_{173}$	1 −1 1 2 1 1 2 0
${\mathbf{f}}_{175}$	1 −1 0 2 2 1 2 0	${\mathbf{f}}_{177}$	1 −1 1 1 0 −1 2 0	${\mathbf{f}}_{179}$	2 −1 1 1 0 −1 2 0
${\mathbf{f}}_{181}$	1 −2 1 1 0 −1 2 0	${\mathbf{f}}_{183}$	1 −1 0 1 1 −1 2 0	${\mathbf{f}}_{185}$	2 −1 0 1 1 −1 2 0
${\mathbf{f}}_{187}$	1 −2 0 1 1 −1 2 0	${\mathbf{f}}_{189}$	2 −1 1 1 1 −1 2 0	${\mathbf{f}}_{191}$	1 −2 1 1 1 −1 2 0
${\mathbf{f}}_{193}$	2 −2 1 1 1 −1 2 0	${\mathbf{f}}_{195}$	0 2 0 −1 −1 0 −2 0	${\mathbf{f}}_{197}$	0 1 0 −2 −1 −1 −2 0
${\mathbf{f}}_{199}$	0 0 0 0 0 0 0 1	${\mathbf{f}}_{201}$	1 0 0 0 0 0 0 1	${\mathbf{f}}_{203}$	1 1 0 0 0 0 0 1
${\mathbf{f}}_{205}$	0 1 −1 0 0 0 0 1	${\mathbf{f}}_{207}$	1 1 −1 0 0 0 0 1	${\mathbf{f}}_{209}$	0 0 0 1 0 0 0 1
${\mathbf{f}}_{211}$	1 0 0 1 0 0 0 1	${\mathbf{f}}_{213}$	1 1 0 1 0 0 0 1	${\mathbf{f}}_{215}$	1 0 1 1 0 0 0 1
${\mathbf{f}}_{217}$	1 0 0 0 1 0 0 1	${\mathbf{f}}_{219}$	1 0 −1 0 1 0 0 1	${\mathbf{f}}_{221}$	1 1 −1 0 1 0 0 1
${\mathbf{f}}_{223}$	1 0 0 1 1 0 0 1	${\mathbf{f}}_{225}$	0 1 −1 0 0 1 0 1	${\mathbf{f}}_{227}$	0 0 0 1 0 1 0 1
${\mathbf{f}}_{229}$	0 1 0 1 0 1 0 1	${\mathbf{f}}_{231}$	1 1 0 1 0 1 0 1	${\mathbf{f}}_{233}$	0 1 −1 1 0 1 0 1
${\mathbf{f}}_{235}$	0 1 −1 0 1 1 0 1	${\mathbf{f}}_{237}$	1 1 −1 0 1 1 0 1	${\mathbf{f}}_{239}$	0 1 −2 0 1 1 0 1
${\mathbf{f}}_{241}$	0 0 0 1 1 1 0 1	${\mathbf{f}}_{243}$	1 0 0 1 1 1 0 1	${\mathbf{f}}_{245}$	1 1 0 1 1 1 0 1
${\mathbf{f}}_{247}$	0 1 −1 1 1 1 0 1	${\mathbf{f}}_{249}$	1 1 −1 1 1 1 0 1	${\mathbf{f}}_{251}$	1 0 0 0 0 −1 0 1
${\mathbf{f}}_{253}$	0 1 −1 1 1 2 0 1	${\mathbf{f}}_{255}$	1 0 0 1 0 0 1 1	${\mathbf{f}}_{257}$	1 −1 1 2 0 0 1 1
${\mathbf{f}}_{259}$	1 0 −1 0 1 0 1 1	${\mathbf{f}}_{261}$	1 0 0 1 1 0 1 1	${\mathbf{f}}_{263}$	2 0 0 1 1 0 1 1
${\mathbf{f}}_{265}$	1 −1 0 1 1 0 1 1	${\mathbf{f}}_{267}$	2 −1 0 1 1 0 1 1	${\mathbf{f}}_{269}$	2 −1 1 1 1 0 1 1
${\mathbf{f}}_{271}$	1 0 −1 1 1 0 1 1	${\mathbf{f}}_{273}$	1 −1 −1 1 1 0 1 1	${\mathbf{f}}_{275}$	1 −1 1 2 1 0 1 1
${\mathbf{f}}_{277}$	2 −1 1 2 1 0 1 1	${\mathbf{f}}_{279}$	2 −1 0 1 2 0 1 1	${\mathbf{f}}_{281}$	2 0 −1 1 2 0 1 1
${\mathbf{f}}_{283}$	1 −1 −1 1 2 0 1 1	${\mathbf{f}}_{285}$	1 0 0 1 1 1 1 1	${\mathbf{f}}_{287}$	1 0 −1 1 1 1 1 1
${\mathbf{f}}_{289}$	1 1 −1 1 1 1 1 1	${\mathbf{f}}_{291}$	1 0 0 2 1 1 1 1	${\mathbf{f}}_{293}$	2 0 0 2 1 1 1 1
${\mathbf{f}}_{295}$	1 −1 0 2 1 1 1 1	${\mathbf{f}}_{297}$	1 −1 1 2 1 1 1 1	${\mathbf{f}}_{299}$	1 0 −1 2 1 1 1 1
${\mathbf{f}}_{301}$	1 0 −2 0 2 1 1 1	${\mathbf{f}}_{303}$	2 0 0 1 2 1 1 1	${\mathbf{f}}_{305}$	1 −1 0 1 2 1 1 1
${\mathbf{f}}_{307}$	1 0 −1 1 2 1 1 1	${\mathbf{f}}_{309}$	2 0 −1 1 2 1 1 1	${\mathbf{f}}_{311}$	1 −1 −1 1 2 1 1 1
${\mathbf{f}}_{313}$	1 0 −2 1 2 1 1 1	${\mathbf{f}}_{315}$	2 0 0 2 2 1 1 1	${\mathbf{f}}_{317}$	1 −1 0 2 2 1 1 1
${\mathbf{f}}_{319}$	1 0 −1 2 2 1 1 1	${\mathbf{f}}_{321}$	2 −1 1 1 0 −1 1 1	${\mathbf{f}}_{323}$	2 −1 0 0 1 −1 1 1
${\mathbf{f}}_{325}$	2 0 −1 0 1 −1 1 1	${\mathbf{f}}_{327}$	2 −1 0 1 1 −1 1 1	${\mathbf{f}}_{329}$	2 −1 1 1 1 −1 1 1
${\mathbf{f}}_{331}$	1 0 −1 1 2 2 1 1	${\mathbf{f}}_{333}$	1 1 −2 1 2 2 1 1	${\mathbf{f}}_{335}$	1 0 −1 2 2 2 1 1
${\mathbf{f}}_{337}$	0 1 0 0 0 0 −1 1	${\mathbf{f}}_{339}$	1 1 0 0 0 0 −1 1	${\mathbf{f}}_{341}$	0 1 −1 0 0 0 −1 1
${\mathbf{f}}_{343}$	0 1 −1 −1 0 0 −1 1	${\mathbf{f}}_{345}$	0 1 0 0 −1 0 −1 1	${\mathbf{f}}_{347}$	0 1 0 0 0 1 −1 1
${\mathbf{f}}_{349}$	0 1 −1 0 0 1 −1 1	${\mathbf{f}}_{351}$	0 2 −1 0 0 1 −1 1	${\mathbf{f}}_{353}$	0 1 0 1 0 1 −1 1
${\mathbf{f}}_{355}$	0 1 −1 0 1 1 −1 1	${\mathbf{f}}_{357}$	0 2 −2 −1 1 1 −1 1	${\mathbf{f}}_{359}$	0 2 −2 0 1 2 −1 1
${\mathbf{f}}_{361}$	2 0 0 1 1 0 2 1	${\mathbf{f}}_{363}$	2 −1 0 1 1 0 2 1	${\mathbf{f}}_{365}$	2 0 −1 1 1 0 2 1
${\mathbf{f}}_{367}$	1 −1 −1 1 1 0 2 1	${\mathbf{f}}_{369}$	2 0 0 2 1 0 2 1	${\mathbf{f}}_{371}$	1 −1 0 2 1 0 2 1
${\mathbf{f}}_{373}$	2 −1 0 2 1 0 2 1	${\mathbf{f}}_{375}$	2 −1 1 2 1 0 2 1	${\mathbf{f}}_{377}$	2 −1 0 1 2 0 2 1
${\mathbf{f}}_{379}$	2 0 −1 1 2 0 2 1	${\mathbf{f}}_{381}$	1 −1 −1 1 2 0 2 1	${\mathbf{f}}_{383}$	2 −1 −1 1 2 0 2 1
${\mathbf{f}}_{385}$	2 −1 0 2 2 0 2 1	${\mathbf{f}}_{387}$	1 0 0 2 1 1 2 1	${\mathbf{f}}_{389}$	2 0 0 2 1 1 2 1
${\mathbf{f}}_{391}$	1 −1 0 2 1 1 2 1	${\mathbf{f}}_{393}$	1 0 −1 2 1 1 2 1	${\mathbf{f}}_{395}$	2 0 −1 1 2 1 2 1
${\mathbf{f}}_{397}$	1 −1 −1 1 2 1 2 1	${\mathbf{f}}_{399}$	2 0 0 2 2 1 2 1	${\mathbf{f}}_{401}$	1 −1 0 2 2 1 2 1
${\mathbf{f}}_{403}$	2 −1 0 2 2 1 2 1	${\mathbf{f}}_{405}$	1 0 −1 2 2 1 2 1	${\mathbf{f}}_{407}$	2 0 −1 2 2 1 2 1
${\mathbf{f}}_{409}$	1 −1 −1 2 2 1 2 1	${\mathbf{f}}_{411}$	2 −1 0 1 1 −1 2 1	${\mathbf{f}}_{413}$	1 0 −1 2 2 2 2 1
${\mathbf{f}}_{415}$	0 0 1 0 0 0 0 −1	${\mathbf{f}}_{417}$	0 0 1 0 −1 0 0 −1	${\mathbf{f}}_{419}$	0 0 1 0 −1 −1 0 −1
${\mathbf{f}}_{421}$	0 0 1 −1 −1 −1 0 −1	${\mathbf{f}}_{423}$	1 −1 2 −1 −1 −2 0 −1	${\mathbf{f}}_{425}$	0 0 0 0 0 0 1 −1
${\mathbf{f}}_{427}$	1 −1 1 0 0 −1 1 −1	${\mathbf{f}}_{429}$	1 −1 2 1 −1 −1 1 −1	${\mathbf{f}}_{431}$	1 −2 2 0 0 −2 1 −1
${\mathbf{f}}_{433}$	1 −1 2 0 −1 −2 1 −1	${\mathbf{f}}_{435}$	1 −2 2 0 −1 −2 1 −1	${\mathbf{f}}_{437}$	0 0 1 −1 −1 −1 −1 −1
${\mathbf{f}}_{439}$	0 0 1 −1 −1 −2 −1 −1	${\mathbf{f}}_{441}$	0 0 1 −2 −1 −2 −1 −1	${\mathbf{f}}_{443}$	0 0 2 −1 −2 −2 −1 −1
${\mathbf{f}}_{445}$	0 0 1 −2 −2 −2 −1 −1	${\mathbf{f}}_{447}$	1 −2 1 1 1 0 2 −1	${\mathbf{f}}_{449}$	1 −2 1 1 0 −1 2 −1
${\mathbf{f}}_{451}$	1 −2 2 1 0 −1 2 −1	${\mathbf{f}}_{453}$	1 −2 1 1 1 −1 2 −1	${\mathbf{f}}_{455}$	1 1 −1 1 1 1 0 2
${\mathbf{f}}_{457}$	1 1 −2 1 2 1 0 2	${\mathbf{f}}_{459}$	0 1 −2 1 1 2 0 2	${\mathbf{f}}_{461}$	1 1 −1 1 2 2 0 2
${\mathbf{f}}_{463}$	1 1 −2 1 2 2 0 2	${\mathbf{f}}_{465}$	2 0 0 1 1 0 1 2	${\mathbf{f}}_{467}$	2 0 −1 1 1 0 1 2
${\mathbf{f}}_{469}$	2 0 −1 1 2 0 1 2	${\mathbf{f}}_{471}$	2 0 0 2 1 1 1 2	${\mathbf{f}}_{473}$	1 0 −1 2 1 1 1 2
${\mathbf{f}}_{475}$	1 0 −1 1 2 1 1 2	${\mathbf{f}}_{477}$	2 0 −1 1 2 1 1 2	${\mathbf{f}}_{479}$	2 1 −1 1 2 1 1 2
${\mathbf{f}}_{481}$	1 0 −2 1 2 1 1 2	${\mathbf{f}}_{483}$	2 1 −2 1 2 1 1 2	${\mathbf{f}}_{485}$	2 0 0 2 2 1 1 2
${\mathbf{f}}_{487}$	1 0 −1 2 2 1 1 2	${\mathbf{f}}_{489}$	2 0 −1 2 2 1 1 2	${\mathbf{f}}_{491}$	2 1 −1 2 2 1 1 2
${\mathbf{f}}_{493}$	1 1 −2 1 2 2 1 2	${\mathbf{f}}_{495}$	1 0 −1 2 2 2 1 2	${\mathbf{f}}_{497}$	1 1 −1 2 2 2 1 2
${\mathbf{f}}_{499}$	2 1 −1 2 2 2 1 2	${\mathbf{f}}_{501}$	1 1 −2 2 2 2 1 2	${\mathbf{f}}_{503}$	0 1 −2 0 1 1 −1 2
${\mathbf{f}}_{505}$	1 2 −2 0 1 1 −1 2	${\mathbf{f}}_{507}$	0 2 −2 0 1 2 −1 2	${\mathbf{f}}_{509}$	2 0 −1 2 2 1 2 2

Applying Equation (10), it is readily verified that for all zone vectors ${\mathbf{z}}_k^{*}$ with components $\mid z_l\mid \le 4$, $l=1,2,\dots ,8$, the facet vectors ${\mathbf{f}}_j\in \mathcal{F}\left({\Sigma }_0^1\right)$ belong to layers ${\mathsf{L}}_i\left({\mathbf{z}}_k^{*}\right)$, $-n\le i\le n$, where $n\ge 2$. Therefore, by Theorem 1 $\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$ is as much minimal as maximal.

In order to calculate the ${\Sigma }_0^1$-subcone, all triplets

$${\mathbf{f}}_i,{\mathbf{f}}_j,{\mathbf{f}}_k\in \mathcal{F}\left({\Sigma }_0^1\right)$$

that fulfill the first two belt conditions (8) are determined. Their number is $N_b=1114$ and the number of half-spaces ${\mathsf{H}}_i$ therefore becomes $3N_b$. Because of the high complexity of the ${\Sigma }_0^1$-subcone, the direct computation of ${\Sigma }_0^1$ as well as of its $\Phi$-subcones is not practicable with small computers. Instead, existence charts may be defined which intersect the ${\Sigma }_0^1$-subcone.

According to Equation (20), any further form ${\mathsf{Q}}_2\in {\Sigma }_0^1$ can be found viz.:

$${\mathsf{Q}}_2=\left(\begin{array}{cccccccc}\hfill 2.00000& \hfill -1.01967& \hfill -1.03513& \hfill 0.04098& \hfill -1.10914& \hfill 1.04969& \hfill -1.04278& \hfill -1.05855\\ \hfill -1.01967& \hfill 2.00000& \hfill 1.01937& \hfill 0.05179& \hfill 1.02822& \hfill -1.05449& \hfill 1.03948& \hfill 0.12220\\ \hfill -1.03513& \hfill 1.01937& \hfill 2.00000& \hfill -1.06200& \hfill 1.02597& \hfill 0.05389& \hfill 1.02432& \hfill 1.09848\\ \hfill 0.04098& \hfill 0.05179& \hfill -1.06200& \hfill 2.00000& \hfill 0.02372& \hfill -1.07686& \hfill -1.09367& \hfill -1.03318\\ \hfill -1.10914& \hfill 1.02822& \hfill 1.02597& \hfill 0.02372& \hfill 2.00000& \hfill -1.05930& \hfill 0.03858& \hfill 0.02027\\ \hfill 1.04969& \hfill -1.05449& \hfill 0.05389& \hfill -1.07686& \hfill -1.05930& \hfill 2.00000& \hfill 0.02207& \hfill 0.02867\\ \hfill -1.04278& \hfill 1.03948& \hfill 1.02432& \hfill -1.09367& \hfill 0.03858& \hfill 0.02207& \hfill 2.00000& \hfill 1.03045\\ \hfill -1.05855& \hfill 0.12220& \hfill 1.09848& \hfill -1.03318& \hfill 0.02027& \hfill 0.02867& \hfill 1.03045& \hfill 2.00000\end{array}\right).$$

The parallelohedron $\mathsf{P}\left({\mathsf{Q}}_2\right)$ is primitive and therefore has the maximal number 510 of facets, as well as 241,956 vertices, and 7016 zones all of which are open, and it proves that ${\mathsf{Q}}_{E_8}$ lies on the boundary of ${\Sigma }_0^1$.

The three forms

$${\mathsf{Q}}_{E_8},{\mathsf{Q}}_1,{\mathsf{Q}}_2\in {\Sigma }_0^1$$

determine a 2-section ${\Pi }^2$ through the ${\Sigma }_0^1$-subcone. The axes ${\overline{\mathbf{x}}}_1$, and ${\overline{\mathbf{x}}}_2$ define a cartesian coordinate system with an origin in ${\mathsf{Q}}_{E_8}$.

Each $\mathsf{Q}\in {\Pi }^2$ is obtained by

$$\mathsf{Q}={\mathsf{Q}}_{E_8}+\sum _{i=1}^2{\lambda }_i{\overline{\mathbf{x}}}_i,{\lambda }_i\in IR.$$

The condition (20) is used to decide if $\mathsf{Q}$ is interior to ${\Sigma }_0^1$. Considering that $\mathcal{F}\left({\Sigma }_0^1\right)$ is an invariant for ${\Sigma }_0^1$, the parallelohedron $\mathsf{P}\left(\mathsf{Q}\right)$ is easily computed.

In what follows, the surrounding of the ${\Sigma }_0^1$-subcone in the section ${\Pi }^2$ will be investigated.

First, all walls ${\mathsf{W}}_k^A$, $0\le k\le k^{\prime }$ containing ${\mathsf{Q}}_{E_8}$ are determined along the four straight line segments

$$\begin{gathered} 0.1{\overline{\mathbf{x}}}_1+{\lambda }_2{\overline{\mathbf{x}}}_2,-0.1\le {\lambda }_2\le 0.1, \\ -0.1{\overline{\mathbf{x}}}_1+{\lambda }_2{\overline{\mathbf{x}}}_2,-0.1\le {\lambda }_2\le 0.1, \\ {\lambda }_1{\overline{\mathbf{x}}}_1+0.1{\overline{\mathbf{x}}}_2,-0.1\le {\lambda }_1\le 0.1, \\ {\lambda }_1{\overline{\mathbf{x}}}_1-0.1{\overline{\mathbf{x}}}_2,-0.1\le {\lambda }_1\le 0.1, \end{gathered}$$

forming a quadrangle around the center $E_8$. Applying the method of nested intervals, the border point ${\mathsf{Q}}_k$ between two neighboring ${\Sigma }_0^k$- and ${\Sigma }_0^{k+1}$-subcones is easily determined within an $ϵ$-limit. The value of $ϵ$ is chosen to be

$$ϵ=det\left(\mathsf{Q}\right){10}^{-10}.$$

The point ${\mathsf{Q}}_k$ corresponds to a limiting parallelohedron $\mathsf{P}\left({\mathsf{Q}}_k\right)$ which is characterized to have some vertex $\mathbf{v}\in \mathsf{P}\left({\mathsf{Q}}_k\right)$ where at least d+1 facets meet. Thus, the wall normal ${\mathbf{n}}_k$ perpendicular to the wall ${\mathsf{W}}_k^A$ can easily be calculated by Equation (16).

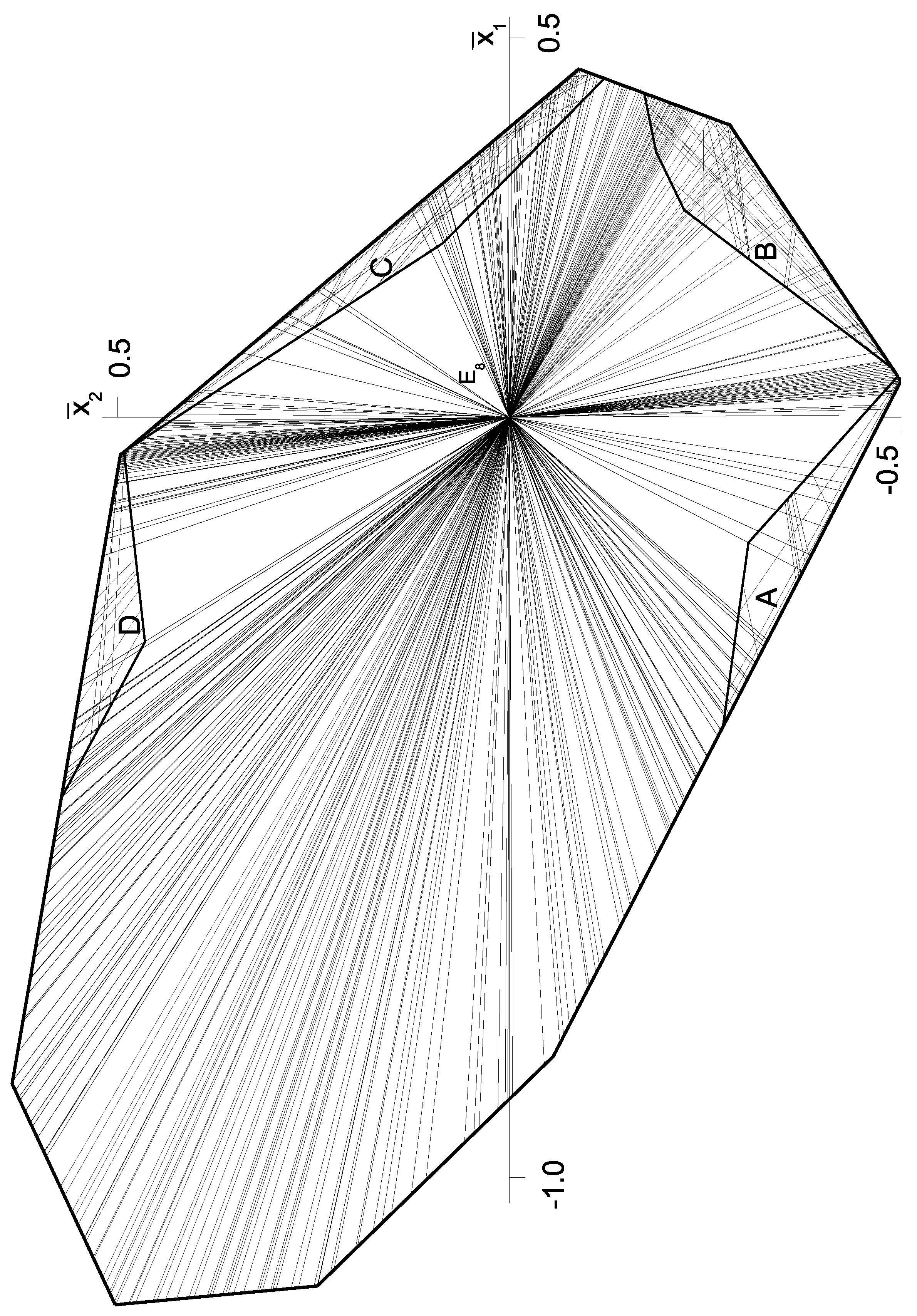
Next, the walls ${\mathsf{W}}_m^B$, $0\le m\le m^{\prime }$ are determined along a radial straight line in ${\Pi }^2$ going out from the center $E_8$ and lying between two neighboring border lines corresponding to walls ${\mathsf{W}}_k^A$ and ${\mathsf{W}}_{k+1}^A$. Applying the method of nested intervals, the border point ${\mathsf{Q}}_m$ between two neighboring ${\Sigma }_0^m$- and ${\Sigma }_0^{m+1}$-subcones is easily determined within an $ϵ$-limit. Thus, the wall normal ${\mathbf{n}}_m$ perpendicular to the wall ${\mathsf{W}}_m^B$ can easily be calculated by Equation (16). This process is continued until at some $m^{\prime }$ a ${\Sigma }_1^{m^{\prime }+1}$ is reached. This step has to be repeated along radial straight lines in various directions in order to fix in ${\Pi }^2$ the border of the cluster ${\mathsf{C}}_{E_8}$. Thereby, the sectors A, B, C, and D were discovered which are shown in Figure 1.

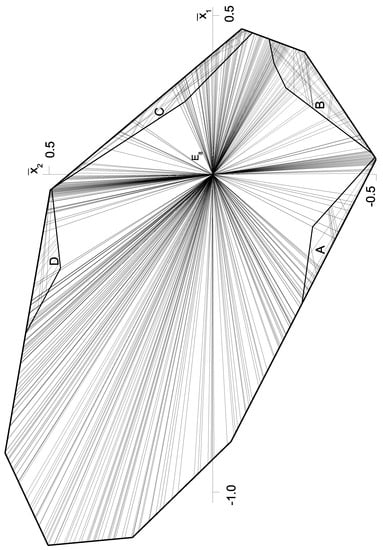
Figure 1. Existencechart through the ${\mathsf{C}}_{E_8}$-cluster in $E^8$.

5. Results

In Section 3, an optimal basis was used in order to compute the parallelohedron $\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$. This has the effect that the components of the facet vectors of $\mathsf{P}\left({\mathsf{Q}}_{E_8}\right)$ as well as of $\mathsf{P}\left({\mathsf{Q}}_1\right)$ lie in the set $\{-2,-1,0,1,2\}$ only as can be seen from Table 2 and Table 3, respectively. Therewith, the computing time is considerably reduced.

A generic ${\Sigma }_0$-subcone first occurs in $E^{6\times 6}$. In [7], it was shown that there exists just one class of arithmetically equivalent ${\Sigma }_0$-subcones. The subcone itself contains at least $192,493,630$ combinatorial types of $\Phi$-subcones of positive volume. In $E^{8\times 8}$ several, non-equivalent clusters can be found each of which contains a large number of non-equivalent ${\Sigma }_0$-subcones of positive volume. It shows that there exists a highly complex cluster ${\mathsf{C}}_{E_8}$ of ${\Sigma }_0^i$-subcones. In Figure 1, the section through ${\mathsf{C}}_{E_8}$ is shown. Only the border lines of the ${\Sigma }_0^i$-subcones are drawn. Each border line corresponds to a wall ${\mathsf{W}}_j$ having wall normal ${\mathbf{n}}_j$ of a certain ${\Sigma }_0^l$-subcone, and therefore, has a representation as a tensor product

$${\mathbf{n}}_j={\mathbf{f}}_a\otimes {\mathbf{f}}_b,{\mathbf{f}}_a,{\mathbf{f}}_b\in \mathcal{F}\left({\Sigma }_0^l\right).$$

There exist two kinds of walls. Walls ${\mathsf{W}}^{\left(in\right)}$ that separate two adjacent ${\Sigma }_0$-subcones, and walls ${\mathsf{W}}^{\left(out\right)}$ that separate a ${\Sigma }_0$-subcone from a adjacent ${\Sigma }_1$-subcone. In order to determine all walls, it would require computing a huge number of $\Phi$-subcones which at present is far out of reach.

The walls containing ${\mathsf{Q}}_{E_8}$ all belong to the class ${\mathcal{W}}^A$ of order 3780 under the group ${\mathcal{G}}_{E_{8r}}$, whereof 607 intersect ${\Pi }^2$ within the ${\mathsf{C}}_{E_8}$-cluster. A representative wall normal ${\mathbf{n}}_1^A$ of ${\mathsf{W}}_1^A\in {\mathcal{W}}^A$ is given by the tensor product

$${\mathbf{n}}_1:=({\mathbf{f}}_1\otimes {\mathbf{f}}_{13}),{\mathbf{f}}_1,{\mathbf{f}}_{13}\in \mathcal{F}\left({\Sigma }_0^1\right)$$

(see Table 3). Although the walls ${\mathsf{W}}_i^A\in {\mathcal{W}}^A$ are equivalent, the ${\Sigma }_0^i$-subcones in the ${\mathsf{C}}_{E_8}$-cluster are not equivalent.

The border lines in the ${\Pi }^2$-section do not necessarily extend over the whole cluster. When several border lines intersect then some border lines may end at the point of intersection. In Figure 1, it is seen that many of the walls ${\mathsf{W}}_i\in {\mathcal{W}}^{\left(in\right)}$ end in the center $E_8$. We have not investigated this behavior in detail because the substructure in sectors A, B, C, and D proved to be highly complicated.