Abstract
A general theory is presented to analyze the time-dependent, transient diffusiophoresis of a charged spherical colloidal particle in an uncharged gel medium containing a symmetrical electrolyte when an electrolyte concentration gradient is suddenly applied. We derive the inverse Laplace transform of an approximate expression for the relaxation function R(t), which describes the time-course of the ratio of the diffusiophoretic mobility of a weakly charged spherical colloidal particle, possessing a thin electrical double layer, to its steady-state diffusiophoretic mobility. The relaxation function depends on the mass density ratio of the particle to the electrolyte solution, the particle radius, the Brinkman screening length, and the kinematic viscosity. However, it does not depend on the type of electrolyte (e.g., KCl or NaCl), which affects only the steady-state gel diffusiophoretic mobility. It is also found that the expression for the relaxation function in transient gel diffusiophoresis of a weakly charged spherical colloidal particle with a thin electrical double layer takes the same form as that for its transient gel electrophoresis.
1. Introduction
The zeta potential of colloidal particles is a key parameter in the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory of colloidal suspension stability [1,2,3,4,5,6,7,8,9,10,11,12,13]. It can be determined through electrokinetic techniques, including electrophoresis and diffusiophoresis. Both electrophoresis and diffusiophoresis are fundamental electrokinetic phenomena that govern the motion of charged colloidal particles in liquid media. Electrophoresis involves particle migration under an externally applied electric field, while diffusiophoresis is driven by an electrolyte concentration gradient.
Extensive theoretical studies have explored diffusiophoresis in various colloidal systems, including rigid spheres [14,15,16,17,18,19,20,21,22,23,24,25,26,27] and soft particles with polyelectrolyte coatings [13,28]. One of the key applications of diffusiophoresis is in drug delivery systems (DDS), where electrolyte concentration gradients can guide particles toward specific regions or tissues, enabling more precise and efficient therapeutic interventions. Additionally, as diffusiophoresis operates without external energy input, it is particularly advantageous in microfluidic environments.
The electrokinetic behavior of colloidal particles is commonly examined in free-solution environments, where colloidal particles migrate in an electrolyte solution without spatial constraints. However, electrokinetics in porous media, such as gel electrophoresis, has both theoretical and practical significance [29,30,31]. When particles travel through the pores of a gel matrix, they experience two primary interactions: (i) short-range steric effects from particle-gel friction and (ii) long-range hydrodynamic interactions. In densely cross-linked gels, where pore sizes are smaller than the particles, steric effects dominate. Conversely, in dilute gels, where the pore size is significantly larger than the particle, long-range hydrodynamic interactions become more influential. The polymer network within a gel can be treated as a porous structure filled with an electrolyte solution, following the Brinkman-Debye-Bueche model [32,33], where polymer segments act as friction centers within the fluid. Using this framework, numerous theoretical studies have explored the diffusiophoresis of rigid particles [34,35,36,37,38,39,40,41,42,43] and soft particles [13,44,45,46,47,48,49].
Sambamoorthy and Chu [50] and Bhaskar and Bhattacharyya [51] developed a theoretical framework for the diffusiophoresis of charged spherical particles in porous gels. Their studies introduced governing equations for particle mobility in gel environments and outlined numerical methods to evaluate these mobilities. Our recent research [52] built upon these foundational works, further generalizing the theoretical framework to derive a more comprehensive expression for particle motion in gel diffusiophoresis.
Despite growing recognition of diffusiophoresis, most prior studies have concentrated on steady-state conditions, where the electrolyte concentration gradient remains unchanged over time, leading to a constant particle velocity. While this steady-state behavior is well understood, transient diffusiophoresis—where particles respond to a suddenly imposed concentration gradient—remains largely unexplored. Understanding this transient response is critical for practical applications, as real-world scenarios often involve abrupt environmental changes rather than perfectly stable conditions. This knowledge gap contrasts with transient electrophoresis, which has been extensively studied. In transient electrophoresis, researchers have analyzed how colloidal particles accelerate after an electric field is suddenly applied, eventually reaching a steady-state velocity. Foundational studies by Morrison [53,54] and Ivory [55,56], later expanded by Keh and collaborators [57,58,59,60,61,62,63,64] as well as others [65,66,67,68,69,70], have provided detailed insights into transient electrophoresis across various particle types [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70], including rigid spheres [53,56,58,59,60,64,66,69], cylinders [54,61,62,67], porous particles [63], and soft particles [15]. Research has also addressed transient gel electrophoresis, investigating time-dependent particle behavior in polymer gel matrices [71,72,73,74,75,76].
However, research on transient diffusiophoresis, in which an electrolyte concentration gradient is suddenly imposed and the resulting particle dynamics are examined, remains scarce in the literature. Our recent theoretical analysis [77] established a general framework for time-dependent transient diffusiophoresis in a free electrolyte solution, focusing on weakly charged spherical colloidal particles with a thin electric double layer.
In the present paper, we further extend our recent work on transient free-solution diffusiophoresis [77] to examine a previously unexplored type of transient electrokinetics—transient gel diffusiophoresis of a spherical colloidal particle. Investigating this phenomenon is essential for understanding particle transport in complex environments, such as porous media and biological systems, where electrolyte concentration gradients play a crucial role.
2. Theory
Consider a charged spherical colloidal particle with radius a, relative permittivity εp, and mass density ρp, carrying zeta potential ζ in an uncharged polymer gel medium containing an electrolyte solution with viscosity η and relative permittivity εr. The Brinkman-Debye-Bueche continuum medium [32,33] is applied, where polymer segments act as resistance centers dispersed throughout the gel medium, generating frictional forces on the liquid as it moves through the gel medium. The gel medium is treated as a homogeneous continuum medium containing electrolyte ions with a density of ρel(r) at position r. The electrolyte is assumed to be a symmetrical type with valence z, allowing for different ionic drag coefficients λ+ for cations and λ− for anions. A spherical coordinate system (r, θ, ϕ) is employed with its origin at the center of the particle (Figure 1). The concentrations (number densities) of cations and anions in the electrolyte solution at position r and time t are denoted as n+(r, t) and n−(r, t), respectively, while n∞ represents their concentrations beyond the electrical double layer surrounding the particle.
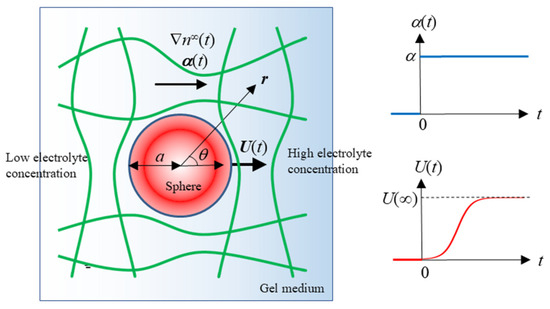
Figure 1.
Transient gel diffusiophoresis of a spherical colloidal particle with radius a moving with a transient diffusiophoretic velocity U(t) in an electrolyte concentration gradient field ∇n∞(t) or a(t).
Suppose that at time t = 0, a step electrolyte concentration gradient ∇n∞(t) is abruptly applied along the polar axis θ = 0, such that
We now define a vector α(t) as
with
and
Here, α(t) and α, respectively, denote the magnitudes of α(t) and α, e is the elementary charge, k is the Boltzmann constant, and T is the absolute temperature. Then, the particle starts moving with a diffusiophoretic velocity U(t) in the direction parallel to ∇n∞(t) or α(t) (Figure 1). The diffusiophoretic mobility μ(t) is defined as
We consider the following assumptions: (i) The liquid is treated as incompressible. (ii) The applied electrolyte concentration gradient field α(t) is sufficiently weak such that both the particle velocity U(t) and the liquid velocity u(r, t) remain proportional to α(t). This allows us to neglect the terms involving the square of the liquid velocity in the Navier-Stokes equation. (iii) The slipping plane, defined as the plane where the liquid velocity u(r, t) at position r (r, 0, 0) relative to the particle velocity is zero, coincides with the particle surface at r = a. Here, r represents the radial distance from the particle center. (iv) Electrolyte ions cannot penetrate the particle surface. (v) In the absence of α(t), the electrolyte ion distribution follows the Boltzmann distribution, and the equilibrium potential Ψ(0)(r) is governed by the Poisson-Boltzmann equation. (vi) The relative permittivity εp of the particle is much lower than that of the surrounding electrolyte solution εr (εp « εr), making εp nearly negligible. (vii) The Brinkman-Debye-Bueche continuum medium model [32,33] is employed, in which the polymer segments are regarded as resistance centers, exerting frictional forces with a frictional coefficient γ on the liquid flowing through the gel medium.
Under assumptions (i) through (vii), we derive the following fundamental electrokinetic equations governing the liquid velocity u(r, t) = (ur(r, t), uθ(r, t), 0) at position r and time t, as well as the velocity v+(r, t) of cations and v−(r, t) of anions, which are similar to those for transient gel electrophoesis and transient diffusiophoesis of a sphere [75,77]:
Here, ε0 is the permittivity of a vacuum, p(r, t) is the pressure, ρel(r, t) represents the charge density (given by Equation (10)), and Ψ(r, t) represents the electric potential. Equations (6) and (7) are the Navier-Stokes equation and the continuity equation for incompressible flow u(r, t) (condition (i)), where the term ρ0(u·∇)u is omitted (condition (ii)). The term involving the frictional coefficient γ in Equation (6) represents the frictional force exerted on the liquid flow by the polymer segments in the polymer gel medium. The presence of the particle velocity U(t) in Equation (6) results from the fact that the particle is chosen as the reference frame for the coordinate system. Equation (8) describes the flow of the electrolyte ions as driven by both the fluid motion u(r, t) and the gradient of the electrochemical potentials of cations μ+(r, t) and anions μ−(r, t), which are given by Equation (11) with being a constant. Equation (9) is the continuity equation for the cations and anions, while Equation (12) is the Poisson equation. Equation (13) is the equation of motion of the particle, in which FH(t) and FE(t) are, respectively, the hydrodynamic and electric forces acting on the particle and are given by
The initial conditions at t = 0 and the boundary conditions at the particle surface (r = a) and far from it (r → ∞) must be satisfied as [77]
where = r/r and is the unit normal vector pointing outward from the particle surface. Equations (16) and (17) imply that both the particle and the liquid are at rest at time t = 0. Equation (18) implies that the slipping plane, where u(r, t) = 0, is located on the particle surface (condition (iii)). Equations (19) and (20) follow from Equation (13) and condition (iv), respectively [77].
For a weak field α(t), the deviations δn±(r, t), δΨ(r, t), δμ±(r, t), and δρel(r, t) of n±(r, t), Ψ(r, t), μ±(r, t), and ρel(r, t) from their equilibrium values (i.e., those in the absence of the electrolyte concentration gradient field α(t)) are small. We may thus write
where the superscript (0) denotes the equilibrium quantities in the absence of α(t), which depend only on r, and is constant and independent of r.
Let us assume that the equilibrium concentration obeys the Boltzmann distribution, and the equilibrium electric potential Ψ(0)(r) satisfies the Poisson-Boltzmann equation (condition (v)), namely:
with
where y(r) is the scaled equilibrium electric potential, and ĸ is the Debye-Hückel parameter (where 1/ĸ is the Debye length). The following boundary conditions for n±(0)(r) and ψ(0)(r) must be satisfied:
Under an applied electrolyte concentration gradient field ∇n∞(t) or α(t), the boundary condition of δn±(r, t) at distances far from the particle is expressed as
The far-field boundary condition for δΨ(r, t) can be derived as follows. The ionic flows v±(r, t) induced by α(t) generate a macroscopic electric field E(t), known as the diffusion potential field, which nullifies the net electric current so that δΨ(r, t) does not vanish as r→∞. The electric current density i(r, t) at position r and time t is given by
By substituting Equations (8), (10), (21), and (23) into Equation (33) and ignoring the products of small quantities u(r, t), δn±(r, t), and δμ±(r, t), we have
With the help of the relation
which is derived from Equations (11) and (19)–(21), Equation (32) reduces to
Beyond the electrical double layer around the particle (r→∞),
and thus Equation (32) becomes
where E(t) is the magnitude of E(t). Since i(r, t) must be zero far from the particle (r→∞), we find from Equation (32) that
Here β is defined as
We thus obtain
By combining Equations (32), (35), and (41), we obtain the following far-field boundary condition for δμ±(r, t):
By inserting Equations (19)–(22) into Equation (6) and neglecting the products of small quantities u(r, t), δn±(r, t), δΨ(r, t), and δμ±(r, t) (condition (ii)), we obtain
and from Equations (8) and (9)
Furthermore, symmetry considerations allow us to express [29,36]:
where h(r, t), ϕ±(r, t), and Y(r, t) are functions of r and t. By substituting Equations (45)–(47) into Equations (36) and (37), we arrive at the following equations for h(r, t), ϕ±(r, t), and Y(r, t)
with
Here λ is the Brinkman parameter (where 1/λ is the Brinkman screening length), and L is a Differential operator defined as
G(r, t) is defined as
and
is the kinematic viscosity. The initial and boundary conditions, given by Equations (16)–(20) and (42), can be rewritten in terms of h(r, t), ϕ±(r, t), and Y(r, t) as follows [77]:
The transient gel diffusiophoretic mobility μ(t) (defined by Equation (5)) can be obtained from Equation (45), viz.:
Here, h(r, t) is the solution to Equation (48), which can be most conveniently solved using the Laplace transformation with respect to time t. The Laplace transforms , , and of h(r, t), G(r, t), and μ(t), respectively, are given by:
From Equations (60), (61), and (73), we obtain the following general expression for :
The Laplace transform of Equation (48) thus gives
which can be solved to yield
The transient gel diffusiophoretic mobility μ(t) can be obtained by applying the numerical inverse Laplace transform to Equation (67). It is possible to derive an approximate expression applicable for the practically important case of a weakly charged spherical particle with a thin electrical double layer (ĸa » 1) and a negligibly small εp (εp « ε0). In this case, it can be shown that Y(r) becomes equal to ϕ±(r), simplifying the solution of Equation (49) for ϕ±(r), as shown below. For the low zeta potential case, by solving Equations (48)–(50), G(r, t) is found to be independent of t so that G(r, t) can be rewritten as G(r) and can be expressed as
where the low-zeta potential approximation for y(r) is given by
For particles with a thin electrical double layer (ĸa » 1), the electric potential Ψ(0)(r) becomes almost zero beyond the electrical double layer at r = a+ 1/ĸ. In Equation (67) for that involves Ψ(0)(r), putting r = a + (r − a) makes (r − a)/a of the order of 1/(ĸa), which can be regarded as a small quantity. By expanding around r = a and retaining terms up to the order of ((r − a)/a)2, we obtain the following large-ĸa approximate form for for ĸa » 1:
where the relation (Equation (68)) has been used.
From Equation (69), we obtain the following large-ĸa approximate expression for the steady-state gel diffusiophoretic mobility μ(∞) using the relation :
Here the large-ĸa approximate expression of μ(∞) correct to the order of ζ2 has been derived in Ref. [52] as
By combining Equations (70) and (72), we obtain
Applying the inverse Laplace transform to Equation (73) yields
where:
which can be estimated numerically. Equation (74), combined with Equation (75), is the required expression for the transient gel diffusiophoretic mobility μ(t).
3. Results and Discussion
In the present paper, we have considered the time-dependent transient gel diffusiophoresis of a charged spherical colloidal particle. Compared to electrophoresis, diffusiophoresis has the advantage of inducing particle motion without requiring an external electric field, making it applicable in situations where electric fields may be undesirable. Furthermore, compared to free-solution diffusiophoresis, gel diffusiophoresis offers better control over particle transport due to the constrained environment provided by the gel matrix. Additionally, while steady-state gel diffusiophoresis describes the long-term motion of particles under a constant concentration gradient, transient gel diffusiophoresis captures the dynamic response of particles to a suddenly applied electrolyte concentration gradient, which is essential for understanding time-dependent behaviors in complex environments.
To the best of our knowledge, no experimental studies on transient gel diffusiophoresis have been reported. Therefore, we propose the following experimental approach to validate the theoretical predictions: Experimentally, suddenly applying an electrolyte concentration gradient to a suspension of colloidal particles, as described by Equation (1), for transient gel diffusiophoresis is significantly more difficult than suddenly applying an electric field for transient electrophoresis. A possible method is to first establish an electrolyte concentration gradient in a polymer gel medium containing an electrolyte solution and then introduce colloidal particles into the system at t=0. This approach may allow for controlled observation of transient gel diffusiophoresis and provide experimental validation of the theoretical model.
We derived a closed-form approximate expression for the inverse Laplace transform of the transient gel diffusiophoretic mobility, μ(t), of a weakly charged spherical colloidal particle with a thin electrical double layer (ĸa » 1), given by Equation (74) as combined with Equation (54). It can be shown that, under conditions of low zeta potential and thin electrical double layer (ĸa » 1), the approximate expression for the transient gel diffusiophoretic mobility takes the same form as that for the transient gel electrophoretic mobility [75]. However, it should be noted that despite the similarity between transient gel diffusiophoresis and gel electrophoresis, the steady-state mobility of μ(∞) is different between gel diffusiophoresis and gel electrophoresis, reflecting different driving forces. In the case of the gel electrophoresis of a weakly charged spherical colloidal particle with a thin electrical double layer, μ(∞) is given by [75],
The function R(t) given by Equation (75) can be interpreted as a relaxation function, which describes how the transient gel diffusiophoretic mobility μ(t) changes from its initial value of zero to its final steady-state value μ(∞). As mentioned above, R(t) takes the same form for the transient gel electrophoresis and diffusionphoresis. It is important to note that R(t) does not depend on the ionic drag coefficients λ±, making it independent of the specific electrolyte type (e.g., KCl or NaCl). On the other hand, μ(∞) depends on the specific electrolyte type, as shown in Equation (72) through the parameter β defined by Equation (40).
Figure 2 presents a 3D plot of R(t) as a function of the scaled particle radius λa and the scaled time νt/a2, calculated using Equation (75) for two values of the particle-to-solution mass density ratio ρp/ρ0, that is, ρp/ρ0 = 2 (a) and 10 (b).
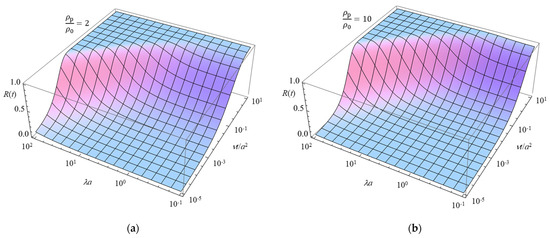
Figure 2.
Relaxation function R(t) for the transient gel diffusiophoresis of a spherical colloidal particle with radius a and a thin electrical double layer (ĸa » 1), defined as R(t) = μ(t)/μ(∞). The 3D plot of R(t) is shown as a function of λa, λ being the Brinkman parameter, and the scaled time νt/a2, calculated using Equation (75) for ρp/ρ0 = 2 (a) and 10 (b).
Figure 2 illustrates how the transient response of particle mobility is influenced by the mass density ratio ρp ρ0. Heavier particles (ρp/ρ0 = 10) exhibit a slower relaxation toward their steady-state mobility μ(∞), requiring a longer time to approach equilibrium. This trend is consistent with the theoretical model, as the particle inertia becomes more significant at higher mass density ratios, leading to a delayed response to the imposed electrolyte concentration gradient.
Moreover, Figure 2 demonstrates that the relaxation time required for μ(t) to reach its steady-state value μ(∞) decreases as λa increases. This behavior can be explained by Equation (72) for μ(∞), which shows that μ(∞) itself decreases with increasing λa. An increase in λa corresponds to either a larger Brinkman parameter λ or a larger particle radius a, both of which enhance the hydrodynamic resistance exerted by the polymer segments in the gel. As a result, the particle experiences greater resistance from the polymer matrix, making it more difficult to migrate through the gel, thereby leading to a reduction in its steady-state diffusiophoretic mobility μ(∞). As a result, the difference between the initial and steady-state mobility becomes smaller for larger λa, leading to a shorter relaxation time. This finding highlights the role of hydrodynamic interactions in gel diffusiophoresis, where the Brinkman parameter λ characterizes the extent of the fluid velocity field penetration into the gel network. A higher λa corresponds to stronger hydrodynamic screening, which reduces the overall mobility and accelerates the transient response. Thus, Figure 2 provides insight into how both the mass density ratio and the Brinkman parameter influence the time-dependent behavior of transient gel diffusiophoresis, agreeing with the theoretical predictions.
The present study demonstrates that while the steady-state mobility μ(∞) is primarily a function of the scaled particle radius λa and the zeta potential ζ, the transient mobility μ(t) exhibits additional dependencies on the scaled time νt/a2 and the mass density ratio ρp/ρ0. This highlights a fundamental distinction between transient diffusiophoresis in gels and traditional gel electrophoresis, where transient effects are often neglected. The dependence of μ(t) on ρp/ρ0 suggests that transient mobility carries information about particle inertia, which is absent in the steady-state analysis. Thus, analyzing μ(t) provides a more comprehensive understanding of particle motion in gels, offering deeper insights into the underlying transport mechanisms compared to steady-state mobility alone.
For the case of large t, which corresponds to small s in Equation (73), the inverse Laplace transform of Equation (75) can be derived analytically as follows. For small s, Equation (73) reduces to
from which we obtain
or
with
Here T can be regarded as the relaxation time. which describes how T depends on λa, and ρp/ρ0, and νt/a2. The relaxation time T for the transient gel diffusiophoresis is shorter than the relaxation time T for the transient free-solution gel diffusiophoresis (with λ = 0) by a factor 1 + λa + λ2a2/9. This shows that T decreases as λa increases.
4. Conclusions
We have developed a theory of the transient gel diffusiophoresis of a charged spherical colloidal particle in an uncharged polymer gel medium, subjected to sudden electrolyte concentration gradients. The relaxation function R(t) (Equation (75)) characterizes the time-dependent gel diffusiophoretic mobility of a weakly charged spherical colloidal particle with a thin electrical double layer (ĸa » 1). Our results show that R(t) is determined by the particle-to-solution mass density ratio ρp/ρ0, the Brinkmann screening parameter λ, the particle radius a, and the kinematic viscosity ν of the solution, while it does not depend on the specific electrolyte type (e.g., KCl or NaCl), which only affects the steady-state gel diffusiophoretic mobility (Equation (72)).
Funding
This research reserved no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Derjaguin, B.V.; Landau, D.L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Physicochim. USSR 1941, 14, 633–662. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Derjaguin, B.V. Theory of Stability of Colloids and Thin Films; Springer: New York, NY, USA, 1989. [Google Scholar]
- van de Ven, T.G.M. Colloidal Hydrodynamics; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Lyklema, J. Fundamentals of Interface and Colloid Science, Solid-Liquid Interfaces; Elsevier: Amsterdam, The Netherlands, 1995; Volume 2. [Google Scholar]
- Delgado, A.V. (Ed.) Electrokinetics and Electrophoresis; Dekker: New York, NY, USA, 2000. [Google Scholar]
- Dukhin, A.S.; Goetz, P.J. Ultrasound for Characterizing Colloids: Particle Sizing, Zeta Potential, Rheology; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Spasic, A.; Hsu, J.-P. (Eds.) Finely Dispersed Particles. Micro-. Nano-, Atto-Engineering; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Masliyah, J.H.; Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tadros, T.F. (Ed.) Colloid Stability. The Role of Surface Forces—Part 1; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Lee, E. Theory of Electrophoresis and Diffusiophoresis of Highly Charged Colloidal Particles; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Ohshima, H. Fundamentals of Soft Interfaces in Colloid and Surface Chemistry; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Derjaguin, B.V.; Dukhin, S.S.; Korotkova, A.A. Diffusiophoresis in electrolyte solutions and its role in the mechanism of film formation of cationic latex by ionic deposition. Kolloidn. Zh. 1961, 23, 53–58. [Google Scholar]
- Prieve, D.C. Migration of a colloidal particle in a gradient of electrolyte concentration. Adv. Colloid Interface Sci. 1982, 16, 321–335. [Google Scholar] [CrossRef]
- Prieve, D.C.; Anderson, J.L.; Ebel, J.P.; Lowell, M.E. Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 1984, 148, 247–269. [Google Scholar] [CrossRef]
- Prieve, D.C.; Roman, R. Diffusiophoresis of a rigid sphere through a viscous electrolyte solution. J. Chem. Soc. Faraday Trans. 2 1987, 83, 1287–1306. [Google Scholar] [CrossRef]
- Pawar, Y.; Solomentsev, Y.E.; Anderson, J.L. Polarization effects on diffusiophoresis in electrolyte gradients. J. Colloid Interface Sci. 1993, 155, 488–498. [Google Scholar] [CrossRef]
- Keh, H.J.; Wei, Y.K. Diffusiophoretic mobility of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 2000, 16, 5289–5294. [Google Scholar] [CrossRef]
- Keh, H.J. Diffusiophoresis of charged particles and diffusioosmosis of electrolyte solutions. Curr. Opin. Colloid Interface Sci. 2016, 24, 13–22. [Google Scholar] [CrossRef]
- Gupta, A.; Rallabandi, B.; Howard, A.; Stone, H.A. Diffusiophoretic and diffusioosmotic velocities for mixtures of valence-asymmetric electrolytes. Phys. Rev. Fluids 2019, 4, 043702. [Google Scholar] [CrossRef]
- Gupta, A.; Shim, S.; Stone, H.A. Diffusiophoresis: From dilute to concentrated electrolytes. Soft Matter 2020, 16, 6975–6984. [Google Scholar] [CrossRef] [PubMed]
- Shin, S. Diffusiophoretic separation of colloids in microfluidic flows. Phys. Fluids 2020, 32, 101302. [Google Scholar] [CrossRef]
- Wilson, J.L.; Shim, S.; Yu, Y.E.; Gupta, A.; Stone, H.A. Diffusiophoresis in multivalent electrolytes. Langmuir 2020, 36, 7014–7020. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Approximate analytic expressions for the diffusiophoretic velocity of a spherical colloidal particle. Electrophoresis 2022, 43, 752–756. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Diffusiophoretic velocity of a large spherical colloidal particle in a solution of general electrolytes. Colloid Polym. Sci. 2021, 299, 1877–1884. [Google Scholar] [CrossRef]
- Majhi, S.; Bhattacharyya, S.; Gopmandal, P.P. Impact of laterally mobile surface charge on diffusiophoresis of hydrophobic rigid colloids. J. Fluid Mech. 2024, 997, A8. [Google Scholar] [CrossRef]
- Majee, P.S.; Ohshima, H. On diffusiophoresis of a soft particle with a hydrophobic Inner core: A semianalytical study. Langmuir 2025, 41, 1469–1479. [Google Scholar] [CrossRef]
- Ogston, A.G.; Preston, B.N.; Wells, J.D. On the transport of compact particles through solutions of chain-polymers. Proc. R. Soc. Lond. A 1973, 333, 297–316. [Google Scholar]
- Johnson, E.M.; Berk, D.A.; Jain, R.K.; Deen, W.M. Hindered diffusion in agarose gels: Test of effective medium model. Biophys. J. 1996, 70, 1017–1026. [Google Scholar] [CrossRef] [PubMed]
- Stigter, D. Influence of agarose gel on electrophoretic stretch, on trapping, and on relaxation of DNA. Macromolecules 2000, 33, 8878–8889. [Google Scholar] [CrossRef]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. 1947, 1, 27–34. [Google Scholar] [CrossRef]
- Debye, P.; Bueche, A.M. Intrinsic viscosity, diffusion, and sedimentation rate of polymers in solution. J. Chem. Phys. 1948, 16, 573–579. [Google Scholar] [CrossRef]
- Allison, S.A.; Xin, Y.; Pei, H. Electrophoresis of spheres with uniform zeta potential in a gel modeled as an effective medium. J. Colloid Interface Sci. 2007, 313, 328–337. [Google Scholar] [CrossRef]
- Allison, S.A.; Pei, H.; Xin, Y. Review modeling the free solution and gel electrophoresis of biopolymers: The bead array-effective medium model. Biopolymers 2007, 87, 102–114. [Google Scholar] [CrossRef]
- Mohammadi, M.; Hill, R.J. Steady electrical and micro-rheological response functions for uncharged colloidal inclusions in polyelectrolyte hydrogels. Proc. R. Soc. A 2010, 466, 213–235. [Google Scholar] [CrossRef]
- Hsu, J.P.; Huang, C.H.; Tseng, S. Gel electrophoresis: Importance of concentration-dependent permittivity and double-layer polarization. Chem. Eng. Sci. 2012, 84, 574–579. [Google Scholar] [CrossRef]
- Hsu, J.P.; Huang, C.H.; Tseng, S. Gel electrophoresis of a charge-regulated, bi-functional particle. Electrophoresis 2013, 34, 785–791. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, S.; De, A.; Gopmandal, P.P. Electrophoresis of a colloidal particle embedded in electrolyte saturated porous media. Chem. Eng. Sci. 2014, 118, 184–191. [Google Scholar] [CrossRef]
- Hill, R.J. Electrokinetics of nanoparticle gel-electrophoresis. Soft Matter 2016, 12, 8030–8048. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, S.; De, S. Gel electrophoresis and size selectivity of charged colloidal particles in a charged hydrogel medium. Chem. Eng. Sci. 2016, 141, 304–314. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; De, S. Nonlinear effects on electrophoresis of a charged dielectric nanoparticle in a charged hydrogel medium. Phys. Fluids 2016, 28, 092006. [Google Scholar] [CrossRef]
- Ohshima, H. Electrophoretic mobility of a charged spherical colloidal particle in an uncharged or charged polymer gel medium. Colloid Polym. Sci. 2019, 297, 719–728. [Google Scholar] [CrossRef]
- Li, F.; Allison, S.A.; Hill, R.J. Nanoparticle gel electrophoresis: Soft spheres in polyelectrolyte hydrogels under the Debye-Hückel approximation. J. Colloid Interface Sci. 2014, 423, 129–142. [Google Scholar] [CrossRef] [PubMed]
- Allison, S.A.; Li, F.; Hill, R.J. The electrophoretic mobility of a weakly charged “soft” sphere in a charged hydrogel: Application of the Lorentz reciprocal theorem. J. Phys. Chem. B 2014, 118, 8827–8838. [Google Scholar] [CrossRef]
- Allison, S.A.; Li, F.; Le, M. Electrophoretic mobility of a dilute, highly charged “soft” spherical particle in a charged hydrogel. J. Phys. Chem. B 2016, 120, 8071–8079. [Google Scholar] [CrossRef] [PubMed]
- Le, L. Numerical Calculation of Gel Electrophoretic Mobility for “Soft” Spherical Nanoparticle. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2017. [Google Scholar]
- Ohshima, H. Gel electrophoresis of a soft particle. Adv. Colloid Interface Sci. 2019, 271, 101977. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Electrophoretic mobility of a soft particle in a polymer gel medium. Colloids Surfaces A Physicochim. Eng. Asp. 2021, 618, 126400. [Google Scholar] [CrossRef]
- Sambamoorthy, S.; Chu, H.C. Diffusiophoresis of a spherical particle in porous media. Soft Matter 2023, 19, 1131–1143. [Google Scholar] [CrossRef]
- Bhaskar, B.; Bhattacharyya, S. Diffusiophoresis of a highly charged rigid colloid in a hydrogel incorporating ion steric interactions. Phys. Fluids 2023, 35, 102023. [Google Scholar] [CrossRef]
- Ohshima, H. Gel diffusiophoresis of a spherical colloidal particle. Fluids 2024, 9, 203. [Google Scholar] [CrossRef]
- Morrison, F.A. Transient electrophoresis of a dielectric sphere. J. Colloid Interface Sci. 1969, 29, 687–691. [Google Scholar] [CrossRef]
- Morrison, F.A. Transient electrophoresis of an arbitrarily oriented cylinder. J. Colloid Interface Sci. 1971, 36, 139–145. [Google Scholar] [CrossRef]
- Ivory, C.F. Transient electroosmosis: The momentum transfer coefficient. J. Colloid Interface Sci. 1983, 96, 296–298. [Google Scholar] [CrossRef]
- Ivory, C.F. Transient electroosmosis of a dielectric sphere. J. Colloid Interface Sci. 1984, 100, 239–249. [Google Scholar] [CrossRef]
- Keh, H.J.; Tseng, H.C. Transient electrokinetic flow in fine capillaries. J. Colloid Interface Sci. 2001, 242, 450–459. [Google Scholar] [CrossRef]
- Keh, H.J.; Huang, Y.C. Transient electrophoresis of dielectric spheres. J. Colloid Interface Sci. 2005, 291, 282–291. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.C.; Keh, H.J. Transient electrophoresis of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 2005, 21, 11659–11665. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.C.; Keh, H.J. Startup of electrophoresis in a suspension of colloidal spheres. Electrophoresis 2015, 36, 3002–3008. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.C.; Keh, H.J. Transient electroosmosis in the transverse direction of a fibrous porous medium. Colloids Surf. A Physicochem. Engin. Asp. 2015, 481, 577–582. [Google Scholar] [CrossRef]
- Li, M.X.; Keh, H.J. Start-up electrophoresis of a cylindrical particle with arbitrary double layer thickness. J. Phys. Chem. B 2020, 124, 9967–9973. [Google Scholar] [CrossRef]
- Lai, Y.C.; Keh, H.J. Transient electrophoresis of a charged porous particle. Electrophoresis 2020, 41, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.C.; Keh, H.J. Transient electrophoresis in a suspension of charged particles with arbitrary electric double layers. Electrophoresis 2021, 42, 2126–2133. [Google Scholar] [CrossRef] [PubMed]
- Khair, A.S. Transient phoretic migration of a permselective colloidal particle. J. Colloid Interface Sci. 2012, 381, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Approximate analytic expression for the time-dependent transient electrophoretic mobility of a spherical colloidal particle. Molecules 2022, 27, 5108. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Transient electrophoresis of a cylindrical colloidal particle. Fluids 2022, 7, 342. [Google Scholar] [CrossRef]
- Ohshima, H. Transient electrophoresis of colloidal particles in a salt-free medium. Front. Lab Chip Technol. 2024, 3, 1438672. [Google Scholar] [CrossRef]
- Ohshima, H. Transient electrophoresis of spherical colloidal particles in a multi-particle suspension. Colloid Polym. Sci. 2024, 302, 1407–1413. [Google Scholar] [CrossRef]
- Ohshima, H. Transient electroosmosis on a soft surface. Colloids Interfaces 2025, 9, 12. [Google Scholar] [CrossRef]
- Saad, E.J.; Faltas, M.S. Time-dependent electrophoresis of a dielectric spherical particle embedded in Brinkman medium. Z. Angew. Math. Phys. 2018, 69, 43. [Google Scholar] [CrossRef]
- Saad, E.J. Start-up Brinkman electrophoresis of a dielectric sphere for Happel and Kuwabara models. Math. Methods Appl. Sci. 2018, 41, 9578–9591. [Google Scholar] [CrossRef]
- Saad, E.J. Unsteady electrophoresis of a dielectric cylindrical particle suspended in porous medium. J. Mol. Liq. 2019, 289, 111050. [Google Scholar] [CrossRef]
- Sherief, H.H.; Faltas, M.S.; Ragab, K.E. Transient electrophoresis of a conducting spherical particle embedded in an electrolyte-saturated Brinkman medium. Electrophoresis 2021, 42, 1636–1647. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Transient gel electrophoresis of a spherical colloidal particle. Gels 2023, 9, 356. [Google Scholar] [CrossRef]
- Ayman, M.; Saad, E.I.; Faltas, M.S. Transient electrophoresis of a conducting cylindrical colloidal particle suspended in a Brinkman medium. Z. Angew. Math. Phys. 2024, 75, 53. [Google Scholar] [CrossRef]
- Ohshima, H. Transient diffusiophoresis of a spherical colloidal particle. Colloids Interfaces 2025, 9, 7. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).