Abstract
This paper proposes the optimization relaxation approach based on the analogue Hopfield Neural Network (HNN) for cluster refinement of pre-classified Polarimetric Synthetic Aperture Radar (PolSAR) image data. We consider the initial classification provided by the maximum-likelihood classifier based on the complex Wishart distribution, which is then supplied to the HNN optimization approach. The goal is to improve the classification results obtained by the Wishart approach. The classification improvement is verified by computing a cluster separability coefficient and a measure of homogeneity within the clusters. During the HNN optimization process, for each iteration and for each pixel, two consistency coefficients are computed, taking into account two types of relations between the pixel under consideration and its corresponding neighbors. Based on these coefficients and on the information coming from the pixel itself, the pixel under study is re-classified. Different experiments are carried out to verify that the proposed approach outperforms other strategies, achieving the best results in terms of separability and a trade-off with the homogeneity preserving relevant structures in the image. The performance is also measured in terms of computational central processing unit (CPU) times.
1. Introduction
In recent years, the increasing number of Polarimetric Synthetic Aperture Radar (PolSAR) sensors has been demanding solutions for different applications based on the data they provide. One of these applications is data classification to identify the nature of the different structures in the imaged surfaces, based on the microwave backscattered signal. Terrain and land-use classifications are important applications of PolSAR data, where many supervised and unsupervised classification methods have been proposed [1–5]. Du and Lee [6] use the fuzzy c-means clustering algorithm for unsupervised segmentation of multi-look PolSAR data, whereas for classification they measure distances derived from the complex Wishart distribution. Grandi et al.[7] apply a wavelet-based approach in order to also capture texture orientation.
An important objective of the use of PolSAR data for quantitative remote sensing applications is to extract physical information from the observed scene. Cloude and Pottier [8–10] proposed a method to extract averaged parameters from experimental PolSAR data using a smoothing algorithm based on second order statistics. This method is based on the eigen-analysis of the coherency matrix, where the mean scattering mechanism is characterized by the entropy H and the mean alpha angle that are employed for its classification. Pottier and Lee [11] proposed another unsupervised classification method that improves the capability to distinguish between different classes whose cluster centers end in the same zone, also considering the anisotropy parameter A.
Lee et al.[12] developed a supervised algorithm based on the complex Wishart probability density function (pdf) for the polarimetric covariance matrix, based on the maximization of pdfs. The main drawback of this approach is that as a supervised algorithm, this method requires training data. Later on, Lee et al.[13] proposed an unsupervised classification approach that uses the method introduced in [9,10] to initially classify the PolSAR data. The initial classification map defines training sets for a classification scheme based on the Wishart pdf. The classification results are then employed as training sets for the next iteration using the Wishart classifier (different than the pdf) proposed in [12]. An improvement of the classification results is observed by increasing the number of iterations.
In this paper, we propose a new method based on a Hopfield Neural Network (HNN) optimization approach, initially proposed by Hopfield and Tank [14,15]. The results obtained by the unsupervised Wishart classifier are improved thanks to the HNN, while preserving the unsupervised nature of the Wishart approach.
An important advantage of the HNN optimization mechanism is its ability to build networks of nodes where each node is characterized by its state. The initial states of these nodes are obtained from the unsupervised Wishart approach. These states are then iteratively updated during the HNN process, taking into account the previous states and two types of external influences exerted by other nodes in its neighborhood. The external influences are mapped as two consistencies under the form of consistency coefficients. Both are embedded into an energy term, which is minimized also considering the states of the node to be updated and the states of its neighbors. At each iteration, under the HNN approach, the pixels in the image under classification are considered for a new cluster assignment, i.e., for re-classification, based on the updated states of the nodes, a cluster separability measure is computed to determine the quality of the new classification. This measure corresponds to the clustering validity criterion based on the cluster separation measure as defined in [16].
The HNN process is an optimization approach trying to achieve a minimum energy value. Nevertheless, a trade-off must be established between maximum cluster separability and minimum energy value. The definition of the consistency coefficients involved under the HNN approach constitutes the main contribution of this paper, inspired by the consideration that pixels that are near to the scene display similar properties and probably belong to the same region [17]. In [18] we proposed a similar network architecture with an optimization process based on Deterministic Simulated Annealing (DSA). Thanks to the HNN design, we still achieve a classification improvement with respect to the DSA approach. The HNN approach is also tested against two classification strategies based on post filtering, as explained in Section 3.2. This justifies the use of the HNN proposal for improving the Wishart classification in PolSAR images.
The paper is organized as follows. In Section 2 the HNN scheme is proposed. We give details about the complex Wishart classifier and the theory about the cluster separability measures, because they are required by the HNN process. The performance of the method is illustrated in Section 3, where a comparative study against the original maximum likelihood Wishart-based approach is carried out. Finally, Section 4 provides a discussion of some related topics and the final conclusions.
2. Hopfield Neural Network Optimization Process
2.1. Decomposition and Wishart Classifier
Before the HNN optimization process is applied, the Wishart-based classification process described in [13] is carried out, which is synthesized as follows:
- The polarimetric scattering information may be represented for each image pixel by the Pauli scattering vector . Hence, is the Hermitian product of the target vector of the one-look ith pixel. PolSAR data need to be multilook processed for speckle reduction by averaging n neighboring pixels. The coherency matrix is then obtained as,where the superscripts * and t denote the complex conjugate and matrix transposition, respectively.
- From the coherency matrices, we apply the H/ᾱ decomposition process as a refined scheme to parameterize polarimetric scattering problems. The scattering entropy, H, is a key parameter in determining the degree of statistical disorder, in such a way that H = 0 indicates the presence of a single scattering mechanism and H = 1 results when three scattering mechanisms with the same power are present in the resolution cell. The angle ᾱ characterizes the scattering mechanism as proposed in [8–10].
- The next step is to classify the PolSAR data into nine classes in the H/ᾱ plane, although zone three never contains pixels. These classes include different types of scattering mechanisms present in the scene, such as vegetation (grass, bushes), water surface (ocean or lakes) or city block areas. Section 3.3 includes a description and discussion about the content of these classes.
- Hence, the classification process results in eight valid zones or clusters, where each class is identified as wj or j, i.e., in our approach j varies from one to nine. Then, we compute the initial cluster center of coherency matrices for all pixels belonging to each zone (class wj) according to the number of pixels nj belonging to the class wj as follows,
- Compute the distance measure for each pixel i characterized by its coherence matrix ⟨T⟩i to the cluster center as follows,
- Assign the pixel to the class with the minimum distance,
- Verify if the termination criterion is met, otherwise set t = t + 1 and return to Step 1. The termination criterion is set to a prefixed number of iterations tmax. Nevertheless, the criteria that we adopt are the following: assuming that at each iteration t we have pixels belonging to the class wj and at the next iteration t + 1 the pixels belonging to the same class are , if the relative difference between both quantities is below a certain percentage, then the process also stops. We experimented with thresholds between ±0.5% and ±5%.
2.2. Cluster Separation Measures
- The dispersion within clusters (Dii): The Dii is defined as the averaged distance between all the pixels within the cluster wi to the cluster center Vi. It measures the compactness of cluster wi and is given by,where the large Dii indicates the dispersion of the pixels into the cluster.
- The distance between two clusters (Dij) is defined as,where the large Dij values indicate the high separation of these two clusters.
- The cluster separability (Rij) involves two clusters and is defined as,a small Rij value indicates that these two clusters are well separated; Rij is the Davies-Bouldin index [16] in classical clustering approaches, here adapted to PolSAR data classification. This quantity measures the quality of the partition, i.e., the clustering quality.
Based on the above measures, the goal of the proposed re-classification is to achieve a small dispersion into the clusters and large distances between pairs of clusters, which leads to a small Rij value. To quantitatively verify the performance of the proposed methodology, and also in order to meet the termination criterion, we compute the global averaged cluster separability with the following equation,
where nw is the number of Rij combinations with i ≠ j, i.e., nw = 36.
2.3. The Hopfield Neural Network for Improving the Wishart Classification
Here, we introduce the HNN architecture and some preliminary considerations, its dynamical behavior, the energy definition and the summary of the HNN process.
2.3.1. Preliminary Considerations and Network Architecture
At this stage, once the Wishart classifier has performed an initial classification, all the pixels have been classified into eight clusters or zones. A label identifying the zone is assigned to each pixel. The objective of the HNN is to perform a re-classification to modify the individual pixel’s labels based on consistency criteria with respect to the labels assigned to the surrounding pixels. We consider this re-labeling as a region homogenization process. When a pixel changes its label, the pixel is assigned to a different class. This implies that their coherency matrices change and, consequently, the cluster centers also change according to Equation (2). This behavior is similar to the one carried out during the iteration in the Wishart classification process. The main difference with respect to the Wishart classifier comes from the nature of the change, that in the case of the HNN process the changes are forced by the neighbors. At this point, four questions arise when applying the HNN process:
- How can we achieve that a pixel changes its current label so that it is classified as belonging to a different class?
- How can we achieve that a pixel does not change its label when its neighbors have identical labels as the label of the pixel under analysis?
- How can we achieve maximum cluster separability?
- When can we consider that no more changes are required?
The first question may be answered by considering that a pixel is classified to belong to a cluster if its distance to the corresponding cluster center is the minimum of all distances to all the cluster centers. Assuming that the pixel i has been labeled as belonging to a cluster different to that of its neighbor pixel k, without loss of generality, consider that i belongs to the cluster wj and k to the cluster wm. This means that the more similar the distances to the same cluster center for both pixels, the more probable that the pixel i changes its label to look like that of the pixel k. Instead of using distances directly, we can map them to a defined range, as defined in Equation (9), obtaining the support that a pixel receives with respect to a cluster and the same reasoning applies. The second question can be answered by considering that if a pixel i has a label identical to those of its neighbors, it does not need to change its current label. The third question requires that these changes must be oriented to preserve maximum cluster separability. Based on the above three considerations, we will define two contextual coefficients, called regularization and separation. The contextual term refers to the consideration of the central pixel and its neighbors. The regularization coefficient controls the changes based on the supports received from the pixels belonging to the clusters. The separation coefficient controls the cluster separability, hence justifying its name. Finally, the fourth question may be answered by taking into account that no more changes are required if we achieve the maximum degree of stability. This is equivalent to achieving a minimum value in the energy function defined in the HNN process.
Previously, we have considered the influence exerted by the pixels in the neighborhood over the central pixel. Nevertheless, not only the influence of the neighbors must be taken into account, but also the own effect of the central pixel in order to avoid an excessive influence of the neighbors. We call this influence the self-influence. The HNN is an energy optimization approach, which can embed contextual and self-influence, with the advantage that it can avoid local minima.
According to Equation (4), a pixel i belongs to the cluster wj if the distance to the corresponding cluster center is the minimum of all distances to the remaining clusters. Based on these distances, we define the support received by the pixel i for belonging to the cluster wj as follows:
where t denotes, as before, the iteration number. The sub index h varies from 1 to m, i.e., it represents the nine zones from h = w1 to h = m = w9. As we observe, the support
varies in the range (–1, +1]. Indeed, if
then
and if
then
. Under the above transformation, the decision rule in Equation (4) can be expressed as a function of the support at the iteration t, according to Equation (9), which expresses that the pixel i belongs to the cluster wj,
Equation (10) indicates that the pixel i belongs to the cluster wj because the support received by the pixel for this cluster is the greatest of all supports received for the remaining clusters.
For each cluster wj, we build a network of q nodes, netj, where the topology of this network is established by the spatial distribution of the pixels in the M × N-pixel image to be classified. Each node i in the netj is associated with the pixel location (x,y) in the image, i.e., i ≡ (x, y) and q = M × N. The node i in the netj is initialized with the support provided by the Wishart classifier through Equation (9) at the last iteration. These initial support values are also the initial network states associated with the nodes in the networks. Through the HNN, the state of each node is reinforced or punished iteratively based on the influences exerted by their neighbors and also through its self-influence. With this, we are trying to make better decisions based on more stable state values through Equation (10). Figure 1 shows the flowchart for the overall procedure and illustrates the architecture and the set of networks built to implement the HNN paradigm.
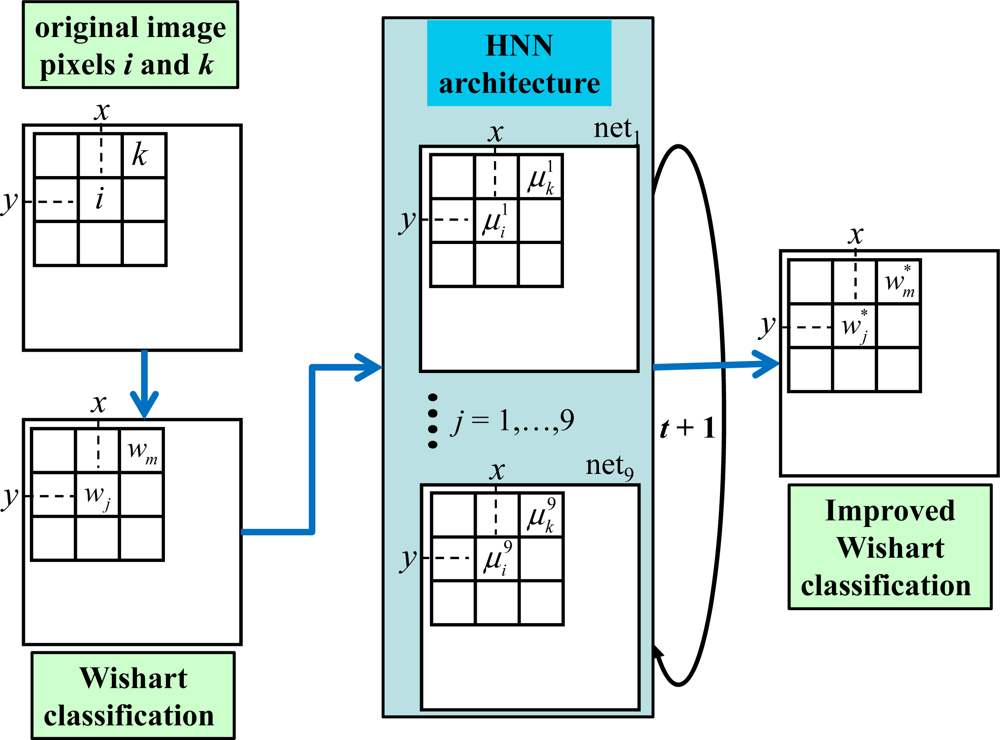
Figure 1.
Flowchart of the overall procedure and architecture for the Hopfield Neural Network (HNN) paradigm.
As one may observe from Figure 1, we obtain a first classification based on the Wishart classification, where each pixel is labeled as belonging to a class, i to wj and k to wm; from the Wishart classification we build the j nets (j = 1 to 9). Every node with its state value or support
on each netj is associated with a pixel i on the original image, both with identical locations (x,y). The states at each network are updated according to the number of iterations t. After the HNN convergence, a re-classification is obtained, where each pixel could change its label, this fact is indicated by the super-index in
and
for pixels i and k respectively.
2.3.2. Dynamics of the Hopfield Neural Network
The HNN paradigm has been widely used for solving optimization problems. This implies fixing two characteristics [19]: its activation dynamics and the associated energy function, which decreases as the network evolves.
The HNN is a recurrent network containing feedback paths from the outputs of the nodes back into their inputs, so that the response of such a network is dynamic. This means that after applying a new input, the output is calculated and fed back to modify the input. The output is then recalculated, and the process is repeated iteratively. Successive iterations produce smaller and smaller output changes, until eventually the outputs become constant, i.e., at this moment the network achieves an acceptable stability.
The connection weights between the nodes in the network netj may be considered to form a matrix Qj. To illustrate the Hopfield networks in more detail, consider the special case of a Hopfield network with a symmetric matrix. The input to the ith node comes from two sources: external inputs and inputs from the other nodes. The total input
to node i is then given by Equation (11).
where the
value represents the output of the kth node;
is the weight of the connection between nodes i and k; and
represents an external input bias value which is used to set the general level of excitability to the network. There are two types of Hopfield networks, namely [19,20]: (a) The analog ones in which the states of the neurons are allowed to vary continuously in an interval, such as [−1, +1] and; (b) the discrete ones in which these states are restricted to the binary values −1 and +1. The drawback of these binary networks is that they oscillate between different binary states, and settle down into one of many locally stable states. Hopfield has shown that analog networks perform better since they have the ability to smooth the surface of the energy function, which prevents the system from being stocked in local minima [14,15].
For analog Hopfield networks, the total input into a node is converted into an output value by a sigmoid monotonic activation function instead of a thresholding operation employed in the case of discrete Hopfield networks [21]. The dynamic of a node is then defined by:
where
is the sigmoid activation function and Li is a time constant which can be set to one for simplicity [20,22]. We have considered the sigmoid activation function to be the hyperbolic tangent function [20],
as this function is differentiable, smooth and monotonic. A detailed discussion about the settings of the time step dt and gain β−1 can be found in [19]. As dt increases, the probability that the energy falls into a local minimum increases also. According to some experiments carried out by Joya et al.[19], where this parameter has been set to values in the range 1 to 10−2, the best performance is achieved with the minimum value (i.e., 10−2), hence we have fixed it to 10−3, which is an order of magnitude smaller than the one experimented in [19].
The way to avoid that a continuous network cannot find a solution due to the existence of local minimum, and therefore to make the network converge to a solution state, is to decrease β along the simulation, theoretically until β = 0. This strategy resembles a simulated annealing process starting with a high enough β, where the network evolves until a stable state (which is not a solution) is reached, then β is decreased and the network evolves again up to a new stable state, and so on; the process ends when β becomes zero, and at this moment the stable state reached should be a global minimum. According to the results reported in [23,24], we have tested the following scheduling strategy β(βt where t is the iteration number. We have computed β0 as follows [25]: (a) given the original data with dimensions x and y coming from the Wishart classifier, they are down-sampled by a factor of
in both dimensions, and then we compute the energy as in Equation (19) after the initialization of the networks netj; (b) we choose an initial β0, that permits about 80% of all transitions to be accepted, i.e., transitions that decrease the energy function, and it is changed until this percentage is achieved; (c) we compute the M transitions ΔEk and we look for a value for β for which
after rejecting the higher order terms of the Taylor expansion of the exponential, β = 8⟨ΔEk⟩, where ⟨·⟩ is the mean value. In our experiments, for the set of images we have employed, we have obtained ⟨ΔEk⟩ = 5.83, resulting in β0 = 46.64, with a similar order of magnitude as reported in [26]. Taking into account that β(t) = 0, t →+∞ and considering t = 106, we obtain β = 3.38, i.e., β−1= 0.30. In our image classification approach, we have carried out different experiments by applying the above scheduling and also assuming a fixed gain, without apparent improvement in the final results. Hence, we set the gain to 0.30 during the complete process.
The model provided in Equation (12) is the classical Hopfield circuit [14,15,27], which follows from the Cohen-Grossberg dynamical systems [28]. In [27] the global stability of these systems is proven under the positivity assumption dg/dt > 0, and considering that the coefficient in the left term of Equation (12) is also positive. Because g is the hyperbolic tangent function, the first condition is true. Although some studies carried out by Lee and Chuang [29] in Hopfield neural networks have been addressed solving the problem of optimal asymmetric associative memories, we have found the classical approach studied in [21] and [28] to be acceptable, where it is shown that a recurrent network is stable if the matrix is symmetrical with zeros on its diagonal, that is, if
for all i and k and
for all neurons i. Additionally, the global stability is favored when the bias
varies slowly. In our design, this is also true according to the discussion in Section 2.3.4. The stability of the Hopfield neural network has also been studied under different perspectives in [21]. Hence, it belongs to the important class of feedback neural network models that are globally stable.
2.3.3. Energy Definition
The quantity describing the state of each network netj, called energy, is defined as follows,
The total energy for the c available networks is,
According to the results reported in [21], the integral term in Equation (13) is bounded by βj ln 2 ≈ 0.19 when
is +1 or −1 and is null when
is zero. In our experiments, we have verified that this term does not contribute to the network stability and only the energy is increased in a small amount with respect to the other two terms in Equation (13). Hence, for simplicity, we have removed it from Equation (13).
The continuous Hopfield model described by the system of nonlinear first-order differential Equation (12) represents a trajectory in the phase space, which seeks out the minimum of the energy function in Equation (13).
The HNN approach tries to achieve the most stable configuration for the network based on energy minimization. Now, the problem is to define the coefficients involved in the energy function, so that the network stability coincides with the minimum energy value. Hence, we need to define the meaning of stability for a node. A node is stable if its state remains invariable with iterations.
The term
is a combination of two coefficients representing the mutual influence exerted by the k neighbors over i, namely: (a) A regularization coefficient, which computes the consistency between the states of the nodes in a given neighborhood for each netj; (b) a separation coefficient which computes the consistency between the clusters in terms of separability, where high separability values are suitable. The neighborhood
is defined as the n-connected spatial region in the network around the node i, taking into account the mapping between the pixels in the image and the nodes in the networks. The regularization coefficient is computed at the iteration t as follows,
where
and
are defined above. From Equation (15) we can observe that
ranges in (−1, +1], where +1 is obtained with
, measuring that both states have identical values, i.e., maximum consistency between the nodes. On the contrary, if
and
take the most extreme and opposite values, such as
and
or vice versa, then
, which is its lower limit expressing minimum consistency between the nodes i and k. The definition of the regularization coefficient establishes maximum consistency for similar state values between the central node and its neighbors. This is intended for region homogenization, where other definitions should still be possible if different effects are desired, such as those concerned with the enhancement of specific and genuine features.
The separation coefficient at the iteration t is computed taking into account the labels assigned to the pixels associated to the nodes according to the classification decision rule given in Equation (10). Assume that the pixels i and k are classified in the clusters wr and ws, respectively, i.e., labeled as r and s. Because we are trying to achieve maximum separability between clusters, we compute the averaged cluster separability according to Equation (16). We compute the separabilities between the pixel i and its k neighbors in
A low Rrs value, equivalently a high
, expresses that the clusters wr and ws are well separated. Based on this assumption, the separation coefficient is defined as,
This coefficient embeds the concept of cluster separability defined in Equation (7) and participates in the calculation of the total energy through Equation (19).
Equation (16) expresses the relative weight of the averaged cluster separability between clusters wr and ws and the averaged cluster separabilities between wr and the clusters wu in
. The Coefficients 2 and 1 in Equation (16) are introduced so that cik(t) is in the range (−1, +1]. This mapping is made to achieve the same range as
. Note that the separation coefficient is independent of j, i.e., of the netj, as the labeling to calculate this coefficient involves the states of all networks. This implies that it is the same for all networks.
Once the regularization and separation coefficients have been specified, we search for an energy function such that the energy is low when both consistencies are high and vice versa. This energy is expressed as follows, where the dependence from the iteration t is suppressed for simplicity,
where A is a positive constant to be defined later on, sgn is the signum function and ν, ς, are the number of negative values in the set
or
, i.e., given
,
;
is introduced to cancel the self-contribution of the node i because it is considered later under the self-data information.
Both coefficients are computed based on the influences exerted by the nodes in the neighborhood
. This implies that the state for each node evolves according to the information provided by the majority in the neighborhood, ignoring its own contribution. This may lead to an incorrect state for the node under consideration. To overcome this drawback, we assume that each node must contribute to the evolution of its own state through the self-data information. The self-data information is modeled as a self-consistency based on the hypothesis that a node in the netj with the maximum support
must be labeled as belonging to the cluster wj and vice versa. This implies that a node with high/low support must have a high/low state value simultaneously. Under this assumption, the self-consistency is mapped as an energy function as follows,
where the constant B is a positive number to be defined later on. So, if the node i has a low/high
value, it implies that EB at each iteration is minimal, as expected.
2.3.4. Derivation of the Connection Weights and External Inputs for the HNN
Assuming contextual consistencies, Equation (17), and self-data information, Equation (18), we derive the energy function defined in Equation (13), which is to be minimized by optimization under the HNN framework,
By comparison of the Expressions (13) and (19), without the integral term in Equation (13), it is easy to derive the connection weights and the external input bias as follows,
According to the discussion in Section 2.3.2, to ensure the convergence to a stable state [28], symmetrical inter-connection weights and no self-feedback are required, i.e., we see that by setting A = B = 1, both conditions can easily be derived from Equation (19). Also, the external input bias must vary slowly to ensure the network stability. As the network is initially loaded with the supports provided by Equation (9), which are computed from the Wishart classifier, the network optimization process starts with a high degree of stability, and these values change slowly. Additionally, the definition of the neighborhood establishes that only small numbers of neurons are interconnected. It is also well-known that this contributes to the stability [30].
The energy in Equation (19) represents a trade-off between the data and contextual information coming from the spatial environment surrounding the node (pixel) i and also its self-data information. The Constants A and B could be fixed so that they tune the influence of each term in Equation (19). We have carried out several experiments verifying that the above setting is appropriated in our approach.
Equation (12) describes the time evolution of the network, the total input to the neuron is computed by solving such equation with the Runge-Kutta method. Finally, the state is also computed according to Equation (12). As we can see, the energy in Equation (19) is obtained by considering the state values and a kind of attractiveness derived from both the data and contextual consistencies. The derivation of an energy function with attractiveness between fixed points has been well addressed in [31] for discrete Hopfield memories preserving symmetrical weights and without self-feedback. Hence, we can assume that under the attractiveness of data and contextual consistencies, our analog Hopfield approach performs appropriately.
As mentioned in the introduction, a DSA approach has also been applied to improve the Wishart classification in PolSAR data, where an energy function is also minimized with the same network architecture and identical consistency coefficients as the ones defined in Equations (15) and (16). As we will see later, HNN outperforms DSA. This is because in the HNN approach, the energy term embeds both consistency coefficients and also the self-data information, unlike in DSA, where only the consistency coefficients are involved. Moreover, there is another important reason behind this outperformance, which is due to the updating process concerning the nodes in the networks. In the DSA approach, a linear combination, involving nodes states and consistency coefficients, is applied instead of the differential Equation (12) used in HNN. The linear combination in the DSA approach is made through a parameter that represents the trade-off between the influence exerted by the neighborhood (consistency coefficients) and the self-information. Also, in the DSA approach the combination of both consistency coefficients is carried out by a linear combination, where a second parameter establishes the trade-off between both coefficients. The HNN approach avoids these two parameters, which must be experimentally discovered, gaining advantage with respect to the DSA because they are unnecessary and no setting is required.
2.3.5. Summary of the HNN-Based Image Classifier
After mapping the energy function onto the Hopfield neural network, the image classification process is achieved by letting the networks evolve until they reach stable states, i.e., when no changes occur in the states of its nodes during the updating procedure. The whole image classification procedure can be summarized as follows:
- Initialization: create a network netj for each cluster wj. For each netj create a node i at each pixel location (x,y) from the image to be classified; t = 0 (iteration number); load each node with the state value , i.e. the support provided by the Wishart-based classifier, Equation (9); compute and through Equation (20); set ε = 0.01 (a constant to accelerate the convergence); tmax = 4 (maximum number of iterations allowed, see Section 3.2); set the constant values as follows: Li = 1; β = 3.38; dt = 10−3. Define nc as the number of nodes that change their state values at each iteration. The iterations in this discrete approach represent the time evolution involved in Equation (12).
- HNN process: set t = t + 1 and nc = 0; for each node i in netj compute using the Runge-Kutta method and update , both according to Equation (12) and ifthen nc = nc + 1; when all nodes i have been updated, if nc ≠ 0 and t < tmax then go to Step 2 (new iteration), else stop.
- Outputs: updated for each node; it is the degree of support for the cluster wj, see Figure 1. The node i is classified as belonging to the cluster with the greatest degree.
Because the proposed HNN approach tries to achieve the maximum cluster separability based on the minimization of an energy function, the optimal convergence criterion should be: “maximum cluster separability with minimum energy”. Nevertheless, we have verified during our experiments that both are not met simultaneously. Indeed, whereas the energy generally decreases continuously, although in a smooth way, with the number of iterations, the averaged cluster separability coefficient R̄, given by Equation (8), decreases and then increases its value after several iterations, as we will see later on. That is, the averaged cluster separability is worse after the iteration where R̄ changes its value although the energy still decreases. Hence, a trade-off must be established between both criteria. We have considered the cluster separability as the priority criterion, but considering that the energy is decreasing although it has not reached its global minimum value. In summary, the convergence criterion is finally: “choose the results obtained in the iteration t with the maximum cluster separability, minimum averaged separability coefficient R̄, where the energy value is lower than in the previous iteration”.
3. Experimental Results
In order to assess the validity and performance of our proposed classification approach, we use the well-tested NASA/JPL AIRSAR L-band image of the San Francisco Bay (SFB). The dimensions of the data are 900 × 1,024 pixels. This image displays several areas, including urban areas where thin structures induce neighboring pixels to belong to different clusters. The HNN tries to smooth these types of areas. Nevertheless, this information is preserved in the original image, either after the Wishart approach or even before the Wishart approach is triggered.
Additionally, we have considered a second PolSAR dataset at C-band. In this case, data were acquired by the EMISAR system property of the Danish Center for Remote Sensing on the Baltic Sea Lakes. These data are 512 × 512 pixels in size and display large targets, where the HNN tries to induce smoothing.
3.1. Design of a Test Strategy
In order to assess the validity and performance of the proposed approach, we have designed the following test strategy. Because our proposed HNN approach starts after the iterative Wishart classification process, the first task consists of the determination of the best number of iterations suitable for the Wishart process. This is carried out by executing this process from one to kmax, fixed to eight in our experiments: this value is set based on the observation that for a number of iterations greater than eight, the averaged separability values always get worse. For each iteration, we compute the averaged separability value according to Equation (8) for the classification obtained at this iteration, and we select the number of iterations kw with the minimum averaged separability coefficient value R̄. The classification results obtained for kw are the inputs for our HNN optimization approach.
Once the best number of iterations is obtained for Wishart, as it is explained in Section 2.1, we fix the maximum number of iterations, tmax, for the HNN process. We have set tmax to four because after experimentation, we verified that more iterations were not suitable due to an over-smoothing of the textured regions.
We tested the HNN for the following three neighborhood regions:
,
and
i.e., with window sizes of 3 × 3, 5 × 5 and 7 × 7, respectively. As before, and as expected, bigger neighborhoods produce excessive smoothing. The best neighborhood is the one with the minimum averaged separability value R̄, which is achieved with 3 × 3, as shown in the next section.
3.2. Results
According to the above strategy, Table 1 displays the results obtained at the different steps for the SFB image. The averaged separability coefficient values for the complex Wishart classifier, computed through Equation (8) are displayed for iterations 1 to kmax = 7.

Table 1.
Averaged separability values for the Wishart classifier against the number of iterations.
As one can see, the best cluster separability is achieved for two iterations, because at this number we obtain the minimum averaged separability coefficient. This is the number of iterations employed for the Wishart classifier, i.e., kw = 2.
Table 2 displays the averaged separability values for the HNN and DSA approaches against the number of iterations varying from one to tmax and for the specified neighborhoods.

Table 2.
Averaged separability values R̄ for the HNN and Deterministic Simulated Annealing (DSA) against the number of iterations.
As one may observe from the results in Table 2, the HNN approach always achieves the best performance at the first iteration and DSA at the second one. In both case, with a neighborhood of
we obtain the best performance. This is in the end the neighborhood employed for the rest of the experiments. The results obtained with
and
are obviously worse; one explanation is because with these values, the number of neighbors forcing the change of the state values of the central pixel is large; according to Equations (15) and (16), this implies that there are pixels belonging to different clusters trying to modify the value of the central pixel. Figure 2 displays the averaged separability values for the first two iterations of the complex Wishart approach according to the values in Table 1 and the eight iterations of the HNN (solid line) and DSA (dashed line) taking into account the best performances according to the values in Table 2 with
. As mentioned, the HNN receives as input the classification results obtained by the complex Wishart classifier at the second iteration where the Wishart approach achieves its best performance; the DSA approach also receives identical input. The HNN approach achieves the best average separability at Iteration 1, obtaining a minimum value much clearer than that obtained by the DSA. In short, HNN outperforms DSA in terms of number of iterations with similar or better qualitative classification results than DSA, as explained later on. This represents an important result taking into account that the HNN process, unlike DSA, is controlled by the energy decrease.
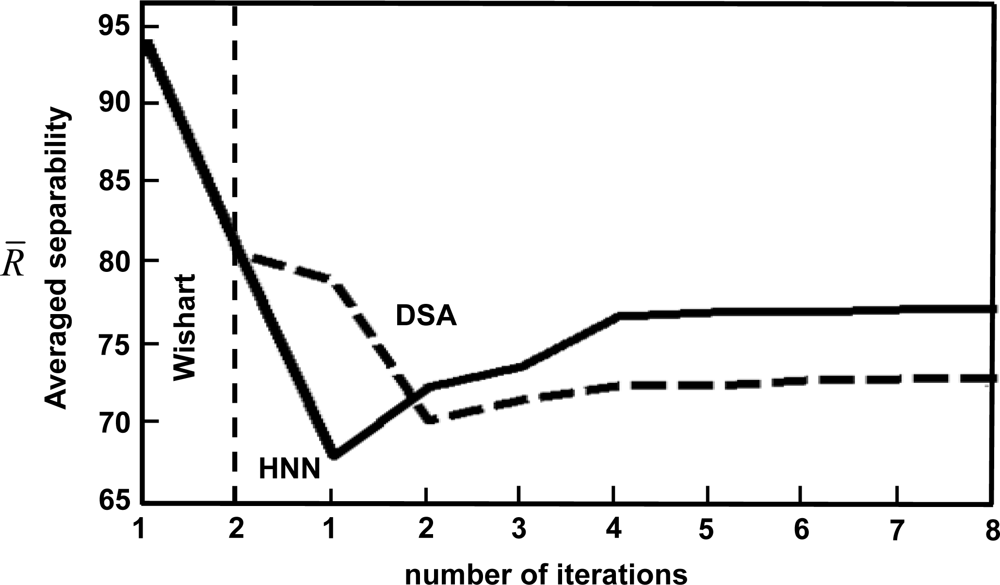
Figure 2.
Averaged separability values for the first two iterations of the Wishart classifier and the best performance achieved with HNN and DSA during the four iterations according to Table.
Figure 3 shows the variation of the energy considering both approaches. The energy in the HNN part is computed exactly through Equations (14) and (19). In the complex Wishart classifier there is no explicitly defined energy function. Nevertheless, for comparison purposes, and after each iteration of the Wishart process, we build the same architecture as the one used for the HNN, Section 2.2, Point 1, i.e., nine networks. The states of the nodes in these networks are obtained by applying Equation (9), once the distances have been calculated. The distances allow us to classify each pixel as belonging to a cluster according to Equation (10). So, once the state’s values and the classification are known, we can use Equations (19), (20) and (14) to compute the energy at the iteration t of Wishart.
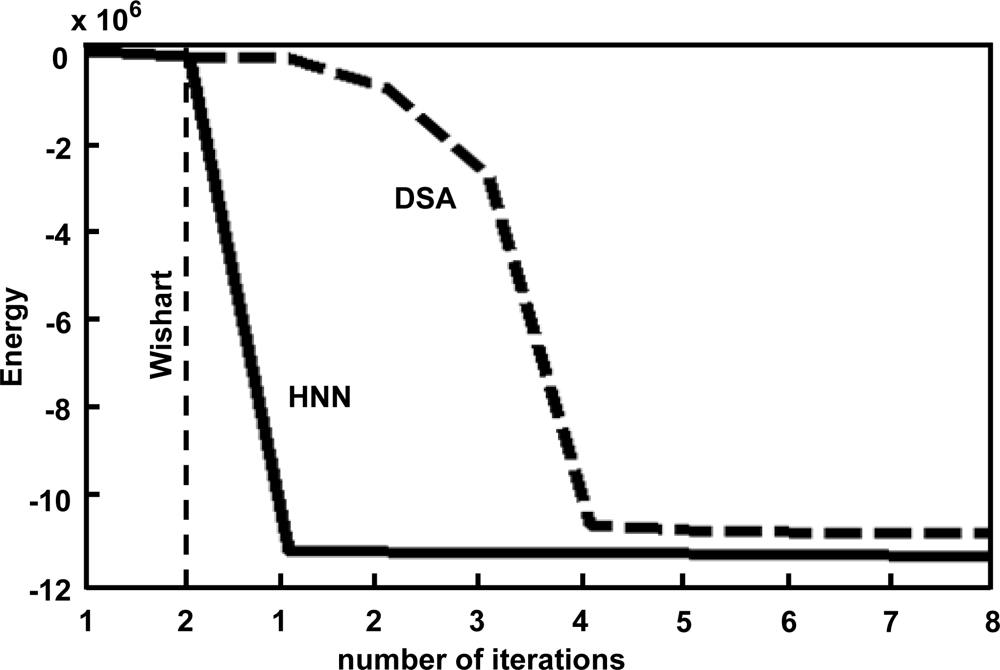
Figure 3.
Energy variation against the number of iterations for Wishart and HNN.
As we can see from Figure 3, the slope for HNN is greater than the one for the DSA at the first iteration, where HNN achieves its best performance, see Table 2. HNN achieves a high degree of stability from the first iteration, where the slope becomes insignificant but always decreases as mentioned before. In DSA, the energy also decreases from the first iteration but at a slower rate. A certain degree of stability is not reached until the fourth iteration. In both cases, when the stability is achieved, similar energy values are obtained.
We compared our proposed HNN approach and the DSA in [18] against Majority (MAJ) and iterated conditional mode (ICM) [32] post filtering classification strategies, where the following criterion has been applied: the class that is the most present in the neighborhood of the pixel is favored. For the ICM we have defined the following energy function, considering the contextual information
where δ is the symbol of Kronecker, which is expressed as: δ(wi, wk) = −1 if wi= wk and δ(wi, wk) = 0 if wi ≠ wk, wi and wk are the corresponding clusters. The goal is to maximize iteratively the a posteriori probability expressed as pi(t) = exp{−Ui/β(t)} or equivalently, to minimize the total energy function U(t) = ∑iUi/β(t), where β(t) is the scheduling defined as in our HNN approach, as it is inspired in [32]. For comparison purposes, we always apply the same number of iterations in the HNN and ICM case. For the DSA, we prefer to consider two iterations, because this is the number of iterations where it achieves its best performance. The MAJ is not an iterative approach.
In order to evaluate the degree of homogeneity induced by the Wishart, the HNN, the DSA, the MAJ and the ICM approaches, we apply the following criterion: given a neighborhood, here
according to the previous results, maximum homogeneity occurs when a unique cluster appears in the neighborhood and minimum homogeneity occurs if nine clusters appear, therefore the homogeneity varies from one (maximum) to nine (minimum), we map linearly these values so that the homogeneity Hi for
ranges in [0,1] for maximum and minimum homogeneities. Finally, we compute the homogeneity for the whole image as the average of the individual homogeneities for the image with size q = M × N
Figure 4(a) displays the classification results obtained by the complex Wishart classifier approach after the two programmed iterations, based on the assumption expressed above. Figure 4(b) displays the classification results obtained by the proposed HNN approach after the first iteration according to the discussion above based on the results shown in Table 2. Figure 4(c) displays the values obtained by DSA after the second iteration, because at this iteration it achieves a similar performance in terms of averaged separability as the one obtained by HNN, see Table 2. They both were obtained with a neighborhood of
, i.e., a window of 3 × 3 pixels. Figure 4(d,e) displays the results obtained by the ICM after the first iteration and the Majority approaches, respectively. The color bar indicates the color assigned to each one of the nine clusters. The data and classification results in Figure 4(a) are the inputs for the HNN, the DSA and the ICM, from which the results in Figure 4(b–d) are obtained after the corresponding optimization process.
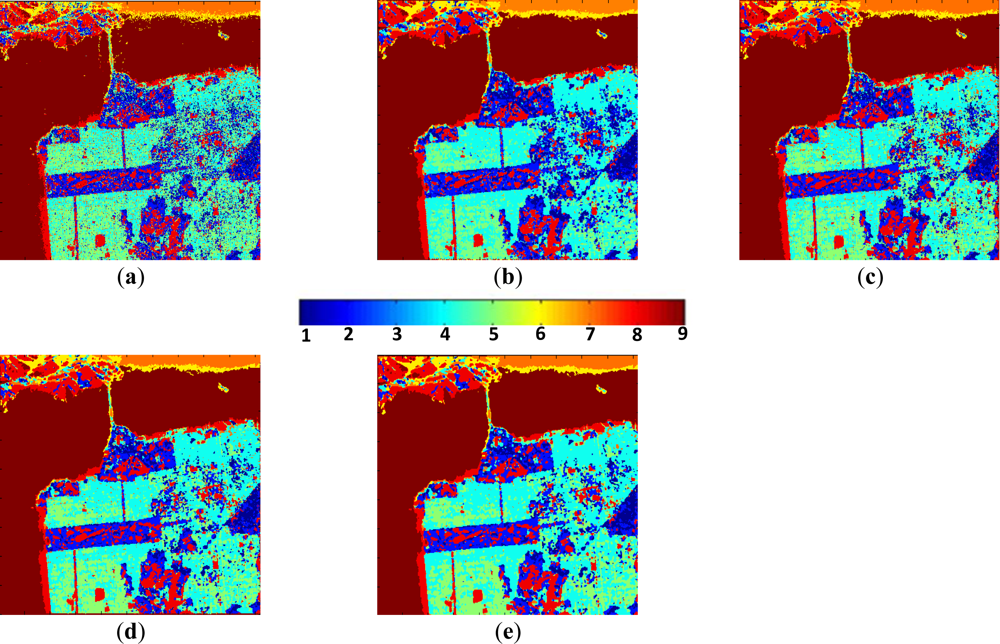
Figure 4.
(a) Classification by the Wishart approach after two iterations. (b) Classification by the proposed HNN optimization approach after the first iteration with a window size of 3 × 3. (c) Classification results for DSA after the second iteration. (d) Classification results by the iterated conditional mode (ICM) after the first iteration. (e) Classification results by Majority.
Results in Figure 4(b,c) are similar, however with some small differences. This is because the cluster separability values obtained for these two images are similar, i.e., 67.7 for the HNN and 67.8 for the DSA approaches, as displayed in Table 3.

Table 3.
Averaged Cluster Separability values (R̄), Homogeneities (H̄) and central processing unit (CPU) times for Wishart, HNN, DSA, ICM and Majority (MAJ) for San Francisco Bay (SFB) image.
Figures 5 and 6 display three detailed areas extracted from the images in Figures 4(a,b,d) and 4(e), respectively. The first ones range from pixels 25 to 400 in the x-size and 25 to 200 in the y-size. The second ones range from pixels 300 to 650 in the x-size and 500 to 850 in the y-size. As one can observe, a high degree of homogenization appears on the classification results obtained with the proposed approach, as compared against the results provided by Wishart (Figures 5(a) and 6(a)). We can also see in Series (c) and (d) how large areas try to absorb smaller areas; this implies a loss of some details that appear on the images in (b).
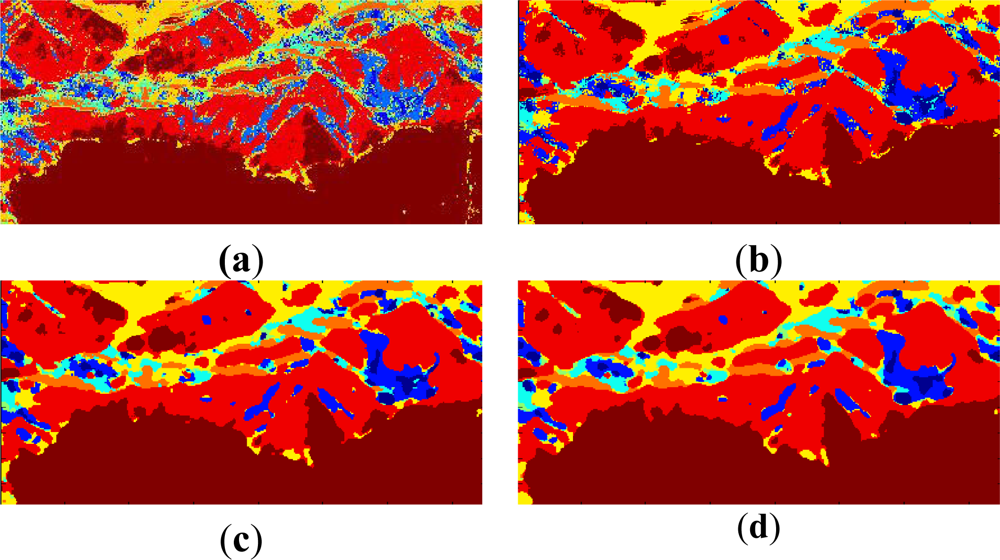
Figure 5.
Expanded area corresponding to mountains extracted from Figure 4. (a) by the Wishart approach classification after two iterations, (b) by HNN optimization approach after the first iteration, (c) by ICM after the first iteration, (d) Majority.
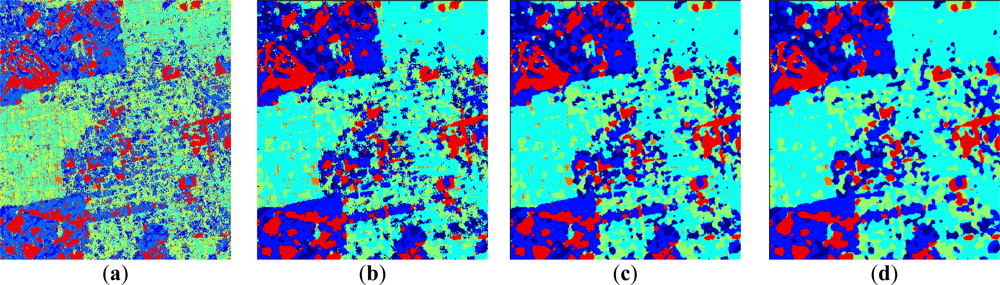
Figure 6.
Expanded area corresponding to a city extracted from Figure 4. (a) Wishart with two iterations. (b) HNN with one iteration. (c) ICM with one iteration. (d) Majority.
Table 3 displays the average separabilities (R̄) and homogeneities (H̄) from the four methods analyzed (Wishart, HNN, DSA, ICM and MAJ) for the SFB image. The values for Wishart (two iterations), HNN and ICM (one iteration) and DSA (two iterations); these data are those displayed in Tables 1 and 2, respectively. The last row displays the average CPU times in minutes per iteration for Wishart, HNN, DSA, ICM and MAJ. The time in Wishart and DSA must be increased by two, i.e., the number of iterations used.
We also applied our HNN strategy for the C-band PolSAR image on the Baltic Sea Lakes (BSL). Figure 7(a) displays the results obtained by Wishart after three iterations, Figure 7(b) the results achieved by HNN in the second iteration, And Figure 7(c) the results of DSA after two iterations (because of its similar performance to HNN with these iterations). Figure 7(d,e) display the classification results obtained by ICM after two iterations (as HNN) and Majority, respectively. The neighborhood was
.
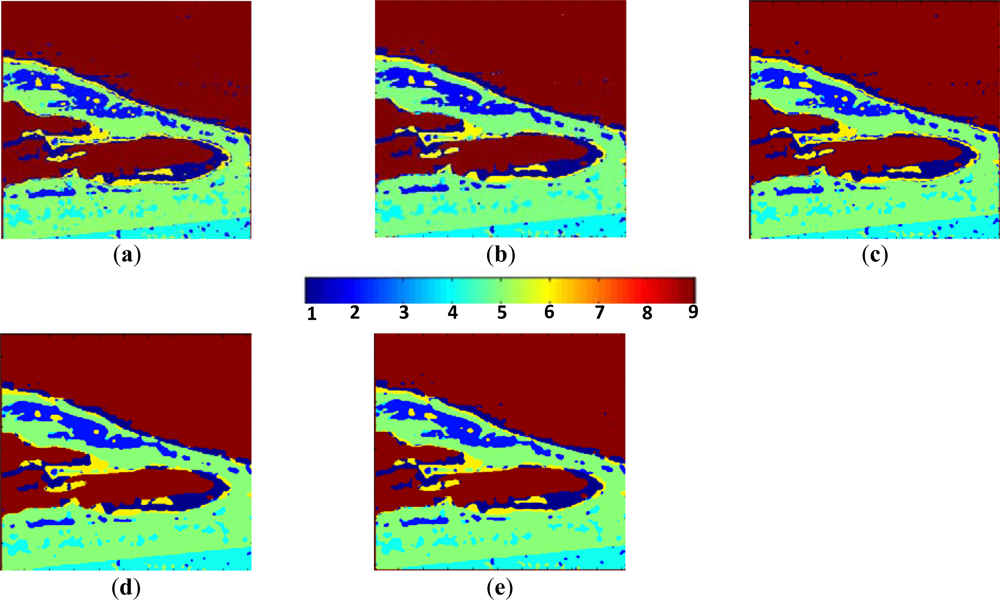
Figure 7.
(a) Classification by Wishart after three iterations. (b) Classification by the proposed HNN optimization approach after the first iteration with a window size of 3×3. (c) Classification results for DSA after two iterations. (d) Classification results by the ICM after the first iteration. (e) Classification results by Majority.
Table 4 displays the average separabilities (R̄) and homogeneities (H̄) from the four methods analyzed (Wishart, HNN, DSA, ICM and MAJ) for the BSL image. The last row displays the average CPU times in minutes per iteration for Wishart, HNN, DSA, ICM and MAJ. For the Wishart and the DSA approaches, the time must be increased by the number of iterations, i.e., two.

Table 4.
Averaged Cluster Separability values (R̄), Homogeneities (H̄) and CPU times for Wishart, HNN, DSA, ICM and MAJ for Baltic Sea Lakes (BSL) image.
3.3. Discussion
From the results above, we have verified that both the HNN and the DSA approaches achieve similar performances in terms of separability but with an important nuance. The HNN approach requires less iterations than the DSA approach to achieve the convergence. For the SFB dataset, the HNN requires a unique iteration and the DSA two iterations, and for BSL two and three iterations. From Figure 2, we can see that HNN and DSA obtain similar separability values in the first and second iterations. An important issue that needs to be considered concerns the HNN network stability. The fact that satisfactory classification results are obtained in the first iteration does not mean that the network has achieved a high degree of stability. Indeed, the energy continues to decrease, which means that it is still not stable. We have verified that the energy in HNN achieves a high degree of stability after the fourth iteration, but in terms of classification this number of iterations produces unacceptable over-homogenization in some regions of the image, which is detected by the increase of the averaged cluster separability value R̄. As mentioned before, DSA begins somewhat smoother than HNN, achieving its stabilization from the iteration four on. This means that a local instability in DSA appears before iteration four, which is not present in HNN. Additionally, HNN always evolves toward stable states. This behavior represents an improvement with respect to DSA.
Three main consequences can be derived from this evidence: (a) Both optimization strategies (HNN and DSA) are suitable for improving the Wishart classification results; (b) the dynamical behavior of HNN is more effective than DSA in capturing both the mutual influences exerted by the neighborhood and the self-influence; (c) HHN does not require the definition of two parameters to establish the trade-off of both mutual and self-influences.
HNN also outperforms ICM and MAJ in terms of averaged separability. This means that the greater the separabilities the better the classification decisions.
From the point of view of homogeneity, ICM and MAJ achieve slightly greater degrees of homogeneity. As the number of iterations increases, the classification results also display a high degree of homogenization. Although the general goal of the methods studied is designed toward homogenization, if this is excessive, the result is an over-homogenization, where relevant structures in the images could vanish. To deal with this problem, a trade-off must be achieved between preserving as many relevant structures as possible and the image homogenization. This is solved by the HNN and DSA optimization strategies, because they consider not only the neighbors but also explicitly the own node or pixel which is being updated, both under the corresponding energy term, which for HNN is defined in Equation (19). Moreover, the ability for mapping both coefficients (regularization and separation) into the HNN, Equation (19), makes this strategy an important contribution to obtaining better clustering.
Another important support coming from HNN and DSA is that both processes can be controlled by energy minimization. As displayed in Figure 3, with respect to the SFB image, the energy decreases as the number of iterations increases. During the two iterations of the Wishart, the energy is practically constant, but during the HNN process the energy clearly decreases with an important slope in the first iteration. The slope of DSA is also high, but in the third iteration. This means that the system under the HNN quickly achieves high stability in terms of energy. This implies, from the point of view of the classification, that the regions generally appear with a high degree of homogenization also after the first iteration. As mentioned before, successive iterations produce an over-homogenization effect and all the pixels in a given region are re-classified as belonging to the same cluster. We have verified that by establishing a trade-off between cluster separability and energy minimization, we can achieve the results displayed in Figure 4(b) or 4(c), representing an improvement in terms of quality with respect to the result obtained by the complex Wishart approach displayed in Figure 4(a). This trade-off determines the convergence criterion for the HNN as described in Section 2.3.5 and also for DSA in [18]. The same behavior is observed in the BSL dataset. The ICM method is also based on an energy minimization, and the energy also behaves with a similar tendency, but it does not include the separation coefficient representing a shortcoming with respect to HNN and DSA.
As reported in the work of Lee et al.[13] and also of Sánchez-Lladó et al.[18], we have verified that during the HNN optimization process, several cluster centers are shifted between the clusters changing their positions.
In [13] and [18] some qualitative improvements with respect to the SFB image are justified based on this fact, therefore the same is applicable in our approach, as summarized below. Hence, under a qualitative point of view, the observation of the images in Figures 4 and 5 allows to make the following considerations:
- The low entropy vegetation consisting of grass and bushes belonging to the cluster w2 has been clearly homogenized, this is because there are many pixels belonging to w4 in these areas re-classified as belonging to w2.
- The three distinct surface scattering mechanisms of the ocean surface identified in [13] are clearly displayed in Figure 4, i.e., they appear under the cluster labeled as w6 (area of high entropy), w8 (ripples, near the coast) and w9 (smooth ocean surface).
- Also, in accordance with [13], the areas with abundant city blocks display medium entropy scattering. We have homogenized the city block areas removing pixels in areas that belong to clusters w1 and w2, so that they are re-classified as belonging to w4 and w5 as expected.
- Some structures inside other broader regions are correctly isolated. This occurs in the rectangular area corresponding to a park, where the internal structures with high entropy are clearly visible [33].
- Additionally, the homogenization effect can be considered as a mechanism for speckle noise reduction during the classification phase, avoiding the early filtering for classification tasks.
From the qualitative point of view the qualitative analysis is more difficult in the image BSL, because the original image displays large and relatively high homogeneity areas, but still we can see how ICM and MAJ tend to eliminate some structures, because the specific self-influences coming from the pixels to which they belong are ignored during the updating process and all pixels in the neighborhood contribute equally.
4. Conclusions
This paper focuses on the performance of the optimization Hopfield Neural Network (HNN) strategy as a suitable method to improve the Polarimetric Synthetic Aperture Radar (PolSAR) data classification results obtained by the standard Wishart classifier. The proposed methodology has been tested considering two different datasets: An L-band PolSAR dataset over the San Francisco Bay (SFB) and a C-band PolSAR dataset over the region of the Baltic Sea Lakes (BSL). HNN has been favorably compared against existing strategies including the Deterministic Simulated Annealing (DSA), which is also based on optimization, ICM and Majority. This comparison is based on the computation of averaged class separability values. We also obtain results, which improve the ones obtained by the standard Wishart classifier. For SFB, these values are 65.5 for HNN, 67.8 for DSA, 71.5 for ICM, 93.1 for MAJ and 78.3 for Wishart. For BSL, the values are 22.4 for HNN, 22.4 for DSA, 24.2 for ICM, 25.9 for MAJ and 24.3 for Wishart. In both cases, lower values indicate better performances.
We achieve homogenization while preserving the most important structures inside broader areas. The proposed approach could be helpful to other procedures, like the one proposed in [34], where different labels from PolSAR data analysis are assigned to groups of pixels instead of the isolated pixels.
HNN has a greater ability than DSA to capture and embed the information coming from the neighboring pixels and also from the own pixel under classification. Unlike DSA, HNN does not require two additional parameters to combine both types of information: (a) A constant representing the trade-off between regularization and separation coefficients like the ones defined in Equations (15) and (16); (b) a coefficient that determines the influence of each node and its neighbors during the updating of the first.
Although the proposed HNN and DSA approaches were designed for homogenization purposes, these optimization approaches are able to enhance specific features, such as buildings or trees in forests, by redefining the regularization coefficient. Indeed, instead of applying reinforcement for similarities of the states between the central pixel and its neighbors, i.e. maximum consistency, we can apply maximum consistency for dissimilarities. This arises when the emphasis is put on differentiation rather than on similarity. Thus, HNN and also DSA are sufficiently flexible in this respect. Moreover, due to the flexibility of the HNN, we can define as many contextual coefficients (constraints) as required with the intention to capture different effects. These coefficients should be conveniently embedded under the energy function according to Equations (14) and (19).
The main drawback of the proposed approach is its relatively high computational cost, which is also inherent to the five approaches involved in our experiments. In SFB these times in minutes are: Wishart (6.01), HNN (2.02), DSA (4.62), ICM (2.28) and MAJ (2.35). In BSL they are: Wishart (2.20), HNN (0.76), DSA (0.77), ICM (0.75) and MAJ (0.81).
HNN is also able to assume any type of separability measures like the Fischer linear discriminant analysis [7], which is proposed as future work.
The effectiveness of this classification approach has been illustrated by the well-tested NASA/JPL AIRSAR L-band data of the San Francisco bay, where detailed and specific scattering mechanisms are preserved. The second test with the C-band dataset has shown the capability to deal with large distributed areas resulting in a preservation of the polarimetric scattering information and a noticeable reduction of the speckle noise component.
In this paper, we have considered an initial classification derived from a target decomposition theorem based on the eigen-analysis of the coherency matrix. With the aim to favor the physical interpretation of the physical information that may be extracted from PolSAR data, in the future, additional efforts should be extended to consider alternative target decomposition theorems for classification based on a direct physical interpretation of the coherency matrix [35]. HNN can be extended by defining new regularization and separation coefficients to cope with this situation.
Acknowledgments
This work has been partially funded by National I+D project TEC2011-28201-C02-01. The authors would like to thank the NASA/JPL and the Danish Center for Remote Sensing for providing the data employed in this study. Thanks are due to the anonymous referees for their very valuable comments and suggestions.
References
- Lee, J.S.; Grunes, M.R.; Pottier, E.; Ferro-Famil, L. Unsupervised terrain classification preserving scattering characteristics. IEEE Trans. Geosci. Remote Sens 2004, 42, 722–731. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ferro-Famil, L.; Pottier, E.; Lee, J.S. Unsupervised classification of multifrequency and fully polarimetric SAR images based on the H/A/Alpha-Whisart classifier. IEEE Trans. Gosci. Remote Sens 2001, 39, 2332–2342. [Google Scholar]
- Benz, U.; Pottier, E. Object Based Analysis of Polarimetric SAR Data in alpha-Entropy-Anisotropy Decomposition Using Fuzzy Classification by eCognition. Proceedings of IEEE Int. Geoscience and Remote Sensing Symposium (IGARSS ’01), Sydney, Australia, 9–13 July 2001; pp. 1427–1429.
- Hara, Y.; Atkins, R.G.; Yueh, S.H.; Shin, R.T.; Kong, J.A. Application of neural networks to radar image classification. IEEE Trans. Geosci. Remote Sens 1994, 32, 100–110. [Google Scholar]
- Du, L.; Lee, J.S. Fuzzy classification of earth terrain covers using complex polarimetric SAR data. Int. J. Remote Sens 1996, 17, 809–826. [Google Scholar]
- Grandi, G.D.; Lucas, R.M.; Kropacek, J. Analysis by wavelet frames of spatial statistics in SAR data for characterizing structural properties of forests. IEEE Trans. Geosci. Remote Sens 2009, 47, 494–507. [Google Scholar]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens 1996, 34, 498–518. [Google Scholar]
- Cloude, S.R.; Pottier, E. Application of the H/A/a polarimetric decomposition theorem for land classification. Proc. SPIE 1997, 3120, 132–143. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of PolSAR. IEEE Trans. Geosci. Remote Sens 1997, 35, 68–78. [Google Scholar]
- Pottier, E.; Lee, J.S. Unsupervised Classification Scheme of Pol-SAR Images Based on the Complex Wishart Distribution and the H/A/α Polarimetric Decomposition Theorem. Proceedings of EUSAR, Munich, Germany, 23–25 May 2000; pp. 265–268.
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens 1994, 15, 2299–2311. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Ainsworth, T.; Du, L.J.; Schuler, D.; Cloude, S. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier. IEEE Trans. Geosci. Remote Sens 1999, 37, 2249–2258. [Google Scholar]
- Hopfield, J.J.; Tank, D.W. Neural computation of decisions in optimization problems. Biol. Cyber 1985, 52, 141–152. [Google Scholar]
- Hopfield, J.J.; Tank, D.W. Computing with neural circuits: A model. Science 1986, 233, 625–633. [Google Scholar]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Machine Intell 1979, 1, 224–227. [Google Scholar]
- Wang, D. The time dimension for scene analysis. IEEE Trans. Neural Netw 2005, 16, 1401–1426. [Google Scholar]
- Sánchez-Lladó, F.J.; Pajares, G.; López-Martínez, C. Improving the Wishart synthetic aperture radar image classifications through deterministic simulated annealing. ISPRS J. Photogramm 2011, 66, 845–857. [Google Scholar]
- Joya, G.; Atencia, M.A.; Sandoval, F. Hopfield neural networks for optimization: Study of the different dynamics. Neurocomputing 2002, 43, 219–237. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Macmillan College Publishing Co.: New York, NY, USA, 1994. [Google Scholar]
- Qiao, H.; Peng, J.; Xu, Z.B. Nonlinear Measures: A new approach to exponential stability analysis for Hopfield-type neural networks. IEEE Trans. Neural Netw 2001, 12, 360–370. [Google Scholar]
- Yu, S.S.; Tsai, W.H. Relaxation by the Hopfield Neural Network. Pattern Recog 1992, 25, 197–209. [Google Scholar]
- Kasetkasem, T.; Varshney, P.K. An image change detection algorithm based on Markov Random field models. IEEE Trans. Geosci. Remote Sens 2002, 40, 1815–1823. [Google Scholar]
- Starink, J.P.; Backer, E. Finding point correspondences using simulated annealing. Pattern Recog 1995, 28, 231–240. [Google Scholar]
- van Laarhoven, P.M.J.; Aarts, E.H.L. Simulated Annealing: Theory and Applications; Kluwer Academic Publishers: Boston, MA, USA, 1988. [Google Scholar]
- Hajek, B. Cooling schedules for optimal annealing. Math. Operation Res 1988, 13, 311–329. [Google Scholar]
- Kosko, B. Neural Networks and Fuzzy Systems: A Dynamical Systems Approach to Machine Intelligence; Prentice-Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Cohen, M.A.; Grossberg, S.G. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cyber 1983, 13, 815–826. [Google Scholar]
- Lee, D.L.; Chuang, T.C. Designing asymmetric Hopfield-type associative memory with higher order Hamming stability. IEEE Trans. Neural Netw 2005, 16, 1464–1476. [Google Scholar]
- Zhao, Z.Q. A novel modular neural network for imbalanced classification problems. Pattern Recog. Lett 2009, 30, 783–788. [Google Scholar]
- Müezzinoglu, M.K.; Güzelis, C.; Zurada, J.M. An energy function-based design method for discrete Hopfield associative memory with attractive fixed points. IEEE Trans. Neural Netw 2005, 16, 370–378. [Google Scholar]
- Idbraim, S.; Aboutajdine, D.; Mammass, D.; Ducrot, D. Classification of Remote Sensing Imaging by an ICM Method with Constraints: Application in Land Cover Cartography. Proceedings of IEEE International Conference on Multimedia Computing and Systems (ICMCS’09), Ouarzazate, Morocco, 2–4 April 2009; pp. 472–477.
- Google Earth. The Google Earth Product Family. Available online: http://www.google.es/intl/es/earth/index.html (accessed on 20 September 2012).
- Turner, D.; Woodhouse, I.H. An icon-based synoptic visualization of fully polarimetric radar data. Remote Sens 2012, 4, 648–660. [Google Scholar]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S-E.; Kobayashi, H.; Singh, G. Three-component power decomposition for polarimetric SAR data based on adaptive volume scatter modeling. Remote Sens 2012, 4, 1559–1572. [Google Scholar]