Abstract
A decomposition scheme was applied to ALOS/PALSAR data obtained from a fast-growing tree plantation in Sumatra, Indonesia to extract tree stem information and then estimate the forest stand volume. The scattering power decomposition of the polarimetric SAR data was performed both with and without a rotation matrix and compared to the following field-measured forest biometric parameters: tree diameter, tree height and stand volume. The analytical results involving the rotation matrix correlated better than those without the rotation matrix even for natural scattering surfaces within the forests. Our primary finding was that all of the decomposition powers from the rotated matrix correlated significantly to the forest biometric parameters when divided by the total power. The surface scattering ratio of the total power markedly decreased with the forest growth, whereas the canopy and double-bounce scattering ratios increased. The observations of the decomposition powers were consistent with the tree growth characteristics. Consequently, we found a significant logarithmic relationship between the decomposition powers and the forest biometric parameters that can potentially be used to estimate the forest stand volume.
1. Introduction
In recent years, industrial plantations have been rapidly expanding in many parts of the world due to a number of factors: paper companies require a stable supply of pulp, electric power companies are interested in producing biofuel feed-stocks and other companies anticipate the expansion of carbon-trading. Plantation expansions seem inevitable because of the annually increasing global demand for paper. Therefore, it is becoming increasingly clear that the sustainable use of industrial plantations requires continuous investigation to monitor their land productivity and estimate the forest stand volume for commercial purposes.
Earth surface surveys currently take full advantage of remote satellite sensing technology. Both optical and microwave satellites provide key information on forest resources that are very important for the sustainable management of the environment. However, the persistent presence of water vapor and clouds makes continuous monitoring using optical satellite data unfeasible particularly over tropical regions.
Microwave radar imaging satellites are therefore expected to conduct periodic forest monitoring. Polarimetric synthetic aperture radar (POLSAR) is an advanced technology that provides image data with phase (scattering matrix) information, which has made it a center of attention in recent years as an effective instrument for identifying land cover and estimating forest biomass [1–7].
In POLSAR data analysis, the normalized radar cross section (σ0) is used as a calculated parameter [5,7–9]. However, there is a great deal of interest in making effective use of other parameters derived from the decomposition of the polarimetric information from the target. The target decomposition theorem has been developed to extract surface features from radar polarimetry data. Both the three-component scattering model developed in [10] and the entropy/alpha decomposition method developed in [11] have been commonly used and are currently being improved for more accurate target classification [12–15]. The Freeman and Durden approach [16] was developed based on the three-component scattering model, which represents the surface, double-bounce and volume (canopy) scatterings. This scheme was further improved by the addition of a helix scattering term as a fourth component and the modification of the volume scattering model [12]. Furthermore, Yamaguchi et al. [13] improved the four-component decomposition scheme using matrix rotation to enhance the results by allowing oriented urban areas previously and mistakenly included in the volume scattering component as double-bounce scattering to be distinguished. In addition to the POLSAR data, there has been an increase in research on the use of Polarimetric Interferometry SAR (POLinSAR) techniques [2,6] particularly for tree height estimations.
In this study, we examine the polarimetric SAR image decomposition scheme. A few studies have attempted to retrieve forest structural parameters, such as the tree diameter, tree height and timber volume, using polarimetric decomposition theorems. Garestier et al. [1] conducted an eigenvector decomposition scheme that showed a linear correlation between the anisotropy and tree height using a P-band over pine trees. Gonçalves et al. [4] reported the usefulness of the volume scattering derived from the Freeman and Durden decomposition and several other backscattering coefficients for tropical forests using the L-band. Notably, targets in both of these studies [1,4] had thick stems, and the studied tropical forests [4] had a dense canopy. Moreover, very few studies have examined the fast-growing tree forests with thin stems and low canopy densities. Fast-growing trees in the commercial Eucalyptus plantations were investigated using backscattering coefficients from the JERS-1 single-polarization SAR image [17] and by interferometry SAR [2] for biomass estimation.
It is well known that the accuracy of forest biometric parameter estimations is site-dependent [8,18] and affected by the forest structure [19,20], shape and dimensions of leaves and stems [21], and the ground conditions. Little is known about the backscattering characteristics of Acacia trees under a power decomposition scheme.
In our previous work [22], we obtained the following characteristic features for the backscattering cross section of an L-band SAR over planted Acacia forests: (i) the regression between the normalized radar cross section (σ0) and the forest stand parameter fits a negative quadratic curve because of the stronger backscattering from approximately two year old trees, and the weaker backscattering from both trees younger than two years and more mature trees; (ii) the optical NDVI values for trees older than two years tend to decrease. These findings suggest that the L-band SAR is strongly affected by the acacia tree foliage.
Therefore, the aim of this study was to extract tree trunk information for the planted Acacia Mangium forests via the decomposition of multi-polarimetric SAR data, and find out the relationship between the decomposition powers and the in-situ forest biometric data through an integrated analysis. From the above findings, we attempted to formulate a methodology for estimating the forest stand volume.
2. Study Area
The study area is located in the southeastern part of the island of Sumatra, Indonesia (Figure 1(a)). There are approximately 10 units in the plantation area managed by the plantation company with each one being considered a maximum management unit. Our targeted area was the unit (Unit V) situated between 3°36′48″S and 3°58′54″S latitude and 103°50′42″E and 103°58′23″E longitude (Figure 1(b)). It covers approximately 282.9 km2 with an altitude ranging from 41 to 253 m (average of 111.5 m) above sea level and a slope varying from 0 to 14.9 degree (3.4° on average).
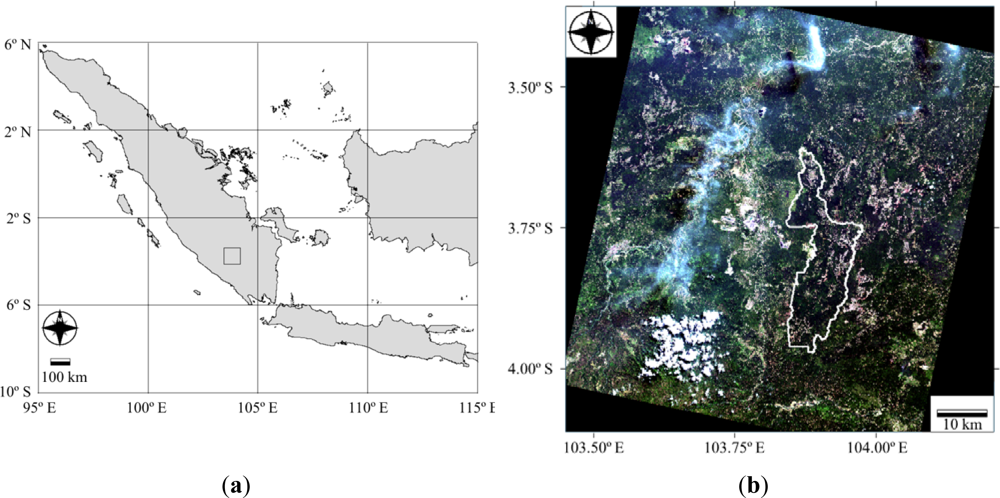
Figure 1.
(a) The location of the study area in Sumatra, Indonesia (small black square). (b) The area of Unit V (white line) superimposed on a true color composite image from ALOS AVNIR2 data.
The total plantation area covers 134.7 km2 (equivalent to 47.9%) of the total area of Unit V (the unit area is not used exclusively for industrial plantations). The mean annual rainfall varies between 2,000 and 3,000 mm per year. This area has a tropical climate; a dry season prevails between June and September, and a rainy season prevails between October and May with two rainfall peaks in December–January and March–April. The average daily temperature is 29 °C, the average minimum temperature is 21 °C and the average maximum temperature is 32 °C.
The plantation area consists of a single-layer forest of Acacia Mangium, which is a fast-growing tree normally harvested between 6 and 7 years after planting the seedlings. Tree planting in this area began in 1990 with the approval of the Indonesian Government on initially unproductive sites where alang-alang (Imperata cylindrica) grass and poor secondary forests dominated [23].
3. Data Sets
3.1. Field Measured Forest Biometric Data
Datasets containing the forest biometric parameters (hereafter forest parameters) for the period from 2006–2008 were made available by the Indonesian tree planting company. These forest parameters are obtained via regular ground-based observations performed at the permanent sample plots (PSPs) marked by the yellow colored circles in Figure 2. The 32 PSPs are randomly distributed within the plantation area (Unit V) for collecting the in-situ data. The company conducts field observations once a year for every PSP. The data observed from the PSPs contain the following parameters: (1) tree diameter at breast height (DBH) in centimeters, (2) tree height (H) in meters and (3) tree density or tree numbers per hectare (N). Additionally, (4) the form factor of the Acacia Mangium stems in this plantation area was also provided by the company. Both the DBH and H were measured for all of the trees, and N was counted within the perimeter of each PSP. The DBH and standing tree height were measured using a diameter tape and clinometer, respectively, while the form factor of the stem was measured on felled sample trees.
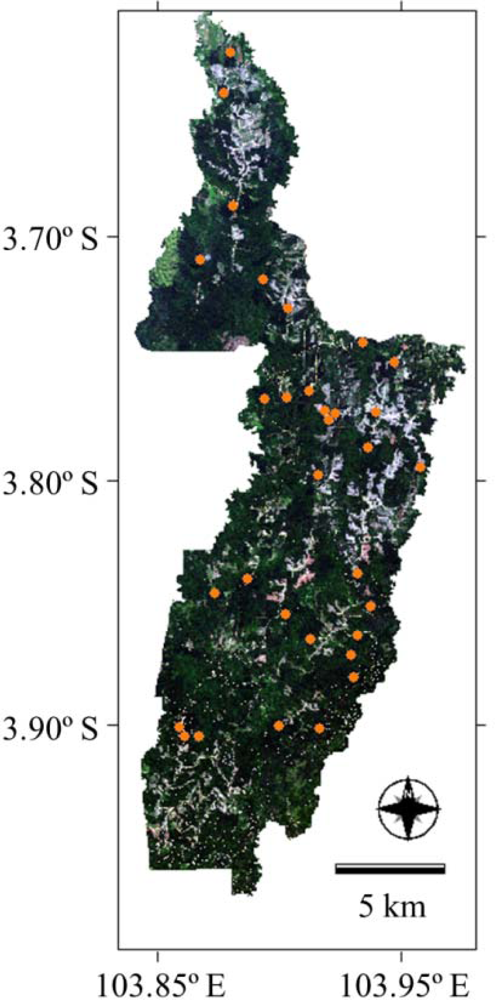
Figure 2.
Unit V represented using a true color composite image. Yellow circles mark the permanent sample plots (PSPs) where the field observations were conducted.
The perimeter of each PSP is rhomb-shaped with 31.6 m diagonals within which individual trees are placed three meters apart in a triangular pattern. This arrangement provides 60 trees growing in each 0.05 ha PSP. The planting and harvesting of the trees are conducted once for each forest stand. Unit V is composed of 3,668 forest stands, which means that the PSPs only represent 0.87% of the total number of forest stands.
In addition to the numerical database mentioned above, the following geographical information, which is essential for GIS (Geographical Information System) analyses, was provided by the planting company: (i) the point vector data for the PSPs (Figure 2) and (ii) polygon vector data for the forest stand boundaries (see 2nd figure in Section 5.1 for reference).
3.2. Satellite Data Sets
We used satellite imagery taken by the ALOS (Advanced Land Observing Satellite) provided by the JAXA (Japan Aerospace Exploration Agency). This satellite was loaded with PALSAR (Phased Array type L-band Synthetic Aperture Rader) microwave L-band sensors (wavelength: 23 cm) that enabled the acquisition of polarimetric radar data with a multi-polarization mode. The spatial resolution was 30 m in the range direction and 5 m in the azimuth direction. The full polarimetric data with four polarizations (HH + HV + VH + VV) used in this study were acquired on 20 May 2007 with an off-nadir angle of 21.5° in the ascending orbit. These are the only full-polarimetric PALSAR data available for the 2006–2008 period when the field observational data were also acquired. The precipitation on the data acquisition date reached 0.5 mm with a 3-day average (18–20 May) of 1.3 mm before the observation. Level 1.1 datasets consisting of complex scattering data were both utilized and analyzed with the ground-observed forest parameters using MATLAB, IDRISI and GIS software for image processing and Cartalinx for vector format editing.
4. Analysis Methodology
4.1. Forest Biometric Parameters
First, the averaged DBH and H values for each PSP were calculated. Second, the basic forest biometric parameters (DBH, H and N) for the date the satellite image was taken were interpolated using linear regression analysis between two known points, that is, the anterior and posterior ground observation values. The above procedure is necessary because the ground observations are conducted all year round throughout the entire plantation area, which means the observations were not all made at the same time for all of the PSPs in Unit V and not on the same day as the satellite data. The initial DBH, H and N values on the planted date were used for the interpolation of PSPs with young trees and only a single ground measurement. These initial values were estimated using sigmoidal growth curves, which yield 1.91 cm and 1.07 m for DBH and H, respectively [22]. The initial N value calculated based on the planting pattern and interval is 1,200 trees/ha.
These interpolated DBH, H and N values were used with a stem volume form factor of 0.48 [24] to calculate the forest stand volume (V) per hectare (in m3/ha) as follows:
4.2. Satellite Remote Sensing Data
4.2.1. Covariance and Coherency Matrix
The covariance matrix ([C]) and coherency matrix ([T]) of the second order statistics were first calculated [25]. In the case of reciprocity [10], where SVH = SHV, the covariance matrix is given as the following:
where the superscript * denotes complex conjunction, and SHH, SVV and SHV indicate the scattering matrix components for the HH, VV and HV polarizations, respectively. The coherency matrix can be calculated by the unitary transformation of the covariance matrix using the following equation:
where † denotes complex conjunction and transposition, and the unitary matrix ([Up]) is expressed as
4.2.2 Pre-Processing of the PALSAR Data
The following radiometric and geometric corrections were performed because the level 1.1 PALSAR datasets were calibrated by JAXA. First, for the speckle filtering of the radiometric correction, a boxcar filter (i.e., a moving average filter) with 0.25:0.5:0.25 weighting factors in only the azimuthal direction was applied to both the covariance and coherency matrices. This filter reduced the short wavelength modes of the Fourier spectrum F(k) as expressed by F(k)(cos(kΔx/2))2, where Δx is the spatial resolution in the azimuth direction. The applied look number was 3 (1 × 3 window). This window size seems relatively small for reducing the speckle noise [26]. However, we adopted this look number because the spatial scale of some forest stands was exceedingly small, for example, 0.0011 km2. The filtered covariance and coherency matrices are denoted as ⟨[C]⟩ and ⟨[T]⟩, respectively.
For the geometric corrections, the slant to ground range conversion was applied in order to both correct the incidence angle of the radar beam and to register the remotely sensed imagery to a reference system grid (the Universal Transverse Mercator (UTM) coordinate system). Considering that the study area is almost flat, it was assumed that the relief influence was small, and the local topographic effects were therefore not accounted for. The inverse distance weighted (IDW) interpolation method was then applied with a weighting factor of one. The pixel spacing was consequently set to 30 m in the range direction and 15 m in the azimuth direction based on the speckle filtering size.
4.2.3. Rotation of Coherency Matrix
We used the four-component scattering model for image decompositions both with and without the matrix rotation developed by Yamaguchi et al. [12,13]. Importantly, while the four-component scattering model was developed for urban settings, it applies to any scenario because it is a general theoretical decomposition for any polarimetric data. The helix power is the same as the circular polarization power and can be caused by a spaced and oriented dipole structure (branches) dependent on frequency.
The rotated coherency matrix ⟨[T(θ)]⟩ can be obtained from the matrix ⟨[T]⟩ and a rotation matrix [Rp(θ)], which are defined as
and
respectively, and using the following transformation:
The rotation angle (θ) can be obtained using
The rotation angle was calculated for each filtered pixel. The rotated coherency matrix is transformed into a covariance matrix using a unitary matrix denoted as ⟨[C(θ)]⟩ and calculated by
The covariance matrix and coherency matrix are mutually convertible via a unitary transformation. Consequently, they are mathematically equivalent and contain the same information [25].
4.2.4. Decomposition of Covariance and Rotated Covariance Matrices
Yamaguchi et al. [12] proposed a four-component scattering model based on the covariance matrix for the polarimetric SAR data decomposition. We applied this method to the ALOS/PALSAR data for both the covariance matrix ⟨[C]⟩ and rotated covariance matrix ⟨[C(θ)]⟩ to obtain the decomposition powers, which consist of the surface scattering, double-bounce scattering, canopy (volume) scattering and helix scattering. The four-component scattering terms from the covariance matrix ⟨[C]⟩ are expressed as
while the terms from the rotated covariance matrix ⟨[C(θ)]⟩ are specified by
where fs, fd, fc as well as fh, and fs(θ), fd(θ), fc(θ) and fh(θ) are the expansion coefficients (f) needing to be evaluated, and ⟨[C]⟩s, ⟨[C]⟩d, ⟨[C]⟩c and ⟨[C]⟩h are the scattering models for the surface, double-bounce, canopy and helix scatterings, respectively. Each of the four-component powers, P (Ps, Pd, Pc, Ph) from ⟨[C]⟩ and P(θ) (Ps(θ), Pd(θ), Pc(θ), Ph(θ)) from the rotated ⟨[C(θ)]⟩, can be determined from the traces of fs⟨[C]⟩s, fd⟨[C]⟩d, fc⟨[C]⟩c and fh⟨[C]⟩h and fs(θ)⟨[C]⟩s, fd(θ)⟨[C]⟩d, fc(θ)⟨[C]⟩c and fh(θ)⟨[C]⟩h, respectively.
It is worth mentioning that the third parameter in Equations (10) and (11) is normally referenced as the volume scattering and denoted by a “v” in the subscript. However, in this paper, we analyzed the relationship with the stand volume. Hence, the term “canopy scattering” is used instead of “volume scattering” and “c” is used in the subscript to avoid confusion. We note that the subscript “c” is commonly used for helix scattering; however, we use the subscript “h” for the helix component.
4.3. Correlation Analysis between Forest Biometric Parameters and Decomposition Powers
The polarimetric SAR information was statistically compared to the ground observations of the forest parameters (DBH: diameter at breast height, H: height and V: stand stem volume). Statistical comparisons were first performed between the base 10 logarithms of the forest parameters (log10DBH, log10H and log10V) and (i) the base 10 logarithms of the decomposition powers, P (log10P), from the covariance matrix ⟨[C]⟩, and (ii) those for P(θ) (log10P(θ)) from the rotated covariance matrix ⟨[C(θ)]⟩.
The decadic logarithm is often used to investigate the relationship between microwave backscattering and forest parameters [2,17]. Moreover, acacia trees grow rapidly between the ages of 0 and 3 years with annual increments of approximately 4–5 cm/year for the DBH and approximately 4 m/year for the tree height, and these growth rates progressively decrease after 3 years [22]. Therefore, the logarithmic conversion of the forest parameters is instrumental in determining the linear relationship via correlation analysis.
The forest parameters were then compared to the decomposition power, P(θ), normalized by the total power (TP), namely, P(θ)/TP (Ps(θ)/TP, Pd(θ)/TP, Pc(θ)/TP and Ph(θ)/TP). This calculation indicates the variation in the ratio of the decomposition powers to the total power between pixels. The TP is calculated as follows:
A linear correlation analysis was performed between the PSP forest parameters and the average decomposition powers from the forest stands. This approach is based on the assumption that each forest stand is a uniform entity because it is managed as a whole as mentioned above. Such analyses based on forest stand information are common in other studies as well [1,4,5,20,27].
The vector data of the PSPs and forest stands were geo-referenced with the satellite raster data using ground control points (GCPs), which yielded a total RMS (root mean square) error of 8.27 m. The polygon boundary of the forest stands were rasterized and optimized with edge treatment to extract the satellite data. To obtain an edge-eroded forest stand, any pixels within the forest stand boundary and designated buffer zones, which are approximately 15 m from the boundary line, were eliminated from the area. Moreover, forest stands less than 0.0144 km2 in area (equal to 120 m × 120 m) were excluded from further analysis. Consequently, 26 forest stands remained as those with PSPs, and only the edge-eroded forest stands with enough dimensions were utilized in the following analyses.
5. Data Analysis Results
5.1. Visual Interpretation of Decomposition SAR Image
Figure 3(a–c) shows the composite images of the decomposition powers, RGB = double-bounce, canopy and surface scattering for log10P, log10P(θ) and P(θ)/TP, respectively, for the forest stands in Unit V. There was not much difference between the first two images (Figure 3(a–b)), whereas the P(θ)/TP image (Figure 3(c)) showed a significant color change relative to those for the log10P and log10P(θ).
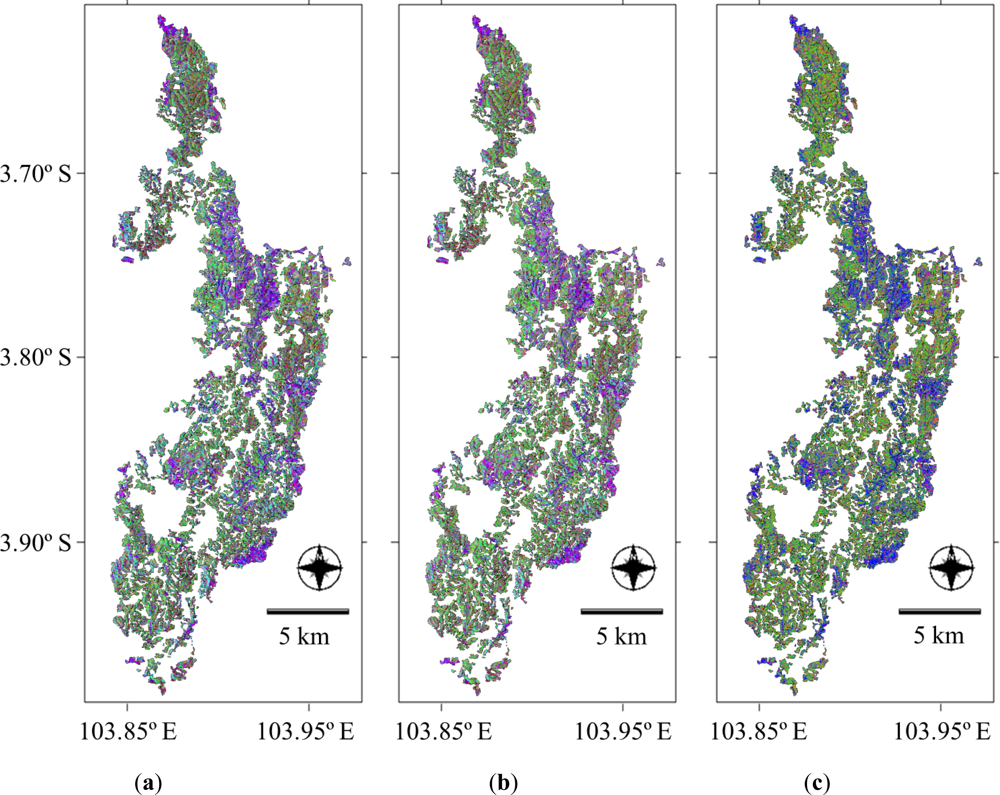
Figure 3.
Composite images of the decomposition powers (RGB = double-bounce/canopy/surface scattering) for (a) log10P, (b) log10P(θ) and (c) P(θ)/TP.
Notably, each forest stand had similar color tones. The portions where the blue color dominates in Figure 3(c) indicate the dominance of surface scattering in places with exposed ground in young forest stands without a thicker and extended canopy or those between harvesting and planting periods. The regions with green color have strong canopy scattering from canopy structures containing leaves and branches.
Figure 4(a) shows an enlarged portion from Figure 3(c) with the forest stand vectors marked by a thin black line. Figure 4(b) shows the same area as Figure 4(a) using the base 10 logarithm of tree age as the attribute. The inflection point in the figure is −0.3 (equal to 0.5 years old), which markedly illustrates the difference between the younger and mature stands. The tree age refers to the number of years since the seedling was planted. The transparent polygons in Figure 4(b) have no tree age data. Indeed, the forest growth is not fully proportional to the tree age. However, the only data that was available for the entire forest stand was the tree age. Hence, we compare Figure 4(a,b). The blue parts in Figure 4(a) are mostly blue in Figure 4(b) and denote younger trees, whereas the green parts in Figure 4(a) are shown in red in Figure 4(b) and indicate older trees. Note that the colors within some forest stands are not consistent with current understanding. These anomalies are attributed to the time lag since the latest harvesting information was available.
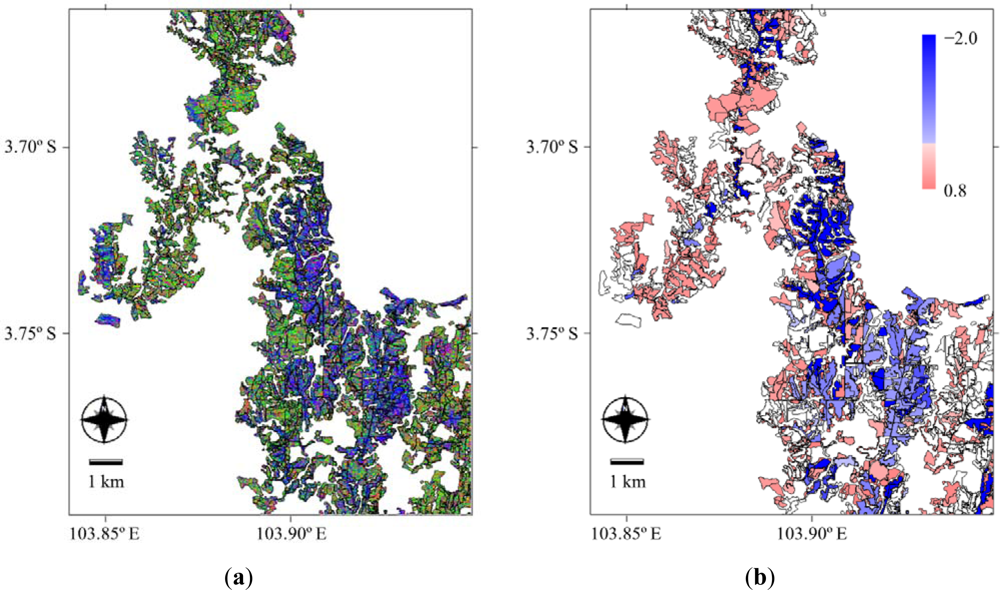
Figure 4.
(a) Enlarged portion of the composite P(θ)/TP image (Figure 3(c)) with the forest stand vector data, which are shown by a thin black line; (b) forest stand polygons with a base 10 logarithm of the tree age (inflection point = −0.3). The transparent polygons have no tree age data.
5.2. Forest Biometric Parameters and Decomposition Powers
The decomposition powers were separately extracted from and averaged over each of the forest stands containing a PSP for the comparison to the ground-based observation data of the forest parameters. Details of the field-measured data used in this study were given in [19]. The correlation analysis was performed between the base 10 logarithms of the forest stand parameters, namely, log10DBH (Figure 5(a)), log10H (Figure 5(b)) and log10V (Figure 5(c)) on the x-axis and the base 10 logarithms of each of the decomposition powers (log10P) on the y-axis.
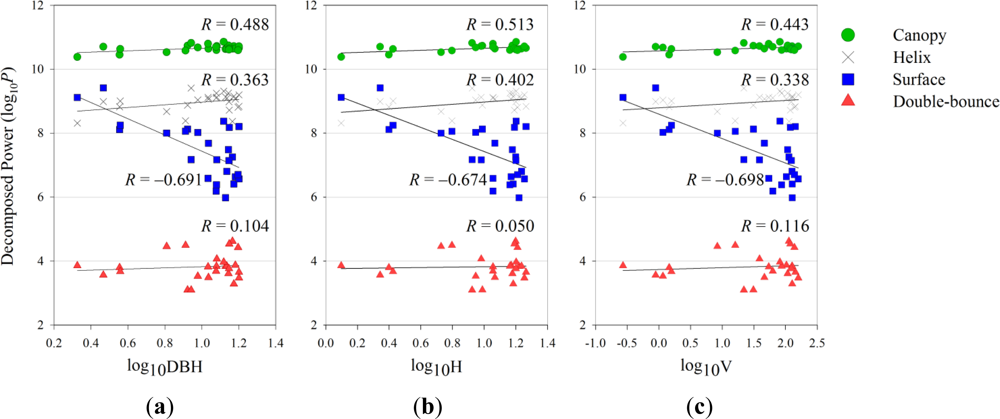
Figure 5.
Correlation analysis between the base 10 logarithms of the (a) tree diameter at breast height (DBH). (b) tree height and (c) forest stand volume on the x-axis and the base 10 logarithms of the decomposition powers (P) (surface, double-bounce, canopy and helix scatterings) calculated from the covariance matrix (log10Ps, log10Pd, log10Pc and log10Ph) on the y-axis.
The decomposition power shown in Figure 5 includes the following: (1) Ps, the surface scattering (the blue colored squares), (2) Pd, the double-bounce scattering (red colored triangles), (3) Pc, the canopy scattering (green colored circles) and (4) Ph, the helix scattering (cross marks). The same symbols and colors are also used in Figures 6–7. The fourth helix scattering is known to primarily occur in urban areas but not natural land-cover environments and is only shown for reference.
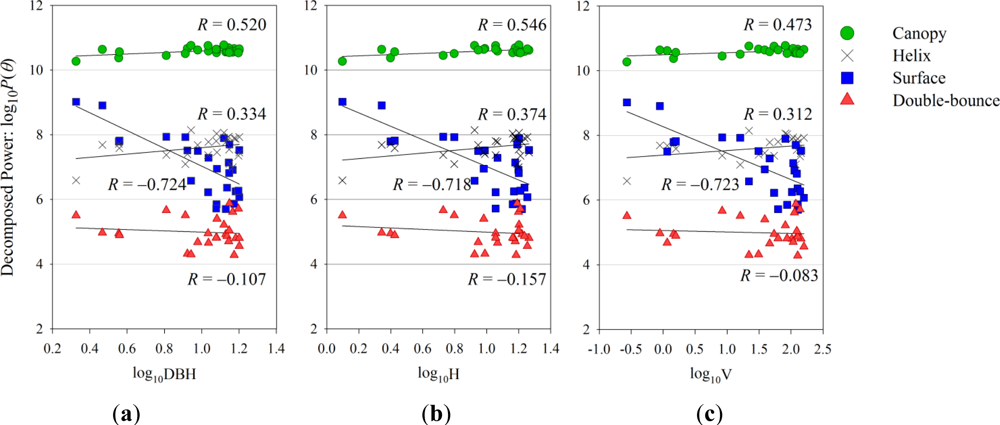
Figure 6.
(a–c) Same as in Figure 5(a–c), except the decomposition powers are calculated from the rotated covariance matrix of log10Ps(θ), log10Pd(θ), log10Pc(θ) and log10Ph(θ) on the y-axis.
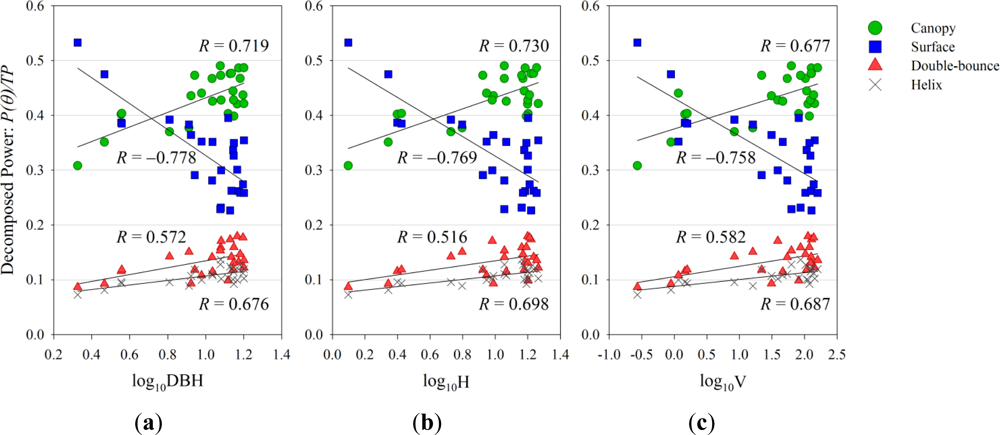
Figure 7.
Correlational analysis (a) between the base 10 logarithms of DBH (log10DBH) and the ratios of the decomposition powers to the total power (P(θ)/TP), (b) between log10H and P(θ)/TP, (c) between log10V and P(θ)/TP, including Ps(θ)/TP, Pd(θ)/TP, Pc(θ)/TP and Ph(θ)/TP.
Similarly, Figure 6(a–c) shows the results from the analysis between the same forest parameters and the base 10 logarithms of P(θ). A Pearson’s correlation coefficient (R) was calculated to evaluate the linear dependence of log10P and log10P(θ) on the forest parameters (Table 1(a–b)).

Table 1.
Correlation coefficients (R) between the base 10 logarithms of the forest parameters and the base 10 logarithms of the decomposition powers: (a) P calculated from the covariance matrix and (b) P(θ) from the rotated covariance matrix.
The trends in the relationship between log10P and log10P(θ) on the one side and the base 10 logarithm of DBH, H and V on the other side are almost identical for each scattered power. However, the P(θ) correlation (Figure 6) is slightly better than that of P (Figure 5) for the surface and canopy scatterings. The surface scattering has a significantly negative correlation (R ≈ −0.70) and the canopy scattering has a medium positive correlation (R ≈ 0.50) with the forest parameters as the forest grows older, whereas the double-bounce scattering does not show any correlation (R ≈ ±0.10).
Figure 7(a–c) illustrates the relationship between the base 10 logarithm of the forest parameters and P(θ)/TP. The correlations became clearer and stronger than those of P (Figure 5(a–c)) and P(θ) (Figure 6(a–c)) for all the decomposition powers. The correlation coefficients were substantially improved especially for the double-bounce and canopy scatterings, which have correlation coefficients above 0.50 and 0.65, respectively. The P-values were less than 0.001 for the surface and volume scatterings and less than 0.002 for the double-bounce scattering (except for H), which indicate the statistical significance of the correlations (Table 2).

Table 2.
Correlation coefficients (R) and P-values between the base 10 logarithms of the forest parameters DBH (log10DBH), height (log10H) and stand volume (log10V) and the P(θ)/TP; ratios of the decomposition powers to the total power.
5.3. Forest Stand Volume Estimation using Decomposition Powers
According to the results discussed in Section 5.2, the P(θ)/TP values correlated well with the stand volume (V) values with an R = −0.758, 0.582 and 0.677 for the surface, double-bounce and canopy scatterings, respectively (Table 2). Based on these findings, we empirically derived the following estimation formula for the forest stand volume as a function of the ratio of these three scattering components, namely, Ps(θ)/TP, Pd(θ)/TP and Pc(θ)/TP:
The nonlinear regression line was as follows:
Figure 8 shows a scatter diagram and logarithmic regression line with the calculated parameter on the x-axis and the base 10 logarithm of the stand volume (log10V) on the y-axis. The determinant coefficient (R2) is 0.557 for a P-value below 0.001. The statistical test results of the nonlinear regression analysis and the analysis of variance are shown in Table 3.
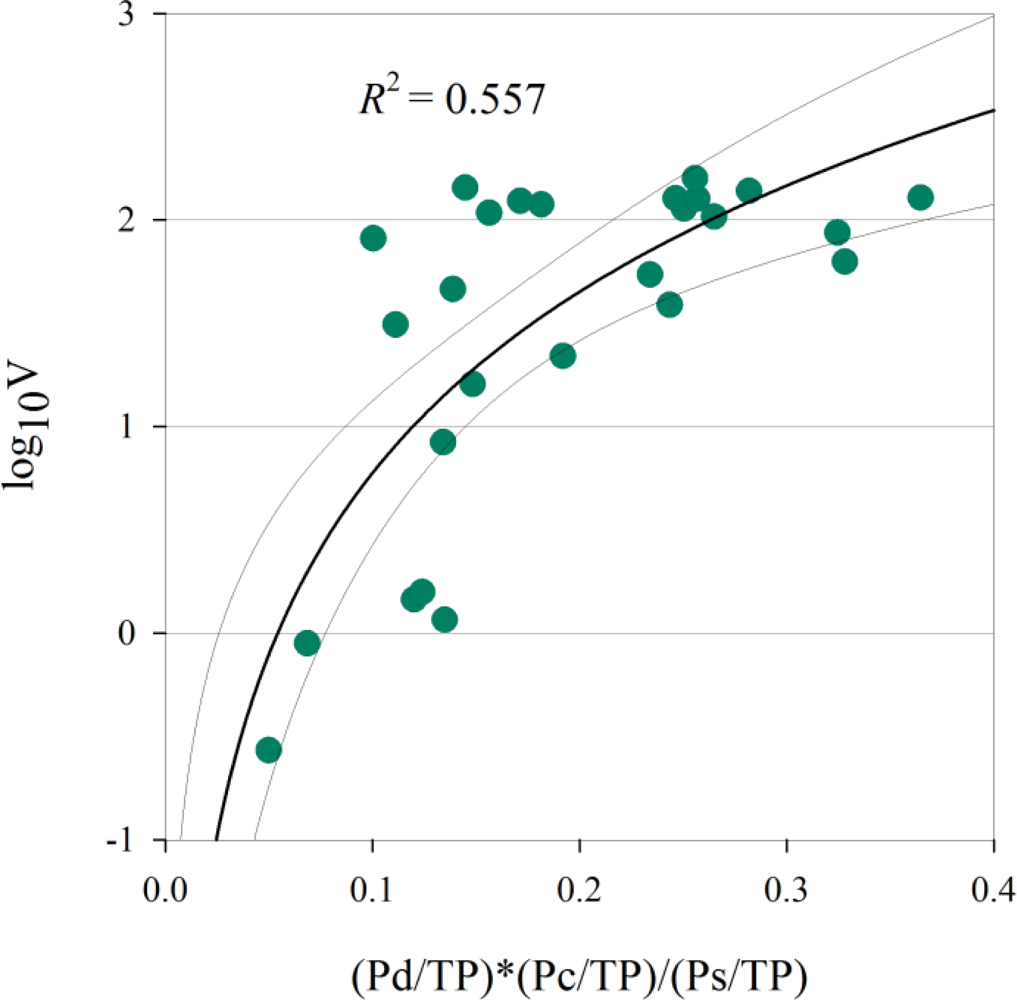
Figure 8.
Scatterplot and logarithmic regression (thick line) of the parameters with the decomposition powers divided by the total power (P(θ)/TP) on the x-axis and the base 10 logarithm of the stand volume (log10V) on the y-axis. The 95% confidence band is shown by thin lines.

Table 3.
Statistical test of the logarithmic regression shown in Figure 8. The degrees of freedom are displayed in the DF column, the calculated sum of the square terms is displayed in the SS column, and the mean square terms are displayed in the MS column. The corresponding F statistics and P-values are also provided.
6. Discussion
6.1. Differences among Decomposition Powers
Comparing Figure 5(a–c) to Figure 6(a–c) indicates that the P and P(θ) scattered powers are characterized by the same correlation to the forest parameters: a high negative correlation for the surface scattering, a medium positive correlation for the canopy scattering and no correlation for the double-bounce scattering. Two of the composite images (Figure 3(a,b)) did not show any clear distinctions between these parameters. However, P(θ), which is derived from the rotated matrix, showed a slightly higher correlation than P for both the surface and canopy scatterings.
Combining the power decomposition scheme with the matrix rotation method [13] enhanced the results in oriented urban areas, which are difficult to distinguish from the vegetation and were previously classified as part of the canopy scattering. However, it is apparent from the current analysis that the new scheme can be useful for forest identification even in areas covered by forest vegetation.
Our approach is based on calculating the ratio of the decomposition powers to the total power (Figure 7(a–c)), which leads to new insights into the relationship between the decomposition powers and forest parameters. The obtained results indicate a very significant and improved correlation for all of the decomposition powers. This approach is based on the fact that the total backscattered power varies between pixels. Thus, the ratio indicates the contribution of the decomposition powers to the total power in terms of the scattering characteristics for each pixel as previously described by Freeman and Durden [10]. Our previous work [22] indicated a similar σ0 level for both young and more mature trees. Hence, ratio calculations would be an effective approach to determine the forest structural parameters, especially in the present study area.
Furthermore, a comparison between the composite P(θ)/TP image in Figure 4(a) and the tree age in Figure 4(b) clearly demarcates the bare ground and less vegetated land, either because of harvesting or other causes. This explicitly demonstrates that the decomposition images derived from the multi-polarimetric SAR data have potential for forest management studies.
6.2. Physical Understanding of Scattering Characteristics
Gonçalves et al. [4] used airborne L-band SAR data to apply the Freeman and Durden decomposition scheme [10]. They showed that all of the scattering contributions to the total power were positively correlated (after removal of outliers) to the stem volume of the tropical forests. However, the physical significance of the observed trends was not discussed. In this study based on the results of the decomposition powers divided by the total power (Figure 7(a–c)), the surface scattering power relative to the total power revealed a significant negative correlation, whereas both the volume and double-bounce relative scatterings had strong positive correlations to the forest parameters. The physical explanation for these observed relationships is the following: as the forests grow, (i) the decreasing exposure of the bare ground reduces the surface scattering, while (ii) the canopy layer grows thicker and more expansive, which increases the canopy scattering, and (iii) the tree trunk and height growth increase the double-bounce scattering, which can be generated from the ground and the trunk intersecting at a right angle. These findings are consistent with both the forest growth mechanisms and physical characteristics of microwave backscattering.
Because the physical characteristics of the double bounce scattering model are dependent on the tree trunk and surface interactions [10] and the analytical results showed the consistency between the forest growth and double-bounce scattering with a clear positive correlation (Figure 7(c)), we consider the double-bounce scattering to be an important physical parameter for estimating the stem (stand) volume. In their forest biometric parameter estimation, Grastier et al. [1] demonstrated that saturation of the decomposed parameters (anisotropy) for the L-band occurred in young pine forests when the trees grew taller than 6 m. They found a clear linear correlation between the forest height and anisotropy of the P-band, while the saturation effect was observed in the other decomposed parameters, including the alpha angle and entropy. In this study, we analyzed Acacia forests up to seven years old and approximately 20 m height, and there appeared to be no saturation for any of the decomposition powers in relation to the forest parameters.
The plots in Figure 7(a–c) vary vertically in the mature phase because of the logarithmic base conversion of the forest parameters on the x-axis. As mentioned above, converting to a log scale translates to a better fit for the regression line; however, this correlation deteriorates in the mature phase due to slower growth. This finding suggests that the growth phase and mature phase should be considered separately from the growth curve derived from the ground-based observation data of the forest structural parameters.
6.3. Possibility of Estimating the Forest Stand Volume
Gonçalves et al. [4] attempted to model the stem volume using a multi-linear regression of several SAR incoherent and coherent attributes. In this study, an estimate of the stand volume (the base 10 logarithm of the stand volume) using the calculated parameters from the decomposition powers for P(θ)/TP (Equation (13)) is presented (Figure 8), aided by Equation (14) and achieved a relatively high correlation (R2 = 0.557, P-value < 0.001). Only 26 sample data plots were available for our analysis, which is statistically very small, especially for young trees. However, this sample size compares favorably to previous works [1,2,4,6], where the number of plots ranged from 13 to 27, which strongly emphasizes the need for more field observations. For our future work, we will strive to collect and accumulate basic data for the purpose of such an application. Although single-year data are used in the current study, we expect to be able to model and realize stem volume and forest biomass estimations based on data compiled over several years with more sample plots.
6.4. Uncertainties in the Relationship between the Decomposition Powers and Forest Structural Parameters
The double-bounce scattering showed a statistically significant increase in the correlation analysis with the forest stand volume (Figure 7(c), Table 2), and the statistical validity was demonstrated for the forest stand volume estimations (Figure 8, Table 3) using the decomposition powers of P(θ)/TP (Equation (13)). However, the double-bounce scattering had the weakest correlation of all the four-component scatterings to the stand volume (R = 0.582), and the standard error of estimate of 0.563 appeared to be sufficiently large for practical use in stand volume estimation. Moreover, it is apparent that some plots had higher volumes (log10V ≈ 2) at lower x-axis values. These plots commonly displayed lower Pd(θ) and higher Pc(θ), which leads to a lower Ps(θ).
We think that these uncertainties in the relationship between the decomposition powers and forest structural parameters are associated with some vestigial canopy effects, which seem to be persistent, especially for the double-bounce scattering, and are difficult to model. The scattering model developed accounting for the Acacia forest structure yields a more accurate estimation result.
7. Concluding Remarks
In many parts of the world, the number and size of industrial plantations have increased in recent years and especially in the tropics, where fast-growing trees are cultivated to supply paper materials that are currently under increasing global demand. We aimed to estimate the forest stand volume of Acacia plantations located in Sumatra, Indonesia. The 4-component power decomposition scheme was applied to the ALOS/PALSAR data to compare the decomposition powers to the field-measured biometric parameters, such as the tree diameter, height and stand volume.
Our findings are as follows: (i) the decomposition powers derived from the rotated matrix were better correlated to the forest parameters than those derived from the non-rotated matrix; (ii) all of the decomposition powers had more significant correlations with the forest parameters when divided by the total power (R ≈ −0.768 for surface scattering, R ≈ 0.558 for double-bounce scattering and R ≈ 0.709 for canopy scattering) rather than when using the decomposition powers themselves (R ≈ −0.722 for surface scattering, R ≈ −0.028 for double-bounce scattering and R ≈ 0.513 for canopy scattering); (iii) the surface scattering ratio of the total power decreased considerably (R = −0.758), whereas the double-bounce and canopy scattering ratios increased (R = 0.582 and R = 0.677, respectively), as the forests grow, i.e., the stand volume increased.
These outcomes, especially (iii), are consistent with both forest and backscattering characteristics: (1) the surface scattering decreases as the exposure of the bare ground decreases, (2) the canopy scattering increases as the canopy layer grows thicker and expands and (3) the double-bounce scattering, which is supposed to physically reflect the stem or stand volume, increases as the tree diameter and height increase.
Our future research goal is to improve stand volume and biomass estimation to increase the practical application of the present methodology to industrial plantations of fast-growing trees and to investigate the effects of the forest structure on the microwave SAR data by comparing decomposition power characteristics for other tree types.
Acknowledgments
This work was supported by the Coordination Funds for Promoting Space Utilization of the Ministry of Education, Culture, Sports, Science and Technology in Japan, the research grant for Mission Research on Sustainable Humanosphere from Research Institute for Sustainable Humanosphere (RISH), Kyoto University and by the APU Academic Research Subsidy from Ritsumeikan Asia Pacific University. We gratefully acknowledge the MHP Plantation Company, Sumatra, Indonesia, for their kind cooperation in providing the field observational data. We are also deeply grateful to the staff of the R&D and Planning Sections of the MHP Company for their kind and continuous support during our field surveys.
References and Notes
- Garestier, F.; Dubois-Fernandez, P.C.; Guyon, D.; Le Toan, T. Forest biophysical parameter estimation using L-and P-band polarimetric SAR data. IEEE Trans. Geosci. Remote Sens 2009, 47, 3379–3388. [Google Scholar]
- Gama, F.F.; Dos Santos, J.R.; Mura, J.C. Eucalyptus biomass and volume estimation using interferometric and polarimetric SAR data. Remote Sens 2010, 2, 939–956. [Google Scholar]
- Lonnqvist, A.; Rauste, Y.; Molinier, M.; Hame, T. Polarimetric SAR data in land cover mapping in boreal zone. IEEE Trans. Geosci. Remote Sens 2010, 48, 3652–3662. [Google Scholar]
- Goncalves, F.; Santos, J.; Treuhaft, R. Stem volume of tropical forests from polarimetric radar. Int. J. Remote Sens 2011, 32, 503–522. [Google Scholar]
- He, Q.S.; Cao, C.X.; Chen, E.X.; Sun, G.Q.; Ling, F.L.; Pang, Y.; Zhang, H.; Ni, W.J.; Xu, M.; Li, Z.Y. Forest stand biomass estimation using ALOS PALSAR data based on LiDAR-derived prior knowledge in the Qilian Mountain, Western China. Int. J. Remote Sens 2012, 33, 710–729. [Google Scholar]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing performance of L- and P-band polarimetric interferometric SAR data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens 2012, 50, 714–726. [Google Scholar]
- Paradzayi, C.; Annegarn, H.J. Estimating potential woody biomass in communal savanna woodlands from synthetic aperture radar (SAR). Int. J. Appl. Geospat. Res 2012, 3, 53–62. [Google Scholar]
- Santoro, M.; Fransson, J.E.S.; Eriksson, L.E.B.; Magnusson, M.; Ulander, L.M.H.; Olsson, H. Signatures of ALOS PALSAR L-band backscatter in Swedish forest. IEEE Trans. Geosci. Remote Sens 2009, 47, 4001–4019. [Google Scholar]
- Clewley, D.; Lucas, R.; Accad, A.; Armston, J.; Bowen, M.; Dwyer, J.; Pollock, S.; Bunting, P.; McAlpine, C.; Eyre, T.; et al. An approach to mapping forest growth stages in Queensland, Australia through integration of ALOS PALSAR and Landsat sensor data. Remote Sens 2012, 4, 2236–2255. [Google Scholar]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens 1998, 36, 963–973. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens 1997, 35, 68–78. [Google Scholar]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens 2005, 43, 1699–1706. [Google Scholar]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens 2011, 49, 2251–2258. [Google Scholar]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S.-E.; Kobayashi, H.; Singh, G. Three-component power decomposition for polarimetric SAR data based on adaptive volume scatter modeling. Remote Sens 2012, 4, 1559–1572. [Google Scholar]
- Sugimoto, M.; Ouchi, K.; Nakamura, Y. Four-component scattering power decomposition algorithm with rotation of covariance matrix using ALOS-PALSAR polarimetric data. Remote Sens 2012, 4, 2199–2209. [Google Scholar]
- Richards, J.A. Remote Sensing with Imaging Radar. Signals and Communication Technology Series; Springer-Verlag; Berlin/Heidelberg, Germany, 2009. Available online: http://www.springer.com/engineering/electronics/book/978-3-642-02019-3 (accessed on 3 September 2012).
- Austin, J.M.; Mackey, B.G.; Van Niel, K.P. Estimating forest biomass using satellite radar: An exploratory study in a temperate Australian Eucalyptus forest. For. Ecol. Manag 2003, 176, 575–583. [Google Scholar]
- Hoekman, D.H.; Quiriones, M. Land cover type and biomass classification using AirSAR data for evaluation of monitoring scenarios in the Colombian Amazon. IEEE Trans. Geosci. Remote Sens 2000, 38, 685–696. [Google Scholar]
- Balzter, H.; Baker, J.R.; Hallikainen, M.; Tomppo, E. Retrieval of timber volume and snow water equivalent over a Finnish boreal forest from airborne polarimetric synthetic aperture radar. Int. J. Remote Sens 2002, 23, 3185–3208. [Google Scholar]
- Rowland, C.S.; Balzter, H.; Dawson, T.P.; Luckman, A.; Patenaude, G.; Skinner, L. Airborne SAR monitoring of tree growth in a coniferous plantation. Int. J. Remote Sens 2008, 29, 3873–3889. [Google Scholar] [Green Version]
- Macelloni, G.; Paloscia, S.; Pampaloni, P.; Marliani, F.; Gai, M. The relationship between the backscattering coefficient and the biomass of narrow and broad leaf crops. IEEE Trans. Geosci. Remote Sens 2001, 39, 873–884. [Google Scholar]
- Kobayashi, S.; Widyorini, R.; Kawai, S.; Omura, Y.; Sanga-Ngoie, K.; Supriadi, B. Backscattering characteristics of L-band polarimetric and optical satellite imagery over planted acacia forests in Sumatra, Indonesia. J. Appl. Remote Sens 2012, 6, 063525. [Google Scholar]
- Kawai, S.; Widyorini, R. Sustainable Forest Management and Regional Environment in South-East Asia. Proceedings of the Second International Conference of Kyoto University Global COE Program in Search of Sustainable Humanosphere in Asia and Africa, Kyoto, Japan, 12–14 March 2008.
- Gunawan, R.; Wahyono, R. Faktor Bentuk (Form Factor) Acacia Mangium (in Indonesian); Technical Note of Research and Development Division; PT Musi Hutan Persada: South Sumatera, Indonesia, 2004; pp. 1–3. [Google Scholar]
- Yamaguchi, Y. Radar Polarimetry from Basic to Applications: Radar Remote Sensing Using Polarimetric Information (in Japanese); The Institute of Electrtonics, information and Communication Engineers Press: Tokyo, Japan, 2007; pp. 80–100. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric SAR Speckle Filtering. In Polarimetric Radar Imaging: from Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009; pp. 143–178. [Google Scholar]
- McNeill, S.; Pairman, D. Stand age retrieval in production forest stands in New Zealand using C-and L-band polarimetric radar. IEEE Trans. Geosci. Remote Sens 2005, 43, 2503–2515. [Google Scholar]