Monitoring Maize Yield Variability over Space and Time with Unsupervised Satellite Imagery Features
Highlights
- Simple, computationally efficient machine learning methods can reliably predict agricultural outcomes in data-scarce environments using publicly available imagery.
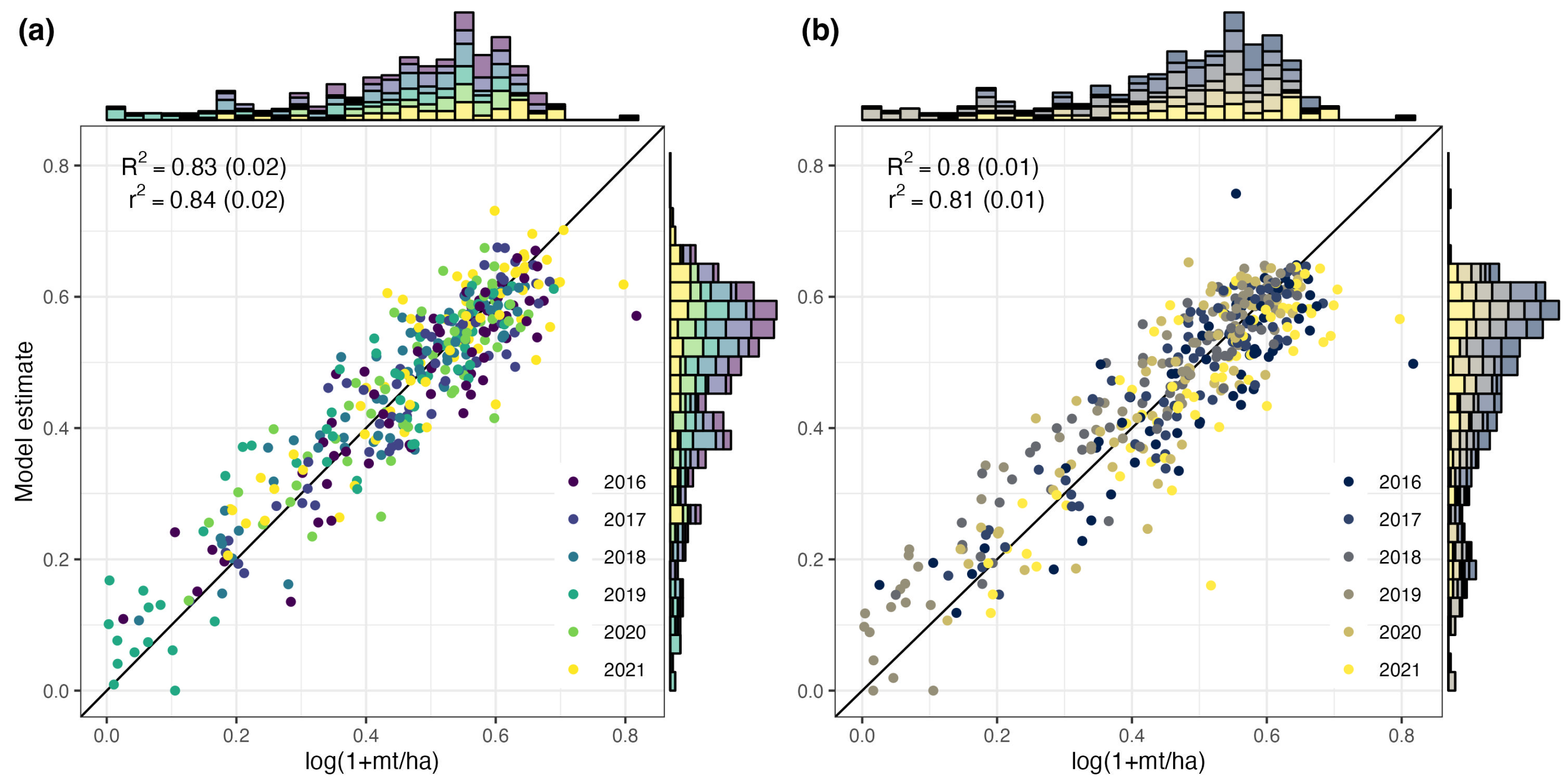
- Task-agnostic random convolutional features (RCFs) from satellite imagery achieve an out-of-sample of 0.83 in predicting maize yields across space and time in Zambia (2016–2021), outperforming traditional NDVI-based approaches.
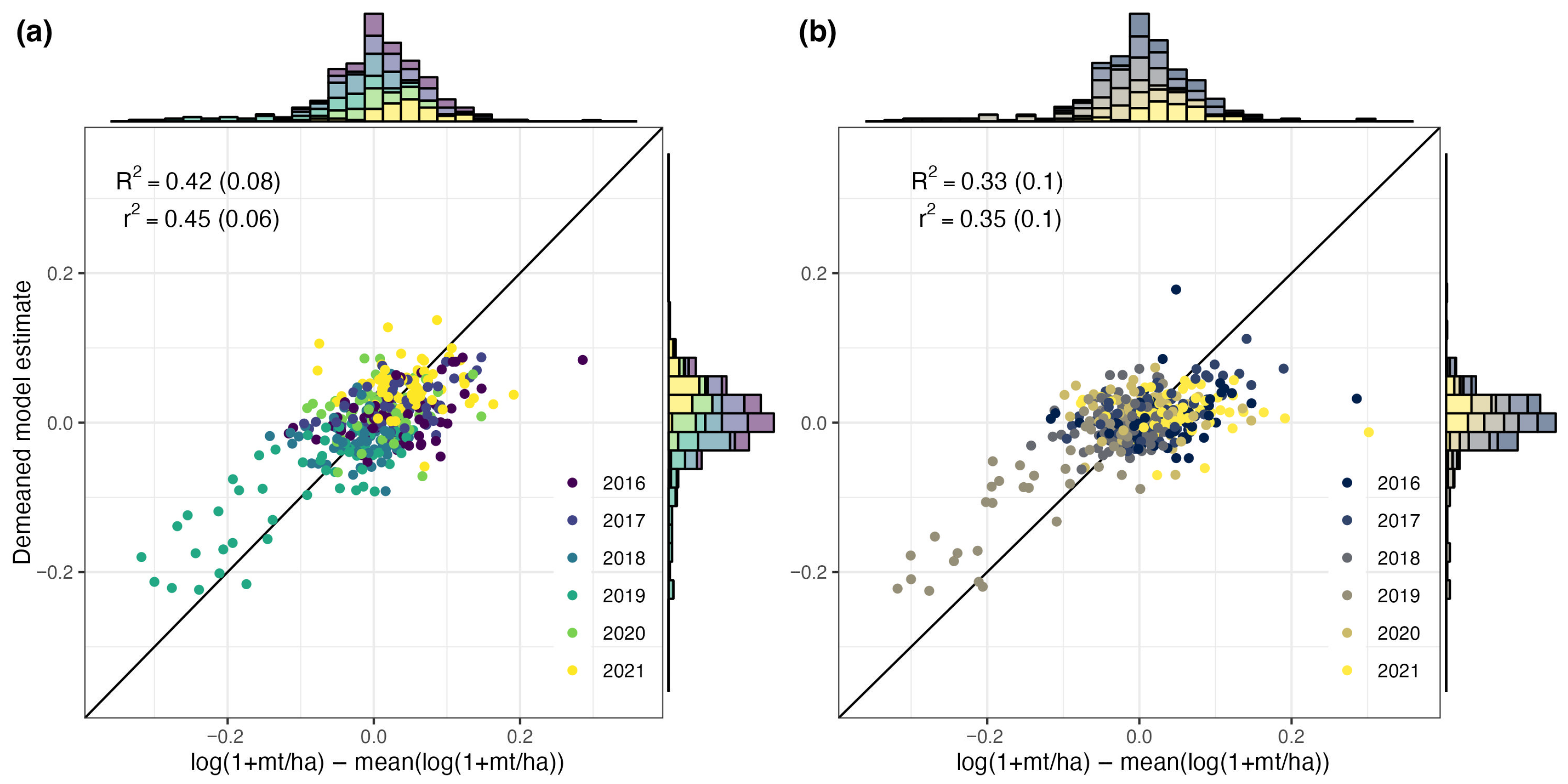
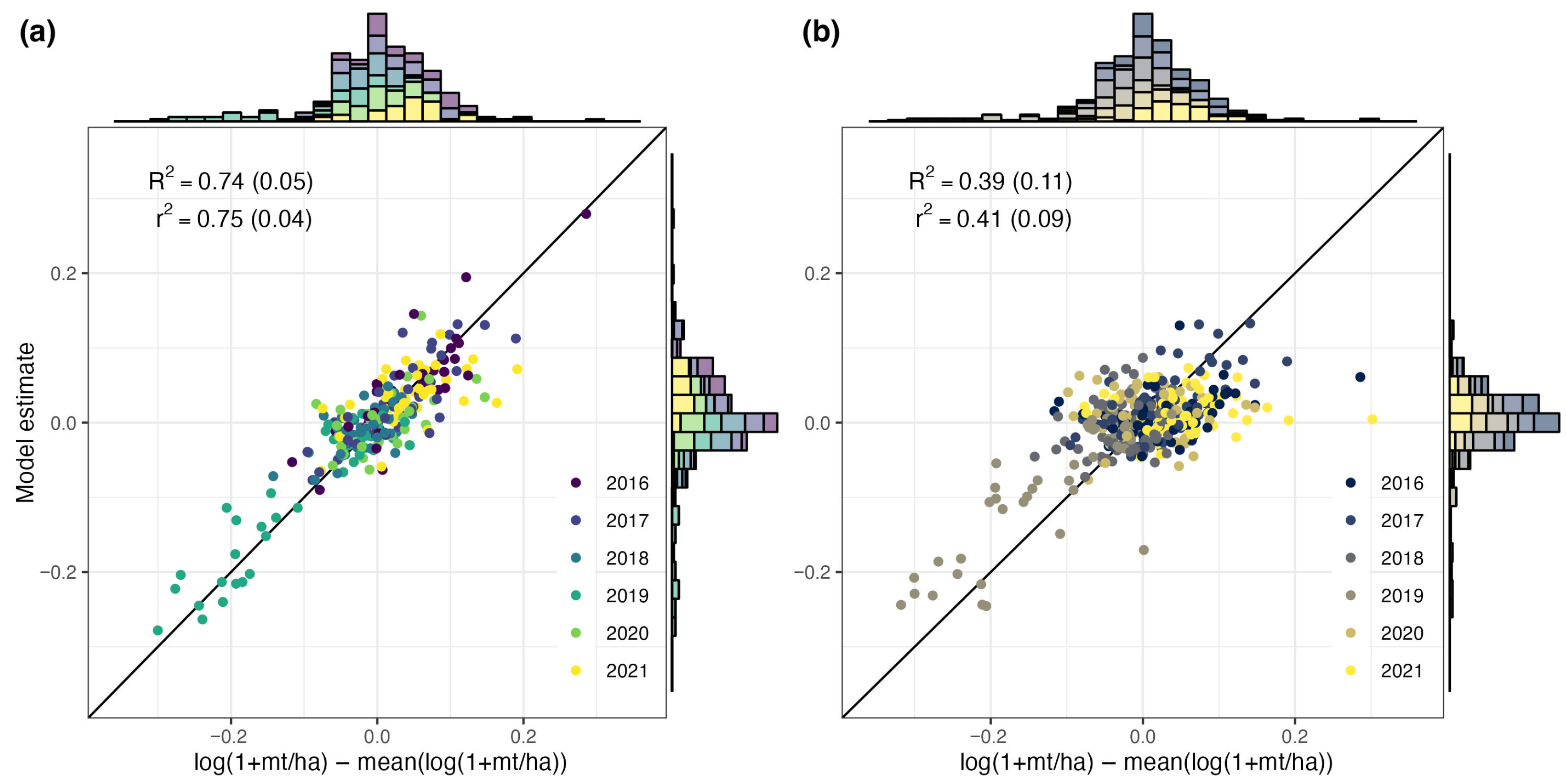
- RCF models achieve strong performance, predicting exclusively temporal variation in yields ( = 0.74) when explicitly trained on temporal anomalies and substantially outperforming NDVI-based approaches ( = 0.39).
- Effective crop-monitoring systems are feasible without expensive proprietary data or computationally intensive deep learning methods.
- Imagery-based monitoring can accurately detect temporal yield anomalies, enabling governments and agencies to target interventions like the expansion or release of government grain stocks, food aid, and agricultural insurance payouts.
- Task-agnostic satellite features offer a scalable, multipurpose alternative to traditional vegetation indices, as the same RCF features can be reused across different prediction tasks (income, forest cover, water availability) without customization.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Context
2.2. Data
2.2.1. Crop Forecast Survey (CFS)
2.2.2. Cropland Data
2.2.3. Satellite Imagery
2.2.4. Normalized Difference Vegetation Index (NDVI)
2.2.5. Temperature and Precipitation
2.3. Methods
2.3.1. Standardized Grid for Location Sampling
2.3.2. Selecting Imagery in Sampled Locations
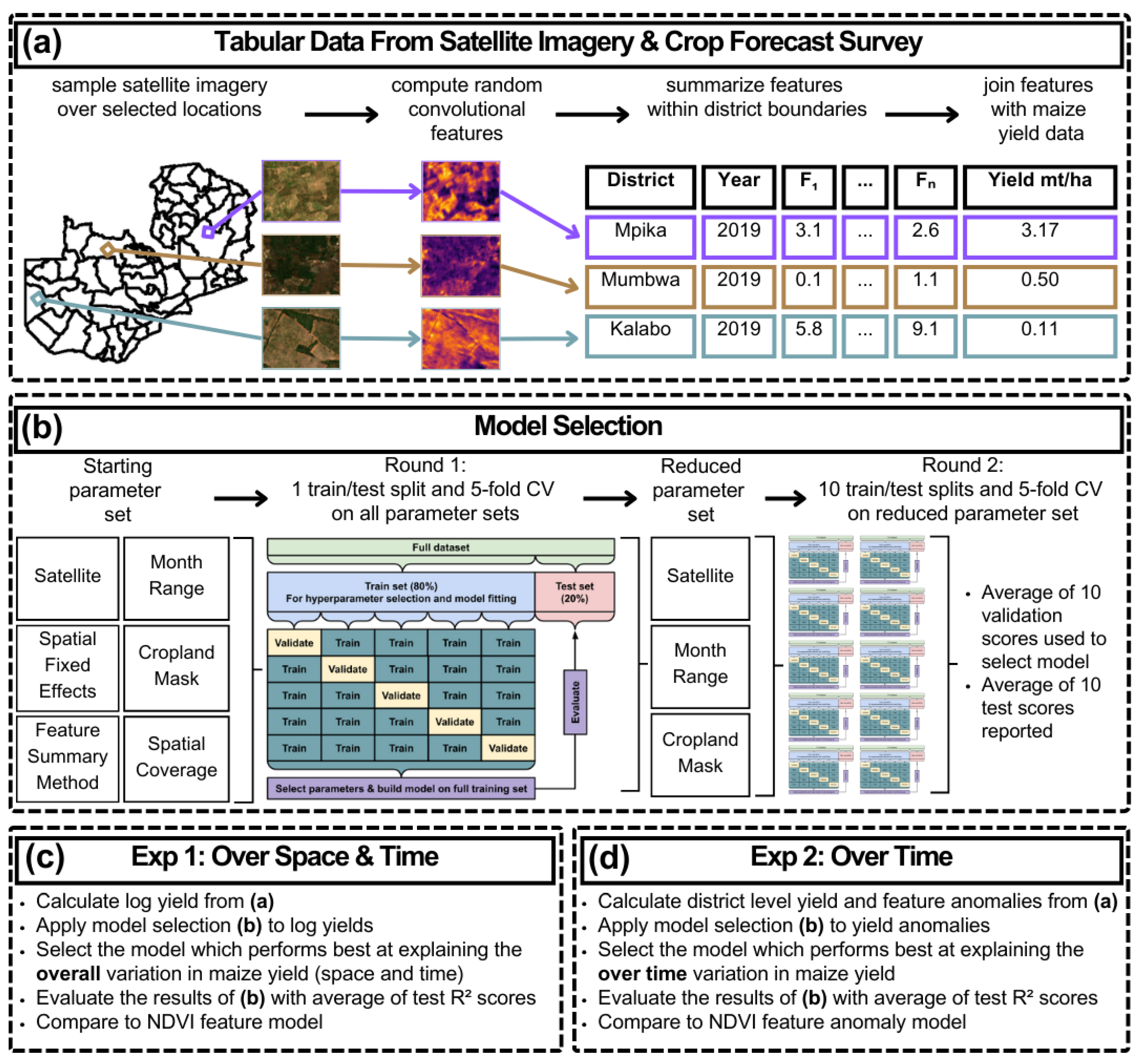
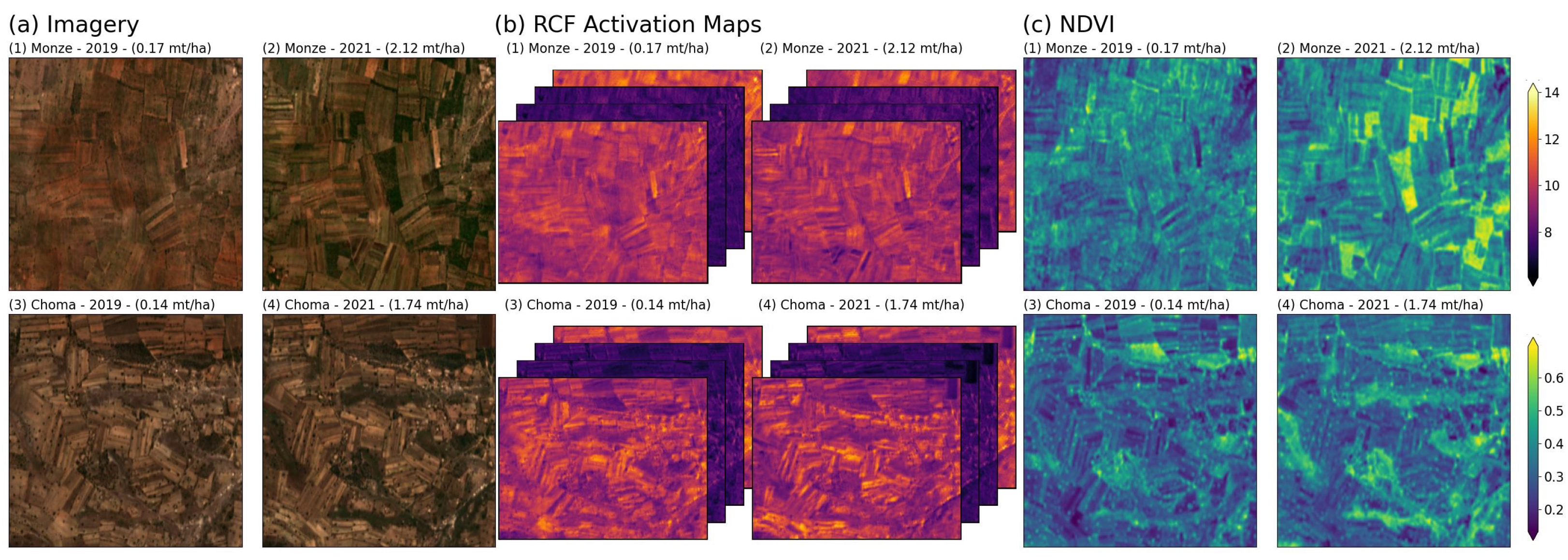
2.3.3. Feature Extraction and Processing
2.3.4. Feature Imputation
2.3.5. Feature Summarization
2.3.6. Model Specification and Tuning
2.3.7. Model Selection
2.3.8. Model Evaluation
2.3.9. Experiments Overview
2.3.10. Predicting Maize Yields over Space and Time
2.3.11. Isolating Predictive Performance over Time
2.3.12. Model Customization for Temporal Prediction
2.3.13. Establishing an NDVI Performance Benchmark
3. Results
3.1. Maize Yield Predictions over Space and Time
3.2. Temporal Performance of Spatiotemporal Models
3.3. Maize Yield Predictions Optimized for Temporal Performance
3.4. Enhancing RCF with NDVI
4. Discussion
4.1. Advantages of Approach
4.2. Model Sensitivity
4.2.1. Cloud Cover
4.2.2. Image Sampling Density
4.2.3. Number of Features
4.2.4. Ablation Study
4.3. Limitations and Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burke, M.; Driscoll, A.; Lobell, D.B.; Ermon, S. Using Satellite Imagery to Understand and Promote Sustainable Development. Science 2021, 371, eabe8628. [Google Scholar] [CrossRef]
- Darra, N.; Anastasiou, E.; Kriezi, O.; Lazarou, E.; Kalivas, D.; Fountas, S. Can Yield Prediction Be Fully Digitilized? A Systematic Review. Agronomy 2003, 13, 2441. [Google Scholar] [CrossRef]
- Joshi, A.; Pradhan, B.; Chakraborty, S.; Behera, M.D. Winter Wheat Yield Prediction in the Conterminous United States Using Solar-Induced Chlorophyll Fluorescence Data and XGBoost and Random Forest Algorithm. Ecol. Inform. 2023, 77, 102194. [Google Scholar] [CrossRef]
- Perez, A.; Yeh, C.; Azzari, G.; Burke, M.; Lobell, D.; Ermon, S. Poverty prediction with public landsat 7 satellite imagery and machine learning. arXiv 2017, arXiv:1711.03654. [Google Scholar] [CrossRef]
- Nakalembe, C.; Becker-Reshef, I.; Bonifacio, R.; Hu, G.; Humber, M.L.; Justice, C.J.; Keniston, J.; Mwangi, K.; Rembold, F.; Shukla, S.; et al. A review of satellite-based global agricultural monitoring systems available for Africa. Glob. Food Secur. 2021, 29, 100543. [Google Scholar] [CrossRef]
- Carletto, C.; Jolliffe, D.; Banerjee, R. From Tragedy to Renaissance: Improving Agricultural Data for Better Policies. J. Dev. Stud. 2015, 51, 133–148. [Google Scholar] [CrossRef]
- World Bank. World Development Indicators 2024; Technical Report; World Bank: Washington, DC, USA, 2024. [Google Scholar]
- Wani, S.P.; Sreedevi, T.K.; Rockström, J.; Ramakrishna, Y.S. Rainfed Agriculture—Past Trends and Future Prospects. In Rainfed Agriculture: Unlocking the Potential, 1st ed.; Wani, S.P., Rockström, J., Oweis, T., Eds.; CABI: Wallingford, UK, 2009; pp. 1–35. [Google Scholar] [CrossRef]
- Shakoor, U.; Saboor, A.; Baig, I.; Afzal, A.; Rahman, A. Climate Variability Impacts on Rice Crop Production in Pakistan. Pak. J. Agric. Res. 2015, 28, 19–27. [Google Scholar]
- Apata, T.G. Effects of Global Climate Change on Nigerian Agriculture: An Empirical Analysis. CBN J. Appl. Stat. 2011, 2, 31–50. [Google Scholar]
- Granados, R.; Soria, J.; Cortina, M. Rainfall Variability, Rainfed Agriculture and Degree of Human Marginality in North Guanajuato, Mexico. Singap. J. Trop. Geogr. 2017, 38, 153–166. [Google Scholar] [CrossRef]
- Idso, S.; Pinter, P.; Hatfield, J.; Jackson, R.; Reginato, R. A Remote Sensing Model for the Prediction of Wheat Yields Prior to Harvest. J. Theor. Biol. 1979, 77, 217–228. [Google Scholar] [CrossRef]
- Rasmussen, M.S. Assessment of Millet Yields and Production in Northern Burkina Faso Using Integrated NDVI from the AVHRR. Int. J. Remote Sens. 1992, 13, 3431–3442. [Google Scholar] [CrossRef]
- Labus, M.P.; Nielsen, G.A.; Lawrence, R.L.; Engel, R.; Long, D.S. Wheat Yield Estimates Using Multi-Temporal NDVI Satellite Imagery. Int. J. Remote Sens. 2002, 23, 4169–4180. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting Crop Yield Using Remotely Sensed Vegetation Indices and Crop Phenology Metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Petersen, L.K. Real-time prediction of crop yields from MODIS relative vegetation health: A continent-wide analysis of Africa. Remote Sens. 2018, 10, 1726. [Google Scholar] [CrossRef]
- Guo, Z.; Chamberlin, J.; You, L. Smallholder maize yield estimation using satellite data and machine learning in Ethiopia. Crop Environ. 2023, 2, 165–174. [Google Scholar] [CrossRef]
- Kaneko, A.; Kennedy, T.W.; Mei, L.; Sintek, C.; Burke, M.; Ermon, S.; Lobell, D.B. Deep Learning for Crop Yield Prediction in Africa. In Proceedings of the International Conference on Machine Learning AI for Social Good Workshop, Long Beach, CA, USA, 10–15 June 2019; pp. 33–37. Available online: https://aiforsocialgood.github.io/icml2019/accepted/track1/pdfs/20_aisg_icml2019.pdf (accessed on 16 October 2025).
- Muruganantham, P.; Wibowo, S.; Grandhi, S.; Samrat, N.H.; Islam, N. A Systematic Literature Review on Crop Yield Prediction with Deep Learning and Remote Sensing. Remote Sens. 2022, 14, 1990. [Google Scholar] [CrossRef]
- El Sakka, M.; Mothe, J.; Ivanovici, M. Images and CNN Applications in Smart Agriculture. Eur. J. Remote Sens. 2024, 57, 2352386. [Google Scholar] [CrossRef]
- Victor, B.; Nibali, A.; He, Z. A Systematic Review of the Use of Deep Learning in Satellite Imagery for Agriculture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 2297–2316. [Google Scholar] [CrossRef]
- Rolf, E.; Proctor, J.; Carleton, T.; Bolliger, I.; Shankar, V.; Ishihara, M.; Recht, B.; Hsiang, S. A Generalizable and Accessible Approach to Machine Learning with Global Satellite Imagery. Nat. Commun. 2021, 12, 4392. [Google Scholar] [CrossRef]
- Brown, C.F.; Kazmierski, M.R.; Pasquarella, V.J.; Rucklidge, W.J.; Samsikova, M.; Zhang, C.; Shelhamer, E.; Lahera, E.; Wiles, O.; Ilyushchenko, S.; et al. AlphaEarth Foundations: An Embedding Field Model for Accurate and Efficient Global Mapping from Sparse Label Data. arXiv preprint 2025, arXiv:2507.22291. [Google Scholar] [CrossRef]
- Corley, I.; Robinson, C.; Dodhia, R.; Ferres, J.M.L.; Najafirad, P. Revisiting pre-trained remote sensing model benchmarks: Resizing and normalization matters. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 3162–3172. [Google Scholar]
- Sherman, L.; Proctor, J.; Druckenmiller, H.; Tapia, H.; Hsiang, S.M. Global High-Resolution Estimates of the United Nations Human Development Index Using Satellite Imagery and Machine-learning. NBER Work. Pap. Ser. 2023, 31044. [Google Scholar] [CrossRef]
- Khachiyan, A.; Thomas, A.; Zhou, H.; Hanson, G.; Cloninger, A.; Rosing, T.; Khandelwal, A.K. Using Neural Networks to Predict Microspatial Economic Growth. Am. Econ. Rev. Insights 2022, 4, 491–506. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Mushtaq, S.; Kath, J.; Nguyen-Huy, T.; Reymondin, L. Satellite-Based Data for Agricultural Index Insurance: A Systematic Quantitative Literature Review. Nat. Hazards Earth Syst. Sci. 2025, 25, 913–927. [Google Scholar] [CrossRef]
- GRID3 Inc. GRID3 Use Case Report District Boundaries Harmonisation in Zambia; GRID3 Inc.: New York, NY, USA, 2020. [Google Scholar]
- Potapov, P.; Turubanova, S.; Hansen, M.C.; Tyukavina, A.; Zalles, V.; Khan, A.; Song, X.P.; Pickens, A.; Shen, Q.; Cortez, J. Global Maps of Cropland Extent and Change Show Accelerated Cropland Expansion in the Twenty-First Century. Nat. Food 2022, 3, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.; Chisanga, B.; Drimie, S.; Kennedy, G. Nutrition Transition in Zambia: Changing Food Supply, Food Prices, Household Consumption, Diet and Nutrition Outcomes. Food Secur. 2019, 11, 371–387. [Google Scholar] [CrossRef]
- Melkani, A.; Mason, N.M.; Mather, D.L.; Chisanga, B. Smallholder Maize Market Participation and Choice of Marketing Channel in the Presence of Liquidity Constraints: Evidence from Zambia; AgEcon Search: St. Paul, MN, USA, 2019. [Google Scholar]
- Dorosh, P.A.; Dradri, S.; Haggblade, S. Regional Trade, Government Policy and Food Security: Recent Evidence from Zambia. Food Policy 2009, 34, 350–366. [Google Scholar] [CrossRef]
- Morgan, S.N.; Mason, N.M.; Levine, N.K.; Zulu-Mbata, O. Dis-Incentivizing Sustainable Intensification? The Case of Zambia’s Maize-Fertilizer Subsidy Program. World Dev. 2019, 122, 54–69. [Google Scholar] [CrossRef]
- Sleimi, R.; Ghosh, S.; Amarnath, G. Development of Drought Indicators Using Machine Learning Algorithm: A Case Study of Zambia. Technical Report, CGIAR Climate Resilience Initiative 2022. Available online: https://cgspace.cgiar.org/handle/10568/127620 (accessed on 16 October 2025).
- Hadunka, P.; Baylis, K. Staple Crop Pest Damage and Natural Resources Exploitation: Fall Army Worm Infestation and Charcoal Production in Zambia. In Proceedings of the 2022 Agricultural Applied Economics Association Annual Meeting, Anaheim, CA, USA, 31 July–2 August 2022. [Google Scholar] [CrossRef]
- Thurlow, J.; Zhu, T.; Diao, X. The Impact of Climate Variability and Change on Economic Growth and Poverty in Zambia; IFPRI: Washington, DC, USA, 2008. [Google Scholar]
- Delwart, S. Sentinel-2 User Handbook; European Space Agency (ESA): Paris, France, 2015. [Google Scholar]
- U.S. Geological Survey. Landsat 8 (L8) Data Users Handbook; Technical Report; U.S. Geological Survey: Reston, VA, USA, 2019.
- Senay, G.B.; Velpuri, N.M.; Bohms, S.; Budde, M.; Young, C.; Rowland, J.; Verdin, J.P. Chapter 9—Drought Monitoring and Assessment: Remote Sensing and Modeling Approaches for the Famine Early Warning Systems Network. In Hydro-Meteorological Hazards, Risks and Disasters; Shroder, J.F., Paron, P., Baldassarre, G.D., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 233–262. [Google Scholar] [CrossRef]
- Lobell, D.B.; Hicke, J.A.; Asner, G.P.; Field, C.B.; Tucker, C.J.; Los, S.O. Satellite Estimates of Productivity and Light Use Efficiency in United States Agriculture, 1982–1998. Glob. Change Biol. 2002, 8, 722–735. [Google Scholar] [CrossRef]
- Mkhabela, M.S.; Mkhabela, M.S.; Mashinini, N.N. Early Maize Yield Forecasting in the Four Agro-Ecological Regions of Swaziland Using NDVI Data Derived from NOAA’s-AVHRR. Agric. For. Meteorol. 2005, 129, 1–9. [Google Scholar] [CrossRef]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical Regression Models Using NDVI, Rainfall and Temperature Data for the Early Prediction of Wheat Grain Yields in Morocco. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 438–452. [Google Scholar] [CrossRef]
- Burke, M.; Lobell, D.B. Satellite-Based Assessment of Yield Variation and Its Determinants in Smallholder African Systems. Proc. Natl. Acad. Sci. USA 2017, 114, 2189–2194. [Google Scholar] [CrossRef]
- Lobell, D.B.; Azzari, G.; Burke, M.; Gourlay, S.; Jin, Z.; Kilic, T.; Murray, S. Eyes in the sky, boots on the ground: Assessing satellite-and ground-based approaches to crop yield measurement and analysis. Am. J. Agric. Econ. 2020, 102, 202–219. [Google Scholar] [CrossRef]
- Yang, C.; Odvody, G.N.; Thomasson, J.A.; Isakeit, T.; Nichols, R.L. Change Detection of Cotton Root Rot Infection over 10-Year Intervals Using Airborne Multispectral Imagery. Comput. Electron. Agric. 2016, 123, 154–162. [Google Scholar] [CrossRef]
- Kumar, S.; Röder, M.S.; Singh, R.P.; Kumar, S.; Chand, R.; Joshi, A.K.; Kumar, U. Mapping of Spot Blotch Disease Resistance Using NDVI as a Substitute to Visual Observation in Wheat (Triticum aestivum L.). Mol. Breed. 2016, 36, 95. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, J.; Chen, Y. NDVI-based Vegetation Responses to Climate Change in an Arid Area of China. Theor. Appl. Climatol. 2015, 126, 213–222. [Google Scholar] [CrossRef]
- Wang, R.; Cherkauer, K.; Bowling, L. Corn Response to Climate Stress Detected with Satellite-Based NDVI Time Series. Remote Sens. 2016, 8, 269. [Google Scholar] [CrossRef]
- Didan, K. MODIS/Terra Vegetation Indices Monthly L3 Global 0.05Deg CMG V061; Dataset; NASA EOSDIS Land Processes Distributed Active Archive Center: Sioux Falls, SD, USA, 2021. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS Monthly High-Resolution Gridded Multivariate Climate Dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Drivers of Within-Field Spatial and Temporal Variability of Crop Yield across the US Midwest. Sci. Rep. 2018, 8, 14833. [Google Scholar] [CrossRef]
- Aiken, E.; Rolf, E.; Blumenstock, J. Fairness and Representation in Satellite-Based Poverty Maps: Evidence of Urban-Rural Disparities and Their Impacts on Downstream Policy. arXiv preprint 2023, arXiv:2305.01783. [Google Scholar] [CrossRef]
- Li, J.; Roy, D.P. A Global Analysis of Sentinel-2A, Sentinel-2B and Landsat-8 Data Revisit Intervals and Implications for Terrestrial Monitoring. Remote Sens. 2017, 9, 902. [Google Scholar] [CrossRef]
- Carrol, R.J.; Rupert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models: A Modern Perspective, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Ratledge, N.; Cadamuro, G.; De La Cuesta, B.; Stigler, M.; Burke, M. Using Machine Learning to Assess the Livelihood Impact of Electricity Access. Nature 2022, 611, 491–495. [Google Scholar] [CrossRef]
- Proctor, J.; Carleton, T.; Sum, S. Parameter Recovery Using Remotely Sensed Variables; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2023. [Google Scholar]
- Beyer, M.; Wallner, M.; Bahlmann, L.; Thiemig, V.; Dietrich, J.; Billib, M. Rainfall Characteristics and Their Implications for Rain-Fed Agriculture: A Case Study in the Upper Zambezi River Basin. Hydrol. Sci. J. 2015, 61, 321–343. [Google Scholar] [CrossRef]
- Van Ittersum, M.K.; van Bussel, L.G.J.; Wolf, J.; Grassini, P.; van Wart, J.; Guilpart, N.; Claessens, L.; de Groot, H.; Wiebe, K.; Mason-D’Croz, D.; et al. Can Sub-Saharan Africa Feed Itself? Proc. Natl. Acad. Sci. USA 2016, 113, 14964–14969. [Google Scholar] [CrossRef]
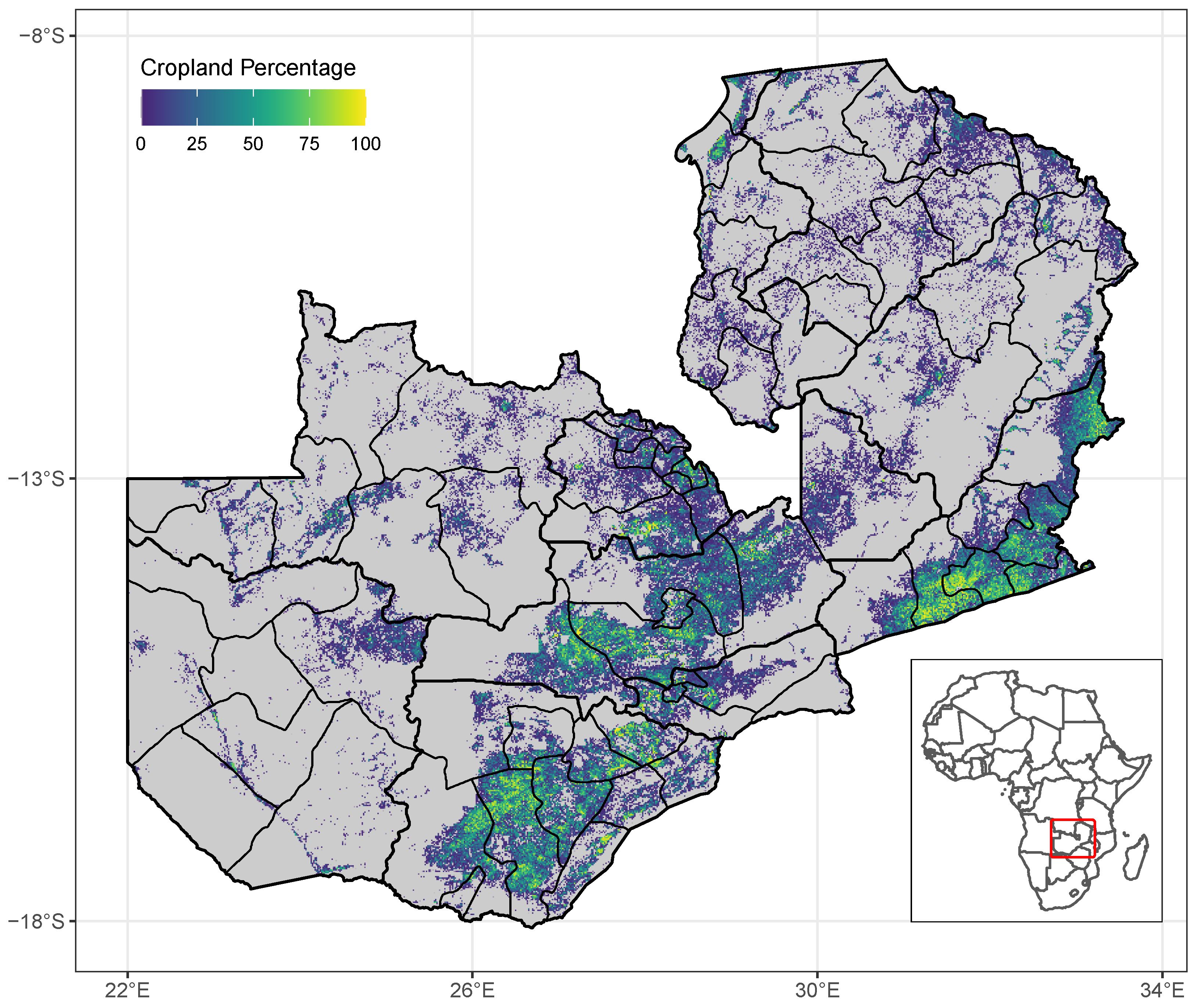
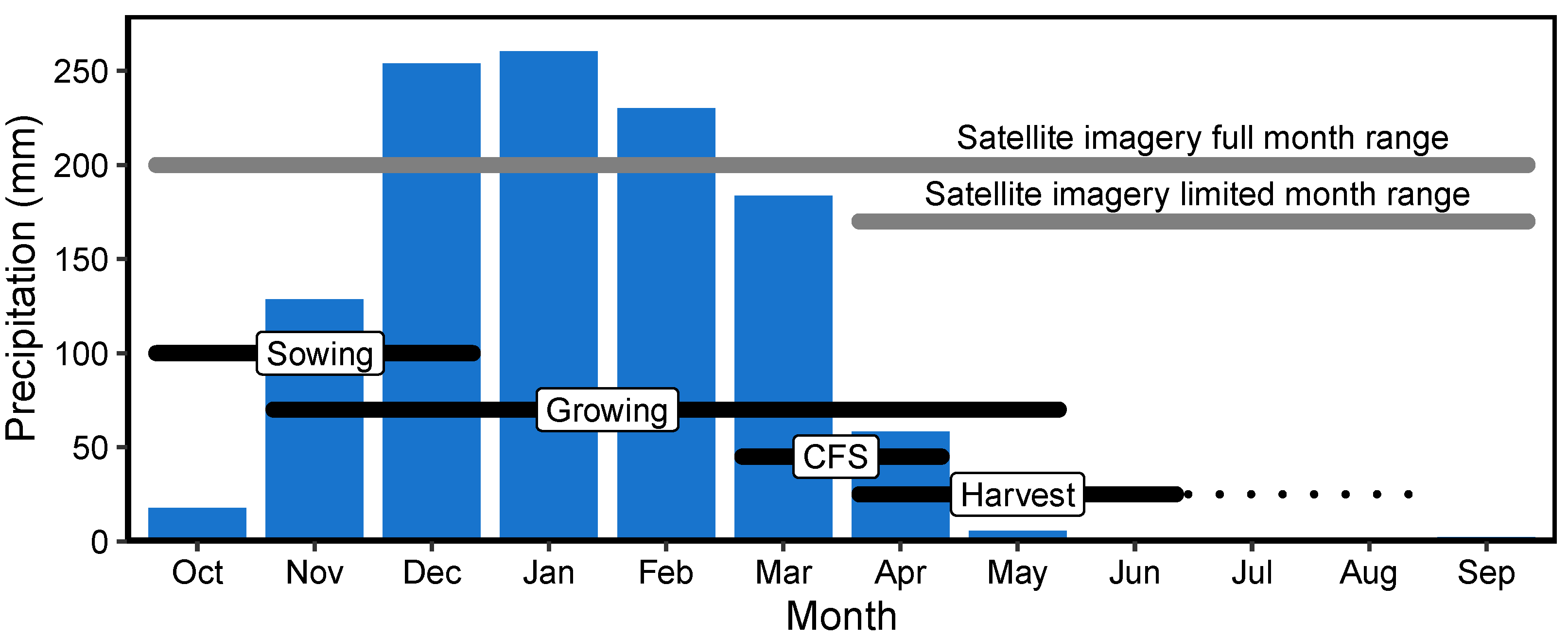
| Satellite | Sensor | Overlap with CFS | Spectral Band (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | G | B | NIR | SWIR1.6 | SWIR2.2 | CA | |||
| Sentinel-2 | MSI | 2016–2022 | 0.65–0.68 | 0.54–0.58 | 0.46–0.52 | 0.78–0.90 | – | – | – |
| Landsat 5 | TM | 2009–2013 | 0.63–0.69 | 0.52–0.60 | 0.45–0.52 | 0.76–0.90 | 1.55–1.75 | 2.08–2.35 | – |
| Landsat 7 | ETM+ | 2009–2021 | 0.63–0.69 | 0.53–0.61 | 0.45–0.52 | 0.78–0.90 | 1.55–1.75 | 2.09–2.35 | – |
| Landsat 8 | OLI | 2013–2021 | 0.64–0.67 | 0.53–0.59 | 0.45–0.51 | 0.85–0.88 | 1.57–1.65 | 2.11–2.29 | 0.43–0.45 |
| Sensor Platform | Spectral Bands | Spatial Coverage | Month Range | Crop Mask | Feature Summary Method | District Fixed Effects | Year Range |
|---|---|---|---|---|---|---|---|
| Landsat-C2-L2 | R, G, B, NIR, SWIR1, SWIR2 | 19,598 | 4–9 | TRUE | Simple mean | TRUE | 2016–2021 |
| Sentinel-2-L2a | R, G, B, NIR | 15,058 | 1–12 | TRUE | Simple mean |
| Sensor Platform | Spectral Bands | Spatial Coverage | Month Range | Crop Mask | Feature Summary Method | Year Range |
|---|---|---|---|---|---|---|
| Landsat-8-C2-L2 | AOT, R, G, B, NIR, SWIR1, SWIR2 | 15,058 | 1–12 | TRUE | Simple mean | 2016–2021 |
| Sentinel-2-L2a | R, G, B | 3772 | 1–12 | TRUE | Simple mean |
| Variables | Overall | Demeaned | Anomaly | Overall | Demeaned | Anomaly |
|---|---|---|---|---|---|---|
| Test | Test | Test | Test | Test | Test | |
| RCF1, NDVI, T | 0.846 | 0.465 | 0.582 | 0.852 | 0.490 | 0.609 |
| RCF1, NDVI | 0.838 | 0.449 | 0.586 | 0.844 | 0.478 | 0.611 |
| T, NDVI | 0.834 | 0.421 | 0.514 | 0.840 | 0.440 | 0.539 |
| RCF1 | 0.832 | 0.422 | 0.583 | 0.838 | 0.452 | 0.607 |
| P, T, NDVI | 0.832 | 0.410 | 0.508 | 0.837 | 0.433 | 0.534 |
| P, NDVI | 0.815 | 0.361 | 0.435 | 0.823 | 0.383 | 0.467 |
| RCF2, NDVI, T | 0.812 | 0.427 | 0.743 | 0.820 | 0.484 | 0.759 |
| T | 0.807 | 0.313 | 0.378 | 0.813 | 0.356 | 0.432 |
| RCF2, NDVI | 0.806 | 0.406 | 0.734 | 0.814 | 0.465 | 0.749 |
| NDVI | 0.804 | 0.331 | 0.387 | 0.814 | 0.354 | 0.412 |
| RCF2 | 0.803 | 0.393 | 0.739 | 0.811 | 0.451 | 0.751 |
| P, T | 0.802 | 0.294 | 0.369 | 0.808 | 0.338 | 0.428 |
| P | 0.699 | 0.006 | 0.049 | 0.717 | 0.080 | 0.113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molitor, C.; Cohen, J.; Lewin, G.; Cognac, S.; Hadunka, P.; Proctor, J.; Carleton, T. Monitoring Maize Yield Variability over Space and Time with Unsupervised Satellite Imagery Features. Remote Sens. 2025, 17, 3641. https://doi.org/10.3390/rs17213641
Molitor C, Cohen J, Lewin G, Cognac S, Hadunka P, Proctor J, Carleton T. Monitoring Maize Yield Variability over Space and Time with Unsupervised Satellite Imagery Features. Remote Sensing. 2025; 17(21):3641. https://doi.org/10.3390/rs17213641
Chicago/Turabian StyleMolitor, Cullen, Juliet Cohen, Grace Lewin, Steven Cognac, Protensia Hadunka, Jonathan Proctor, and Tamma Carleton. 2025. "Monitoring Maize Yield Variability over Space and Time with Unsupervised Satellite Imagery Features" Remote Sensing 17, no. 21: 3641. https://doi.org/10.3390/rs17213641
APA StyleMolitor, C., Cohen, J., Lewin, G., Cognac, S., Hadunka, P., Proctor, J., & Carleton, T. (2025). Monitoring Maize Yield Variability over Space and Time with Unsupervised Satellite Imagery Features. Remote Sensing, 17(21), 3641. https://doi.org/10.3390/rs17213641






