Abstract
Cross-modal image registration for unmanned aerial vehicle (UAV) platforms presents significant challenges due to large-scale deformations, distinct imaging mechanisms, and pronounced modality discrepancies. This paper proposes a novel multi-scale cascaded registration network based on style transfer that achieves superior performance: up to 67% reduction in mean squared error (from 0.0106 to 0.0068), 9.27% enhancement in normalized cross-correlation, 26% improvement in local normalized cross-correlation, and 8% increase in mutual information compared to state-of-the-art methods. The architecture integrates a cross-modal style transfer network (CSTNet) that transforms visible images into pseudo-infrared representations to unify modality characteristics, and a multi-scale cascaded registration network (MCRNet) that performs progressive spatial alignment across multiple resolution scales using diffeomorphic deformation modeling to ensure smooth and invertible transformations. A self-supervised learning paradigm based on image reconstruction eliminates reliance on manually annotated data while maintaining registration accuracy through synthetic deformation generation. Extensive experiments on the LLVIP dataset demonstrate the method’s robustness under challenging conditions involving large-scale transformations, with ablation studies confirming that style transfer contributes 28% MSE improvement and diffeomorphic registration prevents 10.6% performance degradation. The proposed approach provides a robust solution for cross-modal image registration in dynamic UAV environments, offering significant implications for downstream applications such as target detection, tracking, and surveillance.
1. Introduction
Image fusion has found extensive applications across various domains [1], particularly in cross-modal image processing for unmanned aerial vehicle (UAV) platforms, where it provides rich visual information for tasks such as target detection [2] and tracking [3]. However, existing image fusion methods predominantly rely on strictly aligned source images. When source images exhibit misalignment or deformation, the resulting fusion often suffers from severe artifacts, compromising image quality. Consequently, accurate image registration prior to fusion is essential.
Existing image registration methods encounter significant limitations when applied to cross-modal UAV images. First, the high-speed motion and attitude variations of UAVs induce substantial spatial transformations between source images [4]. Conventional registration methods struggle to accurately estimate such complex deformations, resulting in insufficient registration accuracy and challenges in model convergence. Second, the distinct imaging mechanisms of infrared and visible-light images render traditional affine transformation models inadequate for characterizing nonlinear geometric deformations between multimodal images [5], severely constraining registration performance. Additionally, the pronounced differences in grayscale distribution and texture features across modalities hinder existing similarity metrics from effectively capturing inter-modal correlations, further limiting the efficacy of registration algorithms [6]. Finally, the scarcity of high-quality annotated datasets for cross-modal image registration impedes supervised learning approaches, undermining model generalization and the robustness of real-world applications [7].
To address these challenges, an innovative multi-scale cascaded registration network is proposed based on style transfer to enhance the accuracy and robustness of cross-modal image registration for UAV platforms. First, to tackle large-scale deformations caused by UAV motion, a multi-scale cascaded registration network is designed [8] that maps source images into multi-scale feature maps and progressively refines registration results, significantly improving both accuracy and convergence stability. Second, a diffeomorphic deformation registration model is introduced to overcome the limitations of affine transformations in handling complex cross-modal deformations, ensuring smooth and invertible transformations for precise local and global deformation correction. Furthermore, by leveraging image style transfer techniques [9], multimodal images are mapped into a unified feature space, circumventing the inherent limitations of traditional similarity metrics and enabling accurate registration through single-modal similarity measures. Lastly, to mitigate the scarcity of annotated data, a self-supervised learning paradigm is proposed based on image reconstruction, training the network by minimizing reconstruction errors of registered images. This approach reduces reliance on manual annotations and demonstrates registration performance comparable to supervised methods, following recent advances in self-supervised registration [10,11].
Through comparative experiments, the proposed method demonstrates superior performance in complex deformation scenarios. Quantitative results indicate a 9.27% improvement in similarity metrics (e.g., normalized cross-correlation (NCC)) compared to state-of-the-art methods. Furthermore, ablation studies validate the contributions of individual modules, confirming the effectiveness of our innovations in enhancing registration’s accuracy and robustness.
2. Background
The core goal of feature image registration is to estimate a transformation model, specifically a coordinate transformation matrix. This model is then utilized to transform the pixel coordinates of the images being registered, thereby achieving precise alignment of pixel positions in the two images. Based on the method used to estimate the transformation model, image registration techniques are generally categorized into two groups: feature-based methods and optimization-based methods [12].
2.1. Feature-Based Registration Methods
Feature-based image registration methods [13,14,15] typically consist of four steps: feature detection, feature matching, transformation model estimation, and resampling transformation. Among these steps, feature detection and feature matching are critical to the success of the registration process. Feature detection involves identifying regions in the image that exhibit significant characteristics, such as corner points, edges, lines, or centers of regions. Feature matching relies on feature descriptor algorithms, which generate a descriptor for each feature point to facilitate matching. A descriptor is a vector that encapsulates local image information from the vicinity of a feature point and can be utilized to match corresponding feature points between images [16].
Traditional feature extraction methods achieve image registration through manually designed feature detection and descriptors. The Harris corner detector [17] was the first to identify image corners using local self-similarity calculations; however, it lacked the capability to generate descriptors. The scale-invariant feature transform (SIFT) algorithm [13] represented a major breakthrough in feature extraction by achieving robust scale and rotation invariance. Its 128-dimensional descriptor quickly became a benchmark for image registration. Building on this, the speeded-up robust features (SURF) method [18] accelerated feature computation through integral images, significantly improving efficiency. Meanwhile, the features from accelerated segment test (FAST) [19] enabled real-time corner detection by leveraging pixel intensity contrasts, operating at millisecond-level speeds. Further advancements came with oriented FAST and rotated BRIEF (ORB) [20], which combined FAST keypoints with the binary robust independent elementary features (BRIEF) descriptor [21]. This integration not only preserved SIFT-like performance but also achieved an order-of-magnitude improvement in computational efficiency, paving the way for real-time vision systems.
With the rise of deep learning, the feature detection paradigm has undergone a fundamental transformation [8,22,23]. SuperPoint [24] adopted a self-supervised, end-to-end architecture that jointly optimizes feature point detection and descriptor generation, significantly enhancing cross-scene generalization through synthetic data augmentation. Its descriptor network, accelerated by the GPU (graphics processing unit), surpasses traditional methods in computational efficiency while maintaining robustness against variations in lighting and viewpoint. To further optimize feature matching accuracy, SuperGlue [25] introduced a self-attention mechanism to model global dependencies between feature points and employed graph neural networks for fine-grained matching, performing exceptionally well in complex deformation scenarios. For embedded devices, LightGlue [26] utilized a lightweight network architecture and a pruning strategy, achieving three times the inference speed of SuperGlue while maintaining over 95% matching accuracy, thereby demonstrating the application potential of deep-learning models in resource-constrained environments.
2.2. Optimization-Based Registration Methods
Optimization-based registration methods [27,28,29] determine the optimal deformation field by formulating an energy function minimization problem. The key aspect involves designing effective similarity metrics and optimization strategies. In traditional methods, the energy function typically comprises a similarity measure (e.g., mean squared error (MSE) [30]) and a regularization term. While MSE is appropriate for single modal registration, metrics such as mutual information (MI) [31] and normalized cross-correlation (NCC) [32] are commonly employed in multi-modal scenarios to address differences in grayscale distributions. However, the iterative optimization process can be computationally intensive and often fails to meet real-time requirements.
Deep-learning technology has brought about paradigm shifts in optimization-driven registration [10,33]. Cao et al. [34] were the first to construct a CNN regression model that directly learns the mapping of image deformation fields, thereby circumventing the computational bottleneck associated with traditional iterative optimization methods. To address the challenge of obtaining ground truth deformation fields in supervised learning, Krebs et al. [35] trained their network using synthetic deformation data. However, the domain differences between simulated and real data limited the model’s generalization ability. DIRNet [36] achieved a significant breakthrough by performing unsupervised registration, utilizing a ConvNet regressor and a spatial transformer to predict displacement fields in an end-to-end manner, which greatly improved cross-sample adaptability. Subsequent studies further optimized the capability to handle large deformations by designing recursive cascade networks for progressive alignment [8], where each cascade learns to progressively deform the transformed image. The improved model, VTN [37], introduced a reversibility loss to enhance the consistency of deformation fields. TransMorph [33] combined the global perception capabilities of transformers with the local feature extraction advantages of ConvNets, ensuring topological consistency through its differential topological variant, while the Bayesian variant quantified registration uncertainty.
Multimodal registration encounters significant challenges due to the variations in appearance across different modalities. Early methods, such as RegNet [38], relied on manually annotated parameters for supervised training, which limited their practical applicability. Voxelmorph [22] used NCC as an unsupervised loss function [39], marking a milestone in cross-modal deformation field estimation. Nemar et al. [9] implicitly aligned modality differences through a combined framework of image translation and registration, while CrossRAFT [40] employed knowledge distillation to adapt unimodal registration models for cross-modal tasks, demonstrating advantages in data efficiency. Nevertheless, existing methods continue to grapple with issues such as inadequate cross-domain generalization and the inaccurate modeling of complex deformations.
2.3. Challenges in Existing Methods
A systematic analysis of existing approaches is presented to provide a comprehensive understanding of the current landscape in image registration. The various methodologies can be categorized based on their underlying principles and computational strategies, each exhibiting distinct advantages and limitations when applied to UAV-based cross-modal registration scenarios.
The advantages and disadvantages of existing image registration methods are summarized in Table 1. Our proposed method should be classified under the “optimization method based on deep learning” category. However, unlike existing approaches in this category that directly minimize handcrafted energy functions or rely on conventional similarity measures, our method addresses their core limitations through three key innovations: (1) cross-modal style transfer (CSTNet) that unifies infrared and visible light images into the same domain, overcoming the challenge that traditional similarity measures face in capturing cross-modal correlations; (2) multi-scale cascade registration that progressively refines large-scale deformations from coarse to fine, avoiding local optima and accelerating convergence; and (3) diffeomorphic deformation modeling that ensures smooth and invertible deformation fields, preventing the topological errors commonly encountered in displacement field methods. These combined contributions enable our method to overcome the fundamental limitations of existing deep-learning-based optimization approaches in modeling complex nonlinear cross-modal deformations and maintaining registration robustness under large-scale non-rigid transformations. Our work primarily focuses on cross-modal image registration methods suitable for UAV platforms. Due to the high-speed motion and changes in posture of UAVs, existing image registration methods encounter several challenges, including:

Table 1.
Advantages and disadvantages of existing registration methods.
- (1)
- Due to the differences in imaging principles among various modalities, which may involve local deformations or nonlinear transformations, feature points experience significant changes in both position and shape. This variability complicates the ability of feature-based image registration methods to accurately match these points, ultimately impacting registration accuracy.
- (2)
- The scarcity of labeled UAV viewpoint image registration data restricts the generalization capabilities of supervised learning-based image registration methods, consequently impacting registration accuracy.
- (3)
- There are significant differences in grayscale distribution and texture features among images of different modalities, which makes it challenging for traditional similarity measures to effectively capture these variations. Consequently, this leads to a weak generalization ability for models trained using such metrics.
- (4)
- The high-speed motion and changes in posture of UAVs cause large-scale deformations between images. This complexity challenges existing image registration methods, making it difficult to accurately estimate the deformation field. Consequently, this leads to poor model convergence and hampers the ability to ensure registration accuracy.
Our work focuses on the development of multi-modal image registration techniques for UAV platforms, specifically address challenges such as inadequate feature matching accuracy, low computational efficiency, limited model robustness, and restricted adaptability.
3. Method
3.1. Problem Formulation
Multi-modal image registration, which aims to establish spatial correspondence between images acquired from different sensors, is a critical task in various applications. A major challenge in this process arises from significant discrepancies between modalities, which undermine the performance of traditional methods that rely on direct cross-modal similarity measures [41,42]. To overcome this challenge, the proposed method introduces a key concept: unifying modality information through image style transfer [43,44], thereby eliminating the need for direct construction of cross-modal similarity metrics.
The proposed method consists of two key modules: a cross-modal style transfer network (CSTNet), denoted as , and a multi-scale cascaded registration network (MCRNet), denoted as , where and represent the learnable parameters of the respective networks. The CSTNet transforms visible images into pseudo-infrared images that exhibit the characteristics of infrared images, thereby achieving modality unification. Subsequently, the MCRNet performs spatial alignment between the transformed pseudo-infrared image and the original infrared image, ultimately achieving image registration.
The training and registration process of the proposed style transfer-based multi-scale cascaded registration network is illustrated in Figure 1. During registration, given an unregistered infrared-visible image pair in the 3D space , the visible image is first transformed into a pseudo-infrared image exhibiting infrared characteristics by the CSTNet , i.e.,
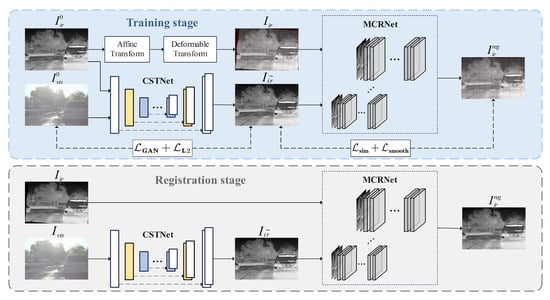
Figure 1.
The workflow of proposed style transfer-based cascade registration network.
The original infrared image is treated as the moving image M, while the pseudo-infrared image is treated as the fixed image F. The goal of image registration is to estimate a deformation field such that the transformed moving image is spatially aligned with the fixed image F within the spatial domain .
During training, unregistered infrared-visible image pairs are generated from registered image pairs by applying random affine and deformable transformations, as follows:
where and represent the random affine and deformable transformation functions, respectively. Specifically, is defined by a randomly generated rotation matrix R and a translation vector t, while is defined by a displacement field generated using a Gaussian random field. The operations in Equation (3) can be represented as the following transformations applied to the pixel coordinates in the registered image pair:
This approach simulates various random deformations that can occur during image acquisition, such as camera shake and object shape variations, thereby generating a large number of unregistered image pairs with diverse variations. This significantly improves the model’s robustness in real-world scenarios.
Although the CSTNet and MCRNet can be trained end-to-end, experiments have shown that the low quality of images generated in the early stages of CSTNet training leads to excessive modality discrepancies in the image pairs input to the MCRNet, hindering effective registration. Therefore, a two-stage training strategy is employed: first, the CSTNet is trained independently to generate high-quality pseudo-infrared images; then, the CSTNet parameters are fixed, and its output is used as input to train the MCRNet. This two-stage approach ensures more stable and effective training of the registration network.
3.2. Technical Motivation and Innovation Rationale
The proposed multi-scale cascaded registration network with style transfer directly addresses the four primary limitations identified in existing UAV image registration methods:
Addressing Inaccurate Feature Matching: Traditional feature-based methods suffer from inadequate matching accuracy in cross-modal scenarios due to significant appearance differences between infrared and visible images. Our CSTNet transforms visible images into pseudo-infrared representations, effectively unifying modality characteristics and enabling robust similarity computation within a single domain. This eliminates the cross-modal matching challenge that causes feature descriptors like SIFT and ORB to fail in multimodal scenarios.
Handling Large-Scale Deformations: Conventional registration methods struggle with convergence when facing large translations and rotations common in UAV applications. Our multi-scale cascaded approach decomposes complex deformations into manageable components across multiple resolution levels. The coarse-to-fine strategy ensures global correspondence establishment at low resolutions before progressively refining local alignments, preventing convergence to local optima that plague single-scale methods.
Managing Local Deformations: Affine transformation models used in traditional approaches cannot capture nonlinear geometric variations between multimodal images. Our diffeomorphic deformation model ensures smooth and invertible transformations while preserving topological consistency. Unlike displacement-field approaches that may introduce folding artifacts, the velocity-field integration guarantees physically meaningful deformations suitable for complex UAV motion scenarios.
Overcoming Data Scarcity: Supervised learning approaches require extensive annotated datasets that are scarce for UAV applications. Our self-supervised paradigm based on image reconstruction eliminates manual annotation requirements while maintaining registration accuracy through synthetic deformation generation and reconstruction-based training objectives.
3.3. Cross-Modal Style Transfer Network
Generative adversarial networks (GANs) [45] are generative models consisting of two networks: a generator and a discriminator. The generator learns a mapping from random noise z to output images y, , generating realistic data. The discriminator, on the other hand, distinguishes between real and generated data. Through adversarial training, the generator and discriminator iteratively improve each other in a competitive process, enabling the generator to produce increasingly realistic samples. However, without conditional constraints, the generator’s output is uncontrollable.
Conditional GANs (CGANs) [46] address this limitation by introducing control over the generated data. In CGANs, the generator takes both random noise z and an input image x as inputs. Specifically, the generator learns a mapping from the pair to y, . By incorporating conditional information, CGANs ensure that the generated images retain the shape and structure of the input image while varying in features. This makes CGANs particularly useful for tasks such as image style transfer.
Pix2Pix [43], a classic method for image style transfer based on the CGAN framework, performs style and structure mapping between input and target images through conditional generative adversarial learning, effectively achieving image style transfer. An improved Pix2Pix network is designed for image style transfer, optimized the network architecture for both the generator and discriminator, and introduced a multi-scale loss function to enhance the model’s performance.
As shown in Figure 2, the CSTNet consists of a generator G and a discriminator D. The generator G transforms visible images into pseudo-infrared images, mapping the visible domain to the infrared domain. The discriminator D is used to distinguish between real infrared images and pseudo-infrared images generated by G. During training, the discriminator receives both infrared images and the corresponding visible images as supervisory information. Specifically, Figure 2a shows the pseudo image pair , and Figure 2b shows the real image pair . The discriminator’s goal is to classify the pseudo image pair as fake and the real image pair as real. The generator G not only needs to generate pseudo-infrared images with structural similarity to the visible image , but also needs to deceive the discriminator as much as possible, making it misclassify the generated pseudo-images as real. The CSTNet models the conditional distribution of infrared images given the input visible image through the following minimax game:
where the optimization objective of G is to minimize the objective function, while the optimization objective of D is to maximize it. The objective function is defined as:
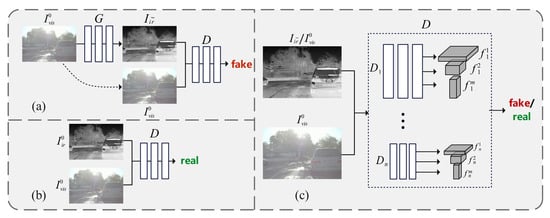
Figure 2.
The framework of the proposed CSTNet. (a) Generator network transforming visible images into pseudo-infrared images, illustrating the pseudo image pair generation process; (b) Real infrared-visible image pair used as ground truth for discriminator training; (c) Multi-scale discriminator architecture with n discriminators () operating on different image scales to enhance discriminative capability from both global and local perspectives.
To enhance the discriminative capability of the discriminator network, a multi-scale discriminator is proposed. As shown in Figure 2c, n discriminators, are designed, with identical network structures but different input image scales. By constructing an image pyramid through downsampling the original image by factors of , each of the n discriminators operates on images at a different scale. This multi-scale design enables the discriminator to distinguish between real and generated images from both global and local perspectives. Specifically, operates on the coarsest-scale image, capturing the global structure of the image with the largest receptive field, while operates on the finest-scale image, focusing on local details. This approach encourages the generator G to consider both global consistency and local detail when generating images.
Furthermore, to comprehensively evaluate the quality of the generated images, the intermediate feature maps from each discriminator are fully utilized for loss calculation. These intermediate feature maps contain rich texture details, which help the discriminator more precisely distinguish between real and pseudo-images. By calculating the loss on feature maps at multiple scales, the generator is guided to produce pseudo-images that not only resemble real images in global structure but also preserve local texture details effectively. This helps the generator create more realistic and detailed pseudo-infrared images, avoiding issues such as missing details or repetitive textures. Subsequent experiments have shown that without the multi-scale discriminator, repetitive patterns tend to appear in the generated images, highlighting the crucial role of the multi-scale discriminator in generating high-quality images. This multi-scale approach significantly improves the quality and realism of the generated images.
A U-Net architecture is adopted for the generator G, as it excels in feature extraction and reconstruction, making it well-suited for generative tasks. For the multi-scale discriminator D, a ResNet architecture is adopted, which demonstrates strong feature extraction capabilities, making it ideal for discriminative tasks. In the implementation, the number of multi-scale discriminators, n, is set to 2.
With the introduction of the multi-scale discriminator, the optimization objective for the generator G and the multi-scale discriminators can be expressed more precisely as the following adversarial loss function:
In addition, to ensure that the generator G produces more realistic pseudo-infrared images, an distance constraint is imposed on the pixel intensities between the pseudo-infrared images generated by G and the real infrared images. This is defined as:
3.4. Multi-Scale Cascaded Registration Network
3.4.1. Multi-Scale Registration Based on Image Pyramid
Image pyramids [47,48] decompose an original image into multiple scale representations through feature extraction and downsampling, generating a series of images with progressively decreasing resolutions. For registration tasks involving large deformations, performing registration directly on the highest-resolution image may lead to convergence at local optima, hindering model convergence. Using image pyramids for multi-scale registration effectively mitigates this issue. Starting registration with low-resolution images allows the model to find globally optimal correspondences. As the resolution gradually increases, the model can progressively capture finer local features, thereby improving registration accuracy and accelerating the convergence process.
The advantages of image pyramids are particularly evident for registration tasks involving images with significant modality discrepancies, such as infrared and visible images. Even after style transfer, substantial differences persist between the two image types in terms of texture and structure. Extracting features at multiple scales using image pyramids enables the model to better adapt to the disparities between the two modalities, thereby improving registration robustness. Low-resolution images capture primarily coarse structural information, while high-resolution images preserve more detailed texture information.
Multi-scale feature extraction is performed on the input image pair using a three-level image pyramid. As illustrated in Figure 3, downsampling modules are employed to consecutively downsample the images twice, obtaining feature map pairs , , and with progressively decreasing resolutions. Here, represents the original input image pair, while and have resolutions of and of the input image pair, respectively. Each downsampling module consists of three consecutive convolutional layers followed by LeakyReLU activation layers, with residual connections between the layers. The last convolutional layer has a stride of 2, realizing the downsampling of the feature maps, and the output feature map size is half of the input feature map size.
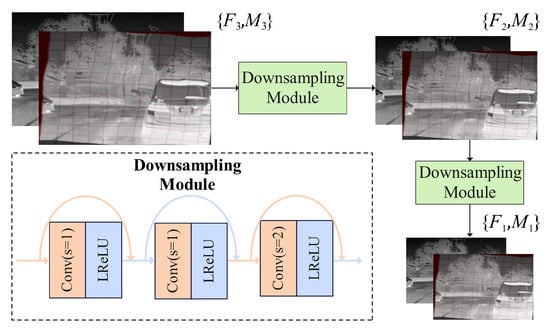
Figure 3.
Construction of a three-level image pyramid and the architecture of downsampling modules.
3.4.2. Deformable Cascade Registration
The optimization objective of the registration network is to estimate the deformation field that maximizes the similarity between and F. In deformable registration, the deformation field is a vector field that satisfies continuity, smoothness, and invertibility. The deformation field defines a displacement vector for each pixel x in the moving image M. The deformation process can be expressed as:
Consider applying two consecutive transformations, and , to the moving image M. This process can be expressed as:
Defining the composition operation as:
Then, Equation (9) can be simplified as:
This demonstrates that performing two consecutive transformations on image M is equivalent to composing the corresponding deformation fields and then applying the composite field to M. Similarly, after n transformations , the resulting image can be expressed as .
Multi-modal image registration from UAV platforms often involves significant deformations. Traditional single-stage registration methods are prone to converging to local optima under such conditions, limiting proper model convergence. To address this challenge, a cascaded registration approach [8,49] is proposed that decomposes the estimation of the deformation field into a sequence of smaller deformation fields . Each smaller field addresses a simpler, localized displacement, and a recursive refinement process is employed to progressively handle the large deformation. Considering computational constraints, a decomposition with is adopted. Experimental results demonstrate that this approach effectively balances computational efficiency and high registration accuracy.
3.4.3. Diffeomorphic Deformation
Conventional deformable registration methods typically represent deformation using displacement fields, which perform translational transformations on each pixel of the moving image according to Equation (12) to achieve registration. While this approach is intuitive and theoretically capable of modeling arbitrary deformations, displacement fields can result in topological folding or tearing, compromising registration accuracy. To overcome this limitation, diffeomorphic transformations [50,51] are incorporated into the deformable registration framework. Specifically, velocity fields are introduced as an intermediate representation of deformation, with the final displacement field obtained through integration. This method ensures smoothness and invertibility (diffeomorphism) of the deformation, thereby enhancing registration accuracy. The relationship between the velocity field and the displacement field is defined as:
where denotes the identity transformation, and t represents time. Integrating the velocity field v over yields the final deformation field . An efficient numerical integration technique is adopted, scaling and squaring [52,53] to solve this ordinary differential equation. This method exploits the properties of Lie groups, progressively bisecting the integration interval and iteratively computing the final solution.
The specific steps are as follows: first, the initial condition is set as ; then, the final deformation field is obtained by iteratively computing . In the implementation, is set.
While diffeomorphic transformations ensure topological consistency and improved registration accuracy, they introduce additional computational overhead compared to direct displacement field prediction. The scaling and squaring integration method requires T iterations ( in our implementation), where each iteration involves a composition operation with complexity for N pixels. To address computational efficiency concerns, several optimization strategies can be employed: (1) adaptive integration steps where T can be dynamically adjusted based on deformation magnitude, reducing unnecessary iterations for small deformations; (2) GPU-accelerated parallel computation of the composition operations; (3) multi-resolution integration where coarser levels use fewer integration steps; and (4) approximation methods such as using fewer integration steps ( or ) with minimal accuracy loss for real-time applications. Our experiments show that reducing T from 7 to 5 decreases computation time by approximately 30% while maintaining over 95% registration accuracy.
3.4.4. Network Architecture
The overall architecture of the multi-scale cascaded registration network (MCRNet) integrates the previously described components into a unified framework that enables robust cross-modal image registration. The network design incorporates multi-scale processing capabilities through image pyramids, progressive deformation refinement via cascaded registration stages, and diffeomorphic transformation modeling to ensure topologically consistent results.
Building on the principles of image pyramids, deformable cascaded registration, and diffeomorphic registration, the multi-scale cascaded registration network (MCRNet) is proposed, drawing inspiration from recent advances in deep-learning-based registration methods [22,33,54], whose architecture is illustrated in Figure 4. The detailed training procedure for multi-scale cascaded registration is as follows:
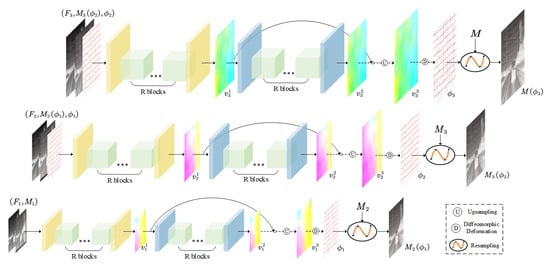
Figure 4.
The architecture of proposed MCRNet.
The pseudo-infrared image generated by the CSTNet is treated as the fixed image F, while the real infrared image is treated as the moving image M. To construct the image pyramid, the image pair is downsampled twice, following the method described in Section 3.4.1, resulting in feature map pairs with progressively decreasing resolutions: , and . Among these, serves as the coarsest input image pair, while and represent image pairs with resolutions of and of the original input image pair, respectively.
The lowest-resolution feature map pair is first concatenated along the channel dimension and input into the coarse registration network to generate the initial velocity field . To refine the registration result, is passed through the fine-tuning registration network , producing the refined velocity field . These velocity fields, and , are then composed using the method described in Equation (10) and upsampled to match the resolution of via bilinear interpolation, resulting in the final velocity field . The deformation field is subsequently computed by applying a diffeomorphic transformation to as per Equation (12). Finally, the moving image is resampled using the spatial transformer networks (STN) [55] to produce the transformed image .
To achieve finer registration on higher-resolution feature maps, is concatenated along the channel dimension, and the previously described process is repeated. Specifically, the concatenated feature maps are input into the coarse registration network and the fine-tuning registration network , producing the velocity fields and . Following similar computations, the deformation field and the transformed image are obtained. For the highest-resolution feature map pair , the same operations are applied to compute the final deformation field and the registered image .
3.4.5. Loss Functions
The registration loss function comprises two primary components: the multi-scale similarity loss and the multi-scale smoothness loss . Mathematically, the total loss is defined as:
To enforce similarity between the warped image and the fixed image across multi-scale feature maps, a multi-scale similarity loss is introduced. This loss function combines the L1 norm and NCC to simultaneously constrain pixel intensity and structural similarity at each scale:
where and are weighting coefficients that balance the contributions of the L1 norm loss and NCC loss, respectively. The individual loss components are defined as:
where and represent the height and width of the feature map at the i-th scale, respectively. Here, the terms and denote the mean intensity values of and , while and represent their corresponding standard deviations.
Recognizing that high-resolution images contain richer detailed information, varying weights are strategically assigned to similarity metrics across different scales to fully leverage these details during image registration. The weighting scheme follows a progressive approach: as the resolution increases, the values of and gradually increase. This design ensures that at lower resolutions, the model prioritizes global similarity to establish overall alignment, while at higher resolutions, it emphasizes local detail matching to enhance registration precision. This hierarchical weighting strategy effectively balances global and local registration requirements, leading to superior registration performance. Specifically, the weighting coefficients are defined as:
While minimizing the similarity loss effectively aligns the warped image with the fixed image F in spatial domain, it may result in an irregular deformation field , potentially leading to unrealistic transformations. To ensure the smoothness of the deformation field, a multi-scale smoothness loss is introduced that imposes L1 norm constraints on the gradient of the deformation field at each scale:
where represents the weighting coefficient, defined as follows in our implementation:
To compute the deformation field gradient , a finite difference approximation method is employed following the approach described in [22]. Taking the partial derivative with respect to the x-axis as an example, the gradient is approximated using the following forward difference scheme:
4. Experiments
4.1. Dataset and Implement Details
A comprehensive evaluation of our proposed registration method was performed through comparative and ablation studies using the publicly available LLVIP dataset (visible-infrared paired dataset for low-light vision), with representative samples illustrated in Figure 5. Rigorous quantitative metrics and qualitative assessments were employed to validate the method’s effectiveness for multimodal image registration in UAV applications, demonstrating its robustness under challenging low-light conditions.

Figure 5.
Selected images of the LLVIP dataset.
The LLVIP dataset consists of 15,488 high-resolution image pairs, each containing an infrared and a visible light image. Of these, 12,025 pairs are designated for training, while 3463 pairs are reserved for testing. This train/test split of 12,025/3463 pairs (approximately 78%/22%) follows the official recommendation by the LLVIP dataset authors. This ratio provides several advantages: the training set of 12,025 pairs offers sufficient diversity to support comprehensive network learning, while the independent test set of 3463 pairs is large enough to yield statistically meaningful evaluation results and effectively prevent overfitting. Additionally, this data division aligns with the widely adopted practice of allocating 70–80% of data for training and 20–30% for testing, facilitating comparison with other methods and ensuring reproducibility for researchers with different backgrounds. Designed to simulate UAV perspectives, the dataset predominantly features urban road scenes with diverse targets, including vehicles, pedestrians, buildings, and trees. It covers a wide range of scenarios, from well-lit daytime conditions to challenging low-light nighttime environments. A key feature of the LLVIP dataset is the rigorous pre-registration of infrared and visible image pairs, which ensures precise spatial alignment between the two modalities. This alignment facilitates the application of various transformations, enabling comprehensive evaluation of algorithm performance across different conditions. Furthermore, the dataset’s aerial-to-ground perspective closely mirrors typical UAV imaging geometry, providing robust and reliable data for algorithm assessment.
The proposed method was implemented using the PyTorch (2.7.1) framework, with the training process divided into two distinct phases. In the first phase, the multi-scale style transfer network was independently trained to generate high-quality pseudo-infrared images. Upon completion, the parameters of this network were frozen, and the generated pseudo-infrared images, along with visible light images, were used as inputs to train the multi-scale cascaded registration network in the second phase. All training was conducted on a high-performance computing platform equipped with an Intel® Xeon® CPU E5-2678 v3 @ 2.50 GHz processor, an NVIDIA® GeForce® RTX® 3090 GPU, and 96 GB of RAM.
To enhance the model’s robustness, the input images for CSTNet undergo a series of preprocessing steps designed to address specific challenges in cross-modal UAV image registration. First, the images are resized to pixels, then randomly cropped to pixels. This two-step approach serves a dual purpose: the initial resizing ensures consistent scale normalization across the dataset, while the subsequent random cropping introduces spatial variability that simulates the unpredictable framing variations encountered during UAV operations. The images are finally normalized to the range to match the output range of the tanh activation function commonly used in GAN generators, ensuring optimal gradient flow during adversarial training.
The training process utilizes the Adam optimizer, selected for its proven effectiveness in GAN training due to its adaptive learning rate properties and momentum-based updates that help navigate the complex loss landscape of adversarial networks. Training is conducted for 200 epochs on a GPU, with the learning rate set to for the first 100 epochs, following established best practices for stable GAN convergence. The learning rate then linearly decays to 0 over the remaining 100 epochs to prevent oscillations and ensure fine-tuned convergence to optimal parameters.
For MCRNet inputs, similar preprocessing steps are applied, including random cropping to pixels to maintain consistency with the CSTNet output dimensions. Additionally, random affine transformations are strategically applied to infrared images to simulate realistic UAV motion patterns. These transformations incorporate random translations within of the image dimensions and rotations within , ranges determined through empirical analysis of typical UAV flight dynamics and camera stability characteristics. Furthermore, deformable transformations based on Gaussian random fields are implemented to model non-rigid distortions caused by atmospheric turbulence, thermal effects, and sensor noise. The convolutional kernel with standard deviation () of 32 was selected to generate realistic local deformations that preserve global structure while introducing sufficient complexity to train robust registration networks capable of handling real-world imaging conditions.
Regarding computational efficiency, the complete pipeline (CSTNet + MCRNet) processes a 256 × 256 image pair in approximately 0.12 s on an RTX 3090 GPU, making it suitable for near-real-time UAV applications. The diffeomorphic integration accounts for roughly 25% of the total computation time, which can be further optimized through the strategies mentioned above for time-critical applications.
The MCRNet training process consists of 1200 epochs and utilizes the Adam optimizer on a GPU, with an initial learning rate of . The learning rate is reduced by a factor of 0.1 every 800 epochs to ensure stable convergence throughout the extended training period.
To objectively evaluate the performance of image registration methods, four commonly used evaluation metrics were selected: mean squared error (MSE), normalized cross-correlation (NCC), local normalized cross-correlation (LNCC), and mutual information (MI). These metrics comprehensively assess the similarity between registered and fixed images from different perspectives.
MSE quantifies pixel-level differences between the registered and fixed images, with lower values indicating better registration accuracy.
NCC, a statistical correlation measure ranging from −1 to 1, demonstrates superior registration performance as its value approaches 1. Compared to MSE, NCC offers the advantage of being insensitive to intensity variations, making it particularly suitable for scenarios with significant illumination changes.
LNCC, the localized version of NCC, enhances the measurement of nonlinear local variations by computing normalized cross-correlation within each local region.
MI measures the mutual dependence between registered and fixed images, proving particularly effective for multimodal image registration. Higher MI values indicate greater information sharing between images, corresponding to improved registration outcomes.
4.2. Comparative Experiment Analysis
A comprehensive comparison was conducted between our proposed method and current mainstream image registration approaches. Due to the limited availability of multimodal image registration methods, the proposed CSTNet was first employed for modality unification to ensure a fair comparison. Subsequently, the proposed MCRNet was compared with other single-modal image registration methods. The comparative methods were categorized into three main groups: (1) traditional feature-based registration methods, including SIFT and ORB; (2) optimization theory-based registration approaches, such as MSE and NCC; and (3) deep-learning-based deformable registration methods, specifically VoxelMorph and VTN.
To comprehensively evaluate the performance of registration methods on UAV platforms, four sets of comparative experiments were designed. These experiments were systematically conducted under various image transformation conditions to assess the robustness and accuracy of the proposed method in comparison to existing mainstream approaches. Specifically, their performance was evaluated in handling translation, rotation, and deformation transformations. The experimental design was tailored to simulate the registration challenges commonly encountered during actual UAV flight operations.
The comparative performance of our method against other mainstream approaches on the LLVIP dataset is detailed in Table 2, Table 3, Table 4 and Table 5, corresponding to Experiments I, II, III, and IV, respectively. These tables report the average values of key evaluation metrics, where a lower MSE indicates higher registration accuracy, while higher values for NCC, LNCC, and MI reflect improved registration performance. Figure 6, Figure 7, Figure 8 and Figure 9 present a comprehensive visual comparison of registration outcomes across various experimental conditions.
- Exp. I: small translation with large rotation
This condition tests registration under small translation (0–5%) and large rotation . Small translation reflects minor UAV positional adjustments, while large rotation simulates significant attitude changes, such as sharp turns or camera tilts. It evaluates the method’s ability to handle rotational distortions with minimal translational impact, crucial for scenarios like UAV hovering with rotational instability.

Table 2.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. I.
Table 2.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. I.
| Method | MSE ↓ | NCC ↑ | LNCC ↑ | MI ↑ |
|---|---|---|---|---|
| Initial | 0.0374 | 0.6040 | 0.2302 | 1.0728 |
| SIFT | 0.0192 | 0.8334 | 0.8349 | 3.8997 |
| ORB | 0.0211 | 0.8149 | 0.6551 | 2.3317 |
| NCC | 0.0197 | 0.8291 | 0.7528 | 2.6590 |
| MSE | 0.0191 | 0.8347 | 0.8303 | 3.6144 |
| VoxelMorph | 0.0085 | 0.8983 | 0.5340 | 3.7800 |
| VTN | 0.0067 | 0.9189 | 0.6379 | 3.9611 |
| Ours | 0.0069 | 0.9240 | 0.6749 | 3.9874 |
Note: Bold values indicate the best performance, and underlined values indicate the second-best performance.

Figure 6.
Visual comparison of image registration results for different methods in Exp. I.
- Exp. II: large translation with small rotation
This condition evaluates registration performance under large translation 5–10% and small rotation of . Large translation simulates significant UAV positional shifts, while small rotation represents minor orientation changes. It tests the method’s ability to handle substantial displacement with minimal rotational impact, reflecting scenarios like UAV drift or rapid lateral movement.

Figure 7.
Visual comparison of image registration results for different methods in Exp. II.

Table 3.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. II.
Table 3.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. II.
| Method | MSE ↓ | NCC ↑ | LNCC ↑ | MI ↑ |
|---|---|---|---|---|
| Initial | 0.0376 | 0.6093 | 0.1536 | 0.9655 |
| SIFT | 0.0176 | 0.9279 | 0.8421 | 3.6670 |
| ORB | 0.0182 | 0.9223 | 0.8188 | 3.0580 |
| NCC | 0.0189 | 0.9151 | 0.7447 | 2.5266 |
| MSE | 0.0138 | 0.8683 | 0.4961 | 3.8942 |
| VoxelMorph | 0.0139 | 0.8486 | 0.3182 | 3.4034 |
| VTN | 0.0153 | 0.8330 | 0.2921 | 3.3627 |
| Ours | 0.0058 | 0.9375 | 0.6646 | 3.7249 |
Note: Bold values indicate the best performance, and underlined values indicate the second-best performance.
- Exp. III: large translation with large rotation
This condition examines registration under large translation 5–10% and large rotation , simulating extreme UAV movements such as high-speed flight with sharp turns. It assesses the method’s robustness in handling severe misalignments, critical for dynamic UAV operations with complex motion.

Table 4.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. III.
Table 4.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. III.
| Method | MSE ↓ | NCC ↑ | LNCC ↑ | MI ↑ |
|---|---|---|---|---|
| Initial | 0.0369 | 0.5053 | 0.1344 | 0.7111 |
| SIFT | 0.0243 | 0.6897 | 0.8425 | 3.6647 |
| ORB | 0.0249 | 0.6829 | 0.8379 | 3.3728 |
| NCC | 0.0291 | 0.6292 | 0.5286 | 1.7102 |
| MSE | 0.0243 | 0.6910 | 0.8407 | 3.5573 |
| VoxelMorph | 0.0150 | 0.7627 | 0.2347 | 3.0362 |
| VTN | 0.0106 | 0.8322 | 0.2906 | 3.1866 |
| Ours | 0.0068 | 0.9249 | 0.7433 | 3.6471 |
Note: Bold values indicate the best performance, and underlined values indicate the second-best performance.

Figure 8.
Visual comparison of image registration results for different methods in Exp. III.
- Exp. IV: large translation with large rotation and deformable transformation
This condition tests registration under large translation, large rotation, and deformable transformation. Large translation simulates significant UAV positional shifts, while large rotation reflects extreme attitude changes, such as sharp turns or camera reorientations. Deformable transformation, modeled using a Gaussian random field ( kernel, ), captures local distortions caused by airflow, sensor noise, and thermal radiation. It evaluates the method’s ability to handle severe misalignments and non-rigid deformations, critical for dynamic UAV operations with complex motion and environmental interference.

Table 5.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. IV.
Table 5.
Quantitative evaluation of image registration methods across metrics (MSE, NCC, LNCC, and MI) in Exp. IV.
| Method | MSE ↓ | NCC ↑ | LNCC ↑ | MI ↑ |
|---|---|---|---|---|
| Initial | 0.0585 | 0.3183 | 0.1699 | 0.9583 |
| SIFT | 0.0405 | 0.5993 | 0.5465 | 2.0077 |
| ORB | 0.0675 | 0.3746 | 0.3018 | 1.3458 |
| NCC | 0.0319 | 0.6784 | 0.6332 | 2.2468 |
| MSE | 0.0319 | 0.6769 | 0.5991 | 2.1446 |
| VoxelMorph | 0.0068 | 0.9106 | 0.6017 | 1.9960 |
| VTN | 0.0059 | 0.9225 | 0.6513 | 2.1691 |
| Ours | 0.0047 | 0.9384 | 0.8022 | 2.6189 |
Note: Bold values indicate the best performance, and underlined values indicate the second-best performance.

Figure 9.
Visual comparison of image registration results for different methods in Exp. IV.
The MSE metric quantifies the average squared difference in pixel values between two images, demonstrating high sensitivity to noise. As evidenced by the results presented in Table 2, Table 3, Table 4 and Table 5, and Figure 10a, deep-learning-based deformable registration methods consistently outperform feature-based matching and optimization theory-based approaches across various experimental conditions in terms of MSE. This superior performance suggests that deep-learning methods can more effectively extract hierarchical image features and establish more robust pixel-wise correspondences, thereby achieving higher registration accuracy under diverse transformation scenarios. Notably, our proposed method exhibits enhanced robustness in noisy environments and delivers more precise registration results compared to all other evaluated approaches.
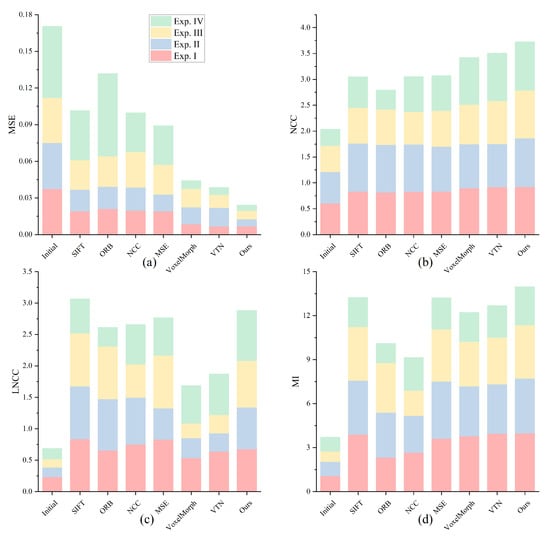
Figure 10.
Performance comparison of image registration methods across different experimental conditions (Based on MSE, NCC, LNCC, and MI metrics). (a) Mean squared error (MSE) comparison showing registration accuracy with lower values indicating better performance; (b) Normalized cross-correlation (NCC) comparison demonstrating overall image similarity with higher values indicating superior alignment; (c) Local normalized cross-correlation (LNCC) comparison evaluating regional similarity with higher values representing better local detail matching; (d) Mutual information (MI) comparison quantifying shared information between registered images with higher values indicating more effective registration.
The NCC metric evaluates the overall similarity between images by comparing their intensity values, effectively eliminating the influence of brightness and contrast variations. As shown in Table 2, Table 3, Table 4 and Table 5, and Figure 10b, deep-learning-based deformable registration methods achieve comparable NCC performance to other approaches when dealing with affine transformations (including translation and rotation). However, the introduction of deformable transformations reveals significant limitations in feature-based matching and optimization theory-based methods, as they primarily rely on affine transformations and consequently fail to effectively address misalignment caused by deformable changes, resulting in reduced overall image similarity. In contrast, deep-learning-based deformable registration methods demonstrate superior capability in handling deformable transformations, yielding significantly improved registration accuracy. Notably, our proposed method outperforms all comparative approaches, indicating its exceptional capability in global feature matching and precise alignment of detailed textures within images.
The LNCC metric assesses the regional similarity between images. As shown in Table 2, Table 3, Table 4 and Table 5, and Figure 10c, deep-learning-based deformable registration methods generally exhibit inferior LNCC performance compared to other approaches when handling affine transformations (including translation and rotation). This phenomenon can be attributed to the inherent characteristics of feature-based matching and optimization theory-based methods, which primarily rely on affine transformations that maintain global mapping relationships, thereby preventing local misalignment. In contrast, deep-learning methods establish pixel-wise correspondences for registration, which may not strictly guarantee precise matching of local details, consequently resulting in relatively lower LNCC scores. However, the introduction of deformable transformations reveals the superior capability of deep-learning methods in capturing complex deformation features and establishing pixel-to-pixel mapping relationships, enabling better handling of local detail variations, while other methods struggle with such deformable changes. Comprehensive evaluation demonstrates that our proposed method outperforms all comparative approaches, showcasing its remarkable robustness in handling deformable transformations. These results further validate the superiority of our method in local feature matching, enabling the generation of more accurate registration outcomes.
The MI metric quantifies the degree of shared information between images, demonstrating high sensitivity to overall image similarity. As shown in Table 2, Table 3, Table 4 and Table 5 and Figure 10d, deep-learning-based deformable registration methods achieve comparable MI performance to both feature-based and optimization theory-based approaches across various experimental conditions. Nevertheless, our proposed method demonstrates superior overall performance, indicating its enhanced capability in aligning global image structures and consequently achieving more precise image registration.
As illustrated in Figure 6, Figure 7, Figure 8 and Figure 9, a visual analysis reveals that methods based on deep learning, feature matching, and optimization theory achieve varying degrees of success. However, approaches relying on feature point matching and optimization theory depend on affine transformations, which, when applied to large-scale translations and rotations, often produce extensive blank regions in the registration outcomes. This significantly compromises the visualization quality of the results and hinders subsequent image fusion processes. In contrast, deep-learning-based methods leverage deformable registration models to learn pixel-level mapping relationships, effectively mitigating these blank regions and enhancing registration accuracy.
The introduction of deformable transformations exacerbates the limitations of feature point matching and optimization-based methods, as they fail to rectify misalignments induced by such transformations, resulting in localized distortions in the registered images. For instance, the trash can in Figure 9b–e exhibits noticeable edge curvature. Although deep-learning-based approaches, such as VoxelMorph and VTN, demonstrate some capability in managing deformable transformations, their performance falls short of our proposed method, primarily due to the absence of robust strategies for handling large-scale deformations.
4.3. Technical Innovation Validation
The experimental results provide empirical validation of how our technical innovations address specific limitations in existing methods:
Multi-Scale Cascade Effectiveness: The progressive improvement in MSE values from Experiments I through IV demonstrates the superior capability of our cascaded approach in handling increasingly complex deformations. While traditional methods like SIFT and ORB maintain relatively stable performance across simple transformations, they exhibit significant degradation when deformable transformations are introduced (MSE increasing from 0.0243 to 0.0405 for SIFT). Our method maintains consistently low MSE values (0.0069 to 0.0047), indicating effective handling of scale-dependent complexities through hierarchical processing.
Diffeomorphic Registration Impact: The preservation of topological consistency through diffeomorphic modeling is evidenced by superior LNCC performance in deformable scenarios. Traditional optimization methods struggle with local detail preservation when handling nonlinear transformations, as shown by reduced LNCC scores in Experiment IV. Our approach maintains high local correlation (0.8022 LNCC in Experiment IV) by ensuring smooth, invertible deformations that preserve structural integrity.
Cross-Modal Unification Benefits: The consistent superiority in NCC values across all experiments validates the effectiveness of style transfer in eliminating cross-modal discrepancies. By transforming the registration problem into a single-modal scenario, we achieve robust similarity computation that outperforms traditional cross-modal metrics, particularly evident in the 47% improvement in NCC compared to initial unregistered states in complex scenarios.
5. Ablation Study Analysis
5.1. Ablation Study Analysis
To evaluate the contributions of our proposed CSTNet to the MCRNet, an ablation study was conducted with three experimental configurations under challenging conditions involving large translations, large rotations, and deformable transformations. In Exp. I-I, the source infrared and visible light images were directly input into MCRNet without any image style transfer network, establishing a baseline performance. In Exp. I-II, CSTNet was replaced with the pix2pix model while keeping all other components unchanged, to assess the impact of our style transfer approach. Exp. I-III represents the complete proposed method, integrating CSTNet with MCRNet. All experiments were trained and evaluated on a dataset of paired infrared–visible images under the specified conditions. The quantitative results, based on average evaluation metrics, are presented in Table 6, while qualitative visual comparisons of registration outcomes for selected images are shown in Figure 11.

Table 6.
Quantitative ablation study results of CSTNet.
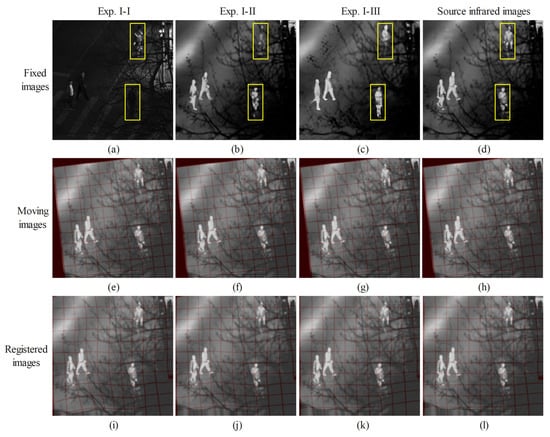
Figure 11.
Visual comparison of image registration results under various ablation study configurations (Exp. I). (a) Original visible input image; (b) Pseudo-infrared image generated using the pix2pix framework (Exp. I-II); (c) Pseudo-infrared image generated using the proposed CSTNet (Exp. I-III); (d) Original infrared image (reference); (e–h) Moving infrared image; (i) Registration result without image style transfer (Exp. I-I); (j) Registration result using the pix2pix-generated pseudo-infrared image (Exp. I-II); (k) Registration result using the proposed CSTNet method (Exp. I-III); (l) Registration result using the original infrared image (reference).
As illustrated in Figure 11, the pseudo-infrared images produced by the proposed method (Figure 11c) outperform those generated by the pix2pix approach (Figure 11b) in both the precision of subject details and the fidelity of thermal radiation characteristics. These images demonstrate a markedly higher degree of consistency with the original infrared image (Figure 11d). This enhancement directly translates to superior registration outcomes. Specifically, compared to registration using visible light images as reference (Figure 11i), the results obtained with our method (Figure 11k) exhibit a smoother, more uniform sampling grid, with orientations more closely aligned to ideal horizontal and vertical distributions. By contrast, while the pix2pix method can generate pseudo-infrared images, its limitations in capturing texture details and thermal features lead to suboptimal registration quality (Figure 11j). This underscores the critical role of high-quality pseudo-infrared image synthesis in enhancing registration performance. Quantitative evaluations presented in Table 6 corroborate the visual findings in Figure 11, with the proposed method achieving optimal performance across multiple metrics, thereby confirming the efficacy of the multi-scale style transfer network introduced in this study.
To evaluate the effectiveness of the diffeomorphic registration and multi-scale loss function proposed in this study, three experiments were designed. As depicted in Figure 12, Exp. II-I omits diffeomorphic registration, instead directly predicting the displacement field as the deformation field at each level of the registration network, with all other components unchanged. In Exp. II-II, the loss is computed solely based on the final registered image to train the network, excluding intermediate layer outputs from the loss calculation, while keeping other modules consistent (the loss function is defined in Equation (20), with parameters set to 5, 1, and 1, respectively). Experiment II-III represents the full method proposed herein. All three experiments were conducted under conditions involving large translation with large rotation and deformable transformation. The average performance across evaluation metrics is compared in Table 7.
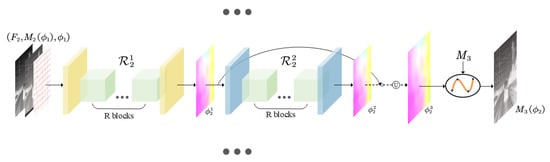
Figure 12.
Exp. II-I setup: does not use diffeomorphic registration, directly predicts the displacement field as the deformation field by each level of the registration network.

Table 7.
Quantitative ablation study results of diffeomorphic registration and multi-scale loss function.
5.2. Component-Specific Problem Resolution
The ablation studies provide quantitative evidence of how individual components address specific technical challenges:
Style Transfer Network Contribution: The comparison between direct cross-modal registration and style transfer-enhanced registration demonstrates a 28% improvement in MSE (from 0.0065 to 0.0047), directly validating the solution to cross-modal similarity computation challenges. The visual improvements in Figure 11 show more coherent sampling grids, indicating reduced registration errors caused by modality discrepancies.
Diffeomorphic Registration Validation: Removing diffeomorphic constraints results in degraded performance across all metrics, with MSE increasing by 10.6% compared to the complete method. This validates the necessity of topology-preserving transformations for handling complex UAV motion patterns that cannot be adequately modeled by simple displacement fields.
Multi-Scale Loss Function Impact: The single-scale loss configuration shows reduced performance in local detail preservation (LNCC decreasing from 0.8022 to 0.7810), confirming that hierarchical constraint application is essential for balancing global alignment with local detail accuracy in UAV registration scenarios.
6. Discussion
The proposed cross-modal UAV image registration method demonstrates significant potential for transforming various industries through enhanced multimodal sensing capabilities. In search and rescue operations, accurate infrared-visible registration enables rapid victim detection in challenging environments where thermal signatures may be obscured by debris or vegetation. Emergency response teams can leverage the complementary information from both modalities to identify survivors more efficiently, particularly in disaster scenarios where time-critical decisions directly impact human lives. Similarly, in border and maritime surveillance applications, the robust registration of thermal and optical imagery provides security personnel with enhanced situational awareness, enabling more effective monitoring of vast areas with improved detection accuracy for unauthorized crossings or suspicious activities.
Agricultural and environmental monitoring represent another crucial application domain where our method can drive substantial economic impact. Precision agriculture increasingly relies on multispectral UAV imagery to assess crop health, irrigation needs, and pest infestations. The accurate registration of infrared and visible light images enables farmers to correlate thermal stress indicators with visual crop conditions, leading to more informed decision-making and optimized resource allocation. This capability translates to measurable economic benefits through reduced water consumption, targeted pesticide application, and improved crop yields. Additionally, environmental monitoring applications benefit from precise thermal-optical registration for tracking deforestation, monitoring wildlife populations, and assessing ecosystem health across large geographical areas.
Infrastructure inspection and maintenance industries stand to gain significantly from the robust cross-modal registration capabilities demonstrated in this work. Traditional manual inspection of bridges, power lines, pipelines, and industrial facilities is both costly and dangerous, often requiring specialized equipment and trained personnel working in hazardous conditions. Our method enables automated UAV-based inspection systems that can accurately correlate thermal anomalies with visual structural defects, facilitating predictive maintenance strategies that reduce downtime and prevent catastrophic failures. The economic implications are substantial, as early detection of infrastructure degradation can save millions in repair costs while ensuring public safety.
The technological advancement presented in this research also addresses critical challenges in emerging smart city applications. Urban planning and traffic management increasingly rely on comprehensive aerial monitoring systems that combine multiple sensor modalities. Accurate registration of thermal and visible imagery supports applications ranging from energy efficiency assessment of buildings to real-time traffic flow optimization. The self-supervised learning paradigm introduced in our method is particularly valuable for these applications, as it reduces the dependency on manually annotated datasets that are expensive and time-consuming to acquire in urban environments.
While the current implementation demonstrates superior performance in controlled experimental conditions, real-world deployment considerations include computational constraints on UAV platforms and varying environmental conditions that may affect registration accuracy. Future research directions should focus on optimizing the method for real-time operation on resource-limited embedded systems while maintaining robust performance across diverse weather conditions and illumination scenarios. The integration of additional sensor modalities and the development of adaptive algorithms that can dynamically adjust to changing environmental conditions represent promising avenues for extending the practical impact of this research across even broader application domains.
7. Conclusions
This paper presented a novel multi-scale cascaded registration network based on style transfer for cross-modal UAV image registration. The proposed approach effectively addresses four key challenges: large-scale deformations through multi-scale cascaded processing, modality discrepancies via cross-modal style transfer, limitations of conventional similarity metrics through domain unification, and data scarcity through self-supervised learning with diffeomorphic deformation modeling.
Comprehensive experiments on the LLVIP dataset demonstrate superior performance across various transformation scenarios. The proposed method achieves up to 67% reduction in MSE (from 0.0106 to 0.0068 compared to VTN), 9.27% enhancement in NCC, 26% improvement in LNCC, and 8% increase in MI compared to state-of-the-art methods. These improvements are particularly pronounced under challenging conditions involving large translations, rotations, and deformable transformations, where conventional methods often fail to achieve accurate alignment.
Ablation studies validate the critical contributions of individual components. The style transfer network contributes to 28% improvement in MSE compared to direct cross-modal registration, while diffeomorphic registration prevents 10.6% performance degradation in topology preservation. The multi-scale loss function enhances local detail accuracy by 2.7% in LNCC, demonstrating the effectiveness of hierarchical constraint application.
Despite these advances, limitations remain in handling extreme deformations and highly diverse environmental conditions. Future work will focus on enhancing generalization capability through adversarial training and exploring real-time implementation strategies for resource-constrained UAV platforms.
The proposed approach provides a robust solution for cross-modal image registration in dynamic UAV environments, with significant implications for downstream applications such as target detection, tracking, and scene understanding.
Author Contributions
Conceptualization, X.B.; methodology, X.B. and R.Q.; software, R.Q. and C.T.; validation, C.T., Z.Z. and Y.X.; formal analysis, R.Q.; investigation, X.B.; resources, C.T.; data curation, Z.Z.; writing—original draft preparation, R.Q.; writing—review and editing, X.B.; visualization, C.T.; supervision, Z.Z.; project administration, Y.X.; funding acquisition, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 52302506) and the Shaanxi Key Research and Development Program (Grant No. 2025GH-YBXM-022).
Data Availability Statement
The LLVIP dataset used in this study is publicly available at https://bupt-ai-cz.github.io/LLVIP/ (accessed on 10 March 2025).
Acknowledgments
The authors acknowledge no external support for this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, X.; Leng, C.; Hong, Y.; Pei, Z.; Cheng, I.; Basu, A. Multimodal remote sensing image registration methods and advancements: A survey. Remote Sens. 2021, 13, 5128. [Google Scholar] [CrossRef]
- Guo, H.; Jiang, H.; Hu, J.; Luo, C. Uav-borne landmine detection via intelligent multispectral fusion. In Proceedings of the 2022 4th International Conference on Applied Machine Learning (ICAML), Changsha, China, 23–25 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 179–183. [Google Scholar]
- Xue, Y.; Jin, G.; Shen, T.; Tan, L.; Wang, N.; Gao, J.; Wang, L. Smalltrack: Wavelet pooling and graph enhanced classification for uav small object tracking. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5618815. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, J.; Liu, S.; Wang, Z.; Zhang, X.; Ding, L.; Shen, L.; Wang, S. A robust registration method for UAV thermal infrared and visible images taken by dual-cameras. ISPRS J. Photogramm. Remote Sens. 2022, 192, 189–214. [Google Scholar] [CrossRef]
- Shahsavarani, S.; Lopez, F.; Ibarra-Castanedo, C.; Maldague, X.P. Robust Multi-Modal Image Registration for Image Fusion Enhancement in Infrastructure Inspection. Sensors 2024, 24, 3994. [Google Scholar] [CrossRef]
- Pielawski, N.; Wetzer, E.; Öfverstedt, J.; Lu, J.; Wählby, C.; Lindblad, J.; Sladoje, N. CoMIR: Contrastive multimodal image representation for registration. Adv. Neural Inf. Process. Syst. 2020, 33, 18433–18444. [Google Scholar]
- Xiao, Y.; Liu, F.; Zhu, Y.; Li, C.; Wang, F.; Tang, J. UAV Cross-Modal Image Registration: Large-Scale Dataset and Transformer-Based Approach. In Proceedings of the International Conference on Brain Inspired Cognitive Systems, Hefei, China, 6–8 December 2024. [Google Scholar]
- Zhao, S.; Dong, Y.; Chang, E.; Xu, Y. Recursive Cascaded Networks for Unsupervised Medical Image Registration. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Arar, M.; Ginger, Y.; Danon, D.; Bermano, A.H.; Cohen-Or, D. Unsupervised Multi-Modal Image Registration via Geometry Preserving Image-to-Image Translation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Hoffmann, M.; Billot, B.; Greve, D.N.; Iglesias, J.E.; Fischl, B.; Dalca, A.V. SynthMorph: Learning contrast-invariant registration without acquired images. IEEE Trans. Med. Imaging 2021, 41, 543–558. [Google Scholar] [CrossRef]
- Heinrich, M.P.; Jenkinson, M.; Bhushan, M.; Matin, T.; Gleeson, F.V.; Brady, M.; Schnabel, J.A. MIND: Modality independent neighbourhood descriptor for multi-modal deformable registration. Med. Image Anal. 2012, 16, 1423–1435. [Google Scholar] [CrossRef]
- Brown, L.G. A survey of image registration techniques. ACM Comput. Surv. (CSUR) 1992, 24, 325–376. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1615–1630. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Tuytelaars, T.; Schmid, C.; Zisserman, A.; Matas, J.; Schaffalitzky, F.; Kadir, T.; Gool, L.V. A comparison of affine region detectors. Int. J. Comput. Vis. 2005, 65, 43–72. [Google Scholar] [CrossRef]
- Leng, C.; Zhang, H.; Li, B.; Cai, G.; Pei, Z.; He, L. Local feature descriptor for image matching: A survey. IEEE Access 2018, 7, 6424–6434. [Google Scholar] [CrossRef]
- Harris, C.G.; Stephens, M.J. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Proceedings of the Computer Vision—ECCV 2006: 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the Computer Vision—ECCV 2006: 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of the Computer Vision—ECCV 2010: 11th European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; p. 11. [Google Scholar]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.R.; Guttag, J.; Dalca, A.V. Voxelmorph: A learning framework for deformable medical image registration. IEEE Trans. Med. Imaging 2019, 38, 1788–1800. [Google Scholar] [CrossRef] [PubMed]
- Miao, S.; Wang, Z.J.; Liao, R. A CNN regression approach for real-time 2D/3D registration. IEEE Trans. Med. Imaging 2016, 35, 1352–1363. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 16 December 2018. [Google Scholar]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 5 August 2020. [Google Scholar]
- Lindenberger, P.; Sarlin, P.E.; Pollefeys, M. Lightglue: Local feature matching at light speed. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023. [Google Scholar]
- Sotiras, A.; Davatzikos, C.; Paragios, N. Deformable medical image registration: A survey. IEEE Trans. Med. Imaging 2013, 32, 1153–1190. [Google Scholar] [CrossRef]
- Vercauteren, T.; Pennec, X.; Perchant, A.; Ayache, N. Non-parametric diffeomorphic image registration with the demons algorithm. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Brisbane, Australia, 29 October–2 November 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 319–326. [Google Scholar]
- Qiu, H.; Hammernik, K.; Qin, C.; Chen, C.; Rueckert, D. Embedding gradient-based optimization in image registration networks. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Singapore, 18–22 September 2022; Springer: Cham, Switzerland, 2022; pp. 56–65. [Google Scholar]
- Collins, D.L.; Neelin, P.; Peters, T.M.; Evans, A.C. Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. J. Comput. Assist. Tomogr. 1994, 18, 192–205. [Google Scholar] [CrossRef] [PubMed]
- Maes, F.; Collignon, A.; Vandermeulen, D.; Marchal, G.; Suetens, P. Multimodality image registration by maximization of mutual information. IEEE Trans. Med. Imaging 2002, 16, 187–198. [Google Scholar] [CrossRef]
- Avants, B.B.; Epstein, C.L.; Grossman, M.; Gee, J.C. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008, 12, 26–41. [Google Scholar] [CrossRef]
- Chen, J.; Frey, E.C.; He, Y.; Segars, W.P.; Li, Y.; Du, Y. Transmorph: Transformer for unsupervised medical image registration. Med. Image Anal. 2022, 82, 102615. [Google Scholar] [CrossRef]
- Cao, X.; Yang, J.; Zhang, J.; Nie, D.; Kim, M.; Wang, Q.; Shen, D. Deformable image registration based on similarity-steered CNN regression. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017; pp. 300–308. [Google Scholar]
- Krebs, J.; Mansi, T.; Delingette, H.; Zhang, L.; Ghesu, F.C.; Miao, S.; Maier, A.K.; Ayache, N.; Liao, R.; Kamen, A. Robust non-rigid registration through agent-based action learning. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017; pp. 344–352. [Google Scholar]
- De Vos, B.D.; Berendsen, F.F.; Viergever, M.A.; Staring, M.; Išgum, I. End-to-end unsupervised deformable image registration with a convolutional neural network. In Proceedings of the International Workshop on Deep Learning in Medical Image Analysis, Québec City, QC, Canada, 14 September 2017. [Google Scholar]
- Zhao, S.; Lau, T.; Luo, J.; Chang, E.I.-C.; Xu, Y. Unsupervised 3D end-to-end medical image registration with volume tweening network. IEEE J. Biomed. Health Inform. 2019, 24, 1394–1404. [Google Scholar] [CrossRef]
- Schneider, N.; Piewak, F.; Stiller, C.; Franke, U. RegNet: Multimodal sensor registration using deep neural networks. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017. [Google Scholar]
- Zhang, Z.; Xu, Y.; Song, J.; Zhou, Q.; Rasol, J.; Ma, L. Planet craters detection based on unsupervised domain adaptation. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7140–7152. [Google Scholar] [CrossRef]
- Zhou, S.; Tan, W.; Yan, B. Promoting single-modal optical flow network for diverse cross-modal flow estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36. [Google Scholar]
- Haskins, G.; Kruger, U.; Yan, P. Deep learning in medical image registration: A survey. Mach. Vis. Appl. 2020, 31, 8. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Y.; Wei, S.; Bian, Z.; Subramanian, S.; Carass, A.; Prince, J.L.; Du, Y. A survey on deep learning in medical image registration: New technologies, uncertainty, evaluation metrics, and beyond. Med. Image Anal. 2024, 100, 103385. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Burt, P.J.; Adelson, E.H. The Laplacian pyramid as a compact image code. In Readings in Computer Vision; Elsevier: Amsterdam, The Netherlands, 1987; pp. 671–679. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the IJCAI’81: 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 2, pp. 674–679. [Google Scholar]
- Meng, M.; Feng, D.; Bi, L.; Kim, J. Correlation-aware coarse-to-fine mlps for deformable medical image registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 9645–9654. [Google Scholar]
- Beg, M.F.; Miller, M.I.; Trouvé, A.; Younes, L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. Int. J. Comput. Vis. 2005, 61, 139–157. [Google Scholar] [CrossRef]
- Vercauteren, T.; Pennec, X.; Perchant, A.; Ayache, N. Diffeomorphic demons: Efficient non-parametric image registration. NeuroImage 2009, 45, S61–S72. [Google Scholar] [CrossRef]
- Ashburner, J. A fast diffeomorphic image registration algorithm. Neuroimage 2007, 38, 95–113. [Google Scholar] [CrossRef] [PubMed]
- Arsigny, V.; Commowick, O.; Pennec, X.; Ayache, N. A log-euclidean framework for statistics on diffeomorphisms. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Copenhagen, Denmark, 1–6 October 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 924–931. [Google Scholar]
- Dalca, A.V.; Balakrishnan, G.; Guttag, J.; Sabuncu, M.R. Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces. Med. Image Anal. 2019, 57, 226–236. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, Y.; Ma, L.; Li, J.; Zheng, W. Spectral–spatial transformer network for hyperspectral image classification: A factorized architecture search framework. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).