Study on Exposure Time Difference Compensation Method for DMD-Based Dual-Path Multi-Target Imaging Spectrometer
Abstract
1. Introduction
2. Design and Analysis of the DMD-Based Dual-Path Multi-Target Imaging Spectrometer
2.1. Optical Design
2.2. Analysis of the Exposure Time Difference
3. Velocity Vector Field Model in Complex Motion States
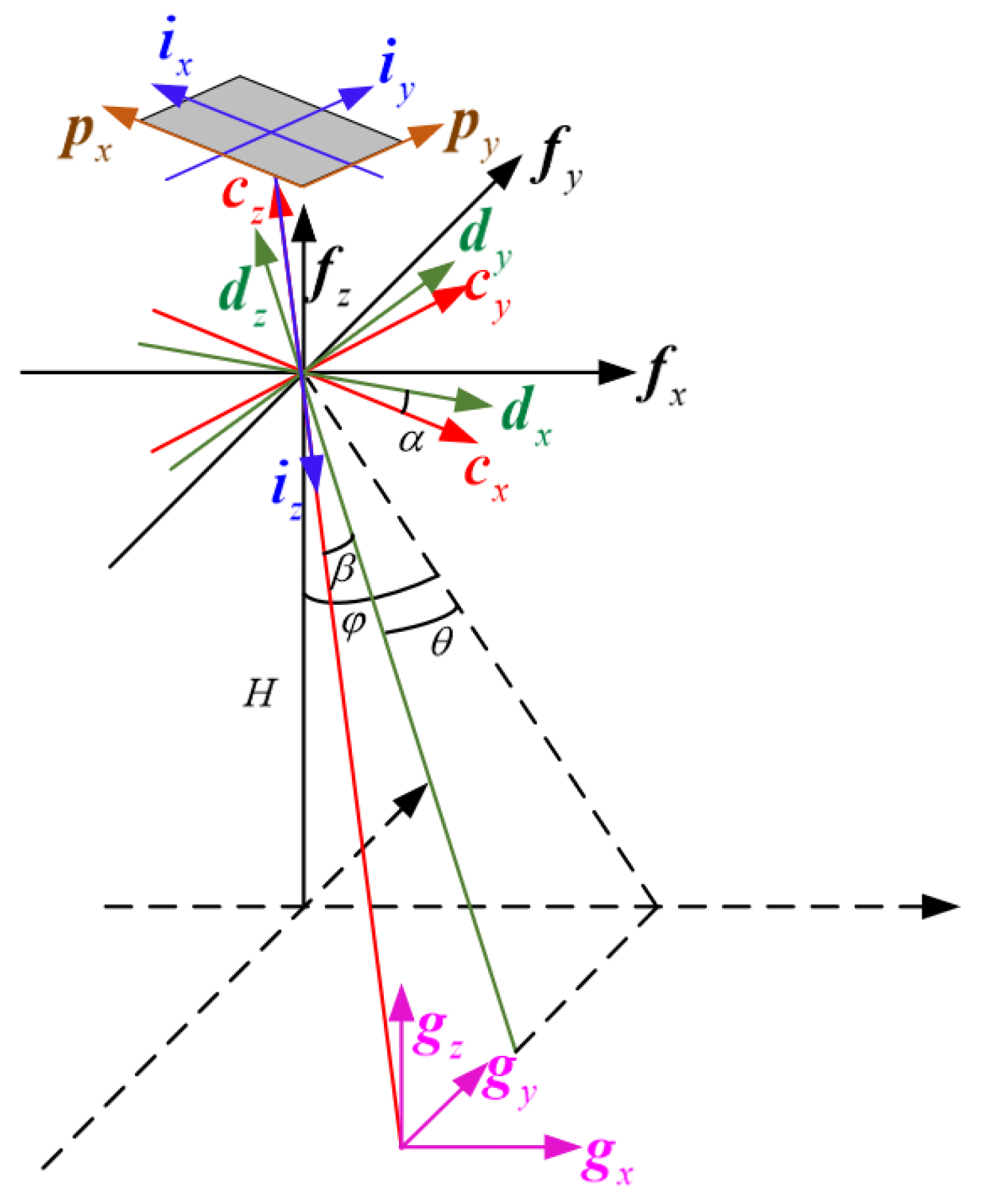
3.1. Ground Target-Dmd Instantaneous Mapping Model
- (1)
- Aircraft flight trajectory coordinate system : The coordinate origin is located at the aircraft’s center of mass, with the pointing in the direction of flight, the pointing vertically toward the sky, and the completing the right-handed coordinate system. Unless otherwise specified, the vectors and coordinates in this paper are all expressed in this coordinate system;
- (2)
- Aircraft coordinate system : The coordinate origin is located at the aircraft’s center of mass. When the aircraft’s attitude angles change (pitch angle is , roll angle is , and yaw angle is ), the aircraft flight trajectory coordinate system is rotated around the by , around the by , and around the by to obtain the aircraft coordinate system ;
- (3)
- Camera coordinate system : The camera is fixed to the aircraft via a pod. Ignoring installation errors, it is assumed that the origin of the camera coordinate system is located at the aircraft’s center of mass. The camera coordinate system is obtained by rotating the aircraft coordinate system around the by angle , and then around the by angle ;
- (4)
- Ground coordinate system : The coordinate origin is the intersection of the and the ground at time t = 0, the and the have the same direction, the and the have the same direction, and the is perpendicular to the ground, pointing upwards;
- (5)
- Image plane coordinate system : The origin of the image plane coordinate system is located at the center of the DMD. When the aircraft and camera have no attitude change, the lies in the plane of the detector and points in the direction of the aircraft’s flight, while the points toward the terrain target along the optical axis;
- (6)
- DMD coordinate system : The origin of the DMD coordinate system is located at the lower-right corner of the DMD. The is aligned with the of the image plane coordinate system, and the is aligned with the of the image plane coordinate system.
3.2. Velocity Vector Field Model
4. Exposure Time Difference Compensation
4.1. When the Image Points Are Still Within the Field of View
4.2. When the Image Points Are Outside the Field of View
5. Simulation
5.1. Exposure Time Difference Compensation Method
5.2. Attitude Compensation Method
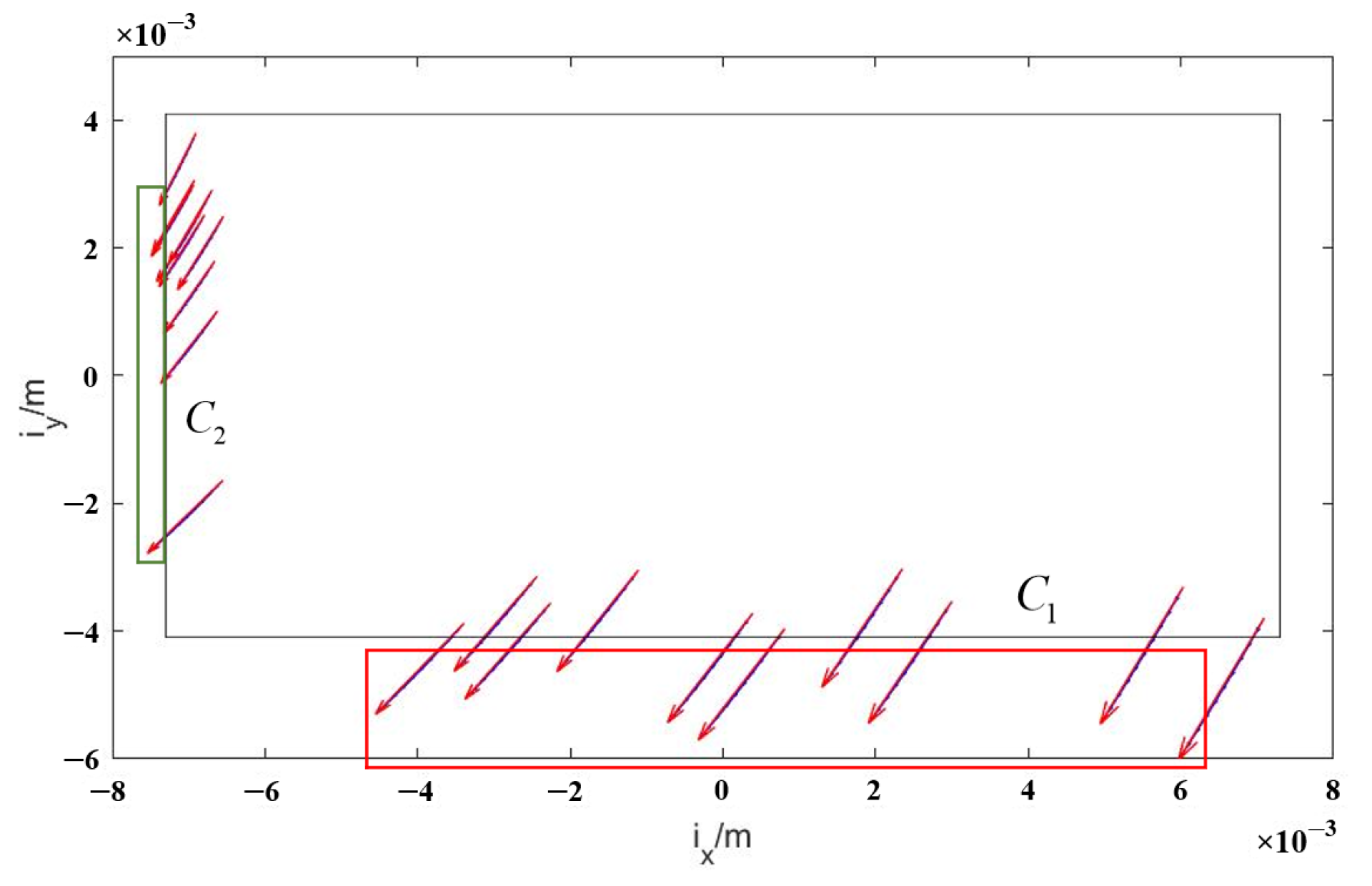
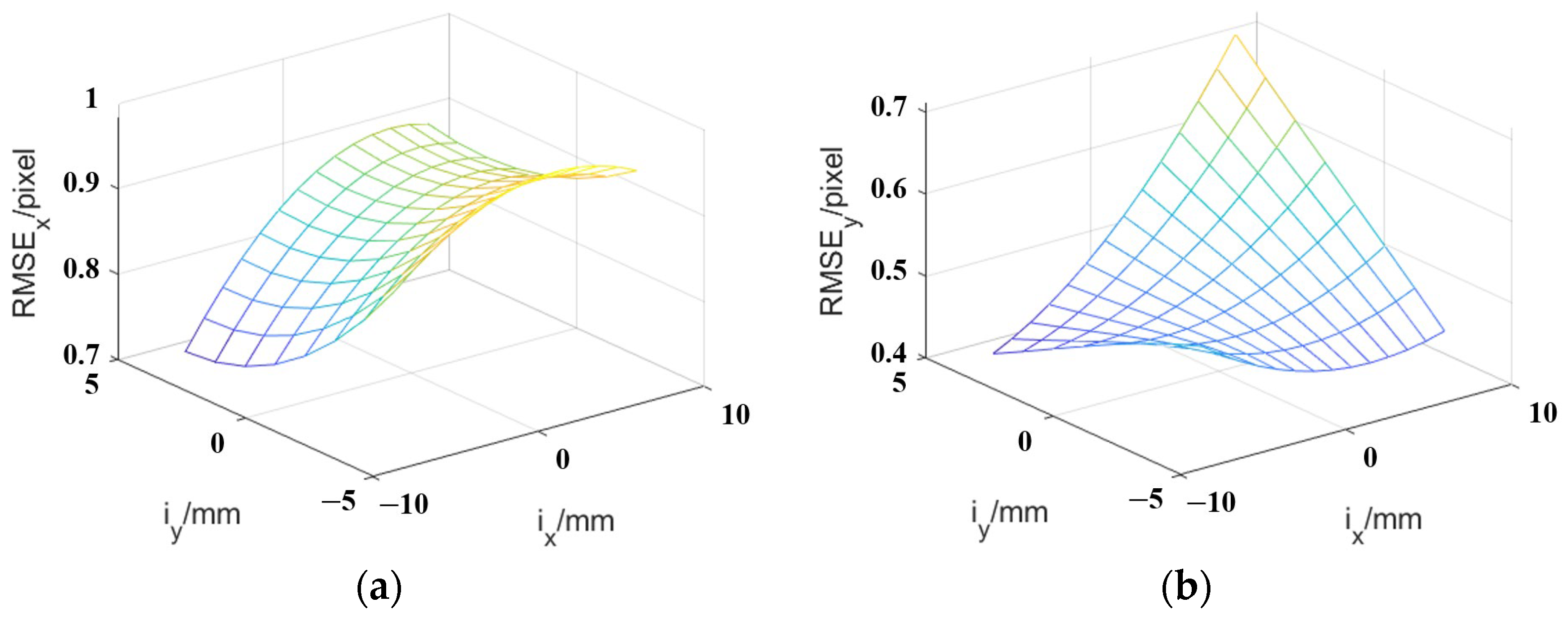
5.3. Error Analysis
- Displacement vector calculation errors caused by discrete integration;
- Velocity vector calculation errors caused by measurement errors in the aircraft’s state parameters;
- Target positioning errors caused by errors in the aircraft’s state parameters.
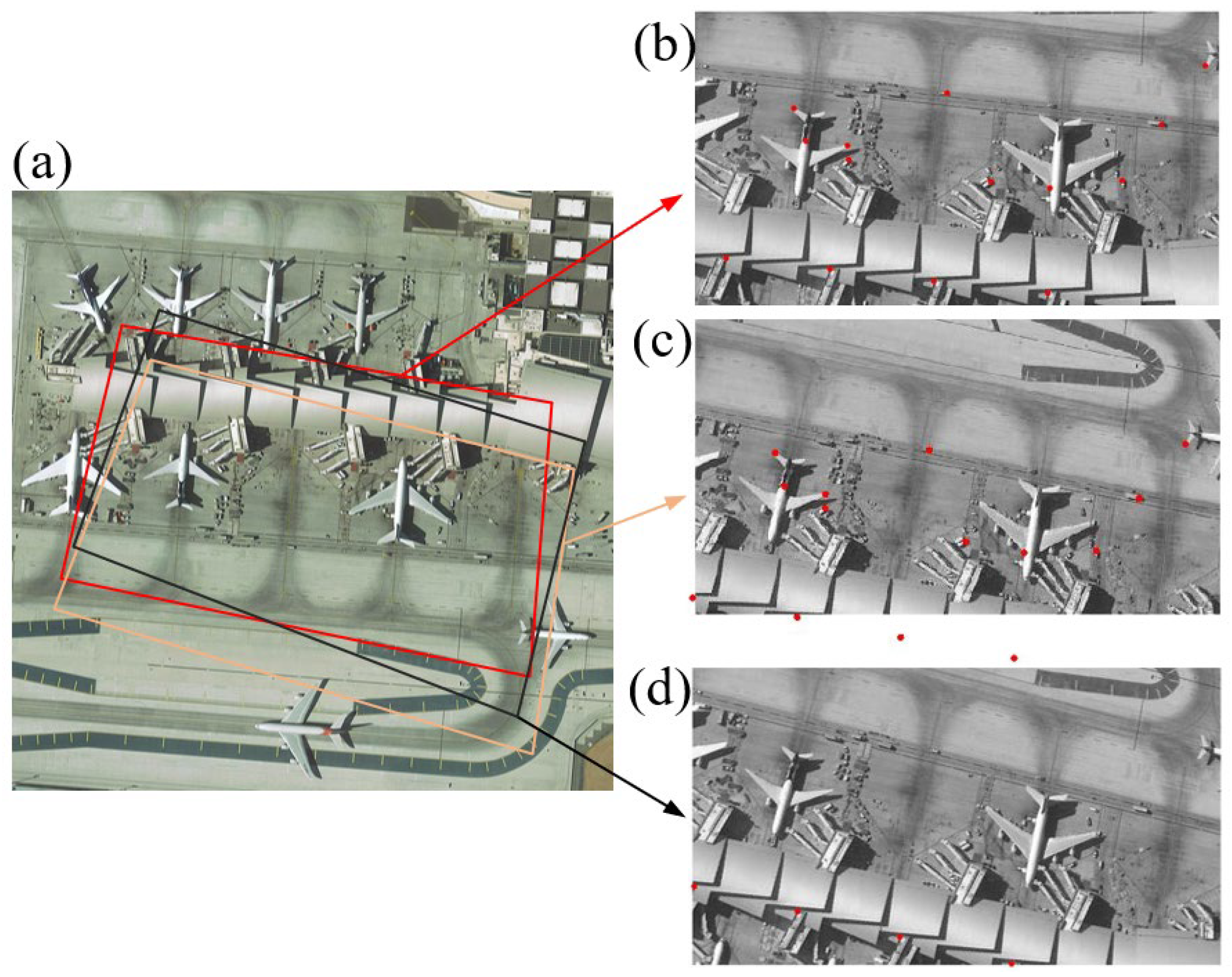
6. Experiment
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goetz, A.F.H. Three Decades of Hyperspectral Remote Sensing of the Earth: A Personal View. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Ma, R.; Zhou, W. Soil Nutrients Inversion in Open-pit Coal Mine Reclamation Area of Loess Plateau, China: A Study Based on ZhuHai-1 Hyperspectral Remote Sensing. Land Degrad. Dev. 2024, 35, 5210–5223. [Google Scholar] [CrossRef]
- Jagpal, R.K.; Quine, B.M.; Chesser, H.; Abrarov, S.M.; Lee, R. Calibration and In-Orbit Performance of the Argus 1000 Spectrometer-the Canadian Pollution Monitor. J. Appl. Remote Sens 2010, 4, 049501. [Google Scholar] [CrossRef][Green Version]
- Guo, X.; Liu, H.; Zhong, P.; Hu, Z.; Cao, Z.; Shen, M.; Tan, Z.; Liu, W.; Liu, C.; Li, D.; et al. Remote Retrieval of Dissolved Organic Carbon in Rivers Using a Hyperspectral Drone System. Int. J. Digit. Earth 2024, 17, 2358863. [Google Scholar] [CrossRef]
- Möckel, T.; Dalmayne, J.; Schmid, B.; Prentice, H.; Hall, K. Airborne Hyperspectral Data Predict Fine-Scale Plant Species Diversity in Grazed Dry Grasslands. Remote Sens. 2016, 8, 133. [Google Scholar] [CrossRef]
- Xiang, T.-Z.; Xia, G.-S.; Zhang, L. Mini-Unmanned Aerial Vehicle-Based Remote Sensing: Techniques, Applications, and Prospects. IEEE Geosci. Remote Sens. Mag. 2019, 7, 29–63. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-Based Photogrammetry and Hyperspectral Imaging for Mapping Bark Beetle Damage at Tree-Level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- Uto, K.; Seki, H.; Saito, G.; Kosugi, Y. Characterization of Rice Paddies by a UAV-Mounted Miniature Hyperspectral Sensor System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 851–860. [Google Scholar] [CrossRef]
- Jia, J.; Chen, J.; Zheng, X.; Wang, Y.; Guo, S.; Sun, H.; Jiang, C.; Karjalainen, M.; Karila, K.; Duan, Z.; et al. Tradeoffs in the Spatial and Spectral Resolution of Airborne Hyperspectral Imaging Systems: A Crop Identification Case Study. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5510918. [Google Scholar] [CrossRef]
- Yuan, L.; Xie, J.; He, Z.; Wang, Y.; Wang, J. Optical Design and Evaluation of Airborne Prism-Grating Imaging Spectrometer. Opt. Express 2019, 27, 17686. [Google Scholar] [CrossRef]
- Wang, B.; Ruan, N.; Guo, C.; Wang, Y.; Wang, Z.; Zhong, X. Optical System Design of Airborne Light and Compact High Resolution Imaging Spectrometer. Acta Opt. Sin. 2015, 35, 1022001. [Google Scholar] [CrossRef]
- Luo, G.-Y.; Wang, B.-D.; Chen, Y.-Q.; Zhao, Y.-L. Design of Visible Near Infrared Imaging Spectrometer on Unmanned Aerial Vehicle. Acta Photonica Sin. 2017, 46, 0930001. [Google Scholar] [CrossRef]
- Eikenberry, S.; Elston, R.; Raines, S.N.; Julian, J.; Hanna, K.; Hon, D.; Julian, R.; Bandyopadhyay, R.; Bennett, J.G.; Bessoff, A.; et al. FLAMINGOS-2: The Facility near-Infrared Wide-Field Imager & Multi-Object Spectrograph for Gemini. In Proceedings of the Conference on Ground-Based and Airborne Instrumentation for Astronomy, Orlando, FL, USA, 25 May 2006. [Google Scholar]
- Zhu, Y.; Hu, Z.; Wang, L.; Wang, J.; Hou, Y.; Tang, Z.; Dai, S.; Wu, Z.; Chen, Y. Construction and commissioning of LAMOST low resolution spectrographs. Sci. Sin. Phys. Mech. Astron. 2011, 41, 1337–1341. (In Chinese) [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Yan, Q.; Geng, T.; Ma, Z.; Liu, Y.; Cui, X. Influence of Misalignment on Output of Astronomical Large-Core Fibers of Multi-Object Fiber Spectroscopic Telescopes. In Proceedings of the Conference on Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, Edinburgh, UK, 26 June–1 July 2016. [Google Scholar]
- Shan, Y.; Zhu, Z.; Tan, H.; Ji, H.; Ma, D. Optical Design of a Multi-Object Fiber-Fed Spectrograph System for Southern Spectroscopic Survey Telescope. Opt. Commun. 2021, 499, 127188. [Google Scholar] [CrossRef]
- McLean, I.S.; Steidel, C.C.; Epps, H.; Matthews, K.; Adkins, S.; Konidaris, N.; Weber, B.; Aliado, T.; Brims, G.; Canfield, J.; et al. Design and Development of MOSFIRE: The Multi-Object Spectrometer for Infrared Exploration at the Keck Observatory. In Proceedings of the Conference on Ground-based and Airborne Instrumentation for Astronomy III, San Diego, CA, USA, 27 June–2 July 2010. [Google Scholar]
- Moon, D.-S.; Sivanandam, S.; Kutyrev, A.S.; Moseley, S.H.; Graham, J.R.; Roy, A. The Development of Ground-Based Infrared Multi-Object Spectrograph Based on the Microshutter Array. In Proceedings of the 5th Conference on Ground-Based and Airborne Instrumentation for Astronomy, Montréal, QC, Canada, 22 June 2014. [Google Scholar]
- Burns, D.E.; Oh, L.H.; Li, M.J.; Kelly, D.P.; Kutyrev, A.S.; Moseley, S.H. 2-D Electrostatic Actuation of Microshutter Arrays. J. Microelectromech. Syst. 2016, 25, 101–107. [Google Scholar] [CrossRef]
- Li, M.J.; Brown, A.-D.; Burns, D.E.; Kelly, D.P.; Kim, K.; Kutyrev, A.S.; Moseley, S.H.; Mikula, V.; Oh, L. James Webb Space Telescope Microshutter Arrays and Beyond. J. Micro/Nanolith. Mems Moems 2017, 16, 025501. [Google Scholar] [CrossRef]
- Travinskya, A.; Vorobiev, D.; Ninkov, Z.; Raisanen, A.; Quijada, M.A.; Smee, S.A.; Pellish, J.A.; Schwartz, T.; Robberto, M.; Heap, S.; et al. Evaluation of Digital Micromirror Devices for Use in Space-Based Multi-Object Spectrometer Application. J. Astron. Telesc. Instrum. Syst. 2017, 3, 035003. [Google Scholar] [CrossRef]
- Yang, J.; Liu, X.; Zhang, L.; Zhang, L.; Yan, T.; Fu, S.; Sun, T.; Zhan, H.; Xing, F.; You, Z. Real-Time Localization and Classification of the Fast-Moving Target Based on Complementary Single-Pixel Detection. Opt. Express 2025, 33, 11301–11316. [Google Scholar] [CrossRef]
- Spanò, P.; Zamkotsian, F.; Content, R.; Grange, R.; Robberto, M.; Valenziano, L.; Zerbi, F.M.; Sharples, R.M.; Bortoletto, F.; De Caprio, V.; et al. DMD Multi-Object Spectroscopy in Space: The EUCLID Study. In Proceedings of the UV/Optical/IR Space Telescopes: Innovative Technologies and Concepts IV, San Diego, CA, USA, 2 August 2009. [Google Scholar]
- Fourspring, K.D.; Ninkov, Z.; Kerekes, J.P. Scattered Light in a DMD Based Multi-Object Spectrometer. In Proceedings of the Conference on Modern Technologies in Space- and Ground-Based Telescopes and Instrumentation, San Diego, CA, USA, 27 June 2010. [Google Scholar]
- Robberto, M.; Donahue, M.; Ninkov, Z.; Smee, S.A.; Barkhouser, R.H.; Gennaro, M.; Tokovinin, A. SAMOS: A Versatile Multi-Object-Spectrograph for the GLAO System SAM at SOAR. In Proceedings of the Conference on Ground-Based and Airborne Instrumentation for Astronomy VI, Edinburgh, UK, 26–30 June 2016. [Google Scholar]
- Gibson, G.M.; Dienerowitz, M.; Kelleher, P.A.; Harvey, A.R.; Padgett, M.J. A Multi-Object Spectral Imaging Instrument. J. Opt. 2013, 15, 085302. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.; Liu, C.; Fan, X.; Li, L.; Xia, J.; Ding, Y.; Liu, H. Optical System Design Based on DMD and Triple-Pass TIR Prism for Asteroid Exploration. Opt. Express 2023, 31, 43198. [Google Scholar] [CrossRef]
- Tan, Y.; Li, X.; Zhang, L. Application and Development Trend of Hyperspectral Remote Sensing in Crop Research. Chin. Agric. Sci. Bull. 2024, 40, 141–148. [Google Scholar]
- El-Alem, A.; Chokmani, K.; Laurion, I.; El-Adlouni, S.E. Comparative Analysis of Four Models to Estimate Chlorophyll-a Concentration in Case-2 Waters Using MODerate Resolution Imaging Spectroradiometer (MODIS) Imagery. Remote Sens. 2012, 4, 2373–2400. [Google Scholar] [CrossRef]
- Wang, Z. Research on High Precision LOS Stabilization and Image Motion Compensation Control Technology of Aeronautical Photoelectric Stabilization Platform. Ph.D. Dissertation, University of Chinese Academy of Sciences, Beijing, China, 2019. [Google Scholar]
- Xu, T.; Yang, X.; Wang, S.; Han, J.; Chang, L.; Yue, W. Imaging Velocity Fields Analysis of Space Camera for Dynamic Circular Scanning. IEEE Access 2020, 8, 191574–191585. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, Y.; Liu, C.; Xie, P.; Ma, W.; Lu, Y.; Kong, X. Study of the Image Motion Compensation Method for a Vertical Orbit Dynamic Scanning TDICCD Space Camera. Opt. Express 2023, 31, 41740. [Google Scholar] [CrossRef]
- Du, J.; Yang, X.; Zhou, M.; Tu, Z.; Wang, S.; Tang, X.; Cao, L.; Zhao, X. Fast Multispectral Fusion and High-Precision Interdetector Image Stitching of Agile Satellites Based on Velocity Vector Field. IEEE Sens. J. 2022, 22, 22134–22147. [Google Scholar] [CrossRef]
- Cao, Z.; Kooistra, L.; Wang, W.; Guo, L.; Valente, J. Real-Time Object Detection Based on UAV Remote Sensing: A Systematic Literature Review. Drones 2023, 7, 620. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Liu, T.; Lin, Z.; Wang, S. DAGN: A Real-Time UAV Remote Sensing Image Vehicle Detection Framework. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1884–1888. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Yu, J.; Cheng, B.; Hao, L. Remote Sensing Ship Target Detection and Recognition Method. Remote Sens. Inf. 2020, 35, 64–72. [Google Scholar]
- Li, K.; Wan, G.; Cheng, G.; Meng, L.; Han, J. Object Detection in Optical Remote Sensing Images: A Survey and a New Benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 159, 296–307. [Google Scholar] [CrossRef]
- Jin, G.; Yang, X.; Zhang, X.; Jiang, L.; Wang, M. Error Analysis and Integration of Aircraft-Based Electro-Optical Imaging Tracking Measurement Equipment. In Analysis of Error and Image Motion in Airborne Electro-Optical Imaging and Tracking Measurement System, 1st ed.; National Defense Industry Press: Beijing, China, 2018; pp. 26–30. [Google Scholar]
- Xiong, T. Design of High-Precision Multi-Mems Gyroscope and Research on Filter Algorithm. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Zeng, X.; Xian, S.; Wang, K.; Si, P.; Wu, Z. A Random Error Compensation Method for MEMS Gyroscope Based on Improved EMD and ARMA. Acta Armamentarii 2024, 45, 3287–3306. [Google Scholar]
- Hu, T. Precision Checking Method and Example of Long Distance GPS RTK Measurement. GNSS World China 2018, 43, 67–69. [Google Scholar]
- Li, X.; Huang, J.; Li, X.; Yuan, Y.; Zhang, K.; Zheng, H.; Zhang, W. GREAT: A Scientific Software Platform for Satellite Geodesy and Multi-Source Fusion Navigation. Adv. Space Res. 2024, 74, 1751–1769. [Google Scholar] [CrossRef]
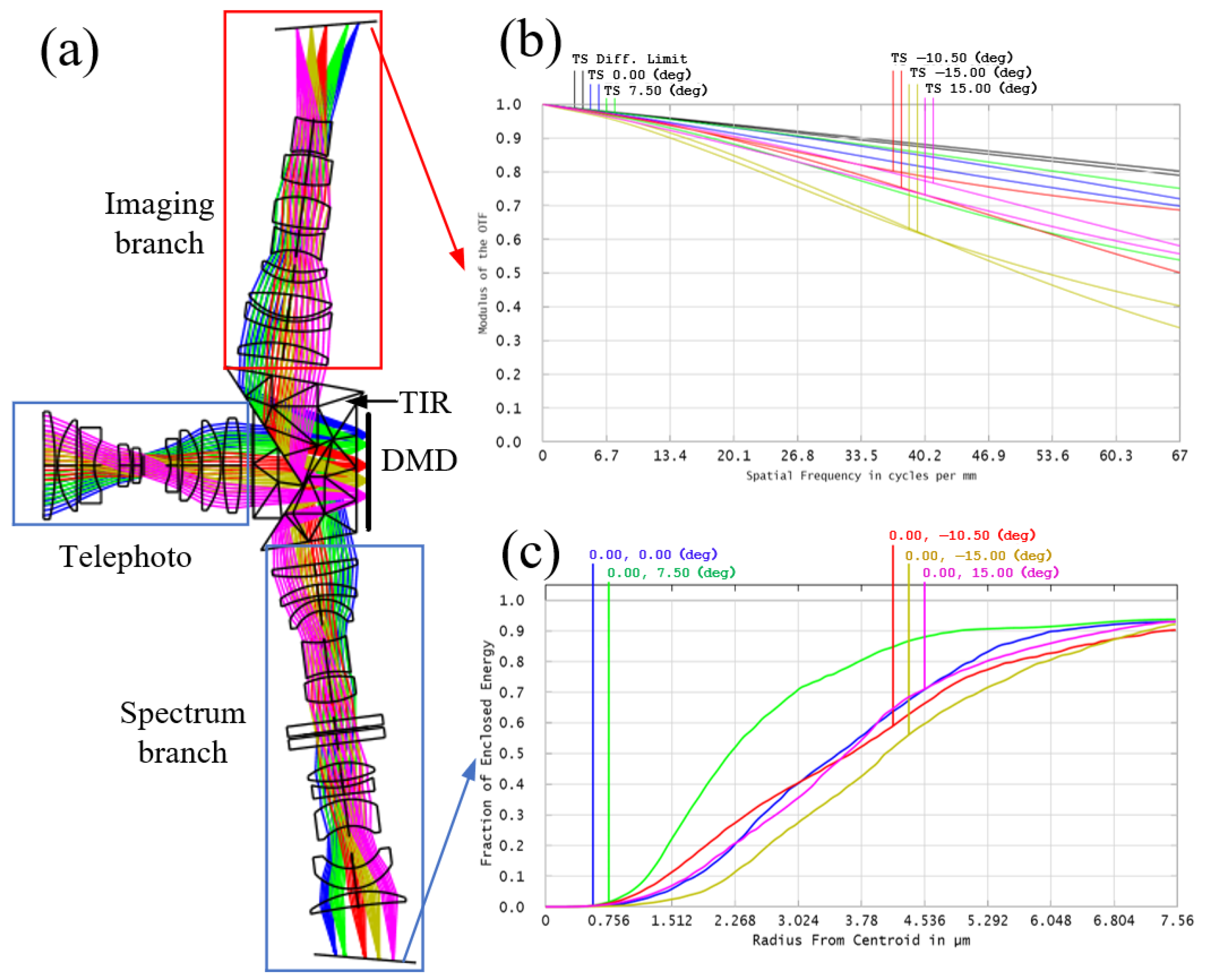
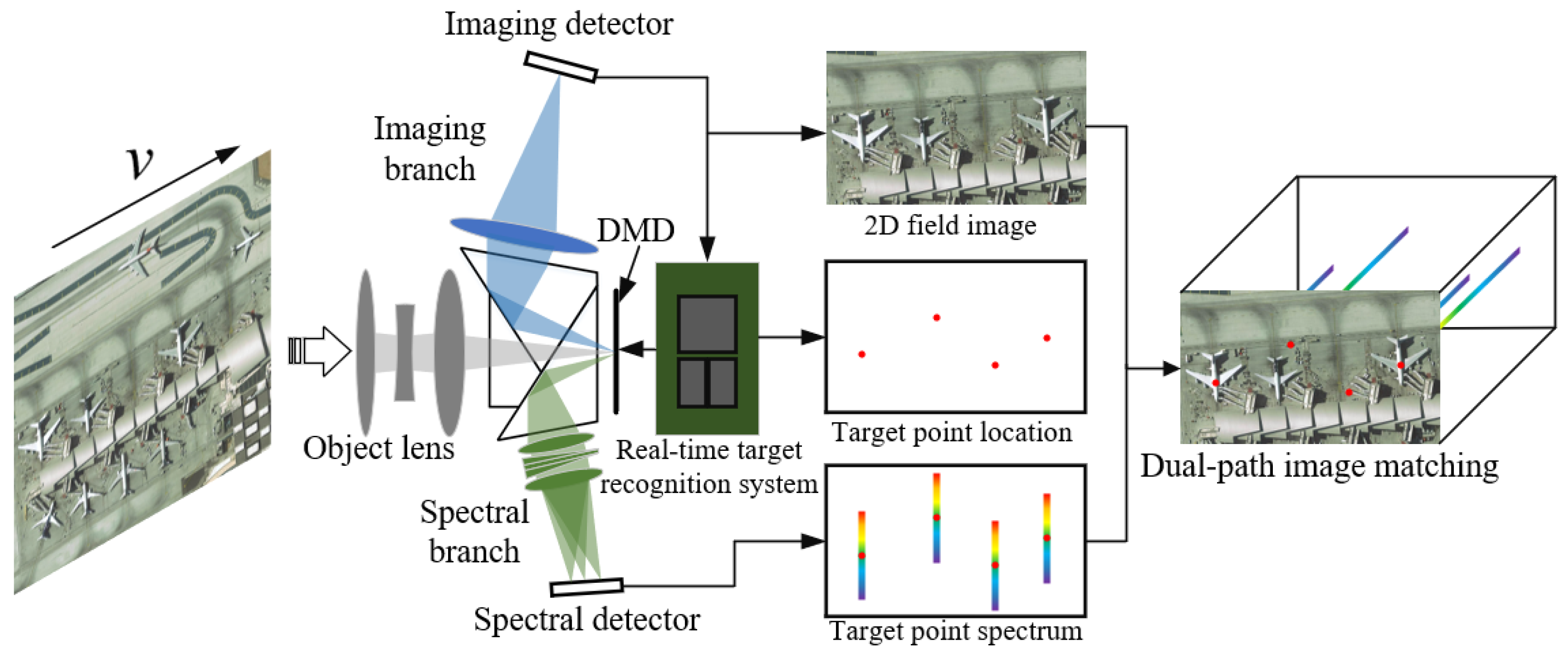






| Optical System Parameter | Numerical Value |
|---|---|
| Spectral range | 400–800 nm |
| F-number | 4 |
| Telescope focal length | 30 mm |
| Field of view | 27.2° × 15.5° |
| Instantaneous field of view | 0.252 mrad |
| Spectral resolution | 2 nm |
| Parameter | Numerical Value | Parameter | Numerical Value |
|---|---|---|---|
| Flight altitude | 5000 m | Flight speed | 30 m/s |
| Airborne platform pitch angle | 5° | Airborne platform pitch angular velocity | 2°/s |
| Airborne platform roll angle | 3° | Airborne platform roll angular velocity | 2°/s |
| Airborne platform yaw angle | 4° | Airborne platform yaw angular velocity | 2°/s |
| Pod yaw angle | 6° | Pod yaw angular velocity | 2°/s |
| Pod pitch angle | 10° | Pod pitch angular velocity | 2°/s |
| Telescope focal length | 0.03 m | DMD pixel size | 7.56 μm × 7.56 μm |
| Attitude Compensation Time | Monte Carlo Simulation Iterations | Number of Successes |
|---|---|---|
| 0.02 s | 10,000 | 0 |
| 0.03 s | 10,000 | 2 |
| 0.04 s | 10,000 | 6 |
| Compensation Method | Distance |
|---|---|
| In this paper | 66.7735 pixel |
| The optimal scheme corresponding to 0.03 s | 8.0373 pixel |
| The optimal scheme corresponding to 0.04 s | 31.9742 pixel |
| Aircraft Information | Error Range |
|---|---|
| Flight altitude | Better than 0.15 m |
| Flight speed | Better than 0.04 m/s |
| Attitude angle | Horizontal Accuracy: Better than 0.02° Direction Localization Accuracy: Better than 0.1° |
| Attitude angular velocity | Better than 0.01°/s |
| Error Sources | RMSE in the x-Direction (Pixel) | RMSE in the y-Direction (Pixel) |
|---|---|---|
| Displacement vector calculation errors | 0.1878 | 0.2355 |
| Velocity vector calculation errors | 0.1416 | 0.1875 |
| Target positioning errors | 0.8744 | 1.1821 |
| Parameter | Numerical Value | Parameter | Numerical Value |
|---|---|---|---|
| Initial pitch angle | −11.9146° | Flight altitude | 1.615 m |
| Initial roll angle | −6.3269° | Flight speed | 0.0258 m/s |
| Roll angular velocity | 2°/s | Telescope focal length | 0.025 m |
| Pitch angular velocity | 0.2°/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yang, J.; Liu, C.; Wang, C.; Zhang, G.; Ding, Y. Study on Exposure Time Difference Compensation Method for DMD-Based Dual-Path Multi-Target Imaging Spectrometer. Remote Sens. 2025, 17, 2021. https://doi.org/10.3390/rs17122021
Zhao Y, Yang J, Liu C, Wang C, Zhang G, Ding Y. Study on Exposure Time Difference Compensation Method for DMD-Based Dual-Path Multi-Target Imaging Spectrometer. Remote Sensing. 2025; 17(12):2021. https://doi.org/10.3390/rs17122021
Chicago/Turabian StyleZhao, Yingming, Jianing Yang, Chunyu Liu, Chen Wang, Guoxiu Zhang, and Yi Ding. 2025. "Study on Exposure Time Difference Compensation Method for DMD-Based Dual-Path Multi-Target Imaging Spectrometer" Remote Sensing 17, no. 12: 2021. https://doi.org/10.3390/rs17122021
APA StyleZhao, Y., Yang, J., Liu, C., Wang, C., Zhang, G., & Ding, Y. (2025). Study on Exposure Time Difference Compensation Method for DMD-Based Dual-Path Multi-Target Imaging Spectrometer. Remote Sensing, 17(12), 2021. https://doi.org/10.3390/rs17122021






