High-Fidelity 3D Gaussian Splatting for Exposure-Bracketing Space Target Reconstruction: OBB-Guided Regional Densification with Sobel Edge Regularization
Abstract
1. Introduction
- (1)
- Conventional 3D reconstruction pipelines such as SfM and MVS rely on photometric consistency across views for feature extraction and correspondence matching. In exposure bracketing sequences, however, rapid exposure changes may introduce large inter-frame brightness gaps that violate this assumption, so reliable matches can become scarce and the reconstruction can often be incomplete or even fail.
- (2)
- Low-exposure images preserve highlight details, whereas high-exposure frames reveal shadow information. Fully exploiting these complementary cues without blurring or artifacts requires balancing their contributions during optimization. Because each exposure emphasizes different content, naïve fusion or independent per-frame optimization could lose critical details or introduce inconsistencies, making this a complex and still largely unexplored problem. The key challenge is how to integrate information from multiple exposures in a region-adaptive manner so that the reconstructor automatically identifies and refines areas that are difficult across all exposures while maintaining consistent global geometry and texture fidelity.
- We propose the first 3DGS-based approach for exposure-bracketed reconstruction, combining an exposure-aware OBB densification strategy to refine error-prone regions and Sobel-edge regularization to preserve structural consistency across exposures.
- To the best of our knowledge, we propose an approach for directly processing exposure bracketing image sequences within the 3DGS framework to achieve high-fidelity 3D reconstruction of space targets. This approach effectively leverages complementary information across different exposure images via a novel joint optimization strategy, directly addressing the challenges posed by exposure bracketing.
- Additionally, we release OBR-ST, a new optical space-target dataset that supplies precise ground-truth camera poses for exposure-bracketing research. Experiments on OBR-ST as well as on the public SHIRT dataset show that our approach consistently delivers denser and more accurate point clouds than the baseline 3DGS, thereby lifting both geometry and texture metrics and confirming its strong capacity to generalize.
2. Related Work
2.1. Traditional Multi-View Geometry Methods
2.2. Deep Learning-Driven Methods
2.3. Neural Implicit Representations
2.4. Explicit Gaussian Representations
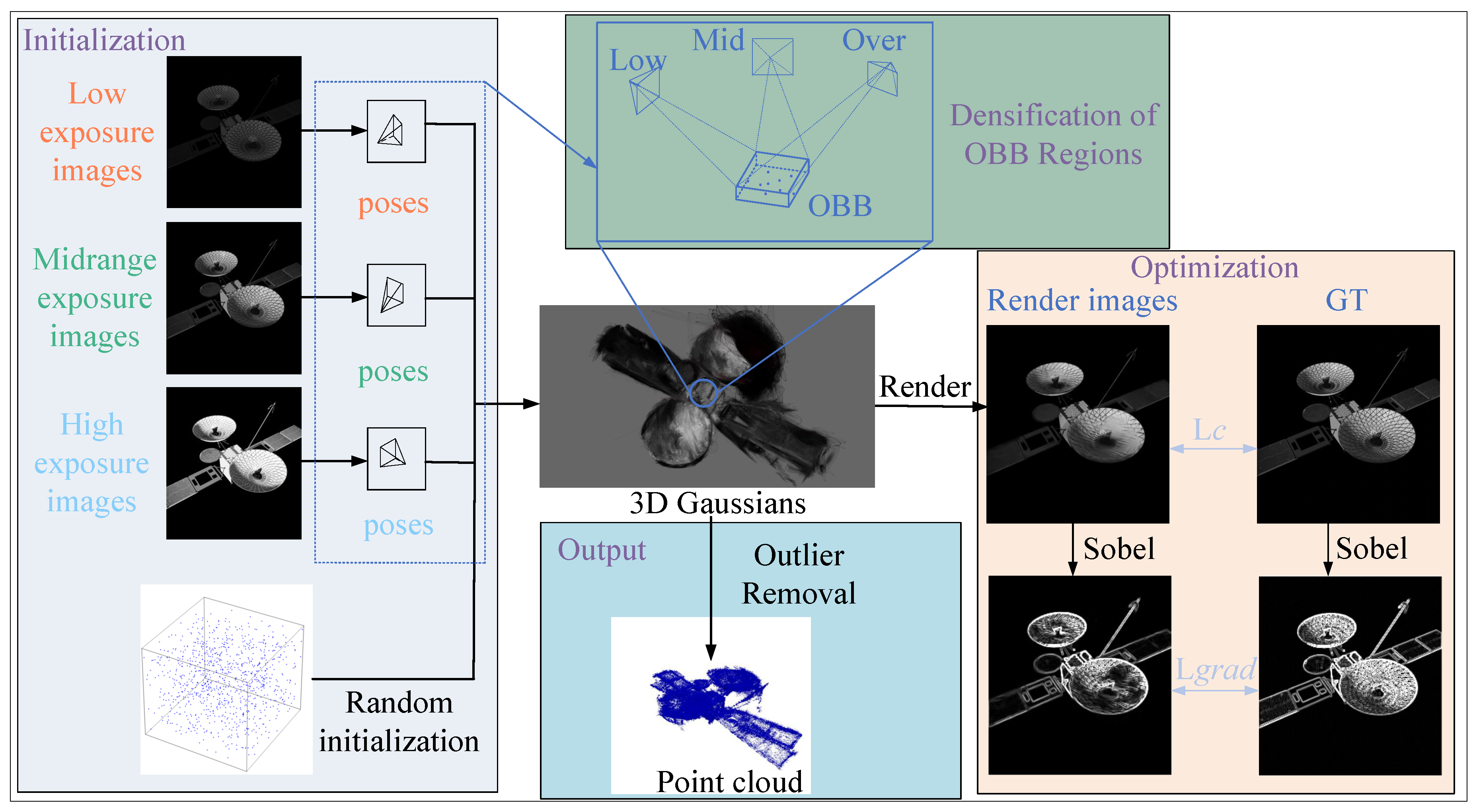
3. Methodology
3.1. Overall Framework
3.2. Preliminaries: 3D Gaussian Splatting
3.3. Sobel Edge Regularization
3.4. Exposure Bracketing OBB Regional Densification
3.4.1. Exposure Bracketing Constraint
- Highlight Detail Preservation: The low-exposure image effectively captures texture and edge features in brightly illuminated regions, preventing detail loss due to overexposure that might occur under other exposure conditions.
- Shadow Region Structure Recovery: The high-exposure image reveals structural information within shadow regions, filling in information that is missing in low-exposure conditions due to insufficient brightness.
- Overall Structure Balance Maintenance: The medium-exposure image provides a baseline representation of the object’s overall form, establishing a continuous transition between highlight and shadow regions.
3.4.2. OBB Region Densification
3.5. Initialization and Optimization
4. Dataset
4.1. Simulation Inputs
- Space target model: We acquire six distinct space target models from NASA’s publicly available 3D model repository. These models are uniformly processed by converting them into the .obj format for subsequent import into the Blender software. Furthermore, we utilize the corresponding material properties available on the NASA website to ensure visual fidelity.
- Orbital information (TLE): We configure a simulation scenario featuring a natural fly-around trajectory. From this scenario, we extract the corresponding TLE data for the chaser and the target during the simulated rendezvous phase.
4.2. Blender Rendered Images
- Scene setup: The Blender camera is designated as the chaser and the imported 3D model represents the target. To reflect the visual characteristics of outer space, the scene background is set to black.
- Illumination: To accurately compute the Sun’s position relative to both space targets, we use the ephemeris file de421.bsp, provided by NASA’s Jet Propulsion Laboratory (JPL). The resulting solar vector is used to position and orient the primary light source (implemented as a sun or planar lamp) within Blender, simulating directional solar illumination.
- Relative pose: The relative position and attitude of the chaser with respect to the target are dynamically updated at each time step based on orbital calculations derived from the input TLE data.
- Exposure variation: To replicate exposure bracketing used in real onboard imaging systems, we periodically vary the camera’s exposure settings across consecutive frames, cycling through low—0.05 ms, medium—0.1 ms, and high—0.2 ms exposure levels.
- Noise simulation: Gaussian noise is added to the rendered images to emulate noise.
4.3. Simulation Output
5. Experiments and Results
5.1. Datasets
- OBR-ST dataset: This task-specific dataset contains six distinct space target models. Each model is depicted in 363 images, split into 198 training, 99 test, and 66 validation samples. The dedicated validation split supports the training regime of NeRF-based methods for orbital targets.
- SHIRT dataset: For the publicly available SHIRT dataset, we adopted a processing strategy similar to that used for OBR-ST. We selected the first 363 images from each category and divided them (per category) into 198 training images, 99 test images, and 66 validation images. The original camera pose information was converted into a format compatible with the NeRF synthetic dataset conventions, enabling direct integration into NeRF training pipelines.
5.2. Implementation Details
- Processor: Intel® Core™ i9-14900KS @ 3.20 GHz (14th gen)
- Graphics Processing Unit (GPU): NVIDIA GeForce RTX 4090 with 24 GB GDDR6X memory
- Memory: 64 GB
- Operating System: Ubuntu 20.04
- Deep Learning Framework: PyTorch 2.0.0, with CUDA 11.8
5.3. Evaluation Metrics
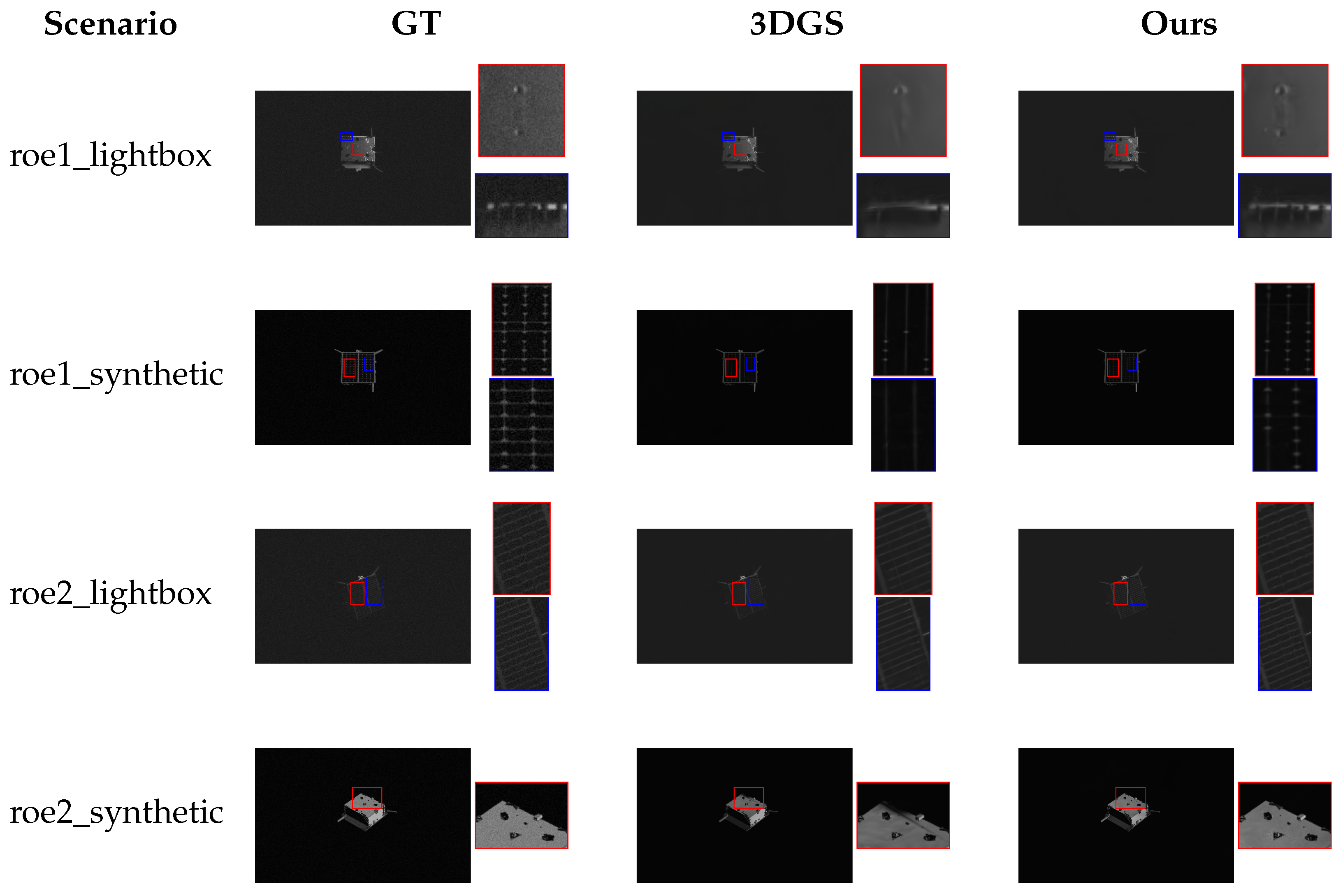
5.4. Qualitative Comparison
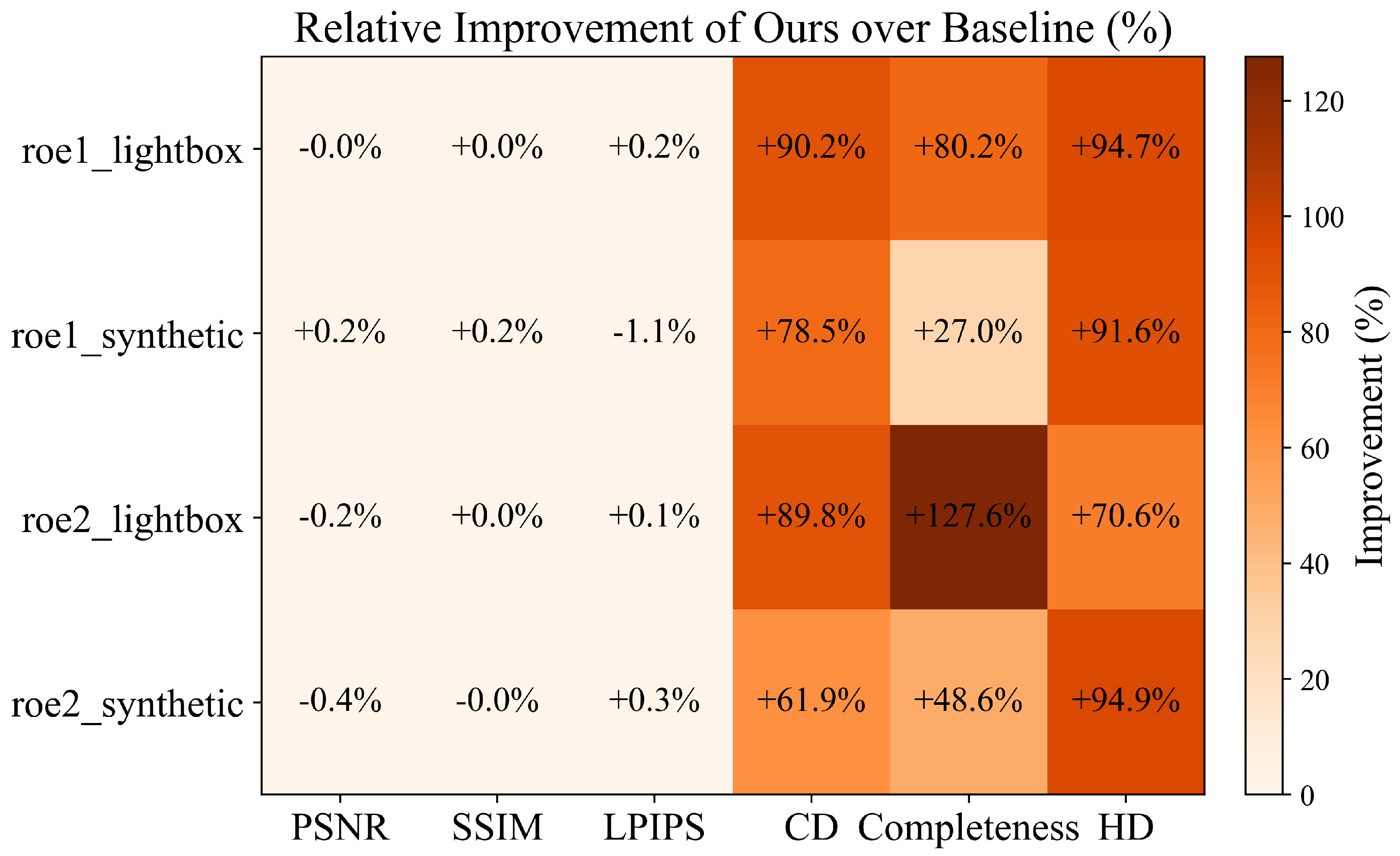
5.5. Quantitative Comparison
5.6. Ablation Study
5.7. Evaluation on SHIRT Dataset
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Wei, Q.; Zhang, W.; Wu, J.; Jiang, Z. Sequential-image-based space object 3D reconstruction. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 273–279. [Google Scholar]
- Sun, Q.; Zhao, L.; Tang, S.; Dang, Z. Orbital motion intention recognition for space non-cooperative targets based on incomplete time series data. Aerosp. Sci. Technol. 2025, 158, 109912. [Google Scholar] [CrossRef]
- Nguyen, V.M.; Sandidge, E.; Mahendrakar, T.; White, R.T. Characterizing Satellite Geometry via Accelerated 3D Gaussian Splatting. Aerospace 2024, 11, 183. [Google Scholar] [CrossRef]
- Dung, H.A.; Chen, B.; Chin, T.J. A spacecraft dataset for detection, segmentation and parts recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Nashville, TN, USA, 20–25 June 2021; pp. 2012–2019. [Google Scholar]
- Cutler, J.; Wilde, M.; Rivkin, A.; Kish, B.; Silver, I. Artificial Potential Field Guidance for Capture of Non-Cooperative Target Objects by Chaser Swarms. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–12. [Google Scholar]
- Piazza, M.; Maestrini, M.; Di Lizia, P. Monocular relative pose estimation pipeline for uncooperative resident space objects. J. Aerosp. Inf. Syst. 2022, 19, 613–632. [Google Scholar] [CrossRef]
- Piazza, M.; Maestrini, M.; Di Lizia, P. Neural Network-Based Pose Estimation for Noncooperative Spacecraft Rendezvous. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4638–4658. [Google Scholar]
- Forshaw, J.; Lopez, R.; Okamoto, A.; Blackerby, C.; Okada, N. The ELSA-D End-of-Life Debris Removal Mission: Mission Design, In-Flight Safety, and Preparations for Launch. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 17–20 September 2019; p. 44. [Google Scholar]
- Forshaw, J.; Okamoto, A.; Bradford, A.; Lopez, R.; Blackerby, C.; Okada, N. ELSA-D—A Novel End-of-Life Debris Removal Mission: Mission Overview, CONOPS, and Launch Preparations. In Proceedings of the First International Orbital Debris Conference (IOC), Houston, TX, USA, 9–12 December 2019; p. 6076. [Google Scholar]
- Barad, K.R.; Richard, A.; Dentler, J.; Olivares-Mendez, M.; Martinez, C. Object-centric Reconstruction and Tracking of Dynamic Unknown Objects Using 3D Gaussian Splatting. In Proceedings of the International Conference on Space Robotics (ISPARO), Luxembourg, 24–27 June 2024; pp. 202–209. [Google Scholar]
- Luo, J.; Ren, W.; Gao, X.; Cao, X. Multi-Exposure Image Fusion via Deformable Self-Attention. IEEE Trans. Image Process. 2023, 32, 1529–1540. [Google Scholar] [CrossRef]
- Xiong, Q.; Ren, X.; Yin, H.; Jiang, L.; Wang, C.; Wang, Z. SFDA-MEF: An Unsupervised Spacecraft Feature Deformable Alignment Network for Multi-Exposure Image Fusion. Remote Sens. 2025, 17, 199. [Google Scholar] [CrossRef]
- Lowe, D. Object Recognition from Local Scale-Invariant Features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Frahm, J. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Cui, H.; Shen, S.; Gao, W.; Hu, Z. Efficient Large-Scale Structure from Motion by Fusing Auxiliary Imaging Information. IEEE Trans. Image Process. 2015, 24, 3561–3573. [Google Scholar]
- Wu, C. Towards Linear-Time Incremental Structure from Motion. In Proceedings of the International Conference on 3D Vision (3DV), Seattle, WA, USA, 29 June–1 July 2013. [Google Scholar]
- Scharstein, D.; Szeliski, R.; Zabih, R. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. In Proceedings of the IEEE Workshop Stereo Multi-Baseline Vision (SMBV), Kauai, HI, USA, 9–10 December 2001; pp. 131–140. [Google Scholar]
- Khan, R.; Akram, A.; Mehmood, A. Multiview Ghost-Free Image Enhancement for In-the-Wild Images with Unknown Exposure and Geometry. IEEE Access 2021, 9, 24205–24220. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J.; Li, L.; Li, X.; Chen, F. Application of MVSNet in 3D Reconstruction of Space Objects. Chin. J. Lasers 2022, 49, 2310003. [Google Scholar]
- Luo, K.; Guan, T.; Ju, L.; Wang, Y.; Chen, Z.; Luo, Y. Attention-Aware Multi-View Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1587–1596. [Google Scholar]
- Zhang, W.; Li, Z.; Li, G.; Zhou, L.; Zhao, W.; Pan, X. AGANet: Attention-Guided Generative Adversarial Network for Corn Hyperspectral Images Augmentation. IEEE Trans. Consum. Electron. 2024. early access. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Li, G.; Zhuang, P.; Hou, G.; Zhang, Q.; Li, C. GACNet: Generate Adversarial-Driven Cross-Aware Network for Hyperspectral Wheat Variety Identification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5503314. [Google Scholar] [CrossRef]
- Liu, Z.; Fang, T.; Lu, H.; Zhang, W.; Lan, R. MASFNet: Multiscale Adaptive Sampling Fusion Network for Object Detection in Adverse Weather. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4702815. [Google Scholar] [CrossRef]
- Yang, H.; Xia, H.; Chen, X.; Sun, S.; Rao, P. Application of Image Fusion in 3D Reconstruction of Space Target. Infrared Laser Eng. 2018, 47, 926002. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.; Tancik, M.; Barron, J.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Kerbl, B.; Kopanas, G.; Leimkuehler, T.; Drettakis, G. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Trans. Graph. 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Zou, Y.; Li, X.; Jiang, Z.; Liu, J. Enhancing Neural Radiance Fields with Adaptive Multi-Exposure Fusion: A Bilevel Optimization Approach for Novel View Synthesis. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 7882–7890. [Google Scholar]
- Cui, Z.; Chu, X.; Harada, T. Luminance-GS: Adapting 3D Gaussian Splatting to Challenging Lighting Conditions with View-Adaptive Curve Adjustment. arXiv 2025, arXiv:2504.01503. [Google Scholar]
- Gupta, M.; Iso, D.; Nayar, S.K. Fibonacci Exposure Bracketing for High Dynamic Range Imaging. In Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, NSW, Australia, 1–8 December 2013; pp. 1473–1480. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Park, T.H.; D’Amico, S. Rapid Abstraction of Spacecraft 3D Structure from Single 2D Image. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Taud, H.; Mas, J.F. Multilayer Perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.F., Escobar, F., Eds.; Springer International Publisher: Cham, Switzerland, 2018; pp. 451–455. [Google Scholar]
- Fu, T.; Zhou, Y.; Wang, Y.; Liu, J.; Zhang, Y.; Kong, Q.; Chen, B. Neural Field-Based Space Target 3D Reconstruction with Predicted Depth Priors. Aerospace 2024, 11, 997. [Google Scholar] [CrossRef]
- Fei, B.; Xu, J.; Zhang, R.; Zhou, Q.; Yang, W.; He, Y. 3D Gaussian as a New Era: A Survey. arXiv 2024, arXiv:2402.07181. [Google Scholar]
- Wu, T.; Yuan, Y.; Zhang, L.; Yang, J.; Cao, Y.; Yan, L.; Gao, L. Recent Advances in 3D Gaussian Splatting. Comput. Vis. Media 2024, 10, 613–642. [Google Scholar] [CrossRef]
- Bao, Y.; Ding, T.; Huo, J.; Liu, Y.; Li, Y.; Li, W.; Gao, Y.; Luo, J. 3D Gaussian Splatting: Survey, Technologies, Challenges, and Opportunities. IEEE Trans. Circuits Syst. Video Technol. 2025. early access. [Google Scholar] [CrossRef]
- Zhao, Y.; Yi, J.; Pan, Y.; Chen, L. 3D Reconstruction of Non-Cooperative Space Targets of Poor Lighting Based on 3D Gaussian Splatting. Signal Image Video Process. 2025, 19, 509. [Google Scholar] [CrossRef]
- Du, X.; Wang, Y.; Yu, X. MVGS: Multi-View-Regulated Gaussian Splatting for Novel View Synthesis. arXiv 2024, arXiv:2410.02103. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Lever, J.; Krzywinski, M.; Altman, N. Principal Component Analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, W.; Lao, Y.; He, T.; Zhao, H. Pixel-GS: Density Control with Pixel-Aware Gradient for 3D Gaussian Splatting. In European Conference on Computer Vision; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2024; pp. 326–342. [Google Scholar]
- Park, T.H.; Martens, M.; Lecuyer, G.; Izzo, D.; D’Amico, S. SPEED+: Next-Generation Dataset for Spacecraft Pose Estimation across Domain Gap. In Proceedings of the IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–15. [Google Scholar]
- Park, T.H.; D’Amico, S. Adaptive Neural-Network-Based Unscented Kalman Filter for Robust Pose Tracking of Noncooperative Spacecraft. J. Guid. Control Dyn. 2023, 46, 1671–1688. [Google Scholar] [CrossRef]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. MVSNet: Depth Inference for Unstructured Multi-View Stereo. In European Conference on Computer Vision; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; pp. 785–801. [Google Scholar]




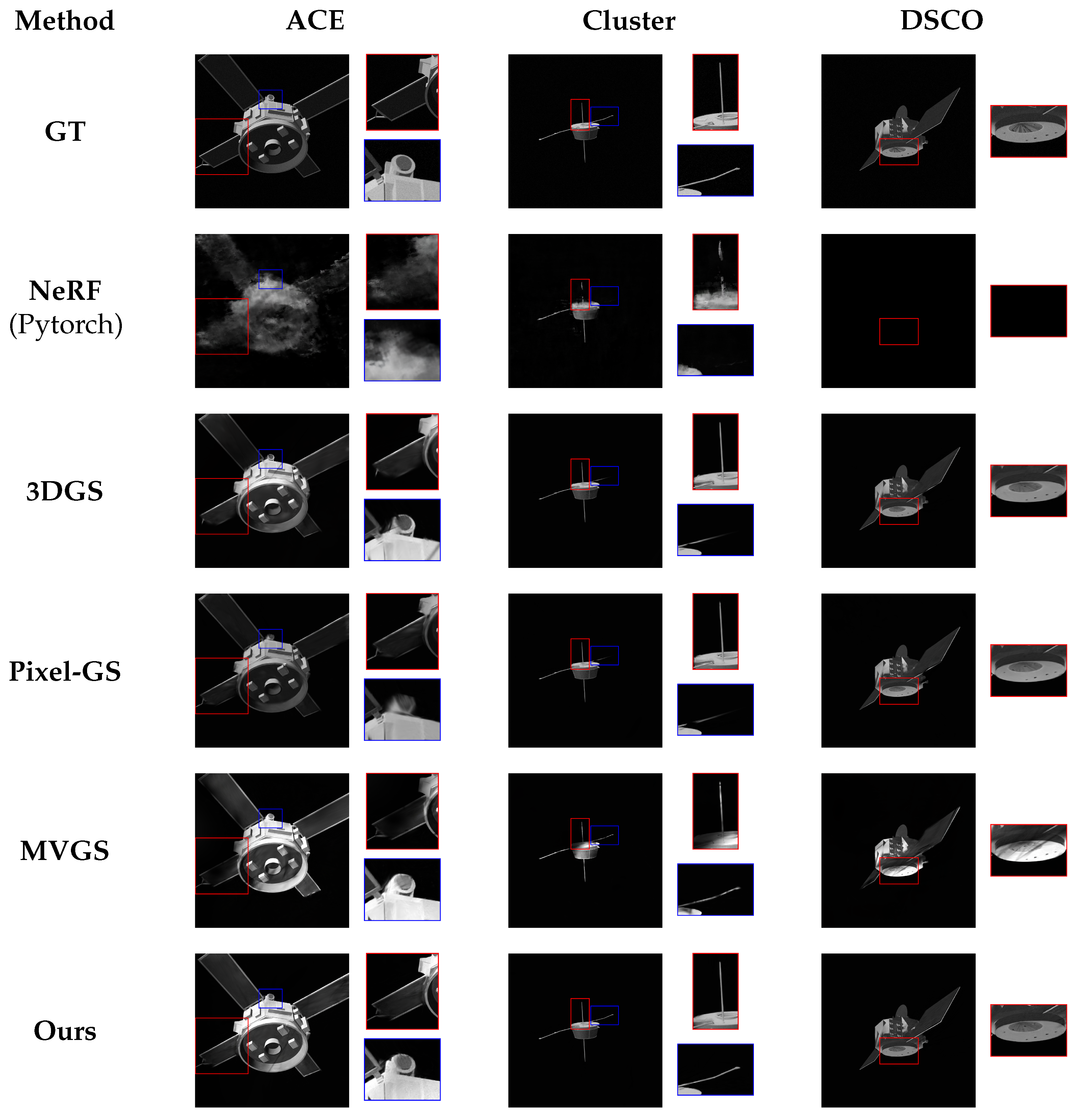

| Module | NeRF (Pytorch) | 3DGS | Pixel-GS | MVGS | Ours |
|---|---|---|---|---|---|
| ACE | 23.5424 | 26.0240 | 25.9689 | 23.4592 | 26.2057 |
| Cluster | 25.8187 | 28.1415 | 28.1223 | 27.8028 | 28.5121 |
| DSCO | 21.0549 | 28.5198 | 28.5737 | 27.7245 | 28.5951 |
| MM | 23.5226 | 29.2306 | 29.3822 | 28.1745 | 29.6908 |
| SHO | 20.6217 | 23.0715 | 23.2382 | 20.4337 | 23.4519 |
| TDRS | 0.3025 | 25.3843 | 25.4555 | 24.1252 | 25.7606 |
| Average | 19.1438 | 26.7286 | 26.7902 | 25.6850 | 27.0361 |
| Module | NeRF (Pytorch) | 3DGS | Pixel-GS | MVGS | Ours |
|---|---|---|---|---|---|
| ACE | 0.6777 | 0.8332 | 0.8340 | 0.8080 | 0.8341 |
| Cluster | 0.7421 | 0.8485 | 0.8486 | 0.8443 | 0.8494 |
| DSCO | 0.4950 | 0.8337 | 0.8337 | 0.8280 | 0.8341 |
| MM | 0.5267 | 0.8415 | 0.8430 | 0.8354 | 0.8461 |
| SHO | 0.6115 | 0.7663 | 0.7681 | 0.7155 | 0.7681 |
| TDRS | 0.0329 | 0.8201 | 0.8206 | 0.8033 | 0.8241 |
| Average | 0.5143 | 0.8239 | 0.8247 | 0.8085 | 0.8260 |
| Module | NeRF (Pytorch) | 3DGS | Pixel-GS | MVGS | Ours |
|---|---|---|---|---|---|
| ACE | 0.5058 | 0.4797 | 0.4783 | 0.4932 | 0.4731 |
| Cluster | 0.4890 | 0.4812 | 0.4805 | 0.4808 | 0.4776 |
| DSCO | 0.5272 | 0.4859 | 0.4846 | 0.4870 | 0.4821 |
| MM | 0.5297 | 0.4767 | 0.4723 | 0.4819 | 0.4646 |
| SHO | 0.5540 | 0.4931 | 0.4878 | 0.5179 | 0.4737 |
| TDRS | 0.8245 | 0.4810 | 0.4790 | 0.4836 | 0.4697 |
| Average | 0.5717 | 0.4829 | 0.4804 | 0.4874 | 0.4735 |
| Module | MVSNet | 3DGS | Pixel-GS | MVGS | Ours |
|---|---|---|---|---|---|
| ACE | 0.4098 | 0.1445 | 0.1206 | 0.7274 | 0.0283 |
| Cluster | 0.1269 | 0.2192 | 0.2345 | 0.8368 | 0.0426 |
| DSCO | 0.3722 | 0.1372 | 0.1510 | 0.2285 | 0.0314 |
| MM | 0.3439 | 0.1843 | 0.1520 | 0.5305 | 0.0419 |
| SHO | 0.2204 | 0.0807 | 0.0852 | 0.4972 | 0.0773 |
| TDRS | 0.2816 | 0.1129 | 0.1218 | 0.6108 | 0.0374 |
| Average | 0.2925 | 0.1465 | 0.1442 | 0.4774 | 0.0431 |
| Module | MVSNet | 3DGS | Pixel-GS | MVGS | Ours |
|---|---|---|---|---|---|
| ACE | 40.6683 | 60.3806 | 76.4285 | 58.7431 | 87.5466 |
| Cluster | 14.7993 | 51.5432 | 59.1408 | 66.5348 | 78.1119 |
| DSCO | 31.6447 | 47.7257 | 55.4674 | 59.2630 | 66.6131 |
| MM | 38.1166 | 71.9740 | 81.2636 | 76.8022 | 91.5039 |
| SHO | 20.4281 | 22.1142 | 29.9984 | 26.5029 | 36.7657 |
| TDRS | 48.0172 | 45.5344 | 56.8314 | 61.4799 | 72.1282 |
| Average | 32.2790 | 49.8787 | 59.8550 | 61.6677 | 72.1116 |
| Module | MVSNet | 3DGS | Pixel-GS | MVGS | Ours |
|---|---|---|---|---|---|
| ACE | 1.6787 | 4.1167 | 3.1101 | 3.6667 | 0.1361 |
| Cluster | 0.9062 | 3.5868 | 2.9471 | 3.8028 | 0.2404 |
| DSCO | 1.6141 | 3.3337 | 3.5116 | 4.3244 | 0.1619 |
| MM | 1.3774 | 3.7419 | 2.6208 | 2.9278 | 0.3942 |
| SHO | 1.0621 | 2.3937 | 3.0082 | 4.0570 | 1.2159 |
| TDRS | 1.6926 | 3.3094 | 3.2736 | 3.6618 | 0.8767 |
| Average | 1.3885 | 3.4137 | 3.0786 | 3.6200 | 0.5042 |
| Structure | PSNR↑ | SSIM↑ | LPIPS↓ | CD↓ | Completeness Percentage ↑ | HD↓ |
|---|---|---|---|---|---|---|
| 3DGS (Baseline) | 26.7286 | 0.8239 | 0.4829 | 0.1465 | 49.8787 | 3.4137 |
| +Sobel | 26.8931 | 0.8248 | 0.4783 | 0.0416 | 66.7511 | 0.3824 |
| +OBB | 26.8282 | 0.8248 | 0.4765 | 0.0396 | 66.5106 | 0.5884 |
| ALL (Ours) | 27.0361 | 0.8260 | 0.4735 | 0.0431 | 72.1116 | 0.5042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Ren, X.; Yin, H.; Jiang, L.; Wang, C.; Wang, Z. High-Fidelity 3D Gaussian Splatting for Exposure-Bracketing Space Target Reconstruction: OBB-Guided Regional Densification with Sobel Edge Regularization. Remote Sens. 2025, 17, 2020. https://doi.org/10.3390/rs17122020
Jiang Y, Ren X, Yin H, Jiang L, Wang C, Wang Z. High-Fidelity 3D Gaussian Splatting for Exposure-Bracketing Space Target Reconstruction: OBB-Guided Regional Densification with Sobel Edge Regularization. Remote Sensing. 2025; 17(12):2020. https://doi.org/10.3390/rs17122020
Chicago/Turabian StyleJiang, Yijin, Xiaoyuan Ren, Huanyu Yin, Libing Jiang, Canyu Wang, and Zhuang Wang. 2025. "High-Fidelity 3D Gaussian Splatting for Exposure-Bracketing Space Target Reconstruction: OBB-Guided Regional Densification with Sobel Edge Regularization" Remote Sensing 17, no. 12: 2020. https://doi.org/10.3390/rs17122020
APA StyleJiang, Y., Ren, X., Yin, H., Jiang, L., Wang, C., & Wang, Z. (2025). High-Fidelity 3D Gaussian Splatting for Exposure-Bracketing Space Target Reconstruction: OBB-Guided Regional Densification with Sobel Edge Regularization. Remote Sensing, 17(12), 2020. https://doi.org/10.3390/rs17122020






