A New Multimodal Map Building Method Using Multiple Object Tracking and Gaussian Process Regression
Abstract
1. Introduction
- A robot-based map building framework is proposed that utilizes model-free multiple object tracking (MOT) integrated with dynamic object information along with 2D occupancy maps derived from SLAM.
- We propose a multimodal map, called the TA map, that represents the level of target activity on the OG map. This map can help with path planning for autonomous navigation.
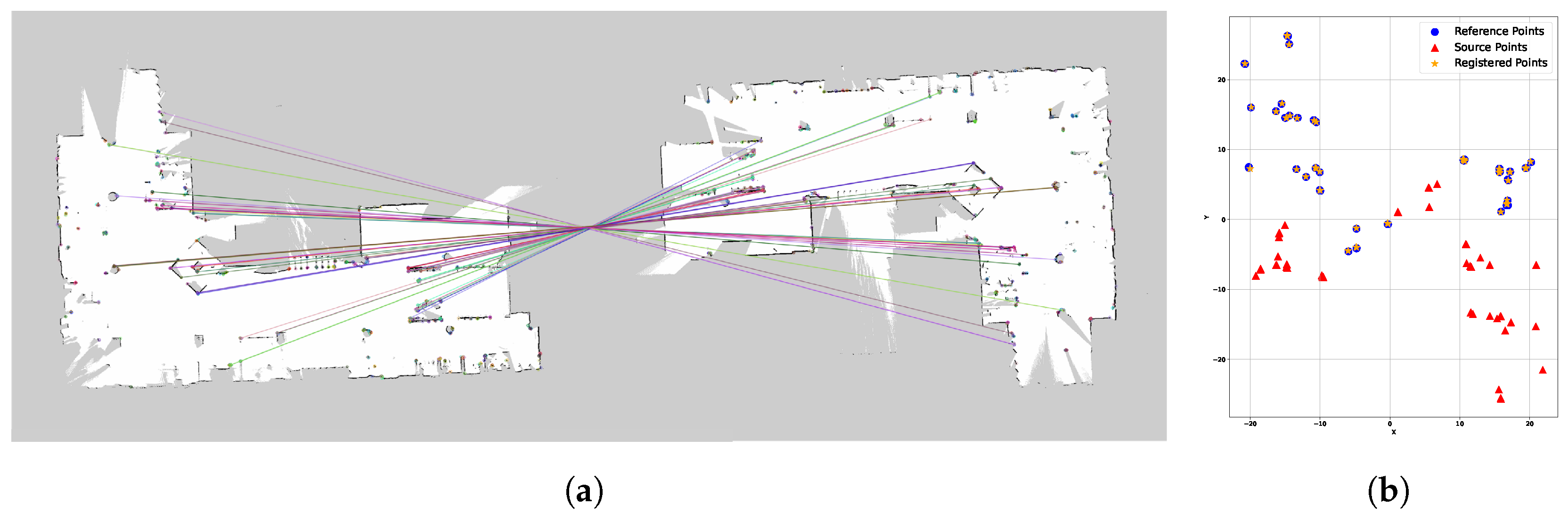
- A registration of multiple target trajectories is developed to create a generalized map. Thus, sensor data obtained under various dataset acquisition conditions, such as different times, routes, and starting points, can be integrated into a single multimodal map.
2. Related Work
2.1. Multiple Object Tracking (MOT)
2.2. Maps Containing Dynamic Object Information
2.3. Map Building with Gaussian Process
3. Problem Statement
3.1. Problem Definition
3.2. Basic Idea
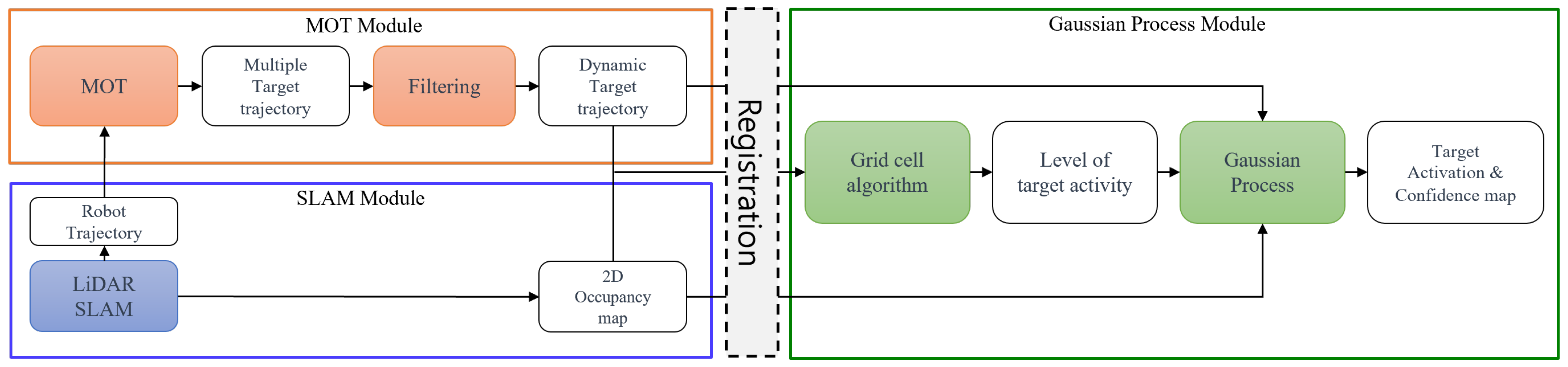
4. Proposed Method
4.1. Overview
4.2. Multiple Target Trajectories and Filtering
4.2.1. LiDAR Coordinates to World Coordinates
4.2.2. Dummy Target Filtering
| Algorithm 1: Dummy target filtering |
|
- Minimal pose variation: non-dynamic objects exhibit minimal changes in their poses over time.
- Low velocity: they have a low or negligible velocity since they remain stationary.
- Compactness: non-dynamic objects tend to have compact spatial distributions, resulting in small-sized vectors.
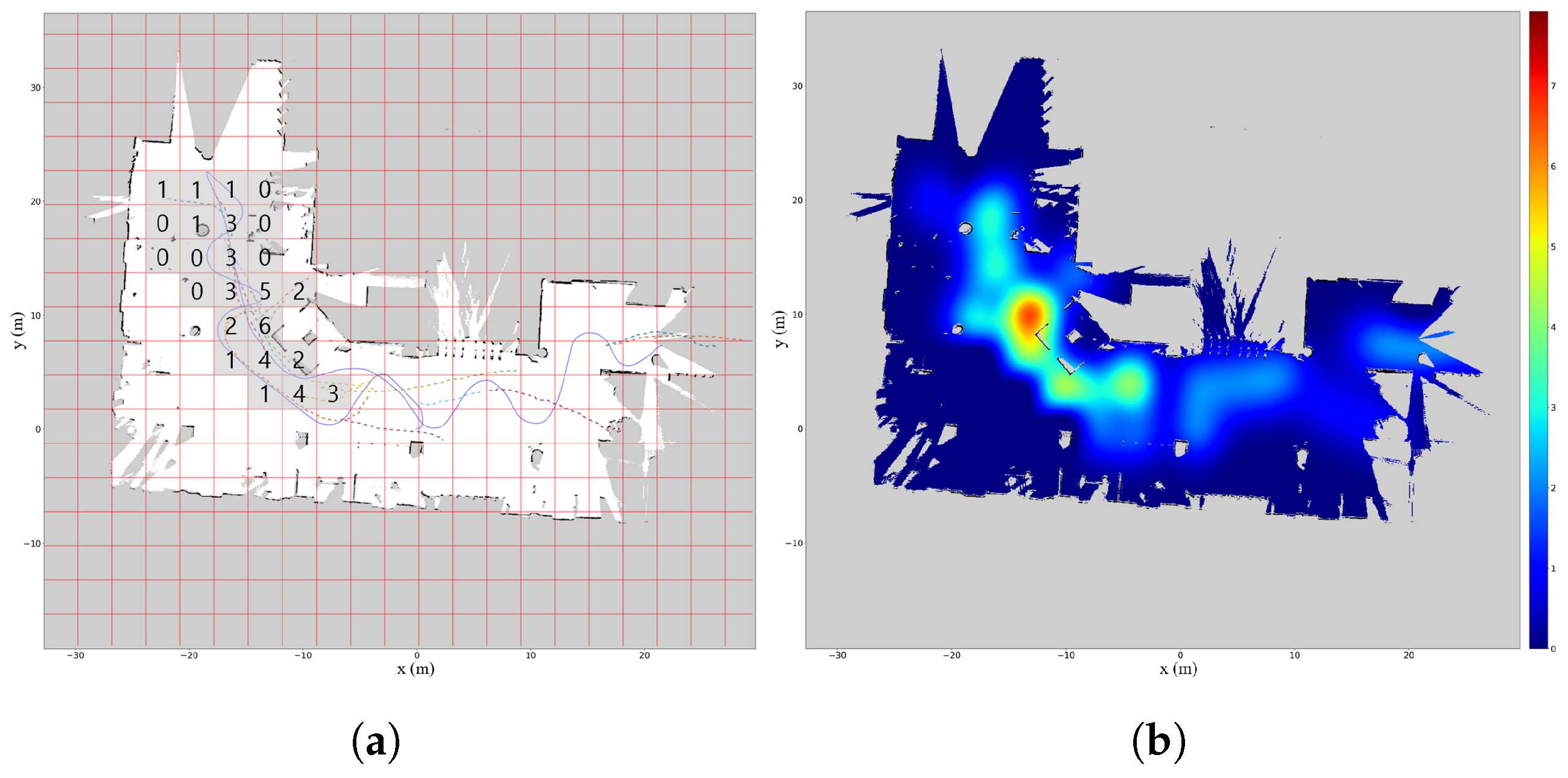
4.3. TA Map Generation with GPR
| Algorithm 2: Grid cell algorithm |
|
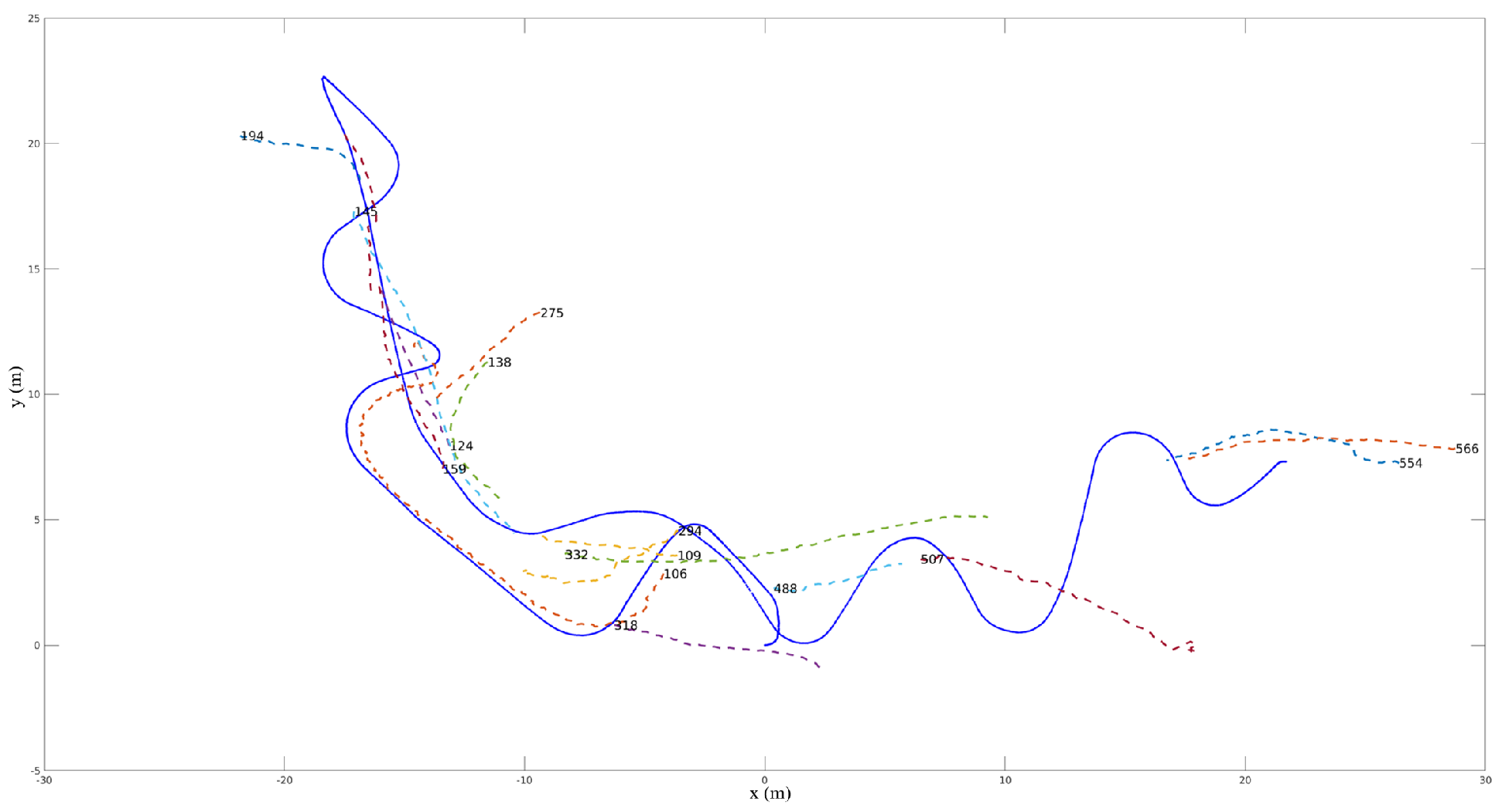
4.4. Registration of Multiple Target Trajectories
5. Experiments
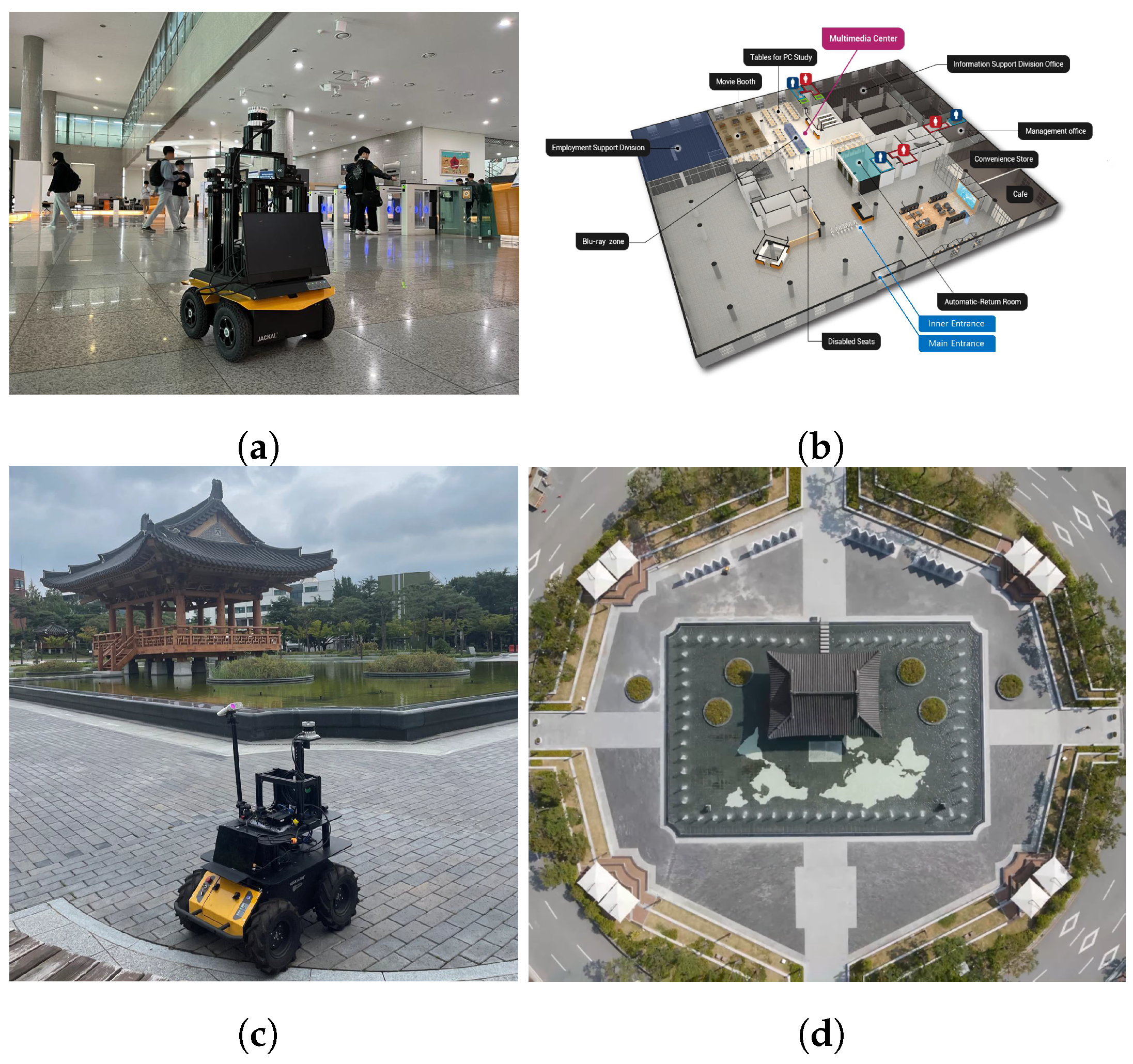
5.1. Platform
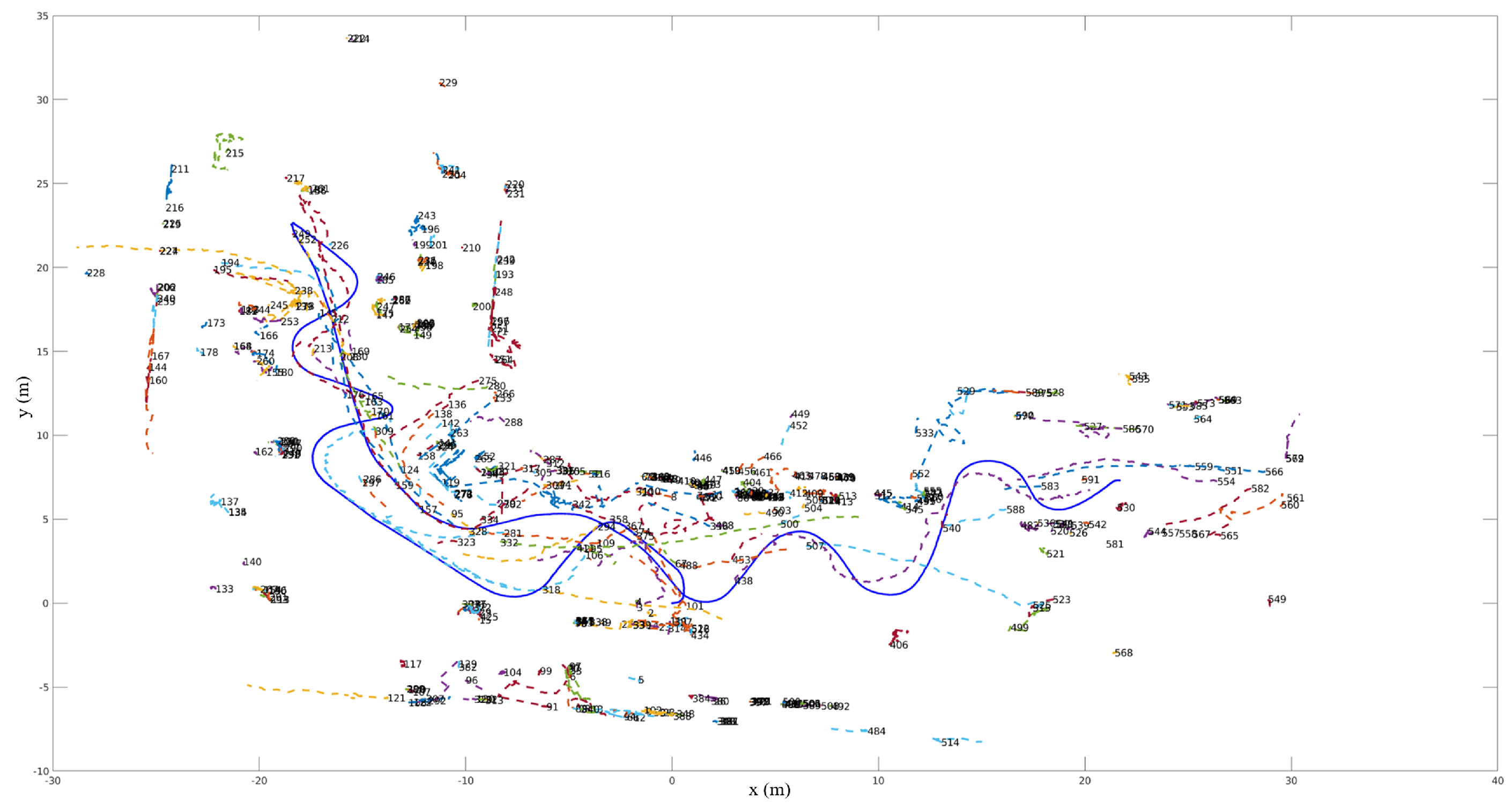
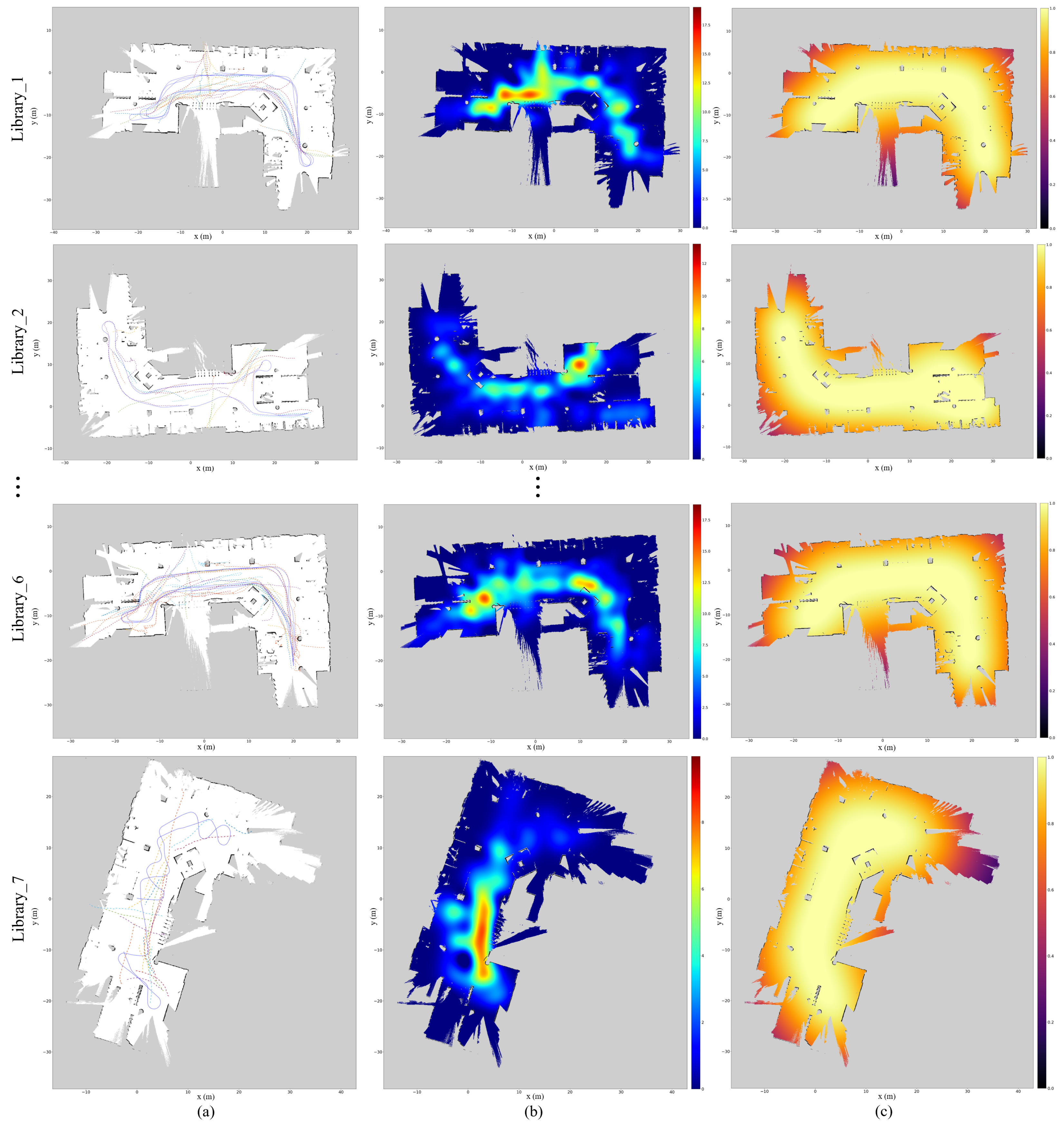
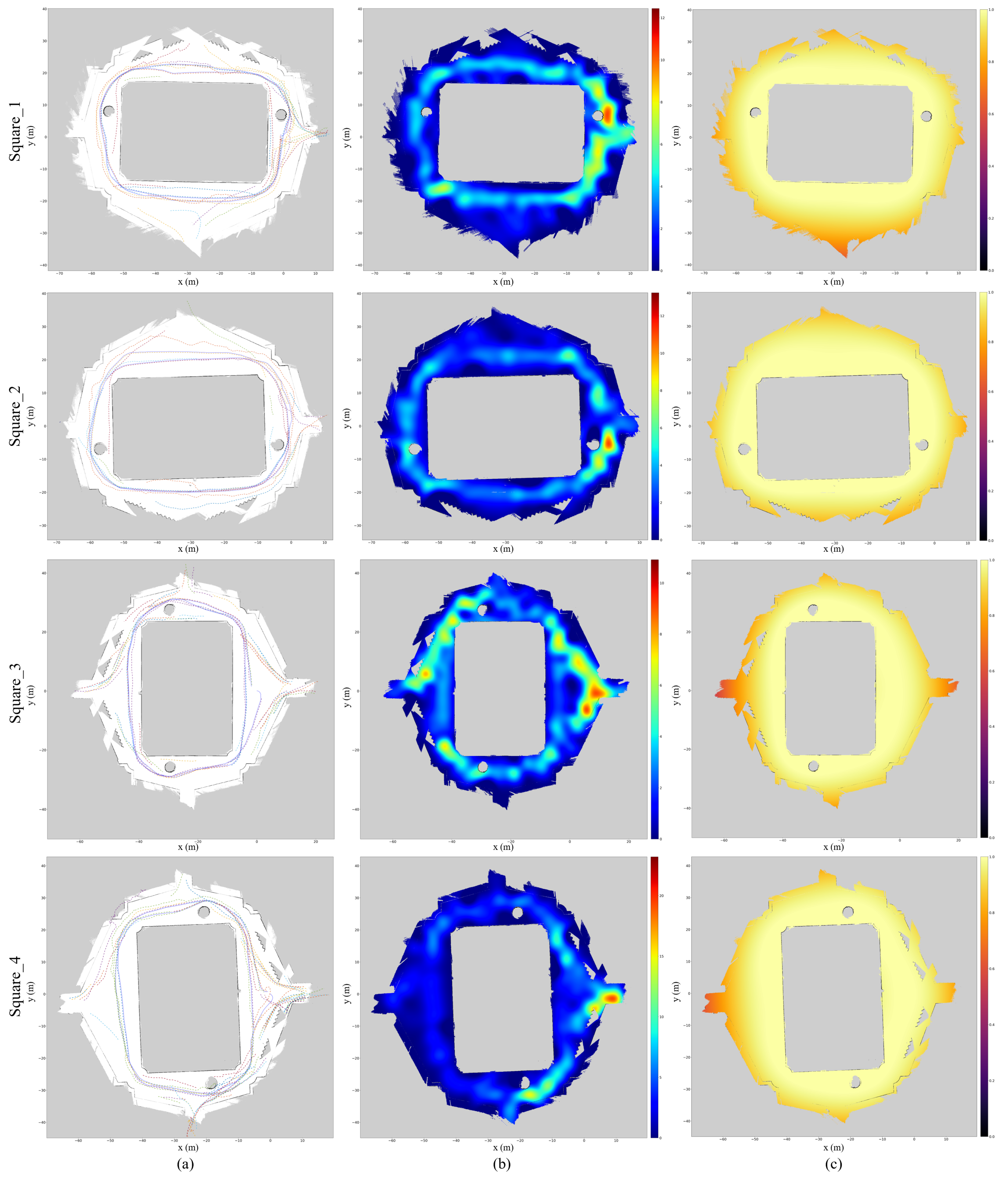
5.2. Results for Single Datasets
5.3. Results for Registered Datasets
5.4. Path Planning on the TA Map
6. Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jo, H.; Cho, H.M.; Jo, S.; Kim, E. Efficient grid-based Rao–Blackwellized particle filter SLAM with interparticle map sharing. IEEE/ASME Trans. Mechatron. 2018, 23, 714–724. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Bai, C.; Xiao, T.; Chen, Y.; Wang, H.; Zhang, F.; Gao, X. Faster-LIO: Lightweight tightly coupled LiDAR-inertial odometry using parallel sparse incremental voxels. IEEE Robot. Autom. Lett. 2022, 7, 4861–4868. [Google Scholar] [CrossRef]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1271–1278. [Google Scholar]
- Ambruş, R.; Bore, N.; Folkesson, J.; Jensfelt, P. Meta-rooms: Building and maintaining long term spatial models in a dynamic world. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1854–1861. [Google Scholar]
- Lim, H.; Hwang, S.; Myung, H. ERASOR: Egocentric ratio of pseudo occupancy-based dynamic object removal for static 3D point cloud map building. IEEE Robot. Autom. Lett. 2021, 6, 2272–2279. [Google Scholar] [CrossRef]
- Ruchti, P.; Burgard, W. Mapping with dynamic-object probabilities calculated from single 3d range scans. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 6331–6336. [Google Scholar]
- Kim, G.; Kim, A. Remove, then revert: Static point cloud map construction using multiresolution range images. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 10758–10765. [Google Scholar]
- Choi, B.; Jo, H.; Kim, E. Normal Distribution Mixture Matching based Model Free Object Tracking Using 2D LIDAR. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Venetian Macao, Macau, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 455–461. [Google Scholar]
- Merugu, S.; Jain, K.; Mittal, A.; Raman, B. Sub-scene target detection and recognition using deep learning convolution neural networks. In ICDSMLA 2019: Proceedings of the 1st International Conference on Data Science, Machine Learning and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1082–1101. [Google Scholar]
- Haq, M.A.; Rahim Khan, M.A. DNNBoT: Deep neural network-based botnet detection and classification. Comput. Mater. Contin. 2022, 71, 1729–1750. [Google Scholar]
- Zhang, R.; Cao, Z.; Yang, S.; Si, L.; Sun, H.; Xu, L.; Sun, F. Cognition-Driven Structural Prior for Instance-Dependent Label Transition Matrix Estimation. IEEE Trans. Neural Netw. Learn. Syst. 2024. [Google Scholar] [CrossRef] [PubMed]
- Pomerleau, F.; Krüsi, P.; Colas, F.; Furgale, P.; Siegwart, R. Long-term 3D map maintenance in dynamic environments. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3712–3719. [Google Scholar]
- Linder, T.; Breuers, S.; Leibe, B.; Arras, K.O. On multi-modal people tracking from mobile platforms in very crowded and dynamic environments. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 5512–5519. [Google Scholar]
- Cheng, S.; Yao, M.; Xiao, X. DC-MOT: Motion deblurring and compensation for multi-object tracking in UAV videos. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 789–795. [Google Scholar]
- Jafari, O.H.; Mitzel, D.; Leibe, B. Real-time RGB-D based people detection and tracking for mobile robots and head-worn cameras. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 5636–5643. [Google Scholar]
- Samal, K.; Kumawat, H.; Saha, P.; Wolf, M.; Mukhopadhyay, S. Task-driven rgb-lidar fusion for object tracking in resource-efficient autonomous system. IEEE Trans. Intell. Veh. 2021, 7, 102–112. [Google Scholar] [CrossRef]
- Shen, L.; Guo, H.; Bai, Y.; Qin, L.; Ang, M.; Rus, D. Group Multi-Object Tracking for Dynamic Risk Map and Safe Path Planning. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 6292–6298. [Google Scholar]
- Gong, H.; Sim, J.; Likhachev, M.; Shi, J. Multi-hypothesis motion planning for visual object tracking. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 619–626. [Google Scholar]
- Rudenko, A.; Palmieri, L.; Doellinger, J.; Lilienthal, A.J.; Arras, K.O. Learning occupancy priors of human motion from semantic maps of urban environments. IEEE Robot. Autom. Lett. 2021, 6, 3248–3255. [Google Scholar] [CrossRef]
- Almonfrey, D.; do Carmo, A.P.; de Queiroz, F.M.; Picoreti, R.; Vassallo, R.F.; Salles, E.O.T. A flexible human detection service suitable for Intelligent Spaces based on a multi-camera network. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718763550. [Google Scholar] [CrossRef]
- Kucner, T.P.; Magnusson, M.; Schaffernicht, E.; Bennetts, V.H.; Lilienthal, A.J. Enabling flow awareness for mobile robots in partially observable environments. IEEE Robot. Autom. Lett. 2017, 2, 1093–1100. [Google Scholar] [CrossRef]
- Wang, Z.; Jensfelt, P.; Folkesson, J. Building a human behavior map from local observations. In Proceedings of the 2016 25th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), New York, NY, USA, 26–31 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 64–70. [Google Scholar]
- Zhang, R.; Tan, J.; Cao, Z.; Xu, L.; Liu, Y.; Si, L.; Sun, F. Part-Aware Correlation Networks for Few-shot Learning. IEEE Trans. Multimed. 2024. [Google Scholar] [CrossRef]
- Vintr, T.; Yan, Z.; Duckett, T.; Krajník, T. Spatio-temporal representation for long-term anticipation of human presence in service robotics. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2620–2626. [Google Scholar]
- MacKay, D.J. Introduction to Gaussian processes. NATO ASI Ser. F Comput. Syst. Sci. 1998, 168, 133–166. [Google Scholar]
- Ebden, M. Gaussian processes: A quick introduction. arXiv 2015, arXiv:1505.02965. [Google Scholar]
- Wang, J. An intuitive tutorial to Gaussian processes regression. arXiv 2020, arXiv:2009.10862. [Google Scholar]
- Guo, H.; Meng, Z.; Huang, Z.; Kang, L.W.; Chen, Z.; Meghjani, M.; Ang, M.; Rus, D. Safe path planning with gaussian process regulated risk map. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Venetian Macao, Macau, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2044–2051. [Google Scholar]
- West, A.; Tsitsimpelis, I.; Licata, M.; Jazbec, A.; Snoj, L.; Joyce, M.J.; Lennox, B. Use of Gaussian process regression for radiation mapping of a nuclear reactor with a mobile robot. Sci. Rep. 2021, 11, 13975. [Google Scholar] [CrossRef] [PubMed]
- O’Callaghan, S.T.; Singh, S.P.; Alempijevic, A.; Ramos, F.T. Learning navigational maps by observing human motion patterns. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4333–4340. [Google Scholar]
- Stuede, M.; Schappler, M. Non-parametric Modeling of Spatio-Temporal Human Activity Based on Mobile Robot Observations. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 126–133. [Google Scholar]
- Molina, S.; Cielniak, G.; Duckett, T. Robotic exploration for learning human motion patterns. IEEE Trans. Robot. 2021, 38, 1304–1318. [Google Scholar] [CrossRef]
- Brščić, D.; Kanda, T.; Ikeda, T.; Miyashita, T. Person tracking in large public spaces using 3-D range sensors. IEEE Trans. Hum.-Mach. Syst. 2013, 43, 522–534. [Google Scholar] [CrossRef]
- Cheeseman, P.; Smith, R.; Self, M. A stochastic map for uncertain spatial relationships. In Proceedings of the 4th International Symposium on Robotic Research, Santa Clara, CA, USA, 9–14 August 1897; MIT Press Cambridge: Cambridge, MA, USA, 1987; pp. 467–474. [Google Scholar]
- Umeyama, S. Least-squares estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 376–380. [Google Scholar] [CrossRef]
- GPy. GPy: A Gaussian Process Framework in Python. 2012. Available online: http://github.com/SheffieldML/GPy (accessed on 17 July 2024).
- Jeonbuk National University. Floor Guide of Central Library. Available online: https://dl.jbnu.ac.kr/webcontent/info/79 (accessed on 3 June 2024).
- Jeonbuk University Promotional Video (Campus). Available online: https://www.youtube.com/watch?v=QEoti0R8uT4 (accessed on 3 June 2024).
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved techniques for grid mapping with rao-blackwellized particle filters. IEEE Trans. Robot. 2007, 23, 34–46. [Google Scholar] [CrossRef]




| Dataset | Dummy Target Filtering | Map | Length of Robot Trajectory (m) | Time | |||
|---|---|---|---|---|---|---|---|
| Initial IDCount | Dynamic ID Count | In Pixels | In Metric | Resolution | |||
| Library_1 | 1412 | 49 | 1368 × 1051 | 68.4 × 52.55 | 0.05 | 347.395 | 10 m 51 s |
| Library_2 * | 751 | 18 | 1408 × 1166 | 72.45 × 51.35 | 146.64 | 4 m 12 s | |
| Library_3 | 393 | 10 | 1454 × 1177 | 72.7 × 58.85 | 93.641 | 3 m 48 s | |
| Library_4 | 591 | 15 | 1250 × 1116 | 62.5 × 55.8 | 115.277 | 4 m 29 s | |
| Library_5 | 599 | 18 | 1410 × 1060 | 70.55 × 53.3 | 114.795 | 16 m 10 s | |
| Library_6 | 2024 | 60 | 1450 × 1050 | 72.5 × 52.5 | 359.211 | 14 m 13 s | |
| Library_7 | 790 | 23 | 1191 × 1304 | 59.55 × 65.2 | 125.316 | 5 m 23 s | |
| Total | 6500 | 203 | - | - | - | 1302.275 | 49 m 11 s |
| Square_1 | 1147 | 34 | 1783 × 1639 | 89.15 × 81.95 | 0.05 | 346.735 | 15 m 18 s |
| Square_2 | 1102 | 28 | 1705 × 1493 | 85.25 × 74.65 | 350.736 | 15 m 37 s | |
| Square_3 | 1496 | 67 | 1946 × 1893 | 97.3 × 94.65 | 345.129 | 16 m 47 s | |
| Square_4 * | 1323 | 78 | 1800 × 1754 | 89.55 × 87.7 | 353.522 | 16 m 10 s | |
| Total | 5068 | 207 | - | - | - | 1396.122 | 63 m 52 s |
| Metric | OG Map [4] | OG Map [41] | TA Map | ||
|---|---|---|---|---|---|
| Case 1 | Activity Level | Mean | 2.299 | 2.171 | 2.146 |
| Variance | 3.785 | 3.262 | 2.984 | ||
| Max | 7.836 | 7.846 | 5.500 | ||
| Length of path (m) | 52.747 | 55.189 | 54.674 | ||
| Case 2 | Activity Level | Mean | 2.131 | 2.124 | 2.074 |
| Variance | 4.131 | 4.229 | 3.701 | ||
| Max | 7.837 | 7.847 | 7.847 | ||
| Length of path (m) | 26.317 | 26.400 | 26.990 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, E.; Lee, S.J.; Jo, H. A New Multimodal Map Building Method Using Multiple Object Tracking and Gaussian Process Regression. Remote Sens. 2024, 16, 2622. https://doi.org/10.3390/rs16142622
Jang E, Lee SJ, Jo H. A New Multimodal Map Building Method Using Multiple Object Tracking and Gaussian Process Regression. Remote Sensing. 2024; 16(14):2622. https://doi.org/10.3390/rs16142622
Chicago/Turabian StyleJang, Eunseong, Sang Jun Lee, and HyungGi Jo. 2024. "A New Multimodal Map Building Method Using Multiple Object Tracking and Gaussian Process Regression" Remote Sensing 16, no. 14: 2622. https://doi.org/10.3390/rs16142622
APA StyleJang, E., Lee, S. J., & Jo, H. (2024). A New Multimodal Map Building Method Using Multiple Object Tracking and Gaussian Process Regression. Remote Sensing, 16(14), 2622. https://doi.org/10.3390/rs16142622







