SRBPSwin: Single-Image Super-Resolution for Remote Sensing Images Using a Global Residual Multi-Attention Hybrid Back-Projection Network Based on the Swin Transformer

Abstract

Remote sensing images usually contain abundant targets and complex information distributions. Consequently, networks are required to model both global and local information in the super-resolution (SR) reconstruction of remote sensing images. The existing SR reconstruction algorithms generally focus on only local or global features, neglecting effective feedback for reconstruction errors. Therefore, a Global Residual Multi-attention Fusion Back-projection Network (SRBPSwin) is introduced by combining the back-projection mechanism with the Swin Transformer. We incorporate a concatenated Channel and Spatial Attention Block (CSAB) into the Swin Transformer Block (STB) to design a Multi-attention Hybrid Swin Transformer Block (MAHSTB). SRBPSwin develops dense back-projection units to provide bidirectional feedback for reconstruction errors, enhancing the network’s feature extraction capabilities and improving reconstruction performance. SRBPSwin consists of the following four main stages: shallow feature extraction, shallow feature refinement, dense back projection, and image reconstruction. Firstly, for the input low-resolution (LR) image, shallow features are extracted and refined through the shallow feature extraction and shallow feature refinement stages. Secondly, multiple up-projection and down-projection units are designed to alternately process features between high-resolution (HR) and LR spaces, obtaining more accurate and detailed feature representations. Finally, global residual connections are utilized to transfer shallow features during the image reconstruction stage. We propose a perceptual loss function based on the Swin Transformer to enhance the detail of the reconstructed image. Extensive experiments demonstrate the significant reconstruction advantages of SRBPSwin in quantitative evaluation and visual quality.

1. Introduction

Remote sensing technology is a comprehensive method for large-scale Earth observation at the present stage, with wide-ranging applications in various fields, such as military, civilian, and agricultural ones [1]. Remote sensing images, as the data bases for the analysis and application of remote sensing technology, play essential roles in the direction of remote sensing target detection [2], scene recognition [3], target segmentation [4], change detection [5], and other directions. The quality of remote sensing images directly influences analysis outcomes, wherein spatial resolution is a critical parameter for assessing image quality. HR images offer greater clarity and contain richer high-frequency textural information, thereby enhancing the utilization value of HR remote sensing images. However, in reality, satellites are affected by the imaging environment and sensors, resulting in the LR remote sensing images generally acquired [6,7]. In response to the aforementioned practical problem, the most straightforward approach is to upgrade the hardware parameters of the satellite sensor. Nevertheless, this solution is complex and costly. Consequently, adopting software algorithms for post-processing, especially single-image super-resolution reconstruction (SISR) techniques, has emerged as a pragmatic and cost-effective means for reconstructing HR remote sensing images from LR remote sensing images.

SISR is a low-level computer vision task that aims to reconstruct an HR image containing more high-frequency information by utilizing limited information from a single LR image [8]. The popularity of this research direction is attributed to the valuable role played by the resulting HR images in various high-level computer vision applications [9,10,11]. Numerous scholars have conducted extensive research in the field of SISR. Currently, SISR methodologies can be classified into the three following main categories: interpolation-based [12,13], reconstruction-based [14], and learning-based approaches [15,16].

In recent years, with the remarkable success of deep learning (DL) across various domains, it has also found applications in addressing SISR challenges. Since Dong et al. [17] pioneered the introduction of CNN methods to solve the SISR problem, they have far surpassed traditional methods in performance. CNN-based SISR methods have also emerged with various architectures, such as residual learning [18,19] and dense connections [20,21]. The SISR task aims to minimize the reconstruction error between SR images and HR images. Iterative back projection (IBP) [22] ensures the reconstruction quality of SR images by propagating bidirectional reconstruction errors between LR and HR domains. Haris et al. [23] designed the Deep Back-projection Network (DBPN) to implement the IBP process. The DBPN utilizes CNNs to construct iterative up-projection and down-projection units, realizing the back-projection mechanism for reconstruction error correction. Although the CNN-based methods mentioned above achieved remarkable results in reconstructing natural images, the limitations of convolutional kernels prevent CNNs from performing global modeling [24]. Recently, the Vision Transformer (ViT) [25] demonstrated remarkable performance in both high-level [26,27] and low-level vision tasks [28,29], owing to its global feature extraction capabilities. Notably, the emergence of the Swin Transformer [30] as a backbone further enhanced the performance of SISR algorithms [31,32]. However, feature extraction along the channel dimension does not receive the same attention, and local features are neglected, causing difficulty in recovering detail effectively. Furthermore, window-based multi-head self-attention (W-MSA) and shifted window-based multi-head self-attention (SW-MSA) methods are utilized to achieve global information interaction, resulting in substantial computational overhead during training. Consequently, an effective and computationally considered method is expected to be developed for further performance optimization.

Unlike natural images, remote sensing images possess the characteristics of complex spatial structure distribution, multiple targets, and a variety of target scales and shapes. Their complexity poses significant challenges for the SR reconstruction of remote sensing images. Therefore, it is essential that the network not only focuses on global information to ensure consistency in spatial structure distribution, but also captures local details. These two aspects are crucial for restoring the integrity of target forms and shapes across different scales.

Focusing on the above issues, we propose a back-projection network based on the Swin Transformer—SRBPSwin—for adapting the characteristics of remote sensing images and enhancing the performance of SR reconstruction. Unlike the DBPN, which uses CNNs to build projection units, a Multi-attention Hybrid Swin Transformer Block (MAHSTB) is designed to build dense up-projection and down-projection units, providing a back-projection mechanism for feature errors at different resolutions. The MAHSTB employs channel and spatial attention, enabling the STB to model both channel and local information simply yet effectively. Therefore, the images reconstructed by SRBPSwin maintain structural consistency between cross-scale targets, restore large-scale image textures, and reconstruct the details of targets and scenes. Crucially, by implementing back projection, the network more comprehensively exploits feature information across different resolutions, reducing the reconstruction error between SR and HR images. Furthermore, a perceptual loss function is developed, based on transformer feature extraction, to minimize feature-level discrepancies, achieving more accurate super-resolution results.

The main contributions of this article are summarized as follows.

(1) SRBPSwin Networks: We propose a Swin Transformer-based dense back-projection network for the SISR reconstruction of remote sensing images. The developed network provides closed-loop feedback for reconstruction errors across different resolution spaces, enabling the perception and extraction of authentic texture features.

(2) Multi-Attention Hybrid Swin Transformer Block (MAHSTB): To address the challenges in super-resolution (SR) reconstruction caused by the abundance and diverse shapes of targets in remote sensing images, we improve the Swin Transformer Block (STB) with Channel and Spatial Attention Blocks (CSABs). This enhancement allows for further refinement of texture features, while maintaining computational cost, to overcome the shortcomings of position insensitivity and ignoring channel and local features when using (S)W-MSA in STB.

(3) Perception Loss Strategy based on Swin Transformer Feature Extraction: Utilizing the superior feature extraction capabilities of the pre-trained Swin Transformer network, we design an improved perceptual loss function. It effectively constrains the training process from the perspective of feature maps and significatively improves the quality of the reconstructed images.

(4) We conduct extensive experiments on various classes from the NWPU-RESISC45 dataset. The obtained experimental results confirm the effectiveness of the proposed method.

The remaining sections of this paper are organized as follows: Section 2 provides a concise overview of related work. Section 3 offers a detailed explanation of the proposed methodology. Section 4 presents experimental results on the NWPU-RESISC45 dataset. A discussion of the experimental results is presented in Section 5. The conclusions and perspectives for future work are provided in Section 6.

2. Related Work

2.1. Back Projection Based on CNNs

SR reconstruction is generally described as an iterative reduction in errors between SR and HR images. Back projection, as described in [22], is an effective method for minimizing reconstruction errors by providing feedback for the reconstruction errors. Haris et al. [23] pioneered the design of the DBPN model, combining back projection with CNNs. By utilizing multiple interconnected up-sample and down-sample layers, the method allows the for alternation of feature maps between HR and LR states. This approach provides a feedback mechanism for projection errors at different resolutions, resulting in superior reconstruction performance.

Building upon DBPN, Liu et al. subsequently designed two additional models: the Back-projection and Residual Network (BPRN) [33] and Attention-based Back-projection Network (ABPN) [34]. The BPRN model enhances the learning of HR features by incorporating convolutions that connect the up-sample features from the DBPN in the form of residual connections to the end. This enhancement enables the network to capture HR characteristics better, ultimately improving the quality of the reconstructed images. On the other hand, the ABPN is based on the BPRN, introducing residual connections in both the up-sample and down-sample layers. Additionally, the ABPN model integrates spatial attention modules after each down-sample layer, enhancing the effectiveness of LR feature propagation to the subsequent up-sample stage.

Although the aforementioned CNN-based back-projection SISR methods have demonstrated promising performance on natural images, the pixel information and structure of remote sensing images are more intricate than natural images. Therefore, the error feedback mechanism provided by back projection can effectively enhance the quality of reconstructed remote sensing images. However, due to the limitations of convolutional kernels, these methods may encounter challenges in capturing global information, thus impacting the quality of the reconstruction results. Consequently, it is imperative to design an SR method based on back projection for remote sensing images. This method should fully utilize pixel and structural information to effectively model global information in remote sensing images.

2.2. Vision Transformer-Based Models

With the remarkable success of transformers in natural language processing [35], they have naturally garnered attention in computer vision. In classic computer vision tasks, such as object detection [27,36], image classification [26,30], and image segmentation [28], methods based on the ViT [26] have achieved performance superiority beyond traditional CNNs in capturing global information and modeling long-range dependencies. In low-level visual tasks, such as image restoration, in order to obtain better visual representation capabilities for ViT, several studies [28,29,37,38,39,40,41] have demonstrated that introducing convolutional operations within the ViT framework can enhance its visual representation capabilities. The emergence of the Swin Transformer [30] has elevated the vast potential of the transformer in computer vision. The Swin Transformer enhances feature extraction in the ViT by utilizing a shift-window mechanism to model distant dependencies. Consequently, Swin Transformer-based methods have promoted development in SISR. Inspired by earlier work in image restoration, Liang et al. [31] utilized the Swin Transformer as a backbone network and incorporated convolutional layers for shallow feature extraction. They introduced SwinIR for SISR, achieving performance surpassing the CNN-based SISR algorithms. Building upon SwinIR, Chen et al. [32] proposed channel attention mechanisms within the Swin Transformer Block by utilizing pixel performance. They also introduced overlapping cross-attention modules to enhance feature interactions between adjacent windows, effectively aggregating cross-window information and achieving superior reconstruction performance compared to SwinIR.

Although STB promotes the extraction of global spatial features, the extraction of channel-wise features needs equal attention. Additionally, the (S)W-MSA can cause insensitivity to pixel positions and neglect local feature details. Consequently, its performance can be further improved.

2.3. Deep Learning-Based SISR for Remote Sensing Images

In remote sensing, HR images are expected to be obtained, leading to the extensive application of SISR. The development of SISR in remote sensing parallels the trends observed in natural image SISR. With rapid advancements in DL, the utilization of CNNs for remote sensing image SR reconstruction has demonstrated performance far surpassing traditional algorithms. This approach has become mainstream in remote sensing image SR reconstruction algorithms.

Lei et al. [42] first introduced a CNN called the Local–Global Combination Network (LGCNet) for remote sensing image super-resolution reconstruction. Liu et al. [43] introduced the saliency-guided remote sensing image super-resolution, which utilizes saliency maps to guide the network in learning more high-resolution saliency maps and provide additional structural priors. Huang et al. [44] proposed the Pyramid Information Distillation Attention Network (PIDAN), which employs the Pyramid Information Distillation Attention Block (PIDAB) to enable the network to perceive a wider range of hierarchical features and further improve the recovery ability of high-frequency information. Zhao et al. [45] proposed the second-order attention generator adversarial attention network (SA-GAN), which leverages a second-order channel attention mechanism in the generator to fully utilize the prior information in LR images. Chen et al. [46] presented the Residual Split-attention Network (RSAN), which utilizes the multipath Residual Split-attention (RSA) mechanism to fuse different channel dimensions to promote feature extraction and ensure that the network focuses more on regions with rich details. Wang et al. [47] proposed the Multiscale Enhancement Network (MEN), incorporating a Multiscale Enhancement Module (MEM), which utilizes a parallel combination of convolutional layers comprising kernels of varying sizes to refine the extraction of multiscale features, thereby enhancing the network’s reconstruction capabilities. Zhang et al. [48] introduced the Dual-resolution Connected Attention Network (DRCAN), which constructs parallel branches—an LR branch and an HR branch—to integrate features at different spatial resolutions in order to enhance the details of reconstructed images. In response to the complex structure, large variation in target scale, and high pixel similarity of remote sensing images, the above-mentioned methods, although utilizing techniques like residual learning and channel attention to enhance the global modeling capacity of CNNs, still fail to effectively overcome the limitations of local feature extraction by convolutional kernels. Therefore, the design of a more effective SISR method for adaptation to remote sensing images remains crucial.

To address the limitations of CNNs in remote sensing image super-resolution reconstruction, we propose SRBPSwin, a super-resolution reconstruction algorithm based on the Swin Transformer. SRBPSwin effectively perceives global image features and employs up-projection and down-projection layers to transmit reconstruction errors. Additionally, it introduces a CSAB to mitigate the inability of the STB to capture both channel-wise and local features. The SRBPSwin can better utilize remote sensing image features, ultimately improving the quality of the SR reconstruction.

3. Methodology

In this section, firstly, we begin by presenting the overall framework of SRBPSwin. Secondly, we introduce the MAHSTB and the Dense Back-projection Unit. Finally, we introduce the loss function utilized for training.

3.1. Network Architecture

As illustrated in Figure 1, the proposed SRBPSwin consists of the four following stages: shallow feature extraction, shallow feature refinement, dense back-projection, and image reconstruction. The stages of shallow feature refinement and dense back projection comprise multiple MAHSTBGs (MAHSTB cascade post-processing modules). These post-processing modules include Patch Fixing, Patch Expanding, and Patch Shrinking. The architecture of incorporating convolutional layers before and after the Swin Transformer results in a better visual representation [31,32,37,38,39].

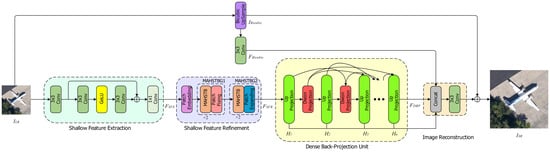
Figure 1. The overall architecture of SRBPSwin. $\oplus$ indicates the element-wise sum.

The shallow feature extraction stage comprises a $3\times 3$ convolutional layer, a residual block, and a $1\times 1$ convolutional layer. Given an input LR image $I_{LR}\in R^{H\times W\times C_{in}}$ (where $H$, $W$, and $C_{in}$ are the height, width, and number of input channels of the LR image, respectively), the shallow feature extraction stage produces feature maps $F_{SFE}\in R^{H\times W\times C}$ ($C$ represents feature channels). The shallow feature refinement stage comprises a Patch Embedding layer and two MAHSTBGs. The Patch Embedding layer partitions the input LR image into non-overlapping $4\times 4$ patches, reducing the dimensions of the feature maps by a factor of 4. MAHSTBG1 employs the Patch Fixing operation to maintain the feature maps’ dimensions and the number of feature channels. To prevent the reduction in feature map size caused by Patch Embedding from hindering feature extraction in deeper network layers, the Patch Expanding operation is utilized to up-sample and restore the feature maps to their original dimensions, thereby obtaining the refined shallow feature $F_{SFR}\in R^{H\times W\times 2C}$. The core of SRBPSwin is the Dense Back-projection Unit, composed of a series of Up-projection Swin Units and Down-projection Swin Units. It extracts back-projection features and transfers reconstruction errors; the obtained dense back-projection feature is $F_{DBP}\in R^{rH\times rW\times 2C}$ ($r$ is the scale factor). For the reconstruction stage, $I_{LR}$ obtains $I_{Bicubic}\in R^{rH\times rW\times C}$ through bicubic up-sampling. Then, a $3\times 3$ convolutional layer is applied to generate $F_{Bicubic}\in R^{rH\times rW\times 2C}$. The high-resolution features $[H_1,H_2,\dots H_n]$ obtained from the $n$ Up-projection Units are concatenated with $F_{Bicubic}$ and $F_{DBP}$. The concatenated features are processed through another $3\times 3$ convolutional layer and then added to $I_{Bicubic}$, resulting in an SR image $I_{SR}\in R^{rH\times rW\times C_{in}}$.

3.2. Multi-Attention Hybrid Swin Transformer Block (MAHSTB)

The structure of MAHSTB is illustrated in Figure 2. The CSAB is inserted in the STB parallel to W-MSA and SW-MSA. We multiply the output of the CSAB by a small constant to prevent conflicts between CSAM and (S)W-MSA during feature representation and optimization. Hence, for a given input feature $F_{in}$, the resulting output feature $F_{out}$, obtained through MAHSTB, is represented as follows:

$$\begin{array}{rr}{F}_{(S)W\text{-}MSA }=& H_{(S)W\text{-}MSA}(H_{LN}(F_{in}))+\alpha H_{CSAB}(F_{in})+F_{in}\hfill \\ F_{out }=& H_{MLP}(H_{LN}(F_{(S)W\text{-}MSA }))+F_{(S)W\text{-}MSA }\hfill \end{array}$$

(1)

where $F_{(S)W\text{-}MSA}$ are intermediate features and $H_{LN}$, $H_{CSAB}$, $H_{W\text{-}MSA}$, $H_{SW\text{-}MSA}$, and $H_{MLP}$ are LayerNorm, CSAB, W-MSA, SW-MSA, and Multi-layer Perceptron operations, respectively.

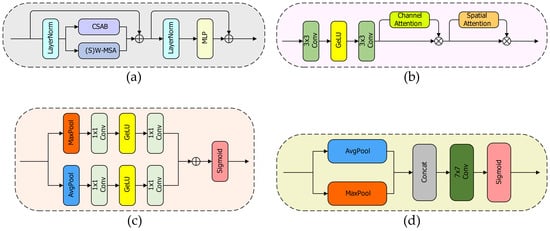
Figure 2. (a) Multi-attention Hybrid Swin Transformer Block (MAHSTB). (b) Channel- and Spatial-attention Block (CSAB). (c) Channel attention (CA) block. (d) Spatial attention (SA) block. $\oplus$ indicates the element-wise sum. $\otimes$ indicates the element-wise product.

For a given input feature of size $h\times w\times c$ (where $h$, $w$, $c$ are the height, width, and number of input channels of the input feature, respectively), the first step involves partitioning the input feature into $hw/M^2$ ($M$ represents the window size) non-overlapping local windows, each of size $M\times M$, to obtain local window features $F_W\in R^{M\times M\times c}$. Secondly, self-attention is computed within each window. $query$, $key$, and $value$ are linearly mapped to $Q$, $K$, and $V$, respectively. Ultimately, self-attention within each window is computed as follows:

$$\mathrm{Attention}(Q,K,V)=\mathrm{SoftMax}(Q{K}^T/\sqrt{d}+B)V$$

(2)

where $d$ is the dimension of $query/key$ and $B$ is the relative position encoding. In addition, as in [34], cross-window connections between adjacent non-overlapping windows are achieved by setting the shift size to half the window size during the shift window stage.

CSAB consists of two $3\times 3$ convolutional layers interconnected by a GELU activation. We controlled the number of channels in two convolutional layers through a compression constant $\beta$ to reduce computational cost [32]. Specifically, for input features with a number of channels $C$, the first convolutional layer reduces the number of channels to $C/\beta$, followed by GELU activation, and then the second convolutional layer restores the number of channels to $C$. Lastly, the method described in [49] is introduced to implement channel attention (CA) and spatial attention (SA) to improve the ability of STB to capture both channel and local features.

3.3. Dense Back-projection Unit (DBPU)

DBPU is constructed by the interleaved connection of $N$ Up-projection Swin Units and $N-1$ Down-projection Swin Units. The structures of the Up-projection Swin Unit (UPSU) and Down-projection Swin Unit (DPSU) are illustrated in the Figure 3. An UPSU consists of three MAHSTBG blocks. Specifically, Group-1 and Group-3 consist of two MAHSTBs and Patch Expanding, while Group-2 consists of two MAHSTBs and Patch Shrinking. The Patch Shrinking operation reduces the sizes of the input features without changing the number of feature channels. Group-1 and Group-3 achieve the up-sampling process, while Group-2 accomplishes the down-sampling process. The Up-projection process is represented as follows:

$$\begin{array}{ccc}\hfill {\widehat{L}}_{t-1}& =\hfill & H_{Concat}([L_1,\dots ,L_{t-1}])\hfill \\ \hfill H_t^0& =\hfill & H_{PE}(H_{MAHSTB2}(H_{MAHSTB1}({\widehat{L}}_{t-1})))\hfill \\ \hfill L_t^0& =\hfill & H_{PS}(H_{MAHSTB2}(H_{MAHSTB1}(H_t^0)))\hfill \\ \hfill e_t^l& =\hfill & L_t^0-{\widehat{L}}_{t-1}\hfill \\ \hfill H_t^1& =\hfill & H_{PE}(H_{MAHSTB2}(H_{MAHSTB1}(e_t^l)))\hfill \\ \hfill H_t& =\hfill & H_t^0+H_t^1\hfill \end{array}$$

(3)

where $H_{PE}$ and $H_{PS}$ represent the Patch Expanding and Patch Shrinking operations, respectively.

Figure 3. (a) Up-projection Swin Unit (UPSU). (b) Down-projection Swin Unit (DPSU). $\oplus$ indicates the element-wise sum. $\ominus$ indicates the element-wise difference.

The UPSU initially takes the LR feature maps, $[L_1,\dots ,L_{t-1}]$, generated by all previous DPSU outputs, and concatenates them to form ${\widehat{L}}_{t-1}$ as input, establishing a dense connection. These are mapped to the HR space, yielding $H_t^0$. Subsequently, $H_t^0$ is back projected to the LR space, generating $L_t^0$. By subtracting $L_t^0$ from ${\widehat{L}}_{t-1}$, the LR space back-projection error $e_t^l$ is obtained. Then, $e_t^l$ is mapped to the HR space as $H_t^1$. Finally, $H_t$ is obtained by summing $H_t^0$ and $H_t^1$, completing the UPSU operation.

The DPSU operation is similar to that of the UPSU. It aims to map input HR feature maps $[H_1,\dots ,H_t]$ to the LR feature map $L_t$. The process is illustrated as follows:

$$\begin{array}{ccc}\hfill {\widehat{H}}_t& =\hfill & H_{Concat}([H_1,\dots ,H_t])\hfill \\ \hfill L_t^0& =\hfill & H_{PS}(H_{MAHSTB2}(H_{MAHSTB1}({\widehat{H}}_t)))\hfill \\ \hfill H_t^0& =\hfill & H_{PE}(H_{MAHSTB2}(H_{MAHSTB1}(L_t^0)))\hfill \\ \hfill e_t^h& =\hfill & H_t^0-{\widehat{H}}_t\hfill \\ \hfill L_t^1& =\hfill & H_{PS}(H_{MAHSTB2}(H_{MAHSTB1}(e_t^h)))\hfill \\ \hfill L_t& =\hfill & L_t^0+L_t^1\hfill \end{array}$$

(4)

The UPSU and DPSU are alternately connected, enabling the feature maps to alternate between HR and LR spaces, providing a feedback mechanism for the projection error in each projection unit and achieving self-correction.

3.4. Loss Function

In order to enhance the textural details of SR images, the developed loss function consists of $L_1$, a norm loss, and a perceptual loss. Firstly, the fundamental $L_1$ norm loss is defined as follows:

$$L_1={‖I_{HR}-I_{SR}‖}_1$$

(5)

Inspired by [18,34], we utilize the Swin Transformer, pre-trained with ImageNet-22K weights, to construct the perceptual loss function.

$$L_{Swin}={‖\varphi (I_{HR})-\varphi (I_{SR})‖}_1$$

(6)

where $\varphi (\cdot )$ represents the feature maps obtained by the complete Swin-B network.

Finally, the optimization loss function for the entire network is defined as follows:

$$L=L_1+\gamma L_{Swin}$$

(7)

where $\gamma$ is a scalar to adjust the contribution of the perceptual loss.

4. Experimentation

4.1. Datasets

This study utilized the NWPU-RESISC45 [50] remote sensing dataset, comprising 45 classes of remote sensing scene data, with 700 images in each class, and resulting in a total of 31,500 RGB images at spatial resolutions ranging from 0.2 to 30 m, each sized 256 × 256 pixels. We randomly selected 100 images from each class as a training dataset, 10 as a validation dataset, and 10 as a testing dataset. Consequently, the final dataset consisted of 4500 images in the training dataset, 450 in the validation dataset, and 450 in the testing dataset. Meanwhile, to ensure the authenticity of the experimental results, there was no intersection among the training, validation, and testing datasets.

4.2. Experimental Settings

In this study, we focused on the 2$\times$ and 4$\times$ scale factors. LR images were obtained by down-sampling HR images using bicubic interpolation [51], considering the corresponding HR images as ground truth. Additionally, training images were augmented through random horizontal and vertical flips. The images were converted to the YCbCr color space, and training was performed on the Y channel [52]. The SR results were evaluated by calculating the peak signal-to-noise ratio (PSNR) [53] and structural similarity (SSIM) [54] on the Y channel.

We employed the Adam optimizer [55] for model training, with ${\beta }_1=0.9$ and ${\beta }_2=0.99$. The initial learning rate was set to 10⁻⁴, and there were 1000 total training epochs. For the 2$\times$ scale factor, the batch size was set to 2, and the number of feature channels C was set to 96. For the 4$\times$ scale factor, the batch size was set to 4, and the number of feature channels C was set to 48. The number of up-sample units N was set to 2. The proposed method was implemented utilizing the PyTorch framework version 1.11. All experiments were conducted on an NVIDIA GeForce RTX 3090 GPU.

4.3. Evaluation Index

Given a real HR image, the PSNR value of the SR reconstructed image is obtained as follows:

$$MSE(x,y)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{(x_i-y_i)}^2}$$

(8)

$$PSNR(x,y)=10{\log }_{10}\frac{{255}^2}{MSE(x,y)}$$

(9)

where $x_i$ and $y_i$ represent the values of the $i$-th pixel in $x$ and $y$, respectively, and $n$ represents the number of pixels in the image. A higher PSNR value indicates better image quality for the reconstructed image. The SSIM calculation formula is described as follows:

$$SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}$$

(10)

where ${\mu }_x$, ${\mu }_y$, ${\sigma }_x$, ${\sigma }_y$, ${\sigma }_{xy}$ are the mean, standard deviation, and covariance of $x$ and $y$, respectively, while $C_1$ and $C_2$ are constants.

4.4. Ablation Studies

We designed two sets of ablation experiments on the NWPU-RESISC45 dataset, with a scale factor of 2$\times$, to verify the effectiveness of the MAHSTB and perceptual Swin loss.

The first set of ablation experiments consisted of three models: Base, Base + CAB, and Base + CSAB(MAHSTB). The Base model is a basic network under only STB. The Base + CAB model replaces CSAB of MAHSTB with CAB. Figure 4 shows the PSNR results of the three models on the validation dataset, showing that the curve of the proposed Base + CSAB model is significantly higher than those of the Base and Base + CAB models. Table 1 presents the quantitative results of experiment 1 on the test dataset, indicating that Base + CSAB achieves the best SR performance. Compared to Base, Base + CAB improves the PSNR by 0.866 dB, indicating that introducing channel attention in parallel at the (S)W-MSA position in the STB enhances the network’s feature representation capability. Furthermore, Base + CSAB increases PSNR by 0.866 dB and 1.165 dB, respectively, compared to Base and Base + CAB. This shows that adding SA after CAB to form CSAB offers a more effective visual representation enhancement in the STB than using CAB only.

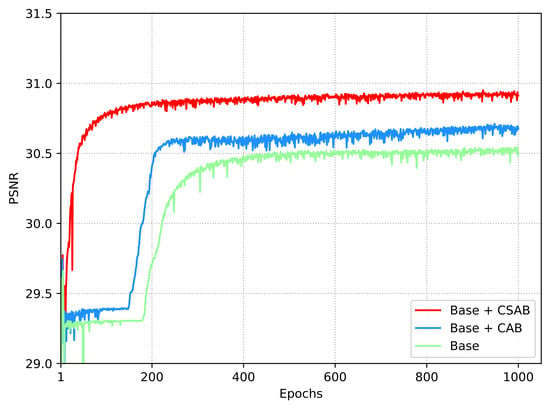
Figure 4. PSNR curves of our method, based on using CSAB or not. Base refers to the network that uses only STB, while Base + CSAB denotes MAHSTB. The results are compared on the validation dataset with a scale factor of 2$\times$ during the overall training phase.

Table 1. Ablation studies to verify the effectiveness of CSAB with a scale factor of 2$\times$ on the testing dataset. Base refers to the network that uses only STB, while Base + CSAB denotes MAHSTB. Red represents the best score.

Component	SRBPSwin
Base	√	√	√
CAB	-	√	-
CSAB	-	-	√
PSNR	32.113	32.412	33.278
SSIM	0.906	0.912	0.924

Figure 5 illustrates the qualitative results of image reconstruction by Base, Base + CAB, and Base + CSAB. For better comparison, we marked the area to be enlarged on the left side of the HR image with a red box and provided local close-ups of the reconstructed area under different methods on the right side. It is observed that Base + CSAB achieves the best visual performance. In “airport_296” and “industrial_area_694”, the reconstructed images show clearer details and sharper edges for the runway ground markings and industrial buildings. In “harbor_368”, the network-reconstructed ship details are more abundant. For “runway_045”, the image texture is more naturally reconstructed by the network. These qualitative results demonstrate that the multi-attention hybrid approach achieved by Base + CSAB enables the STB to utilize the self-attention mechanism for global feature modeling, while also capturing channel and local features, thereby enhancing the quality of the reconstructed images.

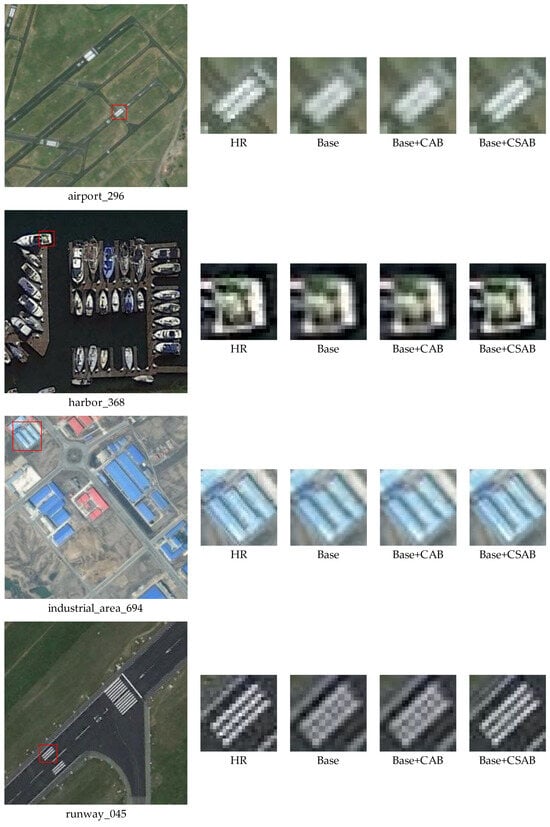
Figure 5. Visual comparison of ablation study to verify the effectiveness of MAHSTB; Base refers to the network that uses only STB, while Base + CSAB denotes MAHSTB. We used a red box to mark the area for enlargement on the left HR image. On the right, we present the corresponding HR image and the results reconstructed by the different methods.

The second set of experiments involved training SRBPSwin using the loss function $L_1$ alone, and a composite loss function $L_1+\gamma L_{Swin}$ ($\gamma =0.1$). Figure 6 shows the results of the second set of experiments on the validation dataset. It can be observed that the PSNR curve under $L_1+\gamma L_{Swin}$ is higher than that under $L_1$. Additionally, Table 2 presents the results of the testing dataset. SRBPSwin trained with $L_1$ achieves a PSNR of 32.917 dB, and SRBPSwin trained with $L_1+\gamma L_{Swin}$ achieves a PSNR of 33.278 dB, showing an improvement of 0.361 dB. This suggests that constructing the perceptual Swin loss function enhances the texture and details in the reconstructed images, utilizing the Swin Transformer with pre-trained weights from ImageNet-22K.

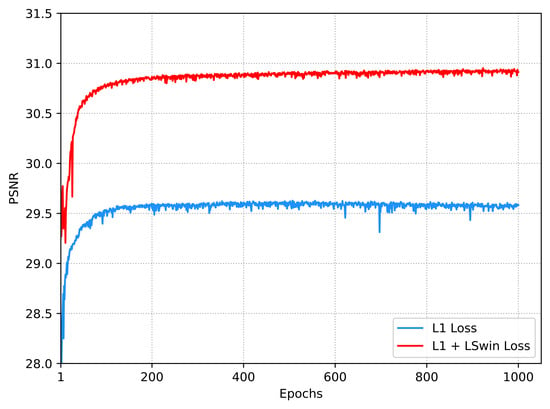
Figure 6. PSNR curves of our method, based on using $L_{Swin}$ or not. The results are compared on the validation dataset with a scale factor of 2$\times$ during the overall training phase.

Table 2. Ablation studies to verify the effectiveness of $L_{Swin}$ with a scale factor of 2× on the testing dataset. Red represents the best score.

Loss Function	SRBPSwin
L1	√	√
LSwin	-	√
PSNR	32.917	33.278
SSIM	0.921	0.924

Figure 7 shows the qualitative results of the $L_1$ loss function and the composite loss function. It indicates that the composite loss function $L_1+\gamma L_{Swin}$ achieves the best visual outcomes. Training the network with $L_1+\gamma L_{Swin}$ yields clearer edges for the airplane target in “airplane_170”. In “church_183”, the network recovers abundant details for the textural features of the building. For “railway_station_505”, the reconstructed station texture appears more refined. In “tennis_court_468”, the restored court looks more natural. These qualitative results validate that $L_{Swin}$ effectively reduces the feature distance and enhances the SR reconstruction capability of the network.

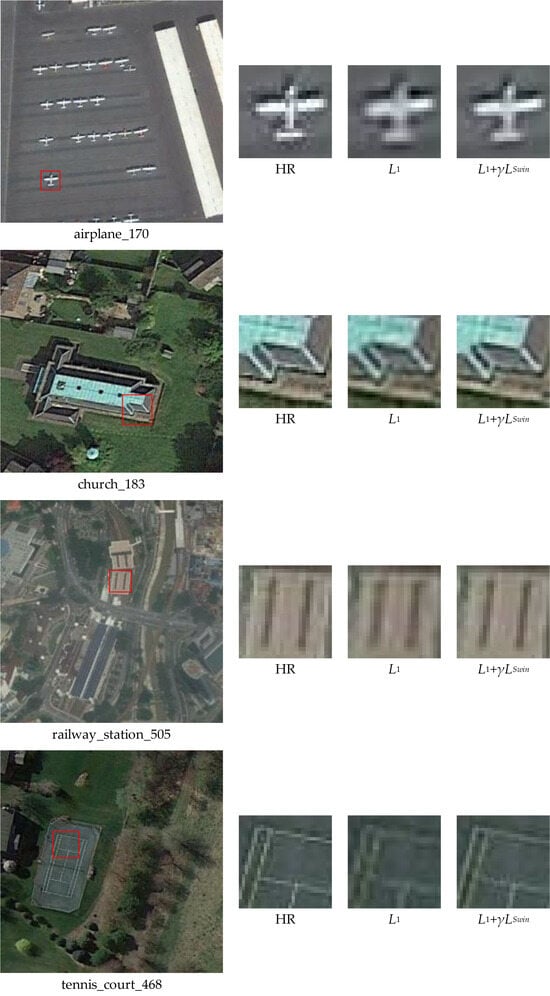
Figure 7. Visual comparison of ablation study to verify the effectiveness of $L_{Swin}$. We used a red box to mark the area for enlargement on the left HR image. On the right, we present the corresponding HR image and the results reconstructed using the different loss functions.

4.5. Comparison with Other CNN-Based Methods

We further compare our method with several open-source SR methods, including the SRCNN [17], VDSR [56], SRRESNet [18], EDSR [19], DBPN [23], LGCNET [42] models. All of these methods were trained and tested under the same conditions for a fair comparison.

Figure 8 and Figure 9 illustrate the quantitative comparison results of the PSNR curves on the validation dataset for the above methods at 2$\times$ and 4$\times$ scale factors. It can be observed that, at the 2$\times$ scale factor, the proposed SRBPSwin starts to surpass other methods in PSNR after the 400th epoch. Similarly, at the 4$\times$ scale factor, SRBPSwin begins to outperform in PSNR after the 500th epoch.

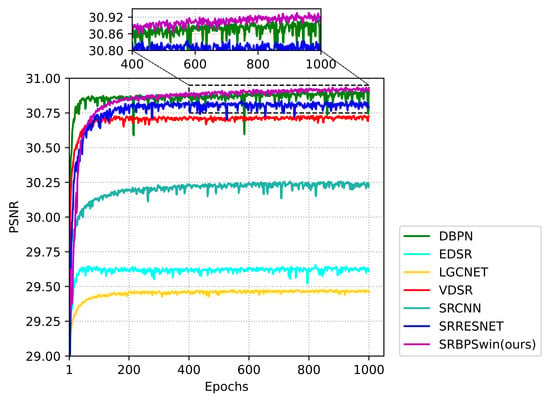
Figure 8. PSNR comparison for different methods on the validation dataset with a scale factor of 2$\times$ during the training phase.

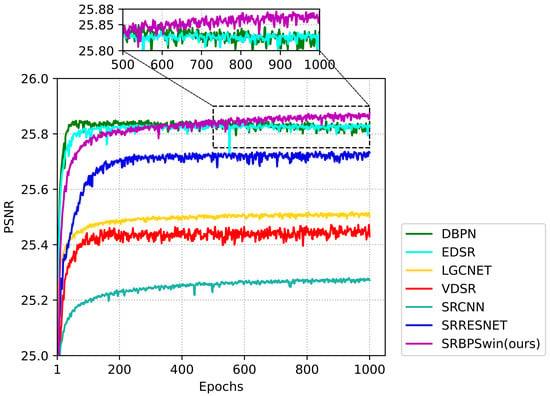
Figure 9. PSNR comparison for different methods on the validation dataset with a scale factor of 4$\times$ during the training phase.

Table 3 and Table 4 present the average quantitative evaluation results at the 2$\times$ and 4$\times$ scales on the 45 classes of testing datasets for all of the methods above. In these tables, PSNR and SSIM scores ranking first in each class are highlighted in red, while scores ranking second are highlighted in blue. If a method achieves the top ranking in both the PSNR and SSIM scores for a given class, it is considered as having the best reconstruction performance.

Table 3. Mean PSNR (dB) and SSIM values of each class of our NWPU-RESISC45 testing dataset for each method. The results are evaluated on a scale factor of 2$\times$. The best result is highlighted in red, while the second is highlighted in blue.

NWPU-RESISC45	SRCNN	VDSR	SRRESNET	LGCNET	EDSR	DBPN	Ours
	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM
airplane	34.551/0.947	35.317/0.954	35.378/0.955	35.231/0.953	35.474/0.955	35.578/0.956	35.733/0.958
airport	32.667/0.923	33.188/0.929	33.244/0.930	33.087/0.928	33.291/0.930	33.335/0.930	33.440/0.933
baseball_diamond	33.375/0.920	33.823/0.927	33.898/0.928	33.763/0.926	33.929/0.928	33.971/0.928	34.101/0.932
basketball_court	32.084/0.901	32.876/0.913	32.978/0.915	32.727/0.911	33.012/0.915	33.050/0.916	33.112/0.918
beach	31.913/0.892	32.128/0.895	32.160/0.896	32.107/0.896	32.161/0.896	32.178/0.896	32.274/0.899
bridge	34.045/0.946	34.526/0.951	34.622/0.951	34.462/0.950	34.646/0.951	34.721/0.952	34.796/0.954
chaparral	28.308/0.863	28.536/0.870	28.579/0.871	28.513/0.870	28.594/0.871	28.618/0.872	28.711/0.875
church	29.208/0.877	29.673/0.889	29.744/0.890	29.588/0.887	29.778/0.890	29.823/0.891	29.932/0.893
circular_farmland	36.060/0.952	37.058/0.958	37.088/0.958	36.886/0.957	37.162/0.958	37.206/0.959	37.477/0.962
cloud	40.355/0.965	40.665/0.967	40.533/0.967	40.584/0.967	40.699/0.967	40.724/0.967	41.107/0.970
commercial_area	30.821/0.921	31.237/0.927	31.302/0.928	31.175/0.926	31.348/0.928	31.383/0.929	31.465/0.930
dense_residential	26.665/0.871	27.158/0.884	27.288/0.886	27.138/0.883	27.278/0.886	27.349/0.887	27.376/0.888
desert	37.156/0.949	37.652/0.952	37.583/0.953	37.535/0.952	37.692/0.953	37.675/0.953	38.073/0.956
forest	32.015/0.886	32.115/0.889	32.168/0.889	32.117/0.889	32.177/0.889	32.192/0.889	32.299/0.893
freeway	32.925/0.907	33.514/0.917	33.583/0.918	33.408/0.915	33.638/0.918	33.684/0.919	33.818/0.921
golf_course	35.689/0.943	36.003/0.945	36.056/0.946	35.979/0.945	36.069/0.946	36.099/0.946	36.249/0.949
ground_track_field	30.928/0.912	31.334/0.919	31.422/0.921	31.305/0.919	31.430/0.920	31.474/0.921	31.521/0.923
harbor	26.480/0.914	26.946/0.922	27.124/0.925	26.983/0.923	27.148/0.925	27.240/0.927	27.175/0.927
industrial_area	30.586/0.912	31.317/0.922	31.376/0.923	31.158/0.921	31.442/0.923	31.515/0.924	31.575/0.926
intersection	29.510/0.896	30.168/0.909	30.357/0.911	30.101/0.908	30.415/0.911	30.490/0.912	30.532/0.915
island	40.677/0.976	41.160/0.978	41.184/0.978	41.070/0.978	41.230/0.978	41.252/0.978	41.614/0.980
lake	34.128/0.924	34.363/0.927	34.401/0.928	34.335/0.927	34.396/0.927	34.410/0.928	34.565/0.931
meadow	37.087/0.919	37.247/0.922	37.299/0.923	37.240/0.922	37.306/0.922	37.320/0.923	37.556/0.927
medium_residential	31.060/0.886	31.369/0.892	31.442/0.893	31.359/0.892	31.458/0.893	31.495/0.893	31.552/0.895
mobile_home_park	28.642/0.877	29.284/0.890	29.422/0.892	29.232/0.889	29.437/0.892	29.510/0.893	29.578/0.895
mountain	35.091/0.931	35.329/0.934	35.351/0.934	35.295/0.932	35.366/0.934	35.371/0.934	35.547/0.937
overpass	30.434/0.893	31.485/0.909	31.616/0.911	31.286/0.906	31.704/0.912	31.757/0.913	31.696/0.914
palace	31.937/0.913	32.404/0.920	32.472/0.921	32.363/0.919	32.485/0.921	32.537/0.921	32.701/0.924
parking_lot	26.923/0.853	27.598/0.870	27.809/0.872	27.528/0.868	27.810/0.872	27.958/0.875	27.925/0.878
railway	29.275/0.857	29.738/0.872	29.799/0.872	29.646/0.868	29.847/0.874	29.889/0.875	29.913/0.877
railway_station	32.288/0.915	32.845/0.923	32.911/0.924	32.725/0.922	32.963/0.924	33.007/0.925	33.167/0.929
rectangular_farmland	34.705/0.893	35.405/0.898	35.474/0.898	35.275/0.899	35.502/0.898	35.546/0.900	35.730/0.900
river	34.817/0.931	35.198/0.936	35.229/0.937	35.115/0.935	35.220/0.936	35.249/0.936	35.408/0.939
roundabout	30.711/0.891	31.176/0.900	31.251/0.902	31.108/0.899	31.295/0.902	31.327/0.902	31.491/0.905
runway	37.137/0.959	38.456/0.965	38.287/0.965	38.113/0.964	38.576/0.966	38.732/0.967	38.874/0.969
sea_ice	35.153/0.952	35.547/0.955	35.580/0.956	35.426/0.955	35.628/0.956	35.652/0.956	35.900/0.959
ship	32.067/0.911	32.559/0.918	32.606/0.919	32.463/0.917	32.666/0.919	32.704/0.920	32.738/0.922
snowberg	29.495/0.929	29.929/0.935	29.982/0.936	29.886/0.936	30.048/0.937	30.086/0.937	30.170/0.938
sparse_residential	30.908/0.871	31.229/0.877	31.357/0.878	31.197/0.876	31.353/0.878	31.366/0.879	31.418/0.881
stadium	32.357/0.933	33.009/0.942	33.044/0.942	32.864/0.940	33.112/0.943	33.148/0.943	33.274/0.945
storage_tank	28.752/0.884	29.301/0.897	29.387/0.898	29.244/0.896	29.404/0.899	29.466/0.899	29.479/0.901
tennis_court	29.521/0.873	29.994/0.886	30.093/0.887	29.958/0.884	30.105/0.887	30.159/0.888	30.193/0.891
terrace	35.043/0.927	35.567/0.936	35.624/0.937	35.457/0.934	35.642/0.937	35.685/0.937	35.865/0.940
thermal_power_station	32.606/0.928	33.171/0.936	33.218/0.936	33.077/0.934	33.274/0.937	33.307/0.937	33.424/0.940
wetland	36.409/0.941	36.671/0.945	36.703/0.944	36.638/0.944	36.715/0.944	36.753/0.944	36.957/0.948

Table 4. Mean PSNR (dB) and SSIM values of each class of our NWPU-RESISC45 testing dataset for each method. The results are evaluated on a scale factor of 4$\times$. The best result is highlighted in red, while the second is highlighted in blue.

NWPU-RESISC45	SRCNN	VDSR	SRRESNET	LGCNET	EDSR	DBPN	Ours
	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM
airplane	28.245/0.817	28.913/0.835	29.253/0.845	28.824/0.833	29.409/0.848	29.451/0.849	29.491/0.849
airport	27.109/0.740	27.479/0.756	27.738/0.765	27.414/0.753	27.780/0.768	27.838/0.769	27.919/0.770
baseball_diamond	28.656/0.767	28.896/0.777	29.107/0.784	28.890/0.776	29.158/0.787	29.176/0.787	29.120/0.787
basketball_court	26.973/0.712	27.379/0.732	27.656/0.743	27.329/0.729	27.755/0.748	27.812/0.749	27.832/0.749
beach	27.588/0.741	27.807/0.748	27.917/0.752	27.775/0.748	27.938/0.753	27.943/0.752	27.975/0.754
bridge	29.206/0.840	29.480/0.849	29.741/0.855	29.453/0.848	29.767/0.856	29.803/0.857	29.808/0.856
chaparral	23.808/0.635	24.001/0.645	24.188/0.655	24.023/0.646	24.226/0.658	24.247/0.660	24.315/0.661
church	24.187/0.668	24.403/0.680	24.617/0.692	24.407/0.680	24.683/0.697	24.717/0.699	24.732/0.698
circular_farmland	30.720/0.837	31.318/0.850	31.639/0.857	31.252/0.849	31.700/0.858	31.761/0.859	31.773/0.860
cloud	33.935/0.867	34.161/0.870	34.250/0.873	34.058/0.869	34.251/0.873	34.265/0.872	34.384/0.875
commercial_area	25.113/0.727	25.276/0.735	25.552/0.747	25.346/0.738	25.596/0.750	25.589/0.750	25.663/0.752
dense_residential	21.817/0.622	21.920/0.631	22.226/0.649	22.010/0.636	22.268/0.655	22.295/0.659	22.324/0.657
desert	30.579/0.786	31.041/0.797	31.079/0.802	30.913/0.795	31.136/0.803	31.145/0.801	31.341/0.807
forest	27.153/0.613	27.133/0.616	27.264/0.623	27.197/0.618	27.287/0.625	27.242/0.623	27.302/0.625
freeway	27.392/0.694	27.821/0.713	28.077/0.722	27.745/0.709	28.125/0.726	28.203/0.728	28.134/0.725
golf_course	30.122/0.814	30.484/0.822	30.728/0.827	30.520/0.823	30.782/0.829	30.789/0.829	30.826/0.830
ground_track_field	25.859/0.725	26.100/0.738	26.363/0.748	26.134/0.738	26.413/0.751	26.441/0.752	26.437/0.751
harbor	21.046/0.724	21.139/0.735	21.500/0.756	21.266/0.741	21.579/0.759	21.644/0.766	21.597/0.761
industrial_area	24.717/0.695	25.149/0.717	25.459/0.731	25.046/0.712	25.537/0.736	25.571/0.738	25.621/0.738
intersection	23.831/0.672	24.053/0.688	24.320/0.702	24.103/0.689	24.363/0.705	24.442/0.709	24.427/0.708
island	34.134/0.902	34.667/0.909	34.855/0.912	34.572/0.908	34.848/0.912	34.850/0.912	34.961/0.913
lake	28.635/0.731	28.722/0.735	28.850/0.740	28.747/0.736	28.875/0.742	28.852/0.741	28.904/0.742
meadow	32.405/0.774	32.517/0.778	32.617/0.780	32.517/0.778	32.623/0.781	32.647/0.781	32.640/0.781
medium_residential	25.956/0.668	26.150/0.676	26.321/0.685	26.165/0.678	26.405/0.688	26.416/0.689	26.427/0.688
mobile_home_park	23.623/0.654	23.844/0.665	24.193/0.681	23.954/0.670	24.251/0.686	24.305/0.689	24.320/0.686
mountain	29.597/0.754	29.708/0.759	29.823/0.763	29.723/0.759	29.831/0.764	29.803/0.762	29.887/0.767
overpass	25.497/0.677	26.001/0.703	26.330/0.718	25.876/0.696	26.455/0.724	26.628/0.728	26.434/0.722
palace	26.540/0.724	26.846/0.735	27.098/0.746	26.854/0.736	27.159/0.750	27.171/0.750	27.223/0.751
parking_lot	22.135/0.609	22.203/0.619	22.464/0.635	22.324/0.624	22.532/0.641	22.543/0.645	22.632/0.658
railway	25.116/0.632	25.294/0.646	25.470/0.656	25.284/0.643	25.527/0.660	25.575/0.663	25.555/0.661
railway_station	26.388/0.703	26.758/0.720	27.030/0.732	26.722/0.718	27.089/0.737	27.141/0.739	27.154/0.737
rectangular_farmland	29.607/0.753	30.095/0.771	30.367/0.781	29.970/0.768	30.403/0.783	30.448/0.784	30.512/0.785
river	29.628/0.765	29.834/0.774	29.995/0.780	29.813/0.773	30.035/0.782	30.008/0.781	30.079/0.783
roundabout	25.524/0.682	25.847/0.697	26.064/0.708	25.822/0.696	26.112/0.711	26.158/0.712	26.173/0.711
runway	30.652/0.840	31.547/0.859	31.872/0.867	31.321/0.855	31.890/0.868	32.117/0.871	32.218/0.872
sea_ice	28.266/0.788	28.458/0.794	28.713/0.802	28.473/0.796	28.718/0.803	28.735/0.804	28.855/0.808
ship	27.288/0.762	27.597/0.775	27.809/0.782	27.575/0.773	27.822/0.784	27.894/0.786	27.856/0.785
snowberg	23.271/0.732	23.491/0.741	23.697/0.754	23.526/0.746	23.756/0.756	23.754/0.757	23.864/0.760
sparse_residential	26.569/0.645	26.740/0.655	26.895/0.661	26.744/0.654	26.957/0.665	26.914/0.664	26.955/0.664
stadium	26.309/0.750	26.667/0.766	26.962/0.778	26.641/0.764	27.029/0.782	27.037/0.783	27.079/0.783
storage_tank	24.469/0.686	24.693/0.702	24.961/0.715	24.750/0.702	25.027/0.720	25.078/0.722	25.056/0.721
tennis_court	25.167/0.667	25.323/0.676	25.568/0.688	25.401/0.679	25.603/0.691	25.641/0.693	25.634/0.691
terrace	29.323/0.746	29.678/0.762	29.861/0.770	29.605/0.758	29.928/0.774	29.883/0.773	29.927/0.773
thermal_power_station	26.422/0.714	26.706/0.728	26.935/0.737	26.692/0.727	27.002/0.742	26.990/0.741	27.063/0.743
wetland	30.892/0.791	31.062/0.797	31.176/0.800	31.046/0.796	31.237/0.802	31.186/0.801	31.287/0.804

Obviously, at the 2$\times$ scale factor, our approach achieved the best PSNR/SSIM results in 42 out of the 45 classes, while the second-best DBPN attained the best PSNR/SSIM in only one class out of the remaining three. At the 4$\times$ scale factor, our method achieves the best PSNR/SSIM results in 26 classes, whereas the second-best DBPN achieves the best PSNR/SSIM results in only 10 out of the remaining 19 classes.

Table 5 presents the overall average quantitative evaluation results for each method on the testing dataset at the 2$\times$ and 4$\times$ scale factors, indicating the superiority of our SRBPSwin model over other methods.

Table 5. Performance comparison of different methods on our NWPU-RESISC45 testing dataset for scale factors of 2$\times$ and 4x. The best result is highlighted in red, while the second is highlighted in blue.

Method	Scale	NWPU-RESISC45
		PSNR/SSIM
SRCNN	×2	32.501/0.913
VDSR	×2	33.006/0.920
SRRESNET	×2	33.067/0.921
LGCNET	×2	32.928/0.919
EDSR	×2	33.109/0.921
DBPN	×2	33.155/0.922
Ours	×2	33.278/0.924
SRCNN	×4	27.144/0.730
VDSR	×4	27.431/0.742
SRRESNET	×4	27.658/0.751
LGCNET	×4	27.418/0.741
EDSR	×4	27.708/0.754
DBPN	×4	27.737/0.755
Ours	×4	27.773/0.755

Figure 10 and Figure 11 show several qualitative comparison results of the above methods. For better comparison, we marked the areas with significant differences after reconstruction utilizing different methods with red rectangles in the HR images. Additionally, localized close-ups of these regions, after reconstruction by each method, are provided on the right side.

Figure 10. Visual comparison of some representative SR methods and our model at the 2$\times$ scale factor.

Figure 11. Visual comparison of some representative SR methods and our model at the 4$\times$ scale factor.

Figure 10 presents the comparison results at the 2$\times$ scale factor. From the illustration, it is evident that the reconstruction results of SRBPSwin are the best compared to other methods. The proposed SRBPSwin yields abundant wing features in “airplane_311”. In “basketball_court_684”, more venue details have been reconstructed. In “church_305”, the reconstructed roof edges are clearer. In “thermal power station_141”, the signage on the chimney is reconstructed with more textures. Figure 11 presents the comparison results at the 4$\times$ scale factor. The illustration shows that the proposed SRBPSwin exhibits more distinct edges in the airport ground signage in “airport_031”. In “basketball_court134”, the reconstructed field lines are more precise. In “commercialid_area_199”, the reconstructed roof area features are more prominent. In “runway_199”, the correct runway markings are reconstructed.

5. Discussion

In this section, we will further discuss the impact of the proposed SRBPSwin.

(1)

Comparison with other methods: The experimental results in Section 4.5 demonstrate that the proposed SRBPSwin method achieves superior SR performance compared with the SRCNN, VDSR, SRRESNET, LGCNET, EDSR, and DBPN models. At a scale factor of 2$\times$, our method restored sharp edges and reconstructed rich details. At a scale factor of 4$\times$, the reconstructed images maintained their shapes in more naturally, without introducing redundant textures. It confirms that the back-projection mechanism in SRBPSwin effectively provides feedback for reconstruction errors, thereby enhancing the reconstruction performance of the proposed network.

(2)

The impacts of the multi-attention hybrid mechanism: Based on the quantitative results of ablation study 1 in Section 4.4, the introduction of CAB improved PSNR by 0.279 dB, compared with STB. After combining CSAB, the PSNR increased by 0.866 dB and 1.165 dB under CAB and STB, respectively, indicating that the multi-attention hybrid mechanism significantly enhanced the network’s SR performance. Additionally, it verifies that the fusion of CSAB improved the ability of both the capture channel and local features of STB. Qualitative results further demonstrate that utilizing CSAB reconstructed local fine textures accurately and achieved sharper edges.

(3)

The impacts of the perceptual loss strategy based on the Swin Transformer: Analysis of the quantitative results from ablation study 2 in Section 4.4 indicates that the $L_1+\gamma L_{Swin}$ loss led to a PSNR improvement of 0.361 dB, compared to the $L_1$ loss. This demonstrates that the $L_{Swin}$ perceptual loss strategy enhanced the reconstruction performance of the network at the feature map level. Qualitative results further show that images exhibit better detail recovery and appear more natural under the composite loss.

(4)

Limits of our method: Firstly, the STB in SRBPSwin incurs significant computational overhead when calculating self-attention, resulting in slower training speeds. Secondly, while the network does not introduce artifacts at large-scale factors, the reconstructed images tend to appear smooth.

6. Conclusions

This study introduces a Swin Transformer-based model, SRBPSwin, based on the Swin Transformer. The main contribution of this research is the design of the Multi-attention Hybrid Swin Transformer Block (MAHSTB) to improve the feature representation of the Swin Transformer Block for high-resolution reconstruction. Furthermore, the MAHSTB is employed to construct dense up-projection and down-projection units, providing a back-projection mechanism for feature errors at different resolutions. The presented method achieves more accurate SR results. Additionally, we incorporate a Swin Transformer with ImageNet-22K pre-trained weights as a perceptual loss function, developing our method to enhance the quality of reconstructed remote sensing images. Extensive experiments and ablation studies validate the effectiveness of our proposed method.

However, the computation of self-attention incurs significant computational overhead, leading to longer training times. Additionally, with increasing scale factor, the reconstructed images become smoother. In future work, we plan to further develop the network to become more lightweight, aiming to accelerate the training process and incorporate multiscale up-sample branches to extract features at various scales, thereby enhancing the network’s reconstruction capabilities.