Navigation Resource Allocation Algorithm for LEO Constellations Based on Dynamic Programming

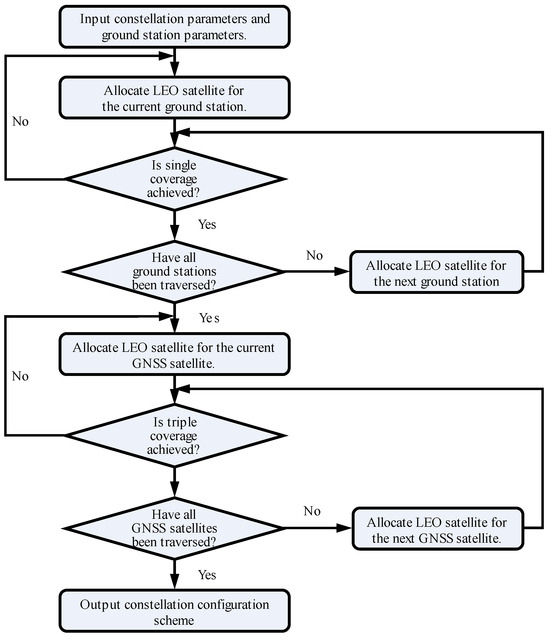
Abstract

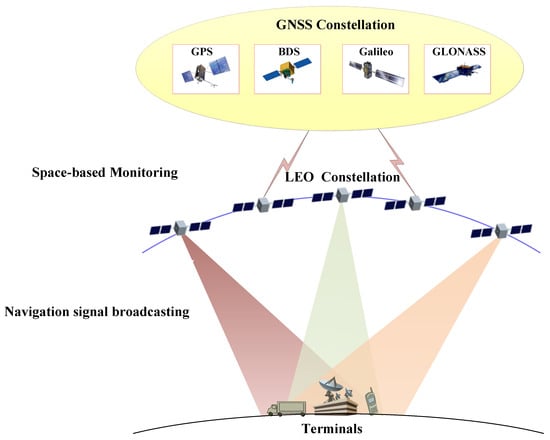
Navigation resource allocation for low-earth-orbit (LEO) constellations refers to the optimal allocation of navigational assets when the number and allocation of satellites in the LEO constellation have been determined. LEO constellations can not only transmit navigation enhancement signals but also enable space-based monitoring (SBM) for real-time assessment of GNSS signal quality. However, proximity in the frequencies of LEO navigation signals and SBM can lead to significant interference, necessitating isolated transmission and reception. This separation requires that SBM and navigation signal transmission be carried out by different satellites within the constellation, thus demanding a strategic allocation of satellite resources. Given the vast number of satellites and their rapid movement, the visibility among LEO, medium-earth-orbit (MEO), and geostationary orbit (GEO) satellites is highly dynamic, presenting substantial challenges in resource allocation due to the computational intensity involved. Therefore, this paper proposes an optimal allocation algorithm for LEO constellation navigation resources based on dynamic programming. In this algorithm, a network model for the allocation of navigation resources in LEO constellations is initially established. Under the constraints of visibility time windows and onboard transmission and reception isolation, the objective is set to minimize the number of LEO satellites used while achieving effective navigation signal transmission and SBM. The constraints of resource allocation and the mathematical expression of the optimization objective are derived. A dynamic programming approach is then employed to determine the optimal resource allocation scheme. Analytical results demonstrate that compared to Greedy and Divide-and-Conquer algorithms, this algorithm achieves the highest resource utilization rate and the lowest computational complexity, making it highly valuable for future resource allocation in LEO constellations.

1. Introduction

Recent advancements in Low-Earth-Orbit (LEO) constellations have significantly impacted satellite navigation systems due to their lower orbital altitude, which minimizes signal path attenuation and maximizes signal reception power [1]. Utilizing LEO constellations for navigation enhancement could substantially improve the performance of existing satellite navigation systems [2]. According to a survey of the current LEO constellations, building a LEO navigation enhancement system based on LEO global communication constellations is one of the mainstream solutions in the future, such as Iridium, SpaceX, OneWeb, and Hongyan [3]. Thus, optimizing the use of satellite resources in LEO constellations to enhance navigational capabilities while minimizing communication bandwidth usage becomes imperative. The primary problem addressed in this paper is the optimal allocation of navigation resources in LEO constellations. This involves strategically distributing satellite functions to maximize the efficiency of navigation enhancement functions while minimizing resource expenditure.

LEO navigation enhancement functions mainly include navigation signal transmission and space-based monitoring (SBM) [4,5,6]. Navigation signal transmission refers to LEO satellite transmission navigation enhancement signals to ground users to achieve information enhancement or signal enhancement of GNSS signals; SBM refers to configuring high-precision GNSS monitoring receivers on LEO satellites to receive downlink signals of GNSSs and analyze the quality of these signals.

Suppose the frequency band of SBM is consistent with or close to that of LEO navigation signals; the transmission power of LEO navigation signals is much higher than the receiving power of GNSS signals, which will cause strong interference to SBM. To solve this problem, transceiver isolation is usually used; that is, SBM or navigation signal enhancement functions are implemented on different LEO satellites. Therefore, satellite resources used for SBM need to be rationally allocated to maximize the need for SBM and navigation signal enhancement.

Since the GNSS system is a pure navigation system and does not have communication and SBM functions, it does not have the above problems. Therefore, the current research on the optimal allocation of satellite navigation resources mainly focuses on the allocation and scheduling of inter-satellite links. To improve the communication capabilities of inter-satellite links in navigation constellations, Chang [7] and Yan [8] took reducing call blocking probability and inter-satellite communication delay as optimization goals, respectively, and used the simulated annealing algorithm to solve the problems of discontinuous connections. GNSS satellite network link allocation problem; Werner [9] designed a topological inter-satellite link allocation algorithm for broadband LEO satellite systems, which prioritizes inter-satellite communication; Wu [10] used the mean-variance theory optimizes the network link capacity under random business conditions; Tan [11] and Yang [12] proposed a random link allocation scheme for satellite optical networks based on laser links, randomly generated an arbitrarily connected network topology; Sun [13] proposed an algorithm with a constant time interval for inter-satellite link topology transformation with the minimization of PDOP value as the optimization goal; Zhou [14], with link stability as a prerequisite, proposed an extensive weighted inter-satellite link allocation scheme that optimized both link latency and link switching performance. Liu [15,16], aiming to fully utilize the limited communication terminal resources on board the satellite, put forward a link allocation scheme based on the perfect matching model. This scheme transforms the link allocation into a perfect matching problem of a mixed complete bipartite graph. The inter-satellite link solution derived from this approach can be applied to all communication terminals on the satellite.

Inter-satellite links for navigation satellites need to take into account the dual requirements of communication and measurement. Shi [17,18] applied the Greedy Algorithm to the link allocation of inter-satellite communication and inter-satellite observation can ensure that the number of inter-satellite observations is maximized while reducing the communication cost of the entire network as much as possible; Wang [19] proposed a method based on the average of the entire network A link allocation algorithm weighted by the observation position accuracy factor and the entire network delay. The optimization goal of this algorithm is to minimize the link cost; Huang [20] proposed an inter-satellite link allocation suitable for GNSS satellite networks, a cascade optimization design method that takes into account both communication and ranging capabilities; Yang [21] proposed a group-based time slot scheduling method to obtain more ranging observation data and realize satellite and ranging Fast communication with a short delay between measurement and control stations. Lin [22], Zhu [23], and Sun [24] used genetic algorithms for inter-satellite communication and ranging link allocation in navigation constellations, which improved the operating efficiency of the algorithm to a certain extent but had shortcomings such as poor fault tolerance and slow convergence speed of the algorithm.

In summary, existing research on satellite navigation resource allocation solves the problem of link resource allocation between navigation satellites in the same orbit. The goal is to utilize all resources to maximize inter-satellite communication or ranging needs, and the navigation resource allocation in LEO constellations is to use as few resources as possible to maximize navigation enhancement capabilities among all resources, and the mission goals are different; secondly, because the number of satellites in previous navigation constellations is small, usually only dozens, and each satellite only needs to consider the link allocation between itself and surrounding satellites visible in a short period, and the calculation amount is generally not large. Future LEO satellite systems are usually mega-constellations composed of hundreds to thousands of satellites, and LEO satellites move extremely fast, resulting in complex and changeable visibility between LEO satellites and mid- and high-orbit satellites. Moreover, in order to achieve global optimization, it is necessary to consider the visibility of the LEO constellation period and the least common multiple of the GNSS constellation period, which may last for several months. Therefore, the computational complexity of the navigation resource allocation problem in the LEO constellation is extremely high.

At present, there is almost no research on the optimal allocation of navigation resources in LEO constellations. Based on the characteristics of the LEO navigation augmentation system, this paper proposes an optimal allocation algorithm for LEO constellation navigation resources based on dynamic programming.

The structure of this article is as follows: Section 2 establishes a network model for LEO constellation navigation resource allocation and gives the constraints and objective functions of resource allocation. Section 3 proposes a navigation resource allocation algorithm based on Dynamic Programming (NRAA-DP). Section 4 analyzes the performance of the algorithm through simulation, including resource utilization and computational complexity. Section 5 summarizes the work of this paper.

2. Model Analysis of LEO Constellation Navigation Resource Allocation

2.1. Network Model

The navigation resource allocation for the LEO constellation needs to consider two primary types of LEO navigation enhancement functions: navigation signal transmission and SBM. The system architecture is shown in Figure 1.

Figure 1. LEO constellation navigation enhanced function architecture diagram.

As depicted in Figure 1, individual LEO satellites are dedicated to a single function—either navigation signal transmission or SBM—but not both simultaneously. This segregation is essential because the power of navigation signals significantly exceeds that of the signals received for SBM. Consequently, if the frequencies of SBM and navigation signal transmission are similar or overlap, substantial interference ensues. To mitigate this, satellites are configured with transceiver isolation, whereby different satellites within the constellation are assigned to either navigation signal transmission or SBM. This ensures that each satellite is optimized for its specific function without cross-interference.

2.1.1. LEO Navigation Signal Transmission

LEO navigation signal transmission refers to the transmission of navigation enhancement signals by LEO satellites to ground users to achieve information enhancement or signal enhancement of GNSS signals. The optimization goal is to optimize global coverage performance. Specifically, it is to use the minimum number of LEO satellites to achieve uniform global coverage when the coverage requirements are determined.

In order to present the global coverage of the satellite navigation system more intuitively, the following takes the BDS navigation system as an example. As shown in Table 1, the BDS navigation system constellation consists of 3 GEO satellites, 3 IGSO satellites, and 24 GEO satellites.

Table 1. BDS navigation system constellation parameters.

Track Type	GEO	IGSO	MEO
Number of satellites	3	3	24
Constellation allocation	80°E, 110.5°E, 140°E	Evenly distributed at 118°E	Walker (24/3/1)
Orbital inclination	0°	55°	55°
Orbital height	35,789 km	35,786 km	21,528 km

The trajectory data of the BDS constellation in the simulation of this article are based on the two rows of orbital ephemeris data provided by Celestrak (http://celestrak.com/), accessed on 13 June 2023. The satellite position data are generated in the STK 11.6 software based on the ephemeris data at a 60 s sampling interval. Figure 2 is the generated three-dimensional spatial allocation diagram of the BDS constellation, and Figure 3 is the BDS sub-satellite point trajectory diagram. It is noteworthy that Figure 2 and Figure 3 are not from the same moment in time.

Figure 2. BDS constellation three-dimensional space allocation diagram. The red line represents the IGSO orbit, the green line represents the GEO orbit, and the blue line represents the MEO orbit.

Figure 3. BDS constellation subsatellite point trajectory chart.

The satellite cutoff altitude angle, set at 10°, refers to the minimum elevation angle at which a satellite can be considered visible. This angle is chosen to avoid signal obstructions near the horizon and ensure reliable communication. The ground latitude and longitude sampling interval to 5°. Through STK 11.6 software simulation, the BDS global average coverage multiplicity and GDOP value distribution are shown in Figure 4 and Figure 5, respectively [25], which show the global coverage of BDS lasting 48 h. Due to the existence of GEO and IGSO satellites, BDS has better coverage performance in the East Eighth District (near 120°E). Moreover, the higher the coverage multiplicity, the lower the GDOP value.

Figure 4. Global average coverage of BDS.

Figure 5. Global GDOP value distribution of BDS.

2.1.2. LEO Space-Based Monitoring

Currently, the four major global navigation satellite systems (GNSS), including GPS, GLONASS, GALILEO, and BDS, have been widely used. To provide better services, the four systems all use ground-based augmentation integrity monitoring (GAIM) [5] to monitor the integrity of GNSS navigation signals. In GAIM, there is a need to realize the dense distribution of ground systems around the world to ensure global integrity monitoring, which is very expensive and difficult to achieve. Therefore, the GNSSs also adopt satellite autonomous integrity monitoring (SAIM) [6]. However, since SAIM directly collects and detects radio frequency (RF) signals or intermediate frequency (IF) signals, it is impossible to evaluate the impact of antennas and wireless channels on navigation signals.

Hein proposed SBM at the Stanford Position Navigation and Timing (PNT) Conference in 2010 [4]. In SBM, after passing through the transmitting antenna and wireless channel, the GNSS signals are received by antennas of other satellites and analyzed by signal monitoring devices of other satellites. SBM greatly simplifies the traditional GAIM, breaks through geographical constraints, and can obtain a high signal-to-noise ratio (SNR). Therefore, SBM has great advantages in signal monitoring. Previously, due to the same orbital altitude of GNSS satellites, it was difficult for GNSS satellites to receive downlink navigation signals from other GNSS satellites. The emergence of the LEO navigation system makes SBM possible.

SBM in the LEO constellation can instantly monitor existing navigation signals. The optimization goal is to optimize the SBM coverage performance, specifically to use the least number of LEO satellites to achieve uniform coverage of the GNSS system under the condition that the multiple requirements for GNSS satellite coverage are determined. Multiple requirements for GNSS satellite coverage refer to the various performance metrics, such as coverage multiplicity and geometric dilution of precision (GDOP), that need to be met to ensure robust and reliable navigation services.

The condition that the navigation signals of GNSS satellites can be monitored by LEO satellites is that GNSS satellites are visible to LEO satellites. The spatial geometric position relationship between GNSS satellites and LEO satellites is crucial for determining visibility. This relationship is depicted in Figure 6, which shows how LEO satellites must have an unobstructed line of sight to GNSS satellites for effective monitoring. In the Figure, the GNSS satellite is visible to the LEO satellite L1, but the GNSS satellite and the LEO satellite L2 cannot send and receive signals due to the Earth’s obstruction, so there is no visibility between them.

Figure 6. GNSS satellites and LEO satellites.

In summary, the conditions for judging visible GNSS satellites from low-orbit satellites are as follows:

(1)

The line-of-sight vectors of low-orbit satellites and GNSS satellites are not blocked by the Earth;

(2)

The elevation angle of the receiving antenna of the low-orbit satellite is within the coverage range of the beam angle of the transmitting antenna of the GNSS satellite.

When the ephemeris and respective antenna elevation angle constraints of the low-orbit constellation and the GNSS constellation are known, the visual situation between the LEO constellation and the GNSS constellation can be calculated through STK 11.6 software simulation or through the analytical algorithm [26]. This analytical algorithm considers satellite ephemeris data and antenna elevation constraints, which can ensure accurate visibility predictions by accounting for the dynamic positions and orientations of both LEO and GNSS satellites. Since satellite motion is periodic and deterministic, the visibility of the GNSS constellation from the LEO constellation at each moment can be calculated in advance.

2.2. Constraints and Objective Functions

From the above analysis, it can be seen that the LEO constellation navigation enhancement system has both navigation signal transmission and SBM functions, and its resource allocation algorithm must comprehensively consider the navigation signal transmission and SBM performance.

For navigation signal transmission performance, the optimization goal is the global coverage of the constellation. First, you need to select the ground stations used for constellation coverage assessment. If there is $P$ a total ground station, the ground station can be expressed as $S{N}_r$, $r=1,2,\cdots ,P$. Suppose there are $N$ LEO satellites in a LEO constellation; then, the LEO satellite can be expressed as $S{L}_i$, $i=1,2,\cdots ,N$. If a LEO satellite $S{L}_i$ and a ground station are visible $S{N}_r$ at a certain moment $t$, then there is a visible link between them, defined as $V\left(t,S{L}_i,S{N}_r\right)$. Express the complete return period of a LEO constellation as $T_1$. When the satellite constellation is determined, its trajectory is periodic and fixed. Therefore, the visibility of ground stations to LEO satellites within the time period $T_1$ encompasses the visibility of ground stations to LEO satellites at any given time. All visible links between LEO satellites and ground stations within the time period $T_1$ constitute the visible link set of the navigation signal broadcasting network, defined as $V{S}_1$, and can be expressed as

$$V{S}_1={\left\{V_1(t,S{L}_i,S{N}_r)\right\}}_{t\in T_1,i\in [1,2,\cdots ,N],r\in [1,2,\cdots ,P]}$$

(1)

Some links are selected from the visible link set $V{S}_1$ as navigation signal transmission links. All links used for navigation signal broadcasting within the time period $T_1$ constitute the activated link set of the navigation signal broadcasting network, which is defined as $W{S}_1$, and can be expressed as

$$W{S}_1={\left\{V_2(t,S{L}_i,S{N}_r)\right\}}_{t\in T_1,i\in [1,2,\cdots ,N],r\in [1,2,\cdots ,P]}$$

(2)

The constraints of the navigation signal transmission network are as follows:

(1) The navigation signal transmission link must first be a visible link; that is, the activated link set of the navigation signal transmission network is a subset of the visible link set, expressed as

$$W{S}_1\subseteq V{S}_1$$

(3)

(2) The different requirements for navigation signal enhancement impose varying demands on global constellation coverage. For instance, achieving independent four-satellite positioning similar to the GNSS system requires global coverage of at least quadruple. Doppler positioning, similar to the Iridium system, only requires single global coverage. Joint positioning with GNSS satellite signals does not have explicit requirements for global coverage. To reduce computational complexity, this paper analyzes the constellation with the goal of achieving single global coverage as an example. In this condition, there is at least one navigation signal transmission link for any time $t$ and any ground station $S{N}_k$, which can be expressed as

$$\left|\left\{V(t_0,S{L}_{i_0},S{N}_{r_0})\right\}\right|\ge 1,V(t_0,S{L}_{i_0},S{N}_{r_0})\in W{S}_1,\forall r_0\in \left[1,2,\cdots ,P\right],\forall t_0\in T_1$$

(4)

where $\left|·\right|$ represents the number of elements in the set.

The set of LEO satellites $U{S}_1$ used for navigation signal transmission is expressed as

$$U{S}_1=\left\{S{L}_{i_0}\right\},i_0\in \left[1,2,\cdots ,N\right]$$

(5)

For SBM performance, the optimization goal is the coverage of GNSS constellations. Assuming that there are $M$ GNSS satellites, then the GNSS satellites can be expressed as $S{G}_j$, $j=1,2,\cdots ,M$. If a LEO satellite $S{L}_i$ and a GNSS satellite $S{G}_j$ are visible at a certain moment $t$, then there is a visible link between them, defined as $V\left(t,S{L}_i,S{G}_j\right)$. The complete return period of the two constellations of the LEO constellation and the GNSS constellation is expressed as $T_2$. When the satellite constellation is determined, its trajectory is periodic and fixed, so the visibility of the two constellations within a time period $T_2$ includes the visibility of the two constellations at any time. All visible links between LEO satellites and GNSS satellites within the time period $T_2$ constitute the visible link set of the SBM network, which is defined as $V{S}_2$ and can be expressed as

$$V{S}_2={\left\{V_1(t,S{L}_i,S{G}_j)\right\}}_{t\in T_2,i\in [1,2,\cdots ,N],j\in [1,2,\cdots ,M]}$$

(6)

Some links are selected from the visible link set $V{S}_2$ as SBM links. All links used for SBM in the time period $T_2$ constitute the activated link set of the SBM network, which is defined as $W{S}_2$, which can be expressed as

$$W{S}_2={\left\{V_2(t,S{L}_i,S{G}_j)\right\}}_{t\in T_2,i\in [1,2,\cdots ,N],j\in [1,2,\cdots ,M]}$$

(7)

The constraints of the SBM network are as follows:

(1) The SBM link must first be a visible link; that is, the activated link set of the SBM network is a subset of the visible link set, expressed as

$$W{S}_2\subseteq V{S}_2$$

(8)

(2) In order to achieve integrity monitoring and multiple voting of GNSS and improve the global integrity of GNSS, LEO constellations should have at least triple coverage of GNSS satellites [25]. At least triple coverage is required for SBM performance to ensure redundancy and reliability in signal monitoring. This level of coverage allows for cross-verification of data from multiple satellites, enhancing the accuracy and robustness of the monitoring process. In this condition, there are at least three monitoring links for any GNSS satellite $S{G}_j$ at any time $t$, which can be expressed as

$$\mathrm{card}\left(\left\{V(t_0,S{L}_{i_0},S{G}_{j_0})\right\}\right)\ge 3,V(t_0,S{L}_{i_0},S{G}_{j_0})\in W{S}_2,\forall j_0\in \left[1,2,\cdots ,M\right],\forall t_0\in T_2$$

(9)

where the ‘card()’ function is used to represent the cardinality of a set, which is the number of elements in the set. The set of LEO satellites $U{S}_2$ used for SBM is expressed as

$$U{S}_2=\left\{S{L}_{i_0}\right\},i_0\in \left[1,2,\cdots ,N\right]$$

(10)

Since LEO satellites need to be isolated from receiving and transmitting, SBM or navigation signal transmission functions are implemented on different LEO satellites. Therefore, a certain LEO satellite can only be used to realize one function of SBM or navigation signal transmission at the same time, that is, a collection of LEO satellites for navigation signal transmission $U{S}_1$ and a collection of LEO satellites for SBM. The sets $U{S}_2$ have no intersection, expressed as

$$U{S}_1\cap U{S}_2=\varnothing$$

(11)

The number of LEO satellites used for navigation enhancement is expressed as $nS$. Since the optimization goal of low-orbit constellation navigation resources is to use the least number of satellites to achieve navigation signal broadcast and SBM functions, the objective function is expressed as

$$\mathrm{Minimize}:nS=\left|U{S}_1\cup U{S}_2\right|$$

(12)

The objective function is subject to the constraints of the above Equations (1)–(11). By sorting out the constraints, we can obtain

$$\{\begin{array}{l}W{S}_1\subseteq V{S}_1\\ \left|\left\{V(t_0,S{L}_{i_0},S{N}_{r_0})\right\}\right|\ge 1,V(t_0,S{L}_{i_0},S{N}_{r_0})\in W{S}_1,\forall r_0\in \left[1,2,\cdots ,P\right],\forall t_0\in T_1\\ W{S}_2\subseteq V{S}_2\\ \left|\left\{V(t_0,S{L}_{i_0},S{G}_{j_0})\right\}\right|\ge 3,V(t_0,S{L}_{i_0},S{G}_{j_0})\in W{S}_2,\forall j_0\in \left[1,2,\cdots ,M\right],\forall t_0\in T_2\\ U{S}_1\cap U{S}_2=\varnothing \end{array}$$

(13)

3. Navigation Resource Allocation Algorithm Based on Dynamic Programming

3.1. Algorithm Principle

Dynamic Programming, as an operational research method, is adept at resolving complex decision processes across multiple stages [26,27,28]. Central to this method is Bellman’s principle of optimality, which simplifies the problem-solving process by breaking down a multi-stage Decision problem into manageable, single-stage problems. This is achieved through a fundamental recursive relationship that allows for the continuous transformation of the Decision process. Each stage builds upon the previous one, enabling a systematic approach to solving each segment in sequence. As illustrated in Figure 7, Bellman emphasized that the optimal strategy for a multi-level Decision process possesses a critical characteristic: irrespective of the initial state and decision, if any stage and state are considered the initial point, the subsequent decisions must align to form an overall optimal strategy. Specifically, if there is a Decision process whose initial state is $K$ level, and its optimal strategy is $\left\{w(0),w(1),\cdots ,w(K-1)\right\}$, then, for $w(0)$$K-1$ the level-level Decision process whose initial state is, the decision set $\left\{w(1),\cdots ,w(K-1)\right\}$ must be the optimal strategy. The principle of optimality provides a simple and effective method for solving optimization problems in multi-level Decision processes and provides a theoretical basis for deriving recursive equations.

Figure 7. Dynamic programming algorithm schematic diagram.

Next, we outline the parameters commonly employed in dynamic programming algorithms [29]:

(1)

Stage: Decompose the given optimization problem into several interconnected stages according to spatial or temporal characteristics, and stage variables are often used $k$ to represent them;

(2)

Status: used to describe the characteristics of the stage. A state is a single variable or vector. In this algorithm, it is assumed that the subjects under study exhibit ‘memorylessness’, which is the Markov property. This means that future states depend only on the current state and are independent of past states and decisions. $s_k$ is commonly used to represent the state variables of the $k$-th stage;

(3)

State space: The set of values of state variables $s_k$ becomes a state set, which is represented by $S_k$;

(4)

Decision: Upon a given state in a particular stage, various decisions can be made to derive the state of the subsequent stage. Such decisions are termed Decision. The variables used to describe these decisions are called decision variables, commonly denoted as ${\mu }_k\left(s_k\right)$ to represent the decision variable at stage $k$ when the state is $s_k$;

(5)

State transition: In dynamic programming, the state of the current stage results from the combined effect of the state and the decision of the previous stage. If the state at stage $k$ is given as $s_k$, and the decision made is ${\mu }_k\left(s_k\right)$, then the state at stage $k+1$, denoted as $s_{k+1}$, is fully determined. The state transition in the context of satellites involves moving from one configuration of resource allocation to another, considering the visibility and isolation constraints of the satellites involved. Their relationship can be expressed by $s_{k+1}=T_k\left(s_k,{\mu }_k\right)$ where $T_k\left(s_k,{\mu }_k\right)$ is called the state transition function, illustrating the evolutionary relationship between successive stages;

(6)

Strategy: In real-world problems, the values of decision variables are often confined within a certain range, known as the permissible decision set. This range is typically denoted as $D_k\left(s_k\right)$, representing the permissible decision set starting from state $s_k$ at stage $k$, thus ${\mu }_k\left(s_k\right)\in D_k\left(s_k\right)$;

(7)

Stage indicator function: The benefit measure of a decision made from a given state in a particular stage is called the stage utility function, denoted as $v_k\left(s_k,{\mu }_k\right)$;

(8)

Performance index function: The objective function used to compare the quality of selected strategies is known as the performance index function.

Therefore, according to the dynamic programming algorithm, the problem of optimal allocation of LEO constellation navigation resources can be decomposed into multiple single-stage navigation resource allocation sub-problems. In this paper, each ground station coverage sub-problem and each GNSS satellite monitoring sub-problem are treated as a single-stage process. Since there are $P$ ground stations and $M$ GNSS satellites, there are a total of $P+M$ sub-problems. The goal is to find the optimal resource allocation for each sub-problem, which involves determining the minimum number of LEO satellites required to achieve single coverage for each ground station and triple coverage for each GNSS satellite. When solving each sub-problem, the solutions obtained from the previous stages are considered. For example, when solving for the optimal satellite configuration for the $P$-th ground station, the optimal satellite configurations for the previous $P-1$ ground stations are taken into account. If the optimal satellite configuration for the previous $P-1$ ground stations already covers the $P$-th ground station, then no additional satellites are needed. By integrating the solutions of the P+M sub-problems in this manner, we can obtain an approximate optimal solution for the overall problem, which covers $P$ ground stations and $M$ GNSS satellites.

From the constraints and objective functions described in the previous section, the parameters of the navigation resource allocation algorithm based on dynamic programming (NRAA-DP) are as follows:

(1)

Stage: Each coverage sub-problem for ground stations and each monitoring sub-problem for GNSS satellites constitutes a single-stage process, resulting in a total of $P+M$ stages, denoted as the stage variable $k=P+M$. Different low Earth orbit navigation enhancement systems prioritize tasks differently; in this section, LEO navigation signals transmission is considered a higher priority than SBM. This means achieving uniform global coverage of the constellation takes precedence over uniform coverage of GNSS. Thus, in dynamic programming, the first $P$ stages cover ground stations, followed by MM stages covering GNSS satellites;

(2)

Status: When $k\le P$, the state variable $s_k$ represents that LEO satellites have achieved at least single-layer coverage for $k$ ground stations. When $P<k\le M$, $s_k$ indicates that LEO satellites have achieved at least single-layer coverage for $P$ ground stations and at least triple-layer coverage for $k$ GNSS satellites;

(3)

State space: $S_k$ is the set of all possible values for the state variable $s_k$;

(4)

Decision: The decision variable ${\mu }_k\left(s_k\right)$ for stage $k$ needed to achieve state $s_k$ is the set of LEO satellites required for that state;

(5)

State transition: The state transition function $T_k\left(s_k,{\mu }_k\right)$ defines the set of additional LEO satellites required to transition from state $s_k$ to state $s_{k+1}$;

(6)

Strategy: The permissible decision set $D_k\left(s_k\right)$ includes all available LEO satellites, denoted as $D_k\left(s_k\right)=\left\{S{L}_{i_0}\right\}$, $i_0=1,2,\cdots ,N$, thus the decision variable ${\mu }_k\left(s_k\right)\in D_k\left(s_k\right)$;

(7)

Stage indicator function: The stage indicator function $v_k\left(s_k,{\mu }_k\right)$ aims to minimize the number of LEO satellites used to achieve the state $s_k$, represented as $\mathrm{Minimize}:\left|{\mu }_k\left(s_k\right)\right|$. The stage indicator function is constrained by Equation (13);

(8)

Performance index function: The performance index function quantifies the minimum number of LEO satellites required to achieve the final state, which includes at least single coverage for $P$ ground stations and at least triple coverage for $M$ GNSS satellites. This corresponds to the objective function in Equation (12), denoted as $\mathrm{Minimize}:nS=\left|U{S}_1\cup U{S}_2\right|$. The performance index function is subject to the constraints specified in Equation (13).

3.2. Algorithm Process

The complete process of NRAA-DP is shown in Figure 8. This algorithm can be summarized into six specific steps, detailed as follows:

Figure 8. Flowchart of the NRAA-DP.

Step 1: Initialize Parameters. Initialize the active link sets for both the navigation signal transmission network, $W{S}_1$, and the SBM network, $W{S}_2$, to be empty. Set the initial identifier for the ground stations as $r_0=1$, with the required coverage time denoted by $T_0$, where $T_0=T_1$. For GNSS satellites, set the initial identifier as $j_0=1$, with the monitoring duration required indicated by $T_0^{\prime }$, where $T_0^{\prime }=T_2$;

Step 2: Determine the visible link set $V{S}_1$. Calculate the set of visible links, $V{S}_1$, between the LEO constellation and ground stations within the time interval $T_0$;

Step 3: Determine the optimal LEO satellite allocation to achieve single-layer coverage of ground stations. The specific steps are as follows:

Step 3.1: Determine the optimal LEO satellite for covering the ground station. Utilize the visible link set $V{S}_1$ to calculate the LEO satellite that can cover the ground station $S{N}_{r_0}$ for the longest duration within the time interval $T_0$, denoted as $S{L}_{i_0}$;

Step 3.2: Update $V{S}_1$ and $W{S}_1$. Remove all visible links containing $S{L}_{i_0}$, denoted as $V(t,S{L}_{I_0},S{N}_r)$, from $V{S}_1$ and add them to $W{S}_1$;

Step 3.3: Update $U{S}_1$ sum $T_0$. Add LEO satellites $S{L}_{i_0}$ to $U{S}_1$ and remove the duration that satellite $S{L}_{i_0}$ can cover ground station $S{N}_{r_0}$ from the time interval $T_0$;

Step 3.4: Determine $T_0$ whether it is 0. If $T_0=0$, let $T_0=T_1$, $r_0=r_0+1$, then go to Step 3.1; otherwise, go to Step 3.1 directly;

Step 3.5: When $r_0=P$, the optimal LEO satellite allocation that achieves single-layer coverage of all ground stations can be obtained, denoted as $U{S}_1$;

Step 4: Determine the visible link set $V{S}_2$. Calculate the set of visible links, $V{S}_2$, between the remaining LEO satellites, excluding $U{S}_1$, and the GNSS constellation within the time interval $T_0^{\prime }$;

Step 5: Determine the optimal allocation of LEO satellites to achieve triple coverage of GNSS satellites. The specific steps are as follows:

Step 5.1: Determine the best LEO satellite for monitoring GNSS satellites. According to $V{S}_2$, calculate the LEO satellite that can monitor $S{G}_{j_0}$ for the longest duration within the given time period $T_0^{\prime }$, denoted as $S{L}_{i_0}$;

Step 5.2: Update $V{S}_2$ and $W{S}_2$. Remove all visible links containing $S{L}_{i_0}$, denoted as $V(t,S{L}_{i_0},S{G}_j)$, from $V{S}_2$ and add them to $W{S}_2$;

Step 5.3: Update $U{S}_2$ and $T_0^{\prime }$. Add the LEO satellite $S{L}_{i_0}$ to $U{S}_2$ and remove the duration when GNSS satellites $S{G}_{j_0}$ can be monitored by $S{L}_{i_0}$ from $T_0^{\prime }$.

Step 5.4: Determine whether $T_0^{\prime }$ is 0. If $T_0^{\prime }\ne 0$, go to Step 5.1; otherwise, go to the next Step.

Step 5.5: Check if triple coverage of the GNSS satellite $S{G}_{j_0}$ has been achieved. If it is satisfied, $\left|\right\{V(t,S{L}_i,S{G}_{j_0})\left\}\right|$, $\left|\right\{V(t_0,S{L}_i,S{G}_{j_0})\left\}\right|\in W{S}_2,\forall t_0\in T_2$, let $T_0^{\prime }=T_2$,$j_0=j_0+1$, and then go to Step 5.1; if it is not satisfied, let $T_0^{\prime }$ equal to the time period in which triple coverage of $S{G}_{j_0}$ has not been achieved, and then go to Step 5.1.

Step 5.6: When $j_0=M$, the optimal allocation of LEO satellites for achieving triple coverage of all GNSS satellites is obtained, denoted as $U{S}_2$.

Step 6: Obtain the optimal navigation resource allocation scheme for the LEO constellation. The optimal allocation scheme for LEO navigation signal transmission and SBM is denoted as $U{S}_2\cup U{S}_1$, and $nS=|U{S}_2\cup U{S}_1|$ represents the number of LEO satellites used.

Based on the above scheme, the pseudocode for the NRAA-DP is shown in Algorithm 1.

Algorithm 1. Pseudocode of the NRAA-DP: Navigation Resource Allocation Algorithm based on Dynamic Programming

Input: Constellation parameters, $P$, $M$, $T_1$, $T_2$ Output: $U{S}_1$, $U{S}_2$ and $nS$ begin 1: Initialization:$W{S}_1=W{S}_2=\left\{\right\}$,$r_0=j_0=1$, $T_0=T_1$, $T_0^{\prime }=T_2$. 2: Generate $V{S}_1$. 3: while $r_0\le P$ do. 4:         while $T_0\ne 0$ do. 5:                Get the best satellite $S{L}_{i_0}$ for covering $S{N}_{r_0}$. 6:                Update $V{S}_1$, $W{S}_1$, $U{S}_1$ and $T_0$. 7:          end while 8:         $T_0=T_1$, $r_0=r_0+1$. 9: end while 10: Generate $V{S}_2$. 11: while $j_0\le M$ do. 12:         while $\left|\left\{V(t,S{L}_i,S{G}_{j_0})\right\}\right|<3$ do. 13:               while $T_0^{\prime }\ne 0$ do. 14:                     Get the best satellite $S{L}_{i_0}$ for monitoring $S{G}_{j_0}$. 15:                     Update $V{S}_2$, $W{S}_2$, $U{S}_2$ and $T_0^{\prime }$. 16:               end while 17:                 Update $T_0^{\prime }$. 18:         end while 19:        $T_0^{\prime }=T_2$, $j_0=j_0+1$. 20: end while 21:  $nS=\left|U{S}_1\cup U{S}_2\right|$ end

The visibility matrix between LEO satellites and ground stations in Step 2 and the visibility matrix between LEO satellites and GNSS satellites in Step 10 can be calculated through analytical algorithms [25] or obtained via STK 11.6 software simulation. Steps 4 to 8 will repeat $P$ times, each time calculating the minimum additional LEO satellites required to achieve single coverage for the ground stations and adding them to $U{S}_1$. Steps 12 to 19 will repeat $M$ times, each time calculating the minimum additional LEO satellites required to achieve triple coverage for the current GNSS satellites and adding them to $U{S}_2$. Finally, output the final $U{S}_1$, $U{S}_2$, and $nS$. $U{S}_1\cup U{S}_2$ represents the optimal allocation scheme for LEO navigation signal transmission and SBM in the LEO constellation, and $nS$ represents the minimum number of LEO satellites required.

4. Performance Analysis

4.1. Parameter Settings

To evaluate the performance of the NRAA-DP, this section primarily assesses the algorithm’s resource utilization and computational complexity. The results are compared with those of the Divide and Conquer Algorithm (DCA) [30] and the Greedy Algorithm (GA) [17]. The core concept of the DCA is to divide the multi-stage problem into multiple single-stage problems, with no interrelation between the stages. Each stage is solved individually to obtain a subset of LEO satellites that can achieve single coverage for each ground station and triple coverage for each GNSS satellite. The union of all these subsets forms the final solution. The core concept of the GA is to first sort the LEO satellites based on their visibility to the ground stations from best to worst. LEO satellites are then sequentially selected and added to the constellation allocation set until single coverage for all ground stations is achieved. The remaining LEO satellites are subsequently sorted based on their visibility to the GNSS satellites from best to worst. LEO satellites are again sequentially selected and added to the constellation allocation set until triple coverage for all GNSS satellites is achieved. The constellation allocation set at this point represents the final solution.

The GNSS constellation simulated in this paper is the BDS constellation, including 3 GEO satellites, 3 IGSO satellites, and 24 MEO satellites. The simulated low Earth orbit constellation consists of 216 satellites, including 72 satellites in near-polar orbits and 144 satellites in inclined orbits. In order to reduce the calculation amount, the simulation time is set to 7 days, from 9 October 2021 12:00:00 to 16 October 2021 13:00:00, with a step of 1 min. The parameters of the BDS constellation and LEO constellation are shown in Table 2.

Table 2. Parameters of BDS and LEO constellation.

Parameter	BDS Constellation	LEO Constellation
Orbital type	GEO/IGSO/MEO	Near-Polar	Inclined
Number of satellites	3/3/24	72	144
Number of orbital planes	1/3/3	6	12
Number of satellites per plane	3/1/8	12	12
Orbital Altitude	36,000 km/36,000 km/21,500 km	1175 km	1150 km
Inclination	0°/55°/55°	55°	87°

Figure 9 shows the three-dimensional spatial allocation of the two constellations based on a comprehensive of the above constellation parameters. The near-polar orbital LEO satellites are labeled as P0101–P0612, and the inclined orbital LEO satellites are labeled as I0101–I1212. The first two digits represent the orbital plane number, while the last two digits represent the satellite number within each orbital plane. For example, P0506 indicates the sixth LEO satellite in the fifth near-polar orbital plane, and I1010 indicates the 10th LEO satellite in the 10th inclined orbital plane.

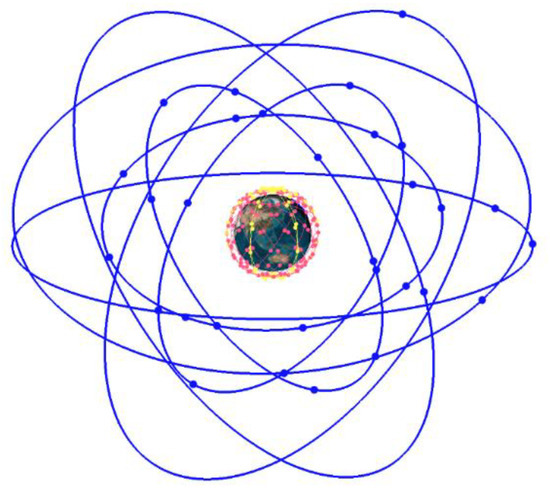
Figure 9. The distribution diagram of the LEO constellation and BDS constellation. The blue lines represent the orbital planes of the BDS constellation, the yellow lines indicate the near-polar orbital planes of the LEO constellation, and the red lines denote the inclined orbital planes of the LEO constellation.

Through simulation analysis using STK 11.6 software, it was found that over a period of 7 days, there are a total of 556,021 visible links between the two constellations, all of which are intermittent, with durations ranging from 0.6 s to 5.8 h. For example, Figure 10 shows the set of visible links between the LEO satellite I0101 and BDS satellites over a period of 4 h. For the LEO satellite I0101, there are a total of 77 intermittent links within this 4-h period. Similarly, the visibility situation between 216 LEO satellites and BDS satellites over 7 days is even more complex and variable.

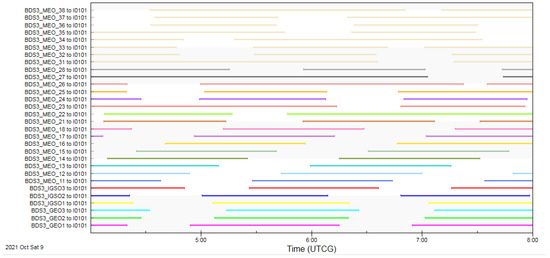
Figure 10. Visual links between LEO satellite S0101 and BDS satellites within 4 h. Lines of different colors represent different visible links.

Due to the symmetrical characteristics of global coverage in the east-west and north-south hemispheres within a complete orbital period of the constellation, only 19 ground stations in the northern hemisphere along the 0° longitude from 0° to 90°N, sampled every 5°, are selected for simplicity when evaluating global coverage performance [31], as shown in Figure 11.

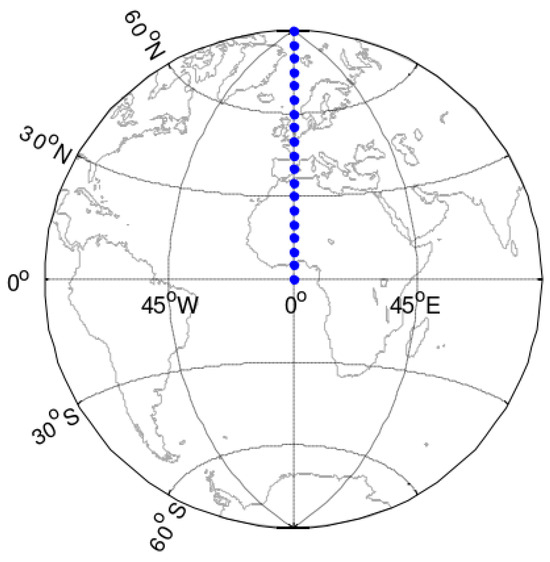
Figure 11. Distribution map of ground stations used for evaluating constellation global coverage. The blue circles represent ground stations in the northern hemisphere along the 0° longitude from 0° to 90°N.

Through simulation analysis using STK 11.6 software, it was found that over a period of 7 days, there are a total of 152,190 visible links between the LEO constellation and the 19 ground stations, all of which are intermittent, with durations ranging from 1.1 s to 14.8 min. For example, Figure 12 shows the set of visible links between the LEO satellite I0101 and a ground station over a period of 4 h. For the LEO satellite I0101, there are a total of 19 intermittent links within this 4-h period. Similarly, the visibility situation between 216 LEO satellites and the ground stations over 7 days is even more complex and variable.

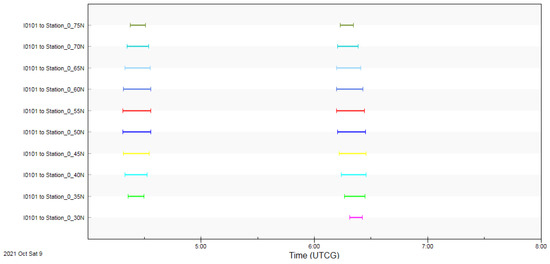
Figure 12. Visible links between the LEO satellite I0101 and the ground stations. Lines of different colors represent different visible links.

4.2. Resource Utilization

The proposed dynamic programming algorithm, the Greedy Algorithm (GA), and the Divide and Conquer Algorithm (DCA) are used for navigation resource allocation of the LEO constellation. The number of LEO satellites required to achieve global single coverage and triple coverage for the BDS constellation are 118, 165, and 201, respectively. The specific constellation allocation results of different algorithms are shown in Table 3.

Table 3. Constellation allocation results of different algorithms.

Algorithm	Number of Satellites in the Resource Allocation Scheme	Satellites Used for Navigation Signal Transmission (NST)		Satellites Used for Space-Based Monitoring (SBM)
		Inclined Orbit	Near-Polar Orbit	Inclined Orbit	Near-Polar Orbit
NRAA-DP	118	96	13	4	5
GA	165	82	72	11	0
DCA	201	103	54	38	6

To more intuitively display the constellation allocation results, the results from Algorithm 1 are shown in Figure 13, Figure 14 and Figure 15. In these Figures, the horizontal axis represents the orbital plane number, and the vertical axis represents the satellite number within each orbital plane.

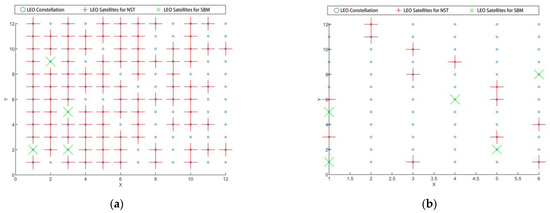
Figure 13. Constellation distribution map of the resource allocation scheme by NRAA-DP. (a) Inclined orbit satellites. (b) Near-polar orbit.

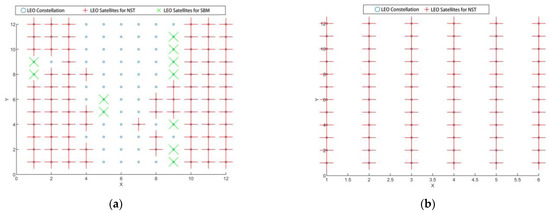
Figure 14. Constellation distribution map of the resource allocation scheme by GA. (a) Inclined orbit satellites. (b) Near-polar orbit.

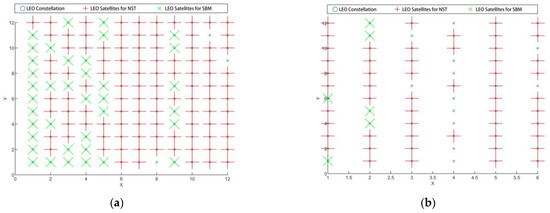
Figure 15. Constellation distribution map of the resource allocation scheme by DCA. (a) Inclined orbit satellites. (b) Near-polar orbit.

Based on the resource allocation schemes obtained from different algorithms in Table 3, the set of visible links between the LEO constellation and the ground stations can be used to derive the global coverage performance of the different constellation resource allocation schemes, as shown in Figure 16. The results indicate that all three constellation allocation schemes meet the requirement for single coverage at all times. Additionally, the average minimum coverage multiplicities for ground stations achieved by the constellation allocation schemes obtained from the three algorithms are 1.2, 3.2, and 2.5, respectively; the average coverage multiplicities are 4.5, 7.9, and 7.5, respectively; and the maximum coverage multiplicities are 8.7, 13.2, and 12.7, respectively.

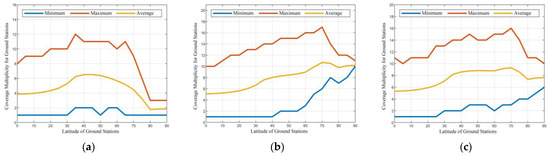
Figure 16. Coverage performance of different navigation resource allocation schemes for ground stations. (a) NRAA-DP. (b) GA. (c) DCA.

Based on the resource allocation schemes obtained from different algorithms in Table 3 and the set of visible links between the two constellations, the coverage performance of different constellation allocation schemes for the BDS satellites can be derived, as shown in Figure 17. The results indicate that all three constellation resource allocation schemes meet the requirement for triple coverage at all times. Additionally, the average minimum coverage multiplicities for all BDS satellites achieved by the constellation allocation schemes obtained from the three algorithms are 3, 3, and 22.7, respectively; the average coverage multiplicities are 6, 8, and 30.3, respectively; and the maximum coverage multiplicities are 7.7, 11.3, and 37.4, respectively.

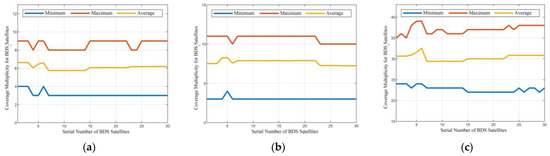
Figure 17. Coverage performance of different navigation resource allocation schemes for BDS satellites. (a) NRAA-DP. (b) GA. (c) DCA.

The results from Figure 16 and Figure 17 are summarized in Table 4.

Table 4. Coverage performance of different navigation resource allocation schemes.

Algorithm	Number of Satellites in the Resource Allocation Scheme	Coverage Multiplicity for Ground Stations			Coverage Multiplicity for BDS Satellites
		Minimum	Average	Maximum	Minimum	Average	Maximum
NRAA-DP	118	1.2	4.5	8.7	3	6	7.7
GA	165	3.2	7.9	13.2	3	8	11.3
DCA	201	2.5	7.5	12.7	2 2.7	30.3	37.4

As shown in Table 4, the navigation resource allocation schemes obtained from all three algorithms can simultaneously achieve LEO satellites’ navigation signal transmission and SBM functions, meeting the requirements for global single coverage and triple coverage of GNSS satellites. The NRAA-DP proposed in this paper yields the optimal solution, with the least number of satellites in the constellation allocation and the highest utilization of LEO satellite resources. The satellite numbers in the resource allocation schemes obtained from the GA and the DCA are 1.4 times and 1.7 times that of the NRAA-DP, respectively, leading to redundant navigation resources, occupying communication resources, and reducing the overall resource utilization of the LEO constellation.

This inefficiency arises because the DCA isolates the multi-stage problem into several single-stage problems without considering the solutions of other stages while optimizing each stage. This results in locally optimal solutions for each single-stage problem rather than a globally optimal solution. Similarly, as a centralized algorithm, the GA is prone to getting trapped in local optima. In contrast, the NRAA-DP considers the solution of the previous stage in each single-stage problem, thus achieving an approximate global optimum.

4.3. Computational Complexity

As shown in Figure 10, the visibility between LEO satellites and BDS satellites is highly complex and variable, with 556,021 visible links observed over 7 days. To ensure triple coverage at any given moment, it is necessary to calculate the least common multiple (LCM) of the orbital periods of the LEO constellation and the BDS constellation, which can span several months. During this period, the number of visible links between LEO satellites and BDS satellites can reach millions. Therefore, it is essential to evaluate the complexity of the navigation resource allocation algorithm.

Assume there are $N$ LEO satellites, $M$ GNSS satellites, and $P$ ground stations. There are a total of $Y$ visible links between LEO satellites and ground stations, and $Z$ visible links between the LEO constellation and the GNSS constellation. On average, each LEO satellite has $Y/N$ visible links to ground stations and $Z/N$ visible links to GNSS satellites. Each ground station has $Y/P$ visible links to LEO satellites, and each GNSS satellite has $Z/M$ visible links to LEO satellites. The number of LEO satellites required for the allocation obtained by different algorithms is $S_1+S_2$, where $S_1$ is the number of LEO satellites used for navigation signal transmission, and $S_2$ is the number of LEO satellites used for SBM.

As shown in Algorithm 1, in the NRAA-DP, the first Step is to determine the LEO satellite allocation for navigation signal transmission. Step 3 and Step 4 each require one logical operation, Step 5 requires $Y$ addition operations and $N$ logical operations, Step 6 requires $4Y/N$ logical operations, and Step 8 requires one addition operation. Throughout the entire process, Steps 4 to 6 are repeated $S_1$ times and Steps 3 and 8 are repeated $P$ times. Next, the LEO satellite allocation for SBM is determined. Step 11, Step 12, and Step 13 each require one logical operation, Step 14 requires $Z$ addition operations and $N$ logical operations, Step 15 requires $4Z/N$ logical operations, and Step 19 requires one addition operation. Throughout the entire process, Steps 12 to 15 are repeated $S_2$ times, and Steps 11 and 19 are repeated $M$ times.

In the GA, the LEO satellites are first sorted based on their visibility to the ground stations from best to worst, requiring $Y$ addition operations and $N$ logical operations. Then, LEO satellites are sequentially selected and added to the navigation signal transmission satellite set. For each additional LEO satellite, the current coverage situation needs to be evaluated, requiring $2PY/N$ logical operations. This Step is repeated $S_1$ times. Next, the LEO satellites are sorted based on their visibility to the GNSS satellites from best to worst, requiring $Z$ addition operations and $N-S_1$ logical operations. LEO satellites are then sequentially selected and added to the SBM satellite set. For each additional LEO satellite, the current coverage situation needs to be evaluated, requiring $2MZ/N$ logical operations. This Step is repeated $S_2$ times.

In the DCA, each ground station’s requirement for single coverage by LEO satellites is solved individually, requiring $YP/S_1$ addition operations and $P/S_1·\left(N+2Y/N+1\right)$ logical operations each time. This step is repeated $P$ times. Then, for each GNSS satellite, the requirement for triple coverage by LEO satellites is solved individually, requiring $ZM/S_2$ addition operations and $M/S_2·\left(N-S_1+2Z/N+1\right)$ logical operations each time. This step is repeated $M$ times.

Table 5 compares the computational complexity of these three algorithms. The values in parentheses below each cell indicate the computational complexity of the simulation cases discussed in this section.

Table 5. Comparison of the computational complexity of three algorithms.

Algorithm	Logical Operation	Addition Operation
NRAA-DP	$\begin{array}{c}(1+N+4Y/N)S_1+P+(1+N+4Z/N)S_2+M\\ (8.6\times {10}^6)\end{array}$	$\begin{array}{c}Y{S}_1+P+Z{S}_2+M\\ (2.1\times {10}^5)\end{array}$
GA	$\begin{array}{c}2S_{1}PY/N+2S_{2}MZ/N+2N-S_1\\ (5.8\times {10}^7)\end{array}$	$\begin{array}{c}Y+Z\\ (7.1\times {10}^5)\end{array}$
DCA	$\begin{array}{c}{{(N+2Y/N+1)P^2/S}_1+(N-S_1+2Z/N+1)M^2/S}_2\\ (1.1\times {10}^8)\end{array}$	$\begin{array}{c}{Y{P}^2/S}_1+{Z{M}^2/S}_2\\ (1.2\times {10}^7)\end{array}$

As shown in Table 5, the NRAA-DP has the lowest complexity among the three algorithms. Moreover, this advantage in computational complexity increases with the number of LEO satellites and GNSS satellites. Running the above three algorithms on the same MATLAB simulation platform on the same computer, the program execution times were 145 s, 562 s, and 1807 s, respectively, further validating this conclusion.

In summary, the DCA exhibits moderate resource utilization but has high computational complexity due to its recursive nature. Specifically, it requires significantly more iterations and computations to achieve optimal coverage, leading to longer processing times. Conversely, the GA demonstrates lower computational complexity by following a heuristic approach, which involves sequentially selecting satellites based on visibility criteria. However, this method may result in suboptimal resource utilization, as it does not consider the global optimum solution.

5. Conclusions

This paper proposes a navigation resource allocation algorithm based on dynamic programming (NRAA-DP) for the problem of navigation resource allocation in LEO constellations. Under this algorithm, a network model for LEO constellation navigation resource allocation is first established. Within the constraints of visibility time windows and onboard transceiver isolation, the objective is to use the minimum number of LEO satellites to achieve navigation signal transmission and SBM. The mathematical expressions for the resource allocation constraints and optimization objectives are derived, and the dynamic programming method is used to solve the optimal resource allocation scheme. The analysis results indicate that this algorithm can obtain the global optimal solution with relatively low computational complexity. Compared to the Greedy Algorithm (GA) and the Divide and Conquer Algorithm (DCA), the resource allocation scheme obtained by this algorithm has the highest resource utilization rate and the lowest computational complexity. When the GNSS constellation is the BDS constellation, and the LEO constellation size is 216 satellites, the resource utilization rate of the NRAA-DP algorithm is 1.4 times and 1.7 times higher than that of the GA and DCA, respectively, and it has the lowest computational complexity among the three algorithms. This advantage increases with the size of the constellation. By optimizing the allocation of navigation resources, the NRAA-DP algorithm enhances the overall efficiency of the LEO constellation. In addition, efficient resource allocation translates to fewer satellites required to achieve the desired coverage and performance. This reduction in the number of satellites can substantially lower the operational and maintenance costs associated with managing large LEO constellations. In summary, the NRAA-DP algorithm not only improves the efficiency and effectiveness of the LEO constellation but also offers substantial cost savings. Future research will focus on incorporating more complex constraints, such as multi-mission requirements and inter-satellite communication limits. Additionally, we plan to test the algorithm with different GNSS constellations to evaluate its adaptability and robustness.