Seamline Optimization Based on Triangulated Irregular Network of Tiepoints for Fast UAV Image Mosaicking
Abstract
1. Introduction
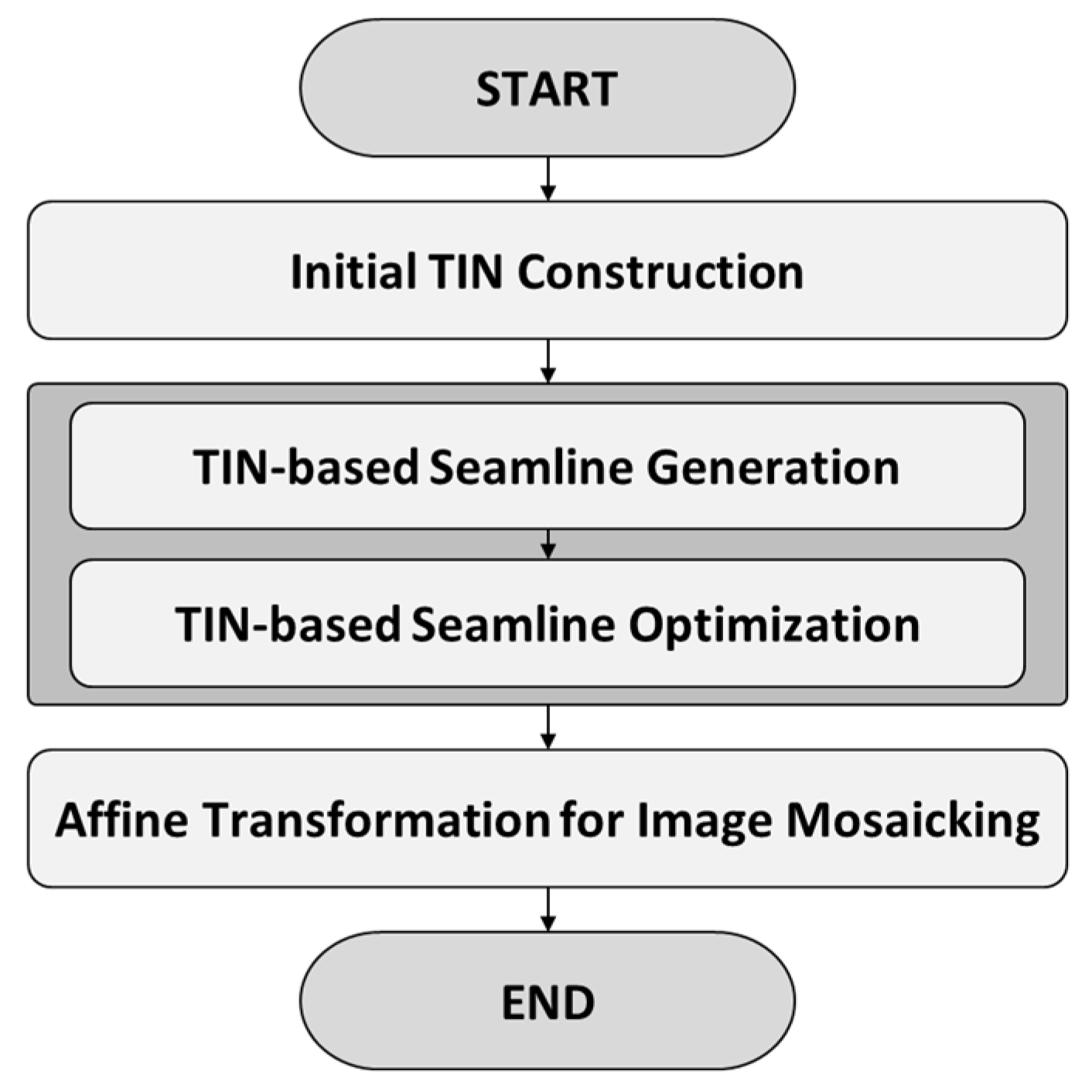
2. Materials and Methods
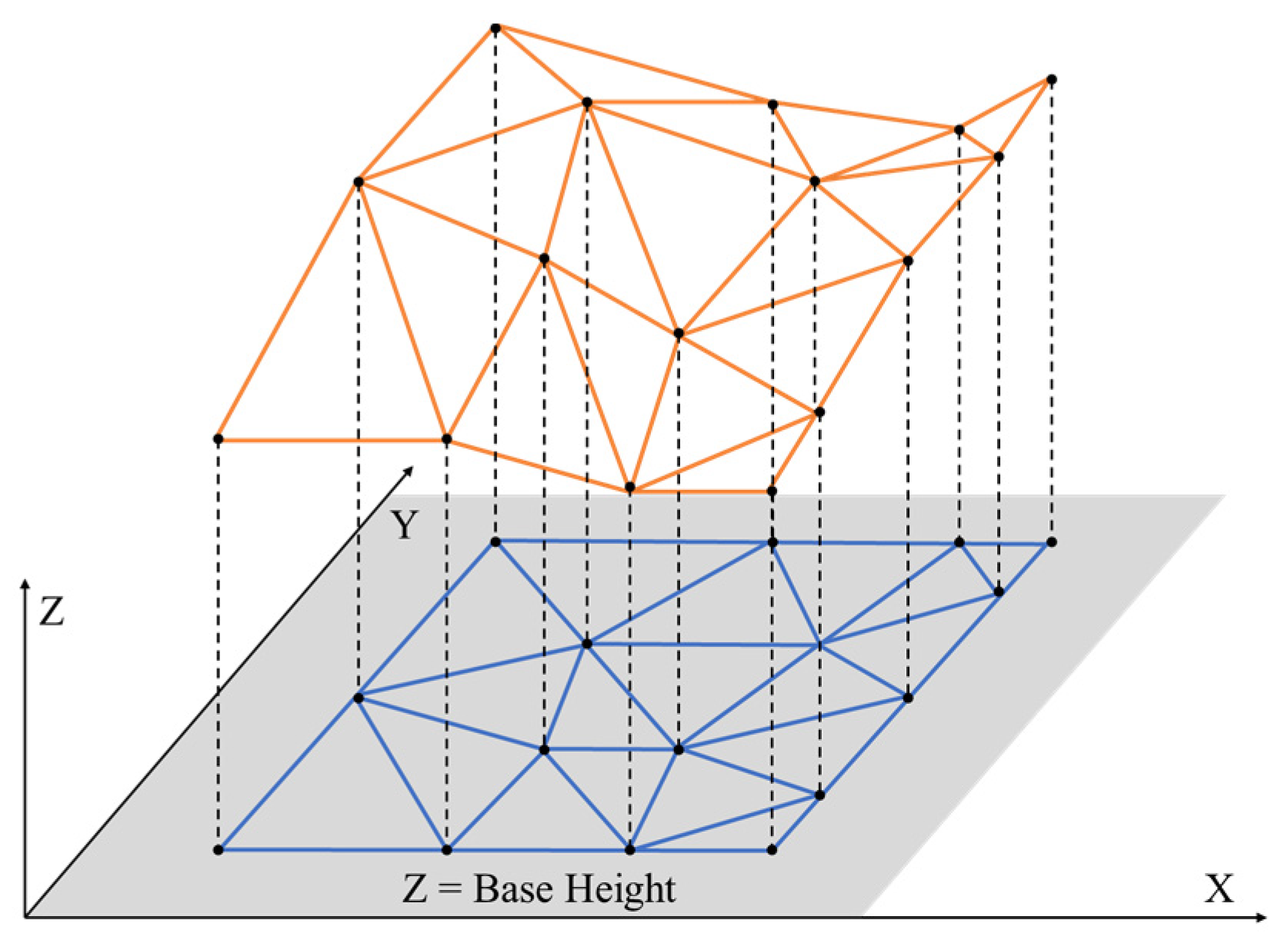
2.1. Initial TIN Construction
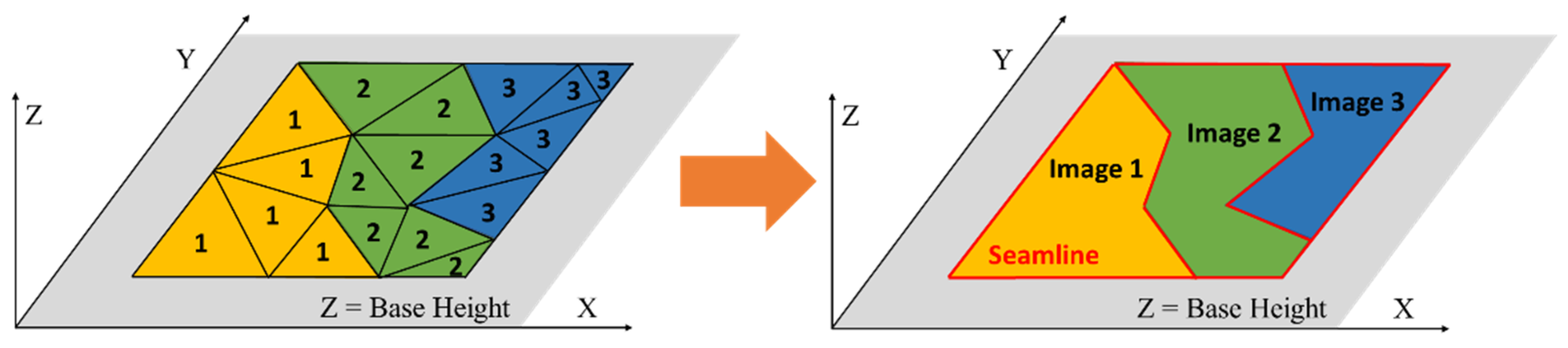
2.2. TIN-Based Seamline Generation
2.3. TIN-Based Seamline Optimization
2.4. Affine Transformation for Image Mosaicking
3. Experiment Results
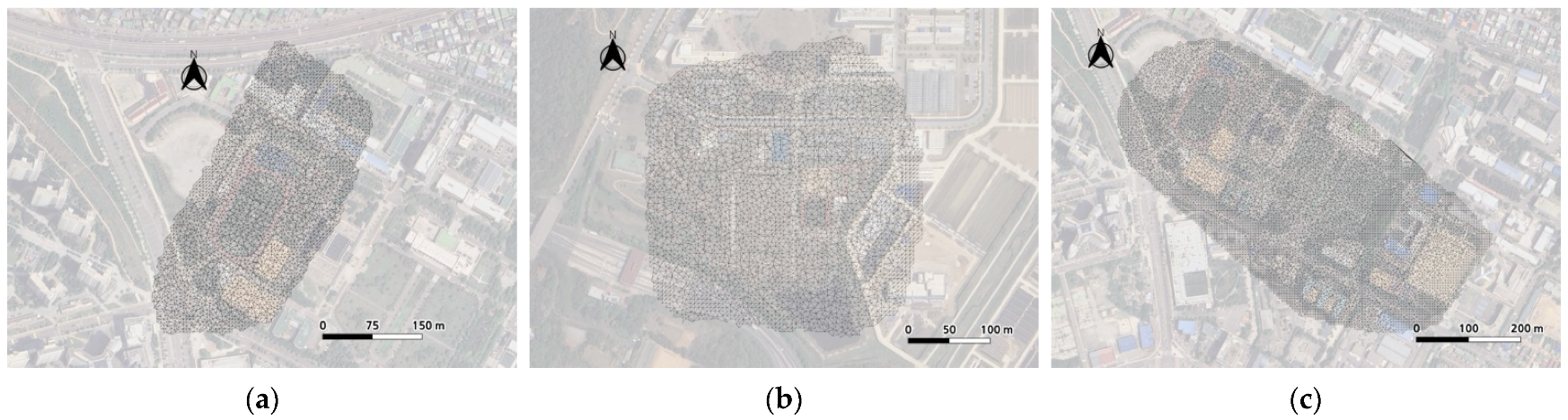
3.1. Results of Intial TIN Construction
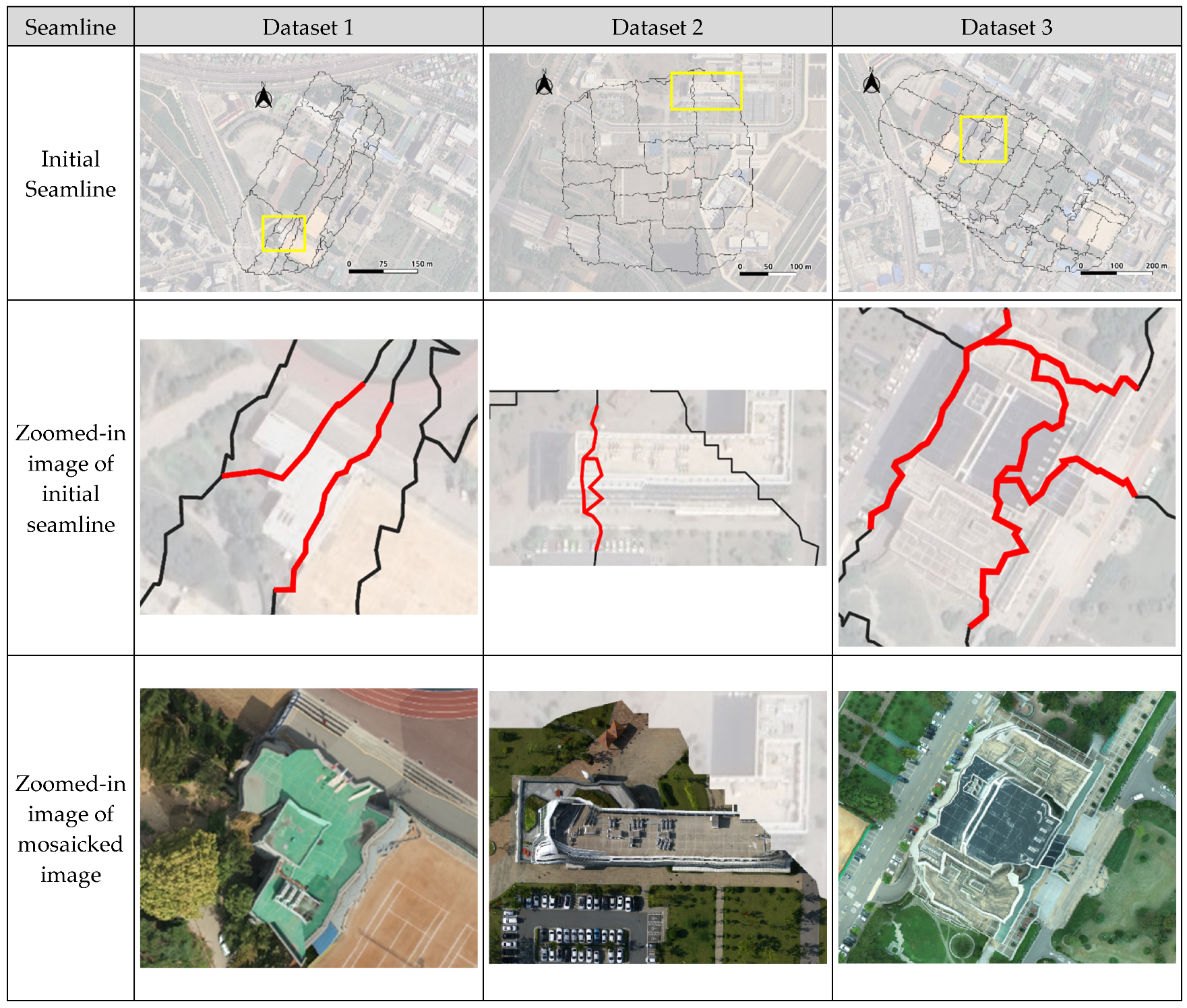
3.2. Results of TIN-Based Seamline Generation
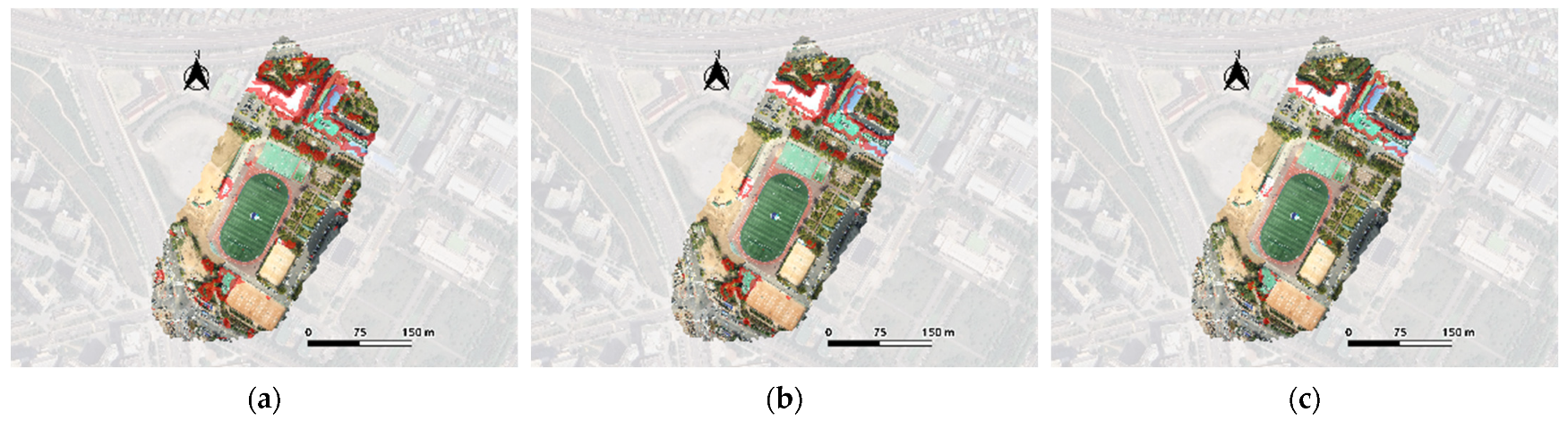
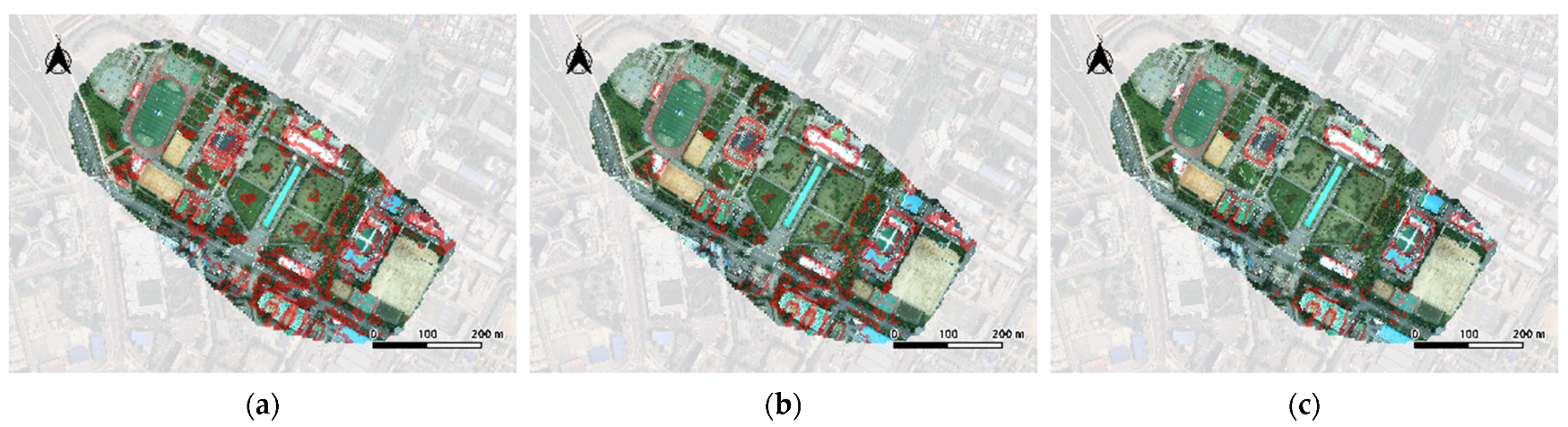
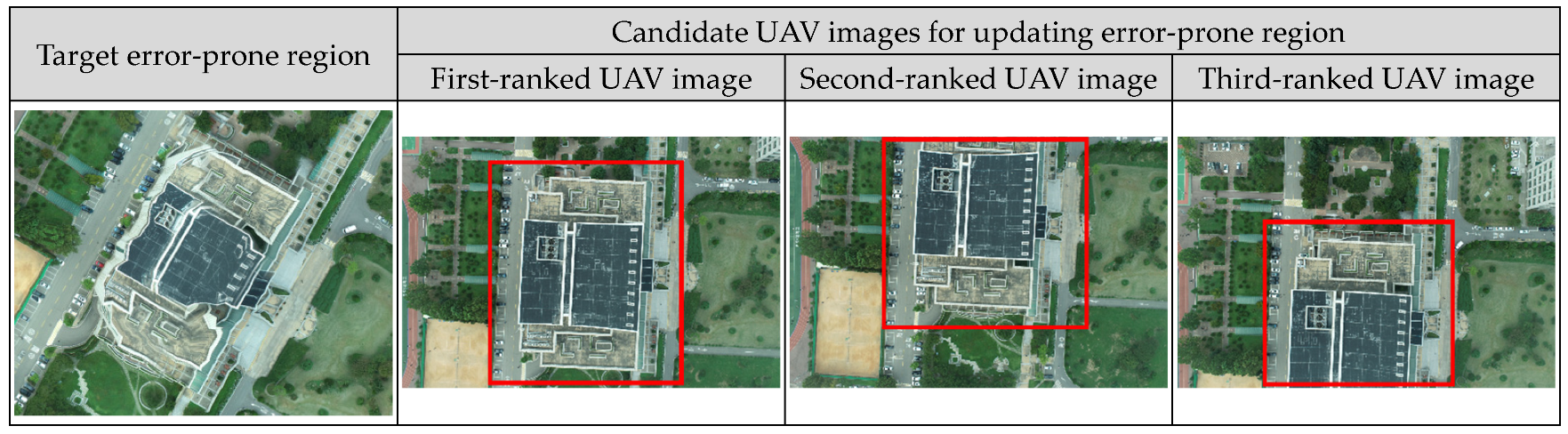
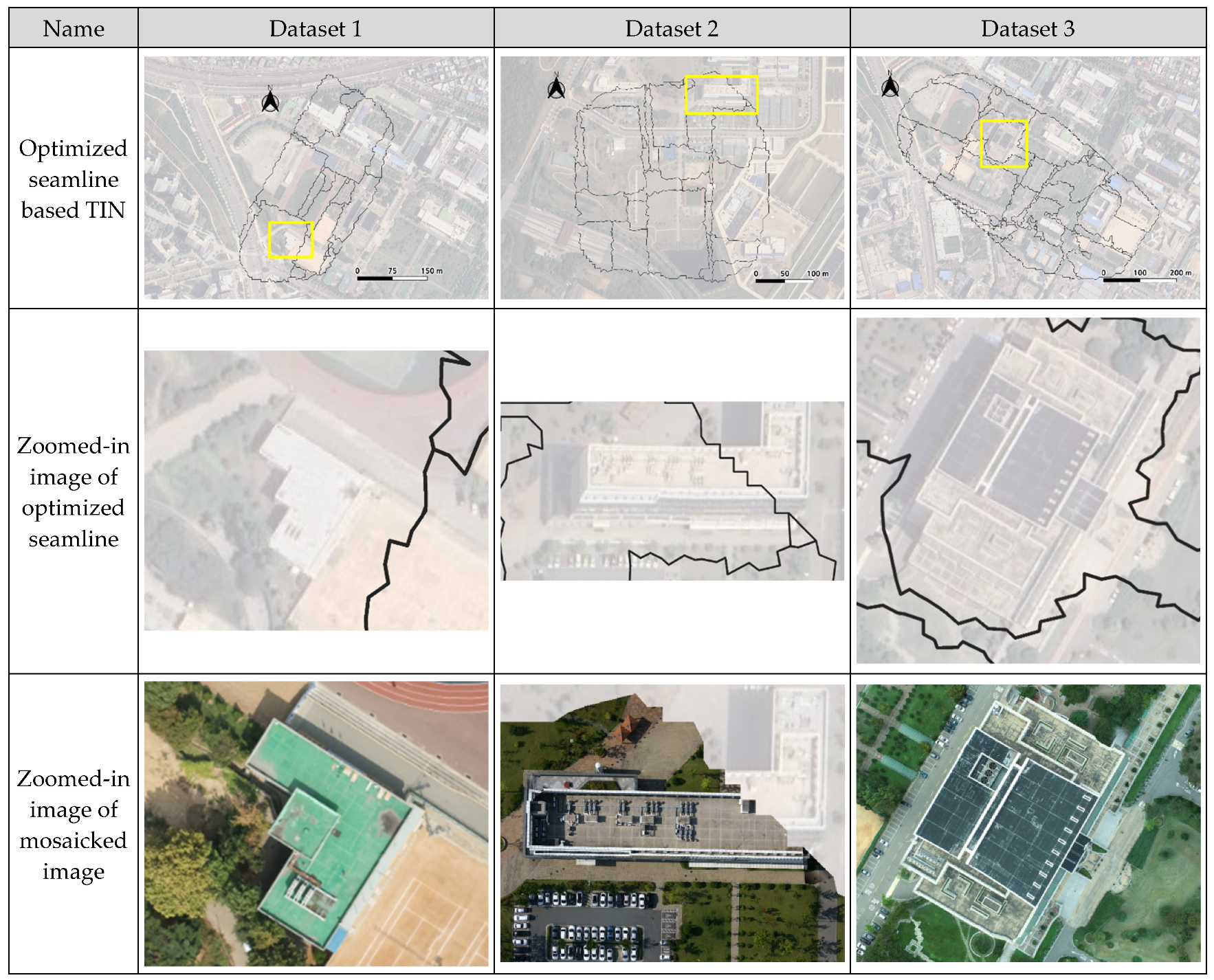
3.3. Results of TIN-Based Seamline Optimization
3.4. Final Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A review on UAV-based applications for precision agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef]
- Tsouros, D.C.; Triantafyllou, A.; Bibi, S.; Sarigannidis, P.G. Data acquisition and analysis methods in UAV-based applications for Precision Agriculture. In Proceedings of the 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini, Greece, 29–31 May 2019. [Google Scholar]
- Chan, B.; Guan, H.; Jo, J.; Blumenstein, M. Towards UAV-based bridge inspection systems: A review and an application perspective. Struct. Monit. Maint. 2015, 2, 283–300. [Google Scholar] [CrossRef]
- Rhee, S.; Kim, T.; Kim, J.; Kim, M.C.; Chang, H.J. DSM Generation and Accuracy Analysis from UAV Images on River-side Facilities. Korean J. Remote Sens. 2015, 31, 183–191. [Google Scholar] [CrossRef]
- Park, S.; Park, N.W. Effects of class purity of training patch on classification performance of crop classification with convolutional neural network. Appl. Sci. 2020, 10, 3773. [Google Scholar] [CrossRef]
- Avola, D.; Cinque, L.; Foresti, G.L.; Martinel, N.; Pannone, D.; Piciarelli, C. A UAV video dataset for mosaicking and change detection from low-altitude flights. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 2139–2149. [Google Scholar] [CrossRef]
- Li, X.; Feng, R.; Guan, X.; Shen, H.; Zhang, L. Remote sensing image mosaicking: Achievements and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 8–22. [Google Scholar] [CrossRef]
- Li, T.; Jiang, C.; Bian, Z.; Wang, M.; Niu, X. A review of true orthophoto rectification algorithms. IOP Conf. Ser. Mater. Sci. Eng. 2019, 780, 022035. [Google Scholar] [CrossRef]
- Shoab, M.; Singh, V.K.; Ravibabu, M.V. High-precise true digital orthoimage generation and accuracy assessment based on UAV images. J. Indian Soc. Remote Sens. 2021, 50, 613–622. [Google Scholar] [CrossRef]
- Jiang, Y.; Bai, Y. Low–high orthoimage pairs-based 3D reconstruction for elevation determination using drone. J. Constr. Eng. Manag. 2021, 147, 04021097. [Google Scholar] [CrossRef]
- Kim, J.I.; Kim, H.C.; Kim, T. Robust mosaicking of lightweight UAV images using hybrid image transformation modeling. Remote Sens. 2020, 12, 1002. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, B.; Li, M.; Liao, X.; Li, W. Improved seam-line searching algorithm for UAV image mosaic with optical flow. Sensors 2018, 18, 1214. [Google Scholar] [CrossRef]
- Yuan, Y.; Fang, F.; Zhang, G. Superpixel-based seamless image stitching for UAV images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1565–1576. [Google Scholar] [CrossRef]
- Yuan, S.; Yang, K.; Li, X.; Cai, H. Automatic seamline determination for urban image mosaicking based on road probability map from the D-LinkNet neural network. Sensors 2020, 20, 1832. [Google Scholar] [CrossRef]
- Li, L.; Yao, J.; Liu, Y.; Yuan, W.; Shi, S.; Yuan, S. Optimal seamline detection for orthoimage mosaicking by combining deep convolutional neural network and graph cuts. Remote Sens. 2017, 9, 701. [Google Scholar] [CrossRef]
- Dai, Q.; Fang, F.; Li, J.; Zhang, G.; Zhou, A. Edge-guided composition network for image stitching. Pattern Recognit. 2021, 118, 108019. [Google Scholar] [CrossRef]
- Yoon, S.J.; Kim, T. Fast UAV Image Mosaicking by a Triangulated Irregular Network of Bucketed Tiepoints. Remote Sens. 2023, 15, 5782. [Google Scholar] [CrossRef]
- Tareen, S.A.K.; Saleem, Z. A comparative analysis of sift, surf, kaze, akaze, orb, and brisk. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018. [Google Scholar]
- Liu, Y.; He, M.; Wang, Y.; Sun, Y.; Gao, X. Farmland aerial images fast-stitching method and application based on improved sift algorithm. IEEE Access 2022, 10, 95411–95424. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Wu, F.L.; Fang, X.Y. An improved RANSAC homography algorithm for feature based image mosaic. In Proceedings of the 7th WSEAS International Conference on Signal Processing, Computational Geometry & Artificial Vision, Athens, Greece, 24–26 August 2007; pp. 202–207. [Google Scholar]
- Thompson, M.M.; Eller, R.C.; Radlinski, W.A.; Speert, J.L. Manual of Photogrammetry, 6th ed.; American Society for Photogrammetry and Remote Sensing (ASPRS): Falls Church, VA, USA, 2013; pp. 121–159. [Google Scholar]
- Lin, Y.C.; Zhou, T.; Wang, T.; Crawford, M.; Habib, A. New orthophoto generation strategies from UAV and ground remote sensing platforms for high-throughput phenotyping. Remote Sens. 2021, 13, 860. [Google Scholar] [CrossRef]
- Park, D.; Cho, H.; Kim, Y. A TIN compression method using Delaunay triangulation. Int. J. Geogr. Inf. Sci. 2001, 15, 255–269. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, Y.; Wang, H.; Li, B.; Hu, H.M. A novel projective-consistent plane based image stitching method. IEEE Trans. Multimed. 2019, 21, 2561–2575. [Google Scholar] [CrossRef]
- Shin, J.I.; Cho, Y.M.; Lim, P.C.; Lee, H.M.; Ahn, H.Y.; Park, C.W.; Kim, T. Relative radiometric calibration using tie points and optimal path selection for UAV images. Remote Sens. 2020, 12, 1726. [Google Scholar] [CrossRef]
- Ban, S.; Kim, T. Relative Radiometric Calibration of UAV Images for Image Mosaicking. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 361–366. [Google Scholar] [CrossRef]
- Jarahizadeh, S.; Salehi, B. A Comparative Analysis of UAV Photogrammetric Software Performance for Forest 3D Modeling: A Case Study Using AgiSoft Photoscan, PIX4DMapper, and DJI Terra. Sensors 2024, 24, 286. [Google Scholar] [CrossRef]












| Specification | Dataset 1 | Dataset 2 | Dataset 3 |
|---|---|---|---|
| Platform | SmartOne | KD-2 Mapper | Phantom4 RTK |
| Manufacturer (City, Country) | Smartplanes (Jävrebyn, Sweden) | Keva Drone (Daejeon, Republic of Korea) | DJI (Shenzhen, China) |
| Flight type | fixed wing | fixed wing | rotary wing |
| Number of images | 56 | 60 | 118 |
| Image size (pixel) | 4928 × 3264 | 7952 × 5304 | 5472 × 3648 |
| Overlap (%) | end: 70, side: 80 | end: 70, side: 80 | end: 75, side: 85 |
| Height of flight (m) | 150 | 180 | 180 |
| GSD 1 (m) | 0.0389 | 0.0242 | 0.0492 |
| Dataset Name | Dataset 1 | Dataset 2 | Dataset 3 |
|---|---|---|---|
| Number of candidate tiepoints | 73,294 | 112,451 | 175,615 |
| Number of initial point clouds | 39,041 | 65,555 | 53,062 |
| Initial point cloud conversion ratio (%) | 53.27 | 58.30 | 30.22 |
| Reprojection error of initial point cloud (pixel) | 0.9316 | 1.0243 | 0.9869 |
| Dataset Name | Dataset 1 | Dataset 2 | Dataset 3 |
|---|---|---|---|
| Number of sampled point clouds | 3922 | 4614 | 10,009 |
| Number of TIN facets | 7112 | 8465 | 18,936 |
| Processing time for point cloud sampling and TIN construction (seconds) | 1.35 | 0.39 | 0.55 |
| Name | Ranked | Unsuitability (Pixels) |
|---|---|---|
| Dataset 1 | 1 | 477.83 |
| 2 | 521.74 | |
| 3 | 606.03 | |
| Dataset 2 | 1 | 691.68 |
| 2 | 1309.21 | |
| 3 | 1427.27 | |
| Dataset 3 | 1 | 97.98 |
| 2 | 509.69 | |
| 3 | 679.41 |
| Name | Method | Mosaic Error (Pixels) |
|---|---|---|
| Dataset 1 | Image mosaicking without seamline optimization | 22.5521 |
| Image mosaicking with seamline optimization | 1.0929 | |
| Dataset 2 | Image mosaicking without seamline optimization | 11.6237 |
| Image mosaicking with seamline optimization | 0.9848 | |
| Dataset 3 | Image mosaicking without seamline optimization | 31.7093 |
| Image mosaicking with seamline optimization | 2.1861 |
| Name | Method | Processing Time for Mosaicking |
| Dataset 1 | Proposed method | 8 s |
| Commercial software | 14 min 36 s | |
| Dataset 2 | Proposed method | 16 s |
| Commercial software | 29 min 21 s | |
| Dataset 3 | Proposed method | 24 s |
| Commercial software | 29 min 34 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, S.-J.; Kim, T. Seamline Optimization Based on Triangulated Irregular Network of Tiepoints for Fast UAV Image Mosaicking. Remote Sens. 2024, 16, 1738. https://doi.org/10.3390/rs16101738
Yoon S-J, Kim T. Seamline Optimization Based on Triangulated Irregular Network of Tiepoints for Fast UAV Image Mosaicking. Remote Sensing. 2024; 16(10):1738. https://doi.org/10.3390/rs16101738
Chicago/Turabian StyleYoon, Sung-Joo, and Taejung Kim. 2024. "Seamline Optimization Based on Triangulated Irregular Network of Tiepoints for Fast UAV Image Mosaicking" Remote Sensing 16, no. 10: 1738. https://doi.org/10.3390/rs16101738
APA StyleYoon, S.-J., & Kim, T. (2024). Seamline Optimization Based on Triangulated Irregular Network of Tiepoints for Fast UAV Image Mosaicking. Remote Sensing, 16(10), 1738. https://doi.org/10.3390/rs16101738







