Abstract
In a hyperspectral image classification (HSIC) task, manually labeling samples requires a lot of manpower and material resources. Therefore, it is of great significance to use small samples to achieve the HSIC task. Recently, convolutional neural networks (CNNs) have shown remarkable performance in HSIC, but they still have some areas for improvement. (1) Convolutional kernel weights are determined through initialization and cannot be adaptively adjusted based on the input data. Therefore, it is difficult to adaptively learn the structural features of the input data. (2) The convolutional kernel size is single per layer, which leads to the loss of local information for a large convolutional kernel or global information for a small convolutional kernel. In order to solve the above problems, we propose a plug-and-play method called dynamic convolution based on structural re-parameterization (DCSRP). The contributions of this method are as follows. Firstly, compared with traditional convolution, dynamic convolution is a non-linear function, so it has more representation power. In addition, it can adaptively capture the contextual information of input data. Secondly, the large convolutional kernel and the small convolutional kernel are integrated into a new large convolutional kernel. The large convolutional kernel shares the advantages of the two convolution kernels, which can capture global information and local information at the same time. The results in three publicly available HSIC datasets show the effectiveness of the DCSRP.
1. Introduction
Hyperspectral images (HSIs) are the information of objects captured by hyperspectral imaging sensors in hundreds of spectral bands. They have a high spectral dimension and high spatial resolution. HSIs have both image information and spectral information. Image information can be used to distinguish the external characteristics of the objects, such as size and shape. The spectral information can characterize various properties of the object, such as physical, chemical, and material characteristics. The comprehensive information on HSIs lays the foundation for hyperspectral image classification (HSIC) technologies. HSIC is an important task; it involves assigning a category to each pixel in a hyperspectral image (HSI) through rich spectral and spatial information. As the development of HSIC technologies continues, HSIC technologies are widely applied in geological exploration [1,2], agriculture [3], forestry [4], environmental monitoring [5] and the military industry [6,7,8]. So far, researchers have proposed numerous methods for HSIC, which can be mainly divided into non-deep-learning-based methods and deep-learning-based methods.
In the task of HSIC, researchers have proposed various non-deep-learning-based methods to fully utilize the spectral information of HSIs, including random forest (RF) models [9], Bayesian models [10], k-nearest neighbors (KNN) [11], etc. Though the above algorithms that utilize spectral information are effective, to some extent, they overlook the spatial structural relationships between neighboring pixels of HSIs, and these structural relationships can enhance the performance of methods. In order to leverage the spatial structural relationships of HSIs and achieve satisfactory results, researchers have proposed various methods that utilize spectral-spatial information. Some examples include Markov random fields [12], sparse representation [13], metric learning [14] and compound kernels [15,16]. There is a problem of spectral information redundancy in HSIs. In order to alleviate the impact of this problem, researchers have proposed some dimensionality reduction techniques, such as principal component analysis (PCA) [17,18].
Compared with non-deep-learning methods, deep-learning-based approaches show great advantages in HSIC, because they can automatically learn complex features of HSIs. These methods include stacked autoencoder (SAE) models [19,20], Boltzmann machines [21], deep belief networks (DBN) [22,23], etc. Chen et al. [24] first introduced the SAE into HSIC. This method proposed a spectral-spatial joint deep neural network that can hierarchically extract deep-level features, leading to higher classification accuracy. In [19], the noise of the image was reduced by a band-by-band nonlinear diffusion method, and a restricted Boltzmann machine was used to extract higher-level features. The experiments prove the effectiveness of the method. Li et al. [22] employed a DBN in HSIC, utilizing a multi-layer DBN to extract features and achieving good results. In addition, tensor-based models are suitable for extracting features and classification of HSIs [25]. In recent years, convolutional neural networks (CNNs) [24,26,27] have become one of the most essential neural network architectures and have attracted the widespread attention of researchers. CNNs can not only promote the development of hyperspectral classification task through HSI restoration [28] and denoising [29] tasks, but they also improve HSIC accuracy through their excellent performance.
In [30], the proposed method can learn discriminative features among a large number of spectral-spatial features and achieve excellent results. Roy et al. proposed HybridSN [31], which can learn spectral-spatial features more effectively and can also learn more abstract spatial features, which helps to improve classification accuracy. Li et al. [22] proposed the two-stream 2D CNN architecture, which can simultaneously acquire spectral features, local spatial features and global spatial features. Not only this, but this method can adaptively fuse feature weights in two parallel streams, thereby improving the expressiveness of the network. In [32], an end-to-end residual spectral-spatial attention network (RSSAN) was proposed. This method can effectively suppress useless band information and spatial information through the spectral attention and spatial attention module, refining features in the feature-learning process. Finally, in order to avoid overfitting of training results, in the residual block, a sequential spectral-spatial attention module was implemented. In [33], the method proposed by the authors can effectively fuse feature maps of different levels and scales and can adaptively capture direction-aware and position-sensitive information, thereby improving classification accuracy. In [34], the author proposed a space-spectrum dense convolution neural network framework, FADCNN, based on a feedback attention mechanism. This method uses semantic features to enhance the attention map through the feedback attention mechanism. In addition, the network can better refine features by better mining and fusing spectral-spatial features.
Although the above CNNs have achieved satisfactory results, like most methods, to obtain a larger receptive field, they all use a stack of many small convolution kernels (the size is three). At present, some researchers have shown that large convolution kernels can build a large effective receptive field [35], which can improve the performance of CNNs. However, using large kernels is not widespread in CNN architectures. Only a few architectures employ large spatial convolution (the size is larger than three), such as AlexNet [36], Inception [37,38,39] and some architectures derived from neural architecture search [40,41,42,43]. Recently, some researchers have employed large kernels in order to design advanced CNN architectures. For example, Liu et al. [44] successfully increased the convolution kernel size to 7 × 7 and significantly improved the performance of the network. Shang et al. [45] proposed a method based on Multi-Scale Cross-Branch Response and Second-Order Channel Attention (MCRSCA), which utilizes 5 × 5 kernels to capture rich and complementary spatial information. The authors of [46] introduced the Multi-Scale Random Convolution Broad Learning System (MRCBLS). This method utilizes different large sizes of convolution kernels. By combining multi-scale spatial features extracted from different kernel sizes, a good HSIC result is achieved. In [47], the proposed method employs 5 × 5 convolution kernels in an end-to-end manner to extract spectral-spatial features. In [48], the proposed model aggregates convolution kernel features of different sizes, which helps to improve the performance of the network.
To obtain a large and effective receptive field and further enhance the performance of CNNs under small sample conditions, we propose a plug-and-play method called structural re-parameterization dynamic convolution (DCSRP). The contributions of this method are as follows: (1) Dynamic convolution is a nonlinear function. It has more representation power, and it can enhance the feature representation capability of the convolution layer. (2) A large kernel is allowed to capture global features and local features by fusing a small kernel into a large kernel, hence improving the performance of the large kernel.
2. Materials and Methods
In this subsequent part, we provide an elaborate explanation of DCSRP. We firstly describe the data preprocessing. Next, we provide a summary of the complete architecture of the DCSRP and show how it can be used. Then, we introduce dynamic convolution in detail in Section 3 and structural re-parameterization in Section 4.
2.1. Data Preprocessing
In our experiments, the input data are in the form of data cube. We use to represent the original input HSI cube: H means the height of the input cube, W means the width of the input cube, and C means the spectral dimension of the input cube. Firstly, PCA is applied to reduce the dimensions of the data. Then, each pixel is taken as the center to obtain the input 3D patches. The class of the center pixels represents the ground-truth of these patches.
2.2. Overall Framework of Proposed Method
CNNs have achieved advanced results in HSIC. Compared to small convolution kernels, large convolution kernels can enhance the receptive field more effectively and can bring higher shape bias rather than texture bias [49], which can make full use of the spatial information of HSI. At present, to enlarge the receptive fields, a typical fashion is overlapping using a stack of small kernel convolutions [50,51,52]. However, some research findings indicate that too many layers will lead to the opposite result [53]. To obtain a large and effective receptive field and further enhance the HSIC accuracy of CNNs under small sample conditions, we propose DCSRP. DCSRP increases the model complexity without increasing the depth of the network, improving the performance of the model. The better performance of the proposed approach can be attributed to the following two factors. One is using multiple convolution kernels in each layer instead of a single kernel and aggregating these kernels in a non-linear manner, which enhances the representation of HSI information. The other is the addition of a smaller kernel to the larger kernel, enabling the larger kernel to effectively capture smaller-scale features and slightly larger global features of HSI, which enhances the feature extraction capability of the model. Figure 1 shows the structure of DCSRP. Next, we describe the data flow of the proposed method.
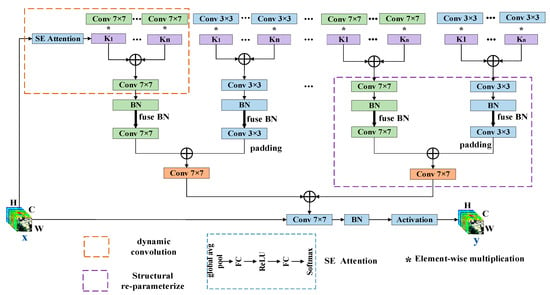
Figure 1.
Overall framework of proposed method.
We define x as the input HSI data block, and the size of x is H × W × C. The x will first go through the dynamic convolution part, which can enhance the representation of HSI information. The detailed process is as follows. The x will calculate the weight of the convolution kernel through squeeze-and-excitation (SE) attention, which can extract features that are beneficial to improving the accuracy of HSI classification by establishing connections between channels. During this process, first, the spatial information of x is compressed through the global average pooling layer, and the size of x becomes 1 × 1 × C. Then, x will go through two FC layers (with a ReLU activation function in the middle), and the sizes of x are 1 × 1 × C/r, 1 × 1 × C/r and 1 × 1 × k, respectively. We denote the number of attention weights by k and set k as 2. Thirdly, attention weights are generated through softmax. Fourthly, the generated weights will act on k convolution kernels. The specific operation consists of the k weights being multiplied by k convolution kernel parameters, respectively. Finally, k convolution kernels are added and aggregated into a convolution kernel. Since the generated weights will change as the x changes, the aggregated convolution kernel weights will also change, and the dynamic arises from this. Dynamic convolution will generate n groups of convolution kernels with a size of 7 × 7 and 3 × 3, and the size of n can be freely set. After dynamic convolution comes the structural re-parameterization part, which can enhance the feature extraction capability of the model. The specific operations include the convolution kernels of sizes 7 × 7 and 3 × 3 being fused with the Batch Normalization (BN) layer, respectively. Then, the 7 × 7 and the 3 × 3 n groups of convolution kernels are integrated into n new 7 × 7 convolution kernels. The specific operation consists of expanding the 3 × 3 convolution kernel into a 7 × 7 convolution kernel by padding zeros, and the two 7 × 7 convolution kernels are added and aggregated into a convolution kernel. Because there are n groups of 7 × 7 and 3 × 3 convolution kernels, n 7 × 7 convolution kernels will be generated. These 7 × 7 convolution kernels are added to generate a 7 × 7 convolution kernel. The 7 × 7 convolution kernel will extract features of HSI data. After passing through the BN layer and activation function, the output y is obtained, whose size is H × W × C.
As shown in Figure 2, as a plug-and-play method, the using method of DCSRP is simple. When there is a necessity to enhance the original network model’s performance, simply substitute the traditional convolution layer in the original network with DCSRP. When a new network needs to be built, the method of DCSRP is the same as that of the traditional convolution layer. Figure 2 is an example of using DCSRP and displays the network structures used in the verification. In this network, the input data first pass through two convolution layers, and the data size remains constant. Then, the data go through a global average pooling layer. Finally, the classification result is obtained through the fully connected layer. Figure 2a is the original convolution network structure, Figure 2b uses a dynamic convolution network structure, and Figure 2c uses a DCSRP network structure.

Figure 2.
An example of using DCSRP. (a) Original network structure; (b) using DYConv network structure; (c) using DCSRP network structure.
2.3. Dynamic Convolution
To improve the accuracy of the network in the HSIC task, the currently popular approach is to increase the complexity of the neural network by increasing the depth of the network. However, too many layers can lead to disappointing results. Thus, we propose DCSRP. This approach increases model complexity in a new way and improves the feature representation capability of the network. Figure 3 illustrates the structure of the dynamic convolution.

Figure 3.
The framework of dynamic convolution.
Figure 3 shows a dynamic convolution layer. There are k convolution kernels in dynamic convolution; these convolution kernels have a uniform kernel size, input and output dimensions. We define x as the input HSI data block. The input x first undergoes SE attention, which extracts features that are beneficial to improving the accuracy of HSI classification by establishing connections between channels. For an HSI data block of size H × W × C, after SE attention, the size of the HSI data becomes 1 × 1 × k. SE attention makes full use of spatial and spectral information of HSI data and generates attention weights. Then, these attention weights are applied to k convolution kernels using multiplication. Thirdly, these convolution kernels are aggregated into one convolution kernel using addition, which extracts HSI information with more expressive capability. Finally, after passing through a BN layer and an activation function, the output y is obtained. Due to the padding zero operation, the output HSI data have the same size as the input HSI data. Dynamic convolution enhances the representation of HSI information by aggregating multiple convolution kernels that can extract effective channel information. It should be noted that the convolutional kernel that is ultimately aggregated changes based on variations in the input—hence the name dynamic convolution.
represents the traditional convolution process, where represents the weight matrix, represents the bias, and represents the activation function (e.g., ReLU). represents the process of dynamic convolution, which aggregates several (k) linear functions. The process can be described as follows:
where represents the attention weight for the k-th linear function . It should be noted that the total weight and total bias have the same attention weights. The attention weights are not fixed; they will change when input x is changed. They represent the optimal set of linear models for input. The aggregated model is a non-linear function. Therefore, dynamic convolution has a stronger capacity for feature representation.
We employ the SE [43] method to generate the attention weights for k convolution kernels. SE can extract features that are beneficial to improving the accuracy of HSI classification by establishing connections between channels. Figure 4 is the structure of the SE method. We use to denote the original feature maps of the HSIs for an HSI data block of size H × W × C. Firstly, the global spatial information of HSI data is squeezed (Fsq) by global average pooling, obtaining a column vector of size 1 × 1 × C, which includes the attention weights for each channel. This process can be represented as:

Figure 4.
Framework of squeeze-and-excitation method.
This operation has some advantages. The first is that the filters using a local receptive field can utilize extra-regional context information to a certain extent. Secondly, the excitation (Fex) operation will use the information aggregated in the squeeze operation, aiming to capture channel-wise dependencies. This operation consists of two fully connected layers and a ReLU function, which can learn non-linear interactions between channels and ensure emphasis on multiple channels. Through this operation, a column vector is obtained. Thirdly, the final output of the features is obtained by rescaling (Fscale) the transformation output. The process can also be described by the following formula:
where , represents channel-wise multiplication between the feature maps and .
2.4. Structural Re-Parameterization
CNNs have achieved satisfactory results in HSIC, but most networks are designed with small kernels. In recent years, researchers have proved that in the design of convolution neural network models, compared with small convolution kernels, large convolution kernels can build large and effective receptive fields and can extract more spatial information of HSIs. Therefore, some advanced convolution models apply large convolution kernels and show attractive performance and efficiency. Although a large convolution kernel shows better performance, directly increasing the convolution kernel size may lead to the opposite result in HSIC. In order to solve this problem, we propose DCSRP, which better extracts the detailed features and slightly larger global features of HSIs. Specifically, the large convolution kernel and the small convolution kernel are fused with a BN layer, respectively. Then, the small convolution kernel is made the same size as the large convolution kernel by padding zero. Finally, the two large convolution kernels are added and aggregated into a convolution kernel. Therefore, the large kernel can capture small-scale patterns, thus improving the performance of the model.
Figure 5 is an example of re-parameterizing a small kernel (e.g., 3 × 3) into a larger kernel (e.g., 7 × 7). We denote the kernel of a 3 × 3 convolutional layer with input channels and output channels as . Similarly, we denote the kernel of a 7 × 7 convolutional layer with input channels and output channels as . For example, there is an HSI data block of size , and after the convolution operation, its size becomes . For the ease of clarifying processes, we set and to be 2. , , and are used to represent the accumulated mean, standard deviation, learned scaling factor and bias of the BN layer following the 3 × 3 convolution layer. Similarly, , , , are used to represent the accumulated mean, standard deviation, learned scaling factor and bias of the BN layer following the 7 × 7 convolution layer. Let and be the input HSI data and output HSI data, respectively. Then, ∗ is used to represent the convolution operator. In the example, , , and . The output features can be represented as:
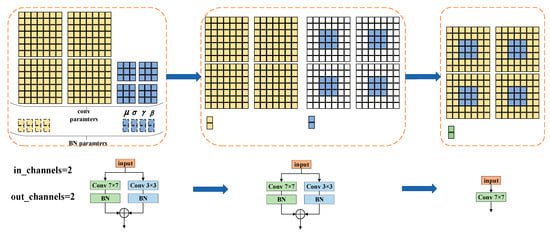
Figure 5.
An example of structural re-parameterization. For ease of visualization, we assume in channels = out channels = 2; thus, the 3 × 3 layer has four 3 × 3 matrices, and the 7 × 7 layer has four 7 × 7 matrices.
The calculation formula for the feature maps after the batch normalization (BN) layer is as follows:
where represents the HSI feature maps of the input in the BN layer, and i represents the value of the i-th channel of . Additionally, .
After fusing the BN and convolution layer into a convolution layer, let be the kernel and bias converted from . We have:
The above process can be described as follows. The first step is to fuse the 7 × 7 convolution layer and the 3 × 3 convolution layer with the BN layer, respectively. After such transformations, one 7 × 7 kernel, one 3 × 3 kernel and two bias vectors are obtained. Then, the two independent bias vectors are fused into a bias vector by addition. The final 7 × 7 kernel is obtained by adding the 3 × 3 kernel onto the 7 × 7 kernel center. The detailed process is first to pad the 3 × 3 kernel to 7 × 7 with zero-padding; then, the two 7 × 7 kernels are added up.
3. Experiments
In the first part of this section, we provide a detailed description of the three public HSI datasets that are used in the experiments. In the second part, we introduce the experimental configuration. The last part gives the experiment results.
3.1. Data Description
3.1.1. Indian Pines
The Indian Pines (IP) dataset was acquired using the AVIRIS sensor at an Indian pine test site in the northwestern part of Indiana. The spatial size of the dataset is 145 × 145, and the number of spectra is 224. The dataset creators further refined the dataset by removing spectra that caused interference, resulting in a final spectral dimension of 200. Excluding background pixels in the IP, there are a total of 10,249 pixels that can be used for classification, which can be categorized into 16 classes. In Figure 6, (a) is the false color image, (b) is the label map, and (c) is the corresponding color label. Detailed information on training samples and testing samples of the IP dataset is shown in Table 1.

Figure 6.
The Indian Pines dataset. (a) False color image. (b) Label map. (c) The corresponding color labels.

Table 1.
The number of samples used for training and testing in the IP dataset.
3.1.2. University of Pavia
The University of Pavia (PU) dataset was acquired using the ROSIS sensor at the University of Pavia in northern Italy. The spatial size of the dataset is 610 × 340, and the number of spectra is 115. The dataset creators further refined the dataset by removing spectra that caused interference, resulting in a final spectral dimension of 103. Excluding background pixels in the PU dataset, there are a total of 42,776 pixels that can be used for classification, which can be categorized into 9 classes. In Figure 7, (a) is the false color image, (b) is the label map, and (c) is the corresponding color label. The detailed information on training samples and testing samples of the PU dataset is shown in Table 2.

Figure 7.
The University of Pavia dataset. (a) False color image. (b) Label map. (c) The corresponding color labels.

Table 2.
The number of samples used for training and testing in the PU dataset.
3.1.3. Salinas
The Salinas (SA) dataset was acquired using the AVIRIS sensor over the Salinas Valley in California. The spatial size of the dataset is 512 × 217, and the number of spectra is 224. The dataset creators further refined the dataset by removing spectra that caused interference, resulting in a final spectral dimension of 204. Excluding background pixels in the SA dataset, there are a total of 54,129 pixels that can be used for classification, which can be categorized into 16 classes. In Figure 8, (a) is the false color image, (b) is the label map, and (c) is the corresponding color label. The detailed information on training samples and testing samples in the SA dataset is shown in Table 3.

Figure 8.
The Salinas dataset. (a) False color image. (b) Label map. (c) The corresponding color labels.

Table 3.
The number of samples used for training and testing in the SA dataset.
All the experiments in this paper were conducted in the IP, PU and SA. The experimental data information for the three datasets is shown in Table 1, Table 2, Table 3. The training data are randomly selected and non-overlapping.
In the experiments in this paper, 5 samples were selected from each class in the HSI as training samples, and the remaining samples were used as test samples. The numbers of training samples in the IP, PU and SA datasets are 80, 45 and 80, respectively, and the numbers of test samples are 10,169, 42,731 and 54,049, respectively.
3.2. Experimental Configuration
The paper utilizes an Intel(R) Core(TM) i9-10900K CPU @ 3.70 GHz, along with an Nvidia RTX 4090 graphics processing unit. The code was run on a Windows 10 environment. The compiler and deep-learning framework used are PyTorch 1.8.1 and Python 3.9, respectively.
In the experiment, we use the Kappa coefficient (Kappa), average accuracy (AA) and overall accuracy (OA) to evaluate the effectiveness of the methods. Kappa measures the agreement between model predictions and actual classifications. AA represents the average accuracy across different categories. OA represents the quantity of accurately classified pixels relative to the total quantity of pixels.
3.3. Experimental Results
3.3.1. Ablation Studies
To demonstrate the superiority of the DCSRP method, we conducted ablation experiments. The results are presented in Table 4.

Table 4.
Experimental results of ablation studies.
To validate the effectiveness of the proposed DCSRP method, experiments are performed with three datasets, and a simple two-layer convolution layer and 5 samples were randomly selected for each class as the training samples. Firstly, we use traditional convolution as a baseline. According to the experimental results of Section 4, on each dataset, we adopt the optimal experimental parameters in the experiments. The following gives the specific parameter information of each dataset. In the IP dataset, the size of the input data blocks is 13 × 13 × 40, the number of parallel convolution kernels is 3, and the kernel size is 9 × 9. In the PU dataset, the size of the input data blocks is 25 × 25 × 10, the number of parallel convolution kernels is 5, and the kernel size is 9 × 9. In the SA dataset, the size of the input data blocks is 23 × 23 × 50, the number of parallel convolution kernels is 5, and the kernel size is 7 × 7. Secondly, we use dynamic convolution to obtain the results from the three datasets and compare the dynamic convolution with the traditional convolution. The results demonstrate that dynamic convolution can improve the performance of the model. This is because multiple convolution kernels are used in the convolution layer, and these parallel kernels are aggregated in a non-linear manner using attention mechanisms, thereby improving the feature representation capability of the model. Finally, we use the proposed method to obtain the results from the three datasets and compare the proposed method with dynamic convolution. The results show that OA, AA and Kappa increased with different degrees in the three datasets. This is because the proposed method enhances the performance of the convolution kernel. Adding a relatively smaller kernel into a larger kernel enables the larger kernel to capture smaller-scale features, resulting in improved classification accuracy.
It can be seen from Table 4 that replacing traditional static convolution with dynamic convolution can improve the model’s performance. In the IP dataset, there is an increase of 2.70% in OA, 1.67% in AA and 3.16% in Kappa compared to the baseline. In the PU dataset, the three metrics increased by 2.34%, 1.70% and 2.63%, respectively. Similarly, in the SA dataset, there are improvements in OA, AA and Kappa by 1.46%, 1.86% and 1.65%, respectively. Moreover, when replacing dynamic convolution in the model with the proposed method, the performance is further enhanced. In the IP, PU and SA datasets, there are respective increases of 1.80%, 0.52% and 0.35% in OA, 1.67%, 0.55% and 0.05% in AA, and 1.84%, 0.56% and 0.42% in Kappa. Overall, the results of the ablation experiments demonstrate that the proposed method not only improves the model’s feature representation capability but also enhances the performance of large kernels, thereby strengthening the final classification results.
3.3.2. Compared Results in Different Methods
In order to ascertain the validity of the proposed method, we conducted experiments utilizing the following models, including SSRN [30], HybridSN [31], BSNET [54], 3D2DCNN [55], SSAtt [56], SpectralNET [57], JigsawHSI [48] and HPCA [33]. We compared the results obtained from the original networks with the results obtained by replacing the 2D convolution layers in the original networks with the dynamic convolution and proposed method. Table 5 presents the overall accuracy of the different methods on different models in the three datasets. The detailed experimental results are presented in Table 6, Table 7, Table 8. In Table 6, Table 7, Table 8, TC represents using the traditional convolution network structure, DC represents using the dynamic convolution network structure, and PM represents using the proposed method network structure. According to the experimental results of Section 4, on each dataset, we adopt the optimal experimental parameters in the experiments. The following includes the specific parameter information of each dataset. In the IP dataset, the size of the input data blocks is 13 × 13 × 40, the number of parallel convolution kernels is 3, and the kernel size is 9 × 9. In the PU dataset, the size of the input data blocks is 25 × 25 × 10, the number of parallel convolution kernels is 5, and the kernel size is 9 × 9. In the SA dataset, the size of the input data blocks is 23 × 23 × 50, the number of parallel convolution kernels is 5, and the kernel size is 7 × 7.

Table 5.
The overall accuracy of different methods on different models in the three datasets.

Table 6.
The classification results of different methods on different models in the IP dataset.

Table 7.
The classification results of different methods on different models in the PU dataset.

Table 8.
The classification results of different methods on different models in the SA dataset.
In the IP dataset, Table 6 displays the classification results of the different methods on the different models. As evident from Table 6, under the same experimental conditions, when the dynamic convolution is added, compared with the experimental results of traditional convolution, the specific results of the increase in OA are 2.24%, 0.75%, 0.52%, 0.70%, 0.51%, 0.93%, 2.21% and 0.83% in SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA. When the proposed method is added, compared with the experimental results of dynamic convolution, it further enhances the OA by 0.87%, 1.45%, 3.11%, 1.56%, 0.89%, 1.30%, 0.83% and 2.59% for SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA, respectively. We compare the results by adding the proposed method and traditional method. The specific results of the increase in OA are 3.11%, 2.20%, 3.63%, 2.26%, 1.40%, 2.23%, 3.04% and 3.42% in SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA. In the PU dataset, Table 7 displays the classification results of different methods on different models. As evident from Table 7, under the same experimental conditions, when the dynamic convolution is added, compared with the experimental results of traditional convolution, the specific results of the increase in OA are 2.39%, 0.69%, 1.01%, 0.41%, 0.86%, 1.42%, 0.89% and 0.64% in SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA. When the proposed method is added, we compare the results adding the proposed method and dynamic convolution, which further enhances the OA by 2.19%, 1.45%, 0.35%, 2.18%, 0.78%, 1.21%, 0.67% and 2.01% for SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA. We compare the results by adding the proposed method and the traditional method. The specific results of the increase in OA are 4.58%, 2.14%, 1.36%, 2.59%, 1.64%, 2.63%, 1.56% and 2.65% in SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA. In the SA dataset, Table 8 displays the classification results of the different methods on the different models. As evident from Table 8, under the same experimental conditions, when the dynamic convolution is added, compared with the experimental results of traditional convolution, the specific results of the increase in OA are 0.43%, 0.87%, 0.29%, 0.37%, 0.36%, 1.00%, 0.63% and 0.42% in SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA. When the proposed method is added, compared with the experimental results of dynamic convolution, it further enhances the OA by 0.50%, 0.65%, 1.37%, 0.59%, 0.94%, 0.51%, 0.68% and 0.61% for SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA. We compare the results by adding the proposed method and the traditional method. The specific results of the increase in OA are 0.93%, 1.52%, 1.66%, 0.96%, 1.30%, 1.51%, 1.31% and 1.03% in SSRN, HybridSN, BSNET, 3D2DCNN, SSAtt, SpectralNET, JigsawHSI and HPCA.
Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 visually display the different models’ comparative results of the experiments in the IP, PU and SA datasets and show the classification maps of the IP, PU and SA datasets. As evident from Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, when adding the proposed method, the classification reduction maps have smoother boundaries and edges, effectively demonstrating the superiority of the proposed method.

Figure 9.
(a–i) are the classification maps of different methods in the IP dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 10.
(a–i) are the classification maps of the dynamic convolution that is added to different methods in the IP dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 11.
(a–i) are the classification maps of the proposed method that is added to different methods in the IP dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 12.
(a–i) are the classification maps of different methods in the PU dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 13.
(a–i) are the classification maps of the dynamic convolution that is added to different methods in the PU dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 14.
(a–i) are the classification maps of the proposed method that is added to different methods in the PU dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 15.
(a–i) are the classification maps of the proposed method that is added to different methods in the SA dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 16.
(a–i) are the classification maps of the dynamic convolution that is added to different methods in the SA dataset. (a) Label map; (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.

Figure 17.
(a–i) are the classification maps of the proposed method that is added to different methods in the SA dataset. (a) Label map. (b–i) are the classification maps of different methods. (b) SSRN; (c) HybridSN; (d) BSNET; (e) 3D2DCNN; (f) SSAtt; (g) SpectralNET; (h) JigsawHSI; (i) HPCA.
Figure 18, Figure 19, Figure 20 more intuitively show the changed situation in the OA of the different models when adding the dynamic convolution and the proposed method in IP, PU and SA. Purple corresponds to the experimental results for each model when employing the traditional convolution. Green corresponds to the experimental results for each model when employing the dynamic convolution. Orange corresponds to the experimental results for each model when employing the proposed method.

Figure 18.
The OA situation of different models when adding the different methods is shown in IP dataset.

Figure 19.
The OA situation of different models when adding the different methods is shown in PU dataset.

Figure 20.
The OA situation of different models when adding the different methods is shown in SA dataset.
3.3.3. Experimental Results of Different Sizes of Convolutional Kernels
In this section, we verify the mutual encouragement between the large convolutional kernel and the small convolutional kernel. We adopt the optimal experimental parameters on different datasets. Table 9, Table 10, Table 11, Table 12, Table 13, Table 14 show the experimental results of the three datasets. SC represents the experimental results of using the small convolutional kernel; BC represents the experimental results of using the large convolution kernel; SBC represents the experimental results of using the concat operation to add the results of the small convolution kernel and the large convolution kernel. PRO represents the experimental results of using the proposed method.

Table 9.
Comparing four methods results of different sizes of convolutional kernels in IP dataset.

Table 10.
Comparing remaining methods results of different sizes of convolutional kernels in IP dataset.

Table 11.
Comparing four methods results of different sizes of convolutional kernels in PU dataset.

Table 12.
Comparing remaining methods results of different sizes of convolutional kernels in PU dataset.

Table 13.
Comparing four methods results of different sizes of convolutional kernels in SA dataset.

Table 14.
Comparing remaining methods results of different sizes of convolutional kernels in SA dataset.
We enumerate the comparison results in different models and describe the results in the order of the OA of the proposed method with the OA of SC, BC and SBC. Table 9 and Table 10 are the results of the IP dataset. In SSRN, the OA increased by 2.19%, 3.54% and 1.49%, respectively.
In HybridSN, the OA increased by 1.97%, 2.20% and 1.47%. respectively. In BSNET, the OA increased by 3.24%, 3.63% and 4.91%, respectively. In 3D2DCNN, the OA increased by 0.20%, 2.26% and 1.39%, respectively. In SSAtt, the OA increased by 1.39%, 1.40% and 3.25%, respectively. In SpectralNET, the OA increased by 1.64%, 2.23% and 2.23%, respectively; In JigsawHSI, the OA increased by 2.23%, 0.05% and 3.04%, respectively. In HPCA, the OA increased by 2.32%, 3.42% and 2.17%, respectively.
Table 11 and Table 12 show the results of the PU dataset. In SSRN, the OA increased by 7.16%, 4.58% and 3.65%, respectively. In HybridSN, the OA increased by 1.66%, 2.14% and −0.78%, respectively. In BSNET, the OA increased by 2.54%, 1.36% and 0.36%, respectively. In 3D2DCNN, the OA increased by 2.42%, 2.59% and 1.59%, respectively. In SSAtt, the OA increased by 5.19%, 1.64% and 2.03%, respectively. In SpectralNET, the OA increased by 3.12%, 2.63% and 0.75%, respectively. In JigsawHSI, the OA increased by 1.32%, 1.56% and 0.93%, respectively. In HPCA, the OA increased by 0.93%, 2.65% and 1.88%, respectively. Although the proposed method gives results that are lower than the those of SBC in HybridSN, the results of the proposed method are higher than the results in other models.
Table 13 and Table 14 show the results of the SA dataset. In SSRN, the OA increased by 2.04%, 0.93% and 0.44%, respectively. In HybridSN, the OA increased by 1.37%, 1.55% and −0.16%, respectively. In BSNET, the OA increased by 2.64%, 1.66% and 1.55%, respectively. In 3D2DCNN, the OA increased by 2.42%, 0.96% and −0.37%, respectively. In SSAtt, the OA increased by 0.45%, 1.30% and 3.60%, respectively. In SpectralNET, the OA increased by 3.84%, 1.51% and 1.91%, respectively. In JigsawHSI, the OA increased by 3.22%, 1.31% and 0.73%, respectively. In HPCA, the OA increased by 0.83%, 1.03% and 0.86%, respectively. Although the results of the proposed method are lower than the results of SBC in HybridSN and 3D2DCNN, the results of the proposed method are competitive. At the same time, the results of the proposed method are higher than those in the other models.
In summary, the experimental results can prove the mutual encouragement between the large convolutional kernel and the small convolutional kernel of the proposed method.
4. Discussion
4.1. The Influence of the Number of Parallel Re-Parameterization Kernels on Experimental Results
Different inputs produce different attention weights, which leads to the weights of the re-parameterized convolution kernel being different. The different numbers of parameterized convolution kernels will have a certain impact on the experimental results. In order to determine the optimal number of kernels, we compared the results with different numbers of convolution kernels. Five sets of experiments were conducted, with the number of parallel kernels being one, two, three, four, five and six, respectively. Figure 21 displays the experimental results.
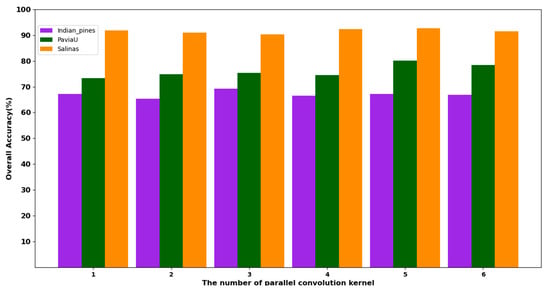
Figure 21.
The results of parallel convolution kernels with different numbers in three datasets.
As evident from Figure 21, in the IP dataset, the best result is obtained when the number of parallel convolutional kernels is three. In the PU and SA datasets, the best results are obtained when the number of parallel convolutional kernels is five. Therefore, there is a non-linear relationship between the number of convolution kernels and the experimental results.
4.2. The Influence of Different Channel and Spatial Sizes on Experimental Results
We compared the results of different spatial sizes and spectral dimensions, aiming to identify the optimal spatial size and spectral dimension for each dataset.
The number of spectral dimensions in the extracted 3D patches indicates how much spectral information is available for HSIC. In the experiments, the spectral dimensions were set to {10, 20, 30, 40, 50, 60, 70}. In order to obtain the optimal number of dimensions, we use the control variable method and set the spatial size to 17 × 17 in the IP, PU and SA.
Figure 22 displays the experimental results of the OA with different spectral dimensions in different datasets. In the IP dataset, increasing the spectral dimension initially leads to an improvement in OA, followed by a subsequent decrease. Notably, the highest OA is observed when the spectral dimension is 40. Conversely, the PU dataset exhibits a different trend. Initially, the OA decreases with an increase in the spectral dimension, followed by an increase and ultimately another decrease. The optimal number of channels for the highest OA is observed at 10. Moving on to the SA dataset, as the number of channels increases, the OA first improves and then declines. The highest OA is achieved when the number of channels is 50. Consequently, the optimal spectral dimension varies across the three datasets. Specifically, for the IP, PU and SA datasets, the proposed method determined the optimal spectral dimensions to be 40, 10 and 50, respectively.

Figure 22.
The experimental results of OA with different spectral dimensions in three datasets.
The spatial size in the extracted 3D patches indicates how much spatial information is available for HSIC. In this paper, the effect of spatial size on the performance of the proposed method is verified in three datasets. In the experiments, the spatial size was set to {11 × 11, 13 × 13, 15 × 15, 17 × 17, 19 × 19, 21 × 21, 23 × 23, 25 × 25, 27 × 27, 29 × 29}, and the number of channels of the IP, PU and SA datasets was set to 40, 10 and 50, respectively.
Figure 23 displays the experimental results of the OA with different spatial sizes in different datasets. For the IP dataset, there is a clear decreasing trend in OA with an increase in spatial size. The highest OA is achieved when the spatial size is 13 × 13. The PU dataset does not exhibit a discernible trend in OA as the spatial size increases. Notably, the OA achieves its maximum when the spatial size is configured as 25 × 25. Turning to the SA dataset, the OA demonstrates a pattern of first decreasing, then increasing and subsequently decreasing again with the increase in spatial size. The highest OA is attained when the spatial size is 23 × 23. Consequently, the optimal spatial size varies across the three datasets. Specifically, for the IP, PU and SA datasets, the results determine the optimal spatial sizes to be 13 × 13, 25 × 25 and 23 × 23, respectively.
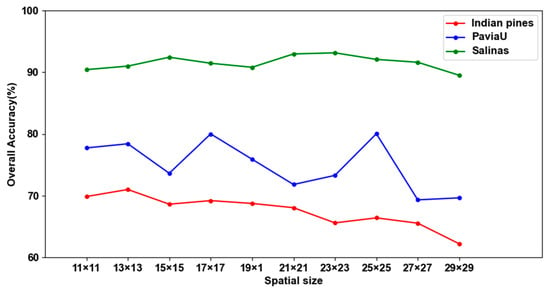
Figure 23.
The experimental results of OA with different spatial sizes in three datasets.
4.3. The Influence of Different Re-Parameterization Kernel Sizes
Adding relatively smaller kernels to larger kernels can allow the large kernel to capture small-scale features. Therefore, the experimental results will change with the size of the large kernel. To determine the optimal size of the kernel, we compared the results of adding a 3 × 3 kernel to larger kernels of different sizes, such as {5 × 5, 7 × 7, 9 × 9, 11 × 11 and 13 × 13}. Figure 24 displays the experimental results.
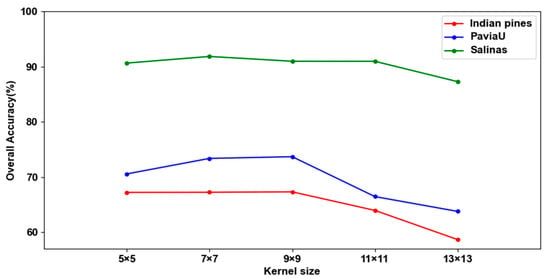
Figure 24.
The results of different re-parameterization kernel sizes in three datasets.
In Figure 24, the experimental results generally exhibit a pattern of initially increasing and subsequently decreasing in the three datasets. This trend may be attributed to the limitation of input spatial sizes. When the kernel size is 13 × 13, the experimental results decrease significantly. This may be because the size of the convolution kernel is similar to the size of the input data. The optimal result is attained with a kernel size of 7 × 7 in the SA dataset, and in the IP and PU datasets, the finest results are obtained when the kernel size is 9 × 9. Therefore, there is a non-linear relationship between the size of the kernel and the experimental results.
5. Conclusions
This paper proposes a plug-and-play method called structural re-parameterization dynamic convolution. Firstly, dynamic convolution is a non-linear function, so it has more representation power. In addition, it can adaptively capture the contextual features of input data. Secondly, the large convolutional kernel and the small convolutional kernel are integrated into a new large convolutional kernel, which can capture global information and local information at the same time. To validate the effectiveness of the proposed method, we compared the experimental results of the original network with the results obtained by adding the proposed method to the original network on three datasets. The results illustrate that the proposed method is proficient at extracting spatial features and improving the model’s performance.
Author Contributions
Conceptualization: C.D. and X.L.; methodology: C.D. and X.L.; validation: X.L., J.C., M.Z. and Y.X.; investigation: X.L., J.C., M.Z. and Y.X.; writing—original draft preparation: C.D. and L.Z.; writing—review and editing: C.D. and X.L.; supervision: C.D. and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundations of China (grant no. 61901369, grant no. 62101454) and the Xi’an University of Posts and Telecommunications Graduate Innovation Foundation (grant no. CXJJYL2022040).
Data Availability Statement
The Indiana Pines, University of Pavia and Salinas datasets are available online at https://ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes#userconsent (accessed on 1 May 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Flores, H.; Lorenz, S.; Jackisch, R.; Tusa, L.; Contreras, I.C.; Zimmermann, R.; Gloaguen, R. UAS-based hyperspectral environmental monitoring of acid mine drainage affected waters. Minerals 2021, 11, 182. [Google Scholar] [CrossRef]
- Gao, A.F.; Rasmussen, B.; Kulits, P.; Scheller, E.L.; Greenberger, R.; Ehlmann, B.L. Generalized unsupervised clustering of hyperspectral images of geological targets in the near infrared. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 4294–4303. [Google Scholar]
- Zhou, S.; Sun, L.; Ji, Y. Germination Prediction of Sugar Beet Seeds Based on HSI and SVM-RBF. In Proceedings of the 4th International Conference on Measurement, Information and Control (ICMIC), Harbin, China, 23–25 August 2019; pp. 93–97. [Google Scholar]
- Haq, M.A.; Rahaman, G.; Baral, P.; Ghosh, A. Deep learning based supervised image classification using UAV images for forest areas classification. J. Indian Soc. Remote Sens. 2021, 49, 601–606. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; An, Z.; Jiang, Z.; Ma, Y. A novel spectral-unmixing-based green algae area estimation method for GOCI data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 437–449. [Google Scholar] [CrossRef]
- Makki, I.; Younes, R.; Francis, C.; Bianchi, T.; Zucchetti, M. A survey of landmine detection using hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2017, 124, 40–53. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Nigam, R.; Bhattacharya, B.K.; Kot, R.; Chattopadhyay, C. Wheat blast detection and assessment combining ground-based hyperspectral and satellite based multispectral data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 473–475. [Google Scholar] [CrossRef]
- Gualtieri, J.A.; Cromp, R.F. Support Vector Machines for Hyperspectral Remote Sensing Classification. In Proceedings of the 27th AIPR Workshop: Advances in Computer-Assisted Recognition, Washington, DC, USA, 14–16 October 1998; SPIE: Bellingham, WA, USA, 1999; Volume 3584, pp. 221–232. [Google Scholar]
- Jain, V.; Phophalia, A. Exponential Weighted Random Forest for Hyperspectral Image Classification. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3297–3300. [Google Scholar]
- Chen, Y.; Lin, Z.; Zhao, X. Riemannian manifold learning based k-nearest-neighbor for hyperspectral image classification. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 1975–1978. [Google Scholar]
- Wu, Z.; Shi, L.; Li, J.; Wang, Q.; Sun, L.; Wei, Z.; Plaza, J.; Plaza, A. GPU parallel implementation of spatially adaptive hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1131–1143. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Cheng, G.; Li, Z.; Han, J.; Yao, X.; Guo, L. Exploring hierarchical convolutional features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6712–6722. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized composite kernel framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, J.; Chen, C.L.P. Extreme learning machine with composite kernels for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 2351–2360. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, R.; Wu, Q. Hyperspectral image classification based on PCA network. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016. [Google Scholar]
- Gao, F.; Dong, J.; Li, B.; Xu, Q. Automatic change detection in synthetic aperture radar images based on PCANet. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1792–1796. [Google Scholar] [CrossRef]
- Zhou, S.; Xue, Z.; Du, P. Semisupervised stacked autoencoder with cotraining for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3813–3826. [Google Scholar] [CrossRef]
- Shi, C.; Pun, C.M. Multiscale superpixel-based hyperspectral image classification using recurrent neural networks with stacked autoencoders. IEEE Trans. Multimed. 2019, 22, 487–501. [Google Scholar] [CrossRef]
- Midhun, M.E.; Nair, S.R.; Prabhakar, V.T.N.; Kumar, S.S. Deep Model for Classification of Hyperspectral Image Using Restricted Boltzmann Machine. In Proceedings of the International Conference on Interdisciplinary Advances in Applied Computing, Amritapuri, India, 10–11 October 2014; pp. 1–7. [Google Scholar]
- Li, T.; Zhang, J.; Zhang, Y. Classification of Hyperspectral Image Based on Deep Belief Networks. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 5132–5136. [Google Scholar]
- Jiang, Z.; Pan, W.D.; Shen, H. Universal Golomb–Rice Coding Parameter Estimation Using Deep Belief Networks for Hyperspectral Image Compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3830–3840. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Yang, J.; Xiao, L.; Zhao, Y.Q.; Chan, J.C.W. Variational regularization network with attentive deep prior for hyperspectral–multispectral image fusion. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J.; Pla, F. Capsule networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2145–2160. [Google Scholar] [CrossRef]
- Li, X.; Ding, M.; Gu, Y.; Pižurica, A. An End-to-End Framework for Joint Denoising and Classification of Hyperspectral Images. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3269–3283. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Huang, S.; Liao, W.; Chan, J.; Kong, S. Multilayer sparsity-based tensor decomposition for low-rank tensor completion. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6916–6930. [Google Scholar] [CrossRef] [PubMed]
- Zilong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar]
- Kumar, R.S.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D-2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar]
- Li, X.; Ding, M.; Pizurca, A. Deep feature fusion via two-stream convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2615–2629. [Google Scholar] [CrossRef]
- Ding, C.; Chen, Y.; Li, R.; Wen, D.; Xie, X.; Zhang, L.; Wei, W.; Zhang, Y. Integrating hybrid pyramid feature fusion and coordinate attention for effective small sample hyperspectral image classification. Remote Sens. 2022, 14, 2355. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.-I. Feedback attentionbased dense CNN for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501916. [Google Scholar]
- Luo, W.; Li, Y.; Urtasun, R.; Zemel, R. Understanding the effective receptive field in deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2016, 29, 2476. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Guo, Z.; Zhang, X.; Mu, H.; Heng, W.; Liu, Z.; Wei, Y.; Sun, J. Single path one-shot neural architecture search with uniform sampling. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 544–560. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for Mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Barret, Z.; Le Quoc, V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Shang, R.; Chang, H.; Zhang, W.; Feng, J.; Li, Y. Hyperspectral image classification based on multiscale cross-branch response and second-order channel attention. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5532016. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, Z.; Chen, C.L.P. Multiscale random convolution broad learning system for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 5503605. [Google Scholar] [CrossRef]
- Jayasree, S.; Khanna, Y.; Mukhopadhyay, J. A CNN with Multiscale Convolution for Hyperspectral Image Classification Using Target-Pixel-Orientation Scheme. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Moraga, J.; Duzgun, H.S. JigsawHSI: A network for hyperspectral image classification. arXiv 2022, arXiv:2206.02327. [Google Scholar]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Scaling up Your Kernels to 31 × 31: Revisiting Large Kernel Design in CNNs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11963–11975. [Google Scholar]
- Radosavovic, I.; Kosaraju, R.P.; Girshick, R.; He, K.; Dollár, P. Designing Network Design Spaces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10428–10436. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Cai, Y.; Liu, X.; Cai, Z. BS-Nets: An end-to-end framework for band selection of hyperspectral image. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1969–1984. [Google Scholar] [CrossRef]
- Ge, Z.; Cao, G.; Li, X.; Fu, P. Hyperspectral image classification method based on 2D–3D CNN and multibranch feature fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5776–5788. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Liu, Q.; Ghamisi, P.; Bhattacharyya, S.S. Hyperspectral image classification with attention-aided CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2281–2293. [Google Scholar] [CrossRef]
- Chakraborty, T.; Trehan, U. Spectralnet: Exploring spatial-spectral waveletcnn for hyperspectral image classification. arXiv 2021, arXiv:2104.00341. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).