Figure 1.
The interpretation of STANAG 1241 using the Venn diagram.
Figure 1.
The interpretation of STANAG 1241 using the Venn diagram.
Figure 2.
The diagram of the information-fusion process in the information-fusion center (IFC) for two sensors. Explanations: mi a BBA measure vector of i-th sensor; mF, a generalized BBA measure vector that is a part of the electronic entity record in the IFC; EER, an electronic entity record in the IFC database.
Figure 2.
The diagram of the information-fusion process in the information-fusion center (IFC) for two sensors. Explanations: mi a BBA measure vector of i-th sensor; mF, a generalized BBA measure vector that is a part of the electronic entity record in the IFC; EER, an electronic entity record in the IFC database.
Figure 3.
The diagram of the information-fusion process in the information-fusion center (IFC) for two sensors and electronic entity record from the IFC database. Explanations: mi, a BBA measure vector of i-th sensor; mF, a generalized BBA measure vector that is a part of the electronic entity record in the IFC; EER, an electronic entity record in the IFC database.
Figure 3.
The diagram of the information-fusion process in the information-fusion center (IFC) for two sensors and electronic entity record from the IFC database. Explanations: mi, a BBA measure vector of i-th sensor; mF, a generalized BBA measure vector that is a part of the electronic entity record in the IFC; EER, an electronic entity record in the IFC database.
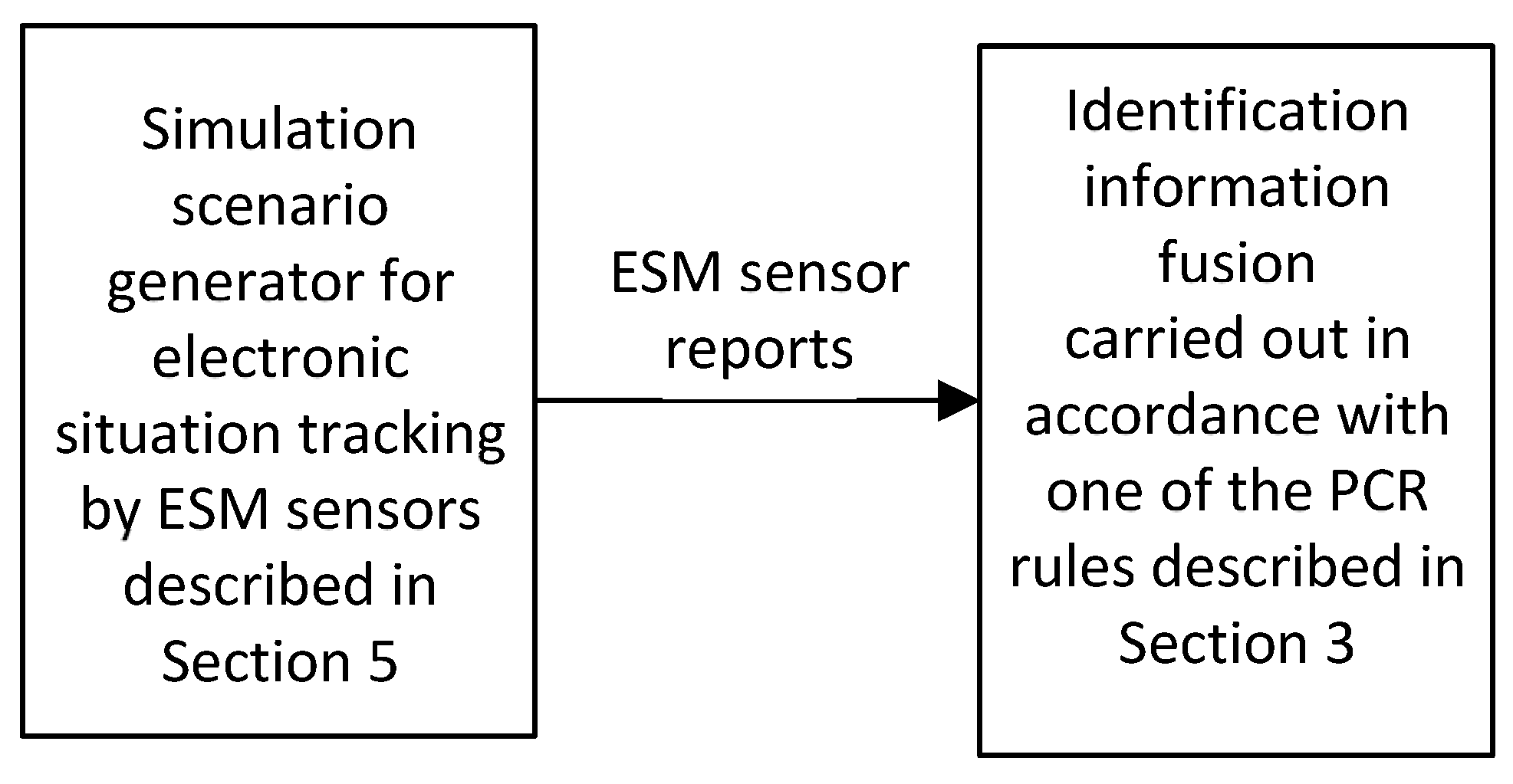
Figure 4.
The general diagram of simulation experiments of fusion of identification information from ESM sensors.
Figure 4.
The general diagram of simulation experiments of fusion of identification information from ESM sensors.
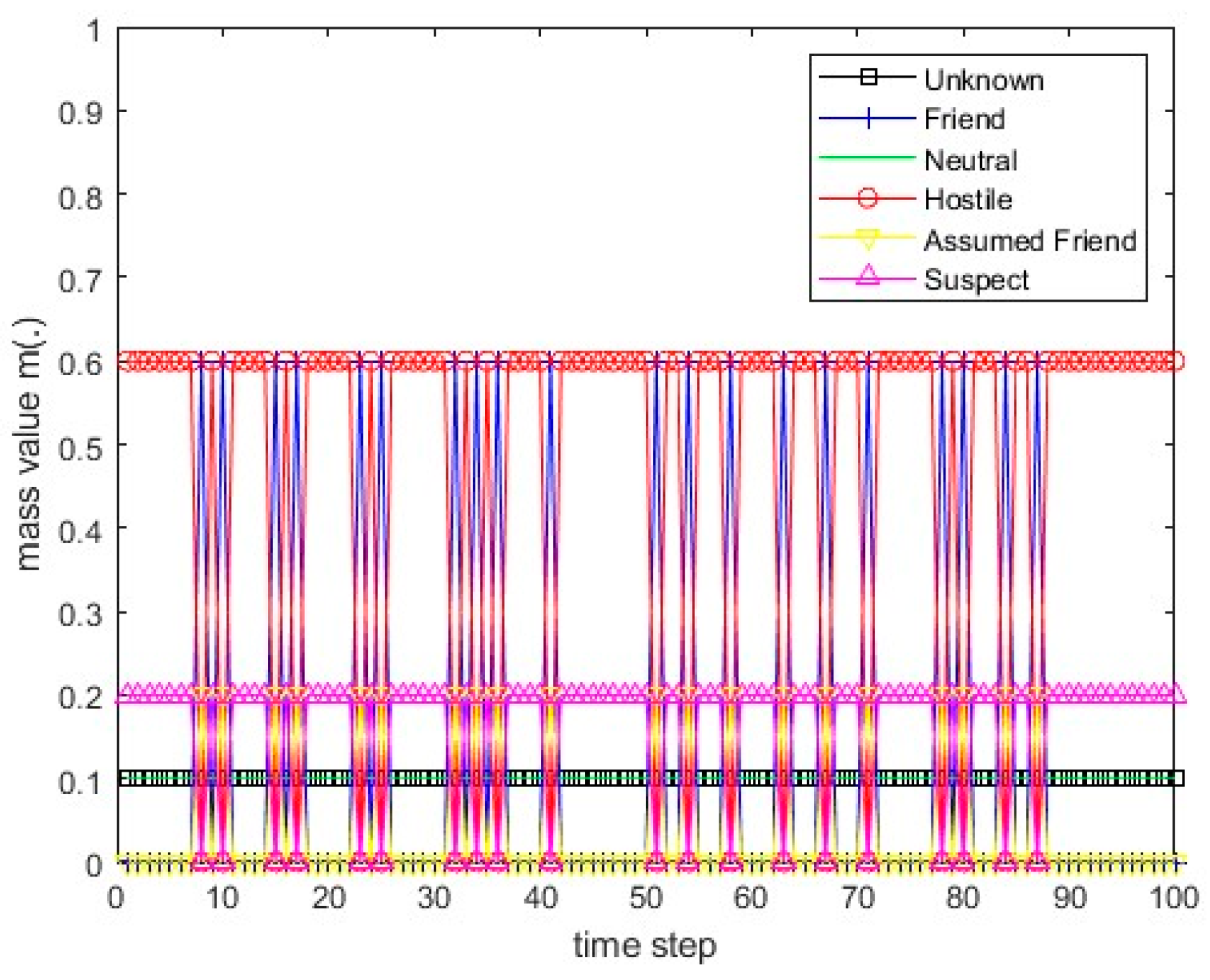
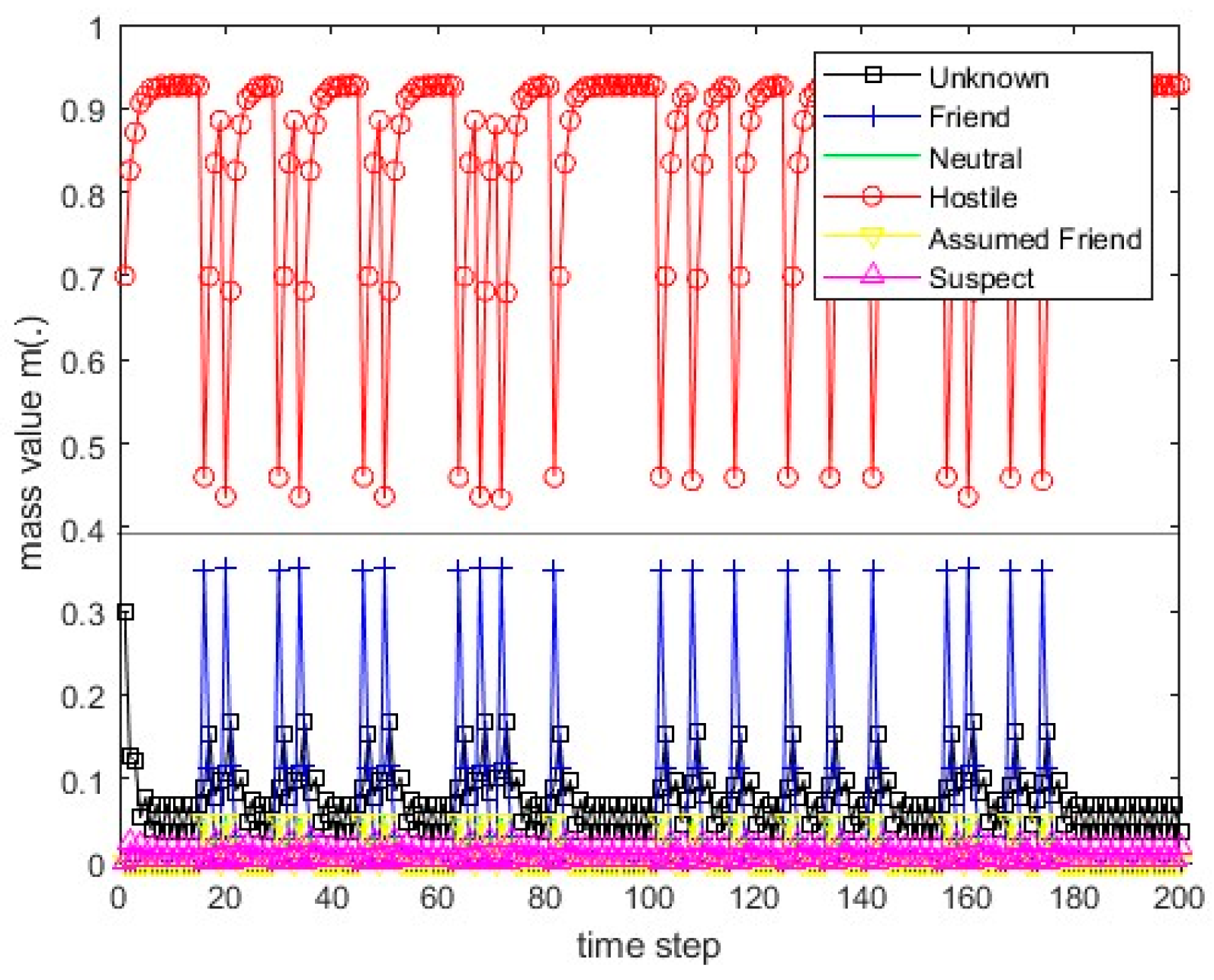
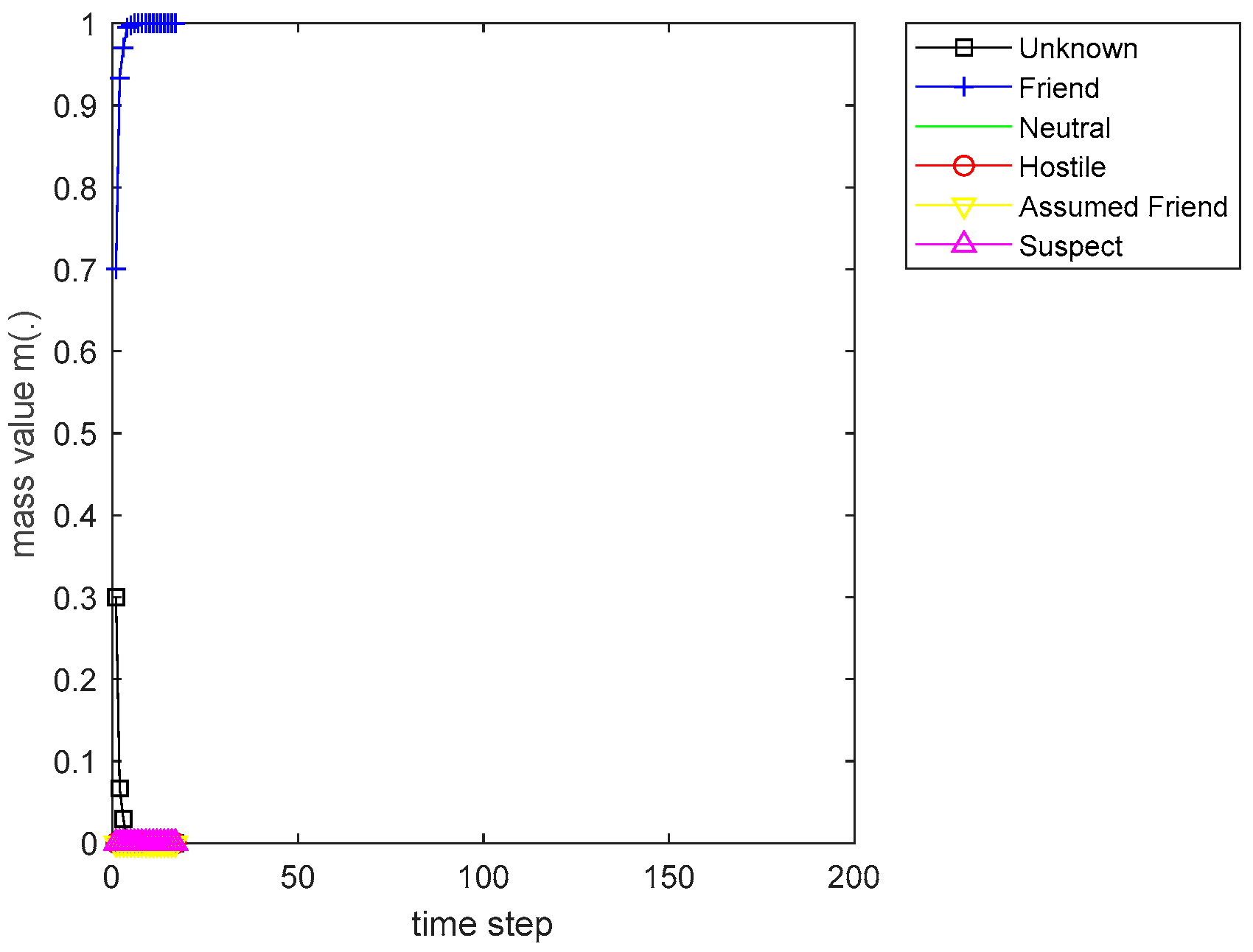
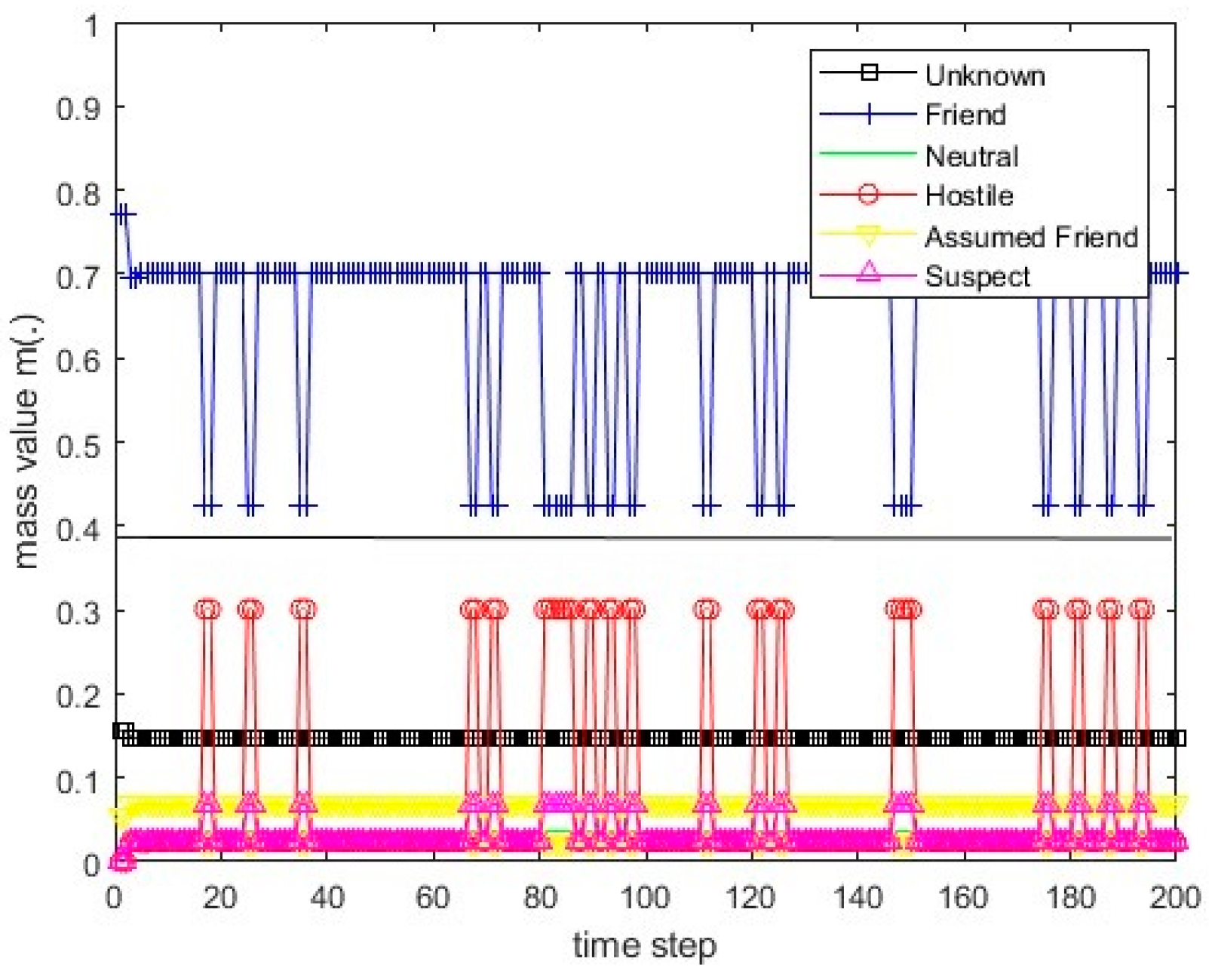
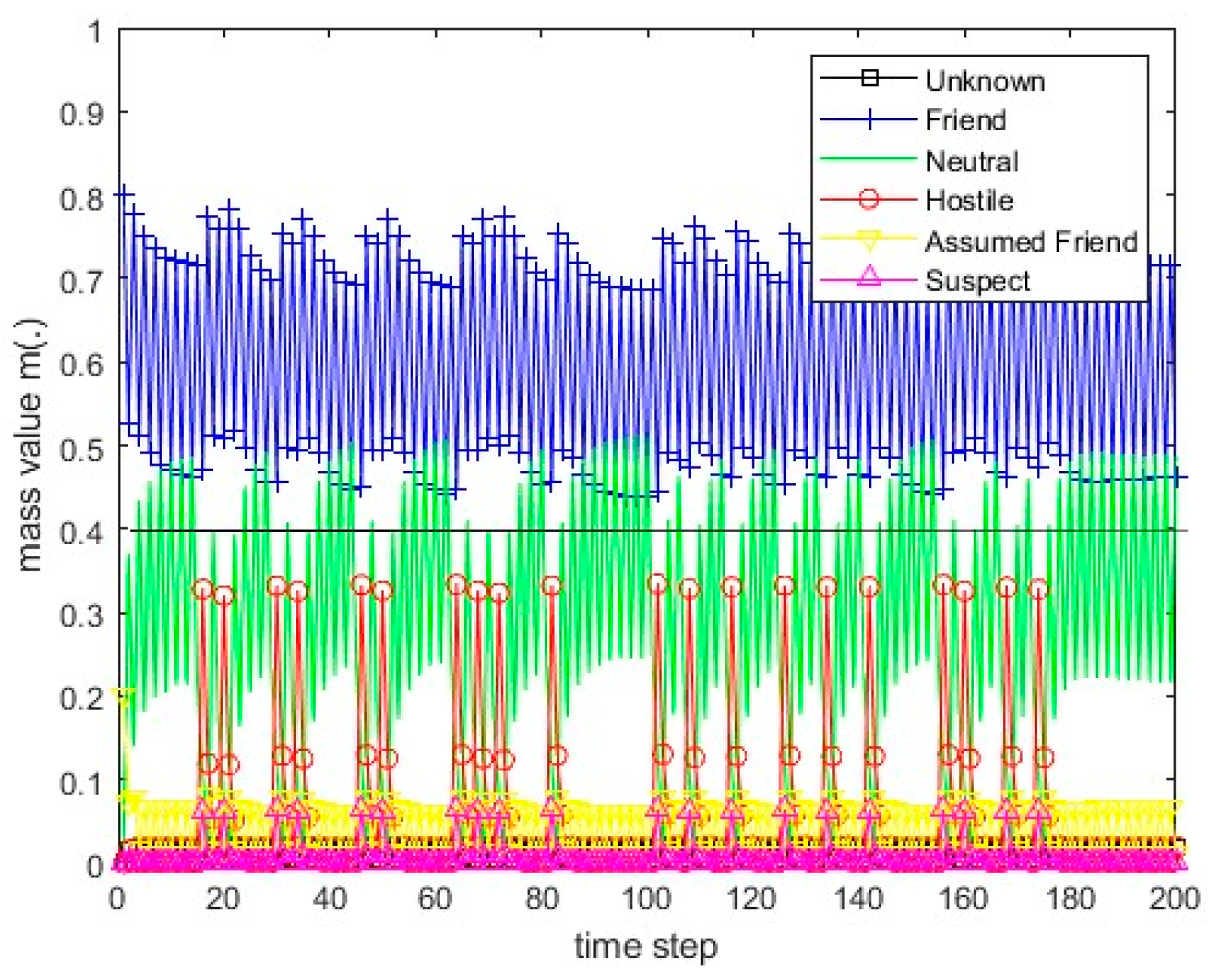
Figure 5.
The course of scenarios number 1, 2, and 5 for sensor 1.
Figure 5.
The course of scenarios number 1, 2, and 5 for sensor 1.
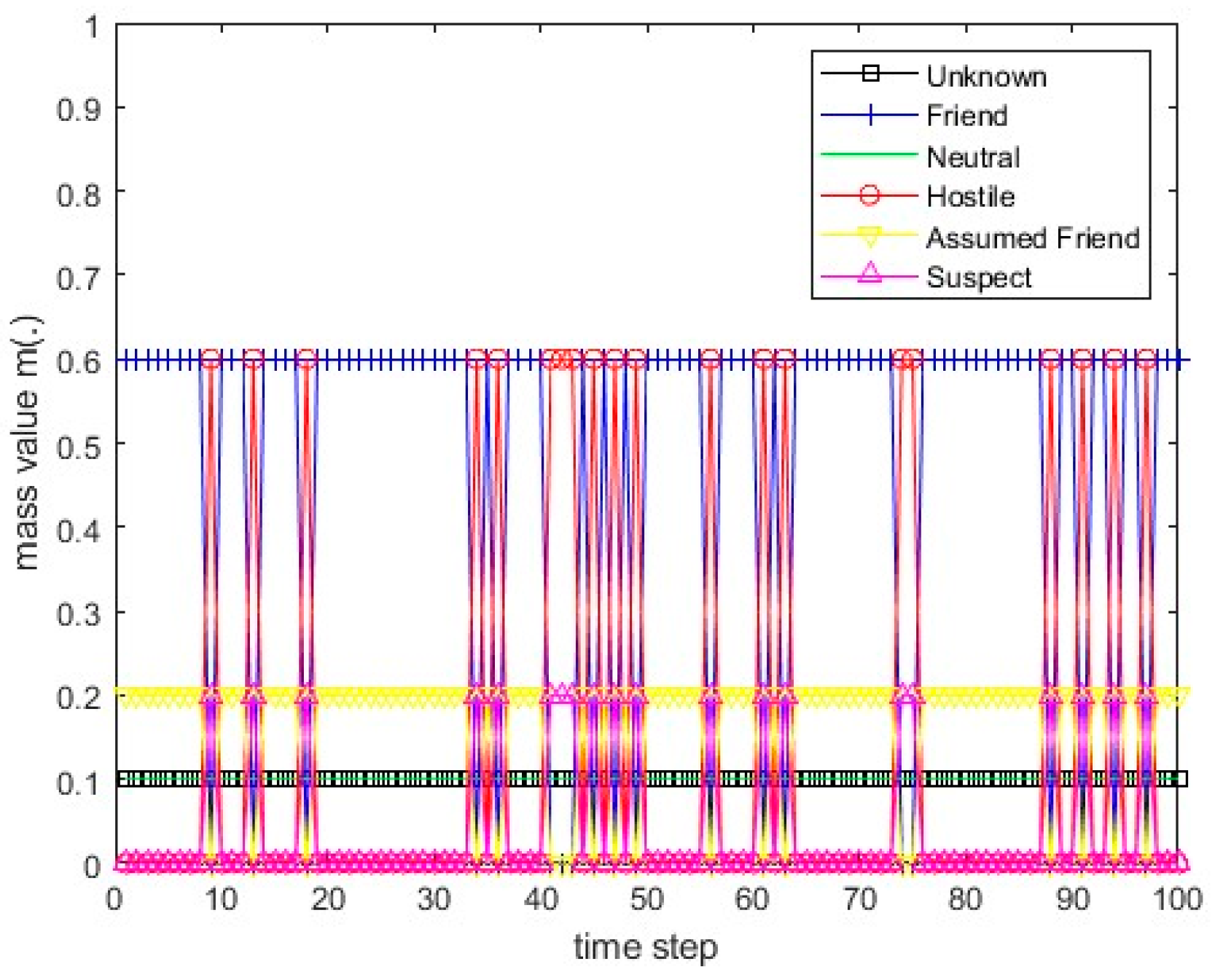
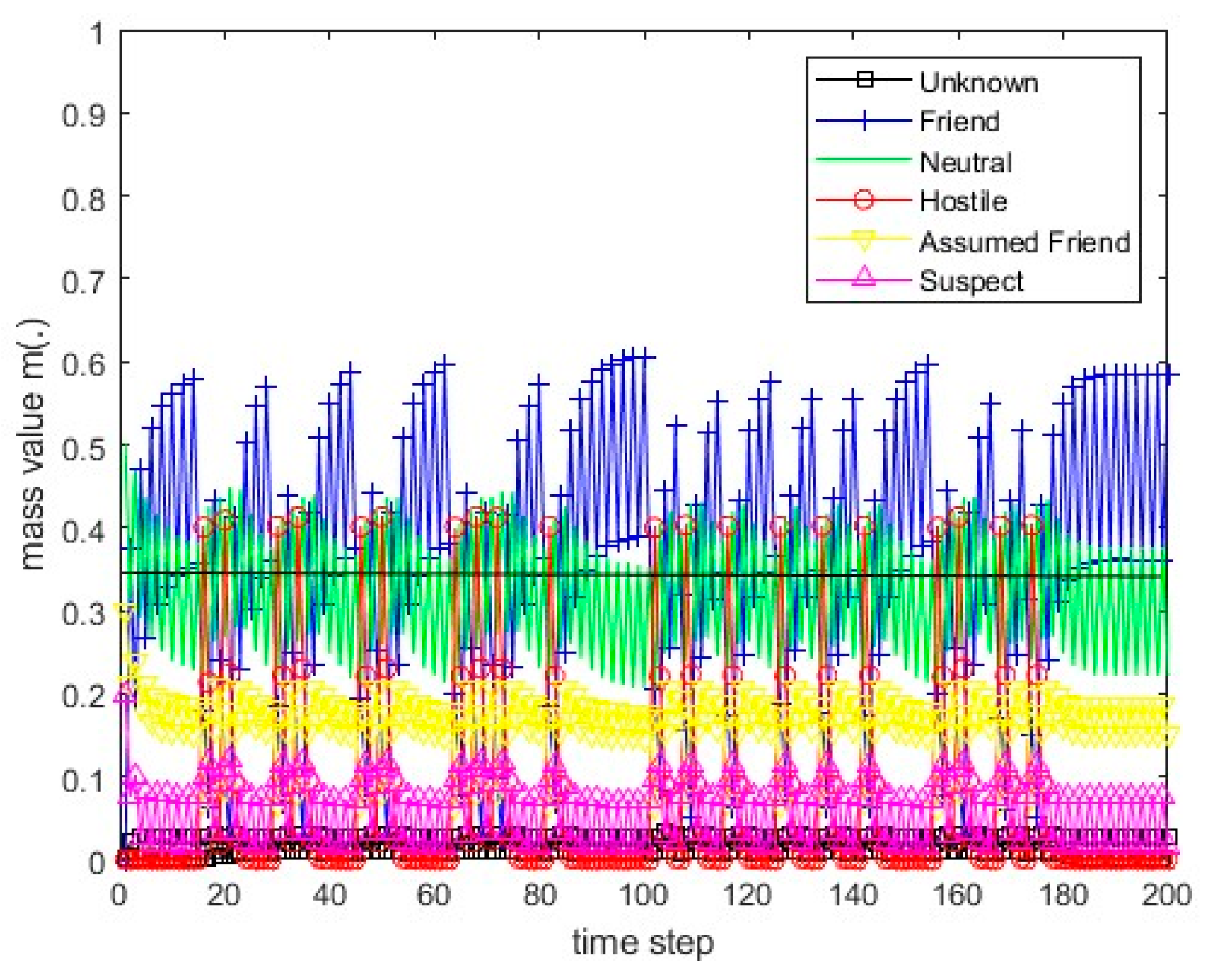
Figure 6.
The course of scenarios number 3, 4, and 6 for sensor 1.
Figure 6.
The course of scenarios number 3, 4, and 6 for sensor 1.
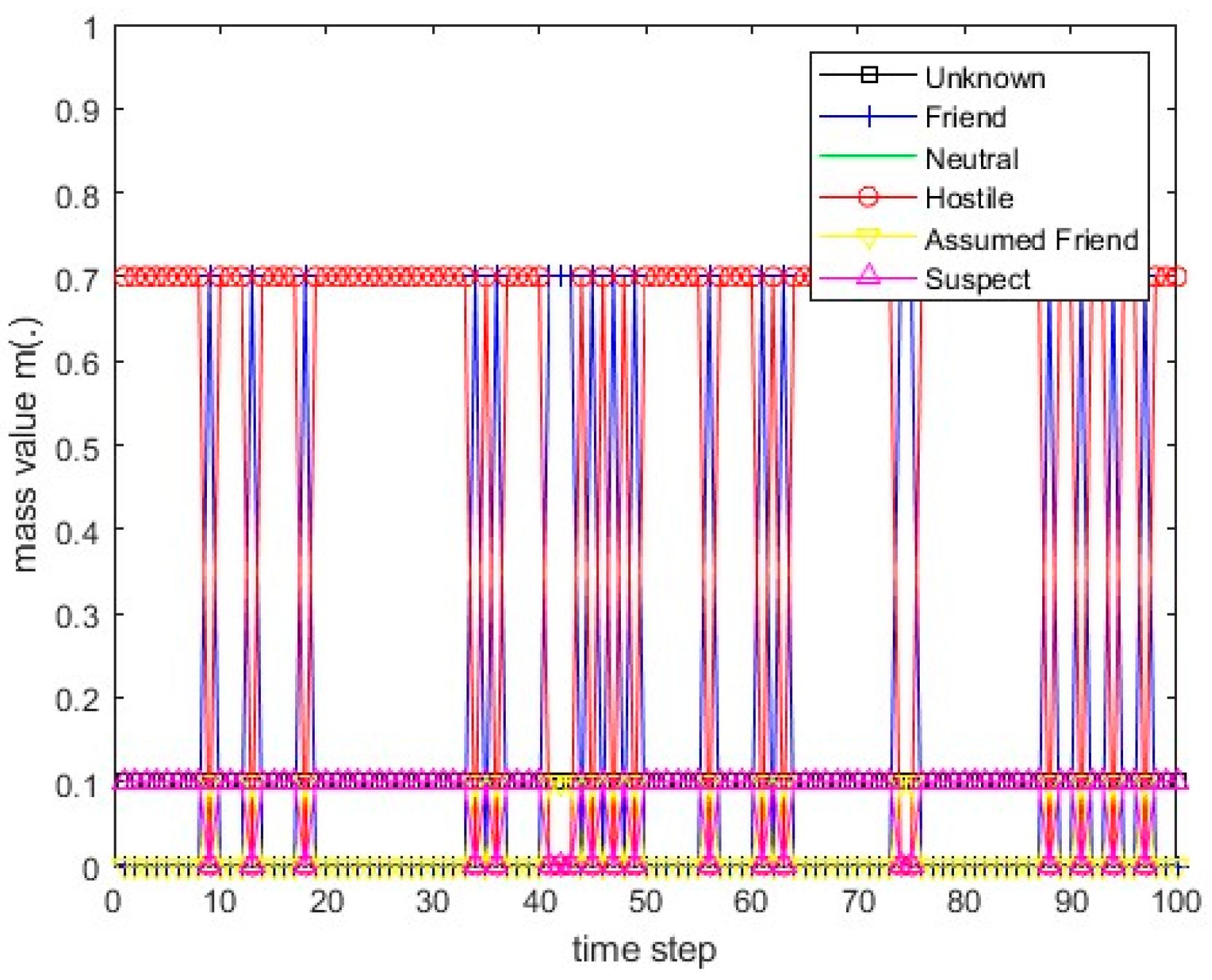
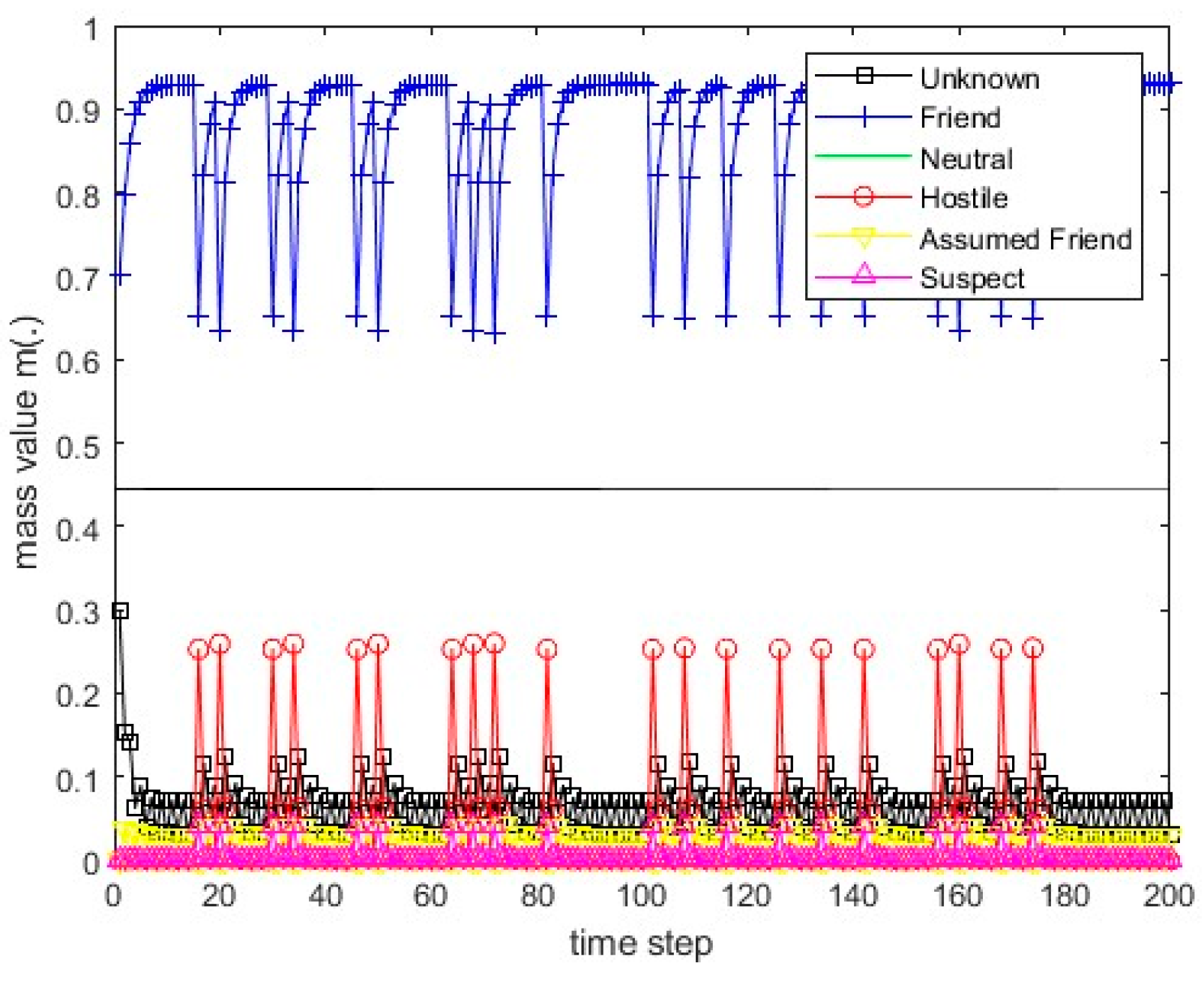
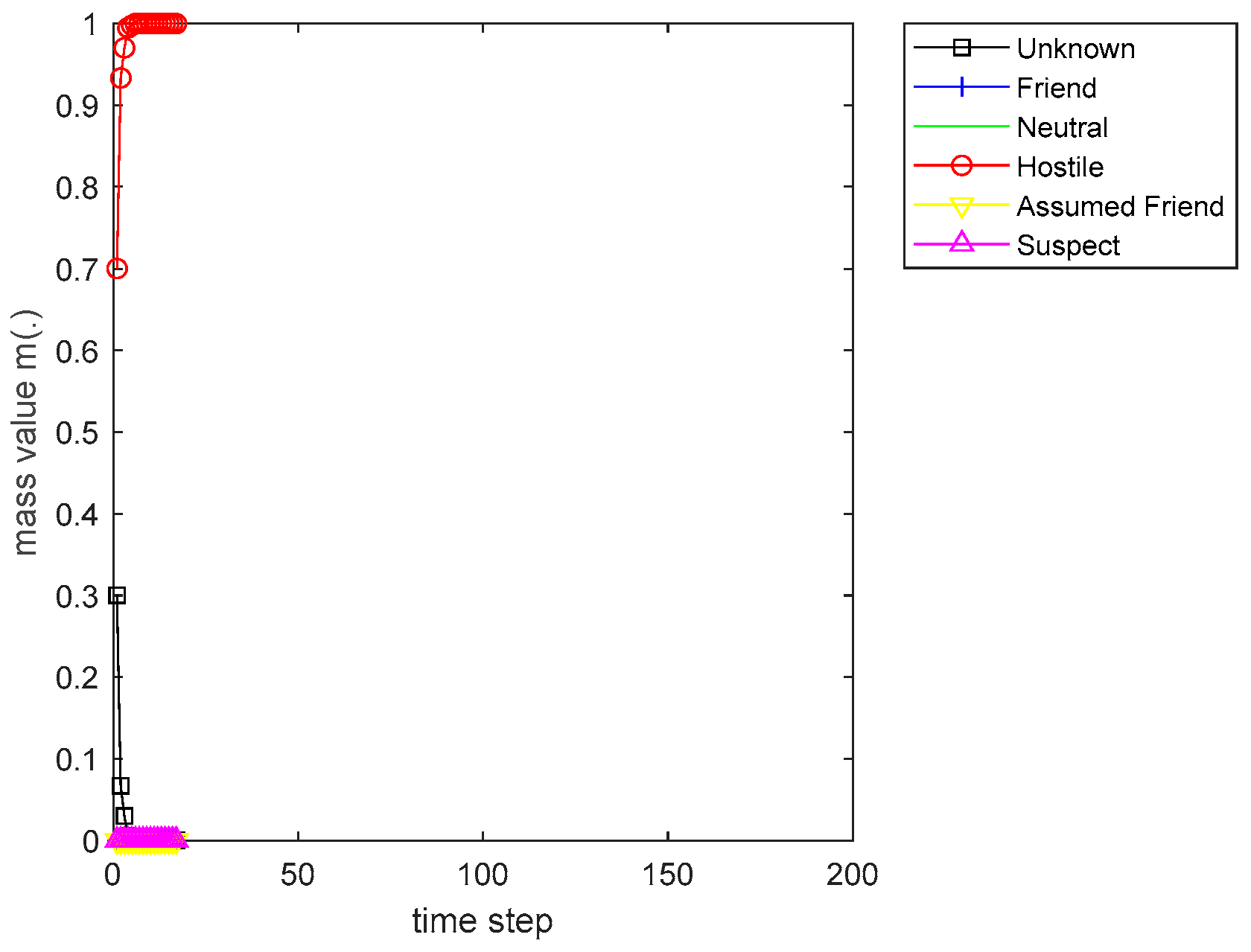
Figure 7.
The course of scenario number 1 for sensor 2.
Figure 7.
The course of scenario number 1 for sensor 2.
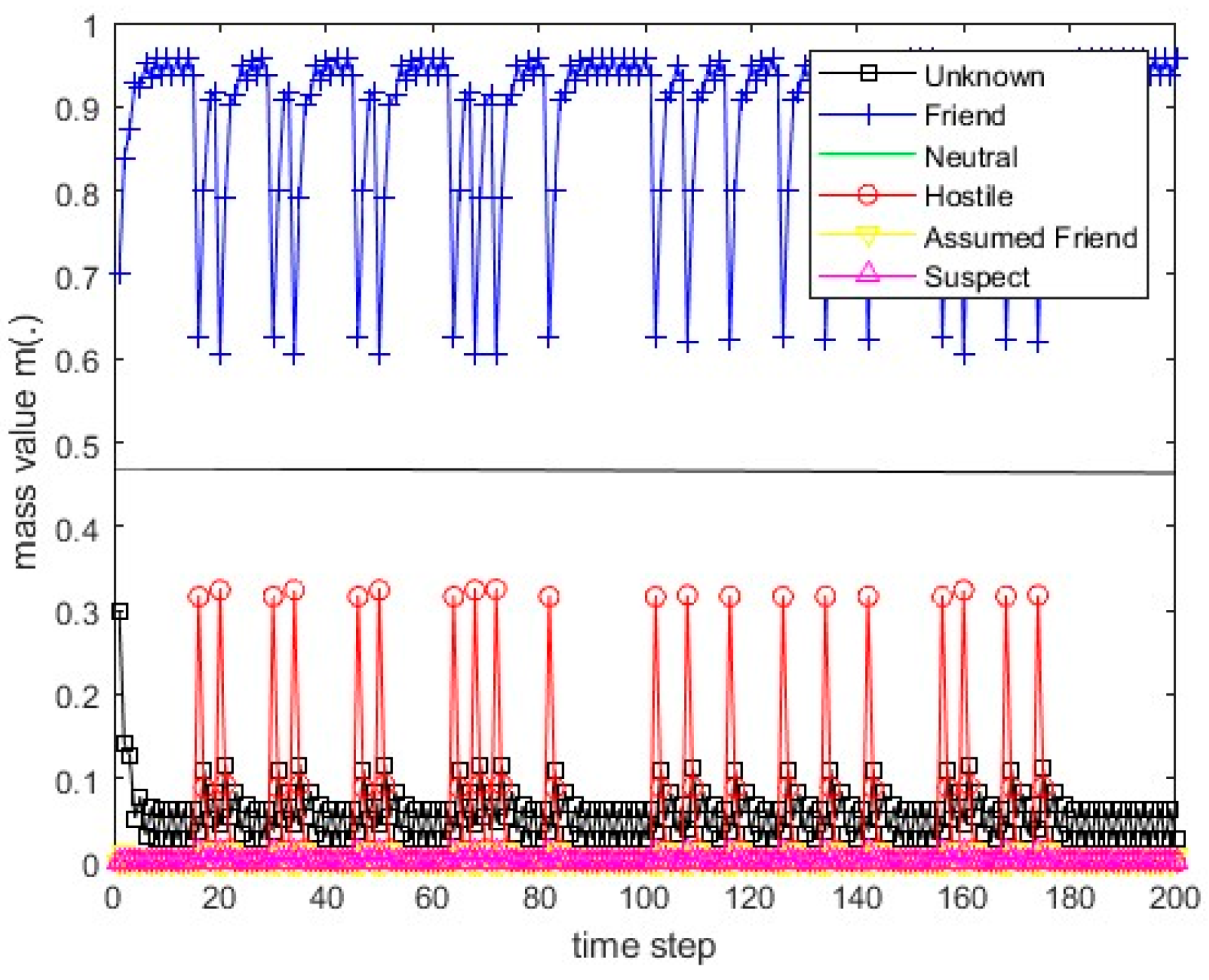
Figure 8.
The course of scenario number 2 for sensor 2.
Figure 8.
The course of scenario number 2 for sensor 2.
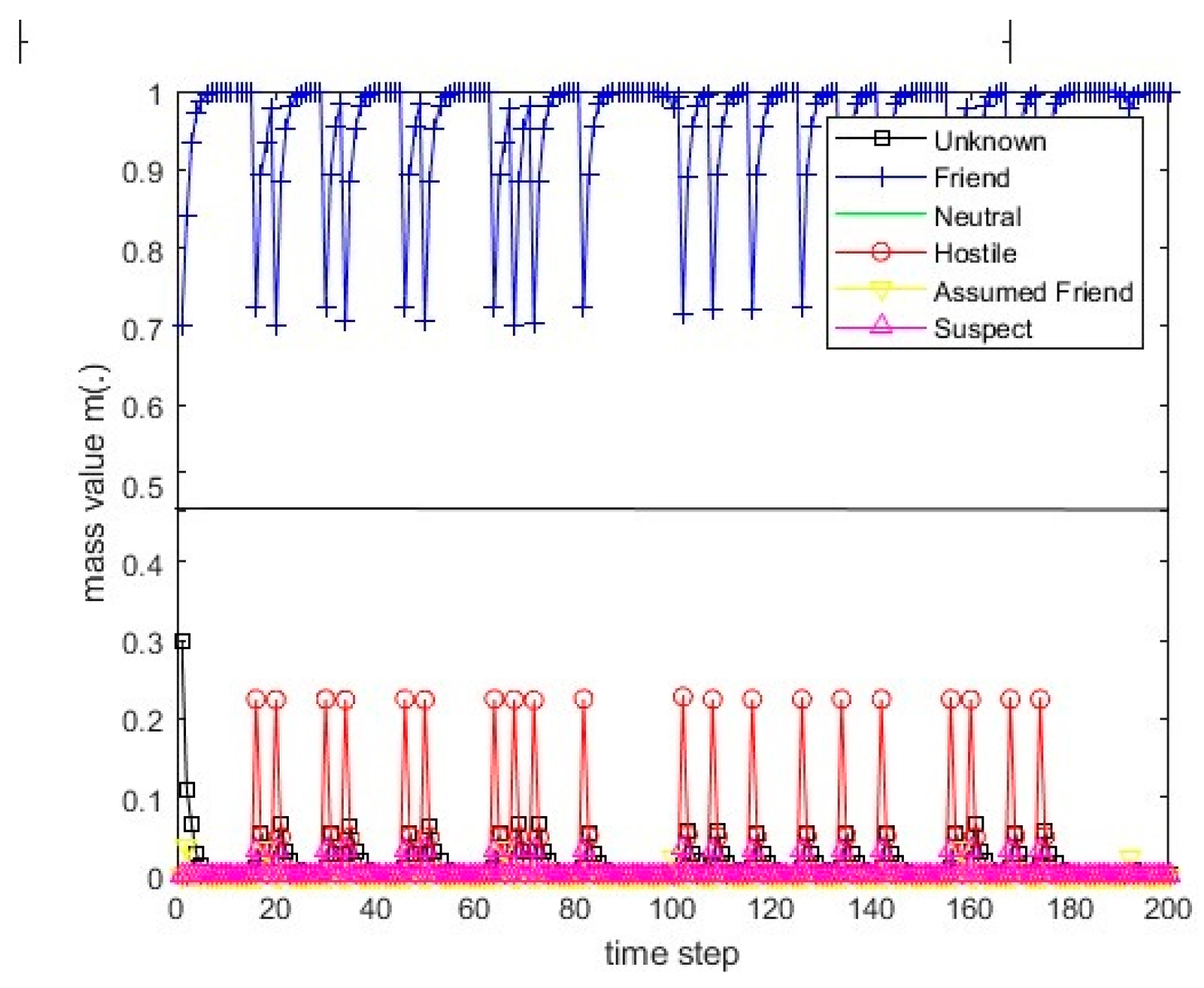
Figure 9.
The course of scenario number 3 for sensor 2.
Figure 9.
The course of scenario number 3 for sensor 2.
Figure 10.
The course of scenario number 4 for sensor 2.
Figure 10.
The course of scenario number 4 for sensor 2.
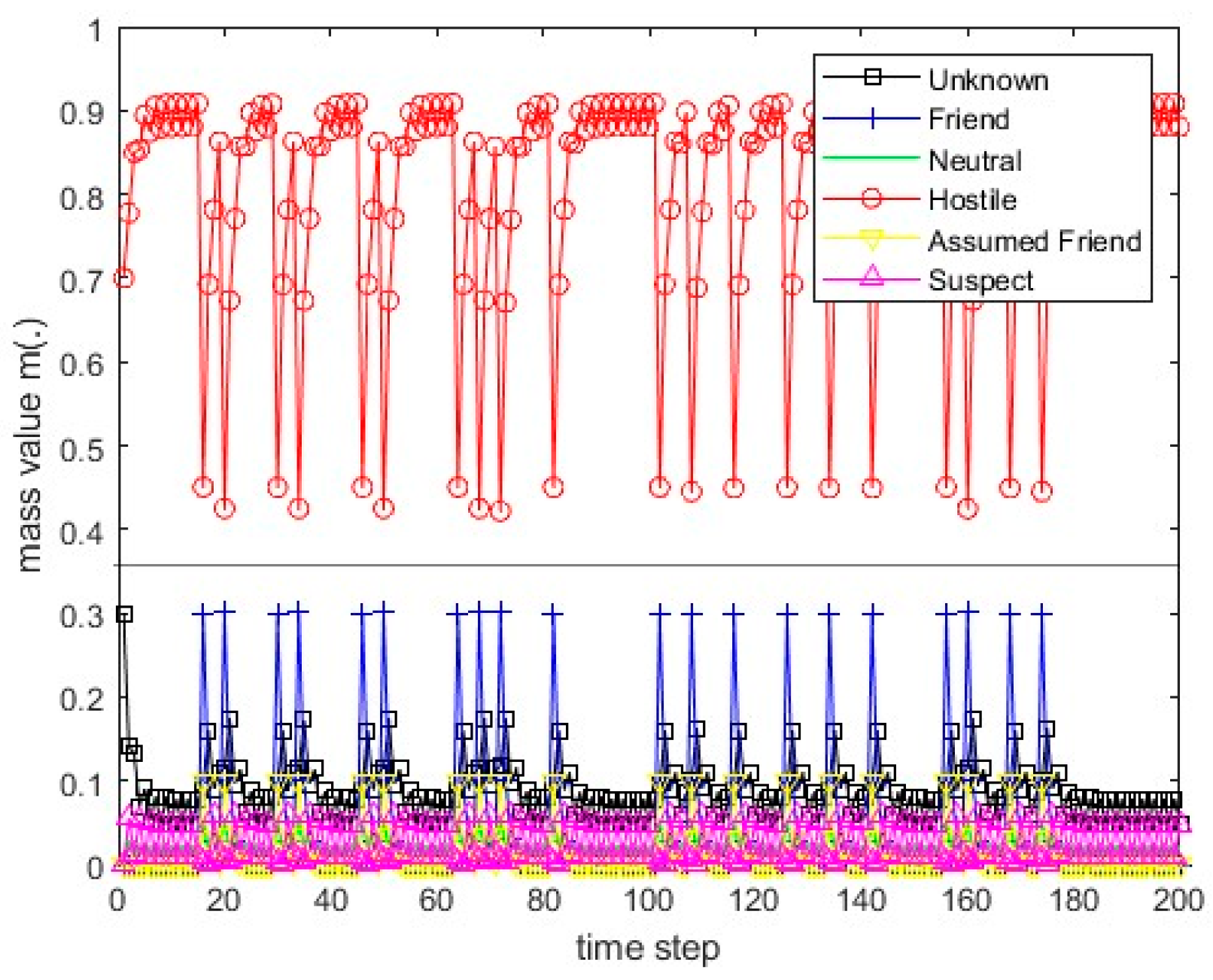
Figure 11.
The course of Monte Carlo scenario number 5 for sensor 2.
Figure 11.
The course of Monte Carlo scenario number 5 for sensor 2.
Figure 12.
The course of Monte Carlo scenario number 6 for sensor 2.
Figure 12.
The course of Monte Carlo scenario number 6 for sensor 2.
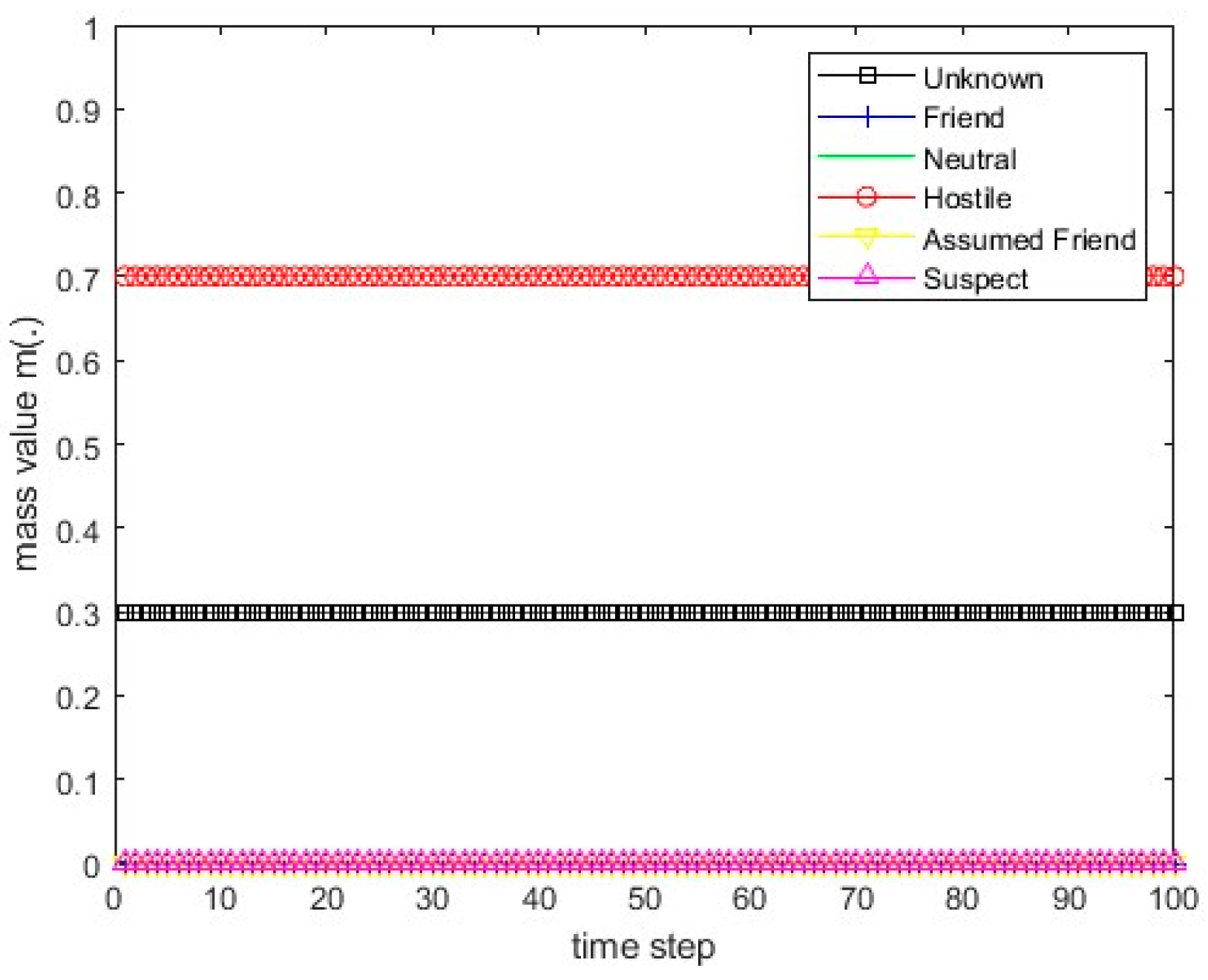
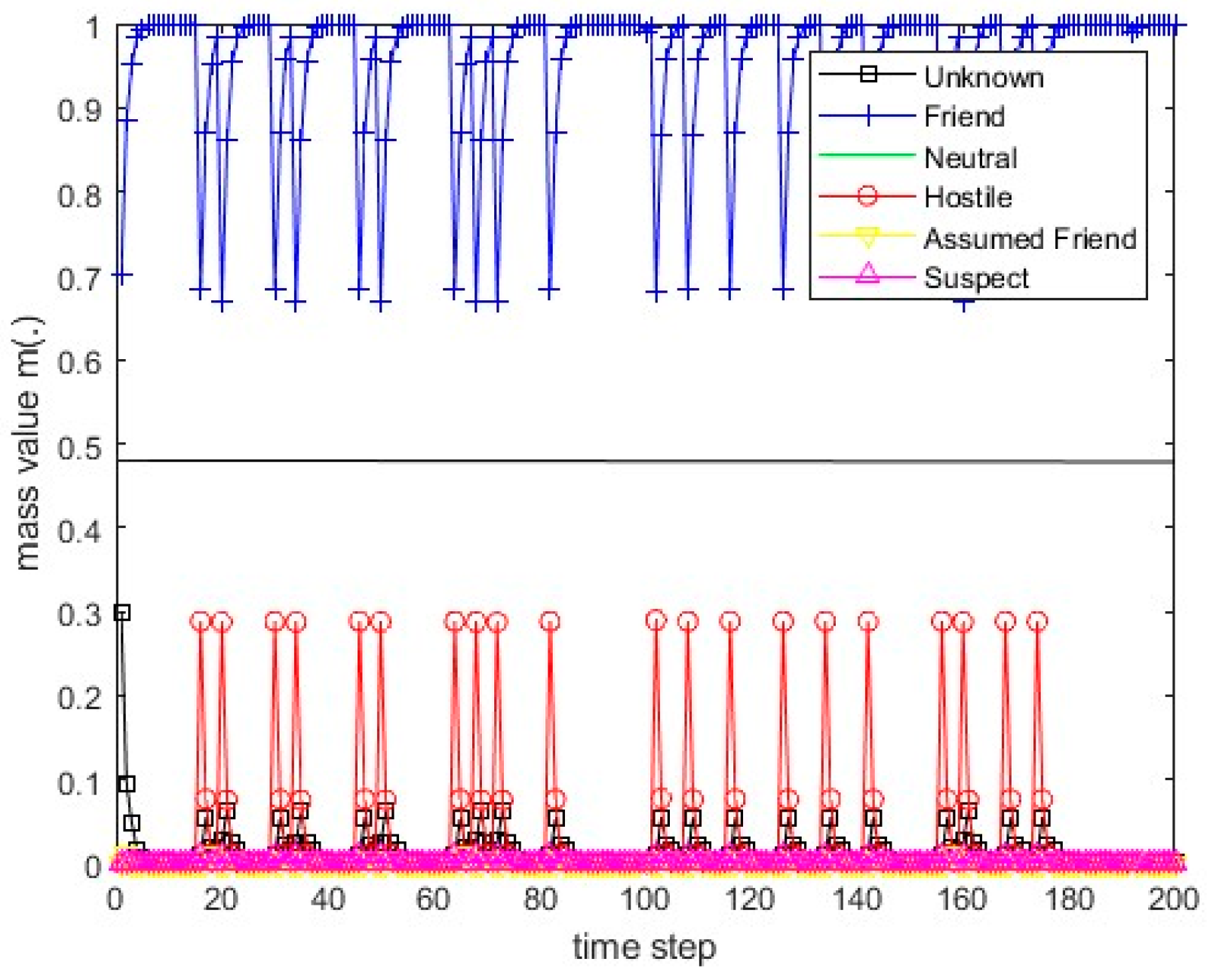
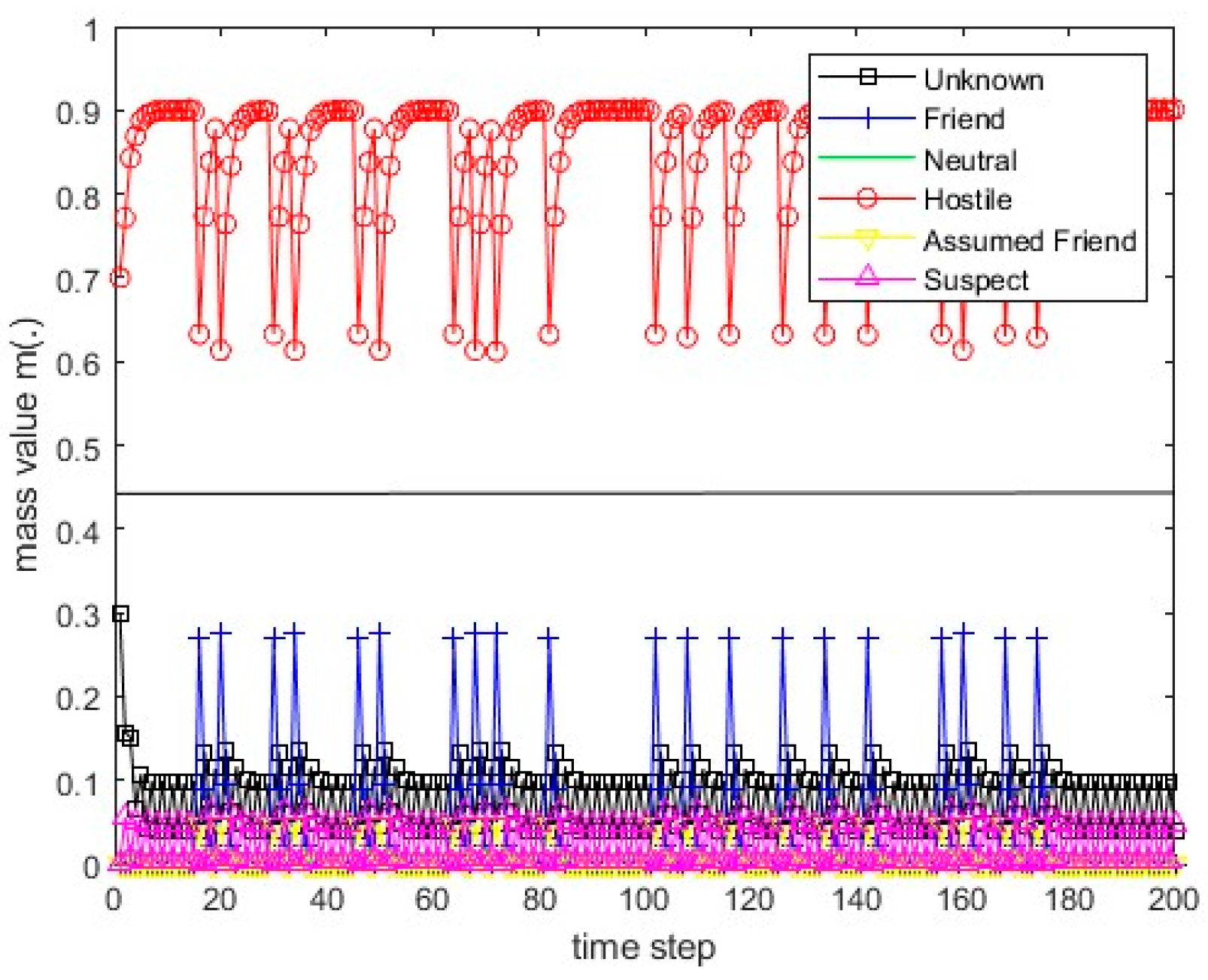
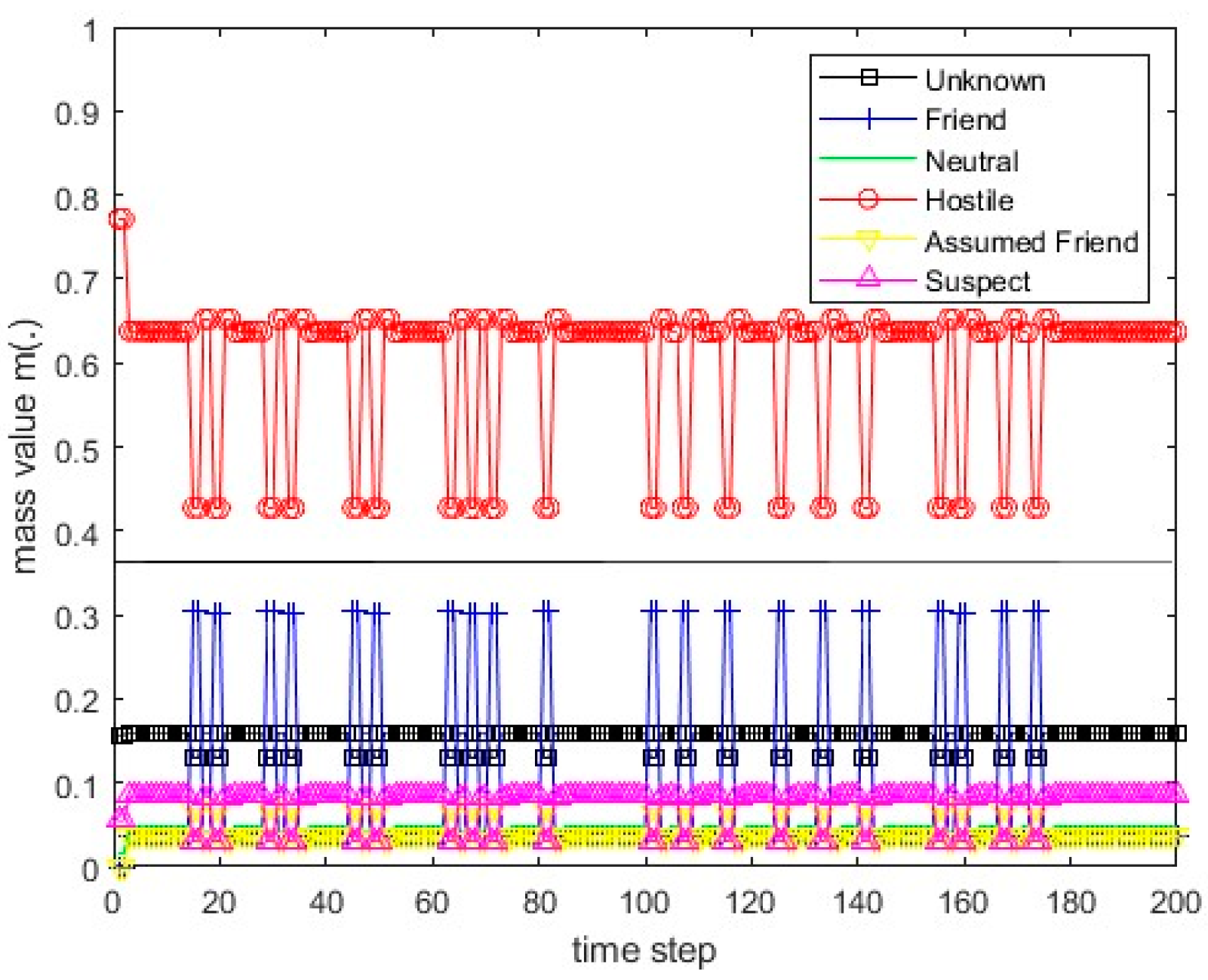
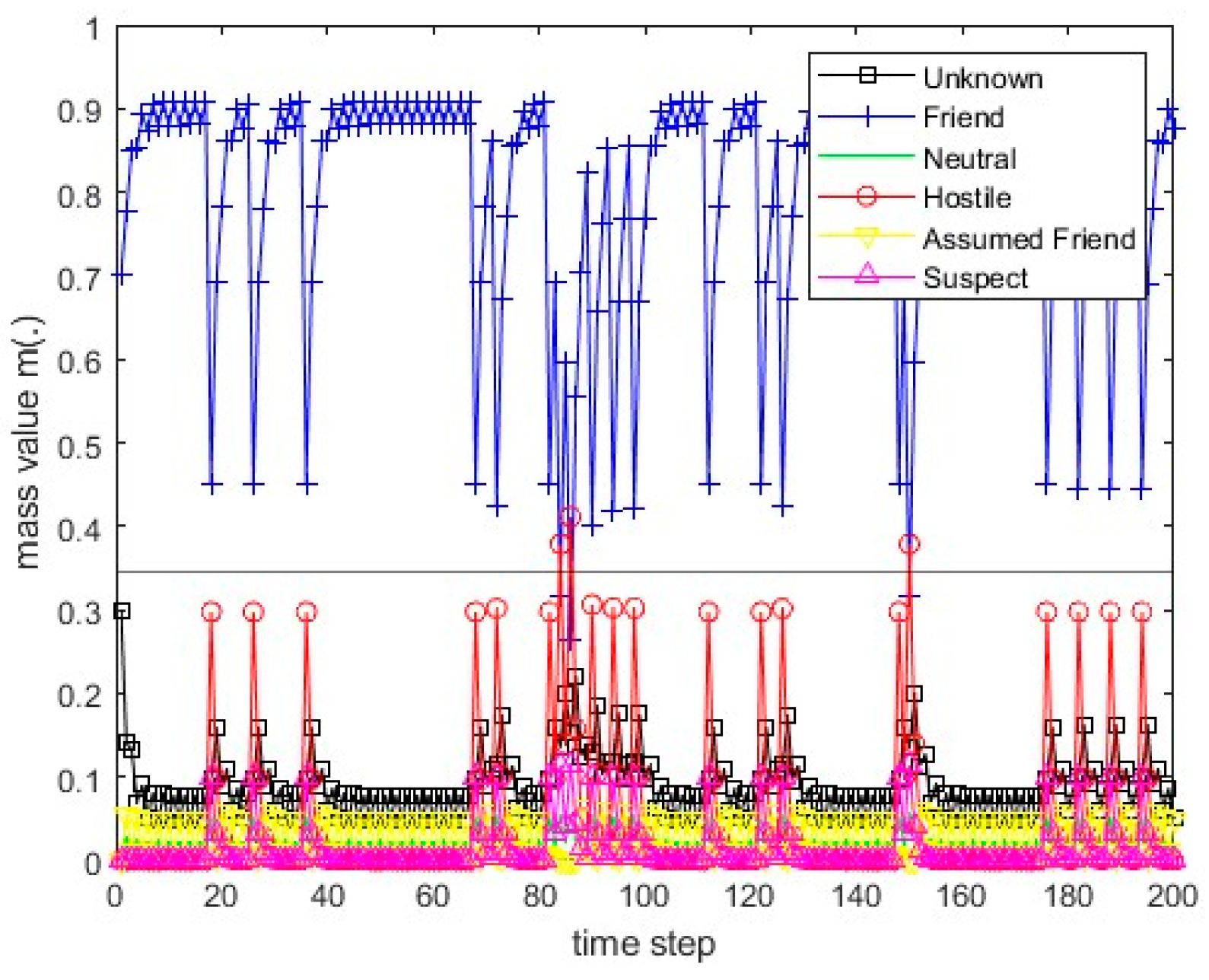
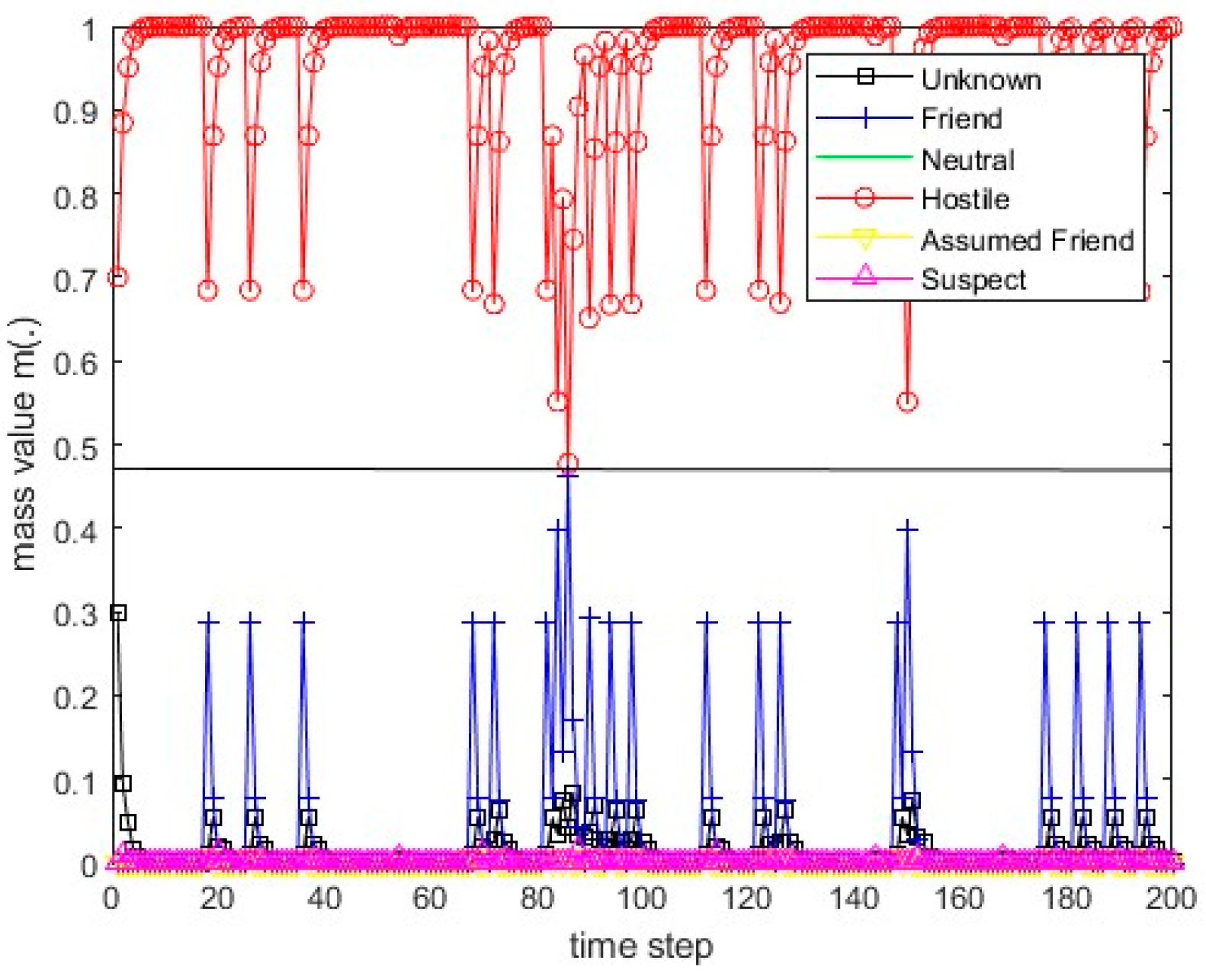
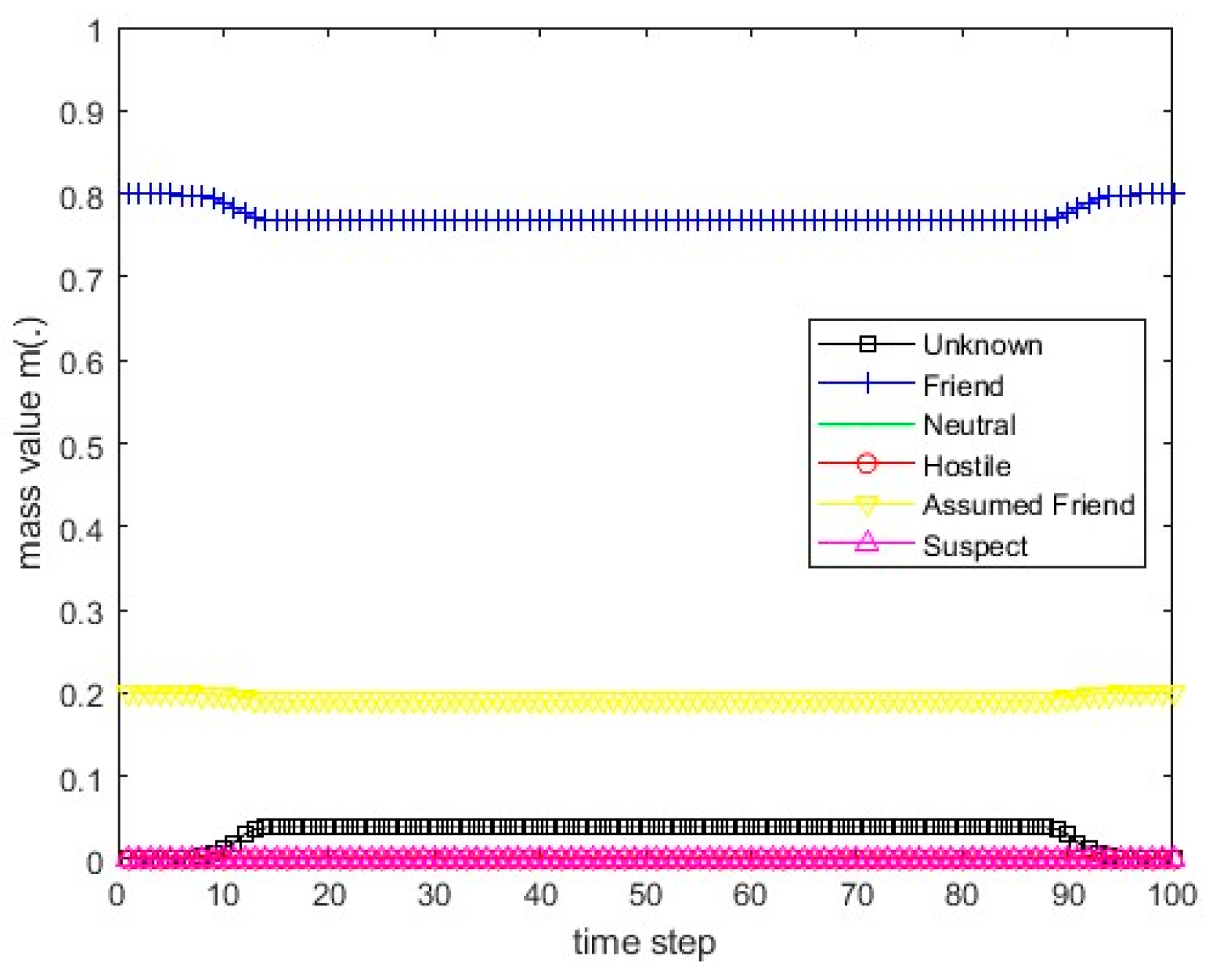
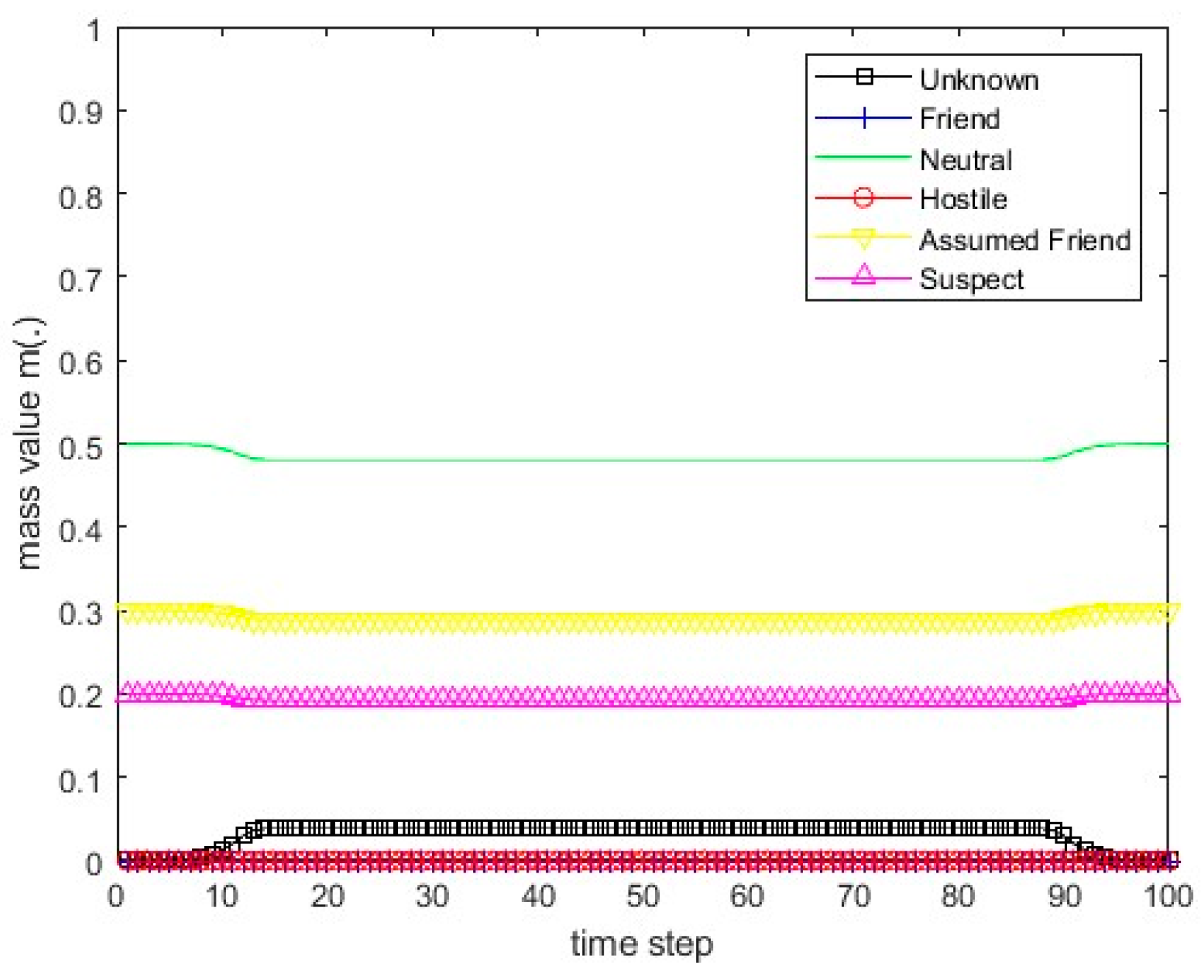
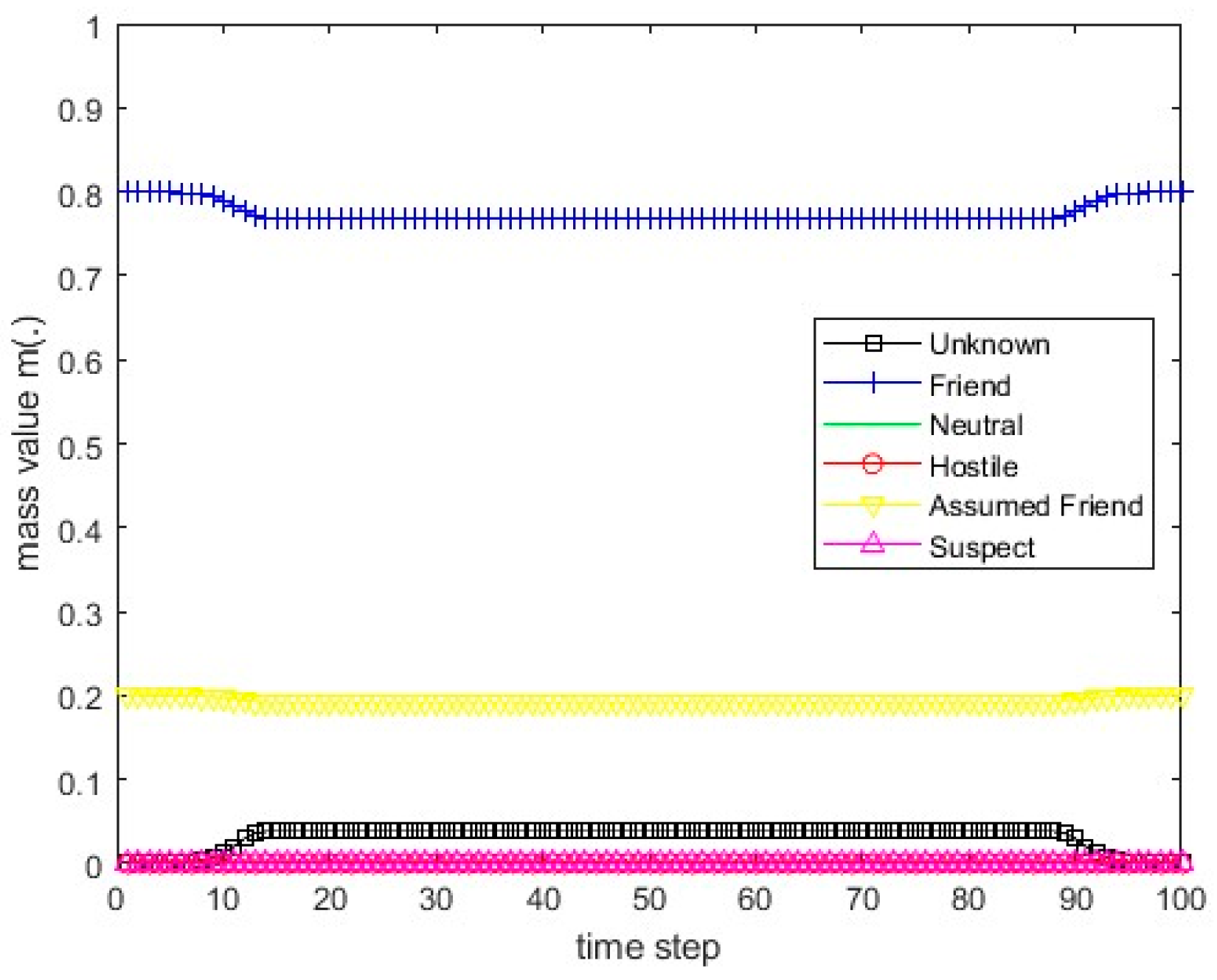
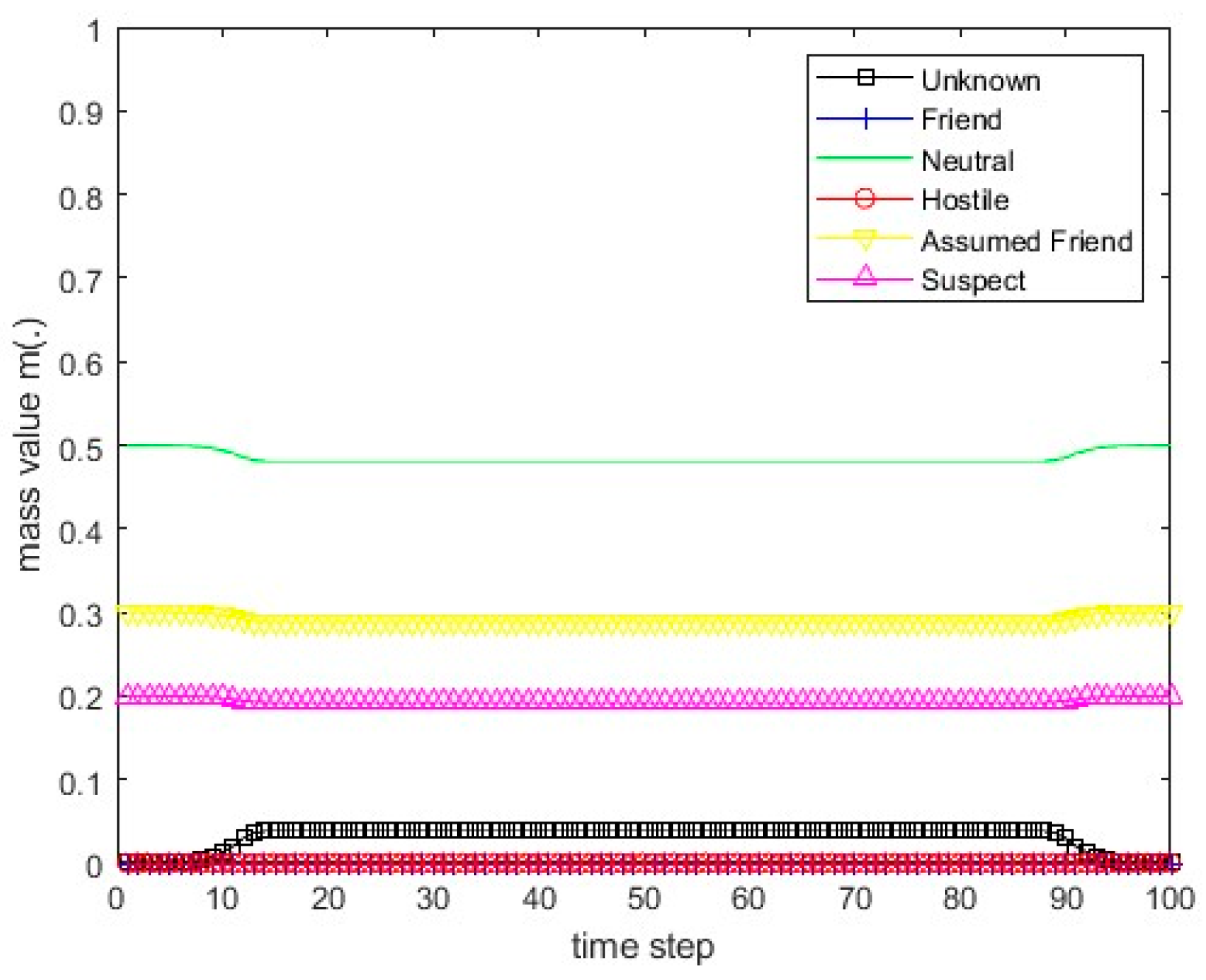
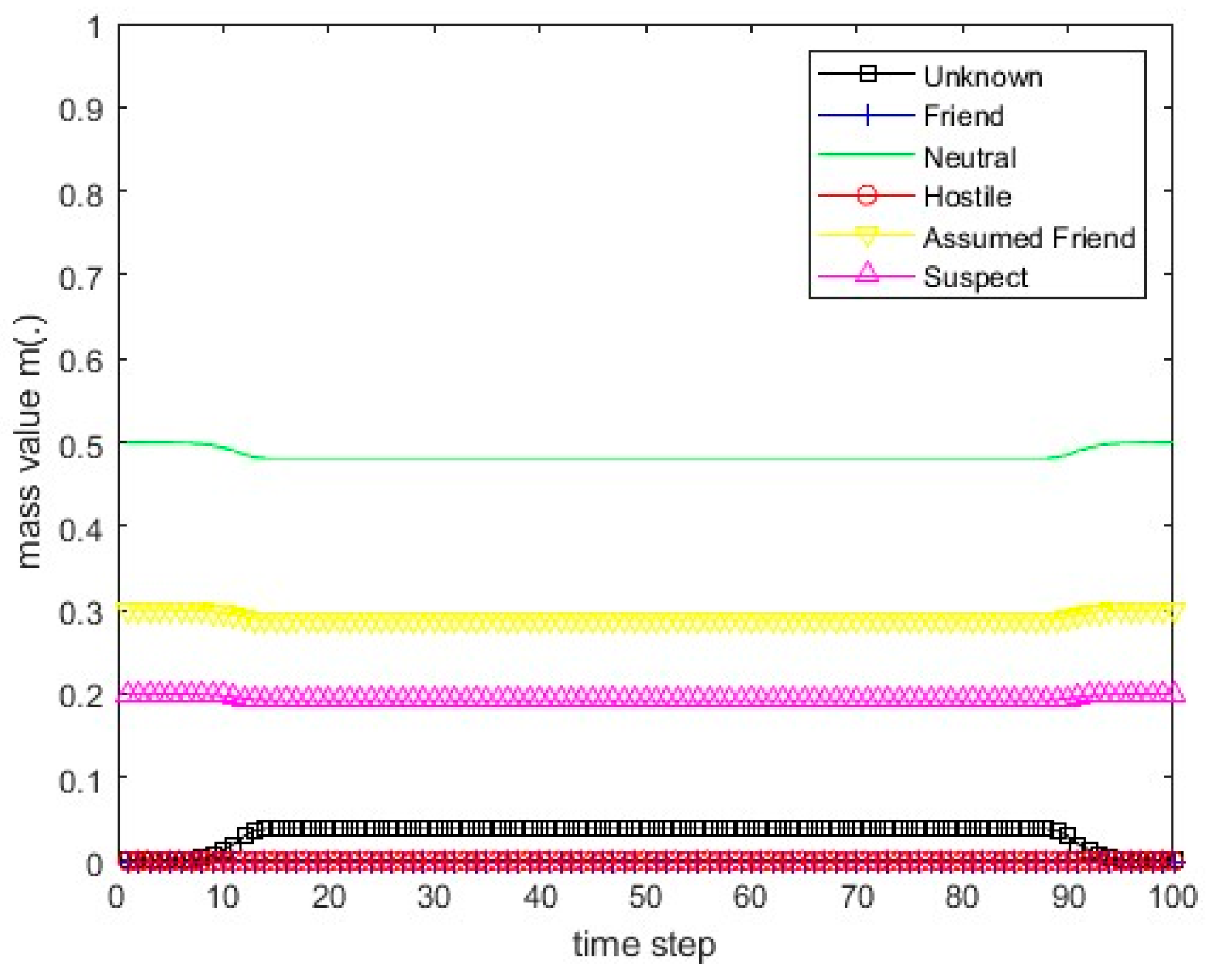
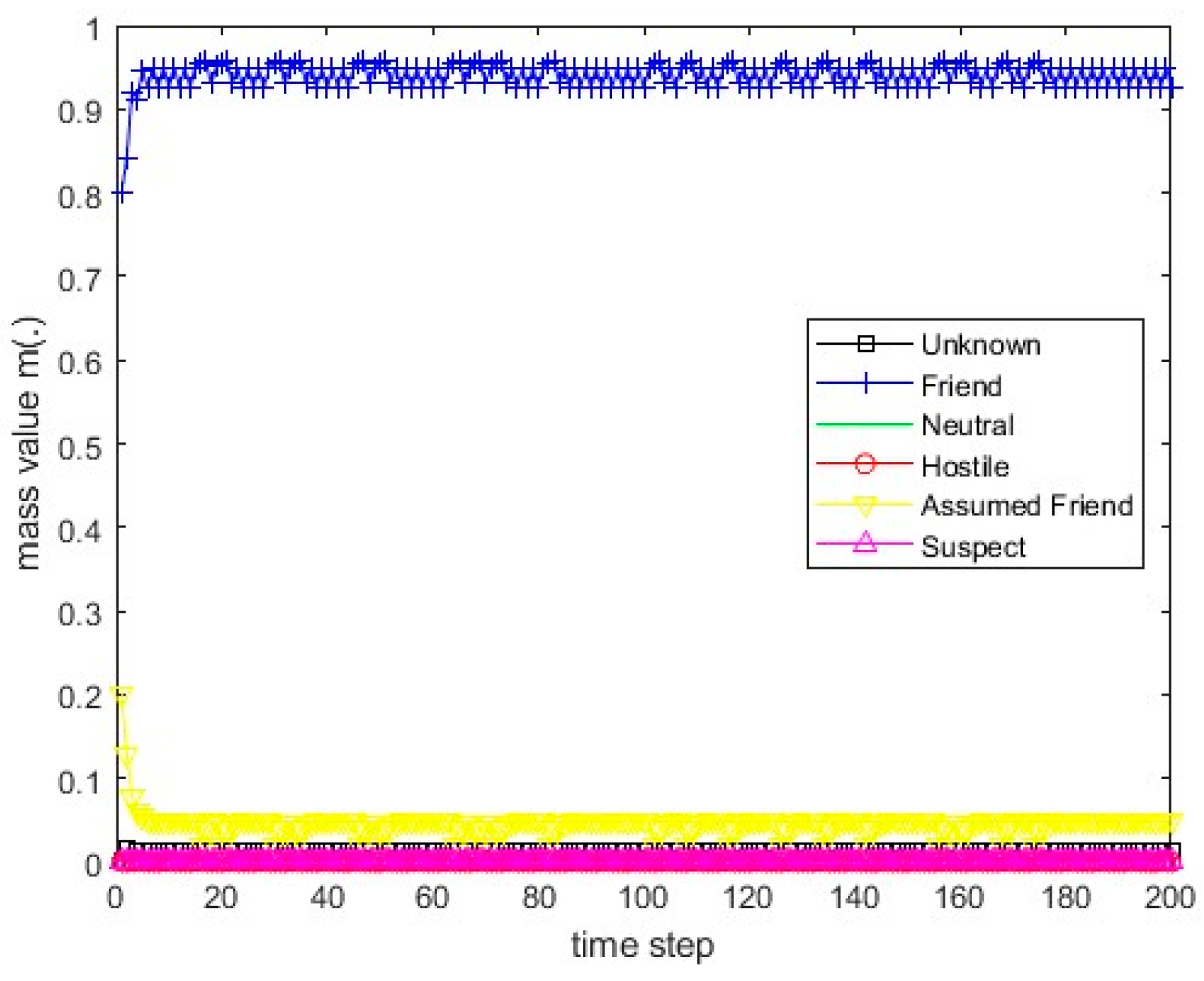
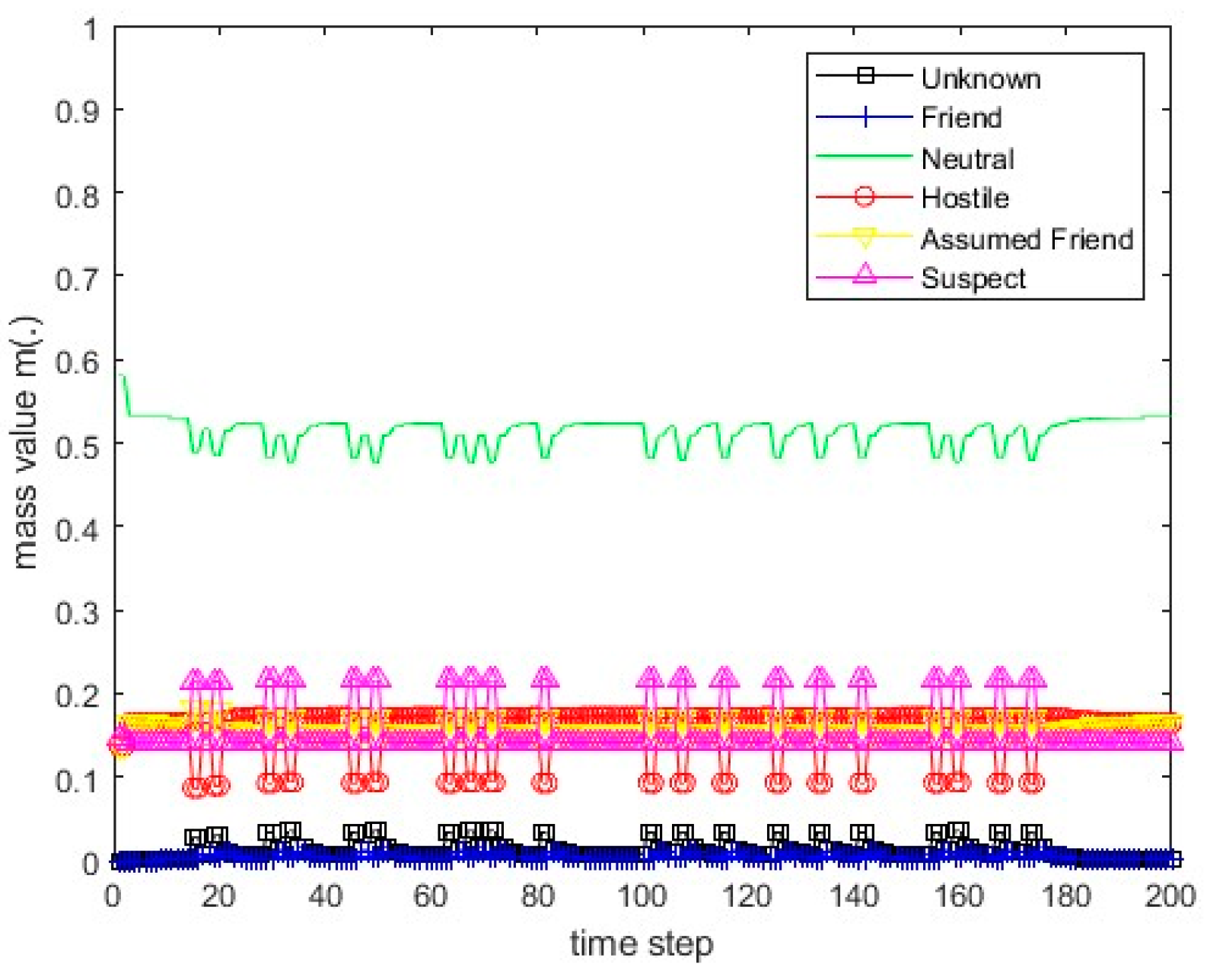
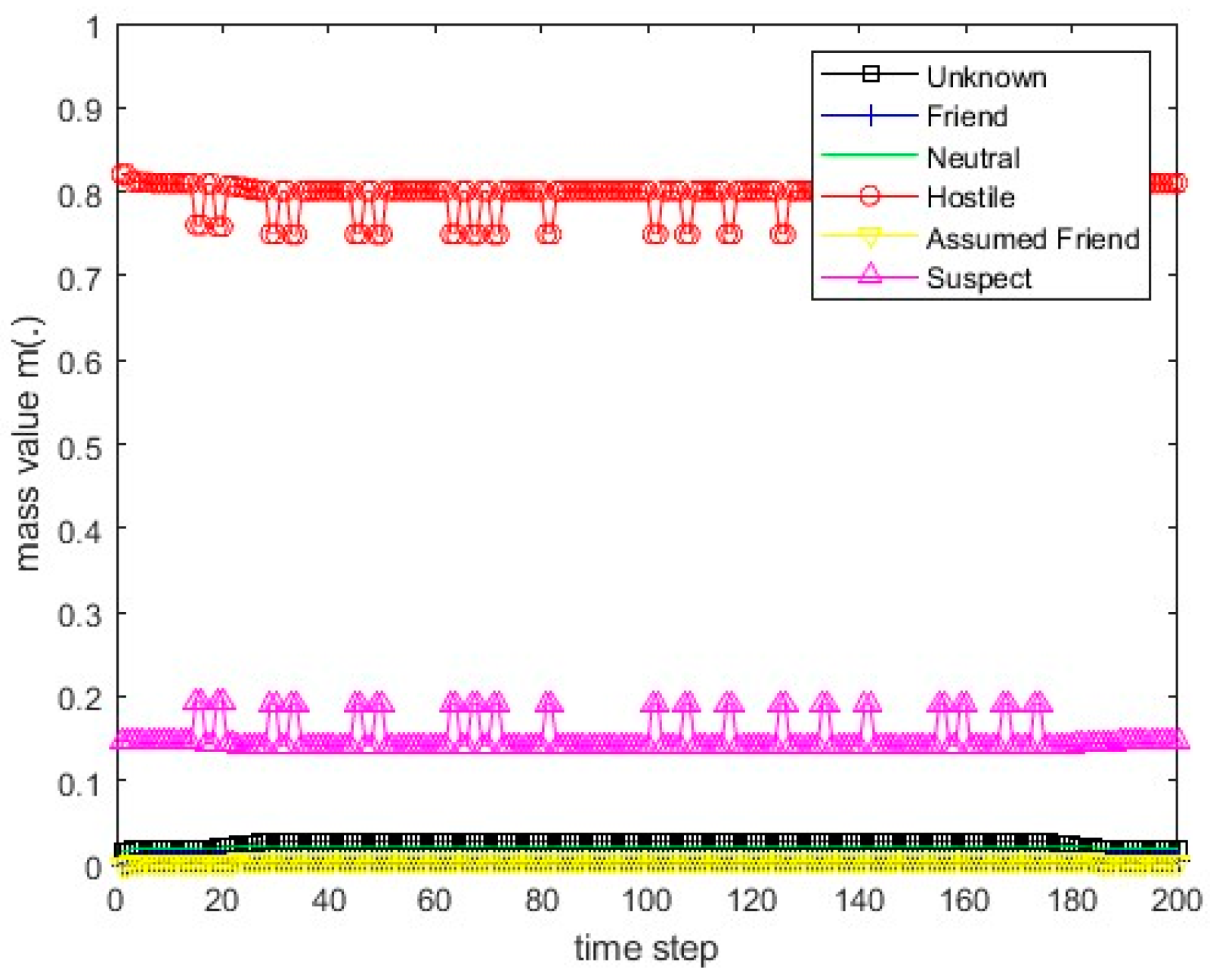
Figure 13.
The values of the resulting belief mass for scenario 1 and Dempster’s rule.
Figure 13.
The values of the resulting belief mass for scenario 1 and Dempster’s rule.
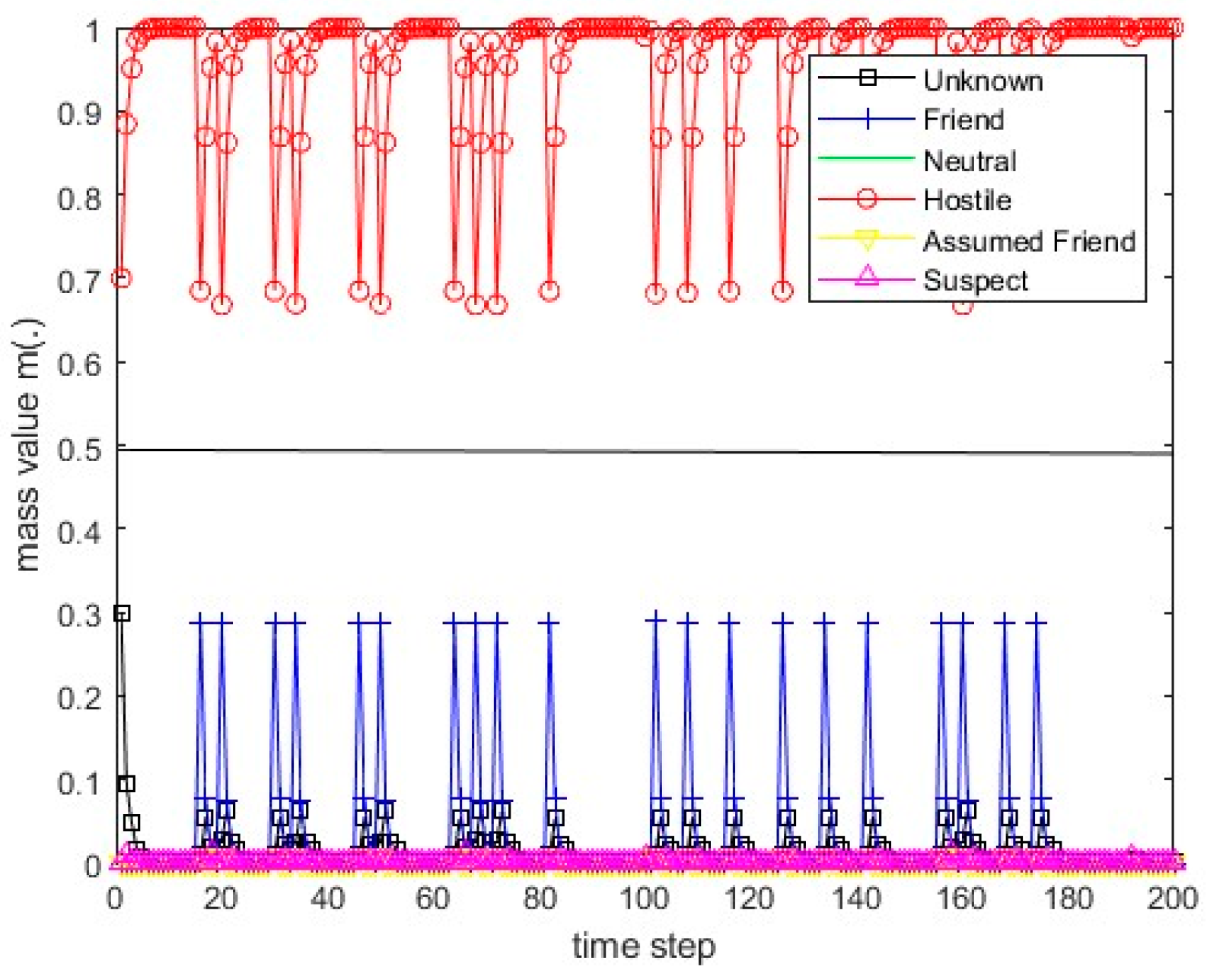
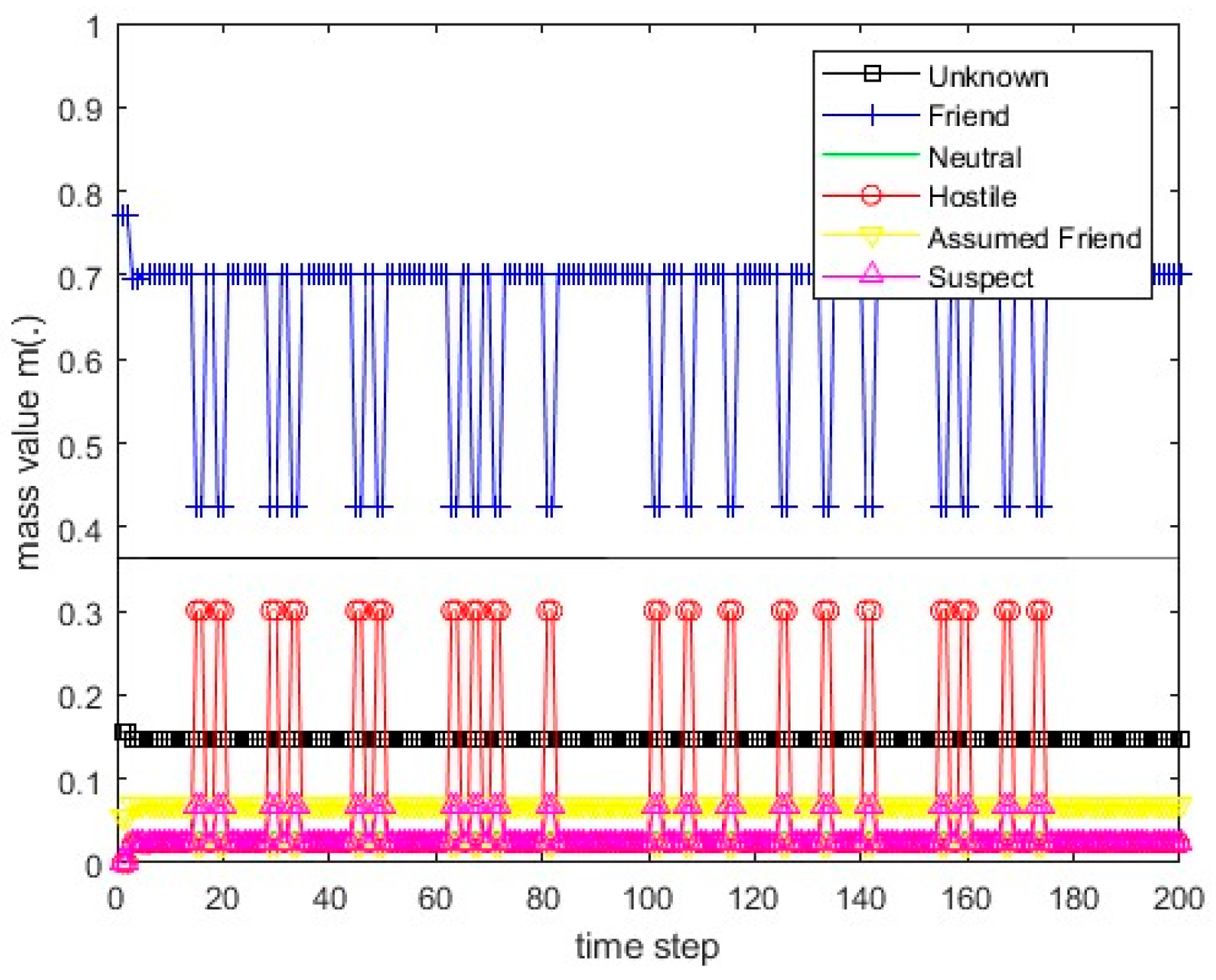
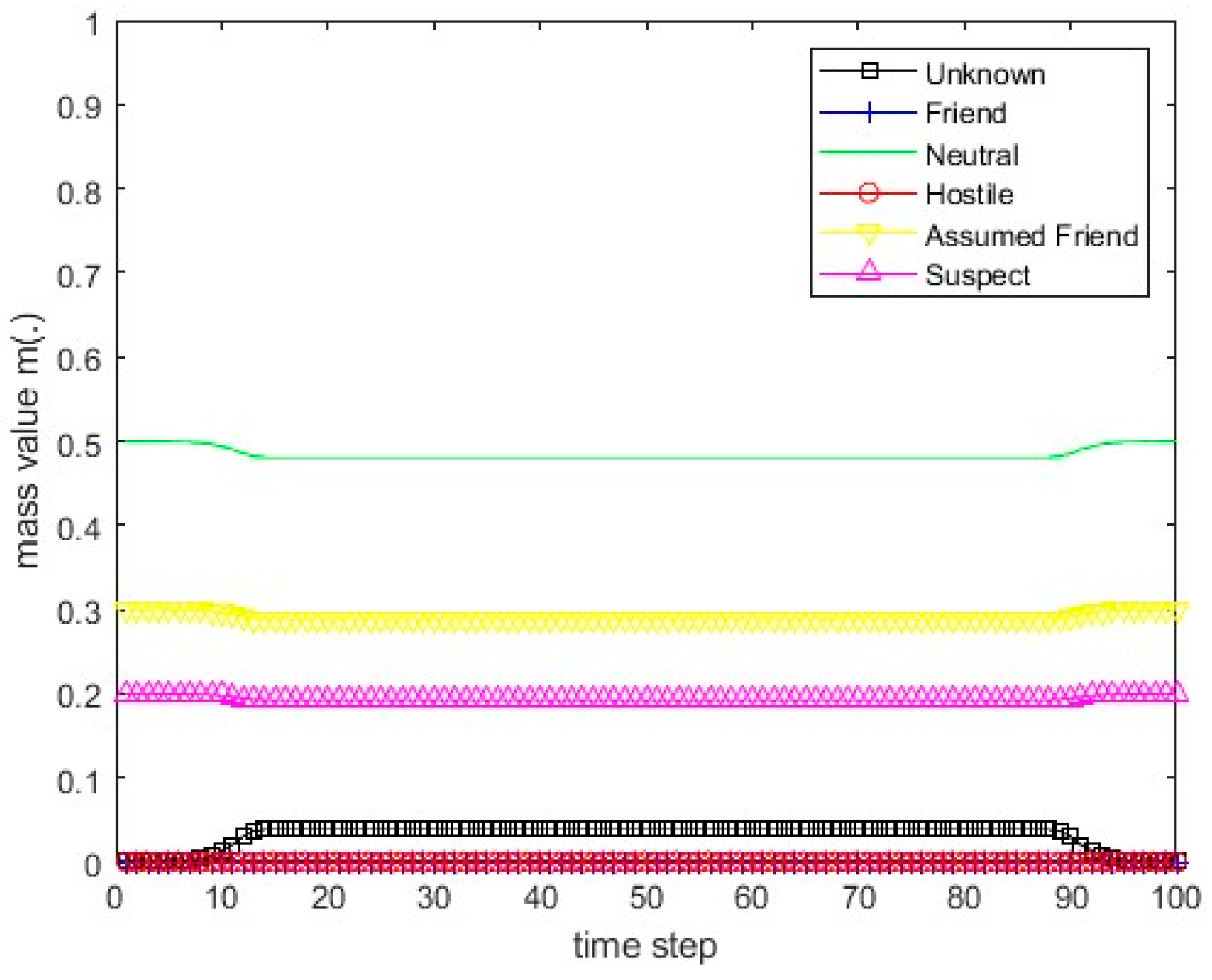
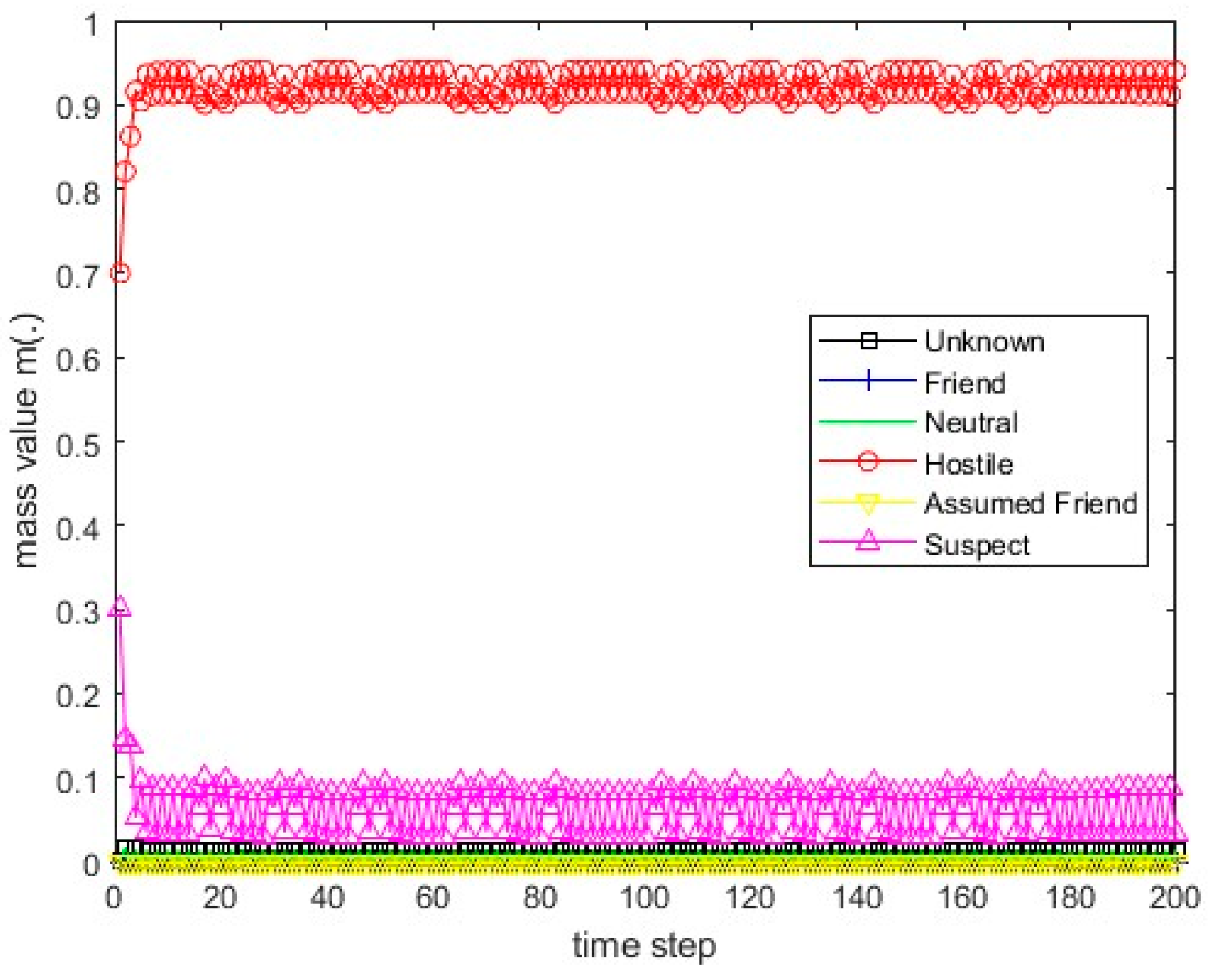
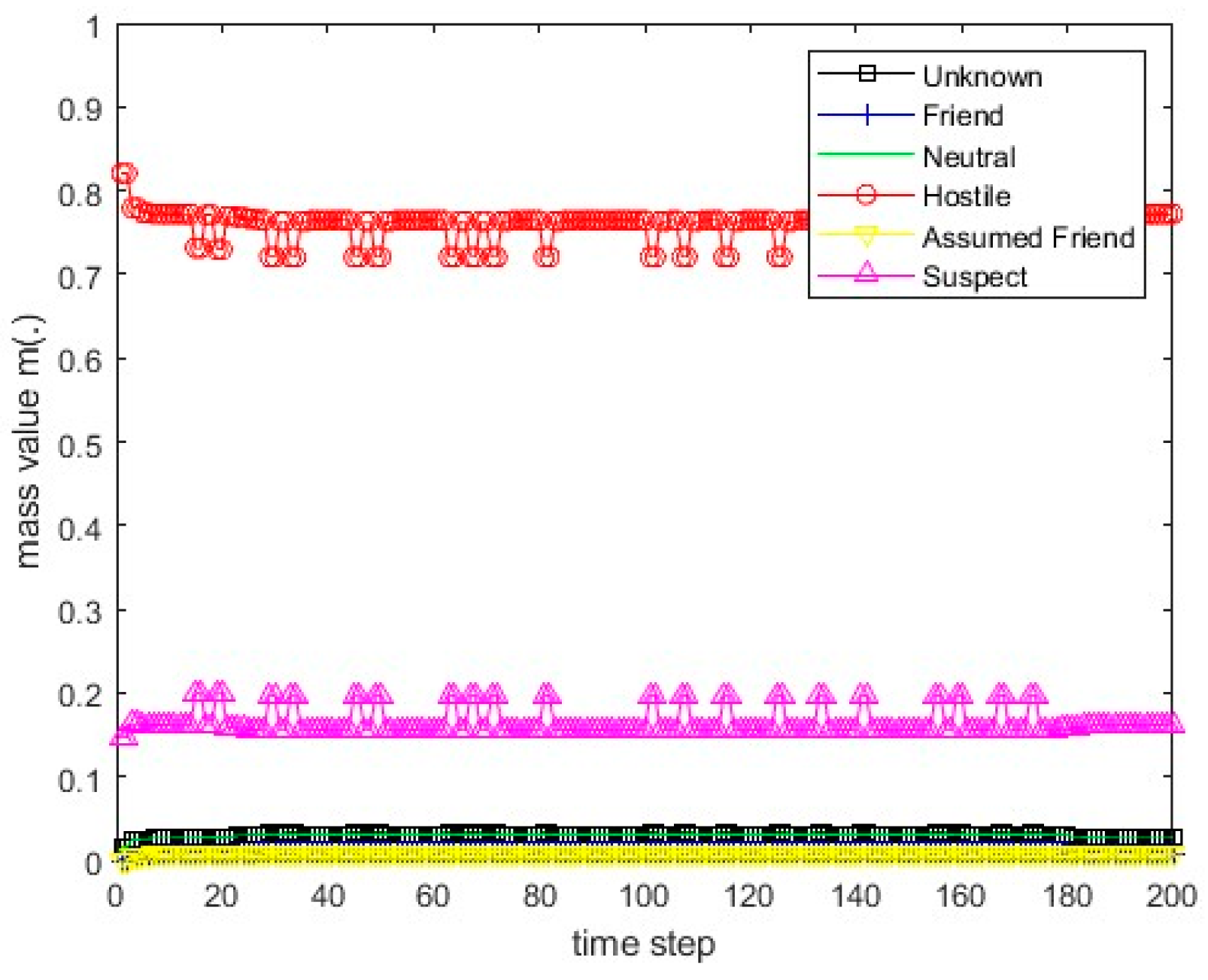
Figure 14.
The values of the resulting belief mass for scenario 3 and Dempster’s rule.
Figure 14.
The values of the resulting belief mass for scenario 3 and Dempster’s rule.
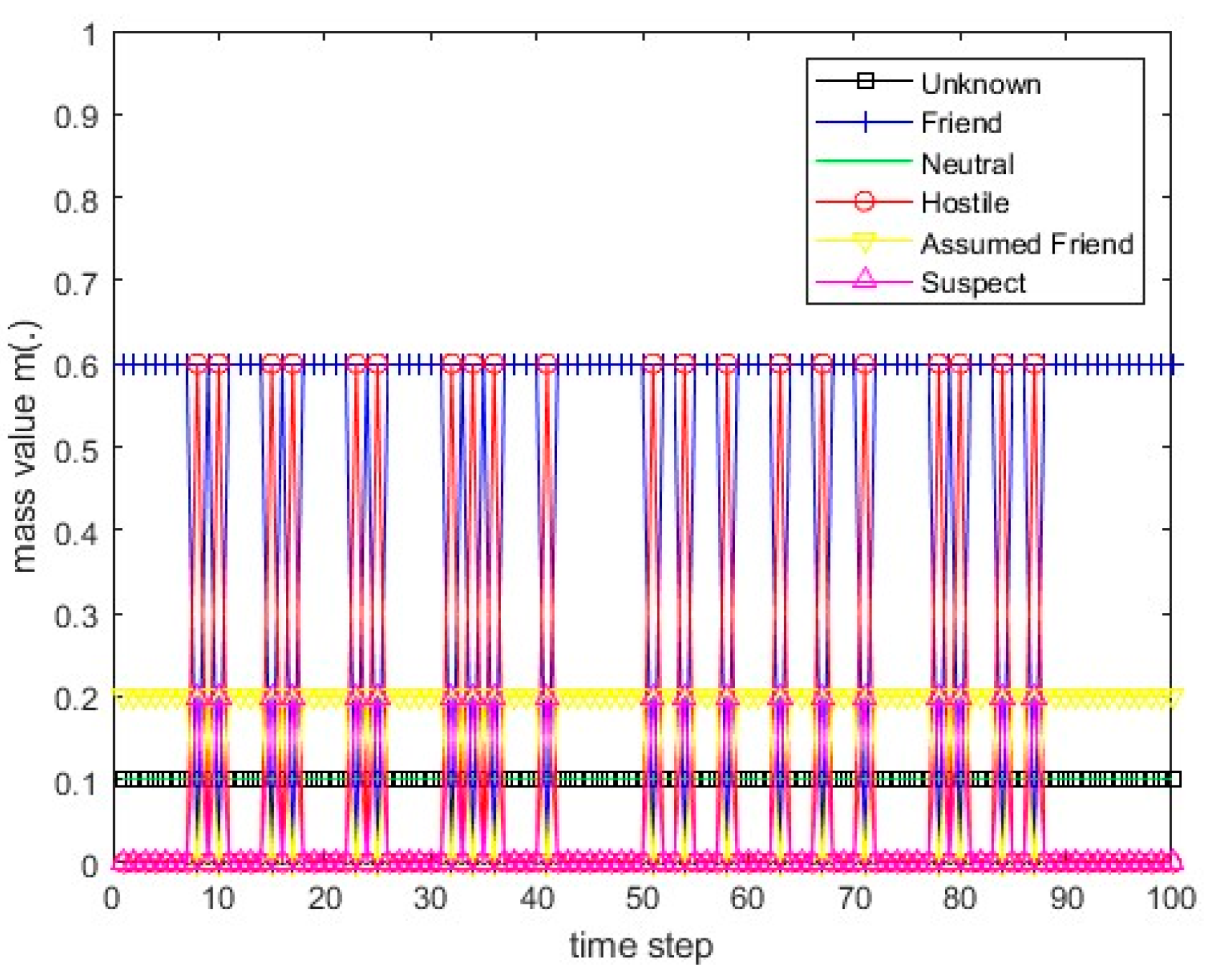
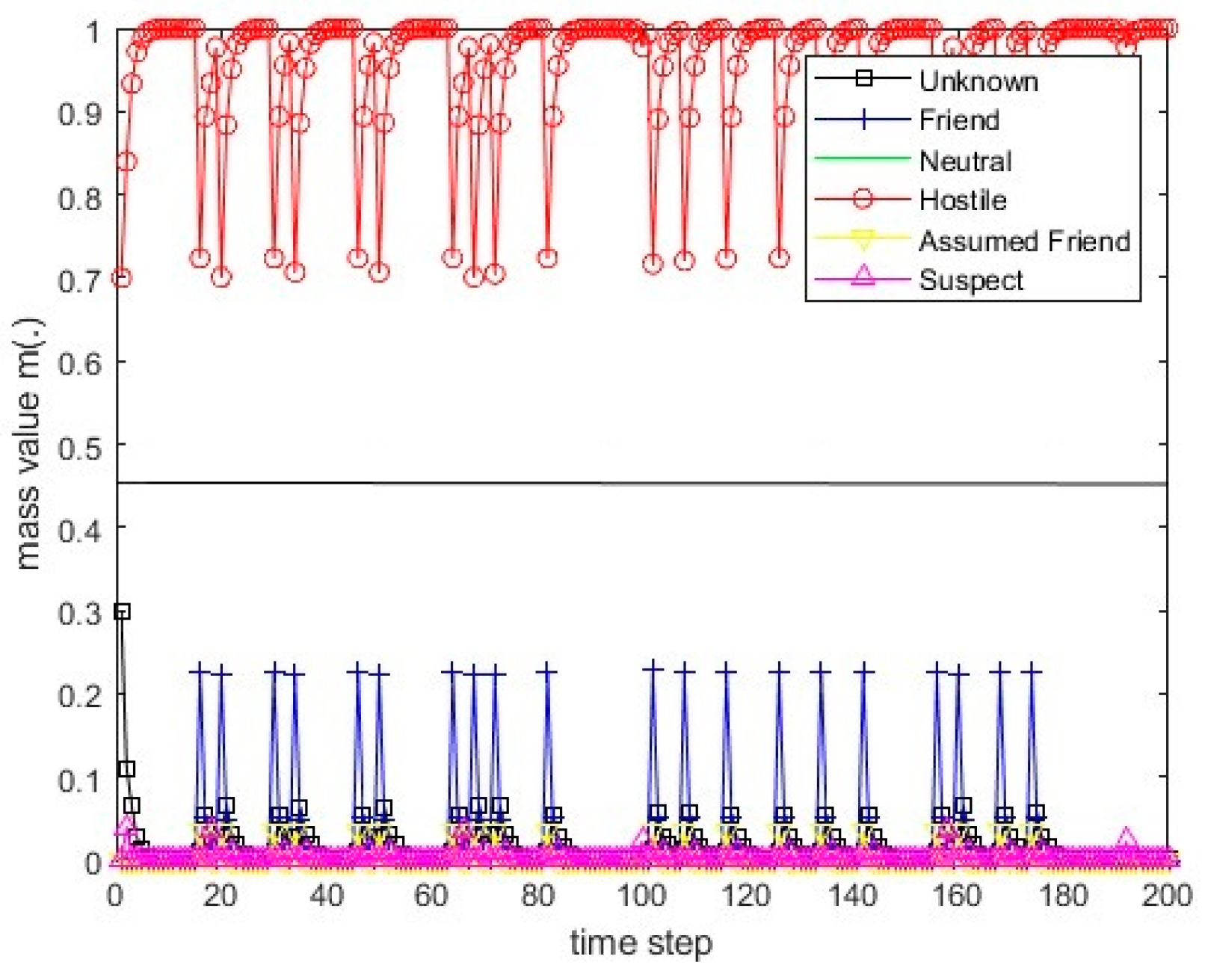
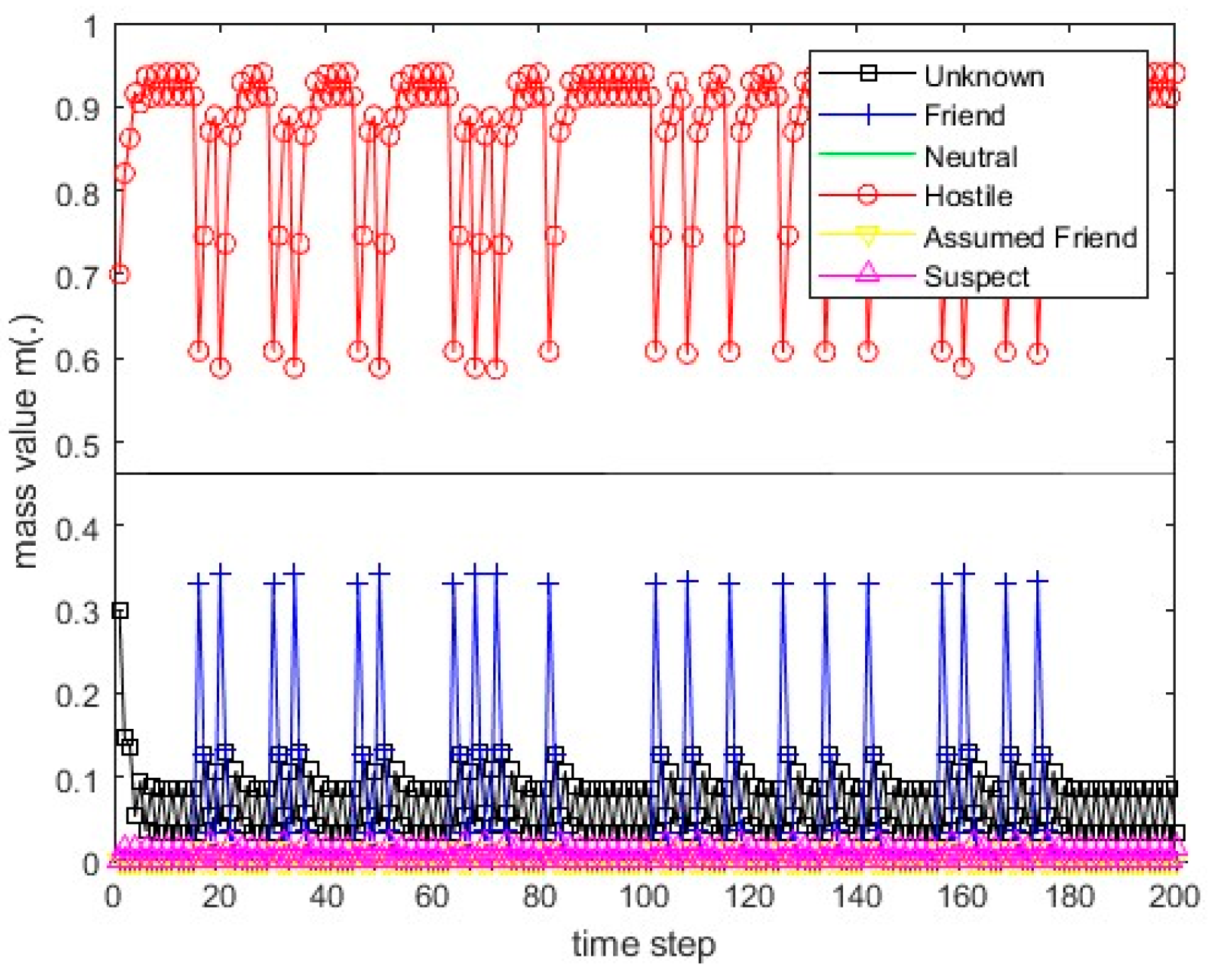
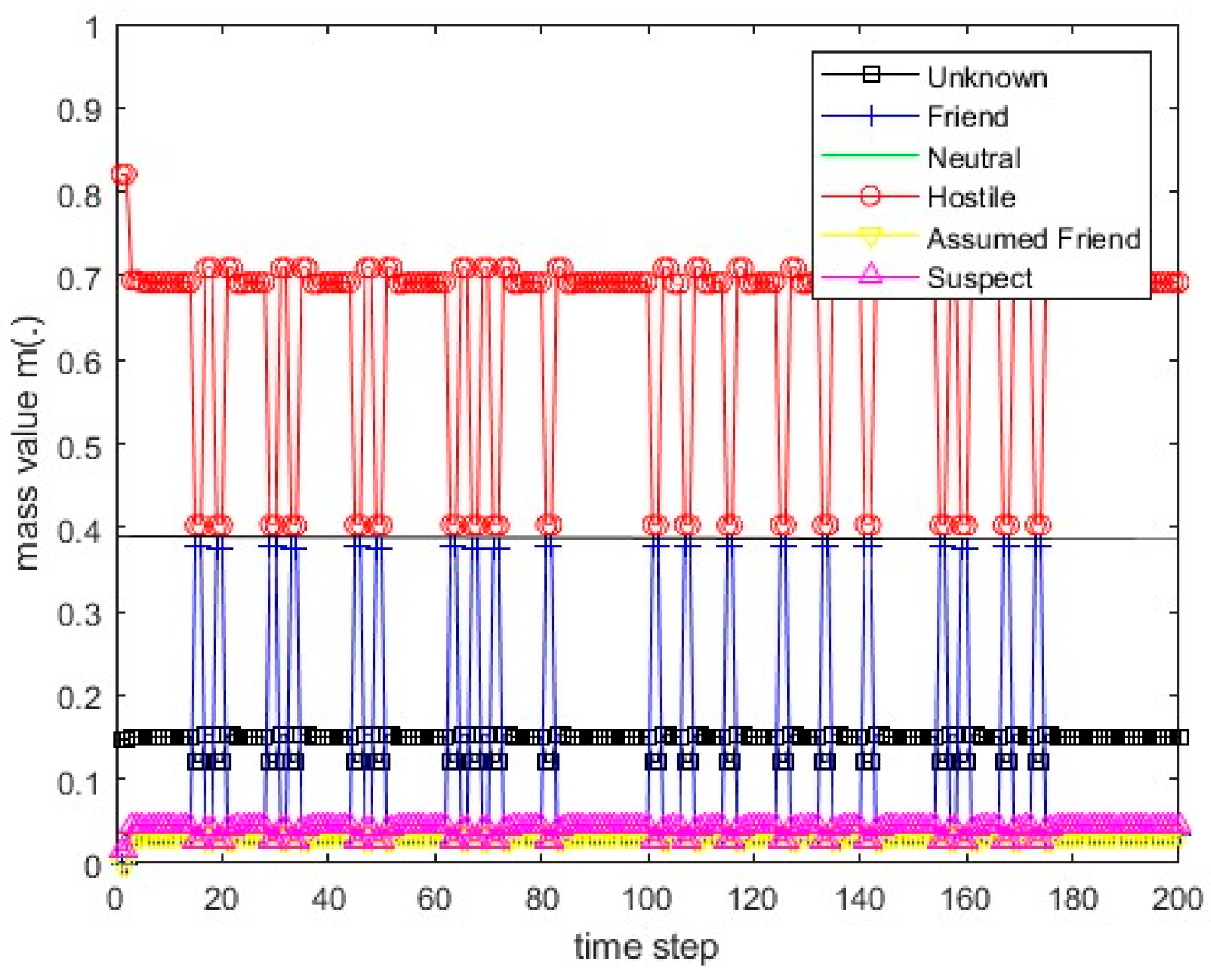
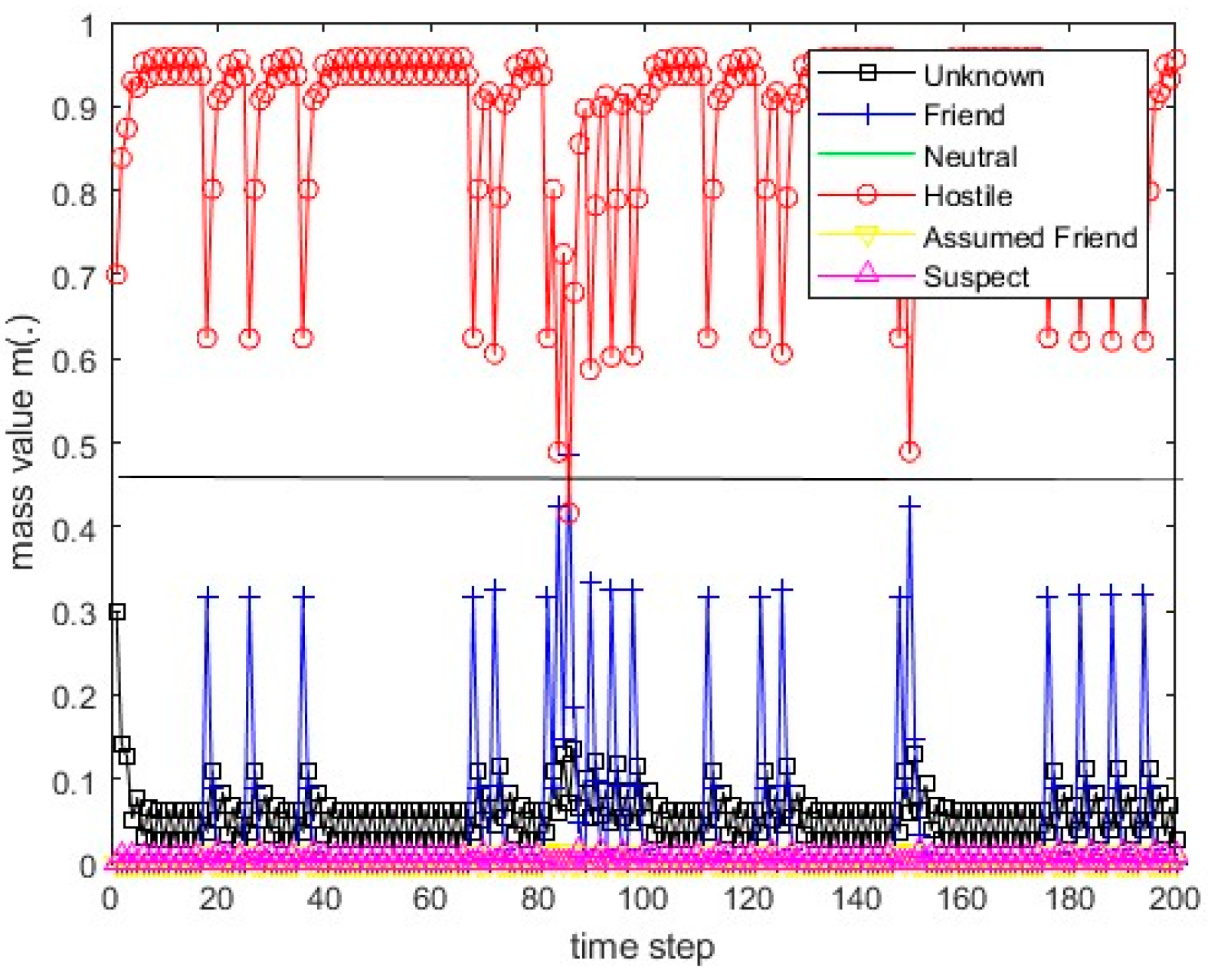
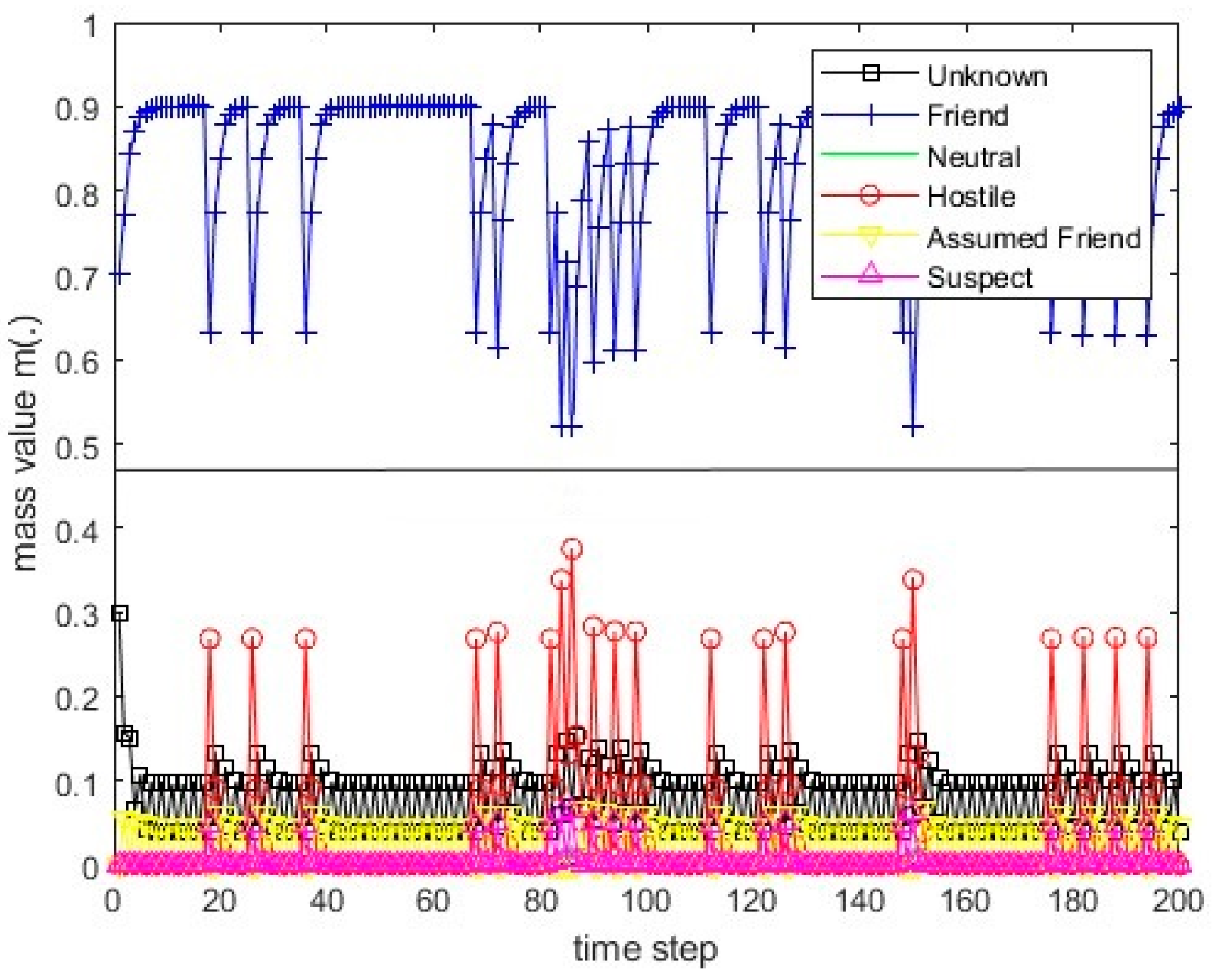
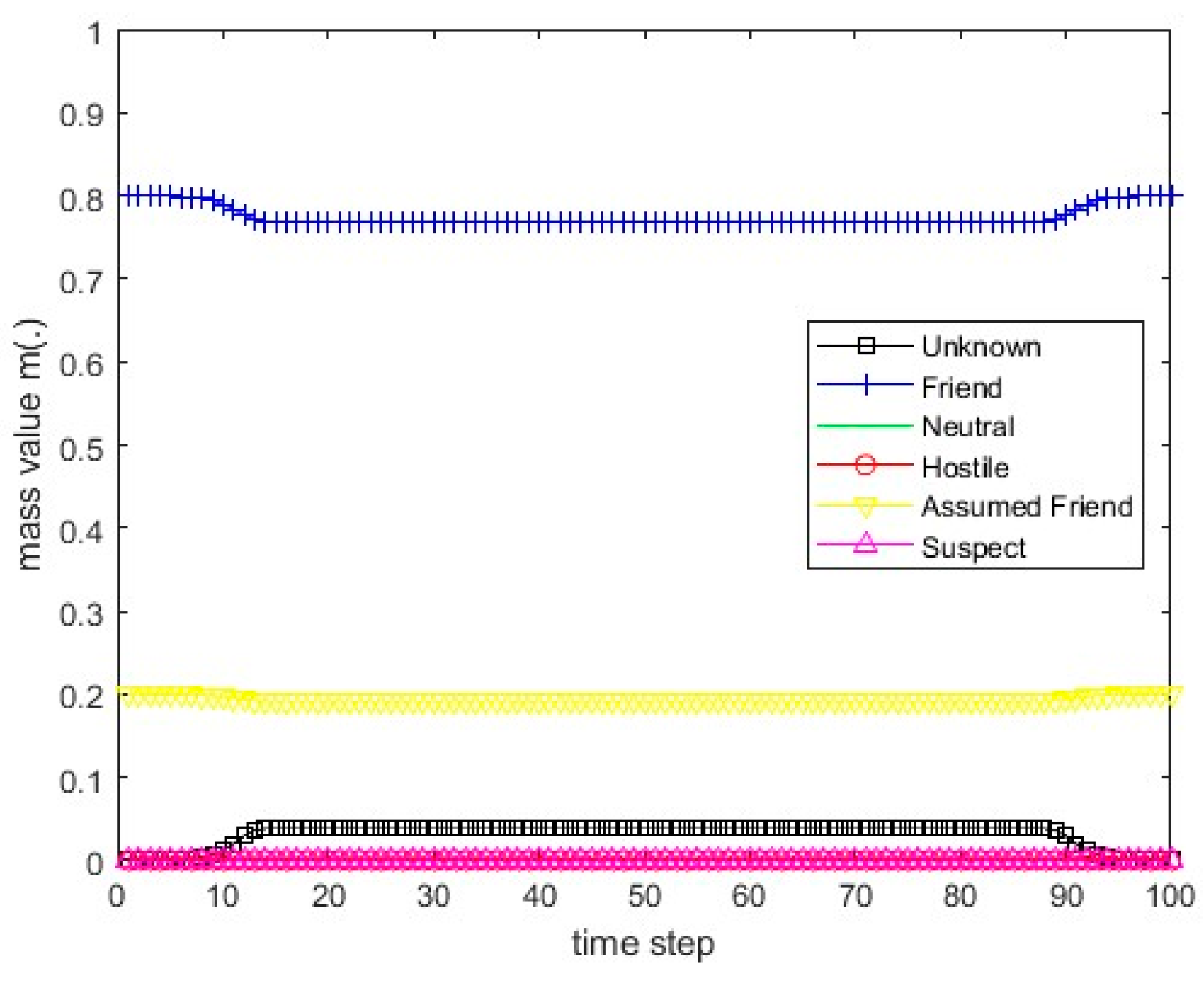
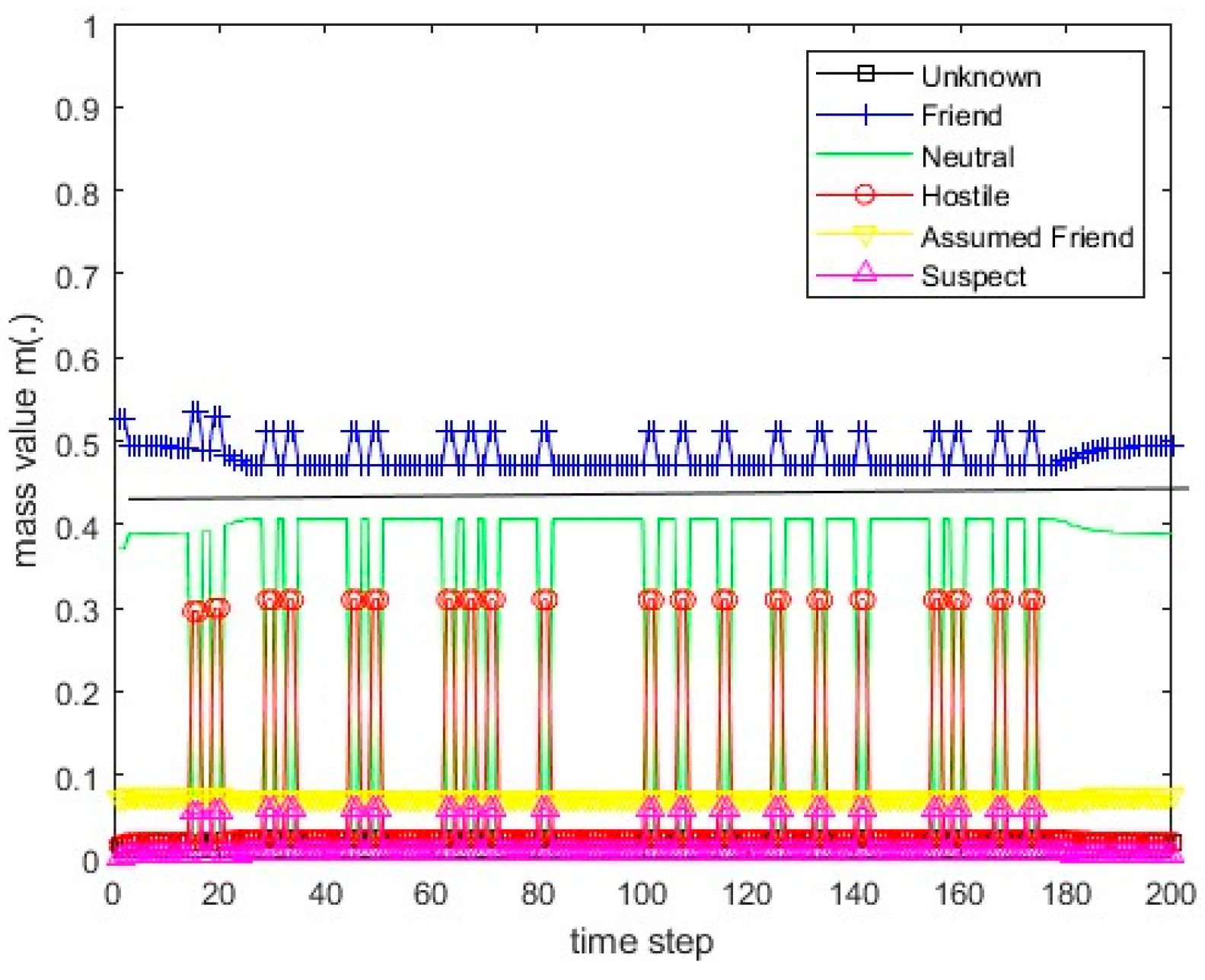
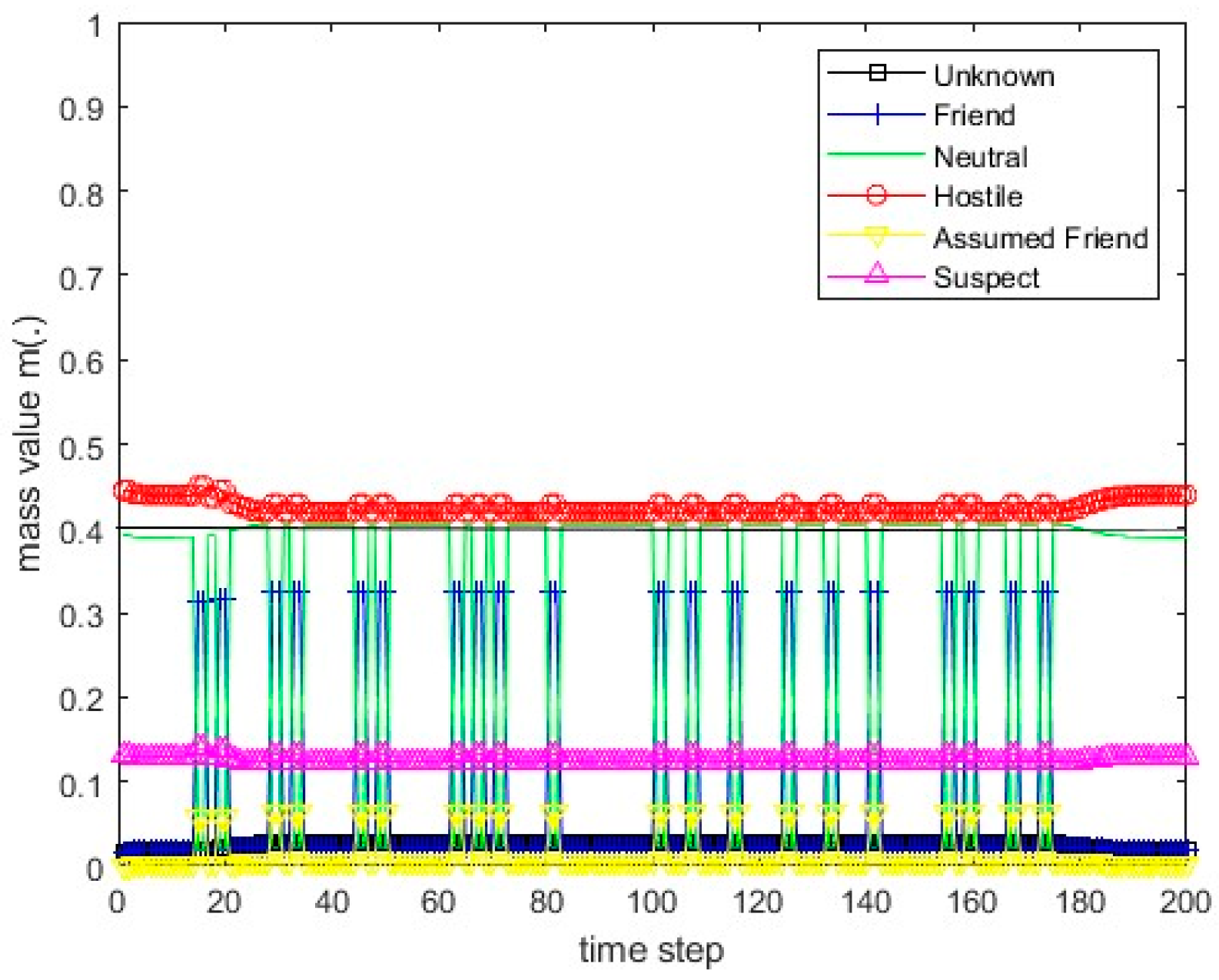
Figure 15.
The values of the resulting belief mass for scenario 1 and the PCR1 rule.
Figure 15.
The values of the resulting belief mass for scenario 1 and the PCR1 rule.
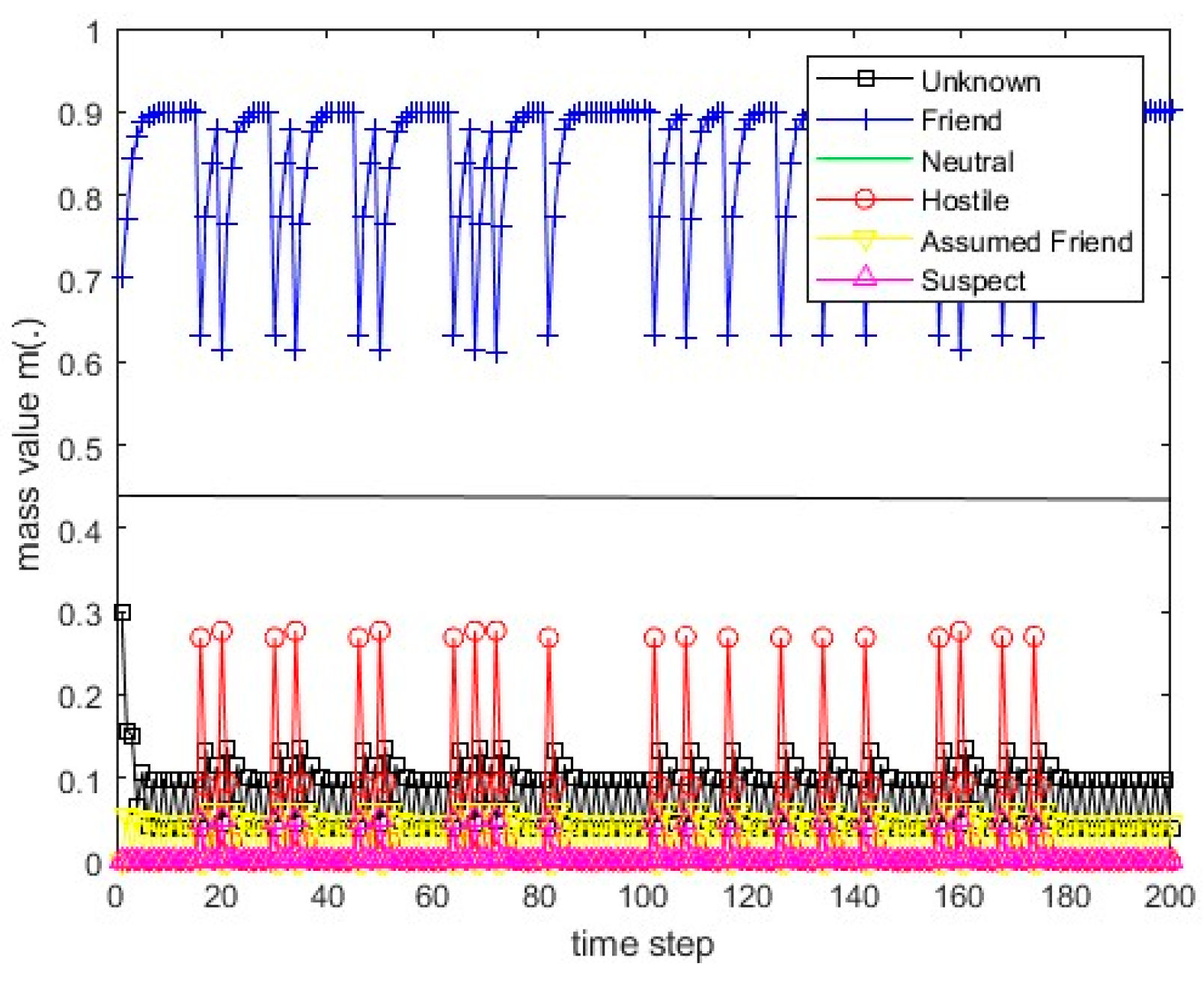
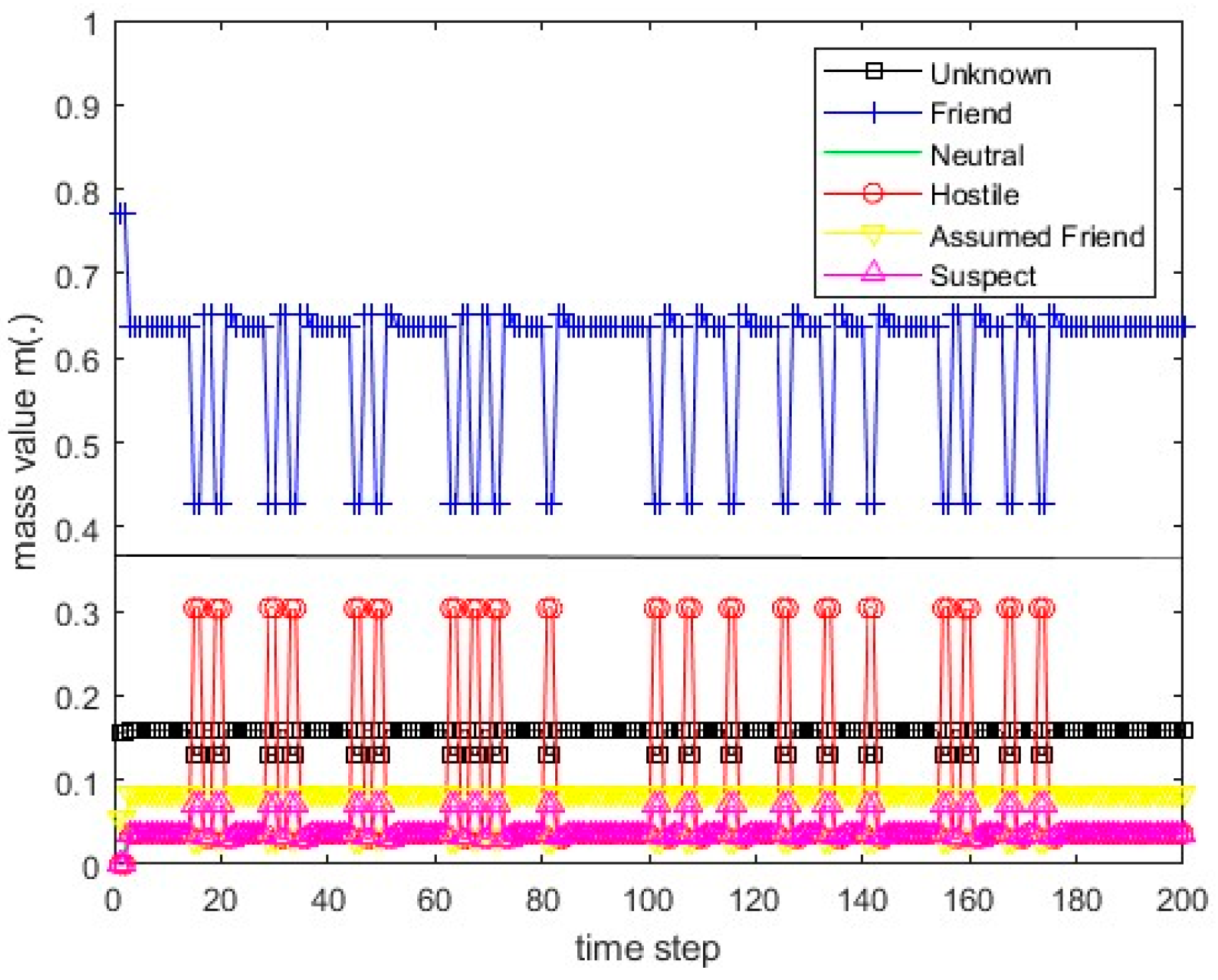
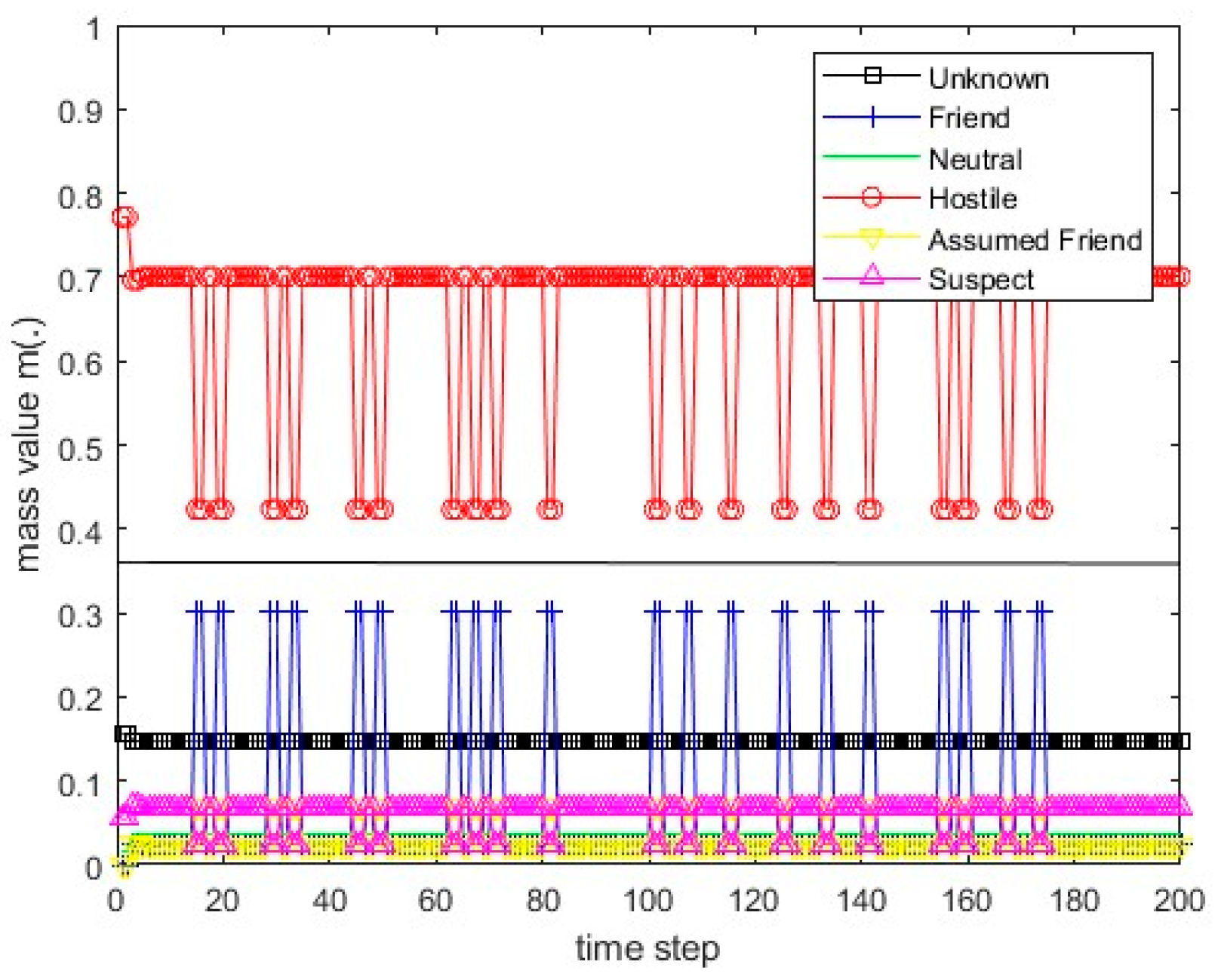
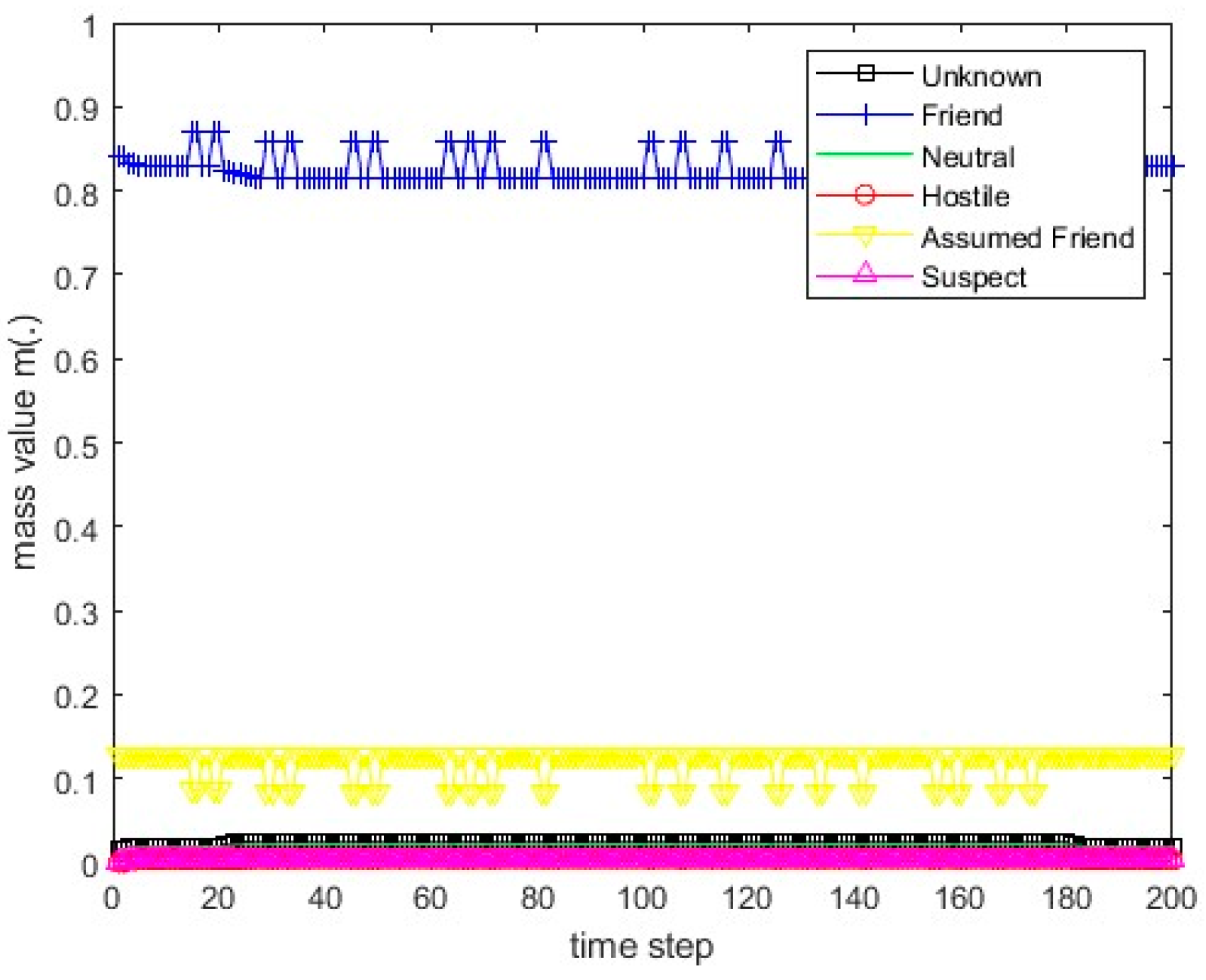
Figure 16.
The values of the resulting belief mass for scenario 2 and the PCR1 rule.
Figure 16.
The values of the resulting belief mass for scenario 2 and the PCR1 rule.
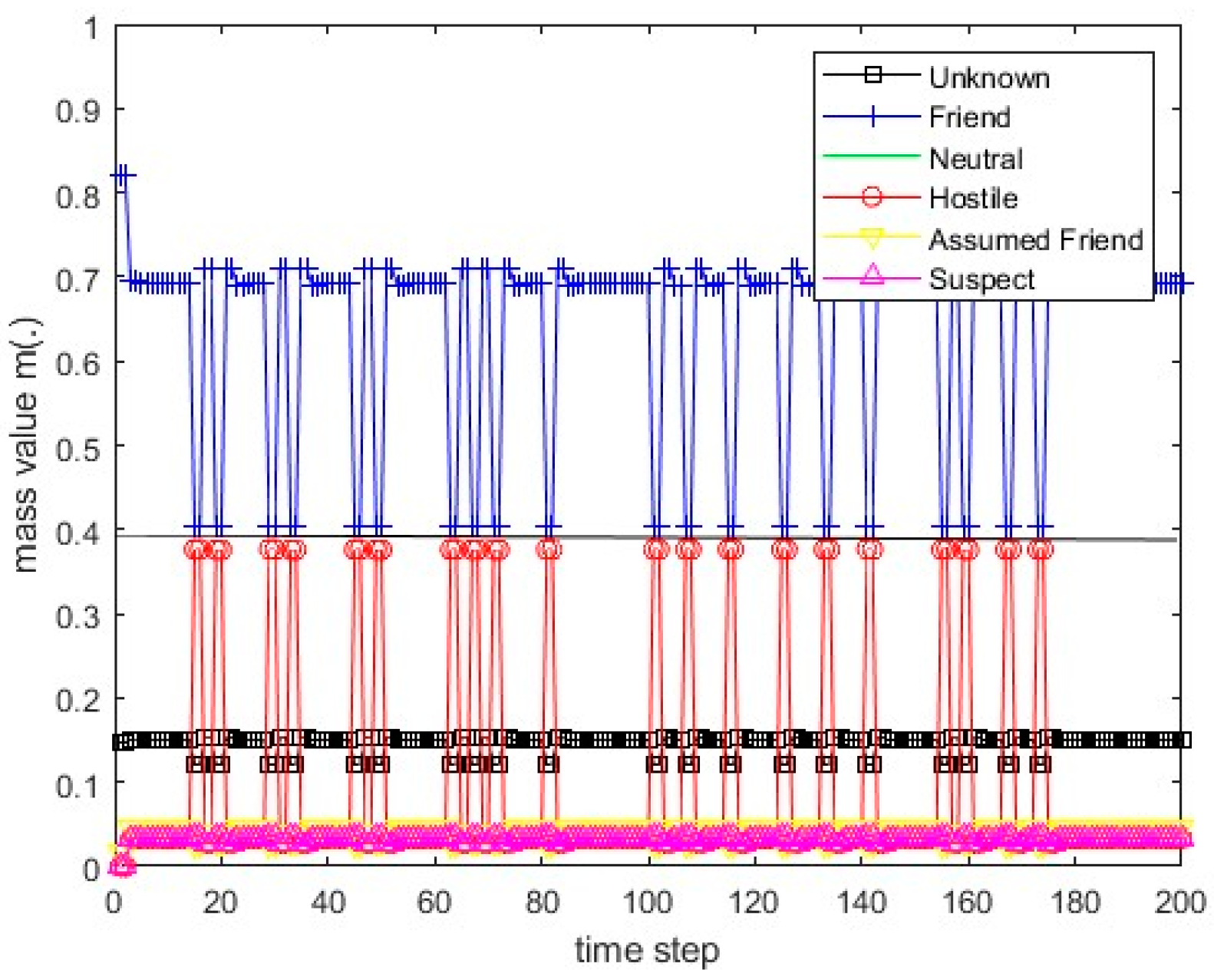
Figure 17.
The values of the resulting belief mass for scenario 3 and the PCR1 rule.
Figure 17.
The values of the resulting belief mass for scenario 3 and the PCR1 rule.
Figure 18.
The values of the resulting belief mass for scenario 4 and the PCR1 rule.
Figure 18.
The values of the resulting belief mass for scenario 4 and the PCR1 rule.
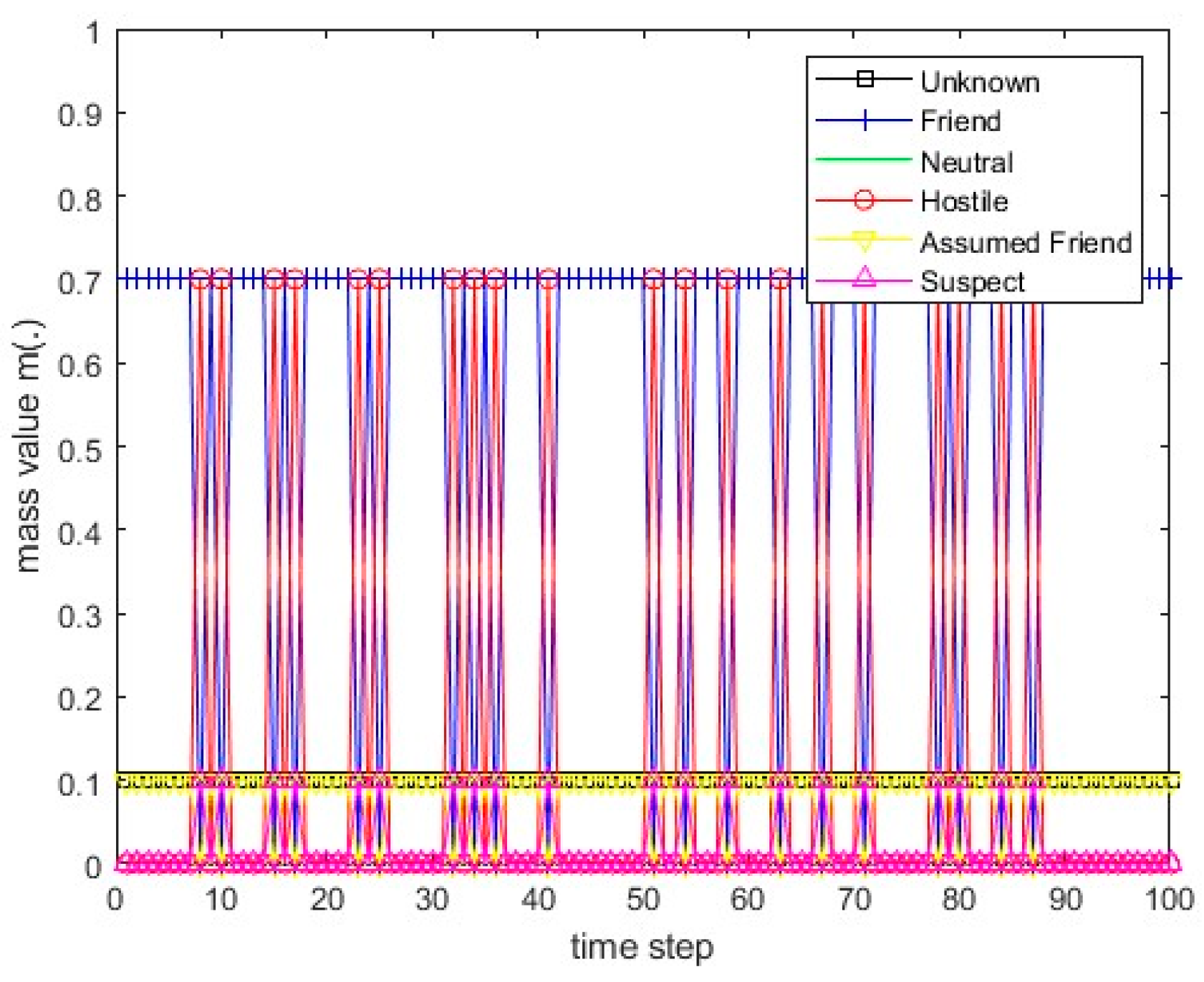
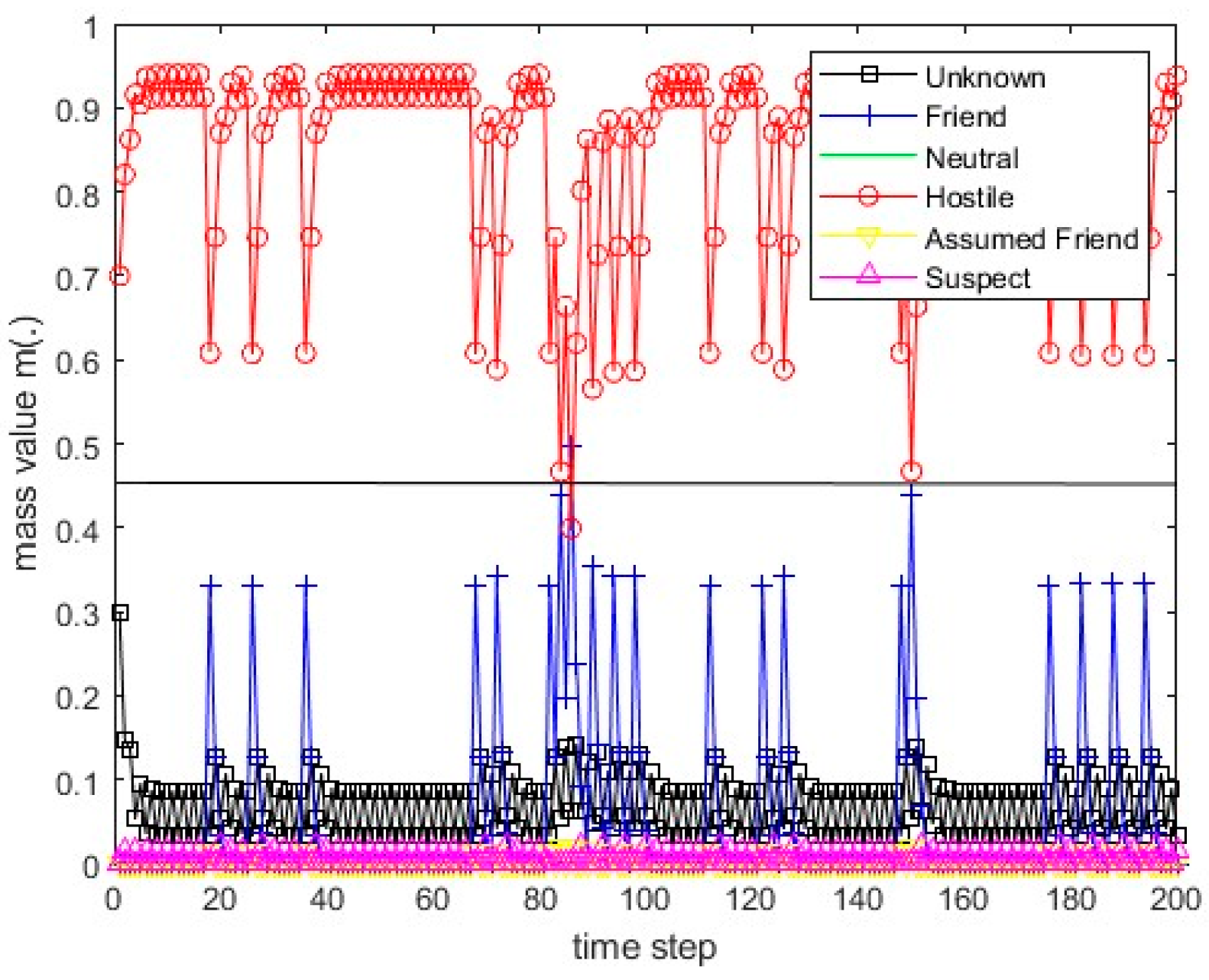
Figure 19.
The values of the resulting belief mass for scenario 1 and the PCR3 rule.
Figure 19.
The values of the resulting belief mass for scenario 1 and the PCR3 rule.
Figure 20.
The values of the resulting belief mass for scenario 2 and the PCR3 rule.
Figure 20.
The values of the resulting belief mass for scenario 2 and the PCR3 rule.
Figure 21.
The values of the resulting belief mass for scenario 3 and the PCR3 rule.
Figure 21.
The values of the resulting belief mass for scenario 3 and the PCR3 rule.
Figure 22.
The values of the resulting belief mass for scenario 4 and the PCR3 rule.
Figure 22.
The values of the resulting belief mass for scenario 4 and the PCR3 rule.
Figure 23.
The values of the resulting belief mass for scenario 1 and the PCR4 rule.
Figure 23.
The values of the resulting belief mass for scenario 1 and the PCR4 rule.
Figure 24.
The values of the resulting belief mass for scenario 2 and the PCR4 rule.
Figure 24.
The values of the resulting belief mass for scenario 2 and the PCR4 rule.
Figure 25.
The values of the resulting belief mass for scenario 3 and the PCR4 rule.
Figure 25.
The values of the resulting belief mass for scenario 3 and the PCR4 rule.
Figure 26.
The values of the resulting belief mass for scenario 4 and the PCR4 rule.
Figure 26.
The values of the resulting belief mass for scenario 4 and the PCR4 rule.
Figure 27.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 2 BBAs.
Figure 27.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 2 BBAs.
Figure 28.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 2 BBAs.
Figure 28.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 2 BBAs.
Figure 29.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 2 BBAs.
Figure 29.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 2 BBAs.
Figure 30.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 2 BBAs.
Figure 30.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 2 BBAs.
Figure 31.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 3 BBAs.
Figure 31.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 3 BBAs.
Figure 32.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 3 BBAs.
Figure 32.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 3 BBAs.
Figure 33.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 3 BBAs.
Figure 33.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 3 BBAs.
Figure 34.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 3 BBAs.
Figure 34.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 3 BBAs.
Figure 35.
The values of the resulting belief mass for scenario 1 and the PCR6 rule for 3 BBAs.
Figure 35.
The values of the resulting belief mass for scenario 1 and the PCR6 rule for 3 BBAs.
Figure 36.
The values of the resulting belief mass for scenario 2 and the PCR6 rule for 3 BBAs.
Figure 36.
The values of the resulting belief mass for scenario 2 and the PCR6 rule for 3 BBAs.
Figure 37.
The values of the resulting belief mass for scenario 3 and the PCR6 rule for 3 BBAs.
Figure 37.
The values of the resulting belief mass for scenario 3 and the PCR6 rule for 3 BBAs.
Figure 38.
The values of the resulting belief mass for scenario 4 and the PCR6 rule for 3 BBAs.
Figure 38.
The values of the resulting belief mass for scenario 4 and the PCR6 rule for 3 BBAs.
Figure 39.
The values of the resulting belief mass for Monte Carlo scenario 5 and Dempster’s rule.
Figure 39.
The values of the resulting belief mass for Monte Carlo scenario 5 and Dempster’s rule.
Figure 40.
The values of the resulting belief mass for Monte Carlo scenario 6 and Dempster’s rule.
Figure 40.
The values of the resulting belief mass for Monte Carlo scenario 6 and Dempster’s rule.
Figure 41.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR1 rule.
Figure 41.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR1 rule.
Figure 42.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR1 rule.
Figure 42.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR1 rule.
Figure 43.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR3 rule.
Figure 43.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR3 rule.
Figure 44.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR3 rule.
Figure 44.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR3 rule.
Figure 45.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR4 rule.
Figure 45.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR4 rule.
Figure 46.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR4 rule.
Figure 46.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR4 rule.
Figure 47.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR5 rule for 2 BBAs.
Figure 47.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR5 rule for 2 BBAs.
Figure 48.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR5 rule for 2 BBAs.
Figure 48.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR5 rule for 2 BBAs.
Figure 49.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR5 rule for 3 BBAs.
Figure 49.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR5 rule for 3 BBAs.
Figure 50.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR5 rule for 3 BBAs.
Figure 50.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR5 rule for 3 BBAs.
Figure 51.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR6 rule for 3 BBAs.
Figure 51.
The values of the resulting belief mass for Monte Carlo scenario 5 and the PCR6 rule for 3 BBAs.
Figure 52.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR6 rule for 3 BBAs.
Figure 52.
The values of the resulting belief mass for Monte Carlo scenario 6 and the PCR6 rule for 3 BBAs.
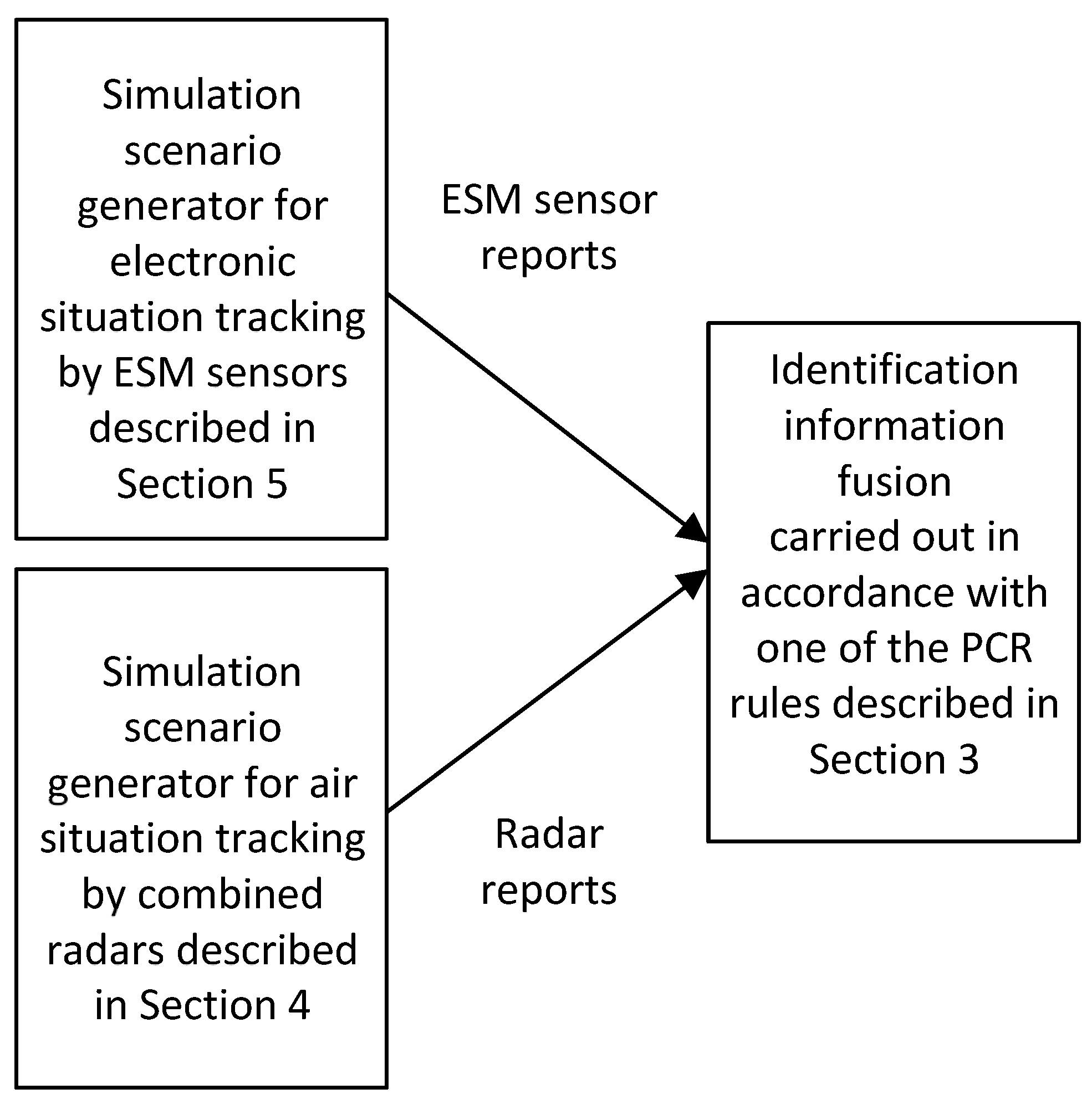
Figure 53.
The general diagram of simulation experiments of fusion of identification information from radars and ESM sensors.
Figure 53.
The general diagram of simulation experiments of fusion of identification information from radars and ESM sensors.
Figure 54.
The course of scenarios number 1 and 4 for sensor 1.
Figure 54.
The course of scenarios number 1 and 4 for sensor 1.
Figure 55.
The course of scenarios number 2 and 5 for sensor 1.
Figure 55.
The course of scenarios number 2 and 5 for sensor 1.
Figure 56.
The course of scenarios number 3 and 6 for sensor 1.
Figure 56.
The course of scenarios number 3 and 6 for sensor 1.
Figure 57.
The course of scenario number 1 for sensor 2.
Figure 57.
The course of scenario number 1 for sensor 2.
Figure 58.
The course of scenario number 2 for sensor 2.
Figure 58.
The course of scenario number 2 for sensor 2.
Figure 59.
The course of scenario number 3 for sensor 2.
Figure 59.
The course of scenario number 3 for sensor 2.
Figure 60.
The course of scenario number 4 for sensor 2.
Figure 60.
The course of scenario number 4 for sensor 2.
Figure 61.
The course of scenario number 5 for sensor 2.
Figure 61.
The course of scenario number 5 for sensor 2.
Figure 62.
The course of scenario number 6 for sensor 2.
Figure 62.
The course of scenario number 6 for sensor 2.
Figure 63.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 2 BBAs.
Figure 63.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 2 BBAs.
Figure 64.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 2 BBAs.
Figure 64.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 2 BBAs.
Figure 65.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 2 BBAs.
Figure 65.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 2 BBAs.
Figure 66.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 2 BBAs.
Figure 66.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 2 BBAs.
Figure 67.
The values of the resulting belief mass for scenario 5 and the PCR5 rule for 2 BBAs.
Figure 67.
The values of the resulting belief mass for scenario 5 and the PCR5 rule for 2 BBAs.
Figure 68.
The values of the resulting belief mass for scenario 6 and the PCR5 rule for 2 BBAs.
Figure 68.
The values of the resulting belief mass for scenario 6 and the PCR5 rule for 2 BBAs.
Figure 69.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 3 BBAs.
Figure 69.
The values of the resulting belief mass for scenario 1 and the PCR5 rule for 3 BBAs.
Figure 70.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 3 BBAs.
Figure 70.
The values of the resulting belief mass for scenario 2 and the PCR5 rule for 3 BBAs.
Figure 71.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 3 BBAs.
Figure 71.
The values of the resulting belief mass for scenario 3 and the PCR5 rule for 3 BBAs.
Figure 72.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 3 BBAs.
Figure 72.
The values of the resulting belief mass for scenario 4 and the PCR5 rule for 3 BBAs.
Figure 73.
The values of the resulting belief mass for scenario 5 and the PCR5 rule for 3 BBAs.
Figure 73.
The values of the resulting belief mass for scenario 5 and the PCR5 rule for 3 BBAs.
Figure 74.
The values of the resulting belief mass for scenario 6 and the PCR5 rule for 3 BBAs.
Figure 74.
The values of the resulting belief mass for scenario 6 and the PCR5 rule for 3 BBAs.
Figure 75.
The values of the resulting belief mass for scenario 1 and the PCR6 rule for 3 BBAs.
Figure 75.
The values of the resulting belief mass for scenario 1 and the PCR6 rule for 3 BBAs.
Figure 76.
The values of the resulting belief mass for scenario 2 and the PCR6 rule for 3 BBAs.
Figure 76.
The values of the resulting belief mass for scenario 2 and the PCR6 rule for 3 BBAs.
Figure 77.
The values of the resulting belief mass for scenario 3 and the PCR6 rule for 3 BBAs.
Figure 77.
The values of the resulting belief mass for scenario 3 and the PCR6 rule for 3 BBAs.
Figure 78.
The values of the resulting belief mass for scenario 4 and the PCR6 rule for 3 BBAs.
Figure 78.
The values of the resulting belief mass for scenario 4 and the PCR6 rule for 3 BBAs.
Figure 79.
The values of the resulting belief mass for scenario 5 and the PCR6 rule for 3 BBAs.
Figure 79.
The values of the resulting belief mass for scenario 5 and the PCR6 rule for 3 BBAs.
Figure 80.
The values of the resulting belief mass for scenario 6 and the PCR6 rule for 3 BBAs.
Figure 80.
The values of the resulting belief mass for scenario 6 and the PCR6 rule for 3 BBAs.
Table 1.
Transformation of the base belief assignment mass into the secondary belief assignment mass.
Table 1.
Transformation of the base belief assignment mass into the secondary belief assignment mass.
| Base Identification → | FB | NB | HB |
|---|
| FS |
| 0 | 0 |
| NS | 0 |
| 0 |
| HS | 0 | 0 |
|
| AF |
|
| 0 |
| S | 0 |
|
|
Table 2.
Belief mass values for the second sensor for scenarios 1 and 5.
Table 2.
Belief mass values for the second sensor for scenarios 1 and 5.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0.6 | 0.1 | 0 | 0.2 | 0 | 0.1 |
| Incorrect identification (20% of events) | 0 | 0.1 | 0.6 | 0 | 0.2 | 0.1 |
Table 3.
Belief mass values for the second sensor for scenario 2.
Table 3.
Belief mass values for the second sensor for scenario 2.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0.7 | 0.1 | 0 | 0.1 | 0 | 0.1 |
| Incorrect identification (20% of events) | 0 | 0.1 | 0.7 | 0 | 0.7 | 0.1 |
Table 4.
Belief mass values for the second sensor for scenario 3.
Table 4.
Belief mass values for the second sensor for scenario 3.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0 | 0.1 | 0.6 | 0 | 0.2 | 0.1 |
| Incorrect identification (20% of events) | 0.6 | 0.1 | 0 | 0.2 | 0 | 0.1 |
Table 5.
Belief mass values for the second sensor for scenarios 4 and 6.
Table 5.
Belief mass values for the second sensor for scenarios 4 and 6.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0 | 0.1 | 0.7 | 0 | 0.1 | 0.1 |
| Incorrect identification (20% of events) | 0.7 | 0.1 | 0 | 0.1 | 0 | 0.1 |
Table 6.
Transformation of the base belief assignment mass into the secondary belief assignment mass for combined primary and secondary surveillance radar.
Table 6.
Transformation of the base belief assignment mass into the secondary belief assignment mass for combined primary and secondary surveillance radar.
| (Scenario Nr, Base Identification) → | (1,FB) | (2,NB) | (3,HB) |
|---|
| FS | 0.8 | 0 | 0 |
| NS | 0 | 0.5 | 0 |
| HS | 0 | 0 | 0.7 |
| AF | 0.2 | 0.3 | 0 |
| S | 0 | 0.2 | 0.3 |
Table 7.
Belief mass values for the second sensor (ESM) for scenario 1.
Table 7.
Belief mass values for the second sensor (ESM) for scenario 1.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0.6 | 0.1 | 0 | 0.2 | 0 | 0.1 |
| Incorrect identification (20% of events) | 0 | 0.1 | 0.6 | 0 | 0.2 | 0.1 |
Table 8.
Belief mass values for the second sensor (ESM) for scenario 2.
Table 8.
Belief mass values for the second sensor (ESM) for scenario 2.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0 | 0.5 | 0.3 | 0 | 0.2 | 0 |
| Incorrect identification (20% of events) | 0 | 0.4 | 0.2 | 0 | 0.3 | 0.1 |
Table 9.
Belief mass values for the second sensor (ESM) for scenario 3.
Table 9.
Belief mass values for the second sensor (ESM) for scenario 3.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0 | 0.1 | 0.7 | 0 | 0.1 | 0.1 |
| Incorrect identification (20% of events) | 0 | 0.1 | 0.6 | 0 | 0.2 | 0.1 |
Table 10.
Belief mass values for the second sensor (ESM) for scenario 4.
Table 10.
Belief mass values for the second sensor (ESM) for scenario 4.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0.1 | 0.7 | 0.1 | 0 | 0 | 0.1 |
| Incorrect identification (20% of events) | 0 | 0.1 | 0.6 | 0 | 0.2 | 0.1 |
Table 11.
Belief mass values for the second sensor (ESM) for scenario 5.
Table 11.
Belief mass values for the second sensor (ESM) for scenario 5.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0.6 | 0.1 | 0 | 0.2 | 0 | 0.1 |
| Incorrect identification (20% of events) | 0 | 0.1 | 0.6 | 0 | 0.2 | 0.1 |
Table 12.
Belief mass values for the second sensor (ESM) for scenario 6.
Table 12.
Belief mass values for the second sensor (ESM) for scenario 6.
| Type of Identification | F | N | H | AF | S | U |
|---|
| Correct identification (80% of events) | 0.1 | 0.7 | 0.1 | 0 | 0 | 0.1 |
| Incorrect identification (20% of events) | 0.6 | 0.1 | 0 | 0.2 | 0 | 0.1 |