Abstract
We studied the kinematic behaviour of active landslides at several localities in the area of Panachaikon Mountain, Achaia (Peloponnese, Greece) using Sentinel (C-band) InSAR time series analysis. We processed LiCSAR interferograms using the SBAS tool, and we obtained average displacement maps for the period 2016–2021. We found that the maximum displacement rate of each landslide is located at about the center of it. The average E-W velocity of the Krini landslide is ~3 cm/year (toward the east) and 0.6 cm/year downward. The line-of-sight (LOS) velocity of the landslide (descending orbit) compares well to a co-located GNSS station within (±) 3 mm/yr. Our results also suggest a correlation between rainfall and landslide motion. For the Krini landslide, a cross-correlation analysis of our data suggests that the mean time lag was 13.5 days between the maximum seasonal rainfall and the change in the LOS displacement rate. We also found that the amount of total seasonal rainfall controls the increase in the displacement rate, as 40–550% changes in the displacement rate of the Krini landslide were detected, following to a seasonal maximum of rainfall values at the nearby meteorological station of Kato Vlassia. According to our results, it seems that large part of this mountainous region of Achaia suffers from slope instability that is manifested in various degrees of ground displacement greatly affecting its morphological features and inhabited areas.
1. Introduction
The movement of an active landslide can be efficiently captured by the InSAR measurements [,,,]. Through InSAR time series analysis, the velocity of the ground movement can be measured with an accuracy of a few mm/yr (e.g., []). This remote sensing technique can provide an accurate identification of the area affected by active landslides and can also assist through hillslope monitoring by detecting potential slope failures. We use the term “active landslide” for landslide bodies that have a long history of affecting the area above and around them, especially the road network that requires constant maintenance. As active landslide (according to []) is considered a landslide that is currently moving and includes first time movements and reactivations.
The InSAR time series method has been applied successfully in a range of landslide studies, not only to locate landslide bodies, but also to identify spatial-temporal patterns of movement []. The analysis of The InSAR-generated displacement time series has the potential to identify periods of accelerated landslide deformation and to evaluate possible correlations with different triggers (rainfall, earthquakes). Large landslides and debris flows form a frequently occurring geohazard posing significant risk to lives and livelihoods.
Landslide phenomena have been previously recognized and mapped in Greek territory using InSAR techniques. Recently, Vassilakis et al. [] used interferometric processing of TerraSAR-X data to estimate ground displacement rates of a large landslide inside a coal mine in western Macedonia; Kontoes et al., [] produced susceptibility maps for the landslides in western Greece using ERS/ENVISAT data; Elias et al. [] used ERS/ENVISAT/Sentinel-1 data to monitor slope stability upstream from an artificial dam; Tsangaratos et al., [] examined the identification of mass movements due to landslides on Lefkada island with InSAR time series analysis using the TERRAFIRMA data (produced by the persistent scatterers interferometry—PSI technique). Kyriou & Nikolakopoulos, [] mapped the landslides south of Patras using interferometric processing (offset-tracking method); several other studies on critical locations used InSAR technology [,].
The Achaia prefecture in NW Peloponnese (Greece), is an area strongly affected by localized subsidence and landslides [,,,,,,], especially the mountainous area near the villages of Krini, Pititsa and Sella (Figure 1; [,]). These villages are located on the north-facing slopes of the mountain Panachaiko (maximum elevation 1926 m; Figure 1a), and all of them are affected by active landslide phenomena []. The NW Peloponnese shows spatially and temporally diverse climatic conditions across its area, mostly due to irregular topography and different atmospheric circulation patterns. Overall, the climate is typical Mediterranean and exhibits large seasonal variations with mild, wet winters and hot, dry summers []. The wet period usually extends from October through May [].
In this study we used Sentinel-1 (C-band) InSAR displacement data to map the active landslides and monitor their kinematics. We compared our InSAR results to a co-located GNSS station at one of the sites. We then cross-correlated our InSAR time series to the rainfall data from a nearby meteorological station of NOA. We demonstrated a robust correlation between maximum rainfall and an increase in displacement rates.
2. Study Area
The study area is close to the Gulf of Corinth which is considered to be a paradigm of an active rift system in Greece (Figure 1; []) and is among the fastest extending continental regions in the world [,,,]. This rift was formed by normal slip on large, E-W striking fault segments that extend the crust of central Greece in a N-S direction. The length of the Corinth rift is 130 km, and the width is 20–40 km. The deepest sea depth is ~900 m, and the major peaks of the mountains around the Gulf of Corinth are ~2500 m. The south coast of the Corinth rift is uplifting, whereas the north part is subsiding [,,,,,]. From space geodesy data (GNSS) we know that the Peloponnese (southern part) moves faster toward the southwest than the Greek mainland (with respect to the “stable” Europe; [,,]). The net result from this movement is that these two areas move away from each other with an average speed of 1 cm/year while the rate of movement increases from east to west [,]. The onshore active faults have normal kinematics with the main active structures being north-dipping faults visible along the southern coast of the Gulf of Corinth, while the rest are located offshore in the central part of the rift [,,,]. Moreover, the study area has rugged relief, several rivers flowing in the general N-S direction (Figure 1), many narrow valleys and numerous other erosional landforms such as triangular faceted spurs on the footwall of active faults [,,,]. Moderate to strong earthquakes occur frequently, inducing additional geological phenomena such as slow and continuous ground displacements in the area [,,].
The area of Achaia specifically has been the focus of many studies concerning landslide events and vulnerability in the last decade [,,,,,,,,,,]. The lithological condition of this area is one of the most controlling parameters for landslide occurrence [,]. The higher density of landslide occurrence is in Pliocene and Pleistocene fluvio-terrestrial and clastic flysch formations []. The most common triggering mechanisms are the seismicity, the steepness of slopes, heavily fractured rocks in the source areas and heavy rainfall [,]. The artificial and natural parts of the terrain slopes along a road, as well as the hydrographic axes of river networks, are also considered important factors for landslide manifestation [,]. From these common factors Koukis et al. [] proposed two main triggering mechanisms for large mass movements in the area, i.e., the excessive rainfall resulting in high pore pressure in the rocks during these events and strong earthquakes resulting in dynamic loading conditions at the failure surface. Therefore, the increased permeability of the rock formations produced by earthquakes (due to strong ground motion and/or fissuring) together with events or periods of intense rainfall are the main factors for the intensity of landslide events.
The bedrock geology of Achaia comprises mainly carbonates (Figure 1b). According to IGME (institute of Geological and Mineral Exploration) maps [,], the study area is part of the Olonos–Pindos geotectonic zone of the Hellenides and mainly comprises limestone, schists and cherts of the Triassic–Jurassic age, covered by thinly bedded limestones with radiolarites of the Cretaceous age. A transition zone overlays the radiolarites, including limestones, shales, cherts and marls, leading to typical flysch sequence sediments of the Upper Eocene []. The syn-rift rocks are Pliocene–Quaternary age sedimentary rocks such as marls, sandstones, conglomerates and alluvial fan deposits.
In this paper we focus our research on the northern / eastern slopes of Panachaiko mountain, with emphasis on well-known landslide activity near the villages of Krini, Pititsa and the monastery of Agia Eleoussa (Figure 1a). In particular, the area around Krini (elevation 775 m; Figure 1b) mostly consists of the Upper Cretaceous–Palaeocene flysch. The flysch mainly includes beds of sandstone and marls (rarely), alternating with thin pelagic limestone, about 50 m thick [,]. During 1985 an IGME investigation about a landslide observed at the southern part of Krini was conducted in this area. According to the field report [], the sliding area close to the village consists of Neogene clay and marl sediments overlapped by a weathered material about 1.5–2 m thick. The Krini landslide is a large earth flow with a mainly E-W slope-parallel displacement trend, which in its eastern (lower) part converts to a translational slide (based on the categorization proposed by [,,]). This is possibly due to changes in lithology. It can be seen in the geological map (Figure 1b), that the landslide extent changes from flysch and its weathered mantle (upper part towards west) to limestone. Krini also displays many characteristics of an earth flow as described by [] with long periods of relative slow to very slow movement alternating with more rapid surges. This type of mass movement has also allowed settlements (such as the village of Krini) and roads to be built on top of the landslide, a common occurrence in many earthflows around the world [,]. During 2021 we visited this area and observed numerous landslides near the village, some of them affecting parts of the road network. Apart from the large slope failures, many small-scale shallow landslides were also observed. Those were affecting the weathered cover of both flysch and Neogene (marl and clay) units.
The village of Pititsa (elevation 650 m; Figure 1b) is also located inside the Upper Cretaceous–Palaeocene flysch, but in this locality the flysch is comprised of sandstone alterations with limestone intercalations and marls. North and east of the village, the flysch is overlapped by Pliocene–Pleistocene blue marls and sandy clays. The Pititsa landslide can also be categorized as an earth flow with the same characteristics as the main body of the Krini landslide but mostly maintaining the lithological homogeneity throughout. The main displacement here is also E-W. To the west of Pititsa, the village of Sella is also affected by active landslides, however, it is built upon terrestrial deposits (Figure 1b; [,]).

Figure 1.
(a) shaded relief Map of northeastern Achaia showing the area of interest (box) including the villages where landslides have occurred; (b) simplified geological map [,]. The landslide of the village of Krini is located on flysch, and the Pititsa landslide is located on flysch and on Pliocene deposits. Active faults are shown with black lines, and red-dashed outlines represent the boundaries of the landslides (ticks on the downthrown side).
3. Data, Methods and Results
3.1. SAR Data Processing
The processing of InSAR time series analysis was completed using the LiCSBAS, an open-source package that integrates with LiCSAR products [,,]. The processing chain and schematic description of data/methods used are shown in the flow chart of Figure S2. LiCSAR produced interferograms (wrapped and unwrapped) from SLC (single look complex) data of Sentinel-1 acquisitions. The interferograms were multilooked with a factor of 20 × 4 in range and azimuth (46 × 56 m spacing) and spatially filtered by a GAMMA adaptive power spectrum filter with an alpha value of 1.0 to decrease noise [,]. With the SNAPHU software, LiCSAR unwraps the phase in two dimensions using a statistical cost technique []. We employed unwrapped interferograms and coherence images that were geocoded with a pixel spacing of 0.001 degree (100 m) and converted to GeoTIFF format for our time series analysis. We used the frames with ID: 080D_05196_131104 for descending track and 175A_05184_121313 for ascending track, respectively. For ascending and descending track (see Figure S1), we used 346 and 317 available interferograms from the LiCSAR portal, respectively (out of 99 and 120 SAR images, respectively; see Table S1 for image dates).
The areas of interest are in the center-east of the frames ID 175A and 080D (Figure S1). The time span for the ascending track ranges was from 2015 to 2021 and for the descending from 2016 to 2021, respectively (see Table S1). Before the main processing, a tropospheric correction was applied on the unwrapped products using the generic atmospheric correction online service for InSAR (GACOS) data ([]; pixel size 10 × 10 km). GACOS utilizes the iterative tropospheric decomposition (ITD) model to separate stratified and turbulent signals from tropospheric total delays. The tropospheric corrections were used in GeoTIFF format. To evaluate the success of the correction, the calculation of standard deviation (STD) of unwrapped phase before and after the GACOS correction and the reduction rate of the STD was performed through the LiCSBAS software []. The STD of unwrapped phases for each interferogram was typically lower (see correlation diagrams in Figure 2 and Figure 3; see also reduction of STD through the interferograms in Figures S3 and S4), indicating that this tropospheric correction approach greatly reduced tropospheric noise. We see in the diagrams (Figure 2 and Figure 3) that the reduction of STD for the dataset of ascending orbit is lower (reduction rate 29.57%) than the reduction of STD for the descending orbit (36.29%).
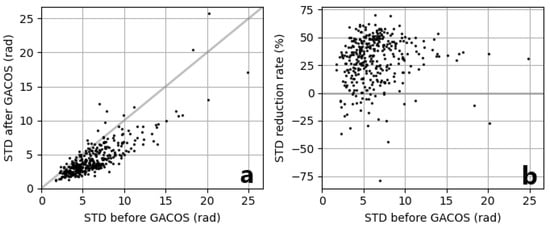
Figure 2.
Correlation diagram showing standard deviation: (a), of unwrapped phases before and after the GACOS corrections and their reduction rates; (b), for ascending track 175. The gray line denotes a 1:1. The reduction of STD for the ascending orbit is moderate. The STD decreased from 6.35 rad to 4.41 rad on average with a mean reduction rate 29.57%.
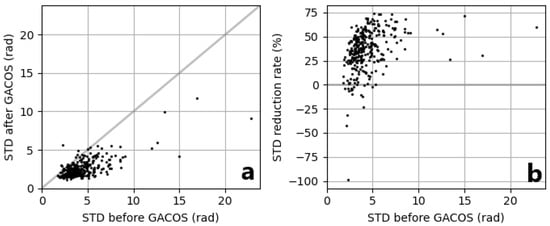
Figure 3.
Correlation diagram showing standard deviation: (a), of unwrapped phases before and after the GACOS corrections and their reduction rates; (b), for descending track 80. The grey line denotes a 1:1. The STD decreased from 4.36 rad to 2.61 rad on average with a mean reduction rate 36.29%.
After the tropospheric correction, we performed the quality check function of LiCSBAS. Statistics such as average phase coherence (we applied a 0.3 threshold) and percentage of genuine unwrapped pixels are used to identify bad data. We also performed the network refinement by interferometric loop closure [] and removed 100 interferograms (95 ascending and 5 descending orbit) from further processing. Unwrapped data may contain unwrapping mistakes, which can result in serious errors in the derived time series and should be eliminated or addressed prior to use. Moreover, after the quality checks, we applied the small baseline (SB) inversion on the network of interferograms (Figure 4). The least-squares approach was then used to get the mean displacement velocity (LOS) from the cumulative displacements. We used the NSBAS approach [] to produce a more realistic time series of displacement even with a disconnected network (Figure 4). We selected the SBAS technique because it works well in the vegetated and rural areas such as the mountainous Achaia region, due to the use of distributed scatterers.
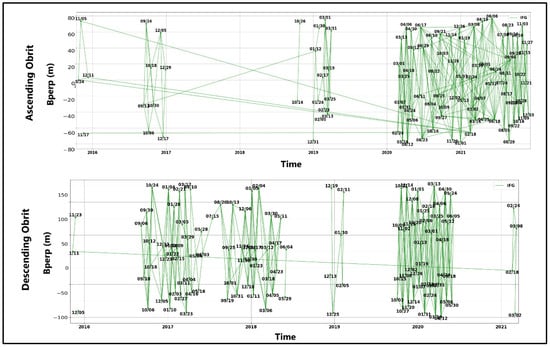
Figure 4.
Perpendicular baseline configuration and network of the 346 small baseline interferograms formed from 99 Sentinel-1A images (ascending track, top panel) and network of the 317 SB interferograms formed from 120 Sentinel-1A images used in this study (descending track, bottom panel). Vertical lines indicate the network gaps.
We also used the percentile bootstrap method to calculate the LOS velocity’s standard deviation from cumulative displacements. The next processing step was the masking of noisy pixels in the time series and the spatiotemporal filtering of time series. Finally, topography-correlated components (linear with elevation) were subtracted with deramping (see Figures S5 and S6), and we obtained the LOS velocity maps for each satellite track (Figure 5).

Figure 5.
Displacement maps in LOS direction for the broader areas of Krini (a,b) and Pititsa villages (c,d) for ascending track and descending track (a) shows the displacement map for ascending track; and (b), for descending track around the village of Krini, respectively. The Figure 5c,d corresponds to displacement map for ascending and descending track around the villages of Pititsa and Sella, respectively.
After the main processing, we decomposed the LOS displacement data to east-west (E-W) and up-down (U-D) components assuming that the north-south (N-S) displacement is very small due to the track’s imaging geometry of the Sentinel-1 satellite [,].
In the area around the village of Krini (Figure 1), an active landslide is present (Figure 5a,b). More active landslides are also located near the villages of Graikas, Pititsa and Sella and to the monastery of Agia Eleoussa (Figure 5c,d). In those locations we measured LOS velocities up to −55 mm/yr for the ascending track (Figure 5a). We obtained similar velocities, up to 30 mm/yr for the descending track (Figure 5b). Note that the values of LOS displacements are referenced to a local reference point which is located about 30 km south of the area of interest (see Figure S1 for location), and it is considered stable (free of gravitational or tectonic displacements).
Then, we produced maps of the east-west and up-down components, assuming that the north-south component was neglected due to the track’s geometry of the Sentinel-1 satellite. We found that all active landslides were moving east and downward (subsidence, Figure 6a,b). All the affected areas are located on the east-facing slopes and in the foothills of Panachaiko mountain (Figure 1).
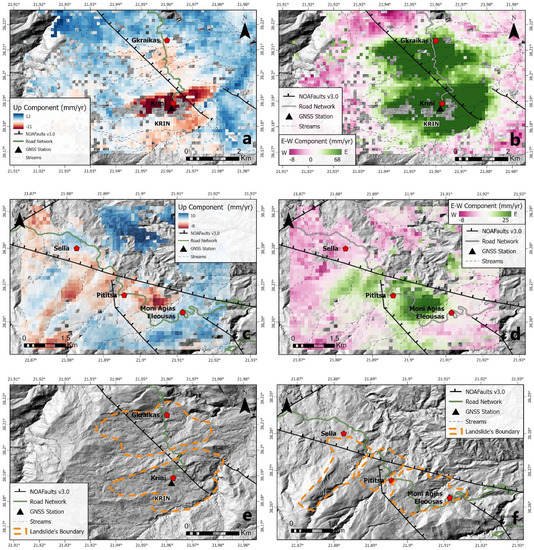
Figure 6.
Displacement-rate maps in mm/yr: Up (a,c) and E-W (b,d), component after the decomposition of InSAR data for the broader areas of Krini and Pititsa villages, respectively; (e), showing the landslides’ outlines for Krini and Graikas landslides; and (f), showing the landslides’ outlines for the monastery Agia Eleoussa and the villages of Pititsa and Sella.
We traced the boundaries of the active landslides using the InSAR motion data on the E-W component (Figure 6e,f). We note that our motion data refer to the period 2016–2021 (Figure 4), so it is possible that landslides mapped in previous studies in the same area [,] have changed their motion patterns. In our study we measured the mean velocity of the larger landslides (Krini and Agia Eleoussa (see areas enclosed by orange lines in Figure 6e,f)) by a statistical approach and not by referring to a single pixel. The mean velocity of the Krini landslide was found to be 6 mm/yr downward (nearly 0.6 cm/year) and 28.7 mm/yr (nearly 3 cm/year) eastward. The mean velocity of the Agia Eleoussa landslide was found to be 1.8 mm/yr (~0.2 cm/year) downward and 7.7 mm/yr (~0.8 cm/year) eastward. We also computed the histograms of the velocities from both ascending and descending tracks and the Up and E-W components of the movement for Krini and Agia Eleoussa, respectively (Table 1, Figure 7 and Figure 8). The area affected by the Krini landslide is 4,080,000 square meters (m2). The area of the active landslide around the village of Pititsa is 800,000 square meters (m2), and the area of the landslide near the monastery of Agia Eleoussa is 1,600,000 square m2. It is probable that the two landslides are in fact part of one feature (mass movement). However, the uncertainty in our InSAR motion rates (~3 mm/yr LOS, see Figure 5c,d) is within the values we mapped in the area between the two landslides.

Table 1.
Table of mean and median velocities of active landslides in the village of Krini and at the monastery of Agia Eleoussa. The landslide outlines are shown in Figure 6e,f. The period of observation was 2016–2020.
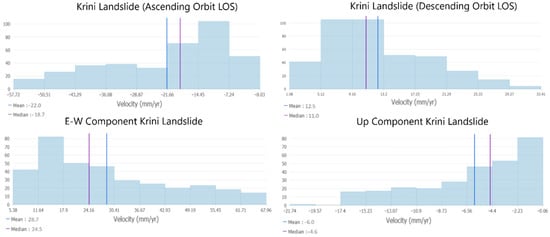
Figure 7.
Histograms of LOS/E-W/U-D velocities of active landslides in the village of Krini (Affected area: 4,080,000 m2).
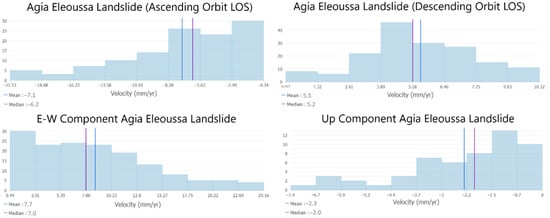
Figure 8.
Histograms of LOS/E-W/U-D velocities of active landslides in the Agia Eleoussa area (Affected area: 1,600,000 m2).
3.2. Rainfall Data
We also collected rainfall data of stations located in the Achaia prefecture (from the database of []) to identify possible temporal patterns of ground movement that could be correlated with the rainfall. The wet season lasts from October to May, during which the total rainfall accounts for 93% of the annual rainfall. The month with the highest precipitation is December, with a mean rainfall of 128.9 mm, followed by November (124.7 mm). August is the lowest with a mean rainfall of 7.0 mm, followed by July (8.8 mm) [].
We used the daily rain data of three meteorological stations of NOA (Kalavrita, Panaxaiko and Kato Vlassia stations (Figure 1)) for the same time span (2015–2021) as with the InSAR and GNSS time series. These stations are located at similar elevations to and within 20 km from the landslides. The data are plotted in Figure 9, Figure 10 and Figure 11.
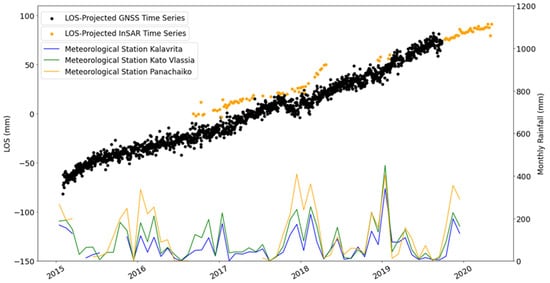
Figure 9.
LOS-Projected GNSS time series (KRIN station: black points) and InSAR position time series (orange points: descending orbit) of the pixel which contains the GNSS station. Also, blue, green and orange lines represent the rainfall of the meteorological stations Kalavrita, Kato Vlassia and Panachaiko (see Figure 1 for station localities).
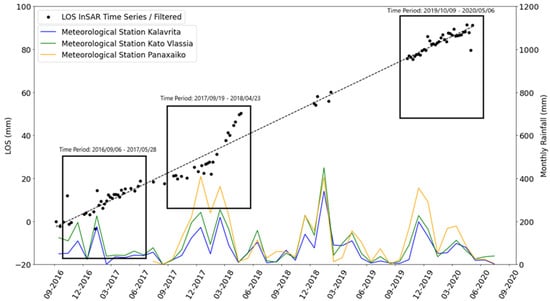
Figure 10.
Graph showing LOS position time series for the Krini landslide descending track (080D). Blue, green and orange lines represent the average monthly rainfall of the meteorological stations Kalavrita, Kato Vlassia and Panachaiko, respectively (right axis). The three black boxes represent the time periods what are used for further processing (see Figure 11). The dashed line indicates the linear fit of the InSAR data for the whole period of observations (25 mm/yr).
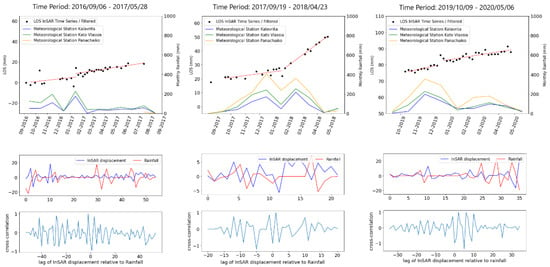
Figure 11.
Graphs showing InSAR position time series and average monthly rainfall (Kato Vlassia station, top panel) for each time period corresponding graphs showing cross-correlation results (signal-converted waveforms, middle panel; correlation between the two waveforms, lower panel). The corresponding displacement rates are reported in Table 2.
3.3. Validation of InSAR Time Series with GNSS Data
To compare our InSAR displacements (velocities) with other geodetic data, we used the GPS observations of the permanent station KRIN of the Corinth Rift Laboratory (CRL) NFO of EPOS (http://crlab.eu/ (accessed on 20 December 2021).). Published GNSS data (30-s daily positions; []) were used. We visited the station in May 2021, and we confirmed the stability of the antenna (see Figure S7). We transformed the GNSS components into LOS through the equation []:
Dr = du × cos(inc) − (sin(inc) × (dn × cos(ah-3 × pi/2) + de × sin(Ah-3 × pi/2)))
Ah-3 × Pi/2 corresponds to the angle to the azimuth look direction, which is perpendicular to the satellite heading; inc is the radar incidence angle; and du, dn, de are the corresponding up, north and east displacements derived from GNSS solutions (Figure S8).
The GNSS time series and the InSAR time series analysis show slightly different displacement rates (Figure 9, descending orbit). The GNSS rate is slightly greater than the InSAR rate; the displacement rate from GNSS is 28 mm/yr and from InSAR time series it is 25 mm/yr (see Figure S9), providing a deviation of 3 mm/yr or 12% of the GNSS rate. This rate difference is expected as it is related to the difference in absolute terms between the point measurement of displacement, which corresponds to the GNSS time series (i.e., the motion of the antenna reference point or ARP), and the ‘pixel’ measurement on the ground, which corresponds to the InSAR time series. Note that the InSAR time series represent the mean value of displacement within a pixel size 100 × 100 m, i.e., enclosing the building where the GNSS antenna is located. This small deviation in rates may indicate: (a) the “smoothing” effect of InSAR; and (b) the possible occurrence of differential movements inside subareas which each SAR pixel covers. To complete the comparison—validation—we also projected the KRIN GNSS data into the LOS-ascending orbit geometry, confirming similar rates of motion (48 vs. 55 mm/yr, respectively; see time-series diagram in Figure S10).
4. Discussion
4.1. Landslide Motion and Rainfall Pattern
There are many publications concerning rainfall triggers for landslides for the areas of central and southern Europe (e.g., [,,]). The most common parameters used for rainfall threshold definition is intensity (of both antecedent cumulated rainfall and event rainfall) and duration []. The effect of the antecedent rainfall depends heavily on the hydrological conductivity of the landslide mass, and only rainfall events with a large amount of precipitation are considered capable of triggering the increase of deformation rate of deep-seated landslides. The authors of [] noted in their case that the time lag for peak precipitation and peak deformation rate may be up to 20 days, while [] found a 12-day relation. Since proximal rainfall data is available for Achaia (Figure 1), we examined the correlation between the rainfall patterns and the seasonal movement of the Krini landslide because for this landslide the displacement rate is well constrained by the co-located GNSS station (Figure 9 and Figure S10). For this purpose, we used a signal processing method, the cross correlation []. We used this approach to convert our data to signal and compare them, so that we could determine if a time delay (time lag) exists between the maximum peaks of the time series of rainfall and of InSAR, respectively. The cross-correlation technique is used to measure the similarity of two time series as a function of the displacement of one relative to the other and to detect correlations among these two series []. We applied this technique to the daily rainfall dataset, which could play an important role in the movement of a landslide and to the InSAR time series. We used the InSAR time series of the descending track due to the completeness of its dataset during the period 2016–2020 rather than the time series from the ascending track (Figure 4). First, we resampled and interpolated the daily rainfall data to fit it to the time span of the InSAR time series. Because it was complete, we selected the data from the meteorological station Kato Vlassia (Figure 1a) and then performed the correlation for motions (displacements) of the Krini landslide.
We applied the cross correlation to the two time series, especially to three subperiods (see boxes in Figure 10). These time periods consisted of three sets of eight months of observations that had complete datasets. We selected to work with three separate time periods because our InSAR time series contains network gaps (Figure 4) which correspond to gaps in the time series. We used the following time periods: 6 September 2016–28 May 2017, 19 September 2017–23 April 2018 and 9 October 2019–6 May 2020. We calculated the displacement rate before and after the changes of the displacements through fitting the trendline to the data (Table 2). We observed in Figure 11 that when changes of the displacement rate were detected previously, a seasonal maximum of rainfall values occurred. Two of the three time periods showed an increase of displacement rate of about 40%, while the total seasonal rainfall (8 months) was quite similar (~700 mm, Table 2). The period September 2017–April 2018 showed an increase of the displacement rate of about 550%. This result was accompanied by a large amount of total rainfall (~1000 mm, Table 2). These findings allowed us to correlate the amount of total rainfall with the positive displacement rate (increase) of an active landslide. Through the cross-correlation method, we computed the time lag between the maximum peaks of InSAR and rainfall (Figure 11 lower panel; Table 2). The mean time lag (of the three periods) was 13.5 days between the maximum value of rainfall and the change in the InSAR displacement rate. The changes in InSAR displacement rates occurred on 28 January 2017, 23 January 2018 and 20 December 2019, respectively. Moreover, due to the large number of ascending orbit data available during the winter–spring period in 2020–2021 (Figure 4), we performed a separate cross correlation using the InSAR position time series (ascending orbit) against the daily rainfall data from the Kato Vlassia station (see Figure S11). Again, we found a 330% increase in the displacement rate of the landslide following a large interval of rainfall with a time lag of 12 days (see Table 2, last line). The change in the displacement rate of the Krini landslide occurred on 18 February 2021. Thus, whatever S1 orbit data we use in the case of Achaia, we always find this pattern, i.e., an increase in the landslide displacement rate following heavy rainfall.

Table 2.
Displacement rate A corresponds to the linear displacement rate of the Krini landslide (descending orbit) before the maximum seasonal rainfall is reached, and linear displacement rate B corresponds to the displacement rate following the rainfall peak (see Figure 11 for trendlines). The total rainfall corresponds to the total rain during each time period. The displacement rate A & B values of the last line (period 2020–2021) refers to the ascending orbit data.
4.2. Kinematic Characteristics of the Landslides
The Krini, Agia Eleoussa monastery and Pititsa are active landslides whose motion was measured by InSAR time series analysis for the period 2016–2021. First, we identified the moving pixels in the InSAR data (draped over the high-resolution DEM, Figure 6) and delineated the landslide boundary. We examined the decomposed velocities and found that the maximum displacement rate of each landslide is located at about the center of each landslide (Figure 12). Then, through InSAR mapping we identified more cases of mass movement than these three well-known landslides in the broader research area. In particular, we identified two additional active landslides, one around the village of Graikas (3 km north of Krini), and another around the village of Sella (Figure 5c,d and Figure 6c,d). Our results showed that a large part of this mountainous region suffers from slope instability that is manifested in various degrees of ground displacement that greatly affects its morphological features and inhabited areas. To validate these results, we provide field photographs of active landslides (taken on 7 May and 10 September 2021) which agree with our InSAR findings (Figure 12).

Figure 12.
Maps showing U-D component of displacement rate (left panel, 2016–2021). Upper panel map includes the landslide of Krini and Graikas, and the bottom panel map includes the landslides of Pititsa and Agia Eleoussa, respectively. On the right side we provide field photos with numbers corresponding to the green markers on the maps.
In addition, the NOAFAULTs database of active faults of Greece [,] contains two active, north-dipping normal faults that affect the area of the active landslides. In particular, the Pititsa landslide seems to be located at the hanging wall of the Panachaiko fault segment, the Agia Eleoussa is situated between two faults (Panachaiko F. and Pititsa F.), while the Krini and Graikas landslides overlay the Panachaiko fault trace (Figure 1b). We could not find in the literature a fine-scale geological map showing the fault traces with high planimetric accuracy, so we had to rely on the coarse information provided by the NOAFAULTs database. In addition, there is no geodetic or geological evidence for any fault creep along these faults, so the tectonic influence of the landslide mobility is uncertain. However, we cannot exclude the possibility of a strong earthquake during the Holocene along these faults and so to further mobilize these landslides.
Furthermore, due to the lack of fine-scale geological mapping in this region, the lithological contacts are based on 1:50.000 scale maps where both cartographic accuracy and lithology detail are reduced. Nevertheless, the area around the Eleoussa monastery landslide consists mainly of flysch and unconformably overlying Neogene deposits, with small chert (Lower–Upper Cretaceous) and limestone (Jurassic) occurrences (Figure 12, point 7). In the area around Krini (Figure 1b, Figure 12 and Figure 13), we observed that the main body of the landslide is located near the contact between the “lower” flysch formation and the pelagic limestone of the Upper Cretaceous age. In addition, the main body of the landslide extends to areas consisting of Neogene sedimentary (clastic) formations. This comes in accordance with the observations made by [,,] on the same region, where they attribute the highly sheared and weathered nature of flysch and Neogene sediments for contributing to the instability of the area. The weakened state of these clastic sediments influences the reactivation of ground motions when nearby seismic activity and heavy rainfall occurs.
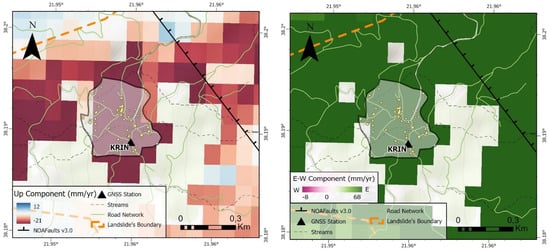
Figure 13.
Maps showing InSAR velocities in the area of the village of Krini (shaded polygon: period 2016–2021). Up component (left), E-W component (right). Yellow boxes indicate houses, and black triangle shows the location of the GNSS station.
Inside the village of Krini itself, we mapped downward velocities up to 2.1 cm/year and eastward velocities up to 6.8 cm/year, respectively (Figure 13). The InSAR coverage of surface motion is discontinuous because of the scarcity of ascending orbit acquisitions (spring 2017–2018, Figure 4 and Table S1), yet there is robust geodetic (InSAR) evidence that the whole village as well as the road access to it, from both north and east directions, is affected by the deep-seated landslide.
Deep-seated landslides are characterized by long-term gradual deformation of millimeter to decimeter scale per year []. Their movement can be divided into slow and acceleration deformation phases, triggered by increased intensity in precipitation []. The deformation rate in deep-seated landslides is mainly controlled by hydrometeorological conditions. Their sliding behavior is a result of the relation of the shear strength of the soil to the shear (sliding) force applied by the gravitational forces acting on the landslide mass, a balance that the hydrological condition of the area can greatly affect []. This may be also the case for the Krini deep-seated landslide. We interpret its kinematic behavior as a result of seasonal changes in rainfall. For the first time, we determined the correlation between rainfall and movement of this landslide. Through the cross-correlation method, the maximum correlation between the two series were about 13.5 days. In all three time-periods studied there was an increase of displacement rate right after a period with rainfall. We suggest that the spatiotemporal pattern of movement is modulated by the seasonal rainfall which in turn, allows us to expect an increase of displacement rate of the landslide of Krini at the end of the rainy season and at the beginning of the dry period. In addition, a moderate to strong earthquake in this area could increase the displacement rate of the landslide, but such a case has not yet been demonstrated.
5. Conclusions
The main findings of this paper are:
- i.
- The Krini, Agia Eleoussa monastery and Pititsa landslides are active landslides whose motion was measured by InSAR (C-band) time series analysis for the period 2016–2021.
- ii.
- We processed LiCSAR interferograms using the SBAS tool and we obtained average displacement maps. The results indicate slow ground motions toward the east and downward (subsidence).
- iii.
- The maximum displacement rate of each landslide is located at about the center of each landslide.
- iv.
- Our results point that there is a correlation between rainfall and landslide motion. For the Krini landslide, we found the mean time lag to be 13.5 days between the maximum rainfall and the maximum of LOS displacement (descending orbit data).
- v.
- The displacement rates of the Krini active landslide increase after a period of rainfall. Two of the three time periods examined showed an increase in the displacement rate by about 40% when the total rainfall was quite similar (~700 mm). The period September 2017–April 2018 showed an increase in the displacement rate by about 550%. This result was accompanied by a large amount of total rainfall (~1000 mm).
- vi.
- Our findings suggest that the amount of total rainfall could control the amount of increase of the displacement rate of an active landslide.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14040844/s1, Figure S1. ESRI map with the ID frames of LicSAR Portal (red outline is descending; blue outline is ascending frame). Green rhomb indicates the location of the reference point used in the InSAR analysis. Figure S2. Data processing flow chart used in this study. The arrows indicate input/output actions. The products are shown in orange. Figure S3. Unw_org corresponds to the interferogram before the GACOS correction, and Unw_cor corresponds to the interferogram after the GACOS correction. The standard deviation (STD) decreased from 3.2 rad to 2.4 rad. The reduction rate for this interferogram is 26.6%. The dates of the interferometric pair are 24 January 2019 and 17 February 2019. (Ascending Orbit). Figure S4. Unw_org corresponds to the interferogram before the GACOS correction, and Unw_cor corresponds to the interferogram after the GACOS correction. The standard deviation (STD) decreased from 5.2 rad to 2.2 rad. The reduction rate for this interferogram is 60.1%. The dates of the interferometric pair are 13 December 2016 and 4 January 2017. (Descending Orbit). Figure S5. Graph showing the time series of displacement of the village of Krini corresponding to the pixel enclosing the GNSS station (ascending orbit). Vel(1) indicates the velocity of this pixel (blue line) after the spatio-temporal filtering and deramping. Figure S6. Graph showing the time series of displacement of the village of Krini corresponding to the pixel enclosing the GNSS station (descending orbit). Vel(1) indicates the velocity of this pixel (blue line) after the spatio-temporal filtering and deramping. Figure S7. Field photograph showing the antenna of KRIN GNSS Station. View to the northeast. Photograph was taken on 7 May 2021. Figure S8. Graph showing the geometry of the LOS velocity vector. 34.58° is the incidence angle in the Krini study area. Figure S9. Graph showing the trend differences between InSAR and GNSS LOS displacements (descending orbit) of the same dates during the common period of observation (58 common dates). For comparison, the blue-line indicates a perfect (1:1) correlation. Figure S10. LOS-Projected GNSS Time series (KRIN station; black points) and InSAR position time series (orange points, ascending orbit) of the pixel which contains the GNSS station. Figure S11. Graphs showing position time series and average monthly rainfall (Kato Vlassia station, top panel) for the period September 2020–May 2021 and corresponding graphs (middle and lower panel) showing cross-correlation results. The corresponding displacement rates are reported in Table 2. Table S1. Dataset of Sentinel-1 SAR acquisitions of ascending and descending orbit used in this study.
Author Contributions
Conceptualization, A.G. and V.T.; methodology, V.T., A.G.; soft-ware, V.T.; validation, V.T., A.G. and I.K. (Ioannis Karamitros); formal analysis, V.T.; investigation, V.T., A.G.; resources, E.E., I.K. (Ioannis Karamitros); data curation, V.T., E.E. and I.K. (Ioannis Karamitros); writing—original draft preparation, V.T., A.G., I.K. (Ioannis Karamitros); writing—review and editing, V.T., A.G., I.K. (Ioannis Karamitros), E.E., I.K. (Ioannis Koukouvelas), E.S.; visualization, V.T.; supervision, A.G., I.K. (Ioannis Koukouvelas), E.S.; project administration, A.G.; funding acquisition, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the research project ‘Platform of multidimensional monitoring with micro sensors of Enceladus of Hellenic Supersite-PROION’ with Grant Number: MIS-5070928. https://proion-hellas.eu/ (accessed on 20 January 2022).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The InSAR data are freely accessible through the LiCSAR—Copernicus portals; The rainfall data are available through www.meteo.gr (data accessed on 20 December 2021); GNSS observations (daily files) are available via the CNRS-CRL web portal.
Acknowledgments
We thank the CRL team which operated the GNSS station KRIN. Thanks to PROION partners for comment and discussions. We acknowledge concession for the use of ESRI products licensed to the Hellenic National Tsunami Warning Center, National Observatory of Athens, through the project “HELPOS—Hellenic Plate Observing System” (MIS 5002697). HELPOS is implemented under the Action “Reinforcement of the Research and Innovation Infrastructure”, funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014–2020) and co-financed by Greece and the European Union (European Regional Development Fund). We acknowledge KTIMATOLOGIO S.A. for kindly providing the digital elevation model. We also thank Vassileios Tsironis, Athina Psalta and Ioannis Fountoulakis for their help with cross-correlation techniques. We also thank Sotiris Valkaniotis and Helena Partheniou for comments and discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- Aslan, G.; Foumelis, M.; Raucoules, D.; De Michele, M.; Bernardie, S.; Cakir, Z. Landslide Mapping and Monitoring Using Persistent Scatterer Interferometry (PSI) Technique in the French Alps. Remote Sens. 2020, 12, 1305. [Google Scholar] [CrossRef]
- Solari, L.; Del Soldato, M.; Raspini, F.; Barra, A.; Bianchini, S.; Confuorto, P.; Casagli, N.; Crosetto, M. Review of Satellite Interferometry for Landslide Detection in Italy. Remote Sens. 2020, 12, 1351. [Google Scholar] [CrossRef]
- Kontoes, C.; Loupasakis, C.; Papoutsis, I.; Alatza, S.; Poyiadji, E.; Ganas, A.; Psychogyiou, C.; Kaskara, M.; Antoniadi, S.; Spanou, N. Landslide Susceptibility Mapping of Central and Western Greece, Combining NGI and WoE Methods, with Remote Sensing and Ground Truth Data. Land 2021, 10, 402. [Google Scholar] [CrossRef]
- Elias, P.; Valkaniotis, S.; Ganas, A.; Papathanassiou, G.; Bilia, A.; Kollia, E. Satellite SAR interferometry for monitoring dam deformations: The case of Evinos dam, central Greece. In Proceedings of the Eighth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2020), Paphos, Cyprus, 16–18 March 2020; Volume 11524, p. 115241I. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide Types and Processes, Transportation Research Board. US Natl. Acad. Sci. Spec. Rep. 1996, 247, 36–75. [Google Scholar]
- Singleton, A.; Li, Z.; Hoey, T.; Muller, J.P. Evaluating sub-pixel offset techniques as an alternative to D-InSAR for monitoring episodic landslide movements in vegetated terrain. Remote Sens. Environ. 2014, 147, 133–144. [Google Scholar] [CrossRef]
- Vassilakis, E.; Foumelis, M.; Erkeki, A.; Kotsi, E.; Lekkas, E. Post-event surface deformation of Amyntaio slide (Greece) by complementary analysis of Remotely Piloted Airborne System imagery and SAR interferometry. Appl. Geomat. 2020, 13, 65–75. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Loupasakis, C.; Nikolakopoulos, K.; Angelitsa, V.; Ilia, I. Developing a landslide susceptibility map based on remote sensing, fuzzy logic and expert knowledge of the Island of Lefkada, Greece. Environ. Earth Sci. 2018, 77, 363. [Google Scholar] [CrossRef]
- Kyriou, A.; Nikolakopoulos, K. Assessing the suitability of Sentinel-1 data for landslide mapping. Eur. J. Remote Sens. 2018, 51, 402–411. [Google Scholar] [CrossRef]
- Papoutsis, I.; Kontoes, C.; Alatza, S.; Apostolakis, A.; Loupasakis, C. InSAR Greece with Parallelized Persistent Scatterer Interferometry: A National Ground Motion Service for Big Copernicus Sentinel-1 Data. Remote Sens. 2020, 12, 3207. [Google Scholar] [CrossRef]
- Psychogyiou, C.; Papoutsis, I.; Kontoes, C.; Poyiadji, E.; Spanou, N.; Klimis, N. Multi-temporal Monitoring of slow moving Landslides in south Pindus mountain range, Greece. In Proceedings of the Fringe 2015 Workshop, Frascati, Italy, 23–27 March 2015; pp. 23–27. [Google Scholar]
- Koukis, G.; Sabatakakis, N.; Ferentinou, M.; Lainas, S.; Alexiadou, X.; Panagopoulos, A. Landslide phenomena related to major fault tectonics: Rift zone of Corinth Gulf, Greece. Bull. Eng. Geol. Environ. 2009, 68, 215–229. [Google Scholar] [CrossRef]
- Lebourg, T.; El Bedoui, S.; Hernandez, M. Control of slope deformations in high seismic area: Results from the Gulf of Corinth observatory site (Greece). Eng. Geol. 2009, 108, 295–303. [Google Scholar] [CrossRef]
- Elias, P.; Briole, P. Ground Deformations in the Corinth Rift, Greece, Investigated Through the Means of SAR Multitemporal Interferometry. Geochem. Geophys. Geosystems 2018, 19, 4836–4857. [Google Scholar] [CrossRef]
- Del Soldato, M.; Del Ventisette, C.; Raspini, F.; Righini, G.; Pancioli, V.; Moretti, S. Ground deformation and associated hazards in NW peloponnese (Greece). Eur. J. Remote Sens. 2018, 51, 710–722. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y.; Tsangaratos, P.; Ilia, I.; Wang, X. Combining Evolutionary Algorithms and Machine Learning Models in Landslide Susceptibility Assessments. Remote Sens. 2020, 12, 3854. [Google Scholar] [CrossRef]
- Sabatakakis, N.; Koukis, G.; Vassiliades, E.; Lainas, S. Landslide susceptibility zonation in Greece. Nat. Hazards 2012, 65, 523–543. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Ganas, A.; Koukouvelas, I. Landsliding phenomena in NW Peloponnese, Greece: A test-site of the EC LEWIS research project. Geophys. Res. Abstr. 2006, 8, 04402. [Google Scholar]
- Papathanou, M. Small Scale Displacements within Landslides in the Region of Pititsa Using Earth Surveying and Photogrammetry. Master’s Thesis, University of Patras: Rio-Patras, Greece; 97, (unpublished).
- Katrantsiotis, C. Holocene Environmental Changes and Climate Variability in the Eastern Mediterranean: Multiproxy Sediment Records from the Peloponnese Peninsula, SW Greece. Ph.D. Thesis, Department of Physical Geography, Stockholm University, Stockholm, Sweden, 2019. [Google Scholar]
- Bernard, P.; Lyon-Caen, H.; Briole, P.; Deschamps, A.; Boudin, F.; Makropoulos, K.; Papadimitriou, P.; Lemeille, F.; Patau, G.; Billiris, H.; et al. Seismicity, deformation and seismic hazard in the western rift of Corinth: New insights from the Corinth Rift Laboratory (CRL). Tectonophysics 2006, 426, 7–30. [Google Scholar] [CrossRef]
- Clarke, P.J.; Davies, R.R.; England, P.C.; Parsons, B.; Billiris, H.; Paradissis, D.; Veis, G.; Cross, P.A.; Denys, P.H.; Ashkenazi, V.; et al. Crustal strain in central Greece from repeated GPS measurements in the interval 1989-1997. Geophys. J. Int. 1998, 135, 195–214. [Google Scholar] [CrossRef]
- Chousianitis, K.; Ganas, A.; Evangelidis, C.P. Strain and rotation rate patterns of mainland Greece from continuous GPS data and comparison between seismic and geodetic moment release. J. Geophys. Res. Solid Earth 2015, 120, 3909–3931. [Google Scholar] [CrossRef]
- Briole, P.; Ganas, A.; Elias, P.; Dimitrov, D. The GPS velocity field of the Aegean. New observations, contribution of the earthquakes, crustal blocks model. Geophys. J. Int. 2021, 226, 468–492. [Google Scholar] [CrossRef]
- Elias, P.; Kontoes, C.; Papoutsis, I.; Kotsis, I.; Marinou, A.; Paradissis, D.; Sakellariou, D. Permanent Scatterer InSAR Analysis and Validation in the Gulf of Corinth. Sensors 2009, 9, 46–55. [Google Scholar] [CrossRef]
- Trikolas, C.; Koskeridou, E.; Tsourou, T.; Drinia, H.; Alexouli-Livaditi, A. Pleistocene marine deposits of the Aigialia region (N. Peloponnesus). Bull. Geol. Soc. Greece 2004, 36, 826–835. [Google Scholar] [CrossRef][Green Version]
- Palyvos, N.; Sorel, D.; Lemeille, F.; Mancini, M.; Pantosti, D.; Julià, R.; Triantaphyllou, M.; De Martini, P.M. Review and New Data on Uplift Rates at the W Termination of the Corinth Rift and the Ne Rion Graben Area (Achaia, Nw Peloponnesos). Bull. Geol. Soc. Greece 2018, 40, 412–424. [Google Scholar] [CrossRef][Green Version]
- Avallone, A.; Briole, P.; Agatza-Balodimou, A.M.; Billiris, H.; Charade, O.; Mitsakaki, C.; Nercessian, A.; Papazissi, K.; Paradissis, D.; Veis, G. Analysis of eleven years of deformation measured by GPS in the Corinth Rift Laboratory area. Comptes Rendus Geosci. 2004, 336, 301–311. [Google Scholar] [CrossRef]
- Roberts, P.G.; Koukouvelas, I. Structural and seismological segmentation of the Gulf of Corinth fault system: Implications for models of fault growth. Ann. Geofis. 1996, 39, 619–646. [Google Scholar]
- Roberts, G.; Ganas, A. Fault-slip directions in central and southern Greece measured from striated and corrugated fault planes: Comparison with focal mechanism and geodetic data. J. Geophys. Res. Earth Surf. 2000, 105, 23443–23462. [Google Scholar] [CrossRef]
- Koukouvelas, I.; Stamatopoulos, L.; Katsonopoulou, D.; Pavlides, S. A paleoseismological and geoarchaeological investigation of Eliki fault, Gulf of Corinth, Greece. J. Struct. Geol. 2001, 23, 531–543. [Google Scholar] [CrossRef]
- Verrios, S.; Zygouri, V.; Kokkalas, S. MORPHOTECTONIC ANALYSIS IN THE ELIKI FAULT ZONE (GULF OF CORINTH, GREECE). Bull. Geol. Soc. Greece 2004, 36, 1706–1715. [Google Scholar] [CrossRef]
- Palyvos, N.; Pantosti, D.; De Martini, P.M.; Lemeille, F.; Sorel, D.; Pavlopoulos, K. The Aigion-Neos Erineos coastal normal fault system (western Corinth Gulf Rift, Greece): Geomorphological signature, recent earthquake history, and evolution. J. Geophys. Res. Earth Surf. 2005, 110, B09302. [Google Scholar] [CrossRef]
- Tsimi, C.; Ganas, A.; Soulakellis, N.; Kairis, O.; Valmis, S. MORPHOTECTONICS OF THE PSATHOPYRGOS ACTIVE FAULT, WESTERN CORINTH RIFT, CENTRAL GREECE. Bull. Geol. Soc. Greece 2018, 40, 500–511. [Google Scholar] [CrossRef]
- Verroios, S.; Zygouri, V. Geomorphological Analysis of Xilokastro Fault, Central Gulf of Corinth, Greece. Geosciences 2021, 11, 516. [Google Scholar] [CrossRef]
- Zygouri, V.; Koukouvelas, I.K. Landslides and natural dams in the Krathis River, north Peloponnese, Greece. Bull. Eng. Geol. Environ. 2019, 78, 207–222. [Google Scholar] [CrossRef]
- Rozos, D.; Bathrellos, D.; Skilodimou, D. Landslide Susceptibility Mapping of the northeastern part of Achaia Prefecture using analytical hierarchical process and GIS techniques. Bull. Geol. Soc. Greece 2010, 43, 1637–1646. [Google Scholar] [CrossRef][Green Version]
- Rozos, D.; Bathrellos, G.D.; Skillodimou, H.D. Comparison of the implementation of rock engineering system and analytic hierarchy process methods, upon landslide susceptibility mapping, using GIS: A case study from the Eastern Achaia County of Peloponnesus, Greece. Environ. Earth Sci. 2010, 63, 49–63. [Google Scholar] [CrossRef]
- Kavoura, K. Landslide Inventory Map Using GIS Tools and Field Experience—The Case of Achaia Prefecture, Western Greece. Master’s Thesis, University of Patras, Rio-Patra, Greece, 2013; p. 98. [Google Scholar]
- Polykretis, C.; Ferentinou, M.; Chalkias, C. A comparative study of landslide susceptibility mapping using landslide susceptibility index and artificial neural networks in the Krios River and Krathis River catchments (northern Peloponnesus, Greece). Bull. Eng. Geol. Environ. 2015, 74, 27–45. [Google Scholar] [CrossRef]
- Konstantopoulos, K.; Miliaresis, G.C.; Desk, S. Unsupervised landslide risk dependent terrain segmentation on the basis of historical landslide data and geomorphometrical indicators. SDRP J. Earth Sci. Environ. Stud. 2018, 3, 1–9. [Google Scholar] [CrossRef][Green Version]
- Tsangaratos, P.; Loupasakis, C.; Rozos, D.; Ilia, I. Landslide susceptibility assessments using the k-Nearest Neighbor algo-rithm and expert knowledge. Case study of the basin of Selinounda River 2015, Achaia County, Greece. In Proceedings of the SafeChania 2015. The Knowledge Triangle in the Civil Protection Service Center of Mediterranean Architecture, Chania, Greece, 10–14 June 2015; pp. 10–14. [Google Scholar]
- Sabatakakis, N.; Tsiambaos, G.; Rondoyanni, T.; Papanakli, S.; Kavoura, K. Deep-Seated Structurally Controlled Landslides of Corinth Gulf Rift Zone, Greece: The Case of Panagopoula Landslide. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015; Paper Number: ISRM-13CONGRESS-2015-273. ISBN 978-1-926872-25-4. [Google Scholar]
- Guzzetti, F.; Ardizzone, F.; Cardinali, M.; Rossi, M.; Valigi, D. Landslide volumes and landslide mobilization rates in Umbria, central Italy. Earth Planet. Sci. Lett. 2009, 279, 222–229. [Google Scholar] [CrossRef]
- Tavoularis, N.; Papathanassiou, G.; Ganas, A.; Argyrakis, P. Development of the Landslide Susceptibility Map of Attica Region, Greece, Based on the Method of Rock Engineering System. Land 2021, 10, 148. [Google Scholar] [CrossRef]
- Loftus, D.L.; Tsoflias, P. Geological Map of Greece in scale 1:50000. NAFPAKTOS Map Sheet; Institute of Geology and Mineral Exploration: Athens, Greece, 1971. [Google Scholar]
- Tsoflias, P. Geological Map of Greece in scale 1:50000. KHALANDRITSA Map Sheet; Institute of Geology and Mineral Exploration: Athens, Greece, 1984. [Google Scholar]
- Eleftheriou, A. Geotechnical Report on the Areas of Elekistra–Argyra and Krini Villages of the Achaia District; IGME: Athens, Greece, 1985; p. 13. [Google Scholar]
- Varnes, D.J. Slope movement types and processes. Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Bertolini, G.; Guida, M.; Pizziolo, M. Landslides in Emilia-Romagna region (Italy): Strategies for hazard assessment and risk management. Landslides 2005, 2, 302–312. [Google Scholar] [CrossRef]
- Morishita, Y.; Lazecky, M.; Wright, T.J.; Weiss, J.R.; Elliott, J.R.; Hooper, A. LiCSBAS: An Open-Source InSAR Time Series Analysis Package Integrated with the LiCSAR Automated Sentinel-1 InSAR Processor. Remote Sens. 2020, 12, 424. [Google Scholar] [CrossRef]
- COMET-LiCS Sentinel-1 InSAR Portal. Available online: https://comet.nerc.ac.uk/COMET-LiCS-portal/ (accessed on 26 May 2021).
- LiCSBAS: LiCSBAS Package to Conduct InSAR Time Series Analysis Using LiCSAR Products. Available online: https://github.com/yumorishita/LiCSBAS (accessed on 26 May 2021).
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Gamma SAR and interferometric processing software. In Proceedings of the ERS-ENVISAT Symposium 2000, Gothenburg, Sweden, 16–20 October 2000. [Google Scholar]
- Wegmüller, U.; Werner, C.; Strozzi, T.; Wiesmann, A.; Frey, O.; Santoro, M. Sentinel-1 IWS mode support in the GAMMA software. In Proceedings of the 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015. [Google Scholar]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, W.; Xu, B.; Wei, G. Assessing the use of GACOS products for SBAS-INSAR deformation monitoring: A case in Southern California. Sensors 2019, 19, 3894. [Google Scholar] [CrossRef]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali Fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef]
- López-Quiroz, P.; Doin, M.P.; Tupin, F.; Briole, P.; Nicolas, J.M. Time series analysis of Mexico City subsidence constrained by radar interferometry. J. Appl. Geophys. 2009, 69, 1–15. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31, L01607. [Google Scholar] [CrossRef]
- Motagh, M.; Shamshiri, R.; Haghshenas-Haghighi, M.; Wetzel, H.-U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Kotroni, V.; Bezes, A.; Koletsis, I.; Kopania, T.; Lykoudis, S.; Mazarakis, N.; Papagiannaki, K.; Vougioukas, S. The automatic weather stations NOANN network of the National Observatory of Athens: Operation and database. Geosci. Data J. 2017, 4, 4–16. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Wei, Z.-L.; Shang, Y.-Q.; Sun, H.-Y.; Xu, H.-D.; Wang, D.-F. The effectiveness of a drainage tunnel in increasing the rainfall threshold of a deep-seated landslide. Landslides 2019, 16, 1731–1744. [Google Scholar] [CrossRef]
- Tomás, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using wavelet tools to analyse seasonal variations from InSAR time-series data: A case study of the Huangtupo landslide. Landslides 2015, 13, 437–450. [Google Scholar] [CrossRef]
- Bracewell, R. Pentagram Notation for Cross Correlation. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1965; pp. 46, 243. [Google Scholar]
- Ganas, A. NOAFAULTS KMZ Layer Version 3.0 (2020 Update) (Version V3.0) [Data Set]. Zenodo 2020. [Google Scholar] [CrossRef]
- Ganas, A.; Tsironi, V.; Kollia, E.; Delagas, M.; Tsimi, C.; Oikonomou, A. Recent upgrades of the NOA database of active faults in Greece (NOAFAULTs). In Proceedings of the 19th General Assembly of WEGENER, Grenoble, France, 10–13 September 2018; pp. 10–13. [Google Scholar]
- Natijne, A.L.; Lindenbergh, R.C.; Bogaard, T.A. Machine Learning: New Potential for Local and Regional Deep-Seated Landslide Nowcasting. Sensors 2020, 20, 1425. [Google Scholar] [CrossRef]
- Villaseñor-Reyes, C.I.; Dávila-Harris, P.; Delgado-Rodríguez, O. Multidisciplinary approach for the characterization of a deep-seated landslide in a semi-arid region (Cañón de Yerbabuena, San Luis Potosí, Mexico). Landslides 2021, 18, 367–381. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).