Effect of Time Window on Satellite and Ground-Based Data for Estimating Chlorophyll-a in Reservoirs
Abstract
:1. Introduction
2. Materials and Methods
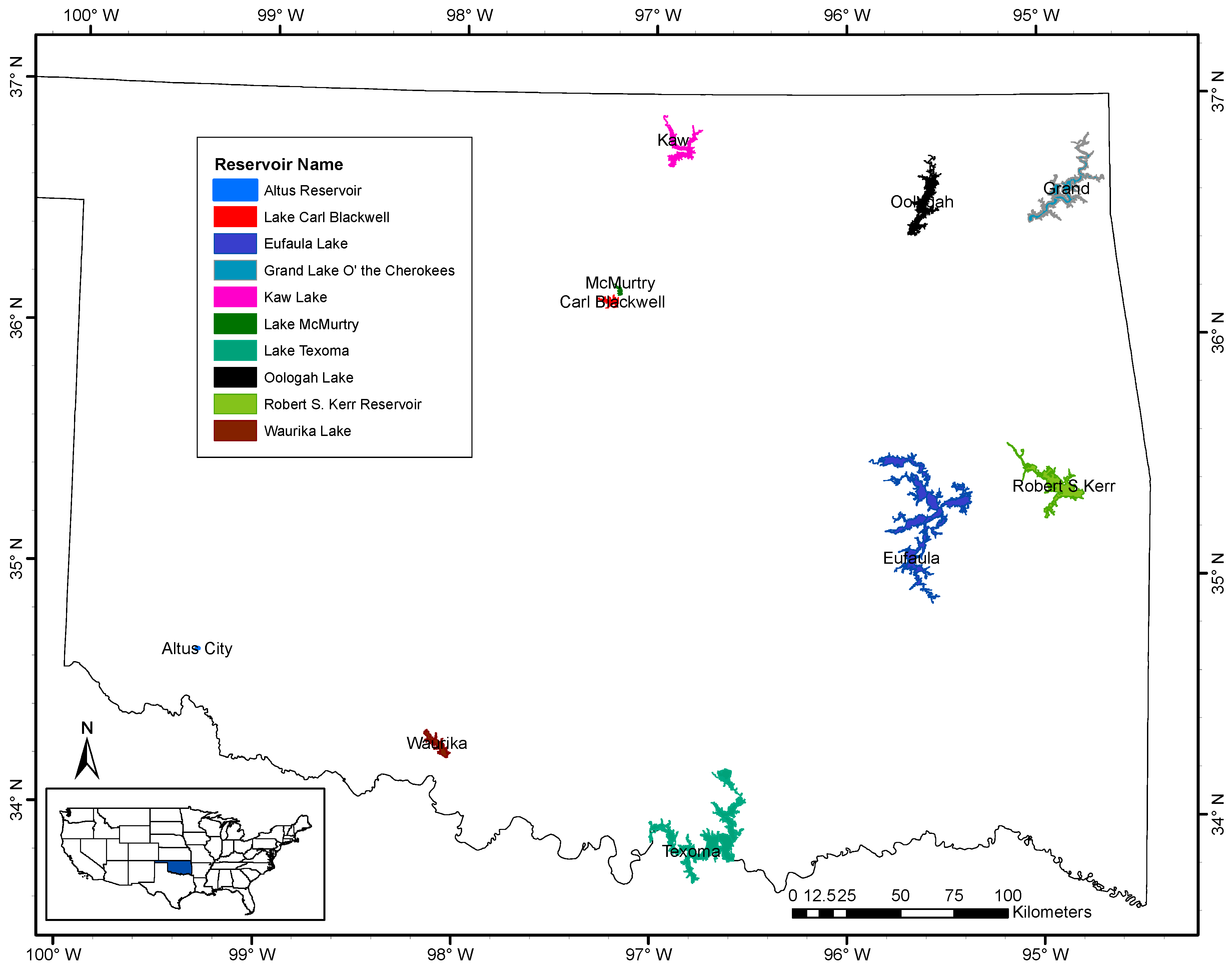
2.1. Study Area
2.2. Water Quality Data
2.3. Image Acquisition and Processing
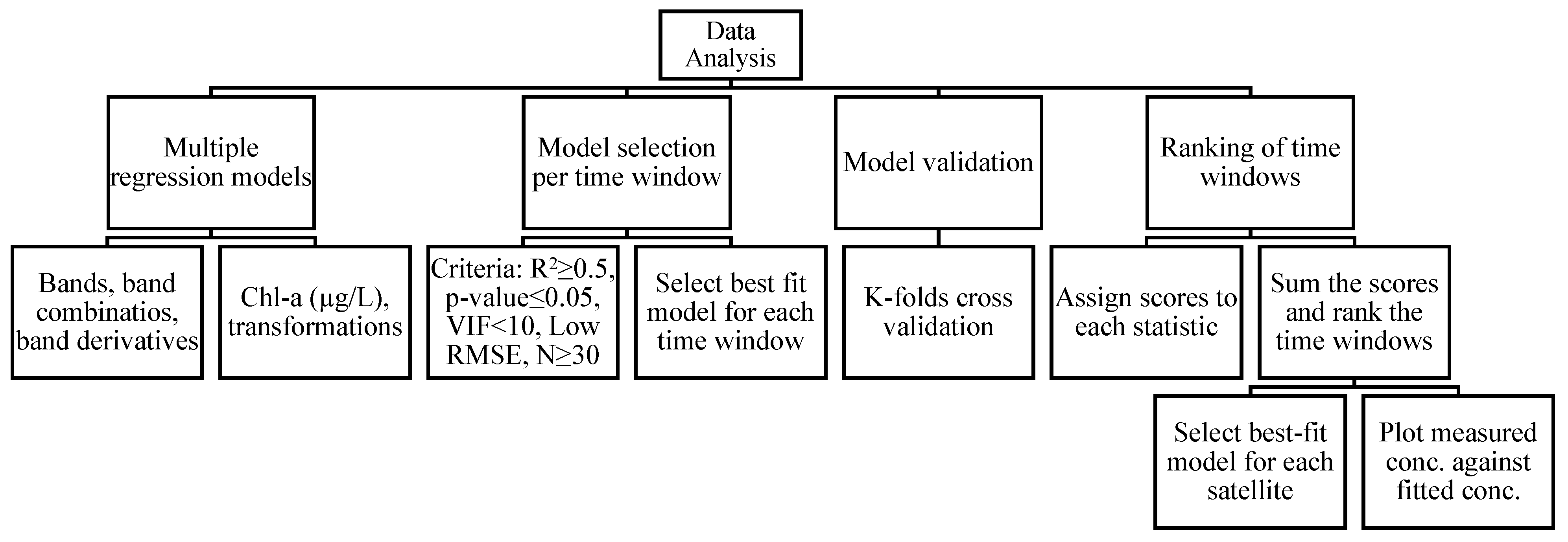
2.4. Data Analysis
- Building multiple regression models for each time window;
- Selection of the best fit model for each time window;
- Validation of the best fit model for each time window;
- Ranking of the time windows based on the statistics of their best fit models.
2.4.1. Building and Selection of Best Fit Models
2.4.2. Validation of the Best Fit Models
- Model-1: Trained on Fold-2 + Fold-3 +…. Fold-10; Test on Fold-1; Record R2 & RMSE;
- Model-2: Trained on Fold-1 + Fold-3 +…. Fold-10; Test on Fold-2; Record R2 & RMSE;
- Model-10: Trained on Fold-1 + Fold-2 +…. Fold-9; Test on Fold-10; Record R2 & RMSE.
2.4.3. Ranking of the Best Fit Models
3. Results
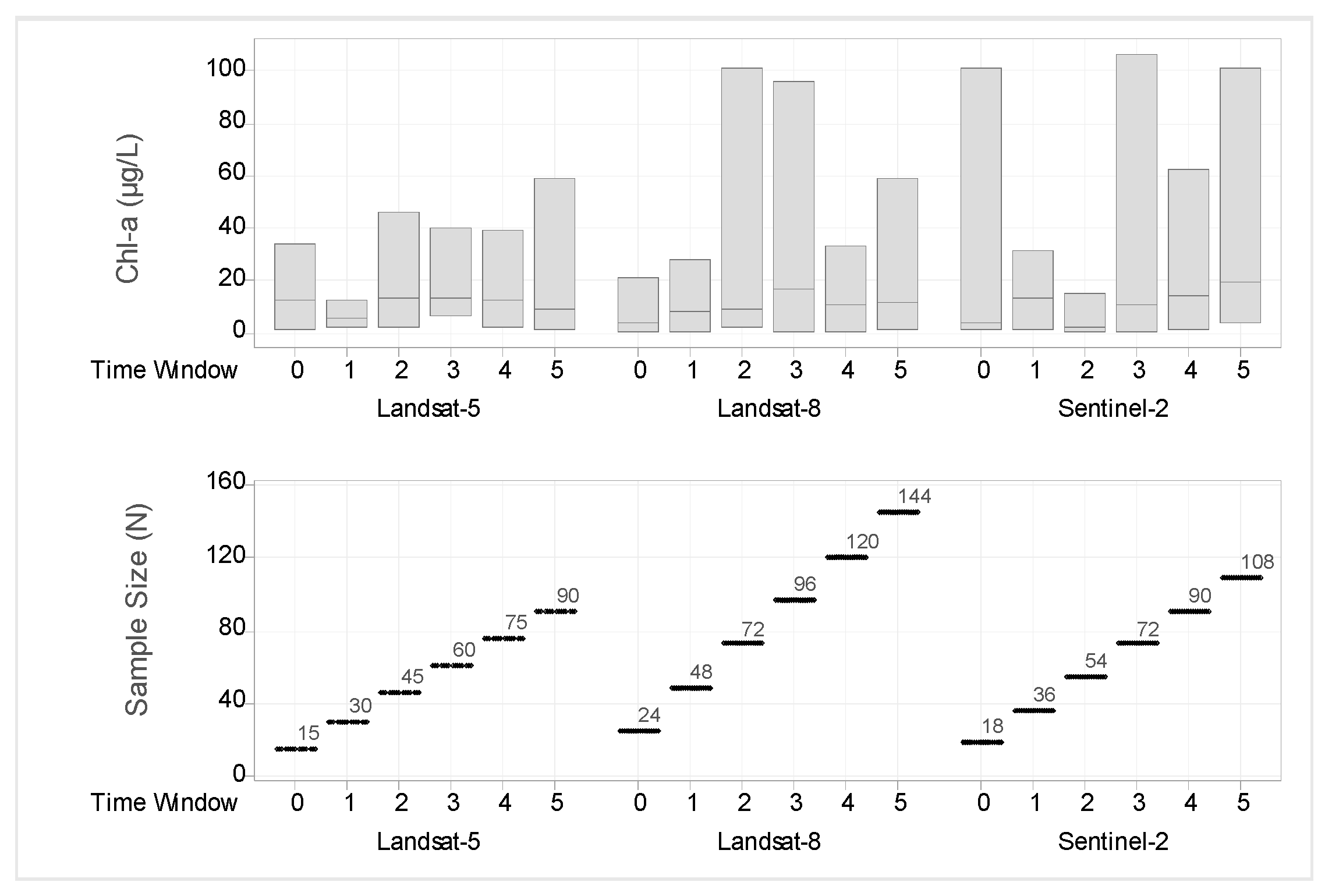
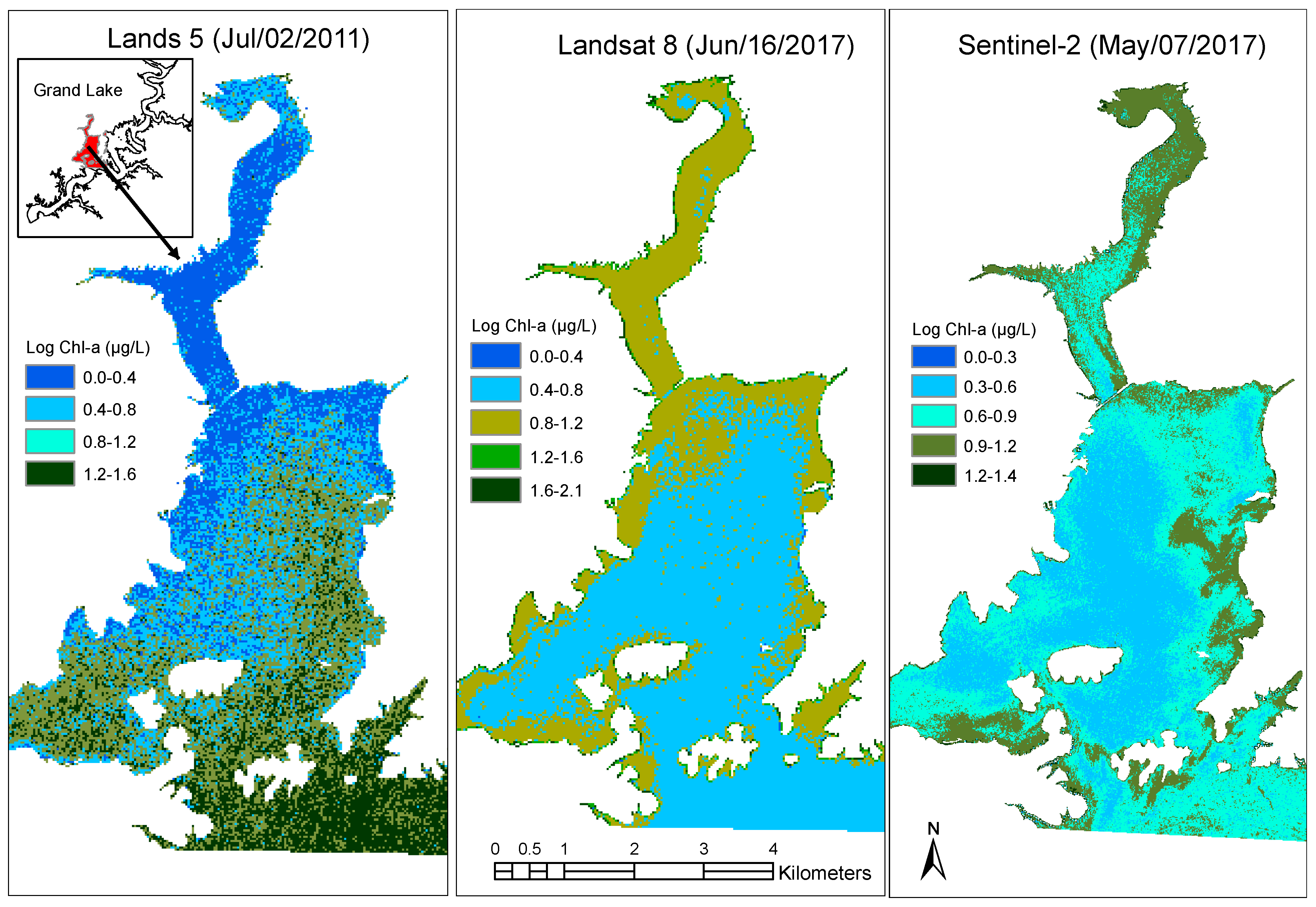
3.1. Range of Data
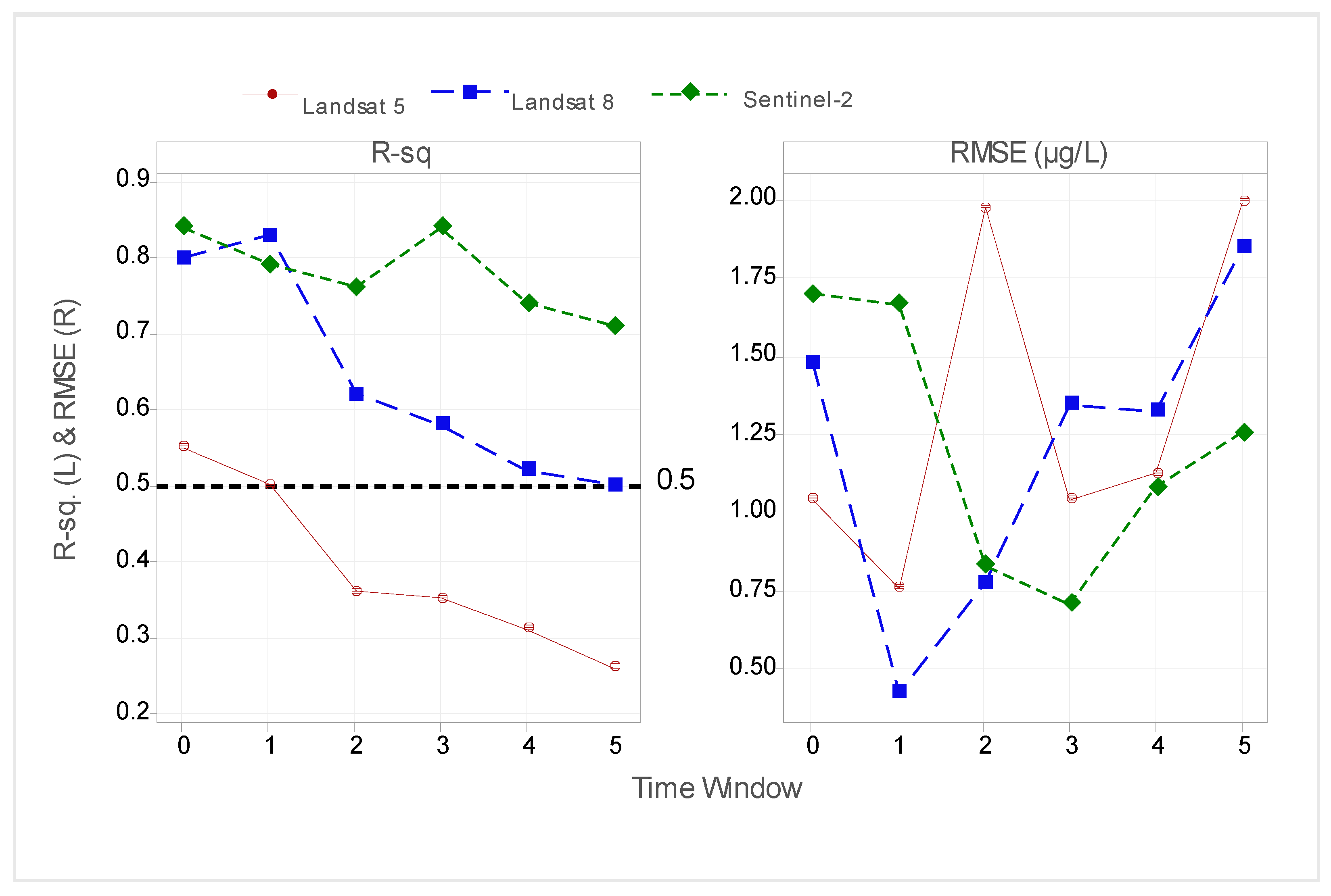
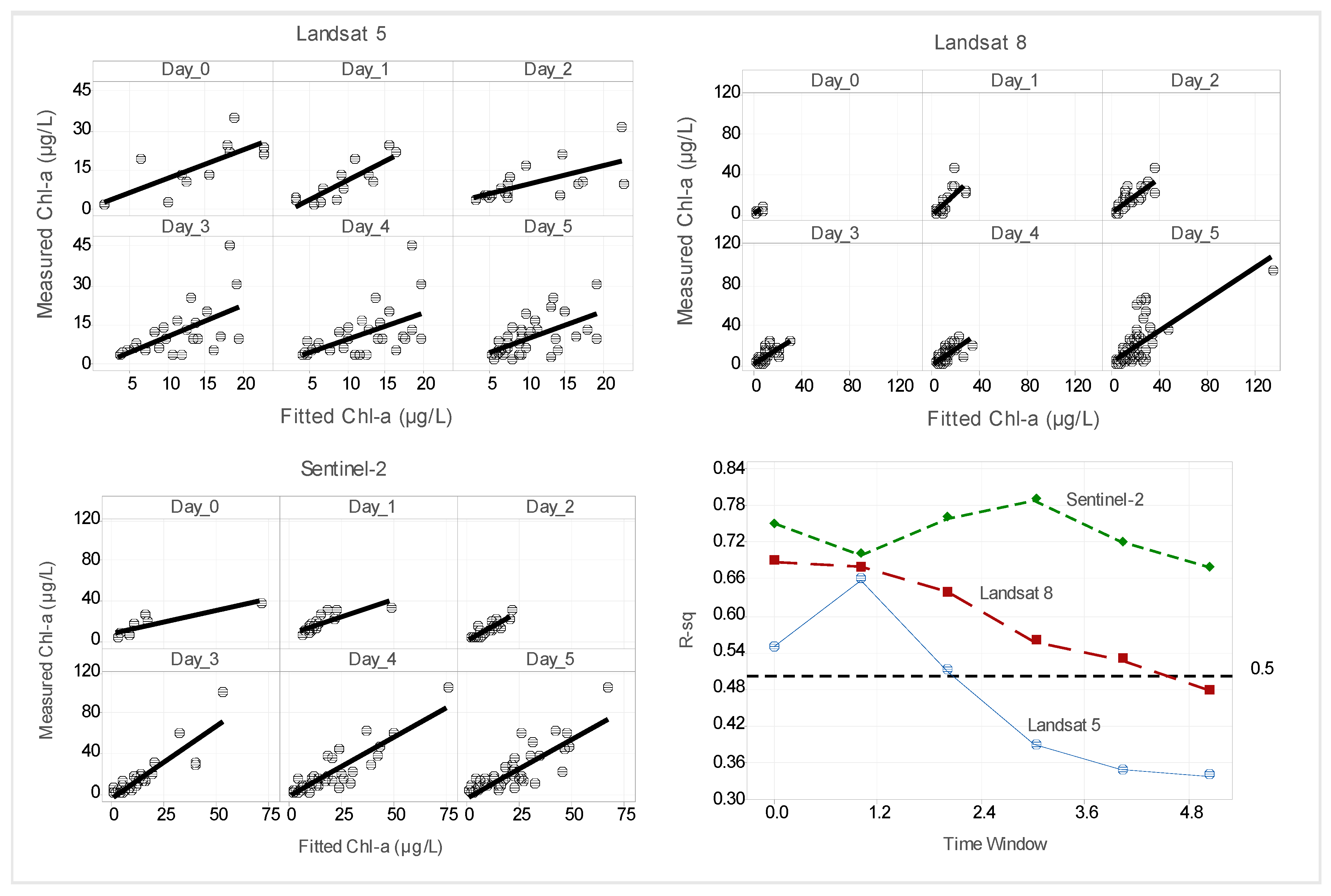
3.2. Best Fit Model per Time Window
3.3. Validation of the Best-Fit Models per Time Window
3.4. Ranking of the Time Windows Based on Their Respective Statistics
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, D.M.; Glibert, P.M.; Burkholder, J.M. Harmful algal blooms and eutrophication: Nutrient sources, composition, and consequences. Estuaries 2002, 25, 704–726. [Google Scholar] [CrossRef]
- Codd, G.A. Toxins of freshwater cyanobacteria. Microbiol. Sci. 1984, 1, 48–52. [Google Scholar] [PubMed]
- He, J.; Zhang, Y.; Wu, X.; Yang, Y.; Xu, X.; Zheng, B.; Deng, W.; Shao, Z.; Lu, L.; Wang, L.; et al. A study on the relationship between metabolism of Cyanobacteria and chemical oxygen demand in Dianchi Lake, China. Water Environ. Res. 2019, 91, 1650–1660. [Google Scholar] [CrossRef] [PubMed]
- Hudnell, H.K. The state of U.S. freshwater harmful algal blooms assessments, policy and legislation. Toxicon 2010, 55, 1024–1034. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.W.; Lazorchak, J.M.; Howard, M.D.A.; Johnson, M.V.; Morton, S.L.; Perkins, D.A.K.; Reavie, D.E.; Scott, I.G.; Smith, S.A.; Steevens, J.A. Are Harmful Algal Blooms Becoming the Greatest Inland Water Quality Threat to Public Health and Aquatic Ecosystems? Environ. Toxicol. Chem. 2016, 35, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Kirk, J. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Zeng, L.; Li, D. Development of In Situ Sensors for Chlorophyll Concentration Measurement. J. Sens. 2015, 5, 903509. [Google Scholar]
- Kuha, J.; Järvinen, M.; Salmi, P.; Karjalainen, J. Calibration of in situ chlorophyll fluorometers for organic matter. Hydrobiologia 2020, 847, 4377–4387. [Google Scholar] [CrossRef] [Green Version]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Qaulity Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [Green Version]
- Tan, W.; Liu, P.; Liu, Y.; Yang, S.; Feng, S. A 30-Year Assessment of Phytoplankton Blooms in Erhai Lake Using Landsat Imagery: 1987 to 2016. Remote Sens. 2017, 9, 1265. [Google Scholar] [CrossRef] [Green Version]
- Bramich, J.; Bolch, C.J.S.; Fischer, A. Improved red-edge chlorophyll-a detection for Sentinel 2. Ecol. Indic. 2021, 120, 106876. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, L.; Duran-Llacer, I.; González-Rodríguez, L.; Abarca-del-Rio, R.; Cárdenas, R.; Parra, O.; Martínez-Retureta, R.; Urrutia, R. Spectral analysis using LANDSAT images to monitor the chlorophyll-a concentration in Lake Laja in Chile. Ecol. Inform. 2020, 60, 101183. [Google Scholar] [CrossRef]
- Yacobi, Y.Z.; Moses, W.J.; Kaganovsky, S.; Sulimani, B.; Leavitt, C.B.; Gitelson, A.A. NIR-red reflectance-based algorithms for chlorophyll-a estimation in mesotrophic inland and coastal waters: Lake Kinneret case study. Water Res. 2011, 45, 2428–2436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, L. Estimating chlorophyll-a concentration using first-derivative spectra in coastal water. Int. J. Remote Sens. 2007, 26, 5235–5244. [Google Scholar] [CrossRef]
- Kuhn, C.; Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Becker, B.L.; Lusch, D.P.; Qi, J. Identifying optimal spectral bands from in situ measurements of Great Lakes coastal wetlands using second-derivative analysis. Remote Sens. Environ. 2005, 97, 238–248. [Google Scholar] [CrossRef]
- Liu, H.; Lee, S.; Chahl, J.S. Transformation of a high-dimensional color space for material classification. J. Opt. Soc. Am. A 2017, 34, 523–532. [Google Scholar] [CrossRef]
- Yan, Y.; Bao, Z.; Shao, J. Phycocyanin concentration retrieval in inland water: A comparative review of the remote sensing techniques and algorithms. J. Great Lakes Res. 2018, 44, 748–755. [Google Scholar] [CrossRef]
- Mansaray, A.S.; Dzialowksi, A.R.; Martin, M.E.; Wagner, K.L.; Gholizadeh, H.; Stoodley, S.H. Comparing PlanetScope to Landsat-8 and Sentinel-2 for Sensing Water Quality in Reservoirs in Agricultural Watersheds. Remote Sens. 2021, 13, 1847. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Noor, K.; Herbert, K. Modelling Reservoir Chlorophyll-a, TSS, and Turbidity Using Sentinel-2A MSI and Landsat-8 OLI Satellite Sensors with Empirical Multivariate Regression. J. Sens. 2020, 2020, 8858408. [Google Scholar] [CrossRef]
- Buma, W.G.; Lee, S. Evaluation of Sentinel-2 and Landsat 8 Images for Estimating Chlorophyll-a Concentrations in Lake Chad, Africa. Remote Sens. 2020, 12, 2437. [Google Scholar] [CrossRef]
- Molkov, A.A.; Fedorov, S.V.; Pelevin, V.V.; Korchemkina, E.N. Regional Models for High-Resolution Retrieval of Chlorophyll a and TSM Concentrations in the Gorky Reservoir. Remote Sens. 2019, 11, 1215. [Google Scholar] [CrossRef] [Green Version]
- Boucher, J.; Weathers, K.C.; Norouzi, H.; Steele, B. Assessing the effectiveness of Landsat 8 chlorophyll a retrieval algorithms for regional freshwater monitoring. Ecol. Appl. 2018, 28, 1044–1054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kloiber, S.M.; Brezonick, P.L.; Olmanson, L.G.; Bauer, M.E. A procedure for regional lake water clarity assessment using Landsat multispectral data. Remote Sens. Environ. 2002, 82, 38–47. [Google Scholar] [CrossRef]
- McCullough, I.M.; Loftin, C.S.; Sader, S.A. Combining lake and watershed characteristics with Landsat TM data for remote estimation of regional lake clarity. Remote Sens. Environ. 2012, 123, 109–115. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Urbanski, J.A.; Wochna, A.; Bubak, I.; Grzybowski, W.; Lukawska-Matuszewska, K.; Lacka, M.; Sliwinska, S.; Wojtasiewicz, B.; Zajaczkowski, M. Application of Landsat 8 imagery to regional-scale assessment of lake water quality. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 28–36. [Google Scholar] [CrossRef]
- Keith, D.; Rover, J.; Green, J.; Zalewsky, B.; Charpentier, M.; Thursby, G.; Bishop, J. Monitoring algal blooms in drinking water reservoirs using the Landsat-8 Operational Land Imager. Int. J. Remote Sens. 2018, 39, 2818–2846. [Google Scholar] [CrossRef]
- Torbick, N.; Corbiere, M. A Multiscale Mapping Assessment of Lake Champlain Cyanobacterial Harmful Algal Blooms. Int. J. Environ. Res. Public Health 2015, 12, 11560–11578. [Google Scholar] [CrossRef] [Green Version]
- Dodds, W.; Whiles, M. Freshwater Ecology: Concepts and Environmental Applications of Limnology, 2nd ed.; (paper back); Academic Press: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Boyer, T.A.; Daniels, B.; Melstrom, R.T. Algal Blooms in Oklahoma: Economic Impacts. 2017, pp. AGEC-1063-1–AGEC-1063-2. Available online: https://extension.okstate.edu/fact-sheets/algal-blooms-in-oklahoma-economic-impacts.html# (accessed on 4 January 2022).
- Mason, A.M.; Triplett, J.R. Controlling Environmental Crisis Messages in Uncontrollable Media Environments: The 2011 Case of Blue-Green Algae on Grand Lake O’ the Cherokees, OK. In Communicating Cimate-Change and Natural Hazard Risk and Cultivating Resilience: Case Studies for a Multi-Disciplinary Approach; Springer: Cham, Switzerland, 2016; Volume 45, pp. 189–204. [Google Scholar]
- OWRB Web Resource. Monitoring and Assessment, Oklahoma Water Resources Board. 2018. Available online: https://www.owrb.ok.gov/quality/monitoring/monitoring.php (accessed on 4 January 2022).
- ESA. Copernicus Open Access Hub. European Space Agency. 2022. Available online: https://scihub.copernicus.eu/ (accessed on 2 February 2022).
- Kupssinsku, L.S.; Guimaraes, T.T.; de Souza, E.M.; Zanotta, D.C.; Veronez, M.R.; Gonzaga, L.; Mauad, F.F. A Method for Chlorophyll-a and Suspended Solids Prediction through Remote Sensing and Machine Learning. Sensors 2020, 20, 2125. [Google Scholar] [CrossRef] [Green Version]
- Minitab. Minitab 21 Support. 2022. Available online: https://support.minitab.com/en-us/minitab/21/?SID=0 (accessed on 2 February 2022).
- Topp, S.N.; Pavelsky, T.M.; Jensen, D.; Simard, M.; Ross, M.R.V. Research trends in the use of remote sensing for inland water quality science: Moving towards multidisciplinary applications. Water 2020, 12, 169. [Google Scholar] [CrossRef] [Green Version]
- Olmanson, L.G.; Bauer, M.E.; Brezonick, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Kimmel, B.L.; Groger, A.W. Factors Controlling Primary Production in Lakes and Reservoirs: A Perspective. Lake Reserv. Manag. 1984, 1, 277–281. [Google Scholar] [CrossRef]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 4th ed.; Pearson: London, UK, 2015. [Google Scholar]
- Ansper, A.; Alikas, K. Retrieval of Chlorophyll a from Sentinel-2 MSI Data for the European Union Water Framework Directive. Remote Sens. 2018, 11, 64. [Google Scholar] [CrossRef] [Green Version]
- Pereira-Sandoval, M.; Ruiz-Verdu, A.; Tenjo, C.; Delegido, J.; Urrego, P.; Pena, R.; Vicente, E.; Soria, J.; Soria, J.; Morena, J. Calibration and Validation of Algorithms for the Estimation of Chlorophyll-A in Inland Waters with Sentinel-2. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.M.; Lichtenthaler, H.K. Detection of Red Edge Position and Chlorophyll Content by Reflectance Measurements near 700 nm. J. Plant Physiol. 1996, 148, 501–508. [Google Scholar] [CrossRef]

| Time Window | Sampling before Satellite Overpass | Same Day | Sampling after Satellite Overpass | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | ||||||||||
| 1 | −1 | 0 | 1 | ||||||||
| 2 | −2 | −1 | 0 | 1 | 2 | ||||||
| 3 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | ||||
| 4 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | ||
| 5 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
| Time Window | R2 | RMSE | R2 (cv) | RMSE (cv) | VIF | Significance | N | Score | |
|---|---|---|---|---|---|---|---|---|---|
| Landsat 5 | 0 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 12 |
| 1 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 13 | |
| 2 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 12 | |
| 3 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 12 | |
| 4 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 12 | |
| 5 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 12 | |
| Landsat 8 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 13 |
| 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 | |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 | |
| 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 | |
| 4 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 13 | |
| 5 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 13 | |
| Sentinel-2 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 13 |
| 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 | |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 | |
| 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 | |
| 4 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 | |
| 5 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kayastha, P.; Dzialowski, A.R.; Stoodley, S.H.; Wagner, K.L.; Mansaray, A.S. Effect of Time Window on Satellite and Ground-Based Data for Estimating Chlorophyll-a in Reservoirs. Remote Sens. 2022, 14, 846. https://doi.org/10.3390/rs14040846
Kayastha P, Dzialowski AR, Stoodley SH, Wagner KL, Mansaray AS. Effect of Time Window on Satellite and Ground-Based Data for Estimating Chlorophyll-a in Reservoirs. Remote Sensing. 2022; 14(4):846. https://doi.org/10.3390/rs14040846
Chicago/Turabian StyleKayastha, Priya, Andrew R. Dzialowski, Scott H. Stoodley, Kevin L. Wagner, and Abubakarr S. Mansaray. 2022. "Effect of Time Window on Satellite and Ground-Based Data for Estimating Chlorophyll-a in Reservoirs" Remote Sensing 14, no. 4: 846. https://doi.org/10.3390/rs14040846
APA StyleKayastha, P., Dzialowski, A. R., Stoodley, S. H., Wagner, K. L., & Mansaray, A. S. (2022). Effect of Time Window on Satellite and Ground-Based Data for Estimating Chlorophyll-a in Reservoirs. Remote Sensing, 14(4), 846. https://doi.org/10.3390/rs14040846









