Abstract
NeQuick2 is a three-dimensional ionospheric electron density empirical model that uses numerical integration to calculate the total electron content along any line-of-sight (LOS). As one of the most commonly used three-dimensional ionospheric models, it is necessary to objectively evaluate the accuracy and stability of NeQuick2 over a long period, especially over the mid-latitudes of the northern hemisphere where most of the ground-based GNSS stations are distributed. Therefore, different methods are used in this study to evaluate the accuracy of the NeQuick2 model from 2008 to 2021, including comparison with the International Global Navigation Satellite System Global Ionosphere Maps (IGSG), Jason2 Vertical Electron content (VTEC), and self-consistent evaluation. The comparison with IGSG shows that the standard deviation (STD) value is about 2.59 TECU. The accuracy of the IGSG and NeQuick2 model over ocean regions shows that the bias of IGSG is more significant than that of the NeQuick2 model. The mean STD value is 2.09 TECU for IGSG, and the corresponding value is 3.18 TECU for the NeQuick2 model, which is about 50% worse than IGSG. The dSTEC assessment results indicate that the variation in bias for IGSG is more stable than that of the NeQuick2 model. The mean STD value is 0.86 and 1.52 TECU for IGSG and NeQuick2 model, respectively. The conclusion could be made that NeQuick2 model represents the average ionosphere electron content and its accuracy fluctuates with solar conditions. Compared with the IGSG, the NeQuick2 model always underestimates TEC value, especially in low solar activity periods and compared with Jason2, the TEC values obtained by NeQuick2 model are overestimated, but the degree of overestimation is smaller than that of IGSG.
1. Introduction
The ionosphere is the ionized region in the outer layer of the Earth’s atmosphere. It is closely related to human high-tech activities and even daily life. Free electrons and ions in the ionosphere can change the transmission speed and generate refraction, reflection, and scattering of radio waves, which results in absorption of the radio signals at different degrees and rotation of the polarization plane. In fact, under the influence of solar activity, geomagnetic activity, and natural disaster, the density of free electrons and ions has complex characteristics of disturbance and variation at different scales such as time and space. Ionosphere modeling is an essential part of global space weather change exploiting and monitoring. It is crucial to understand the specific effects of radio signals traveling through the ionosphere. Thus, studying the mechanism, evolution process, and impact of the ionosphere and climate change is of great significance. In particular, when the radio wave signal emitted by the Global Navigation Satellite System (GNSS) propagates in the ionosphere, an error of several meters to tens of meters will occur, which is one of the primary error sources restricting GNSS users, particularly single-frequency GNSS users, from high-precision positioning.
The rapid development of real-time Precise Point Positioning (PPP) has put forward novel and higher requirements for real-time Ionosphere modeling. Dual-frequency GNSS users can utilize dispersion effects to eliminate ionosphere delay errors by ionosphere-free (IF) combination. However, the IF combination would cause the observation coupling clock error and differential code deviation (DCB) [1]. Single-frequency GNSS users can only adopt the ionosphere correction models. Researching and constructing a high-precision real-time ionosphere model can help weaken the ionosphere influence and speed up the convergence of PPP.
Generally, there are different approaches to describe the ionosphere, including physical models [2,3], mathematical models based on different algorithms [4,5,6,7], and empirical models [8,9,10,11]. Due to the limitation of communication capability and real-time ionosphere variation, physical models and mathematical models are not widely used. The Total Electron Content (TEC) of the ionosphere is considered as a crucial parameter to describe the characteristics of the ionosphere variation, and the value of TEC is proportional to the amount of ionosphere delay received by the radio wave signal. In recent years, with the development of multi-system GNSS, GNSS TEC observations have provided a wealth of data sources for the study of ionosphere variations and have made significant progress, which facilitates the construction and verification of ionosphere empirical models [12]. Therefore, empirical models based on TEC are often used in GNSS navigation and positioning with high precision and real-time requirements.
At present, commonly used ionosphere models suitable for GNSS navigation and positioning include the two-dimensional empirical ionosphere model, the three-dimensional ionosphere model, and the global ionosphere model (GIM) [6]. The two-dimensional ionosphere models, such as Klobuchar, use the greater than zero part of the cosine function to describe the daytime ionosphere delay, and a fixed constant to describe the nighttime ionosphere delay. The period and amplitude of the cosine function are related to the geomagnetic latitude, day of the year (DOY), and solar activity at the pierce point. During the quiet ionosphere period, it can correct only 50%~70% of ionosphere delay [13,14]. In addition, due to the assumption of single-layer ionosphere, the vertical characteristics of the ionosphere are ignored. However, the dispersion effect in the upper layer of the ionosphere is more serious, which will cause a more significant projection error [12]. Therefore, its accuracy is limited, which cannot meet the demand of real-time high-precision positioning and cannot reflect the real-time variation characteristics. The three-dimensional ionosphere models adopt electron density as the modeling object to obtain the vertical electron density distribution layers [14]. Thus, numerical integration can calculate the TEC in any direction passing through the ionosphere. Moreover, key parameters can be transmitted through broadcast ephemeris, which is suitable for real-time applications. The GIMs provided by different ionosphere associate analysis centers have higher precision than other methods. However, there is a delay of several days in the release of the high-precision model, which results that real-time monitoring of ionosphere and correction of propagation delay cannot be achieved. In addition, the IGS ground-based monitoring stations distribute unevenly in the global scale. Therefore, users often use broadcast ionosphere and real-time TEC models for navigation and positioning. Compared with other approaches, the three-dimensional empirical models can be applied to describe the averaged condition of the ionosphere for the long term [15]. They could provide relatively high-accuracy ionosphere correction, and overcome the limitations of the commonly used two-dimensional model. This could help achieve accurate monitoring of space weather and satisfy high-precision GNSS PPP demands.
Generally, there are two commonly used three-dimensional models, i.e., the International Reference Ionosphere (IRI) model and the NeQuick model. In terms of the IRI model, it uses observations provided by different methods (such as global ionosphere sounder, incoherent scattering radar, sounding rocket data, etc.), and is constructed by introducing solar activity index and geomagnetic activity index, with integrating multiple atmospheric models [10,11]. Furthermore, it is the International Standardization Organization (ISO) standard for the ionosphere. The IRI-Plas model is the latest proposed for extension of the IRI model to the plasmasphere [16,17]. Many studies have been performed to evaluate its accuracy from different aspects, such as its accuracy over specific regions [18,19,20,21,22], under different geomagnetic or solar conditions [23,24,25], and its topside part constructions [26,27,28]. These studies showed that the IRI model can describe the physical properties of the ionosphere. However, the IRI model can only calculate the TEC value in the vertical direction, which might limit their applications. For the NeQuick model, it is a three-dimensional electron density empirical model originally constructed for the GALILEO system to correct the ionosphere delay. The electron density can be calculated based on the input parameters such as time, location and solar activity index, and can obtain the TEC value over a specified altitude range by integration. Currently, there are three officials versions of NeQuick, which mainly include the NeQuick 1 model [8,29], NeQuick2 model [9] and NeQuick G model [30]. Among them, the coefficients of the NeQuickG model is broadcasted by the Galileo satellite system, which are mainly applied for ionospheric correction in real-time. The NeQuick2 is an updated version for the NeQuick1 model, which is estimated by multiple Epstein layers with optimized parameters and the NeQuick2 can calculate the TEC value in the LOS direction directly based on the input azimuth angle, elevation angle and the height between the station and the satellite. Meanwhile, some evaluations of the NeQuick model have been performed in recent years [31,32,33].
The increasing demands for ionosphere physics and space geodetic applications makes it essential to understand the accuracy of the three-dimensional models [13]. Some relevant researches have been published, with most of them based on comparative studies in specific regions or under specific circumstances. The slant electron content extracted from the NeQuick2 model can be applied for ionosphere mapping function error analysis [34]. Furthermore, the topside part of the NeQuick2 model has been the default option for the IRI model. The study performed by [35] validates that the accuracy of the IRI-2016 model and NeQuick2 model are nearly the same and both are worse than that of IGSG. The results indicate that the hourly mean biases of Ne-Quick2 is about −2.5 TECU compared to IGSG, the Root Mean Square (RMS) value of empirical models is 6.0 relative to Jason2-VTEC, and the RMS value is about 2.6 TECU compared with dSTEC values derived from the selected stations. However, the long-term globally statistical analysis of the empirical model may be affected by partial ionospheric anomalies. In addition, the difference between the IRI model and NeQuick2 model has been studied in detail [27,36,37,38], and the results show that the performance of the IRI model is similar with that of NeQuick2 model. To further understand the empirical model characters at long-term and large-scale, NeQuick2 is employed as the object model in this study.
Limited by the spatiotemporal properties of the ionosphere and the distribution of ground monitoring stations, the correction effect is strongly related to the latitudes of the stations and solar activity. The correction effectiveness of the empirical model near the equator and high latitude region is usually relatively poor in long-term statistics. Although there are many GNSS monitoring and tracking stations around the world, which can achieve high-precision and all-time monitoring, the monitoring stations are unevenly distributed worldwide, and most of them are located in the northern hemisphere. In addition, there are few ground-based monitoring stations in the ocean and the North and South Poles, resulting in fewer ionosphere data in areas with harsh natural conditions such as the ocean and the poles. This will restrict the accuracy and reliability of the model in the corresponding regions. The ionosphere in low latitudes changes dramatically, especially near the equator, which is greatly affected by solar radiation. Its lower layer structure is more complex, and therefore is called the equatorial anomalies. Moreover, there are polar day and polar night effects in high latitude regions. Most sudden extreme weather conditions cannot be considered in the construction of each empirical model at present. Thus, its accuracy characteristics are bound to decrease significantly under extreme climate conditions. Large deviations in extreme conditions may overwhelm the statistical properties of the deviations in normal conditions, which generally occupy the most of the time. In general, the ionosphere in the mid-latitudes is relatively quiet, with obvious seasonal and diurnal variations. For long-term statistical evaluation of empirical model bias, it is necessary to consider minimizing the impact of occasional extreme weather conditions on the overall results. Therefore, to evaluate the accuracy of the NeQuick2 model in long-term more reasonably, this paper selects the mid-latitudes of the northern hemisphere as the analysis area.
Thus, this study evaluates the performance of the NeQuick2 model over the mid-latitudes of the northern hemisphere in detail from different aspects. A brief introduction of the NeQuick2 model is presented first. Afterward, the assessment methods, such as validation over the ocean and self-consistency evaluation method are illustrated. The evaluation results of the NeQuick2 model will be shown in Section 4. Finally, Section 5 gives the summaries and conclusions of this study.
2. NeQuick2 Model Introduction
The NeQuick model is a three-dimensional electron density semi-empirical model used by the Galileo system for single-frequency users to correct the ionosphere. It can be used easily and can be used for mapping function error analysis. Furthermore, it is mainly based on the topside sounding data, which means that it has the advantage that absolute TEC values are calculated based on real measurements of plasma frequency and electron density. With the gradual establishment of Galileo and the enrichment of related data, the NeQuick model is constantly updated, and the calculation of its parameter has been modified in the new versions. The TEC calculated by NeQuickG is regarded as a function of time, longitude, latitude, height, and a small set of ionosphere correction parameters updated continuously by ground segments [30]. The calculated parameters are transmitted to the Galileo users as parts of the navigation message. NeQuick2 [9] model is the latest version of the NeQuick model, which is developed at the Aeronomy and Radio propagation Laboratory of the Abdus Salam International Centre for Theoretical Physics (ICTP), Trieste, Italy, and at the Institute for Geophysics, Astrophysics and Meteorology (IGAM) of the University of Graz, Austria. Compared with the NeQuick1 model, the structure of the model did not change, but the formulation of some specific parameters, which related to the bottom side and topside part, have been modified. Besides, computational efficiency has also been improved by applying specific revisions to the computer package. The NeQuick2 web model is also available at https://t-ict4d.ictp.it/nequick2/nequick-2-web-model (last access: 11 August 2022).
The ionospheric charged electrons and ions have different changing rules at different heights, positions, and times [39]. Generally, the distribution of ionospheric electron density in the vertical direction can be divided into D, E, and F layers. The F layer can be further divided into the F1 layer and the F2 layer. The D layer is the layer closest to the ground in the ionosphere, its height ranges from 60 to 90 km, and the electron content density is low in the D layer. The F layer is the middle region of the ionosphere, about 130~600 km above the ground, and the electron concentration is the largest. The electron distribution is mainly affected by the neutral wind and the earth’s magnetic field. At the same time, since the electron density of the F layer accounts for the largest proportion in the whole ionosphere, the large-scale change of the ionosphere is related to the change of this layer. The F1 layer appears in mid-latitude areas in summer and usually disappears at night. The height of the F2 layer is higher than that of the F1 layer, and it is the main area for reflecting high-frequency radio waves. The NeQuick2 model uses semi-Epstein layers with modeled thickness parameters to describe the electron density of the ionosphere ranging from 90 km to the peak altitude of the F2 layer [9]. In other words, the NeQuick2 model mainly concentrates on the E, F1, and F2 layers.
Therefore, to model the ionosonde parameters, such as foE, foF1, foF2, and M(3000)F2, three profile anchor points, i.e., the layer peak of E, F1, and F2 layer are applied in NeQuick2. The basic inputs are position, time, and solar flux (or sunspot number). The electron density along any ground-to-satellite ray-path and the corresponding TEC could be calculated by numerical integration. The Epstein layer can be represented as [9]:
where is the layer peak electron density, is the layer peak height, and is the layer thickness parameter. With different expressions of the parameters, the bottom side and top side of the NeQuick2 could be expressed as a sum of semi-Epstein layers. In addition, the thickness parameters take different values for different layers [9]. Parameters used in different layers are summarized in Table 1. As shown in the table, the thickness parameters should take different values for bottom side and topside of each layer, and it is worth noting that hmF2 is a function of M(3000)F2 [9].

Table 1.
Summary of NeQuick2 basic parameters.
Moreover, the Titheridge model based on the seasonal relationship with solar zenith angle is adopted to calculate foE and foF1 [9]. The ITU-R coefficients are used to compute median values of foF2 and M(3000)F2, which are provided in the NeQuick package one file a month. In addition, a worldwide grid MODIP data file is provided in the package to calculate geomagnetic inclination. It should be noted that the MODIP file needs to be updated every five years to consider the natural changes in the Earth’s magnetic field.
In a word, the values of the NeQuick2 model depend on solar activity, e.g., monthly-mean sunspot number index (R12) or solar radio flux index (F10.7), month, and universal time. In this study, the input parameters include time, location, and daily solar activity index (F10.7). The altitude range is from 50 km to 20,200 km, which is consistent with the range area of GIM generated by ground-based GNSS observation.
3. Models Assessment Methods
As mentioned earlier, different models are built on different data sources, which can no doubt lead to differences between models. Limited by the acquisition of the ionosphere TEC truth value, multiple methods need to be adopted to evaluate the model from as many aspects as possible. In addition, long-term comparisons are adopted to eliminate this effect as much as possible. This section first presents various methods for evaluating the NeQuick2 model, including the model evaluation by final GIM products provided by IGS (IGSG), the model accuracy assessment over ocean regions with the Jason2 VTEC products, and the model accuracy evaluation using the dSTEC self-consistency check method by GNSS raw observation data. The theory and feasibility of each evaluation method are briefly introduced. Then the precision factor and principle used in the evaluation process are explained.
3.1. The Final GIM Provided by IGS
Nowadays, seven ionosphere associate analysis centers (IAACs) can provide GIMs, which are generated by their fitting algorithm and have a good agreement [40,41]. The GIMs are mostly computed from dual-frequency measurements gathered at global scale. They contain the worldwide distribution of VTEC with a specific spatial and temporal resolution. The accuracy of GIM products provided by different analysis centers is roughly the same, about 2~8 TECU [40,42]. To provide a comprehensive ionosphere product to users, IGS employed weighted mean method with self-consistency test to combine the GIMs provided by Center for Orbit Determination in Europe (CODE), Universitat Politècnica de Catalunya/IonSAT (UPC), European Space Operations Center of European Space Agency (ESA), and Jet Propulsion Laboratory (JPL) [42]. IGSG final products have relatively higher accuracy and can obtain the VTEC values globally. Furthermore, the mid-latitudes of northern hemisphere have the most ground-based stations, which could avoid the impact of data source lacking of IGSG and ensure the accuracy of IGSG to a certain extent. Therefore, the final IGSG products is regarded as the VTEC reference to calculate the long-term and large-scale difference concerning the NeQuick2 model in mid-latitudes of northern hemisphere.
3.2. Assessment over the Oceanic Region
There are few GNSS monitoring stations in marine areas, so the ground-based ionosphere monitoring data sources are scarce over the ocean. Using mathematical model fitting and extrapolation might not entirely make up for the lack of data, resulting in low accuracy and even negative values of the constructed ionosphere TEC model in these areas.
Jason 2 was an Earth satellite designed to make observations of ocean topography. The mission was a follow-on to the French–American Jason 1 mission, which began collecting data on sea-surface levels in 1992. The Jason satellites are equipped with dual-frequency altimeters containing two frequencies, i.e., a Ku-band ( = 13.575 GHz) and a C-band ( = 5.3 GHz). Thus, VTEC data can be derived from the Ku-band frequency’s vertical phase ionosphere delay [43]. The orbit is designed at an altitude of 1336 km. Besides, as we can see from Figure 1, the repeat trajectory of Jason2 satellite mainly range from 65°S to 65°N and can cover most of the oceanic regions. Additionally, the ionosphere data calculated from Jason is not correlated with the ionosphere data extracted from the ground-based GNSS. Therefore, the VTEC provided by the Jason2 satellite is applied in this research to assess the accuracy of the NeQuick2 model over oceanic regions. Meanwhile, the accuracy of the IGSG over the ocean could also be validated by this assessment process.
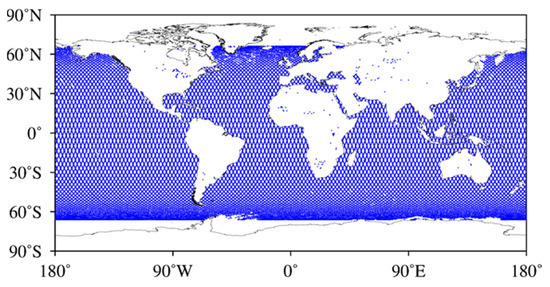
Figure 1.
Trajectory of Jason2 satellite for its repeat cycle.
Generally, Jason VTEC is obtained by pseudo-range ionosphere delay correction of Ku-band. The specific formula could be expressed as below:
where is the ionosphere delay correction of Ku-band; is the frequency of Ku-band in GHz.
It is worth noting that this method can only obtain VTEC in a small range on the satellite’s operating path below the satellite’s orbital altitude. However, this altitude range already covers the most interval of ionosphere range. At the same time, the observation noise of the obtained VTEC is relatively large, and there is a constant deviation of about 3~5 TECU from the VTEC extracted by the ground-based GNSS [44,45,46]. Due to the high noise level of the altimeter, a sliding window of 15–25 s is usually used to extract TEC with the method of the median filter. The accuracy of the smoothed VTEC is better than one TECU [47]. Therefore, the missing part of the VTEC calculated by Jason2 could be considered as a systematic deviation. This system deviation will only affect the deviation value of the evaluation results, and will not affect the stability of the evaluation results.
To reflect the real accuracy in the applications, analysis will be made according to the real modeled ionospheric correction values, which is more consistent with the actual situation, and the altitude range is still from 50 km to 20,200 km for the NeQuick-2 model when compared to Jason2. Although there will be a constant deviation from the ionosphere corrections calculated to the Jason2 orbital plane, the range of ionosphere heights calculated by NeQuick2 and IGSG is still consistent. By this way, it can also reflect the characteristics and differences of the NeQuick2 model in calculating the TEC value of the top model of the ionosphere, and the comparison could be more comprehensive and more valuable.
3.3. Self-Consistency Evaluation
The dSTEC method was first proposed in reference [48]. As shown in Figure 2, the method uses dual-frequency carrier-phase observations to calculate the Slant Total Electron Content (STEC) of the slanted path [49]. Then the differential STEC (dSTEC) could be extracted by the difference of STEC with respect to that with the enormous elevation within a continuous arc. It has lower noise levels, and thus, multipath effects can be used to validate the accuracy of ionosphere models [50]. The dSTEC calculation formula could be expressed as below:
where represents the STEC value of the line of sight between satellite and receiver at the epoch ; represents the value of geometry-free combination at epoch ; and the subscript denotes the max elevation. In addition, the STEC value of IGSG at these epochs could be converted from the VTEC interpolation value by mapping functions. The detailed processing steps can be found in the reference proposed in [49].
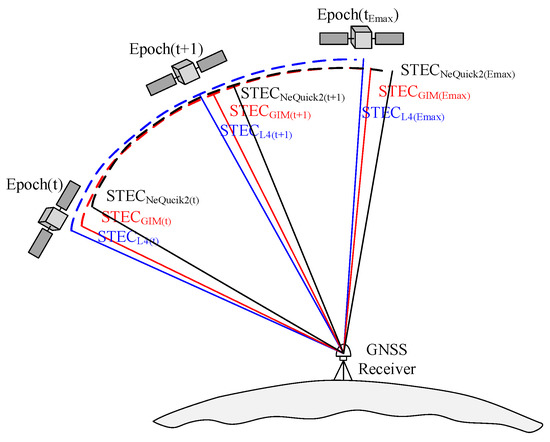
Figure 2.
Schematic diagram of the evaluation principle of dSTEC.
Generally, the accuracy of dSTEC can be better than 0.1 TECU and free from any assumption or model errors. Hence, the dSTEC assessment method is applied to evaluate the self-consistency of the NeQuick2 model in this research.
3.4. Accuracy Index
According to the NeQuick2 model, VTEC values at ionosphere pierce points with specific detection ranges can be calculated using the numerical integration method. The calculation formula can be simplified as follows:
where, and , respectively, represent the detection range corresponding to different types of ionosphere data; represents VTEC values calculated at pierce points using the NeQuick2 model for different types of ionosphere data; represents the integration of the electron density over the corresponding observation path.
Therefore, bias and standard deviation (STD) error could be utilized to quantify the accuracy of the NeQuick2 model, which can be defined as follows:
where represents the total number of VTEC values used for comparisons, and denotes the VTEC values derived from the NeQuick2 model and the mean VTEC values or reference VTEC values, respectively.
4. Results and Discussions
In this section, the above model evaluation methods are processed with various measured observation data to evaluate the accuracy and stability of the NeQuick2 model in the mid-latitudes of the northern hemisphere over a long period. The results are given through the following experiments in multiple aspects.
4.1. Data Collection
In order to present the performance of the NeQuick2 model comprehensively for a long period over the mid-latitudes of the northern hemisphere and consider the influence of multiple solar conditions, the test period is chosen from the day of the year (DOY) 001, 2008 to DOY 365, 2021. The solar condition (F10.7 index) and geomagnetic condition (Dst. index) for the period are shown in Figure 3. As can be seen from the figure, this solar cycle contains low, medium, and high solar conditions. In addition, it should be noted that there is a super geomagnetic storm near DOY 076, 2015. It has a considerable influence on the ionosphere, which has been well studied [51,52].
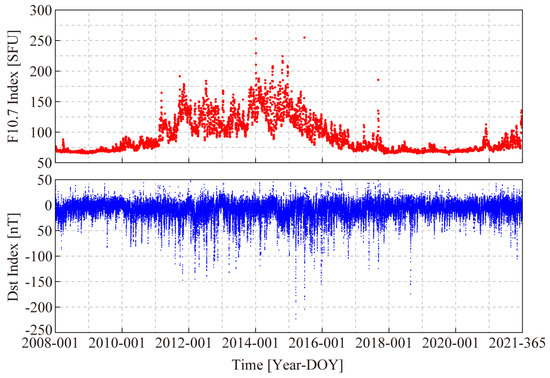
Figure 3.
Solar and geomagnetic conditions at the evaluation period.
The IGS final GIM model could serve as a reference to evaluate NeQuick2. The distribution of IGSG generation stations used in this paper is shown in the green five-pointed star in Figure 4. Although the accuracy and reliability of IGSG have been significantly improved in recent decades, its performance is related to the distribution of ground-based GNSS stations. Thus, to make the assessment more persuasive, this study also employs the dSTEC evaluation method for further assessment. The distribution of dSTEC assessment stations is also plotted in Figure 4 as red dots. As shown in the figure, the stations used for dSTEC assessment are evenly distributed over the test region and are not used to generate the IGSG model.
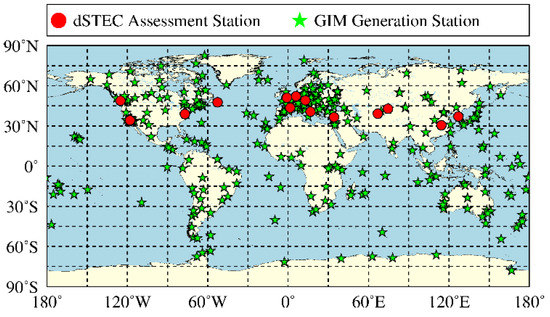
Figure 4.
Distribution of ground-based GNSS station used for assessment.
4.2. Validation with IGS Final GIM
To better understand the differences between the NeQuick2 model and IGSG, three scenarios were used to conduct the analysis. To reflect the error of projection function and focus on the application in GNSS positioning, validation experiments also pay attention to hourly and daily variations in models. The statistics of the hourly and daily results will also reflect the long-term statistic characters of the model to a certain extent.
Firstly, taking IGSG as the reference benchmark, biases of the NeQuick2 model during high solar activity and low solar activity days were analyzed. Furthermore, the average bias and standard deviation in the NeQuick2 model over a long-time period were analyzed. In addition, the average deviation between the NeQuick2 model and IGSG was calculated every two hours in one day to gain insight into the accuracy and stability of the model.
The difference of the NeQuick2 model compared with IGSG on different solar condition days over the mid-latitude region is illustrated in Figure 5. As we can see, the maximum deviation is about 30 TECU on high solar condition days, while the value is about 15 TECU on low solar condition days. The maximum values mainly appear at the lower latitudes and fluctuate with the sun activities. The maximum negative difference is about −10 TECU over other regions. The results indicate that the NeQuick2 model underestimated the TEC values on low and high solar condition days except the region with high solar conditions compared with IGSG.
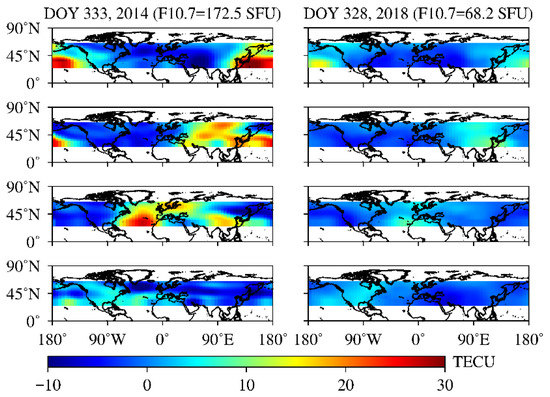
Figure 5.
The differences between the NeQuick2 and IGSG on high and low solar condition days is presented above. Figures from top to bottom denote 00:00, 06:00, 12:00, and 18:00 UTC, respectively. The left and right figures present the high solar condition day and low solar condition day, respectively.
The time series of daily mean bias and standard deviation (STD) values between the NeQuick2 and IGSG are presented in Figure 6. Corresponding to the solar activity conditions in Figure 3, Figure 6 notably indicates that the variation in bias and STD values is highly related to the solar conditions. Specifically, on low solar condition days, e.g., the days from DOY 001, 2008 to DOY 001, 2011 and the days from DOY 001, 2017 to DOY 365, 2021, the biases are more stable than other periods, which are mainly concentrated around zero TECU. On the other days with medium and high solar conditions, the biases mainly range from −10 to 10 TECU. In terms of STD values, they mainly range from 2 to 6 TECU. On low solar condition days, the STD values mainly range from 2 to 3 TECU. While on high solar condition days, the STD values mainly range from 3 to 6 TECU. Meanwhile, the mean value of biases is −1.53 TECU, while the mean value of STD is 2.59 TECU.
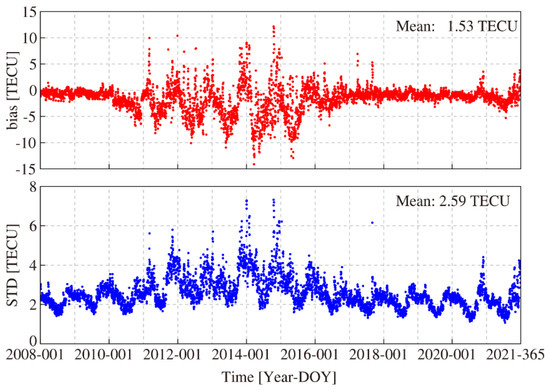
Figure 6.
Time series of NeQuick2 with respect to IGSG during the test period.
Furthermore, the average biases and STD during the whole test period of the NeQuick2 model compared every two hours with IGSG is shown in Figure 7. The result shows that the absolute bias values are smaller than two TECU from UTC 0 to 16 o’clock, while the absolute bias values are large than two TECU for UTC 18, 20, and 22 o’clock. In terms of STD values, the values are smaller than three TECU, and only a few differences exist in one day. This indicates that the accuracy of the NeQuick2 model is stable for each hour and compared with IGSG, the NeQuick2 model usually underestimates the TEC values at the range of −1 to −2 TECU.
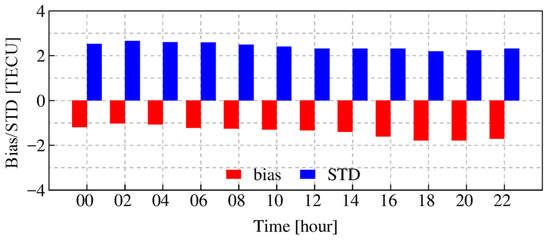
Figure 7.
Statistical results of NeQuick2 model with respect to IGSG every two hours.
4.3. Assessment of NeQuick2 Model over the Ocean
To evaluate the performance of the NeQuick2 model over the ocean, this section adopts the Jason2 satellite VTEC data to conduct targeted evaluations. Taking Jason2 VTEC as the reference value, the deviations in the VTEC values of the IGSG and the NeQuick2 model were compared and analyzed.
The Jason2 satellite had a life time from DOY 186, 2008 to DOY 273, 2019. The time series of daily mean bias and STD for IGSG and NeQuick2 model concerning Jason2 VTEC is presented in Figure 8. As we can see, the biases of IGSG and NeQuick2 model both have periodical variation related to the solar condition. For the bias time series, the variation in IGSG is mainly about 2 to 6 TECU, which is much more stable than that of the NeQuick2 model. The variation in the NeQuick2 model is mainly from −5 to 10 TECU. Significantly, for the NeQuick2 model, the biases are near zero TECU on low solar condition days, while there are more considerable variations on high solar condition days. In terms of STD values, the STD values are mainly from 2 to 3 TECU, which are better than the NeQuick2 model. The STD values of the NeQuick2 model mainly range from 2 to 8 TECU, while the values on high solar condition days are more significant than that of low solar condition days. The mean STD value is 2.09 TECU for IGSG and the mean STD value is 3.18 TECU for the NeQuick2 model, which is about 50% worse than IGSG. As mentioned above, the VTEC over the ocean area extracted from IGSG is mainly estimated by fitting of the VTEC from ground-based stations. Due to the mid-latitudes of the northern hemisphere having the densest ground-based stations, the IGSG could maintain relatively high accuracy and stability.
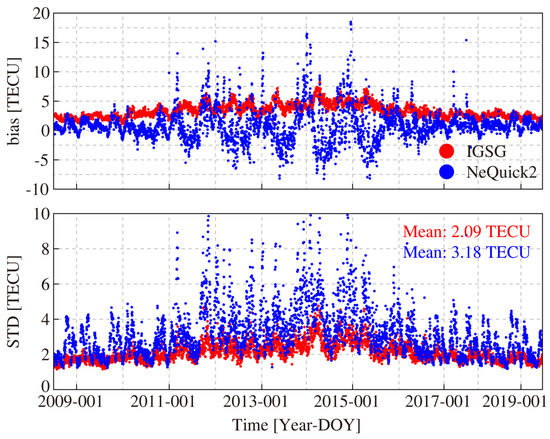
Figure 8.
Time series of IGSG and NeQuick2 with respect to Jason2 VTEC during the test period.
It is also worth noting that the outputs of the ionosphere simulation function used by the NeQuick2 model is related to solar activity as well as latitude and longitude. However, the Jason2 satellite has a revisit cycle of about 10 days. There would exist small changes in latitudes and latitudes when the Jason2 satellite revisits the adjacent orbits after 10 days, and most importantly, during 2011 to 2015, the Sun is in a period of high solar activity. As a result, during this period, there exists large biases for NeQuick2 model as compared to Jason2.
Figure 9 presents the mean deviation between Jason2 VTEC and IGSG and the NeQuick2 model over the mid-latitude region in high solar condition year (2014) and low solar condition year (2018). The results show that the bias of IGSG is more significant than that of the NeQuick2 model. The deviation values mainly range from 4 to 8 TECU for IGSG in high solar condition years, and the values would be 2 to 4 TECU in low solar condition years. In terms of the NeQuick2 model, the deviation values mainly range from 0 to 4 TECU in high solar condition years and 0 to 2 TECU in low solar condition years.
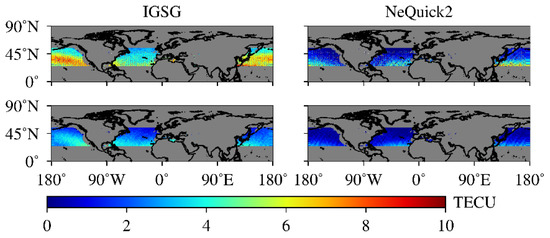
Figure 9.
The distribution of the mean deviations of the IGSG and NeQuick2 model with respect to the reference of Jason2 VTEC. Figures from top to bottom denote high solar condition year and low solar condition year, respectively.
Moreover, the Jason2 VTEC does not include the electron content on the path from Jason2 altitude to GNSS satellite altitude. Thus, compared with Jason2 VTEC, the IGSG always overestimate the TEC values in years of high or low solar conditions. Besides, the mean value of the NeQuick2 model is near the same as Jason2 VTEC.
Furthermore, the statistical result of the IGSG and NeQuick2 model concerning Jason2 VTEC for each year is plotted in Figure 10. As we can see, the average bias of IGSG for each year is more significant than that of the NeQuick2 model. However, the STD values are more stable for IGSG, and the variation is related to the solar condition. In terms of the NeQuick2 model, the maximum STD value would be more significant than four TECU, and it is about three TECU for IGSG.
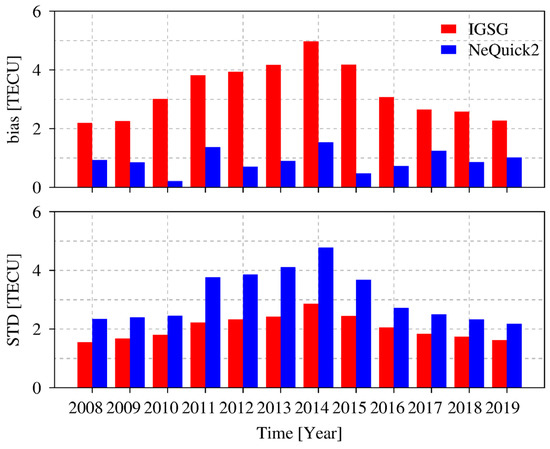
Figure 10.
Statistical results of IGSG and NeQuick2 with respect to Jason2 VTEC for each year.
In Figure 8, it can be clearly seen that the IGSG is always overestimating VTEC values compared to Jason2. This is in line with expectations since Jason2 is not measuring TEC up to a GPS satellite height. This is different with IGSG, as the biases of NeQuick2 fluctuate relatively more dramatically compared to Jason2, although the average biases of NeQuick2 is smaller than that of IGSG. This is also reasonable since NeQuick2 is constructed based on the monthly average representations of ionosphere. According to the comparison present in Figure 10, it is found that NeQuick2 is also overestimating VTEC values on average compared to Jason2. To illustrate the specific differences, the year 2012 is taken as an example. Detailed biases comparison results of the year 2012 are shown in Figure 11.
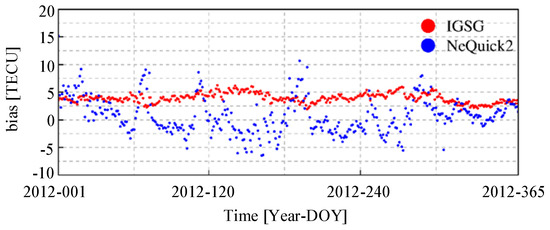
Figure 11.
Daily average biases of IGSG and NeQuick2 with respect to Jason2 VTEC during the year 2012.
As can be seen from Figure 11, in 2012, the VTEC values of NeQuick2 model are greater than the VTEC values obtained by Jason2 in most cases. The VTEC biases of NeQuick2 with respect to Jason2 mainly range from −5 to 10 TECU, and the average value of them is above zero, which means that the NeQuick2 model also overestimates the VTEC value on average in mid-latitudes.
Furthermore, to analyze the overestimation and underestimation VTEC proportion of NeQuick2 compared to Jason2 in long-term, statistical characters in each year have been summarized in Table 2. As can be seen from Table 2, compared with Jason2 VTEC values, both the proportions and average values of the NeQuick2 overestimation are smaller than those of the NeQuick2 underestimation. Even though the results of the NeQuick2 underestimation are more concentrated as shown in Figure 8, at long-term, NeQuick2 is also overestimating the VTEC on average.

Table 2.
Bias Statistical characters of NeQuick2 with respect to Jason2 from 2008 to 2019.
4.4. Self-Consistency Evaluation
To further validate the accuracy of ionosphere models, the dSTEC method is used to evaluate the self-consistency of the IGSG and NeQuick2 models.
The statistical results assessed by the dSTEC method for IGSG and the NeQuick2 model are shown in Figure 12. Results show that the variation in bias for IGSG is more stable than that of the NeQuick2 model. The variation in bias for IGSG is around 0 to 1 TECU. The value is −3 to 3 TECU on a high solar condition day and −1 to 0 TECU on a low solar condition day for the NeQuick2 model. On the other side, the STD value of IGSG is smaller than that of the NeQuick2 model, and the variation is related to the solar condition. The variation in STD for the IGSG and NeQuick2 model mainly ranges from 0.50 to 2 and 1 to 3 TECU, respectively. The mean STD value is 0.86 and 1.52 TECU for IGSG and NeQuick2 model, respectively.
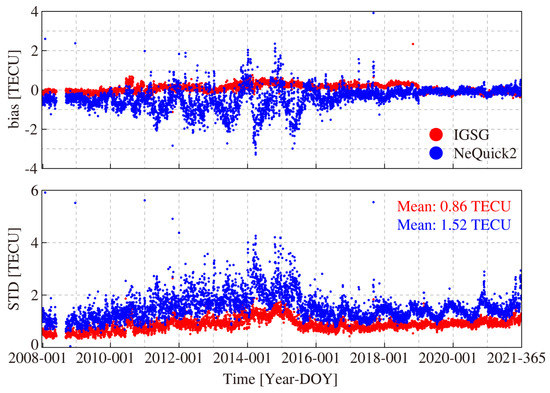
Figure 12.
The time series of IGSG and NeQuick2 were assessed by the dSTEC method during the test period.
The statistical STD of IGSG and NeQuick2 models for the different ground-based stations is illustrated in Figure 13. The figure indicates that the STD values of IGSG are smaller than 1.50 TECU, and most of them are smaller than one TECU. In terms of the NeQuick2 model, the STD values mainly range from 1 to 2 TECU and have a considerable variation for different stations.
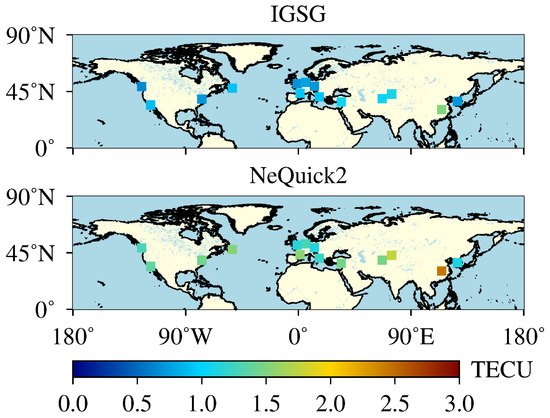
Figure 13.
The STD of dSTEC assessment results of each station for IGSG and NeQuick2 during the test period.
5. Conclusions
As the representative three-dimensional empirical model, NeQuick2 can be employed to calculate the total electron content along a specific LoS at any given altitude, which can overcome the limitations of the commonly used two-dimensional models. Meanwhile, with the increasing demands for ionosphere physics research and the continuous expansion of space geodetic applications, it is necessary to evaluate the long-term accuracy of three-dimensional ionosphere models. Long-term accuracy analysis in mid-latitudes could minimize the impact of occasional extreme weather conditions on the statistical characters of the empirical model and most ground-based stations are located in the mid-latitudes of northern hemisphere. Therefore, understanding the accuracy of the NeQuick2 model over the mid-latitudes of the northern hemisphere in long-term is of great importance. Hence, the accuracy assessments have been made from 2008 to 2021 by different methods, such as the comparison with IGSG and Jason2 VTEC, self-consistency evaluation method, and so forth. The assessment results are listed as follows:
- (1)
- The comparison with IGSG shows that the maximum deviation can be about 30 TECU on high solar condition days, which mainly appear at the lower latitudes and fluctuates with the sun activities. Moreover, the maximum deviation is about 15 TECU on low solar condition days. In addition, the STD values mainly range from 2 to 6 TECU, with a mean STD value of 2.59 TECU. For different hours, the absolute bias is smaller than two TECU from UTC 0 to 16 o’clock, while the absolute value will be larger than two TECU for UTC 18, 20, and 22 o’clock. In terms of STD values, the values are mainly smaller than three TECU, and there are few differences between hours.
- (2)
- Compared with Jason2, the accuracy of the IGSG and NeQuick2 model over ocean regions shows that the bias of IGSG is more significant than that of the NeQuick2 model. In addition, the difference between IGSG and NeQuick2 model has a periodical variation, which is highly related to the solar condition. The mean STD value is 2.09 TECU for IGSG. and the mean STD value is 3.18 TECU for the NeQuick2 model, which is about 50% worse than IGSG. The maximum STD value would be more significant than four TECU in high solar condition years for the NeQuick2 model, and the corresponding value is about eight TECU for IGSG.
- (3)
- The dSTEC assessment results indicate that the variation in the biases for IGSG is more stable than that of the NeQuick2 model. In addition, the STD value of IGSG is smaller than that of the NeQuick2 model. The mean STD value is 0.86 and 1.52 TECU for IGSG and NeQuick2 model, respectively. The statistical STD values of the IGSG and NeQuick2 model for different ground-based stations indicate that the STD value of IGSG is smaller than 1.50 TECU, and most of them are smaller than one TECU. In terms of the NeQuick2 model, the STD value mainly ranges from 1 to 2 TECU and has a notable variation for different stations.
The long-term analysis results show that the NeQuick2 model could represent the average TEC of the ionosphere. Compared with the IGSG, the NeQuick2 model always underestimates TEC value, especially in low solar activity periods. And compared with Jason2, The TEC values obtained by the NeQuick2 model are overestimated, but the degree of overestimation is smaller than that of IGSG. The results can provide a reference for the performance of the NeQuick2 model in practical application.
Author Contributions
Conceptualization, E.W.; Funding acquisition, E.W.; Investigation, Z.S.; Methodology, L.W.; Software, L.W.; Validation, S.X.; Writing—original draft, L.W.; Writing—review & editing, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Scholarship Council (No. 201806270184), National Natural Science Foundation of China (No. 41874036), Education Commission of Hubei Province of China (Grant No. Q20212801), Open Research Fund Program of the Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, China (Grant No. 20-01-03, 21-01-04).
Acknowledgments
The authors would like to thank the Telecommunications/ICT for Development (T/ICT4D) Laboratory of the Abdus Salam International Centre for Theoretical Physics, Trieste, Italy for providing the open source calculation code, and IGS (International GNSS Service) for providing global GNSS observation data and navigation data. NOAA is also acknowledged for providing Jason2 VTEC observation data. The numerical calculations in this paper have been done on the supercomputing system in the Supercomputing Center of Wuhan University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Su, K.; Jin, S. Three Dual-Frequency Precise Point Positioning Models for the Ionospheric Modeling and Satellite Pseudorange Observable-Specific Signal Bias Estimation. Remote Sens. 2021, 13, 5093. [Google Scholar] [CrossRef]
- Scherliess, L.; Schunk, R.W.; Sojka, J.J.; Thompson, D.C. Development of a physics-based reduced state Kalman filter for the ionosphere. Radio Sci. 2004, 39, 1–12. [Google Scholar] [CrossRef]
- Schunk, R.W.; Scherliess, L.; Sojka, J.J.; Thompson, D.C.; Anderson, D.N.; Codrescu, M.; Minter, C.; Fuller-Rowell, T.J.; Heelis, R.; Hairston, M.; et al. Global Assimilation of Ionospheric Measurements (GAIM). Radio Sci. 2004, 39, 1–11. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.; Sanz, J. New approaches in global ionospheric determination using ground GPS data. J. Atmos. Sol.-Terr. Phys. 1999, 61, 1237–1247. [Google Scholar] [CrossRef]
- Feltens, J. Development of a new three-dimensional mathematical ionosphere model at European Space Agency/European Space Operations Centre. Space Weather 2007, 5. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Xu, P.; Han, W.; Ge, M.; Shi, C. Eliminating negative VTEC in global ionosphere maps using inequality-constrained least squares. Adv. Space Res. 2013, 51, 988–1000. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. SHPTS: Towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2015, 89, 331–345. [Google Scholar] [CrossRef]
- Leitinger, R.; Zhang, M.L.; Radicella, S.M. An improved bottomside for the ionospheric electron density model NeQuick. Ann. Geophys. 2009, 48. [Google Scholar] [CrossRef]
- Nava, B.; Coïsson, P.; Radicella, S. A new version of the NeQuick ionosphere electron density model. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Zhang, Y.; Mertens, C.J.; Truhlik, V.; Richards, P.; McKinnell, L.-A.; Reinisch, B.W. The International Reference Ionosphere 2012—A model of international collaboration. J. Sp. Weather Space Clim. 2014, 4, A07. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Sp. Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Prol, F.; Hoque, M. Topside Ionosphere and Plasmasphere Modelling Using GNSS Radio Occultation and POD Data. Remote Sens. 2021, 13, 1559. [Google Scholar] [CrossRef]
- Liu, T.; Yu, Z.; Ding, Z.; Nie, W.; Xu, G. Observation of Ionospheric Gravity Waves Introduced by Thunderstorms in Low Latitudes China by GNSS. Remote Sens. 2021, 13, 4131. [Google Scholar] [CrossRef]
- Nina, A. Modelling of the Electron Density and Total Electron Content in the Quiet and Solar X-ray Flare Perturbed Ionospheric D-Region Based on Remote Sensing by VLF/LF Signals. Remote Sens. 2021, 14, 54. [Google Scholar] [CrossRef]
- Feltens, J.; Angling, M.; Jackson-Booth, N.; Jakowski, N.; Hoque, M.; Hernández-Pajares, M.; Aragon-Angel, A.; Orús, R.; Zandbergen, R. Comparative testing of four ionospheric models driven with GPS measurements. Radio Sci. 2011, 46, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Gulyaeva, T.L.; Huang, X.; Reinisch, B.W. Plasmaspheric extension of topside electron density profiles. Adv. Sp. Res. 2002, 29, 825–831. [Google Scholar] [CrossRef]
- Bilitza, D.; McKinnell, L.-A.; Reinisch, B.; Fuller-Rowell, T. The international reference ionosphere today and in the future. J. Geod. 2011, 85, 909–920. [Google Scholar] [CrossRef]
- Zakharenkova, I.; Cherniak, I.; Krankowski, A.; Shagimuratov, I. Vertical TEC representation by IRI 2012 and IRI Plas models for European midlatitudes. Adv. Sp. Res. 2014, 55, 2070–2076. [Google Scholar] [CrossRef]
- Adewale, A.; Oyeyemi, E.; Cilliers, P.; McKinnell, L.; Adeloye, A. Low solar activity variability and IRI 2007 predictability of equatorial Africa GPS TEC. Adv. Sp. Res. 2012, 49, 316–326. [Google Scholar] [CrossRef]
- Olawepo, A.; Adeniyi, J.; Oluwadare, E. TEC variations and IRI-2012 performance at equatorial latitudes over Africa during low solar activity. Adv. Sp. Res. 2017, 59, 1800–1809. [Google Scholar] [CrossRef]
- Patel, N.; Karia, S.; Pathak, K. Comparison of GPS-derived TEC with IRI-2012 and IRI-2007 TEC predictions at Surat, a location around the EIA crest in the Indian sector, during the ascending phase of solar cycle 24. Adv. Sp. Res. 2016, 60, 228–237. [Google Scholar] [CrossRef]
- Wan, Q.; Ma, G.; Li, J.; Wang, X.; Fan, J.; Li, Q.; Lu, W. A comparison of GPS-TEC with IRI-TEC at low latitudes in China in 2006. Adv. Sp. Res. 2017, 60, 250–256. [Google Scholar] [CrossRef]
- Adebesin, B.; Ikubanni, S.; Adebiyi, S.; Joshua, B. Multi-station observation of ionospheric disturbance of March 9 2012 and comparison with IRI-model. Adv. Sp. Res. 2013, 52, 604–613. [Google Scholar] [CrossRef]
- Oyeyemi, E.; Adewale, A.; Adeloye, A.; Olugbon, B. An evaluation of the IRI-2007 storm time model at low latitude stations. Adv. Sp. Res. 2013, 52, 1737–1747. [Google Scholar] [CrossRef]
- Sharma, D.; Aggarwal, M.; Bardhan, A. Variability of ionospheric parameters during solar minimum and maximum activity and assessment of IRI model. Adv. Sp. Res. 2017, 60, 435–443. [Google Scholar] [CrossRef]
- Klenzing, J.; Simões, F.; Ivanov, S.; Bilitza, D.; Heelis, R.; Rowland, D. Performance of the IRI-2007 model for equatorial topside ion density in the African sector for low and extremely low solar activity. Adv. Sp. Res. 2013, 52, 1780–1790. [Google Scholar] [CrossRef] [Green Version]
- Jamjareegulgarn, P.; Supnithi, P.; Hozumi, K.; Tsugawa, T. Study of ionospheric topside variations based on NeQuick topside formulation and comparisons with the IRI-2012 model at equatorial latitude station, Chumphon, Thailand. Adv. Sp. Res. 2017, 60, 206–221. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Liu, L.; Wan, W.; Ning, B. Comparison of the observed topside ionospheric and plasmaspheric electron content derived from the COSMIC podTEC measurements with the IRI_Plas model results. Adv. Sp. Res. 2017, 60, 222–227. [Google Scholar] [CrossRef]
- Coisson, P.; Radicella, S.M.; Nava, B.; Leitinger, R. Low and equatorial latitudes topside in NeQuick. J. Atmos. Sol.-Terr. Phys. 2008, 70, 901–906. [Google Scholar] [CrossRef]
- Montenbruck, O.; Rodriguez, B.G. NeQuick-G performance assessment for space applications. GPS Solut. 2020, 24, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Yuan, Y.; Li, Z.; Li, Y.; Huo, X.; Li, M. An examination of the Galileo NeQuick model: Comparison with GPS and JASON TEC. GPS Solut. 2016, 21, 605–615. [Google Scholar] [CrossRef]
- Migoya-Orué, Y.; Folarin-Olufunmilayo, O.; Radicella, S.; Alazo-Cuartas, K.; Rabiu, A. Evaluation of NeQuick as a model to characterize the Equatorial Ionization Anomaly over Africa using data ingestion. Adv. Sp. Res. 2017, 60, 1732–1738. [Google Scholar] [CrossRef]
- Ahoua, S.M.; Habarulema, J.B.; Obrou, O.K.; Cilliers, P.J.; Zaka, Z.K. Evaluation of the NeQuick model performance under different geomagnetic conditions over South Africa during the ascending phase of the solar cycle (2009–2012). Ann. Geophys. 2018, 36, 1161–1170. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Wang, Z.; An, J.; Liu, J.; Wang, N.; Li, H. Influence of spatial gradients on ionospheric mapping using thin layer models. GPS Solut. 2018, 22, 2. [Google Scholar] [CrossRef]
- Chen, J.; Ren, X.; Zhang, X.; Zhang, J.; Huang, L. Assessment and Validation of Three Ionospheric Models (IRI-2016, NeQuick2, and IGS-GIM) From 2002 to 2018. Sp. Weather 2020, 18, e2019SW002422. [Google Scholar] [CrossRef]
- Liu, A.; Wang, N.; Li, Z.; Wang, Z.; Yuan, H. Assessment of NeQuick and IRI-2016 models during different geomagnetic activities in global scale: Comparison with GPS-TEC, dSTEC, Jason-TEC and GIM. Adv. Sp. Res. 2019, 63, 3978–3992. [Google Scholar] [CrossRef]
- Cherniak, I.; Zakharenkova, I. NeQuick and IRI-Plas model performance on topside electron content representation: Spaceborne GPS measurements. Radio Sci. 2016, 51, 752–766. [Google Scholar] [CrossRef] [Green Version]
- Okoh, D.; Onwuneme, S.; Seemala, G.; Jin, S.; Rabiu, B.; Nava, B.; Uwamahoro, J. Assessment of the NeQuick-2 and IRI-Plas 2017 models using global and long-term GNSS measurements. J. Atmos. Sol.-Terr. Phys. 2018, 170, 1–10. [Google Scholar] [CrossRef]
- Pignalberi, A.; Giannattasio, F.; Truhlik, V.; Coco, I.; Pezzopane, M.; Consolini, G.; De Michelis, P.; Tozzi, R. On the Electron Temperature in the Topside Ionosphere as Seen by Swarm Satellites, Incoherent Scatter Radars, and the International Reference Ionosphere Model. Remote Sens. 2021, 13, 4077. [Google Scholar] [CrossRef]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C.; et al. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2018, 92, 691–706. [Google Scholar] [CrossRef] [Green Version]
- Wielgosz, P.; Milanowska, B.; Krypiak-Gregorczyk, A.; Jarmołowski, W. Validation of GNSS-derived global ionosphere maps for different solar activity levels: Case studies for years 2014 and 2018. GPS Solutions 2021, 25, 1–15. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Imel, D. Evaluation of the TOPEX/POSEIDON dual-frequency ionosphere correction. J. Geophys. Res. Earth Surf. 1994, 99, 24895–24906. [Google Scholar] [CrossRef]
- Li, M.; Zhang, B.; Yuan, Y.; Zhao, C. Single-frequency precise point positioning (PPP) for retrieving ionospheric TEC from BDS B1 data. GPS Solut. 2018, 23, 18. [Google Scholar] [CrossRef]
- Hu, A.; Li, Z.; Carter, B.; Wu, S.; Wang, X.; Norman, R.; Zhang, K. Helmert-VCE-aided fast-WTLS approach for global ionospheric VTEC modelling using data from GNSS, satellite altimetry and radio occultation. J. Geodesy 2018, 93, 877–888. [Google Scholar] [CrossRef]
- Jee, G.; Schunk, R.W.; Scherliess, L. Analysis of TEC data from the TOPEX/Poseidon mission. J. Geophys. Res. Earth Surf. 2010, 109. [Google Scholar] [CrossRef]
- Jee, G.; Lee, H.-B.; Kim, Y.H.; Chung, J.-K.; Cho, J. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: Ionospheric perspective. J. Geophys. Res. Sp. Phys. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Orus, R.; Cander, L.R.; Hernández-Pajares, M. Testing regional vertical total electron content maps over Europe during the 17–21 January 2005 sudden space weather event. Radio Sci. 2007, 42, 1–12. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X.; Freeshah, M. Performance evaluation of real-time global ionospheric maps provided by different IGS analysis centers. GPS Solut. 2019, 23, 1–17. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Roma-Dollase, D.; Krankowski, A.; García-Rigo, A.; Orús-Pérez, R. Methodology and consistency of slant and vertical assessments for ionospheric electron content models. J. Geod. 2017, 91, 1405–1414. [Google Scholar] [CrossRef]
- Jin, S.; Jin, R.; Kutoglu, H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J. Geod. 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Ray, S.; Roy, B.; Paul, K.S.; Goswami, S.; Oikonomou, C.; Haralambous, H.; Chandel, B.; Paul, A. Study of the effect of 17–18 March 2015 geomagnetic storm on the Indian longitudes using GPS and C/NOFS. J. Geophys. Res. Sp. Phys. 2017, 122, 2551–2563. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).