Quadrotor Autonomous Navigation in Semi-Known Environments Based on Deep Reinforcement Learning ^†

Abstract

In the application scenarios of quadrotors, it is expected that only part of the obstacles can be identified and located in advance. In order to make quadrotors fly safely in this situation, we present a deep reinforcement learning-based framework to realize autonomous navigation in semi-known environments. Specifically, the proposed framework utilizes the dueling double deep recurrent Q-learning, which can implement global path planning with the obstacle map as input. Moreover, the proposed framework combined with contrastive learning-based feature extraction can conduct real-time autonomous obstacle avoidance with monocular vision effectively. The experimental results demonstrate that our framework exhibits remarkable performance for both global path planning and autonomous obstacle avoidance.

1. Introduction

With the development of unmanned aerial vehicle (UAV) technology, the application field of UAV has also expanded. As the quadrotor is one of the most widely used kinds of UAVs, its applications, such as searching, tracking and transportation, require it to fly safely in cities, forests, and other non-clearance areas. Thus, autonomous flight capability becomes more and more critical, leading massive research work efforts to achieve it. In all the quadrotor operation scenarios, semi-known environments with part of the obstacles identified and located are commonly encountered. For instance, the general navigation map may mark all the buildings and mountains, ignoring details such as trees or billboards. The effective autonomous flight of the quadrotor needs to make a reasonable response to the unknown obstacles encountered while making efficient use of prior known environmental information. Therefore, global path planning and autonomous obstacle avoidance are both indispensable for safe flight.

Global path planning methods utilize the environmental information to generate a feasible path to guide the quadrotor from the starting position to the goal position. The commonly used global path planning algorithms such as Dijkstra [1] and rapidly-exploring random tree (RRT) [2] are widely applied in quadrotors and robots. However, the successful implementation of these algorithms requires that the environment model is established based on the environmental information in advance. Moreover, the computational complexity of these methods is directly related to the complexity of the environment.

Autonomous obstacle avoidance methods are used to deal with the obstacle en-countered without prior information. These methods update the nearby environment observation based on the on-board sensor information and decide obstacle avoidance action on top of these observations. Methods based on simultaneous localization and mapping (SLAM) [3,4,5] have achieved remarkable results. In [6], The proposed SLAM algorithm covers the entire areas with obstacles after 1000 iterations, while a random-based algorithm mapped only the 87% after 5000 iterations. In [7], the robot avoided the two pedestrians through the proposed obstacle avoidance design and returned back to home position in the test. In [8], the experiments showed that the proposed algorithm could successfully identify and avoid moving and static obstacles of different quantities. The SLAM-based methods have successfully been applied in many quadrotors and robots. However, they may cease to be effective when faced with unlisted/untextured obstacles and require extensive computing resources for the on-board processor [9].

The development of deep reinforcement learning [10,11,12] provides a new way for global path planning and obstacle avoidance. Deep reinforcement learning results in the global path planning not requiring a detailed environment model and for invalid paths to be explored. For obstacle avoidance, deep reinforcement learning-based methods can function on pixel-level data directly, significantly reducing the computational pressure, for it no longer relies on real-time feature matching. However, previous research has usually considered that environmental obstacles are either completely known or completely unknown. Then, only global path planning or autonomous obstacle avoidance is studied separately. But the single solution of the two problems is not enough to support the quadrotor to fly effectively and safely in semi-known environments.

In order to effectively solve the problem of safe flight in semi-known environments, it is necessary to propose feasible and easy-to-use global path planning and autonomous obstacle avoidance methods, considering the application characteristics of quadrotors. In this paper, a decision framework based on dueling double deep recurrent Q network (D3RQN) is proposed. The global path planning and autonomous obstacle avoidance can be both solved on top of the proposed framework. When applied to global path planning, the trained model can take the obstacle map as input, generating a possible path from starting position to the goal position without collision detection during planning. Moreover, an unsupervised contrastive learning based perception module is proposed in this paper. After adding the pre-processing perception module trained with unsupervised contrast learning, the model can be successfully applied in monocular vision-based autonomous obstacle avoidance. The models are trained in multiple simulation scenarios, and the trained models validate the effectiveness in evaluation.

2. Related Works

Learning-based Global Path Planning. Traditional global path planning methods transform observations of global environments into detailed environment models. Then, various path planning algorithms are applied to these models. Although the global path planning is based on known environmental conditions, the modeling process is still time-consuming and laborious. Due to the development of deep reinforcement learning, researchers have proposed a series of global path planning methods to avoid cumbersome environment modeling and improve algorithm execution efficiency. In [13], a novel learning-based algorithm is proposed for planetary rovers, which can plan paths directly from orbital images with a success rate of more than 92%. Motion Planning Networks (MPNet) [14] uses neural networks to learn general near-optimal heuristics for path planning in seen and unseen environments. MPNet was evaluated to plan motion for a Baxter robot in several challenging and cluttered environments, and the success rate was 87.8%, which is about 5% higher than other solvers such as batch informed trees. Yu et al. [15] proposed a learning-based end-to-end path planning algorithm with safety constraints, which achieved the average success rate of 94.4% in three different simulation scenarios. In [16], a novel end-to-end neural network architecture called a three-dimensional path planning network (TDPP-Net) is proposed to realize DNN-based 3D path planning, which requires a large number of data with labeled optimal actions to implement supervised imitation learning. The researches mentioned above have made good progress in global path planning, but they consider that all obstacles are known globally, which is difficult in practical application.

Perception With Monocular Vision. For conducting effective obstacle avoidance in a semi-known environment, it is essential to perceive the obstacles that are not on the map. Quadrotors are usually equipped with monocular cameras to sense surrounding environments. And the depth estimation method is often used to improve the perception ability of the monocular camera. Research based on supervised learning-based depth estimation [17,18,19,20,21] trains depth estimation networks using external supervision signals. These signals are generated from the groundtruth of the scene depth information obtained by external sensors, such as Kinetic, LIDAR, etc. Since the datasets with groundtruth are usually difficult to obtain, semi-supervised learning [22] and unsupervised/self-supervised learning [23,24,25,26] based depth estimation methods are proposed. These studies adopt the view consistency from different perspectives as supervision to train the depth estimation model, which avoids the tedious preparation process of data with groundtruth. However, the data preparation still requires left-right consistency, sequence consistency, or other prerequisites, limiting the form of training data.

Contrastive Learning For Visual Representation. Contrastive learning methods extract low-dimensional features from high-dimensional observations by maximizing the feature similarity between the positive samples and minimizing that of the negative ones. Based on the extracted features, the follow-up tasks can get better data efficiency. In multiple detection and segmentation tasks, Momentum Contrast (MoCo) [27,28] achieved improved efficiency than its ImageNet supervised counterpart in seven detection or segmentation tasks. In [29], the accuracy of the linear classifier trained on self-supervised representations matches the performance of the supervised pre-training representations. Laskin et al. [30] extracts high-level features from raw pixels using contrastive learning and performs off-policy control on top of the extracted features, achieving state of-the-art data-efficiency on pixel-based RL tasks across several benchmark environments in Atari. However, previous researches mainly focused on solving tasks like classification or recognition rather than environmental perception.

Reinforcement Learning For Obstacle Avoidance. Researchers adopt deep reinforcement learning algorithms to learn the obstacle avoidance policy. These studies train agents to operate obstacle avoidance actions on top of high dimensional observation of the surrounding environments. Some of those studies [31,32,33] adopt end-to-end architecture. Although the sensor types and specific model structures are different in those studies, they make obstacle avoidance decisions directly based on sensor data. Some other methods [34,35,36,37] consider obstacle avoidance as a combination of two actions, perception and decision-making. They process the raw sensor data to obtain the by-products such as depth estimation and semantic segmentation, and then make decisions based on them. However, different from the method proposed in this paper, none of them applies unsupervised contrastive learning to obstacle avoidance.

3. Proposed Method

To realize autonomous navigation in semi-known environments, this paper divides the semi-known environment into known and unknown parts, and proposes solutions respectively. Global path planning is used to deal with the known obstacles, and autonomous obstacle avoidance is for the unknown parts. In this section, we present the Dueling Double Deep Recurrent Q-learning, which can solve these two problems.

3.1. Dueling Double Deep Recurrent Q-Learning

For the global path planning problem, we assume that all obstacles are known, and the problem can be regarded as a Markov decision process (MDP). However, considering the limited observational ability of the on-board fixed monocular camera, the quadrotor autonomous obstacle avoidance can only be treated as a partially observable Markov decision process (POMDP). Thus, the proposed dueling double deep recurrent Q-learning is required to work on both MDP and POMDP.

3.1.1. Problem Formulation

The path planning and obstacle avoidance problem in this paper are defined as tuple $⟨\mathcal{S},\mathcal{A},\mathcal{T},\mathcal{R},\mathsf{\Omega },\mathcal{O}⟩$. Here $\mathcal{S}$ is the set of states, referred to the system state space. $\mathcal{A}$ is the set of actions, referred to the action space of the quadrotor. $\mathcal{T}$ is the set of transitions, which describes how the state updates according to the chosen action and current state. $\mathcal{R}$ is the set of rewards obtained by the agent for executing each action. Here $\mathsf{\Omega }$ is the set of observations, referred to the global environment information for global path planning or sensor information for obstacle avoidance, while $\mathcal{O}$ is the set of the probability distributions. At each time step $t$, the agent receives the observation $o_t\in \mathsf{\Omega }$, the proposed action $a_t\in \mathcal{A}$ and the reward $r_t$ that given by the reward function $\mathcal{R}\left(s_t,a_t\right)$. The system generates a new state $s_{t+1}$ according to the transition model $\mathcal{T}\left(s_{t+1}|s_t,a_t\right)$, while the agent updates the observation to $o_{t+1}$.

In global path planning, the observation $o_t$ equals the state $s_t$. The action $a_t$ can be sampled from the policy $\pi =P(a_t|s_t)$. The expectation of accumulative reward can be approximated by action-state-value function $Q(s_t,a_t)$. The solution is the optimal policy $\pi$, which maximizes the accumulative future reward $\mathbb{E}\left[{\displaystyle \sum _t^{\infty }{\gamma }^t}R\left(s_t,a_t\right)\right]$, where $\gamma$ is the discount factor. The optimal Q-value function can be computed using the Bellman equation

$$Q^{*}\left(s_t,a_t\right)={\mathbb{E}}_{s_{t+1}}\left[r_t+\gamma {\max }_{a_{t+1}}{Q}^{*}\left(s_{t+1},a_{t+1}\right)|s_t,a_t\right]$$

(1)

For POMDP like obstacle avoidance with monocular vision, the observation $o_t$ can not represent the whole picture of the system state $s_t$, leading the estimating Q-value $Q(o_t,a_t|\pi )\ne Q(s_t,a_t|\pi )$. Therefore, in this paper, the recurrency mechanism is adopted for extracting useful environment information from sequential observations, making a good estimation of the state $s$ from the observation $o$.

3.1.2. Network Structure

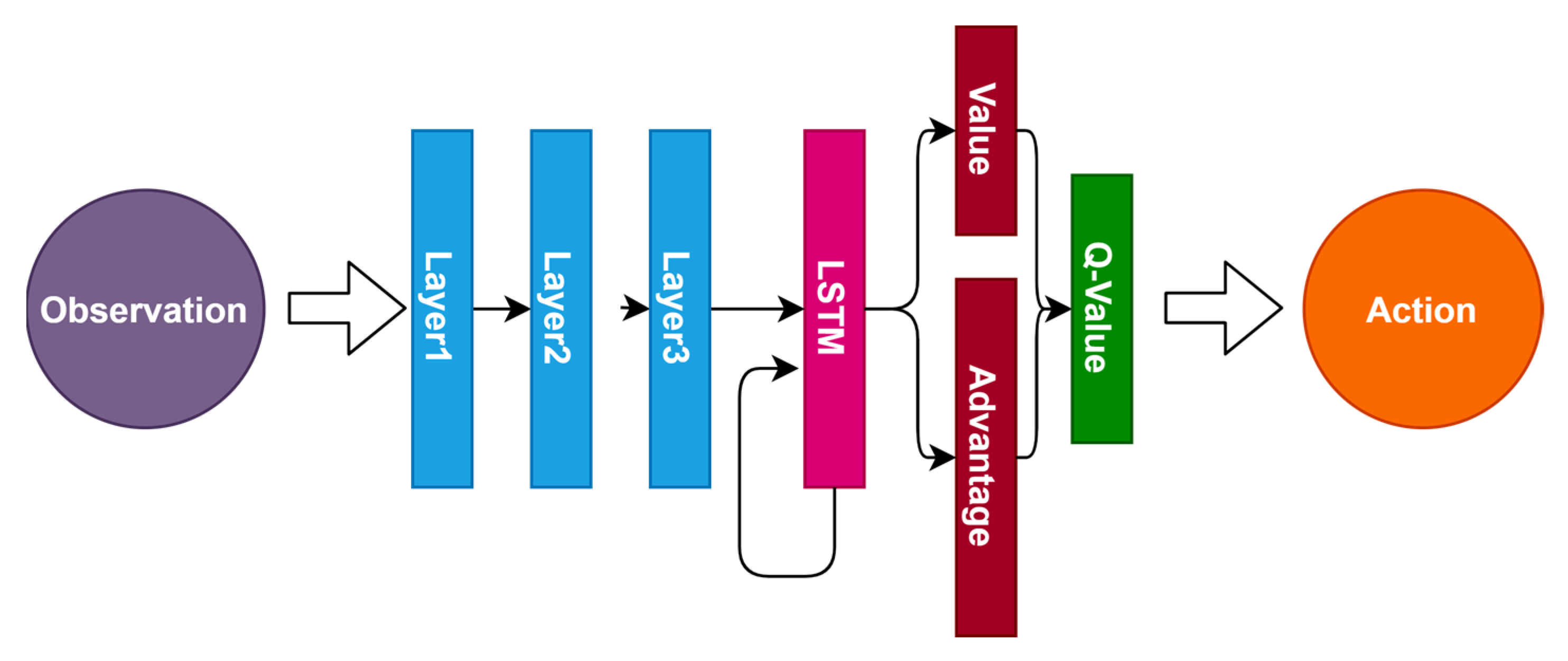
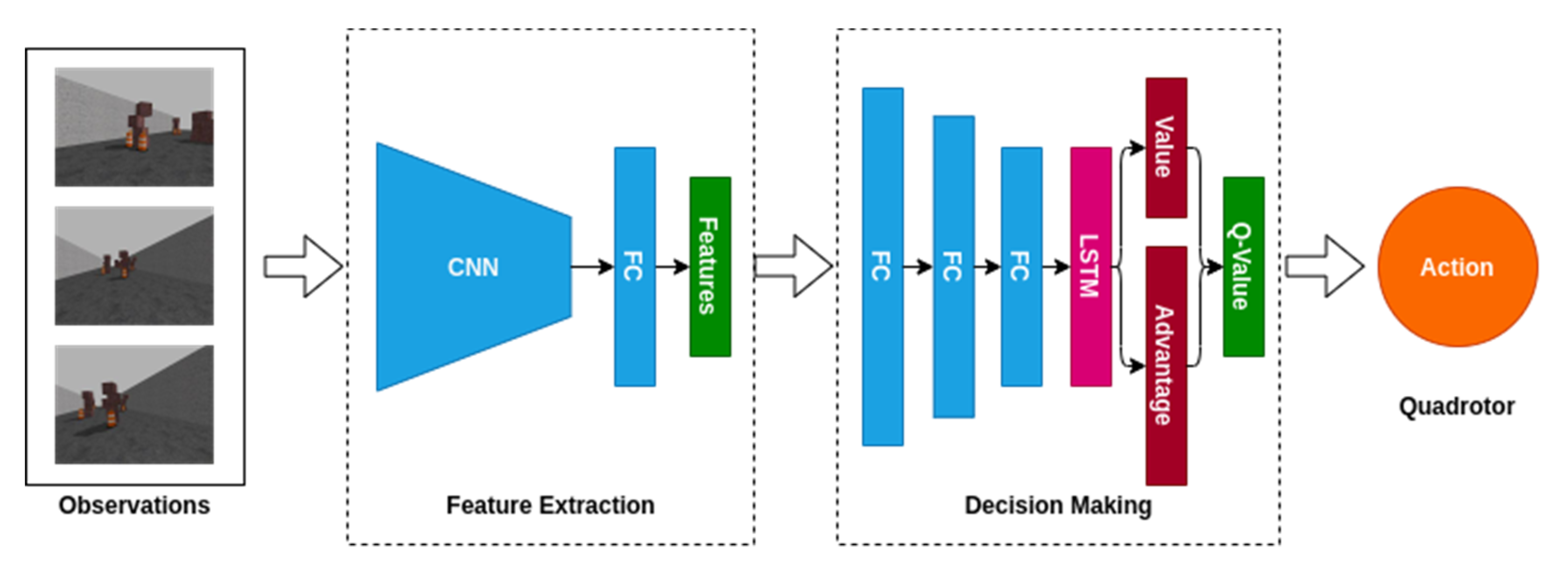
Researchers have proposed the deep recurrent Q network (DRQN) [38] by augmenting a recurrency to DQN which can effectively improve the performance of the agent in POMDP. Moreover, the dueling and double technology [39,40] have been proved to improve the performance and training speed, while solving the problem of overoptimistic value estimation. Based on these previous research results, we proposed the Dueling Double Deep Recurrent Q Network (D3RQN) by combining the DRQN and dueling network. To be specific, one fully connected layer of the dueling network is replaced with an LSTM layer. In the D3RQN, two streams are used to compute the value and advantage functions. The first two or three layers can be either convolutional layers or fully connected layers. The network structure of the D3RQN is shown in Figure 1.

Figure 1. The network structure of the D3RQN.

3.1.3. Value Function Estimation

In the original dueling network, the Q value is constructed by the values and advantage function as follows

$$Q^{\pi }(s,a)=A^{\pi }(s,a)+V^{\pi }(s)$$

(2)

Since the state $s$ is not obtainable in a POMDP, the Q value and loss function at time $t$ is defined as

$$Q^{\pi }({\mathsf{\Omega }}_t,a_t)=A^{\pi }({\mathsf{\Omega }}_t,a_t)+V^{\pi }({\mathsf{\Omega }}_t)$$

(3)

and

$${\mathcal{ℒ}}_t(\theta )\hspace{0.17em}=\hspace{0.17em}{\mathbb{E}}_{{\mathsf{\Omega }}_t,a_t,r_t,{\mathsf{\Omega }}_{t+1}}[{(y_t^{D3RQN}\hspace{0.17em}-\hspace{0.17em}Q({\mathsf{\Omega }}_t,a_t;\theta ))}^2],$$

(4)

with

$$y_t^{D3RQN}\hspace{0.17em}=\hspace{0.17em}{r}_t\hspace{0.17em}+\hspace{0.17em}\gamma {\max }_{a_{t+1}}Q({\mathsf{\Omega }}_{t+1},a_{t+1};{\theta }^{-}),$$

(5)

where ${\mathsf{\Omega }}_t$ represents the observation sequence before time $t$, and ${\theta }^{-}$ is the parameters of a fixed and separate target network. Hence, the network can learn the value function estimation by minimizing the loss function. The policy is derived as:

$$a_t=\pi \left({\mathsf{\Omega }}_t\right)=\arg {\max }_a\widehat{Q}\left({\mathsf{\Omega }}_t,a\right)$$

(6)

3.2. Global Path Planning

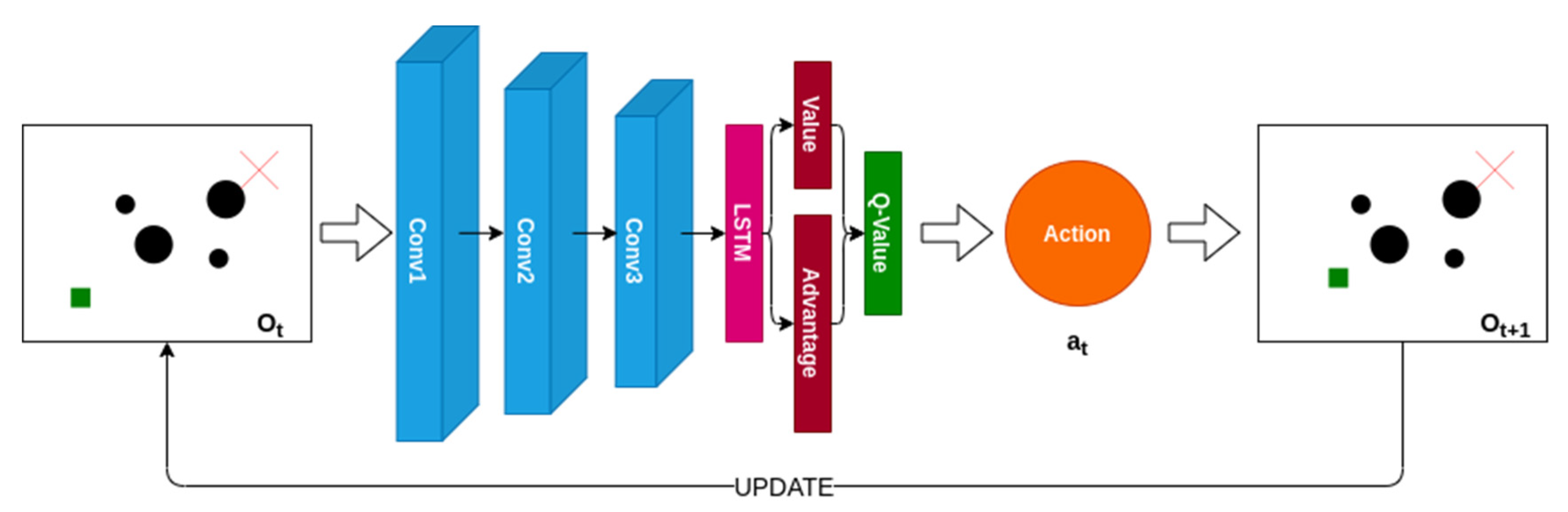
The proposed global path planning method adopts a progressive strategy, as shown in Figure 2. The D3RQN model is used as the planner to select the optimal action according to previous observations, and then update the next position of the quadrotor. Repeat this operation until the quadrotor reaches the destination. The collection of optimal actions constitutes the feasible path of the quadrotor in the environment.

Figure 2. The architecture of the proposed global path planning method.

3.2.1. Planner Network

The parameter setting of planner network is shown in Table 1. All convolutional layers are followed by ReLU activation.

Table 1. Parameter Setting for the Global Path Planning Network.

Layer	Input Size	Output Size	Kernel	Stride	Padding
Conv1	3	6	8	4	0
Conv2	6	12	4	2	0
Conv3	12	24	3	2	0
LSTM	1152	1152	-	-	-
FC (advantage)	1152	12	-	-	-
FC (value)	1152	1	-	-	-

Note: Conv is short for convolutional layer, LSTM for lstm layer and FC for fully connected layer.

3.2.2. Observation Space

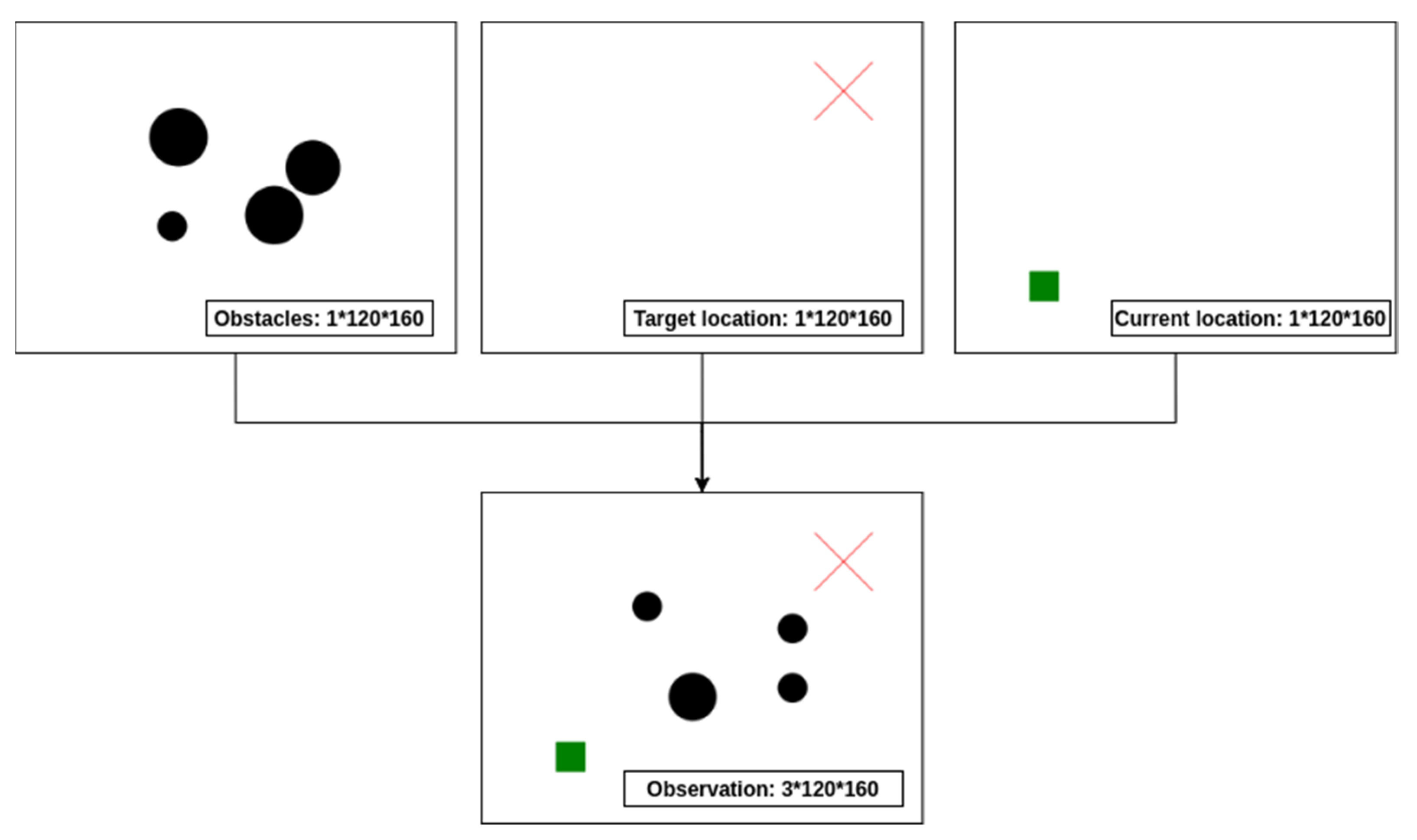
The observation is composed of obstacle information, goal location information and current location information. As shown in Figure 3, the obstacle information, goal location information and current location information are transformed into 1 × 120 × 160 (channel × height × width) tensors respectively. Furthermore, the global observation is composed of the three tensors, which is transformed into a 3 × 120 × 160 tensor.

Figure 3. The generation of path planning global environment observation.

3.2.3. Action Space

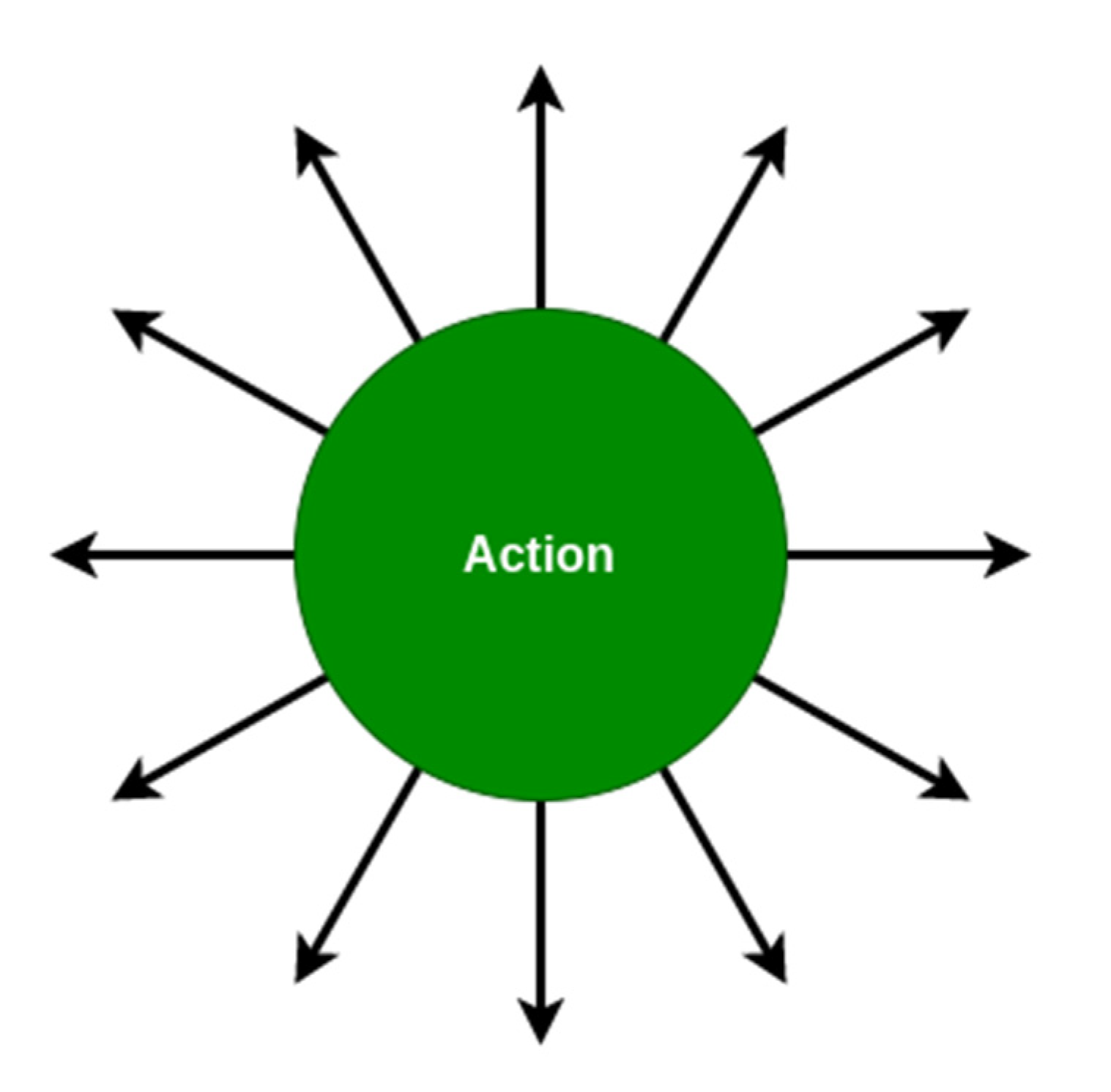
The action setting includes 12 possible directions with a fixed displacement length on the two-dimensional map. The directions of the twelve actions are evenly distributed at an angle of 30 degrees, as shown in Figure 4.

Figure 4. The quadrotor action definition in global path planning.

3.2.4. Reward Function

The reward function of the global path planning model is defined as

$$r_t=\{\begin{array}{ll}10\hfill & ifreach\hfill \\ -10\hfill & ifcollide\hfill \\ K*(d_{curr}-d_{next}-d_{step})\hfill & otherwise\hfill \end{array}$$

(7)

where the $d_{curr}$ is the distance between the current location and the goal location, the $d_{next}$ is the distance between the next location and the goal location, and the $d_{step}$ is the length of a step. K is a constant, which is three here. In this design, the reward is generally negative before reaching the goal, which can avoid the agent’s ineffective wandering.

3.3. Autonomous Obstacle Avoidance

In order to demonstrate the adaptability of the proposed quadrotor autonomous obstacle avoidance method, the fixed on-board monocular camera is used as the only sensor. The operation of the proposed method includes two key steps, feature extraction and decision making, as shown in Figure 5. For dealing with the observation data more effectively, the proposed method utilizes unsupervised contrastive learning to train a CNN-based encoder for preprocessing, which can extract the scene representation features from the image data captured by the monocular camera. High-dimensional image data is compressed into a one-dimensional feature vector by the encoder, which greatly improves the efficiency of the downstream obstacle avoidance task. Furthermore, the dueling double deep recurrent Q-learning is used to train the obstacle avoidance policy, which can select the optimal quadrotor action based on the scene representation features. The selected actions work on the outer loop control of the quadrotor for realizing obstacle avoidance.

Figure 5. The architecture of the proposed framework.

3.3.1. Random Data Augmentation

Recently, contrastive learning methods have achieved remarkable results in unsupervised classification tasks. Random data augmentation is widely applied in those methods [27,28,29] to transform any sample into related views of the same example. The composition of multiple data augmentation operations is the key to train the encoder to extract effective representations. Among the data augmentation operators, crop, resize, flip and cutout are usually used. However, these data augmentation operators mentioned above may change the spatial structure of the scene observations, leading the trained encoder to fail in extracting the representation of the spatial information. In this paper, a stochastic data augmentation composition is introduced to learn the spatial representation of the scene. The augmentation policy used to train the encoder includes random perspective, random color jitter, random grayscale, random cutout and random Gaussian blur. Note that the random cutout used in our framework is limited with its area and aspect ratio, which can eliminate its negative impact on representing the spatial information. The data augmentation operators are visualized in Figure 6.

Figure 6. The data augmentation operators applied in the framework. Each augmenta tion transforms data stochastically with some random internal parameters. (a) Raw, (b) Random perspective, (c) Random color jitter, (d) Random grayscale, (e) Random cutout, (f) Random Gaussian blur.

3.3.2. Feature Extraction Network

Perception with contrastive representation learning requires the encoder to gain the feature extraction policy. The encoder $\mathsf{ℰ}$ in our framework is mainly based on a multi-layer CNN, followed by a fully connected layer. The encoder returns an abstract feature vector $z_i=\mathcal{E}\left[\mathsf{𝒟}\left(o_i\right)\right]$, where $o$ is the observation of onboard monocular camera, $i$ is the index of observation and $\mathcal{D}$ donates the random data augmentation. The parameter setting of the encoder is shown in Table 2. All convolutional layers are followed by ReLU activation, while the fully connected layer is followed by Sigmoid activation. The model structure of the encoder is shown in the dotted box on the left side of Figure 5. The 320 × 240 RGB images are compressed into 1 × 256 feature vectors via the encoder.

Table 2. Parameter Setting for the Encoder.

Layer	Input Size	Output Size	Kernel	Stride	Padding
Conv1	3	32	7	2	3
Conv2	32	32	7	0	3
Conv3	32	64	5	2	2
Conv4	64	64	5	0	2
Conv5	64	128	3	2	1
Conv6	128	128	3	0	1
Conv7	128	256	3	2	1
Conv8	256	256	3	0	1
Conv9	256	128	3	2	1
Conv10	128	128	3	0	1
FC	10,240	256	-	-	-

3.3.3. Contrastive Loss

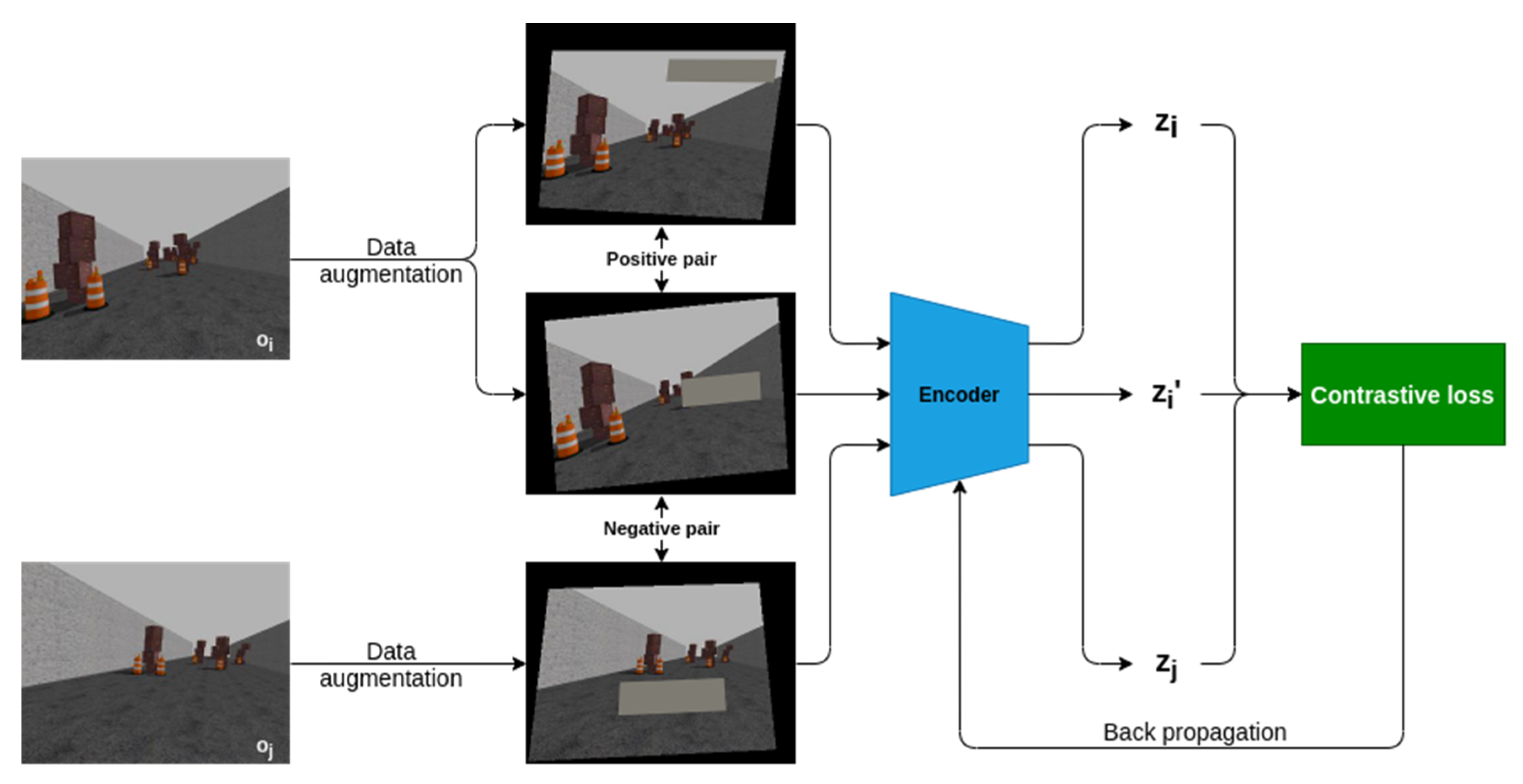
For training the encoder, random data augmentation is used to generate both positive and negative sample pairs. Two samples generated from any sample with different augmentation operators are considered as a positive pair. And two samples generated from two different samples with any augmentation operators are considered as a negative pair. The encoder should learn to maximize the similarity of the representation feature extracted from any positive pair, while minimizing that of any negative pair. The process of training the encoder is shown in Figure 7. The contrastive loss is introduced to train the encoder, which can be defined as follows

$${\mathcal{L}}_{cs}=\mathrm{Dif}\left(z_i,z_i{}^{\prime }\right)+\left[1-\mathrm{Dif}\left(z_i,z_j\right)\right]$$

(8)

Figure 7. The process of training the encoder.

Here $z_i$ and $z_i{}^{\prime }$ denote the feature vectors extracted from the same observation with different data augmentation, while $z_i$ and $z_j$ are the feature vectors from different observations. And $\mathrm{Dif}(\cdot ,\cdot )$ here can be defined as the normalized Euclidean distance to measure the difference between two representation vectors. Its value ranges from 0 to 1, where 0 means two vectors are exactly the same, and 1 means just the opposite.

3.3.4. Decision Making Network

In order to solve the problem of insufficient observation, the decision module in the proposed method can make use of sequential environment information before the current time for more effective obstacle avoidance decisions. The decision module in our method is also based on the D3RQN as in the global path planning section. This decision-making network is shown in the right dotted box of Figure 5, and corresponding parameters are shown in Table 3. The first three fully connected layers are followed by ReLU activation.

Table 3. Parameter Setting for the Decision Module.

Layer	Input Size	Output Size
FC1	256	1024
FC2	1024	1024
FC3	1024	1024
LSTM	1024	1024
FC (advantage)	1024	5
FC (value)	1024	1

3.3.5. Observation and Action Space

The observation for operating the decision-making is the extracted feature vector from the encoder mentioned in Section 3.3.2. The flight action setup of the quadrotor is defined in Table 4.

Table 4. Quadrotor Action Definitions.

Action Number	Linear Velocity (m/s)	Angular Velocity (rad/s)
	(x, y, z)	(x, y, z)
1	(2, 0, 0)	(0, 0, 0)
2	(2, 0, 0)	(0, 0, 0.25)
3	(2, 0, 0)	(0, 0, −0.25)
4	(2, 0, 0)	(0, 0, 0.5)
5	(2, 0, 0)	(0, 0, −0.5)

3.3.6. Reward Function

In the training of the decision making module, the reward function is defined as

$$r_t=\{\begin{array}{ll}{d}_{nst}\hfill & if{d}_{nst}>0.5m\hfill \\ -1\hfill & otherwise\hfill \end{array}$$

(9)

here the $d_{nst}$ is the distance to the nearest obstacle at time $t$, and the safe distance is considered to be 0.5 m.

4. Experiments

The global path planning and autonomous obstacle avoidance model proposed in this paper are implemented using the PyTorch framework. All the training and evaluation are running on an NVIDIA GeForce RTX 2070 GPU, 16 GB RAM and Intel Core i7 processor machine.

4.1. Global Path Planning

4.1.1. Training Setup

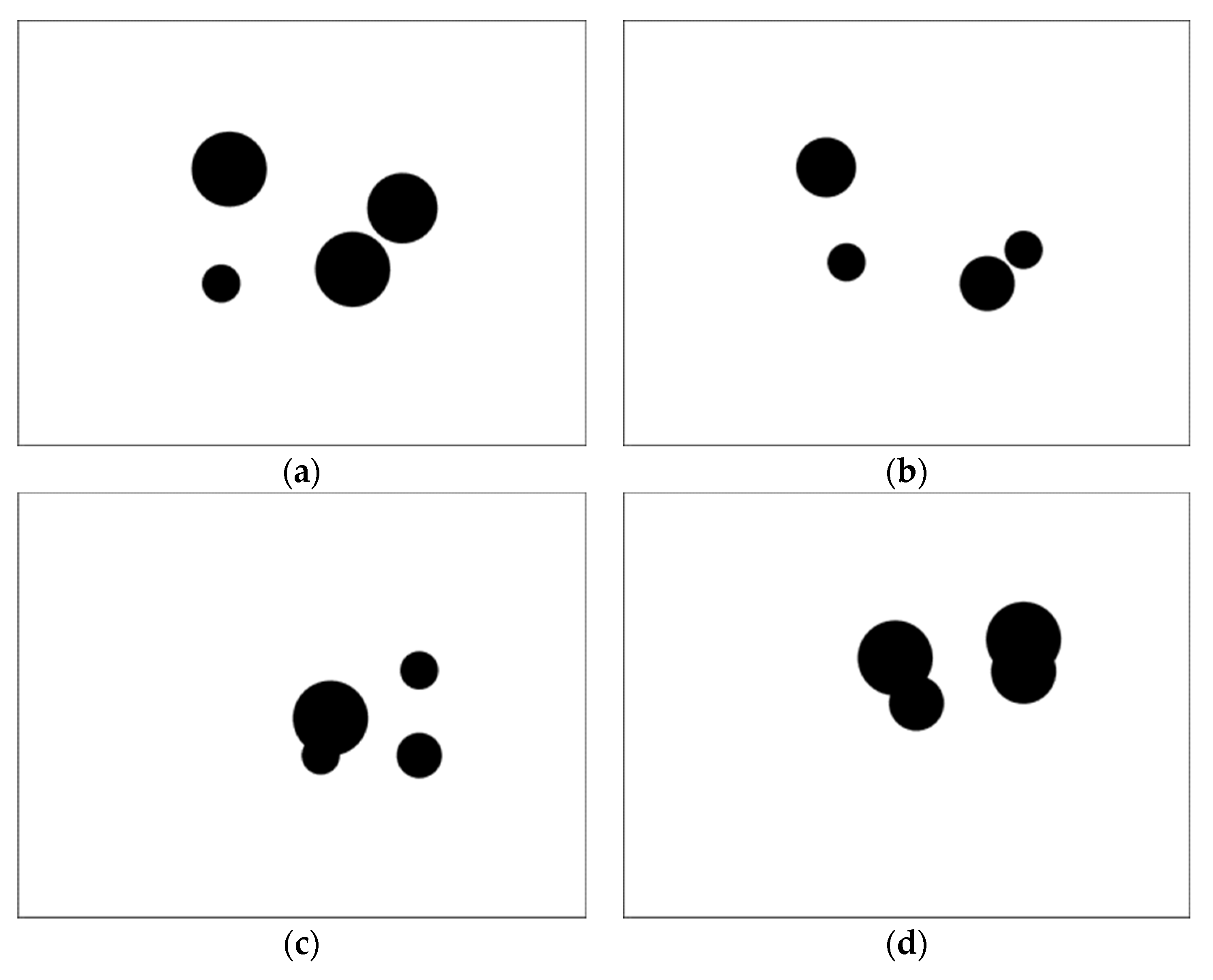
The training of the global path planner is set up with random obstacle generation. The position and size of multiple obstacles change randomly in each training iteration. The random obstacle information is transformed into a 120*160 tensor, shown in Figure 8. And the random obstacle information is used to form observation variables with goal location information and current location information, as mentioned in Section 3.2.

Figure 8. The random obstacle generation for training the path planner. (a) Random obstacle case 1, (b) Random obstacle case 2, (c) Random obstacle case 3, (d) Random obstacle case 4.

The hyperparameters of training the global path planner are shown in Table 5. And the global path planning algorithm is presented in Algorithm 1.

Algorithm 1. Algorithm for global path planning

Require: max epoch number $E{p}_{max}$

Require: planner network $f_p$ and parameters of planner network ${\theta }_p$

Require: random action rate $\beta$

Require: current location $l_c$ and goal location $l_g$

Training phase

$Ep=0$

while $Ep\le E{p}_{max}$ do

Reset the initial state

$t=0$, local memory = []

while$l_c\ne l_g$ do

Obtain current observation ${\mathsf{\Omega }}_t$

Randomly generate ${\beta }_t\in [0,1]$

if ${\beta }_t\le \beta$ then

Randomly choose an action $a_t$

else

Choose action $a_t$ based on $f_p\left({\mathsf{\Omega }}_t\right)$ and Equation (6)

end if

Update current location $l_c$

Receive reward $r_t$ and ${\mathsf{\Omega }}_{t+1}$ in environment

Append data $\left({\mathsf{\Omega }}_t,a_t,r_t,{\mathsf{\Omega }}_{t+1}\right)$ to local memory

$t=t+1$

end while

Push local memory into replay buffer M

Randomly select one batch of training data in M

Calculate loss based on Equation (4)

Upate ${\theta }_p$ to minimize loss

$Ep=Ep+1$

end while

Return $f_p$ and ${\theta }_p$

Testing phase

Reset the initial state

$\mathrm{path}=\left[l_c\right]$

while $l_c\ne l_g$ do

Obtain current observation ${\mathsf{\Omega }}_t$

Choose optimal action $a_t$ based on $f_p\left({\mathsf{\Omega }}_t\right)$ and Equation (6)

Update current location $l_c$ and append it into path

end while

Return path

Table 5. Hyperparameters of Training the Global Path Planner.

Parameters	Value
Map size	120*160
Obstacle number	4
Batch size	32
Discount factor	0.99
Learning rate	0.00005
Input sequence length	5
Action number	12
Step length	7
Target network update frequency	1000
Optimizer	Adam

4.1.2. Results Analysis

The trained global path planner is evaluated in scenarios with randomly generated obstacles. The proposed global path planner is compared with the planners based on DQN, dueling double deep Q network (D3QN) and classic RRT. All these planners for comparison have the same action space. The DQN, the D3QN and the proposed global path planner have the same number of network layers. The DQN has three convolutional layers followed by two fully connected layers. The first four layers of D3QN are the same with those in the DQN, and the fifth layer is divided into two branches for computing advantage and value. The proposed planner is based on D3RQN, whose network can be obtained by replacing the fourth layer of D3QN with a LSTM layer. Moreover, the DQN and D3QN have the same training hyperparameters as the proposed planner.

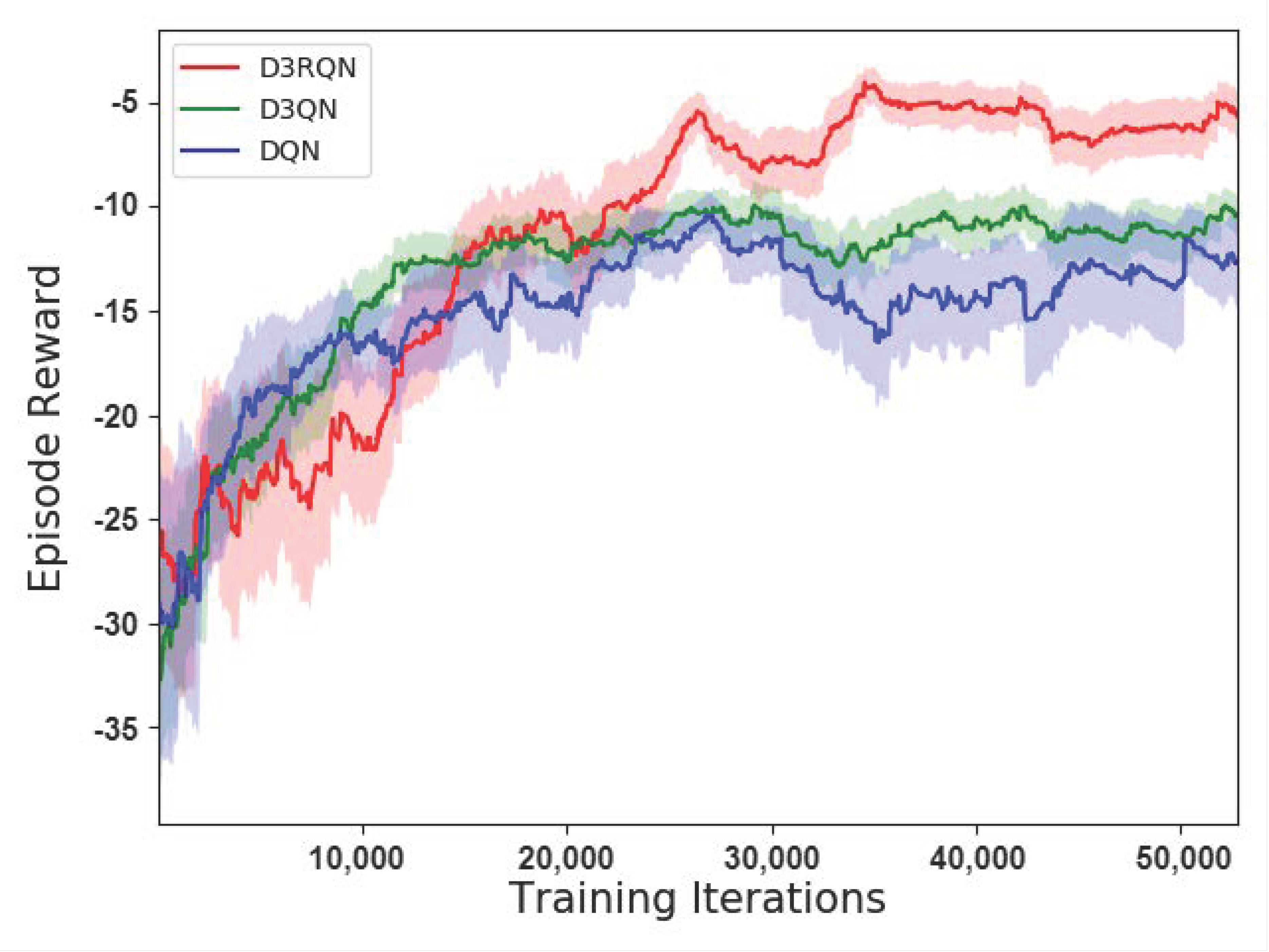
The learning curves of the planners are shown in Figure 9 and the path planning results are shown in Figure 10.

Figure 9. The learning curves of the global path planning models.

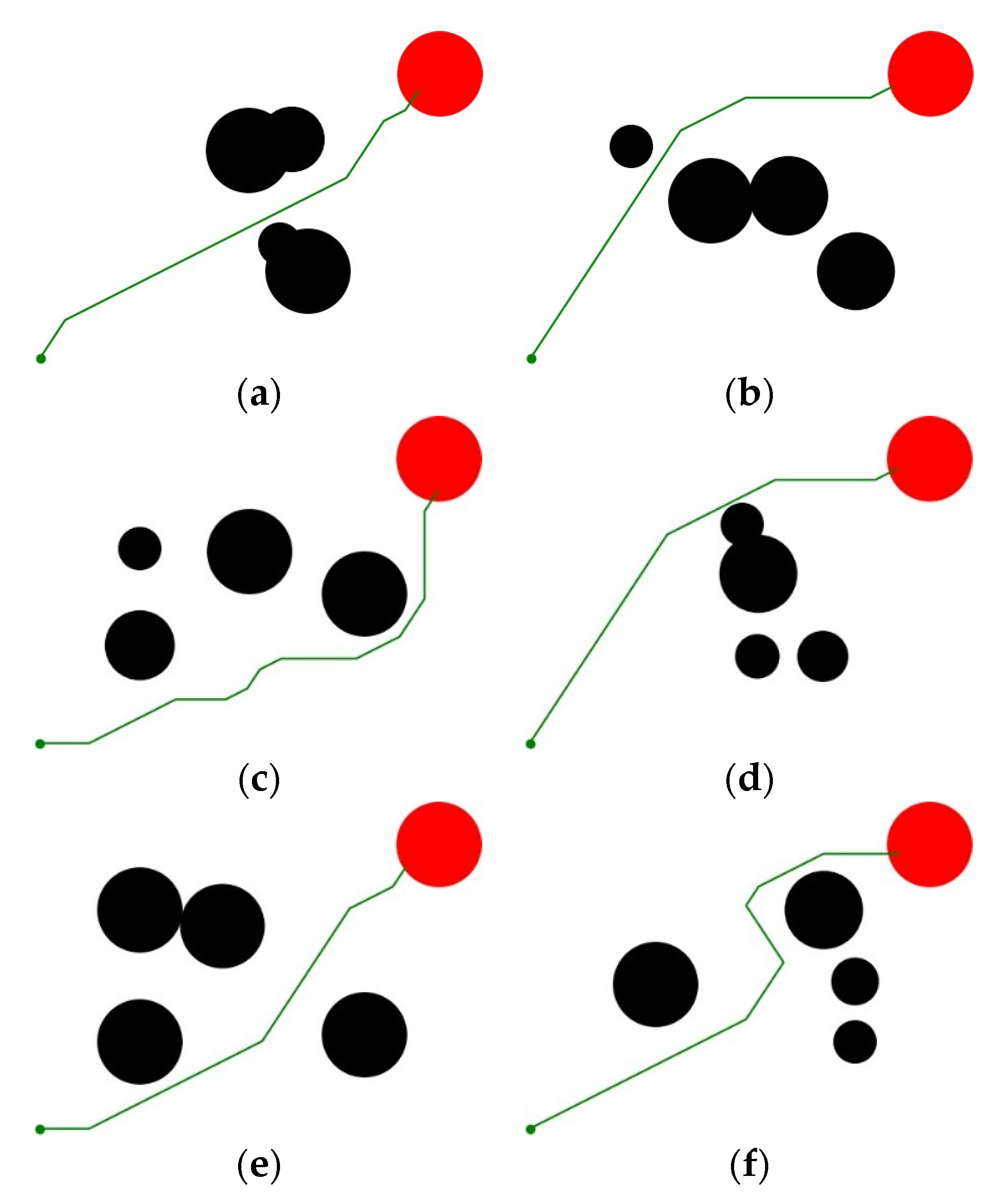
Figure 10. The global path planning results of the proposed method. (a) Result 1, (b) Result 2, (c) Result 3, (d) Result 4, (e) Result 5, (f) Result 6.

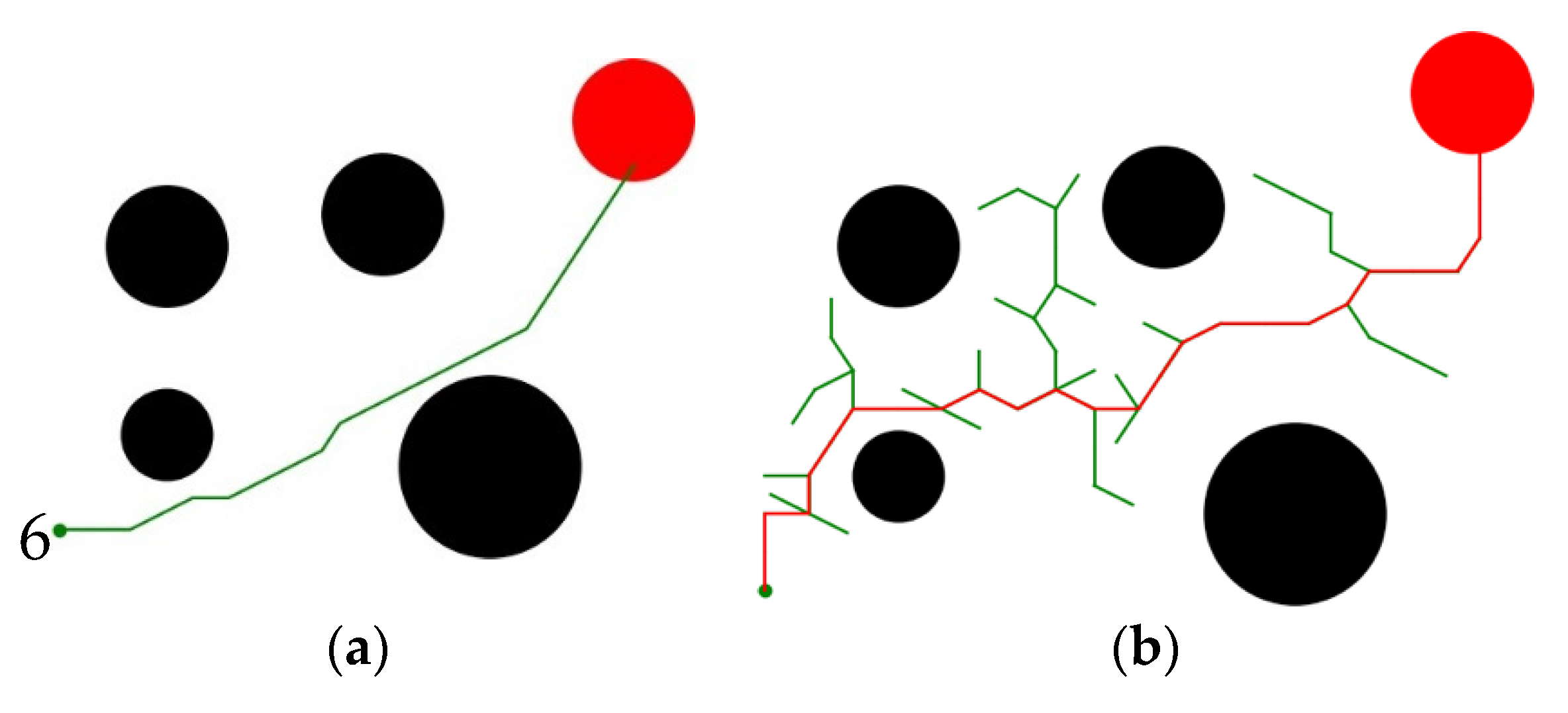
Table 6 shows the performance of different planners. The performance comparison of our planner and the RRT planner in the same scene is shown in Figure 11. It shows that our method has better planning efficiency than the traditional heuristic method for avoiding invalid attempts and collision detection. Moreover, the generated path is more optimized and smoother.

Table 6. The global path planning performance of different planners.

Policy	SR (30 Steps)	SR (50 Steps)	SR (100 Steps)	AS
Random	0	0	0	-
DQN	0.612	0.625	0.629	24.22
D3QN	0.735	0.738	0.740	23.95
RRT	0.926	0.968	0.997	39.68
D3RQN	0.972	0.973	0.973	22.31

Note: SR is short for success rate, AS is short for average steps when successful.

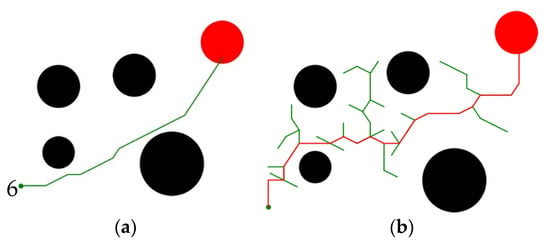
Figure 11. The global path planning results comparison. (a) D3RQN, (b) RRT.

4.2. Autonomous Obstacle Avoidance

4.2.1. Training Setup

The planner is trained and evaluated in the ROS Gazebo simulation environment, shown in Figure 12. The framework learns to extract low dimensional representation features from the high dimensional visual observations, and select the optimal action for obstacle avoidance. The visual observations are the RGB images captured by the fixed on-board camera in the simulation.

Figure 12. The Basic Training Environments for Our Framework in Gazebo. (a) Front view, (b) Top view.

The framework is trained with a step-by-step strategy. The encoder for extracting the representation features is trained first with the raw scene images. Then the D3RQN for conducting obstacle avoidance is trained based on the pre-trained encoder. The training images are collected in the simulation environments by the monocular camera on the manually controlled quadrotor. The hyperparameters of training the encoder are shown in Table 7.

Table 7. Hyperparameters of Training the Encoder.

Parameters	Value
Image number	10,000
Batch size	64
Learning rate	0.00005
Image size	3*240*320
Feature dim	256
Optimizer	Adam

The D3RQN is trained to estimate the current Q-value over the last several observations, which means the last several representation feature vectors generated by the pre-trained encoder in the framework. The hyperparameters of training the D3RQN are shown in Table 8. And the obstacle avoidance algorithm is presented in Algorithm 2.

Algorithm 2. Algorithm for obstacle avoidance

Require: Encoder network $\mathcal{E}$ and parameters of the Encoder ${\theta }_{\mathcal{E}}$ Require: D3RQN $f_d$ and parameters of D3RQN ${\theta }_d$ Require: max epoch number for training the Encoder $E{p}_{max}^{\mathcal{E}}$ Require: max epoch number for training the D3RQN $E{p}_{max}^d$ Require: random data augmentation $\mathcal{D}$ Require: max step number $T_{max}$ Require: random action rate $\beta$ Encoder training phase     $E{p}^{\mathcal{E}}=0$         while $E{p}^{\mathcal{E}}\le E{p}_{max}^{\mathcal{E}}$ do             Randomly select two batch of training data $o_i$ and $o_j$             Extract feature vector $z_i=\mathcal{E}\left[\mathcal{D}\left(o_i\right)\right]$, $z_i{}^{\prime }=\mathcal{E}\left[{\mathcal{D}}^{\prime }\left(o_i\right)\right]$, $z_j=\mathcal{E}\left[\mathcal{D}\left(o_i\right)\right]$             Calculate loss based on Equation (8)             Update ${\theta }_{\mathcal{E}}$ to minimize loss             $E{p}^{\mathcal{E}}=E{p}^{\mathcal{E}}+1$         end while         Return $\mathcal{E}$ and ${\theta }_{\mathcal{E}}$ D3RQN training phase         $E{p}^d=0$         while $E{p}^d\le E{p}_{max}^d$ do             Reset the initial state             $t=0$, local memory = []             while no collide do                 Obtain current observation ${\mathsf{\Omega }}_t$                 Randomly generate ${\beta }_t\in [0,1]$                 if ${\beta }_t\le \beta$ then                     Randomly choose an action $a_t$                 else                     Choose action $a_t$ based on $f_d\left[\mathcal{E}\left({\mathsf{\Omega }}_t\right)\right]$ and Equation (6)                 end if                 Update current quadrotor location                 Receive reward $r_t$ and ${\mathsf{\Omega }}_{t+1}$ in environment                 Append data $\left({\mathsf{\Omega }}_t,a_t,r_t,{\mathsf{\Omega }}_{t+1}\right)$ to local memory                 $t=t+1$             end while                 Push local memory into replay buffer $M$                 Randomly select one batch of training data in $M$                 Calculate loss based on Equation (4)             Upate ${\theta }_d$ to minimize loss             $E{p}^d=E{p}^d+1$          end while         Return $f_d$ and ${\theta }_d$ Testing phase         Reset the initial state         $t=0$         while $t\le T_{max}$ and no collide do             Obtain current observation ${\mathsf{\Omega }}_t$             Choose optimal action $a_t$ based on $f_d\left[\mathcal{E}\left({\mathsf{\Omega }}_t\right)\right]$ and Equation (6)             Update quadrotor location             $t=t+1$         end while         if $t=T_{max}$ then             Return success         end if

Table 8. Hyperparameters of Training the D3RQN.

Parameters	Value
Batch size	32
Discount factor	0.99
Learning rate	0.00005
Input sequence length	5
Action time interval	0.4 s
Target network update frequency	400
Optimizer	Adam

4.2.2. Results Analysis

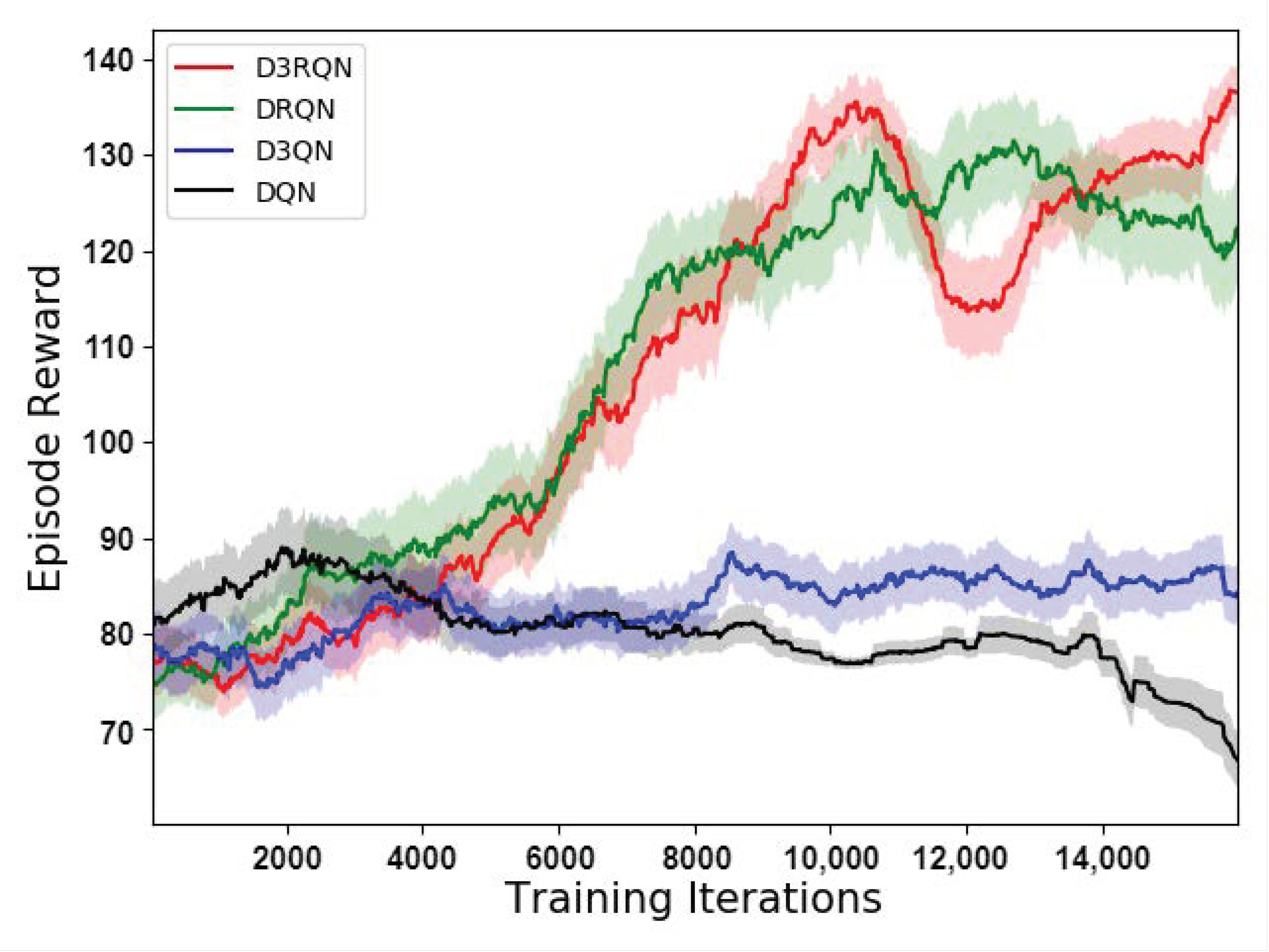
The trained framework is evaluated in several test simulation scenarios. If the quadrotor flies more than 50 steps safely, it is considered a success. The obstacle avoidance performance of the proposed framework is evaluated by calculating the success rate after 2000 times test flight. Some other policies, such as straight, random, DQN, DRQN and D3QN are also implemented in this paper as a comparison. All these methods for comparison have the same action space. The DQN, the D3QN, the DRQN and the proposed framework have the same number of network layers. The DQN has four fully connected layers. The first three layers of D3QN are the same with those in DQN, and the fourth layer is divided into two branches for computing advantage and value. The DRQN can be obtained by replacing the third layer of DQN with a LSTM layer. And the proposed framework can be obtained by replacing the third layer of D3QN with a LSTM layer. Moreover, all the models have the same training hyperparameters. Figure 13 displays the learning curves of these models.

Figure 13. The learning curve of the obstacle avoidance models.

The evaluation results are shown in Table 9. And Figure 14 presents the test scenario and corresponding success trajectory. Note that the success rate is the average of the test results in three different scenarios. The typical obstacle avoidance failure mode is shown in Figure 15. In this case, the quadrotor passes through the side of the obstacle. The obstacle is outside the field of vision of the on-board camera, and the quadrotor fails to maintain a safe distance from the obstacle and collides. Expanding the vision field of the sensor or increasing the number of sensors will help to solve this problem, and these improvement measures will be considered in future work.

Table 9. The evaluation results of the trained framework.

Policy	Training Time	Execution Frequency	Success Rate
Straight	-	-	0
Random	-	-	0.002
DQN	10.2 h	15 Hz	0.113
D3QN	11.5 h	15 Hz	0.144
DRQN	16.1 h	15 Hz	0.732
D3RQN	16.0 h	15 Hz	0.996

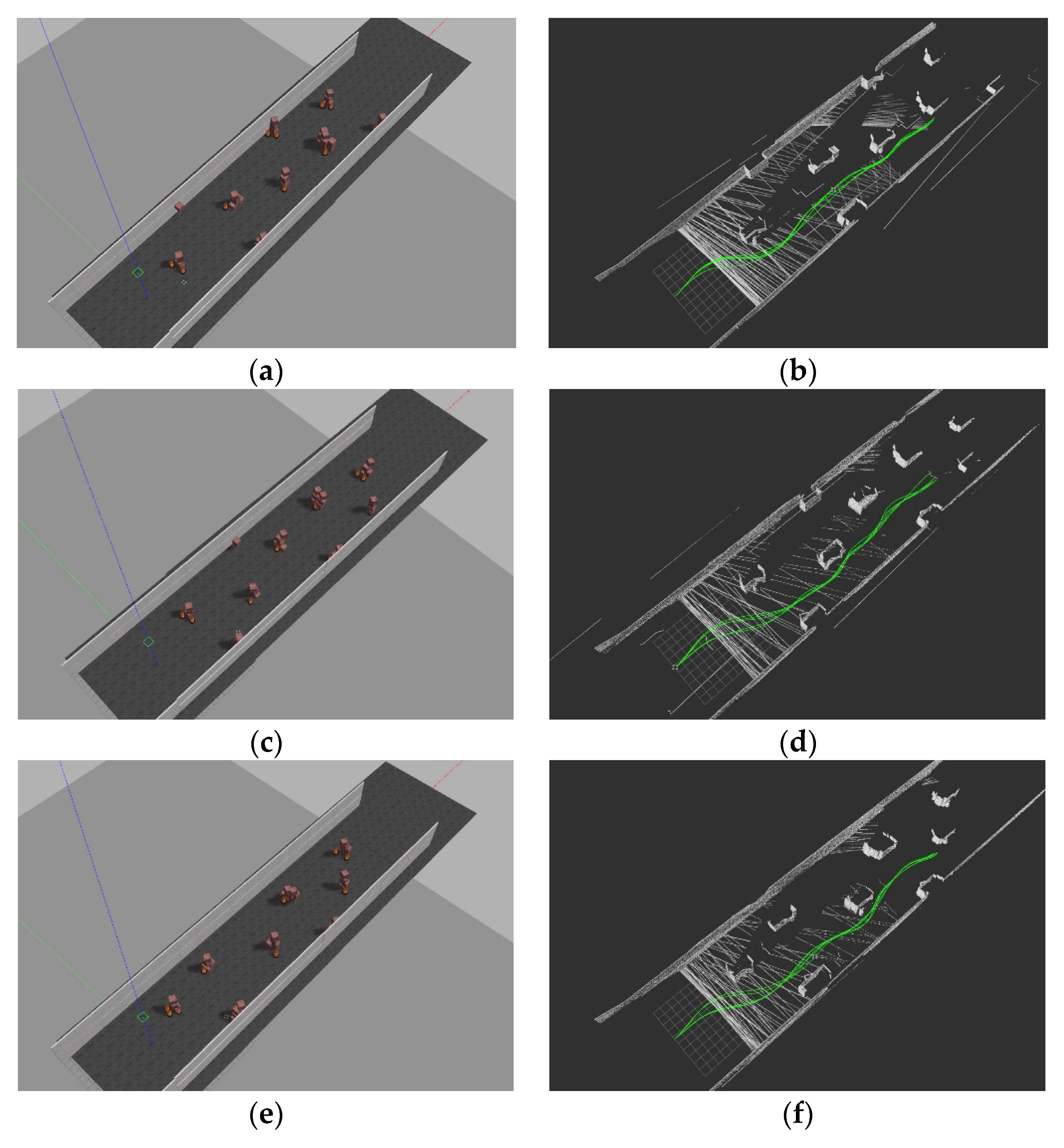
Figure 14. The test scenarios and corresponding success trajectories. (a) Test scenario 1, (b) Trajectory in scenario 1, (c) Test scenario 2, (d) Trajectory in scenario 2, (e) Test scenario 3, (f) Trajectory in scenario 3.

Figure 15. The case when the proposed method fails.

5. Discussion

In this paper, a deep reinforcement learning-based framework is proposed for quadrotor autonomous navigation in semi-known environments. The proposed framework can be applied to global path planning and autonomous obstacle avoidance. This framework has the characteristics as follows:

• In this paper, an multi-layer CNN based encoder is used for extracting the visual representation of onboard camera observations, which is trained with unsupervised contrastive learning. The trained encoder is applied to autonomous obstacle avoidance of the quadrotor. Its training requires no groundtruth or special format for the training dataset, while some other perception methods based on depth estimation via unsupervised learning require a special format for training datasets such as left-right consistency or sequence consistency [23,24,25,26]. Moreover, the trained encoder in this paper is only 42.2 MB, and the total number of parameters is 4,379,680. The depth estimation model is 126.4 MB in [24] with a total number of 31,596,900 parameters. So the proposed encoder model is more lightweight, making it more suitable for quadrotor applications.
• The proposed method can be used in global path planning. Compared with other traditional methods like RRT, our method has the ability to generate feasible paths more effectively. In the process of path planning, our method does not need detection or random path exploration, so it has higher execution efficiency. In each step of path planning, it selects the optimal action according to the trained policy. In the evaluation, it successfully plans the path with an average of 22.31 steps, which is much lower than the 39.68 steps of RRT. Also, its path planning success rate is also better than its competitors DQN and D3QN.
• In this paper, the conduction of autonomous obstacle avoidance of the quadrotor was undertaken based on the image data captured by a fixed on-board monocular camera. The autonomous obstacle avoidance can be considered as POMDP. The incomplete observation of the sensor leads to the significant performance degradation of the DQN and D3QN models. In the evaluation, the success rate of the DQN and D3QN was only slightly higher than 10%. By adding a recurrent neural network layer, the DRQN and D3RQN model can reduce the negative impact of incomplete observation, and significantly improve the success rate. By combining the dueling and double technique, the performance of the D3RQN model is further improved, reaching more than 99% in the evaluation. Moreover, the whole obstacle avoidance model, combined with the preprocessing encoder, can run at a maximum frequency of 15 Hz on the test computer, so it is possible to control an actual quadrotor.

6. Conclusions

In this paper, we proposed a decision model based on D3RQN. We demonstrated that the proposed model can plan a feasible path with obstacle map information as input. The evaluation results show that it has higher execution efficiency than a classic path planner like RRT and a higher success rate than some other learning-based models such as DQN or D3QN. Moreover, we also propose an unsupervised contrastive learning-based encoder to extract the visual representation. Combined with the decision model mentioned above, this encoder can be used to perform autonomous obstacle avoidance. The evaluation conducted in ROS gazebo proves its effectiveness. In our future work, we are interested in implementing and testing the proposed method on a real quadrotor combined with more kinds of sensors. It is also important to realize the avoidance of moving obstacles in future research.