Abstract
The use of carrier phase data is the main driver for high-precision Global Navigation Satellite Systems (GNSS) positioning solutions, such as Real-Time Kinematic (RTK). However, carrier phase observations are ambiguous by an unknown number of cycles, and their use in RTK relies on the process of mapping real-valued ambiguities to integer ones, so-called Integer Ambiguity Resolution (IAR). The main goal of IAR is to enhance the position solution by virtue of its correlation with the estimated integer ambiguities. With the deployment of new GNSS constellations and frequencies, a large number of observations is available. While this is generally positive, positioning in medium and long baselines is challenging due to the atmospheric residuals. In this context, the process of solving the complete set of ambiguities, so-called Full Ambiguity Resolution (FAR), is limiting and may lead to a decreased availability of precise positioning. Alternatively, Partial Ambiguity Resolution (PAR) relaxes the condition of estimating the complete vector of ambiguities and, instead, finds a subset of them to maximize the availability. This article reviews the state-of-the-art PAR schemes, addresses the analytical performance of a PAR estimator following a generalization of the Cramér–Rao Bound (CRB) for the RTK problem, and introduces Precision-Driven PAR (PD-PAR). The latter constitutes a new PAR scheme which employs the formal precision of the (potentially fixed) positioning solution as selection criteria for the subset of ambiguities to fix. Numerical simulations are used to showcase the performance of conventional FAR and FAR approaches, and the proposed PD-PAR against the generalized CRB associated with PAR problems. Real-data experimental analysis for a medium baseline complements the synthetic scenario. The results demonstrate that (i) the generalization for the RTK CRB constitutes a valid lower bound to assess the asymptotic behavior of PAR estimators, and (ii) the proposed PD-PAR technique outperforms existing FAR and PAR solutions as a non-recursive estimator for medium and long baselines.
1. Introduction
The use of Global Navigation Satellite Systems (GNSS) carrier phase observations is fundamental for supplying high-precision Positioning, Navigation, and Timing (PNT) data [1]. In contrast to standard code-based positioning, such carrier phase observations are ambiguous and require the estimation of integer unknowns, also denoted ambiguities, along with the dynamical parameters of the target. Regression for a mixture of real- and integer-valued parameters, also known as mixed model, implies a Maximum Likelihood Estimation (MLE) problem and a real-to-integer mapping of the ambiguities. The latter process is referred to as Integer Ambiguity Resolution (IAR) [2], and its performance is key to achieve precise positioning estimates.
Real-Time Kinematic (RTK) is a high-precision localization procedure, for which the position of a rover is determined with respect to a geolocated base station [3,4]. RTK represents an example of mixed model whose associated MLE can be solved through a three-step process [5]:

with float and IAR corresponding to least squares (LS) adjustment for real- and integer-valued parameter estimation, respectively. The fixed solution improves the positioning solution by virtue of the integer constraints on the ambiguities, although the presence of a single wrongly estimated ambiguity can lead to a worsened positioning solution. Thus, the validity test allows determining whether the output of the IAR process may or not be trusted. If the ambiguities cannot be fixed with high confidence, the original float estimate is preserved instead.
The estimation of the complete vector of ambiguities can be a challenging task, provided that a single bias or inaccuracy in a carrier phase pseudorange could potentially spoil the estimation. A representative example of the former relates to medium and long baseline RTK positioning, due to the atmospheric residuals. Even though the use of multi-GNSS, multi-frequency observations strengthens the model, the probability of correctly estimating the integer vector, also known as success rate, tends to decrease with a raise on the number of observations [6]. The conventional procedure of estimating all the ambiguities, known as Full Ambiguity Resolution (FAR), is specially sensitive to the aforementioned challenges. Two alternatives are typically considered to alleviate the former limitation:
- 1.
- Increasing the observation time span and/or applying recursive estimation, particularly when the atmospheric residuals become part of the state estimate.
- 2.
- Applying Partial Ambiguity Resolution (PAR), which relaxes the integer estimation over the complete set of ambiguities to a subset instead.
This work focuses on PAR solutions for snapshot estimation, i.e., non-recursive estimation for which only the observations received at a time instant are considered. This case is particularly relevant for safety-critical vehicular applications, for which high availability of precise positioning is required in an instantaneous manner [7,8,9,10]. Thus, PAR identifies a subset of ambiguities to fix upon certain criteria, e.g., success rate maximization, failure rate minimization, etc. The question resides on how can one determine which ambiguities to fix. Answering this question leads to the different selection heuristics, such as signal-to-noise ratio [11,12], Ambiguity Dilution of Precision (ADOP) [13], or minimum bias [14]. Alternatively, the framework of Generalized Integer Aperture (GIA), introduced by Brack in his series of work [15,16,17,18], extends the concepts from Integer Aperture to PAR to jointly perform real-to-integer mapping and subset selection.
This work introduces Precision-Driven PAR (PD-PAR), a PAR subset selection criteria based on the projection of the integer ambiguities into the positioning domain. As the precision of the fix positioning solution is conditioned on the quality of the float estimates (for the position and ambiguity elements) and their associated covariance, PD-PAR identifies the combination of ambiguities which grants a target positioning precision requirement (i.e., the minimal precision needed for an use-case application) prior to the actual integer estimation. To achieve that end, we propose an algorithm workflow and demonstrates that PD-PAR subset criteria selection leads to a lower degree of ambiguity cross-correlation and a higher probability of correctly estimating those ambiguities.
Furthermore, we propose a Cramér–Rao Bound (CRB) for the analytical assessment of PAR estimators’ performance. Among the families of estimation bounds, the CRB stands out for its straightforward calculation, being the lowest bound in the mean squared error (MSE) sense and asymptotically attained by MLEs. While an extensive literature on lower and upper bounds exists for real [19,20,21,22] and integer estimation [23,24,25], the general CRB for the mixed estimation problem was only recently introduced [26,27]. This work leverages the CRB for the mixed problem and generalizes it for the mixed model with PAR estimation. Thus, we can analytically acknowledge the performance of PAR estimators and its relation with respect to the conventional FAR approaches. This generalized form of CRB for the mixed model and PAR allows to address the performance of the proposed PD-PAR, while serving as benchmark for other PAR estimators.
The performance of conventional FAR and PAR solutions as well as the proposed PD-PAR is analyzed in a twofold manner: first, a Monte Carlo experiment over a synthetic scenario illustrates the estimation performance for conventional FAR, PAR and the proposed PD-PAR estimators for a range of baseline distances of up to 60 km; then, real data collected for a medium baseline scenario are used as further analysis. The results show that (i) the general CRB for the mixed PAR model is correct and there exist estimators which asymptotically attain it and (ii) PD-PAR is a promising subset selection criteria for PAR, particularly attractive for applications requiring high availability of precise positioning in a snapshot manner (e.g., driverless vehicles or autonomous robots).
The remaining of the article is as follows. Section 2 provides background on RTK and the mixed model estimation. Section 3 discusses the state-of-the-art PAR methods and introduces the PD-PAR scheme. The theoretical estimation bound for the PAR mixed model is provided in Section 4. Section 5 presents the experimentation and associated results. Finally, Section 6 outlines the work and proposes future research lines.
2. RTK and the Mixed Model
Let us consider GNSS satellites being simultaneously tracked over a particular frequency where the position of the rover is determined with respect to a stationary base station of accurately known coordinates. RTK positioning applies a double difference (DD) combination code/carrier measurements to minimize the effect of nuisance parameters, e.g., atmospheric delays, satellites’ position, and clock errors. Therefore, the vector of observations is composed by the sized vector of DD carrier phase and code observables. RTK is associated with the mixed real- and integer-valued model, or simply mixed model, expressed as
where are full rank design matrices and is the covariance matrix for the observations. Within the context of RTK, the vector constitutes the baseline vector between the rover and the base, such that and is the vector of carrier phase DD ambiguities. In that case, the design matrices and are defined as follows:
where is the carrier wavelength, is the n-dimensional identity matrix, is the n-dimensional null matrix, and is the dimensional unit column vector. Additionally, is the geometry matrix, composed by the unit satellite steering vectors, and is the single-difference matrix operator. More detailed description on the mixed model can be found in [28] (Ch. 21, 23). The definition of the observations’ covariance matrix is as
where are the zenith-referenced variances for the undifferenced carrier phase and code observables, respectively, and is the weighting diagonal matrix, expressed typically as function of the satellite elevation [29,30].
As aforementioned, the DD observation combination allows eliminating atmospheric delays as long as the distance between base and rover locations is sufficiently small (i.e., below 10 km). As this distance grows, different residual biases become prominent: the difference in line-of-sight vectors towards satellites from rover and base, tropospheric, and ionospheric delays. While the first two can be generally overseen, ionospheric residuals strongly jeopardize RTK positioning performance. For medium baselines (i.e., below 50 km), the ionospheric delay for each undifferenced observation can be treated as an additional zero-mean normal-distributed noise term, known as the ionospheric-weighted model [31,32], whose variance is modeled as a function of the satellite elevation and the baseline distance [33]. Then, the covariance matrix associated with the ionospheric delays is added to the observations covariance matrix and expressed as
with ⊗ denoting the Kronecker product. Note that a correlation between carrier phase and code measurements becomes apparent, as the differential ionospheric biases affect them both. For long baseline distances, the ionospheric model becomes weak in terms of IAR. Therefore, multi-frequency observations are required and the ionospheric delay for each link is added to the real parameters vector and recursively estimated. This work is focused on instantaneous positioning in short and medium baseline lengths considering the ionospheric-weighted model in Equation (4) within the observations’ stochastic modeling.
Mixed Model Estimation
Solving the linear system of equations in Equation (1) leads to an optimization problem with mixed real and integer parameter estimation. From a MLE perspective, its estimation follows a weighted least-squares (LS) formulation:
where is a weighted norm. Although an explicit solution to Equation (5) is unknown, the decomposition of the previous quadratic form into the sum of three LS adjustments is well known [5] and expressed as follows:
where is the real-valued least-square ambiguity vector with a variance-covariance matrix and is the least-square vector conditioned on having as variance-covariance matrix with the adjustments being commonly denoted as float, IAR, and fixed solution estimations. Next, each of these processes are shortly described:
- Float solution:
- during the first step of Equation (6a), the integer nature of the carrier ambiguities is neglected and, instead, a conventional WLS for real-valued parameters is employed. The result of this estimation is denoted as float solution, whose distribution is described bywith the covariance matrix gathering the uncertainty on the estimates and their correlation;
- Integer Ambiguity Resolution:
- the second minimization problem Equation (6b) constitutes the Integer Least Squares (ILS) adjustment, a real-to-integer mapping such thatwith a many-to-one mapping operator (i.e., different real values lead to the very same integer value). In this context, an integer estimator is described by its pull-in regions, which describe a subset of real numbers which “pull” to the same integer vector [25]. Pull-in regions result extremely useful to understand the success rate , i.e., the probability that an estimated integer vector match the true one . The ILS success rate is upper bounded by the bootstrapped (BS) success rate [23], for which an exact close-form expression existswith the cumulative normal distribution, and the ith conditional variance (i.e., the ith diagonal value of the diagonal matrix from an LDL decomposition on , ). Hereinafter, ILS is considered as integer estimator (i.e., ), due to its optimality properties [25].After the float estimation, the ambiguities’ covariance matrix presents a high correlation among ambiguities which hinders the IAR process (i.e., integer rounding (IR) and IB performance is jeopardized, while ILS increases its computational load). To overcome this limitation, integer reparametrizations, also known as Z-transformations, are typically applied. The general class of Z-transformations issuch that all the elements of and its inverse are integer numbers. Due to the integer constraints on , the complete decorrelation of the ambiguities is not possible, although it can be considerably reduced through a sequence of integer approximated Gauss transformations and permutations [34]. Thus, the minimization of Equation (6a) is instead expressed and resolved in the Z-space, asand, afterwards, the original ambiguity space can be reconstructed from .IAR also includes a validation step to determine the reliability of the integer estimate. Thus, an integer solution is accepted only if the success rate is sufficiently high or the validity test is passed. Thus, the integer mapping Equation (8) can be described in a more flexible way aswith and being a generic testing function and threshold value, respectively. The criteria for testing function leads to model- and data-driven rules. Model-driven rules are solely dependent on the strength of the model, i.e., the ambiguities’ covariance matrix , with the operator expressed aswith the failure rate (i.e., ) and the target probability of estimating the wrong integer solution. Thus, model-driven implies accepting a solution whenever the success rate is sufficiently high or, in other words, only if the BS upper bound success rate is high enough. Alternatively, data-driven rules take into consideration the real-valued estimate and express the operator aswhere one can distinguish, for instance, the ratio and difference tests (RT and DT), whose test functions are given bywith the best counter-hypothesis to , and , the threshold values for RT and DT, respectively. The underlying challenge relates to choosing a threshold value adequate for different geometries or number of frequencies used. The fixed failure rate test (FF-RT) is a well-known solution to that challenge [35,36], for which the RT threshold value is chosen upon a target failure rate and the strength of the model. Hereinafter, this work considers FF-RT as validation test, for which the integer estimate is accepted if it guarantees a sufficiently low failure rate and, otherwise, the real-valued ambiguity solution is kept.
- Fixed solution:
- the last minimization (6c) improves the vector of real-valued parameters upon the knowledge of the integer ambiguities , driving to high accuracy positioning, denoted as fixed solution. The mean and covariance for the fixed solution, , are based on the projection of the integer ambiguities into the position domain, aswith the fixed solution inheriting its high precision from the carrier phase observables. Notice that the precision gain occurs only when estimated integer ambiguities coincide with the true ones, but this information is unknown in a real system. Alternatively, a fixed solution is considered only when the probability of a correct ambiguities fixing is sufficiently high (i.e., when the validity test is passed). Otherwise, the complete set of integer estimates is disregarded, i.e., , and the fixed solution does not adjust the original float solution. PAR is a distinct alternative for finding the integer solution for only a subset of ambiguities, explained in the sequel.
3. Partial Ambiguity Resolution Strategies
Let us denote with the index for the subset of ambiguities to be fixed, such that
where denotes the set of possible non-empty index combinations with cardinality and the complementary set indicates the ambiguities to remain real-valued. The real-to-integer mapping function now becomes , and it is different among estimators.
In general, the use of PAR leads to a suboptimal solution for the mixed problem in Equation (5), as one intends at solving the alternative
with
and only when , Equation (19) is equivalent to the original mixed estimation (5). While it appears illogical, aiming at solving a suboptimal problem, the use of PAR may improve the overall performance of an estimator for the mixed model by increasing the success rate for some ambiguities in contrast to all of them.
The challenge resides on the choice of the subset of ambiguities to fix. The set is not known beforehand and it is to be determined along with the integer estimation process. Adopting the same nomenclature than the validity tests, strategies for the subset selection are distinguished in model- and data-driven. An instance of model-driven PAR employs the IB success rate in Equation (9) to determine the subset that assures a solution with a failure rate lower than the target , such that
and the conditional variance of the ith transformed ambiguity. The Z-transformed ambiguities are assumed to be sorted such that presents the highest precision (). Then, an ILS solution for the subset is assured to present a sufficiently low failure rate.
For data-driven PAR techniques, the choice of the set also depends on the vector of float estimates . Doing so is equivalent to extending the validity test in Equation (14) to, at most, the possible combinations. Thus, an integer estimator computes a solution for a particular and then a RT-DT test as in Equation (15) is applied. The workflow is summarized in Algorithm 1 and as follows: first, the float solution for Equation (6a) is obtained; second, the ambiguities are Z-transformed and sorted in increasing order of precision; then, an integer estimate is determined for the set of ambiguities and a data-driven test checks its reliability; this process is sequentially performed eliminating the less precise ambiguity each time until the test is passed. While this practice has been shown to perform effectively [37,38], it can be computationally very demanding, as the number of estimation instances is not known beforehand.
| Algorithm 1: Data-Driven PAR |
 |
Alternatively, the framework of Generalized Integer Aperture (GIA) estimation, introduced by Brack in his series of works [15,16,17,39], extends the concepts on IAR and PAR to describe selective pull-in regions and their aperture. Thus, GIA estimators procure a joint subset selection, integer estimation, and test validation upon the aperture of the decision regions. To do so, the best counter-hypothesis for each of the n ambiguities is tested against the corresponding ambiguities of the overall best solution. For instance, the GIA difference test (GIA-DT) describes the subset selection as
where is the best counter-hypothesis to for which the i-th element is different and is a threshold value. In analogy to the FF-RT, the threshold value can be dynamically estimated upon a particular target failure rate [16].
Precision-Driven PAR Scheme
Although data- and model-driven schemes are widely used, they only take into account the ambiguities derived from the real-valued parameters estimation and the information brought by the covariance matrix of the ambiguities. While the requirement of a minimal precision for the fixed solution has been discussed in the context of PAR [18] (Ch. 4), its consideration as subset selection criteria has not yet been proposed. Precision-driven PAR fulfills this end using the projection of the ambiguities into the fixed positioning domain as ambiguity subset selection criteria. Thus, one aims at finding a reduced number of ambiguities which guarantee certain target positioning precision criteria for the fixed position solution, while retaining a sufficiently low failure rate . Notice that the precision requirement refers to the minimal positioning precision required by a particular application (e.g., automobile lane detection may require decimeter-level precision [40], while vessel mooring assistance might entail a precision of a few centimeters [41]).
Thus, the PAR problem in Equation (24) can be reformulated to be subject to a minimal positioning accuracy, as
where denotes the trace operator. Unlike Equations (16) and (17), the fixed solution for a PAR estimator is expressed in terms of the subset of ambiguities fixed, as
and, as remains invariant with the subset choice, the selection can be realized so that
so that one may omit performing integer estimation if the associated positioning precision does not match the target . The procedure to operate PD-PAR consists on recursively finding the subset with best associated precision and whether a reliable integer solution exists (i.e., passing the validity test assures that the success rate is sufficiently high). If the position precision criteria is not fulfilled, a fixed solution cannot be estimated for the subset . The subset searching is based on Equation (27) that follows from Equation (17). Instead, if the precision is sufficient but a reliable solution is unavailable, the size of the subset reduces and the recursion is repeated.
Algorithm 2 proposes a top-bottom (the number of ambiguities to integer-map decreases with the iterations) workflow for PD-PAR, with the binomial coefficient where n is the length vector of DD carrier phase and code observables and s is the number of discarded observations. Notice that PD-PAR is indeed a model-driven PAR estimator, as the decision to whether accept or not a solution follows from any data-driven rules given in Equation (14), with the peculiarity that the subset selection is realized based on how good the ambiguities are projected into the positioning domain. Moreover, the Z-transform is estimated for each subset size which greatly reduces the degree of decorrelation among ambiguities at the cost of a slightly superior computational complexity. As for other data-driven approaches, the number of iterations until a subset can be reliably integer estimated is unknown. However, whenever the satellite geometry is poor or the model is weak, one can rapidly disregard any integer estimation, provided that a potential fixed solution would not comply with a target positioning precision. This latter is solved with a satellite selection via convex geometry as discussed in [42], which relates a bottom-top search would aim at finding the subset with the minimum number of ambiguities to satisfy the precision.
| Algorithm 2: Precision-Driven PAR |
 |
We notice that the complexity of the proposed PD-PAR is higher than its DD-PAR counterpart. More precisely, the computational complexity is dominated by the “subset listing” and “find best subset” operations in Algorithm 2, with being the asymptotic time complexity of the algorithm. This can be substantially higher than current methods; however, we would like to highlight that the additional computational complexity can be dealt with by the ever growing computational power of today’s GNSS devices [43,44], as we observed when running our experiments.
4. CRB for the PAR Mixed Model
This section summarizes the main result in [27], which recently derived the CRB for the estimation of the mixed model in Equation (5), and extends its use to the PAR mixed model. Let us reformulate the problem as
The CRB provides a lower bound on the variance of any locally unbiased estimator, and it is used to assess the estimation performance of , the estimator of vector , such that
with the Fisher Information Matrix (FIM) and indicates that is a positive semidefinite matrix. In the case of a mixed model (5), the CRB is given by [27]
with a vector of selected values for the parameter vector . The terms of the CRB are as follows:
where is the kth column of the identity matrix and the test points , .
When considering a PAR estimation problem, its associated mixed model is expressed as
and for notation purpose, let us denote the dimension of the unknown real-valued vector and the total number of unknowns. Furthermore, the design matrix for the real parameters is given by
Thus, the CRB for the mixed model can be generalized to the PAR mixed model as
with also a selected value of , and the CRB matrix terms given by
and, again, test points are , .
New Insights from the CRB for the PAR Mixed Model
For the validation of the for a PD-PAR scheme, a realistic GNSS RTK experiment was simulated. Figure 1 shows the satellite geometry with satellites considered for this experiment at an IGS MGEX station POTS0 in Potsdam, Germany, on 26 March 2019 (DOY 085 12:00 UTC) and where the noise of the code is maintained two orders of magnitude larger than the carrier-phase measurement. To illustrate the performance of the PD-PAR with respect to a FAR scheme, the Root MSE (RMSE) obtained from Monte Carlo runs is used as a performance metric.
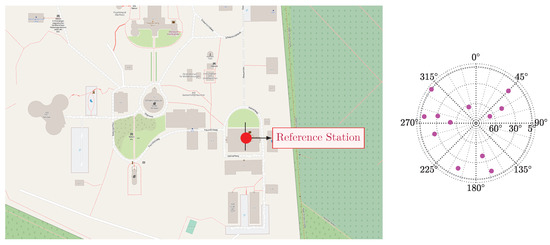
Figure 1.
Right side, IGS MGEX station POTS0 in Potsdam, Germany, as reference station (red mark). Right side, skyplot of the synthetic GNSS scenario.
Figure 2 shows the 3D position RMSE performance for both PD-PAR and FAR schemes. In the plot, the following results are shown:
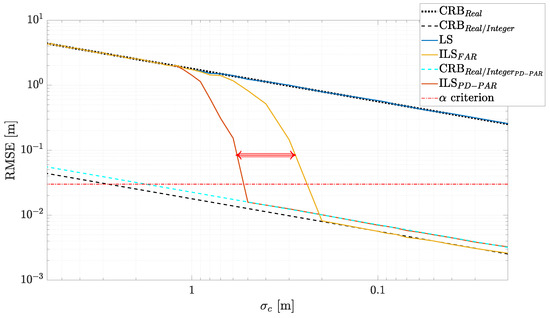
Figure 2.
RMSE and CRB as a function of the code noise standard deviation, , for FAR and PD-PAR schemes illustrating the difference between both asymptotic regions.
- Methods: (i) LS refers to the float solution estimate, (ii) ILS is the estimator that tries to fix all ambiguities, and (iii) ILS is the new PAR scheme proposed in this article. Notice that the horizontal line 5 cm is the specific precision constraint considered in this experiment.
First, notice that the float LS is efficient, that is, it coincides with the CRB. It is also worth pointing out the potential gain of correctly fixing the ambiguities (i.e., correctly using an ILS), that is, the difference between CRB and CRB. As in standard maximum likelihood estimators, we can identify three regions of operation:
- (1)
- For low code-noise levels ( for the FAR and for the PD-PAR), the so-called asymptotic regime, the ILS performance for both FAR and PD-PAR schemes coincides with CRB. This confirms that a correct ILS which considers only a successful IAR is asymptotically efficient. Obviously, there is a slight performance degradation when not fixing all the ambiguities, that is, the asymptotic performance of PD-PAR is slightly larger than with a correct FAR.
- (2)
- At high code-noise levels (), the RMSE performance of both ILS coincides with the float solution LS. In other words, after a certain level of noise, trying to fix the ambiguities is useless, and a correct IAR is never achieved.
- (3)
- The region between the asymptotic convergence to the mixed real/integer bound and the unconstrained float region is the so-called threshold region. Such a threshold provides information on the optimal receiver operation conditions. It is remarkable to see that the PD-PAR threshold appears for larger noise levels when compared to the FAR scheme, which implies that the PD-PAR provides a more reliable single-epoch IAR solution.
Overall, the PD-PAR (which forsakes a given position precision) does not improve the position estimation with respect to a correct FAR, but guarantees the precision criterion and achieves a correct IAR for larger noise values. Taking into account that the main problem in FAR schemes is that under harsh conditions, or with a large number of measurements, they do not achieve a correct IAR, it turns out that the new PD-PAR is a powerful alternative. To further support this statement, we show the success rate for both schemes in Figure 3, where the advantage brought by the PD-PAR is clear. Even for high code-noise levels meter, a PD-PAR scheme maximizes the ILS success rate providing a high reliability when FAR fails.
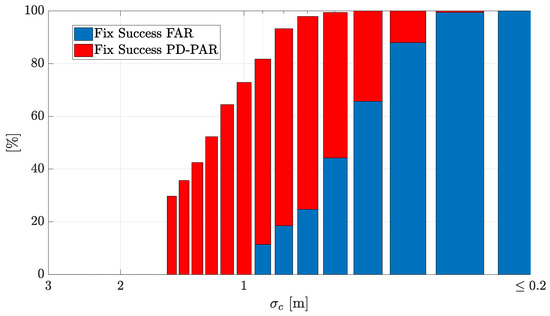
Figure 3.
Comparison of the single-epoch IAR experimental success rate for FAR and PD-PAR schemes. At high code-noise levels , an IAR is still achieved with a precision-aided PAR scheme approach.
5. Evaluation Results
The analysis and evaluation of the RTK performance with three different ambiguity resolutions schemes, i.e., FAR, data-driven PAR [45], and the new precision-aided PAR, are presented in the sequel. An instantaneous dual-frequency GPS+Galileo navigation system was used for the both synthetic and real data evaluation setups.
5.1. Simulation Results
Two hours of GNSS data was used for the simulation setup at an IGS MGEX station POTS0 in Potsdam, Germany, on 26 March 2019 (DOY 085 12:00–14:00 UTC) with a data interval of 30 s. A combined GPS (L1 + L2) and Galileo (E1 + E5a) dual-frequency system was evaluated with a cut-off elevation angle of . Figure 4 illustrates the number of GPS and Galileo satellites along the experiment duration. The failure rate was set to . The analysis of the proposed precision-aided PAR scheme was made for different baseline lengths, and implemented in a non-recursive (snapshot) LS-type float solution manner.
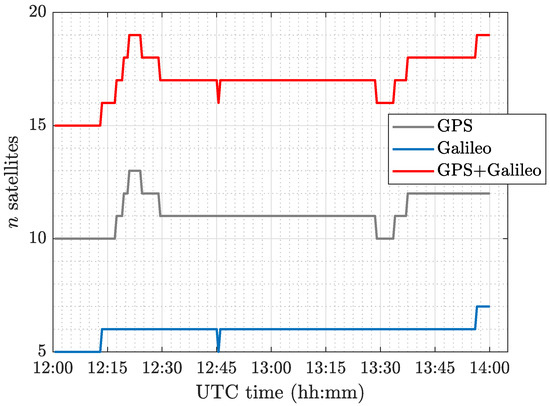
Figure 4.
Number of GPS (L1 + L2) and Galileo (E1 + E5a) satellites for the simulated scenario.
The zenith-referenced (undifferenced) code and carrier phase standard deviations are listed in Table 1. The ionospheric delays and the zenith-references code and carrier phase noises listed in Table 1 are scaled with the elevation dependent function .

Table 1.
Wavelengths and zenith-referenced code and carrier standard deviations for GPS and Galileo observations.
When FAR fails, an ambiguity subset searching algorithm is enforced where the precision-aided condition (27) is fulfilled and following Algorithm 2 described in Section 3 to determine the best subset which allows to reach the minimum precision-aided criterion .
A precision metric cm was defined, and was adjusted with a functional model followed in [16]. Figure 5 shows the results obtained from Monte Carlo runs, considering the model-driven (MD), data-driven (DD), and developed precision-driven (PD) FAR/PAR schemes. It is worth noting from Figure 5 that, when the baseline length increases, the ionospheric delay plays an important role in having a success IAR showing an advantage with a PAR scheme. Figure 5a shows the experimental success rate for the different ambiguity resolution schemes, where it is clear that the MD-PAR scheme has the worst performance when the baseline length grows, in comparison with DD or PD PAR schemes, as only the covariance information is taken into account. Furthermore, notice that an improved availability of successful IAR is provided with the new PD-PAR scheme, which can be seen in Figure 5b. This is because the selection of the best subset to be fixed depends only on the precision domain defined as a function of . The latter is also shown in Figure 6 for only one GNSS constellation, where the PD-PAR scheme achieves the highest success rate.
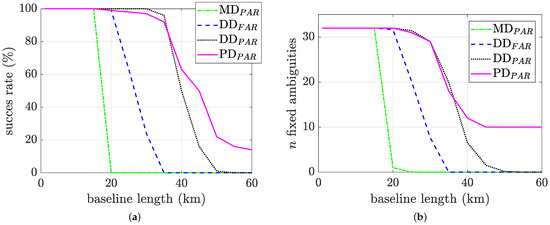
Figure 5.
Model-driven (MD), data-driven (DD), and precision-driven (PD) performance analysis. (a) Experimental success rate. (b) Number of fixed ambiguities.
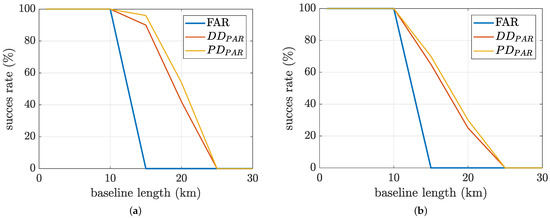
Figure 6.
Comparison with different ambiguity resolution schemes for one GNSS constellation only. (a) GPS (L1 + L2) experimental success rate. (b) Galileo (E1 + E5a) experimental success rate.
In terms of positioning error, Figure 7 plots the 3D position RMSE performance, together with the corresponding CRBs for a MD-PAR, a DD-FAR/PAR, and a PD-PAR scheme. Even when a data-driven scheme offers a prominent approach in terms of MSE, a PD-PAR scheme offers a major availability in having a correct IAR satisfying the position precision criteria and maximizes the ILS success rate.
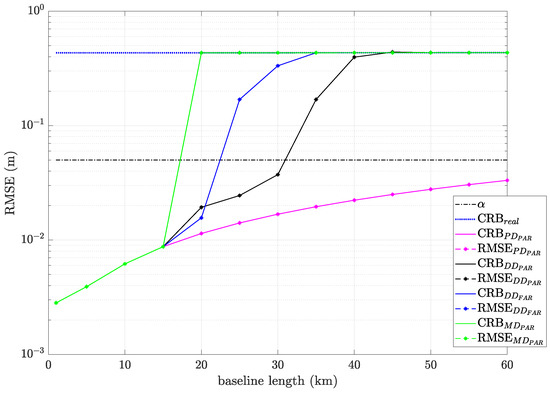
Figure 7.
RMSE for each ambiguity resolution scheme vs baseline length.
5.2. Validation with Real Data
An analysis with real data was performed, providing a comparative for FAR, DD-PAR, and PD-PAR. For that end, twelve hours of data collected at the IGS MGEX stations of PERT and CUT0 in Perth, Australia, on 7 May 2020 (DOY 128 01:00–07:00 UTC) is employed. The CUT0-PERT baseline length is 22.41 km, which may be considered a medium baseline distance. The cut-off elevation angle is set at , and dual-frequency data are used for the GPS and Galileo constellations (L1, L2 for GPS and E1, E5a for Galileo). To provide a fair comparison, this validation focuses only on model-driven validity tests, and MD-PAR is therefore excluded for the comparison. In particular, the FF-RT uses a target failure rate of (as in the simulated experiment) and the minimum target positioning precision is again five cm. The results of real data evaluation are graphically depicted in Figure 8, Figure 9 and Figure 10.
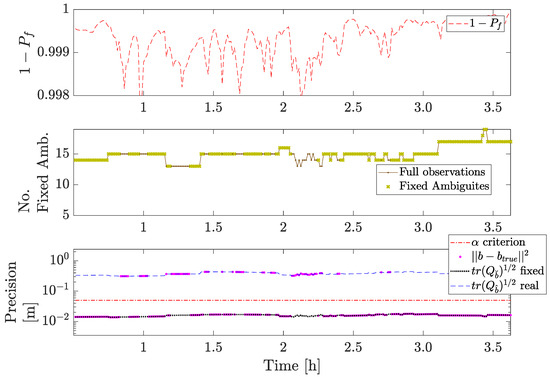
Figure 8.
GPS (L1 + L2) + GAL (E1 + E5a) performance comparative for a FAR scheme.
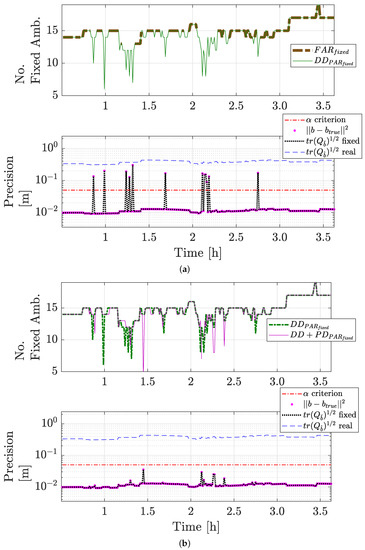
Figure 9.
Comparative of success rate . Number of fixed ambiguities and precision for FAR, Data-Driven PAR, and Data-Driven+precision-aided PAR schemes. (a) GPS (L1 + L2) + GAL (E1 + E5a) performance comparative for a DD-PAR scheme when FAR fails (no fixed solution). (b) GPS (L1 + L2) + GAL (E1 + E5a) performance comparative for the proposed DD+PD PAR scheme when FAR or DD-PAR fails (no fixed solution). Furthermore, PD-PAR guarantees a fixed solution whose fixed positioning errors (and precision) respect the criteria for minimum required positioning precision .
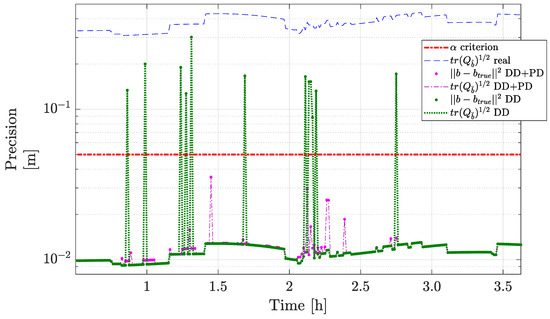
Figure 10.
FAR vs Precision-aided PAR scheme RMSE error positioning performance.
Figure 8 showcases the performance obtained with FAR for a period of 3.5 h. On the top, the IB success rate (upper bound for the ILS one) is shown. On the middle, the number of ambiguities to estimate (dotted solid line) and the number of those which are fixed (marked with green crosses) by FAR. Notice that whenever a green cross is missing, a fixed solution could be reliably estimated by FAR. On the bottom, it is shown the minimum required precision in dashed red color over time, along with the precision for the float and fixed positioning (in blue and black, respectively), and the positioning errors (in pink). Whenever a pink dot appears over the blue line (float precision), a float positioning solution was estimated by FAR, as the integer estimation did not pass the associated FF-RT test. In total, FAR was only able to provide a fixed positioning solution for 88.33% of time, which constitutes the poorest performance in comparison with DD- and PD-PAR.
A direct comparison between DD-PAR is given in Figure 9a for the same 3.5 h period. On the top, it is depicted the fixed number of ambiguities by FAR (in red dashed line) and DD-PAR (in green solid line). It is clear that, while FAR fails at providing a solution for all the ambiguities, DD-PAR manages to reliably estimate a subset of them. In the bottom part of Figure 9a, it is showcased the precision of float and fixed positioning for DD-PAR (in blue dashed and black dotted lines, respectively), as well as the positioning errors (in pink dots). For this period of time, DD-PAR provides a fixed solution for 100% of the time. However, in certain time instances the DD-PAR subset of fixed ambiguities leads to a fixed positioning solution which, while being better than the float one, does not qualify for our minimum positioning precision required. Notice that the errors for the fixed positioning are, at all times, right on top of the associated precision, meaning that there are no wrongly estimated integer ambiguities for this period.
Similarly, the top part of Figure 9b provides a comparison between DD-PAR and PD-PAR, in terms of number of fixed ambiguities. Interestingly, there are epochs in which the number of fixed ambiguities do not agree, mostly due to differences in the subset selection criteria and the repeated Z-transformation applied to each subset search in PD-PAR. On the bottom part of Figure 9b, it is shown the float and fixed positioning precision (dashed blue and black dotted lines, respectively) and the actual positioning errors (in pink dots). A noticeable fact appears close before the 1.5 h point, a moment in which PD-PAR fixes a much lower number of ambiguities than DD-PAR and still the positioning precision and errors are well below the required minimum precision. As for the DD-PAR case, the fact that the positioning errors perfectly align with the estimated precision is due to the ambiguities being correctly estimated for the complete period of time (i.e., the experimental failure rate is null).
Figure 10 shows the precision error for a FAR and the precision-aided PAR scheme with its corresponding . As the precision error with PAR is slightly higher than the precision error with a FAR scheme, this does not has a big impact since the position precision criteria is never violated.
Finally, we take into consideration the complete 12 h of real data to provide a numerical comparison of the availability of high precision positioning solutions, as summarized in Table 2. Thus, the availability of cm-level estimates is higher for PD-PAR in a instantaneous-time ambiguity modus, reaching a of IAR success rate, with a total of discarded ambiguities. The experimental success rate for the integer estimated subset of ambiguities amounts to 100%. In terms of experimental success rate, also FAR and DD-PAR presents no wrongly estimated ambiguities, although the availability of the solution is 88.33% and 98.60%, respectively. Figure 11 shows the correctly fixed solution along with the empirical success rates for 12 h of real data for a DD-PAR and PD-PAR approach, respectively. All epochs were correctly fixed where PD-PAR guarantees a high empirical success rate in comparison with DD-PAR. These results demonstrate that the PD-PAR method makes a best subset ambiguities searching and assures a fixed solution when FAR or a DD-PAR approach fails.

Table 2.
Percentage of fixed solutions for every IAR method for 12 h of real data.
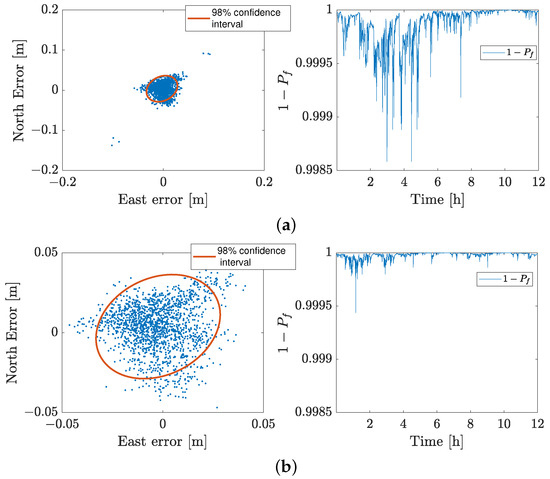
Figure 11.
Horizontal (NE) position scatter plots along with the success rate for 12 h of real data (PERT-CUT0) only for fixed solutions. (a) DD-PAR performance analysis for 12 h of real data. (b) PD-PAR performance analysis for 12 h of real data.
6. Conclusions
This work introduces a novel precision-aided PAR technique that makes a subset ambiguities selection based on the projection of the ambiguities into the position domain, increasing the mapping of real values to integer ones. The CRB for real/integer values presented in this work was used as a tool to verify the consistency and convergence of precision-aided PAR scheme. The bound was compared with the evaluated RMSE together with its corresponding CRB, showing that precision-aided PAR scheme maps real-to-integer values in a consistent manner. Despite the fact that the data-driven PAR method gives a prominent performance in comparison with the model-driven PAR, the precision-aided PAR method presented in this study offers a fix ratio of with a non-violation of the position precision criteria. Furthermore, the precision-aided PAR method provides an availability in having a correct IAR and maximizing the ILS success rate while also having a better efficiency of the mixed real and integer parameter estimation using a precision-aided PAR scheme. The validation of a precision-aided PAR scheme was evaluated and presented using real data showing optimal results. A precision-aided PAR scheme reaches a of IAR success rate in comparison with the data-driven PAR that achieves a of fix ratio when FAR is not always optimal in terms of success rate of ambiguity resolution.
Author Contributions
Conceptualization, D.M.; Data curation, J.M.C.-A.; Formal analysis, J.V.-V.; Funding acquisition, R.Z.; Investigation, J.M.C.-A., D.M., J.V.-V. and P.C; Methodology, J.M.C.-A. and D.M.; Project administration, R.Z.; Supervision, R.Z. and E.C.; Writing—original draft, J.M.C.-A.; Writing—review & editing, D.M., J.V.-V., E.C., and P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Commission grant number 861377-IW-NET and BMVI grant number VB18F1025B and supported by the NSF under Awards CNS-1815349 and ECCS-1845833, and the French DGA/AID under project 2019.65.0068.00.470.75.01.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting the findings of this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2021. [Google Scholar]
- Teunissen, P.J.G. A new class of GNSS ambiguity estimators Artif. Satell. 2002, 37, 111–119. [Google Scholar]
- Langley, R.B.; RTK GPS. GPS World 1998, 70–75. Available online: http://www2.unb.ca/gge/Resources/gpsworld.september98.pdf (accessed on 20 January 2020).
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined BDS, Galileo, QZSS and GPS single-frequency RTK. GPS Solut. 2014. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; de Jonge, P.J.; Tiberius, C.C.C.J.M. The LAMBDA-Method for Fast GPS Surveying. In Proceedings of the International Symposium “GPS Technology Applications”, Bucharest, Romania, 26–29 September 1995; pp. 203–210. [Google Scholar]
- Verhagen, S. Integer ambiguity validation: An open problem? GPS Solut. 2004, 8, 36–43. [Google Scholar] [CrossRef]
- Williams, N.; Wu, G.; Closas, P. Impact of positioning uncertainty on eco-approach and departure of connected and automated vehicles. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1081–1087. [Google Scholar]
- Kassas, Z.M.; Closas, P.; Gross, J. Navigation systems panel report navigation systems for autonomous and semi-autonomous vehicles: Current trends and future challenges. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 82–84. [Google Scholar] [CrossRef]
- Liu, X.; Ribot, M.Á.; Gusi-Amigó, A.; Closas, P.; Garcia, A.R.; Subirana, J.S. RTK Feasibility Analysis for GNSS Snapshot Positioning. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online, 22–25 September 2020; pp. 2911–2921. [Google Scholar]
- Liu, X.; Ribot, M.Á.; Gusi-Amigó, A.; Rovira-Garcia, A.; Subirana, J.S.; Closas, P. Cloud-Based Single-Frequency Snapshot RTK Positioning. Sensors 2021, 21, 3688. [Google Scholar] [CrossRef]
- Parkins, A. Increasing GNSS RTK availability with a new single-epoch batch partial ambiguity resolution algorithm. GPS Solut. 2011, 15, 391–402. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Kalman-filter-based integer ambiguity resolution strategy for long-baseline RTK with ionosphere and troposphere estimation. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation 2010, Portland, OR, USA, 21–24 September 2010. [Google Scholar]
- Teunissen, P.J.G.; Odijk, D. Ambiguity dilution of precision: Definition, properties and application. Proc. ION GPS 1997, 1, 891–899. [Google Scholar]
- Henkel, P.; Günther, C. Partial integer decorrelation: Optimum trade-off between variance reduction and bias amplification. J. Geod. 2010, 84, 51–63. [Google Scholar] [CrossRef]
- Brack, A.; Günther, C. Generalized integer aperture estimation for partial GNSS ambiguity fixing. J. Geod. 2014, 88, 479–490. [Google Scholar] [CrossRef]
- Brack, A. On reliable data-driven partial GNSS ambiguity resolution. GPS Solut. 2015, 19, 411–422. [Google Scholar] [CrossRef]
- Brack, A. Partial ambiguity resolution for reliable GNSS positioning—A useful tool? IEEE Aerosp. Conf. Proc. 2016, 1–7. [Google Scholar] [CrossRef]
- Brack, A. Partial Carrier-Phase Integer Ambiguity Resolution for High Accuracy GNSS Positioning. Ph.D. Thesis, Technische Universität München (TUM), München, Germany, 2019. [Google Scholar]
- Closas, P.; Fernández-Prades, C.; Fernández-Rubio, J.A. Cramér-Rao bound analysis of positioning approaches in GNSS receivers. IEEE Trans. Signal Process. 2009, 57, 3775–3786. [Google Scholar] [CrossRef]
- Das, P.; Ortega, L.; Vilà-Valls, J.; Vincent, F.; Chaumette, E.; Davain, L. Performance limits of GNSS code-based precise positioning: GPS, galileo & meta-signals. Sensors 2020, 20, 2196. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X. Estimation and Tracking-Principles, techniques, and Software; Artech House, Inc.: Norwood, MA, USA, 1993. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Success probability of integer GPS ambiguity rounding and bootstrapping. J. Geod. 1998, 72, 606–612. [Google Scholar] [CrossRef]
- Hassibi, A.; Boyd, S. Integer parameter estimation in linear models with applications to GPS. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. An optimality property of the integer least-squares estimator. J. Geod. 1999. [Google Scholar] [CrossRef]
- Medina, D.; Ortega, L.; Vilà-Valls, J.; Closas, P.; Vincent, F.; Chaumette, E. Compact crb for delay, doppler, and phase estimation—A pplication to gnss spp and rtk performance characterization. IET Radar Sonar Navig. 2020, 14, 1537–1549. [Google Scholar] [CrossRef]
- Medina, D.; Vilà-Valls, J.; Chaumette, E.; Vincent, F.; Closas, P. Cramér-Rao bound for a mixture of real- and integer-valued parameter vectors and its application to the linear regression model. Signal Process. 2021, 179. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O.E. Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Eueler, H.J.; Goad, C.C. On optimal filtering of GPS dual frequency observations without using orbit information. Bull. Géodésique 1991, 65, 130–143. [Google Scholar] [CrossRef]
- Medina, D.; Gibson, K.; Ziebold, R.; Closas, P. Determination of Pseudorange Error Models and Multipath Characterization under Signal-Degraded Scenarios. In Proceedings of the 31st International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2018), Miami, FL, USA, 24–28 September 2018. [Google Scholar] [CrossRef]
- Wielgosz, P. Quality assessment of GPS rapid static positioning with weighted ionospheric parameters in generalized least squares. GPS Solut. 2011, 15, 89–99. [Google Scholar] [CrossRef]
- Paziewski, J.; Wielgosz, P. Investigation of some selected strategies for multi-GNSS instantaneous RTK positioning. Adv. Space Res. 2017, 59, 12–23. [Google Scholar] [CrossRef]
- Odijk, D. Weighting Ionospheric Corrections to Improve Fast GPS Positioning Over Medium Distances. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000. [Google Scholar]
- de Jonge, P.; Tiberius, C. Integer Ambiguity Estimation with the Lambda Method. In GPS Trends in Precise Terrestrial, Airborne, and Spaceborne Applications; Springer: Berlin/Heidelberg, Germany, 1996; pp. 280–284. [Google Scholar] [CrossRef]
- Verhagen, S.; Teunissen, P.J.G. The ratio test for future GNSS ambiguity resolution. GPS Solut. 2013, 17, 535–548. [Google Scholar] [CrossRef]
- Wang, L.; Verhagen, S. A new ambiguity acceptance test threshold determination method with controllable failure rate. J. Geod. 2015, 89, 361–375. [Google Scholar] [CrossRef]
- Verhagen, A.A.; Teunissen, P.J.G.; van der Marel, H.; Li, B. GNSS ambiguity resolution: Which subset to fix? In Proceedings of the International Global Navigation Satellite Systems Society, Sydney, Australia, 15–17 November 2011.
- Odijk, D.; Arora, B.S.; Teunissen, P.J. Predicting the success rate of long-baseline GPS+Galileo (Partial) ambiguity resolution. J. Navig. 2014, 67, 385–401. [Google Scholar] [CrossRef]
- Brack, A. Optimal Estimation of a Subset of Integers with Application to GNSS. Artif. Satell. 2016, 51, 123–134. [Google Scholar] [CrossRef][Green Version]
- Fernandez-Hernandez, I.; Senni, T.; Calle, D.; Cancela, S.; Vecchione, G.A.; Seco-Granados, G. Analysis of High-Accuracy Satellite Messages for Road Applications. IEEE Intell. Transp. Syst. Mag. 2020, 12, 92–108. [Google Scholar] [CrossRef]
- Heßelbarth, A.; Medina, D.; Ziebold, R.; Sandler, M.; Hoppe, M.; Uhlemann, M. Enabling Assistance Functions for the Safe Navigation of Inland Waterways. IEEE Intell. Transp. Syst. Mag. 2020, 12, 123–135. [Google Scholar] [CrossRef]
- Blanco-Delgado, N.; Nunes, F.D. Satellite selection method for multi-constellation GNSS using convex geometry. IEEE Trans. Veh. Technol. 2010, 59, 4289–4297. [Google Scholar] [CrossRef]
- Pany, T.; Dampf, J.; Bär, W.; Winkel, J.; Stöber, C.; Fürlinger, K.; Closas, P.; Garcia-Molina, J. Benchmarking CPUs and GPUs on embedded platforms for software receiver usage. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015; pp. 3188–3197. [Google Scholar]
- Dampf, J.; Pany, T.; Bär, W.; Winkel, J.; Stöber, C.; Fürlinger, K.; Closas, P.; Garcia-Molina, J. More than we ever dreamed possible: Processor technology for GNSS software receivers in the year 2015. Inside GNSS 2015, 10, 62–72. [Google Scholar]
- Brack, A. Reliable GPS + BDS RTK positioning with partial ambiguity resolution. GPS Solut. 2017, 21, 1083–1092. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).