An Algorithm to Retrieve Total Precipitable Water Vapor in the Atmosphere from FengYun 3D Medium Resolution Spectral Imager 2 (FY-3D MERSI-2) Data
Abstract
1. Introduction
2. Data and Methodology
2.1. The FY-3D MERSI-2 Data
2.2. Theoretical Basis for PWV Algorithm Development
2.3. The Ratio Technique for PWV Estimation
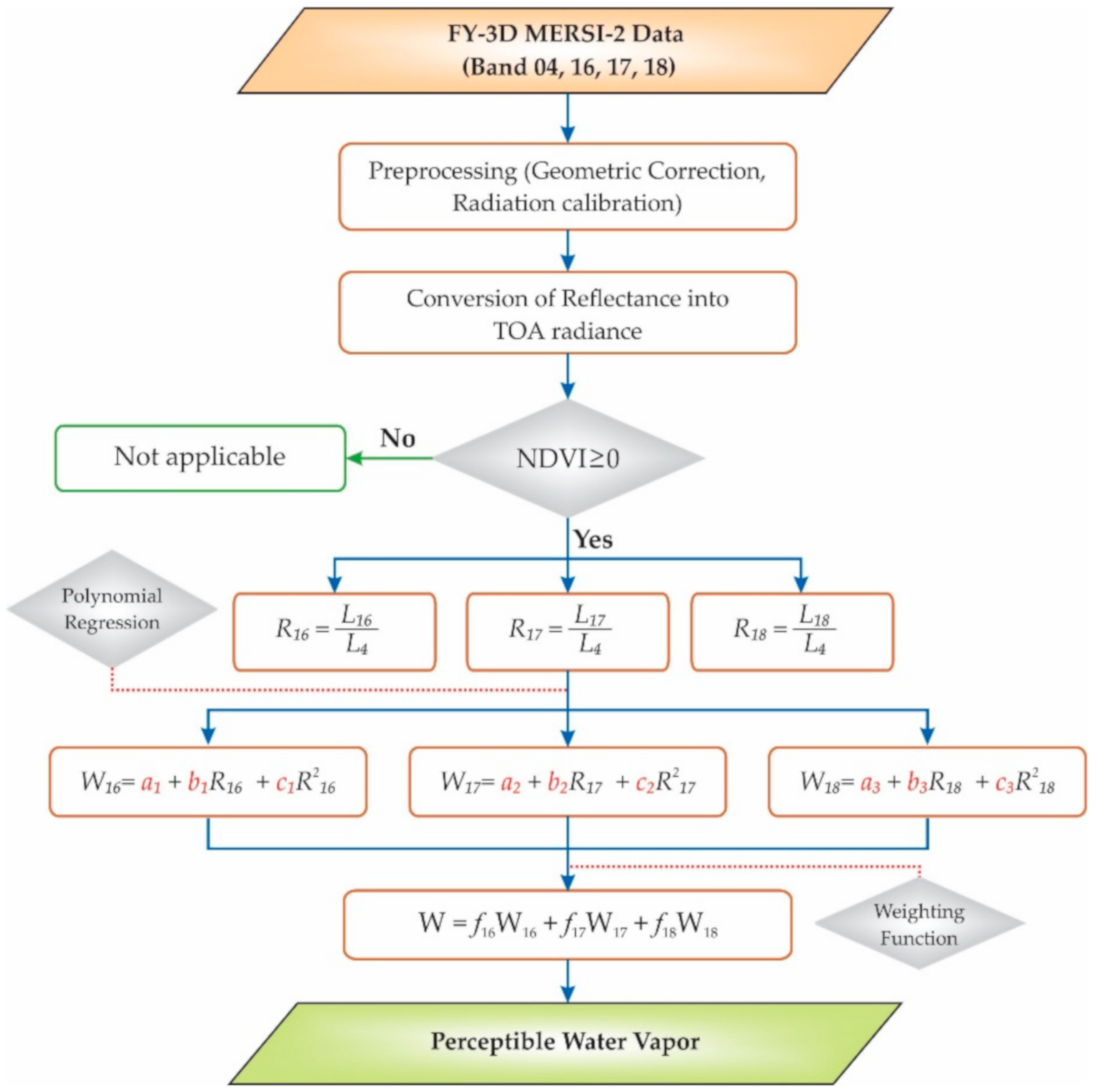
2.4. Algorithm Development for PWV Estimation
2.5. Framework and Technical Procedures
2.6. Validation of the Algorithm
2.7. Sensitivity Analysis
3. Results and Validation
3.1. Precipitable Water from FY-3D NIR Algorithm
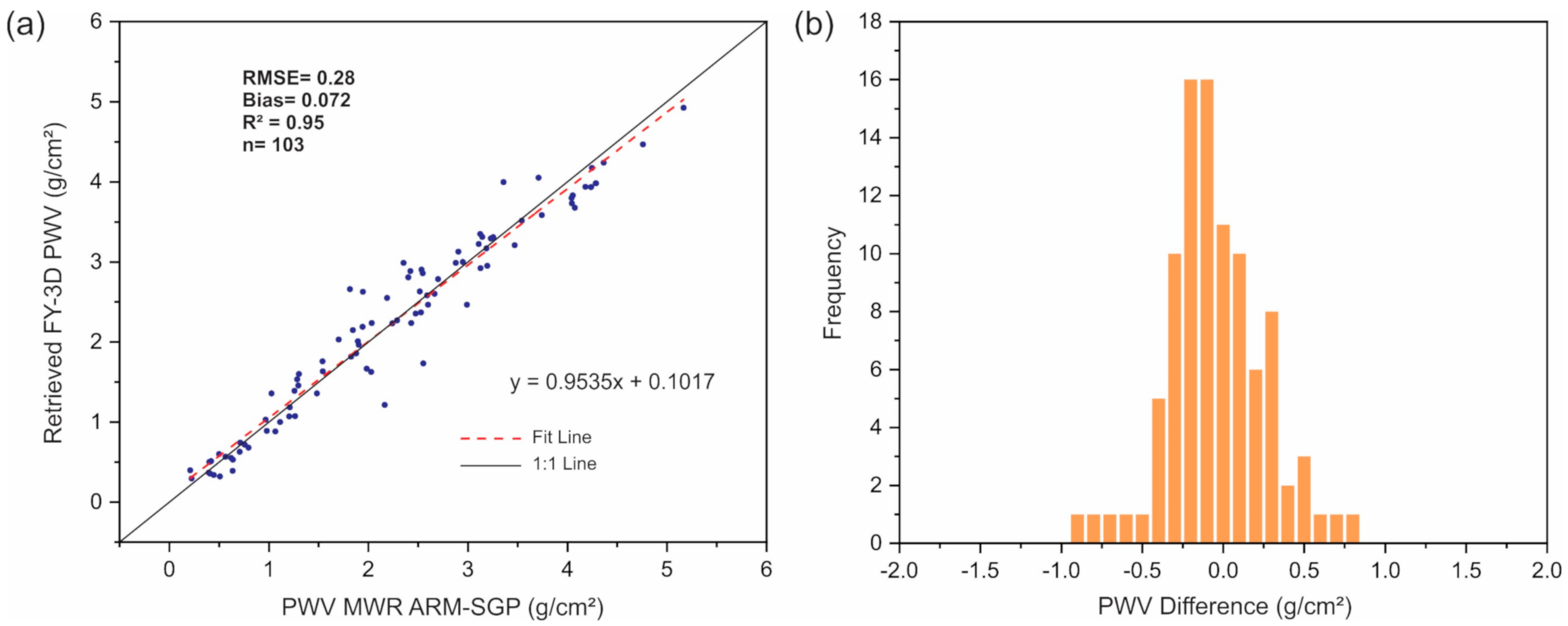
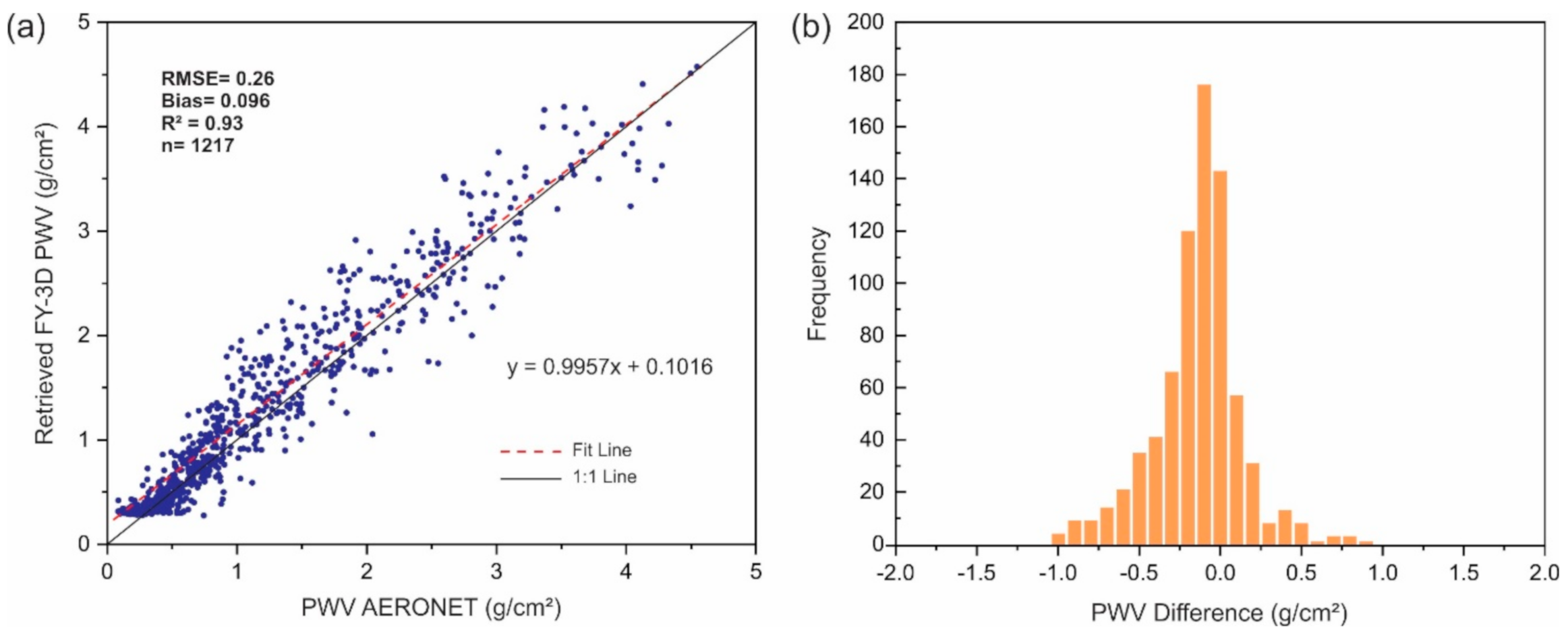
3.2. Validation and Error Analysis
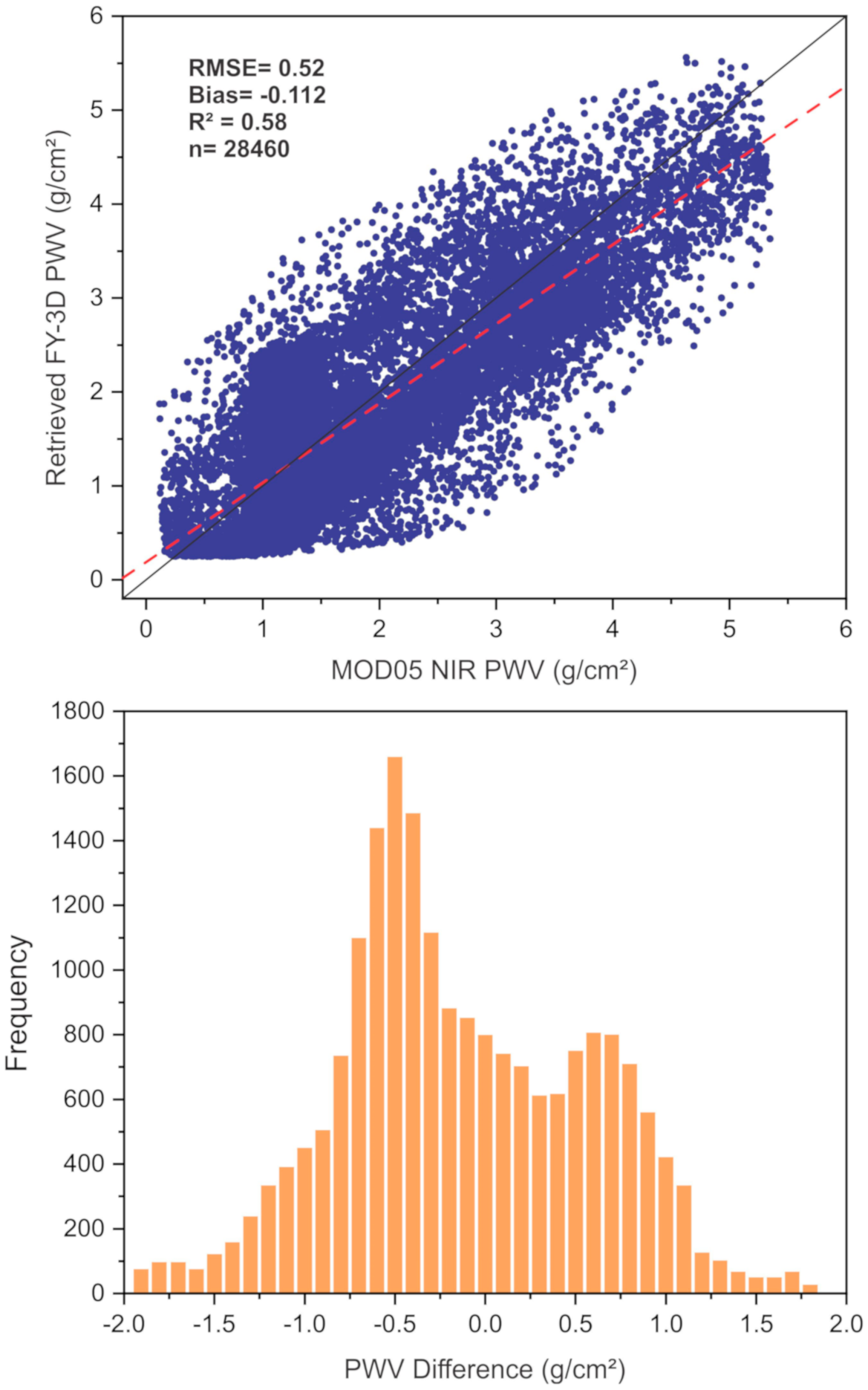
3.3. Comparison with MOD05 Water Vapor Product of MODIS
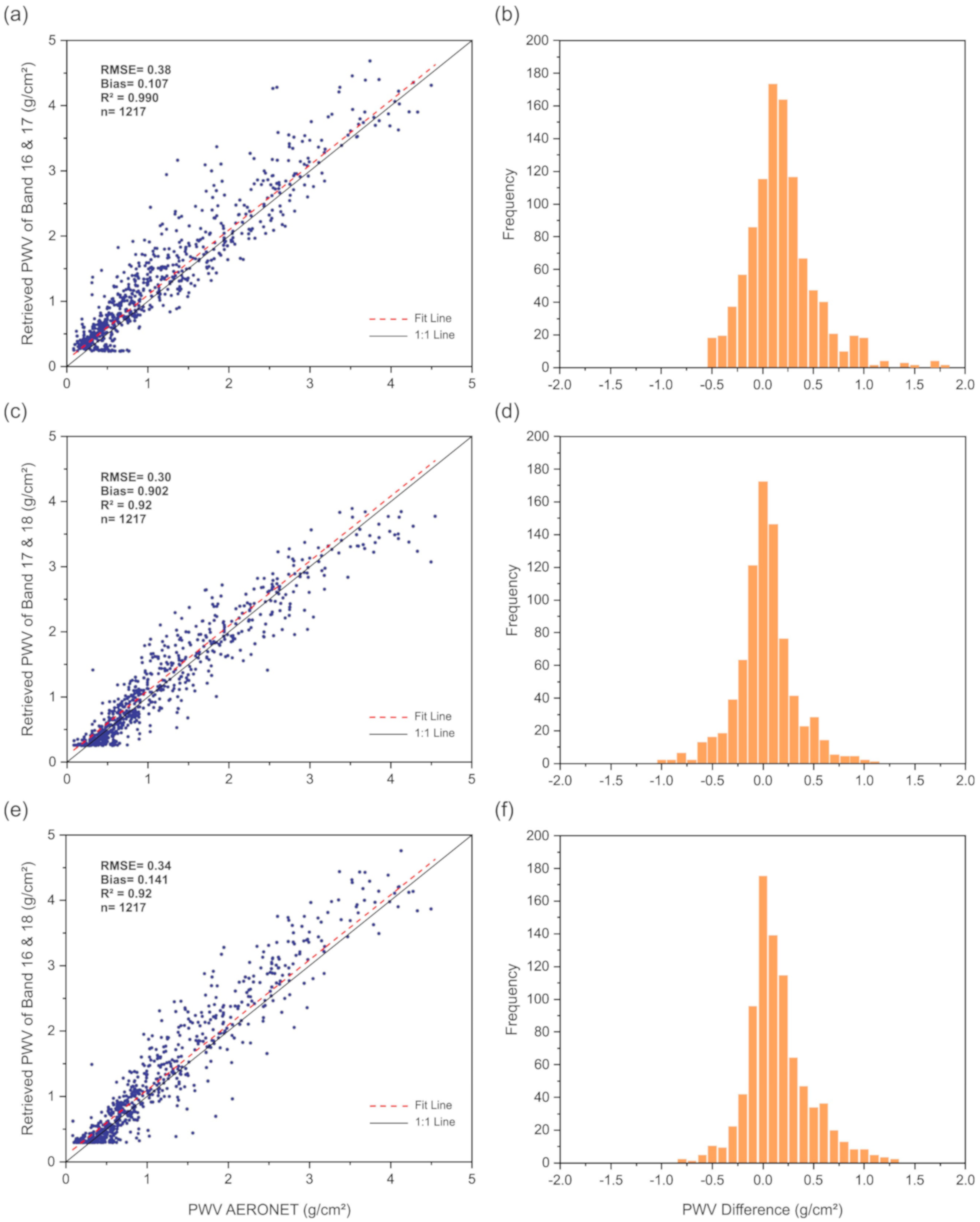
3.4. Comparison with Other Combinations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, T.; Wen, J.; Van der Velde, R.; Meng, X.; Li, Z.; Liu, Y.; Liu, R. Estimation of the Total Atmospheric Water Vapor Content and Land Surface Temperature Based on AATSR Thermal Data. Sensors 2008, 8, 1832–1845. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Ji, D.; Shi, J.; Wang, Y.; Lei, T.; Zhang, P.; Letu, H. The Retrieval of Total Precipitable Water over Global Land Based on FY-3D/MWRI Data. Remote Sens. 2020, 12, 1508. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust Responses of the Hydrological Cycle to Global Warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Niell, A.E.; Coster, A.J.; Solheim, F.S.; Mendes, V.B.; Toor, P.C.; Langley, R.B.; Upham, C.A. Comparison of Measurements of Atmospheric Wet Delay by Radiosonde, Water Vapor Radiometer, GPS, and VLBI. J. Atmos. Ocean. Technol. 2001, 18, 830–850. [Google Scholar] [CrossRef]
- Roman, J.; Knuteson, R.; August, T.; Hultberg, T.; Ackerman, S.; Revercomb, H. A global assessment of NASA AIRS v6 and EUMETSAT IASI v6 precipitable water vapor using ground-based GPS SuomiNet stations. J. Geophys. Res. Atmos. 2016, 121, 8925–8948. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.; Smith, L. Trends and variability in column-integrated atmospheric water vapor. Clim. Dyn. 2005, 24, 741–758. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, L.; Gan, B. Modes and Mechanisms of Global Water Vapor Variability over the Twentieth Century. J. Clim. 2013, 26, 5578–5593. [Google Scholar] [CrossRef]
- Reichardt, J.; Wandinger, U.; Serwazi, M.; Weitkamp, C. Combined Raman lidar for aerosol, ozone, and moisture measurements. Opt. Eng. 1996, 35, 1457–1465. [Google Scholar] [CrossRef]
- Chen, B.; Dai, W.; Liu, Z.; Wu, L.; Xia, P. Assessments of GMI-Derived Precipitable Water Vapor Products over the South and East China Seas Using Radiosonde and GNSS. Adv. Meteorol. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Gao, B.-C.; Goetz, A.F.H. Column atmospheric water vapor and vegetation liquid water retrievals from Airborne Imaging Spectrometer data. J. Geophys. Res. Space Phys. 1990, 95, 3549–3564. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Gao, B.-C. Remote sensing of water vapor in the near IR from EOS/MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 871–884. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Simarro, J.; Nerry, F.; Petitcolin, F. Atmospheric water vapor content over land surfaces derived from the AVHRR data: Application to the Iberian Peninsula. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1425–1434. [Google Scholar] [CrossRef]
- Mao, K.; Shen, X.; Zuo, Z.; Ma, Y.; Liu, G.; Tang, H. An Advanced Radiative Transfer and Neural Network Scheme and Evaluation for Estimating Water Vapor Content from MODIS Data. Atmosphere 2017, 8, 139. [Google Scholar] [CrossRef]
- Sobrino, J.A.; El Kharraz, J.; Li, Z.-L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens. 2003, 24, 5161–5182. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Zhu, R. An Improved Algorithm for Retrieving Atmospheric Water Vapor Using MODIS Near-Infrared Data. In Proceedings of the 2nd International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE) Nanjing, Jiangsu, China, 1 June 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Hu, J.; Tang, S.; Liu, H.; Min, M. An Operational Precipitable Water Vapor Retrieval Algorithm for Fengyun-2F/VLSSR Using a Modified Three-Band Physical Split-Window Method. J. Meteorol. Res. 2019, 33, 276–288. [Google Scholar] [CrossRef]
- McAtee, B.K.; Maier, S.W. A comparison of algorithms for Near-Real Time water vapour retrieval from MODIS. Int. J. Remote Sens. 2006, 27, 5145–5163. [Google Scholar] [CrossRef]
- Varamesh, S.; Hosseini, S.M.; Rahimzadegan, M. Estimation of atmospheric water vapor using MODIS data 1. (case study: Golestan province of Iran). J. Mater. Environ. Sci. 2017, 8, 1690–1695. [Google Scholar]
- Moradizadeh, M.; Momeni, M.; Saradjian, M.R. Estimation and validation of atmospheric water vapor content using a MODIS NIR band ratio technique based on AIRS water vapor products. Arab. J. Geosci. 2013, 7, 1891–1897. [Google Scholar] [CrossRef]
- Fraser, R.; Kaufman, Y. The Relative Importance of Aerosol Scattering and Absorption in Remote Sensing. IEEE Trans. Geosci. Remote Sens. 1985, 625–633. [Google Scholar] [CrossRef]
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Gao, B.-C.; Kaufman, Y.J. Water vapor retrievals using Moderate Resolution Imaging Spectroradiometer (MODIS) near-infrared channels. J. Geophys. Res. Space Phys. 2003, 108, 1–10. [Google Scholar] [CrossRef]
- Berk, A. Voigt equivalent widths and spectral-bin single-line transmittances: Exact expansions and the MODTRAN®5 implementation. J. Quant. Spectrosc. Radiat. Transf. 2013, 118, 102–120. [Google Scholar] [CrossRef]
- Atmospheric Radiation Measurement (ARM). User Facility 2011, updated hourly. MWR Retrievals (MWRRET1LILJCLOU). 2019-08-01 to 2019-12-31, Southern Great Plains (SGP) Central Facility, Lamont, OK (C1). Compiled by K. Gaustad and L. Riihimaki. ARM Data Center. Available online: http://dx.doi.org/10.5439/1285691 (accessed on 20 March 2020).
- Turner, D.D.; Clough, S.A.; Liljegren, J.C.; Clothiaux, E.E.; Cady-Pereira, K.E.; Gaustad, K.L. Retrieving Liquid Water Path and Precipitable Water Vapor from the Atmospheric Radiation Measurement (ARM) Microwave Radiometers. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 3680–3690. [Google Scholar] [CrossRef]
- Turner, D.D.; Lesht, B.M.; Clough, S.A.; Liljegren, J.C.; Revercomb, H.E.; Tobin, D.C. Dry Bias and Variability in Vaisala RS80-H Radiosondes: The ARM Experience. J. Atmos. Ocean. Technol. 2003, 20, 117–132. [Google Scholar] [CrossRef]
- Sano, I.; Mukai, S.; Yamano, M.; Takamura, T.; Nakajima, T.; Holben, B. Calibration and validation of retrieved aerosol properties based on AERONET and SKYNET. Adv. Space Res. 2003, 32, 2159–2164. [Google Scholar] [CrossRef]
- Holben, B.; Eck, T.; Slutsker, I.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.; Kaufman, Y.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Bouffiès, S.; Bréon, F.M.; Tanre, D.; Dubuisson, P. Atmospheric water vapor estimate by a differential absorption technique with the polarisation and directionality of the Earth reflectances (POLDER) instrument. J. Geophys. Res. Space Phys. 1997, 102, 3831–3841. [Google Scholar] [CrossRef]
- Gao, B.-C.; Goetz, A.F.H.; Westwater, E.R.; Conel, J.E.; Green, R.O. Possible Near-IR Channels for Remote Sensing Precipitable Water Vapor from Geostationary Satellite Platforms. J. Appl. Meteorol. 1993, 32, 1791–1801. [Google Scholar] [CrossRef]
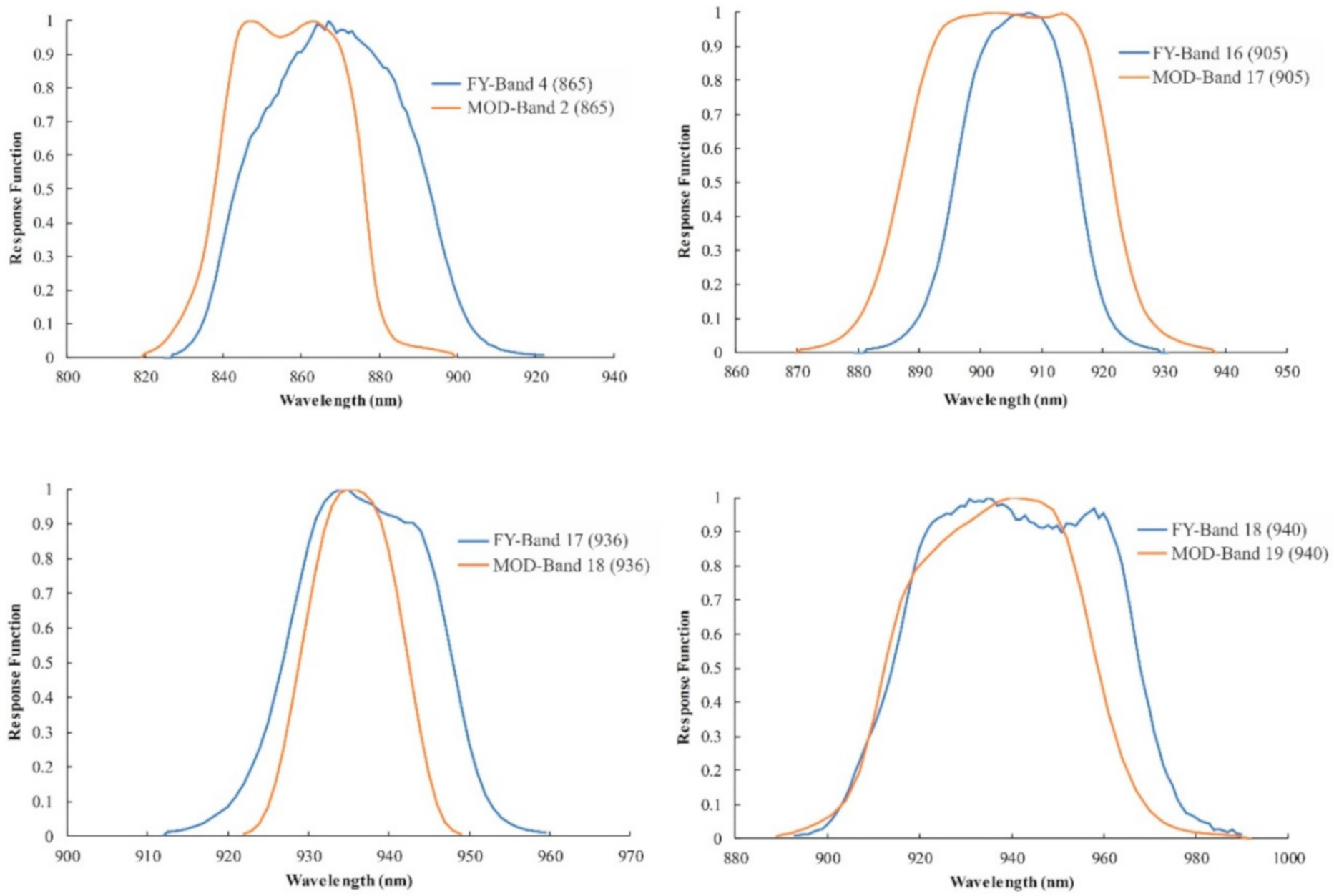
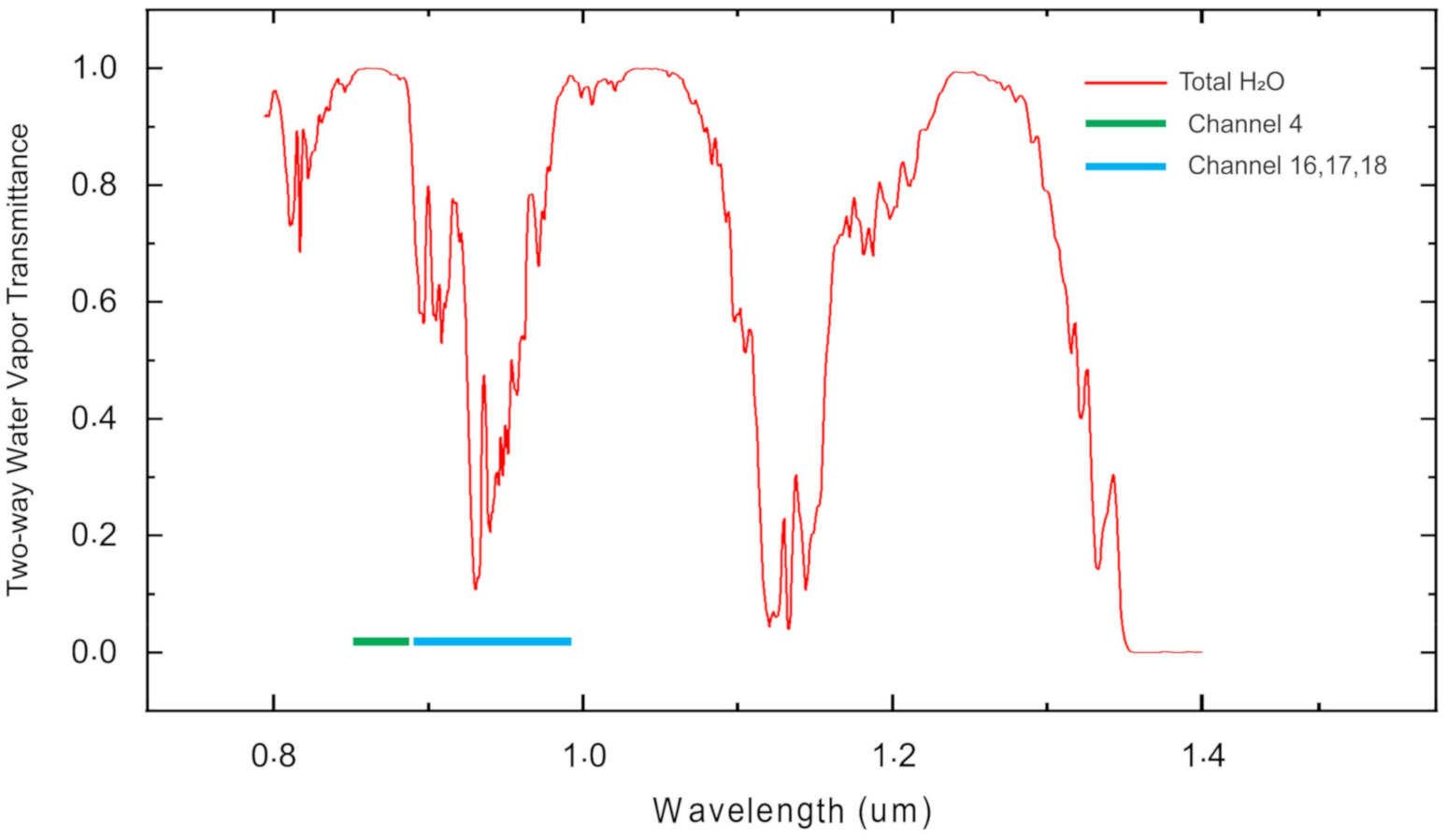
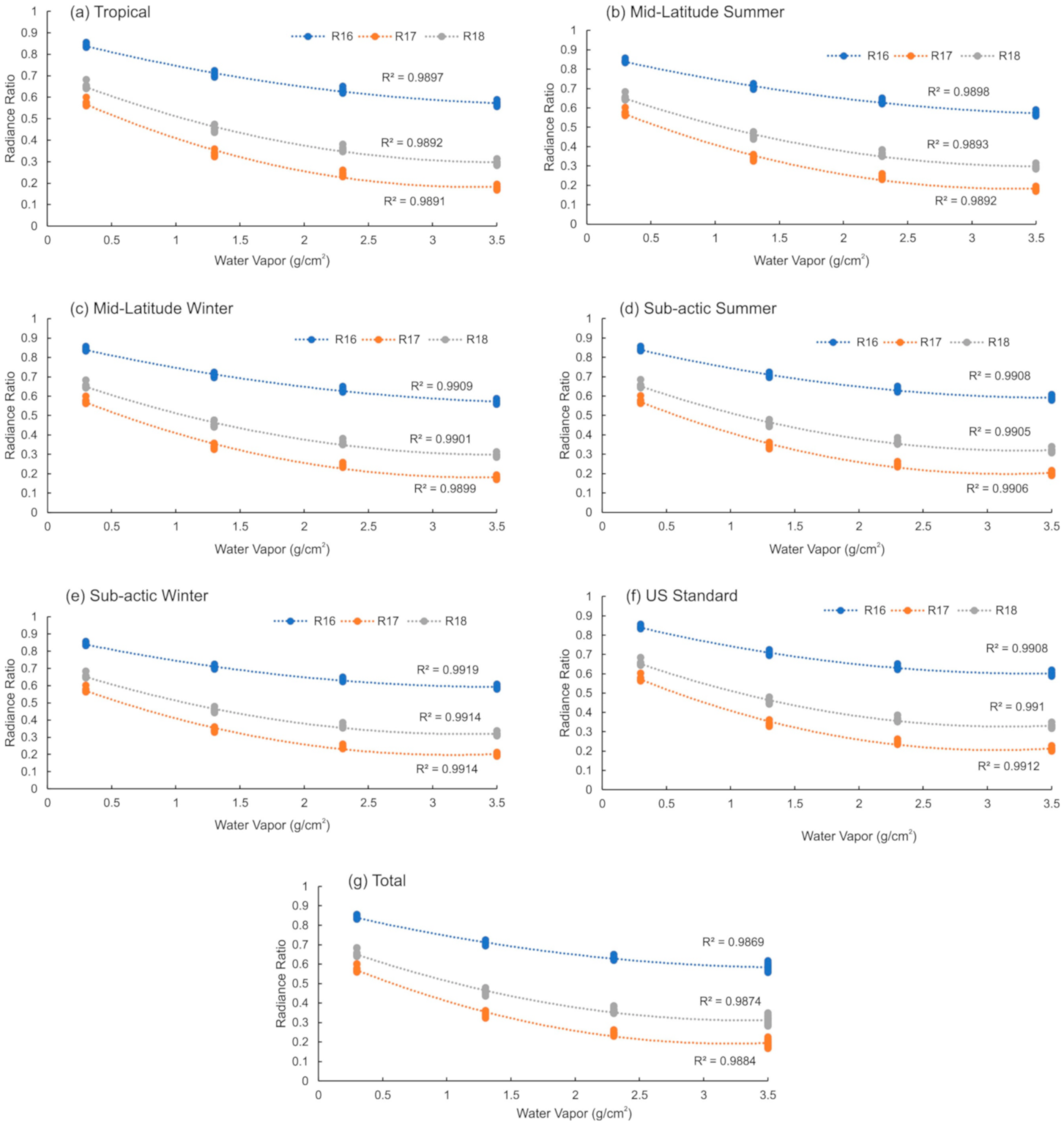

| MODIS Band | Position, µm | FY-3D Band | Position, µm |
|---|---|---|---|
| 2 | 0.865 | 4 | 0.865 |
| 17 | 0.905 | 16 | 0.905 |
| 18 | 0.936 | 17 | 0.936 |
| 19 | 0.940 | 18 | 0.940 |
| Parameter | Value | Instruction |
|---|---|---|
| MODEL | 1, 2, 3, 4, 5, 6 | MLS, TR, MLW, SAS, SAW and US. |
| ITYPE | 2 | Vertical path between two altitudes. |
| IEMSCT | 3 | Radiance/scattering model. |
| Column H2O | 0.3, 1.3, 2.3, 3.5 | Defined column water vapor value g/cm2. |
| Reflectance | −1, −2, −3, −4, −6, −8, −9, −10, −22, −40 | Snow cover, forest, farm, desert, ocean, burnt grass, maple leaf, decayed grass, cloud deck, and old grass. |
| IMULT | −1 | Multiple scattering. |
| LLFLTNM | MERSI2.flt | User-defined MERSI-2 FY-3D sensor filter function. |
| IHAZE | 1 | RURAL extinction, default VIS = 23 km. |
| GNDALT | 0 | Altitude of surface relative to sea level (km). |
| H1ALT | 100 | Altitude of the FY-3D satellite (km). |
| OBSZEN | 180 | Sensor zenith angle (°). |
| V1 | 10,000 | Initial wavenumber (cm). |
| V2 | 13,000 | Final wavenumber (cm). |
| PARM | 45 | Solar zenith angle (°). |
| Station Name | Latitude | Longitude |
|---|---|---|
| UACJ_UNAM_ORS | 31.743 | 106.432W |
| Yuma | 32.644 | 114.583 |
| Goldstone | 35.233 | 116.792 |
| NEON_SRER | 31.911 | 110.835 |
| USGS_Flagstaff_ROLO | 35.215 | 111.634 |
| Modesto | 37.642 | 120.994 |
| NEON_OSBS | 29.689 | 81.993 |
| IMPROVE-Mammoth Cave | 37.132 | 86.148 |
| NASA_Ames | 37.420 | 122.057 |
| ARM_SGP | 36.605 | 97.486 |
| NEON_UKFS | 39.040 | 95.192 |
| Univ_of_Houston | 29.718 | 95.342 |
| NEON_LENO | 31.854 | 88.161 |
| NEON-CPER | 40.812 | 104.744 |
| NEON_NIWO | 40.054 | 105.582 |
| White_Sands_HELSTF | 32.635 | 106.338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbasi, B.; Qin, Z.; Du, W.; Fan, J.; Zhao, C.; Hang, Q.; Zhao, S.; Li, S. An Algorithm to Retrieve Total Precipitable Water Vapor in the Atmosphere from FengYun 3D Medium Resolution Spectral Imager 2 (FY-3D MERSI-2) Data. Remote Sens. 2020, 12, 3469. https://doi.org/10.3390/rs12213469
Abbasi B, Qin Z, Du W, Fan J, Zhao C, Hang Q, Zhao S, Li S. An Algorithm to Retrieve Total Precipitable Water Vapor in the Atmosphere from FengYun 3D Medium Resolution Spectral Imager 2 (FY-3D MERSI-2) Data. Remote Sensing. 2020; 12(21):3469. https://doi.org/10.3390/rs12213469
Chicago/Turabian StyleAbbasi, Bilawal, Zhihao Qin, Wenhui Du, Jinlong Fan, Chunliang Zhao, Qiuyan Hang, Shuhe Zhao, and Shifeng Li. 2020. "An Algorithm to Retrieve Total Precipitable Water Vapor in the Atmosphere from FengYun 3D Medium Resolution Spectral Imager 2 (FY-3D MERSI-2) Data" Remote Sensing 12, no. 21: 3469. https://doi.org/10.3390/rs12213469
APA StyleAbbasi, B., Qin, Z., Du, W., Fan, J., Zhao, C., Hang, Q., Zhao, S., & Li, S. (2020). An Algorithm to Retrieve Total Precipitable Water Vapor in the Atmosphere from FengYun 3D Medium Resolution Spectral Imager 2 (FY-3D MERSI-2) Data. Remote Sensing, 12(21), 3469. https://doi.org/10.3390/rs12213469







