Abstract
Conventional relative kinematic positioning is difficult to be applied in the polar region of Earth since there is a very sparse distribution of reference stations, while precise point positioning (PPP), using data of a stand-alone receiver, is recognized as a promising tool for obtaining reliable and accurate trajectories of moving platforms. However, PPP and its integer ambiguity fixing performance could be much degraded by satellite orbits and clocks of poor quality, such as those of the geostationary Earth orbit (GEO) satellites of the BeiDou navigation satellite system (BDS), because temporal variation of orbit errors cannot be fully absorbed by ambiguities. To overcome such problems, a network-based processing, referred to as precise orbit positioning (POP), in which the satellite clock offsets are estimated with fixed precise orbits, is implemented in this study. The POP approach is validated in comparison with PPP in terms of integer ambiguity fixing and trajectory accuracy. In a simulation test, multi-GNSS (global navigation satellite system) observations over 14 days from 136 globally distributed MGEX (the multi-GNSS Experiment) receivers are used and four of them on the coast of Antarctica are processed in kinematic mode as moving stations. The results show that POP can improve the ambiguity fixing of all system combinations and significant improvement is found in the solution with BDS, since its large orbit errors are reduced in an integrated adjustment with satellite clock offsets. The four-system GPS+GLONASS+Galileo+BDS (GREC) fixed solution enables the highest 3D position accuracy of about 3.0 cm compared to 4.3 cm of the GPS-only solution. Through a real flight experiment over Antarctica, it is also confirmed that POP ambiguity fixing performs better and thus can considerably speed up (re-)convergence and reduce most of the fluctuations in PPP solutions, since the continuous tracking time is short compared to that in other regions.
Keywords:
PPP; double-difference; ambiguity fixing; orbit error; global network; GPS; GLONASS; Galileo; Beidou 1. Introduction
The GNSS (global navigation satellite system) precise kinematic positioning over the polar regions of Earth has always been an important topic, as its trajectory is essential information for any observing and monitoring system via mobile platforms, for example, for airborne gravimetry [1].
Usually, the traditional relative kinematic positioning (RKP), which requires reference stations nearby, is applied in order to remove most of the common biases. An alternative approach is the precise point positioning (PPP) using precise orbit and clock products and observations of a stand-alone receiver. This system usually takes about 30 min for initialization to achieve centimeter-level positioning accuracy and can be significantly improved by the carrier phase ambiguity resolution (AR) technique [2,3,4].
Compared with the positioning in other regions, there are quite few International GNSS Service (IGS) stations. It is also difficult to set up a reference station because of the harsh weather and the adamant soil layers. Therefore, RKP does not always work well over the polar regions. Moreover, satellites are usually tracked at lower elevation and over a shorter continuous period, due to the GNSS constellation with inclined orbit planes. Both observations of short period and at lower elevation bring difficulties in integer ambiguity resolution on one hand, on the other hand they also degrade the accuracy in height components. Therefore, further investigation is still required for PPP and its integer ambiguity resolution applied to the polar regions, although they have been well demonstrated elsewhere.
Nowadays, with the construction of global coverage of the Galileo and Beidou navigation satellite system (BDS), the multi-GNSS, including GPS, GLONASS (Russian GLObal Navigation Satellite System), Galileo and BDS, can provide a great number of satellites for positioning. That means that the poor accuracy of the vertical position due to the lower tracking elevation over Antarctica can be improved considerably. The accuracy of GPS, GLONASS and Galileo final orbit and clock products turns out to be at the same level, since their MGEX (Multi-GNSS Experiment) tracking stations are globally and evenly distributed, whereas there are only about 71 stations with Beidou observations, mainly distributed in Europe and Asia-pacific areas, and only two stations named CAS1 and DAV1 in Antarctica. Because of the insufficiently well distributed stations and a poorly developed solar radiation pressure model [5], the accuracy of the Beidou satellite orbits is relatively low compared to that of the other GNSS satellites, particularly for the BDS Geostationary Earth Orbit (GEO) satellites. The positioning and ambiguity fixing of BDS PPP will be greatly affected since it is dependent of the orbit and clock products. Li et al. [6] and Liu et al. [7] illustrated that the impact of BDS GEO orbit errors is similar for all stations in a regional network as the directions of the satellite to all receivers are almost the same and thus can be assimilated into the uncalibrated phase delays (UPDs). However, the impact difference gets larger for a global network from station to station and is regarded as a main obstacle for ambiguity fixing.
In order to get rid of the disadvantage of RKP and PPP, a method named precise orbit positioning (POP) [8] is applied to process the Antarctica data. This is, in principle, a network solution with fixed satellite orbits, where satellite clock offsets are estimated with a global or large regional reference network instead of a few nearby reference stations. According to Douša [9], 96% of the orbit errors in the radial direction can be compensated by the satellite clock in such a network processing mode. Including more stations will improve the clock estimation, especially when the distribution of the tracking stations is rather sparse over the interesting region. Furthermore, fixing ambiguities with respect to nearby reference stations is in principle easier to PPP ambiguity fixing with possibly contaminated UPDs. Therefore, this approach can achieve a higher positioning performance as well as ambiguity fixing compared to PPP when processing the BDS observations.
In this contribution, we concentrate on the comprehensive study of PPP and POP with aspects of ambiguity fixing and multi-GNSS impact and their improvements in positioning performance for their applications in the polar regions.
The rest of the paper is organized as follows. After the introduction of the basic observation model of multi-GNSS data processing, algorithms of double-difference (DD) ambiguity fixing is introduced for complexity with some special analyses for GLONASS and BDS. Afterwards, with data from the IGS MGEX network and data from a real flight experiment over Antarctica, the performance of single-, dual- and four-system PPP and POP ambiguity fixing, as well as kinematic positioning, are analyzed and investigated. The results, conclusions and perspectives are finally summarized.
2. Precise Orbit Positioning Processing Approach
2.1. Global Navigation Satellite System Observation Model
The GNSS observation equation of pseudorange and carrier phase can be expressed as follows:
where denotes the receiver, the satellite, the wavelength of the carrier phase, the speed of light in a vacuum, the geometric distance between the satellite position at the signal emission time and receiver position at the signal arrival time, and the receiver and satellite clock biases, and the receiver- and satellite-dependent UPDs; and are the code biases for the receiver and satellite. is the integer ambiguity, is the zenith total tropospheric delay, is the slant ionospheric delay, means the ionospheric delay is a function of the frequency and and are the sum of multipath effect error and measurement noise for the carrier phase and pseudorange observations, respectively. Furthermore, the relativistic delay and phase wind-up errors must be corrected with proper models accordingly [10], although they are not explicitly included in the equations.
The ionosphere-free (IF) combination is usually applied to eliminate the first-order ionospheric delays of the code and carrier phase observations. The GNSS code and phase IF combinations are defined as:
where and indicate frequency number and and mean the corresponding frequency. In this study, the L1 and L2 signals are used for GPS and GLONASS, E1 and E5a for Galileo, B1 and B2 for BDS. For simplicity, we will use and to indicate the first and second frequency for all GNSS systems.
In POP data processing, satellite and receiver clock offsets are estimated epoch-by-epoch with a network of reference stations with respect to a selected clock as reference. Usually, we can combine the code biases and with the clock parameters and , which turns out to be and , respectively. What is more, the code and carrier phases share the same receiver clock, so rewriting Equation (1), we have, for the IF observations,
where through the reformation , and , it is considered that the code hardware delay and phase delay will all contribute to the estimation of the ambiguities.
2.2. Ambiguity Fixing
As the whole equations are connected by the estimation of satellite clocks in a network mode, the ambiguity fixing can only be made on a DD-level for POP. For comparison, the PPP ambiguity fixing is also made on a DD-level in this study.
For DD ambiguity fixing, a DD ambiguity is usually expressed as the combination of wide- and narrow-lane (WL and NL) ambiguities for fixing:
where and , and represent two receivers and two satellites, respectively.
The WL ambiguity can be estimated by taking the time average of the Hatch-Melbourne-Wubbena (HMW) [11,12,13] combination of the pseudorange and carrier phase observations. Then, the DD WL ambiguity can be fixed according to its probability by rounding to its nearest integer [2,14].
After WL fixing, the NL ambiguity can be derived with the fixed WL and the float IF ambiguity and fixed in the same way as WL. A DD integer ambiguity can be reconstructed only when both the related WL and NL are fixed, and then as constraints imposed on the normal equations with original UD ambiguities [15].
It should be mentioned that for GLONASS, because of its frequency-division multiple-access (FDMA) strategy, the receiver code hardware delay , as well as the phase delay , are different for satellites with different frequency factors , referred to inter-frequency bias (IFB) for code and carrier phase, respectively. Therefore, they cannot be removed by forming DD ambiguity unless, homogeneous receivers, i.e., the same type of receivers, are used [16]. Since the code and carrier phase IFBs of a particular satellite is the same for all involved receivers, they can be eliminated while forming difference between homogeneous receivers. Through this classification, the IFB causes no effect on WL fixing. Indeed, IFBs can also be estimated and calibrated for integer ambiguity resolution [17].
2.3. Ambiguity Fixing of BeiDouObservations
The BDS satellite-induced code bias is identified in its code observations. Although it has a minor impact on positioning since the code measurements are assigned a much lower weight compared to the carrier phase measurements, the precision and consistence of the WL ambiguity derived from the HMW combination observations are severely affected. The variation of this bias is elevation dependent and can be corrected with empirical correction model for Inclined Geo-synchronous Orbit (IGSO) and Medium altitude Earth Orbit (MEO) satellites [18] and also for GEO satellites [19]. Due to the slight difference in satellite elevation for regional networks, such code bias is almost identical for all receivers and can be absorbed by the WL UPDs at the satellite side [6]. However, when applied in a global network in this study, they can neither be eliminated by DD nor assimilated into the UPDs. Therefore, the code biases of BDS satellites should be corrected before ambiguity fixing. The impact of the correction is shown in Figure 1. We can see that the BDS code observation residuals after correcting the satellite-induced code bias show a typical symbol of elevation-dependent: the higher the elevation angles, the smaller the residuals.
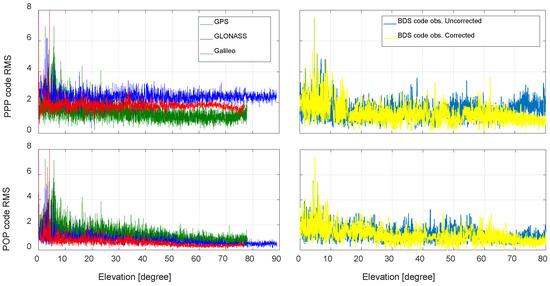
Figure 1.
The RMS values of IF code residuals of PPP and POP solutions. For each system, the code residuals of all involved satellites are lumped together to calculate the RMS values. The Beidou code observations before and after corrected with the satellite-induced code bias are shown in the right two subplots.
Besides the satellite-induced code bias, the poor orbit quality of BDS GEO satellites will also affect the estimation of the float ambiguity as well as the kinematic position significantly. The geometric orbit error for BDS GEO satellites can be expressed as:
where is the direct cosine unit vector at the direction from the receiver to the satellite , is the orbit error in radial, cross and along directions. Li et al. [6] and Liu et al. [7] both use a regional network to force the orbit error to be absorbed by the NL UPDs. However, it is not practical for a global network as the unit vector is different between GEO satellites and global receivers. For PPP ambiguity fixing, the coordinates of reference stations, orbits and clocks are fixed; the orbit errors will be mostly absorbed by the IF ambiguities. Since orbit bias is changing with time, its effect is different on the estimated IF ambiguities depending on the continuous tracking time of each ambiguity besides the station location. This will, consequently, result in inaccurate UPD estimates and, finally, fixing the performance of ambiguity fixing at rover stations. However, the temporal varying orbit error can more likely be assimilated into the satellite clock estimates rather than the float ambiguities. Therefore, for POP, the orbit error will be mainly absorbed by satellite clock parameters rather than the ambiguities, which will lead to a better ambiguity fixing and positioning performance.
In a multi-GNSS analysis, the satellite clock offsets of GPS, GLONASS, Galileo and Beidou may be biased with the constant since the satellite code hardware bias is absorbed by the satellite clock [20]. According to our experimental analysis, when applying such multi-GNSS clock products, the constant bias will be mostly assimilated into the code observation residuals. Here, take the observation data of the MGEX station CAS1 for analysis. The PPP and POP are processed with IF pseudorange and carrier phase measurements, and only the code observation residuals are analyzed. For GPS, even though different satellites have different elevation angles, they generally show a symbol of elevation-dependence: the higher the elevation angles, the smaller the residuals. Therefore, the code residuals of all GPS satellites are ranged according to their elevation angles in ascending order. These code residuals are lumped together to calculate the root mean square (RMS) values with a sampling step size of 0.1 degrees. Such calculation holds for the GLONASS, Galileo and Beidou satellites. Figure 1 shows the RMS of elevation dependent ionosphere-free (IF) code residuals. It can be seen that there exists constant bias in the code residuals of PPP but not POP. That is because when we estimate the satellite clocks in POP, the code bias is not assimilated into the code residuals but into the satellite clocks. What can be concluded here is that the code bias inside the satellite clocks will contribute to the estimation of the float ambiguity and the NL ambiguity fixing since the clocks are involved in the PPP adjustment. Therefore, the estimated UPD should be used together with the corresponding orbit and clock for PPP ambiguity fixing. What can also be found from the POP results is that the code observation residuals are at the same level for each system, therefore, we set equal weights to the code observations of each system.
For multi-GNSS ambiguity fixing, the DD ambiguity is fixed within each system. Since BDS does not have a good coverage outside the Asia-Pacific area and only three to six Galileo satellites can be tracked by Antarctica stations. Therefore, in order to overcome the limitation of the number of valid satellites, GLONASS, Galileo and BDS perform together with GPS, respectively.
3. Validation with Data from International GNSS Service
3.1. Data Description
In order to verify the performance of PPP and POP ambiguity fixing, 136 global multi-GNSS reference stations are selected among which seven (CAS1, DAV1, MAW1, MCM4, OHI3, OHI2 and SYOG) are located in Antarctica. One reason why we use a global network is that the Galileo and BDS satellite clocks cannot be estimated well with a sparse distribution of IGS network around Antarctica. The another is that such a regional network is not sufficient for GLONASS ambiguity fixing since there are not enough exactly the same type of receivers as those in Antarctica. The distribution of these multi-GNSS stations are shown in Figure 2.
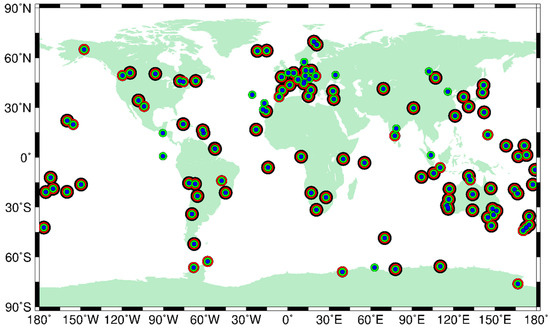
Figure 2.
The distribution of global multi-GNSS network used in this study. The colors represent the tracked GNSS systems on a station, GPS in blue, GLONASS in green, Galileo in red and Beidou in black.
The coordinates of these reference stations are fixed to the IGS weekly solutions. The GFZ (German Research Centre for Geosciences) analysis center final orbit and clock products are used for PPP, whereas the satellite clock offsets are estimated with the network in Figure 2 for POP.
The PPP and POP AR performance in terms of fixing rate and positioning accuracy of solutions of GPS, GPS + GLONASS (GR), GPS + Galileo (GE), GPS + BDS (GC) and all four systems GPS + GLONASS + Galileo + BDS (GREC) are analyzed.
During the data processing, we discovered that observations of the Antarctic stations MAW1 and SYOG cannot be processed properly with significant outliers in the positional estimates, and OHI2 and OHI3 are collocated stations. Therefore, only stations CAS1, DAV1, OHI3 and MCM4 are processed in the kinematic mode, since they observe the most GNSS systems. Observation data from the days of years 1 to 14, 2018 are processed.
In the ambiguity fixing, all possible DD ambiguities between a kinematic station and all the static stations are defined as candidates and are checked for fixing according to the probability test. For the GLONASS fixing, there are quite a few receivers of the same type and with exactly the same firmware and antennas as the receivers in Antarctica used as rovers in the experiment. Therefore, we ignore the differences in the firmware versions of receivers. Four types of the most commonly used receivers for GLONASS ambiguity fixing, namely SEPT POLARX5, TRIMBLE NETR9, JAVAD TRE_G3TH DELTA and LEICA GR25, are selected each for one rover station, respectively. Their distributions are shown in Figure 3.
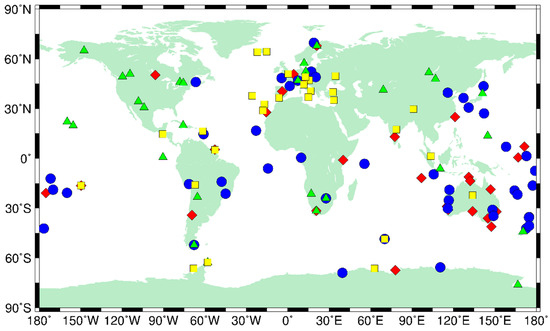
Figure 3.
The distribution of GLONASS stations selected for integer ambiguity fixing. The red diamonds denote the SEPT POLARX5 receivers, the blue dots denote the TRIMBLE NETR9 receivers, the yellow squares denote the JAVAD TRE_G3TH DELTA receivers and the green triangles denote the LEICA GR25 receivers. The firmware versions for different types of receivers are ignored in this study.
3.2. Performance of Ambiguity Fixing
In this study, the DD ambiguity candidates are defined over baselines shorter than a distance of 3500 km and at least with 15 min common observations. For reliable fixing, we excluded DD ambiguities with a standard deviation (STD) larger than 0.15 cycles or a fractional part larger than 0.25 cycles. The fixing rate, defined as the ratio of the number of the fixed and that of all independent DD ambiguities, can be a very efficient indicator to judge the fixing performance. There is an average of 35,013, 51,145, 43662, 39,810 and 65,505 daily independent DD ambiguity candidates can be used with GPS, GR, GE, GC and GREC observations, respectively. We can see that the addition of GLONASS, Galileo and BDS can enhance the estimation of the float solutions, therefore a higher fixing rate can be achieved.
Obviously, the WL fixing does not have any differences for PPP and POP since it is independent of the analysis model and only code and carrier phase observations are applied. Therefore, we only compare the performance of NL fixing.
The fixing percentages with single-, dual- and four-system observations are analyzed. The results are displayed in Figure 4. The average fixing percentage of PPP is 88.4% with GPS-only observations which is generally lower than that of the static processing [6,15] because kinematic stations are involved for fixing. The fixing percentages of POP with GPS, GLONASS and Galileo observations are slightly higher than the corresponding PPP solutions, while the improvement is significant with the BDS observations because of the reduced impact of the orbit errors.
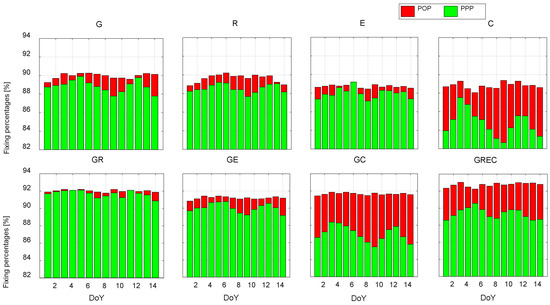
Figure 4.
The fixing percentages of PPP and POP AR with 14 days of single-, dual- and four-system observations. By doing a chi-squared distribution test with a 0.05 level of significance, it is shown that the p-value that indicates the significance-level for the differences between PPP and POP calculated with GLONASS, Galileo, BDS, GR, GE, GC and GREC observations is 0.062, 0.078, 0.0030, 0.25, 0.09, 0.0036 and 0.019, respectively, with respect to GPS. We can see there are significant differences between the PPP and POP results with BDS, GC, and GREC observations.
With the addition of other GNSS observations, a higher fixing rate can be achieved than the GPS-only solution, that is most likely because multi-GNSS enhances the float solution. The average fixing percentages of PPP GC and GREC solutions are only about 86.8 and 89.5%, which are even 5.0 and 2.3% lower than its GR solutions. The major reason is the problem of BDS fixing because of its relatively poor orbit and clock quality. However, the POP can resist such effect, while its GR, GE and GC solutions show almost the same fixing percentage and is higher than that of GPS-only; meanwhile, its GREC solution represents the highest fixing rate of about 92.7%.
Comparing the ambiguity fixing of PPP and POP solutions using GC or GREC observations, the advantage of the POP approach is confirmed that the orbit biases can be absorbed by clock parameters for better estimates of float ambiguities and consequently better fixing performance.
3.3. Performance of Positioning
The PPP and POP integer ambiguity resolution on the four stations CAS1, DAV1, OHI3 and MCM4 are performed. The position differences of the float and fixed solutions calculated with PPP and POP approaches regarding the IGS estimated coordinates for station CAS1 are shown in Figure 5 and Figure 6, respectively. The average RMS values of the station coordinates over 14 days are calculated for each station to assess the performance of the PPP and POP float, as well as fixed solutions; the statistical results are shown in Figure 7.
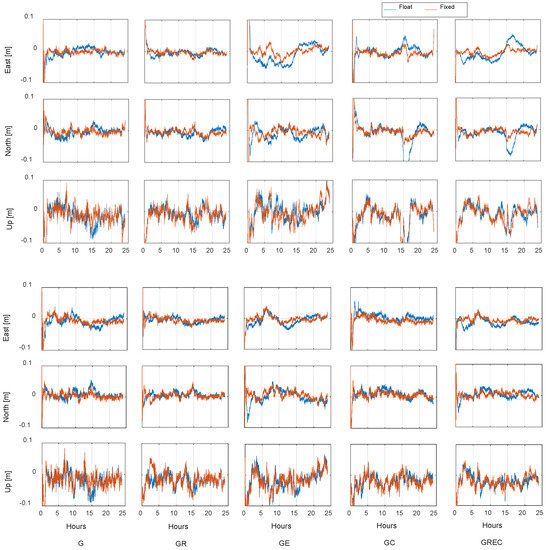
Figure 5.
The single-, dual- and four-system PPP (upper half) and POP (lower half) float and fixed solutions with respect to the IGS nominal position for station CAS1 on 1 January 2018. We can see better performance of POP than PPP with BDS involved solutions.
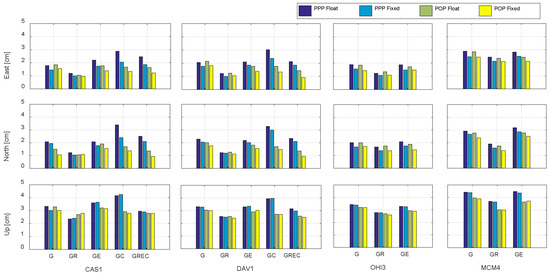
Figure 6.
The average RMS values of kinematic PPP and POP solutions after converged for stations CAS1, DAV1, OHI3 and MCM4 with different types of observations in the east, north and up components. For each day, the RMS values are calculated for each type of solutions, i.e., the PPP float with GPS observations in the east component, with reference to the IGS nominal position. Then the average RMS values are obtained over 14 days.
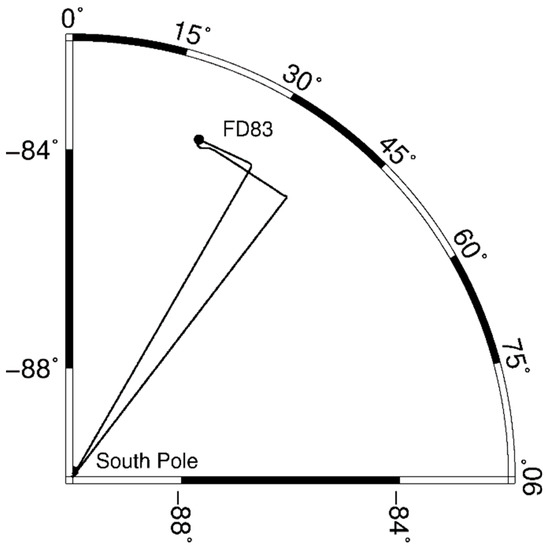
Figure 7.
The trajectory of this flight with the latitude shown on the radius and the longitude on the arc. FD83 is the reference station.
Figure 5 gives us a visual impression that the POP approach has, on average, a better performance than PPP for GE, GC and GREC solutions. Some fluctuations appear in the PPP GE position differences; these fluctuations are possibly caused by the short-term fluctuations in the Galileo satellite clocks. The influence of BDS orbits and clocks on PPP GC and GREC kinematic positioning is significant. Some large positioning errors appear between 14:00 and 16:00. The fixed solutions can improve the accuracy in the horizontal directions, and the RMS value is reduced by 8% and 17% for the east and north components, respectively. However, in the POP solutions, most of the clock the orbit biases are compensated by the clock parameters, the positioning errors caused by the remaining orbit errors are below 5 cm for all components, as shown in the lower half panel in Figure 5. What is more, the POP ambiguity resolution can further improve the positioning performance in the east component and the accuracy is improved by 14%. The differences of PPP and POP positioning results are not significant with GPS and GR observations, which is mainly due to their stable orbit and clock quality derived from globally well distributed stations.
Figure 6 shows the average RMS values of PPP and POP kinematic positioning results regarding the IGS reference over the 14 days. The positioning results on stations CAS1 and DAV1 indicate that the accuracy of the GC and GREC float PPP solutions are relatively poor, and even worse than the corresponding GPS-only solution. This result is mainly caused by the poor quality of BDS orbits. The GE solution shows almost no improvement because of the limit number of available Galileo satellites. Meanwhile the GR solution represents an average improvement of 31.3, 33.1 and 18.5% compared to the GPS-only solution for the east, north and up components, respectively. The PPP fixed solutions can improve the accuracy in the east and north components, i.e., an average improvement of 13.1, 9.5, 16.9, 29.7 and 20.0% with GPS, GR, GE, GC and GREC observations, respectively.
The POP single-, dual- and four-system float solutions are more stable and can achieve higher accuracy than the corresponding PPP float solutions on the four stations, i.e., the average improvements are 12.7, −2.4, 21.0, 28.1 and 6.3% with GPS, GR, GE, GC and GREC observations for the up component. What is more, the POP GR, GE and GC solutions are all better than its GPS-only solution, and its GREC fixed solutions enables the highest average positioning accuracy of 1.2, 1.1 and 2.5 cm, while its GPS-only fixed solution is 2.0, 1.8 and 3.3 cm for the east, north and up components, respectively.
4. Result of a Real Flight Experiment
The European Space Agency (ESA) PolarGap airborne gravimetry campaign was carried out from December 7, 2015 to January 19, 2016 to cover the gravity gap over central Antarctica. A Twin-Otter aircraft was used with three antennas named AIR2, 0158 and SPAN installed on the aircraft to collect the GNSS data. Here, we choose the data collected on day 19 December 2015 for analysis, which covers about 10.5 h from 10:30 to 21:00 (UTC). Most of the flight tracks were done from the South Pole along the meridian to the edge of the region and then back. A dedicated reference station SP2X was installed at the South Pole, i.e., in the middle of the region. Such a track pattern is beneficial for traditional relative kinematic positioning. However, the observation data of SP2X on day December 19 is not available, and we use the data from another reference station called FD83 which was installed in a tented field camp (Figure 7). As the observed satellites on these kinematic receivers are at low elevation angles (less than 60°), a cut-off angle of 7° is applied to fully use all satellites. Since AIR2 observes GR data, 0158 and SPAN observe GPS data, only GPS data is processed for the three antennas in DD, PPP and POP mode for validation. For DD processing only one reference station FD83 is used, while 42 IGS reference stations around Australia are included for PPP and POP processing. The sampling interval of the receivers in the experiment is 1 s.
Unfortunately, it is very difficult to evaluate the positional results of the three approaches, since no “true” or accurate trajectory is available as reference. As the three onboard antennas are fixed on the aircraft, the inter-antenna distance should remain constant during the flight. It should be pointed out that special attention must be paid to the different signal receiving times for the two receivers of a baseline, although they are programmed to receive the signal at the same epoch. The difference could reach more than 1 milli-second due to online clock steering, which is usually shown in the observations as milli-second jumps, for example, the JAVAD DELTA G3T receiver at AIR2. This is a problem mainly for receivers moving with high speed but not for static or kinematic station with moderate speed. The positions are interpolated to the same nominal epoch time to get rid of such influence.
The time series of baseline length of the three processing approaches are calculated and shown in Figure 8. Be aware of that the DD estimates of the first one hour are not shown, because the reference station FD83 was moved during that time period.
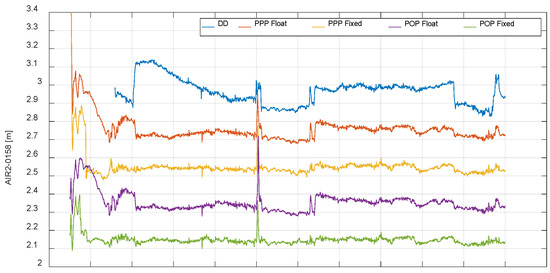
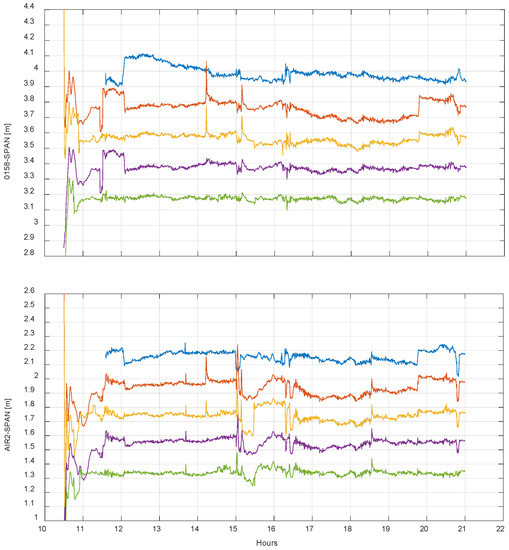
Figure 8.
The time series of baseline length of the three antennas derived from DD, PPP and POP approaches. Both the float as well as fixed solutions are shown for PPP and POP. For clarity, the DD, PPP float, PPP fixed and POP float results are shifted by 0.2, 0.4, 0.6 and 0.8 m, respectively.
In general, there are two time periods of baseline results with larger variations, i.e., 15:00–16:30 and 20:00–21:00 for almost all solutions besides the initialization at the beginning. The variations are more obvious in the two baselines with AIR2 than the baseline 0158–SPAN. This indicates that the data quality of AIR2 might be the reason. The major reason is that in airborne kinematic positioning over Antarctica, the receivers occasionally loosing track, and the gain of satellites observed simultaneously by the ground station and the rover is not beneficial for the estimation of the carrier phase ambiguities. It can be seen in the satellite visibility in Figure 9 that the continuous tracking time of one satellite is usually shorter than that in other regions. Therefore, there will be less DD observations at each epoch for the three baselines. It seems that the aforesaid fluctuations are most likely caused by the insufficient number of DD observations at the AIR2 station, especially during the time 20:00–21:00, which can be seen in Figure 10.
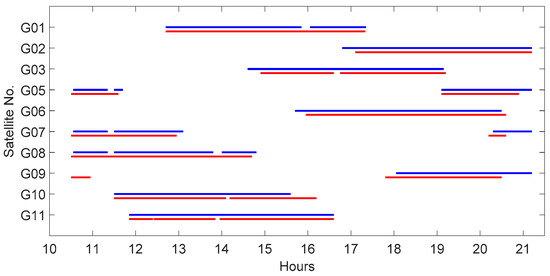
Figure 9.
The satellite visibility tracked by the reference station FD83 (blue) and the rover AIR2 (red). Only 10 satellites are shown here. Receivers losing track of the satellites may introduce biases in the DD solutions.
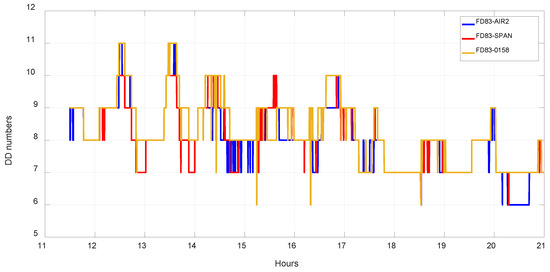
Figure 10.
The number of DD observations used in the processing for the three baselines. During 20:00–21:00, the number is 6 and is not beneficial for the calculation of DD solutions.
The STD values of the three baselines calculated with DD, PPP and POP float and fixed solutions are shown in Figure 11. It is seen that the DD approach does not work well because only a single reference station is used for such a large region, which is, on average, worse than PPP. The POP generally shows a better performance than PPP both in float and fixed solutions, especially in the results of 0158-SPAN, and the errors in the baseline results are almost within 10 cm. Comparing the STD of float and fixed solutions, ambiguity fixing indeed improved the position accuracy significantly. The time series of the fixed solutions shown in Figure 8 are much flatter than their float solutions, and most of the fluctuations and jumps in the float solutions disappeared. This is also proof that the fluctuations and jumps are caused by the poor observation quality of the rovers. From the beginning, it is very clear that ambiguity fixing can also considerably reduce the convergence time, in this case from 1 h to a half hour, on average.
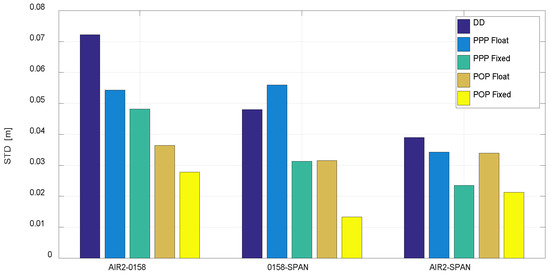
Figure 11.
Statistics of the distances between the three antennas derived from the five types of solutions. It is seen that the POP fixed solutions generate the best baseline results.
Overall, the POP fixed solution has the best performance, with an STD of 1–3 cm for the three baseline results. The ambiguity fixing is very important for airborne kinematic positioning in the polar regions to overcome fluctuations and jumps caused by poor data quality, since the continuous tracking time is usually short and more signal interruptions could occur due to the high dynamical movement.
5. Discussions
For the results presented so far, only the IGS final products are applied and the PPP and POP approaches are all processed in post mode. As the POP approach is independent of the external clock information, it can be seen that it is possible to use different types of IGS products, including the ultra-rapid (observed and predicted orbits and clocks). The accuracy of the ultra-rapid (predicted) satellite clock is 3 ns, the requirement for real-time PPP applications cannot be satisfied. Fortunately, the IGS Real-Time Pilot Project (RTPP) (http://www.rtigs.net) makes it possible to obtain real-time orbits with an accuracy of 5 cm and a clock accuracy of 0.3 ns which is almost the same accuracy as the IGS ultra-rapid (observed) products (3 cm for orbit and 0.15 ns for clock). Therefore, the POP approach can perform better than PPP when applied in real-time applications since it is independent of the real-time clocks. This becomes significant when applied in airborne gravimetry as the gravity results calculated from the GNSS solutions and the gravity measurements can be investigated in real-time.
6. Conclusions
This paper focuses on kinematic positioning over Antarctica with multi-GNSS observations. The conventional PPP and its ambiguity fixing in Antarctic stations are demonstrated to be negatively influenced by the poor orbit quality of the BDS satellites. A network-based approach, named POP, is implemented to overcome such effects. This approach’s ambiguity fixing performance is investigated and compared with PPP.
With data collected from a global network of 136 stations over 14 days, it is demonstrated that the PPP solutions involving BDS are not reliable; some positioning errors larger than 10 cm appear in the horizontal and vertical components with GC observations. However, the orbit errors can be mostly compensated by the satellite clocks when the clock offsets are estimated with a network of reference stations in POP processing. The kinematic positioning errors caused by the remaining orbit errors are below 5 cm. The POP also gives a better ambiguity fixing performance than PPP. A higher fixing rate can be achieved by POP than PPP because of the reduced effect of BDS orbit errors, an average improvement of 5.1 and 3.2%, respectively, can be obtained with GC and GREC observations. The ambiguity fixing can improve the kinematic positioning accuracy for both PPP and POP, and their fixed solutions are compared with their float solutions. Significant improvements of 16.9, 29.7 and 20.0% for PPP with GE, GC and GREC observations, respectively, are obtained. The POP represents relatively slight improvements of 11.2, 17.6 and 13.6% with the same types of observations.
Through a real flight experiment over Antarctica, it is shown that the DD solutions are not always robust under a baseline length up to 750 km. When comparing the baseline results among three antennas installed in an aircraft, it is found that some outliers in the PPP float and fixed baseline results disappear in the POP solutions. The ambiguity fixing can accelerate the convergence and overcome the fluctuations and jumps in the positional estimates. After convergence, the POP fixed solutions generate the best baseline estimates, with a STD of 1–3 cm.
Author Contributions
M.L. conceived the study and wrote the original manuscript; T.X. and K.H. analyzed the experimental results and provided the funding information; B.L., C.F. and F.F. made the data acquisition; all authors had read and contributed to subsequent draft.
Funding
This study is supported by the Chinese Scholarship Council (No. 201506560002) and the National Natural Science Foundation of China (41574013, 41,874,032 and 41731069).
Acknowledgments
We are very grateful to Maorong Ge for his valuable comments and suggestions and our colleagues in GFZ for their kind help, cooperation, and discussion. We are also thankful to Fausto Ferraccilio from the British Antarctic Survey and René Forsberg from the Danish Technical University/National Space Institute for providing GNSS data from ESA’s PolarGAP campaign.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, X.; Forsberg, R. Assessment of long-range kinematic GPS positioning errors by comparison with airborne laser altimetry and satellite altimetry. J. Geod. 2007, 81, 201–211. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J.N. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Goed. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Collins, P.; Lahaye, F.; Héroux, P.; Bisnath, S. Precise Point Positioning with Ambiguity Resolution using the Decoupled Clock Model. In Proceedings of the ION-GNSS-2008, Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
- Laurichesse, D.; Mercier, F. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP. ION. In Proceedings of the GNSS 2007 20th International Technical Meeting of the Satellite Division, Fort Worth, TX, USA, 25–28 September 2007; pp. 839–848. [Google Scholar]
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut. 2018, 22, 11. [Google Scholar] [CrossRef]
- Li, X.X.; Li, X.; Yuan, Y.; Zhang, K.K.; Zhang, X.H.; Wickert, J. Multi-GNSS phase delay estimation and PPP ambiguity resolution: GPS, BDS, GLONASS, Galileo. J. Geod. 2017, 92, 579–608. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Zhu, J.; Ye, S.; Song, W. Real-Time Phase Bias Estimation for BeiDou Satellites Based on Consideration of Orbit Errors. Remote Sens. 2018, 10, 1009. [Google Scholar] [CrossRef]
- Salazar, D.; Hernandez-Pajares, M.; Juan, J.; Sanz, J. GNSS data management and processing with the GPSTk. GPS Solut. 2010, 14, 293–299. [Google Scholar] [CrossRef]
- Douša, J. The impact of errors in predicted GPS orbits on zenith troposphere delay estimation. GPS Solut. 2010, 14, 229–239. [Google Scholar] [CrossRef]
- Kouba, J. A guide to using international GNSS service (IGS) products. 2009. Available online: http://igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf (accessed on 10 February 2019).
- Hatch, R. The synergism of GPS code and carrier measurements. In Proceedings of the Third International Symposium on Satellite Doppler Positioning at Physical Sciences Laboratory of New Mexico State University, Las Cruces, NM, USA, 8–12 February 1982; Volume 2, pp. 1213–1231. [Google Scholar]
- Moulborne, W.G. The case for ranging in GPS-based geodetic systems. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Wübbena, G. Software developments for geodetic positioning with GPS using TI-4100 code and carrier measurements. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 403–412. [Google Scholar]
- Dong, D.; Bock, Y. Global positioning system network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P. Improving carrier-phase ambiguity resolution in global GPS network solutions. J. Geod. 2005, 79, 103–110. [Google Scholar] [CrossRef]
- Wanninger, L. Carrier phase inter-frequency biases of GLONASS receivers. J. Geod. 2012, 86, 139–148. [Google Scholar] [CrossRef]
- Tian, Y.; Ge, M.; Neitzel, F. Particle filter-based estimation of Inter-frequency phase bias for real-time GLONASS integer ambiguity resolution. J. Geod. 2015, 89, 1145–1158. [Google Scholar] [CrossRef]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2014, 19, 639–648. [Google Scholar] [CrossRef]
- Lou, Y.; Gong, X.; Gu, S.; Zheng, F.; Feng, Y. Assessment of code bias variations of BDS triple-frequency signals and their impacts on ambiguity resolution for long baselines. GPS Solut. 2017, 21, 177–186. [Google Scholar] [CrossRef]
- Ge, M.; Chen, J.; Douša, J.; Gendt, G.; Wickert, J. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime. GPS Solut. 2012, 16, 9–17. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).