Abstract
Persistent scatterer interferometry (PSI) is commonly applied to monitor surface displacements with millimetric precision. However, this technique still has trouble estimating non-linear displacements because the algorithm is designed for the slow and linear displacements. Additionally, there is a variety of non-linear displacement types, and finding an appropriate displacement model for PSI is still assumed to be a fairly large task. In this paper, the conventional PSI technique is extended using a non-parametric non-linear approach (NN-PSI), and the performance of the extended method is investigated by simulations and actual observation data processing with TerraSAR-X. In the simulation, non-linear displacements are modeled by the magnitudes and periods of the displacement, and the evaluation of NN-PSI is conducted. According to the simulation results, the maximum magnitude of the displacement that can be estimated by NN-PSI is two and a half times the magnitude of the SAR sensor’s wavelength (2.5 that is roughly equivalent to 8 cm for X-band, 14 cm for C-band, and 60 cm for L-band), and the period of the displacement is about three months. However, this displacement cannot be reconstructed by the conventional PSI due to the limitation, known as the 2 displacement ambiguity. The result of the observation data processing shows that a large displacement with the 2 ambiguity can be estimated by NN-PSI as the simulation results show, but the conventional PSI cannot reconstruct it. In addition, a different approach, Small BAseline Subset (SBAS), is applied to the same data to ensure the accuracy of results, and the correlation between NN-PSI and SBAS is 0.95, while that between the conventional PSI and SBAS is −0.66. It is concluded that NN-PSI enables the reconstruction of non-linear displacements by the non-parametric approach and the expansion of applications to measure surface displacements that could not be measured due to the limitations of the traditional PSI methods.
1. Introduction
Spaceborne synthetic-aperture radar (SAR) sensors are informative resources for measuring surface deformations induced by natural disasters or human activities. In previous decades, differential interferometry (D-InSAR) techniques were considered to be unexceptional methods for measuring ground deformations from SAR data acquisitions [1,2,3,4]. Recently, due to the increase of the availability of SAR data, these techniques have been rapidly extended by using multi-temporal data to raise the accuracy of the resulting displacement with millimetric precision. These multi-temporal D-InSAR approaches [5] are called interferometric stacking techniques [6], and one of the major techniques is called persistent scatterer interferometry (PSI) [7].
PSI is the point target measurement, and it requires a permanently strong backscatter in order to maintain the quality of the estimation with time series data. One of the technical advantages in PSI is that the algorithm operates on the phase time series of each pixel separately, and this PSI feature allows a fine spatial resolution of the final results to be obtained [6]. There are many researches that have adopted the PSI techniques to detect surface displacements, and many types of PSI applications were investigated, such as monitoring landslides [8,9,10,11], infrastructure [12,13,14,15], and mining [16,17,18], with measurements at millimeter scales. Although PSI has been becoming a proven surface-monitoring method, there are also some limitations indicated in several PSI reviews [19,20], and one of the major limitations of PSI is to estimate non-linear displacements. The accuracy of the displacement estimation by PSI is in millimetric order, but the algorithm was designed for the slow and linear displacements in order to avoid the measurement limitation in D-InSAR, called 2 displacement ambiguity [19,20]. Therefore, the non-linear displacements such as fast, large, and periodical motions are wrongly estimated by PSI. In order to overcome this limitation in PSI, some empirical data, complicated models, and parametric approaches are always required. There are some previous studies to solve this limitation. For example, in [21], it is shown that the stochastic model was used in PSI to estimate non-linear motions. In [22,23], the non-linear displacement was estimated using the surrounding pixels. Recently, the tomography technique was also used to improve the PSI techniques in [24,25,26,27,28], but these studies also define some models. Lastly, in [5], the non-linear displacements were estimated by a mixed approach, combining PSI with other approaches, called Small BAseline Subset (SBAS) techniques [29]. Currently, PSI methods for non-linear displacements are mainly based on parametric approaches and / or assumptions on the correlation between displacements of adjacent pixels.
With regards to the measurement of the non-linear displacements by the interferometric stacking, it is quite common that the SBAS technology is used to overcome the limitation of PSI approaches, and it is worth highlighting the differences between the SBAS and PSI approaches in general. The SBAS technique is designed to estimate the displacements for the distributed targets such as vegetated areas. The difficulties of SBAS are to maintain both spatial and temporal coherence from the distributed targets. In order to conduct SBAS successfully, the multiple masters with short temporal and spatial baselines are used to decide the interferometric pairs. One of the significant differences from PSI approaches is that SBAS adopts the spatial phase unwrapping which is applied to overcome 2 displacement ambiguity [30]. The spatial phase unwrapping is the most complicated process in D-InSAR, and to make its process easy, the spectral shift [31] and spatial filter are also adopted. After the unwrapping process, the atmospheric correction is performed and the final displacements are estimated by some inversion methods. Therefore, SBAS is robust to the non-linear displacements, but because of the unwrapping and spatial filters, the resulting displacements are averaged by the adjacent pixels. Consequently, the spatial resolution of SBAS is not as high as that derived by PSI, although SBAS enables reconstruction of non-linear displacements. Based on the core algorithms of SBAS and PSI, it is implicitly indicated that there is no technology enabling reconstruction of non-linear displacements for the point targets that are needed to recognize among some complicated geometry, unless some specific models are formulated.
According to the previous studies, the reconstruction of the non-linear displacement by PSI is needed to improve with a non-parametric approach in order to overcome the 2 displacement ambiguity. Then, it is a significant advantage that the non-linear displacement can be reconstructed by a PSI technique at the same level of SBAS with full spatial resolutions of the SAR sensors. Thus, in this paper, a new PSI approach, which enables reconstruction of non-linear displacements using a non-parametric method, is proposed (non-parametric non-linear PSI: NN-PSI). NN-PSI uses a scattering distribution map (SDM) for the selection of the best height by using temporal coherence, and the displacement is reconstructed with a full spectrum of the displacement phase by a Fourier transform at the selected height. In NN-PSI, no displacement model is defined or invented when reconstructing the displacements. This proposed method is expected to help to simplify the estimation of non-linear displacements with full spatial resolution, and this simplicity will expand the applications of monitoring surface displacements that could not be measured due to the PSI limitations.
In order to investigate the performance of the proposed method, non-linear displacements, including 2 displacement ambiguity and strong non-linearities, are simulated, and the results of NN-PSI with the simulation data are compared with those by the conventional PSI technique (ConvPSI), which is considered to have some limitations to estimate the non-linear displacements. In addition to conducting simulations, an experiment with the actual observation data of TerraSAR-X is conducted. The rest of this paper is structured as follows. In Section 2, the basic concept of NN-PSI is described. In Section 3, the methodology of the simulation is presented. In Section 4, the simulation results are detailed and discussed. In Section 5, an experiment with actual observation data processing is presented. Finally, in Section 6, further discussion and conclusions are presented.
2. Basic Concept and Methodology
2.1. Multi-Baseline Model
The basic concept of NN-PSI is based on the multi-baseline model [32,33], which has been well established in [25,26,27,34,35], and the multi-baseline projection is depicted in Figure 1. The range distance Rn in any azimuth–range pixel (x, r) at the nth (n = 0, …, N) acquisition is expressed with the baseline distance bn, the reference range distance r, and the elevation direction s, and each acquisitions is supposed to have a displacement in the line of sight d(s, tn) in Equation (1):
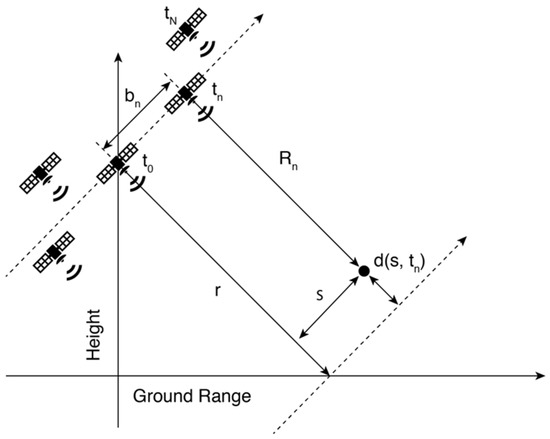
Figure 1.
System geometry in the plane orthogonal to the orbit direction. Each satellite shows the positions of the acquisition antennas over repeated passes [26].
The received complex signal of the object, along the elevation in each acquisition, is expressed as Equation (2):
where is the reflectivity function, is the wavelength of the carrier frequency, and are the range of height, and are the sampling spatial frequencies.
By expanding the exponential velocity term in Fourier harmonics described in [14,34], the displacement component in Equation (2) can be expressed as Equation (3):
where is the spectral distribution associated with the displacement, and are the range of velocity, and are the temporal frequencies. Substituting the exponential velocity term in Equation (2) with Equation (3), it is rewritten to Equation (4):
where is the scattering distribution.
According to Equation (4), a received signal is composed of a 2-D Fourier transform of the scattering distribution in the elevation–velocity plane (EV plane), and using the scattering distribution, individual scatterers with linear displacement show some peaks in an SDM [27,34]. Thus, it is theoretically possible to detect a single scattering point that indicates the best combination of the elevation and mean velocity by selecting the strongest scattering point in the SDM.
2.2. Calculation Procedure
Based on the parameters, height and mean velocity, at a single scattering point in the SDM, the displacement is estimated in the NN-PSI approach. There are a few steps involved in extracting the displacement, and Figure 1 shows these general steps, from the interferogram phase generation to the displacement estimation. It is also shown in Figure 2 that the procedures of ConvPSI and the steps of NN-PSI are the same from the beginning until the single scattering point needs to be detected.
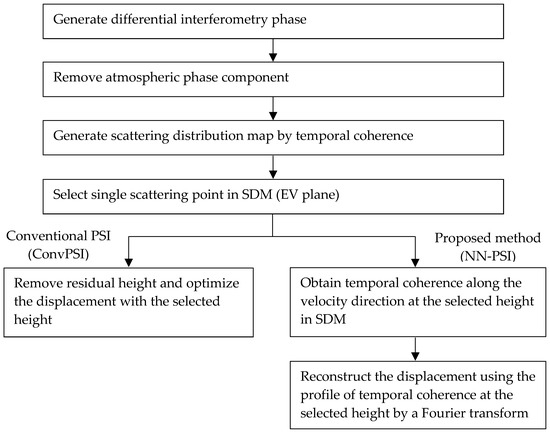
Figure 2.
Process flows of the conventional persistent scatterer interferometry (PSI) and the proposed method.
2.3. Scattering Distribution
Many methods have been proposed to estimate the scattering distribution of in Equation (4), such as the multi-interferogram complex coherence (MICC) [24,36], beamforming (BF), Capon, generalized likelihood ratio test (GLRT), multiple signal classification (MUSIC), and singular value decomposition (SVD), and the advantages of each method are explained well in [28,34]. In our approach, MICC is adopted to estimate the scattering distribution and to generate the SDM for selected height and velocity ranges. MICC is the indicator based on the temporal coherence that shows the goodness of the fit between the observed displacement phase and the modeled one in time series. This indicator provides the scattering distribution that highlights the difference of the velocity [27], and it is estimated by a non-parametric method [22]. MICC is also used in ConvPSI to detect the single scattering point, where the height and mean velocity are optimized. Thus, MICC is well suited to our proposed method. The calculation of the temporal coherence used in MICC is expressed in Equation (5):
where . is the temporal coherence at the given and is the observed phase component of the received complex . The temporal coherence ranging 0 to 1, is used to estimate the stability of the displacement phase at each scattering point in the SDM.
2.4. ConvPSI
In ConvPSI, the maximum of the temporal coherence in an SDM is selected in order to find a single scattering point, as described in Equation (6):
When detecting the single scattering point, the single elevation and mean velocity are also automatically selected according to the point location in the SDM, as depicted in Figure 2. The selected height and velocity are applied to the height and velocity phase components in Equation (4), and it is rewritten to Equation (7):
ConvPSI uses the single height and velocity values, and the scattering distribution is considered to be the maximum (one). The displacement phase component at the selected height can be calculated by the observed signal and given height and velocity.
2.5. NN-PSI
In the NN-PSI approach, the detection of a single scattering point is conducted in the same way as it is in the ConvPSI approach, as expressed in Equation (6). In the ConvPSI procedure, a single height and a mean velocity are selected to derive the final displacement, and the value of the temporal coherence (scattering distribution) is not used when reconstructing it. A significant difference between the proposed method and the ConvPSI approach is that the former uses the profile of the temporal coherences in the velocity direction at the selected height in the SDM [26,27]. Figure 3 illustrates how the single scattering point is determined and how the mean velocities are used in ConvPSI and the proposed approach.
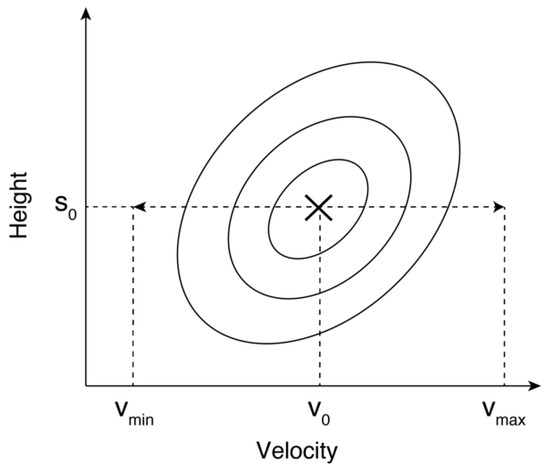
Figure 3.
The single scattering point is selected, where the scattering distribution (temporal coherence) is the maximum. Conventional PSI (ConvPSI) uses a single elevation and a mean velocity , and non-parametric non-linear PSI (NN-PSI) uses a single elevation and the profile (vmin through vmax) of the temporal coherence for the displacement reconstruction.
Once the height is selected in the SDM, Equation (4) is rewritten to Equation (8):
In the equation, only the velocity term remains because the height is selected in the SDM, and the height phase component becomes a known parameter. It is indicated that the scattering distribution is the profile of the temporal coherence in the velocity direction. Now Equation (8), which is the same form as Equation (3), is the velocity Fourier expansion of the scattering distribution, and all of the displacement signals are preserved along the velocity direction in the SDM [27]. The scattering distribution can be estimated with the temporal coherence, and assuming the atmospheric phase component is removed, the velocity phase component , can also be calculated by the observed signal and given velocity and height. Thus, the displacement phase component can be estimated by the Fourier transform from to .
As described in Equation (8), the reconstructed displacement phase is calculated in complex numbers, and the measurement unit of the displacement is still modulo-2π. In order to obtain the real measurement unit, the temporal phase unwrapping is required via a simple phase offset adjustment in the final step of NN-PSI [26]. It is common that some displacement models are implemented to estimate non-linear displacements in general PSI approaches; however, no displacement model is assigned in NN-PSI.
Finally, the atmospheric artifact is often discussed in interferometric stacking approaches. In the simulation, the atmospheric correction is assumed to have been conducted, before the reconstruction of the displacements is performed. For the real data processing explained in the later section, the standard atmospheric correction described in [7] is adopted.
3. Simulation
To investigate the performance of NN-PSI, the displacement phase was modeled as an input phase in this simulation. Then, the SDM was calculated from the modeled phase, and the single scattering point was selected by the highest value of the temporal coherence in the SDM. The selected height and mean velocity were used to reconstruct the final displacement. The initial displacement phase was used for the reference displacement, and the reconstructed displacement was validated by the root mean square error (RMSE) between the original and resulting displacement. The performance of NN-PSI should be evaluated according to the RMSE. In addition to the evaluation of NN-PSI, ConvPSI was also processed with the modeled displacement phase in order to compare the result of ConvPSI with that of NN-PSI. Two principal aspects of NN-PSI were investigated, which are as follows:
- The applicable displacements of NN-PSI were investigated by changing the magnitude and period of the displacements (simulation-1);
- How the velocity ranges that are used in the generation of SDM affect the resulting displacement with NN-PSI was investigated (simulation-2).
For the displacement phase model, the cumulative distribution function (CDF) was used to generate the simulated phase that needs to be reconstructed. The CDF is adequate to express the displacement, along with the magnitude and the period of the displacement, and these two parameters can easily be used in the evaluation of NN-PSI. The displacement models in the simulations are illustrated in Figure 4. The modeled displacement was composed of two periods. The first period had no displacement, and the second period was defined by the CDF period. The no-displacement period was added to this model, before the CDF period, in order to evaluate how NN-PSI should estimate the flat displacement, before the non-linear displacements start. In the CDF period, the displacement model was defined, with a CDF origin that was always defined by half of the given displacement (Dmax) and CDF variance. As shown in Figure 4b, the period of the displacement becomes shorter as the CDF variance is lowered.
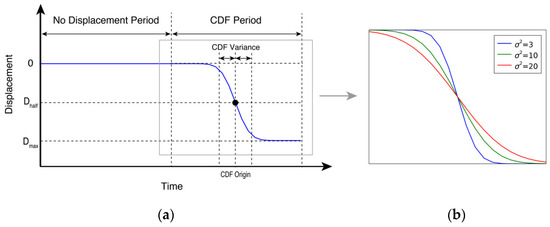
Figure 4.
(a) The displacement model in the simulation. (b) The displacements, with the different cumulative distribution function (CDF) variances in the CDF period shown in (a).
The simulation needed to be as realistic as possible, and the selected conditions of the simulation were similar to the parameters of the current spaceborne satellites. The simulation conditions are summarized in Table 1.

Table 1.
The simulation conditions.
4. Simulation Results and Discussions
4.1. Simulation-1
The RMSE derived from simulation-1 under each condition is plotted in Figure 4. The color of RMSE is represented, from 0 to 0.5λ, and the darkest color (brown) indicates that the RMSE is larger than half of the wavelength that is considered the 2π displacement ambiguity in D-InSAR techniques. Both results obtained by ConvPSI and NN-PSI in Figure 5 show that RMSE increases as Dmax increases. Figure 4a shows that a displacement with a Dmax value of less than 0.25λ is correctly reconstructed by the ConvPSI technique, because the value of RMSE is less than 0.1λ, but a displacement of more than 0.25λ could not be reconstructed, and RMSE increases as Dmax increases. It is also clear that the results obtained using the ConvPSI technique are not affected by the CDF variance, because RMSE remains the same in the CDF variance direction. These results prove that ConvPSI works only with a small displacement, with a Dmax value of less than 0.25λ.
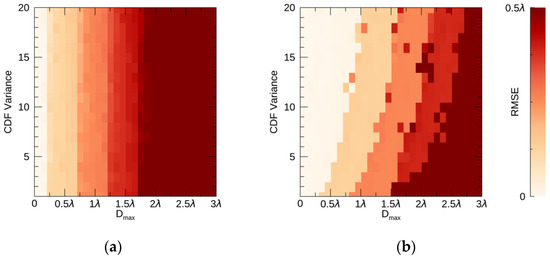
Figure 5.
(a) The root mean square error (RMSE) distribution with the ConvPSI; and (b) the RMSE distribution with the NN-PSI. The vertical axis shows the CDF variance, and the horizontal axis shows the Dmax.
Figure 5b shows the RMSEs calculated with the displacements reconstructed by NN-PSI. Some of the displacements with a Dmax value of more than 0.25λ can be reconstructed, and these RMSEs are less than 0.1λ. When the CDF variance is 20, the displacement with a Dmax value of λ can be reconstructed correctly. When the CDF variance is lowered, the RMSEs tend to be larger, with the same values of Dmax. When the CDF variance is lowered to one, a Dmax value with a minimum RMSE of about 0.25λ is the same as that resulting from the use of ConvPSI. This result indicates that the NN-PSI is dependent on the period of the displacement, and RMSE becomes larger when the CDF variance is smaller. However, it is clear that NN-PSI can adapt to larger displacements that are not handled correctly by ConvPSI.
Figure 5 shows the SDMs and time evolutions of the simulation results under each condition in simulation-1. According to the SDMs, as shown in Figure 6a,c,e, the selected height is 0 m for all SDMs, and the selected velocity is slightly increased as the Dmax is increased. The maximum value of the coherence in the SDM in Figure 5a is highest with a CDF variance of 15 and a Dmax value of 0.25λ, and becomes lower as Dmax increases, as shown in Figure 5c,e. The area of the high coherence values in Figure 6a has a rounded shape, but for the displacement with Dmax values of 0.75λ and 1.5λ, the rounded shape becomes smaller and distorted. This indicates that the displacement that is close to the linear trend shows a rounded shape with high coherence values in the SDM, whereas the non-linear displacement does not strongly show it.
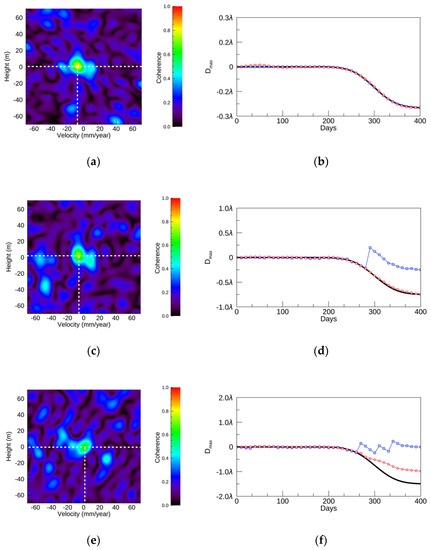
Figure 6.
(a) The scattering distribution map (SDM) with a Dmax value of 0.25 and a CDF variance of 15. The horizontal dashed white line shows the selected height, and the vertical dashed white line shows the selected velocity in the ConvPSI. (b) The resulting displacement of (a). (c) The SDM with a Dmax value of 0.75 and a CDF variance of 15. (d) The resulting displacement of (c). (e) The SDM with a Dmax value of 1.5 and a CDF variance of 15. (f) The resulting displacement of (e). In the time plots, the red, blue, and black lines show the NN-PSI, ConvPSI, and modeled displacements, respectively.
In Figure 6b, it can be seen that both ConvPSI and NN-PSI can reconstruct a displacement that fits the original one, with a CDF variance of 15 and a Dmax value of 0.25λ. With a CDF variance of 15 and a Dmax value of 0.75λ in this simulation, ConvPSI cannot reconstruct the displacement because of the phase jump incurred by the 2λ displacement ambiguity, but the displacement of NN-PSI does not have a phase jump, and the displacement is correctly estimated, as shown in Figure 6d. Neither of the methods can reconstruct the displacement with a CDF variance of 15 and a Dmax value of 1.5λ, as shown in Figure 6f. There are big differences between the resulting displacements and the original one. The result of ConvPSI has several phase jumps, and the result of NN-PSI underestimates the displacement. However, there are no phase jumps in the NN-PSI result.
4.2. Simulation-2
In simulation-2, RMSE is also investigated by changing the velocity range and Dmax, and Figure 7 shows results from both ConvPSI and NN-PSI. In Figure 7a, the displacement with a Dmax value of 0.25 can be reconstructed with an RMSE of 0.1. As Dmax is increased, RMSE increases, and RMSE reaches more than 0.5 when the Dmax is more than 1.75. This result is the same as that from the first simulation and indicates that the velocity range does not influence the results of ConvPSI. In Figure 7b, the displacement with a Dmax value of less than can be reconstructed with an RMSE of 0.1, when the velocity range is set to be wider than a range from −250 to 250 mm/year. In simulation-1, the largest displacement that can be correctly reconstructed is generated with a Dmax value of when the velocity range is set to be from −70 to 70 mm/year (Figure 4b). Thus, increasing the velocity range expands the magnitude of the displacement, of which NN-PSI enables a correct estimation. The maximum Dmax value of a displacement that NN-PSI can reconstruct with a low RMSE is around 2.5 with larger velocity ranges, but beyond this range, RMSE becomes higher with NN-PSI, although the velocity ranges are increased.
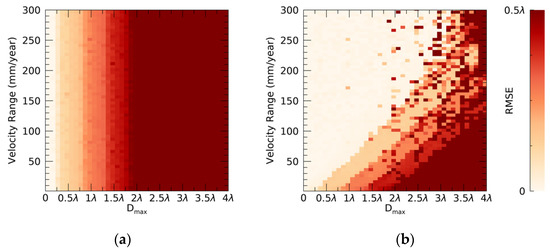
Figure 7.
The results of the simulation for the velocity range: (a) the RMSE distribution with ConvPSI; and (b) the RMSE distribution of NN-PSI.
Figure 8 shows the SDMs and time evolutions in simulation-2. In Figure 8a,c,e,g, the horizontal size of SDM is widened by the velocity range. All SDMs show that the strongest coherence values are located around the point with a height of 0 and a velocity of 0. The shape of the dominant scattering point is a double circle, with Dmax values of 1.5λ and 2.5λ in Figure 8a,c,e, and the shape becomes a horizontal circle as the Dmax is increased in Figure 8g. The right side (positive velocity) of the coherence values at the selected height of 0 are clearly low in the SDMs with a Dmax value of 1.5λ and λ in Figure 8a,c,e, but this pattern is not clear in the SDM with a Dmax value of λ in Figure 8g. This result indicates that a positive mean velocity does not exist in the selected elevation in the SDM, and the resulting displacement becomes a negative direction (subsidence).
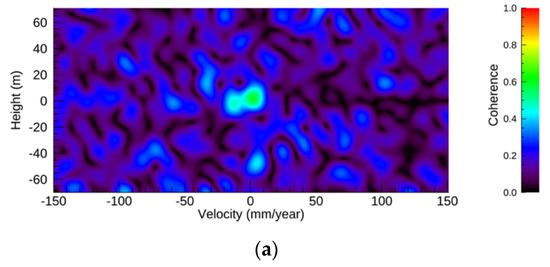
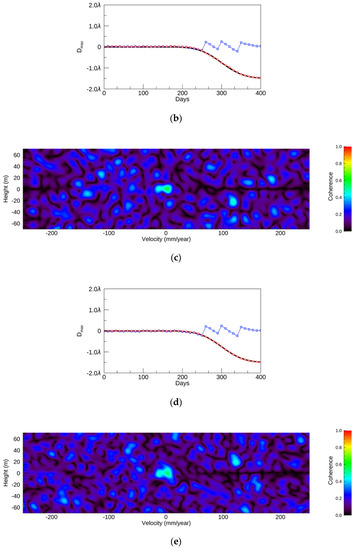
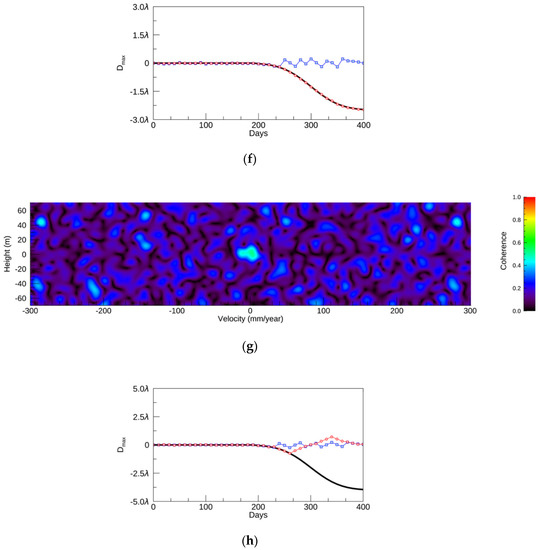
Figure 8.
(a) The SDM with a CDF variance of 1.5 and a velocity range from −150 to 150 mm/year. (b) The original and resulting displacements of (a). (c) The SDM with a CDF variance of 1.5 and a velocity range from −250 to 250 mm/year. (d) The resulting displacements of (c). (e) The SDM with a CDF variance of 2.5 and a velocity range from −250 to 250 mm/year. (f) The resulting displacements of (e). (g) The SDM with a CDF variance of 4 and a velocity range from −300 to 300 mm/year. (h) The resulting displacements of (g). In the time plots, the red, blue, and black lines show NN-PSI, ConvPSI, and modeled displacements, respectively.
The time evolutions are plotted in Figure 8b,d,f,h, and all of the displacements are not reconstructed correctly by ConvPSI. The resulting displacements with Dmax values of 1.5λ and 2.5λ by NN-PSI agree well with the original ones in Figure 8b,d,f. With a Dmax value of 4λ, NN-PSI cannot estimate the displacement, and the result of NN-PSI shows an uplift that is opposite to the original one in Figure 8h. In this case, the estimation is less accurate than that of ConvPSI due to the strong uplift estimated by NN-PSI.
In simulation-2, it is clear that the larger displacements up to a Dmax value of can be estimated by NN-PSI by increasing the velocity range, but the estimation of the displacement becomes less accurate than that of ConvPSI, once the displacement is beyond the capability of NN-PSI. One further advantage of using the wider velocity range in NN-PSI is that the fitting of the resulting displacement is better than with the smaller velocity range. Compared to the time evolutions of simulation-1 and simulation-2, the resulting displacement by NN-PSI, shown by the red line in Figure 6d, has some gaps between the resulting and the original displacements, whereas the output displacements, shown by the red lines in Figure 8d,f, do not have any gaps between the resulting and original displacements.
5. Experiment with Actual Observation Data
In this section, NN-PSI was applied to spaceborne SAR satellite data, TerraSAR-X, over Budapest in Hungary. In Budapest, the construction of the subway called Metro Line 4 was started in 2006, and the line crosses the city for a length of 12.7 km and comprises 16 stations [37], and in the study area subsidence was detected around a newly built underground station [38]. It was also reported that these displacements could not be measured by a ConvPSI approach due to the sudden descent on the order of half of the system wavelength over a period of about three months [6]. Thus, this area was selected to conduct NN-PSI and its performance was compared with that of ConvPSI.
In the last part of this section, the SBAS process was also conducted to ensure the results of PSI approaches. There is a fact that Airbus Defence and Space had already conducted the SBAS process with TerraSAR-X data in this area. The resulting displacements by Airbus Defence and Space had been validated with ground survey data, and the accuracy was confirmed [38]. As described in the Introduction, SBAS is not as good as PSI with the spatial resolution, but it is worth comparing SBAS displacements that should be equivalent to the ground survey data with NN-PSI and checking if the comparison shows the good correspondence as an additional validation.
5.1. ConvPSI and NN-PSI
The purpose of this experiment is to confirm if NN-PSI overcomes the limitation of ConvPSI by using the actual data. The data description is summarized in Table 2, and the distribution of the baseline distances is depicted in Figure 9.

Table 2.
Data description.
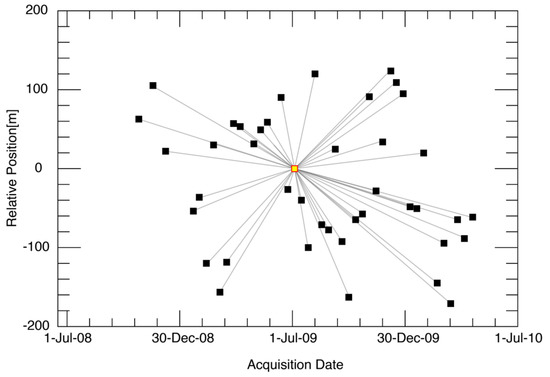
Figure 9.
The combination of the interferometric pairs used in the PSI approaches. The yellow square shows the master acquisition, and the black squares are the slave acquisitions. The horizontal axis shows the date of the acquisition, the vertical axis shows the baseline length in meters, and the gray lines show the combination of the interferometric pairs.
The data processing procedure was followed by the steps described in Figure 1, and the displacements calculated by ConvPSI were compared with those calculated by NN-PSI. Figure 10 shows the mean velocities calculated by ConvPSI. Both NN-PSI and ConvPSI estimated displacements pixel by pixel, and the resulting displacements are presented in point objects, as illustrated in Figure 10.
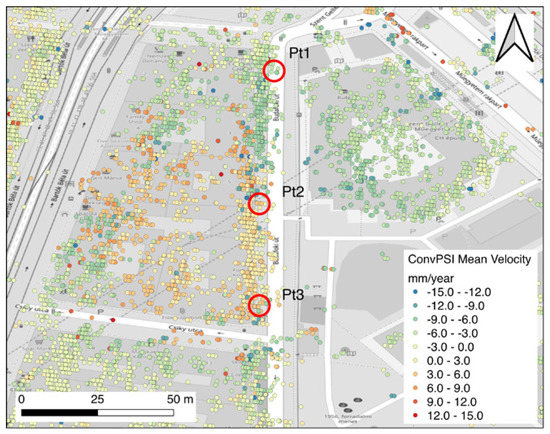
Figure 10.
The distribution of the resulting points of PSI around Szent Gellért Station. The color of the points represents the mean velocity of ConvPSI. Pt1, Pt2, and Pt3 are the selected points, and the time evolutions were investigated. The background map was obtained from OpenStreetMap (OSM).
According to the mean velocities estimated by ConvPSI, the direction of the displacements along Budafoki Street in the center of Figure 9 was changed from subsidence (green) to uplift (red), from north to south, and then the direction was changed from uplift to subsidence at the most south part of the street. Around the station, it was reported in Reference [6] that the subsidence was confirmed by the SBAS technique, so that the points showing uplift are conceived to have some large-scale displacements that ConvPSI wrongly estimated due to the displacement ambiguity.
Three points, indicated by the red circle in Figure 10, were investigated, and the time evolutions derived from each PSI approach were compared in Figure 11. According to the mean velocity values of ConvPSI, Pt1 shows subsidence, and Pt2 and Pt3 show uplift. At Pt1 in Figure 11a, the displacements of ConvPSI and NN-PSI show similar trends. Both displacements turn into subsidence after November 2009, and the amount of the displacement is so small (about 0.2) that ConvPSI and NN-PSI do not have significant difference at Pt1. At Pt2 in Figure 11b, the ups and downs in the ConvPSI displacement are frequent. The displacement of NN-PSI shows a strong subsidence at around November 2009, but the one by ConvPSI shows a strong jump towards the uplift direction over the same period. This jump should be the cause of the displacement ambiguity. At Pt3 in Figure 11c, both displacements of ConvPSI and NN-PSI show a similar pattern before November 2009, but after November 2009, the displacement of NN-PSI has a strong subsidence while ConvPSI shows an opposite displacement, which is a strong uplift. The magnitude of the subsidence is roughly 0.5 (15 mm), and the duration of the subsidence is about 4 months. The displacements derived by the PSI approaches at Pt3 can be explained by the simulation results shown in Figure 5. Because the displacement of NN-PSI at Pt3 is approximately equal to a Dmax value of 0.5 and a CDF variance of 30, and these are allowable parameters for NN-PSI to reconstruct the displacement but not for ConvPSI due to the displacement magnitude larger than a Dmax value of 0.25. As explained by the simulation, the difference between ConvPSI and NN-PSI at Pt3 should come from the computation limitation of ConvPSI, and NN-PSI is still able to measure the displacement, despite the ambiguity.
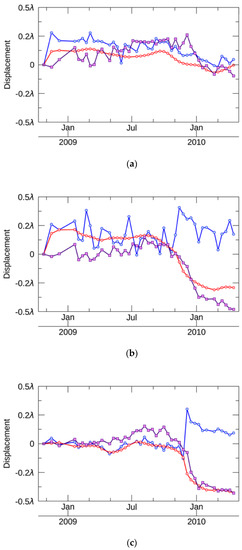
Figure 11.
(a–c) The time evolutions at Pt1, Pt2, and Pt3. In the time plots, the red, blue, and purple lines show NN-PSI, ConvPSI, and Small BAseline Subset (SBAS) displacements, respectively.
5.2. Comparison with SBAS Results
The SBAS approach with the same data of TerraSAR-X was also conducted in order to ensure the results of the simulations and performance of PSI approaches. In the SBAS process, about 300 interferometric pairs were processed to estimate the displacements in the same study area. To compare the results of SBAS with those of PSI approaches, the time evolutions were investigated at the same points indicated in Figure 10, and they are presented in Figure 11.
At Pt1 in Figure 11a, all of the time evolutions calculated by three different methods are similar. At Pt2 and Pt3 in Figure 11b,c, the time evolution of ConvPSI shows the phase jump, while those of SBAS and NN-PSI are identical and able to reconstruct non-linear displacements. In Reference [6], the time evolution of SBAS conducted by Airbus Space and Defence is shown, and the magnitude of the displacement is around 15 mm (0.5), and the date to start the strong subsidence is around October in 2009. That is, the time evolution of SBAS shown in the reference corresponds with those of SBAS and NN-PSI at Pt3. Additionally, the correlation between SBAS and two PSI methods was calculated to understand the difference quantitatively at each point, and the results are presented in Table 3. At Pt1 where the small linear displacement is confirmed, the correlation values of ConvPSI and NN-PSI are relatively low. However, the correlation values of NN-PSI are significantly increased at Pt2 and Pt3 where the non-linear displacements are observed by SBAS. On the other hand, the correlation values of ConvPSI at Pt2 and Pt3 are decreased and become an inverse relation. The results support that NN-PSI can maintain the accuracy of the estimation with non-linear displacements that cannot be estimated by ConvPSI.

Table 3.
The correlation between SBAS and PSI methods.
6. Conclusions
We have extended PSI using the NN-PSI and investigated NN-PSI in order to overcome the large non-linear displacement issues associated with PSI. Two types of simulations were conducted, and the results of NN-PSI were compared with those of the ConvPSI. Additionally, NN-PSI was applied to the actual observation data of TerraSAR-X.
In the first simulation, the applicable displacements that can be measured by NN-PSI were investigated using the CDF, which enables an evaluation of the magnitude (Dmax) and a period (CDF variance) of the displacement. The results show that NN-PSI is able to reconstruct the displacement with a Dmax value of three-quarters of the wavelength (0.75) and a CDF variance of 15, whereas ConvPSI cannot reconstruct the same displacement due to the 2 displacement ambiguity. As for the actual numbers, the displacements of roughly 2, 4, and 18 cm with X-, C-, and L-bands, respectively, over 80 days should be reconstructed by NN-PSI. In the second simulation, the influence of the velocity range was investigated, and it was confirmed that the displacement with a Dmax value of 2.5, which is roughly equivalent to 8 cm for X-band, 14 cm for C-band, and 60 cm for L-band, can be reconstructed with a velocity range from −250 to 250 mm/year. The wider the velocity range, the larger the displacement that can be reconstructed by NN-PSI. The allowable Dmax value is raised by up to three times that in simulation-1, with a wider velocity range.
One of the most significant limitations observed in the simulations is that neither ConvPSI nor NN-PSI could reconstruct a displacement with small CDF variances. The results indicate that displacements that occur over a very short period with a large magnitude, such as a step displacement, cannot be reconstructed. This limitation could be resolved by increasing in the number of the data, but the displacement extraction should be conducted with a limited number of data acquisitions, and the limitation still exists in practical situations.
Regarding the real data processing, it was confirmed that the simulation results were reproduced by NN-PSI and ConvPSI with TerraSAR-X data. Additionally, the SBAS was applied to the same data, and the displacement of NN-PSI agrees well with that of SBAS while that of ConvPSI does not at the points where the non-linear displacement exists. The results with actual observation data also indicate that large-scale non-linear displacements, which ConvPSI wrongly estimates, can be correctly estimated by NN-PSI.
In conclusion, the non-linear displacement with 2 displacement ambiguity can be reconstructed by NN-PSI, without the use of any displacement models and empirical data. With NN-PSI, complete pixel-independent analytics can be conducted with non-linear displacements, which indicates that NN-PSI improves the spatial resolution for the measurement of non-linear displacements, because no spatial filter or spatial unwrapping is implemented in the proposed method.
In this paper, only one type of the non-linear displacement adopted by NN-PSI was shown, but it is expected that NN-PSI enables reconstruction of several types of the displacements such as periodical displacement and subsidence with accelerations, according to our primary experiments. Future work will investigate other types of non-linear displacements with NN-PSI.
Author Contributions
F.O. designed the research and developed the algorithm, with the help of M.D. F.O. conducted the simulation and evaluated the TerraSAR-X data analyzed by M.D. and P.P. M.M. supported the design of the simulation. M.M., M.D. and P.P. validated the results of the simulation and data analysis. F.O. wrote the paper. M.M., M.D. and P.P. edited the paper.
Funding
This research was supported in part by the grant-in-aid for scientific research (KAKENHI No.: 17H02050).
Acknowledgments
The authors would like to thank Airbus Defense and Space for the TerraSAR-X data and relevant information and the Remote Sensing Society of Japan for the support of this publication. The map data from OpenStreetMap contributors were copyrighted and are available from https://www.openstreetmap.org.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rosen, P.A.; Hensley, S.; Joughin, I.R.I.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas—Differential radar interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Peltzer, G.; Rosen, P. Surface Displacement of the 17 May 1993 Eureka Valley, California, Earthquake Observed by SAR Interferometry. Science 1995, 268, 1333–1336. [Google Scholar] [CrossRef] [PubMed]
- Hooper, A.J. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Pasquali, P.; Cantone, A.; Riccardi, P.; Defilippi, M.; Ogushi, F.; Gagliano, S.; Tamura, M. Mapping of Ground Deformations with Interferometric Stacking Techniques. Land Appl. Radar Remote Sens. 2014, 233–259. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Farina, P.; Colombo, D.; Fumagalli, A.; Marks, F.; Moretti, S. Permanent Scatterers for landslide investigations: Outcomes from the ESA-SLAM project. Eng. Geol. 2006, 88, 200–217. [Google Scholar] [CrossRef]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- Tofani, V.; Raspini, F.; Catani, F.; Casagli, N. Persistent scatterer interferometry (PSI) technique for landslide characterization and monitoring. Remote Sens. 2013, 5, 1045–1065. [Google Scholar] [CrossRef]
- Zhao, F.; Mallorqui, J.J. Landslide Monitoring Using Multi-Temporal SAR Interferometry with Advanced Persistent Scatterers Identification Methods and Super High-Spatial Resolution TerraSAR-X Images. Remote Sens. 2018, 10, 921. [Google Scholar] [CrossRef]
- Sousa, J.J.; Bastos, L. Multi-temporal SAR interferometry reveals acceleration of bridge sinking before collapse. Nat. Hazards Earth Syst. Sci. 2013, 13, 659–667. [Google Scholar] [CrossRef]
- Lazecky, M.; Perissin, D.; Lei, L.; Qin, Y.; Scaioni, M. Plover Cove dam monitoring with spaceborne InSAR technique in Hong Kong. In Proceedings of the 2nd Joint International Symposium on Deformation Monitoring, Nottingham, UK, 9–11 September 2013. [Google Scholar]
- Fornaro, G.; Reale, D.; Verde, S. Bridge Thermal Dilation Monitoring with Millimeter Sensitivity via Multidimensional SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 677–681. [Google Scholar] [CrossRef]
- Pratesi, F.; Tapete, D.; Terenzi, G.; Del, C.; Moretti, S. Rating health and stability of engineering structures via classification indexes of InSAR Persistent Scatterers. Int. J. Appl. Earth Obs. Geoinf. 2015, 40, 81–90. [Google Scholar] [CrossRef]
- Ishitsuka, K.; Tsuji, T.; Matsuoka, T.; Nishijima, J. Heterogeneous surface displacement pattern at the Hatchobaru geothermal field inferred from SAR interferometry time-series. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 95–103. [Google Scholar] [CrossRef]
- Wegmüller, U.; Walter, D.; Spreckels, V.; Werner, C.L.; Member, S. Nonuniform Ground Motion Monitoring with TerraSAR-X Persistent Scatterer Interferometry. IEEE Trans. Geosci. Remote Sens. 2010, 48, 895–904. [Google Scholar] [CrossRef]
- Raucoules, D.; Bourgine, B.; de Michele, M.; Le Cozannet, G.; Closset, L.; Bremmer, C.; Engdahl, M. Validation and intercomparison of Persistent Scatterers Interferometry: PSIC4 project results. J. Appl. Geophys. 2009, 68, 335–347. [Google Scholar] [CrossRef]
- Wasowski, J.; Bovenga, F. Investigating landslides and unstable slopes with satellite Multi Temporal Interferometry: Current issues and future perspectives. Engineering Geology 2014, 174, 103–138. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. Isprs. J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Novali, F.; Prati, C.; Rocca, F. SAR Monitoring of Progressive and Seasonal Ground Deformation Using the Permanent Scatterers Technique. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1685–1701. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Lu, Z. Modeling PSInSAR Time Series Without Phase Unwrapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 547–556. [Google Scholar] [CrossRef]
- Ferretti, A.; Bianchi, M.; Prati, C.; Rocca, F. Higher-order permanent scatterers analysis. EURASIP J. Appl. Signal Process. 2005, 2005, 3231–3242. [Google Scholar] [CrossRef]
- Lombardini, F. Differential tomography: A new framework for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 37–44. [Google Scholar] [CrossRef]
- Fornaro, G.; Reale, D.; Serafino, F. Four-dimensional SAR imaging for height estimation and monitoring of single and double scatterers. IEEE Trans. Geosci. Remote Sens. 2009, 47, 224–237. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Let’s Do the Time Warp: Multicomponent Nonlinear Motion Estimation in Differential SAR Tomography. IEEE Geosci. Remote Sens. Lett. 2011, 8, 735–739. [Google Scholar] [CrossRef]
- Budillon, A.; Crosetto, M.; Johnsy, A.C.; Monserrat, O.; Krishnakumar, V.; Schirinzi, G. Comparison of Persistent Scatterer Interferometry and SAR Tomography Using Sentinel-1 in Urban Environment. Remote Sens. 2018, 10, 1986. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for monitoring localized deformation phenomena based on small baseline differential SAR interferograms. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar]
- Pepe, A.; Lanari, R. On the Extension of the Minimum Cost Flow Algorithm for Phase Unwrapping of Multitemporal Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Gatelli, F.; Monti Guarnieri, A.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef]
- Pasquali, P.; Prati, C.; Rocca, F.; Seymour, M.; Fortuny, J.; Ohlmer, E.; Sieber, A.J. A 3-D SAR Experiment with EMSL Data. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS’95, Quantitative Remote Sensing for Science and Application, Firenze, Italy, 10–14 July 1995. [Google Scholar]
- Reigber, A.; Moreira, A. First Demonstration of Airborne SAR Tomography Using Multibaseline L-Band Data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–2152. [Google Scholar] [CrossRef]
- Lombardini, F.; Pauciullo, A.; Fornaro, G.; Reale, D.; Viviani, F. Tomographic Processing of Interferometric SAR Data. IEEE Signal Process. Mag. 2014, 50, 41–50. [Google Scholar]
- Fornaro, G.; Serafino, F.; Soldovieri, F. Three-dimensional focusing with multipass SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41(3), 507–517. [Google Scholar] [CrossRef]
- Maio, A.; De Fornaro, G.; Pauciullo, A. Detection of Single Scatterers in Multidimensional SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2284–2297. [Google Scholar] [CrossRef]
- Peter, K. Space Monitor for Hong Kong Settlement. Available online: https://tunneltalk.com/Satellite-imaging-Sep11-Satellite-eye-on-settlement.php (accessed on 17 September 2019).
- Corne, E. Satellite technology as an aid to map and monitor construction/infrastructure sites anywhere in the world. Proceedings of Geomatics Indaba, Ekurhuleni, South Africa, 11–13 August 2015. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).