Hyperspectral Classification Based on Texture Feature Enhancement and Deep Belief Networks

Abstract

With success of Deep Belief Networks (DBNs) in computer vision, DBN has attracted great attention in hyperspectral classification. Many deep learning based algorithms have been focused on deep feature extraction for classification improvement. Multi-features, such as texture feature, are widely utilized in classification process to enhance classification accuracy greatly. In this paper, a novel hyperspectral classification framework based on an optimal DBN and a novel texture feature enhancement (TFE) is proposed. Through band grouping, sample band selection and guided filtering, the texture features of hyperspectral data are improved. After TFE, the optimal DBN is employed on the hyperspectral reconstructed data for feature extraction and classification. Experimental results demonstrate that the proposed classification framework outperforms some state-of-the-art classification algorithms, and it can achieve outstanding hyperspectral classification performance. Furthermore, our proposed TFE method can play a significant role in improving classification accuracy.

1. Introduction

Hyperspectral imagery with hundreds of narrow spectral channels provides wealthy spectral information. With very high spectral resolution, hyperspectral data has been of great interest in many practical applications, such as in agriculture, environment, surveillance, medicine [1,2,3,4] etc. Hyperspectral classification is a key technique employed in aforementioned applications. A majority of classification methods have been promoted in the last several decades to distinguish physical objects and classify each pixel into a unique land-cover label, such as maximum likelihood [5], minimum distance [6], K-nearest neighbors [7,8], random forests [9], Bayesian models [10,11], neural networks, etc., and their improvements [12,13,14,15]. Among these supervised classifiers, one of the most important classifiers is kernel-based support vector machine (SVM), which can also be considered as a kind of neural network. It can achieve superior hyperspectral classification accuracy via building an optimal hyperplane to best separate training samples.

In addition, sparse representation based on an over-complete signal dictionary has gained great attention in the literature. Sparse representation-based classification (SRC) [16,17,18] and collaborative representation classification (CRC) [19,20] are proposed from a different aspect: they do not adopt the traditional training–testing fashion. Such classification methods do not need any prior knowledge about probability density distribution of the data. To further enhance the performance of SRC and CRC, Du and Li [21] utilized a diagonal weight matrix to adaptively adjust the regularization parameter. To address the issues of Hughes phenomenon in hyperspectral classification, majority of feature extraction and selection algorithms are utilized to delete redundant features from the original data. To further improve performance of hyperspectral classification, multi-features are extracted and employed for classification. For instance, Kang et al. combined spectral and spatial features through a guided filter to process pixel-wise classification map in each class [22]. Several studies [23,24,25] focused on integrating spatial and spectral information in hyperspectral imagery. In addition, texture features are considered to assist hyperspectral classification [26], and modeling of hyperspectral image textures is significant for classification and material identification.

Recent research has highlighted deep learning with deep neural networks, which can learn high-level features hierarchically. They have demonstrated their potential in image classification, which also motivated successful applications of deep models on hyperspectral image classification. The classic deep learning method is convolutional neural networks (CNN), which plays a dominant role in visual-based issues. The local receptive fields of CNN can extract spatial-related features at high levels. Fukushima [27] introduced the motivations of CNNs. Ciresan and Lee et al. [28,29] depicted the invariants of CNNs. Chen et al. proposed 2-D CNN and 3-D CNN [30] to capture deep abstract and robust features, yielding superior hyperspectral classification performance. Although CNNs are typical supervised models, a massive training dataset is needed to trigger their powers. Unfortunately, a limited number of labeled samples are usually given in hyperspectral imagery. Deep belief networks (DBNs) [31] and stacked autoencoders (SAEs) [32] are also very promising deep learning methods for hyperspectral classification with limited training samples.

In this paper, we mainly investigate the DBN for its suitability and practicality to hyperspectral classification. A novel hyperspectral classification framework is proposed based on an optimum DBN. To acquire desirable performance, we also promote an advanced algorithm to enhance the texture features of hyperspectral imagery. The main contributions of this paper are summarized below.

• We first promote a band group method to separate the bands of hyperspectral data into different band groups. Multi-texture features are used to select a sample band in each band group.
• We propose a novel algorithm to enhance the texture features of hyperspectral data. We advocate the use of guided filter to complete the procedure of texture feature enhancement (TFE).
• An optimal DBN structure is proposed with consideration of learning and deep features extraction. The learned features are exploited in Softmax to address the classification problem. Furthermore, with enhanced texture features, accurate classification maps can be generated by considering spatial information.

The rest of the paper is organized into four sections. Section 2 is a brief description of related work. In Section 3, we detail our proposed DBN model. Datasets and parameters setting are demonstrated in Section 4. Experimental results and discussions are depicted in Section 5. Section 6 draws the conclusion of this paper.

2. The Related Work

A deep belief network (DBN) is a model that is first pre-trained in an unsupervised way, and then the available labeled training samples are used to fine-tune the pre-trained model through optimizing a cost function defined over the labels of training samples and their predictions.

The original DBN, published in Science [33], uses a generative model in the pre-training procedure, and uses back-propagation in the fine-tuning stage. This is very useful when the number of training samples is limited, such as in the case of hyperspectral remote sensing. DBN can be efficiently trained in an unsupervised, layer-by-layer manner where the layers are typically made of restricted Boltzmann machines (RBM). Thus, to explain the structure and theory of the DBN, we first describe its main component, the RBM.

2.1. Restricted Boltzmann Machines (RBM)

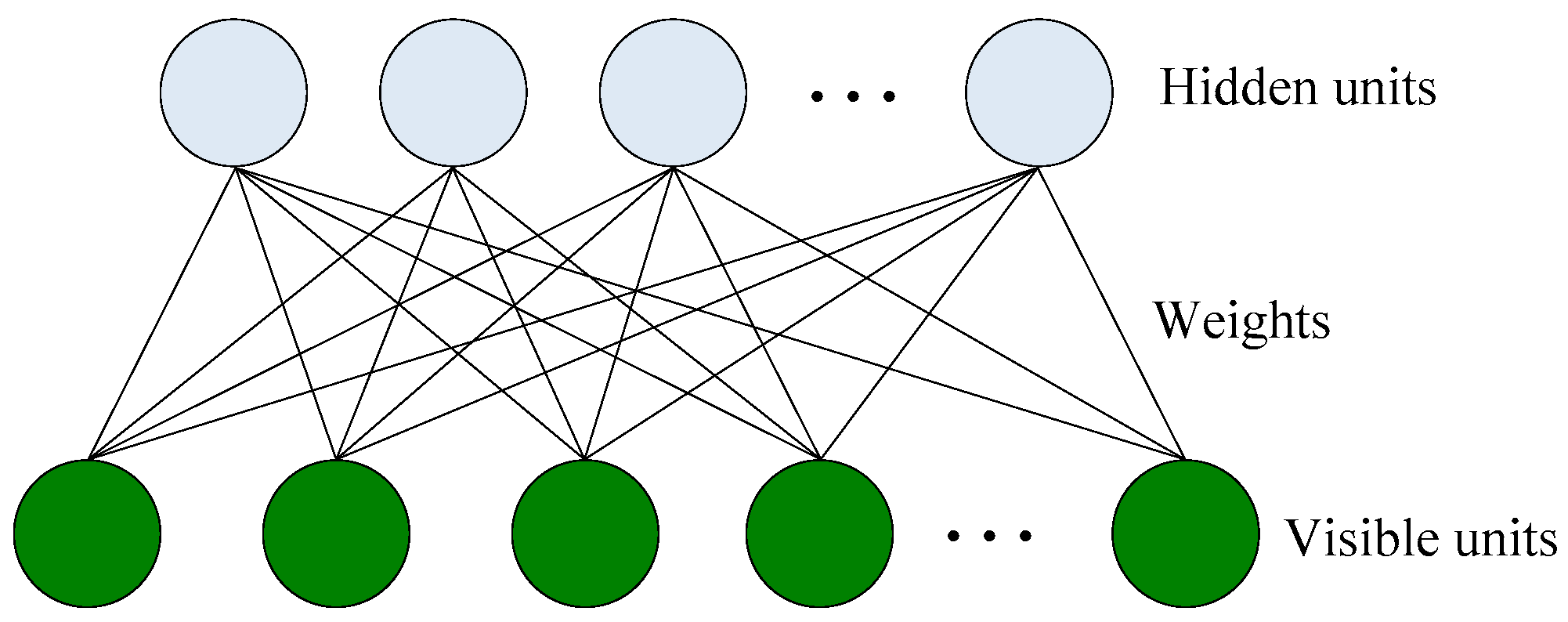
An RBM generally uses unsupervised learning, which can be interpreted as stochastic neural networks. It was originally developed to form a distributed representation. It is a two layer-wise network, which is composed of visible and hidden units. Learning RBM only allows the full connection between visible and hidden units, and does not allow connection between two visible units or connections between two hidden units. With the given visible units, hidden units can be obtained via mapping of visible units. The activations of each neuron in hidden layers are independent. Meanwhile, with the given hidden units, visible units have the same effects. A typical RBM structure is depicted in Figure 1.

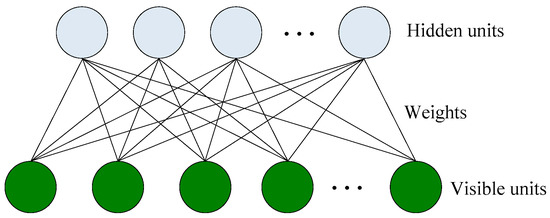
Figure 1. Architecture of Restricted Boltzmann Machines.

The visible units can be represented as $h$, and the hidden units can be expressed as $v$. The RBM model is a kind of energy-based models in which the joint distribution of the layers can be expressed as Boltzmann distribution. Energy-based probabilistic models define a probability distribution through an energy function as:

$$p(v,h|\theta )=\frac{\exp (-E(v,h|\theta ))}{Z(\theta )},$$

(1)

where the normalization constant $Z(\theta )$ is called the partition function by analogy with physical systems:

$$Z(\theta )={\displaystyle \sum _v{\displaystyle \sum _{h}E(v,h;\theta )}}$$

(2)

A joint configuration of the units has an energy given by:

$$\begin{array}{ll}E(v,h;\theta )& =-{\displaystyle {\sum }_{i=1}^n{a}_i{v}_i-{\displaystyle {\sum }_{j=1}^m{b}_j{h}_j-{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^m{v}_i{w}_{ij}}}}}{h}_j\\ & =-a^{T}v-b^{T}h-v^{T}wh\end{array},$$

(3)

where $\theta =\{a_i,b_j,w_{ij}\}$; $w_{ij}$ represents the weight connecting the visible unit i and the hidden unit j; $a_i$ and $b_j$ denote the bias terms of visible and hidden layers, respectively; n and m are the total visible and hidden unit numbers; and $v_i$ and $h_j$ represent the states of visible unit i and hidden unit j.

Due to the specific structure of RBMs, visible and hidden units are conditionally independent, as given by:

$$\begin{array}{l}P(v_i=1|h,\theta )=\sigma (a_i+{\displaystyle {\sum }_i{w}_{ij}{v}_i})\\ P(h_j=1|v,\theta )=\sigma (b_j+{\displaystyle {\sum }_j{w}_{ij}{h}_j})\end{array},$$

(4)

where $\sigma (•)$ is the logistic function defined as

$$\sigma (x)=\frac{1}{1+\exp (-x)}$$

(5)

Overall, an RBM has five parameters: $h$, $v$, $w$, $a$ and $b$, where $w$, $a$ and $b$ are achieved via learning, $v$ is input, and $h$ is output. $w$, $a$ and $b$ can be learned and updated via the contrastive divergence (CD) method as

$$w_{ij}\leftarrow w_{ij}+\lambda (P(h_j|v_i)v_i-P(h_j^r|v_i^r)v_i^r)$$

(6)

$$a_i\leftarrow a_i+\lambda (v_i-v_i^r)$$

(7)

$$b_j\leftarrow b_j+\lambda (h_j-h_j^r)$$

(8)

where $\lambda$ denotes the learning rate, $P(h_j^r|v_i^r)$ represents the reconstructed probability distribution, and $v_i^r$ and $h_j^r$ are the reconstruction of visible and hidden unit, respectively. Once the states of hidden units are chosen, the visible units can be reconstructed via the hidden units sampled via Gibbs method. Then, the states of hidden units are updated through the visible units, so that the hidden units demonstrate the features of reconstruction. The distribution of visible units approximates the distribution of the real data. The learning ability of an RBM depends on whether the hidden units contain enough information of the input data.

2.2. Deep Belief Learning

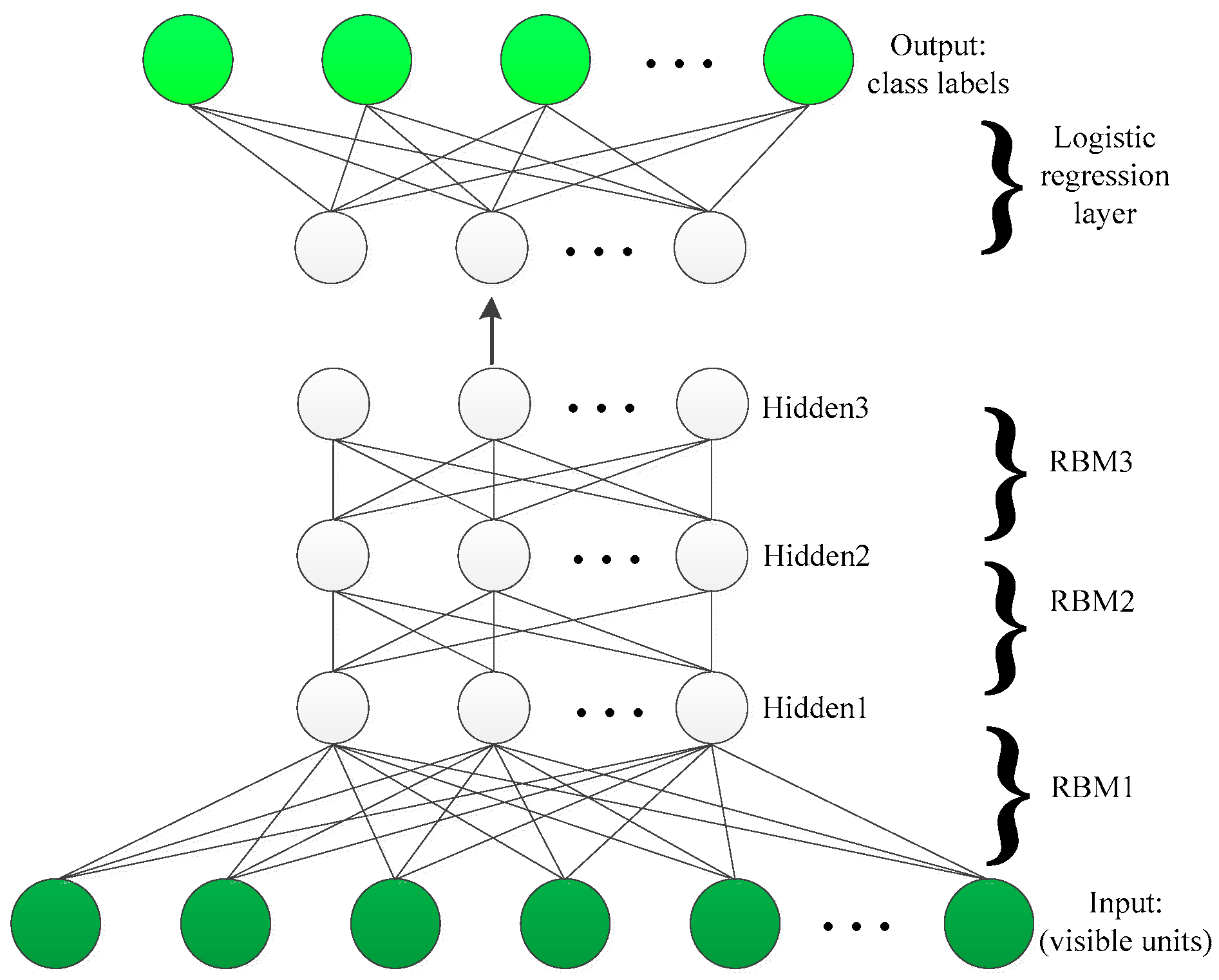
The learning ability of a single hidden layer is limited. To capture the comprehensive information of data, the hidden units of the RBM can be feed as the input (visible units) of another RBM. This kind of layer-by-layer learning structure trained in a greedy manner forms so-called Deep Belief Networks. In this way, DBN can extract deep features of image data. The structure of three-layer DBN is depicted in Figure 2.

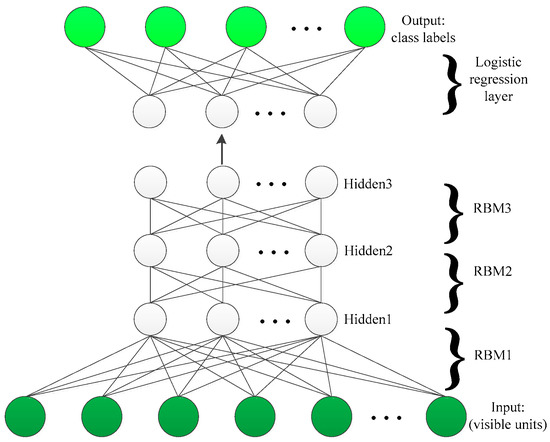
Figure 2. An illustration of three-layer DBN with logistic regression.

The process of training of DBN consists of two parts: pre-training and fine-tuning. The pre-training is an unsupervised training stage that initializes the model in such a way to enhance the efficiency of supervised training. The fine-tuning process can be realized as supervised training stage, which adjusts the classifier’s prediction to match the ground truth of the data.

3. The Proposed Framework

To extract more powerful and invariant features, we propose a novel DBN hyperspectral classification algorithm based on TFE. DBN is composed of several layers of latent factors, which can be deemed as neurons of neural networks. However, the limited training samples in the real hyperspectral image classification task usually lead to many “dead” (never responding) or “potential over-tolerant” (always responding) latent factors (neurons) in the trained DBN. Our proposed framework mainly consists of three steps: band grouping and sample band selection, TFE, and DBN-based classification.

3.1. Band Grouping and Sample Band Selection

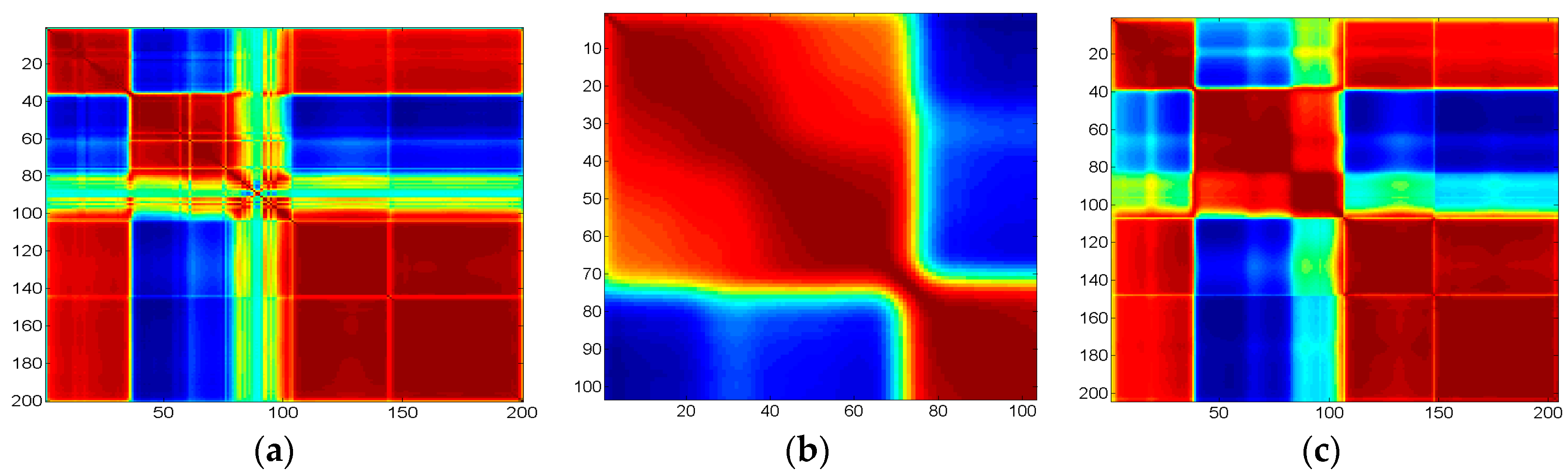
Compared to multispectral imagery, hyperspectral imagery with hundreds of spectral bands has relatively narrow bandwidths. The correlation between spectral bands needs to be considered. In our framework, we calculated all the pair wise correlation coefficient of bands, and then utilized the correlations between adjacent bands. The spectral correlation coefficients in different datasets are depicted in Figure 3.

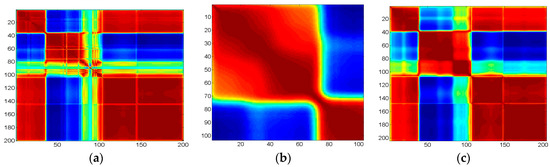
Figure 3. The maps of correlation coefficients of spectral bands in different datasets: (a) Indian Pines; (b) University of Pavia; and (c) Salinas.

We can obtain the correlation coefficient between adjacent bands as:

$${\rho }_{i,j}=corr({\mathrm{B}}_i,{\mathrm{B}}_j)=\mathrm{cov}({\mathrm{B}}_i{,\mathrm{B}}_j)/\sqrt{\mathrm{var}({\mathrm{B}}_i)\mathrm{var}({\mathrm{B}}_j)}$$

(9)

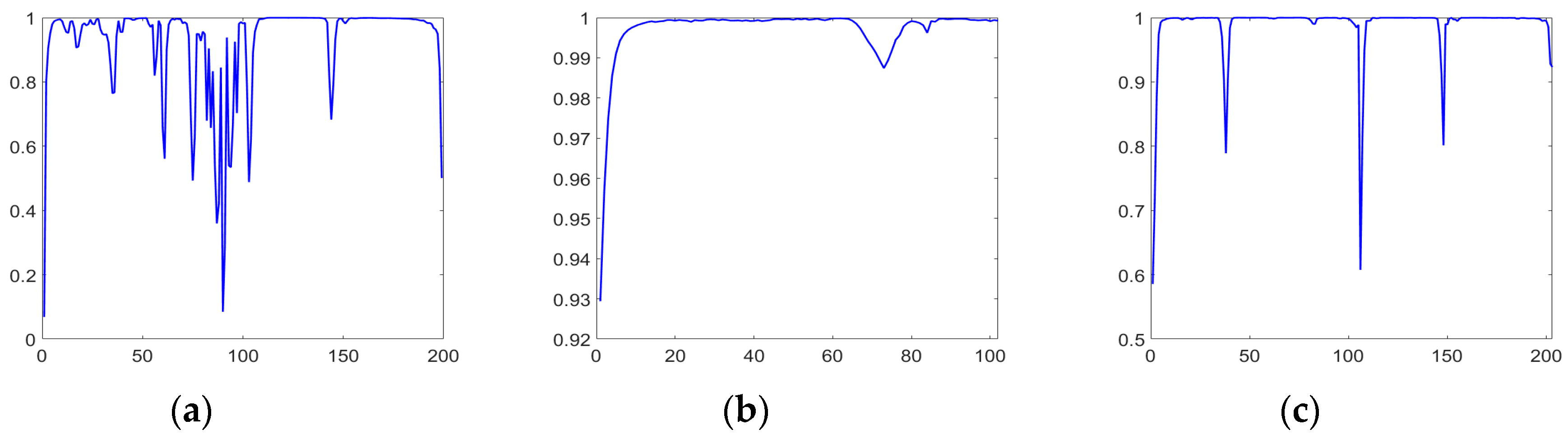
where cov is covariance and var means variance. ${\mathrm{B}}_i$ and ${\mathrm{B}}_j$ represent the $i$-th and $j$-th band channels, respectively. $i=1,2,\dots ,L-1$. Here, L denotes the number of bands of the hyperspectral dataset. Based on Equation (9), the correlation coefficients between adjacent bands in different datasets are calculated, as shown in Figure 4. We can see that the highest correlation coefficient in Indian Pines is 0.9997, and the lowest correlation coefficient is 0.0686. The spectral bands of university of Pavia have strong correlations overall, where the highest correlation coefficient is 0.9998, and the lowest correlation coefficient is 0.9294. The highest correlation coefficient in Salinas is 0.9999, and the lowest correlation coefficient is 0.5856.

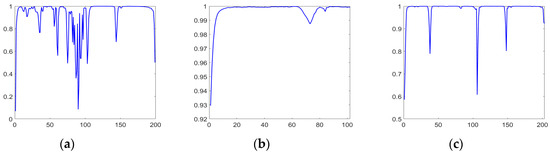
Figure 4. The correlation coefficients of adjacent spectral bands in different datasets: (a) Indian Pines; (b) University of Pavia; and (c) Salinas.

Here, we design an algorithm for grouping bands rationally.

Firstly, calculate the average correlation coefficients of the adjacent bands, denoted as $\overline{C}$, which is utilized as the threshold in the following steps. It can be calculated through:

$$\overline{C}=\frac{1}{L-1}{\displaystyle \sum _{i=1}^{L-1}{\rho }_{i,j}}$$

(10)

where $j=i+1$. If the correlation coefficients of adjacent bands are greater than $\overline{C}$, these two bands are considered to have strong correlation.

Second, search local minimum values from the correlation coefficients between the adjacent bands, denoted as ${\mathsf{\rho }}_{}^{\min }$, where ${\mathsf{\rho }}_{}^{\min }=\text{{}{\rho }_{i,j}|{\rho }_{i,j}\le {\rho }_{i+1,j+1}||{\rho }_{i,j}\le {\rho }_{i-1,j-1}\text{}}$. All the elements in ${\mathsf{\rho }}_{}^{\min }$ are compared with $\overline{C}$. If the inequality $\{{\rho }_{i,j}\in {\mathsf{\rho }}^{\min }\}<\overline{C}$ is satisfied, it indicates that the correlation between the $i$-th band and the $j$-th band is lower than the average correlation value, and the correlation between these two bands is considered to be weak. Then, the corresponding index group {i, j} is recorded and added to the set ${\mathsf{\rho }}^{Loc}$.

Third, band grouping depends on the stored index pairs in ${\mathsf{\rho }}^{Loc}$. For instance, with regard to index pair {i, j}, the i-th band is set as the end band of the former band group and the j-th band is set as the first band of the next band group. Thus, based on the aforementioned rules, all the bands are divided into different band groups $\{G_1,G_2,\cdots ,G_K\}$.

After dividing all the bands of hyperspectral dataset into different band groups, a sample band with the strongest and clearest texture features is searched and selected from each group.

To extract texture features, the gray level co-occurrence matrix (GLCM) has been employed successfully. GLCM [34] is defined as a matrix of frequencies which can extract second order statistics from a hyperspectral image. The distribution in the matrix depends on the angular and distance relationship between pixels. After the GLCM is created, it can be used to compute various features. We choose the five most commonly used features in Table 1 to select a sample band from each band group. The texture feature score of each band can be calculated by Equation (11):

$$T={\displaystyle \sum _{i=1}^5{F}_i}$$

(11)

Table 1. Feature calculated from the normalized co-occurrence matrix $P(i,j)$.

No.	Feature	Formula
$F_1$	Energy	${\displaystyle {\sum }_i{\displaystyle {\sum }_j{P}^2(i,j)}}$
$F_2$	Entropy	${\displaystyle {\sum }_i{\displaystyle {\sum }_{j}P(i,j)}}\log P(i,j)$
$F_3$	Contrast	${{\displaystyle {\sum }_i{\displaystyle {\sum }_j(i-j)}}}^{2}P(i,j)$
$F_4$	Mean	$\frac{1}{m*n}{\displaystyle {\sum }_i{\displaystyle {\sum }_j|i-j|}}P(i,j)$
$F_5$	Homogeneity	${\displaystyle {\sum }_i{\displaystyle {\sum }_j\frac{P(i,j)}{1+|i-j|}}}$

The sample band in each band group can be selected through:

$$g_k\underset{{\mathrm{B}}_{l^k}}{=\arg \max }\left\{T_{{\mathrm{B}}_{l^k}}|{\mathrm{B}}_{l^k}\in G_k\right\},$$

(12)

where $G_k$ represents the $k$-th band group of the dataset, $l^k\in \{1,2,\cdots ,N^k\}$, $N^k$ is the number of bands in the $k$-th band group, and ${\mathrm{B}}_{l^k}$ represent the $l^k$-th band in the $k$-th band group. Finally, the sample band set are comprised of $\{g_1,g_2,\cdots ,g_k\}$.

3.2. Texture Feature Enhancement

As an effective edge-preserving filter, guided filter (GF) was proposed by He in 2012. It can enhance the detail of an image. Texture feature is a kind of important spatial characteristics and also has long history in image processing. In this paper, we utilize the GF in each band group to enhance the texture features of the image.

The general guided image filtering was designed for gray-scale images or color images. It is very easy to extend to multi-channel image. Firstly, the guidance image in our proposed framework is multi-channel image, denoted as $I^M$, which is comprised of the copies of the band with the strongest texture features in each band group. We assume $q_{}^M$ is a linear transform of $I^M$ in a window ${\omega }_k$ centered at the pixel k, and the multi-channel guided filter model can be expressed as

$$q_i^M={(a_k^M)}^T{I}_i^M+b_k^M,\forall i\in {\omega }_k$$

(13)

where $I_i^M$ is a $C\times 1$ vector, and $C$ is the channel number of the input image, $a_k^M$ is a $C\times 1$ coefficient vector, and $q_i^M$ and $b_k^M$ are scalars. The guided filter for multi-channel guidance image becomes

$$\begin{array}{l}{a}_k^M={({\displaystyle {\sum }_k}+\epsilon U)}^{-1}(\frac{1}{|\omega |}{\displaystyle \sum _{i\in {\omega }_k}{I}_i^M{p}_i^M-{\mu }_k\overline{p_k^M}})\\ b_k^M=\overline{p_k^M}-{(a_k^M)}^T{\mu }_k\\ q_i^M={(\overline{a_i^M})}^T{I}_i^M+\overline{b_i^M}\end{array},$$

(14)

where ${\displaystyle {\sum }_k}$ is the $C\times C$ covariance matrix of $I^M$ in ${\omega }_k$, $U$ is an $C\times C$ identity matrix, $p^M$ denotes a filtering input image which is given beforehand according to the application, ${\mu }_k^{}$ is the mean of $I^M$ in ${\omega }_k$, $\overline{p_k^M}$ is the mean of $p_{}^M$ in ${\omega }_k$, and $|\omega |$ represents the number of pixels in ${\omega }_k$.

Then, the extending guided image filtering for multi-channel images will be applied to each band group. For instance, each channel of the guidance image $I^M$ in Equation (14) for the $k$-th band group $G_k$ is the copy of the sample band $g_k$ selected previously.

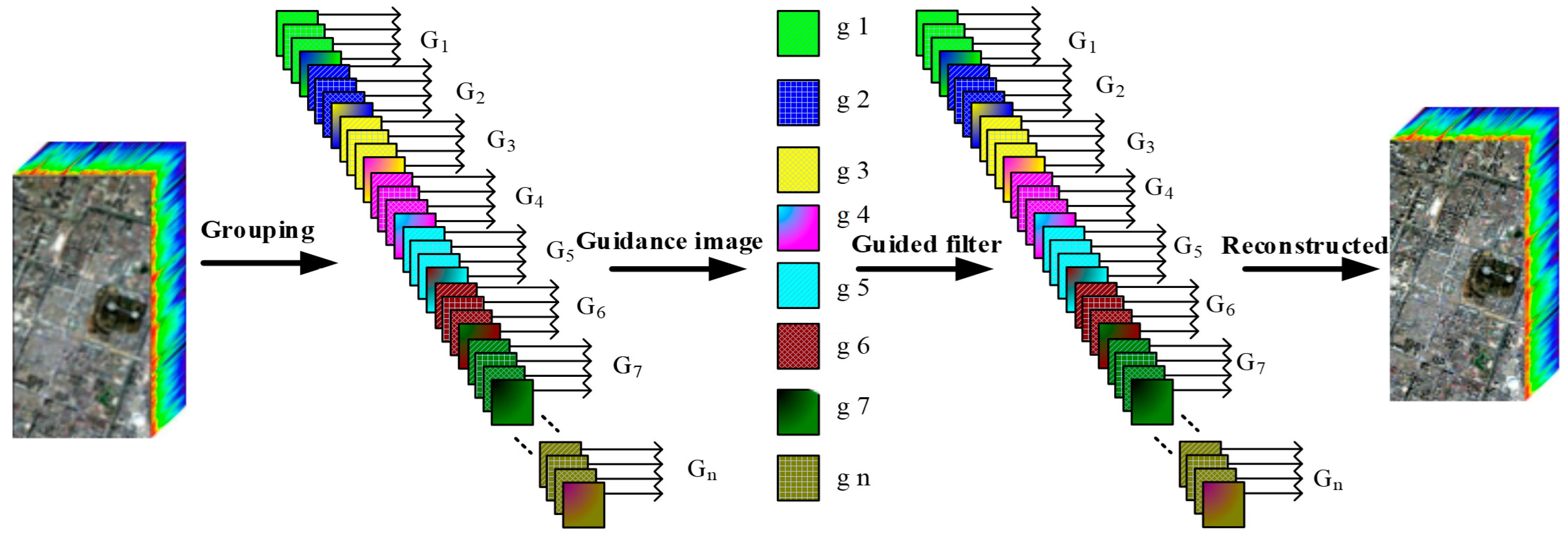
After guided filtering for all groups is completed, the output bands are restored to a hyperspectral image cube according to the band number. Finally, the reconstructed image data with enhanced texture features are obtained through the aforementioned steps. Figure 5 demonstrates the procedure of band grouping and TFE. We can see that, after sample bands with strongest textures are obtained, the reconstructed image data with enhanced texture feature can be achieved through the GF process.

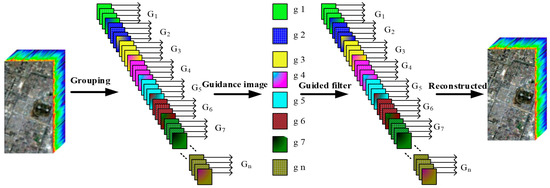
Figure 5. The procedure of band grouping and texture features enhancement.

3.3. DBN Classification Model

In this section, a DBN-based framework for hyperspectral classification with feature enhanced data is developed.

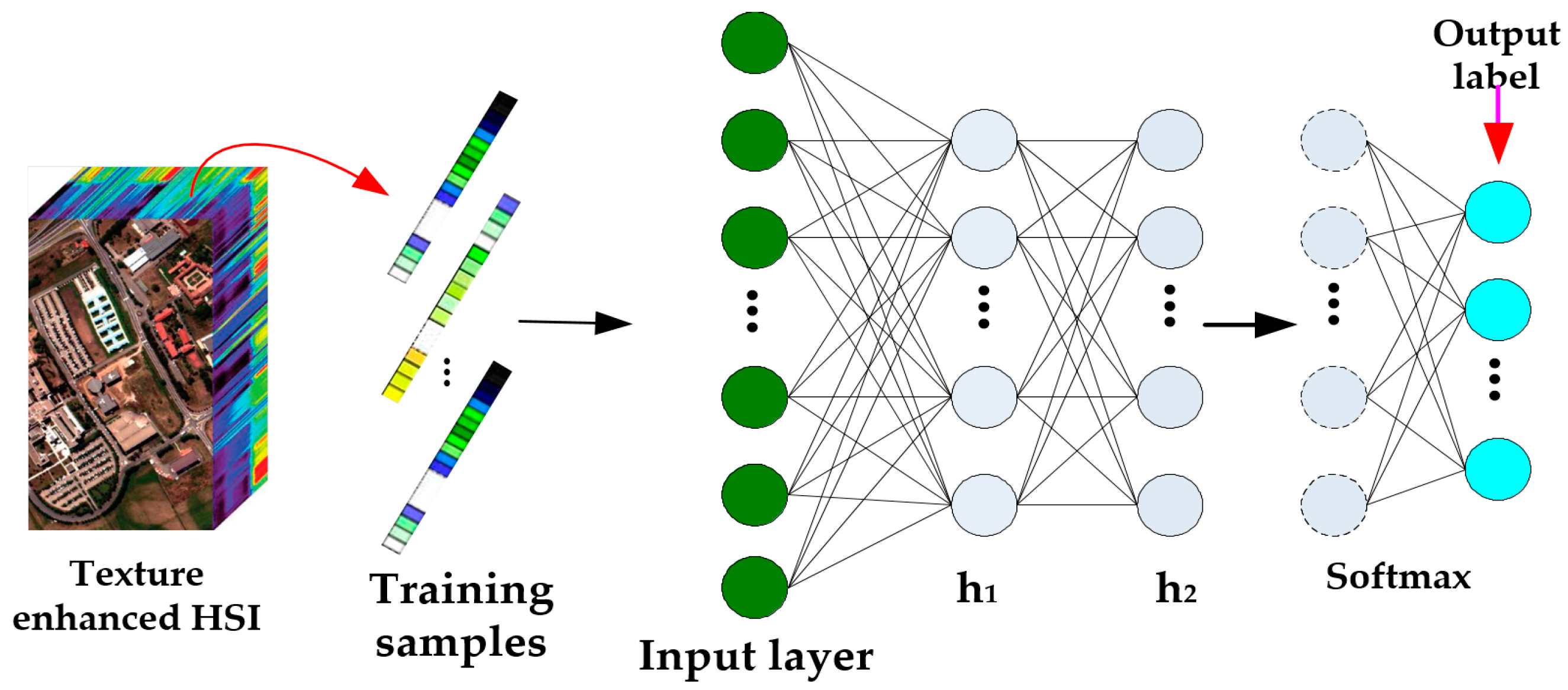
Spectral information is the most significant and direct feature, and can be directly utilized for classification. Architectures of existing methods, such as SVM and KNN, can extract spectral features but not deep enough. Therefore, only a deep architecture can make full use of the texture enhanced hyperspectral image characteristics. However, as the training samples are limited, the overfitting problem often occurs if the network is too deep, so we advocate a novel DBN framework, which has only two hidden layers (Figure 6).

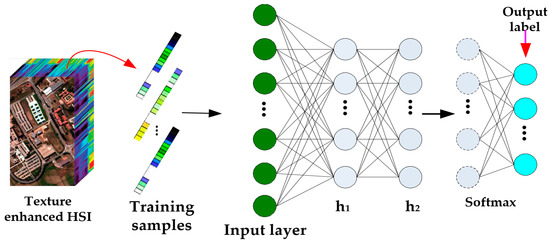
Figure 6. Our proposed DBN network for classification.

The input data consist of training samples that are one-dimensional (1-D) vectors, and each pixel of a training sample is collected from the texture enhanced HSI data. For ease of description, the first hidden layer is denoted as $h_1$ and the second $h_2$. The first layer is learned for extracting features from the input data, and the learned features are preserved in $h_1$. Then, to pursue refined and abstract features, using the features contained in $h_1$ as the visible data of the second layer, $h_2$ keeps the refined features. This procedure is generally called recursive greedy learning for pre-training a DBN.

In practice, learning each layer is often performed through the $n$-step CD, and the weights are updated using Equations (6)–(8).

To fine-tune the DBN and accomplish classification, a Softmax layer is added to the end of the network.

Now, let $X=\{x_1,x_2,\dots ,x_K\}$ be a set of training samples and $Y=\{y_1,y_2,\dots ,y_K\}$ be the corresponding labels, where $x_k={\left[x_{k1},x_{k2},\dots ,x_{kL}\right]}^T$ is the spectral signature of the $k$-th sample with $L$ bands. Utilizing the maximum likelihood method, the objective function can be written as

$$C(\mathsf{\theta })=-{\displaystyle \sum _{k=1}^K\log (P(y_k|x_k),\mathsf{\theta })}=-{\displaystyle \sum _{k=1}^K\log (S_{y_k}(x_k,\mathsf{\theta }))}$$

(15)

where $K$ is the number of training samples, $(P(y_k|x_k),\mathsf{\theta })$ means the distribution of $y_k$ when given $x_k$ with the parameters $\mathsf{\theta }$ of the Softmax layer, and $S_{y_k}(x_k,\mathsf{\theta })$ denotes the output of the Softmax layer of the $k$-th training sample, that is

$$S_{y_k}(x_k,\mathsf{\theta })=\frac{\exp \{-{\displaystyle \sum _{m=1}^M\delta (y_k=m){\mathsf{\theta }}_m^T}{h}^{H_L}\}}{{\displaystyle \sum _{n=1}^M\exp \{-{\mathsf{\theta }}_n^T{h}^{H_L}\}}},$$

(16)

where $H_L$ is the number of the hidden layers, which is set to 2 in our proposed framework, and $M$ is the number of the classes. ${\mathsf{\theta }}_m$ and ${\mathsf{\theta }}_n$ are the parameter vectors for the $m$-th and $n$-th unit of the softmax layer, respectively. $h^{H_L}$ is the output of the $H_L$-th hidden layer, which is calculated via the input data, the weights and bias from the first layer to the $H_L$-th hidden layer. To optimize the objective function, the stochastic gradient descent (SGD) algorithm is used. Finally, the label of each testing pixel is determined via the weights and biases from aforementioned steps.

4. Experiments

4.1. Datasets

In this section, three typical hyperspectral datasets, namely Indian Pines, University of Pavia and Salinas, are employed to compare the proposed DBN classification method with other state-of-the-art methods. In these experiments, we randomly select 300 labeled pixels per class for training, of which 20 samples are utilized for validation. The remaining pixels of labeled data are used for testing. Furthermore, each pixel is uniformly scaled to the range of −1 to 1.

The first experiment is Indian Pines dataset, which was gathered by Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor in northwestern Indiana. There are 220 spectral channels in 0.4 to 2.45 μm region with spatial resolution of 20 m. It consists of 145 × 145 pixels with 200 bands after removing 20 noisy and water absorption bands. Here, we employ 8 large classes in this experiment. The numbers of training and testing samples are listed in Table 2.

Table 2. Number of training and testing samples used in the Indian Pines dataset.

No.	Classes	Training	Testing
1	Corn-notill	300	1160
2	Corn-mintill	300	534
3	Grass-pasture	300	197
4	Hay-windrowed	300	189
5	Soybean-notill	300	668
6	Soybean-mintill	300	2168
7	Soybean-clean	300	314
8	Woods	300	994
	Total	2400	6224

The second dataset with 610 × 340 pixels is the University of Pavia, which was acquired by the Reflective Optics System Imaging Spectrometer (ROSIS) during a flight campaign over Pavia, northern Italy. The ROSIS sensor cover 115 spectral bands from 0.43 to 0.86 μm and the geometric resolution is 1.3 m. Each pixel has 103 bands after discarding bad bands. There are 9 ground-truth classes with the number of labeled samples shown in Table 3.

Table 3. Number of training and testing samples used in the Pavia University dataset.

No.	Classes	Training	Testing
1	Asphalt	300	6331
2	Meadows	300	18,349
3	Gravel	300	1799
4	Trees	300	2764
5	Painted metal sheets	300	1045
6	Bare Soil	300	4729
7	Bitumen	300	1030
8	Self-Blocking Bricks	300	3382
9	Shadows	300	647
	Total	2700	40,076

The third experiment is on Salinas dataset, which was also collected by the AVIRIS sensor, capturing an area over Salinas Valley, California, with a spatial resolution of 3.7 m. The area comprises 512 × 217 pixels with 204 bands after removing noisy and water absorption bands. It mainly contains vegetables, bare soils, and vineyard fields. There are 16 different ground-truth classes, and the numbers of training and testing samples are listed in Table 4.

Table 4. Number of training and testing samples used in the Salinas dataset.

No.	Classes	Training	Testing
1	Brocoli_green_weeds_1	300	1709
2	Brocoli_green_weeds_2	300	3426
3	Fallow	300	1676
4	Fallow_rough_plow	300	1094
5	Fallow_smooth	300	2378
6	Stubble	300	3659
7	Celery	300	3279
8	Grapes_untrained	300	10,971
9	Soil_vinyard_develop	300	5903
10	Corn_senesced_green_weeds	300	2978
11	Lettuce_romaine_4wk	300	768
12	Lettuce_romaine_5wk	300	1627
13	Lettuce_romaine_6wk	300	616
14	Lettuce_romaine_7wk	300	770
15	Vinyard_untrained	300	6968
16	Vinyard_vertical_trellis	300	1507
	Total	4800	49,329

Our experiments are implemented using Matlab 2015b which is manufactured by Mathworks in Massachusetts, US. The CPU we employed is Intel Core i5-3470. The basic frequency is 3.200 GHz. The operation system is Win7 with 64 bits.

4.2. Parameters Tuning and Analysis

In our proposed framework, we have several parameters that need to be adjusted: the number of hidden units, the learning rate, the max epoch and the number of hidden layers. In this section, some tuning experimental results are listed for selecting proper values. Both the number of hidden layers and the number of hidden units in hidden layers play an important role in classification performance. A suitable number of hidden layers and neurons can make full use of texture enhanced hyperspectral data without over-training, and can support a fitting mapping from original hyperspectral data to hyperspectral features. In the training process of DBN, the learning rate controls the pace of learning. It implies that a too large learning rate will lead an unstable output of training, and a too small learning rate will lead a longer training process. Therefore, an appropriate learning rate can expedite our training procedure with satisfactory performance.

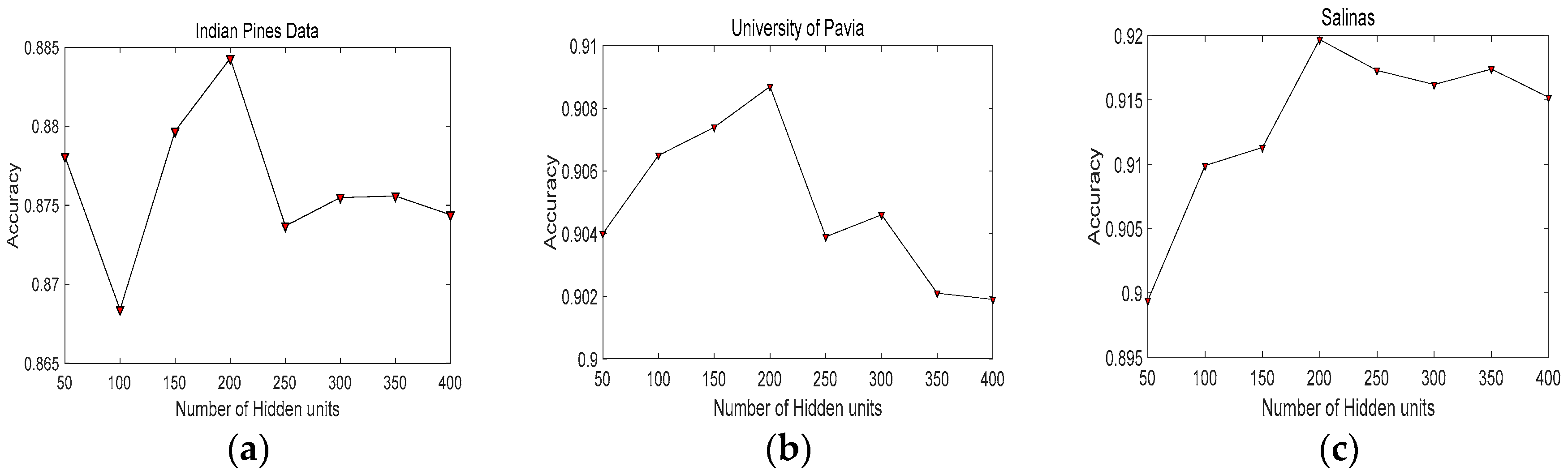
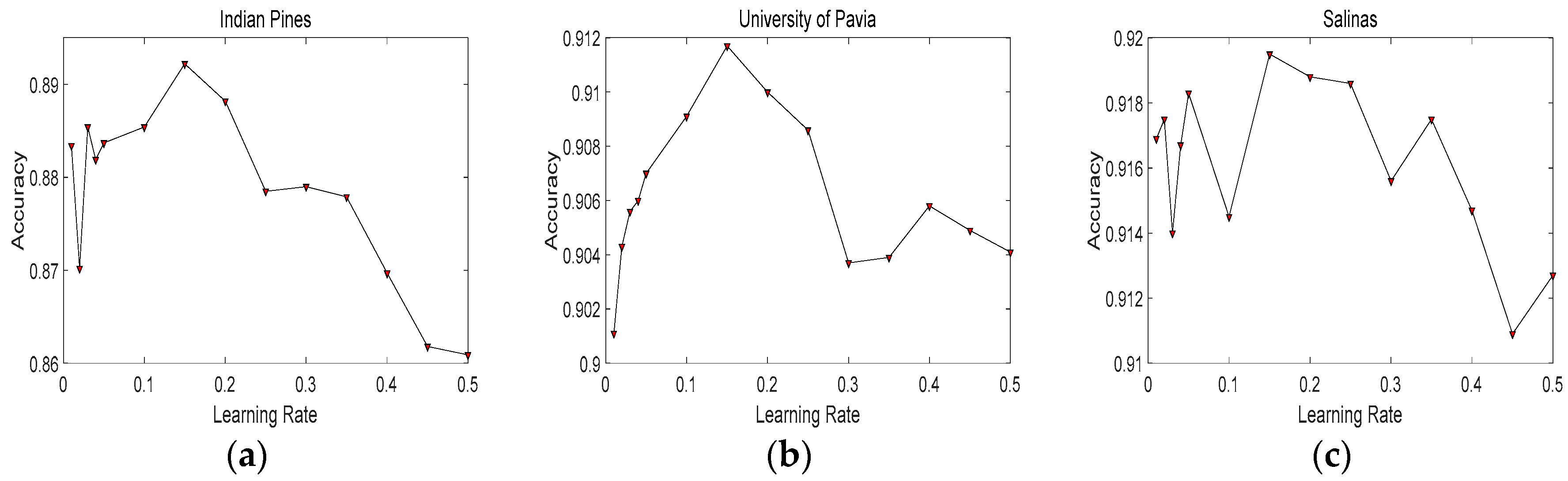
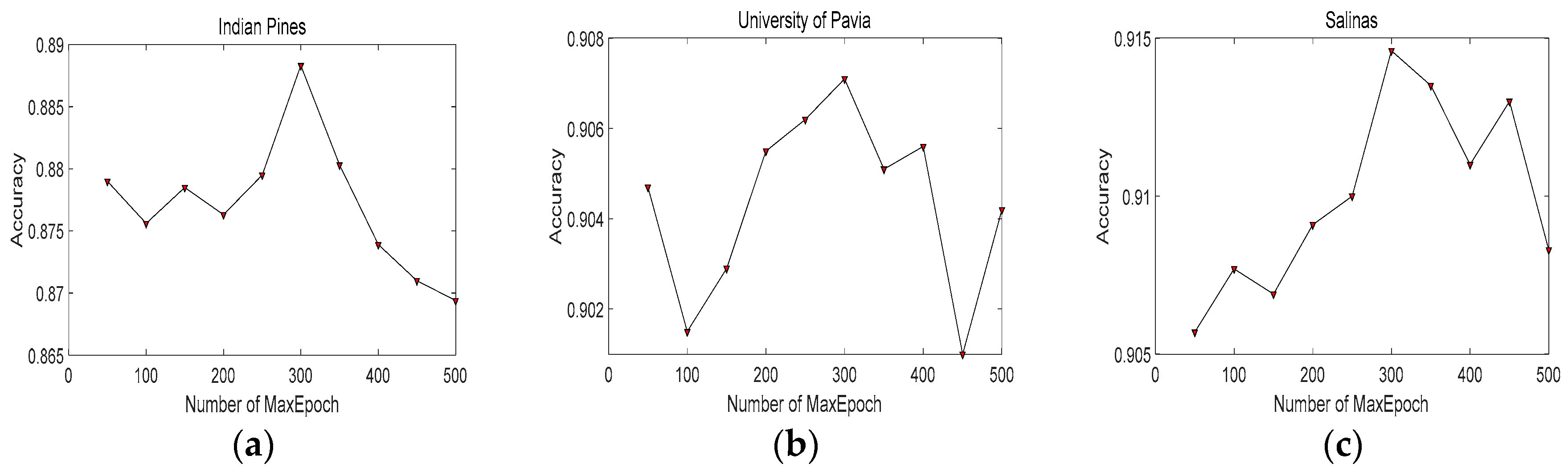
In Figure 7, we can see that our proposed framework achieves best classification accuracy with 200 hidden neurons in each hidden layer. It demonstrates that 200 is a suitable number of hidden neurons. Figure 8 depicts the relationship between accuracies and the learning rates. It can be seen that the values of learning rate from 0.15 to 0.2 can obtain better performance. Therefore, we select 0.15 for the first RBM, and 0.2 for the second RBM. To determine the max epoch, we set the range of max epoch from 50 to 500. Figure 9 demonstrates that, when max epoch reaches 300, our proposed framework can achieve best classification performance. Consequently, the max epoch is set to 300. Table 5 lists the accuracies achieved with different numbers of hidden layers in DBN. When employing two hidden layers, the classification performance of DBN can achieve superior results. Thus, in our proposed framework, we set the number of hidden layers to 2.

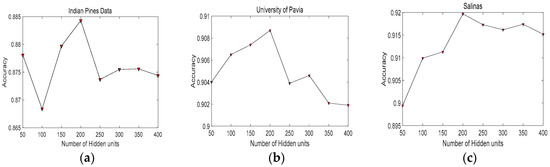
Figure 7. The relationship between accuracies and the number of hidden units in different datasets: (a) Indian Pines; (b) University of Pavia; and (c) Salinas.

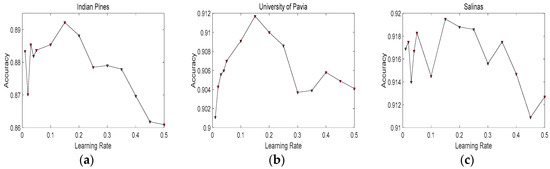
Figure 8. The relationship between accuracies and the learning rates in different datasets: (a) Indian Pines; (b) University of Pavia; and (c) Salinas.

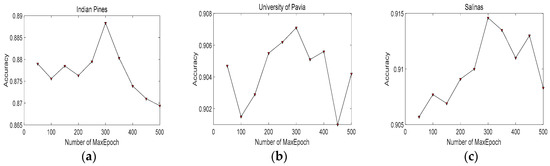
Figure 9. The relationship between accuracies and the numbers of Max epoch in different datasets: (a) Indian Pines; (b) University of Pavia; and (c) Salinas.

Table 5. The accuracies obtained via different numbers of hidden layers in DBN.

Datasets	1 Layer	2 Layers	3 Layers	4 Layers
Indian Pines	0.8919	0.8948	0.8892	0.8432
University of Pavia	0.9090	0.9123	0.9065	0.8994
Salinas	0.9123	0.9228	0.9104	0.9064

In our paper, we utilize Graycomatrix function in Matlab to calculate the GLCM. The parameters used in experiments are “NumLevels” and “Offset”, and they are set to 8 and [0, 3; −3, 3; −3, 0; −3, −3], respectively.

4.3. Evaluation Criteria

The evaluation criteria used in our paper are overall accuracy (OA), average accuracy (AA), precision, and Kappa. Especially, OA, Precision and Kappa are highlighted for assessment of the proposed framework.

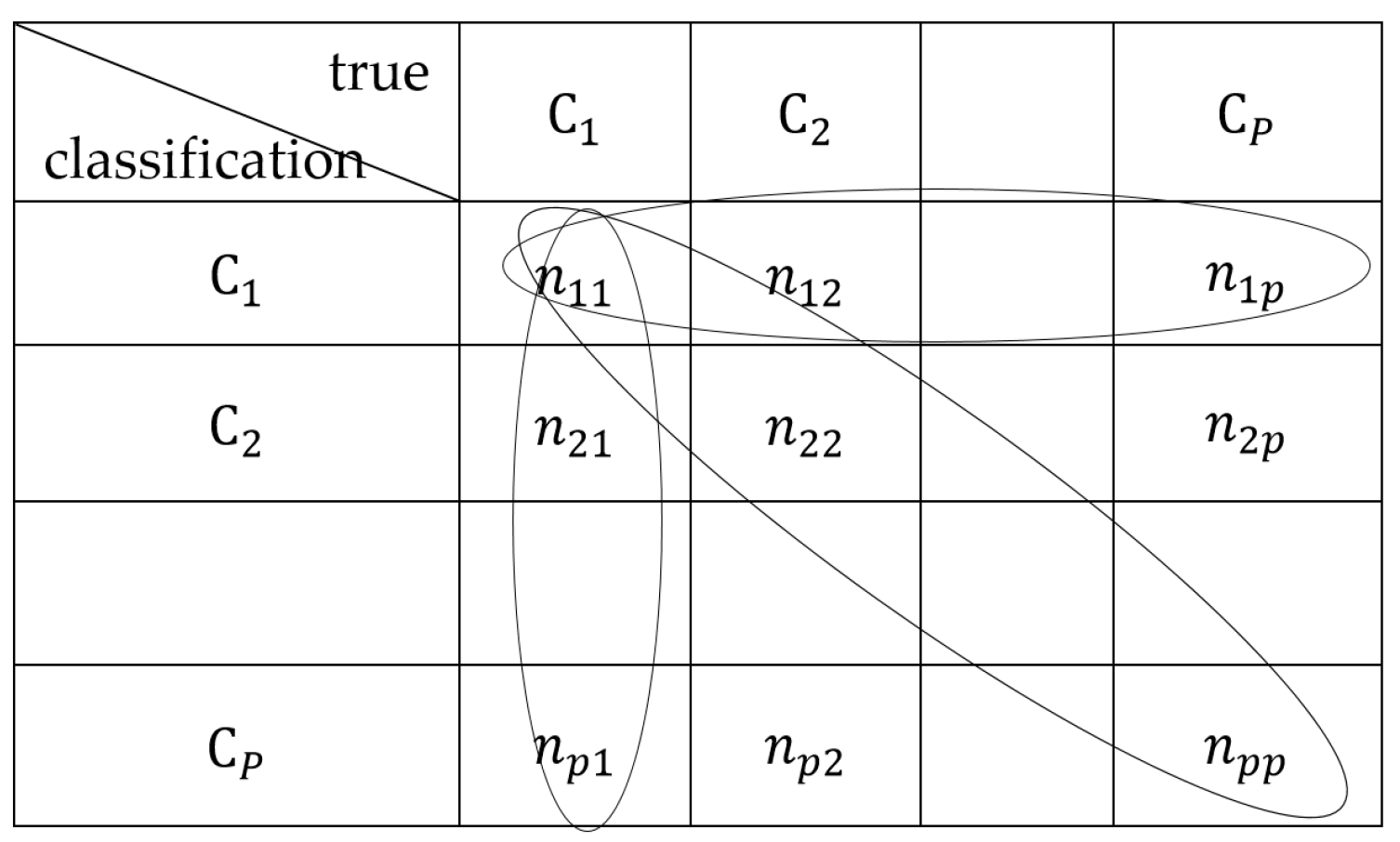
Figure 10 demonstrates a p-class confusion matrix. Based on Figure 10, AA and precision can be derived as [35]

$${\mathrm{P}}_{\mathrm{AA}}=\frac{1}{p}({\displaystyle {\sum }_{i=1}^p\frac{n_{ii}}{{\displaystyle {\sum }_{j=1}^p{n}_{ji}}}})$$

(17)

$${\mathrm{P}}_{precision}=\frac{1}{p}({\displaystyle {\sum }_{i=1}^p\frac{n_{ii}}{{\displaystyle {\sum }_{j=1}^p{n}_{ij}}}})$$

(18)

where p is the number of classes. N is the total number of the hyperspctral image data samples and $N={\displaystyle {\sum }_{i=1}^p{n}_i}$. n_ii is the number of hyperspectral image samples in the i-th class to be classified into the i-th class, and n_ji is the number of hyperspectral image samples in the i-th class to be classified into the j-th class.

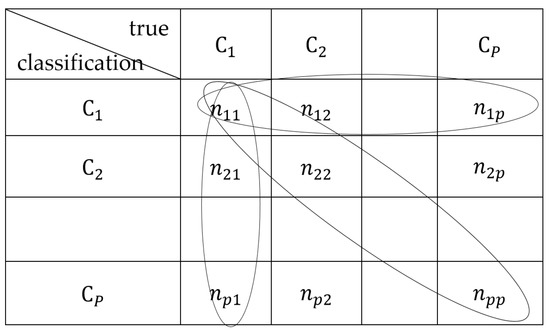
Figure 10. P-class confusion matrix.

We also take the nonparametric McNemar’s test based on the standardized normal test statistic to evaluate the statistical significance in the improvement of OA with different hyperspectral classification algorithms. The McNemar’s test statistic for two different algorithms noted as Algorithm 1 and Algorithm 2 can be calculated as [36]:

$$z=(f_{12}-f_{21})/\sqrt{f_{12}+f_{21}},$$

(19)

where $f_{12}$ denotes the number of samples misclassified using Algorithm 2 but not Algorithm 1, and $f_{21}$ means the number of samples misclassified using Algorithm 1 but not Algorithm 2. $|z|$ is the absolute value of $z$. For 5% level of significance, the $|z|$ value is 1.96. If a $|z|$ value is greater than this quantity, the two classification algorithms have significant discrepancy.

5. Experimental Results and Discussion

In this section, the proposed TFE and the novel classification framework will be evaluated and the relevant results will be summarized and discussed in detail.

5.1. Compared Methods and Band Groups

To analyze and evaluate our proposed algorithm, which combines the TFE and the optimal DBN efficiently, existing algorithm, such as SVM with Radial Basis Function kernel (SVM-RBF), the Radical Basis Function neural network (RBFNN) and CNN, are employed for comparison purpose. Besides, we also compare with a state-of-the-art spectral–spatial algorithm called EPF-G-c [22]. All these algorithms are widely used with excellent performance in hyperspectral image classification tasks, especially EPF-G-c. In addition, for evaluating our proposed texture feature enhancement (TFE) algorithm, we also applied TFE algorithm on the traditional SVM-RBF and RBFNN. All experiments are repeated 10 times with the average classification results demonstrated for comparison.

According to our proposed band grouping solution, the bands of Indian Pines can be divided into 41 groups: 1, 2, 3, 4–17, 18, 19–33, 34, 35, 36, 37–56, 57, 58–60, 61, 62, 63–74, 75, 76, 77–82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92–93, 94, 95, 96–97, 98–102, 103, 104, 105, 106–143, 144, 145, 146–198, 199 and 200. The bands of University of Pavia can be divided into 19 groups: 1, 2, 3, 4, 5, 6, 7, 8–68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78–84 and 85–103. The bands of Salinas can be divided into 21 groups: 1, 2, 3, 4, 5–35, 36, 37, 38, 39, 40, 41–104, 105–106, 107, 108, 109–146, 147, 148, 149–201, 202, 203 and 204. All these band groups are employed in the TFE algorithm.

5.2. Discussion on Effectiveness of the Proposed TFE

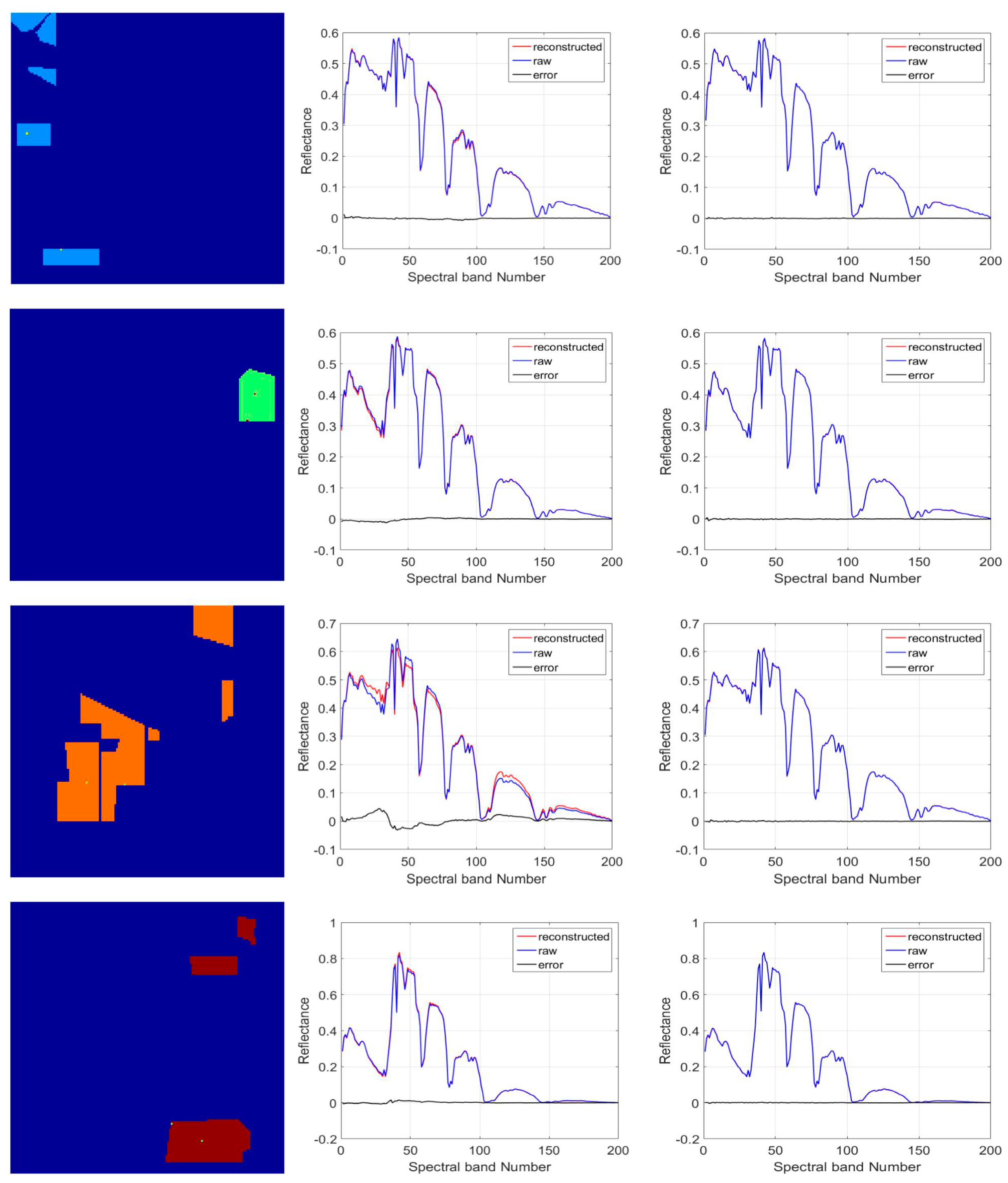
Figure 11 demonstrates the reconstructions of border and inner pixels of four classes after TFE in Indian Pines dataset. The first image of each row depicts the locations of border and inner pixels. The reconstruction and reconstructed error of the border pixel are demonstrated in the second image of each row. Meanwhile, the reconstruction and reconstructed error of the inner pixel are demonstrated in the third image.

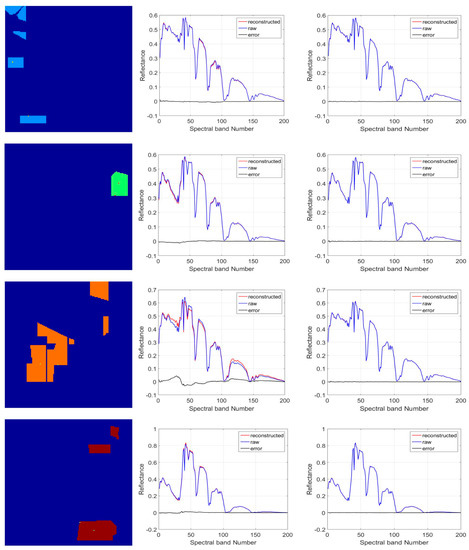
Figure 11. The reconstructions of the border-pixels and inner-pixels of different classes in Indian Pines. First row is the reconstruction information of Class 2, second row is the reconstruction information of Class 4, third row is the reconstruction information of Class 6 and last row is the reconstruction information of Class 8.

In hyperspectral classification, some spectra of the hyperspectral image are distorted through imaging noise or low spatial resolution, especially border-pixels, therefore the difficulty of hyperspectral classification primarily focuses on the correct classification of the border pixels. In Figure 11, it can be seen that, by utilizing TFE, the reconstructed border pixels become different from the original border pixels, and the reconstructed inner pixels are nearly the same as the original inner pixels, which implies that TFE plays an important role for border pixels. TFE can make border pixels distinct with its characteristics and more similar to their original spectra. Hence, the texture feature of the hyperspectral image become more obvious and clear. Consequently, the pixels that are difficult to distinguish can be recognized more easily than before with clearer texture feature. In other words, TFE has a positive effect for enhancing hyperspectral classification performance.

5.3. Discussion on Classification Results and Statistical Test

Table 6 provides the classification performance on Indian Pines achieved by different classification algorithms: SVM, RBFNN, optimal DBN (O_DBN), SVM combined with TFE (SVM_TFE), RBFNN combined with TFE (RBFNN_TFE), CNN, EFP-G-c and our proposed framework. O_DBN denotes the optimal DBN we proposed but without TFE. The SVM_TFE and RBFNN_TFE are two algorithms combined with the TFE method. The classification accuracy of each class is also listed in this table. In Table 6, we can see that our proposed framework can obtain the superior performance compared with other algorithms. Meanwhile, the optimal DBN has the best classification accuracy compared to the other algorithms without TFE, such as SVM and RBFNN. Although EFP-G-c is an outstanding spectral–spatial hyperspectral classification algorithm, our proposed framework utilizing TFE still has slightly better classification accuracy. Besides, SVM_TFE and RBFNN_TFE outperform SVM and RBFNN, respectively. The OA of SVM_TFE is 5.06% greater than SVM, and the OA of RBFNN_TFE is 8.97% higher than RBFNN. Compared with O_DBN, the OA obtained via our proposed framework improved by 8.08% and the Kappa increased by 9.98%. All these facts indicate the successful effects of TFE and demonstrates that our proposed framework and TFE have good influence on Indian Pines in hyperspectral classification.

Table 6. Classification accuracy of different algorithms on Indian Pines.

Class	SVM	RBFNN	O_DBN	SVM_TFE	RBFNN_TFE	CNN	EPF-G-c	Our Proposed
1	0.8578	0.8672	0.8562	0.9069	0.9638	0.9107	0.9757	0.9690
2	0.9251	0.9288	0.9532	0.9625	0.9944	0.7783	0.9736	0.9888
3	0.9391	0.9543	0.9594	0.9594	0.9949	0.8462	0.9314	0.9594
4	0.9841	1	0.9947	1	1	0.9793	0.9793	1
5	0.9162	0.9237	0.9172	0.9506	0.9910	0.7842	0.9268	0.9880
6	0.8054	0.7975	0.8189	0.8962	0.9553	0.9348	0.9855	0.9613
7	0.9363	0.9459	0.9490	0.9522	0.9809	0.8442	0.9873	0.9682
8	0.9940	0.9950	0.9909	1	1	0.9929	0.9881	1
OA	0.8837	0.8854	0.8948	0.9343	0.9751	0.8983	0.9754	0.9756
AA	0.9197	0.9265	0.9270	0.9535	0.9850	0.8838	0.9685	0.9793
Kappa	0.8559	0.8582	0.8617	0.9180	0.9688	0.8736	0.9692	0.9694

Table 7 lists the classification precision achieved via these different classification algorithms. In Table 7, we can see that the precision of our proposed algorithm outperforms SVM, RBFNN, O_DBN, SVM_TFE, RBFNN_TEF, CNN and EPF-G-c. In addition, the methods associated with TFE have better classification precision than without TFE.

Table 7. Classification precision of different algorithms on Indian Pines.

Class	SVM	RBFNN	O_DBN	SVM_TFE	RBFNN_TFE	CNN	EPF-G-c	Our Proposed
1	0.8585	0.8643	0.8563	0.9132	0.9646	0.8440	0.9474	0.9571
2	0.7577	0.7631	0.7496	0.8877	0.9620	0.9270	0.9606	0.9661
3	0.9113	0.9353	0.8400	0.8873	0.9849	0.9492	0.9645	0.9692
4	0.9688	0.9844	0.9495	0.9895	1	1.0000	1	1
5	0.7917	0.7434	0.8037	0.8675	0.9272	0.9087	0.965	0.9396
6	0.9307	0.9341	0.9417	0.9643	0.9862	0.8538	0.9686	0.9836
7	0.7861	0.8710	0.8466	0.8617	0.9716	0.9490	0.9936	0.9882
8	0.9930	0.9940	0.9970	0.9990	1	0.9909	1	1
Precision	0.8747	0.8862	0.8731	0.9213	0.9746	0.9278	0.9750	0.9755

Table 8 and Table 10 present the classification accuracy acquired via different algorithms for University of Pavia and Salinas datasets. Meanwhile, Table 9 and Table 11 also list the precisions obtained through our proposed model and other classification algorithms on different datasets. It is obvious in Table 8 and Table 10 that our proposed framework has better performance than other classification methods. Especially, we can see that all algorithms that integrate TFE outperform those without TFE. By employing the TFE, the performance of SVM increased by 5.78% in University of Pavia and 1.75% in Salinas, while the performance of RBFNN improved by 6.8% in University of Pavia and 1.55% in Salinas. The OA achieved by the proposed framework is 6.55% higher than the OA achieved via optimal DBN in University of Pavia and 3.94% larger than the OA achieved via optimal DBN in Salinas. Furthermore, the proposed classification framework has better performance than CNN and EPF-G-c. As for kappa coefficients, we can see that our proposed framework has better consistency. The possible reason is the ability of our proposed framework, as a deep network, to extract high-level features of data is stronger than the RBFN and the SVM, as shallow networks, thus the description ability of our proposed framework is more stable. In Table 9 and Table 11, the precisions obtained through our proposed model on different datasets are better than precisions achieved via other algorithms. Furthermore, our proposed TFE has a positive effect on classification accuracy.

Table 8. Classification accuracy of different algorithms on University of Pavia.

Class	SVM	RBFNN	O_DBN	SVM_TFE	RBFNN_TFE	CNN	EPF-G-c	Our Proposed
1	0.7466	0.7733	0.8650	0.8534	0.9029	0.9758	0.9579	0.9458
2	0.8442	0.8980	0.9281	0.9058	0.9601	0.9832	0.9993	0.9728
3	0.8533	0.8377	0.8410	0.8922	0.9305	0.7795	0.9511	0.9550
4	0.9801	0.9602	0.9765	0.9772	0.9787	0.9096	0.9677	0.9881
5	0.9990	0.9990	0.9990	0.9981	0.9971	0.9830	0.9372	0.9990
6	0.9108	0.9492	0.9125	0.9558	0.9903	0.8153	0.9263	0.9873
7	0.9456	0.9583	0.8990	0.9544	0.9932	0.6680	0.9885	0.9893
8	0.8430	0.8628	0.8613	0.9101	0.9571	0.8562	0.9421	0.9438
9	1	1	0.9985	1	1	0.9985	0.9895	1.0000
OA	0.8555	0.8888	0.9123	0.9133	0.9568	0.9211	0.9671	0.9696
AA	0.9025	0.9154	0.9201	0.9385	0.9678	0.8855	0.9622	0.9757
Kappa	0.8103	0.8525	0.8824	0.8845	0.9418	0.8943	0.9590	0.9590

Table 10. Classification accuracy of different algorithms on Salinas Dataset.

Class	SVM	RBFNN	O_DBN	SVM_TFE	RBFNN_TFE	CNN	EPF-G-c	Our Proposed
1	0.9965	0.9971	0.9947	0.9982	0.9988	1.0000	1.0000	0.9947
2	0.9947	0.9947	1	0.9956	0.9950	0.9933	0.9994	0.9962
3	0.9976	0.9988	0.9976	0.9976	0.9982	0.9589	0.9994	0.9976
4	0.9963	0.9963	0.9963	0.9954	0.9954	0.9838	0.9973	0.9973
5	0.9886	0.9849	0.9811	0.9874	0.9899	0.9898	0.9992	0.9853
6	0.9981	0.9986	0.9978	0.9981	0.9981	0.9995	0.9984	0.9973
7	0.9970	0.9963	0.9957	0.9960	0.9966	0.9988	0.9989	0.9963
8	0.8606	0.8567	0.8315	0.8761	0.8893	0.8379	0.8690	0.9085
9	0.9934	0.9985	0.9939	0.9942	0.9966	0.9896	0.9911	0.9949
10	0.9661	0.9758	0.9426	0.9698	0.9775	0.8848	0.9715	0.9614
11	0.9987	0.9961	0.9961	0.9987	0.9987	0.8919	1	1
12	0.9994	1	1	0.9994	1	0.9685	0.9992	0.9994
13	0.9968	0.9951	0.9984	0.9951	0.9951	0.9534	0.9987	0.9968
14	0.9792	0.9857	0.9948	0.9857	0.9805	0.9159	0.9978	0.9948
15	0.6972	0.7336	0.7646	0.7941	0.7916	0.7673	0.8856	0.9127
16	0.9920	0.9900	0.9854	0.9920	0.9914	0.9695	1	0.9887
OA	0.9212	0.9266	0.9228	0.9387	0.9421	0.9155	0.9543	0.9622
AA	0.9658	0.9687	0.9669	0.9733	0.9746	0.9439	0.9816	0.9826
Kappa	0.9114	0.9175	0.9133	0.9312	0.9350	0.9051	0.9486	0.9575

Table 9. Classification precision of different algorithms on University of Pavia.

Class	SVM	RBFNN	O_DBN	SVM_TFE	RBFNN_TFE	CNN	EPF-G-c	Our Proposed
1	0.9795	0.9798	0.9675	0.9836	0.9877	0.8531	0.9822	0.9837
2	0.9720	0.9841	0.9763	0.9869	0.9980	0.9341	0.9756	0.9978
3	0.6657	0.6905	0.7568	0.7803	0.8876	0.8766	0.9711	0.9261
4	0.7657	0.8906	0.8207	0.9122	0.9808	0.9678	0.9642	0.9437
5	0.9831	0.9981	0.9849	0.9943	1	0.9981	0.9900	0.9877
6	0.6714	0.7388	0.7735	0.7456	0.8639	0.9484	0.9450	0.9189
7	0.5084	0.5583	0.6515	0.7567	0.8575	0.9592	0.9157	0.9586
8	0.8312	0.8028	0.8645	0.8394	0.8772	0.8752	0.9864	0.9117
9	1	1	0.9985	0.9985	1	0.9985	0.8779	0.9969
Precision	0.8197	0.8492	0.8660	0.8886	0.9392	0.9345	0.9565	0.9583

Table 11. Classification precision of different algorithms on Salinas Dataset.

Class	SVM	RBFNN	O_DBN	SVM_TFE	RBFNN_TFE	CNN	EPF-G-c	Our Proposed
1	0.9988	0.9994	0.9971	0.9994	1	0.9801	1	1
2	0.9985	0.9985	0.9980	0.9994	0.9994	0.9947	0.9995	0.9991
3	0.9744	0.9721	0.9489	0.9830	0.9824	0.9976	0.9782	0.9682
4	0.9909	0.9864	0.9847	0.9918	0.9900	0.9973	0.9991	0.9900
5	0.9941	0.9970	0.9978	0.9920	0.9895	0.9315	0.9987	0.9924
6	0.9995	0.9997	0.9884	0.9992	0.9995	0.9978	0.9997	0.9940
7	0.9966	1	1	0.9951	1	0.9957	0.9991	0.9973
8	0.8209	0.8372	0.8592	0.8729	0.8726	0.8952	0.9162	0.9415
9	0.9956	0.9916	0.9898	0.9931	0.9927	0.9810	0.9475	0.9926
10	0.9517	0.9735	0.8699	0.9534	0.9674	0.9325	0.9627	0.9487
11	0.9808	0.9922	0.8242	0.9935	0.9948	0.9831	0.9994	0.9785
12	0.9909	0.9897	0.9748	0.9933	0.9921	1.0000	0.9987	0.9933
13	0.9777	0.9919	0.9935	0.9871	0.9839	0.9968	0.9920	0.9731
14	0.8737	0.9245	0.8235	0.9256	0.8945	0.9506	0.9359	0.8899
15	0.7803	0.7747	0.7344	0.8187	0.8341	0.5128	0.7777	0.8559
16	0.9701	0.9920	0.9861	0.9658	0.9953	0.9854	0.9946	0.9900
Precision	0.9559	0.9638	0.9356	0.9665	0.9680	0.9458	0.9687	0.9690

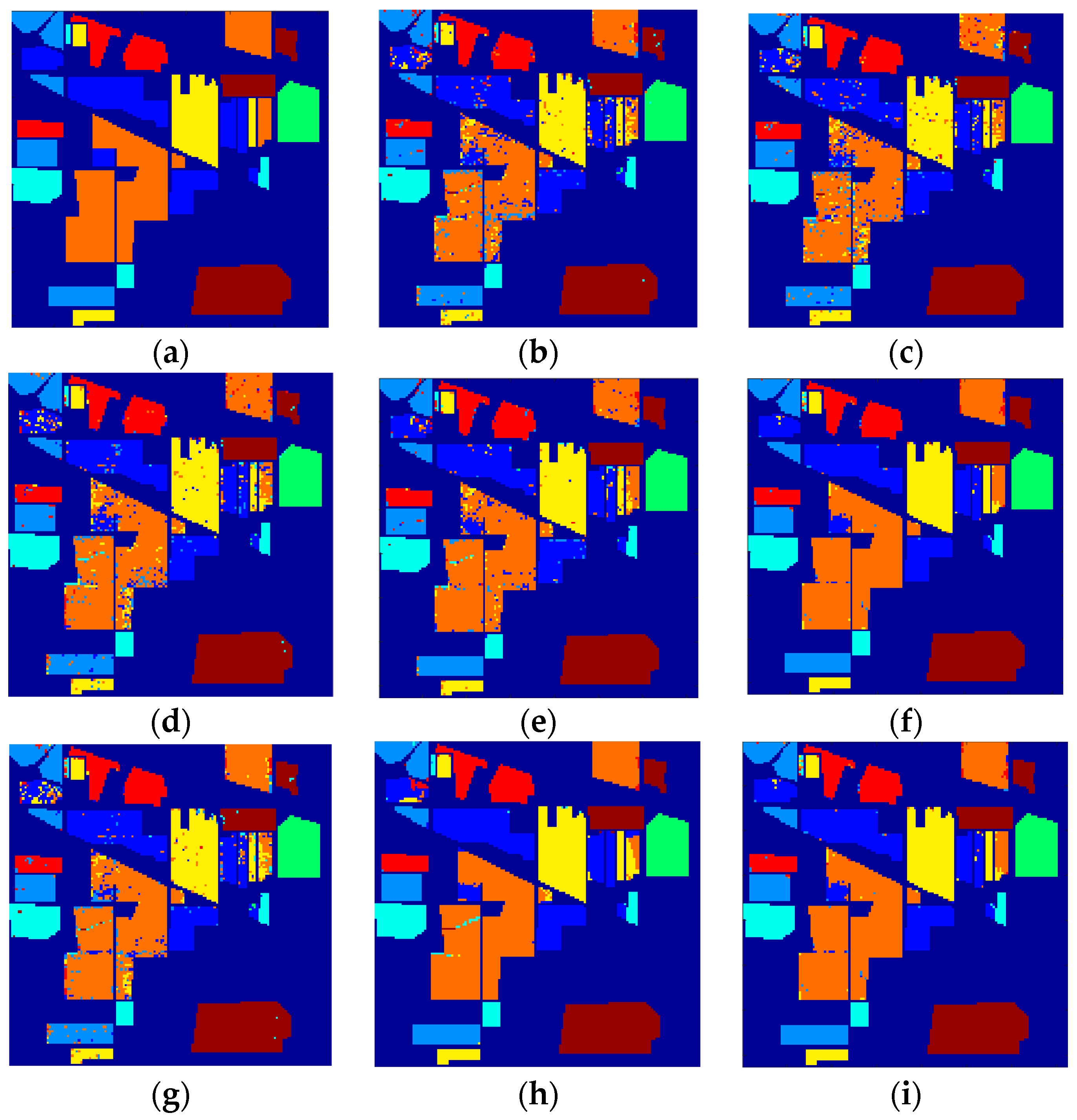
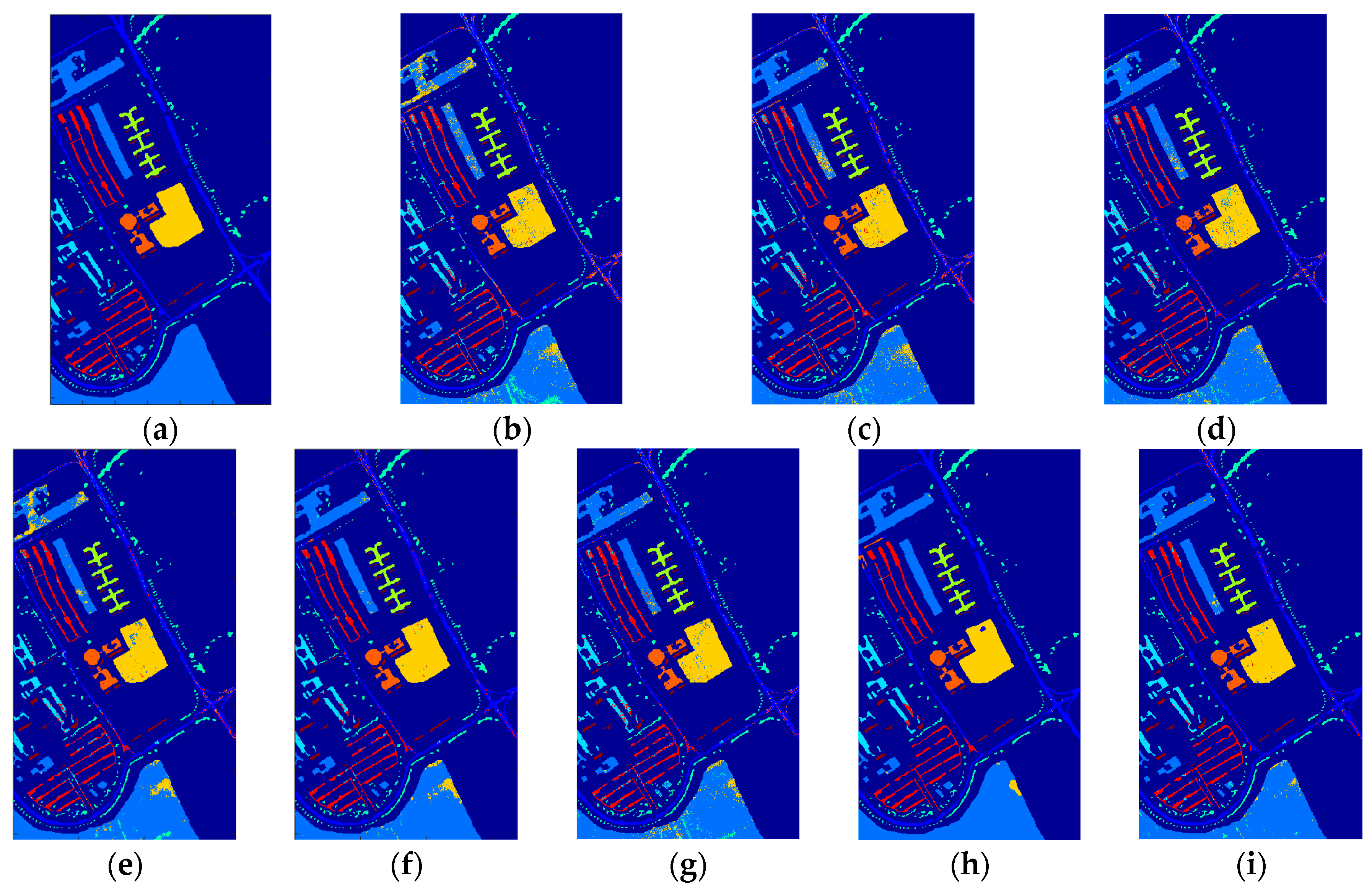
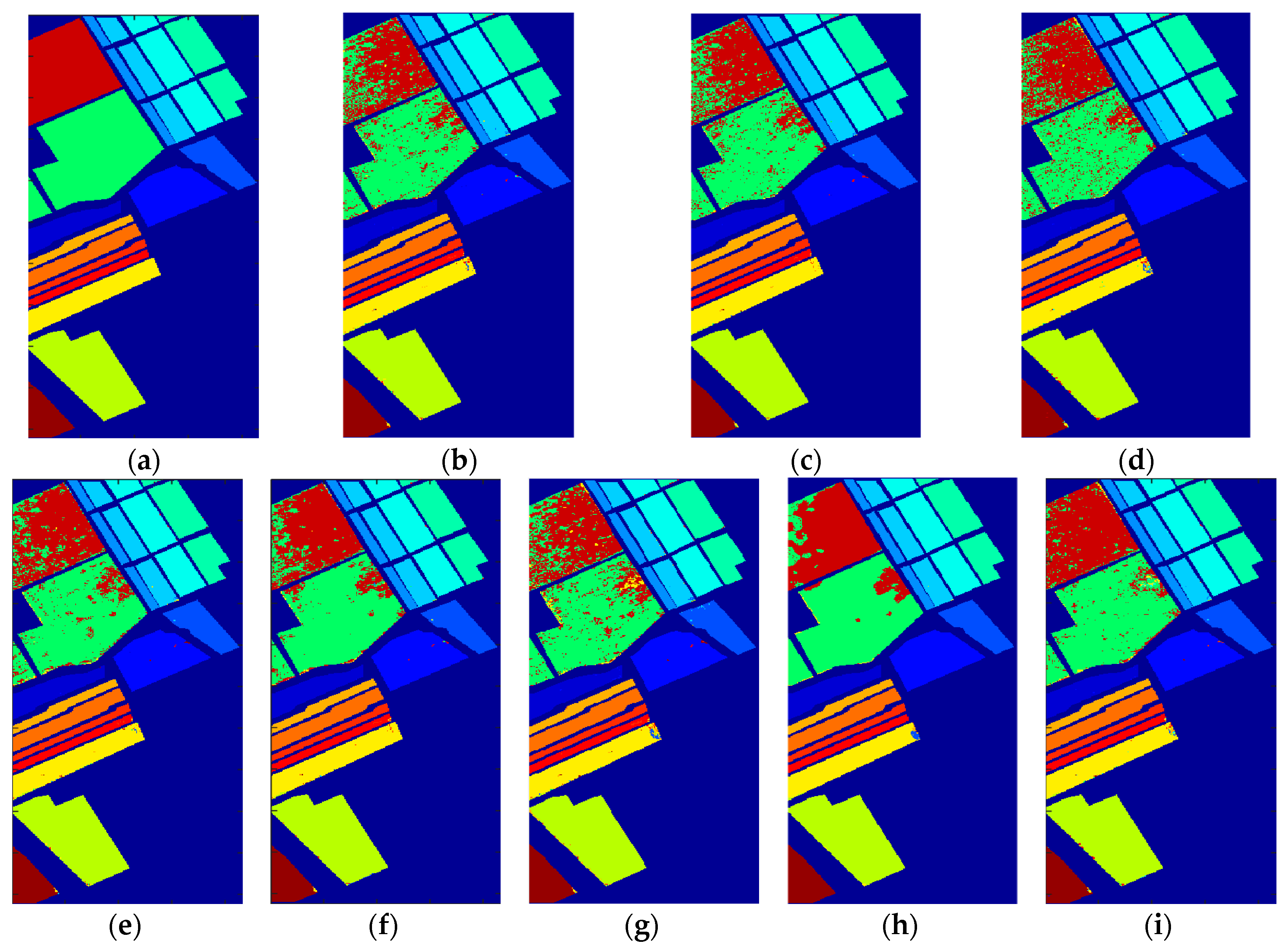
Figure 12, Figure 13 and Figure 14 demonstrate the classification maps obtained in Indian Pines, University of Pavia and Salinas, respectively. Clearly, the classification maps shown in Figure 12, Figure 13 and Figure 14 achieved by our proposed framework are the smoothest and clearest. The classification accuracy of border pixels in these datasets is improved greatly and the boundaries of different classes are more distinct. Compared to other classification algorithms, the results of our proposed framework are better because they contain less salt-and-pepper noise.

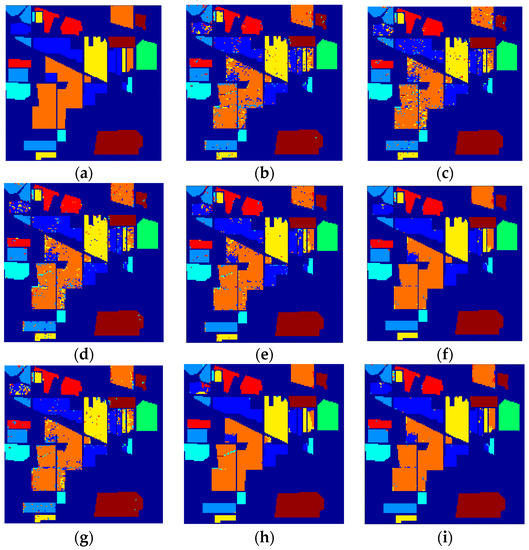
Figure 12. The classification maps obtained via different algorithms in Indian Pines: (a) Ground truth; (b) SVM; (c) RBFNN; (d) O_DBN; (e) SVM_TFE; (f) RBFNN_TFE; (g) CNN; (h) EFP-G-c; and (i) the proposed framework.

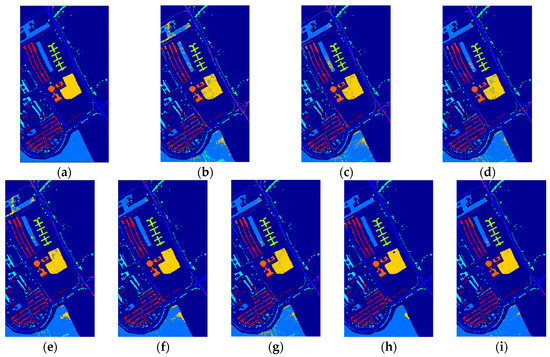
Figure 13. The classification maps obtained via different algorithms in University of Pavia: (a) Ground truth, (b) SVM, (c) RBFNN, (d) O_DBN, (e) SVM_TFE, (f) RBFNN_TFE, (g) CNN, (h) EFP-G-c and (i) the proposed framework.

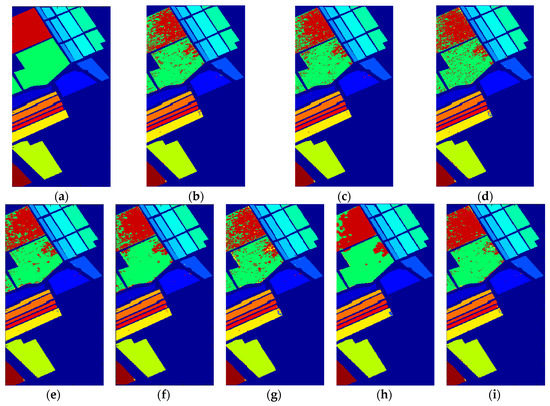
Figure 14. The classification maps obtained via different algorithms in Salinas Dataset: (a) Ground truth, (b) SVM, (c) RBFNN, (d) O_DBN, (e) SVM_TFE, (f) RBFNN_TFE, (g) CNN, (h) EFP-G-c and (i) the proposed framework.

Table 12 presents the average $|z|$ values achieved from Indian Pines, Pavia University and Salinas of the proposed classification framework as well as other classification algorithms. A “yes” here denotes the two classification algorithms in McNemar’s test have significant performance discrepancy. Obviously, the proposed classification framework is statistically different from its counterparts with 5% significance level.

Table 12. ($|z|$ values/Siginificant?) in the McNemar’s Test.

Algorithms	Indian Pines	Pavia University	Salinas
SVM	31.16/Yes	68.33/Yes	41.19/Yes
RBFNN	31.34/Yes	69.27/Yes	41.39/Yes
O_DBN	2.78/Yes	3.74/Yes	3.32/Yes
SVM_TFE	31.95/Yes	73.29/Yes	41.21/Yes
RBFNN_TFE	32.82/Yes	74.84/Yes	42.49/Yes
CNN	3.50/Yes	3.00/Yes	4.49/Yes
EPF_G_c	32.16/Yes	75.13/Yes	41.21/Yes

Note: 5% significance level is selected.

6. Conclusions

In this paper, we investigate a novel hyperspectral classification framework based on an optimal DBN algorithm. In our proposed framework, we develop a new TFE algorithm that employs multi-texture features and band grouping method. The resulting classification framework can offer better classification accuracy than other classic algorithms. To further test our proposed TFE algorithm, a series of experiments based on the combination of the state-of-the-art algorithms and the TFE algorithm are applied on the three classic hyperspectral datasets. Experimental results demonstrate that the algorithms with TFE outperform those without TFE, which implies that our proposed TFE can play an important role in improving hyperspectral classification performance. We believe that the proposed hyperspectral classification framework based on the optimal DBN and TFE is more suitable to process hyperspectral data in practical applications when training samples are limited.