Abstract
The Colville is an Arctic river in the Alaska North Slope. The residents of Nuiqsut rely heavily on the Colville for their subsistence needs. Increased erosion has been reported on the Colville, especially along bluffs, which shaped the goals of this study: to use remote sensing techniques to map and quantify erosion rates and the volume of land loss at selected bluff sites along the main channel of the Colville, and to assess the suitability of automated methods of regional erosion monitoring. We used orthomosaics from high resolution aerial photos acquired in 1955 and 1979/1982, as well as high resolution WorldView-2 images from 2015 to quantify long-term erosion rates and the cubic volume of erosion. We found that, at the selected sites, erosion rates averaged 1 to 3.5 m per year. The erosion rate remained the same at one site and increased from 1955 to 2015 at two of the four sites. We estimated the volume of land loss to be in the magnitude of 166,000 m3 to 2.5 million m3 at our largest site. We also found that estimates of erosion were comparable for manual hand-digitized and automated methods, suggesting our automated method was effective and can be extended to monitor erosion at other sites along river systems that are bordered by bluffs.
1. Introduction
Erosion plays a significant role in the changing environment of a river. It affects water flow, water quality, channel width and depth, and safe use of a river as a transportation corridor. In the Arctic, climate warming severely influences river geomorphic processes, including erosion, especially when a river runs through a continuous permafrost zone [1]. Warmer air and water temperatures lead to more pronounced thermal erosion and toe undercutting of ice-rich permafrost banks, resulting in erosion through massive block failures. This process is unique to rivers flowing through continuous permafrost and results in higher bank erosion rates with increasing bank height, which is uncommon for non-periglacial rivers [2].
The Colville River is frozen seven to eight months of the year, creating a very short ice-free season for intense erosion, transportation, and redeposition of sediment [3]. Climate impacts on river geomorphic processes are particularly relevant to residents of river communities with mixed cash-subsistence economies, who heavily rely on the river to access and harvest subsistence food [4]. There are two established Alaska Native communities along the Colville: Umiat and Nuiqsut. During our field visit we spoke with Nuiqsut residents about changes they perceive to the Colville River and the effects on the community. Residents reported accelerated erosion throughout the river system and difficulty in navigating the river, which has resulted in increasingly limited access to harvest sites upstream. Also, as part of a six-year study to understand social and ecological changes in Alaska and the ability of communities to adapt to those changes, Nuiqsut residents were asked “How has erosion changed along the Colville?”. Of the interviewed residents, 61% reported more or faster erosion along the Colville River now than there used to be, and that increased erosion contributes to changes in the river environment; and 11% reported no change [5].
Some residents believe that the changes in the Colville River are happening due to recent climate warming. Wendler et al. [6] reported an average warming of 2.7 °C across Arctic Alaska from 1979 to 2013, which is far greater than that recorded during any other time period across Alaska as well as across other climate zones. Warmer ground and air temperatures caused earlier river breakups in recent years, leaving the river banks exposed to flowing water for longer periods [7]. Also, changes in seasonality are resulting in very intense and rapid seasonal changes to the Colville, such as lengthening of thawing season, and flooding during the spring snowmelt due to rapid warming [5]. Some studies on erosion in Northern Rivers [1] point to a possible correlation between climate warming and accelerated erosion. We will analyze air temperature, ground temperature, snow depth, and length of summer season data to verify if a similar trend also occurs in the Alaska North Slope, which may contribute to accelerated erosion along the Colville.
The focus of this paper is to investigate riverbank erosion at bluff bound sites of the Colville River using a simple yet robust approach that can be easily repeated on newer images. The goals of this study are (1) to map and estimate erosion rates and volume of land loss at selected bluff sites along the main channel of the Colville River from aerial photos and satellite imagery; and (2) to assess the suitability of automated methods for regional erosion monitoring by comparing mapping results and land volume loss estimates from automated change detection methods and manual hand-digitized measurements. We do this by identifying four sites of heavy erosion and measuring erosion rates at those sites using aerial and satellite imagery from 1955, 1979, 1982, and 2015. We estimate the volume of land loss by using the mapped erosion area and terrain height from a high-resolution Arctic Digital Elevation Model (DEM), which employs a novel yet simple technique. For broader applicability of the research, we deliberately keep the processing approach simple, practical, and easy to repeat.
2. Study Area
The Colville is the longest river in the Alaskan North Slope with a course of 600 km. It drains into a 550 km2 delta, 250 km east of the community of Utqiagvik (formerly Barrow). The Colville River serves as one of the transportation arteries in the North Slope of Alaska, a region with virtually no roads. We chose this river because of its significance to Nuiqsut, a Native village located on the Colville River about 25 km South (upstream) of the river mouth on the Beaufort Sea (Figure 1). Villagers travel great distances on the river, from Umiat to the Beaufort Sea, for subsistence hunting. They frequent this section of the river to reach moose and caribou hunting grounds.
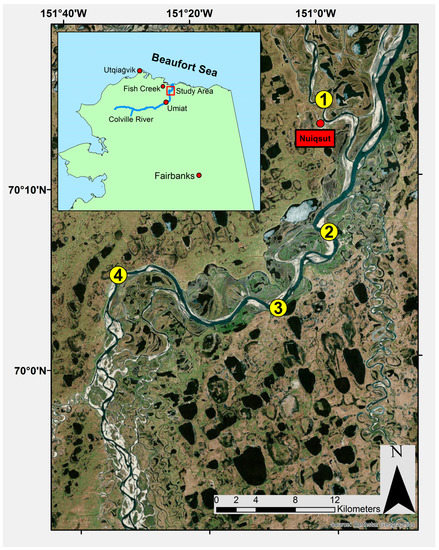
Figure 1.
Study area map showing a stretch of the Colville near the village of Nuiqsut, Alaska (AK). The four sites of heavy erosion studied here are highlighted in yellow.
We focused our study on the bluff bound parts of this frequently used section of the main channel of the Colville River. We used the main channel of the river to study erosion, as this is the primary navigation corridor and the larger channel size also makes it more appropriate for remote sensing-based mapping and investigation. We focused on bluff sites because extensive erosion usually occurs along bluffs [8,9,10,11,12]. Additionally, on nadir-looking remote sensing images, the sharp contrast between the tundra, the bluff face, and the river water is particularly suitable for delineating the water–land boundary, which is necessary to monitor erosion. We selected four bluff sites along the Colville (Figure 1) that suitably represent the variability of bluffs along the Colville. The bluff heights at these sites range from 5–33 m.
3. Data
3.1. Remote Sensing Data
This study focused primarily on the use of remote sensing data (Table 1) to study erosion at selected sites on the Colville over an extended time period (since 1955). These include orthomosaics of the study sites from 1955 and 1979/1982, accessed through the Alaska National Science Foundation Established Program to Stimulate Competitive Research (Alaska NSF EPSCoR) data catalog [13]. The 1955 orthomosaic has an effective spatial resolution of 2 m and was generated using black and white images that were acquired by the US Geological Survey (USGS) in an airborne mission in late July of that year. The 1979/1982 orthomosaic has an effective spatial resolution of 1.7 m and was generated using color infrared images that were acquired during two separate airborne campaigns flown as a part of the Alaska High Altitude Aerial Photography mission. The southern half of the study area was imaged during the summer of 1979, while the northern half was imaged three years later in 1982. For the recent time period, we used a cloud-free WorldView-2 image from Digital Globe Inc. that had a spatial resolution of 1.4 m [14]. Together, these datasets covered a 60-year span (1955–2015), which is an ample amount of time to detect and study large-scale erosion along the river. For ease, in the remainder of this article we refer to the orthomosaics as images, as during the processing we treat them similar to any other satellite image.

Table 1.
Details of remotely sensed data used in this study.
We attempted to locate images for summers in the 2000–2010 time-frame to verify Nuiqsut residents’ statements about accelerated erosion in recent years, but were unable to access cloud-free, high-resolution imagery for that period.
Another key piece of data is the Arctic Digital Elevation Model (ArcticDEM), accessed through the Polar Geospatial Center at the University of Minnesota [15]. We used this 5 m resolution model to estimate and quantify the volume of land loss from the river banks due to erosion.
3.2. Climate Data
Local climate data was accessed through the USGS [16] and Weather Underground [17] websites. We used data from USGS weather stations located around the North Slope of Alaska dating back to 1998. The closest USGS station to Nuiqsut is Fish Creek, located about 40 km NW of Nuiqsut. There is also an Umiat USGS station. Data used from these weather stations included monthly averages of both ground and air temperatures, and snow depth. Annual average air temperature data was also available for the village of Nuiqsut from the weather station located at their airstrip.
4. Methods
4.1. Mapping Erosion by Automated Digital Change Detection
Aerial and satellite images are commonly used to study river and coastal erosion [18]. For temporal monitoring and change detection, it is important to ensure that the different date images have minimal geolocation errors [19]. As mentioned above, we used images from three different time points to study the change over six decades in our study area. The images from 1955 and 1979/1982 were already orthorectified; however, by inspection we found that the geolocation accuracy of these products was off by 4 to 10 m in some places, which was not optimal for our change analysis. For better geolocation accuracy and to reduce misregistration amongst the images we used the 2015 WorldView-2 image as the master/base image and carried out an image-to-image coregistration using tie-points and a first order affine transformation (Figure 2). There were no man-made features on our 1955 image (Nuiqsut village was established in 1974), therefore we used lakes that looked similar between the 1955, 1979/1982, and 2015 images and had a distinguishing feature, such as a jutting peninsula or unique shoreline shape, that could be used as a tie-point. Since there is no way to definitively ascertain the depth of these lakes in the images, a relative water depth analysis was performed between the different years. For this analysis, we chose the lakes to be used as tie points, then measured between two distinguishable features across the same lake in different years. We assumed that lower water would mean a shorter distance between these two shore points and higher water, a farther distance. If a lake had a similar distance between features in both 2015 and earlier dates images, it was used as a tie point. Image-to-image coregistration resulted in the temporal images aligning with an accuracy of 2 m or less, as confirmed by verifying the locations and boundaries of 20 lakes around each study site. Pixel sizes of air photos and images used in this study ranged from 1.4 to 2 m, so a 2 m offset represented 1.5 pixels or less of registration error. This was an acceptable registration error for this study. Rather than resampling all the images to the same pixel size, we decided to keep the original pixel sizes. The small 0.6 m of difference between the 1955 and 2015 image resolutions contributed a negligible amount of error to the land cover mapping.
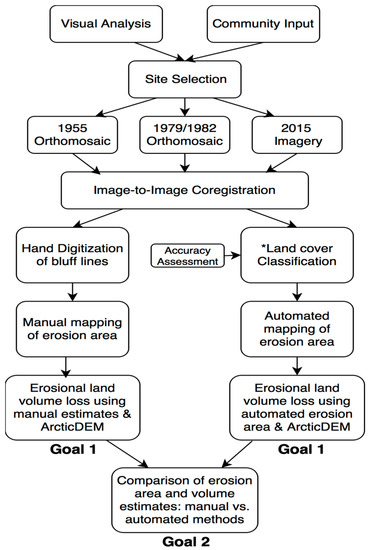
Figure 2.
A flowchart showing the data processing steps from site selection to erosion area and land loss volume estimation.*Land cover classification was performed using a maximum likelihood classifier on the 1979, 1982, and 2015 datasets; whereas, land cover classes (land and water) were manually digitized from the 1955 dataset.
We then performed a supervised classification using a maximum likelihood classifier on three (1979, 1982, and 2015) of the four images, generating three output classes: water, bare ground or sandbar, and tundra. We deliberately limited the number of classes because these were the three minimum classes needed in order to characterize either erosion or deposition. We chose to use a maximum likelihood classifier (MLC) because it can readily accommodate covarying data, a common occurrence with satellite image data, and MLC’s have been proven to perform well over a range of cover types, conditions, and sensing systems [20,21,22,23] Also, the fact that maximum likelihood is one of the most popular classifiers, simple to use, and readily available with free GIS platforms was important to us for potential future erosion monitoring by someone with limited resources.
The 1955 image was a single band panchromatic image. The signature of land cover features, such as tundra, sand bars, and the river, were similar enough that we could not satisfactorily map land cover using a digital classifier. Instead, we mapped the river channel through visual interpretation and manual digitization [24]. The digital signatures of bare ground (bluffs and sandbars) and shrub tundra were very similar in the 1955 panchromatic image, therefore we could not differentiate between the two. This gave us only two land cover classes (water, or land) for the 1955 panchromatic image. Land cover in the remaining images (1979/1982, and 2015) was separated into three classes: water, bare ground or sandbar, and tundra.
Upon completing the classification, we performed an accuracy assessment on each of the classified images [25]. We generated a total of 90 random points, 30 for each class. We then compared the land cover maps to the actual images at these random points and marked them as either matching the correct land cover type or not. Land cover classes were easy to identify on a standard false color composite of near infrared, red, and green bands, displayed in red, green, and blue respectively. Once these points were analyzed, we estimated percentages of overall accuracy based on how many points were correctly classified. User and producer accuracies were also calculated for each class (Table 2). Our 1955 image was hand-digitized and not classified like the others, therefore no accuracy assessment was performed. As seen in Table 2, each of the three images had near or above 95% overall classification accuracy and a Kappa value above 0.9, which ensures high confidence mapping the erosion area.

Table 2.
Accuracy assessment table showing user, producer, overall accuracy, and the Kappa Coefficient for each of the three classified images.
After the accuracy assessment, a digital change detection was performed to identify areas of high erosion or deposition. Each of the three classes from each image was given a unique numerical value. Then, simple band math was performed by multiplying land cover classification images by each other for two different time periods (Figure 3) [26]. This gave a new classified image with nine unique values: three represented no change in land cover type between images; three represented erosion between images shown as either tundra changing to water, tundra changing to bare ground or sandbar, or bare ground or sandbar changing to water; and one outcome represented deposition, i.e., water changing to bare ground or sandbar. The final two outcomes were ignored as they represented water or sandbars turning back into tundra, a scenario which did not take place in this river system over this time scale. Figure 3 shows the classification values for 1979 and 2015 and the resulting table created by multiplying the two classification images. These nine results represented one of four possibilities, as listed at the bottom of the figure.
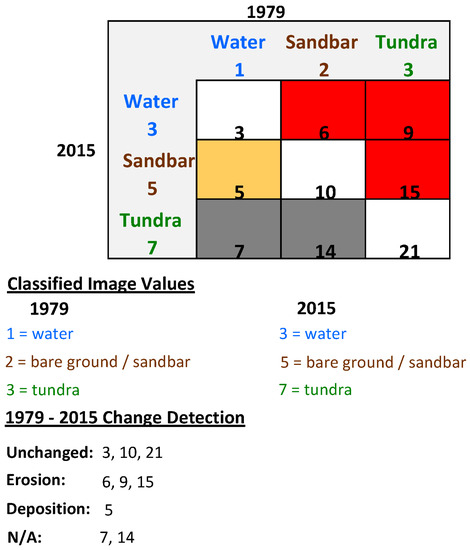
Figure 3.
Multiplying classified images by each other, resulting in values that represent different scenarios between 1979 and 2015.
4.2. Mapping Erosion by Manual Hand-Digitization
In the absence of field measurements, visual interpretation and manual digitization of bluff lines is the only logical approach to assess the accuracy of erosion area estimates from the automated digital change detection method. At the study sites, the river water abuts bluff faces. The simplicity of this land cover lends itself well to accurate mapping of the tundra–bluff and bluff–water boundaries using manual digitization based on visual interpretation.
We manually digitized the bluff lines at the four erosion sites for the years 1955, 1979/1982, and 2015. The digitizing was performed directly on the original images, not on the classified or change detection images (Figure 2). For this study, “bluff line” was defined as the line where tundra can easily be distinguished from either water or sandbar. Using a tundra line on a cliff as our reference point for mapping bluff line erosion eliminates any discrepancies caused by changing water height between images that might cover or uncover patches of sandbar along the banks of the river.
After bluff lines were digitized for the three time periods, we estimated erosion using two measurements. Average erosion between images was calculated by sampling evenly across the digitized shorelines (using 15 transects) and by measuring the perpendicular distance from one year’s bluff line to the next. This was calculated three times for each site: between the bluff lines of 1955 and 1979/1982; 1979/1982 and 2015; and 1955 and 2015. The distance in meters between river bluff lines from different years gave us an erosional distance as well as a timespan, which was converted to an average erosion rate expressed as meters per year (m/year). Then, we estimated the maximum erosion rate at each site using only the transect of greatest value for each year. This maximum distance was also converted to erosion rate in m/year.
4.3. Estimating the Volume of Land Loss
We calculated the cubic volume of land loss due to erosion by measuring the area of our four erosion sites and multiplying that by an average height based on current DEM values. We created vector polygons of the eroded sites based off the bluff lines digitized in the previous step. These polygons represent all of the erosion between 1955–1979/1982, 1979/1982–2015, and 1955–2015 for each site. We then calculated the area of these polygons in square meters.
Elevation data for the 1955 and 1979/1982 bluff lines did not exist for our study sites. We also could not find any published methods to estimate paleo bluff line elevations that could be applied to decadal-scale change detection. To estimate bluff line elevations, we assumed that the current trajectory of changes in elevation and slope across a site reflected the trajectory of changes across the same site in the past. For each site, we plotted five transects across the available DEM: four perpendicular to the shoreline and a fifth running parallel along the whole erosion site (Figure 4). These five transects were plotted to show elevation changes. The average of all five transects was taken and used as the height value, in order to calculate cubic volume loss at all erosional sites with a simple formula:
V: volume of land loss in m3; A: area of erosion in m2; h: bluff height in m).
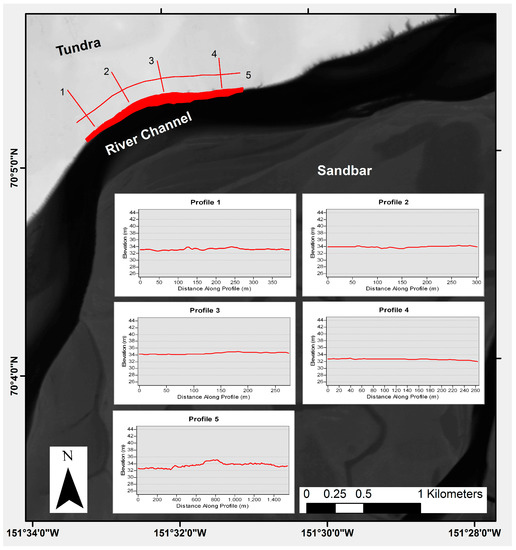
Figure 4.
ArcticDEM at Site 4, showing the digitized erosion area from 1955–2015 (red polygon). The five lines represent transects taken across DEM, in order to calculate the average height of tundra for erosional volume loss estimates. The four overlaid graphs show the profiles of each transect.
4.4. Analysis of Climate Data
We analyzed the annual averages of ground and air temperature and snow depth for the Umiat and Fish Creek sites, and air temperature data from Nuiqsut, to determine any trends in the data and to see if any such trends were statistically significant at a confidence level of 95%. We wanted to learn and report the degree of climate warming and changes in snow cover near the study area because previous studies on Arctic river erosion have identified warming air temperature and increased snow cover as among the drivers of riverbank erosion [1,12].
5. Results
5.1. Mapping Erosion Results
Figure 5 shows the classified map of Site 1, derived from the 2015 WorldView-2 image. The main river channel can easily be distinguished, as can sandbars along the river and the surrounding tundra. The grid-like feature in the bottom center of the image is the village of Nuiqsut. For our classification, roads and buildings most closely resembled bare ground/sandbar and were classified as such. The smaller blue shapes in the tundra are the lakes that litter the North Slope.
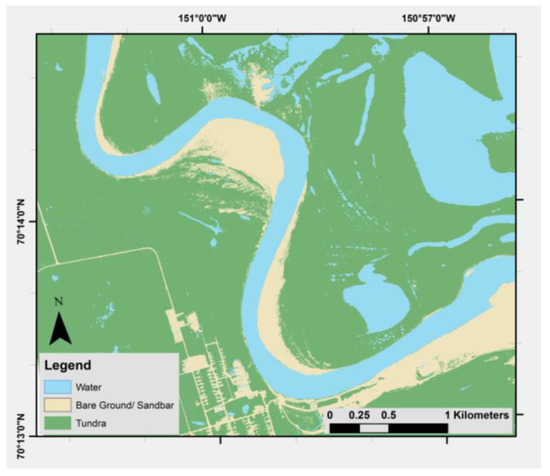
Figure 5.
Land cover classification map of Site 1, processed from the 2015 WorldView-2 image using the maximum likelihood supervised classification method.
Figure 6 shows the areas of heavy erosion near Site 1 between 1955 and 2015. As expected, we see erosion, in red, along the outer bank of the river bends. Also, shown in green is the sandbar migration further into the river channel, representing deposition of sand from upstream.
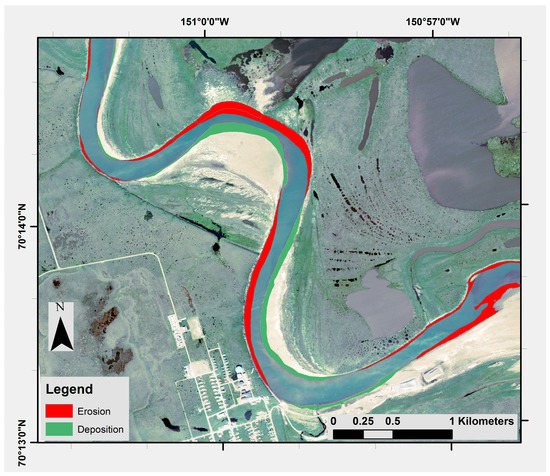
Figure 6.
A change detection layer highlighting erosion and deposition at Site 1 from 1955 to 2015 overlaid on the 2015 WorldView-2 image.
5.2. Volume of Land Loss Results
The measured erosion distances and calculated erosion rates for each of the four study sites (Table 3) were based on the hand-digitized bluff lines generated in this study. In Table 3, the second column from the right shows the cubic volume of erosion calculated from the automated digital change detection method without any input from the user. The percentage of error is shown for each of the cubic volume calculations performed using the digital change detection method. This error value represents the difference in estimation compared to the hand-digitized bluff lines and calculations, which are assumed to be as accurate as possible. A small percentage of error indicates that the automated method can be used as an acceptable substitute for mapping river erosion over large areas where hand-digitization and calculation are unfeasible.

Table 3.
Average and maximum erosion distances and rates for each site over our three time periods, expressed in meters and m/year, as well as the area of each erosion site between 1955 and 2015, with estimated cubic volume loss based on DEM.
As seen in Table 3, Sites 3 and 4 showed increased erosional rates and cubic volume loss since 1979, while Site 1 remained relatively constant over the entire timespan. Site 2 was the only site that showed a slowing down in erosion rate. It is worth noting that Sites 1, 3, and 4 were all located on bends in the river; whereas, Site 2 was along a straight portion of the channel.
For each site, we calculated the average erosion rate for the time periods 1955–1979/1982 and 1979/1982–2015, as well as for the whole period, from 1955 to 2015 (Figure 7). Erosion rates for the 1979/1982–2015 period were either equal to or greater than the 1955–1979/1982 and 1955–2015 erosion rates at three of our four sites (Table 3).
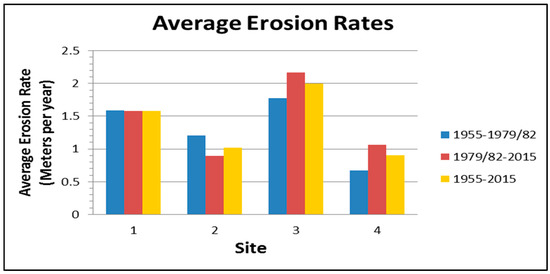
Figure 7.
Bar graph showing erosional rates at our four study sites.
Site 1: Based on hand-digitized erosion analysis, we found that areas of 25,085 m2 and 31,959 m2 were eroded away between 1955 and 1982, and 1982 and 2015, respectively. The total area loss between 1955 and 2015 was 57,044 m2. With an average elevation of 5.04 m, this equals a total cubic volume loss of 287,502 m3. Estimating the average bluff retreat (or erosion) along lines perpendicular to the bluff face, we found similar erosion rates of 1.6 m/year for both 1955–1982 and 1982–2015. When estimating cubic volume loss via automated change detection methods, we came out with very low error percentages compared to hand-digitized measurements: the error percentage was 2.05% when comparing the volume estimates for 1955–1982, while the estimate for 1982–2015 was almost perfect, with an error percentage of 0.44%.
Site 2: This was the only site that actually showed a significant reduction in erosion rates between the 1955–1979 and 1979–2015 time periods. Between 1955 and 2015 we calculated an average erosion rate of 1.21 m/year, whereas we only saw 0.89 m/year average erosion between 1979 and 2015. As shown in Table 3, we saw very similar erosion volumes for both time periods, even though 1955–1979 was a 24-year span and 1979–2015 was a 36-year span. This, again, suggests slower rates of erosion over the 1979–2015 time period. As stated previously in this paper, we are unable to determine whether this slowing is indicative of the whole 36-year period, or if there were slower erosion years closer to 1979 that lowered the average for the past 10 to 15 years, which residents report has been a period of increased erosion. Site 2 had the highest error percentages when comparing cubic volume loss estimates; the 9.21% error percentage for 1955–2015 was far higher than other sites, which had percentages as low as 0.44%.
Site 3: This site exhibited both the fastest erosion rates, as well as the largest area of erosion of any site. Average erosion rates increased from 1.78 m/year to 2.17 m/year between the two included time periods. The maximum erosion rate for Site 3 was 3.5 m/year between 1979 and 2015, which was by far the fastest rate of any site over any time period in our study. There was also a large increase in erosion area between the two time periods, from 51,714 m2 to 97,843 m2. With an average elevation of 7.51 m, this equates to an estimated cubic volume loss of 1,174,534 m3 between 1955 and 2015. With such a large square area of erosion at Site 3, it is important to notice the low error percentages for volume estimates: all three digital change detection estimates were lower than 5% error, and as low as 3.13% error for the estimate between 1979 and 2015.
Site 4: Similar to Site 3, Site 4 exhibited increasing erosion rates. From 1979 to 2015, the site had an average erosion rate of 1.06 m/year, which was a 58% increase from the 1955–1979 timespan and shows an average erosion rate of 0.67 m/year. While Site 4 had the slowest erosion rate of all the sites, it did have the largest calculated cubic volume loss, which could be attributed to the large cliff, over 30m high, that occupied the site. Over the 60-year period from 1955 to 2015, Site 4 saw more than 74,000 m2 of erosion, resulting in 2.5 million m3 of volume loss. Digital change detection for volume estimations at the site came back with low error percentages ranging from 1.8% to 6.2% error.
5.3. Error Analysis
We mapped riverbank erosion at four sites by following two approaches: (1) comparing the location of bluff lines that were hand-digitized using the 1955, 1979/1982, and 2015 images as a base; and (2) using automated change detection between the aforesaid images. As discussed in Section 4.1, we coregistered the 1955 and 1979/1982 images to the 2015 WorldView-2 image. Then, we verified the locational accuracy at 20 sites and observed 2 m or less shift between the images. The pixel sizes of these images ranged from 1.4 m to 2.0 m, so a maximum 2 m of spatial offset represented 1.5 pixels of registration error. In approach (1), we delineated the bluff lines using visual interpretation, and we believe that 0.6 m and 0.3 m differences in pixel sizes had a negligible effect on the accuracy of the bluff line positions, and the estimation of the long-term erosion rate and area. In approach (2), we classified the input images (1979, 1982, and 2015) into three simple land cover classes (water, bare ground, and tundra). The spatial distribution of these classes was such that they were arranged along a sequence of water, bare bluff face, and tundra. Because of this sequential arrangement, the differences in pixel size only affected the pixels along the boundary between two classes. The accuracy of the change detection was, in part, limited by the pixel size of the coarsest resolution input data used. In our study, the 1955 image with 2 m pixel size served as this limiting factor. Given that the lateral bank erosion in the study sites was in the order of tens of meters (at least an order of magnitude higher than the coarsest resolution image), we found the input images appropriate for meeting our change detection needs. In this particular case, the differences in pixel sizes were very small relative to the mapped erosion distances and area, and hence we assumed it had a negligible effect on long-term estimates of erosion rates and area. In the case of approach (1), the only significant source of error in the erosion area mapping was registration error, which propagated into the delineation of the bluff line. The hand-digitized erosion areas at the four sites for all time periods varied from 14,747 m2 to 149,557 m2. In order to find out the maximum possible error in erosion area estimation (i.e., the worst-case scenario), we adopted the buffer analysis approach [27]. Hughes et al. [27] used the buffer analysis approach to demonstrate the implications of georectification error when measuring lateral channel movement. We buffered the erosion areas by 2 m and compared the buffered erosion areas with hand-digitized erosion areas. We found that if the 2 m registration error were constant across an entire erosion site, then it could result in 4.3–12.3% error in erosion area mapping. We found the smallest error of 4.3% for the largest erosion polygon, and largest error of 12.3% for the smallest erosion polygon. In this particular case, the registration error only affected the outline of the erosion area, so an erosion polygon with a lower area to perimeter ratio will tend to have higher error. Since the spatial offset between the images varied across the images and was usually less than 2 m, the actual error in calculation of the hand-digitized erosion area was much less than 12.3%. In the case of approach (2), there are two kinds of error affecting the erosion area estimates: (a) registration error, and (b) land cover classification error. The land cover classification accuracies were 94.4%, 95.6%, and 96.7% for the 1979, 1982, and 2015 images, respectively (Table 2). In the last column of Table 3, we reported the difference between the erosion areas estimated using approach (1) and approach (2) as an error percentage (hand-digitized vs. automated), assuming that the hand-digitization of bluff lines is as accurate as possible. The error in mapping and estimation of erosion area by approach (2) varied from 0.44% to 12.8% (Table 3). Since we used three simple land cover classes (water, bare land, and tundra) to map erosion in the second method, the majority of the misclassified pixels lay along the boundaries between two classes. Therefore, erosion areas with lower area to perimeter ratios tended to have bigger differences with respect to hand-digitized erosion mapping. For example, in Site 2, which was a near vertical and straight bluff, the erosion area had an area to perimeter ratio of 27 and it also showed the highest error estimate of 9.2% (hand-digitized vs. automated); whereas, Site 1, with an area to perimeter ratio of 43, showed the lowest error estimate of 0.64% (Table 3).
5.4. Climate Data Results
Figure 8 and Figure 9 show time series plots of average yearly air temperature, average yearly ground temperature (at 120 cm depth), and average yearly snow depths at USGS weather stations at Fish Creek and Umiat. Air temperature data from the Nuiqsut airport was averaged on a yearly basis and plotted in Figure 10. We also examined snow depth data around the river, based on the assumption that higher snow depths, along with warming air temperatures, result in more meltwater during the spring breakup, which has been demonstrated to contribute to greater river erosion [28]. Regression analyses of air and ground temperature, and snow depth data show a statistically significant positive trend in agreement with climate warming and increased snow cover observed in the environment of other Arctic rivers (e.g., Lena River) experiencing increased erosion [1].
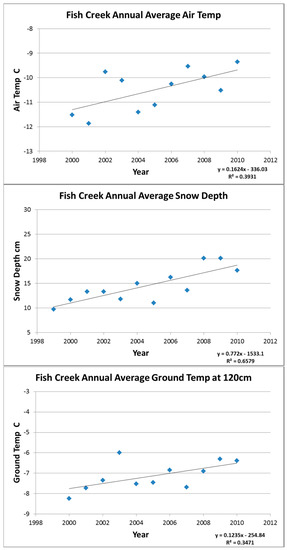
Figure 8.
USGS climate data averaged annually for Fish Creek, with trend lines overlaid.
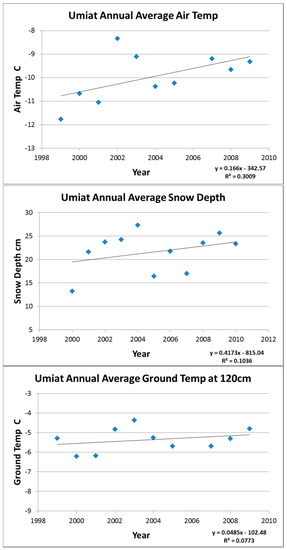
Figure 9.
USGS climate data averaged annually for Umiat, with trend lines overlaid.
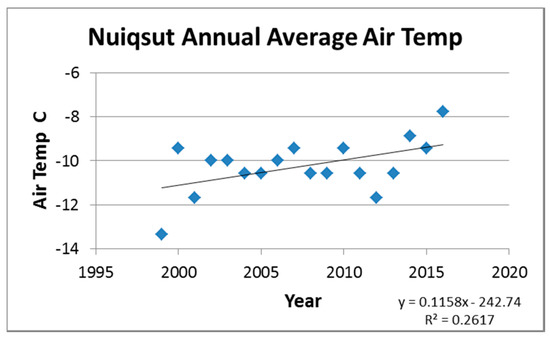
Figure 10.
Airport air temperature data averaged annually for Nuiqsut, with a trend line overlaid.
As shown in the climate graphs, all sites demonstrated trends of warming temperatures and increasing snow depth. A regression calculation was run for each of the plots at a 95% confidence level. This calculation returned positive results for each of the plots, indicating statistically significant positive trends at each site. Even in our short window of climate data, we see significant warming trends, in the magnitude of multiple degrees. This is on par with Wendler’s study on temperature increases in Alaska, which reported an average warming of 2.7 °C across Arctic Alaska from 1979 to 2013, which is a far greater increase than has been observed for any other region or time period in Alaska or for any other climate zones. [6]. This warming has also caused a lengthening of the Arctic melt season at a rate of 4 to 5 days per decade since 1979 [29].
6. Discussion
The Colville’s high-latitude location lends it unique characteristics. Unlike in most non-Arctic regions, river morphology in the Arctic greatly centers on a few short months of the year when the river is not frozen. The few weeks of breakup and flooding, usually between late May and mid-June, are crucial for river erosion, with nearly 50% of annual discharge into the river occurs during the first three to four weeks of breakup [30]. As a result of this heavy discharge, it is estimated that nearly 75% of annual sediment load is transported during these few weeks of breakup and flooding [12]. Much of this sediment load results from thermal erosion; the process of thawing frozen sediments by turbulent water flow and eroding away what is left by mechanical erosion [31]. Flooding after breakup, caused by the melting of snow in the Colville drainage basin, is one of the largest drivers of erosion for the Colville. The most important impacts of climatic changes in terms of Colville River erosion are thus (a) an increase in snowfall during the winter months, and (b) faster snowmelt during breakup, causing more intense flooding.
According to our estimates of riverbank erosion rates at four sites along the Colville, it is evident that erosion has increased at some sites along the Colville since the 1980s, though the rate of increase in erosion varies spatially, and higher bluff sites tend to have more erosion and land loss (Site 3 and Site 4 in this study). This is due to the fact that the type, timing, and severity of riverbank erosion varies with bank composition and height, snow and ice cover, stage and velocity of discharge, air and water temperature, and wind [8,12]. Most of the banks along the Colville, upstream of Nuiqsut, range in height from a few meters to 33 m in some large dune areas (e.g., near Site 4), with a general tendency for height to increase upstream. Walker et al. [12] reported a short-term erosion rate of 1.6 m/year (1982–1985) for an erosional bank on Colville made up of Gubik Formation (a Quaternary deposit of unconsolidated sediments). Our estimates of erosion at the Gubik Formation site (Site 1) suggest a long-term erosion rate of 1.6 m/year for both periods (1955–1982) and (1982–2015), which means that this site has been eroding consistently at 1.6 m/year rate since 1955.
Much higher rates of riverbank erosion have been reported from other Arctic rivers. Costard et al. [8] reported exceptionally high erosion rates of up to 40 m/year along the Lena River banks in specific areas (e.g., concave river banks and heads of islands). Based on a laboratory simulation experiment, they concluded that the exceptional erosion rates were due to a combination of high water temperature and mechanical erosion, in association with the particular geometry of the channel. Are [32] reported average bank retreats of 19–24 m/year on the Lena River during 1953–1961. However, in the Olenek channel of the Lena River delta, the bank retreated at an average rate of 1.7 m/year, which is comparable to the erosion rates we found along the Colville.
Kanevskiy et al. [9] investigated the riverbank retreat at three active yedoma bluff sites along the Itkillik River, a tributary of the Colville River. They reported the highest long-term rates of riverbank erosion ever observed in permafrost regions of North America. For one of their study sites, they reported an average retreat rate for a 680-m-long bluff as 11 m/year (1995–2010). They also found that lower bluffs (height of <4.5 m) tended to have much lower retreat rates. Contrary to this finding, we observed the lowest erosion rate at the tallest bluff site (Site 4: average height of 33 m with an erosion rate of 0.9 m/year during 1955–2015), and the highest erosion rate of 2 m/year (1955–2015) at Site 3, which had an average elevation of 7.5 m.
Stettner et al. [10] estimated cliff top erosion of a permafrost riverbank in the central Lena River Delta. They reported a short-term (2013–2015) mean annual net erosion of 4.1–6.9 m/year, which is close to the reported rates of riverbank cliff-top erosion at the Yana and Indigirka river delta sites [11]. They concluded that the mean annual net erosion at their study site significantly differed from one year to another, and analysis of the role of climate variables on erosion suggested a contingent sensitivity of erosion to temperature and precipitation. Air temperature has a strong influence on erosion, but when temperatures are at or below average precipitation appears to be an important factor. In situations where the cliff top is decoupled from the thermo-erosional processes, its erosion likely results from climate forcing, and depends on bank composition and ground ice content.
Along most parts of the Colville River bank (particularly banks with lower height), development of thermoerosional niches, followed by block collapse, is the dominant process of bank retreat; whereas, along the higher banks, such as Site 4, where the upper part of the bluff is decoupled from the thermo-erosional processes, thermal denudation is the dominant process of bank retreat. Our estimates of riverbank erosion at four sites on the Colville are very similar to the rates reported by Walker et al. [12], and contrast greatly with the erosion rates reported for Siberian rivers [8,10,32], and the Itkilik River [9]. The block collapse that often follows the development of thermoerosional niches accounts for an almost instantaneous retreat that can be as much as 12 m [12]; however, long-term rates, even in susceptible cut banks, rarely exceed 3 m.
The majority of erosion studies analyze erosion in terms of short-term or long-term rates and do not include changes in erosion area or land loss volume [8,10,11,12]. For example, Shur et al. [11] studied river shoreline erosion at 14 sites along the Yana and Indigirka Rivers in North Yakutia and analyzed only average erosion rates. Walker et al. [12] studied riverbank erosion at six sites in the Colville River Delta; however, they reported total land volume loss at only one site. Kanevskiy et al. [9] estimated land volume loss at three bluff sites along the Itkilik River for the short period of 2007–2011 but did not show how the land loss compared with land loss for an earlier period. Stettner et al. [10] estimated only the erosion rate to study riverbank erosion in the central Lena Delta.
The average erosion rate (i.e., erosion distance divided by timespan in year) does not necessarily provide a complete picture of the amount and severity of bank erosion. Hence, to get a better understanding of the riverbank erosion process on the Colville, we not only estimated long-term erosion rates, but also changes in erosion area and volume of land loss. At Site 1 (Gubik Formation), the average erosion rate turned out to be 1.6 m/year for both the 1955–1982 and 1982–2015 periods; however, the estimated erosion area increased from 25,085 m2 during 1955–1982 to 31,959 m2 during 1982–2015. Therefore, in terms of the average erosion rate, the rate of erosion appeared to be consistent at this site, but in reality, erosion had a disproportionally greater effect during the 1982–2015 period. Similarly, at Site 3, the difference in the erosion rate for the period 1955–1979 and 1979–2015 was 1.8 and 2.2 m/year, respectively, but the difference in the erosion area almost doubled from 51,714 m2 to 97,843 m2. At Site 4, the difference in the erosion rate for the period 1955–1979 and 1979–2015 was 0.7 and 1.0 m/year, respectively, but the difference in the erosion area more than doubled from 23,884 m2 to 50,352 m2. When we compared the average erosion rate at Site 1 (1.6 m/year) to Site 4 (1.0 m/year), we saw that Site 1 had a much higher erosion rate. However, Site 4 had the tallest banks (average bank height of 33 m) and the volume of land loss was 1,689,813 m3 for the period 1979–2015, which was 10 times more land volume loss than at Site 1 (average bank height of 5 m) for the same period.
Erosion and deposition also alter the connectivity of secondary channels and lakes to the main channel of the Colville, which impacts fish habitat [33], as well as accessibility of traditional subsistence and historical sites to the residents of Nuiqsut. When the river erodes faster than the channel can carry sediment to the sea, the sediment deposits in the river system itself and can close up smaller channels or create hazardous shallow sites in the main channel. Popular lakes can become inaccessible or drain due to bank erosion [34]. During our fieldwork, we noted an example of this at Site 3, where a large lake had drained in the early summer of 2017, as described by local residents who had previously used the lake as a fishing site (Figure 11). These changes impact the subsistence lifestyle of Nuiqsut residents, who rely heavily on traditional knowledge passed down from generation to generation. Elders possess a wealth of knowledge about the Colville, but in recent times the river has become so dynamic that it is hard to keep up with the changes, posing a real threat to subsistence practices. Updated knowledge of the characteristics and rate of change to the Colville would be valuable information for making management decisions about river access for the community.

Figure 11.
Lake near Site 3 that has drained due to bank erosion.
The accuracy of measuring erosion by hand-digitization versus automated change detection methods is significant for large-scale Arctic river monitoring. In the case of measuring erosion by hand-digitization, the major source of error is registration error, and in the case of the automated change detection method, the major sources of error are registration error and classification error. In both cases, these errors tend to have the greatest effect along the outline of an erosion area or along the boundary between the land cover classes. Therefore, erosion areas with lower area to perimeter ratios tend to have higher error. By minimizing registration error and improving land cover classification accuracy, the overall error in erosion area mapping can be minimized.
We determined that, for the study of a small number of sites such as those in our study, hand-digitized measurements were the most accurate method for estimating erosional rates and areas. However, if the goal of a study is to monitor yearly river erosion on a large scale, our results indicate that automated change detection methods can produce reasonable estimates. This serves to validate a straightforward and rapid process for monitoring river erosion that can be performed by someone with even limited GIS and image processing skills.
Our use of DEM trajectories to estimate paleo cliff elevations may be unique to the Arctic. We are confident in our estimates due to the geomorphology of our study area, a relatively flat region with little change in topography.
7. Conclusions
Analysis of high-resolution data indicates that bank erosion on the Colville River seems to have increased during the past 36 years, from 1979/1982 to 2015, when compared to erosion from 1955 to 2015. Of four erosion sites analyzed, two showed significant increases in yearly erosional rates from 1.8 m/year to 2.2 m/year and from 0.7 m/year to 1.0 m/year. One site showed similar erosion rates of 1.6 m/year between the two time periods, and a fourth site showed a decrease in erosion rates from 1.2 m/year to 0.8 m/year. However, the average erosion rate (i.e., erosion distance divided by timespan) did not necessarily provide a complete and accurate picture of the extent and severity of bank erosion. Hence, to get an accurate understanding of the riverbank erosion process of the Colville, we not only estimated the long-term erosion rates, but also changes in erosion area and the volume of land loss. At Site 3, the average erosion rate for the period 1955–1979 and 1979–2015 was 1.8 and. 2.2 m/year, respectively, but the difference in the erosion area was almost double, from 51,714 m2 to 97,843 m2. At Site 4, the average erosion rate for the period 1955–1979 and 1979–2015 was 0.7 and 1.0 m/year, respectively, but the difference in the erosion area was more than double, from 23,884 m2 to 50,352 m2. When we compared the average erosion rate at Site 1 (1.6 m/year) to Site 4 (1.0 m/year), we saw that Site 1 had a much higher erosion rate. However, Site 4 had the tallest banks (average bank height of 33 m) and the volume of land loss was 1,689,813 m3 for the period 1979–2015, which was ten times more than the volume of land loss at Site 1 (average bank height of 5 m) for the same period.
The novelty of this research is in extending the estimates from two-dimensional surface erosion rates (as reported by most studies) to three-dimensional volumes (i.e., the amount of material eroded). Whereas there is a wealth of literature available on the former, there is very little published on the latter. As per our knowledge, this is the first paper that demonstrates that for an Arctic river, studies on riverbank erosion that use only erosion rate can be inaccurate and grossly conservative. This study validates the significance of mapping erosion areas and estimating land loss volumes to gain an accurate understanding of the amount and severity of riverbank erosion, as in certain areas the volume of land loss can be disproportionately higher than what average erosion rates may suggest. Hence, this study presents not only an improved understanding of the extent and severity of riverbank erosion along parts of the Colville than any previous study, but also valuation of land loss from typical eroding banks using publicly available DEM.
Based on the erosion study results and climate data, it can be safely inferred that climate warming plays a role in erosion on the Colville. These findings are consistent with a study on increased erosion due to climate change on the Lena River in Central Siberia, an Arctic fluvial system similar to the Colville [1]. Air and ground temperature warming trends on the North Slope are likely the catalyst for increased erosion rates through the thawing of permafrost along river bluffs causing massive block failure. Warmer temperatures also mean longer ice-free seasons, which results in a longer period in which the river can erode. Trends of higher snow depths contribute to more meltwater during the spring breakup, which is the main period of erosion for Arctic rivers. If these climate trends continue, it can be inferred that erosion along the Colville will continue to increase, resulting in more problems for the residents of Nuiqsut, who rely on the river to travel to subsistence and historical family sites. Additionally, important village infrastructure, such as a water tank and power plant, is located within 90 m from an eroding bluff (near Site 1). If the rate of erosion intensifies, this will have major economic implications for the village of Nuiqsut.
This study suggests that high-resolution imagery can be effectively used to monitor bluff line erosion along Arctic rivers. This type of monitoring can enhance our understanding of hydro-geomorphological processes along Arctic rivers and provide information for estimates of future change. We have also demonstrated that estimating erosion via automated change detection based on simple classification methods can be as effective as digitizing by hand. This is important for monitoring large study areas or making multiple change observations in areas where hand-digitization is not feasible. We have also successfully used a current DEM to calculate the cubic volume of past erosion, and demonstrated the efficacy of this simple method for paleo topography estimates for relatively flat Arctic regions. This method can be used in certain situations when land topography changes are minimal and no other source of data is available to gauge the height of eroded features.
Though this study returned solid results, it was hampered by several limitations, primarily the lack of high-resolution cloud-free imagery for the 2000–2013 time period. Such imagery would have been ideal in order to examine more recent erosion trends, as local knowledge from Nuiqsut suggests that erosion increases have not been linear since 1979, but almost exponential, with the greatest erosion happening in the past 10 to 15 years. We speculate that climate warming is also warming water temperatures, which can expedite the processes of thermal erosion along riverbanks. Future erosion studies could potentially incorporate more variables, such as water temperature.
This study delivered significant results, crucial to the community of Nuiqsut, while simultaneously adding novel techniques to the remote sensing of river erosion literature. We expect that the regular availability of high-resolution summer imagery in the future will enable continued monitoring of river erosion using the techniques presented in this paper.
Acknowledgments
This work was supported by an Alaska NSF EPSCoR award #OIA-1208927 and the state of Alaska, as well as the Alaska Space Grant and the UAF Global Change Student Research Grant. The authors would like to thank Tom Moran for editorial assistance, Matthew Whitley for help with preparation of the GIS data, and Todd Brinkman for his insight on erosion along the Colville.
Author Contributions
C.P. and S.P. conceived and designed the study; C.P. and S.P. performed the fieldwork; C.P. processed the data; C.P., S.P., and A.P. analyzed the data; C.P. led the writing; S.P. and A.P. contributed to the writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Costard, F.; Gautier, E.; Brunstein, D.; Hammadi, J.; Fedorov, A.; Yang, D.; Dupeyrat, L. Impact of the global warming on the fluvial thermal erosion over the Lena River in Central Siberia. Geophys. Res. Lett. 2007, 34, L14501. [Google Scholar] [CrossRef]
- Tananaev, N.I. Hydrological and geocryological controls on fluvial activity of rivers in cold environments. In Cold and Mountain Region Hydrological Systems under Climate Change: Towards Improved Projections, Proceedings of the H02, IAHS-IAPSO-IASPEI Assembly, Gothenburg, Sweden, 22–26 July 2013; IAHS Publ.: Gothenburg, Sweden, 2013; pp. 161–167. [Google Scholar]
- Walker, H. Some Aspects of Erosion and Sedimentation in an Arctic Delta during Breakup; Coastal Studies Institute, Louisiana State University: Baton Rouge, LA, USA, 1970; pp. 209–219. [Google Scholar]
- BurnSilver, S.; Magdanz, J.; Stotts, R.; Berman, M.; Kofinas, G. Are mixed economies persistent or transitional? Evidence using social networks from Arctic Alaska. Am. Anthropol. 2016, 118, 121–129. [Google Scholar] [CrossRef]
- Schmidt, J.; Kofinas, G.; Brinkman, T. Local Knowledge and Science: Observations of Landscape Change in the Nuiqsut Homelands; University of Alaska Anchorage and Fairbanks: Anchorage, AK, USA; Available online: http://www.alaska.edu/epscor/ (accessed on 18 February 2018).
- Wendler, G.; Moore, B.; Galloway, K. Strong temperature increase and shrinking sea ice in Arctic Alaska. Open Atmos. Sci. J. 2014, 8, 7–15. [Google Scholar] [CrossRef]
- Floyd, A.; Prakash, A.; Meyer, F.; Gens, R.; Liljedahl, A. Applicability of Synthetic Aperture Radar to investigate river ice breakup on the Kuparuk River, Northern Alaska. Arctic 2014, 67, 462–471. [Google Scholar] [CrossRef]
- Costard, F.; Dupeyrat, L.; Gautier, E.; Carey-Gailhardis, E. Fluvial thermal erosion investigations along a rapidly eroding river bank application to the Lena River (central Siberia). Earth Surf. Process. Landf. 2003, 28, 1349–1359. [Google Scholar] [CrossRef]
- Kanevskiy, M.; Shur, Y.; Strauss, J.; Jorgenson, T.; Fortier, D.; Stephani, E.; Vasiliev, A. Patterns and rates of riverbank erosion involving ice-rich permafrost (yedoma) in northern Alaska. Geomorphology 2016, 253, 370–384. [Google Scholar] [CrossRef]
- Stettner, S.; Beamish, A.L.; Bartsch, A.; Heim, B.; Grosse, G.; Roth, A.; Lantuit, H. Monitoring inter-and intra-seasonal dynamics of rapidly degrading ice-rich permafrost riverbanks in the Lena Delta with TerraSAR-X time series. Remote Sens. 2017, 10, 51. [Google Scholar] [CrossRef]
- Shur, Y.; Vasiliev, A.; Kanevsky, M.; Maximov, V.; Pokrovsky, S.; Zaikanov, V. Shore Erosion in Russian Arctic. In Cold Regions Engineering: Cold Regions Impacts on Transportation and Infrastructure, Proceedings of the 11th International Conference on Cold Regions Engineering 2002, Anchorage, AK, USA, 20–22 May 2002; American Society of Civil Engineers: Anchorage, AK, USA, 2002; pp. 736–747. [Google Scholar]
- Walker, J.; Arnborg, L.; Peippo, J. Riverbank erosion in the Colville delta, Alaska. Phys. Geogr. 1987, 61–70. [Google Scholar] [CrossRef]
- Alaska EPSCoR Data Portal. Available online: http://epscor.alaska.edu/search (accessed on 18 January 2018).
- Digital Globe Inc. Available online: https://www.digitalglobe.com (accessed on 18 January 2018).
- Polar Geospatial Center at the University of Minnesota. Available online: https://www.pgc.umn.edu (accessed on 18 January 2018).
- USGS Climate and Active-Layer Data. Available online: https://pubs.usgs.gov/ds/812/introduction.html (accessed on 18 January 2018).
- Weather Underground. Available online: https://www.wunderground.com/weather/us/ak/nuiqsut (accessed on 18 January 2018).
- Winterbottom, S.J.; Gilvear, D.J. A GIS-based approach to mapping probabilities of river bank erosion: Regulated River Tummel, Scotland. River Res. Appl. 2000, 16, 127–140. [Google Scholar] [CrossRef]
- Lawler, D.M. The measurement of river bank erosion and lateral channel change: A review. Earth Surf. Process. Landf. 1993, 18, 777–821. [Google Scholar] [CrossRef]
- Swain, P.; Davis, S. Remote Sensing: A Quantitative Approach; McGraw-Hill Book Co.: New York, NY, USA, 1978; 396p. [Google Scholar]
- Richards, J. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 1986; 292p. [Google Scholar]
- Bolstad, P.; Lillesand, T. Rapid maximum likelihood classification. Photogramm. Eng. Remote Sens. 1991, 57, 67–74. [Google Scholar]
- Otukei, J.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
- Panda, S.K.W.; Whitley, M. Sixty-five Years of Colville River Dynamics and its Impact on Present River Navigability near Nuiqsut, North Slope of Alaska. In Proceedings of the 14th International Circumpolar Remote Sensing Symposium, Homer, AK, USA, 12–16 September 2016; Available online: https://alaska.usgs.gov/science/geography/CRSS2016/posters_and_talks/Whitley_ICRSS_Poster_compressed.pdf (accessed on 23 February 2018).
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Mars, J.; Houseknecht, D. Quantitative remote sensing study indicates doubling of coastal erosion rate in past 50 yr along a segment of the Arctic coast of Alaska. Geology 2007, 35, 583–586. [Google Scholar] [CrossRef]
- Hughes, M.L.; McDowell, P.F.; Marcus, W.A. Accuracy assessment of georectified aerial photographs: Implications for measuring lateral channel movement in a GIS. Geomorphology 2006, 74, 1–16. [Google Scholar] [CrossRef]
- Walker, H.J.; McCloy, J.M. Morphologic Change in Two Arctic Deltas; Arctic Institute of North America: Washington, DC, USA, 1969. [Google Scholar]
- Stroeve, J.; Markus, T.; Boisvert, L.; Miller, J.; Barrett, A. Changes in Arctic melt season and implications for sea ice loss. Geophys. Res. Lett. 2014, 41, 1216–1225. [Google Scholar] [CrossRef]
- Arnborg, L.; Walker, H.J.; Peippo, J. Water discharge in the Colville River. Phys. Geogr. 1966, 48, 195–210. [Google Scholar] [CrossRef]
- Gatto, L.W. Soil Freeze-Thaw Effects on Bank Erodibility and Stability; Accession Number: ADA301818; Cold Regions Research and Engineering Lab: Hanover, NH, USA, 1995; Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a301818.pdf (accessed on 18 January 2018).
- Are, F. Thermal Abrasion of Coasts. In Proceedings of the Fourth International Conference on Permafrost, Washington, DC, USA, 17–22 July 1983; University of Alaska Fairbanks: Fairbanks, AK, USA, 1983; pp. 24–28. [Google Scholar]
- Brubaker, M.; Bell, J.; Dingman, H.; Itta, M.; Kasak, K. Climate Change in Nuiqsut, Alaska, Strategies for Community Health; Publication of the Center for Climate and Health, Alaska Native Tribal Health Consortium: Anchorage, AK, USA, 2014; Available online: http://www.north-slope.org/assets/images/uploads/ANTHC_Nuiqsut_7-31-14_web_FINAL.pdf (accessed on 18 January 2018).
- Jones, B.M.; Arp, C.D. Observing a catastrophic thermokarst lake drainage in northern Alaska. Permafr. Periglac. Process. 2015, 26, 119–128. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).