Abstract
As structures age, air leaks naturally form and can remain undetected for years, resulting in increased utility bills and, in severe cases, structural damage. The traditional method to determine if a structure has developed these leaks is through an energy audit, including blower door testing, which is costly and disturbs normal use of the building. A numerical approach to indicate the presence of air leaks, for instance, a simple mathematic formula requiring only simple building information available to any layman, would be of great value. Within this paper, a formula was developed for climate Zone 5 regions using multiple linear regression models to infer the presence of air leaks using only four input variables. To validate the model, this framework was applied to a series of 700–770 square foot (65.03–71.54 m2) apartment units in Morgantown, West Virginia, USA. The model was determined to be able to accurately estimate the energy consumption of a given unit within this size range with 20% accuracy, which can then be used to ascertain sub-optimal, and thus unsustainable, consumption of energy. This framework can be applied in additional climate zones to create a more robust and generally applicable formula.
1. Introduction to Sustainability-Based Energy Conservation in Buildings
In the last four decades, global energy consumption has increased tremendously as many formerly agrarian nations rapidly industrialize. This industrialization is coupled with rapid urbanization and electrification, substantially increasing energy demand in these nations, the majority of which is supplied by fossil fuels [1]. Estimates by the Energy Information Administration suggest world energy consumption will increase by 53% from 2008 to 2035 [2]. As the global population continues to approach its projected peak of 10.9 billion people in 2100, the demand for energy will continue to rise [3]. Distribution of this energy use is, of course, important to consider. In 2022, commercial and residential energy consumption was 21% and 17% of nationwide electricity consumption in the United States, including energy losses during distribution, respectively [4]. In 2022, it is estimated that 52% of electricity consumed by the average American household was used for space heating and cooling [5].
By ENERGY STAR estimates, between 25% and 40% of energy used for heating and cooling is wasted due to air leaks in the structure [6]. As such, an intact thermal barrier is essential to keeping utility bills low and unnecessary emissions minimal [7,8,9]. These leaks include gaps between doors or windows and their respective framing, penetrations for plumbing and electrical wires, and gaps between building materials, etc. While new structures are generally well sealed, gaps appear and expand naturally as structures age due to the breakdown of seals, pests, and various weathering phenomena [6]. Currently, the primary mode to determine if these gaps are present and need to be addressed is a home energy audit. This audit is costly and invasive, as the technician needs to set up a set of sensors to measure the energy consumption of appliances and complete a blower door test on the structure, which requires occupants to exit for several hours. Rather than relying on this invasive and costly process, a methodology requiring an owner to simply enter information from past electrical bills, the location of the building, occupancy information, and square area would have clear benefits. By facilitating the detection of leaks using a formula rather than an expensive and disruptive energy assessment, ease of access for homeowners and landlords will be dramatically improved and will increase participation.
As 40% of all energy generated is used by buildings, a reduction in unnecessary energy consumption in buildings will result in enormous impacts on global carbon emissions due to the fossil fuel-intensive nature of global energy generation. The research showcased in this paper enables the expedited detection of excess air leakage in buildings, allowing stakeholders to address the problem expediently to ensure the conservation of energy resources used to heat and cool building spaces. The resulting demand reduction from this expedited approach will ensure that future generations enjoy the continued availability of finite natural resources by reducing unnecessary energy consumption in buildings. The three global challenges of environmental conservation, energy security, and socio-economic development can only be addressed by sustainable energy considerations, especially in buildings. While the green transition is underway, sustainable energy usage clearly addresses the requirement that energy, particularly fossil fuel-generated energy, should be consumed as efficiently as possible while remaining affordable. The concept of “sustainable energy” mandates stakeholder responsibility for future generations to access affordable energy, which is only possible through energy efficiency efforts and an effective energy supply chain. The current energy and climate challenges emphasize the necessity of effective and easily accessible approaches to sustainable energy, especially in buildings, as they contribute to a major share of energy usage throughout the world. For environmental, energy security, and economic reasons, sustainable energy use secures resources for future generations so they can enjoy a high quality of life while remaining key contributors to a robust national and world economy.
2. Development of the Model
2.1. Parameters for the New Methodology
To develop the model, an experimentally gathered dataset was composed by collecting data from 15 different small, independent apartments in Morgantown, WV, USA. As stated above, each unit is of similar scale and age. The heating system in each apartment maintains the set point temperature on the thermostat. The amount of heat put into the system or the work performed by the heating furnace/heat pump is determined by the variable factors inside and outside the apartment, which will be detailed in later sections. The data collection was designed in such a manner that the effect of all significant variables is covered and thus can be fitted into the empirical model. The calculations completed herein are based on ASHRAE 90.2 codes, and all the data collected was gathered using HOBO series data loggers produced by Onset, Bourne, MA, USA.
This research process involves considering the variables on the response (ideal energy consumption to actual energy consumption), the floor area, the temperature differences between the internal and external space, the number of occupants, and the number of air changes per hour. Using these variables, a multiple regression model was developed to predict the response variable with respect to the other variables. The research gap being addressed is the development of a remote and cost-effective method to understand the thermal integrity of a building space. The methods to ascertain this aspect, including the use of blower door tests, are not cost-effective and require significant time and expense for installation and generation of results, which need to be interpreted by skilled technicians. A method that instead uses utility bills and the infrastructural depiction of the building space through drawings, which are relatively easy to obtain and analyze, could be followed by interpretation via a simple formula. The model used to create this formula was developed and validated from actual data collected from fifteen apartment units. Each of the apartment buildings was built with a brick and masonry-type exterior, wood paneling, and shingled roof material. The apartment buildings assessed featured a mixture of natural gas and electric heating systems. The apartments were mostly south-facing, while some were north-facing. Each apartment had normal ceiling heights and fenestration systems in a rectangular configuration for all rooms. All the apartments surveyed were located in Morgantown, WV, USA.
2.2. ASHRAE Standards
In order to create this new methodology, many assumptions about the buildings being modeled are necessary. Fortunately, standards organizations, such as ASHRAE 90.2, a residential standard published by the American Society of Heating, Refrigerating, and Air Conditioning Engineers (ASHRAE), provide guidance for meeting minimum energy efficiency requirements in low-rise buildings. By referencing this standard, the model can be developed with substantially less data collection. ASHRAE 90.2 covers the seven climatic zones and has laid down 37 separate prescriptive paths. ASHRAE 90.2 details the energy-efficient design of low-rise buildings and provides minimum requirements for such building designs [10]. These energy efficiency requirements are intended to advance energy efficiency while remaining cost-effective. Compliance with these standards is determined through either prescriptive or systems analysis methods. The prescriptive criterion contains an independent energy requirement for each building component, such as exterior walls or duct insulation. This method is the most user-friendly but is the most stringent and offers the least design flexibility. The second option, the systems analysis approach, bases compliance on achieving an acceptable annual energy cost for the building. This method requires detailed analysis but allows for increased design flexibility, as well as accounting for energy-efficient features such as passive solar or innovative designs [11].
When calculating the values of heat loss by different factors, such as wind and infiltrations, some equations used are from the ASHRAE Handbook 2009, while standard values are applied in other equations (Figure 1).
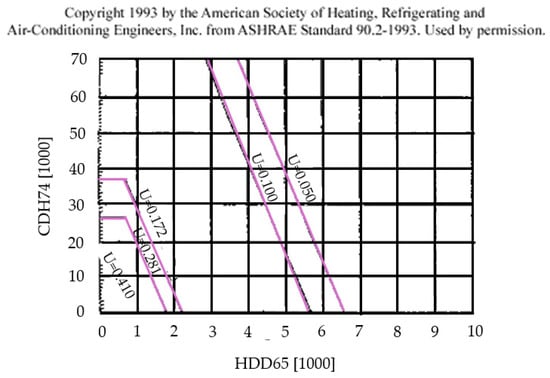
Figure 1.
ASHRAE 90.2 exterior wall required U-factors.
The ideal furnace energy consumption can be evaluated by calculating the heat loss, taking into account the area of the particular structure and the R and U values specified by IECC 2009 for Monongalia County, West Virginia. Table 1 shows the R and U values for West Virginia, while the sections directly following detail the individual values therein.

Table 1.
ASHRAE data points for the West Virginia climate zone.
Buildings, of course, vary substantially, and as such, several notes of clarification are necessary to properly apply these factors.
- (a)
- R-values are minimums. U-factors and SHGC are maximums. R-19 batts compressed into a nominal 2 × 6 ft (0.61 × 1.83 m) framing cavity, such that the R-value is reduced by R-1 or more, shall be marked with the compressed batt R-value in addition to the full thickness R-value.
- (b)
- The fenestration U-factor column excludes skylights. The SHGC column applies to all glazed fenestrations.
- (c)
- “15/19” means R-15 continuous insulated sheathing on the interior or exterior of the home or R-19 cavity insulation at the interior of the basement wall. “10/13” means R-10 continuous insulated sheathing on the interior or exterior of the home or R-13 cavity insulation at the interior of the basement wall.
- (d)
- R-5 shall be added to the required slab edge R-values for heated slabs. Insulation depth shall be the depth of the footing or 2 feet (0.61 m), whichever is less in Zones 1 through 3 for heated slabs.
- (e)
- There are no SHGC requirements in the Marine zone.
- (f)
- Basement wall insulation is not required in warm-humid locations.
- (g)
- Insulation sufficient to fill the framing cavity is required. R-19 is the minimum.
- (h)
- “13 + 5” means R-13 cavity insulation plus R-5 insulated sheathing. If structural sheathing covers 25 percent or less of the exterior, insulated sheathing is not required where structural sheathing is used. If structural sheathing covers more than 25 percent of the exterior, structural sheathing shall be supplemented with insulated sheathing of at least R-2.
- (i)
- The second R-value applies when more than half the insulation is on the interior of the wall.
- (j)
- For impact-rated fenestration complying with Section R301.2.1.2 of the International Residential Code or Section 1608.1.2 of the International Building Code, the maximum U-factor shall be 0.75 in Zone 2 and 0.65 in Zone 3.
With these parameters properly defined, the equation used to quantify ideal furnace energy consumption is as follows:
Ideal Consumption (9 days) =
where
U = Overall heat transfer coefficient, BTU/(h °F )
A = Area,
∆T = Temperature difference (between the inside and outside of the structure), °F
2.3. Energy Usage
In this study, the readings from electric bills and actual meters are used to estimate the energy used by the HVAC units assessed as part of this work. From the data collected from these sources, it was estimated that 41% of total electricity consumption and 60% of total gas consumption were used for space heating. This assertion is of great value when attempting to estimate the consumption of an HVAC unit using only utility bills.
Currently, there is no non-invasive method or straightforward formula to assess the effectiveness of the insulation of a given structure. The only accurate way is to commission an energy audit, which costs anywhere from $300 to $1000, depending on the size of the structure. So, the whole idea of this research is to develop a remote auditing system that will include only the use of energy bills and the construction drawings of the structure. The equation developed in this research will provide a rating of the effectiveness of the thermal blanket of the residential structure or, in simple terms, will show the effectiveness of the structure’s insulation. This method will be substantially more cost-effective for a homeowner while providing data of similar quality.
The primary energy reference in this study is the energy used for heating. As most furnaces in the structures were electric, data was collected by simply measuring power consumption in kWh from the utility meters.
These readings from each electric meter were recorded before and after experimental data collection. The difference between these two values was taken as the total electricity or gas consumption in a particular apartment. As defined by ASHRAE, 41.5% of the total energy used in a residential house is used for heating loads in North America, so 41.5% of the actual consumption in a house (the difference between before and after readings) was assumed to be the energy used for heating during the period of data collection (assumption in the model). Table 2 shows the kWh reading obtained from the electricity meter from each of the apartments.

Table 2.
kWh usage from residential apartments sampled in this study.
Ideal Heat Loss
The ideal heat loss is the theoretical energy loss from a residential structure. This loss is calculated by International Energy Conservation Code (IECC) standards for Monongalia County, WV. This heat loss considers the design and size of the structure along with the R and U values described in the code. The standard also considers the orientation of windows and doors for solar heat gain. In this study, these variations were assumed to be the same for all apartments.
2.4. Response
Response is the ratio of ideal heat loss to actual energy consumption. The response signifies the effectiveness of the thermal envelope in the residence. It is an indicator of how well the structure is insulated and if there is a need to make repairs or changes.
The response of the model is calculated using the formula described above to divide the ideal consumption (calculated) by the actual consumption, which is the noted kWh consumption.
where
Res = Response, no units
Actual Consumption = Actual energy consumption noted from the utility meter, kWh
2.5. Infiltration Leakage Area and the Effect of Wind
In a traditional building assessment, an auditor is dispatched to analyze energy bills over the past few years and benchmark the building energy profile. The auditor then typically interviews the owner about major appliances, observes standard building conditions, and takes measurements to determine energy consumption. Of course, electrical and gas inputs to a structure do not provide an accurate picture of how heat and air move through a structure. Radiant energy from the sun and a sudden increase in leakage due to gusts of wind are consistently varying parameters, which are difficult to account for without significant effort [12,13]. The auditor conducts a blower door test to empirically assess air leakage in the structure, wherein all doors, external vents, and windows are sealed with the exception of a single exterior door that is replaced with a “blower door.” A blower door is a specialized fan used to evacuate air from the structure, creating a pressure difference of −50 Pascals between the interior of the structure and the surrounding environment, known as the CFM50 test. An example of a blower door deployed in an apartment and the CFM50 measurement unit is shown below in Figure 2.

Figure 2.
Blower door test setup and CFM50 reading.
Once the building is depressurized, the fan is turned off, and the opening is sealed. The various leaks in the structure then allow air in from the exterior, slowly repressurizing the structure. By measuring the pressure while the structure repressurizes, the auditor can determine the magnitude of leaks present measured in air change per hour (ACH).
where
ACH = Air change per hour
A = Floor area of the structure
H = Average height of the room in the residence
Q = Cubic feet per minute of air
If the measurement is taken on a day where measurable wind is present, a different formula is used, as wind flow affects the repressurization rate [14] (Table 3).

Table 3.
Basic model of the wind and stack coefficients.
= Leakage area
= Stack coefficient
∆T = Temperature difference between the interior and exterior
= Wind coefficient
U = Wind velocity, mph
In order to gather data to develop the formula in this study, blower door tests were completed on every floor of all three apartment buildings in the study. The purpose of these tests was to determine the leakage area of the units (Table 4). Each floor was depressurized to −50 Pa by the blower door. Once the building was fully depressurized, a gauge installed on the blower door test unit measured the CFM readings, and from these data, the following equations were used to determine the leakage under natural conditions:

Table 4.
Air leakage from each apartment in the study.
Now, to convert cfm to air changes per hour:
where
- n = Lawrence Berkeley Laboratory (LBL) n factor for ventilation, 18.2 (Figure 3)
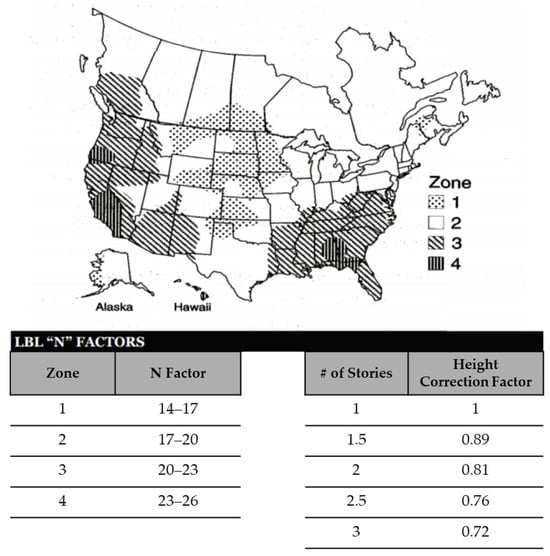 Figure 3. LBL n factor for ventilation.
Figure 3. LBL n factor for ventilation.
The LBL n factor, as depicted in Figure 3, was used to consider ventilation-related heat losses. Thermal equivalence concepts were utilized when considering and determining ventilation heat losses. The factors that impacted ventilation heat losses were the building envelope characteristics and the effectiveness of the fenestration systems. The different ventilation systems, whether they were based on natural air movement or forced air movement, were captured effectively by the thermal heat balance analysis and the LBL n factors.
2.6. Temperature Difference
The temperature difference between the temperature inside and outside of a given structure plays a significant role in determining the effectiveness of the insulation [15]. The temperature inside the apartment or house is governed by the thermostat set point temperature and is affected by air leakage. Figure 4 shows the relationship between heat loss and the set point temperature.
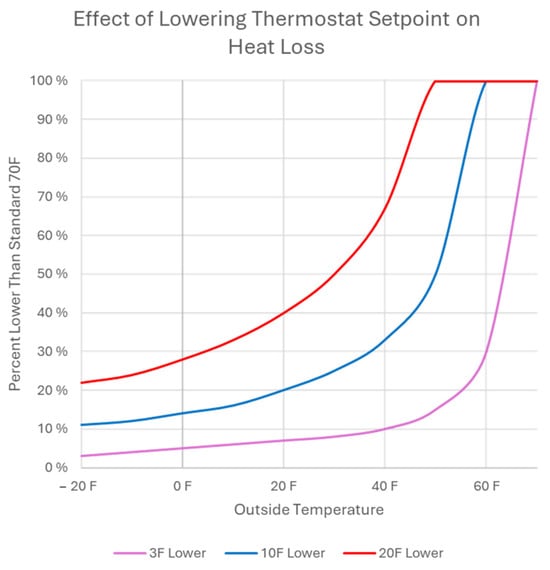
Figure 4.
Effect of lowering the thermostat setpoint on heat loss.
As shown in Figure 4, there is a significant decrease in heat loss as the set temperature decreases [16]. Decreasing the set point temperature will decrease the temperature inside the residence, which, as these data points were recorded in winter, will decrease the temperature difference. As the temperature difference decreases, assuming all conditions remain the same, the heat loss will likewise decrease.
A HOBO data logger was used to record the temperature within the apartment and the relative humidity measurements at constant intervals for a specified period. Specifically, the HOBO U12 Temperature/Relative Humidity/Light/External Data Logger was used. This unit features 12-bit resolution and can store up to 43,000 data points in its onboard memory. The logger can accept a variety of add-on sensors, including temperature and split-core AC current sensors. An example of the data collected from the loggers used is displayed in Figure 5a,b below.
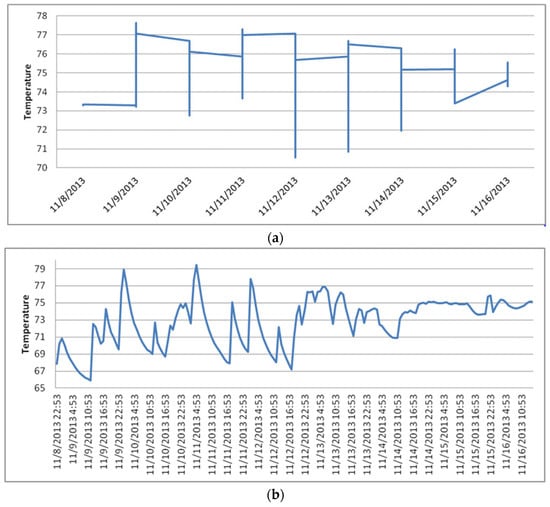
Figure 5.
(a) Hourly temperature data in Building 775, Apt 1. (b) Hourly temperature data in Building 777, Apt 2.
A logging interval of 30 s was used during data collection, which means that a temperature value was recorded inside the apartment every 30 s. In each apartment where the data were recorded, the dataloggers were placed near the thermostat.
The second component required to calculate temperature difference is the local weather conditions. The weather data for empirical modeling, which includes the hourly point temperature, wind speed, precipitation, and weather conditions, were requested and obtained from the National Climatic Data Center. The National Climatic Data Center is responsible for monitoring, assessing, storing, and providing public access to the nation’s climate and historical weather data.
2.7. Occupancy
The next parameter considered for this study was building occupancy. Human metabolic functions dissipate heat from the human body into their surroundings in the form of latent heat and sensible heat. The heat from convection and radiation is sensible heat, and the heat from evaporation is known as latent heat. Under normal conditions, the rate of heat transfer from a human body varies from 100 W when sedentary to 1000 W during intense physical work, as shown in Table 5 [17].

Table 5.
Sensible and latent heat loss from humans.
Therefore, increasing the number of people in a space increases the temperature and thus reduces the demand placed on the heating system during heating months. Though higher occupancy results in lower demand from the central heating unit, increased occupancy also increases the amount of carbon dioxide in a space and correspondingly increases the number of required air changes per hour for proper ventilation. Taking how these two factors affect HVAC load into account, for the empirical modeling completed in this study, a heat generation value of 256 Btu/h (75 Watts) per human occupant was used.
3. Development of the Model and Results
3.1. Design and Development of the Model
After data collection and preliminary calculations, the final variables were as follows:
- (a)
- Response (Ideal energy consumption/Actual energy consumption)
- (b)
- Floor area of the structure
- (c)
- Temperature difference
- (d)
- Number of occupants
- (e)
- Air changes per hour
Multiple linear regression was utilized in this study to establish a relationship between these variables and the response. Multiple linear regression models the relationship of all the variables and the response by fitting a linear equation between the observed data. The dependent variable is called a predictand (response), and the independent variable is known as the predictor. Multiple regression is based on the method of least squares, in which the best fit of the data is obtained by minimizing the sum of the least squares of the vertical deviations from each data point [18].
Standard practice is to use 4–5 data points for each variable in the equation for statistical modeling. In this model, the equation was developed using 15 data points, one from each apartment, and it was found that the adjusted coefficient of determination was a significant value, and validation examples yielded satisfactory results. Each of the apartment buildings was built from a brick and masonry-type exterior with wood paneling and shingled roof material. Apartment buildings using both natural gas and electric heating systems were included in the study. Most apartments surveyed were south-facing, while some were north-facing. Each apartment had normal ceiling heights and fenestration systems in a rectangular configuration for all rooms. All apartments in the sample were located in Morgantown, WV, USA.
Multiple regression is not a time series method, and the variables are sometimes dependent on one another [19]. The following equation illustrates the multiple regression model with two variables describing a space in three-dimensional space of , , and :
In the study, the final regression equation was as follows:
It should be noted that the wind speed data are obtained from the National Climate Data Center website, and thus, all datasets use the same value for wind speed. Due to this, the wind speed factor is rendered insignificant in the regression analysis, but practically, it is a significant factor [13,18]. Notice that the ACH factor used in this study includes the effect of wind because the CFM50 readings from the blower door tests do not neglect heat loss due to winds.
The method used in this research to develop an equation for analyzing the effectiveness of the insulation of a residential apartment or house is regression analysis. Multiple linear regression was completed between the response and the variables (area, occupancy, temperature difference, and air change) every 40 h.
All the calculations were performed in MS Excel, and the calculated values were imported to Minitab 15 to develop the empirical model using multiple linear regression (MLR) (Table 6).

Table 6.
Dataset for empirical modeling.
3.2. Predictors of Multiple Linear Regression
As stated above, the final predictors chosen in the MLR were area, temperature difference, number of occupants, and ACH (air changes per hour). Larger residences feature increased energy usage and, as a result, lose more energy through the walls because larger, older structures leak more compared to smaller, newer structures. Notably, temperature difference has a positive correlation with response, as increasing temperature difference increases energy usage. As the number of occupants increases, the energy used in the building to add heat to the system decreases, prompting a negative correlation. The ACH is dependent on the leakage area of the structure and is directly proportional to the power consumed, resulting in a positive correlation. Scatter plots of the response with all the aforementioned predictands are shown in Figure 6 below.
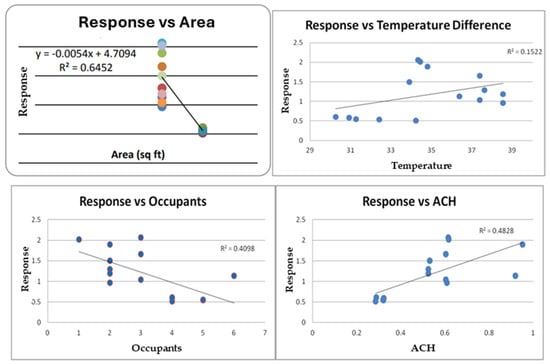
Figure 6.
Plots of the response (predictand) with all the variables.
The reason for comparatively low coefficients of determination compared to the final regression equation, as explained later, for linear fitted values shown in the graphs above is that all the data points were randomly collected, and there may not be a linear relationship with the response. Also, the response is affected by many factors not considered in this study, such as climatic zone, setback control, type of insulation, and grade and type of heating equipment. The scope of this study did not allow for the inclusion of these variables, as all the data were collected in Morgantown, WV, USA.
3.3. Creation of the Model
Multiple linear regression (MLR) was performed using the predictand response R (ideal energy consumption/actual energy consumption) and the predictors (area, temperature difference, number of occupants, air changes per hour, natural CFM, ln(ACH), and ln(natural CFM)). The coefficient of determination (R2) is the proportion of variance accounted for, explained, or described by regression. These response trials were used to narrow down the results obtained by the initial regression analysis. Table 7 and Table 8 show the response and predictors used to develop the model.

Table 7.
Predictand and predictors for the multiple linear regression analysis.

Table 8.
Boundary limits for the variables in the model.
In the first case, regression for thermal barrier response was completed using the following variables: area, temperature difference, number of occupants, and natural ACH. It should be noted that the predictors, natural ACH, natural CFM, ln(ACH), and ln(nCFM), are all variables derived from the same quantity. Hence, only one of these variables can be used as a predictor in the model. Similarly, in the next case, only three variables were used, and so on, with one variable neglected in every case. After these four cases, the variables ACH, natural CFM, ln(ACH), and ln(nCFM) were regressed one by one in the model. Table 8 shows the different multiple linear regressions, the predictor, the coefficients, and the corresponding coefficient of determination.
(Complete results of all the regression trials are documented in the Appendix A).
As shown in Table 8, the coefficient of determination (R2) and the adjusted coefficient of determination (adj R2) for all the multiple linear regression iterations were in the range of 72.3% to 84.7%. This signifies that there was not very much difference in R2 values, and there was not enough explanation for the use of transformation values (ln(ACH) and ln(nCFM)), though the model demonstrated a better p-value by using the ln(ACH) and ln(nCFM) predictors.
After performing a multiple linear regression (MLR) analysis on different combinations of predictand and predictors, it was concluded that the MLR with response vs. area, temperature difference, number of occupants, and air changes per hour produced the best results and the best fit. The p-value associated with ACH was 0.50, which concludes that the variable is not very significant in the equation; however, mathematically, it proves that there is a direct positive relationship between the energy consumed for heating and the air leakage (which affects ACH) (Table 9).

Table 9.
The response (predictand) with all the variables.
3.4. Final Equation, Coefficients, and ANOVA
The final empirical equation developed in this study was as follows:
The variable names are explained in Table 10.

Table 10.
Variables for the final equation.
Table 11 shows the parameter estimates for the model. The table shows the predictors, coefficients, standard error of coefficients, T-test, and p-test values (Table 12 and Table 13). It should be noted that the standard error coefficient and p-test value of the ACH predictor are quite high and are not considered very significant in the empirical equation (Figure 7). But mathematically, it has been proven that there is a significant effect of ACH that cannot be neglected. This relation is proven in the following equations:
where

Table 11.
Parameter estimates of the empirical model.

Table 12.
Summary of fit.

Table 13.
Analysis of variance (ANOVA).
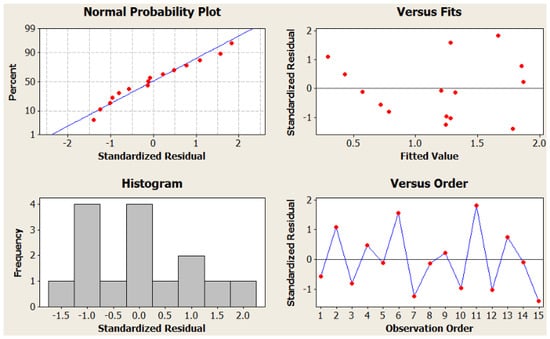
Figure 7.
Residual plots for the response.
= Leakage area,
= Stack coefficient
∆T = Temperature difference
= Wind coefficient
U = Wind velocity, mph
Q = Heat loss
ACH = Air changes per hour
3.5. Model Validation and Final Equation
To validate the model, a second batch of data collection was conducted on several apartments not in the dataset used to create the formula. The full details on the area, temperature difference, and apartment parameters were collected during the visits. The following section utilizes the data collected in these repeat studies to illustrate the function of the empirical model. Of course, the model can be applied to a variety of parameters that were considered and reported above. It should be noted that not all response variables will be applicable to specific indoor and outdoor conditions.
Since all the parameters and their effects were discussed in detail in the previous sections, this section will exclusively focus on the calculations and the values for outputs in table format. The details of the two apartments will be discussed as Apartment A and Apartment B.
- Apartment A:
The product parameters:
Area: 667 (61.97)
Ceiling height: 8 ft (2.44 m)
Temperature difference: 31.11 °F (17.28 °C)
Occupants: 2
CFM50: 935 CFM (26.48 )
- The next step converts the CFM50 data point to ACH:
The model was populated with data collected from Apartment A. The response results were obtained from the model as described in the section below.
The equation is applied as follows:
The product parameters:
Area: 667 ft2 (61.97 m2)
Ceiling height: 8 ft (2.44 m)
Temperature difference: 33.55 °F (18.64 C)
Occupants: 3
CFM50: 940 CFM (26.62 m3/min)
- The next step converts the CFM50 data point to ACH:
The model was populated with data collected from apartment A. The response results were obtained from the model as described in the section below.
The equation is as follows:
This value matches the energy consumption values recorded for this period and will be verified through energy bills.
4. Discussion
The model has been populated with the data collected in the host apartments, and results were obtained.
Table 14 compares the actual energy consumption with predicted energy consumption and states the error found in the model. The actual consumption was observed for one day and then was extrapolated for nine days. An average error of 15% is noted between the predicted values and the actual values of energy consumption.

Table 14.
Comparison of results.
This section verifies that the model is valid and holds well within the 20% error limits and subsets of the range of the values used to populate the empirical model.
This model can be used to predict energy consumption and the effectiveness of the thermal envelope within the limitations. The limitations of the current model are as follows:
- (1)
- The area of the structure should not exceed 770 sq ft. (71.54 m2).
- (2)
- The thermostat inside the structure should not be calibrated, and it should not be programmed for setback control.
- (3)
- The model cannot be used for summer months.
- (4)
- The model can give readings with 30% error.
- (5)
- The empirical model produces meaningful results only when the variables are in the ranges of values used to develop the empirical equation.
- (6)
- ACH will have to be estimated, as it is not possible to perform a blower door test every time the equation/model is used. The process of this calculation is demonstrated below.
- ACH estimation procedure:
- (1)
- The variables should be within the limits mentioned in Table 8 to avoid absurd and negative response values.
- (2)
- For estimating ACH, the following steps should be followed:
- a
- Calculate the effective leakage area using the following table:
S. No Units Best Estimate Minimum Maximum Ceiling in2/ft2 0.026 0.011 0.04 Door Frame, Wood in2/ft2 0.004 0.001 0.004 Door, General in2/ft2 0.015 0.011 0.021 Electrical Outlets in2/ea 0.023 0.012 0.54 Ceiling-wall joint in2/lfte 0.07 0.0075 0.12 Vents in2/ea 1.6 0.39 3.1 Walls, clay brick cavity wall in2/ft2 0.0098 0.0007 0.033 Windows not weather-stripped in2/ft2 0.023 0.011 0.035 - b
- Calculate CFM50:CFM50 = ELA × 10
- c
- Calculate natural CFM:
- d
- Convert natural cfm to air changes per hour:
n = Lawrence Berkeley Laboratory (LBL) n factor for ventilation, 18.2.
- (3)
- Once the response and all the variables are known, the effectiveness of thermal insulation can be assessed using Table 15.
 Table 15. Effectiveness rating in residential households.
Table 15. Effectiveness rating in residential households.
5. Conclusions and Future Work
From the data analysis completed using the multiple linear regression technique, a formula was created to calculate the response when the variables, area, temperature difference, and air changes per hour, are known. The model is limited in its applicability as only relatively small floor area units were tested, no structures tested featured smart thermostats, only traditional thermostats, and only structures in a single city were tested. While the model can be generalized to some extent for various regions and building types, the inherent parametric evaluations are consistent with enabled robustness to prevent increased variability in results.
The response rating was developed after assessing the 15 structures included in this study and analyzing the utility bills of the apartments that were used to formulate the empirical equations. These equations meet the MLR assumptions; the R2 values are quite high for an experimental study, which signifies that they explain a considerable part of the observed variation in the data. Also, the results obtained from the empirical equation for the calculation of response are in reasonable proximity to the experimental values. Consequently, these equations are reliable predictors of the response and effectiveness of the thermal barrier and insulation of a structure.
Empirical equations were also formulated using a combination of other variables; however, the fit was obtained using the final four variables mentioned above. Most of the MLR equations produced satisfactory results and yielded high R2 values. Some of the equations violated the MLR assumptions and were considered unreliable. The empirical model was validated by testing the value of the response from the empirical equation and then comparing it with the energy consumption in kWh in real time.
To check the robustness of the empirical equations, various random values were used to generate response functions, and the results concluded the following limitations in the empirical model explained in Table 16 below.

Table 16.
Effectiveness Limitations of the model.
Therefore, the final conclusions of the study are as follows:
- A good estimate of a structure’s insulation effectiveness and energy consumption in the form of electricity can be computed using the model equation developed.
- The current model will have outliers in specific cases.
- The current model equation is developed only for small apartments located in Zone 5 winter season conditions.
- The model can be used to rate the effectiveness of insulation.
With this baseline proof of concept completed, ongoing research and substantially more data points are required to improve model accuracy and applicability. The system should be refined to include other variables accounting for lesser factors that have smaller effects on the calculation. The development of an empirical model in this study has demonstrated a feasible methodology to help homeowners analyze their furnace heating utilization and insulation effectiveness and determine whether the structure needs any maintenance or modifications. However, as noted, the current model is limited to a very small subset of structures. The following work would further improve the accuracy, robustness, and credibility of the empirical model:
- Populate the current model with data points gathered from additional apartments within the current limiting parameters to improve the accuracy of the baseline equation.
- A new version of the equation should be developed to account for heating energy consumption for a given structure, and the data should be obtained directly, rather than theoretically, by installing a current transducer in the furnace. The current model makes a statistically valid assumption about what percentage of the structure’s power consumption is used for heating, but a directly logged value would increase accuracy significantly.
- Temperature difference readings and energy consumption readings should be taken at shorter intervals over long periods to retrieve more accurate data. The current model was developed to measure the internal temperature for a single day and extrapolate these data to nine days. Measuring the internal temperature of each structure for the full nine days would improve accuracy.
- The model should be updated to include data from apartments and houses that have more than one floor and have an area greater than 770 sq ft (71.54 . While this baseline dataset of small apartments served well to prove the viability of this method of formula generation, the current model is extremely niche in its applications, realistically only useful to landlords of apartment complexes in Morgantown, WV, USA. The model should be updated to include data from assorted apartments and houses that are located outside West Virginia to make it more robust and valid in other parts of the world. Applying the methodology explained herein to a substantially larger dataset would result in a generally applicable formula useful to homeowners and landlords nationwide.
- To improve the accuracy of the response variable, it would be prudent to develop a more accurate model of ideal heating energy consumption by simulating the apartments and houses in eQUEST.
- With the previously explained updates, the model should be validated on an experimental model house where the variables can be controlled and the response/results are already known. This would serve as a useful “control” data point, allowing for the final formula to be adjusted for increased accuracy.
- The model should be expanded with data from additional climate zones to create a new version of the model that is generally applicable rather than constrained to a single climate zone.
Author Contributions
This work is adapted from a thesis written by P.V. in 2014 under a committee of K.M. and B.G. The thesis was adapted into a research paper by J.J.R. in 2024 under the direct supervision of B.G. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are contained within this paper.
Acknowledgments
Special thanks to Terence Musho and Chris Haddox, without whom this research could not have been conducted, and the DOE for their continued support of the Industrial Assessment Center at WVU.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACH | Air Change per Hour |
| CFM | Cubic Feet per Minute |
| ASHRAE | American Society of Heating, Refrigerating, and Air Conditioning Engineers |
| MLR | Multiple Linear Regression |
Appendix A
To provide a better understanding of the various data and plots, an explanation of the different components is presented below.
- Summary of Fit Table
- “R Square” (R2) is the coefficient of determination, which is the proportion of variance accounted for, explained, or described by the regression model. If the regression is perfect, the R2 value is one. If the regression is a failure and the sum of squares of errors equals the total sum of squares, no variance is accounted for by regression and R2 is zero.
- “R Square Adj” is the adjusted R2 value, which measures the proportion of the variation in the predictand accounted for by the predictors. Adjusted R2 allows for the degrees of freedom associated with the sums of squares.
- “Root Mean Square Error” is the square of the differences between values predicted by a model and the observed values being modeled.
- “Mean of Response” is the values of the predictand calculated from the regression parameters and a given value of the predictor. This is an estimate of the mean of the predictand associated with an explanatory value of the predictor. The mean of the response is used in the plots as a horizontal reference point.
- “Observations” are the number of data points used in the regression model.
- Analysis of Variance Table
- “Source” has three rows: one for total variability and one for each of the two pieces comprising the total, model or regression and error or residual. The “C” in “C Total” stands for corrected.
- “DF” is the degrees of freedom. For the model, the number of degrees of freedom is the number of predictors used for the regression. For the error, the degrees of freedom is the number of observations minus the number of predictors minus 1. The degrees of freedom for C Total is the sum of the degrees of freedom for the model and the error.
- “Sum of Squares” is a way to find the function that best fits (least varies from) the data. It is the total variability in the response that is calculated from , where is the sample mean. The “Corrected” in “C Total” refers to subtracting the sample mean before squaring. The amount of variation in the data that cannot be accounted for by this simple method of prediction is given by the total sum of squares. When the regression model is used for prediction, the uncertainty that remains is the variability about the regression line, , where is the predicted value of the predictand. This is the error sum of squares. The difference between the total sum of squares and the error sum of squares is the model sum of squares, which is equal to .
- “Mean Squares” are the sum of squares divided by the corresponding degrees of freedom.
- “F Ratio” is the test statistic used to decide whether a model as a whole has a statistically significant predictive capability; that is, whether the regression sum of squares is big enough, considering the number of variables needed to achieve it. F is the ratio of the model mean square to the error mean square.
- Parameter Estimates Table
- “Term” is the predictor.
- “Estimate” is the regression coefficients in the regression equation.
- “Standard Error” is an estimate of the standard deviation of the regression coefficients.
- “t Ratio” tests the hypothesis that a population regression coefficient is zero when the other predictors are in the model. It is the ratio of the sample regression coefficient to its standard error.
The different models that were tested during the development of the final equation are as follows:
- Regression analysis: response vs. temperature difference, occupants, and ACH

Table A1.
Parameter estimates of the empirical model.
Table A1.
Parameter estimates of the empirical model.
| Predictor | Coeff | SE Coeff | T | P |
|---|---|---|---|---|
| Constant | 2.631 | 1.44 | 1.83 | 0.095 |
| Del T | −0.04881 | 0.04148 | −1.18 | 0.264 |
| Occupants | −0.24173 | 0.06969 | −3.34 | 0.005 |
| ACH | 2.0466 | 0.5417 | 3.78 | 0.003 |

Table A2.
Summary of Fit.
Table A2.
Summary of Fit.
| Regression Statistics | |
| Multiple R | 0.866468 |
| R Square | 0.750767 |
| Adjusted R Square | 0.682794 |
| Standard Error | 0.331462 |
| Observations | 15 |

Table A3.
Analysis of Variance (ANOVA).
Table A3.
Analysis of Variance (ANOVA).
| Df | Sum of Squares | Mean Square | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 4 | 3.6645 | 0.9161 | 13.6743 | 0.0005 |
| Residual | 10 | 0.6700 | 0.0670 | - | - |
| Total | 14 | 0.4344 | - | - | - |
- 2.
- Regression analysis: response vs. area, occupants, and ACH

Table A4.
Parameter estimates of the empirical model.
Table A4.
Parameter estimates of the empirical model.
| Predictor | Coeff | SE Coeff | T | P |
|---|---|---|---|---|
| Constant | 3.26 | 3.19 | 1.02 | 0.33 |
| Area | 0.00 | 0.00 | −0.72 | 0.49 |
| Occupants | −0.16 | 0.10 | −1.68 | 0.12 |
| ACH | 1.19 | 0.90 | 1.33 | 0.21 |

Table A5.
Summary of Fit.
Table A5.
Summary of Fit.
| Regression Statistics | |
|---|---|
| Multiple R | 0.86 |
| R Square | 0.73 |
| Adjusted R Square | 0.66 |
| Standard Error | 0.34 |
| Observations | 15 |

Table A6.
Analysis of Variance (ANOVA).
Table A6.
Analysis of Variance (ANOVA).
| Df | Sum of Squares | Mean Square | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 3 | 3.5 | 1.2 | 10.0 | 0.0018 |
| Residual | 11 | 1.3 | 0.1 | - | - |
| Total | 14 | 4.8 | - | - | - |
- 3.
- Regression analysis: response vs. area, temperature difference, and ACH

Table A7.
Parameter estimates of the empirical model.
Table A7.
Parameter estimates of the empirical model.
| Predictor | Coeff | SE Coeff | T | P |
|---|---|---|---|---|
| Constant | 17.45 | 3.96 | 4.41 | 0.00 |
| Area | −0.02 | 0.00 | −4.59 | 0.00 |
| ACH | −0.06 | 0.65 | −0.09 | 0.93 |
| Del T | −1.14 | 0.05 | −3.11 | 0.01 |

Table A8.
Summary of Fit.
Table A8.
Summary of Fit.
| Regression Statistics | |
|---|---|
| Multiple R | 0.91 |
| R Square | 0.82 |
| Adjusted R Square | 0.77 |
| Standard Error | 0.28 |
| Observations | 15 |

Table A9.
Analysis of Variance (ANOVA).
Table A9.
Analysis of Variance (ANOVA).
| Df | Sum of Squares | Mean Square | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 3 | 3.98 | 1.33 | 16.84 | 0.000201 |
| Residual | 11 | 0.87 | 0.08 | - | - |
| Total | 14 | 4.85 | - | - | - |
- 4.
- Regression analysis: response vs. area, temperature difference, and occupants

Table A10.
Parameter estimates of the empirical model.
Table A10.
Parameter estimates of the empirical model.
| Predictor | Coeff | SE Coeff | T | P |
|---|---|---|---|---|
| Constant | 16.25 | 3.04 | 5.34 | 0.00 |
| Area | −0.01 | 0.00 | −5.39 | 0.00 |
| Del T | −0.14 | 0.04 | −3.28 | 0.01 |
| Occupants | −1.08 | 0.06 | −1.23 | 0.24 |

Table A11.
Summary of Fit.
Table A11.
Summary of Fit.
| Regression Statistics | |
|---|---|
| Multiple R | 0.92 |
| R Square | 0.84 |
| Adjusted R Square | 0.80 |
| Standard Error | 0.26 |
| Observations | 15 |

Table A12.
Parameter estimates of the empirical model.
Table A12.
Parameter estimates of the empirical model.
| Df | Sum of Squares | Mean Square | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 3 | 4.09 | 1.36 | 19.64 | 0.0001 |
| Residual | 11 | 0.76 | 0.07 | - | - |
| Total | 14 | 4.85 | - | - | - |
- 5.
- Regression analysis: response vs. area, temperature difference, occupants, and natural CFM

Table A13.
Parameter estimates of the empirical model.
Table A13.
Parameter estimates of the empirical model.
| Predictor | Coeff | SE Coeff | T | P |
|---|---|---|---|---|
| Constant | 14.12 | 4.41 | 3.20 | 0.01 |
| Area | −0.01 | 0.00 | −2.78 | 0.02 |
| Del T | −0.13 | 0.05 | −2.80 | 0.02 |
| Occupants | −0.11 | 0.08 | −1.38 | 0.20 |
| Natural CFM | 0.01 | 0.01 | 0.68 | 0.51 |

Table A14.
Summary of Fit.
Table A14.
Summary of Fit.
| Regression Statistics | |
|---|---|
| Multiple R | 0.92 |
| R Square | 0.85 |
| Adjusted R Square | 0.79 |
| Standard Error | 0.27 |
| Observations | 15 |

Table A15.
Analysis of Variance (ANOVA).
Table A15.
Analysis of Variance (ANOVA).
| Df | Sum of Squares | Mean Square | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 4 | 4.12 | 1.03 | 14.13 | 0.0004 |
| Residual | 10 | 0.73 | 0.07 | - | - |
| Total | 14 | 4.85 | - | - | - |
- 6.
- Regression analysis: response vs. area, temperature difference, occupants, and log(natural CFM)

Table A16.
Parameter estimates of the empirical model.
Table A16.
Parameter estimates of the empirical model.
| Predictor | Coeff | SE Coeff | T | P |
|---|---|---|---|---|
| Constant | 12.34 | 6.16 | 2.00 | 0.07 |
| Area | −0.01 | 0.00 | −2.23 | 0.05 |
| Del T | −0.13 | 0.05 | −2.75 | 0.02 |
| Occupants | −0.11 | 0.08 | −1.41 | 0.19 |
| Ln (Natural CFM) | 0.38 | 0.52 | 0.74 | 0.48 |

Table A17.
Summary of Fit.
Table A17.
Summary of Fit.
| Regression Statistics | |
|---|---|
| Multiple R | 0.92 |
| R Square | 0.85 |
| Adjusted R Square | 0.79 |
| Standard Error | 0.27 |
| Observations | 15 |

Table A18.
Analysis of Variance (ANOVA).
Table A18.
Analysis of Variance (ANOVA).
| Df | Sum of Squares | Mean Square | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 4 | 4.12 | 1.03 | 14.13 | 0.0004 |
| Residual | 10 | 0.73 | 0.07 | - | - |
| Total | 14 | 4.85 | - | - | - |
- 7.
- Regression analysis: response vs. area, temperature difference, occupants, and log(ACH)

Table A19.
Parameter estimates of the empirical model.
Table A19.
Parameter estimates of the empirical model.
| Predictor | Coeff | SE Coeff | T | P |
|---|---|---|---|---|
| Constant | 13.69 | 4.67 | 2.93 | 0.02 |
| Area | −0.01 | 0.01 | −1.89 | 0.09 |
| Del T | −0.13 | 0.05 | −2.75 | 0.02 |
| Occupants | −0.11 | 0.08 | −1.41 | 0.19 |
| Ln (ACH) | 0.38 | 0.52 | 0.74 | 0.48 |

Table A20.
Summary of Fit.
Table A20.
Summary of Fit.
| Regression Statistics | |
|---|---|
| Multiple R | 0.92 |
| R Square | 0.85 |
| Adjusted R Square | 0.79 |
| Standard Error | 0.27 |
| Observations | 15 |

Table A21.
Analysis of Variance (ANOVA).
Table A21.
Analysis of Variance (ANOVA).
| Df | Sum of Squares | Mean Square | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 4 | 4.13 | 1.03 | 14.25 | 0.0004 |
| Residual | 10 | 0.72 | 0.07 | - | - |
| Total | 14 | 4.85 | - | - | - |
References
- United Nations Climate Action Committee. Available online: https://www.un.org/en/climatechange/raising-ambition/renewable-energy (accessed on 19 March 2024).
- U.S. Energy Information Administration. Available online: https://www.eia.gov/pressroom/releases/press368.php#:~:text=Worldwide%20energy%20consumption%20grows%20by,over%20the%20next%2025%20years (accessed on 19 March 2024).
- Pew Research. Available online: https://www.pewresearch.org/short-reads/2019/06/17/worlds-population-is-projected-to-nearly-stop-growing-by-the-end-of-the-century/ (accessed on 19 March 2024).
- U.S. Energy Information Administration. U.S. Energy Consumption. Available online: https://www.eia.gov/tools/faqs/faq.php?id=86&t=1#:~:text=When%20electrical%20system%20energy%20losses,U.S.%20energy%20consumption%20in%202022.&text=See%20a%20diagram%20of%20U.S.,consumption%20by%20source%20and%20sector (accessed on 19 March 2024).
- U.S. Energy Information Administration. Energy Use in U.S. Households. Available online: https://www.eia.gov/energyexplained/use-of-energy/homes.php (accessed on 19 March 2024).
- Energy Star Building Envelope Improvements. Available online: https://www.energystar.gov/ia/home_improvement/home_sealing/AirSealingFS_2005.pdf (accessed on 19 March 2024).
- Chandhran, K.D.; Elavenil, S. A comprehensive state-of-the-art review of sustainable thermal insulation system used in external walls for reduction in energy consumption in buildings. Int. J. Green Energy 2023, 20, 895–913. [Google Scholar] [CrossRef]
- Sugandha Rathan, N.; Raut, A.; Gnana Rahul, B. Comparative Analysis of Various Insulation Materials for Building Envelope Components. IOP Conf. Ser. Earth Environ. Sci. 2021, 822, 012014. [Google Scholar] [CrossRef]
- Kashiwagi, D.T.; Moor, W.C. The Relationship between Energy Cost and Conservation Measures, Building Design and Insulation Levels. J. Build. Phys. 1993, 16, 375–394. [Google Scholar] [CrossRef]
- ASHRAE 90.2. 1993. Available online: https://www.ashrae.org/news/esociety/newly-revised-standard-90-2-includes-new-performance-specifications-more (accessed on 15 January 2014).
- ASHRAE 90.2. 2009. Available online: http://yanpage.narod.ru/NCMA_TEKs/TEKs/Wce2743723fb62.htm (accessed on 15 January 2014).
- Wojdyga, K. An influence of weather conditions on heat demand in district heating systems. Energy Build. 2008, 40, 2009–2014. [Google Scholar] [CrossRef]
- Mattsson, B. The influence of wind speed, terrain and ventilation system on the air change rate of a single-family house. Energy 2006, 31, 719–731. [Google Scholar] [CrossRef]
- King, P.; Hunt, C.M.; King, J.C.; Trechsel, H.R. Building Air Change Rate and Infiltration Measurements: A Symposium; ASTM International: Conshohocken, PA, USA, 1980; Volume 719. [Google Scholar]
- Asadi, S. Evaluation of the Thermal Performance and Cost Effectiveness of Radiant Barrier Thermal Insulation Materials in Residential Construction. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2011. [Google Scholar]
- Set Back Temperature Control—Utilities Savings Factsheet. Available online: https://www.deq.nc.gov/environmental-assistance-and-customer-service/ias-energy-efficiency/opportunities/setback-temperature-control/download (accessed on 15 January 2014).
- Emery, A.F.; Kippenhan, C.J. A long term study of residential home heating consumption and the effect of occupant behavior on homes in the Pacific Northwest constructed according to improved thermal standards. Energy 2006, 31, 677–693. [Google Scholar] [CrossRef]
- Regression Analysis. Available online: https://hbr.org/2015/11/a-refresher-on-regression-analysis (accessed on 19 March 2024).
- Multiple Linear Regression Analysis. Available online: https://www.reliawiki.com/index.php/Multiple_Linear_Regression_Analysis (accessed on 19 March 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).