The Influence of Communication Strategies of Intelligent Agents in Production Systems on the Shift of Sustainable Solutions

Abstract

Current decision support systems for recommending labor resource allocation and generating production schedules in the systems with decentralized technological process control often fail to account for the impact of participants’ communication strategies on the shifts in target performance indicators, which depend on the alignment between local goals of production units and the global objectives of the system. The goal of the present study is to develop an approach for determining optimal communication parameters among intelligent agents to achieve system-level performance targets using the previously developed multiagent systems (MAS) for optimizing technological processes. The research investigates how agent constraint systems influence both overall system welfare and the individual welfare of agents, considering the shifts in their objective functions driven by preferred communication strategies. A workflow is developed to identify effective constraints. Using this workflow, the study provides recommendations for assigning regional field development plans, accounting for participants’ tendencies toward cooperation. On data where the potential for increasing the region’s flow rate through optimization of labor resource allocation and scheduling of well intervention operations (GTO) does not exceed 6%, the presented solution enabled the development of field plans that result in an additional 1% increase in the predicted oil production region’s flow rate on top of the gain achieved through resource allocation optimization.

1. Introduction

In the context of managerial decision-making within production systems, simulation models are used to enhance the justification of decisions. Decision support systems are often based on simulation models that belong to one of the three classical paradigms. Among these, agent-based modeling offers the greatest potential for capturing individual capabilities of system participants [1]. However, the descriptive capabilities of classical simulation methods are insufficient to achieve the level of realism required by businesses. This limitation stems from the specific nature of production systems. These systems can be viewed as complex organizational structures characterized by integrity and emergence. One of their distinguishing features is structural variability [2]. These characteristics present one of the major challenges in managing a production system, namely, the interdependence of system elements and the processes within them. The integrity of complex systems, coupled with their practical decentralization, creates significant challenges. In particular, it makes it analytically infeasible to identify the dependencies needed to predict the effectiveness of control actions with sufficient accuracy. This property is one of the key drivers for adopting multi-agent models of production systems and highlights the importance of studying the communication strategies of system participants. Agents’ preferences in selecting communication strategies significantly affect the sustainability of decisions obtained via decision support systems.

A project was conducted to explore the applicability of multi-agent systems (MAS) in optimizing technological processes. As part of this effort, an MAS was developed to forecast oil production rates and company expenditures, incorporating the communication strategies of the participating agents [3]. The developed system reflects how preferred communication strategies influence the behavior of agents and the overall efficiency of the system. The model can be used to study how agents’ preferred communication strategies affect the sustainability of system-level decisions [4,5]. These preferred strategies cannot be externally modified. They can only be influenced by the agent itself through its internal moral beliefs. However, it is possible to affect an agent’s decision-making by imposing constraints on its target indicators. This is particularly effective if the agent has a predisposition toward cooperation. This study focuses on identifying constraints on agents’ target indicators under which, given their known communication strategies, the system-level objectives are optimized. The concept of decision sustainability in a multi-agent system is explored. A workflow is proposed for determining effective constraints that ensure the sustainability of solutions, considering the agents’ known communication strategies. Using the proposed workflow, recommendations are presented for planning oilfield development in the region. These recommendations take into account the cooperative tendencies of system participants. The findings of this study contribute to the development of methodological and instrumental tools for decision support in the management of technological processes based on MAS.

2. Materials and Methods

A key concept in this study is the sustainability of solutions in a multi-agent system. Sustainability here refers to the ability of a solution to maintain a superior objective function value compared to alternative solutions under varying search conditions [6].

In multi-agent systems (MAS), the problem of finding a sustainable solution is further complicated by the distributed nature of decision-making, coordination, and potential conflicts between agent goals.

In the context of production planning within MAS, a sustainable solution can be interpreted as:

• a Nash equilibrium—strategic sustainability of interaction;
• an evolutionarily stable strategy (ESS)—behavioral sustainability under mass adherence to established rules;
• a robust solution—retention of feasibility and optimality under changes in environmental parameters.

A sustainable solution in MAS for production planning is defined as a coherent set of agent strategies that simultaneously meet the following criteria:

• Strategically sustainable: no agent (e.g., workshop, production unit, supplier) has an incentive to unilaterally deviate from the adopted strategy, thus satisfying the Nash equilibrium condition.
• Evolutionarily sustainable: if the majority of agents follow this strategy, then deviations by individual agents neither improve their outcomes nor disrupt system coherence (i.e., the strategy qualifies as evolutionarily stable, ESS).
• Robustly sustainable: the solution maintains feasibility and effectiveness under external changes (e.g., demand, resource availability, delivery schedules, equipment condition) within a defined parameter range.

In the last decade, there has been a significant increase in research on the implementation of MAS in various industrial environments. Unlike traditional centralized or hierarchical approaches, this method assumes the presence of multiple decision-makers distributed throughout the production system, who interact and collaborate to achieve globally optimal performance [7].

In the scientific literature, a multi-agent approach to production planning is recognized, proposing systems that balance workstation workloads and enhance scheduling efficiency for mixed-model assembly lines in accordance with the principles of autonomous agent theory [8].

Multi-agent system (MAS) technology can play a significant role in the development of highly responsive production planning systems capable of adapting to dynamic and uncertain demand fluctuations. MAS has been widely applied to address production planning problems in manufacturing systems [9].

A review of existing scientific literature on the application of MAS in production planning revealed several key research directions. First, there are comprehensive review papers discussing the applicability of MAS tools in production planning [8,9]. Second, some works analyze and present specific MAS-based architectural solutions developed for manufacturing systems [8,10]. Third, a number of studies focus on the use of MAS tools for scheduling in production environments [10,11]. Finally, researchers have investigated MAS-based approaches to the integration of production and logistics processes [12,13,14]. Prior work does not explicitly link communication strategies to multi-criteria stability in production planning.

In the scientific literature, agent-based approaches are also applied to the adaptation of energy-optimized production schedules. One such method uses extensive-form game trees to transform and monitor production plans, enabling dynamic adjustment to changing energy prices and disruptions. The model incorporates interactions between a planning agent and energy agents and is validated both in a simulated scenario involving electricity price updates and in a real industrial case addressing unforeseen events [15].

This study introduces the concept and implementation of agent-based adaptation of energy-efficient production schedules using extensive-form games. A game tree is constructed between the scheduler agent and the energy agents. When energy prices fluctuate or disruptions occur (e.g., order shifts, condition changes), the scheduler and energy agents engage in strategic interactions to adapt the schedule. Solution sustainability is measured as the ability to adapt to such changes with minimal performance loss.

In the literature, multi-agent approaches are also used for dynamic scheduling in flexible manufacturing environments subject to random equipment failures. Such models employ autonomous agents to allocate tasks across machines in real time, ensuring continuity of production despite disturbances [16].

The system is agent-based and does not rely on a fixed baseline schedule. Machine agents respond to breakdowns and dynamically allocate tasks. Sustainability in this context is defined as the system’s low sensitivity to disruptions, with performance measured by flowtime under various failure scenarios.

Game-theoretic methods are also applied to project scheduling problems. Here, Nash equilibrium represents a state where no agent has an incentive to unilaterally change the duration of its tasks. The focus is placed on identifying equilibria that minimize overall project completion time, with sustainability understood as the absence of incentives for agents to alter task durations [17].

In contemporary research, reinforcement learning methods combined with multi-agent architectures are also employed for real-time, factory-wide dynamic scheduling. Such approaches enable the representation of specific operational characteristics through specialized agents, while leader–follower coordination mechanisms ensure that local decision-making remains consistent with the overall objectives of the production system [18]. Additionally, a rule-based transformation algorithm is introduced to compensate for errors arising during the training of reinforcement learning agents, thereby preventing significant losses in production capacity. The proposed model delivers robust scheduling performance under demand fluctuations. This research demonstrates that integrating multi-agent reinforcement learning methods with rule-based decision adaptation mechanisms can serve as an effective tool for identifying sustainable solutions in production planning. This approach reduces dependence on expert heuristics and enhances the reliability of manufacturing systems under uncertainty (Table 1).

Table 1. Analysis of Research on the Stability of Multi-Agent System Solutions.

Method Class	Mathematical Apparatus	Reference	Stability Criterion
Game-theoretic models	Extensive-form games, construction of game trees between scheduler and energy agents	Motsch W., Wagner A., Ruskowski M. Autonomous Agent-Based Adaptation of Energy-Optimized Production Schedules Using Extensive-Form Games //Sustainability.—2024.—T. 16.—No. 9.—C. 3612 [15].	System’s ability to adapt to price changes or unexpected events with minimal performance loss
Agent-based dynamic planning	Decentralized task allocation by machine agents, real-time response to equipment failures	Ebufegha A., Li S. Multi-agent system model for dynamic scheduling in flexibile job shop subject to random machine breakdown //2022 Winter Simulation Conference (WSC).—IEEE, 2022.—C. 1719–1730 [16].	Low sensitivity to failures (evaluated via flowtime across different failure scenarios)
Game-theoretic models (equilibrium solutions)	Nash equilibrium for multi-project scheduling with milestones	Šůcha P. et al. Nash equilibrium solutions in multi-agent project scheduling with milestones //European Journal of Operational Research.—2021.—T. 294.—No. 1.—C. 29–41 [17].	Absence of agents’ incentive to change task durations (stability achieved at equilibrium point)
Machine learning in MAS	Multi-agent reinforcement learning (MARL), leader–follower coordination + rule-based conversion algorithm	Jang J. et al. Scalable Multi-agent Reinforcement Learning for Factory-wide Dynamic Scheduling //arXiv preprint arXiv:2409.13571.—2024 [18].	Robustness to demand variability and prevention of production capacity loss through RL-agent decision correction

The stability of decisions made within a production system is influenced by the communication strategies chosen by its participants. Two overarching communication tendencies can be distinguished: convergence and individuality. A communication strategy refers to the agent’s preference for one of these tendencies [19,20,21]. Communication strategies are typically categorized as competitive, cooperative, or coopetitive. This classification is based on differing approaches to joint activity execution. Participants in a production system adopt competitive strategies when joint action aimed at achieving a common goal is not anticipated. A cooperative style is chosen when the achievement of individual goals requires collaborative action. Coopetition, in turn, refers to temporary collaboration between competing participants to jointly achieve certain individual objectives [22]. The effectiveness of communication strategy selection within an organization depends on individual situational factors: the presence of a problem situation, the agent’s constructive capacity, and its a priori assumptions [23]. A problem situation manifests as the agent’s desire to act; constructive capacity refers to the agent’s ability to form a strategy consistent with its desires and capabilities; and a priori assumptions reflect the agent’s understanding of the environment in which it operates. These key aspects influencing the effectiveness of communication strategy choice can be formalized within a multi-agent system model.

A multi-agent system is generally defined as a collection of intelligent agents, an environment, and an organizational structure [24,25]. The BDI model is a common foundation for agent architecture. Its widespread use is supported by its popularity, the variety of available development tools, and a solid theoretical basis for its application in the design of MAS, including ontology-based systems [25,26,27,28,29,30,31]. Of particular interest are practical applications of the MAS approach for managing organizational systems, especially in conflict resolution [32]. Within MAS theory, research is conducted not only on managing conflict in organizational contexts but also on agent communication in general. One line of inquiry focuses on social and moral agents [5,33,34,35], including investigations into how moral preferences influence emergent system properties, manifestations of self-sabotage, and collective welfare [5]. However, the specific relationship between decision stability and agents’ preferred communication strategies in production systems remains underexplored. The studies reviewed in this research served as the foundation for the development of a multi-agent model of a production system. Within the framework of this model, recommendations were formulated for defining constraints on the target indicators of system participants, taking into account their preferred communication strategies.

3. Results

The selection of constraints on the target indicators of system agents must account for the preferred types of communication adopted by participants in the production system. Developing an approach to defining recommended constraints, expressed as requirements for agent performance, requires a deeper investigation. In particular, it is necessary to examine how the agents’ preferred communication strategies influence both the stability of the system’s decisions and its key performance indicators. This study was conducted using a digital model of a multi-agent production system.

Previously, an invariant ontology of multi-agent interactions within a complex production system was developed [3]. Within this model, it is proposed to distinguish between production and support units of the enterprise. These structural units are treated as autonomous decision-making entities within the system, participating in scheduling and resource allocation processes. The model was implemented in Python 3.13. The system enables the generation of recommendations for resource distribution and scheduling in the production system, taking into account the individual goals and capabilities of system participants. Groups of agents were introduced for each type of enterprise unit. Production units are modeled across two hierarchical levels, and a separate enterprise-level agent is also included. Agents are defined according to the BDI paradigm. In this system, the enterprise agent’s primary desire is to maximize production output while minimizing production costs.

Unit agents model the ability of participants within the simulated system to select their preferred communication style during resource distribution. To support this, they are implemented as moral agents. The performance indicators of these agents are adjusted according to their internal beliefs about teamwork. For production units, the individual performance indicator is the volume of output. For support units, it is the number of completed maintenance operations. Agents do not receive direct benefit (i.e., an increase in individual performance indicators) from transferring resources to other agents. However, guided by their personal beliefs, they may choose to allocate resources in favor of another agent or group. This system considers competitive games between agents. The tendency toward cooperation or competition is expressed through the agents’ ability to select a strategy: competition (resource appropriation) or cooperation (resource sharing). This tendency is also encoded in the agents’ desires. Their objective functions include two components. The first is the system-wide performance indicator multiplied by an altruism coefficient. The second is the individual performance indicator multiplied by an egoism coefficient. The altruism coefficient reflects the agent’s inclination toward cooperative strategies and represents a willingness to help others without direct compensation. It ranges from 0 to 1, where 1 indicates a preference for collective welfare regardless of individual outcomes, and 0 denotes a focus on individual performance irrespective of others’ conditions. The egoism coefficient is the inverse of altruism and is calculated as one minus the altruism coefficient. Agents aim to fulfill the system manager’s requirements and will choose competition until the constraints on their individual targets are met. Random variables are introduced into the model to represent agents’ varying performance levels. To manage resource allocation, a multi-agent optimization approach based on bilateral negotiation is implemented, solving the resource distribution problem within the MAS framework [24]. An agent continues participating in resource exchanges until changes in its objective function become negligible. Decision-making is based on forecasts generated using environment objects. This modeling approach allows the representation of key factors influencing enterprise performance (including the needs, motivations, goals, and tasks of participants; their understanding of production technologies; and their methods for evaluating performance [36,37]) in full detail. The model thus serves as a suitable platform for analyzing the impact of agents’ preferred communication strategies on the stability of system decisions.

Three criteria define the stability of solutions in a multi-agent system: evolutionary, strategic, and robust stability. Among these, only agents’ approaches to forecasting the utility of their actions directly influence the robustness of the designed system. This is the only factor that explicitly depends on environmental parameters. At the same time, the communication strategy selected by each agent must significantly affect the system’s performance indicators. To study how communication strategies affect robust stability, determine if random variations in unit efficiency significantly impact system and agent performance when strategies are identical. The evolutionary stability of solutions in the examined system arises from the fact that resource optimization continues until agents’ objective function values cease to change significantly. The communication strategies selected by agents can have a notable impact on evolutionary stability. This is because the agents’ objective functions depend on their tendency toward cooperation and directly influence whether further optimization is necessary. To assess evolutionary stability, it is essential to determine whether changes in agents’ communication preferences result in significant changes in the system’s performance indicators. If such dependence exists, it is necessary to define constraints under which agents’ freedom to choose communication strategies does not lead to solution instability. Since constraints can be imposed on the required performance levels of all agents, the system manager always has the ability to establish specific conditions. Under such conditions, agents are forced to act selfishly, following a single preferred set of communication strategies. Strategic stability can be achieved when changes in agents’ strategies do not lead to significant changes in their performance indicators. To investigate strategic stability, it is necessary to determine whether the agents’ performance indicators change significantly when communication strategy preferences are varied. If such changes are found to be significant, the imposed constraints may be adjusted accordingly: by easing the requirements on individual performance indicators, agents are more likely to select strategies that help them reach a satisfactory state. Stability is sought when the best possible values of the system’s performance indicators are achieved.

Based on the above criteria, a workflow can be developed for identifying recommended constraints on the target performance indicators of agents in a production-oriented multi-agent system, depending on their preferred communication strategies:

• Robust Stability

• Demonstrate the independence of system-level performance indicators from random factors.
• Demonstrate the dependence of system-level performance indicators on the communication strategies preferred by agents, for at least two groups defined by types of communication preferences, for example, groups with different values of the altruism coefficient.

As a result of these steps, it will be shown that the model is insensitive to noise but responsive to agents’ communication strategy choices.

2.

Evolutionary Stability

• Identify a set of agent communication strategy preferences for which the system’s performance indicators do not change significantly. From this set, determine the strategies with maximum utility.

The result of this step is a set of altruism coefficient values for all system agents. For decisions within this set, the system’s performance indicators remain stable. Agents’ strategic choices can be controlled by imposing stricter constraints on their individual performance targets.

3.

Strategic Stability

• Identify a set of agent communication strategy preferences for which the agents’ individual performance indicators do not change significantly. From this set, determine the strategies with maximum utility.

The result of this step is a set of altruism coefficient values for all system agents. For decisions within this set, the agents’ performance indicators remain stable. Agents’ strategic choices can be controlled by relaxing constraints on their performance targets.

4.

Constraint Definition

• Identify the set of constraints under which the stability conditions for the solution are satisfied.

In this methodology, independence from random effects is considered as low sensitivity to small random changes in system parameters. Sensitivity here refers to the dependence of the system’s dynamic properties on changes in its parameters and characteristics. Thus, independence is inherent in systems where small random changes in parameters lead to only minor changes in their performance results.

At this stage, the algorithm is completed. As a result, the constraints on the agents’ target parameters that ensure solution stability and maximize the system’s overall performance indicators are determined.

The computational approaches applied may vary and can be selected according to the specific objectives of the study. By using the proposed workflow to define constraints, it is possible to obtain stable and efficient solutions.

The workflow was tested using a case study of a multi-agent system representing an enterprise in the oil and gas sector. The data used are synthetic but closely approximate real-world conditions. The data on the coordinates of well pads and wells were obtained from open sources. The list of fields for testing, data on the initial flow rate of wells, the expected annual production of the region and the fields, data on the impact of GTO on production changes, data on the number of crews in the region, and the distribution of their roles were obtained earlier during the execution of a commercial project to model the production activity of the region. The scenario includes oilfields within a single region. The initial dataset includes: 1 region, 4 oilfields, 24 well clusters, and an average active well stock (AWS) of 348 wells. The modeling task involves not only increasing the total production rate at the regional level but also meeting the individual production plans of each oilfield. The production rate of a specific well cluster depends on the timing and type of the geological and technical operations (GTO) performed, which makes the scheduling of GTOs a critical factor. Among various GTOs, the following types were considered: drilling, near-wellbore zone treatments (NWZT), remedial cementing operations (RCO), and hydraulic fracturing (HF). The modeling covers a one-year period. In the model, oilfields, well clusters, and service crews are represented by agents participating in resource allocation. Oilfields and well clusters are modeled as agents of production units, while service crews are modeled as agents of support units. The region is modeled as the enterprise-level agent. In this case study on the influence of agents’ preferred communication strategies on solution stability, the primary performance indicator analyzed is the production rate of each agent.

To evaluate the stability of solutions, agents were modeled without production rate constraints, i.e., their production targets were set to zero. Tests were conducted using altruism coefficient values of 0, 0.2, 0.5, 0.8, and 1. For each altruism coefficient, a sample of 70 simulation runs was generated. Within the scope of this study, a difference is considered statistically significant if the deviation exceeds 0.05; deviations below this threshold are considered negligible.

Figure 1 presents density histograms of regional production rate distributions for fixed altruism coefficient values. The data for the given coefficients are not normally distributed. To determine whether the data samples differ significantly at fixed altruism coefficient values, coefficients of variation were calculated for each case. The results are presented in Table 2.

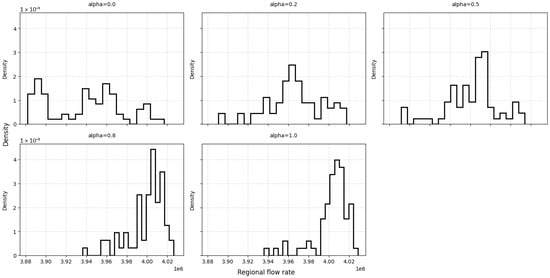
Figure 1. Density histogram of regional production rate for fixed altruism coefficient values in the case study of an oil and gas enterprise.

Table 2. Results of robustness analysis based on the case study of an oil and gas enterprise.

Altruism coefficient	0	0.2	0.5	0.8	1
Coefficient of variation	0.009445	0.006893	0.006569	0.004484	0.004300

As shown, the reported values do not differ significantly.

To determine whether there are significant differences between the regional production rate data groups formed according to different values of the altruism coefficient, the Kruskal–Wallis test was conducted. The test revealed that the values across groups with different altruism coefficients differ significantly at p-value = 0.05 (Table 3).

Table 3. Results of the Kruskal–Wallis and Dunn’s tests.

	0	0.2	0.5	0.8	1
0	1	0.008	0.0675	0	0
0.2	0.008	1	1	0	0
0.5	0.0675	1	1	0	0
0.8	0	0	0	1	1
1	0	0	0	1	1

Dunn’s test indicated statistically significant differences between the following group pairs: 0.0 and 0.2, 0.0 and 0.8, 0.0 and 1.0, 0.2 and 0.8, 0.2 and 1.0, 0.5 and 0.8, and 0.5 and 1.0. Other comparisons showed no significant differences. Statistical significance of differences between this altruism groups is assessed via Kruskal–Wallis and Dunn’s tests. Thus, at least two of the groups differ significantly, indicating that the method is sensitive to the selection of communication strategies. In summary, the system’s target performance indicator does not significantly vary within groups that share the same altruism coefficient, but it does vary significantly between groups with different coefficient values. The robustness of the solution under consideration is therefore confirmed.

Previously, based on Table 3, it was determined that some pairs of strategies do not produce significant differences in outcomes at the regional level. These include the pairs 0.0 and 0.5, 0.2 and 0.5, and 0.8 and 1. These strategies can be included in the set of communication strategies that ensure evolutionary stability. When reapplying the Kruskal–Wallis test to this subset, it was found that no significant differences exist within the group of strategies 0.8 and 1. Thus, to ensure evolutionary stability, it is advisable to retain the strategies from this group by introducing appropriate constraints on oilfield production plans. Accordingly, in the following steps, it is assumed that each agent in the system either uses a single fixed value of the altruism coefficient or selects a value from the set of 0.8 and 1. As shown in Figure 2, higher altruism coefficients are preferred at the regional level.

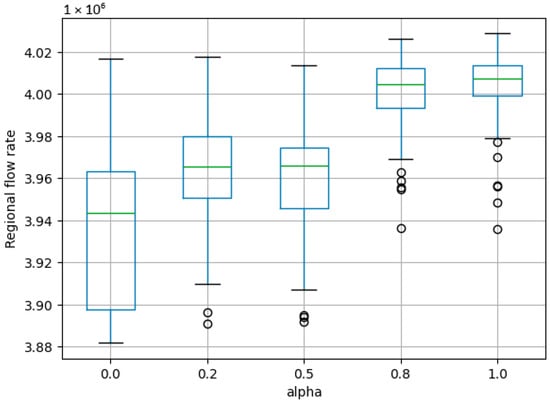
Figure 2. Regional production levels under different altruism coefficient values.

To assess the strategic stability of the solutions, the Kruskal–Wallis and Dunn’s tests were also applied to determine strategy groups with statistically insignificant differences in outcomes for individual oilfields. The Kruskal–Wallis test is a non-parametric alternative to one-way ANOVA, used for comparing three or more independent groups. The null hypothesis of the test assumes that the median values of the variable in the populations from which the samples are drawn do not differ. This test is appropriate for analyzing group data that do not follow a normal distribution [38]. If the Kruskal–Wallis test indicates statistically significant differences in median values among the groups, Dunn’s test is applied as a post hoc method to perform pairwise comparisons and identify the specific group pairs that differ significantly. For the first oilfield, the stable strategy set includes 0, 0.2, 0.5, and 0.8. For the second, third, and fourth oilfields, the set includes 0, 0.2, 0.5, 0.8, and 1. Lower altruism coefficient values are preferable for individual oilfields.

The selection of strategy sets available to agents ultimately depends on the system’s goals. In this case, the primary objective is to maximize regional production. Accordingly, the selected altruism coefficients for the oilfields are 0.8, 1, 1, and 1, respectively. Based on the results, it was decided to revise the production plans for the oilfields. Plans for oilfields 1 and 2 were set at 900,000 units; for oilfields 3 and 4, at 695,000 units. These values were determined through computational experiments. The resulting solution increased average production by approximately one percent compared to the optimization scenario without oilfield-level planning. Within the scope of the current task, this increase is considered significant. The production flow rate of the simulated oil-producing region, with a uniform distribution of crews and with GTO operations performed on wells and well pads in descending order of their initial flow rate, amounts to approximately 3,870,000 tons. The random effect, which determines the success of a GTO operation, alters the region’s flow rate by approximately 10,000 tons. It constitutes about a quarter of one percent. With an optimal schedule and crew allocation, the region’s flow rate reaches approximately 4,080,000 tons, which is 5.5% higher than the initial flow rate value. A change in the region’s flow rate of more than a quarter of a percent is considered significant, as it is not a consequence of random effects. Given the production volumes and the value of the product, any increase in the flow rate is considered meaningful. Moreover, the result remains consistent across multiple simulation runs. This example demonstrates the potential of the proposed approach to defining constraints on the target indicators of agents in a multi-agent production system, taking into account the agents’ preferred communication strategies.

4. Discussion and Conclusions

Based on the presented analysis of the concept of solution stability in the context of multi-agent systems, as well as the review of approaches to modeling moral agents, this study proposes a dedicated workflow. This workflow enables the identification of constraints on agents’ target indicators in such a way that the resulting solution is evolutionarily, strategically, and robustly stable, while remaining efficient. The proposed approach is distinguished from existing methods by its consideration of the full set of factors influencing the performance of an enterprise as a complex organizational system. The results of testing using a case study of an oil and gas enterprise illustrate one possible application of the proposed workflow. This solution contributes to the advancement of methodological and instrumental foundations for the development of decision support systems for managing enterprise technological processes based on a multi-agent approach.

Future research in this direction may build upon these results by introducing adaptable communication strategies for agents, developing practical methods for determining altruism coefficients, and refining the representation of agent goals as a function of their communication strategies. In the future, the proposed approach will be improved through extended statistical analysis. This includes confidence interval estimation and the use of larger Monte Carlo samples. The method will also be tested on a finer grid of altruism coefficient values and on additional datasets describing the oil production region model. These tests will be valuable when conducting simulations with real initial data. The multi-agent system of the oil production region was tested on various datasets, the most indicative of which are three. The dataset presented in the study is one of the most illustrative among those considered. The second dataset includes 248 wells across 4 fields, in which case the region’s production flow rate increased by 1.8%. The third dataset includes 550 wells across 5 fields in the region, and the production flow rate increased by 2.09%. The region presented in the study includes fewer fields compared to the simulated region. When testing on real data, a greater optimization effect is expected. Applying the presented approach to this data will demonstrate the robustness of the obtained solutions when changing the scale of the simulated system. The model used also enables the calculation of time costs associated with conducting GTOs. The presented method will also be applied to the case of multiple objective functions after enhancing the system with solutions for calculating economic indicators.

The modeling approach for altruistic agents can also be further developed. Currently, an agent’s degree of selfishness is determined by an altruism coefficient, the value of which ranges from 0 to 1 and is a real number. The degree of an agent’s altruism can not only be defined by this coefficient influencing the value of its objective function but can also determine its mechanism of action. For instance, the behavior of a selfish agent could fundamentally differ from the currently used cooperative approach and be defined using methods from game theory. Furthermore, the defined range of the coefficient’s value can be adjusted according to the requirements of the subject area. An alternative approach to perceiving moral agents can be considered. Within the presented research, an agent’s altruism is viewed as its willingness to assist other system participants at its own expense. Scientific discourse also presents an approach where the degree of an agent’s tolerance to short-term exploitation is defined. These two approaches are akin and equally worthy of consideration. From solutions implementing this alternative perception of moral agents [39], it would be valuable to adopt the experience of dynamically adjusting the agent’s degree of altruism. The development of the approach for constructing moral agents will be advanced as research continues, following recommendations from experts in the field of organizational management systems.

The proposed solution serves to deepen the theoretical and practical basis for designing decision support systems that utilize multi-agent approaches in industrial process management.