Enhancing Sustainable Supply Chain Performance Prediction Using an Augmented Algorithm-Optimized XGBOOST in Industry 4.0 Contexts
Abstract
1. Introduction
- To develop an augmented algorithm–optimized XGBOOST model that integrates the SSALEO for accurate and robust prediction of supply chain performance.
- To evaluate the predictive accuracy, convergence stability, and generalization capability of the proposed SSALEO-XGBOOST model in comparison with conventional machine-learning and metaheuristic–ML hybrid algorithms.
- To provide actionable insights for the integration of industry technologies, enabling data-driven decision-making that supports efficient and resilient supply chain management.
2. Related Works
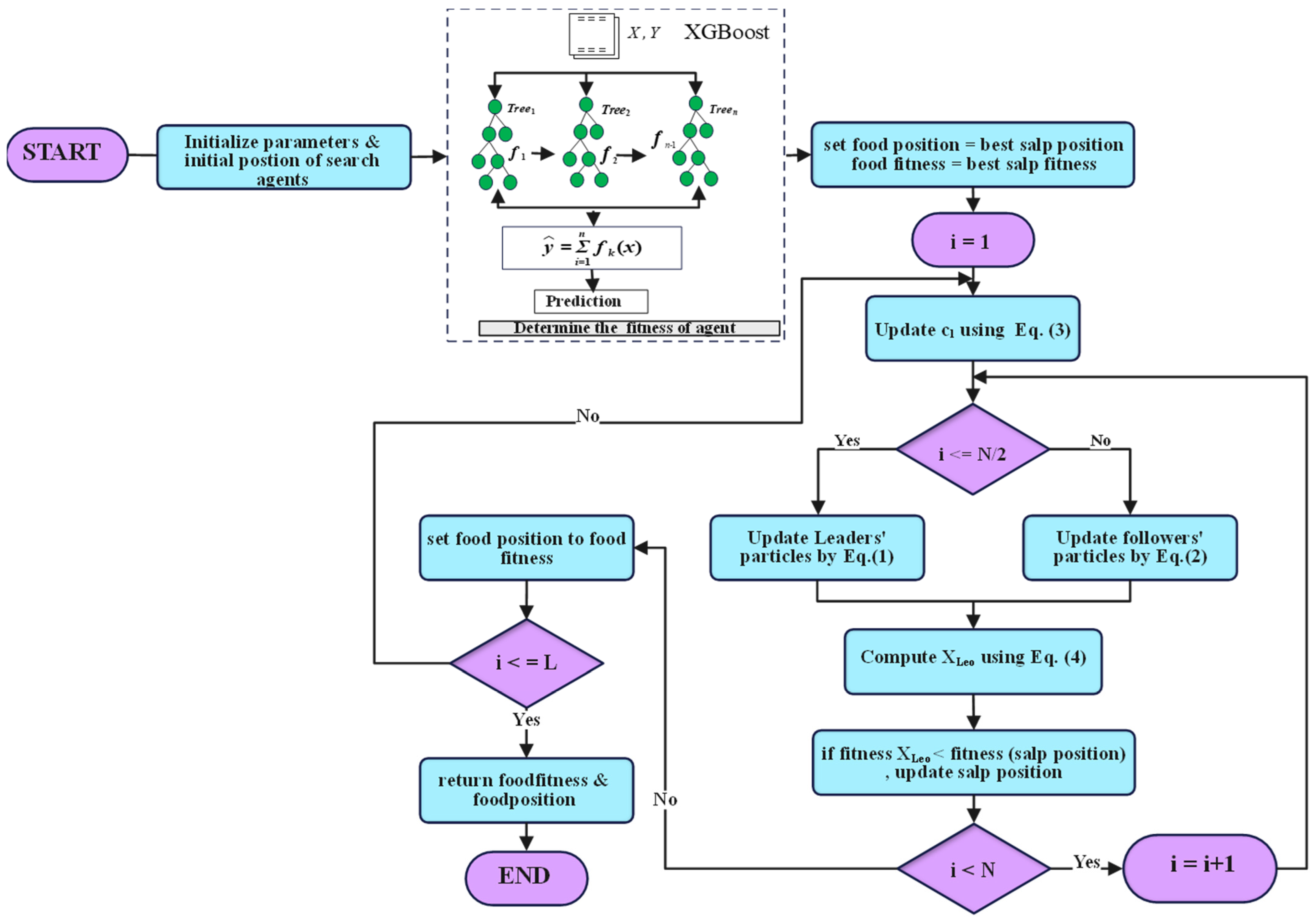
3. Methodology
3.1. Salp Swarm Algorithm (SSA)
3.2. Local Escaping Operator (LEO)
3.3. eXtreme Gradient Boosting (XGBOOST)
3.4. SSALEO-XGBOOST
| Algorithm 1: SSALEO for XGBOOST Hyperparameter Optimization |
| Input: Hyperparameter bounds, , dataset Output: Optimal XGBOOST model 1: Initialize salp population 2: Evaluate fitness using MSE on training data 3. Set best solution 4: for to do 5: Update using Equation (3) 6: for each salp do 7: if then 8: Update leader using Equation (1) 9: else 10: Update follower using Equation (2) 11: end if 12: if then 13: Apply LEO update (Equations (4)–(13)) to 14: end if 15: Clip positions within bounds 16: -evaluate 17: Update if better solution found 18: end for 19: end for 20: Return XGBOOST model with parameters from 21: Evaluate the final model with test data |
3.5. Computational Complexity
4. Experiment and Discussion
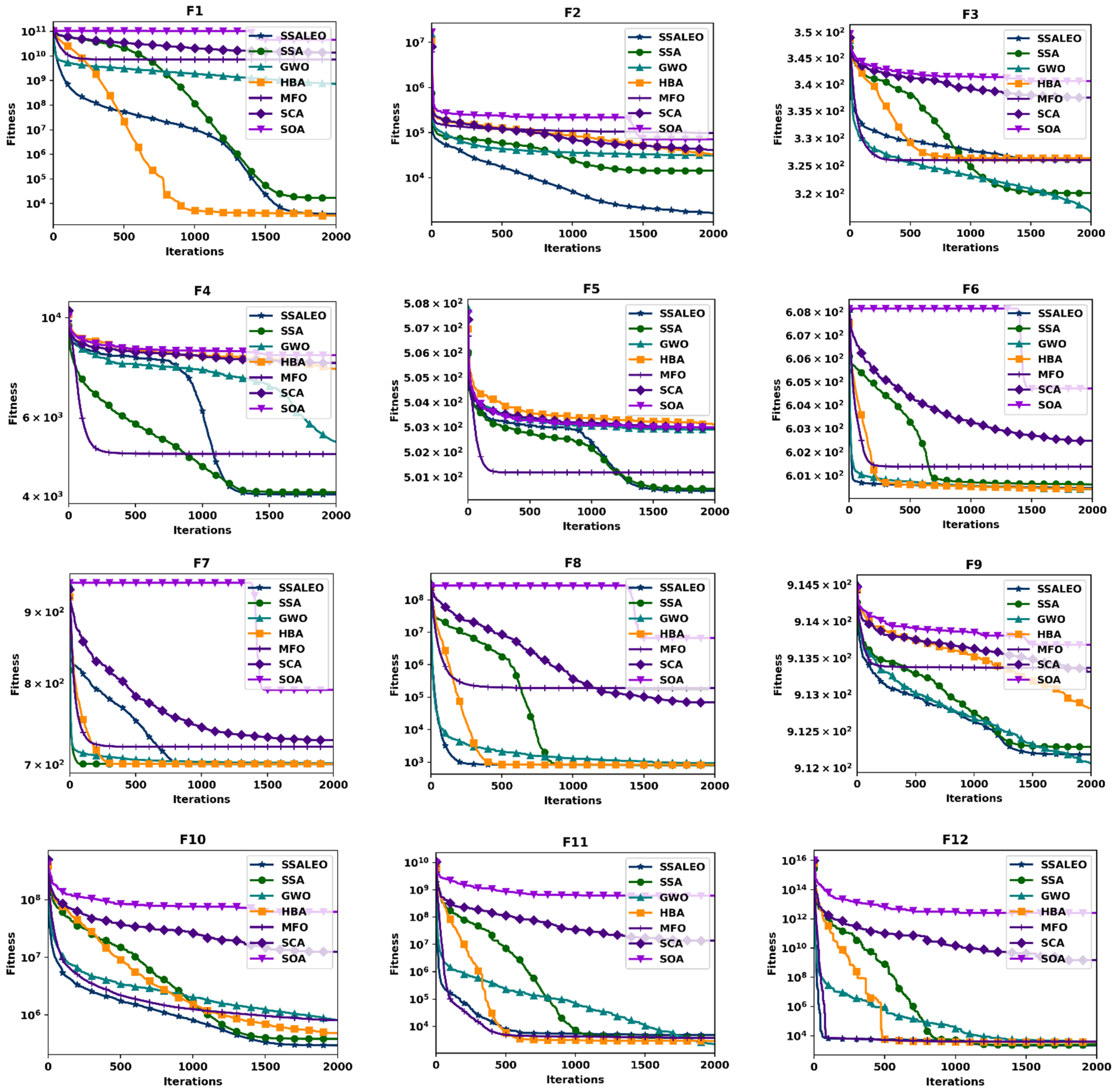
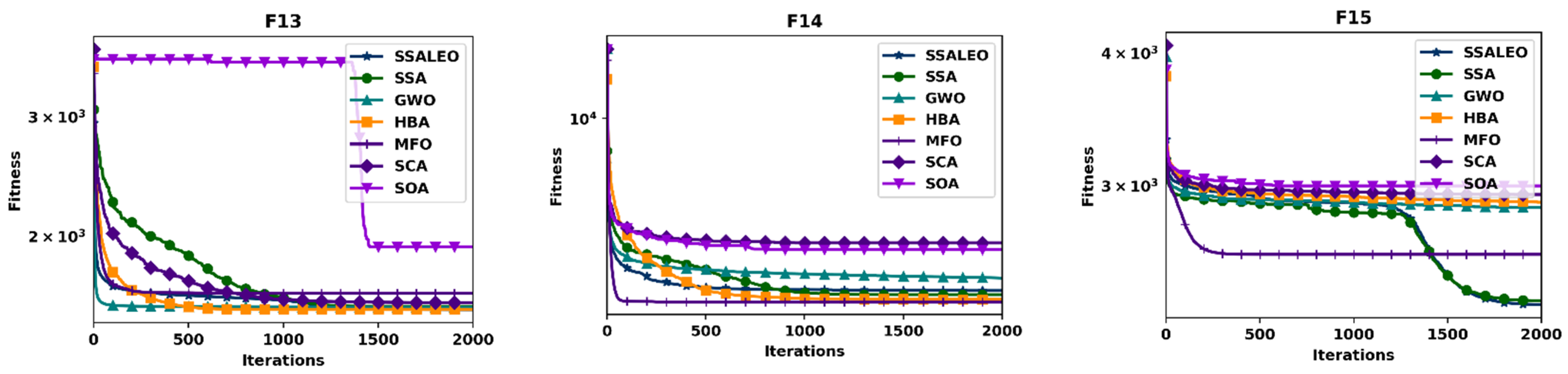
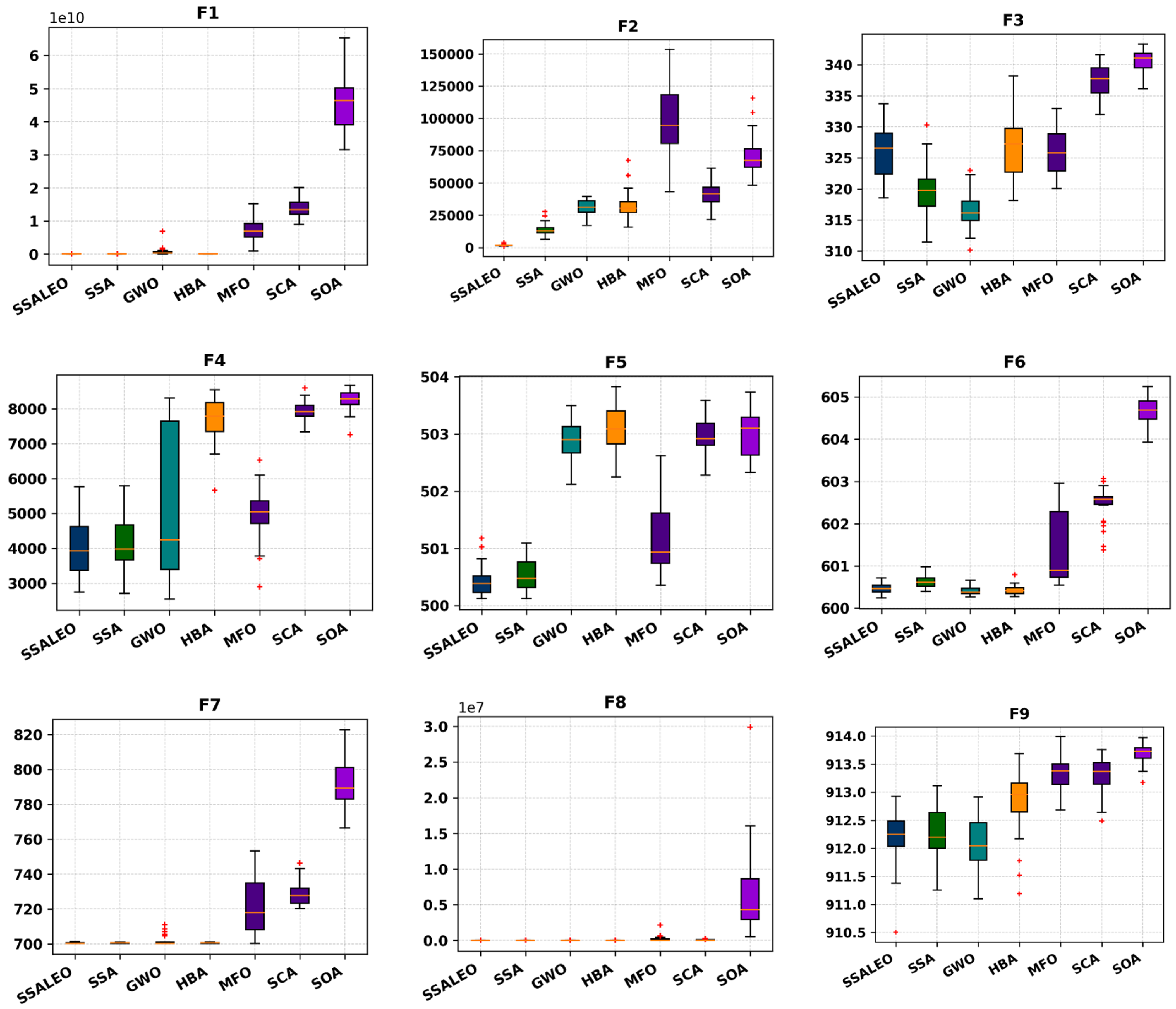
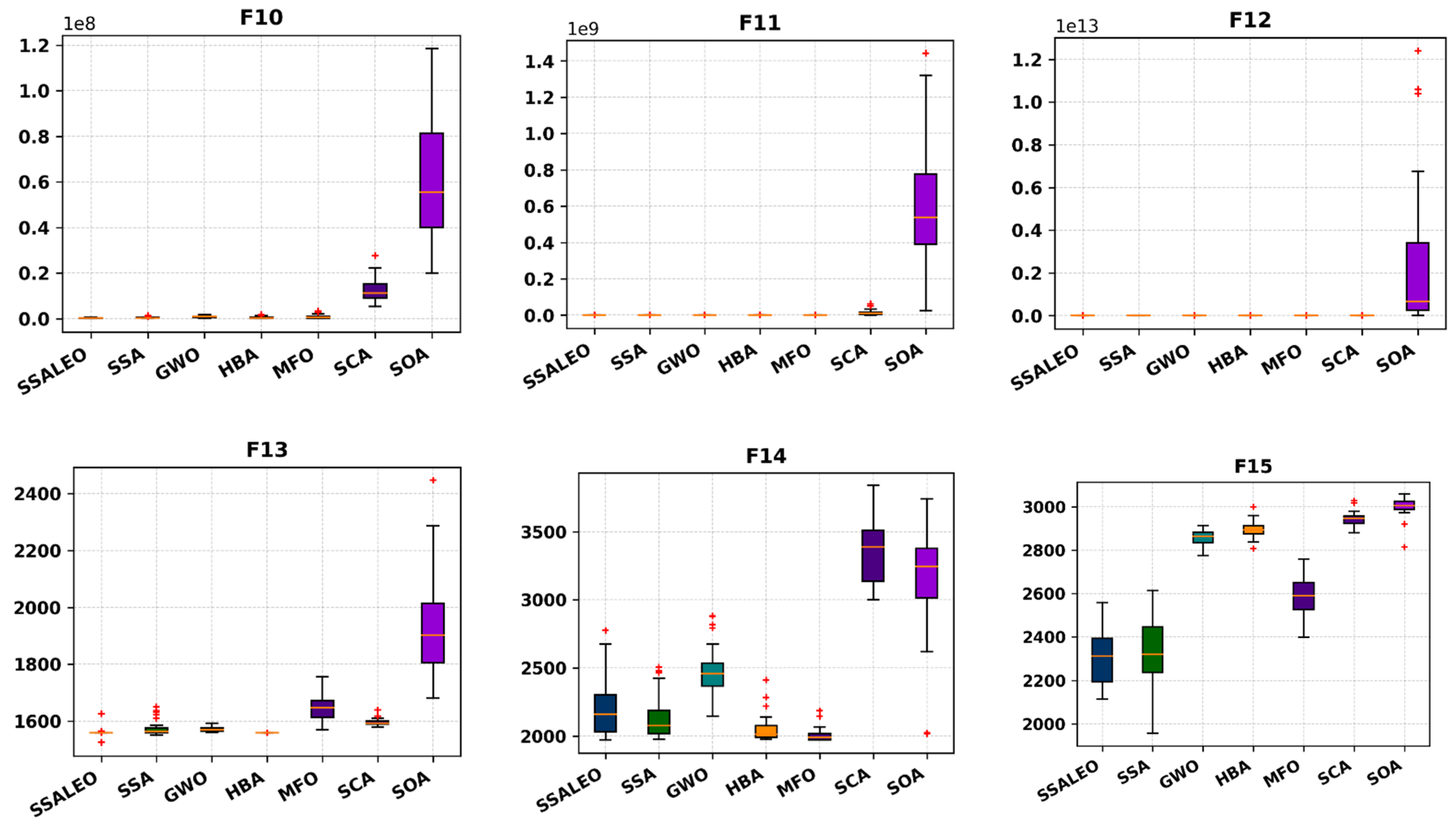
4.1. Benchmark Validation
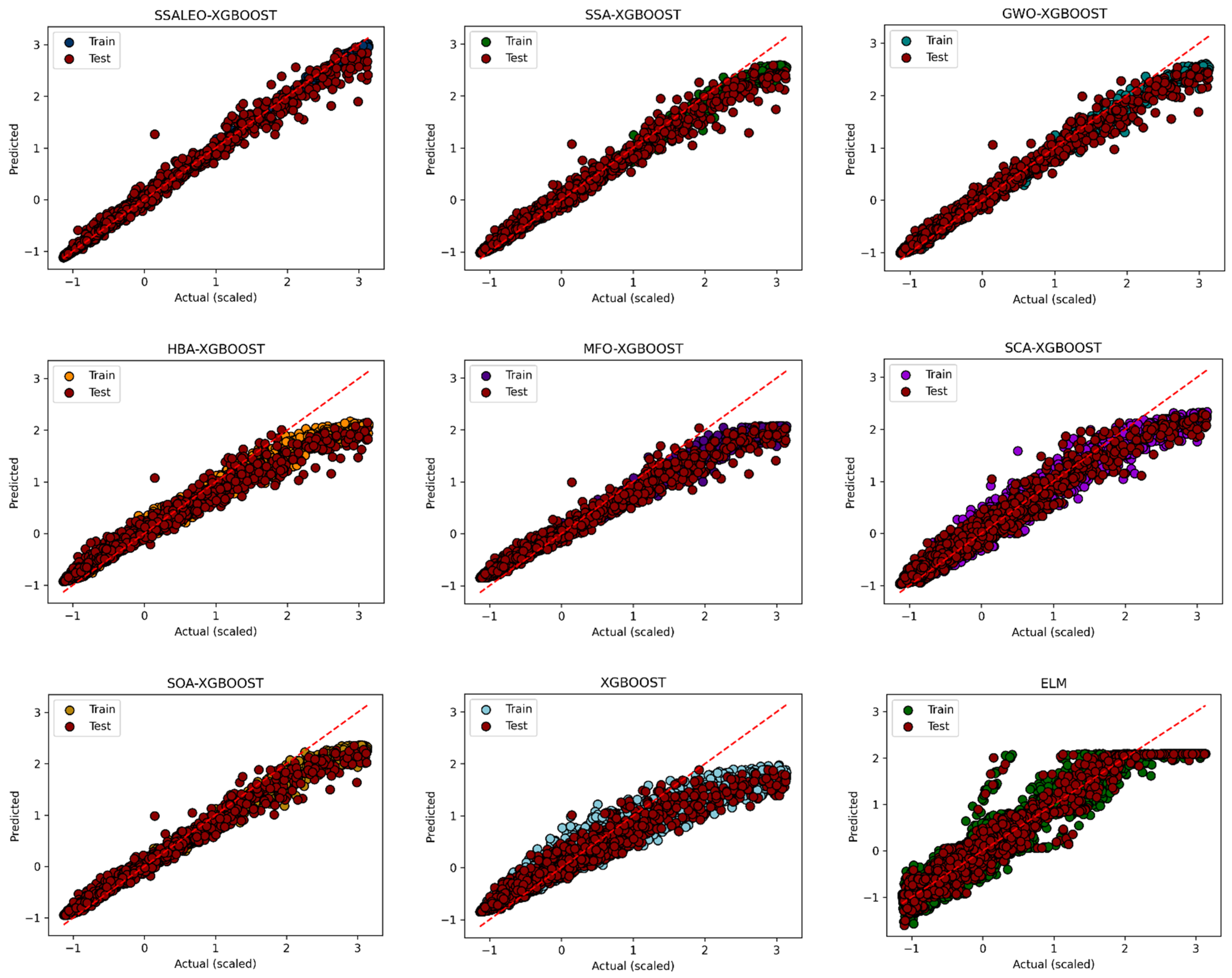
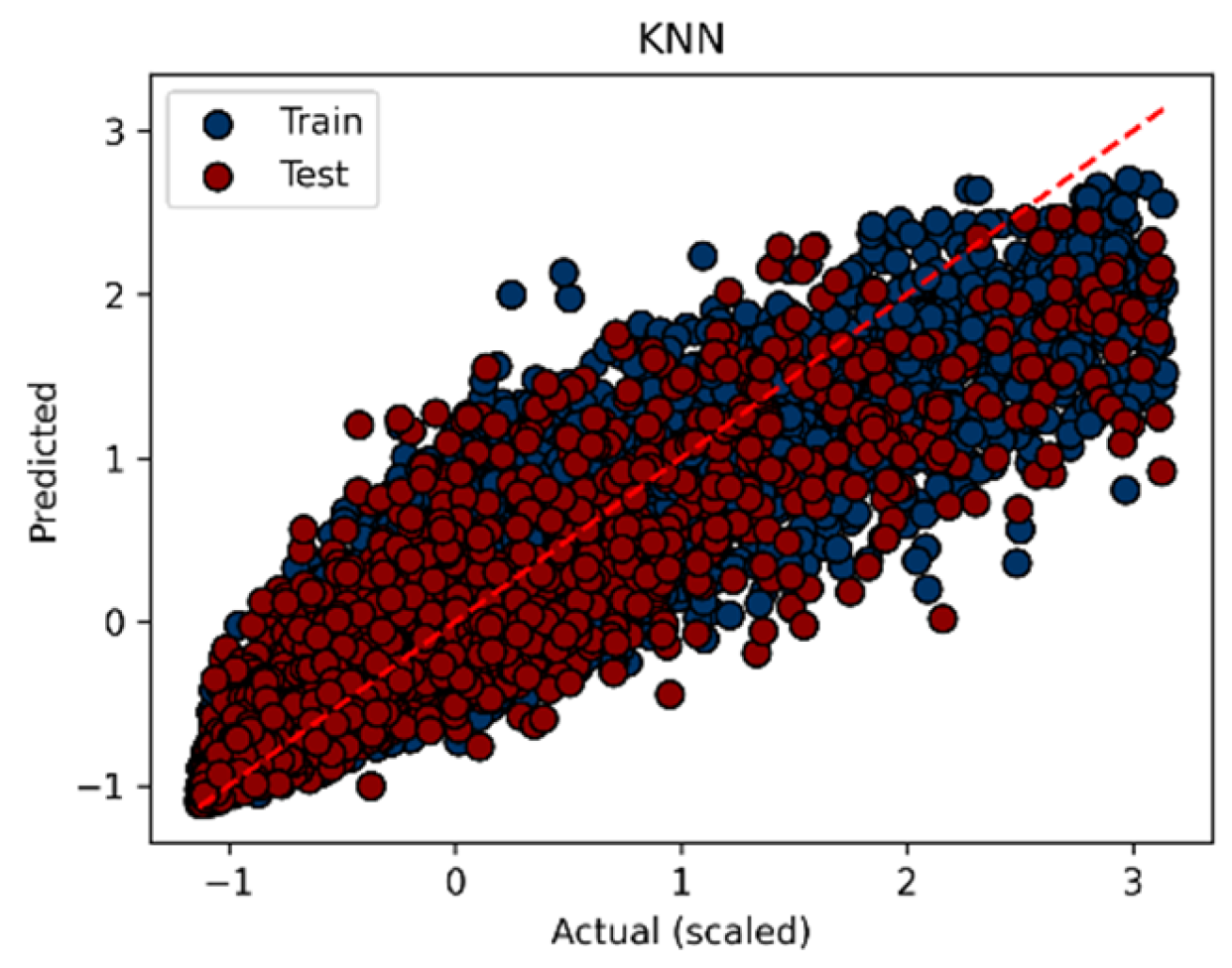
4.2. Supply Chain Prediction
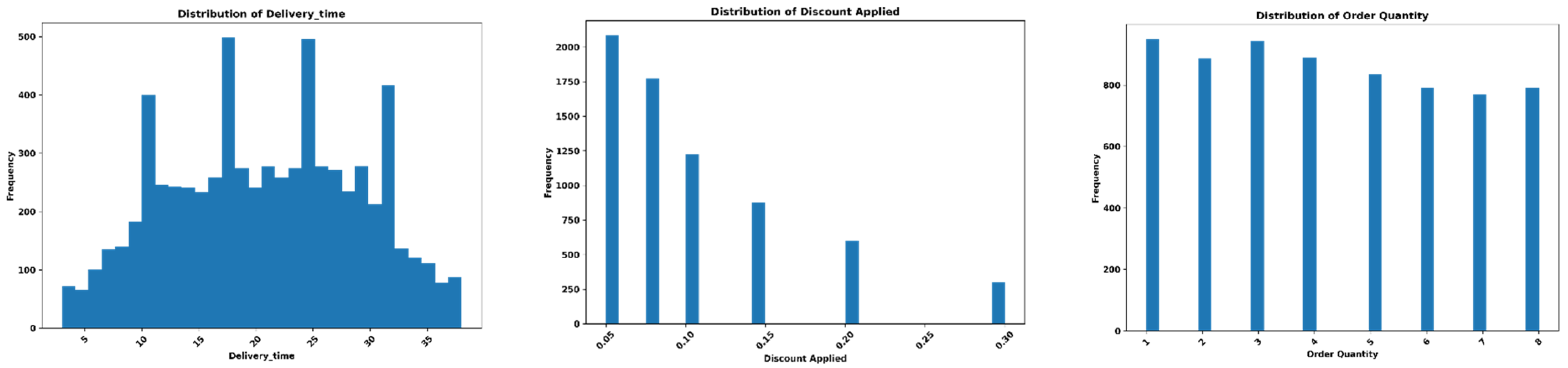
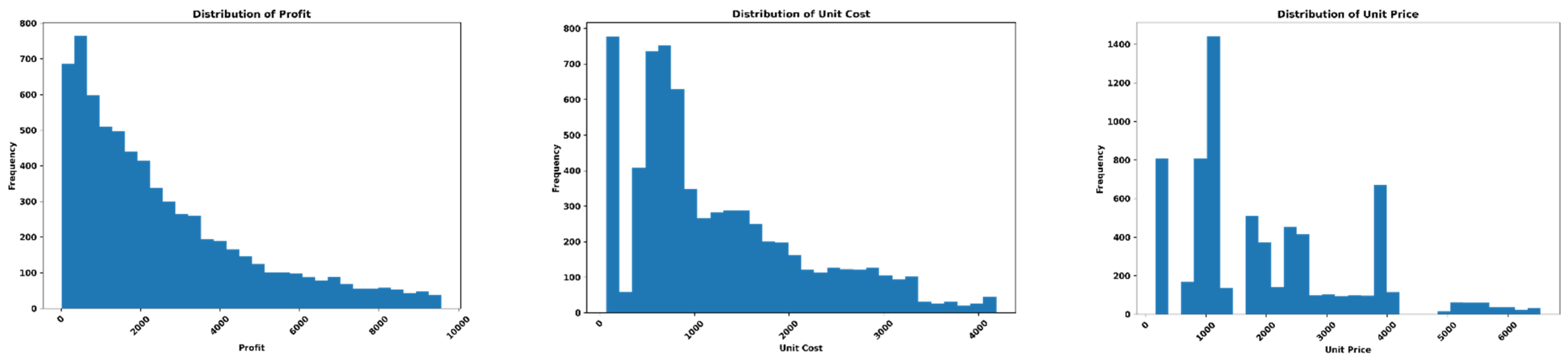
4.2.1. Data
4.2.2. Evaluation Metrics
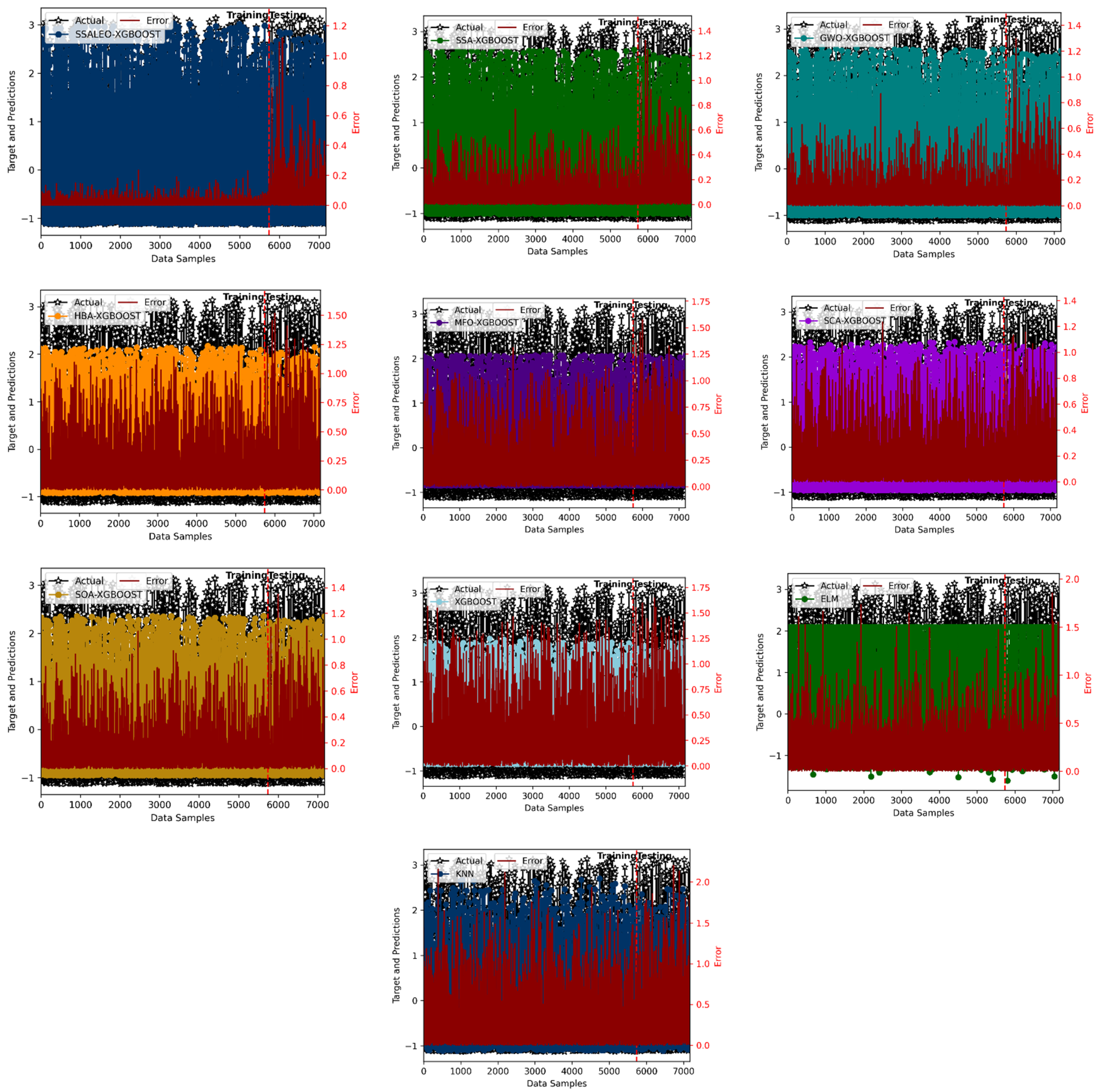
4.2.3. Cross-Validation Experiment
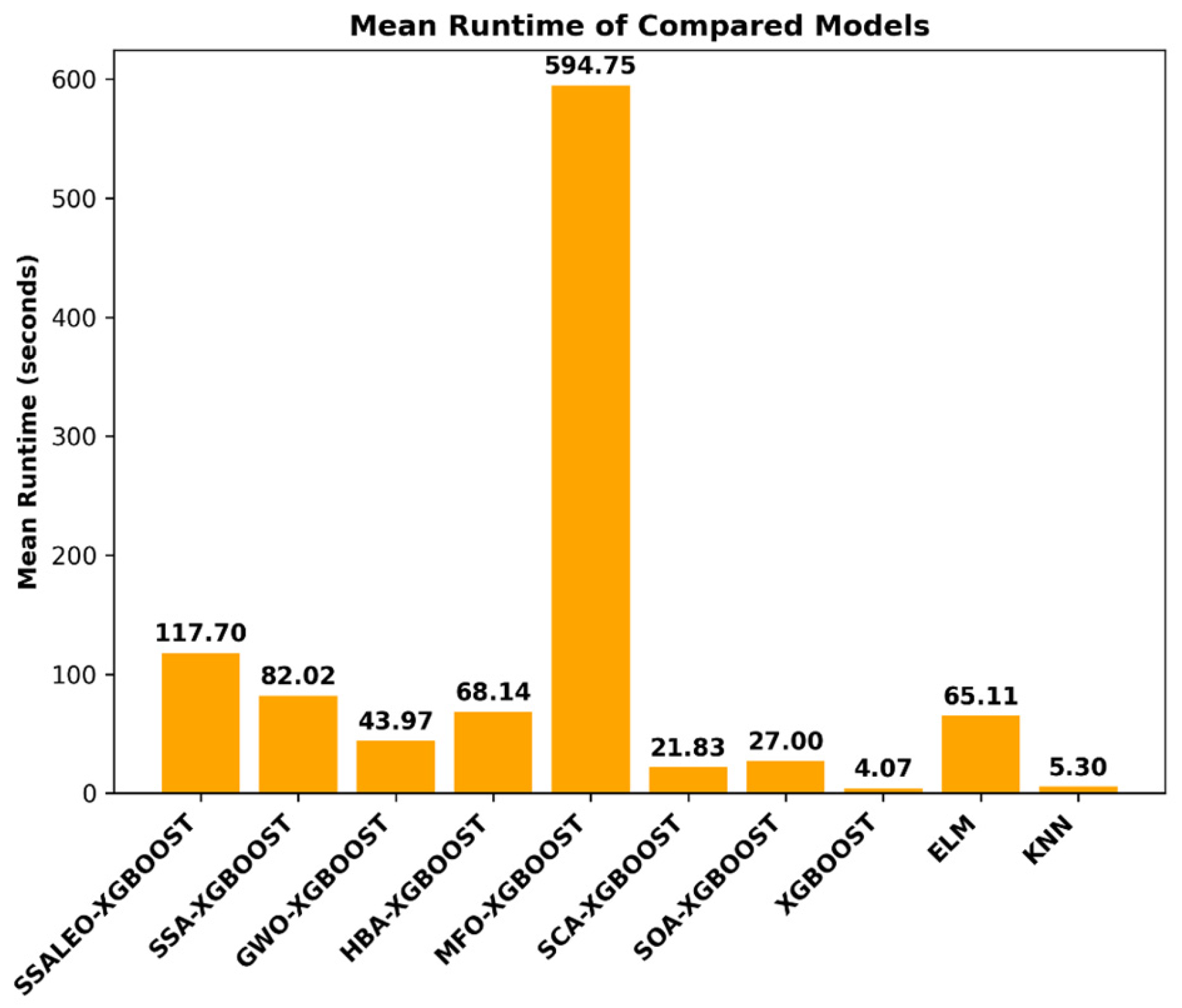
4.2.4. Performance Evaluation over 20 Independent Runs
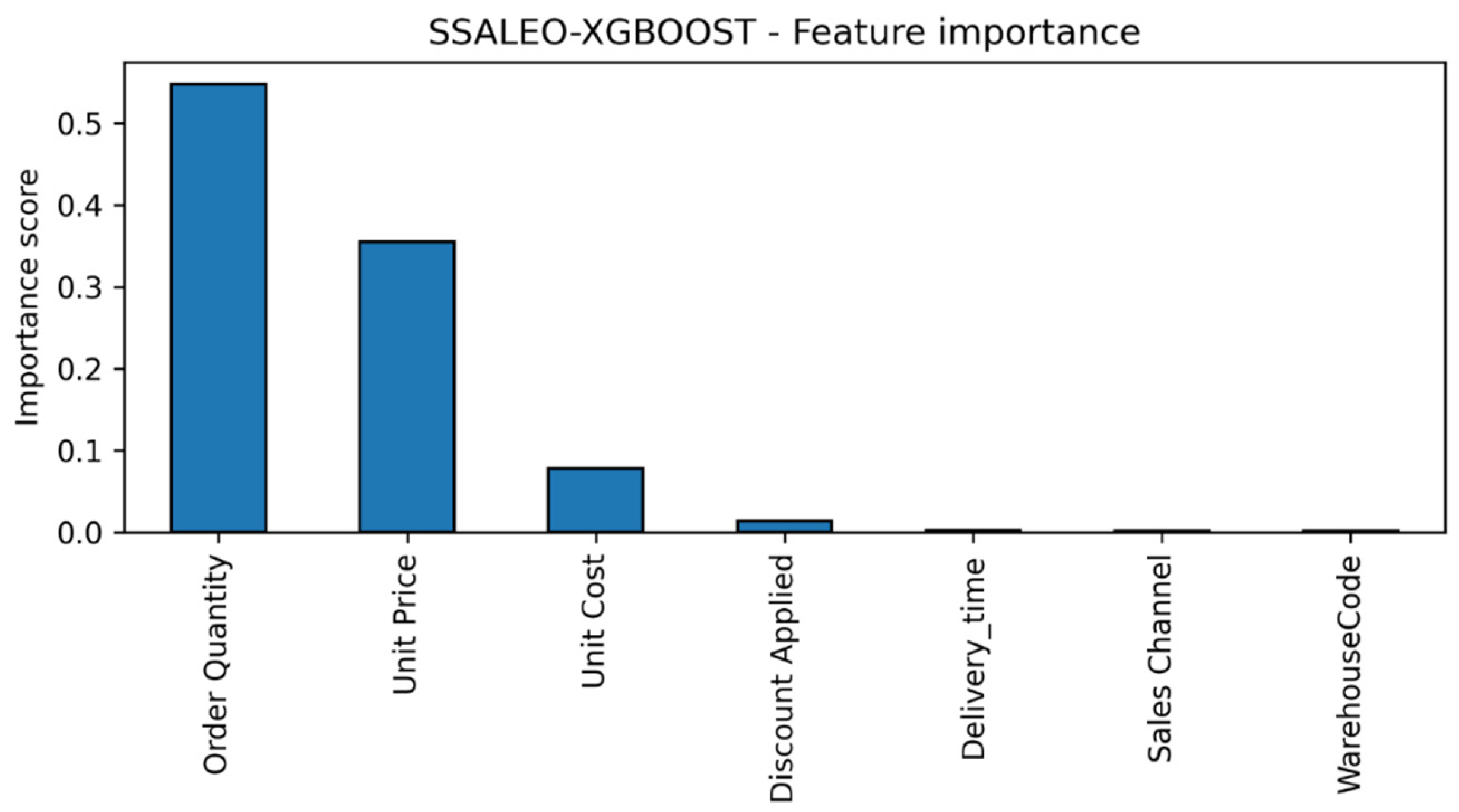
4.2.5. Feature Importance Analysis
4.2.6. Operational Implications of Model Performance
- Optimize Order Quantities: Given the dominant influence of Order Quantity, organizations should prioritize demand forecasting and aggregation strategies to determine optimal order sizes. This involves aligning procurement schedules with demand patterns and negotiating bulk purchase agreements with suppliers to secure volume-based discounts, thereby reducing per-unit costs and enhancing profit margins.
- Refine Pricing Strategies: The significant role of Unit Price underscores the importance of dynamic pricing models that balance competitiveness with profitability. Managers should conduct market analyses to set prices that reflect customer willingness to pay while ensuring sufficient margins to cover costs. Price elasticity studies can further inform adjustments to maximize revenue.
- Enhance Cost Control Measures: While Unit Cost has a moderate impact, it remains a critical lever for profitability. Supply chain teams should explore cost-reduction initiatives, such as process optimization, supplier diversification, or adoption of lean inventory practices, to minimize production and procurement expenses without compromising quality.
- Integrate Model Outputs into Decision-Making: The SSALEO-XGBOOST model should be embedded within decision support systems to provide real-time profit predictions. For instance, managers can simulate the profit impact of adjusting order quantities or pricing strategies under varying market conditions, enabling data-driven decision-making.
4.2.7. Managerial Implications, Limitations, and Future Research Directions
Managerial Implications
Limitations of the Study
Future Research Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, S.; Ragu-Nathan, B.; Ragu-Nathan, T.S.; Subba Rao, S. The impact of supply chain management practices on competitive advantage and organizational performance. Omega 2006, 34, 107–124. [Google Scholar] [CrossRef]
- Ning, L.; Yao, D. The Impact of Digital Transformation on Supply Chain Capabilities and Supply Chain Competitive Performance. Sustainability 2023, 15, 10107. [Google Scholar] [CrossRef]
- Meng, Q.; Zu, G.; Ge, L.; Li, S.; Xu, L.; Wang, R.; He, K.; Jin, S. Dispatching Strategy for Low-Carbon Flexible Operation of Park-Level Integrated Energy System. Appl. Sci. 2022, 12, 12309. [Google Scholar] [CrossRef]
- Maheshwari, S.; Gautam, P.; Jaggi, C.K. Role of Big Data Analytics in supply chain management: Current trends and future perspectives. Int. J. Prod. Res. 2021, 59, 1875–1900. [Google Scholar] [CrossRef]
- Jiang, S.; Yuan, X. Does green credit promote real economic development? Dual empirical evidence of scale and efficiency. PLoS ONE 2025, 20, e0326961. [Google Scholar] [CrossRef] [PubMed]
- Helo, P.; Hao, Y. Artificial intelligence in operations management and supply chain management: An exploratory case study. Prod. Plan. Control 2022, 33, 1573–1590. [Google Scholar] [CrossRef]
- Wen, Y.-H. Shipment forecasting for supply chain collaborative transportation management using grey models with grey numbers. Transp. Plan. Technol. 2011, 34, 605–624. [Google Scholar] [CrossRef]
- Tseng, F.-M.; Yu, H.-C.; Tzeng, G.-H. Applied Hybrid Grey Model to Forecast Seasonal Time Series. Technol. Forecast. Soc. Change 2001, 67, 291–302. [Google Scholar] [CrossRef]
- Quartey-Papafio, T.K.; Javed, S.A.; Liu, S. Forecasting cocoa production of six major producers through ARIMA and grey models. Grey Syst. Theory Appl. 2020, 11, 434–462. [Google Scholar] [CrossRef]
- Jia, X.; Wang, J.; Ma, T.T.; Wang, Q. Grey improvement model for intelligent supply chain demand forecasting. Int. J. Manuf. Technol. Manag. 2025, 39, 334–357. [Google Scholar] [CrossRef]
- Xia, M.; Wong, W.K. A seasonal discrete grey forecasting model for fashion retailing. Knowl.-Based Syst. 2014, 57, 119–126. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Sadeghi, S.; Mooseloo, F.M.; Vandchali, H.R.; Aeini, S. Application of Machine Learning in Supply Chain Management: A Comprehensive Overview of the Main Areas. Math. Probl. Eng. 2021, 2021, 1476043. [Google Scholar] [CrossRef]
- Shen, X.; Li, L.; Ma, Y.; Xu, S.; Liu, J.; Yang, Z.; Shi, Y. VLCIM: A Vision-Language Cyclic Interaction Model for Industrial Defect Detection. IEEE Trans. Instrum. Meas. 2025, 74, 1–13. [Google Scholar] [CrossRef]
- Chen, S.; Long, X.; Fan, J.; Jin, G. A causal inference-based root cause analysis framework using multi-modal data in large-complex system. Reliab. Eng. Syst. Saf. 2026, 265, 111520. [Google Scholar] [CrossRef]
- Qiao, Y.; Lü, J.; Wang, T.; Liu, K.; Zhang, B.; Snoussi, H. A Multihead Attention Self-Supervised Representation Model for Industrial Sensors Anomaly Detection. IEEE Trans. Ind. Inform. 2024, 20, 2190–2199. [Google Scholar] [CrossRef]
- Zhang, B.; Cai, X.; Li, G.; Li, X.; Peng, M.; Yang, M. A modified A* algorithm for path planning in the radioactive environment of nuclear facilities. Ann. Nucl. Energy 2025, 214, 111233. [Google Scholar] [CrossRef]
- Harle, S.M.; Wankhade, R.L. Machine learning techniques for predictive modelling in geotechnical engineering: A succinct review. Discov. Civ. Eng. 2025, 2, 86. [Google Scholar] [CrossRef]
- Rezaei, A.; Abdellatif, I.; Umar, A. Towards Economic Sustainability: A Comprehensive Review of Artificial Intelligence and Machine Learning Techniques in Improving the Accuracy of Stock Market Movements. Int. J. Financ. Stud. 2025, 13, 28. [Google Scholar] [CrossRef]
- Mao, F.; Chen, M.; Zhong, K.; Zeng, J.; Liang, Z. An XGBoost-assisted evolutionary algorithm for expensive multiobjective optimization problems. Inf. Sci. 2024, 666, 120449. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Amjad, M.; Ahmad, I.; Ahmad, M.; Wróblewski, P.; Kamiński, P.; Amjad, U. Prediction of Pile Bearing Capacity Using XGBoost Algorithm: Modeling and Performance Evaluation. Appl. Sci. 2022, 12, 2126. [Google Scholar] [CrossRef]
- Pan, S.; Zheng, Z.; Guo, Z.; Luo, H. An optimized XGBoost method for predicting reservoir porosity using petrophysical logs. J. Pet. Sci. Eng. 2022, 208, 109520. [Google Scholar] [CrossRef]
- Mohammed, S.I.; Hussein, N.K.; Haddani, O.; Aljohani, M.; Alkahya, M.A.; Qaraad, M. Fine-Tuned Cardiovascular Risk Assessment: Locally Weighted Salp Swarm Algorithm in Global Optimization. Mathematics 2024, 12, 243. [Google Scholar] [CrossRef]
- Algwil, A.R.A.; Khalifa, W.M.S. An enhanced moth flame optimization extreme learning machines hybrid model for predicting CO2 emissions. Sci. Rep. 2025, 15, 11948. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Feda, A.K.; Tejani, G.G.; Smerat, A.; Kumar, P.; Agyekum, E.B. Salp Navigation and Competitive based Parrot Optimizer (SNCPO) for efficient extreme learning machine training and global numerical optimization. Sci. Rep. 2025, 15, 13704. [Google Scholar] [CrossRef]
- Li, G.; Cui, Y.; Su, J. A multi-strategy improved snake optimizer for three-dimensional UAV path planning and engineering problems. arXiv 2025, arXiv:2507.14043. [Google Scholar] [CrossRef]
- Elkington, J. Accounting for the Triple Bottom Line. Meas. Bus. Excell. 1998, 2, 18–22. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Mirjalili, S.; Halima, N.B.; Elhosseini, M.A. Comparing SSALEO as a Scalable Large Scale Global Optimization Algorithm to High-Performance Algorithms for Real-World Constrained Optimization Benchmark. IEEE Access 2022, 10, 95658–95700. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, L.; Chen, H.; Zhang, S.; Wang, S.; Peng, H.; Zou, J. An Indoor Fingerprint Positioning Algorithm Based on WKNN and Improved XGBoost. Sensors 2023, 23, 3952. [Google Scholar] [CrossRef] [PubMed]
- Nabavi, Z.; Mirzehi, M.; Dehghani, H.; Ashtari, P. A Hybrid Model for Back-Break Prediction using XGBoost Machine learning and Metaheuristic Algorithms in Chadormalu Iron Mine. J. Min. Environ. 2023, 14, 689–712. [Google Scholar] [CrossRef]
- Mohiuddin, G.; Lin, Z.; Zheng, J.; Wu, J.; Li, W.; Fang, Y.; Wang, S.; Chen, J.; Zeng, X. Intrusion Detection using hybridized Meta-heuristic techniques with Weighted XGBoost Classifier. Expert Syst. Appl. 2023, 232, 120596. [Google Scholar] [CrossRef]
- Kazemi, M.M.K.; Nabavi, Z.; Armaghani, D.J. A novel Hybrid XGBoost Methodology in Predicting Penetration Rate of Rotary Based on Rock-Mass and Material Properties. Arab. J. Sci. Eng. 2024, 49, 5225–5241. [Google Scholar] [CrossRef]
- Mosa, M.A. Optimizing text classification accuracy: A hybrid strategy incorporating enhanced NSGA-II and XGBoost techniques for feature selection. Prog. Artif. Intell. 2025, 14, 275–299. [Google Scholar] [CrossRef]
- Xi, B.; Huang, Z.; Al-Obaidi, S.; Ferrara, L. Predicting ultra high-performance concrete self-healing performance using hybrid models based on metaheuristic optimization techniques. Constr. Build. Mater. 2023, 381, 131261. [Google Scholar] [CrossRef]
- Krishna, A.Y.; Kiran, K.R.; Sai, N.R.; Sharma, A.; Praveen, S.P.; Pandey, J. Ant Colony Optimized XGBoost for Early Diabetes Detection: A Hybrid Approach in Machine Learning. J. Intell. Syst. Internet Things 2023, 10. Available online: https://openurl.ebsco.com/contentitem/doi:10.54216%2FJISIoT.100207?sid=ebsco:plink:crawler&id=ebsco:doi:10.54216%2FJISIoT.100207 (accessed on 11 May 2025). [CrossRef]
- Ozcan, T.; Ozmen, E.P. Prediction of Heart Disease Using a Hybrid XGBoost-GA Algorithm with Principal Component Analysis: A Real Case Study. Int. J. Artif. Intell. Tools 2023, 32, 2340009. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Short-Term Rockburst Damage Assessment in Burst-Prone Mines: An Explainable XGBOOST Hybrid Model with SCSO Algorithm. Rock Mech. Rock Eng. 2023, 56, 8745–8770. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, R.; Lu, Y.; Huang, J. Prediction of Compressive Strength of Geopolymer Concrete Landscape Design: Application of the Novel Hybrid RF–GWO–XGBoost Algorithm. Buildings 2024, 14, 591. [Google Scholar] [CrossRef]
- Iqbal, M.; Fan, Y.; Ahmad, N.; Ullah, I. Circular economy solutions for net-zero carbon in China’s construction sector: A strategic evaluation. J. Clean. Prod. 2025, 504, 145398. [Google Scholar] [CrossRef]
- Iqbal, M.; Ma, J.; Ahmad, N.; Ullah, Z.; Hassan, A. Energy-Efficient supply chains in construction industry: An analysis of critical success factors using ISM-MICMAC approach. Int. J. Green Energy 2023, 20, 265–283. [Google Scholar] [CrossRef]
- Iqbal, M.; Waqas, M.; Ahmad, N.; Hussain, K.; Hussain, J. Green supply chain management as a pathway to sustainable operations in the post-COVID-19 era: Investigating challenges in the Chinese scenario. Bus. Process Manag. J. 2024, 30, 1065–1087. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, in KDD ’16, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N.; Chen, Q. Problem Definitions and Evaluation Criteria for the CEC 2015 Competition on Learning-Based Real-Parameter Single Objective Optimization; Technical Report 201411A; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2014; Volume 29. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- SupplyChainAnalysis [US-Regional-Sales]. Available online: https://www.kaggle.com/code/omarmelzeki/supplychainanalysis-us-regional-sales (accessed on 12 May 2025).
- Khajavi, H.; Rastgoo, A.; Masoumi, F. Enhanced Streamflow Forecasting for Crisis Management Based on Hybrid Extreme Gradient Boosting Model. Iran. J. Sci. Technol. Trans. Civ. Eng. 2025, 49, 5233–5254. [Google Scholar] [CrossRef]
- Bag, S.; Yadav, G.; Dhamija, P.; Kataria, K.K. Key resources for industry 4.0 adoption and its effect on sustainable production and circular economy: An empirical study. J. Clean. Prod. 2021, 281, 125233. [Google Scholar] [CrossRef]


| Optimization Algorithm | Parameter Settings |
|---|---|
| SSALEO | |
| SSA | |
| GWO | |
| HBA | , C = 2 |
| MFO | b = 1, a = [−2, −1] |
| SCA | |
| SOA |
| Function | Metrics | SSALEO | SSA | GWO | HBA | MFO | SCA | SOA |
|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 3.815 × 103 | 1.701 × 104 | 7.346 × 108 | 3.241 × 103 | 7.130 × 109 | 1.391 × 1010 | 4.623 × 1010 |
| STD | 8.432 × 103 | 4.836 × 104 | 1.228 × 109 | 2.715 × 103 | 3.737 × 109 | 2.890 × 109 | 8.314 × 109 | |
| F2 | AVG | 1.644 × 103 | 1.418 × 104 | 3.115 × 104 | 3.287 × 104 | 9.687 × 104 | 4.155 × 104 | 7.141 × 104 |
| STD | 6.723 × 102 | 4.790 × 103 | 5.895 × 103 | 1.040 × 104 | 2.806 × 104 | 7.952 × 103 | 1.458 × 104 | |
| F3 | AVG | 3.260 × 102 | 3.201 × 102 | 3.166 × 102 | 3.264 × 102 | 3.260 × 102 | 3.375 × 102 | 3.406 × 102 |
| STD | 4.260 | 4.335 | 3.049 | 4.543 | 3.724 | 2.567 | 1.806 | |
| F4 | AVG | 4.035 × 103 | 4.085 × 103 | 5.288 × 103 | 7.685 × 103 | 4.969 × 103 | 7.930 × 103 | 8.249 × 103 |
| STD | 7.792 × 102 | 7.287 × 102 | 2.197 × 103 | 6.529 × 102 | 7.551 × 102 | 3 × 102 | 3.040 × 102 | |
| F5 | AVG | 5.004 × 102 | 5.005 × 102 | 5.029 × 102 | 5.031 × 102 | 5.012 × 102 | 5.030 × 102 | 5.030 × 102 |
| STD | 2.724 × 10−1 | 2.772 × 10−1 | 3.330 × 10−1 | 3.858 × 10−1 | 6.420 × 10−1 | 2.780 × 10−1 | 3.955 × 10−1 | |
| F6 | AVG | 6.005 × 102 | 6.006 × 102 | 6.004 × 102 | 6.004 × 102 | 6.014 × 102 | 6.025 × 102 | 6.047 × 102 |
| STD | 1.229 × 10−1 | 1.418 × 10−1 | 9.749 × 10−2 | 1.125 × 10−1 | 8.645 × 10−1 | 4.099 × 10−1 | 3.331 × 10−1 | |
| F7 | AVG | 7.005 × 102 | 7.006 × 102 | 7.016 × 102 | 7.006 × 102 | 7.208 × 102 | 7.288 × 102 | 7.917 × 102 |
| STD | 3.049 × 10−1 | 2.156 × 10−1 | 2.805 | 2.493 × 10−1 | 1.615 × 101 | 6.611 | 1.478 × 101 | |
| F8 | AVG | 8.099 × 102 | 8.104 × 102 | 9.275 × 102 | 8.246 × 102 | 1.881 × 105 | 6.908 × 104 | 6.569 × 106 |
| STD | 3.788 | 4.157 | 1.197 × 102 | 1.286 × 101 | 4.135 × 105 | 6.064 × 104 | 6.052 × 106 | |
| F9 | AVG | 9.122 × 102 | 9.123 × 102 | 9.121 × 102 | 9.128 × 102 | 9.134 × 102 | 9.133 × 102 | 9.137 × 102 |
| STD | 5.114 × 10−1 | 4.615 × 10−1 | 4.465 × 10−1 | 5.568 × 10−1 | 3.258 × 10−1 | 3.237 × 10−1 | 1.710 × 10−1 | |
| F10 | AVG | 2.963 × 105 | 3.859 × 105 | 8.134 × 105 | 4.811 × 105 | 8.118 × 105 | 1.239 × 107 | 6.185 × 107 |
| STD | 1.659 × 105 | 2.754 × 105 | 4.591 × 105 | 4.299 × 105 | 8.034 × 105 | 5.403 × 106 | 2.856 × 107 | |
| F11 | AVG | 4.814 × 103 | 3.758 × 103 | 2.230 × 103 | 2.877 × 103 | 3.724 × 103 | 1.361 × 107 | 6.039 × 108 |
| STD | 6.176 × 103 | 3.860 × 103 | 2.477 × 103 | 3.736 × 103 | 4.202 × 103 | 1.398 × 107 | 3.882 × 108 | |
| F12 | AVG | 2.141 × 103 | 2.375 × 103 | 3.411 × 103 | 3.618 × 103 | 3.958 × 103 | 1.529 × 109 | 2.509 × 1012 |
| STD | 6.019 × 102 | 4.603 × 102 | 7.674 × 102 | 9.717 × 102 | 1.599 × 103 | 2.453 × 109 | 3.470 × 1012 | |
| F13 | AVG | 1.558 × 103 | 1.576 × 103 | 1.571 × 103 | 1.559 × 103 | 1.648 × 103 | 1.596 × 103 | 1.929 × 103 |
| STD | 1.661 × 101 | 2.653 × 101 | 8.259 | 5.392 × 10−2 | 4.752 × 101 | 1.258 × 101 | 1.704 × 102 | |
| F14 | AVG | 2.216 × 103 | 2.138 × 103 | 2.475 × 103 | 2.053 × 103 | 2.008 × 103 | 3.363 × 103 | 3.171 × 103 |
| STD | 2.323 × 102 | 1.611 × 102 | 1.964 × 102 | 9.957 × 101 | 5.084 × 101 | 2.371 × 102 | 4.066 × 102 | |
| F15 | AVG | 2.317 × 103 | 2.336 × 103 | 2.860 × 103 | 2.894 × 103 | 2.584 × 103 | 2.942 × 103 | 2.998 × 103 |
| STD | 1.248 × 102 | 1.652 × 102 | 3.423 × 101 | 3.792 × 101 | 8.845 × 101 | 3.427 × 101 | 4.669 × 101 | |
| Friedman Mean | 1.90 | 2.63 | 3.17 | 3.40 | 4.37 | 5.77 | 6.77 | |
| Friedman Rank | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| p-Values | - | 4.792 × 10−2 | 2.307 × 10−2 | 3.377 × 10−2 | 1.857 × 10−2 | 6.550 × 10−4 | 6.550 × 10−4 |
| SSALEO-XGBOOST | SSA-XGBOOST | GWO-XGBOOST | HBA-XGBOOST | MFO-XGBOOST | SCA-XGBOOST | SOA-XGBOOST | XGBOOST | ELM | KNN | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.9994 | 0.9875 | 0.9755 | 0.9448 | 0.9333 | 0.9696 | 0.9685 | 0.8845 | 0.8057 | 0.7969 |
| STD | 2.279 × 10−5 | 1.706 × 10−4 | 8.329 × 10−3 | 7.266 × 10−3 | 5.366 × 10−4 | 1.421 × 10−2 | 2.525 × 10−3 | 1.714 × 10−3 | 2.421 × 10−2 | 2.116 × 10−3 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| RMSE | AVG | 2.410 × 10−2 | 1.120 × 10−1 | 1.541 × 10−1 | 2.344 × 10−1 | 2.582 × 10−1 | 1.696 × 10−1 | 1.773 × 10−1 | 3.399 × 10−1 | 4.400 × 10−1 | 4.507 × 10−1 |
| STD | 4.703 × 10−4 | 7.610 × 10−4 | 2.715 × 10−2 | 1.515 × 10−2 | 1.038 × 10−3 | 3.989 × 10−2 | 7.086 × 10−3 | 2.518 × 10−3 | 2.746 × 10−2 | 2.345 × 10−3 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| MSE | AVG | 5.810 × 10−4 | 1.254 × 10−2 | 2.447 × 10−2 | 5.519 × 10−2 | 6.668 × 10−2 | 3.036 × 10−2 | 3.147 × 10−2 | 1.156 × 10−1 | 1.943 × 10−1 | 2.031 × 10−1 |
| STD | 2.279 × 10−5 | 1.706 × 10−4 | 8.329 × 10−3 | 7.266 × 10−3 | 5.366 × 10−4 | 1.421 × 10−2 | 2.525 × 10−3 | 1.714 × 10−3 | 2.421 × 10−2 | 2.116 × 10−3 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| ME | AVG | 2.439 × 10−1 | 8.069 × 10−1 | 1.084 | 1.260 | 1.341 | 1.132 | 1.141 | 1.566 | 1.928 | 2.284 |
| STD | 4.938 × 10−2 | 8.174 × 10−2 | 1.802 × 10−1 | 1.681 × 10−1 | 1.141 × 10−1 | 1.999 × 10−1 | 7.780 × 10−2 | 3.918 × 10−2 | 1.062 × 10−1 | 8.292 × 10−2 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| RAE | AVG | 2.410 × 10−2 | 1.120 × 10−1 | 1.541 × 10−1 | 2.344 × 10−1 | 2.582 × 10−1 | 1.696 × 10−1 | 1.773 × 10−1 | 3.399 × 10−1 | 4.400 × 10−1 | 4.507 × 10−1 |
| STD | 4.703 × 10−4 | 7.610 × 10−4 | 2.715 × 10−2 | 1.515 × 10−2 | 1.038 × 10−3 | 3.989 × 10−2 | 7.086 × 10−3 | 2.518 × 10−3 | 2.746 × 10−2 | 2.345 × 10−3 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 |
| SSALEO-XGBOOST | SSA-XGBOOST | GWO-XGBOOST | HBA-XGBOOST | MFO-XGBOOST | SCA-XGBOOST | SOA-XGBOOST | XGBOOST | ELM | KNN | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.9851 | 0.9698 | 0.9624 | 0.9205 | 0.9136 | 0.9524 | 0.9526 | 0.8685 | 0.8047 | 0.7435 |
| STD | 5.763 × 10−4 | 1.894 × 10−3 | 4.950 × 10−3 | 4.163 × 10−3 | 3.064 × 10−3 | 1.340 × 10−2 | 2.952 × 10−3 | 3.845 × 10−3 | 2.954 × 10−2 | 7.051 × 10−3 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| RMSE | AVG | 1.221 × 10−1 | 1.734 × 10−1 | 1.935 × 10−1 | 2.817 × 10−1 | 2.937 × 10−1 | 2.158 × 10−1 | 2.175 × 10−1 | 3.622 × 10−1 | 4.400 × 10−1 | 5.057 × 10−1 |
| STD | 3.840 × 10−3 | 6.334 × 10−3 | 1.527 × 10−2 | 1.195 × 10−2 | 8.742 × 10−3 | 3.428 × 10−2 | 7.211 × 10−3 | 1.152 × 10−2 | 3.335 × 10−2 | 1.107 × 10−2 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| MSE | AVG | 1.493 × 10−2 | 3.012 × 10−2 | 3.766 × 10−2 | 7.951 × 10−2 | 8.635 × 10−2 | 4.774 × 10−2 | 4.734 × 10−2 | 1.313 × 10−1 | 1.947 × 10−1 | 2.559 × 10−1 |
| STD | 9.450 × 10−4 | 2.227 × 10−3 | 6.127 × 10−3 | 6.849 × 10−3 | 5.151 × 10−3 | 1.442 × 10−2 | 3.140 × 10−3 | 8.360 × 10−3 | 2.891 × 10−2 | 1.128 × 10−2 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| ME | AVG | 1.224 | 1.400 | 1.302 | 1.478 | 1.608 | 1.377 | 1.414 | 1.607 | 1.874 | 2.352 |
| STD | 1.116 × 10−1 | 2.124 × 10−1 | 1.949 × 10−1 | 1.958 × 10−1 | 1.837 × 10−1 | 1.804 × 10−1 | 2.075 × 10−1 | 7.056 × 10−2 | 1.426 × 10−1 | 9.469 × 10−2 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | |
| RAE | AVG | 1.222 × 10−1 | 1.735 × 10−1 | 1.934 × 10−1 | 2.817 × 10−1 | 2.938 × 10−1 | 2.156 × 10−1 | 2.176 × 10−1 | 3.620 × 10−1 | 4.399 × 10−1 | 5.056 × 10−1 |
| STD | 2.371 × 10−3 | 5.494 × 10−3 | 1.270 × 10−2 | 7.354 × 10−3 | 5.218 × 10−3 | 3.225 × 10−2 | 6.751 × 10−3 | 5.011 × 10−3 | 3.291 × 10−2 | 6.674 × 10−3 | |
| p-Value | - | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 | 4.311 × 10−2 |
| SSALEO-XGBOOST | SSA-XGBOOST | GWO-XGBOOST | HBA-XGBOOST | MFO-XGBOOST | SCA-XGBOOST | SOA-XGBOOST | XGBOOST | ELM | KNN | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.99941 | 0.98749 | 0.97998 | 0.94365 | 0.93362 | 0.97268 | 0.96109 | 0.88392 | 0.83956 | 0.91833 |
| STD | 1.152 × 10−5 | 3.459 × 10−5 | 6.476 × 10−3 | 1.006 × 10−2 | 2.775 × 10−5 | 1.731 × 10−2 | 1.096 × 10−2 | 1.110 × 10−16 | 3.331 × 10−16 | 1.105 × 10−2 | |
| Best | 0.99943 | 0.98754 | 0.98745 | 0.95164 | 0.93365 | 0.98740 | 0.97166 | 0.88392 | 0.83956 | 0.94367 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.845 × 10−5 | 8.845 × 10−5 | 8.857 × 10−5 | 8.683 × 10−5 | 8.683 × 10−5 | 8.683 × 10−5 | |
| RMSE | AVG | 2.425 × 10−2 | 1.119 × 10−1 | 1.398 × 10−1 | 2.365 × 10−1 | 2.576 × 10−1 | 1.585 × 10−1 | 1.954 × 10−1 | 3.407 × 10−1 | 4.006 × 10−1 | 2.851 × 10−1 |
| STD | 2.386 × 10−4 | 1.541 × 10−4 | 2.205 × 10−2 | 2.015 × 10−2 | 5.336 × 10−5 | 4.690 × 10−2 | 2.661 × 10−2 | 5.551 × 10−17 | 0 | 1.974 × 10−2 | |
| Best | 2.378 × 10−2 | 1.116 × 10−1 | 1.120 × 10−1 | 2.199 × 10−1 | 2.576 × 10−1 | 1.123 × 10−1 | 1.684 × 10−1 | 3.407 × 10−1 | 4.006 × 10−1 | 2.373 × 10−1 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.845 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | |
| MSE | AVG | 5.882 × 10−4 | 1.251 × 10−2 | 2.002 × 10−2 | 5.635 × 10−2 | 6.638 × 10−2 | 2.732 × 10−2 | 3.891 × 10−2 | 1.161 × 10−1 | 1.604 × 10−1 | 8.167 × 10−2 |
| STD | 1.152 × 10−5 | 3.459 × 10−5 | 6.476 × 10−3 | 1.006 × 10−2 | 2.775 × 10−5 | 1.731 × 10−2 | 1.096 × 10−2 | 2.776 × 10−17 | 2.776 × 10−17 | 1.105 × 10−2 | |
| Best | 5.660 × 10−4 | 1.246 × 10−2 | 1.255 × 10−2 | 4.836 × 10−2 | 6.635 × 10−2 | 1.261 × 10−2 | 2.834 × 10−2 | 1.161 × 10−1 | 1.604 × 10−1 | 5.633 × 10−2 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.845 × 10−5 | 8.845 × 10−5 | 8.857 × 10−5 | 8.683 × 10−5 | 8.683 × 10−5 | 8.683 × 10−5 | |
| ME | AVG | 2.315 × 10−1 | 8.122 × 10−1 | 9.250 × 10−1 | 1.164 | 1.317 | 9.895 × 10−1 | 1.131 | 1.564 | 2.157 | 1.635 |
| STD | 1.106 × 10−2 | 2.063 × 10−2 | 8.444 × 10−2 | 7.726 × 10−2 | 9.613 × 10−3 | 1.883 × 10−1 | 9.876 × 10−2 | 2.220 × 10−16 | 0 | 2.526 × 10−1 | |
| Best | 2.067 × 10−1 | 7.671 × 10−1 | 8.239 × 10−1 | 1.081 | 1.308 | 8.099 × 10−1 | 1.010 | 1.564 | 2.157 | 1.154 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | |
| RAE | AVG | 2.425 × 10−2 | 1.119 × 10−1 | 1.398−1 | 2.365 × 10−1 | 2.576 × 10−1 | 1.585 × 10−1 | 1.954 × 10−1 | 3.407 × 10−1 | 4.006 × 10−1 | 2.851 × 10−1 |
| STD | 2.386 × 10−4 | 1.541 × 10−4 | 2.205 × 10−2 | 2.015 × 10−2 | 5.336 × 10−5 | 4.690 × 10−2 | 2.661 × 10−2 | 5.551 × 10−17 | 0 | 1.974 × 10−2 | |
| Best | 2.378 × 10−2 | 1.116 × 10−1 | 1.120 × 10−1 | 2.199 × 10−1 | 2.576 × 10−1 | 1.123 × 10−1 | 1.684 × 10−1 | 3.407 × 10−1 | 4.006 × 10−1 | 2.373 × 10−1 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.845 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 |
| SSALEO-XGBOOST | SSA-XGBOOST | GWO-XGBOOST | HBA-XGBOOST | MFO-XGBOOST | SCA-XGBOOST | SOA-XGBOOST | XGBOOST | ELM | KNN | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.98455 | 0.96850 | 0.96400 | 0.91566 | 0.91068 | 0.95493 | 0.94334 | 0.86727 | 0.74833 | 0.90918 |
| STD | 5.029 × 10−4 | 2.418 × 10−4 | 5.318 × 10−3 | 5.727 × 10−3 | 1.941 × 10−4 | 1.800 × 10−2 | 9.423 × 10−3 | 4.441 × 10−16 | 0 | 1.188 × 10−2 | |
| Best | 0.98544 | 0.96902 | 0.96934 | 0.91990 | 0.91079 | 0.96977 | 0.95206 | 0.86727 | 0.74833 | 0.93515 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | |
| RMSE | AVG | 1.215 × 10−1 | 1.735 × 10−1 | 1.850 × 10−1 | 2.837 × 10−1 | 2.921 × 10−1 | 2.042 × 10−1 | 2.319 × 10−1 | 3.561 × 10−1 | 4.904 × 10−1 | 2.939 × 10−1 |
| STD | 1.974 × 10−3 | 6.655 × 10−4 | 1.305 × 10−2 | 9.393 × 10−3 | 3.168 × 10−4 | 3.718 × 10−2 | 1.855 × 10−2 | 1.665 × 10−16 | 0.000 | 1.953 × 10−2 | |
| Best | 1.180 × 10−1 | 1.721 × 10−1 | 1.712 × 10−1 | 2.766 × 10−1 | 2.920 × 10−1 | 1.700 × 10−1 | 2.140 × 10−1 | 3.561 × 10−1 | 4.904 × 10−1 | 2.489 × 10−1 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | |
| MSE | AVG | 1.477 × 10−2 | 3.010 × 10−2 | 3.440 × 10−2 | 8.059 × 10−2 | 8.534 × 10−2 | 4.306 × 10−2 | 5.414 × 10−2 | 1.268 × 10−1 | 2.405 × 10−1 | 8.677 × 10−2 |
| STD | 4.805 × 10−4 | 2.311 × 10−4 | 5.081 × 10−3 | 5.472 × 10−3 | 1.855 × 10−4 | 1.720 × 10−2 | 9.003 × 10−3 | 2.776 × 10−17 | 1.110 × 10−16 | 1.135 × 10−2 | |
| Best | 1.392 × 10−2 | 2.960 × 10−2 | 2.930 × 10−2 | 7.654 × 10−2 | 8.524 × 10−2 | 2.888 × 10−2 | 4.580 × 10−2 | 1.268 × 10−1 | 2.405 × 10−1 | 6.196 × 10−2 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | |
| ME | AVG | 1.201 | 1.353 | 1.235 | 1.466 | 1.567 | 1.322 | 1.362 | 1.647 | 2.204 | 1.455 |
| STD | 1.050 × 10−1 | 4.515 × 10−2 | 8.630 × 10−2 | 9.293 × 10−2 | 1.961 × 10−2 | 1.082 × 10−1 | 7.936 × 10−2 | 4.441 × 10-16 | 4.441 × 10−16 | 2.644 × 10−1 | |
| Best | 1.026 | 1.294 | 1.075 | 1.317 | 1.521 | 1.140 | 1.197 | 1.647 | 2.204 | 1.100 | |
| p-value | - | 3.385 × 10−4 | 3.317 × 10−1 | 1.204 × 10−4 | 8.857 × 10−5 | 7.796 × 10−4 | 5.934 × 10−4 | 8.857 × 10−5 | 8.857 × 10−5 | 4.550 × 10−3 | |
| RAE | AVG | 1.242 × 10−1 | 1.774 × 10−1 | 1.892 × 10−1 | 2.901 × 10−1 | 2.987 × 10−1 | 2.087 × 10−1 | 2.371 × 10−1 | 3.641 × 10−1 | 5.014 × 10−1 | 3.005 × 10−1 |
| STD | 2.018 × 10−3 | 6.805 × 10−4 | 1.334 × 10−2 | 9.604 × 10−3 | 3.237 × 10−4 | 3.801 × 10−2 | 1.897 × 10−2 | 0 | 1.110 × 10−16 | 1.997 × 10−2 | |
| Best | 1.206 × 10−1 | 1.759 × 10−1 | 1.750 × 10−1 | 2.828 × 10−1 | 2.985 × 10−1 | 1.738 × 10−1 | 2.188 × 10−1 | 3.641 × 10−1 | 5.014 × 10−1 | 2.545 × 10−1 | |
| p-value | - | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 | 8.857 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nsir, N.; Alzubi, A.B.; Adegboye, O.R. Enhancing Sustainable Supply Chain Performance Prediction Using an Augmented Algorithm-Optimized XGBOOST in Industry 4.0 Contexts. Sustainability 2025, 17, 10344. https://doi.org/10.3390/su172210344
Nsir N, Alzubi AB, Adegboye OR. Enhancing Sustainable Supply Chain Performance Prediction Using an Augmented Algorithm-Optimized XGBOOST in Industry 4.0 Contexts. Sustainability. 2025; 17(22):10344. https://doi.org/10.3390/su172210344
Chicago/Turabian StyleNsir, Noreddin, Ahmad Bassam Alzubi, and Oluwatayomi Rereloluwa Adegboye. 2025. "Enhancing Sustainable Supply Chain Performance Prediction Using an Augmented Algorithm-Optimized XGBOOST in Industry 4.0 Contexts" Sustainability 17, no. 22: 10344. https://doi.org/10.3390/su172210344
APA StyleNsir, N., Alzubi, A. B., & Adegboye, O. R. (2025). Enhancing Sustainable Supply Chain Performance Prediction Using an Augmented Algorithm-Optimized XGBOOST in Industry 4.0 Contexts. Sustainability, 17(22), 10344. https://doi.org/10.3390/su172210344





