Abstract
As is well known, due to carbon dioxide emissions, the combustion of lignite in power plants creates environmental pollution. In contrast, nuclear fuels do not produce carbon dioxide emissions. This paper investigates the effects of replacing lignite thermal power plants with small modular nuclear reactors (SMRs) of equivalent rated power and related characteristics. In terms of the emissions criterion, nuclear fuels belong to the same category of clean sources as the sun and wind. A second criterion is the economic one and concerns the operating cost of the nuclear–thermal power plant. Based on the economic criterion, although nuclear reactors require a higher initial invested capital, they have lower fuel costs and lower operating costs than lignite plants, which is important due to their long service life. A third criterion is the effect of the operation mode of an SMR, constant or variable, on the cost of energy production. In terms of the operation mode criterion, two cycles were investigated: the production of a constant amount of energy and the production of a variable amount of energy related to fluctuations in the electric load demand or the operation load-following. Using multi-criteria managerial scenarios, the results of the research demonstrate that the final mean minimal cost of energy generated by hybrid thermal units with small nuclear reactors in constant power output operation is lower than the mean minimal cost of the energy generated in the load-following mode by 2.45%. At the same time, the carbon dioxide emissions in the constant power output operation are lower than those produced in the load-following mode by 2.14%. In conclusion, the constant power output operation of an SMR is more sustainable compared to the load-following operation and also is more sustainable compared to generation by lignite thermal power plants.
1. Introduction
The economic sustainability of power plants involves their financial viability, operational efficiency, and long-term profitability while considering environmental and social impacts [1]. Key factors influencing the economic sustainability of power plants are as follows:
- Efficiency improvements, such as optimizing energy production in hybrid systems, contribute to economic sustainability by lowering operational costs and enhancing resource utilization.
- Renewable energy sources, such as solar and wind, are being integrated into power generation due to their lower environmental impact and potential for cost savings. Hybrid systems with renewable sources address energy variability needs and improve economic sustainability. Hybrid generation with nuclear energy is decarbonizing global energy as part of solutions to boost clean energy in power systems [2].
- Economic sustainability can be assessed using financial metrics such as the levelized cost of energy, net present value, or payback period, which determine the profitability and cost-effectiveness of power plants.
- The adoption of advanced technologies, upgrades in thermal power plants, or hybrid models enhance their economic performance by improving efficiency and adapting to fluctuating power demands, causing financial viability and long-term profitability.
- Economic sustainability is linked to environmental and social factors too. Reducing carbon emissions and adopting sustainable practices can improve public perception and long-term viability. Economic sustainability requires supportive policies and financial incentives to overcome initial investment barriers, especially for emerging technologies.
Thus, the economic sustainability of power plants depends on a combination of financial metrics, technological advancements, renewable energy integration, operational efficiency, and supportive policies.
A hybrid power system is a smart team of different energy sources working together to provide consistent, efficient, and cleaner electricity, especially where a single source is not reliable or sufficient on its own. A hybrid power system combines two or more different types of power sources, typically renewable and non-renewable, to provide a reliable, efficient, and cleaner supply of electricity. Primary power sources are renewables (solar, wind, hydro, and biomass) and conventional sources are coal, diesel oil, and natural gas. Energy storage includes batteries (lithium-ion) and thermal storage (molten salt). Control systems for hybrid systems involve smart energy management to optimize which source supplies power at any time. The hybrid system switches between or combines energy sources based on the availability, demand needs, cost-efficiency, and storage levels. The advantages of hybrid systems are their reliability, fuel savings because they reduce the dependence on fossil fuels, flexibility to operate off-grid or when grid-connected, and lower emissions, especially when renewables replace conventional fuels. Applications are in remote or off-grid regions, islands, disaster relief zones, and industrial operations needing power 24 h/day 7 days/week. Hybrid and renewable energy systems are promising for achieving long-term economic and environmental sustainability [3,4,5].
Nuclear power plants produce electricity without producing pollution. On the other hand, thermal electricity-generating plants based on fossil fuels emit gases such as CO2 [6]. To lower the pollution, electricity generation was directed towards hybrid systems which involve nuclear, thermal, and renewable sources [7,8,9]. Hybrid energy systems have a role in decarbonizing off-grid and remote regions by integrating renewable energy sources with storage and backup solutions. They significantly reduce carbon emissions, improve energy reliability and offer economic benefits, making them a viable and sustainable alternative to traditional fossil fuel-based power generation in isolated areas [10,11,12]. These systems provide reliable, sustainable, and cost-effective electricity, reducing dependence on fossil fuels and enhancing energy access in areas where extending the main grid is impractical. The key benefits of hybrid systems for decarbonization are as follows:
- A significant reduction in carbon emissions and decrease in greenhouse gas emissions by minimizing reliance on diesel generators.
- Enhanced energy access and reliability in isolated regions where hybrid systems have replaced diesel generators, providing consistent electricity for lighting, refrigeration, and communication.
- Economic advantages: while the initial investment in hybrid systems can be substantial, they offer long-term cost savings by reducing fuel expenses and maintenance costs associated with diesel generators.
- Scalability and adaptability. Hybrid systems can be tailored to the specific energy needs and resource availability of different communities.
Hybrid energy systems are transformative for off-grid and remote regions, offering a sustainable pathway to decarbonization. Their ability to provide reliable, clean, and cost-effective energy addresses both environmental concerns and socio-economic development goals. Moreover, these systems empower communities by enhancing energy independence and resilience, particularly in the face of climate change and energy insecurity [10,11,12]. The investment capital for the construction of nuclear power plants is high, but their operating costs are lower than that of fossil fuel plants; nuclear reactors have higher production for a longer lifespan, and the invested capital is spread over more years [13,14,15]. In particular, small modular reactors (SMRs) work without refueling up to 24 months, producing a stable source of power [16,17]. SMRs have higher investment capital compared to large reactors, but have economic benefits for small power systems, such as the autonomous grids in inaccessible zones [18].
Hybrid nuclear–thermal power plants aim to improve the economic flexibility of energy systems by combining the base-load reliability of nuclear energy with the dispatchable or variable output of thermal systems. The economic rationale behind such systems is rooted in maximizing the energy output while minimizing costs and adapting to the variable grid demand, especially under high renewable penetration. Hybrid energy systems integrate nuclear reactors providing a constant thermal output, thermal systems such as concentrated solar power or fossil thermal plants, supplying a flexible peak-load capacity, or storing excess nuclear heat and thermal energy storage. These systems can function in a load-following mode, using stored energy to supply–demand mismatches, and are effective in microgrids or remote grids. Key economic factors are high capital expenditure for nuclear components and moderate for solar and thermal systems and enhanced operational flexibility by thermal storage or integration with industrial processes and a varying levelized cost of electricity which is sensitive to the hybridization ratio, storage size, and market conditions.
A study optimized a nuclear–solar–thermal hybrid plant under load-following constraints and found that adding nuclear power reduces the overall electricity costs compared to pure solar or fossil thermal options. Additionally, multi-criteria decision methods enable economically optimal configurations across different plant sizes and market conditions [19]. Using a software framework [20], another paper analyzed nuclear–wind hybrids, showing that the profitability depends on matching the industrial demand to the nuclear output. Higher renewable penetration increased the value of hybrid flexibility due to the volatility [21]. A techno-economic study of Concentrated Solar Power–nuclear hybrids in isolated grids found that hybridization improved the system’s capacity factor and reduced energy storage requirements, and the Levelized Cost of Electricity (LCOE) decreased with an optimized mix of solar and nuclear power [22]. Hybrid nuclear–thermal power plants offer a viable pathway to economically competitive, flexible, and low-emission electricity generation. Under an appropriate design, such systems can significantly reduce the cost of electricity, buffer renewable intermittency, and improve grid resilience, especially when integrated with energy storage and industrial processes.
A technological review of the concepts of SMRs under development assesses reactor technologies for integration benefits and power system added values. There are uncertainties in their economic attractiveness and these can influence the economics of production [23,24]. There is a potential for SMRs to supply electricity to the grids, allowing for the greater penetration of renewable energy sources and reducing costs [25,26,27]. Multiple SMRs instead of large nuclear power plants reduce the need for frequency regulation.
Following initiatives of other countries [28,29], Greece is exploring the repowering of existent lignite-based units by another of new technology, such as natural gas and nuclear. The nuclear generator can be installed jointly with existing fossil fuel plants to enhance the country’s energy sources and reduce CO2 pollution [30]. The installation on behalf of the Greek Public Power Corporation (PPC) of a combined cycle steam power station includes three generators [31], two heat recovery boilers with an exhaust gas bypass system, condenser, and forced flow cooling tower, and an industrial water treatment complex [32,33]. From PPC’s facilities in Megalopolis, Plant A consists of lignite power plants: Units I and II were built in 1970 with a capacity of 125 MW each, Unit III was built in 1973 and Unit IV was built in 1991, with a capacity of 300 MW each. The exhaust gases are channeled into separate heat recovery boilers and the steam drives the turbines [32,34].
SMRs can work in load-following mode and in the ranges of 50–100% of the rated committed loads, thus improving the economic and environmental aspects [35]. Other situations with load following can be 25–100% of the rated power [36,37]. In load-following mode, the electricity generation is controlled according to the fluctuations in the electric load demand, while the operator monitors the variations in energy generation according to the system necessities [38]. Published reports show that SMRs can work in the load-following mode of operation and can vary their output during different periods, such as day and night. Correspondingly, SMRs can change the generated energy according to the production of energy by renewable sources, such as the wind or sun, mainly in placements of SMRs in locations in isolated areas [19,39].
When a power plant combines nuclear reactors with other forms of generation such as thermal energy, a more efficient and flexible system is created, adapting to grid conditions and energy requirements, which enhances the electricity economy and reduces carbon dioxide emissions [40,41]. As the thermal power plant operates independently of the nuclear reactor, the hybrid system has flexibility in the production, load monitoring, grid stability, and increased economic viability [42,43,44].
The optimization of the economics of the energy generated is multicriteria because of the different kinds and sizes of interconnected generators [45]. The generators which contribute to objective cost functions have different ratings and operating constraints [46]. From the study of the optimization of the economics of energy systems, the reports are related to control, optimization, and software, while the economics’ aspects are of increasing attention too. The economic optimization of hybrid thermal and solar plants studies of solar energy generation is related to the geographical coordinates, time of the year, and solar irradiation [9]. Knowledge from the above publications has been made available for further research and education in the energy sector, offering to the readers innovative scientific ideas [47,48].
From the literature study of methods and techniques for optimizing economic dispatch and commitment in hybrid energy systems, it appears that the economic factor is still of interest. The optimization of the economics of hybrid nuclear–thermal power plants during constant power generation or load-following generation is still under study. In order to minimize electricity costs, the optimal production planning of hybrid nuclear–thermal power plants must take into account the specific characteristics of each power unit and the demand for the electric load. In view of the participation of hybrid plants in the production of electricity either by a constant power output or by a load-following power output, production planning must follow specific requirements such as resolving the impact of operating and maintenance costs and fluctuations in the electrical load in real-time.
The literature shows that research efforts have been made. However, an accurate mathematical method is needed that reflects the effects of changing the electrical load, fuel prices, operating and maintenance costs, and solving the problem of the load demand in real time. The production of electricity by optimizing the cost of electricity must take into account the characteristics of each hybrid nuclear–thermal power plant and the committed electrical load.
This research links the issues mentioned regarding finding an optimal solution for low-cost electricity generation and proposes a scenario-based multi-criteria study to investigate the cost-effective multi-criteria optimization of nuclear reactors operating together with thermal production units. This paper conducts an analysis of the economic feasibility of a nuclear–thermal plant. The main question focuses on optimizing the electricity cost of systems with thermal units so that they can be replaced with SMRs. The goal is to control the power from multiple thermal units and nuclear reactors that either generate constant power or generate power by following the electric load for a given electric load and a given 24 h period. The aspect of economic sustainability in combination with environmental factors is addressed through the optimization of energy production, which is associated with the reduction of carbon dioxide emissions from the replacement of fossil fuels with nuclear fuels.
This paper presents a novel solution for optimizing the economics of energy generated by a hybrid nuclear and thermal power plant. Three scenarios are studied using the optimization methodology. It is concluded that the cost of coal-based electricity generated is higher than that of electricity generated from the nuclear–thermal hybrid system. The main contribution of this work is the development of a new methodology for the study of the final optimal cost of energy produced by hybrid nuclear–thermal power plants. The developed methodology uses a multi-criteria approach. This study is based on investigating the effects of replacing thermoelectric plants with SMRs of equivalent nominal power. Other criteria taken into account are the operating costs. These criteria are applied to the study of different modes of operation: the production of a fixed amount of energy or the production of a variable amount of energy. The numerical results obtained confirm the effectiveness of the developed approach.
This study designs a new approach to the energy economy for modeling and forecasting using multi-criteria management analysis. The approach is compared to the efficiency of thermal units for proper electricity generation. The issue is of interest to those working in the energy industries, including the nuclear industry.
In this paper, the description of a hybrid nuclear–thermal system is in Section 2. The methodology of modeling economic optimization and solving the system using multicriteria decisions is presented in Section 3. Using specific scenarios, the control of the power generated by a nuclear reactor and thermal units operating in a constant output mode or in a load-following mode up to a target load level within a 24 h timeframe is presented in Section 4. Section 5 of this paper discusses the results. Finally, conclusions are made in Section 6, alongside with future research directions. Additionally, the technical data of the system are in Appendix A and nomenclature is in the abbreviation section.
2. System Description
Nuclear reactors have technical limitations when their production must follow the levels of the electrical load. Frequent temperature changes create dependencies between nuclear fuel and shielding that can break and escape fission products [36,49]. For security reasons, a variation in the output power is limited. Thus, when monitoring the levels of the electrical load, the operating limits should be at 50–100% of the rated power of the nuclear reactor during a day [36,37,50]. Considering that in order to recover the initial capital investment, nuclear reactors must constantly operate close to their rated power, it follows that with the function of following the levels of the electric load, nuclear power plants lose part of their economic performance [7]. Therefore, according to economic criteria, the operation of the SMRs in load following is, on the one hand, attractive and must be programmed accurately [51,52]. On the other, fossil fuel power plants are more suitable to cover lower loads in the following mode because of their lower fuel costs and lower initial capital for investment.
In compliance with technological and economic development trends, the power systems are modernized in terms of their structuring, management and operation. Due to the interconnection between these systems and their role in a safe and reliable operation, their management and coordination are very specific and complex tasks.
SMRs offer more flexible and economically efficient nuclear power generation. However, their adoption and operational feasibility—especially in load-following or variable-demand contexts—depend on several technical and economic constraints related to reactor kinetics, ramp rate limitations, and fuel degradation. The economics of SMRs, especially under load-following or variable operation modes, are coupled with technical constraints in the ramp rate (reactor kinetics) and the implications of cyclic operation on fuel integrity and degradation.
Reactor kinetics and ramp rate limitations involve the following:
- Capacity factor reduction: frequent changes in the power output reduce the capacity factor (the time the reactor is running at the rated power), impacting the revenue per MWh.
- Automation and O&M: SMRs are designed for lower staffing and automated control, which could reduce costs associated with more complex kinetics control.
- Faster ramps could increase thermal stress and O&M costs unless materials and systems are specifically engineered to handle it.
- SMRs, particularly those operating without soluble boron, rely on mechanical control systems, which can cause higher local power peaking during rapid load changes. Boron-free designs with continuous control rod insertion increase reactivity feedback complexity and risk fuel hot spots under rapid power transients [53].
- Ramp rate limitations are not only thermal–hydraulic (coolant temperature lag), but are also driven by cladding strain limits and peak linear power constraints, affecting fuel safety margins.
Economic implications of fuel degradation under variable loads operation include the following:
- A shortened fuel life: cycling can reduce the burnup efficiency, increasing the refueling frequency and waste.
- More rigorous fuel performance monitoring is needed, increasing operational costs.
- Advanced fuel premium: SMRs using resilient fuels (metallic or TRISO) may have higher upfront fuel costs, but lower degradation in the variable mode.
- Cyclic thermal and mechanical loading during ramping operations leads to enhanced fission gas release, accelerated cladding creep and oxidation, and an elevated risk of pellet-clad interactions.
- Advanced cladding materials (Cr-coated zirconium, FeCrAl) mitigate these effects, but exhibit mixed results depending on the power peaking and core design [54].
A variable operation reduces the capacity factor, damaging the economics [55]. The ramp rate is constrained by the peak-cladding strain and power peaking. Long cycles (up to 5 years) are possible with low power densities, but restrict the transient response [53]. Advanced cladding and fuel reduce thermal damage in boron-free SMRs, but high peaking factors under ramped conditions require the optimization of control strategies [54].
While SMRs are being designed with flexibility in mind, economic success in variable operation depends on balancing capital cost recovery with new revenue streams from grid services. Reactor kinetics and ramp rate capabilities are technically feasible, but fuel degradation and associated costs must be managed with better materials, monitoring, and operational strategy. Ramp rate limitations are dictated by the fuel temperature, power peaking, and structural strain thresholds, all of which affect long-term fuel integrity. Economic viability under variable operation depends on offsetting the reduced baseload efficiency with revenue from grid services and advanced core/fuel designs.
SMRs are being considered for frequent power ramping or ramp rate cycling. This flexibility introduces concerns regarding the integrity of fuel cladding, the primary barrier preventing the release of fission products. SMRs may undergo frequent power transitions, necessitating the understanding of mechanical–thermal interactions under cycling conditions, especially a Pellet-Cladding Mechanical Interaction (PCMI). Ramp rate cycling in SMRs significantly elevates the risk of fuel cladding degradation due to the intensified PCMI, cyclic mechanical fatigue, and hydride reorientation. High-frequency ramping induces stress accumulation and strain in the cladding, especially near pellet edges, compromising the long-term structural integrity. Mitigation strategies should focus on material innovations and predictive modeling to ensure fuel safety under a flexible operation.
A detailed study examined the diametral strain in cladding during power changes, showing that plastic strain accumulates primarily during rapid power ascents [56]. These strains were directly linked to cladding thinning and mechanical fatigue over time. Using the TRANSURANUS fuel code, a European team modeled the SMR fuel behavior under load-following scenarios. Their work predicted that the ramp frequency and peak power level were dominant factors affecting the cladding creep and fission gas release, suggesting a nonlinear risk of buildup over time [57].
Load-following operations in SMRs introduce economic considerations concerning fuel degradation. SMRs designed for a flexible output may experience increased mechanical and thermal stresses on fuel cladding due to frequent power adjustments. This can lead to accelerated wear and the potential early replacement of fuel assemblies, impacting the overall economic viability of SMRs. Fuel degradation due to load-following operations in SMRs presents economic considerations, including increased fuel and maintenance costs, as well as waste management expenses. Addressing these challenges through material advancements, operational optimization, and predictive maintenance can enhance the economic viability of SMRs in flexible energy markets.
SMRs’ frequent power ramping can cause degradation mechanisms and can reduce the fuel lifespan, necessitating more frequent refueling and increasing operational costs such as rapid temperature changes leading to differential expansion between fuel pellets and cladding, inducing mechanical stress; repeated heating and cooling cycles that can weaken cladding materials over time; and, in zirconium-based claddings, temperature fluctuations which can promote hydride precipitation, embrittling the material.
The economic impact of fuel degradation in load-following SMRs includes the following:
- Increased fuel costs: more frequent fuel replacement due to accelerated degradation raises the cost per megawatt-hour (MWh) of electricity produced;
- Maintenance and downtime: additional inspections and unscheduled maintenance can lead to increased operational expenditures and reduced availability;
- Waste management: higher volumes of spent fuel and associated radioactive waste necessitate expanded storage and disposal solutions, further increasing costs.
Study [58] highlights that SMRs may produce more spent fuel per unit of electricity generated compared to larger reactors due to higher neutron leakage and lower fuel burnup. To address these economic challenges, several strategies can be as follows:
- Advanced fuel materials by using cladding materials with improved resistance to thermal and mechanical stresses can extend fuel life.
- Optimized reactor operation by implementing control strategies that minimize rapid power changes to reduce stress on fuel components.
- Predictive maintenance by utilizing machine learning and AI-driven models to predict fuel degradation enables proactive maintenance, reducing unexpected downtime [59].
The integration of SMRs into the energy mix is driven by promises of flexible deployment, lower upfront capital costs, and improved safety. However, these advantages come with significant trade-offs, particularly in the back end of the nuclear fuel cycle and the management of spent nuclear fuel. SMRs often operate with higher neutron leakage and lower fuel burnup due to their smaller core size and unique fuel designs (e.g., single-batch or once-through fuel cycles). These features lead to higher isotopic decay heat and radiotoxicity, greater volumes of intermediate and high-level waste, and increased requirements for shielding, cooling, and isolation in storage systems [58]. SMRs generate more reactive, voluminous waste than light water reactors (LWRs), increasing management and disposal costs [58].
The cost implications of spent fuel management in SMRs are as follows:
- Storage costs: On-site storage remains the most economical option, especially for early SMR deployment phases. However, with a proliferation of SMRs across distributed sites, the cumulative cost of maintaining multiple secured storage units increases.
- Cost sensitivity: the price of dry storage casks is a significant cost driver; SMRs producing more reactive fuel require more robust (and expensive) cask designs [60].
- Transportation and centralized disposal: More numerous and smaller sites translate to higher transportation costs and infrastructure redundancy. The chemically reactive and heterogeneous waste stream may limit options for co-disposal with conventional LWR waste, necessitating new disposal strategies. Local on-site storage is most cost-effective, but an SMR increases costs and transportation complexities [60].
- Repository design and lifecycle costs: SMRs are likely to increase the total repository footprint needed due to a higher waste volume per unit of energy. Waste packages might require enhanced engineered barriers, further elevating disposal costs.
Increased spent fuel generation from SMRs imposes significant economic burdens on the nuclear fuel cycle’s backend. These include higher costs for shielding, storage, transportation, and waste isolation due to the fuel’s higher reactivity and volume. While on-site storage may offer short-term savings, long-term system-wide costs are expected to rise unless dedicated SMR-compatible repository solutions are developed. Thus, backend fuel costs are not fully internalized in current models [24].
Advanced modeling techniques can predict long-term cladding fatigue in SMRs, though with certain limitations due to ongoing material science changes. Cladding fatigue in SMRs, resulting from mechanical, thermal, and irradiation stresses over time, can compromise the integrity of fuel rods. Given the unique conditions in SMRs, including high burnup rates, frequent load-following cycles, and advanced coolants, predictive modeling can estimate the lifespan and improve safety margins. In SMRs, the extended operational life and the transient loads increase the importance of predictive fatigue analysis. Advanced fatigue modeling integrates the following:
- Microstructure evolution models which simulate radiation-induced defects [61]. Study [61] demonstrates the coupling of irradiation-induced microstructure evolution with mechanical property changes, forming the basis for predictive models;
- Multiphysics simulations link thermal, mechanical, and chemical degradation mechanisms [62] and reviews failure mechanisms in ferritic and austenitic cladding materials under extreme conditions, highlighting modeling needs.
- Time-series and machine learning methods: used in structural health monitoring to extrapolate long-term behavior from in-service data [63].
While no single model can fully predict cladding fatigue in all SMR contexts, the integration of physics-based and data-driven models provides a pathway toward reliability. Validation remains a key challenge, requiring long-term irradiation data and in situ monitoring. Continued advancements in multiscale modeling and AI-enhanced monitoring systems are expected to close current prediction gaps.
Advanced modeling can predict long-term cladding fatigue in SMRs by capturing microstructural evolution and mechanical degradation processes under irradiation. However, the accuracy and generalizability of these models depend on ongoing validation with experimental and operational data, especially under the diverse operating conditions of future SMR designs.
The primary task is accomplished by the Energy Management System (EMS) which is assuring the energy balance between the power generation and consumption. The EMS controls the power flow; coordinates power generation, the integration of renewable resources, and the reliability of components; coordinates the interconnected operation of power systems; manages the electricity market; and coordinates an optimal and economic power dispatch [64].
Figure 1 shows the energy generation system. It consists of an Energy Management System (EMS), the nuclear power unit—SMR—thermal units (Thi), and electrical loads. In the case study, the energy system consists of one small modular reactor (SMR) and three thermal generation units which work with lignite Th1–Th3. The EMS executes energy management, controls the distribution of power between the generation and electric load during the time periods and operating conditions. Thus, the EMS, according to the electric loads, switches to different options to achieve the balance of powers when power resources and loads fluctuate. Additionally, the EMS controls the nuclear production by SMRs. The thermal units and the nuclear reactor operate independently.

Figure 1.
Generation system with nuclear and thermal units.
The analysis, modeling, and simulation period is focused on a 24 h period during the month of July 2024, because that is when there are the higher electrical loads according to the IPTO (Independent Power Transmission Operator of Greece) [65]. As can be seen from Figure 2a, in July, the demand is higher than the other months of the year [66]. However, the method of analysis, modeling, and simulation developed in this work is generalized, can be applied to any other time duration, and can include seasonal variations, long-term data, and multi-day patterns.
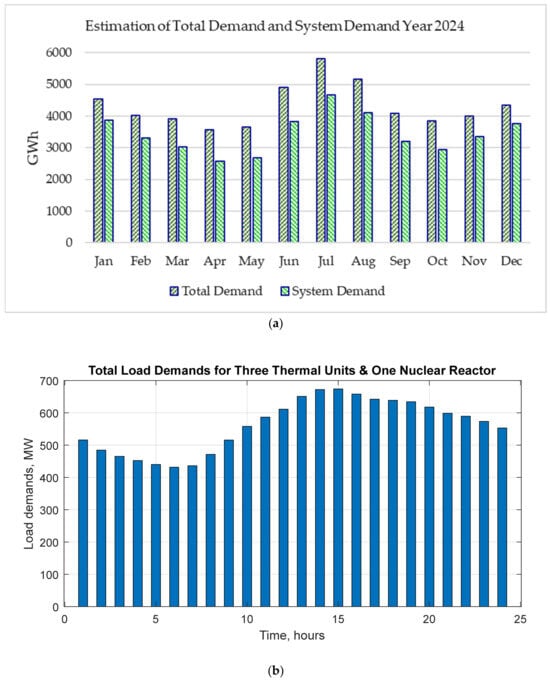
Figure 2.
(a) Total demand and system demand per month in year 2024 in Greece [66]; (b) Electric total load demands in July 2024 at the studied area [65].
The total demand is the generation on the mainland and the interconnected islands required to supply the load. The estimation of the total demand includes the estimation of the system demand and the estimation of the demand covered by production units connected to the network. The network generation results from certified measurements for the medium voltage and for the low voltage [66]. The system demand is the generation produced by units (conventional and RES) connected to the system that is required to cover the system load. The estimation of the system demand includes the demand of high-voltage consumers, mines, and self-production, the demand in system–network boundary substations, system losses, and the flow to the Crete island interconnection [66].
The considered varying electrical loads in July during 24 h are shown in Figure 2b. The total load is with data from the month of July 2024 [65]. The electrical load is assumed at values between the total minimum and maximum amounts of power of the thermal units. The thermal units have the data given in Table A1 from Appendix A [67]. The thermal units are located in Megalopolis, Greece [32,33,68]. The system involves the addition of a nuclear reactor that will replace one of the existing old thermal units, such as Megalopolis I, in order to reduce the overall gas emissions from lignite combustion. When the SMR generates power in the system, the power generated by the thermal units for the same committed loads is reduced.
3. Modeling the System
The first criterion aims tο lower the emissions of carbon dioxide by replacing fossil fuels such as lignite with nuclear fuels. The combustion of lignite in thermal power units creates environmental pollution due to emissions of CO2. In contrast, nuclear fuels do not produce CO2 emissions. In this context, one lignite thermal power unit can be replaced by one SMR of equivalent rated power.
A second criterion concerns the economics of generated electrical energy and aims to minimize the operating cost of the hybrid nuclear–thermal power plant. The basis on the economic criterion is that nuclear reactors have lower fuel costs and lower operating costs than lignite power units.
A third criterion is the effect of the operation process of the SMR on the cost of energy production. In terms of the operation process, two duty cycles were investigated: (i) the generation of a constant amount of energy and (ii) the generation of a variable amount of energy dependent on fluctuations of the electric load demand, which is the load-following operation.
To control the generating units both in the constant output power and in a load-following operation, with technical constraints, and, at the same time, to optimize the total costs of energy in the system is the aim of this research [19,69].
Nuclear plants have a lifetime of 40–60 years, depending on the maintenance and upgrades. A commissioned nuclear reactor continues with the power output for long periods of time and facilitates grid management. SMRs have capacity factors of 90–95% and thus present economic viability to pay back the initial investment. Their costs may be analyzed into capital costs and operational costs. Capital costs refer to costs associated with the plant design, licensing, and construction, interest during construction, and contingency costs. Operational costs involve personnel, materials, equipment, fuel, operation and maintenance (O&M), and decommissioning. The operational costs of SMRs cover the following [70,71]:
- Fuel costs, mainly of uranium or plutonium.
- O&M costs including employee remuneration, equipment maintenance, and overheads.
- Decommissioning costs for dismantling equipment and the disposal of radioactive waste.
- Insurance, regulatory compliance, and licensing costs related to nuclear operations.
The validity of an economic model of a nuclear power plant without considering factors such as efficiency losses and accidents risks on the total cost rate depends on the inclusion and weighting of other key cost factors such as capital costs, fuel expenses, operation, and maintenance costs. In nuclear power plants, other costs are a significant component of total costs [72]. Studies [24,73] suggest that elements such as capital investment, fuel prices, and operational efficiencies play critical roles in the economic viability of nuclear reactors, particularly SMRs and desalination plants. Publication [73] focuses on fuel and operational costs in efficiency optimization, while [24] highlights the cost breakdown in SMRs, showing the importance of factors like other costs.
While these models might miss a portion of the financial picture, they can provide valuable insights into cost optimization through technical and operational efficiencies. There is an impact of taxes on carbon and pollution in nuclear economics; while taxes have environmental and economic implications, their exclusion from models does not invalidate the analysis, but limits the generality when assessing net-benefit scenarios, especially when policy and regulatory environments are key to financial sustainability [74]. Thus, the cost rate of nuclear power plants refers to the total cost of producing electricity per unit of the output, and includes fuel costs (procurement and processing of nuclear fuel) and operational and maintenance costs (O&M). Other costs may be neglected.
The cost rate of a nuclear reactor is found from the total cost of energy per unit of time, including fuel costs and O&M costs. The optimization models include thermal units [46] and nuclear reactor [19]. Thus, the cost rate of a nuclear reactor, , with the number of reactors, , during a duration of time is
where is the power output and is the total cost of the nuclear unit [75].
The objective function is the total operating cost rate of the generators [19,46]. The cost rate per hour is considered, where is power-generated by thermal unit . The sum of the generated is equal to the electrical load , and the power balance constraint is expressed in Equation (2) by the function which is
The total maximum power generated exceeds the load by an amount of reserve of power . There are limits in the generation between the minimum and maximum values, and [46,69].
The nuclear power output to the power system by the reactors is limited to a maximum value :
The power balance of the system with thermal and nuclear units is
Economic optimization to a nuclear and thermal system with an electrical load uses, as the objective function, the total cost rate function . The optimization with constraints for the power balance and power bound of this system is
and is the total operating cost rate of thermal generators and is the total operating cost rate of nuclear reactors. The objective function is
where is the direct cost coefficient of the nuclear unit .
Minimization with constraints can be based on the Lagrangian function , which is equal to the objective function summed with the constraint multiplied by variable lambda , corresponding to the incremental cost rate [46]. The optimal solution results computing the partial derivatives of and the incremental cost rates are
The optimal power dispatch occurs when the marginal cost of each thermal unit equals the Lagrange multiplier when the incremental cost of electricity is balanced across the units. Then, the cost rates are computed from heat rates and fuel costs .
The lambda iteration method introduces small variations in the amounts constrained by the conditions from Equations (4) and (6), and the solutions for optimal costs of thermal powers are in matrix :
The minimal operational costs of thermal units , the total minimal costs of thermal power units , and the total minimal costs of the hybrid nuclear–thermal power plant are computed from Equations (24) and (25), respectively.
The mathematical model and computer program were tested for errors in the input data. Many tests were carried out with varying operating data of the electric power system. By doing repeated checks, we tested the simulation program with many combinations of input variables and data, and we did not encounter a model operation problem. We excluded unforeseen input data errors with additional program logic design control loops to minimize the possibility of future errors’ input and incorrect results. Thus, it was proved that the model is accurate and the program well designed and reliable.
4. Scenarios Studied
In our case study, the power system involves one small modular reactor (SMR), three thermal units (Th1, Th2, and Th3), and varying electrical loads between 430 MW and 675 MW. The data of the thermal units Th1–Th3 are in Table A1, and the data of the SMR are in Table A2 in Appendix A. The rates of heat/hour are given as functions and the cost rate is obtained using Equation (12). The lignite cost coefficient and nuclear cost coefficient are 105 Eur/Gcal and 150 Eur/MWh, respectively.
Three scenarios are studied, which are described in Table 1:

Table 1.
The three scenarios applied to the power system.
- Scenario 1: the SMR generates a constant output power and the three thermal units generate varying outputs;
- Scenario 2: the SMR generates load-following output power and the three thermal units generate varying outputs;
- Scenario 3: the SMR is deactivated and the three thermal units are activated and generate varying outputs. This operation is the base case study for the comparison of the results obtained by activating the SMR in Scenarios 1 and 2.
4.1. Scenario 1: Nuclear Reactor Generates Constant Power; Three Thermal Units Generate Varying Outputs
The nuclear reactor produces rated power over 24 h, between the hours of 1:00 and 24:00. The thermal units Th1–Th3 produce optimal power and reserves of powers, computed using small variations of between 180 < < 194, as shown in Figure 3.
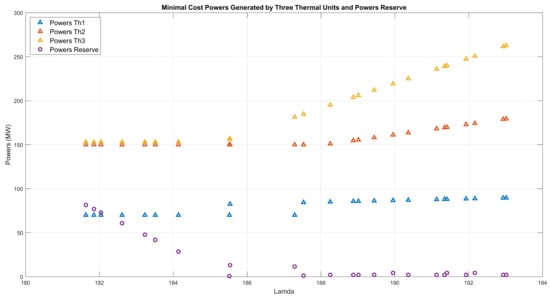
Figure 3.
Scenario 1. The minimal cost powers generated and the reserves of power versus during 24 h. The optimal values are 180 < < 194.
The minimal costs of powers of Th1–Th3 and of nuclear reactor over 24 h are plotted in Figure 4. In Figure 5 are plotted the total minimal cost powers produced by the nuclear reactor, by three thermal units, the reserves of powers and the electrical load over 24 h.
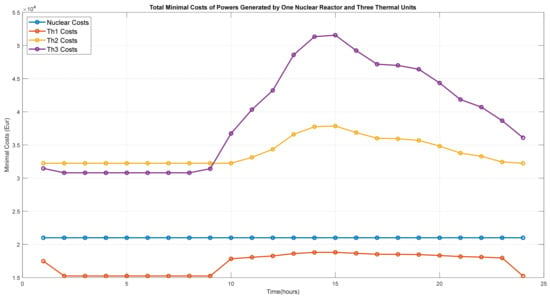
Figure 4.
Scenario 1. Total minimal costs of power generated by nuclear reactor and three thermal units over 24 h.

Figure 5.
Scenario 1. The total electrical load, the thermal powers generated by three thermal units, and the reserves of power over 24 h. The nuclear unit generates constant power.
4.2. Scenario 2: Nuclear Reactor Generates Load-Following Output; Three Thermal Units Generate Varying Output
The minimal cost powers of Th1–Th3 versus lambda are shown in Figure 6. The computed optimal values of are 184 < < 194. In Figure 7 are plotted the total minimal costs of powers generated by the three thermal units and the nuclear reactor in load-following mode over 24 h. In Figure 8 are shown the total electrical load demand, the thermal powers generated by the thermal units, the power generated by the nuclear reactor in the load-following operation, and the reserves of power over 24 h.
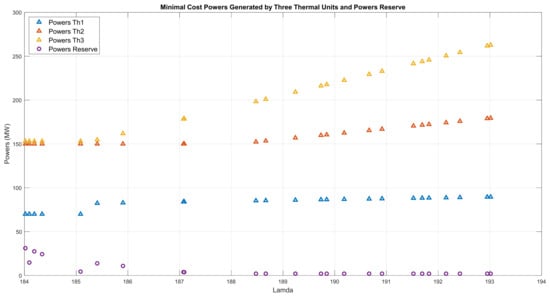
Figure 6.
Scenario 2. The minimal cost powers produced by Th1–Th3 and reserves of powers versus lambda over 24 h. The SMR is load-following. The optimal values are 184 < < 194.
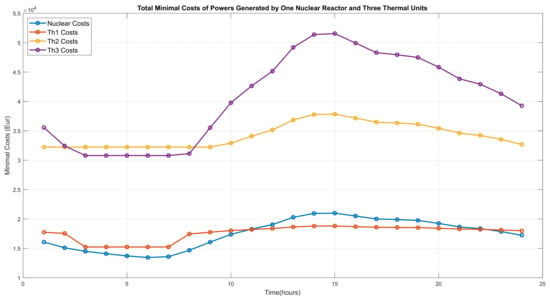
Figure 7.
Scenario 2. Total minimal costs of powers generated from three thermal and nuclear reactors in load-following mode over 24 h.
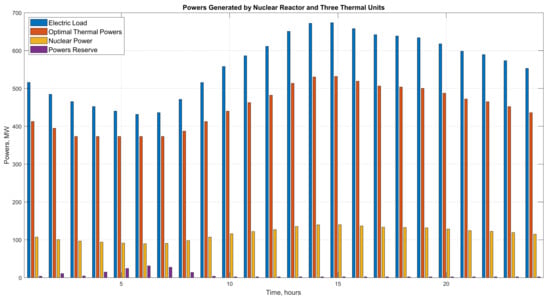
Figure 8.
Scenario 2. The total electrical load, the thermal powers generated by three thermal units, and the reserves of power over 24 h. The SMR generates power in load-following mode.
4.3. Scenario 3: Nuclear Reactor Is Deactivated; Three Thermal Units Generate Varying Output
In Figure 9 are the minimal cost powers produced by Th1–Th3 and the reserves of powers versus , while the SMR is deactivated. The optimal is 188 < < 208. In Figure 10 are the minimal costs of powers of Th1–Th3 over 24 h, while the SMR is deactivated. In Figure 11 are the total minimal costs of the generated powers from thermal units Th1–Th3, the reserves of power, and the electrical load during 24 h, while the SMR is deactivated.
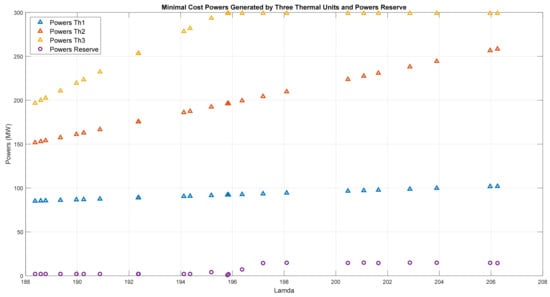
Figure 9.
Scenario 3. The minimal cost powers generated by Th1–Th3 and the reserves of power versus lambda over 24 h. The optimal λ is 188 < < 208. The SMR is deactivated.
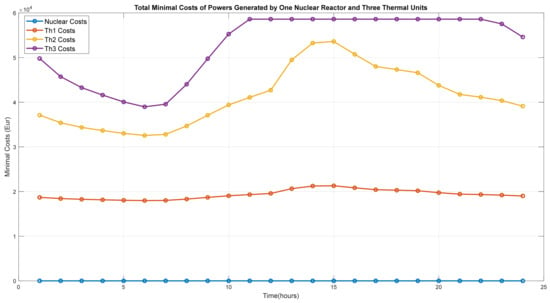
Figure 10.
Scenario 3. Total minimal costs of powers generated from thermal units Th1–Th3 over 24 h. The SMR is deactivated.
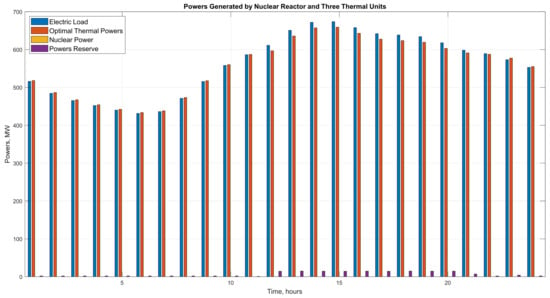
Figure 11.
Scenario 3. The total electrical load, the thermal powers generated by Th1–Th3, and the reserves of power over 24 h. The SMR is deactivated.
5. Results and Discussion
Summing up from the three scenarios studied: in Scenario 1, the system operates with thermal units Th1–Th3 activated, and the nuclear reactor is working in a constant output mode; in Scenario 2, thermal units Th1–Th3 are activated, and the nuclear unit is working in load-following mode; in Scenario 3, the thermal units Th1–Th3 are activated and the nuclear reactor is deactivated. The operation of Scenario 3 is assumed as a reference case study, and its results will be taken as a basis for comparison with those from Scenario 1 and Scenario 2. The data used to solve the operational conditions, i.e., the technical data of the thermal units, the data of the nuclear reactor, and the cost values of fuels, are in Appendix A.
For the case study of electrical loads from Figure 2 and of the three scenarios, Figure 3, Figure 6 and Figure 9 illustrate the minimum costs’ powers produced by the thermal units Th1–Th3 for small variations of during a 24 h period. Regarding the amounts of power generated during 24 h in the three scenarios and considering the same electrical loads from Figure 2, Figure 5, Figure 8 and Figure 11 present the minimum costs’ powers generated with constraints from the nuclear unit and the activated thermal units Th1–Th3 (Figure 5); from the nuclear unit and the activated thermal units Th1–Th3 (Figure 8); and from the deactivated nuclear reactor and activated thermal units Th1–Th3 (Figure 11). The reserves of the powers are shown in Figure 5, Figure 8 and Figure 11, too. From Figure 5, Figure 8 and Figure 11, it is clearly shown that in situations where the nuclear units are operating with a constant output or load following, either activated or deactivated, the thermal units Th1–Th3 regulate their energy production in order to follow the fluctuations of the electrical load, thus compensating the variability in production by the nuclear reactor. Furthermore, the optimal control applied to thermal units places the thermal units at minimal generation levels, thus minimizing CO2 emissions from fossil fuels such as lignite. Figure 12 illustrates the balance of total powers generated during the three Scenarios by the optimal controlled system with nuclear and thermal units, adding the reserves of power generated.
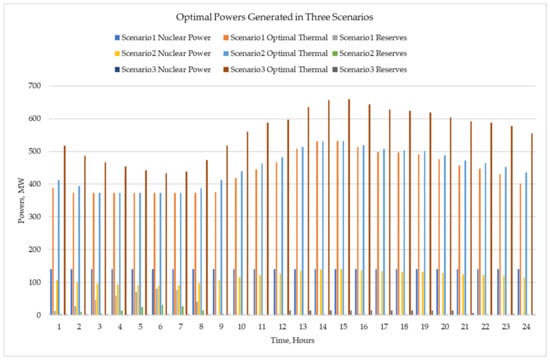
Figure 12.
Balance of total powers generated from nuclear and thermal sources and reserves of powers.
Figure 13 depicts the balance of the total powers generated during the three scenarios and the total electrical load over 24 h: in Scenario 1, a hybrid nuclear and thermal arrangement with it being nuclear in a controlled constant output mode; in Scenario 2, a nuclear and thermal configuration with the nuclear reactor controlled in load-following operation; and in Scenario 3, the three thermal units operate while the SMR is deactivated. Figure 12 and Figure 13 show the detailed situation of the power balance. In Figure 14 are plotted the total optimal costs of powers, and the varying lambda versus time for the three scenarios.
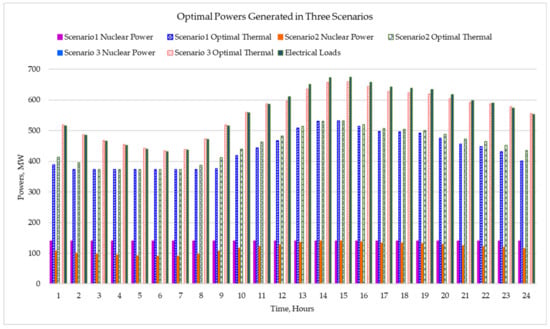
Figure 13.
Balance of total powers generated from nuclear and thermal sources and electrical loads.
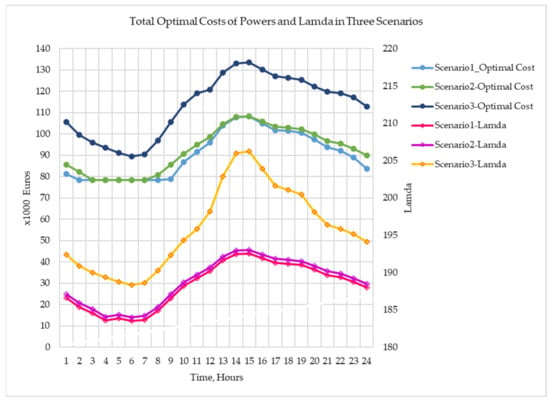
Figure 14.
Total optimal costs of powers and varying lambda versus time for the three scenarios.
Table 2 shows the accumulated results for the three scenarios. The basis for comparison is Scenario 3. Table 2 concentrates the results from the method described in Section 3, for the three Scenarios 1–3 and electric loads during 24 h. Specifically, the results are in the rows titled “Energy, MWh”, “Costs, EUR”, and “Cost/Energy. Eur/MWh”. The results in Table 2 show that over 24 h, thermal units Th1, Th2, and Th3 operate as follows:

Table 2.
Accumulated results for optimal constant nuclear and varying thermal power (Scenario 1), optimal load-following nuclear and varying thermal power (Scenario 2), and varying thermal power (Scenario 3) over 24 h. The basis (100%) is the optimal thermal power (Scenario 3).
- In Scenario 1, at the minimum limits of powers, , , and , between the hours of 24:00 and 9:00, 23:00 and 11:00, and 2:00 and 8:00, respectively. Therefore, during the 24 h, the three thermal units will generate at , , and .
- In Scenario 2, at the minimum limits of powers, , between the hours of 3:00 and 7:00, between 1:00 and 9:00, and between 3:00 and 7:00, respectively. Therefore, during the 24 h, the three thermal units will be at , , and .
- In Scenario 3, at , , and between 22:00 and 11:00, and between 11:00 and 22:00. In Scenario 3 with the SMR deactivated, the Th3 worked at a maximum capacity during the night, 22:00–11:00, and this fact indicates the most polluted situation.
The results of the minimum mean energy cost (Eur/MWh) and the minimum mean power cost (Eur/MW) per generating unit for all scenarios are in Table 3. The same results expressed in a percentage can also be seen in Figure 15, where the trend line is added, showing the decrease in the costs of energy generated related to the selection of the scenarios.

Table 3.
Mean minimum costs of energy and power generated for the three Scenarios.
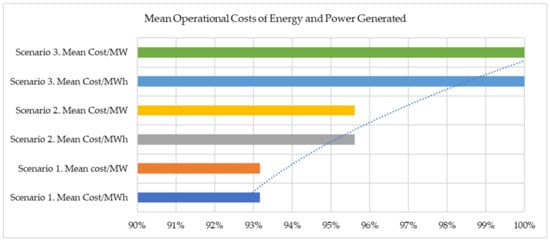
Figure 15.
Mean operational costs of energy and power generated (horizontal bars) and trend of costs (dotted line).
The mean minimum power cost generated by the constant output nuclear reactor and thermal system is at 7.90 Eur/MW (Scenario 1); this value is lower than the minimum mean power cost generated by the nuclear reactor with a load-following output and thermal system at 8.10 Eur/MW (Scenario 2). Also, it is lower than the minimum mean power cost produced by the thermal system alone at 8.47 Eur/MW (Scenario 3), Table 3.
Thus, the value of 8.47 Eur/MW for one MW of power generated by the lignite system is higher than the value of 8.10 Eur/MW for one MW of power generated by the nuclear reactor producing the load-following output with the thermal system. Also, it is higher than the value of 7.90 Eur/MW for one MW of power generated by the constant output nuclear reactor working in parallel with the thermal system (Table 3).
Also, both operations’ constant output and load-following nuclear reactor working in parallel with fossil fuel thermal power units decreases the minimum cost per MW and per MWh compared to the electricity produced from fossil fuels only, Figure 15.
Correspondingly, the cost of the energy produced by the constant output nuclear reactor and thermal system at 189.49 Eur/MWh (Scenario 1) is lower than the cost of energy produced by the load-following output nuclear reactor and thermal system at 194.47 Eur/MWh (Scenario 2), and is lower than the cost of the energy produced by the thermal system alone at 203.38 Eur/MWh (Scenario 3), Table 3.
Table 4 shows the differences expressed in percentages of the mean costs of the energy and power generated, and in Figure 16, the trend line is added: between the constant output and load-following operation (Scenarios 1 and 2), the difference is −2.45%; between the constant nuclear output and nuclear disabled (Scenarios 1 and 3), the difference is −6.83%; and between the load-following nuclear generation and nuclear disabled (Scenarios 2 and 3), the difference is −4.38%. In Figure 16, the differences expressed in the percentage of the mean costs of the energy and power generated are shown and the trend line of differences of costs is added.

Table 4.
Differences of mean costs of Energy and power generated.
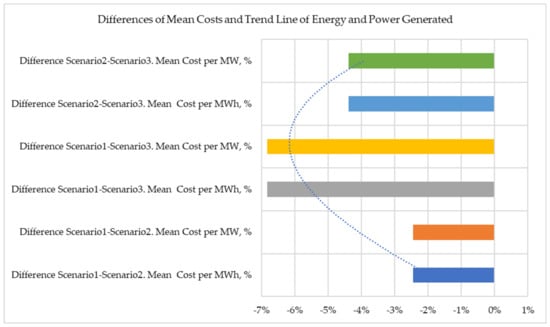
Figure 16.
Differences expressed in percentage of mean costs of energy and power generated (horizontal bars) and trend of differences of costs (dotted line).
The costs of energy of the nuclear and thermal system can be lowered more if the reserves of power are taken into account (shown in Figure 3, Figure 5, Figure 6, Figure 8, Figure 9, Figure 11 and Figure 12). Such reserves of power could be either accumulated in storage systems and later supplied to consumers, or can be supplied to other power systems where there are shortage situations.
The results from this study show that the cost of lignite-based electricity is higher than the cost of electricity produced from a constant output nuclear reactor or from a load-following nuclear reactor with a thermal system. Additionally, the above analysis indicates that nuclear feasibility is influenced by fuel costs and financing [76,77].
As regards the reduction of CO2 emissions related to the energy sources, it emerged that nuclear energy is more cost-effective [78]. Thus, it is expected that plants with renewable sources, such as solar and wind, will generate electricity at a comparable average cost, making them competitive in production from nuclear fuels [79]. In addition, the costs for the production of nuclear energy are related to accidents and waste disposal and are higher compared to renewable energy sources, which are known to have a minimal environmental impact.
Details of the CO2 emission calculation method are provided below.
In Table A3 in Appendix A, the specific CO2 emissions of different fuels in power generation are given [80]. In the case study of the Megalopolis thermal plant, the fuel is lignite. The lignite plant was built in the year 1970 [32], and it can be considered as old.
According to Table A3, Appendix A, in the case study of Megalopolis, the specific emissions including the upstream chain of old lignite power plants are at 1.2 gCO2/MWh [80]. Emissions including the upstream chain are calculated from the primary energy-related CO2 emission factors, including upstream chain emissions and other greenhouses gases as CO2 equivalents divided by the power plant efficiency, in gCO2-eq/kWhel. The amount of energy (in MWh) from Table 2 is multiplied by the specific emission quantity of 1.2 (in gCO2/MWh) and the total quantity in gCO2 is obtained. The procedure is applied successively for the three scenarios.
In Table 5, the computed the CO2 emissions of lignite thermal units and the savings due to the introduction of a nuclear reactor are shown. In Figure 17, the savings of emissions of CO2 due to the introduction of a nuclear reactor in Scenarios 1 and 2 are shown. The results show that the CO2 emissions in Scenario 1 (constant-output SMR) are at 78.53% and are lower than the emissions in Scenario 2 (load-following SMR) of 80.67% which are lower than the emissions from Scenario 3 (SMR deactivated) of 100%.

Table 5.
CO2 emissions of lignite thermal units and savings of CO2 emissions due to introduction of nuclear reactor.
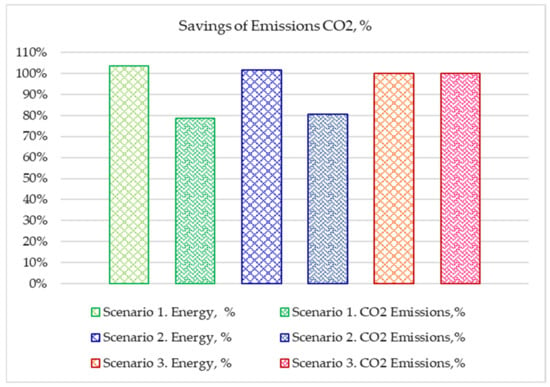
Figure 17.
Savings of CO2 emissions in Scenarios 1 and 2 referred to CO2 emissions in Scenario 3.
The present research calculated the results of the three scenarios that we analyzed and discussed in order to study:
- The minimal cost powers generated and the reserves of power versus ;
- Total minimal costs of power generated by nuclear reactor and by three thermal units during 24 h;
- The total powers generated by a nuclear reactor, by three thermal units, the reserves of power, and the electrical load during 24 h;
- Balance of total powers generated from nuclear and thermal sources and the reserves of powers;
- Total optimal costs of powers and the varying lambda versus time for the three scenarios;
- The results for optimal energy (MWh), optimal costs (Eur), and optimal cost/energy (Eur/MWh);
- The mean minimum costs of energy and power generated for the three scenarios;
- The differences between applying three scenarios in terms of mean minimum costs of energy and power generated;
- The CO2 emissions of lignite thermal units and the savings of CO2 emissions due to introduction of a nuclear reactor.
The three scenarios we chose were considered as the most representative. Even if we analyze more scenarios, the most important results will not change. The most important results are that substituting lignite-based power plants with nuclear reactors reduces electricity costs and, at the same time, reduces environmental pollution from CO2 emissions. Therefore, based on the above the analysis, the results are adequate.
Optimizing energy production in hybrid systems brings efficiency improvements and contributes to economic sustainability by lowering operational costs and enhancing resource utilization. Hybrid systems with renewable energy sources improve economic sustainability. Nuclear energy can be integrated into power generation due to the lower environmental impact and potential for cost savings. Hybrid systems with nuclear energy are important in decarbonizing global energy as part of solutions to boost clean energy in energy systems.
The new information from this study for explaining nuclear energy problems can be introduced in the energy sector and also for education and research. Reports combining mathematics, control systems, power systems, and economics offer new systematic ideas to international readers [81]. Recent developments in technologies have impacted research and education in energy engineering [82] to develop future careers of engineering graduates and researchers. The retrofit by the replacement of fossil fuels power units by SMRs can be introduced in different locations, such as in islands or other isolated areas.
A qualitative and quantitative comparison of the results obtained by this work compared to similar approaches was carried out. Study [19] presents an economic optimization of a hybrid power plant integrating nuclear, solar, and thermal energy sources under load-following conditions. The research employs multi-criteria decision making to minimize electricity production costs while considering operational constraints and varying fuel prices. This study’s findings suggest that incorporating nuclear energy into hybrid systems can reduce electricity generation costs compared to systems relying solely on solar and thermal sources. This approach involves a case study with three scenarios: Scenario 1: a hybrid system with nuclear, solar, and thermal units active; Scenario 2: a hybrid system with active solar and thermal units and a deactivated nuclear unit; and Scenario 3: a system with only active thermal units while with both deactivated nuclear and solar units. This study [19] utilizes optimization techniques to determine the minimum cost of electricity production over a 24 h period, considering factors such as the fuel costs, operational constraints, and load demand. The study’s quantitative results indicate Scenario 1: the average energy cost of 196.63 EUR/MWh; Scenario 2: the average energy cost of 201.00 EUR/MWh; and Scenario 3: the average energy cost of 198.83 EUR/MWh.
These results show that the inclusion of nuclear energy in the hybrid system (Scenario 1) leads to lower electricity production costs compared to the other scenarios.
When comparing this work’s findings with other studies:
- Study [39] discussed the economic and strategic aspects of small modular reactors (SMRs), highlighting their potential for integration into hybrid systems.
- Study [41] provided a critical assessment of SMRs, questioning their economic viability and scalability.
- Study [83] explored the compatibility of nuclear power with renewable energy sources, emphasizing the need for flexible operation.
Studies [19,39,41,83] offer broader perspectives on the integration of nuclear energy into hybrid systems, with varying conclusions on economic benefits and operational challenges.
Our study contributes to addressing hybrid energy systems by providing a case-specific analysis of economic optimization. The findings support the notion that integrating nuclear energy can reduce electricity production costs under certain conditions. This study offers valuable insights into the economic optimization of hybrid power plants combining nuclear and thermal energy sources. The research suggests potential cost benefits of including nuclear energy in thermal systems. However, when compared to other studies in the field, the findings highlight the importance of context-specific analyses and the need for further research to generalize conclusions across different scenarios and system configurations.
6. Conclusions
This paper has investigated the effects of replacing one thermal power unit with one SMR of equivalent rated power, in terms of the minimum cost of the electricity generated by the hybrid nuclear reactor–thermal units system.
Multi-criteria decision making was used to achieve the advantages of cleaner electricity, lower CO2 emissions, and the minimum cost of electricity generated. One criterion is the environmental: lignite causes environmental pollution with carbon dioxide emissions, while nuclear fuels do not produce such emissions. A second criterion is the economic costs associated with the hybrid nuclear–thermal plant operating costs. Based on the economic criterion, although nuclear reactors have a higher initial investment capital, their fuel and operating costs are lower. A third criterion studies how the operating cycle of a nuclear reactor affects the cost of power generation.
Two operating modes were investigated: (i) the generation of a constant quantity of energy and (ii) the generation of a variable quantity of energy depending on fluctuations of the electrical load demand and the load-following mode.
According to the fluctuations of the electrical loads, the optimal operating points are identified and the thermal units adjust their operation to the minimum output power and below the maximum power during the various hours of the day.
Using the multi-criteria scenarios, the results show that the mean minimal cost of energy generated by hybrid SMRs with thermal units in constant output power operation is lower than the mean minimal cost of energy generated in the load-following mode by 2.45%. At the same time, carbon dioxide emissions in constant output power operation are lower than those produced in the load-following mode by 2.14%.
By minimizing the operating costs of the hybrid system, as a result, some of the thermal units have been put at the limit of the minimum power and the corresponding amounts of carbon dioxide emissions have been reduced too. The achievement of the minimum cost depends on the power balance and the operation of the nuclear reactor at a constant power or in the load-following mode. The cost of fuels affects the minimum cost of electricity production. Replacing fossil fuel thermal generators with nuclear ones leads to lower energy costs. To overcome initial investment difficulties with emerging technologies and achieve economic sustainability, economic incentives and supportive policies related to environmental and social factors are needed. Reducing carbon dioxide emissions can improve society’s perception of long-term sustainability.
In conclusion, the constant output power duty cycle of an SMR is more sustainable compared to the load-following duty cycle and also is more sustainable compared to lignite thermal stations. The validation of the results of this feasibility study requires data collection from the operation of a real hybrid nuclear–thermal power plant. However, the construction and commissioning of a real hybrid nuclear–thermal power plant is expected to take place in future years. Then, after the trial operation of the nuclear–thermal power plant, there will be available data from real-time measurements. Therefore, the verification of this feasibility study will be possible in the context of future research.
Future research directions will aim to change economic variables. The study of the volatility of fuel cost on the economics of a hybrid nuclear–thermal power system can become the topic of future research. This study will undertake the design of the model based on the sensitivity of costs. Fuel price volatility and maintenance schedules could be considered as variables.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in this article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
| Lambda, variable corresponding to incremental cost rate | |
| Small variations of lambda | |
| Function expressing the power balance constraint of the hybrid system | |
| Function expressing the power balance constraint of thermal system | |
| Total costs of the nuclear unit | |
| EMS | Energy Management System |
| , | Cost rate of nuclear reactor |
| Objective function, the total operating cost rate of the thermal generators | |
| Cost rate of thermal unit | |
| Objective function, total operating cost rate of the hybrid system | |
| Total operating cost rate of thermal generators | |
| Total operating cost rate of nuclear reactors | |
| Matrix of fuel costs of thermal units | |
| Fuel cost of thermal unit | |
| Matrix of minimal operational costs of thermal units | |
| Total minimal costs of thermal units | |
| Total minimal costs of thermal power plant | |
| Heat rates coefficients | |
| Heat rate of thermal unit | |
| Number of thermal units | |
| Number of nuclear reactors | |
| Lagrangian function | |
| Total number of thermal units | |
| Total number of nuclear units | |
| O&M | Operation and Maintenance |
| Power generated by thermal unit | |
| Power generated by nuclear reactor | |
| Electrical load | |
| , | Limits of generation of thermal units , minimum values, maximum values |
| Nuclear power output to the power system | |
| Nuclear power of reactors | |
| Maximum value nuclear power of reactors | |
| Matrix of optimal costs’ thermal powers | |
| Reserve of power | |
| SMR | Small modular reactor |
| Thi | Thermal unit |
| Cost coefficient of the nuclear unit | |
| Duration of time |
Appendix A
In Table A1, there are the data of three thermal units selected from the Greek power system [67]. In Table A2, there are the data of the nuclear reactors [84]. In Table A3, there are the CO2 emissions data [80].

Table A1.
Data of thermal units Th1–Th3.
Table A1.
Data of thermal units Th1–Th3.
| Thermal Units | (MW) | (MW) | Locations: Peloponese, Greece [68] | |||
|---|---|---|---|---|---|---|
| Th1 | 70 | 130 | 0.00507 | 0.9300 | 55.185 | Megalopoli 1, Megalopoli 2. |
| Th2 | 150 | 300 | 0.00079 | 1.5520 | 56.318 | Megalopoli 3. |
| Th3 | 150 | 300 | 0.00034 | 1.6620 | 31.164 | Megalopoli 4. |

Table A2.
Data of the SMR [84].
Table A2.
Data of the SMR [84].
| Rated Power: | 140 MWe |
| Efficiency: | 45% |
| Main Temperature: | 585 °C |
| Reactor Outlet Temperature: | 650 °C |
| Intermediate Salt: | “Solar”/Nitrate Salt |
| Refueling Type: | Online |

Table A3.
Specific CO2 emissions of fuels in power generation [80].
Table A3.
Specific CO2 emissions of fuels in power generation [80].
| Fuel Type: | Lignite | Hard Coal | Natural Gas | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Old | Modern | Mean | Old | Modern | Mean | New (Turbine) | New (CCGT) | Mean | |
| Direct CO2 emissions. (*) | 1173 | 831 | 1049 | 939 | 663 | 867 | 512 | 340 | 358 |
| CO2 emissions including upstream chain. (**) | 1200 | 850 | 1073 | 1051 | 742 | 970 | 624 | 415 | 436 |
(*) Calculated from the primary energy-related CO2 emission factors. Excluding upstream chain emissions, excluding other greenhouse gases, divided by power plant efficiency. gCO2/kWhel [85]. (**) Calculated from the primary energy-related CO2 emission factors. Including upstream chain emissions and other greenhouses gases as CO2 equivalents CO2-eq, divided by power plant efficiency. gCO2-eq/kWhel [85].
References
- Kartal, M.T.; Santosh, M.; Ulussever, T.; Pata, U.K.; Depren, S.K. A comprehensive review of progress in sustainable development goals from energy and environment perspectives. Energy Strategy Rev. 2024, 56, 101550. [Google Scholar] [CrossRef]
- Froggatt, A.; Schneider, M. Nuclear Power Versus Renewable Energy-A Trend Analysis. Proc. IEEE 2015, 103, 487–490. [Google Scholar] [CrossRef]
- Alonso, G.; Bilbao, S.; del Valle, E. Economic competitiveness of small modular reactors versus coal and combined cycle plants. Energy 2016, 116, 867–879. [Google Scholar] [CrossRef]
- Ioannides, M.G.; Stamelos, A.; Papazis, S.A.; Papoutsidakis, A.; Vikentios, V.; Apostolakis, N. IoT monitoring system for applications with renewable energy generation and electric drives. Renew. Energy Power Qual. 2021, 19, 565–570. [Google Scholar] [CrossRef]
- Papazis, S.A.; Ioannides, M.G.; Fotilas, P.N. An information system for the multiple criteria assessment of renewable energy power plants. Wind Eng. 2000, 24, 81–99. [Google Scholar] [CrossRef]
- Behera, S.; Barisal, A.K.; Behera, S.; Bagal, D.K. Combined Economic Emission Dispatch including Variable Energy Resources. Curr. World Environ. 2024, 19, 2. [Google Scholar] [CrossRef]
- World Nuclear Association, WNA. World Nuclear Performance Report. Available online: https://world-nuclear.org/images/articles/World-Nuclear-Performance-Report-2024.pdf (accessed on 27 November 2024).
- EIA Energy Information Administration. Available online: https://www.eia.gov/tools/ (accessed on 21 July 2024).
- Papazis, S.A. Integrated Economic Optimization of Hybrid Thermosolar Concentrating System Based on Exact Mathematical Method. Energies 2022, 15, 7019. [Google Scholar] [CrossRef]
- Olabode, O.E.; Ajewole, T.O.; Okakwu, I.K.; Alayande, A.S.; Akinyele, D.O. Hybrid power systems for off-grid locations: A comprehensive review of design technologies, applications and future trends. Sci. Afr. 2021, 13, e00884. [Google Scholar] [CrossRef]
- López-Castrillón, W.; Sepúlveda, H.H.; Mattar, C. Off-Grid Hybrid Electrical Generation Systems in Remote Communities: Trends and Characteristics in Sustainability Solutions. Sustainability 2021, 13, 5856. [Google Scholar] [CrossRef]
- Aghapouramin, K. Technical, Economical, and Environmental Feasibility of Hybrid Renewable Electrification Systems for off-Grid Remote Rural Electrification Areas for East Azerbaijan Province, Iran. Technol. Econ. Smart Grids Sustain. Energy 2020, 5, 20. [Google Scholar] [CrossRef]
- IAEA International Atomic Energy Agency. Developing an Economic Performance System to Enhance Nuclear Power Plant Competitiveness, Technical Reports Series No. 406, Vienna. 2002. Available online: www.iaea.org/publications/6118/developing-an-economic-performance-system-to-enhance-nuclear-power-plant-competitiveness (accessed on 17 June 2024).
- IAEA International Atomic Energy Agency. Economic Performance Indicators for Nuclear Power Plants, Technical Reports Series No. 437, Vienna. 2006. Available online: www.iaea.org/publications/7179/economic-performance-indicators-for-nuclear-power-plants (accessed on 17 June 2024).
- Cacuci, D.G. (Ed.) Handbook of Nuclear Engineering; Springer Science & Business Media: New York, NY, USA; Berlin, Germany, 2010; ISBN 978-0-387-98150-5. [Google Scholar]
- ΙAΕA International Atomic Energy Agency. Management Strategies for Nuclear Power Plant Outages, Technical Reports Series No. 449, Vienna. 2007. Available online: www.iaea.org/publications/7385/management-strategies-for-nuclear-power-plant-outages (accessed on 17 June 2024).
- IAEA, International Atomic Energy Agency. Status of Small Reactor Designs Without On-Site Refueling; Nuclear Energy Series, Technical Reports IAEA-TECDOC-1536; IAEA: Vienna, Austria, 2007. [Google Scholar]
- Wang, Y.; Chen, W.; Zhang, L.; Zhao, X.; Gao, Y.; Dinavahi, V. Small Modular Reactors: An Overview of Modeling, Control, Simulation, and Applications. IEEE Access 2024, 12, 39628–39650. [Google Scholar] [CrossRef]
- Papazis, S.A. Economic Optimization of a Hybrid Power Plant with Nuclear, Solar, and Thermal Energy Conversion to Electricity. J. Nucl. Eng. 2025, 6, 2. [Google Scholar] [CrossRef]
- RAVEN Risk Analysis Virtual Environment, Idaho National Laboratory. Available online: https://inl.gov/raven/ (accessed on 7 May 2025).
- Epiney, A.; Rabiti, C.; Talbot, P.; Alfonsi, A. Economic analysis of a nuclear hybrid energy system in a stochastic environment including wind turbines in an electricity grid. Appl. Energy 2020, 260, 114227. [Google Scholar] [CrossRef]
- Son, I.W.; Jeong, Y.; Son, S.; Park, J.H.; Lee, J.-I. Techno-economic evaluation of solar-nuclear hybrid system for isolated grid. Appl. Energy 2022, 306, 118046. [Google Scholar] [CrossRef]
- Nøland, J.K.; Hjelmeland, M.N.; Hartmann, C.; Tjernberg, L.B.; Korpås, M. Overview of Small Modular and Advanced Nuclear Reactors and Their Role in the Energy Transition. IEEE Trans. Energy Convers. 2025. early access. [Google Scholar] [CrossRef]
- Asuega, A.; Limb, B.J.; Quinn, J.C. Techno-economic analysis of advanced small modular nuclear reactors. Appl. Energy 2023, 334, 120669. [Google Scholar] [CrossRef]
- Ioannides, M.G.; Tuduce, R.; Cristea, P.-D.; Papazis, S.A. Wind power generating systems based on double output induction machine: Considerations about control techniques. In Proceedings of the 20th International Conference on Systems, Signals and Image Processing (IWSSIP 2013), Bucharest, Romania, 7–9 July 2013; pp. 103–107. [Google Scholar] [CrossRef]
- IAEA Advanced Reactors Information System (ARIS). Advances in Small Modular Reactor Technology Developments, 2022 Edition. Available online: https://aris.iaea.org/publications/SMR_booklet_2022.pdf (accessed on 27 November 2024).
- Nøland, J.K.; Hjelmeland, M.; Korpås, M.; Tjernberg, L.B. The Potential of Small Modular Reactors to Provide System-Bearing Services in the Future Power Grid. In Proceedings of the 2024 IEEE PES Innovative Smart Grid Technologies Europe (ISGT EUROPE), Dubrovnik, Croatia, 14–17 October 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Bartela, Ł.; Gładysz, P.; Ochmann, J.; Qvist, S.; Sancho, L.M. Repowering a Coal Power Unit with Small Modular Reactors and Thermal Energy Storage. Energies 2022, 15, 5830. [Google Scholar] [CrossRef]
- Luo, B.; Zhang, L.; Li, W.; Zhu, X.; Ye, Y.; Su, Y. Study on Conventional Island Retrofit Strategies for Converting Coal-Fired Power Plants to Nuclear Power Stations in China. Energies 2024, 17, 2912. [Google Scholar] [CrossRef]
- Kostadima, I. Why Greece and Europe Are Turning to Nuclear Energy. Available online: https://www.powergame.gr/energygame/690420/giati-ellada-kai-evropi-strefontai-stin-pyriniki-energeia/ (accessed on 16 July 2024).
- GEVernova Aeroderivative and Heavy-Duty Gas Turbines. Available online: https://www.gevernova.com/gas-power/products/gas-turbines/9f (accessed on 25 March 2025).
- PPC Factories Megalopolis. Available online: https://megalopolis.gr/ergostasia/ (accessed on 21 July 2024).
- Steam Power Station Megalopolis. Available online: https://www.terna.gr/activities/energy/project-combined-cycle-power-plant-in-megalopolis (accessed on 21 July 2024).
- Rompokos, P. Gas Turbines Operating in Greece and Software Development for Industrial Twin Shaft Gas Turbine Model Adaptation Using Operational Data. Diploma Thesis, National Technical University of Athens, Athens, Greece, 2018. [Google Scholar]
- Nguyen, K.H.N.; Rivas, A.; Delipei, G.K.; Hou, J. Reinforcement Learning-Based Control Sequence Optimization for Advanced Reactors. J. Nucl. Eng. 2024, 5, 209–225. [Google Scholar] [CrossRef]
- OECD Nuclear Energy Agency. Technical and Economic Aspects of Load Following with Nuclear Power Plants; OECD Int. At. Energy Agency: Paris, France, 2011; Available online: https://www.oecd.org/en/publications/technical-and-economic-aspects-of-load-following-with-nuclear-power-plants_29e7df00-en.html (accessed on 21 July 2024).
- Brits, Y.; Botha, F.; van Antwerpen, H.; Chi, H.W. A Control Approach Investigation of the Xe-100 Plant to Perform load-following within the Operational Range of 100–25–100%. Nucl. Eng. Des. 2018, 329, 12–19. [Google Scholar] [CrossRef]
- Locatelli, G.; Boarin, S.; Pellegrino, F.; Ricotti, M.E. Load following with small modular reactors (SMR): A real options analysis. Energy 2015, 80, 41–54. [Google Scholar] [CrossRef]
- Locatelli, G.; Bingham, C.; Mancini, M. Small modular reactors: A comprehensive overview of their economics and strategic aspects. Prog. Nucl. Energy 2014, 73, 75–85. [Google Scholar] [CrossRef]
- Veszely, K. Hybrid Combined Cycle Power Plant. In Proceedings of the International Conference Nuclear Energy for New Europe 2002, Kranjska Gora, Slovenia, 9–12 September 2002; pp. 0103.1–0103.8. Available online: https://arhiv.djs.si/proc/gora2002/pdf/0103.pdf (accessed on 23 December 2024).
- Ramana, M.V. Small Modular and Advanced Nuclear Reactors: A Reality Check. IEEE Access 2021, 9, 42090–42099. [Google Scholar] [CrossRef]
- Carelli, M.D.; Garrone, P.; Locatelli, G.; Mancini, M.; Mycoff, C.; Trucco, P.; Ricotti, M.E. Economic features of integral, modular, small-to- medium size reactors. Prog. Nucl. Energy 2010, 52, 403–414. [Google Scholar] [CrossRef]
- Shropshire, D. Economic viability of small to medium-sized reactors deployed in future European energy markets. Prog. Nucl. Energy 2011, 53, 299–307. [Google Scholar] [CrossRef]
- Kuznetsov, V. Options for small and medium sized reactors (SMRs) to overcome loss of economies of scale and incorporate increased proliferation resistance and energy security. Prog. Nucl. Energy 2008, 50, 2–6, 242–250. [Google Scholar] [CrossRef]
- Egieya, J.M.; Muritala Alade Amidu, M.A.; Hachaichi, M. Small modular reactors: An assessment of workforce requirements and operating costs. Prog. Nucl. Energy 2023, 159, 104632. [Google Scholar] [CrossRef]
- Papazis, S.A.; Bakos, G.C. Generalized model of economic dispatch optimization as an educational tool for management of energy systems. Adv. Electr. Comput. Eng. 2021, 21, 75–86. [Google Scholar] [CrossRef]
- Ioannides, M.G.; Papazis, S.A. Development of new curricula in vocational education for the needs of enterprises and employability of graduates. In Proceedings of the 2016 15th International Conference on Information Technology Based Higher Education and Training (ITHET), Istanbul, Turkey, 8–10 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Papazis, S.A.; Ioannides, M.G. Emerging Energy Engineering Education on the Way to Employment. In Learning with Technologies and Technologies in Learning. Lecture Notes in Networks and Systems; Auer, M.E., Pester, A., May, D., Eds.; Springer: Cham, Switzerland, 2022; Volume 456, pp. 655–677. [Google Scholar] [CrossRef]
- Persson, J.; Andgren, K.; Henriksson, H.; Loberg, J.; Malm, C.; Pettersson, L.; Sandström, J.; Sigfrids, T. Additional Costs for Load-Following Nuclear Power Plants. Experiences from Swedish, Finnish, German, and French Nuclear Power Plants; Technical Rapport 12.71; Elforsk: Stockholm, Sweden, 2012. [Google Scholar]
- EUR European Utilities Requirements. Available online: https://www.acer.europa.eu/sites/default/files/events/documents/2021-12/EUR.pdf (accessed on 29 June 2024).
- Boarin, S.; Ricotti, M.E. An evaluation of SMR economic attractiveness. Sci. Technol. Nucl. Install. 2014, 803698, 1–8. [Google Scholar] [CrossRef]
- Yan, X.; Yan, X.; Tachibana, Y.; Ohashi, H.; Sato, H.; Tazawa, Y.; Kunitomi, K. A small modular reactor design for multiple energy applications: HTR50S. Nucl. Eng. Technol. 2013, 45, 401–414. [Google Scholar] [CrossRef]
- Halimi, A.; Shirvan, K. Fuel Behavior Implications of Reactor Design Choices in Pressurized Water SMRs. In Nuclear Technology; Taylor & Francis: Abingdon, UK, 2024; pp. 1–24. [Google Scholar] [CrossRef]
- de Lara, A.; Nguyen, X.H.; Van Uffelen, P.; Shwageraus, E. Comparison of Advanced-Technology-Fuel Options in Soluble Boron-Free Small Modular Reactors. Ann. Nucl. Energy 2025, 218, 111355. [Google Scholar] [CrossRef]
- Alonso, G. Economic Competitiveness of Small Modular Reactors in a Net Zero Policy. Energies 2025, 18, 922. [Google Scholar] [CrossRef]
- Uwaba, T.; Maeda, S.; Mizuno, T.; Teague, M.C. Study on the mechanism of diametral cladding strain and mixed-oxide fuel element breaching in slow-ramp extended overpower transients. J. Nucl. Mater. 2012, 429, 149–158. [Google Scholar] [CrossRef]
- Cantini, F.; Adorni, M.; D’Auria, F. Nuclear Fuel Modelling During Power Ramp. J. Energy 2013, 62, 1–4. [Google Scholar] [CrossRef]
- Krall, L.; Macfarlane, A.; Ewing, R.C. Nuclear waste from small modular reactors. Proc. Natl. Acad. Sci. USA 2022, 119, e2111833119. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.; Khan, A.H.; Verma, R.; Kumar, D.; Kobayashi, K.; Usman, S.; Alam, S. Machine Learning and Artificial Intelligence-Driven Multi-Scale Modeling for High Burnup Accident-Tolerant Fuels for Light Water-Based SMR Applications. In Handbook of Smart Energy Systems; Fathi, M., Zio, E., Pardalos, P.M., Eds.; Springer: Cham, Switzerland, 2023; ISBN 978-3-030-72322-4. [Google Scholar] [CrossRef]
- Brinton, S. Used nuclear Fuel Storage Options Including Implications of Small Modular Reactors. Master’s Thesis, Massachusetts Institute of Technology. Technology and Policy Program, Cambridge, MA, USA, 2014. Available online: http://dspace.mit.edu/handle/1721.1/90067 (accessed on 10 May 2025).
- Wirth, B.D.; Morgan, D.; Kaoumi, D.; Motta, A.T. Microstructure and Property Evolution in Advanced Cladding and Duct Materials Under Long-Term and Elevated Temperature Irradiation: Modeling and Experimental Investigation. Final report for U.S. Department of Energy, Nuclear Energy University Programs, Project 10-392, Battelle Energy Alliance, LLC. 2013. Available online: https://core.ac.uk/display/71289064 (accessed on 10 May 2025).
- Wang, G.; Wang, Z.; Yun, D. Cladding Failure Modelling for Lead-Based Fast Reactors: A Review and Prospects. Metals 2023, 13, 1524. [Google Scholar] [CrossRef]
- Ahmadivala, M.; Sawicki, B.; Brühwiler, E.; Yamalas, T.; Gayton, N.; Mattrand, C.; Orcesi, A. Application of Time Series Methods on Long-Term Structural Monitoring Data for Fatigue Analysis. 2019. Available online: https://infoscience.epfl.ch/record/270411 (accessed on 10 May 2025).
- Rexhepi, V. The dispatch center’s role in the power grid operation and control. Electrotech. Rev. (Elektrotehniski Vestn.) 2023, 90, 1–2, 51–59. [Google Scholar]
- IPTO Independent Power Transmission Operator. Available online: https://www.admie.gr/en/market/reports/monthly-energy-balance (accessed on 5 November 2024).
- IPTO Independent Power Transmission Operator. Available online: https://www.admie.gr/sites/default/files/attached-files/type-file/2025/02/Energy_Report_202412_v2_en.pdf (accessed on 5 May 2025).
- Papanikolaou, D.N. Economic Operation of Power Systems. Master’s Thesis, University of Patras, Patras, Greece, 21 February 2008. [Google Scholar]
- Maps of Greece. Available online: https://earth.google.com/web (accessed on 7 December 2024).
- Conejo, A.J.; Baringo, L. Power System Operations; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 197–216. [Google Scholar] [CrossRef]
- Devezeaux De Lavergne, J.-G.; Thiollière, N. Chapter 2. Nuclear Costs: Methodological Aspects. In Nuclear Economy 1; Percebois, J., Thiolière, N., Eds.; Wiley: Hoboken, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Nuclear Energy Agency, N.E.A. Projected Costs of Generating Electricity, 2020 ed.; OECD Publishing: Paris, France, 2020; Available online: https://www.oecd-nea.org/jcms/pl_51110/projected-costs-of-generating-electricity-2020-edition?details=true (accessed on 27 November 2024).
- Owen, P.S.; Parker, M.B.; Omberg, R.P. Economic analysis of nuclear reactors. In Technical Report, May 1979; Hanford Engineering Development Laboratory: Richland, WA, USA, 1979. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, T.; Ran, K. The Energy-Saving Diagnosis of PWR Nuclear Power Station Based on the Thermo-Economic Analysis Model. In Proceedings of the 18th International Conference on Nuclear Engineering, Xi’an, China, 17–21 May 2010; pp. 137–144. [Google Scholar] [CrossRef]
- Roth, M. Going Nuclear for Climate Mitigation and Energy Systems Modeling of Carbon Dioxide and Air Pollution Taxes. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2020. [Google Scholar] [CrossRef]
- IAEA Power Reactor Information System (PRIS) Database. Available online: http://www.iaea.org/programmes/a2/ (accessed on 31 December 2020).
- Boldon, L.; Sabharwall, P. Small Modular Reactor: First-of-a-Kind (FOAK) and Nth-of-a-Kind (NOAK) Economic Analysis. Idaho National Laboratory, Summer 2014 Report, August 2014, INL/EXT-14-32616. Available online: https://inldigitallibrary.inl.gov/sites/sti/sti/6293982.pdf (accessed on 27 November 2024).
- Cacuci, D.G. Sensitivity Analysis, Uncertainty Quantification and Predictive Modeling of Nuclear Energy Systems. Energies 2022, 15, 6379. [Google Scholar] [CrossRef]
- Kim, H.-S. Comparison of cost efficiencies of nuclear power and renewable energy generation in mitigating CO2 emissions. Environ. Sci. Pollut. Res. 2021, 28, 789–795. [Google Scholar] [CrossRef]
- Ram, M.; Child, M.; Aghahosseini, A.; Bogdanov, D.; Lohrmann, A.; Breyer, C. A comparative analysis of electricity generation costs from renewable, fossil fuel and nuclear sources in G20 countries for the period 2015–2030. J. Clean. Prod. 2018, 199, 687–704. [Google Scholar] [CrossRef]
- Specific Carbon Dioxide Emissions of Various Fuels. Available online: https://www.volker-quaschning.de/datserv/CO2-spez/index_e.php (accessed on 27 November 2024).
- Stamelos, A.P.; Papoutsidakis, A.; Vikentios, V.; Papazis, S.A.; Ioannides, M.G. Experimental Educational System of AC Electric Drives with Internet of Things. In Proceedings of the XXIII International Conference on Electrical Machines ICEM 2018, Alexandroupoli, Greece, 3–6 September 2018; pp. 1497–1502. [Google Scholar] [CrossRef]
- Ioannides, M.G.; Papazis, S.A. Teaching and Research in Emerging Electrical Energy Engineering Education. In Proceedings of the 2021 International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 27–29 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Ingersoll, D.T.; Colbert, C.; Houghton, Z.; Snuggerud, R.; Gaston, J.W.; Empey, M. Can nuclear power and renewables be friends? In Proceedings of the ICAPP International Congress on Advances in Nuclear Power Plants, Nice, France, 3–6 May 2015; no. 15555. Available online: https://international.anl.gov/training/materials/BL/NuScale-Integration-with-Renewables_ICAPP15.pdf (accessed on 24 December 2024).
- Kairos Power. Available online: https://kairospower.com/technology/ (accessed on 6 July 2024).
- Umweltbundesamt 2022, Kohlendioxid-Emissionsfaktoren für Die Deutsche Berichterstattung atmosphärischer Emissionen. Available online: https://umweltbundesamt.de/sites/default/files/medien/361/dokumente/co2_ef_liste_2022_brennstoffe_und_industrie_final.xlsx (accessed on 25 March 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).