The Real-Time Distributed Control of Shared Energy Storage for Frequency Regulation and Renewable Energy Balancing

Abstract

With the increasing integration of renewable energy sources, distributed shared energy storage (DSES) systems play a critical role in enhancing power system flexibility, operational resilience, and energy sustainability. However, conventional scheduling methods often suffer from excessive communication burdens, limited scalability, and poor real-time responsiveness, especially when handling fast-changing frequency regulation signals and fluctuating renewable energy outputs. To address these challenges, this paper proposes a consensus-driven distributed online convex optimization method that enables a decentralized scheduling of energy storage units by leveraging the consensus algorithm for local decision-making while maintaining global consistency. Additionally, an adaptive event-triggered mechanism is designed to dynamically adjust the communication frequency based on system state variations, reducing redundant information exchange and ensuring convergence and stability in a fully distributed environment. Simulation results on the IEEE 14-bus test system show that the strategy reduces the communication load by 33–60% and improves the convergence speed by over 40% compared to baseline methods. It also demonstrates a strong adaptability to storage unit disconnection and reconnection. By enabling a fast and efficient response to grid services such as frequency regulation and renewable energy balancing, the proposed approach contributes to the development of intelligent and sustainable power systems.

1. Introduction

With the increasing integration of renewable energy, wind and photovoltaic power plants face challenges such as power fluctuations and deviation penalties, necessitating dynamic regulation through energy storage systems [1]. Shared energy storage, as a flexible resource allocation method, not only serves users and grid dispatching but also provides real-time leasing services for renewable energy plants, assisting in power smoothing and deviation management to enhance renewable energy utilization [2].

Shared energy storage has received increasing attention in both academia and industry due to its potential to improve energy flexibility, resource utilization, and cost-effectiveness in multi-user scenarios [3,4,5]. Based on the organization of storage resources, shared energy storage systems can be categorized into Centralized Shared Energy Storage (CSES) and Distributed Shared Energy Storage (DSES) [6]. CSES is typically deployed at specific locations in the form of large-scale storage stations, providing services to multiple users [7]. This model benefits from economies of scale and centralized management but also presents challenges such as high construction costs, spatial constraints, a limited flexibility, a strong dependence on the grid infrastructure, and a vulnerability to single-point failures. In contrast, DSES consists of multiple geographically dispersed storage units that coordinate efficiently through intelligent optimization strategies to achieve effective resource sharing [8]. This structure offers a greater flexibility and scalability but also introduces a higher control complexity due to the distributed architecture.

For a DSES system with multiple distributed storage units, optimization scheduling methods can be broadly categorized into centralized optimization scheduling and distributed optimization scheduling [9,10]. Centralized optimization scheduling relies on a central controller to collect global information and perform a unified optimization. Theoretically, this centralized approach provides an optimal coordination solution from a system-wide perspective [11]. However, due to the high computational complexity, extensive communication requirements, and the risk of single-point failures, its application in large-scale DSES is limited [12]. In particular, it struggles to coordinate a large number of storage units in real time, making it difficult to respond quickly to time-sensitive tasks such as frequency regulation [13]. Distributed coordination methods reduce reliance on a central coordinator by employing decentralized optimization strategies, where the optimization process primarily relies on local information exchange among storage units [14]. Each storage unit performs simplified independent computations based on local information rather than solving the full global optimization problem. Through iterative information sharing with neighboring units, the system gradually converges toward a globally optimal solution, effectively reducing computational complexity and improving optimization efficiency. Additionally, this method supports the dynamic integration and withdrawal of storage units, offering strong plug-and-play adaptability. Newly added storage units do not require a reconstruction of the global optimization model; instead, they can compute their local optimization variables and gradually integrate into the system through information exchange with neighboring units. This feature enhances the flexibility and scalability of DSES.

However, decentralized optimization methods that rely solely on local information exchange still face challenges in convergence speed and global consistency. Since each storage unit can only access limited information from neighboring units, the optimization process may converge slowly or, in some cases, fail to ensure that all units ultimately reach a globally optimal solution. Additionally, system topology and communication delays may cause information desynchronization, further affecting optimization performance. To address these issues, consensus algorithms have been widely applied in distributed optimization frameworks to ensure that all storage units gradually reach a consistent decision during iterations [15,16]. By leveraging consensus algorithms, storage units can not only optimize using neighboring information but also adjust their strategies through an iterative mechanism [17,18]. This approach accelerates convergence, enhances optimization stability, and ensures global consistency.

Moreover, uncertainty challenges remain a significant issue in the real-time scheduling of DSES systems. Current research primarily relies on forecast-based methods for optimizing energy storage scheduling [19,20,21]. For relatively stable and long-timescale signals, such as user demand, forecasting methods can effectively capture future load trends with reasonable accuracy. However, for commands requiring a second-level response, such as frequency regulation signals, the rapid fluctuations and high volatility of these signals—heavily influenced by grid conditions, frequency deviations, and other dynamic factors—make traditional forecasting methods insufficiently accurate [22,23]. As a result, the reliance on forecasting in such scenarios can degrade the effectiveness of real-time optimization and scheduling in shared energy storage systems. To address this issue, this paper employs a distributed online convex optimization approach, enabling DSES units to optimize adjustments based on real-time observation data without requiring accurate predictions of future states. By integrating online optimization and convex optimization theory, this method dynamically updates the optimal solution at each time step, allowing the system to adapt to rapid fluctuations in frequency regulation demand and enhance scheduling responsiveness [24]. Furthermore, the distributed optimization framework enables parallel computation across multiple storage units, avoiding the computational bottlenecks and single-point failure risks associated with centralized methods [25,26]. Additionally, the online optimization algorithm improves system adaptability and robustness in uncertain environments by utilizing incremental learning strategies rather than relying on complete historical data.

Distributed optimization relies on information exchange between energy storage units, requiring state synchronization at each iteration [27]. High-frequency communication not only increases bandwidth usage and computational overhead but also introduces potential communication delays, leading to asynchronous information updates that can slow down convergence [28]. Therefore, reducing communication frequency and redundant data exchange while maintaining optimization accuracy and convergence is a key challenge in distributed optimization. To address this issue, this paper introduces an event-triggered control mechanism, where communication is triggered only when state changes exceed a predefined threshold, effectively reducing unnecessary data transmission and improving computational efficiency. In recent years, event-triggered strategies have been applied to large-scale optimization problems, where information is updated only when specific trigger conditions are met [29,30,31,32,33]. This approach reduces communication frequency while ensuring convergence and the stability of the optimization process. However, existing event-triggered strategies still have notable limitations: (1) Fixed-threshold strategies determine communication triggers based on a preset threshold. However, in dynamic system environments, a fixed threshold may not adapt to varying state changes. When system state fluctuations are large, excessive triggering may occur, increasing communication overhead. Conversely, when state variations are small, delayed updates may degrade optimization performance. (2) Decreasing-threshold strategies progressively lower the trigger threshold to approximate the global optimum. However, if the threshold becomes too small, it may lead to an excessive communication frequency, increasing the information transmission burden rather than effectively reducing communication costs.

To address the aforementioned challenges, this paper proposes a distributed online convex optimization method based on consensus algorithms and adaptive event-triggered optimization, which significantly reduces the communication requirements in DSES while ensuring optimization performance. The main contributions of this work are as follows:

(1)

A novel consensus-based distributed online convex optimization method is proposed for the decentralized scheduling of energy storage units. The method leverages Lagrangian relaxation to address global constraints while maintaining scalability and robustness.

(2)

An adaptive event-triggered communication mechanism is developed to minimize communication overhead by dynamically adjusting the transmission threshold according to system states.

(3)

The algorithm’s robustness is demonstrated through simulations of dynamic disconnection and reconnection scenarios, showing a reliable scheduling performance under varying topologies.

2. Optimization Scheduling Modeling of Distributed Shared Energy Storage Systems

2.1. Real-Time Control Framework for Distributed Shared Energy Storage Systems

In practical power grid applications, the deployment of DSES systems on the power supply side is typically integrated with transmission networks and operates in conjunction with electricity markets, renewable energy sources (such as photovoltaic and wind power), and ancillary service markets.

Figure 1 illustrates the real-time control framework of a DSES system, where multiple geographically dispersed storage units collaborate through transmission networks, communication networks, and market mechanisms to achieve optimized energy scheduling. The numbers 1–14 in the figure indicate the bus nodes within the transmission network, where selected nodes are equipped with distributed energy storage units. In the power grid architecture, these storage units are typically deployed at critical nodes within the transmission system, serving electricity leasing, frequency regulation ancillary services, and demand-side management functions, thereby enhancing grid stability and economic efficiency. Each storage unit independently manages charging and discharging based on distributed control strategies and exchanges state information through the communication network. A distributed optimization strategy is employed for autonomous scheduling.

Figure 1. The real-time control framework of a distributed shared energy storage system.

The system adopts a consensus algorithm-driven decentralized cooperative control approach, enabling storage units to coordinate power distribution and dynamically respond to changes in grid demand. Unlike centralized control methods, this approach requires only a limited information exchange between storage units and their neighboring units to achieve globally optimal scheduling, thereby reducing reliance on a centralized controller and improving system flexibility and robustness. Under this architecture, the communication network plays a critical role. It not only supports distributed consensus optimization, ensuring that storage units reach consistent scheduling decisions through local computation and minimal information exchange, but also reduces redundant communication and enhances scheduling efficiency through an event-triggered mechanism.

Figure 2 illustrates the workflow of this study. The demand input module includes two types of signals: user leasing demand at the minute level and frequency regulation (RegD) signals at the second level. The communication mechanism adopts a consensus-based approach to enable information exchange among neighboring storage units while implementing a threshold-based decision rule to reduce unnecessary transmissions and improve communication efficiency. The distributed online optimization framework incorporates consensus optimization and event-triggered mechanisms to facilitate decentralized coordination among storage units. It also handles coupling constraints while minimizing computational and communication overheads. Finally, the simulation verification is conducted using the IEEE 14-bus network to evaluate the proposed method under different scenarios, including convergence analysis, communication overhead assessment, hybrid demand scenarios, and extreme conditions such as disconnection and recovery.

Figure 2. A flowchart of this study.

2.2. The Cost Function of Distributed Energy Storage Units

In shared energy storage systems, each unit must adjust its charging and discharging according to demand. During this process, electrochemical reactions cause internal energy losses, which translate into operational cost penalties. These internal energy loss costs can significantly affect the system’s overall economic performance, particularly when many units operate simultaneously. Therefore, minimizing such losses is essential not only for energy coordination but also for cost-effective operation. To quantify this cost, this paper introduces a dynamic internal energy loss coefficient ${\zeta }_{i,t}$, which is used to evaluate the monetary cost incurred by power transfer inefficiencies:

$${\zeta }_{i,t}={\alpha }_{i,t}\cdot P_{i,t}+{\beta }_{i,t}$$

(1)

where ${\alpha }_{i,t}$ and ${\beta }_{i,t}$ are coefficients determined based on the state of the storage unit and its output power characteristics, reflecting the possible heterogeneity in internal losses among different storage units during operation.

The specific expression for internal energy loss cost in a shared energy storage system is given as follows:

$$C_{\mathrm{inner},i}={\zeta }_{i,t}\cdot P_{i,t}^2=\left({\alpha }_{i,t}\cdot P_{i,t}+{\beta }_{i,t}\right)\cdot P_{i,t}^2$$

(2)

where $P_{i,t}$ represents the charging/discharging power of storage unit $i$ at time $t$. This equation shows that the cost of the internal energy loss depends on the power output. Adjusting the loss coefficient dynamically allows for a flexible coordination among distributed storage units.

Additionally, it is necessary to consider the degradation cost of storage units, as battery lifespan reduction is closely related to the depth of charge/discharge cycles and the frequency of charge–discharge transitions. Therefore, the following equation is used to represent the degradation cost for each storage unit:

$$C_{\mathrm{degradation},i}={\rho }_c\cdot \mathsf{\Delta }{P}_{i,t}$$

(3)

where ${\rho }_c$ is the marginal cost of unit energy loss, estimated using experimental data or historical operation records; $\mathsf{\Delta }{P}_{i,t}$ denotes the energy variation of unit $i$ in the current cycle.

In shared energy storage systems, due to the diversity of storage unit types and differences in operating modes, the aging cost factor ${\rho }_c$ may need to be individually configured for each type of storage unit. For example, soft-packaged battery systems tend to have a lower degradation rate, while nickel–metal hydride battery systems may experience higher aging rates. These variations impose higher requirements on optimization design.

By integrating internal energy loss costs and degradation costs, the total operating cost of a shared energy storage system is expressed as follows:

$$C_{\mathrm{total},i}=C_{\mathrm{inner},i}+C_{\mathrm{degradation},i}$$

(4)

which can be further expanded as follows:

$$C_{\mathrm{total},i}=\left({\alpha }_{i,t}\cdot P_{i,t}+{\beta }_{i,t}\right)\cdot P_{i,t}^2+{\rho }_c\cdot \mathsf{\Delta }{P}_{i,t}$$

(5)

2.3. Optimization Objectives and Constraints of Real-Time Control Strategies

In real-time control, the shared energy storage platform aims to minimize its operational costs while maximizing the revenue obtained from providing services to users and participating in ancillary service markets. The operating cost includes both the internal energy loss cost and the degradation cost of storage units. Meanwhile, revenue arises from two primary sources: user-side leasing and grid-side ancillary services. However, since the online convex optimization framework conventionally adopts a minimization form, we reformulate the original profit-maximization objective as the minimization of negative profit. Specifically, the revenue term is subtracted in the objective function to ensure compatibility with standard online learning formulations. This transformation is mathematically equivalent and does not affect the economic interpretation of the problem. Thus, the optimization objective function is defined as follows:

$$\underset{P_{i,t}}{\min }{\displaystyle \sum }_{t\in T}\left({\displaystyle \sum }_{i\in B}\left(C_{\mathrm{inner},i,t}+C_{\mathrm{degradation},i,t}\right)-{\displaystyle \sum }_{i\in B}{R}_{\mathrm{service},i,t}\right)$$

(6)

where $B$ represents the set of storage units; $C_{\mathrm{inner},i,t}$, $C_{\mathrm{degradation},i,t}$, and $R_{\mathrm{service},i,t}$ denote the internal energy loss cost, degradation cost, and service revenue of the storage unit at time $t$, respectively.

In shared energy storage systems, the overall revenue is derived from the collaborative contribution of all storage units rather than being independently calculated for each unit. Therefore, to simplify the revenue model and incentivize storage units to respond to system demands, this paper adopts a virtual pricing mechanism. By establishing a unified virtual price $p_t$, storage units are guided to perform rational power regulation, and their revenue is defined as follows:

$$R_{\mathrm{service},i,t}=p_t\cdot P_{i,t}$$

(7)

where $p_t$ represents the unit price of electricity in external markets or leasing services to users at time $t$, which is dynamically adjusted based on market conditions; $P_{i,t}$ represents the charging/discharging power of storage unit $i$ at time $t$. This revenue model provides a quantitative formulation of the economic objectives of storage units while aligning their adjustments with real-time market price fluctuations.

The current model treats $p_t$ as a predefined, time-varying signal reflecting external market trends. In practice, this signal can be derived from historical electricity price profiles, predicted spot-market data, or regulatory reward structures. Integrating such data-driven market inputs into the virtual pricing mechanism will be the focus of our future work.

Future extensions may consider the dynamic learning of $p_t$ based on forecasted prices, congestion costs, and ancillary service opportunities. This would strengthen the economic foundation of the model, enabling storage units to participate more effectively in real-world electricity markets and it would improve the coordination between control policies and price-based dispatch strategies.

To ensure the operational safety of storage units and the stability of system regulation, the optimization model must satisfy the following constraints.

The output power of storage units is subject to equipment limitations, defined as follows:

$$P_{i,t}^{\min }\le P_{i,t}\le P_{i,t}^{\max }$$

(8)

where $P_{i,t}^{\min }$ and $P_{i,t}^{\max }$ represent the minimum and maximum power output of storage unit $i$, respectively, which are influenced by storage unit type and real-time operating conditions.

The state of charge (SoC) of storage units must remain within the safe operating range to ensure operational security and equipment longevity, defined as follows:

$$So{C}_{i,t}^{\min }\le So{C}_{i,t}\le So{C}_{i,t}^{\max }$$

(9)

where $So{C}_{i,t}$ denotes the state of the charge of storage unit $i$ at time $t$; $So{C}_{i,t}^{\min }$ and $So{C}_{i,t}^{\max }$ represent the minimum and maximum allowable SoC levels for the storage unit, respectively.

The state of charge of a storage unit dynamically changes over time and is determined by the charging and discharging power. It is specifically expressed as follows:

$$So{C}_{i,t+1}=So{C}_{i,t}+{\displaystyle \frac{{\phi }_i{P}_{i,t}\mathsf{\Delta }t}{E_{i,\max }}}$$

(10)

where ${\phi }_i$ denotes the charging and discharging efficiency of unit $i$, typically less than 1; $E_{i,\max }$ represents the rated maximum energy capacity of unit $i$; $\mathsf{\Delta }t$ is the time step length. The current formula primarily describes the charging response of DESS to renewable energy users. In the global optimization framework, DESS must simultaneously meet multiple user demands and can only be in either a charging or discharging state at any given time, but not both simultaneously. Traditional methods typically introduce 0–1 binary variables (where charging is 1 and discharging is 0), which transform the optimization problem into a Mixed-Integer Programming problem, increasing computational complexity. This study adopts a continuous optimization approach, where the appropriate constraints are selected based on the direct judgment of demand direction (charging or discharging) without additional binary decision variables. As a result, the convexity of the optimization problem is preserved, avoiding non-convexity issues, reducing computational complexity, and improving efficiency, making it more suitable for the real-time scheduling of large-scale DESS.

The shared energy storage system needs to meet real-time external demands, including ancillary service requirements and user leasing requests, defined as follows:

$${\displaystyle \sum }_{i\in B}{P}_{i,t}-D_t=0$$

(11)

where $D_t$ represents the total power demand of the system at time $t$.

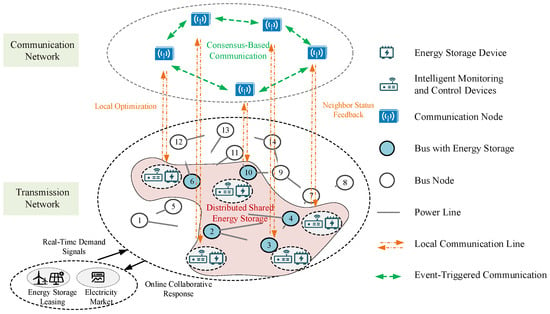
3. Distributed Real-Time Scheduling Framework Based on Consensus Algorithm

3.1. Real-Time Optimization Framework Design Based on Distributed Online Convex Optimization

A distributed energy storage system, due to its geographical dispersion and high communication costs, requires rapid response to scheduling demands. Traditional centralized optimization is constrained by computational burdens and communication latency. Distributed online convex optimization integrates convex optimization, distributed computing, and online optimization, enabling storage units to perform local computations while exchanging critical information via the communication network, thereby achieving decentralized global scheduling.

This method decomposes the global optimization problem into multiple subproblems corresponding to individual storage units. Each unit independently solves its local problem based on local information and exchanges key variables (such as Lagrange multipliers and local solutions) with neighboring units. Through iterative updates, the system gradually converges to the global optimum, enhancing scheduling efficiency and robustness.

In a distributed energy storage system, the objective of the global optimization problem is to achieve a coordinated scheduling of storage units through the communication network. In the context of online convex optimization, this is typically modeled by minimizing a cumulative time-varying loss function, where “loss” refers to a scalar cost function at each time step—not to be confused with physical energy loss. Specifically, the system’s global loss function is defined as follows:

$$f_t\left(x\right)={\displaystyle \sum }_{i\in B}{f}_{i,t}\left(x\right)$$

(12)

where $f_{i,t}\left(x\right)$ represents the local loss function at node $i$ at time $t$, which is typically associated with the operating costs and scheduling objectives of the storage unit. The optimization goal is to minimize the cumulative loss over a finite time horizon $T$:

$$\underset{x\in \mathsf{\Omega }}{\min }{\displaystyle \sum }_{t=1}^T{f}_t\left(x\right)$$

(13)

where $x\in \mathsf{\Omega }$ denotes the optimization variables; $\mathsf{\Omega }$ represents a compact and convex constraint set.

To describe the optimization objective within the system’s time horizon, specifically in relation to the operational costs and revenues of the shared energy storage system, combining the optimization objective defined in Section 2, $f_t\left(x\right)$ can be further expressed as follows:

$$f_t\left(x\right)={\displaystyle \sum }_{i\in B}\left(C_{\mathrm{inner},i,t}+C_{\mathrm{degradation},i,t}\right)-{\displaystyle \sum }_{i\in B}{R}_{\mathrm{service},i,t}$$

(14)

To evaluate the performance of the distributed optimization algorithm, a dynamic regret metric is typically introduced as an evaluation criterion, defined as follows:

$${\mathrm{Reg}}_T^g={\displaystyle \sum }_{t=1}^T{f}_t\left(x_t\right)-{\displaystyle \sum }_{t=1}^T{f}_t\left(x_t^{*}\right)$$

(15)

where $x_t$ represents the decision solution provided by the algorithm at time $t$; $x_t^{*}=\arg \underset{x\in \mathsf{\Omega }}{\min }{f}_t\left(x\right)$ denotes the optimal solution at time $t$.

If the dynamic regret of the algorithm satisfies a sublinear convergence condition $\underset{T\to \infty }{\lim }{\mathrm{Reg}}_T^g/T=0$, then it indicates that the algorithm can gradually converge to the global optimal solution over the long-term operation.

The distributed optimization algorithm enables each storage unit node to independently compute gradients and achieve coordination by exchanging state information over the communication network. Each node computes its gradient $\nabla f_{i,t}\left(x_t\right)$ at time $t$ and updates the local variable using the following formula:

$$x_{t+1,i}=x_{t,i}-\eta \nabla f_{i,t}\left(x_{t,i}\right)$$

(16)

where $\eta >0$ is the learning rate. Subsequently, the node exchanges state information $x_{t+1,i}$ with other nodes in its neighborhood ${\mathcal{N}}_i$ and receives the state values from neighboring nodes.

To ensure global consistency in the optimization process, a consensus constraint must be satisfied, requiring that for all $\left(i,j\right)\in \mathcal{E}$, the condition $x_{t,i}=x_{t,j}$ holds. This consistency can be achieved through distributed consensus algorithms, for example, using a weighted averaging update formula:

$$x_{t+1,i}={\displaystyle \sum }_{j\in {\mathcal{N}}_i}{a}_{ij}{x}_{t,j}$$

(17)

We will further explore how consensus algorithms enforce the consistency condition and analyze its application in distributed energy storage systems.

In practical applications, communication delay is an unavoidable factor in distributed energy storage systems. Communication delays may lead to asynchronous state updates, thereby affecting the sensitivity and efficiency of optimization algorithms. The communication delay ${\tau }_{ij}$ represents the time difference in information transmission between node $i$ and node $j$, i.e., ${\tau }_{ij}=t_{\mathrm{send},ij}-t_{\mathrm{receive},ij}$. To address the delay issue, an asynchronous optimization approach can be adopted, allowing nodes to perform updates even when only partial information has been received.

3.2. The Distributed Optimization Strategy Based on Consensus Algorithm

The consensus algorithm helps distributed storage units agree on a common decision by exchanging information with neighbors. Its core goal is to reach a consistent system state without using a central controller, expressed as follows:

$$\underset{t\to \infty }{\lim }{x}_i^t=x^{\mathrm{op}}$$

(18)

where $x_i^t$ represents the local decision variable of node $i$ at time $t$; $x^{\mathrm{op}}$ is the globally consistent optimal value. In the optimization framework of this paper, $x_i^t$ corresponds to the power decision variable $P_{i,t}$ of storage unit $i$ at time $t$.

In the optimization problem, the power balance constraint ${\displaystyle {\displaystyle \sum }_{i\in B}}{P}_{i,t}-D_t=0$ involves the power decisions of multiple storage units and serves as a global coupling constraint. Since this constraint spans all units, it cannot be enforced locally. We use the Lagrange multiplier method to embed the constraint into each unit’s objective. This allows all units to coordinate indirectly and converge toward a global solution through local updates and communication. To simplify notation, $h_t\left(P\right)={\displaystyle {\displaystyle \sum }_{i\in B}}{P}_{i,t}-D_t=0$ is used to denote this constraint. The Lagrangian form of the optimization objective is then given by the following:

$${\mathcal{L}}_t\left(P,{\lambda }_t\right)={\displaystyle \sum }_{i\in B}{f}_{i,t}\left(P_{i,t}\right)+{\lambda }_t^T{h}_t\left(P\right)$$

(19)

For power limits and state of charge constraints, since these constraints only affect local variables, each storage unit can directly impose these constraints in its local optimization problem without requiring relaxation via the Lagrange multiplier.

Thus, the global optimization problem is formulated as follows:

$$\min {\displaystyle \sum }_{i\in B}{f}_{i,t}\left(P_{i,t}\right)$$

(20)

subject to the following:

$$h_t\left(P\right)={\displaystyle \sum }_{i\in B}{P}_{i,t}-D_t=0,P\in {\mathcal{F}}_B$$

(21)

where $C_{i,t}\left(P_{i,t}\right)$ represents the operational cost of storage unit $i$ at time $t$; the constraint condition $h_t\left(P\right)=0$ ensures power balance across the system; $P$ is the power allocation vector for all storage units, subject to the constraint set ${\mathcal{F}}_B$.

In real-time operation, due to the dynamic and uncertain nature of distributed energy storage systems, the optimization process must be executed in real-time. Therefore, we adopt an online optimization framework and update the solution using a gradient descent method. Specifically, at each time step, each storage unit can only obtain local information and the gradient direction $\nabla f_{i,t+1}$, without access to the globally optimal solution. Consequently, we integrate the local gradient update with a consensus mechanism to ensure simultaneous optimization across all units. The power decision for each unit at time $t$ is formulated as the following optimization problem:

$$\begin{array}{cc}{P}_{i,t}& =\arg \underset{P_{i,t}\in {\mathcal{S}}_i}{\min }\nabla f_{i,t+1}\left(P_{i,t-1}\right)\left(P_{i,t}-P_{i,t-1}\right)+{\displaystyle \frac{1}{2k}}\Vert P_{i,t}-P_{i,t-1}{\Vert }^2\hfill \\ & +\nabla h_t\left(P_{i,t-1}\right)\left(P_{i,t}-P_{i,t-1}\right){\displaystyle {\displaystyle \sum }_{j\in {\mathcal{N}}_i}}{w}_q{\lambda }_{j,t-1}\end{array}$$

(22)

where, to facilitate understanding, the structure of Equation (22) is explained below in terms of three key components: the first term $\nabla f_{i,t+1}\left(P_{i,t-1}\right)\left(P_{i,t}-P_{i,t-1}\right)$ represents the gradient descent term, which optimizes power in the direction of historical gradients, allowing for cost reduction. Since the gradient direction inherently follows the steepest descent path, this term ensures that the storage unit adjusts power toward an optimal schedule. The second term ${\displaystyle \frac{1}{2k}}\Vert P_{i,t}-P_{i,t-1}{\Vert }^2$ is a regularization term, which penalizes drastic changes in power adjustment. This term prevents excessive fluctuations in power output that may affect system stability. The parameter $k$ controls the adjustment rate; larger values of $k$ result in slower power adjustments, leading to a smoother optimization process. The third term $\nabla h_t\left(P_{i,t-1}\right)\left(P_{i,t}-P_{i,t-1}\right){\displaystyle {\displaystyle \sum }_{j\in {\mathcal{N}}_i}}{w}_q{\lambda }_{j,t-1}$ serves as a constraint correction term, where the Lagrange multiplier ${\lambda }_{j,t-1}$ is used to adjust for the global constraint. The consensus algorithm ensures that each storage unit gradually aligns its power decisions with the global power balance constraint by incorporating the weighted information received from its neighboring nodes.

Since the optimization process adopts the Lagrange multiplier relaxation method, the Lagrange multiplier ${\lambda }_{i,t}$ acts as a penalty factor for the global constraint $h_t\left(P\right)$, requiring coordination updates among storage units. Based on the consensus algorithm, each storage unit $i$ can only receive information from neighboring nodes $j$, and its update follows a weighted averaging strategy:

$${\lambda }_{i,t}={\displaystyle \sum }_{j\in B}{w}_{ij}{\lambda }_{j,t-1}+\mathcal{l}{\displaystyle \sum }_{i\in B}{w}_{ij}{y}_{j,t-1}$$

(23)

where $w_{ij}$ is the weight of the adjacency matrix, used to adjust the influence of transmitted information; $y_{i,t}$ is the consensus variable, which is further used to refine the optimization direction in the subsequent steps; $\mathcal{l}$ is the step size parameter, which controls the update rate. This update equation ensures that the Lagrange multiplier ${\lambda }_{i,t}$ gradually converges across all nodes, allowing all storage units to achieve coordinated optimization without a centralized controller.

In a distributed environment, an individual storage unit cannot directly obtain information about the global constraint $h_t\left(P\right)$. Therefore, an auxiliary variable $y_{i,t}$ is introduced as a local estimation of the global constraint. The update formula for the consensus variable $y_{i,t}$ is given by the following:

$$y_{i,t}={\displaystyle \sum }_{j\in B}{w}_{ij}{y}_{j,t-1}+\mathsf{\Delta }{h}_{i,t-1}$$

(24)

In this equation, the first term ${\displaystyle {\displaystyle \sum }_{j\in B}}{w}_{ij}{y}_{j,t-1}$ enables information exchange among neighboring nodes via the consensus algorithm, ensuring a gradual convergence of $y_{i,t}$ across all nodes. The second term $\mathsf{\Delta }{h}_{i,t-1}$ represents the variation of the global constraint $h_t\left(P\right)$ at time $t-1$, which corrects $y_{i,t}$ to reflect the latest changes in the global system state. The core objective of this update strategy is to ensure that storage units share consistent constraint information, thereby enhancing the global feasibility of the optimization process.

4. Adaptive Event-Triggered Mechanism and Algorithm Deployment

4.1. Network Topology and Information Interaction Mechanism

In a DSES system, the communication network serves as a key support for achieving the coordinated optimization and scheduling of storage units. The topology structure not only affects the efficiency and stability of information exchange but also directly influences the system’s response speed to dispatch commands and the feasibility of control strategies.

Under a distributed control framework, storage units exchange information through a neighbor communication mechanism to achieve distributed consensus optimization. The mathematical modeling of the communication network is typically represented by a graph structure $G=\left(\mathcal{V},\varphi \right)$, where the node set $\mathcal{V}$ represents the set of storage units, with each node $i\in \mathcal{V}$ corresponding to a storage unit, and the edge set $\varphi$ represents the communication links between nodes. If there exists a communication link between two nodes $\left(i,j\right)\in \varphi$, it is defined as an edge.

The communication relationship is described using an adjacency matrix $A=\left[a_{ij}\right]\in {ℝ}^{m\times m}$, where the matrix elements $a_{ij}$ satisfy $a_{ij}>0$ if there is communication between nodes $i$ and $j$, and $a_{ij}=0$ if there is no communication. To ensure the stability and fairness of the network, the weight matrix typically satisfies a double stochasticity condition, i.e., ${\displaystyle {\displaystyle \sum }_{j=1}^m}{a}_{ij}=1,{\displaystyle {\displaystyle \sum }_{i=1}^m}{a}_{ij}=1$.

In the communication network of a DSES system, different topology structures determine the methods and efficiency of information exchange. The following three typical topology models are introduced: fully connected topology, ring topology, and randomly sparse connection topology, with their corresponding adjacency matrix expressions provided.

In the communication network of a DSES system, different topology structures determine the methods and efficiency of information exchange. The following provides adjacency matrix representations for three typical topology models: fully connected topology, ring topology, and randomly sparse connected topology.

In a fully connected topology, all storage units can communicate directly, and each node can exchange information with all the other nodes. Taking a system with five storage units as an example, its adjacency matrix $A$ is given by the following:

$$A=\left[\begin{array}{ccccc}0& 1& 1& 1& 1\\ 1& 0& 1& 1& 1\\ 1& 1& 0& 1& 1\\ 1& 1& 1& 0& 1\\ 1& 1& 1& 1& 0\end{array}\right]$$

(25)

where $A_{ij}=1$ represents a communication link between storage units $i$ and $j$, and $A_{ii}=0$ indicates no self-connection.

In a ring topology, each storage unit only communicates with its two adjacent units, forming a closed ring network. This topology reduces communication overhead but may impact the overall system communication performance if some nodes fail. The adjacency matrix $A$ for this topology is given by the following:

$$A=\left[\begin{array}{ccccc}0& 1& 0& 0& 1\\ 1& 0& 1& 0& 0\\ 0& 1& 0& 1& 0\\ 0& 0& 1& 0& 1\\ 1& 0& 0& 1& 0\end{array}\right]$$

(26)

In a randomly sparse connected topology, communication links in the network are randomly selected, with some nodes only communicating with a few others, resulting in a sparse connectivity structure. This topology minimizes communication costs but may lead to higher information transmission delays at certain nodes, potentially affecting the convergence speed of the consensus algorithm. An example adjacency matrix for a randomly sparse connected topology is the following:

$$A=\left[\begin{array}{ccccc}0& 1& 0& 0& 1\\ 1& 0& 1& 0& 0\\ 0& 1& 0& 0& 1\\ 0& 0& 0& 0& 1\\ 1& 0& 1& 1& 0\end{array}\right]$$

(27)

The neighbor set of each node is defined as ${\mathcal{N}}_i=\left\{j\in \mathcal{V}\left|a_{ij}\right.⟩0\right\}$, where neighbors are the storage units that can directly communicate with node $i$. The in-degree and out-degree of a node refer to the size of its neighbor set, defined as $d_i^{-}=\left|{\mathcal{N}}_i\right|$ and $d_i^{+}=\left|{\mathcal{N}}_i\right|$, respectively.

The communication network is typically assumed to be independent of the physical network of the storage system, allowing for a flexible communication topology design. However, in practical applications, power lines often serve as the medium for data transmission, meaning that the network topology may be constrained by the physical layout of the power infrastructure.

4.2. The Design of the Adaptive Event-Triggered Mechanism

The design of the adaptive event-triggered mechanism is based on the idea that the system should dynamically adjust trigger conditions according to the changes in system state, ensuring that the system does not update information at a fixed frequency regardless of state variations. In the optimization framework of this paper, the adaptive event-triggered scheduling (AETS) is primarily implemented as follows.

At each time step $t$, a storage unit only triggers communication when its state error exceeds a certain threshold. The transmission signal of storage unit $i$ at time $t$ is defined as follows:

$$x_{i,t}=\left\{\begin{array}{ll}{x}_{i,t},\hfill & t\in {\theta }_i\hfill \\ x_{i,t-1},\hfill & t\notin {\theta }_i\hfill \end{array}\right.$$

(28)

where $x_{i,t}$ represents the state generated by storage unit $i$ at time $t$, and $x_{i,t-1}$ is the previously transmitted state. Only when $x_{i,t}$ satisfies the trigger condition will it be updated and sent to neighboring nodes; otherwise, the previous value is maintained. ${\theta }_i$ denotes the set of specific time steps when storage unit $i$ needs to transmit information.

Traditional event-triggered mechanisms use a fixed threshold $\delta$, whereas adaptive event-triggered mechanisms allow the threshold to dynamically change over time. If the trigger condition continues to be met, the threshold remains unchanged. However, if a long period has passed without triggering an event, the threshold gradually decreases to ensure that even small state variations are not ignored. The event-trigger condition is defined as follows:

$$t_{i,t+1}=\min \left\{t\in {\theta }_i\Vert t>t_{i,t},\Vert x_{i,t}-x_{i,t-1}\Vert >{\delta }_{i,t}\right\}$$

(29)

where $t_{i,t+1}$ denotes the next triggering time of storage unit $i$, and ${\delta }_{i,t}$ is the dynamically adjusted threshold at the previous time step.

The update rule for ${\delta }_{i,t}$ is given by the following:

$${\delta }_{i,t}=\left\{\begin{array}{ll}{\delta }_{i,t-1},\hfill & \mathrm{if} \mathrm{continuously} \mathrm{riggered}\hfill \\ \gamma {\delta }_{i,t-1},\hfill & \mathrm{if} \mathrm{not} \mathrm{triggered} \mathrm{for} \mathrm{a} \mathrm{long} \mathrm{time}\hfill \end{array}\right.$$

(30)

where $\gamma \in \left(0,1\right)$ is the reduction factor that controls the rate of threshold decay over time. Equation (30) describes a classical static event-triggered mechanism based on error reduction, where $\gamma$ is a fixed reduction factor. To improve the dynamic responsiveness and reduce communication overhead, we further develop the strategy by incorporating an adaptive event-triggered mechanism that adjusts the threshold based on system state variations (see Equation (35)).

Under the adaptive event-triggered mechanism, the signal error $e_i=x_{i,t}-x_{i,t-1}$ must always satisfy the constraint:

$$\Vert x_{i,t}-x_{i,t-1}\Vert \le {\delta }_{i,t}$$

(31)

This constraint ensures that even at lower communication frequencies, system state errors remain controlled, preventing excessive error accumulation that could degrade optimization performance.

The Zeno phenomenon refers to a scenario where an infinite number of events are triggered within a finite time, which, in practical applications, can lead to unnecessary computational and communication overhead. To avoid this issue, the adaptive event-triggered mechanism imposes a minimum time interval $b$ between any two consecutive triggering times $t_{i,t+1}$ and $t_{i,t}$, ensuring that, as follows:

$$t_{i,t+1}-t_{i,t}\ge b$$

(32)

This setting effectively prevents the occurrence of the Zeno phenomenon and improves the robustness of the system.

To ensure the convergence of the optimization algorithm, the adaptive event-triggered mechanism must satisfy the following assumption:

$${\displaystyle \sum }_{t=0}^{\infty }{\epsilon }_t^2=N<\infty$$

(33)

This assumption guarantees that as time progresses, the error threshold will not increase indefinitely while allowing global convergence to be achieved under a reasonable communication frequency.

4.3. Algorithm Implementation Process

This paper uses the power $P_{i,t}$ of storage units as the state variable $x_{i,t}$ in the adaptive event-triggered mechanism. At each time step $t$, the system updates $P_{i,t}$ only when certain trigger conditions are met. Specifically, the trigger condition is defined as follows:

$$\Vert P_{i,t}-P_{i,t-1}\Vert >{\delta }_{i,t}$$

(34)

where ${\delta }_{i,t}$ is the adaptive adjustable trigger threshold, updated according to the following rule:

$${\delta }_{i,t+1}=\sigma {\delta }_{i,t}+\xi \Vert P_{i,t}-P_{i,t-1}\Vert$$

(35)

where $\sigma$ is the forgetting factor, typically set within $\sigma \in \left[0.9,1\right]$, ensuring smooth adjustments of the trigger threshold; $\xi$ is a dynamic adjustment coefficient used to modify the trigger threshold based on the magnitude of state changes.

When the system state changes significantly, ${\delta }_{i,t}$ decreases, increasing the triggering frequency; when system state variations are small, ${\delta }_{i,t}$ increases, reducing unnecessary information exchange.

To improve clarity and facilitate understanding, the proposed online optimization strategy is summarized in Algorithm 1 in the form of pseudo-code. This algorithm integrates the adaptive event-triggered mechanism into a consensus-based distributed online optimization process. At each time step, the algorithm checks the power variation against a dynamic threshold to decide whether to execute updates and exchange information. The threshold itself is updated adaptively, enabling a reduced communication overhead while ensuring coordination and convergence.

Algorithm 1 Adaptive Event-Triggered Distributed Online Optimization Strategy
Input:	Step size $\kappa$, forgetting factor $\sigma$, dynamic adjustment coefficient $\xi$, initial power $P_{i,0}$, initial threshold ${\delta }_{i,0}$, dual variables ${\lambda }_{i,0}$ $y_{i,0}$
Output:	Updated power decision variable $P_{i,t}$
1:	Initialize time step $t\leftarrow 1$
2:	Initialize all variables: $P_{i,0},{\delta }_{i,0},{\lambda }_{i,0},y_{i,0}$
3:	repeat
4:	Compute local gradients $\nabla f_{i,t-1}\left(P_{i,t-1}\right)$, $\nabla h_{i,t-1}\left(P_{i,t-1}\right)$
5:	Calculate $\Vert P_{i,t}-P_{i,t-1}\Vert$
6:	if $\Vert P_{i,t}-P_{i,t-1}\Vert >{\delta }_{i,t}$ then
7:	Update power variable $P_{i,t}$ using Equation (22)
8:	Update Lagrange multiplier ${\lambda }_{i,t}$ using Equation (23)
9:	Update consensus variable $y_{i,t}$ using Equation (24)
10:	Exchange info with neighbors
11:	else
12:	Skip update to reduce communication
13:	end if
14:	Update threshold: ${\delta }_{i,t+1}=\sigma \cdot {\delta }_{i,t}+\xi \cdot \Vert P_{i,t}-P_{i,t-1}\Vert$
15:	Increment time step: $t\leftarrow t+1$
16:	until $\Vert P_{i,t}-P_{i,t-1}\Vert <{\delta }_{\mathrm{final}}$ or $t=T_{\max }$

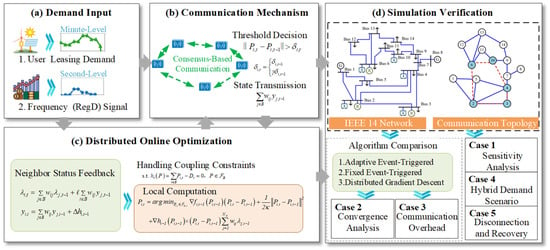
5. Case Study

5.1. Experimental Setup for the Case Study

The IEEE 14-bus system is selected as the test platform, widely used for power system optimization and stability analysis. It consists of 5 generator buses, 11 transmission lines, and 11 load buses, with integrated renewable energy sources and energy storage units to simulate an intelligent grid environment (as shown in Figure 3). Detailed node numbering and equipment parameters are provided in Table 1.

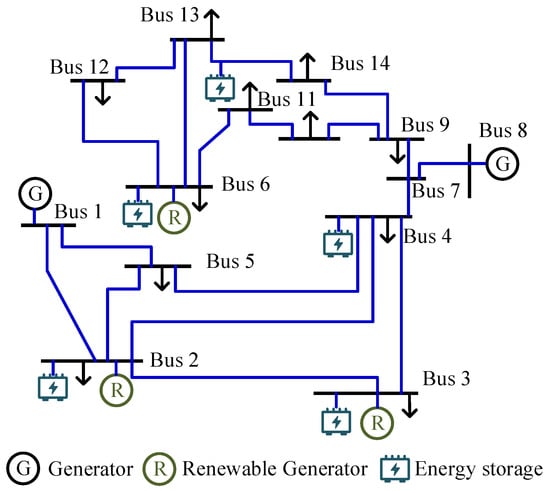
Figure 3. IEEE 14-bus power system test case with integrated renewable generation and energy storage.

Table 1. Parameter settings of distributed BESS units.

Storage Unit ID	Deployment Node	Maximum Power (± kW)	Energy Capacity (kWh)	Initial SoC (%)
BESS-1	3	±30	50	60
BESS-2	10	±30	60	55
BESS-3	6	±30	40	70
BESS-4	4	±35	75	50
BESS-5	2	±30	50	65

Since distributed optimization control is used, each storage unit coordinates with neighbors via a communication network modeled by an adjacency matrix. A ring topology is set as the default, while fully connected and randomly sparse topologies are also analyzed in Case Study 2 to assess their impact on communication load.

The focus is on real-time optimization for storage units participating in frequency regulation services and power leasing. The system operates under a hybrid load scenario, where storage units dynamically adjust power allocation based on PJM RegD frequency regulation commands and renewable energy-based user demand.

Experiments are conducted in Python 3.8. The libraries NumPy (v1.21.0), Pandas (v1.3.0), Matplotlib (v3.4.2), and SciPy (v1.7.0) are used to handle data processing, visualization, and optimization, while NetworkX (v2.6.3) is used to construct the communication network.

The hardware setup includes an Intel i7-12700K processor and 32GB RAM, ensuring efficient computation and data processing.

5.2. A Sensitivity Analysis of Adaptive Event-Triggered Parameters

To assess the behavior of the adaptive event-triggered mechanism under different threshold update strategies, we perform a sensitivity analysis using the power data of BESS 1. The analysis focuses on two key parameters: the forgetting factor $\sigma$, which influences the memory length of past thresholds, and the dynamic adjustment coefficient $\xi$, which determines the responsiveness to power variations. Nine combinations are tested with $\sigma \in \left\{0.6,0.8,0.98\right\}$ and $\xi \in \left\{0.05,0.1,0.2\right\}$.

Figure 4 illustrates the evolution of the adaptive threshold across these combinations. As $\xi$ increases, the mechanism becomes more responsive to power fluctuations, resulting in more frequent threshold adjustments and fewer unnecessary communications. Higher $\xi$ values are especially beneficial during rapid system changes.

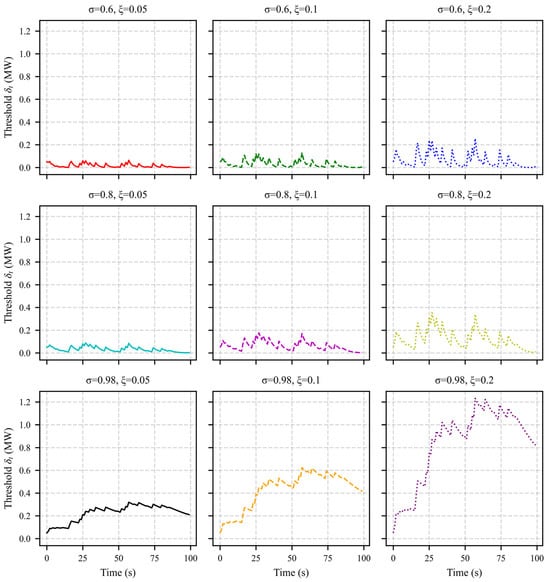
Figure 4. The variation trends of the adaptive threshold under different values of the forgetting factor and dynamic adjustment coefficient.

In contrast, increasing $\sigma$ slows the decay of ${\delta }_{i,t}$, producing smoother and more stable threshold curves. A high $\sigma$ (e.g., 0.98) effectively accumulates historical information, which is advantageous for systems with infrequent or bursty activity.

Overall, for systems with frequent dynamics, a larger $\xi$ (e.g., 0.2) enhances the adaptability. For systems with less frequent events, a larger $\sigma$ (e.g., 0.98) ensures threshold stability. The setting $\sigma =0.98,\xi =0.1$ achieves a good balance and is used in the main implementation.

5.3. A Convergence Performance Comparison of Adaptive Event-Triggered and Other Algorithms

To evaluate the convergence performance of different optimization algorithms, this study experimentally compares the dynamic regret function values of three methods: adaptive event-triggered optimization, fixed event-triggered optimization, and distributed gradient descent. Adaptive event-triggering dynamically adjusts the threshold, reducing computation and communication while ensuring optimization accuracy. In contrast, fixed event-triggering updates at fixed time intervals, lacking the ability to dynamically adjust optimization frequency based on the optimization state. Although distributed gradient descent exhibits a good scalability, it executes computation and communication at every time step, resulting in a slower convergence.

Through comparative experiments, the advantages of adaptive event-triggering in terms of convergence speed, computational efficiency, and stability are verified. The dynamic regret function is used to measure the loss of an algorithm relative to the optimal strategy, providing an intuitive representation of the convergence trend. Figure 5 illustrates the variations in the dynamic regret function for different optimization methods.

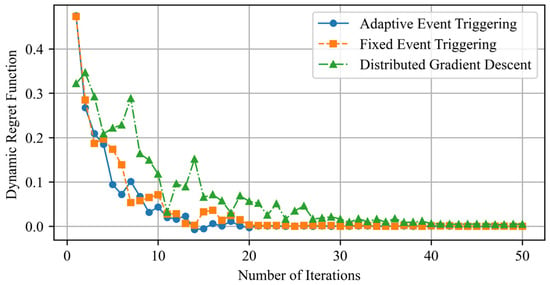
Figure 5. Variation trends of the dynamic regret function for different optimization methods.

Experimental results indicate that the adaptive event-triggered algorithm outperforms traditional methods in optimization convergence speed and stability. This method effectively reduces unnecessary computation and communication, rapidly adjusts during the initial optimization phase to improve convergence efficiency, and maintains stability in later stages, avoiding the computational overhead caused by frequent updates. In contrast, the fixed event-triggered method exhibits a relatively fast initial convergence but stabilizes after 15 iterations. Due to its triggering mechanism, it may result in unnecessary updates or information lag, thereby reducing the overall efficiency. The distributed gradient descent method has the slowest convergence speed, with smaller amplitude fluctuations in the optimization curve, indicating more oscillations in the optimization path, making rapid convergence difficult.

5.4. A Comparative Analysis of Communication Overhead and Consensus Performance Under Different Communication Mechanisms

In the real-time optimization of DSES systems, communication overhead is a key factor in evaluating algorithm efficiency. Excessive communication increases delays, computational costs, and affects real-time performance, while insufficient communication amplifies consensus errors, leading to suboptimal control strategies.

• The Impact of Different Communication Mechanisms on Communication Overhead

Firstly, a comparison was conducted among adaptive event-triggered optimization, fixed event-triggered optimization, and distributed gradient descent, analyzing their impact on the total communication occurrences, the average communication frequency, and the communication data volume during the optimization process. The experimental results are presented in Table 2.

Table 2. A comparison of communication overhead under different communication mechanisms.

Algorithm	Total Communication Count (Times)	Average Communication Count (Times/Unit)	Total Communication Volume (KB)	Consensus Error (Final Value)
Adaptive Event-Triggering	120	24	5.6	0.025
Fixed Event-Triggering	180	36	8.2	0.035
Distributed Gradient Descent	300	60	12.5	0.010

The total communication volume (in KB) is calculated as the total communication count multiplied by the data size per transmission. Each transmission includes state variables, gradient updates, and other optimization-related information. In this experiment, the data size per transmission is assumed to be 0.047 KB, and the total communication volume is derived accordingly.

Experimental results show that the adaptive event-triggered method incurs the lowest communication overhead, reducing the total communication by 33% compared to the fixed event-triggered method and 60% compared to distributed gradient descent. By triggering communication only when necessary, it minimizes redundant data exchanges while maintaining a low consensus error. The fixed event-triggered method results in a higher communication overhead due to fixed-interval updates, leading to unnecessary transmissions at certain time steps, totaling 180 communications. The distributed gradient descent method has the highest communication burden, performing global communication at every iteration, with a total of 300 communications. While it achieves the lowest consensus error, its high communication frequency imposes a significant system load.

2.

The Impact of Network Topology on Communication Overhead

This study further analyzes the impact of different network topologies on communication overhead. Optimization experiments were conducted under ring topology, sparsely connected grid topology, and fully connected topology, with the total communication count, communication per iteration, and consensus error recorded. The results are presented in Table 3.

Table 3. A comparison of communication overhead under different network topologies.

Network Topology	Total Communication Count (Times)	Communication per Iteration (Times)	Consensus Error (Final Value)
Ring Topology	100	2	0.040
Sparse Grid Topology	160	3.2	0.030
Fully Connected Topology	280	5.6	0.010

3.

The Trade-off Analysis Between Communication Efficiency and Consensus Error

Consensus error measures the deviation of decision variables in distributed optimization from the global optimal solution. It is closely related to communication frequency—insufficient communication may result in delayed information exchange, leading to larger optimization deviations among storage units, whereas excessive communication increases computational and communication overhead.

To analyze the trade-off between consensus error and communication overhead, this study records the number of communications required to reach a target consensus error of 0.02 for different optimization methods, along with the iterations needed for convergence. The results are presented in Table 4.

Table 4. The relationship between consensus error and communication overhead.

Algorithm	Target Consensus Error	Communication Count Required	Iterations Required for Convergence
Adaptive Event-Triggering	0.02	110	12
Fixed Event-Triggering	0.02	170	18
Distributed Gradient Descent	0.02	250	40

Experimental results show that the adaptive event-triggered method achieves the target consensus error with minimal communication overhead, requiring only 110 communications and 12 iterations for convergence. By dynamically adjusting communication frequency, it reduces redundancy while maintaining optimization performance.

The fixed event-triggered method takes 170 communications and 18 iterations, indicating that fixed triggering can cause unnecessary communication, leading to a slower convergence.

The distributed gradient descent method requires 250 communications and 40 iterations, imposing the highest communication overhead. While it ensures a high optimization accuracy, its computational burden makes it less suitable for large-scale distributed systems.

5.5. Real-Time Power Scheduling Optimization for Distributed Energy Storage Systems in a Hybrid Load Scenario

In the real-time scheduling of a distributed shared energy storage (DSES) cluster, optimizing power allocation to meet both frequency regulation needs and fluctuating user leasing demands is crucial. Figure 6 presents the input data, including frequency regulation commands, user leasing demand, and the total demand variations over time. Frequency regulation commands fluctuate rapidly with small amplitudes, reflecting real-time grid balancing needs, while user leasing demand changes less frequently, remaining stable over longer periods. This results in multi-level system demand variations, combining short-term fluctuations from frequency regulation with longer-term stability from user leasing requirements.

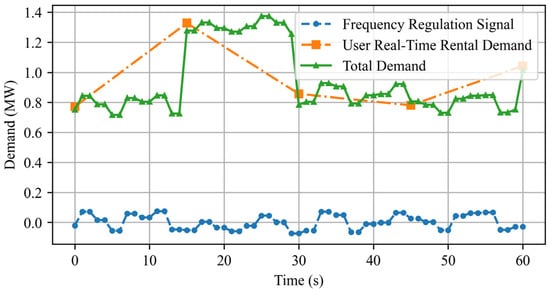
Figure 6. Frequency regulation commands, user leasing demand, and the total demand for case 4.

Figure 7 illustrates the power scheduling trajectory of the proposed distributed online optimization algorithm. Under algorithm guidance, storage units dynamically coordinate power output to adapt to demand fluctuations. When frequency regulation commands fluctuate, storage units adjust the power output accordingly. Similarly, during sudden shifts in user leasing demand, the system rapidly reallocates power to maintain supply–demand balance. Notably, during demand surges, power adjustments remain well balanced, demonstrating that the algorithm ensures both rapid response and controlled adjustments, preventing overreactions that could compromise system stability.

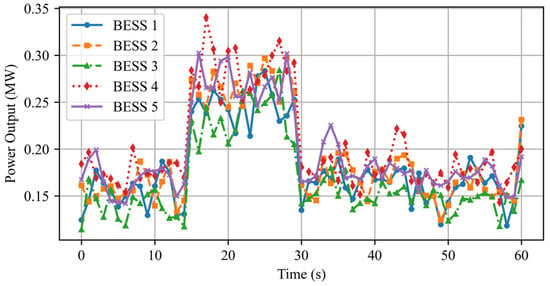
Figure 7. Power scheduling response trajectory of the distributed energy storage system.

In distributed optimization, maintaining a balanced power allocation is as crucial as flexibility. Overloading a few storage units can shorten their lifespan, increase charge–discharge cycles, and accelerate battery degradation. Figure 8 presents the distribution of power scheduling among storage units using a box plot. The results show the uniform power distribution, with no single unit consistently handling excessive load. The box lengths and interquartile ranges indicate that power fluctuations remain within a controlled range, without extreme values, ensuring system-wide balance. The distribution of outliers suggests that while some units experience short-term high loads, these occurrences are sporadic and not persistent. Additionally, the median power outputs of storage units are closely aligned, demonstrating that the proposed optimization algorithm effectively maintains load balance, preventing premature aging due to prolonged high loads. Compared to traditional methods, which may overburden specific storage units, the proposed consensus-based optimization enables dynamic load-sharing across all units. During high-demand fluctuations, storage units coordinate power adjustments locally, avoiding the excessive charging or discharging of individual units. This balanced scheduling not only reduces equipment wear but also enhances system stability under sudden load variations, ensuring long-term efficient operation.

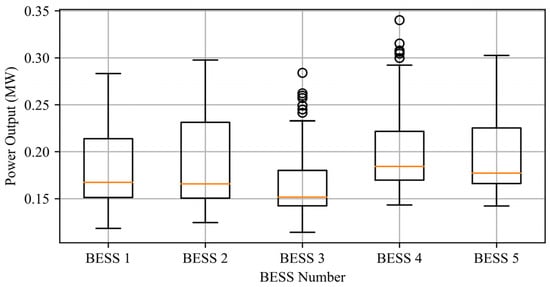
Figure 8. A dispersion analysis of power scheduling in distributed energy storage units.

Figure 9 shows the SoC variations during scheduling. The results indicate that SoC levels remain stable and within the 20–80% safety range, avoiding overcharging and deep discharges, which helps preserve battery lifespan. The proposed optimization method effectively regulates charge–discharge behavior while ensuring synchronized SoC trends across storage units through consensus-based coordination, enabling efficient decentralized operation.

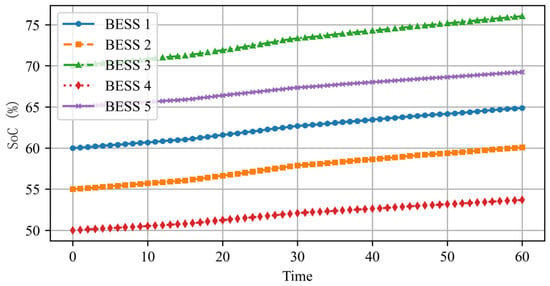
Figure 9. The state of the charge variation of energy storage units for case 4.

5.6. Adaptability and Scalability Analysis Under Storage Unit Disconnection and Reconnection

In DSES operation, storage units may disconnect or rejoin due to maintenance, faults, or system expansion, requiring optimization algorithms to adapt dynamically for stable power scheduling. The proposed distributed online convex optimization algorithm, incorporating consensus mechanisms and adaptive event-triggering, is tested for scalability in this scenario.

A five-unit DSES is simulated, where units operate independently under decentralized optimization, adjusting power output based on demand. From t = 60 to t = 150, storage unit 3 disconnects, and the remaining units compensate for the supply gap. At t = 151, unit 3 rejoins and resumes normal operation. Figure 10 presents the scenario data.

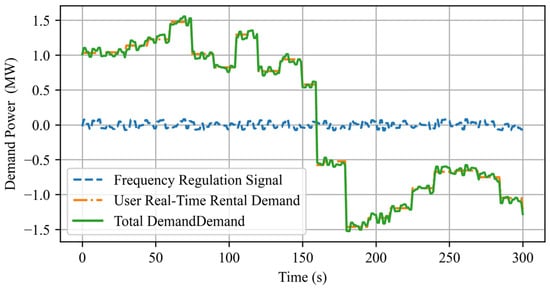
Figure 10. Frequency regulation commands, user leasing demand, and the total demand for case 5.

Figure 11 illustrates the power scheduling trajectory under storage unit disconnection and reconnection. When storage unit 3 disconnects, the system quickly adjusts, with other units increasing their output to compensate. Power trajectories remain stable, ensuring a balanced load distribution. Upon reconnection, unit 3 gradually restores output, and the system returns to pre-disconnection levels smoothly. These results confirm that the algorithm enables a rapid adaptation to unit outages and a stable reintegration, preventing scheduling instability. Figure 12 illustrates the SoC variations.

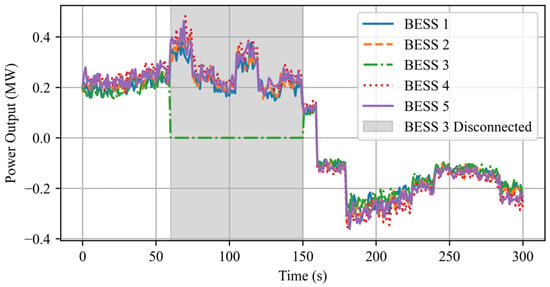
Figure 11. Power scheduling response trajectory.

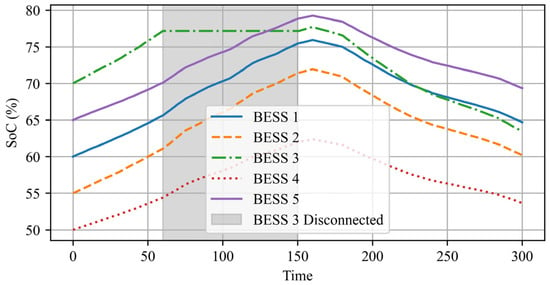
Figure 12. The state of the charge variation of energy storage units for case 5.

Figure 13, Figure 14 and Figure 15 illustrate the power output distribution of storage unit 3 before disconnection, during disconnection, and after reconnection, visualized through box plots to show power dispersion. Before disconnection, all storage units operate normally with a balanced power scheduling, as shown by similar medians and compact interquartile ranges in the box plot. During disconnection, unit 3’s output drops to zero, and other units compensate for the load, leading to higher medians and wider interquartile ranges while maintaining load balance. After reconnection, unit 3 gradually resumes output, the standard deviation decreases, and the system quickly stabilizes, ensuring an equitable power distribution.

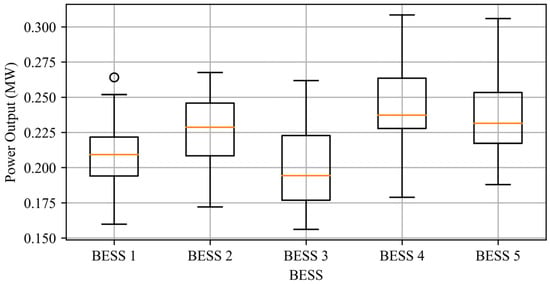
Figure 13. A power dispersion analysis of storage units before the disconnection of storage unit 3.

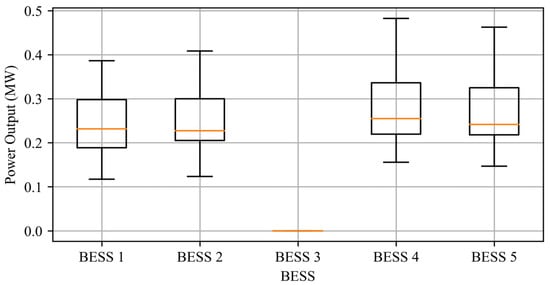
Figure 14. A power dispersion analysis of storage units during the disconnection of storage unit 3.

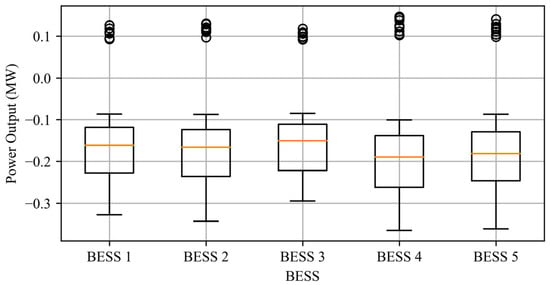
Figure 15. A power dispersion analysis of storage units after the reconnection of storage unit 3.

6. Conclusions

This paper presents a consensus-driven distributed online convex optimization strategy with an adaptive event-triggered mechanism to enhance the scheduling efficiency and scalability of DSES systems. The proposed approach leverages a consensus algorithm to achieve a decentralized and autonomous scheduling of storage units while maintaining global optimization consistency. By incorporating the Lagrangian relaxation method, the strategy effectively handles global power balance constraints, reducing the reliance on a central controller and enhancing system robustness and scalability.

To further improve communication efficiency, an adaptive event-triggered mechanism is developed to dynamically adjust the communication frequency based on system state variations. Instead of using a fixed triggering threshold, the mechanism employs a self-updating threshold that evolves in response to power changes. Communication is activated only when the state deviation exceeds this dynamically adjusted threshold, thereby reducing redundant transmissions while ensuring convergence stability. This approach minimizes communication overhead and enhances the system’s coordination capability under varying operating conditions.

Simulation experiments conducted on the IEEE 14-bus system validate the effectiveness of the proposed strategy. The results demonstrate that communication overhead is reduced by 33–60%, while convergence speed improves by over 40% compared to conventional methods. Moreover, the strategy exhibits strong adaptability in handling dynamic conditions, such as the integration and disconnection of storage units, ensuring stable and efficient scheduling in practical applications.

The proposed optimization framework not only achieves a balance between communication efficiency and optimization accuracy but also enhances the overall scalability of DSES systems. By reducing the reliance on frequent global information exchange, the method ensures a low consensus error while significantly lowering communication costs, making it particularly suitable for large-scale energy storage networks.

Despite the advantages of the proposed method, to improve the real-world applicability of the proposed method, future research will focus on several key directions. Firstly, it is important to develop delay-tolerant and noise-resilient control strategies that enhance robustness under practical communication constraints such as latency, data loss, or asynchronous updates. Secondly, the algorithm can be extended to support multi-time-scale coordination, enabling the integration of real-time control with day-ahead and hour-ahead planning layers commonly used in energy management systems. Thirdly, adaptive parameter tuning mechanisms based on reinforcement learning or real-time performance feedback can be incorporated to improve algorithm adaptability across different system conditions. Finally, conducting hardware-in-the-loop (HIL) simulations and field experiments will be essential to evaluate the deployment feasibility and performance of the proposed strategy in actual shared energy storage systems. These enhancements will collectively strengthen the practicality, robustness, and scalability of the framework, paving the way for real-world implementation.