You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Sustainability
Download PDF
  • Review
  • Open Access

9 July 2021

A Critical Analysis of Job Shop Scheduling in Context of Industry 4.0

,
,
and
1
Department of Mechanical Engineering, Capital University of Science & Technology, Islamabad 44000, Pakistan
2
Department of Engineering, School of Science and Technology, Clifton Campus, Nottingham Trent University, Nottingham NG11 8NS, UK
*
Author to whom correspondence should be addressed.
Sustainability2021, 13(14), 7684;https://doi.org/10.3390/su13147684
This article belongs to the Special Issue Building Sustainable Industry 4.0: Efficiency, Effectiveness, Evaluation, Development Frameworks
Version Notes
Order Reprints

Abstract

Scheduling plays a pivotal role in the competitiveness of a job shop facility. The traditional job shop scheduling problem (JSSP) is centralized or semi-distributed. With the advent of Industry 4.0, there has been a paradigm shift in the manufacturing industry from traditional scheduling to smart distributed scheduling (SDS). The implementation of Industry 4.0 results in increased flexibility, high product quality, short lead times, and customized production. Smart/intelligent manufacturing is an integral part of Industry 4.0. The intelligent manufacturing approach converts renewable and nonrenewable resources into intelligent objects capable of sensing, working, and acting in a smart environment to achieve effective scheduling. This paper aims to provide a comprehensive review of centralized and decentralized/distributed JSSP techniques in the context of the Industry 4.0 environment. Firstly, centralized JSSP models and problem-solving methods along with their advantages and limitations are discussed. Secondly, an overview of associated techniques used in the Industry 4.0 environment is presented. The third phase of this paper discusses the transition from traditional job shop scheduling to decentralized JSSP with the aid of the latest research trends in this domain. Finally, this paper highlights futuristic approaches in the JSSP research and application in light of the robustness of JSSP and the current pandemic situation.

1. Introduction

Scheduling plays a pivotal role in the production facility, as it maximizes the efficiency while minimizing various costs, lead time and cycle time, etc. Several studies have been conducted which analyzed the impact of the flow shop and job shop scheduling problem (JSSP) on manufacturing systems [1,2,3]. JSSP includes job operations with different machine sequences that have different processing times. The scheduling of machine operations can be done under various criteria; for instance, processing time, lead time, makespan, free float, or due dates, etc. [4]. Geyik & Cedimoglu (2004) [5] classified JSSP as an NP-hard optimization problem where different machines are assigned to various jobs while minimizing any of the applicable predefined criteria. Various algorithms and problem-solving techniques (such as first come first serve (FCFS), shortest processing time (SPT), earliest due date (EDD), etc.) have been developed and used over the years to solve JSSP [6,7,8,9,10,11,12,13]. However, as these optimization algorithms usually concentrate on centralized scheduling, these techniques are mainly focused on small-scale problems. While scaling up the problem, significant challenges arise in terms of computational time and cost [14,15]. Therefore, researchers and practitioners have gradually shifted their focus from traditional scheduling arrangement to smart-distributed scheduling (SDS) aided with technological pillars of the Industry 4.0 environment, such as Cyber-Physical Systems (CPS), Big data, Artificial Intelligence (AI), Internet of Things (IoTs), and Social, Mobile, Analytics, Cloud computing (SMAC). The transition from traditional scheduling to SDS faces two major research challenges: the integration of conventional JSSP scheduling techniques with SDS, and the development of new problem-solving techniques required for SDS.
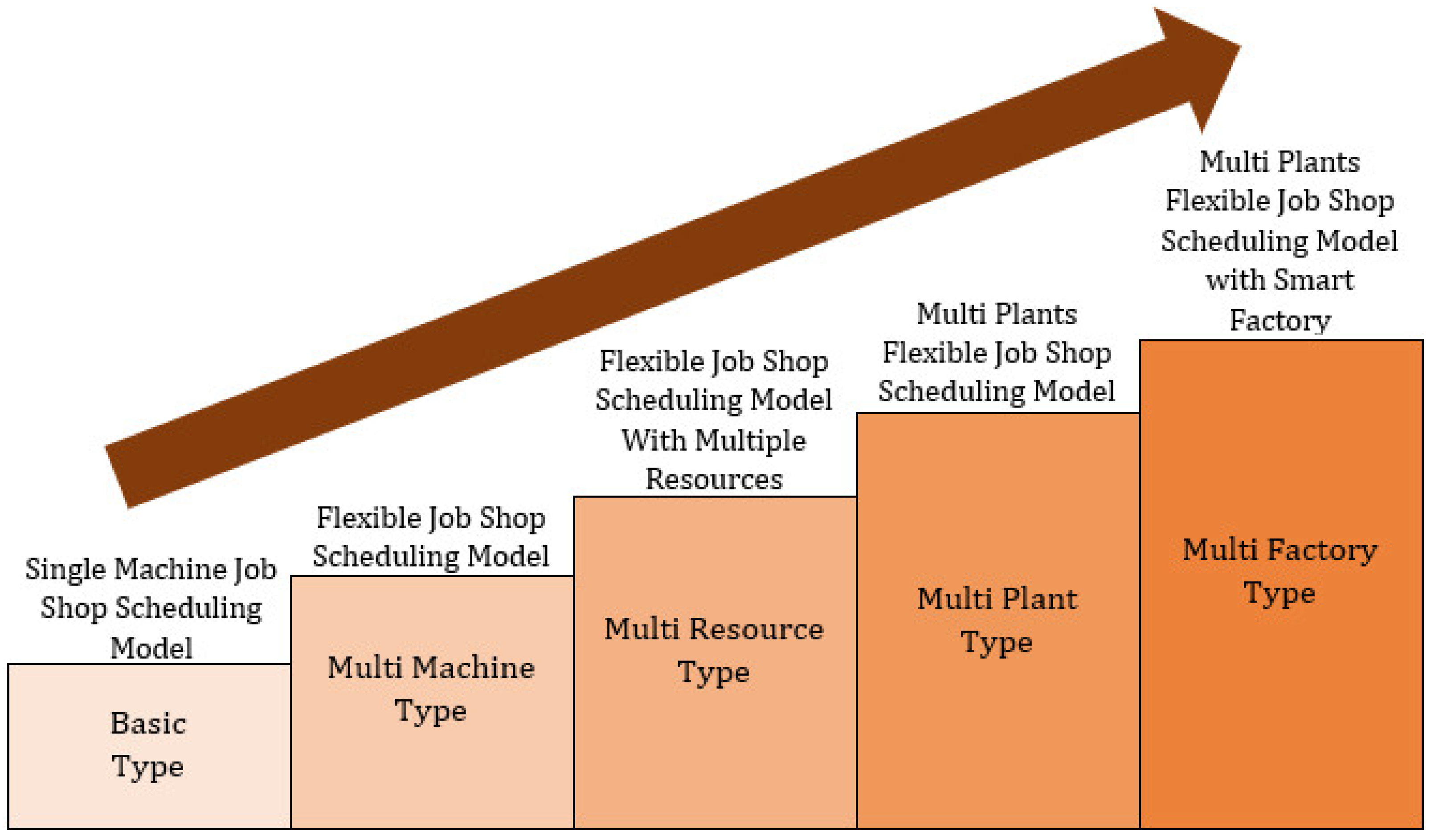
Various models for JSSP have been proposed for improving the operational efficiency of a job shop production facility. Figure 1 presents the classification of JSSP models with varying complexity based on the inclusion of various operational parameters. It is evident from Figure 1 that there is a drive toward the development of smart factories integrated with Industry 4.0. A detailed review of the literature reveals that several studies have reviewed the integration of JSSP with Industry 4.0. Chaudhry & Khan (2016) [16] performed an extensive review of literature from 1990 to 2014 and highlighted various techniques and approaches used to solve the JSSP problem. Their study argued the importance of flexible JSSP, especially in large-scale problems. The study also highlighted that the majority of the studies focused on algorithm development rather than solving real-world application problems. Parveen & Ullah (2010) [17] surveyed the literature to analyze the multi-objective scheduling in the context of flow shop and job shop scheduling environments. Their study highlighted the use of multi-criteria decision-making (MCDM) techniques along with mathematical optimization models to analyze the JSSP. A comprehensive review of job shop scheduling models, algorithms used for JSSPs, and the integration of techniques used in Industry 4.0 for solving JSSP were conducted by Zhang et al. [18]. Their study analyzed solving methods for various JSSPs in the Industry 4.0 environment.
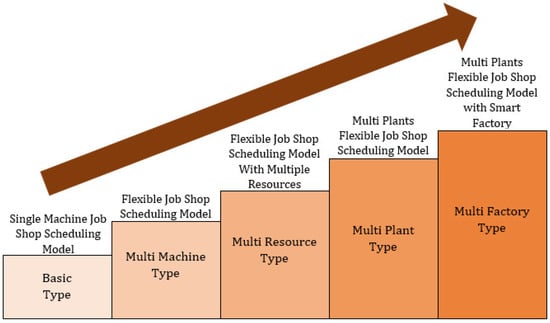
Figure 1. Job shop Scheduling Models and Classifications.
However, the studies discussed above are limited to the generic literature review and have not focused on the emerging trend of robustness and smart scheduling. The review presented in this paper builds on the previous research and contributes by reviewing the up-to-date JSSPs and solving techniques to highlight their current usages and challenges for SDS in the context of Industry 4.0. The research also provides an outlook for the integration of job shop scheduling with the medical industry in wake of the current pandemic situation.
The paper proceeds as follows: Section 2 includes the research objectives of the study; Section 3 includes the review methodology; Section 4 presents the research design used for the comprehensive analysis of the published literature; Section 5 includes the detailed literature review of the articles based on existing models, methodologies, and their advantages along with the limitations of the centralized JSSP problem; Section 6 presents the analysis of decentralization techniques for solving JSSP problems that are used in the Industry 4.0 environment; Section 7 focuses on the analysis of the latest publications on smart scheduling for JSSP; Section 8 presents the robustness in job shop scheduling integrated with Industry 4.0 environment in recent years; Section 9 includes the future research directions; Section 10 includes the conclusion of the study.

2. Research Objectives

Since the development of the first Job Shop Scheduling Problem (JSSP) [19], scheduling has been a research topic of interest amongst researchers and practitioners. JSSP is an NP-hard problem and extensive research has been done to solve its various classifications and complexities. However, there exist limited articles that comprehensively analyze different approaches developed by past researchers. Therefore, this study aims to examine the state-of-the-art literature available on JSSP for channeling it towards the Industry 4.0 implementation. In this regard, the following research questions have been addressed in this study:
  • What is the existing research status of JSSP?
  • How are JSSP models classified?
  • What techniques/algorithms have been used for solving various JSSP classifications and what are their limitations?
  • How JSSP can be integrated with the technological pillars of Industry 4.0?

3. Review Methodology

A systematic literature review-based study is conducted to address the above research questions. Peer-reviewed articles in ISI indexed journals in the context of JSSP (solving techniques/algorithms and integration of JSSP with Industry 4.0) are studied. Three selection criteria for the papers were considered, including (1) paper must be written in English; (2) paper must include the Job Shop Scheduling and Industry 4.0; (3) paper must include quantitative research methodology.
Published papers in international journals among electronic bibliographical sources including Scopus, Google Scholar, and Web of Science were searched by using a combination of different keywords.
In the first stage, keywords and sentence strings—‘Job Shop Scheduling’, ‘Flexible Job Shop Scheduling’, ‘Smart Factory’, ‘Job Shop Scheduling and Industry 4.0’—were employed to identify the relevant literature. The results obtained were then cross compared for possible overlap and checked for duplication.
The second stage of the process involved reviewing and screening the articles based on the above-stated criteria. This involved conducting an initial check with regard to the titles and keywords identified in the articles. From this, a total of 238 papers were identified. The third stage entailed reviewing the abstracts and conclusions of all 238 articles. This reduced the number of articles to 122.

4. Research Design

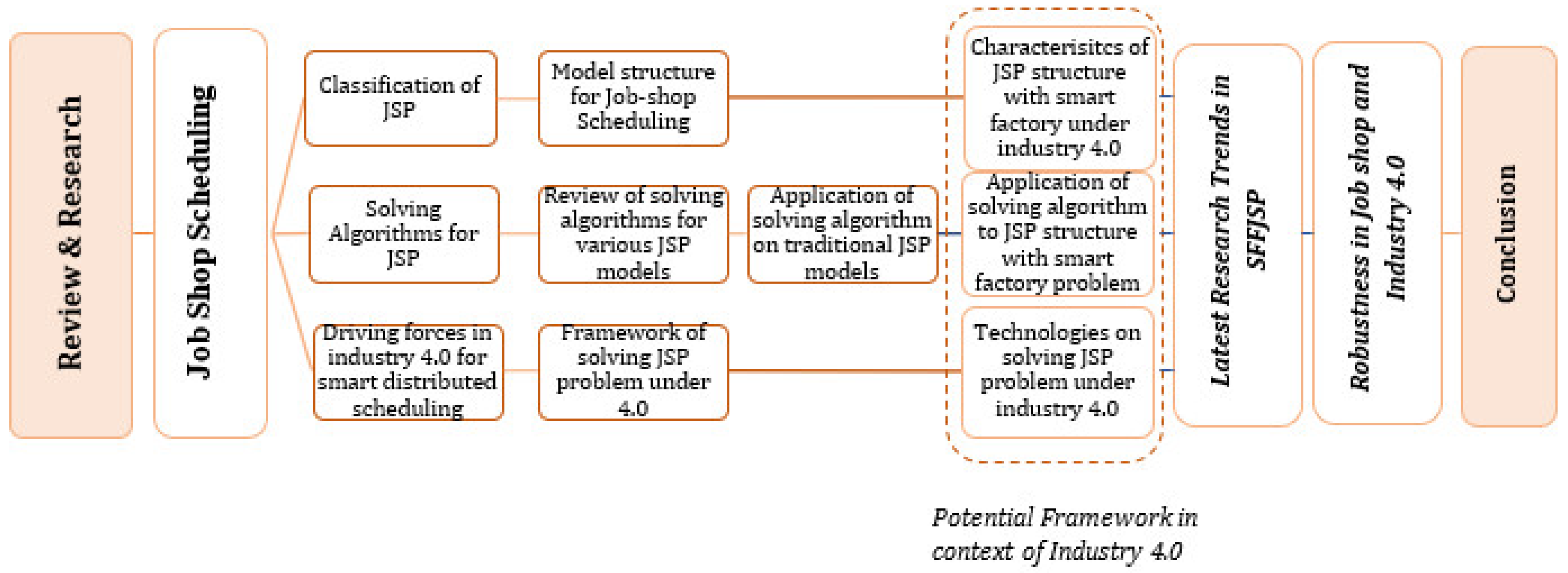
The research on scheduling in the context of Job Shop can be divided into two main categories: (1) problem modeling and (2) problem-solving techniques. JSSP is first classified based on model structures used in the literature. Characteristics of traditional JSSP model structures are analyzed in the context of Industry 4.0. Secondly, the classification and review of algorithms that are used for solving JSSP are done by taking into account both single and hybrid algorithms. Advantages and disadvantages, along with the limitations of the algorithms used in conventional scheduling are analyzed. The challenges of algorithms for using smart distributed scheduling are then highlighted. The driving forces such as IoT, deep learning, AI, cloud computing, and big data are analyzed for smart distributed scheduling. An analysis of the robustness of scheduling in the context of Industry 4.0 is also presented. Figure 2 presents the holistic framework of the research design for this study.
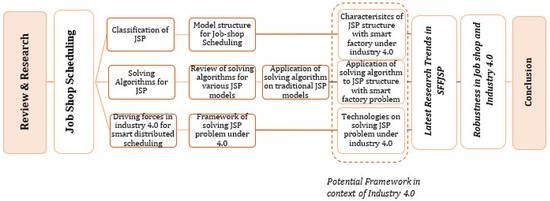
Figure 2. Research Design and Structure.

5. Literature Review

Johnson [19] did the pioneer work on scheduling by formulating the mathematical model with two machines. Garey et al. [20] classified JSSP with more than two machines as an NP-complete problem. The JSSP, as defined by Geyik & Cedimoglu [5], is a set of jobs Ji, where i = 1, 2, 3, …, n need to be scheduled on a set of machines Mj, where j = 1, 2, 3, …, m to minimize the makespan under some defined constraints. Some of the commonly used constraints are as follows Chen et al. [21]:
  • Each job will be assigned to different machines with a specified processing time;
  • Each machine can perform only one job at a moment;
  • The processing time of the job is fixed, and once the job is started it cannot be interrupted for each machining operation [22].
In advance scheduling techniques, the additional constraints such as machine capacity, labor productivity, resource availability, inventory, stock levels, and costs, etc., are also included [23].

5.1. Scheduling Model Structures

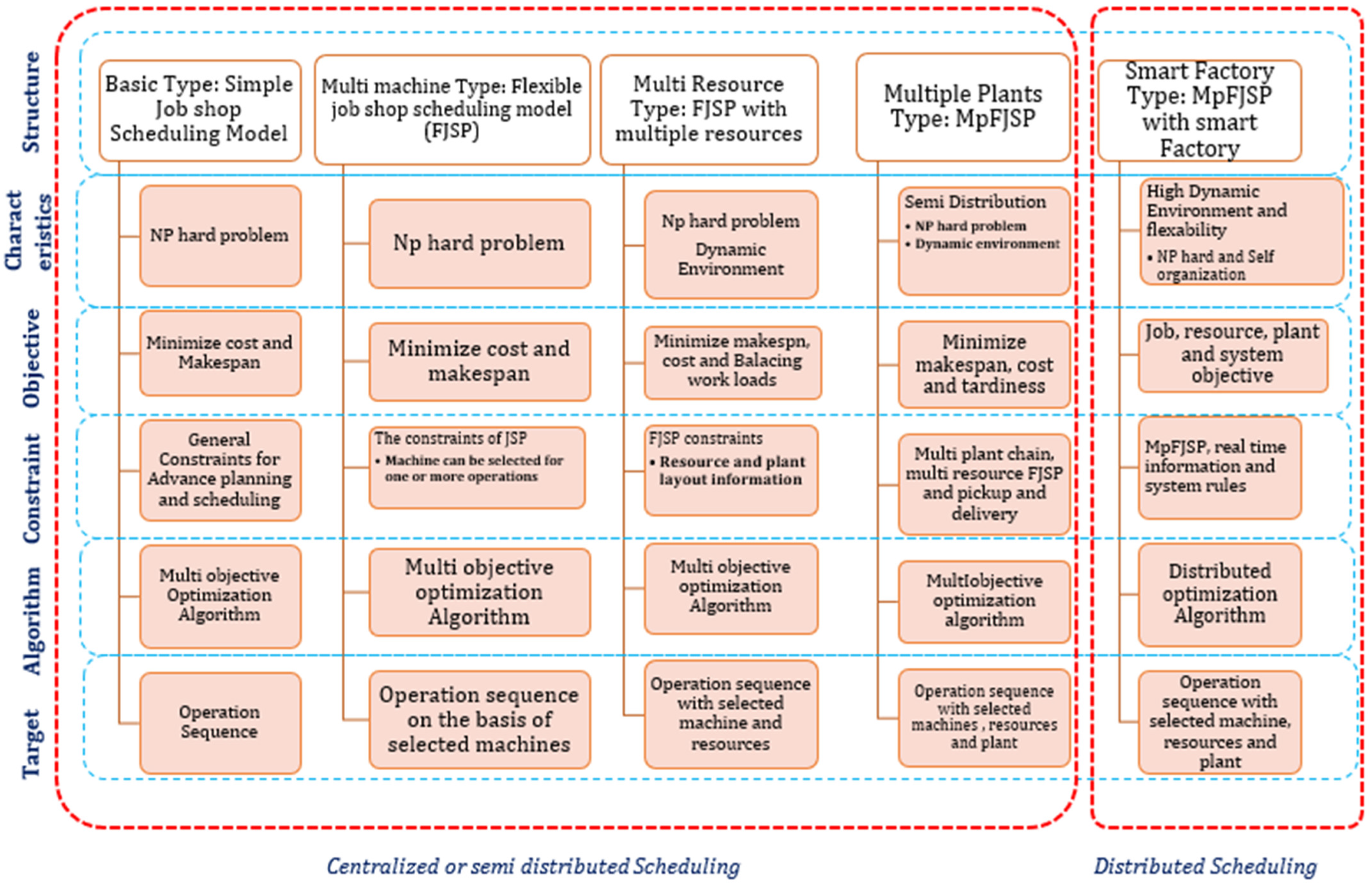
Scheduling can be done based on available resources, assigned jobs, and associated machines. Some review studies [24,25] on scheduling and model structures have analyzed diversified aspects of the scheduling models. The job shop scheduling models can be mainly classified into five types, i.e., performance measures, number of machines, production environment, resource constraint, and processing operations [26]. Based on the literature, JSSP was reclassified into five various types of structures as shown in Figure 3. The basic JSSP problem is an NP-hard problem with a specified operation on a specific machine/machining tool. It is an optimization problem employed to minimize the makespan, maximum lateness, and total weighted tardiness whilst achieving an optimum operation sequence. The Flexible Job Shop scheduling problem (FJSSP) tends to minimize expected makespan and balance the workloads on the selected machines for the optimized solution of an operation sequence [27]. In FJSSP, some or all the machines can be chosen by the algorithm for the desired solution [28]. Both JSSP and FJSSP are frequently used while implementing the algorithms. In Multi resource FJSSP, makespan, cost, and resource consumption are minimized by balancing the workloads [29]. It includes both renewable resources such as machinery and labor, etc., and non-renewable resources such as fuel and material. This type of problem is analyzed either by using disjunctive graphs or by developing the mathematical model [30]. In multi-plant-based FJSSP, multiple plants and transportation among them are also considered while minimizing makespan, costs, tardiness, and transportation distance [31]. This increases complexity and requires high computational power and time to achieve the optimized solution for the operation sequence with selected resources and plants. Due to its dynamic behavior, rescheduling is also required to achieve the optimum solution. The first four structures (i.e., basic type, multi-machine, multi-resource, and multi-plant) models are centralized scheduling models and are not effective for real-time dynamic changes [32]. As all four models are NP-hard problems, the incorporation of the actual dynamics results in increased cost, time and a long recovery period for disruptions in the manufacturing process. To incorporate the disruptions and stochastic environment related to orders, delivery times, machine breakdown, tool failure, and emergency events, etc., smart factory solutions are required in the future. In today’s mass customization and adaptive manufacturing environment, there is a need for smart agents with the features of self-organization and decision making that should be used for scheduling the manufacturing processes. In a smart distributed scheduling problem, the problem is divided into small parallel sub-problems and solved separately either by using a mono or multi-objective approach, using the exact or approximate algorithm. The separated sub-problems simultaneously require less computational time rather than concentrated JSSP to achieve better results.
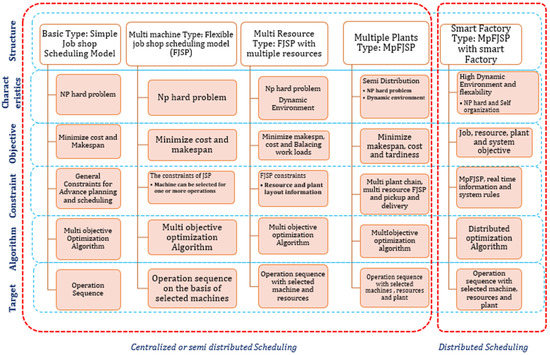
Figure 3. JSSP Structures.

5.2. Classification of Scheduling Algorithm

Various algorithms have been employed in the literature for solving JSSP. Both exact and approximate algorithms are classified, compared, and analyzed in various types of JSSP [33,34]. Table 1 and Table 2 enlist some relevant research to classify the algorithms used in the JSSP problem.
Table 1. Exact Optimization Algorithms for JSSP.
Table 2. Approximate Optimization Algorithms for JSSP.
JSSP can also be classified on the basis of machine tools, i.e., single and multi-machine shops. Various studies analysed the JSSP in the context of performance measures, i.e., cost, lead time, makespan, etc. Production environment also plays a pivotal role in JSSP. It is characterized as deterministic and stochastic. The addition of constraints and characteristics such as the number of plants, types of resources (i.e., renewable and nonrenewable) and type of operations would further classify the JSSP along with increasing the complexity and solution space of the problem.

5.3. Characteristics, Limitations, and Challenges of Exact and Approximate Optimization Methods

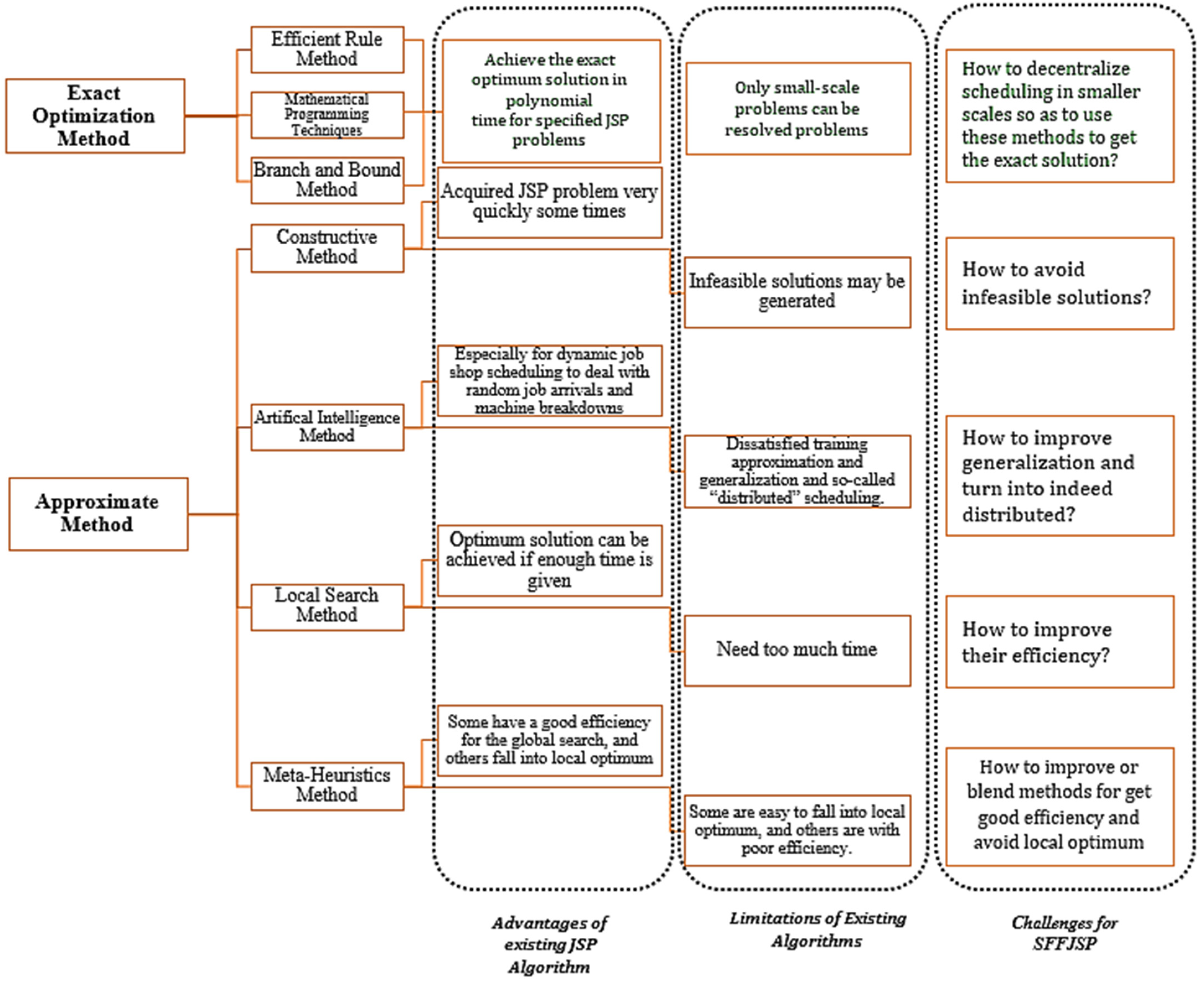
As highlighted in Table 1 and Table 2, optimization methods can be classified into exact and approximate solution approaches. The exact optimization method solves the optimization problem with an effort that grows polynomially with the problem size. It includes efficient rule approaches, mathematical programming approaches, branch definition methods, etc. For NP-hard problems such as JSSP, the exact approaches require exponential effort [80]. In contrast, the approximate optimization method used a dynamic environment with multiple dependent and independent variables. The approximate methods include constructive methods, artificial intelligence, local search, and meta-heuristic algorithms. Approximate methods do not guarantee finding optimal solutions. They are usually designed for a particular problem and tend to exploit problem-specific knowledge. Therefore, the performance of the problem can be often increased by increasing problem specificity and narrowing the application scope [81]. Figure 4 presents the characteristics, limitations, and challenges of optimization algorithms used for JSSP problems.
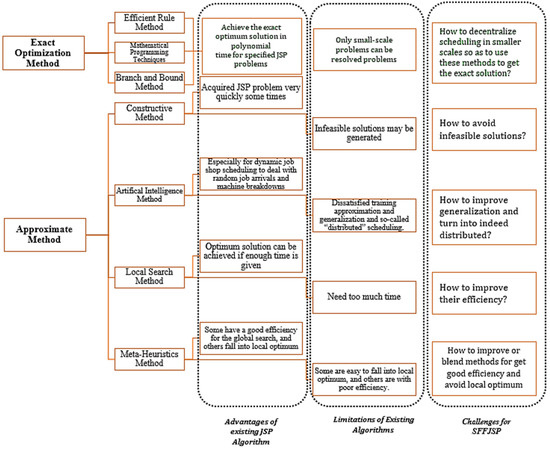
Figure 4. Characteristics and challenges of Optimization Algorithms in context of SFFJSP.

6. Decentralization

With decentralization taking over the manufacturing industry, flexible manufacturing systems have become a top priority which are smart as well as decentralized, and provide the opportunity to achieve autonomist manufacturing [82]. This approach is unlike the centralized and semi-centralized traditional JSSP. With Industry 4.0 making its shift towards smart manufacturing, the traditional JSSP application is expected to be utilizing smart scheduling along with optimization techniques. In the models based on the futuristic approach, the job, resource, system, and plant objectives are allotted to the smart agents. These objectives act as the prime optimization objective for the smart agents for accessing smart distribution scheduling. Optimization through smart agents is based on distributed optimization algorithm feedback. The feedback is related to predefined parameters, system rules, and objectives. With this decentralized approach, Industry 4.0 has emerged as a pioneer in producing faster and easier operation schedules and sequences with predefined resources [83].

6.1. Industry 4.0 Mainspring for Smart Distributed Scheduling

The shift in the production processes to decentralization is obtained through the exchange of information among resources, plants, jobs, and machines [84]. The frequent exchange of information has brought various important aspects under research and implementation, such as: smart factories, cyber-physical systems, cloud computing, and Internet of Things. Artificial Intelligence utilization through deep learning has also emerged as an important solution for solving fast, self-decision problems for smart agents in job shop scheduling.

6.1.1. Internet of Things (IoT)

In the context of a job shop, Internet of Things (IoT) helps in connecting all the desired aspects of the manufacturing systems for the creation of big data [85]. The inclusion of IoT in the job shop scenario has made manufacturing smarter since it has made it more real through the use of real-time data and integration of network information of resources, tools, machines, and personals [86]. This has led to the optimization of the supply chain through improvisation of the production process, meeting demands, and performing jobs quickly.

6.1.2. Cyber-Physical Systems (CPS)

CPS merges the virtual world (computing stimulated process) and the real-world (physical process). Through this system, the physical process and parameters govern the scheduling through virtual models, where the embedded systems, control, and computing technologies govern production through optimized scheduling [87]. The futuristic CPS has become highly advanced and reduced computation and data storage by using advanced tools such as RFID, network gateways, and other tools. Such systems, contrary to traditional CPS, are highly efficient since data analysis is a distributed task, whereas, for the latter case, service agents are required for these tasks [88].

6.1.3. Smart Factory

Smart factories are based on CPS and IoT. In the smart factory concept, employing modules, CPS is more efficient as compared to IoT since it communicates among modules more effectively thus making decentralization possible in many aspects. The difference between traditional centralized job shop scheduling and smart decentralized job shop scheduling is the incorporation of the concept of a smart factory [89]. In a smart factory, a smart agent can decide the scheduling and its assignment based on its plan, choice, goals, current condition, and machining history. Therefore, flexible job shop scheduling models with multi-resources, multi-plants, transportation, and smart factory (SFFJSP) have emerged as a solution to scheduling problems [90].

6.1.4. Cloud Computing

Cloud computing has provided a structure for scheduling in manufacturing. It has provided a service and information sharing platform which has proved to be very fruitful for optimization during scheduling [91]. Cloud computing has enabled the incorporation of multi-plants, multi-suppliers, and multi-logistic providers in the scheduling of optimization procedures [92]. Cloud manufacturing has also eased parallel computing, which reduces the workload, enables distributed decisions for agents, and makes the solution of local problems possible through the use of computing power and big data [93,94].

6.1.5. Deep Learning

Deep learning, in recent years, has emerged as one of the mainstream subjects in machine learning and artificial intelligence. It applies nonlinear models of complex nature for the representation of the relationship between data [95]. It employs big data for the analysis and determination of end relationships between data. Deep learning applies the first come, first serve rule for scheduling in a job shop. The system, either randomly or by optimization, schedules the preliminary sorting. This sorting, with the deep learning technology, leads to self-determination for each job, whether it adjusts to the queue or not [96]. This practice covers two scenarios for each job. In the first scenario, each job judges the preliminary sorting against its delivery time and, if the delivery time is not met, then the job self-decides to override the sequence to achieve its target. In the second scenario, if the preliminary sorting guarantees the delivery time of the job, the job uses deep learning technology with autonomous decision-making for forecasting efficiency, cost, machine utilization, etc. Deep learning and improved learning techniques enable the system to predict failures. As a preventive measure, it enables the system to issue maintenance instructions, keep a record of machine maintenance, measures the jobs involved in the scheduling, and choose their process resources and orders in response. This self-decision process is realized when there is an information transfer among smart jobs and machines. Automated driving technology based on a combination of deep learning with incremental learning makes the logistics transport resourcing smart. Each vehicle and robot can perceive its environment in real-time, choose the shortest route, and avoid congestion dynamically [97]. This decision-making process is realized when there is an information transfer among smart jobs and smart multi-resources. This predictive model is constantly improved through deep learning and data-driven techniques, where data is obtained from the stimulated machining processes and the actual machining processes.

6.2. Implementation Steps of JSSP Structure with SFFJSP

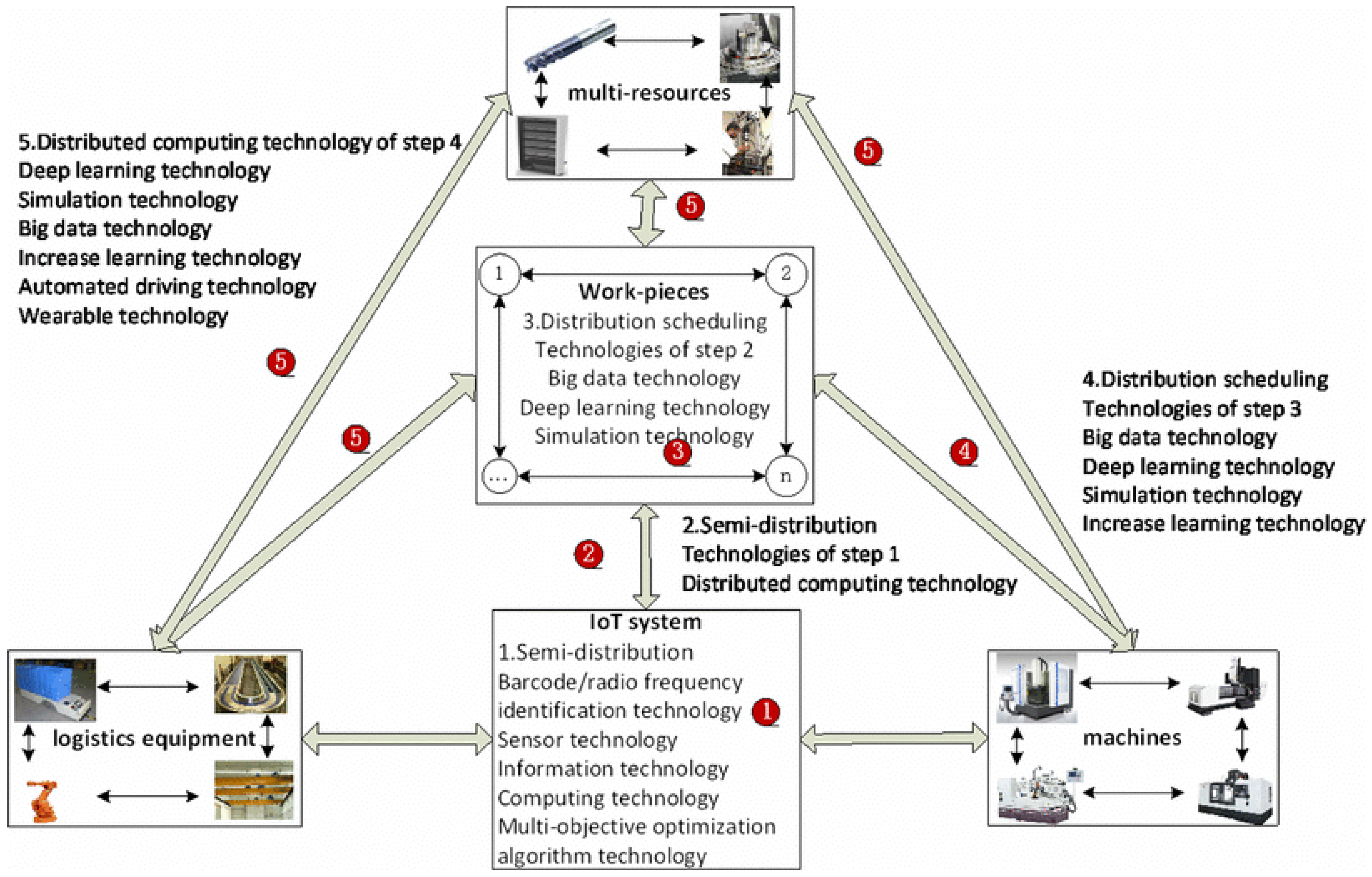
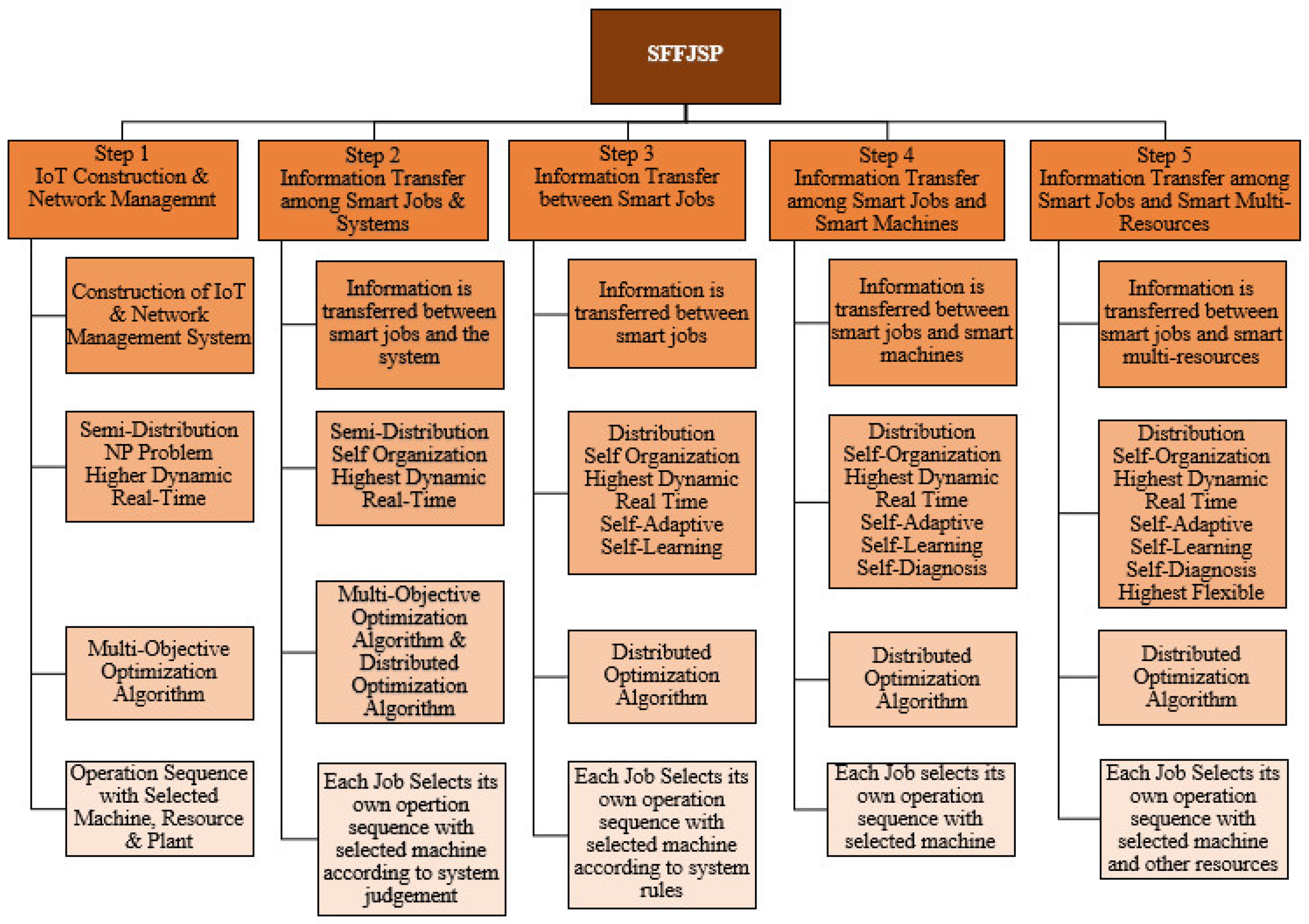
The original centralized scheduling problem can be turned into smart agents-based problems. Framework for the solution of the JSSP problem under Industry 4.0 as summarized by Zhang et al. [18] is shown in Figure 5, and its related SFFJSP implementation is shown in Figure 6.
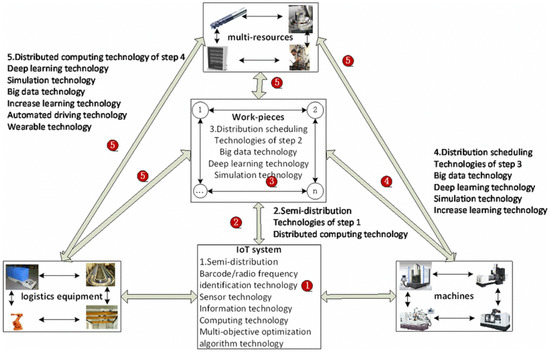
Figure 5. Key enabling technologies for JSSP under Industry 4.0 Reprinted from Zhang et al. (2019) [18].
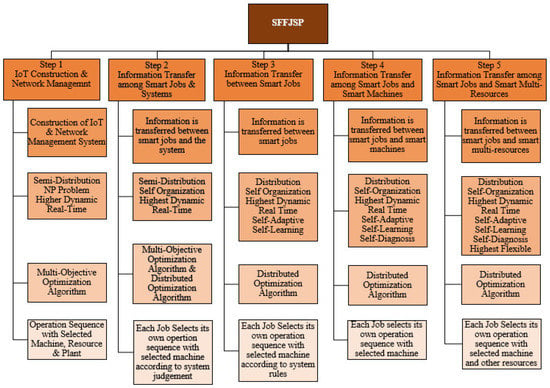
Figure 6. Steps of SFFJSP.

8. Robustness in Job Shop and Industry 4.0

Robustness in the Job Shop environment has been viewed as a concern and a constraint in the past. However, it has been found that, among the robustness and energy efficiency, there exists a clear relationship and there is a tradeoff not only among robustness and makespan but also among energy efficiency and makespan [116]. It can be analyzed and incorporated in the scheduling problem if the processing times are modeled as fuzzy numbers and scheduling is performed through a Hybrid Genetic Algorithm which leads to minimized makespan [117].
Inclusion of additional measures in the robustness problem such as maximal machine workload and makespan objective functions along with uncertainty, when solved through Modified Multi-Objective Evolutionary Algorithm based on Decomposition (m-MOEA/D), leads to a better convergence to the problem as compared with the Multi-Objective Optimization Evolutionary Algorithms (MOEAs) for a Multi-Objective Stochastic Flexible Job Shop Scheduling Problem (MOSFJSSP) [118].
Consideration of pre-defined/predicted disruptions in a JSSP for robustness indicated that small-scale problems give solutions through both the mathematical model and the branch and bound algorithm. For large-scale problems, the aforementioned methods were not found to be viable since the time to solution considerably increased. For large-scale problems, beam search algorithm and particle swarm optimization were found to be better performing. However, a single method could not be singled out for solving the scheduling problem, since each method outperformed the other in different scenarios [119].
Recent studies indicated the effects of robustness in the real time scenario of machine breakdowns. Robustness in the multi-objective optimization with the inclusion of machine breakdowns along with makespan leads to the development of meta-models which, when solved through MOEA, indicates a better convergence and diversity in Pareto solution sets as compared to the slack-based surrogate measures [120,121].

9. Future Research Agenda

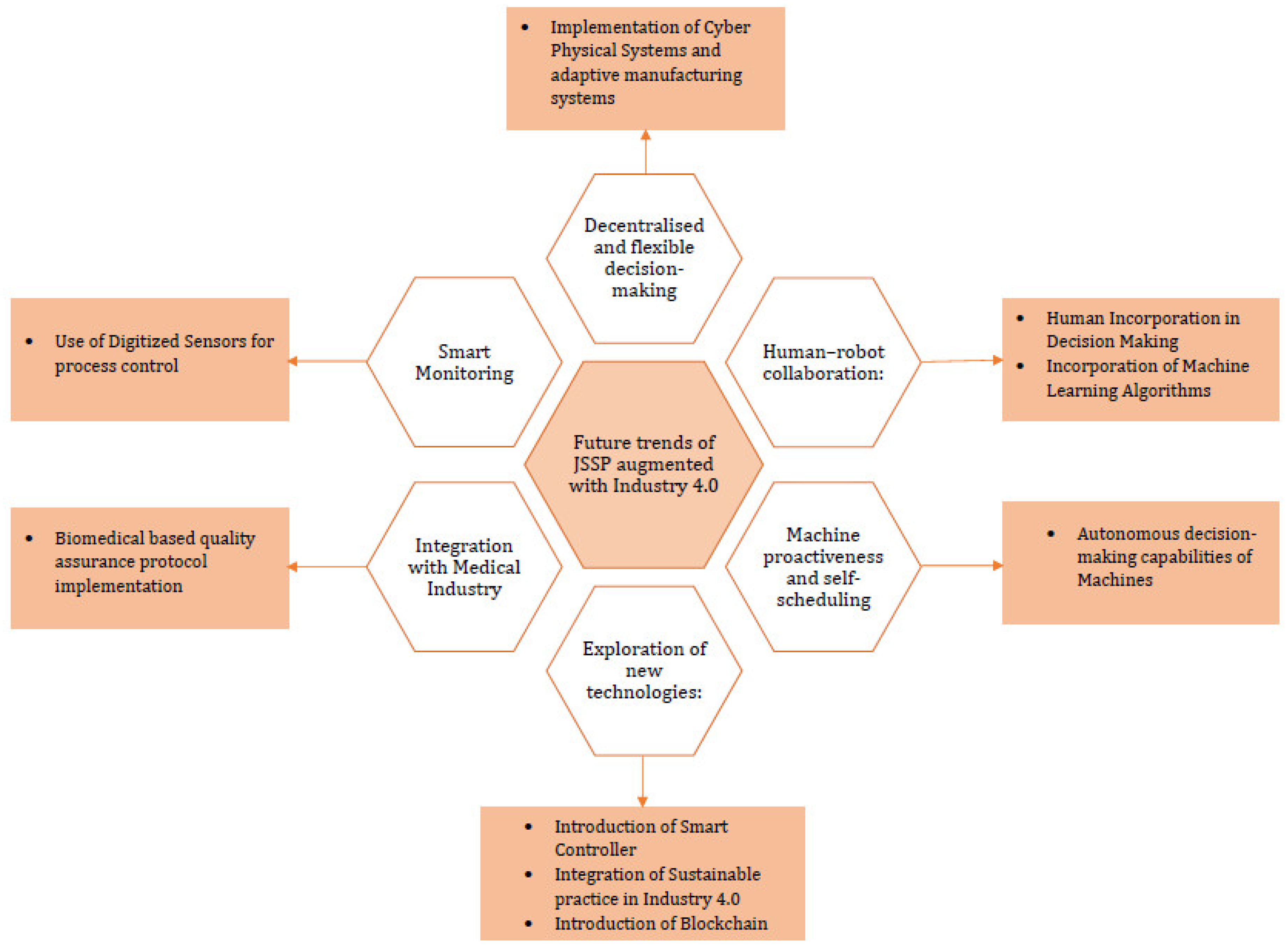
The scope for research in JSSP in the context of Industry 4.0 is still largely untapped and its utility and viability in various applications is still to be explored further. Figure 7 presents the future research agenda of JSSP augmented with Industry 4.0.
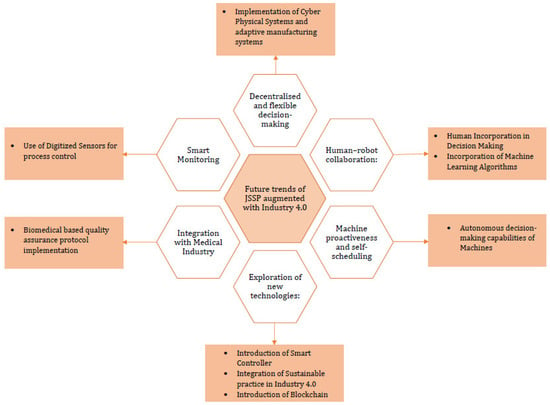
Figure 7. Dimensions of Future Research Perspectives.
  • Incorporation of customized decision-making criteria for machine learning-based decentralized operating systems.
  • Industry 4.0 also provides room for human-machine collaboration where smart machines can assist humans to achieve efficient solutions, as discussed in Berti et al. [122]. Moreover, involvement of human input in decision-making for efficient and sustainable decisions directed towards Industry 5.0 framework.
  • Development of customized smart sensors for manufacturing performance criteria assurance and assessment.
  • Development of specialized sensors and quality assurance procedures for decentralized JSSP for medical-grade manufacturing.
  • Implementation of blockchain and distributed ledger technologies in a manufacturing environment for sharing and retrieving data of machines functions between agents.
  • Determination of sustainability indices for decentralized JSSP.
  • Implementation of sustainability indices and other decision-making criteria for application in decentralized JSSP focused on the concept of Industry 5.0 (fueled by Information Technology and Environmental Sustainability).

10. Conclusions

In the first phase of this paper, the JSSP problem is summarized based on the structural framework and scheduling algorithms. Various studies are classified based on solving algorithms. The advantages and limitations of existing solving methods and challenges for the implementation in the Industry 4.0 environment are highlighted. In the second phase, the futuristic approaches to solving JSSP problems under Industry 4.0 environment are presented with their potential advantages. A framework is presented through which the original centralized scheduling problem can be turned into smart agents-based problems. In the third phase of this study, the latest studies from the year 2017–2021 are analyzed to provide an overview of the latest research trends in SFFJSP.
  • Integration of FJSSP with Industry 4.0 provides a conducive solution regarding computational time, makespan, tardiness, lateness, etc.
  • The latest research trends indicate that conventional JSSP is no more practical to study.
  • Multi machines, multi operations, multi resources with multiple factories and logistics centers should be incorporated in conventional JSSP to evaluate the actual dynamics of the system.
  • Currently, the research focus is on approximate algorithms rather than exact algorithms for solving JSSP and FJSSP. The global and local optimum solution is evaluated with the aid of multi-objective optimization techniques.
  • The metaheuristics approaches have acquired great popularity for solving the JSSP and FJSSP. Recent studies show that hybrid approaches are vastly used for solving JSSP under the Industry 4.0 environment.
  • The use of PID controllers, RFIDs, and barcodes has become a great source of integrating actual plant with its digital part.
  • Recent studies indicate the use of smart agents to determine the efficient sequencing of jobs while minimizing the complexity of JSSPs, is a competitive approach adopted by many scholars.
  • The merger of AI, CPS, deep learning, cloud computing, etc., in JSSPs has outperformed the conventional approaches of finding optimal solutions.

Author Contributions

R.A.L.: literature search and manuscript writing, editing. S.H.: literature search and manuscript writing. S.S.W.: content planning, reviewing and proof reading, manuscript editing. A.K.: content planning, reviewing, proof reading. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare that there is no conflict of interest in the subject matter or materials discussed in this manuscript.

References

  1. Kim, S.C.; Bobrowski, P.M. Impact of sequence-dependent setup time on job shop scheduling performance. Int. J. Prod. Res. 1994, 32, 1503–1520. [Google Scholar] [CrossRef]
  2. Le Gal, P.-Y.; Lyne, P.; Meyer, E.; Soler, L.-G. Impact of sugarcane supply scheduling on mill sugar production: A South African case study. Agric. Syst. 2008, 96, 64–74. [Google Scholar] [CrossRef]
  3. Dalton, D.R.; Mesch, D.J. The Impact of Flexible Scheduling on Employee Attendance and Turnover. Adm. Sci. Q. 1990, 35, 370. [Google Scholar] [CrossRef]
  4. Błażewicz, J.; Ecker, K.H.; Pesch, E.; Schmidt, G.; Weglarz, J. Scheduling Computer and Manufacturing Processes; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
  5. Geyik, F.; Cedimoglu, I.H. The strategies and parameters of tabu search for job-shop scheduling. J. Intell. Manuf. 2004, 15, 439–448. [Google Scholar] [CrossRef]
  6. Della Croce, F.; Tadei, R.; Volta, G. A genetic algorithm for the job shop problem. Comput. Oper. Res. 1995, 22, 15–24. [Google Scholar] [CrossRef]
  7. Nowicki, E.; Smutnicki, C. A Fast Taboo Search Algorithm for the Job Shop Problem. Manag. Sci. 1996, 42, 797–813. [Google Scholar] [CrossRef]
  8. Hurink, J.; Jurisch, B.; Thole, M. Tabu search for the job-shop scheduling problem with multi-purpose machines. Oper. Res. Spectr. 1994, 15, 205–215. [Google Scholar] [CrossRef] [Green Version]
  9. Carlier, J.; Pinson, E. An Algorithm for Solving the Job-Shop Problem. Manag. Sci. 1989, 35, 164–176. [Google Scholar] [CrossRef]
  10. Blazewicz, J.; Domschke, W.; Pesch, E. The job shop scheduling problem: Conventional and new solution techniques. Eur. J. Oper. Res. 1996, 93, 1–33. [Google Scholar] [CrossRef]
  11. Mastrolilli, M.; Gambardella, L.M. Effective neighbourhood functions for the flexible job shop problem. J. Schedul. 2000, 3, 3–20. [Google Scholar] [CrossRef]
  12. Nakano, R.; Yamada, T. Conventional genetic algorithm for job shop problems. ICGA 1991, 91, 474–479. [Google Scholar]
  13. Ye, L.; Yan, C. A genetic algorithm for job-shop scheduling. J. Softw. 2010, 5, 269–274. [Google Scholar]
  14. Chong, C.S.; Low, M.Y.H.; Sivakumar, A.I.; Gay, K.L. A Bee Colony Optimization Algorithm to Job Shop Scheduling. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1954–1961. [Google Scholar]
  15. Qing-Dao-Er-Ji, R.; Wang, Y. A new hybrid genetic algorithm for job shop scheduling problem. Comput. Oper. Res. 2012, 39, 2291–2299. [Google Scholar] [CrossRef]
  16. Chaudhry, I.A.; Khan, A.A. A research survey: Review of flexible job shop scheduling techniques. Int. Trans. Oper. Res. 2016, 23, 551–591. [Google Scholar] [CrossRef]
  17. Parveen, S.; Ullah, H. Review on job-shop and flow-shop scheduling using. J. Mech. Eng. 2011, 41, 130–146. [Google Scholar] [CrossRef] [Green Version]
  18. Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 2019, 30, 1809–1830. [Google Scholar] [CrossRef]
  19. Johnson, S.M. Optimal two-and three-stage production schedules with setup times included. Naval Res. Log. Q. 1954, 1, 61–68. [Google Scholar] [CrossRef]
  20. Garey, M.R.; Johnson, D.S.; Sethi, R. Complexity of Flowshop and Jobshop Scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
  21. Chen, J.C.; Wu, C.-C.; Chen, C.-W.; Chen, K.-H. Flexible job shop scheduling with parallel machines using Genetic Algorithm and Grouping Genetic Algorithm. Expert Syst. Appl. 2012, 39, 10016–10021. [Google Scholar] [CrossRef]
  22. Leusin, M.E.; Frazzon, E.M.; Maldonado, M.U.; Kück, M.; Freitag, M. Solving the Job-Shop Scheduling Problem in the Industry 4.0 Era. Technologies 2018, 6, 107. [Google Scholar] [CrossRef] [Green Version]
  23. Lin, L.; Hao, X.-C.; Gen, M.; Jo, J.-B. Network modeling and evolutionary optimization for scheduling in manufacturing. J. Intell. Manuf. 2011, 23, 2237–2253. [Google Scholar] [CrossRef]
  24. Floudas, C.A.; Lin, X. Continuous-time versus discrete-time approaches for scheduling of chemical processes: A review. Comput. Chem. Eng. 2004, 28, 2109–2129. [Google Scholar] [CrossRef] [Green Version]
  25. Graves, S.C. A Review of Production Scheduling. Oper. Res. 1981, 29, 646–675. [Google Scholar] [CrossRef]
  26. Nouri, H.E.; Driss, O.B.; Khaled, G.A. Classification Schema for the Job Shop Scheduling Problem with Transportation Resources: State-of-the-Art Review. Artif. Intell. Perspect. Intell. Syst. 2016, 464, 249–261. [Google Scholar] [CrossRef]
  27. Kacem, I.; Hammadi, S.; Borne, P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2002, 32, 1–13. [Google Scholar] [CrossRef]
  28. Gholami, O.; Sotskov, Y.N. Solving parallel machines job-shop scheduling problems by an adaptive algorithm. Int. J. Prod. Res. 2013, 52, 3888–3904. [Google Scholar] [CrossRef]
  29. Grobler, J.; Engelbrecht, A.P.; Kok, S.; Yadavalli, S. Metaheuristics for the multi-objective FJSP with sequence-dependent set-up times, auxiliary resources and machine down time. Ann. Oper. Res. 2009, 180, 165–196. [Google Scholar] [CrossRef] [Green Version]
  30. Jones, D.F.; Mirrazavi, S.K.; Tamiz, M. Multi-objective meta-heuristics: An overview of the current state-of-the-art. Eur. J. Oper. Res. 2002, 137, 1–9. [Google Scholar] [CrossRef]
  31. Lee, S.; Moon, I.; Bae, H.; Kim, J. Flexible job-shop scheduling problems with ‘AND’/‘OR’ precedence constraints. Int. J. Prod. Res. 2012, 50, 1979–2001. [Google Scholar] [CrossRef]
  32. Floudas, C.A.; Lin, X. Mixed Integer Linear Programming in Process Scheduling: Modeling, Algorithms, and Applications. Ann. Oper. Res. 2005, 139, 131–162. [Google Scholar] [CrossRef]
  33. Çaliş, B.; Bulkan, S. A research survey: Review of AI solution strategies of job shop scheduling problem. J. Intell. Manuf. 2013, 26, 961–973. [Google Scholar] [CrossRef]
  34. Jain, A.S.; Meeran, S. A State-of-the-Art Review of Job-Shop Scheduling Techniques. 1998. Available online: https://neuro.bstu.by/ai/To-dom/My_research/Papers-0/For-courses/Job-SSP/jain.pdf (accessed on 5 July 2021).
  35. Hefetz, N.; Adiri, I. An Efficient Optimal Algorithm for the Two-Machines Unit-Time Jobshop Schedule-Length Problem. Math. Oper. Res. 1982, 7, 354–360. [Google Scholar] [CrossRef]
  36. Wagner, H.M. An integer linear-programming model for machine scheduling. Nav. Res. Logist. Q. 1959, 6, 131–140. [Google Scholar] [CrossRef]
  37. Manne, A.S. On the Job-Shop Scheduling Problem. Oper. Res. 1960, 8, 219–223. [Google Scholar] [CrossRef] [Green Version]
  38. Lomnicki, Z.A. A “Branch-and-Bound” Algorithm for the Exact Solution of the Three-Machine Scheduling Problem. J. Oper. Res. Soc. 1965, 16, 89. [Google Scholar] [CrossRef]
  39. Sarin, S.C.; Ahn, S.; Bishop, A.B. An improved branching scheme for the branch and bound procedure of schedulingnjobs onmparallel machines to minimize total weighted flowtime. Int. J. Prod. Res. 1988, 26, 1183–1191. [Google Scholar] [CrossRef]
  40. Versteyhe, M.; DeBrouwere, F. Application of non-deterministic uncertainty models to improve resource constraint optimal scheduling. J. Oper. Res. Soc. 2020, 1–12. [Google Scholar] [CrossRef]
  41. McMahon, G.; Florian, M. On Scheduling with Ready Times and Due Dates to Minimize Maximum Lateness. Oper. Res. 1975, 23, 475–482. [Google Scholar] [CrossRef]
  42. Barker, J.R.; McMahon, G.B. Scheduling the General Job-Shop. Manag. Sci. 1985, 31, 594–598. [Google Scholar] [CrossRef]
  43. Rosenkrantz, D.J.; Stearns, R.E.; Lewis, P.M. An analysis of several heuristics for the traveling salesman problem. Fundam. Prob. Comput. 2009, 6, 45–69. [Google Scholar] [CrossRef]
  44. Nawaz, M.; Enscore, E.E.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 1983, 11, 91–95. [Google Scholar] [CrossRef]
  45. Liu, S.Q.; Kozan, E. A hybrid shifting bottleneck procedure algorithm for the parallel-machine job-shop scheduling problem. J. Oper. Res. Soc. 2012, 63, 168–182. [Google Scholar] [CrossRef]
  46. Dauzere-Peres, S.; Lasserre, J.B. A modified shifting bottleneck procedure for job-shop scheduling. Int. J. Prod. Res. 1993, 31, 923–932. [Google Scholar] [CrossRef]
  47. Adams, J.; Balas, E.; Zawack, D. The Shifting Bottleneck Procedure for Job Shop Scheduling. Manag. Sci. 1988, 34, 391–401. [Google Scholar] [CrossRef]
  48. Wenqi, H.; Aihua, Y. An improved shifting bottleneck procedure for the job shop scheduling problem. Comput. Oper. Res. 2004, 31, 2093–2110. [Google Scholar] [CrossRef]
  49. Pesch, E.; Tetzlaff, U.A.W. Constraint Propagation Based Scheduling of Job Shops. Inf. J. Comput. 1996, 8, 144–157. [Google Scholar] [CrossRef]
  50. Sadeh, N.; Fox, M.S. Variable and value ordering heuristics for the job shop scheduling constraint satisfaction problem. Artif. Intell. 1996, 86, 1–41. [Google Scholar] [CrossRef] [Green Version]
  51. Simon, F.Y.-P.; Takefuji, Y. Stochastic neural networks for solving job-shop scheduling. I. Problem representation. In Proceedings of the IEEE International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; pp. 283–290. [Google Scholar]
  52. Simon, F.Y.-P.; Takefuji, Y. Stochastic neural networks for solving job-shop scheduling. II. Architecture and simulations. In Proceedings of the IEEE International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; pp. 283–290. [Google Scholar]
  53. Akyol, D.E.; Bayhan, G.M. A review on evolution of production scheduling with neural networks. Comput. Ind. Eng. 2007, 53, 95–122. [Google Scholar] [CrossRef]
  54. Min, H.-S.; Yih, Y. Selection of dispatching rules on multiple dispatching decision points in real-time scheduling of a semiconductor wafer fabrication system. Int. J. Prod. Res. 2003, 41, 3921–3941. [Google Scholar] [CrossRef]
  55. Bensana, E.; Bel, G.; Dubois, D. OPAL: A multi-knowledge-based system for industrial job-shop scheduling†. Int. J. Prod. Res. 1988, 26, 795–819. [Google Scholar] [CrossRef]
  56. Yun, Y.S. Genetic algorithm with fuzzy logic controller for preemptive and non-preemptive job-shop scheduling problems. Comput. Ind. Eng. 2002, 43, 623–644. [Google Scholar] [CrossRef]
  57. Hajri, S.; Liouane, N.; Hammadi, S.; Borne, P. A controlled genetic algorithm by fuzzy logic and belief functions for job-shop scheduling. IEEE Trans. Syst. Man Cybern. Part B 2000, 30, 812–818. [Google Scholar] [CrossRef] [PubMed]
  58. Kacem, I.; Hammadi, S.; Borne, P. Pareto-optimality approach for flexible job-shop scheduling problems: Hybridization of evolutionary algorithms and fuzzy logic. Math. Comput. Simul. 2002, 60, 245–276. [Google Scholar] [CrossRef]
  59. Kolonko, M. Some new results on simulated annealing applied to the job shop scheduling problem. Eur. J. Oper. Res. 1999, 113, 123–136. [Google Scholar] [CrossRef]
  60. Chen, P.-H.; Shahandashti, S.M. Hybrid of genetic algorithm and simulated annealing for multiple project scheduling with multiple resource constraints. Autom. Constr. 2009, 18, 434–443. [Google Scholar] [CrossRef]
  61. Bouleimen, K.; Lecocq, H. A new efficient simulated annealing algorithm for the resource-constrained project scheduling problem and its multiple mode version. Eur. J. Oper. Res. 2003, 149, 268–281. [Google Scholar] [CrossRef]
  62. Kanaga, E.M.; Valarmathi, M. Multi-agent based Patient Scheduling Using Particle Swarm Optimization. Procedia Eng. 2012, 30, 386–393. [Google Scholar] [CrossRef] [Green Version]
  63. Zorin, D.A.; Kostenko, V.A. Simulated Annealing Algorithm for Job Shop Scheduling on Reliable Real-Time Systems. In Proceedings of the Communications in Computer and Information Science; Springer Science and Business Media LLC: Berlin, Germany, 2015; Volume 509, pp. 31–46. [Google Scholar]
  64. Meeran, S.; Morshed, M.S. A hybrid genetic tabu search algorithm for solving job shop scheduling problems: A case study. J. Intell. Manuf. 2011, 23, 1063–1078. [Google Scholar] [CrossRef]
  65. Turker, A.K.; Aktepe, A.; Inal, A.F.; Ersoz, O.O.; Das, G.S.; Birgoren, B. A Decision Support System for Dynamic Job-Shop Scheduling Using Real-Time Data with Simulation. Mathematics 2019, 7, 278. [Google Scholar] [CrossRef] [Green Version]
  66. Yang, X. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Beckington, UK, 2010; ISBN 9781905986286. [Google Scholar]
  67. Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 11–13 December 1991; Volume 142, pp. 134–142. [Google Scholar]
  68. Zhu, Z.C.; Ng, K.M.; Ong, H.L. A modified tabu search algorithm for cost-based job shop problem. J. Oper. Res. Soc. 2010, 61, 611–619. [Google Scholar] [CrossRef]
  69. Rocholl, J.; Mönch, L. Decomposition heuristics for parallel-machine multiple orders per job scheduling problems with a common due date. J. Oper. Res. Soc. 2019, 1–17. [Google Scholar] [CrossRef]
  70. Gholami, O.; Sotskov, Y.N.; Werner, F.; Zatsiupo, A.S. Heuristic Algorithms to Maximize Revenue and the Number of Jobs Processed on Parallel Machines. Autom. Remote Control 2019, 80, 297–316. [Google Scholar] [CrossRef]
  71. Fonseca, D.J.; Navaresse, D. Artificial neural networks for job shop simulation. Adv. Eng. Inform. 2002, 16, 241–246. [Google Scholar] [CrossRef]
  72. Apt, K.R. Principles of Constraint Programming; Cambridge University Press (CUP): Cambridge, UK, 2003. [Google Scholar]
  73. Rossi, F.; Van Beek, P.; Walsh, T. (Eds.) Handbook of Constraint Programming; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
  74. Adibi, M.; Zandieh, M.; Amiri, M. Multi-objective scheduling of dynamic job shop using variable neighborhood search. Expert Syst. Appl. 2010, 37, 282–287. [Google Scholar] [CrossRef]
  75. Zhang, W.; Wen, J.B.; Zhu, Y.C.; Hu, Y. Multi-Objective Scheduling Simulation of Flexible Job-Shop Based on Multi-Population Genetic Algorithm. Int. J. Simul. Model. 2017, 16, 313–321. [Google Scholar] [CrossRef]
  76. Gholami, O.; Sotskov, Y.N. A fast heuristic algorithm for solving parallel-machine job-shop scheduling problems. Int. J. Adv. Manuf. Technol. 2014, 70, 531–546. [Google Scholar] [CrossRef]
  77. Gholami, O.; Sotskov, Y.N.; Werner, F. A Genetic Algorithm for Hybrid Job-Shop Scheduling Problems with Minimizing the Makespan or Mean Flow Time. J. Adv. Manuf. Syst. 2018, 17, 461–486. [Google Scholar] [CrossRef]
  78. Pongchairerks, P. A self-tuning PSO for job-shop scheduling problems. Int. J. Oper. Res. 2014, 19, 96. [Google Scholar] [CrossRef]
  79. Sha, D.; Hsu, C.-Y. A hybrid particle swarm optimization for job shop scheduling problem. Comput. Ind. Eng. 2006, 51, 791–808. [Google Scholar] [CrossRef]
  80. Thizy, J.-M.; Van Wassenhove, L.N.; Khumawala, B.M. Comparison of exact and approximate methods of solving the uncapacitated plant location problem. J. Oper. Manag. 1985, 6, 23–34. [Google Scholar] [CrossRef]
  81. Rothlauf, F. Design of Modern Heuristics: Principles and Application; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
  82. Iwamura, K.; Sugimura, N. A study on real-time scheduling for autonomous distributed manufacturing systems. In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010; pp. 1352–1357. [Google Scholar]
  83. Hermann, M.; Pentek, T.; Otto, B. Design principles for industrie 4.0 scenarios. In Proceedings of the 2016 IEEE 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016; pp. 3928–3937. [Google Scholar]
  84. Harrison, R.; Vera, D.; Ahmad, B. Engineering the smart factory. Chin. J. Mech. Eng. 2016, 29, 1046–1051. [Google Scholar] [CrossRef]
  85. Wang, J.; Zhang, Y.; Liu, Y.; Wu, N. Multiagent and Bargaining-Game-Based Real-Time Scheduling for Internet of Things-Enabled Flexible Job Shop. IEEE Internet Things J. 2018, 6, 2518–2531. [Google Scholar] [CrossRef] [Green Version]
  86. Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
  87. Mourtzis, D.; Vlachou, E. A cloud-based cyber-physical system for adaptive shop-floor scheduling and condition-based maintenance. J. Manuf. Syst. 2018, 47, 179–198. [Google Scholar] [CrossRef]
  88. Lödding, H.; Riedel, R.; Thoben, K.-D.; von Cieminski, G.; Kiritsis, D. (Eds.) Advances in Production Management Systems. The Path to Intelligent, Collaborative and Sustainable Manufacturing; Springer Science and Business Media LLC: Berlin, Germany, 2017; pp. 127–134. [Google Scholar]
  89. Ortíz, M.A.; Betancourt, L.E.; Negrete, K.P.; De Felice, F.; Petrillo, A. Dispatching algorithm for production programming of flexible job-shop systems in the smart factory industry. Ann. Oper. Res. 2017, 264, 409–433. [Google Scholar] [CrossRef]
  90. Hajrizi, E. Smart Solution for Smart Factory. IFAC Pap. 2016, 49, 1–5. [Google Scholar] [CrossRef]
  91. Narman, H.S.; Hossain, S.; Atiquzzaman, M.; Shen, H. Scheduling internet of things applications in cloud computing. Ann. Telecommun. 2016, 72, 79–93. [Google Scholar] [CrossRef]
  92. Dutta, D.; Joshi, R.C. A genetic. In Proceedings of the International Conference & Workshop on Emerging Trends in Technology—ICWET ’11, Mumbai, India, 25–26 February 2011; pp. 422–427. [Google Scholar]
  93. Zhao, C.; Zhang, S.; Liu, Q.; Xie, J.; Hu, J. Independent Tasks Scheduling Based on Genetic Algorithm in Cloud Computing. In Proceedings of the 2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar]
  94. Masood, A.; Mei, Y.; Chen, G.; Zhang, M. Many-objective genetic programming for job-shop scheduling. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 209–216. [Google Scholar]
  95. Bengio, Y.; LeCun, Y. Scaling Learning Algorithms towards AI. Large-Scale Kernel Mach. 2007, 34, 1–41. [Google Scholar] [CrossRef]
  96. Bengio, Y. Deep learning of representations for unsupervised and transfer learning. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, Bellevue, WA, USA, 2 July 2011; pp. 17–36. [Google Scholar]
  97. Guo, Y.; Liu, Y.; Oerlemans, A.; Lao, S.; Wu, S.; Lew, M.S. Deep learning for visual understanding: A review. Neurocomputing 2016, 187, 27–48. [Google Scholar] [CrossRef]
  98. Niehues, M.; Blum, M.; Teschemacher, U.; Reinhart, G. Adaptive job shop control based on permanent order sequencing. Prod. Eng. 2017, 12, 65–71. [Google Scholar] [CrossRef]
  99. Grieco, A.; Caricato, P.; Gianfreda, D.; Pesce, M.; Rigon, V.; Tregnaghi, L.; Voglino, A. An Industry 4.0 Case Study in Fashion Manufacturing. Procedia Manuf. 2017, 11, 871–877. [Google Scholar] [CrossRef]
  100. Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent Manufacturing in the Context of Industry 4.0: A Review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
  101. Mehrsai, A.; Figueira, G.; Santos, N.; Amorim, P.; Al-mada-Lobo, B. Decentralized vs. Centralized Sequencing in a Complex Job-Shop Scheduling. In Advances in Production Management Systems. The Path to Intelligent, Collaborative and Sustainable Manufacturing; Springer Science and Business Media LLC: Berlin, Germany, 2017; pp. 467–474. [Google Scholar] [CrossRef] [Green Version]
  102. Guizzi, G.; Vespoli, S.; Santini, S. On The Architecture Scheduling Problem Of Industry 4.0. In Proceedings of the CEUR Workshop; CEUR-WS.org: London, UK, 2017; pp. 94–100. [Google Scholar]
  103. Sousa, R.A.; Varela, M.L.R.; Alves, C.; Machado, J. Job shop schedules analysis in the context of Industry 4.0. In Proceedings of the 2017 International Conference on Engineering, Technology and Innovation (ICE/ITMC), Madeira, Portugal, 27–29 June 2017; pp. 711–717. [Google Scholar]
  104. Ivanov, D.; Dolgui, A.; Sokolov, B.; Werner, F.; Ivanova, M. A dynamic model and an algorithm for short-term supply chain scheduling in the smart factory Industry 4.0. Int. J. Prod. Res. 2016, 54, 386–402. [Google Scholar] [CrossRef] [Green Version]
  105. Liu, S.Q.; Kozan, E.; Masoud, M.; Zhang, Y.; Chan, F.T. Job shop scheduling with a combination of four buffering constraints. Int. J. Prod. Res. 2017, 56, 3274–3293. [Google Scholar] [CrossRef]
  106. Ding, K.; Jiang, P. RFID-based production data analysis in an IoT-enabled smart job-shop. IEEE/CAA J. Autom. Sin. 2018, 5, 128–138. [Google Scholar] [CrossRef]
  107. Ahuett-Garza, H.; Kurfess, T. A brief discussion on the trends of habilitating technologies for Industry 4.0 and Smart manufacturing. Manuf. Lett. 2018, 15, 60–63. [Google Scholar] [CrossRef]
  108. Lunardi, W.T.; Cherri, L.H.; Voos, H. A Mathematical Model and a Firefly Algorithm for an Extended Flexible Job Shop Problem with Availability Constraints. In Artificial Intelligence and Soft Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; Volume 1, pp. 235–246. ISBN 9783319912530. [Google Scholar]
  109. Lukasik, S.; Żak, S. Firefly Algorithm for Continuous Constrained Optimization Tasks. In Proceedings of the International Conference on Computational Collective Intelligence, Wroclaw, Poland, 5–7 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 97–106. [Google Scholar]
  110. Yan, B.; Bragin, M.A.; Luh, P.B. Novel Formulation and Resolution of Job-Shop Scheduling Problems. IEEE Robot. Autom. Lett. 2018, 3, 3387–3393. [Google Scholar] [CrossRef]
  111. Heger, J.; Voß, T. Dynamic priority based dispatching of AGVs in flexible job shops. Procedia CIRP 2019, 79, 445–449. [Google Scholar] [CrossRef]
  112. Dolgui, A.; Ivanov, D.; Sethi, S.P.; Sokolov, B. Scheduling in production, supply chain and Industry 4.0 systems by optimal control: Fundamentals, state-of-the-art and applications. Int. J. Prod. Res. 2019, 57, 411–432. [Google Scholar] [CrossRef]
  113. Weber, E.; Tiefenbacher, A.; Gronau, N. Need for Standardization and Systematization of Test Data for Job-Shop Scheduling. Data 2019, 4, 32. [Google Scholar] [CrossRef] [Green Version]
  114. Zhao, M.; Li, X.; Gao, L.; Wang, L.; Xiao, M. An improved Q-learning based rescheduling method for flexible job-shops with machine failures. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 331–337. [Google Scholar]
  115. Liu, P.; Zhang, Q.; Pannek, J. Development of Operator Theory in the Capacity Adjustment of Job Shop Manufacturing Systems. Appl. Sci. 2019, 9, 2249. [Google Scholar] [CrossRef] [Green Version]
  116. Salido, M.A.; Escamilla, J.; Barber, F.; Giret, A.; Tang, D.; Dai, M. Energy efficiency, robustness, and makespan optimality in job-shop scheduling problems. Artif. Intell. Eng. Des. Anal. Manuf. 2015, 30, 300–312. [Google Scholar] [CrossRef]
  117. Rodriguez, I.G.; Puente, J.; Varela, R.; Rodriguez-Vela, C. A Study of Schedule Robustness for Job Shop with Uncertainty. In Proceedings of the Advances in Artificial Intelligence—IBERAMIA 2008, Lisbon, Portugal, 14–17 October 2008; pp. 31–41. [Google Scholar]
  118. Shen, X.-N.; Han, Y.; Fu, J. Robustness measures and robust scheduling for multi-objective stochastic flexible job shop scheduling problems. Soft Comput. 2016, 21, 6531–6554. [Google Scholar] [CrossRef]
  119. Jamili, A. Robust job shop scheduling problem: Mathematical models, exact and heuristic algorithms. Expert Syst. Appl. 2016, 55, 341–350. [Google Scholar] [CrossRef]
  120. Zhang, J.; Yang, J.; Zhou, Y. Robust scheduling for multi-objective flexible job-shop problems with flexible workdays. Eng. Optim. 2016, 48, 1973–1989. [Google Scholar] [CrossRef]
  121. Wu, Z.; Yu, S.; Li, T. A Meta-Model-Based Multi-Objective Evolutionary Approach to Robust Job Shop Scheduling. Mathematics 2019, 7, 529. [Google Scholar] [CrossRef] [Green Version]
  122. Berti, N.; Finco, S.; Battaïa, O.; Delorme, X. Ageing workforce effects in Dual-Resource Constrained job-shop scheduling. Int. J. Prod. Econ. 2021, 237, 108151. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Sustainability in Refugee Camps: A Systematic Review and Meta-Analysis
Previous
Thermal Performance of Compression Ignition Engine Using High Content Biodiesels: A Comparative Study with Diesel Fuel
Next