Abstract
High-efficiency taxiing for safe operations is needed by all types of aircraft in busy airports to reduce congestion and lessen fuel consumption and carbon emissions. This task is a challenge in the operation and control of the airport’s surface. Previous studies on the optimization of aircraft taxiing on airport surfaces have rarely integrated waiting constraints on the taxiway into the multi-objective optimization of taxiing time and fuel emissions. Such studies also rarely combine changes to the airport’s environment (such as airport elevation, field pressure, temperature, etc.) with the multi-objective optimization of aircraft surface taxiing. In this study, a multi-objective optimization method for aircraft taxiing on an airport surface based on the airport’s environment and traffic conflicts is proposed. This study aims to achieve a Pareto optimized taxiing scheme in terms of taxiing time, fuel consumption, and pollutant emissions. This research has the following contents: (1) Previous calculations of aircraft taxiing pathways on the airport’s surface have been based on unimpeded aircraft taxiing. Waiting on the taxiway is excluded from the multi-objective optimization of taxiing time and fuel emissions. In this study, the waiting points were selected, and the speed curve was optimized. A multi-objective optimization scheme under aircraft taxiing obstacles was thus established. (2) On this basis, the fuel flow of different aircraft engines was modified with consideration to the aforementioned environmental airport differences, and a multi-objective optimization scheme for aircraft taxiing under different operating environments was also established. (3) A multi-objective optimization of the taxiing time and fuel consumption of different aircraft types was realized by acquiring their parameters and fuel consumption indexes. A case study based on the Shanghai Pudong International Airport was also performed in the present study. The taxiway from the 35R runway to the 551# stand in the Shanghai Pudong International Airport was optimized by the non-dominant sorting genetic algorithm II (NSGA-II). The taxiing time, fuel consumption, and pollutant emissions at this airport were compared with those of the Kunming Changshui International Airport and Lhasa Gonggar International Airport, which have different airport environments. Our research conclusions will provide the operations and control departments of airports a reference to determine optimal taxiing schemes.
1. Introduction
Air traffic flow has sharply increased with the continuous development of the air transport industry. It is estimated that by 2035, the air traffic flow in Europe will be 1.5 times higher than that in 2012 [1]. An airport is an air traffic hub, and the operational capabilities of airports have reached their limits. Existing infrastructure must be used efficiently, and airport capacity should be increased to improve airport operations [2]. The taxiway system between the runway and the stand is the main bottleneck in many airports that works against their operational capacity. The optimization of aircraft movement on the taxiway is a key problem [3]. This condition can further complicate other elements, such as runway ordering [4,5] and the distribution of stand/departure gates on the airport’s surface [6]. Although taxiing on the airport surface is a small part of running an aircraft, it can significantly influence the operating costs and emissions of airports. Jet engines are designed to run in an optimal state at air cruising speed; however, aircraft taxiing efficiency on the airport surface is relatively low [7]. Estimates indicate that the fuel consumption of single-aisle planes during taxiing in busy airports accounts for 6% of their fuel consumption throughout short-haul flights and reaches 5 million tons worldwide [8]. In 2010, the 37th Conference of International Civil Aviation Organization (ICAO) was focused on environmental protection, and the Committee on Climate Change estimated that carbon emissions caused by air transport in the middle of the 21st century will increase by 7–8 times compared to those in 1990 [9]. The next generation of air transport system (NextGen) of America [10] and Single European Sky ATM Research (SESAR) [11] have emphasized that the optimal control of fuel combustion, operating costs, and delays on the running surface should be recognized. The High-Level Air-Transport Research Team of the Council of Europe plans to realize their zero-emission airport taxiing goal by 2050 [12]. An aircraft taxiing plan for airport surfaces could decrease taxiing delays and cut taxiing costs by a third [13].
Previous studies on aircraft surface control have targeted a range of subjects, including passive, semi-active, and active routes. Research methods on taxiing have become highly effective. However, the trade-offs among the three objectives in reducing taxiing time, fuel consumption, and pollutant emissions are reduced when combined with the factors of taxiing conflict and changes in the airport’s environment (such as airport elevation, field pressure, temperature, etc.) at different altitudes. Therefore, this study aims to propose a multi-objective optimization method for aircraft taxiing on an airport surface that considers both the airport’s environment and traffic conflicts. This research is carried out to find a Pareto-optimized taxiing scheme that can reduce taxiing time, fuel consumption, and pollutant emissions. This study will provide aviation companies with the means to make decisions on saving operation costs. Moreover, this study will provide the operations and management departments of airports the means to increase operational efficiency.
The main contributions and innovations of this study are summarized on the basis of the following considerations:
- (1)
- Previous calculations of aircraft taxiway have excluded the waiting points on the taxiway from the multi-objective optimization of taxiing time and fuel emissions in order to avoid taxiing conflicts. Thus, this study improved the taxiing speed curve by including waiting points and by establishing a multi-objective optimization for aircraft taxiing. Accordingly, the calculation results are close to practical operating conditions.
- (2)
- Previous studies have rarely considered the taxiing multi-objective optimization problem under different airport environments. However, changes in air pressure and the environment at different airports affect the fuel combustion of aircraft engines. Hence, the fuel flows of different aircraft engines were modified in the present study. Moreover, a multi-objective optimization model of aircraft taxiing under different airport environments was constructed.
- (3)
- In this study, a multi-objective optimization for the taxiing time and fuel consumption of different aircraft modes was realized by acquiring their parameters and fuel consumption indexes. Through a multi-objective optimization of different aircraft models, the optimal values of the Pareto fronts were intuitively determined via a comparison of the calculation results, which provided references for the operational control of airport surfaces.
The remainder of this study is organized as follows: Section 2 presents the literature review. Section 3 constructs a multi-objective optimization model for aircraft taxiing and modifies the coefficients of fuel flow and pollutant emission by considering differing airport environments. Section 4 analyzes the taxiing speed curve of aircraft on the airport’s surface. Section 5 solves the algorithm on the basis of the NSGA-II algorithm model. Section 6 is a case study based on the taxiway of the Shanghai Pudong International Airport (ICAO: ZSPD) in order to verify the proposed multi-objective optimization scheme. Section 7 provides the conclusions and future prospects.
2. Literature Review
This section presents a concise literature survey of existing research efforts related to the mathematical models used in taxiing problems, such as fuel consumption and emissions, on the airport’s surface. A brief survey will also be provided. This survey particularly focuses on categorization according to the following issues: (1) the guiding control method of aircraft taxiing and (2) a multi-objective optimization method of taxiing.
2.1. Guiding Control Method of Aircraft Taxiing on the Airport Surface
Aircraft taxiing in a busy airport has attracted the wide attention of scholars in past decades. This study was conducted mainly to provide a guiding control scheme for the taxiing process of the approaching aircraft from the runway to the stand and for the taxiing process of the departing aircraft from the stand to the runway. The ICAO proposed the concept of an advanced surface movement, guidance, and control system (A-SMGCS) to solve this problem [14]. An A-SMGCS is equipped with four basic functions: monitoring, route, guidance, and control. This scheme aims to provide an optimal route and schedule for aircraft during surface taxiing. The proposed scheme will help increase taxiing efficiency on the airport’s surface and reduce the fuel consumption, delays, and potential conflicts via the collaborative optimization of traffic flows during taxiing on the airport’s surface. The A-SMGCS can be divided into three generations through its functions, as shown in Table 1.

Table 1.
The evolution of surface management systems.
In the first generation of passive route and route guiding systems [15], the standard average taxiing time was used for route planning. Chen and Stewart [16] pointed out that the route plans of the current route functions were inadequate for some aircraft because the difference between the route functions and the average taxiing time was ignored. Consequently, the fuel consumption was affected to a certain extent. Lesire [17] pointed out that the route’s plan was to provide a taxiing plan for aircraft on the airport’s surface to ensure that the aviator can control the aircraft’s taxiing speed along a specific route.
In the second generation of A-SMGCS, Atkin et al. [18] and Ravizza et al. [19] proposed a new algorithm on the basis of a sequence chart and calculated the taxiing time of the aircraft by statistical methods and fuzzy rules according to historical take-off and landing times. Both calculation methods were more accurate than the calculation results of the standard lookup. Bakowski et al. [20] increased the calculation accuracy of the time and decreased the space among aircraft through the concept of surface track-based operation. The required time of arrival (RTA) algorithm dynamically calculated the recommended taxiing speed via the residential distance, residual time to RTA, and number of turns. Cheng and Sweriduk [21] realized cockpit automatization for reliable surface operation, reconstructed a cleaned 4D route, and generated a reference route for aircraft taxiing according to the concept of surface operation automatic research. This trace defines the aircraft’s position, speed, and acceleration as constraints to meet the time requirements. Many degrees of freedom (DOFs) are still found in the generation method of the speed curve of the aircraft. The generated speed curve is common.
In the third generation of A-SMGCS, the SESAR project of Europe [11] and the NextGen of America [9] believe that introducing complete 4D traces (4DTS) composed of 3D spaces and time could lay a solid foundation for studies on air traffic. Estimates indicate that introducing 4DTS into taxiing on an airport’s surface may decrease taxiing delays by approximately 55% [22]. During aircraft surface taxiing, since all dimensions are unnecessary, the unique positional information of aircraft can be defined by their route and speed curves.
Therefore, taxiing optimization can be realized via the taxiing speed curve of an aircraft. However, the addition of the speed curve under the existence of barriers into the multi-objective optimization of taxiing time, fuel consumption, and pollutant emissions is a problem that has yet to be solved. In this paper, the taxiing waiting point is added to the speed curve to optimize the multi-objective problem.
2.2. Multi-Objective Optimization Method of Taxiing Time, Fuel Consumption, and Pollutant Emission
Aviation carbon emissions mainly come from pollutants emitted during the combustion of aviation fuel and after air mixed combustion. These emissions include NOx, SO2, CO, unburnt hydrocarbons, CO2, carbon cigarette pellets (soot), particulate matter, and aviation-induced cloudiness [23]. Such emissions can influence the air quality and contribute to the greenhouse effect. At present, CO2 emissions from air transport account for 2.0%–2.5% of total global CO2 emissions by humans [24]. Damage assessment of carbon emissions in air transport, especially in the surface operating environments of airports, has attracted wide attention [25]. Aircraft taxiing on the airport’s surface also adopts a low speed and is in a fully-developed state. Taxiing optimization is of great significance to control fuel consumption and pollutant emissions in airports. Some scholars have carried out deep studies on the multi-objective optimization of taxiing time, fuel consumption, and pollutant emissions on airport surfaces in the past two decades. Smeltink [26] proposed an optimization model for the aircraft taxiing schedule on the airport’s surface and worked on aircraft taxiing via a hybrid integer programming model. An optimal schedule can reduce delays caused by taxiing conflicts as much as possible. In this study, only taxiing time was considered, while the balance between taxiing time, fuel consumption, and pollutant emissions was ignored. Herrero et al. [27] proposed an optimal taxiway planning method based on an improved spatiotemporal flow algorithm and the genetic algorithm; this approach minimized the total taxiing time. However, these authors ignored fuel consumption and pollutant emissions caused by taxiing on the airport’s surface. Simaiakis et al. [28] constructed a queuing theory prediction model to estimate the taxiing time of departing flights from the stand to the runway with consideration given to the mutual influences of different taxiways. Roling and Visser [29] studied the relationship between fuel consumption and taxiing time through surface taxiway optimization. These authors also improved the operational efficiency of the airport and reduced fuel consumption by shortening the total taxiing time. However, the authors did not consider pollutant emissions. Koeners et al. [30] implemented a real-time optimization of runway rankings through a dynamic planning of taxiways to increase runway facility utilization and reduce flight taxiing time.
The aforementioned authors aimed to decrease fuel consumption and pollutant emissions by shortening taxiing time. However, the balance among the three objectives was ignored. Chen and Stewart [16] studied the taxiing traces in the different sections of taxiways via an improved multi-objective optimization method. On the one hand, these taxiing traces provide estimations of aircraft taxiing time. On the other hand, such traces are integrated into the optimal taxiway and scheduling process to determine the optimal taxiway with the shortest total taxiing time and the lowest fuel consumption. However, pollutant emissions were neglected. Ravizza [31] proposed a multi-objective optimization method composed of a chart-based route algorithm and a population adaptive immune algorithm. The author applied this method to discover the distribution of aircraft taxiing speeds; thus, the balance between taxiing time and fuel consumption was analyzed. Nevertheless, the pollutant emissions from surface taxiing were neglected. Balakrishnan et al. [32] constructed a mixed integer linear programming model of aircraft taxiing based on a spatiotemporal network and solved the surface taxiing problem to minimize taxiing time. Weiszer and Chen [33] proposed a multi-objective optimization problem that combines route schedule and speed optimization for aircraft taxiing. These authors investigated the balance between total taxiing time and fuel consumption through comprehensive optimization. However, the authors also ignored the optimization of pollutant emissions. Chen et al. [34] carried out a detailed analysis on the three main emission indices (EIs), CO, HC, and NOx, in airports to determine the conflict objective with a minimum quantity and generate an optimal speed curve. Their results demonstrated that NOx has a strong linear correlation with the combustion of fuels for all types of aircraft. In heavy aircraft, HC and CO emissions should be treated by separating them from taxiing time and fuel consumption. In medium-weight and light aircraft, HC and CO emissions are strongly correlated with taxiing time. This study did not analyze the operational results in plateau airports. Chen and Weiszer [7] introduced a systematic multi-objective speed profile generation framework to generate the optimal unimpeded taxiing speed profile on a given taxiway. This work aims to maintain the solvability of the complicated surface taxiing problem in airports with consideration given to many mutual conflicts. Brownleea et al. [35] proposed a method to estimate the uncertainty of aircraft surface taxiing time based on an adaptive Mamdani fuzzy rule. These authors also improved the time window algorithm for the existing fastest route problems to estimate the fuzzy taxiing time.
In most small airports, taxi times can be fixed because the layouts of terminals and runways usually mean that the current default values are sufficient. In medium and large airports, the configurations of runways and the layouts of terminal buildings can lead to significant differences in the taxi time of arriving and departing flights. When the taxi time changes greatly, factors such as control capacity, aircraft type, average taxi time based on historical data, taxi time based on specific operating conditions, and taxi route will be considered.
The time of aircraft taxiing on the airport’s surface is usually affected by an airport’s weather, airspace capacity, air traffic control capacity, and other factors (such as military activities, sector configuration, and system maintenance) [36]. However, at present, many scholars’ research mainly involves airport capacity and new system procedures, without seriously considering the impact of the airport’s environment and traffic conflicts on operations.
In summary, unlike previous studies, we not only consider a comparison of multi-objective optimization results for different aircraft types but also carry out a multi-objective optimization of airport environment (e.g., the elevation of the airport, field pressure, and temperature) scenarios with or without conflict waiting points and at different altitudes. Thus, our calculation results are more comprehensive, and our research content is more abundant.
3. Multi-Objective Optimization Model of an Aircraft Taxiway
In this study, the parameters independent of the aircraft include the maximum speed, the minimum speed, and the turning speed during surface taxiing; parameters related to aircraft mainly include fuel flow and the pollutant emission index of different aircraft engines, as well as the fuel consumption, pollutant emissions, speed optimization curves and set of aircraft obtained by the multi-objective optimization of aircraft (see Annotations).
3.1. Objective Functions
The optimal speed curve is generated to obtain a group of complete speed curves. The significance of the Pareto optimality is defined by the unimpeded taxiing speed curve of aircraft on taxiway (in this study, there are several optional paths for aircraft to taxi on the airport surface, and one of the paths is marked as to optimize the speed curve). The multi-objective optimization model shortens the taxiing time and decreases the aircraft’s fuel consumption. The following factors were considered: taxiway characteristics, thrust level determined by the given speed curve, weight, engine type, and rolling resistance of aircraft. The objectives for taxiing time and fuel consumption in this study are defined as follows:
where is the objective function of the aircraft taxiing time, and the aircraft engages in unimpeded taxiing on the taxiway . In a given speed curve, , is a function of time. Similarly, expresses the fuel consumption of aircraft (weight type) for taxiing on taxiway at a speed curve of .
The ICAO emission database for calculating fuel consumption [37] lists emission data for most commercial engines. Each engine type provides the fuel flow (kg/s) and EIs (total grams of pollutant emissions from the combustion of each kilogram of fuel) when the rated outputs are 7%, 30%, 85%, and 100%. The pollutants in this database include HC, CO, and NOx. Chen et al. [34] pointed out that a relationship curve between fuel flow and EIs can be fitted by the data when the thrust values are 7%, 30%, 85%, and 100%. Moreover, HC and CO were fitted into exponential functions, while NOx was fitted as a linear function. Therefore, NOx emissions can be overlooked in the multi-objective optimization.
Therefore, the HC and CO emissions can be calculated by the following model:
where is the pollutant emissions of aircraft (, , and are the light, medium-weight, and heavy aircraft, respectively) for taxiing on the taxiway at the speed of . The pollutants include HC, CO, and NOx.
In , the means of the fuel flow and emission coefficients of different pollutant types are not hypothesized during aircraft taxiing. The fuel consumption and pollutant emissions are used as continuous functions of speed changes. The four fixed thrust levels correspond to four different stages. Fuel consumption is calculated by the product of taxiing time in each stage and the corresponding fuel flow. The pollutant emissions are calculated by multiplying fuel consumption with the emission coefficients of different types of pollutants.
3.2. Constraints
- (1)
- The taxiing speed constraint: The maximum and minimum taxiing speeds ( and ) and the taxiing speed at the turning section () were restricted to 25, 10, and 10 knots, respectively; this restriction was applied to ensure the safe and high-efficient surface taxiing of aircraft on airport surfaces, without considering the constraints of taxiway type over taxiing speeds [14];
- (2)
- Taxiing acceleration constraint: The acceleration () was restricted to <0.1 g to ensure the comfort of passengers during the accelerated taxiing of the aircraft [38].
3.3. Modification of Fuel Consumption Coefficient
Data on the fuel flow and EIs were collected from the engine emission database of ICAO to determine the ideal landing and take-off cycles under ISA conditions. However, the geological locations of different airports may vary, and these external conditions can influence the combustion process of aircraft engines. This finding demonstrates that the fuel flow and EIs of engines vary in different airports. The fuel flow and EIs must be modified. In this study, the fuel flow and EIs were modified via the Boeing fuel flow method 2 [39,40].
Under ISA conditions, the modification formulas to transform the sea-level fuel flow () of the single engine of aircraft under taxiing state into the actual fuel flow are
The aircraft taxies on the airport surface in this study, and the taxiing speed is far smaller than the sound velocity. Therefore, the Mach number is approximately zero. The EIs of the aircraft engine from taxiing are also related to environmental pressure, environmental temperature, saturated vapor pressure, and atmospheric relative humidity in airports. Under ISA conditions, the modification formulas to transform into practical EIs are
where k = 1, 2, which represent HC and CO, respectively. Index x is the corresponding engine value in the P3–T3 method. In this study, the default value of x = 1 is adopted [39].
4. Taxiing Time and Fuel Consumption Models Based on the Optimized Speed Curve
4.1. Optimized Speed Curve
During the unimpeded taxiing of aircraft along the given taxiway , the taxiway can be further divided into several sections, and each section includes several sides. Several continuous straight sides generally form a straight section. The turning section is formed by continuous edges, and an angle of at least 30° is evident in the turning section [7].
Aircraft can produce infinite DOFs because they can use taxiing speed as a continuous function of time in each section. Each straight section of the taxiway can be separated into four parts to further simplify the optimization problem of the speed curve. These parts correspond to the four different taxiing stages of the aircraft: acceleration, taxiing at a uniform speed, braking, and fast braking (Figure 1).
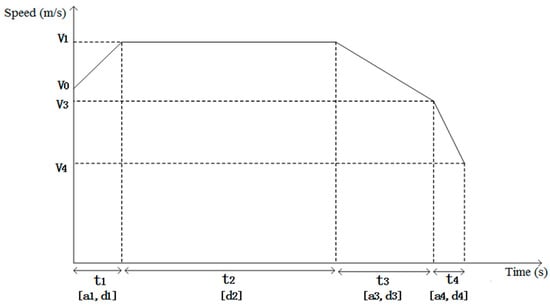
Figure 1.
Speed curves under four taxiing states.
In Figure 1, stage 1 is the acceleration stage, in which the taxiing speed of the aircraft increases from to at a distance of , with an acceleration of . Stage 2 is the taxiing at a uniform speed. In this stage, the aircraft taxies at a uniform speed of until arriving at a distance of . Stages 3 and 4 are the decelerating stages. In these two stages, the aircraft decreases its taxiing speed from to at different rates at the end section. The maximum deceleration in stage 4 is to rapidly increase the taxiing speed to . In stage 3, deceleration is unique and is determined by and . Variable can be derived in reverse under the given , , and . The length of stage 3 is equal to . Therefore, the four independent variables are , , , and , and the unique speed distribution of section is defined.
The ranges of , , , and can be obtained according to [7] to meet the constraints over taxiing speed and taxiing acceleration:
(1) The upper limit of is equal to the maximum acceleration. The lower limit corresponds to the aircraft’s continuous acceleration in the whole section. Moreover, the aircraft taxiing speed at the end of the section must be able to reach . Therefore, the range of is
(2) The limits of are determined after those of are fixed. The lower limit of must be sufficiently long to ensure that the aircraft taxiing speed at the end of a section reaches . The upper limit is determined by and the longest possible period of acceleration (). Therefore, the range of is
(3) If the range of is determined, the taxiing speed can be fixed, and the range of can be calculated by the following equations:
(4) When the feasible range of is determined, the lower limit of is set to zero. Specifically, when no is present, the upper limit of is calculated according to the upper limit of . Therefore, the range of is
As shown in the discretization, when the four variables in each section are fixed, the speed intervals in the above-mentioned figure can be uniquely determined. The taxiing time and fuel consumption can be simultaneously minimized by searching for the optimal values of , , , and , thereby realizing the equilibrium state. In this way, the multi-objective optimization problem for aircraft surface taxiing is solved.
4.2. Taxiing Time, Fuel Consumption, and Pollutant Emission Model
The aircraft taxiing time to transverse one section is obtained on the basis of the above-mentioned section. Therefore, the sum of the taxiing time in different stages is
The aircraft taxiing time for the whole taxiway is:
The following four stages are defined in the straight section: acceleration, uniform speed, braking, and fast braking. In the braking and fast braking stages, the thrust level is set to 5%, and the thrust level is set to 7% at the turn. is obtained through linear interpolation/extrapolation, and the fuel flows are 7% and 30%, which are reported in the emission database of ICAO [37,40]. Therefore, the formulas of fuel consumption and pollutant emissions in section s are
The calculation formulas for the total fuel consumption and pollutant emissions in the whole taxiway are
5. Design of the Solving Algorithm
Since the aircraft surface taxiing path can be divided into several sections, it is necessary to calculate the optimal taxiing speed curve of each section in order to find the optimal solution. On this basis, a non-dominant ranking genetic algorithm with elitism selection strategy was chosen to solve this problem. The high performance of the NSGA-II algorithm [41] in searching the Pareto solution depends on its evolution mechanism, which mainly includes fast non-dominant ranking, congestion distance, and an elitism selection strategy based on non-dominant ranking. In comparison with the other multi-objective algorithms, the NSGA-II algorithm has some advantages. For example, the existing algorithms prefer to use single fitness functions or transform multiple objectives into a single objective (sub-objective). This preference might result in the loss of some important characteristics of the calculated results. However, the NSGA-II algorithm processes multiple objectives by searching the effective Pareto solution. This algorithm not only has good convergence and high calculation efficiency but also meets the requirements for real-time performance. The steps of the NSGA-II Algorithms 1–4 for taxiway optimization on the airport surface are introduced as follows.
5.1. Initialization of Population
Each straight section on the aircraft taxiway is separated into four parts, which correspond to four different taxiing states of the aircraft: acceleration, uniform speed, braking, and fast braking. Specifically, each taxiing section of the aircraft has four independent variables: The acceleration and taxiing distance in stage 1 are and , respectively. The taxiing distances of stages 2 and 4 are and , respectively. A chromosome with four genes was developed, and each sub-chromosome was used to express one decision solution reflecting the values of a1, d1, d2, and d4. In the generation process of the various decision variables, the value ranges must be met. The value ranges of the different variables are equations: (8), (9), (10) and (12).
The genes in each chromosome were generated by random sequences. Therefore, the initialization of the population was accomplished.
5.2. Non-Dominant Ranking
Before selective calculation, the populations were layered and put in their proper order according to the control level of their different members, determined by the value of the objective function, thereby forming different levels of the Pareto front. This process was repeated until all solutions were set into the leading edges. The objective function was determined according to the formula in this study. The values of the decision variables a1, d1, d2, and d4 were integrated into the formula. The fitness of the three objectives of the terminal operation optimization model was designed as (14), (17) and (18).
5.3. Congestion Distance
The congestion distance is allocated once the non-dominant ranking is accomplished. The individuals are chosen on the basis of their levels and congestion distance. Hence, all individuals are allocated to one congestion distance. The congestion distance is allocated according to the front surface. Comparing the congestion distance of two solutions with different front surfaces is meaningless. The congestion distance of the individual () is defined as follows:
5.4. Selection, Crossing, and Variation
The individual quality judgment criteria are as follows: Each individual in the population gets two attributes after fast non-dominant ranking and calculation of the degree of congestion: (1) Non-dominant rank () and (2) degree of congestion (). The dominant and non-dominant relationship between any two individuals in a population can be distinguished on the basis of these two attributes. Individual is better than individual only when and .
In this study, the binary competition method was applied. The offspring population was obtained from the parent population through crossing and variation. Chromosomes in the offspring population that failed to meet the constraints were eliminated. The offspring and parent populations were integrated, and an integrated population was obtained, followed by non-dominant ranking of the integrated population and congestion distance calculation. The elitism selection strategy indicated that was screened from low to high, and then was selected from large to small. The good chromosomes were selected until the population size of the new parent population was . Then, a new parent population was produced. This process was repeated to generate the next generation until the preset number of iterations (300) was reached. The elitism selection strategy adds the optimal individuals into the next generation of the population. Thus, the quality of the solution can be continuously optimized.
| Algorithm 1: cyclical function of subjects |
| 1. The population size (pop) and the number of genetic iterations (GEN) are defined. The population at initialization moment t = 0 is P(0), and its dimension is (4,pop). Each column reflects one decision scheme; the first row to the fourth row are a1, d1, d2, and d4, respectively. 2. Non-dominant ranking of initialized populations. 3. Let t = 0; 4. While t < GEN An offspring population Q(t) is generated by selection, crossing, and variation in the parent population P(t) through the binary bidding method; The integrated population: R(t)←P(t) + Q(t); Non-dominant ranking of R(t) is implemented to generate the ranked population F and N individuals are selected; P (t + 1) is set as an empty set; Let I = 0 While len (P (t + 1)) + len(F[i]) < = N when the new parent population is full (the number of the new parent population reaches N) Degree of congestion is estimated; P (t + 1)←P (t + 1) + F [i] selects from low to high in the ranked population F, and the selected individuals are added into the new parent population; i←i + 1 End while i←I + 1; P (t + 1)←P (t + 1) + F [1:(N-len (P (t + 1))], the congestion distance is added into the population from large to small when the new parent population crosses the border; t←t + 1 End while |
| Algorithm 2: non-dominant ranking |
| 1. Two variables are set and initialized: the number of dominant np = 0; the dominated individual set (sp) is set as an empty set. 2. Determine the highest level of the non-dominant solution set. For p = 1:N For q = 1:N If the individual p dominates the individual q Then the individual q is added into sp Else if the individual p is dominated by the individual q Then np←np + 1 End if End for If np of the individual is 0 Then the Pareto level is p.rank = 1 End if End for 3. Leveling of other individuals. i = 0 While F[i] For q = 1:len(sp) If the number of dominants of the individual (np) is 0 Then this individual is a non-dominant individual If i = 0 Then the Pareto level is added with 2 Else the Pareto level is added with 1 End if End for i←i + 1 End while |
| Algorithm 3: estimation of degree of congestion |
| 1. Initialize the congestion distance in the population set P: P[p].distance = 0. 2. The first objective function is selected: g = 1. 3. While g < G Individuals in the population are ranked from low to high according to the objective function g; The distance between the first and the last individuals in P is set as infinite. While p > 1 && p < len (p-1) Finding the crowding distance of the p-th individual p←p + 1 End while g←g + 1 End while |
| Algorithm 4: calculation of the objective function of individuals |
| The taxi segment ld is defined. For ld = 1:N If a segment is straight, it is optimized Then a1, d1, d2 and d4 are acquired according to encoding; t1, t2, t3, t4 and v1, v2, v3, v4 are calculated. If t1, t2, t3 or t4 have negatives or imaginary values Then The objective functions for this individual are set infinite Else All objective functions are calculated according to the formula Else All objective functions are calculated according to the formula for turns End if End for |
6. Case Study
6.1. Data Source
6.1.1. Taxiway Data of the Aircraft
Figure 2 exhibits a directed graph of the taxiway on the ZSPD, where the taxiways of the approaching aircraft from the runway 35R to the 551# stand are shown.
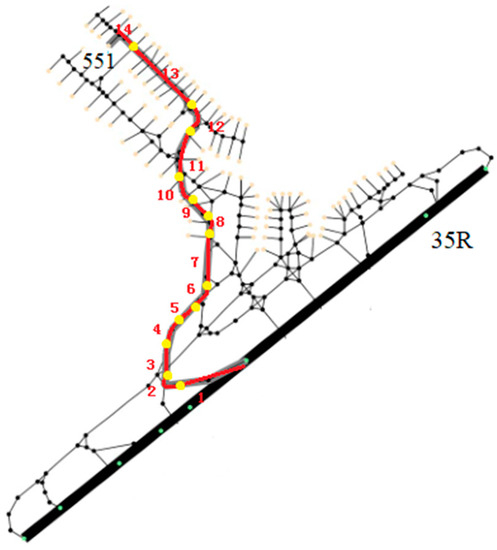
Figure 2.
Directed graph representation of the taxiway at the Shanghai Pudong International Airport.
The red taxiway in Figure 2 can be divided into 14 sections, while Table 2 illustrates the specific aircraft taxiing parameters in each section. The initial speed () at the starting point in section 1 is 10 knots because the approaching aircraft is selected. The aircraft moves along this straight section and can use various speed curves. The aircraft leaves section 1 at a speed of knots. This speed is used as the initial speed () of section 2. Section 2 is a turn, and the aircraft may maintain a constant speed (), which is set to 10 knots. Lastly, section 14 is a straight section that covers the stand, and the aircraft decelerates to zero.

Table 2.
Edges of a specific taxiway for aircraft.
6.1.2. Relevant Data of Aircraft
Learjet35A (light), A320 (medium-weighted), and A333 (heavy) were selected according to the aircraft’s wake flow intervals. The technological indexes of the representative aircraft were selected in the calculation. Table 3 illustrates the technological data and engine types of the three types of aircraft.

Table 3.
Parameters of the representative aircraft.
The fuel flow and EIs of the representative aircraft for the speed of idling, uniform speed, and deceleration during taxiing were obtained through linear interpolation by using the data under 7% and 30% thrust levels. Table A1 in Appendix A illustrates the results.
6.2. Pareto Analysis among Different Optimization Objectives
The Pareto optimization schemes for the four objectives (taxiing time, fuel consumption, HC emissions, and CO emissions) during taxiing for Learjet35A, A320, and A333 on the same taxiway were calculated (Figure 3).
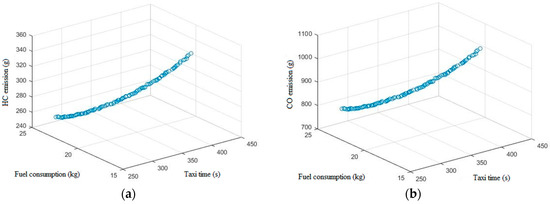
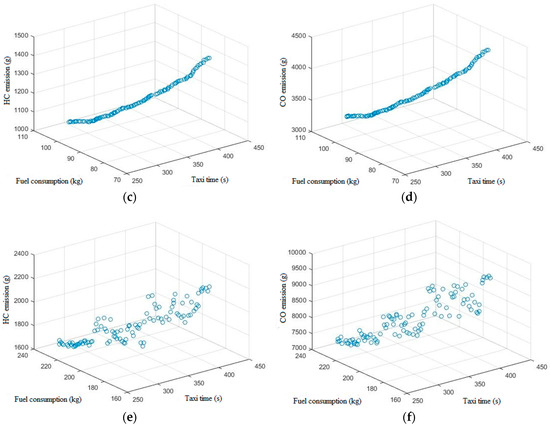
Figure 3.
Pareto fronts of the multi-objective optimization of different aircraft types. (a) Learjet35A Pareto front of taxiing time, fuel consumption, and HC emissions; (b) Learjet35A Pareto front of taxiing time, fuel consumption, and CO emissions; (c) A320 Pareto front of taxiing time, fuel consumption, and HC emissions; (d) A320 Pareto front of taxiing time, fuel consumption, and CO emissions; (e) A333 Pareto front of taxiing time, fuel consumption, and HC emissions; and (f) A333 Pareto front of taxiing time, fuel consumption, and CO emissions.
The optimal Pareto fronts were compared, and some conclusions can be drawn. First, Figure 3 shows that the EI of HC and CO of the light and medium-weight aircraft have significant linear relations with taxiing time and fuel consumption. Specifically, the HC and CO emissions are negatively related with fuel consumption. When the taxiing time is relatively short, the HC and CO emissions are low. The Pareto front of the heavy aircraft is balanced among different objectives. This result demonstrates that the speed curve with high acceleration produces fewer pollutant emissions than the speed curve with lower acceleration and a short taxiing time.
The correlation coefficient matrix of the four optimization objectives of the three aircraft types was calculated (Table 4, Table 5 and Table 6). This task was carried out to further study the correlations between the HC and CO emissions, taxiing time, and fuel consumption.

Table 4.
Correlations among different optimization objectives of the light aircraft.

Table 5.
Correlations among different optimization objectives of the medium-weight aircraft.

Table 6.
Correlations among different optimization objectives of the heavy aircraft.
As shown in the matrixes from Table 4, Table 5 and Table 6, a negative correlation exists between taxiing time and fuel consumption. Specifically, these two objectives have mutual conflicts and a relationship in equilibrium. The HC and CO emissions are positively correlated with taxiing time, but they are negatively correlated with fuel consumption. The correlation coefficients of the HC and CO emissions are relatively similar, thereby verifying that have the same variation trend. This similarity is due to the exponential correlations of the HC and CO emissions with fuel consumption. Therefore, the HC and CO emissions can be ignored while considering the balance among the four objective functions—namely, taxiing time, fuel consumption, HC emissions, and CO emissions.
6.3. Analysis of the Taxiway Optimization Results for Different Aircraft Types
The taxiway optimization for different aircraft types is different due to variations in fuel flow and pollutant emissions. In this section, the aircraft were divided into narrow, wide, and ultra-wide types according to size. Fuel flows were obtained for the narrow (B738 and A320), wide (B777 and A310), and ultra-wide (B747 and A340) types under different taxiing states (Appendix A: Table A2 and Table A3) and applied in the multi-objective optimization of the taxiway. On this basis, the optimized Pareto solution set of the taxiing time and fuel consumption of the aircraft was derived (Figure 4).
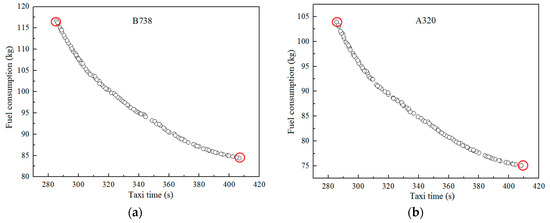
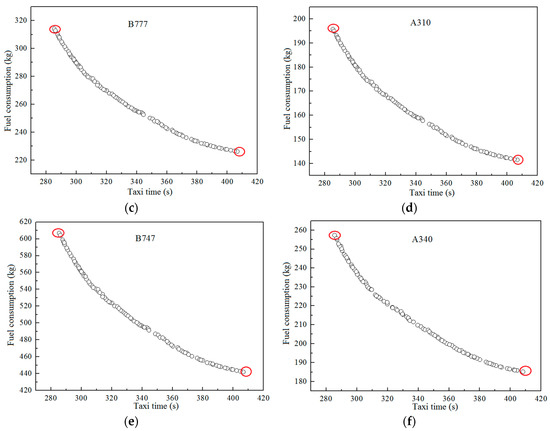
Figure 4.
Pareto fronts on the optimization of taxiing time and fuel consumption of different aircraft types (a) B738; (b) A320; (c) B777; (d) A310; (e) B747; and (f) A340.
Figure 4 demonstrates that the shortest total taxiing time does not represent the aircraft with the lowest fuel consumption of aircraft. On the other hand, the taxiing speed curve that pursues the shortest taxiing time is often accompanied by multiple acceleration and deceleration states, thereby increasing fuel consumption. The two red circles at the two ends of the Pareto curve represent the taxiing speed curves with the shortest taxiing time and lowest fuel consumption. Given the same taxiway, taxiing speed, and acceleration, the optimization results of the taxiing time of the above-mentioned six aircraft are basically the same. However, the optimization results of different aircraft vary due to different fuel flows. The two ends of the Pareto curves of different aircraft after optimization were selected. Table 7 illustrates the results.

Table 7.
Comparison of the two taxiing schemes for different aircraft.
The aforementioned table shows the optimized taxiways of different aircraft. Among the most time-saving taxiing schemes, the taxiing time of different aircraft is 285 s. However, the fuel consumption of all aircraft is high in the Pareto solution set. Among the most fuel-saving taxiing schemes, the fuel consumptions of the narrow aircraft B738 and A320 are 84.44 and 75.05 kg; those of the wide aircraft B777 and A310 are 226.21 and 141.51 kg; and those of the ultra-wide aircraft B747 and A340 are 442.12 and 185.22 kg, respectively. The fuel consumption of all aircraft is 28% lower than that in the time-saving taxiing schemes. Figure 4 demonstrates that the fuel consumption of the Boeing aircraft of all sizes is higher than that of the airbus planes.
Figure 5 presents the taxiing speed curves of the aircraft under the most time-saving and fuel-saving taxiing schemes.
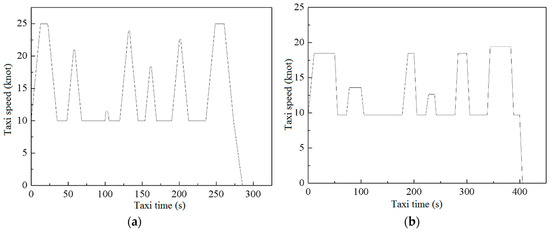
Figure 5.
Speed curves of the aircraft under the most time-saving and fuel-saving taxiing schemes: (a) the most time-saving taxi speed curve; and (b) the fuel economy taxi speed curve.
The aforementioned figure shows that among the most time-saving and fuel-saving taxiing schemes, the maximum taxiing speeds of the aircraft are 25 and 20 knots. The aircraft taxi by minimizing taxiing time. Thus, the acceleration and number of accelerations and decelerations are significantly higher than those under the most fuel-saving taxiing schemes.
6.4. Comparison of the Optimization Results with and without Taxiing Waiting Points
Aircraft might run through one of the other runways during taxiing, and they have to decelerate to zero before running through the runway. In this case, in the corresponding section is set approximately to zero. The initial speed of the next section is the terminal speed of the previous section. Table 8 illustrates the sectional information of the specific waiting points.

Table 8.
Parameters of different sections with taxiing waiting points.
The unimpeded taxiing and taxiing surfaces with conflict waiting of B738, A320, B777, A310, B747, and A340 were optimized. Figure 6 presents the Pareto fronts of the taxiing time and fuel consumption of the different aircraft under two taxiing schemes.
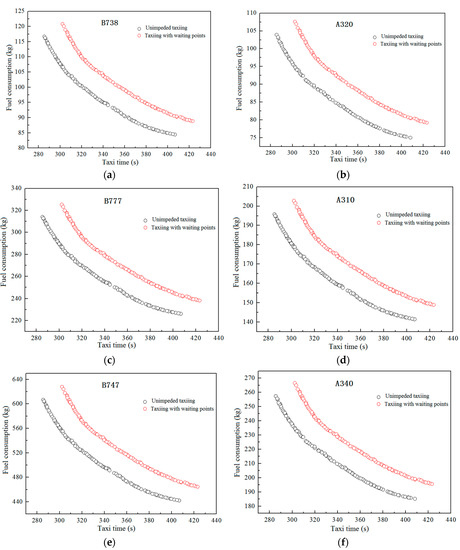
Figure 6.
Comparison of the Pareto fronts of the different aircraft with and without taxiing waiting points. (a) B738; (b) A320; (c) B777; (d) A310; (e) B747; and (f) A340.
Figure 6 demonstrates that the taxiing time and fuel consumption of the six aircraft during taxiing with waiting points are higher than those during unimpeded taxiing. The taxiing time and fuel consumption of all taxiing schemes of each aircraft in the Pareto curve increase at a uniform interval. The two end scheme aircraft, namely, the taxiing schemes with the shortest taxiing times and the least fuel consumption, of the two Pareto curves of different aircraft were selected. Table 9 lists the relevant data.

Table 9.
Comparison of the optimized taxiways with and without waiting points.
This table illustrates that the taxiing times of all six aircraft in the Pareto-optimized schemes with waiting points are 17 s longer than those under unimpeded taxiing. Specifically, the fuel consumptions of B738, A320, B777, A310, B747, and A340 under the most time-saving and fuel-saving schemes increased by 4.13 and 4.42, 3.67 and 4.2, 11.25 and 12.04, 6.95 and 7.44, 21.09 and 22.57, and 9.15 and 10.48 kg, respectively. Although all aircraft have an equal additional taxiing time for the taxiing conflict, the total growth of their fuel consumption is different. B747 shows the highest growth in fuel consumption, whereas A320 presents the lowest growth. The growth of fuel consumption is proportional to the aircraft’s fuel flow. When the fuel flow is high, the growth of the fuel consumption will also be high.
The taxiing time and speed curve of the different aircraft under various taxiing surfaces are generally the same. Thus, A320 was chosen for the case study in the present work. The speed curve and thrust changes of A320 under the most time-saving taxiing scheme were analyzed. Figure 7 presents the results.
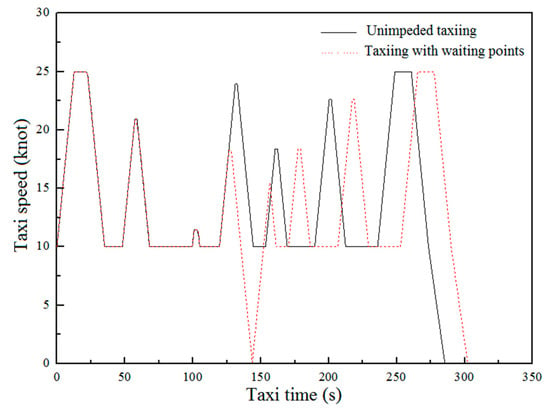
Figure 7.
Comparison of the speed curves of A320 under the most time-saving taxiing schemes with or without waiting points being present.
This figure shows that when waiting points are present, aircraft reach a maximum taxiing speed of 18.26 knots at 126 s upon arrival at a certain taxiing section. The aircraft then begins to decelerate to zero to avoid conflicts, which takes 17 s. When the taxiing speed approaches zero, the aircraft begins to engage in accelerating taxiing. The taxiing speed reaches its peak in this section at 13 s (reaching 15.5 knots). Under unimpeded taxiing, the aircraft do not decelerate to zero. In the above-mentioned taxiing sections, the maximum taxiing speeds of the aircraft under the unimpeded taxiing scheme are higher than those under the taxiing scheme with waiting points.
The comparative results of Figure 7 and Figure 8 show that the braking/thrust ratio of aircraft changes with taxiing speed. When aircraft initiative accelerates taxiing, their thrust is 85,000 N. When aircraft engage in taxiing at a uniform speed, the thrust of the aircraft is kept constant at 15,000 N when they are taxiing at a constant taxiing speed or at a speed of 10 knots. When the aircraft initiate their decelerating speed, the braking force is −65,000 N.
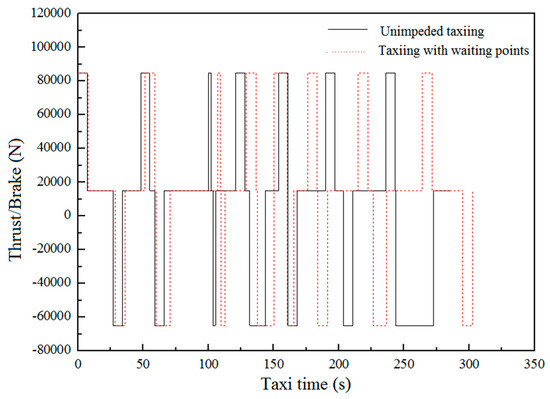
Figure 8.
Comparison of the thrust/braking curves of A320 in the most time-saving taxiing schemes with or without waiting points.
The above-mentioned thrust/braking diagram shows that, under unimpeded taxiing, aircraft begin to engage in taxiing at a uniform speed (10 knots) at 144 s. Here, the aircraft thrust is 15,000 N. Under taxiing with waiting points, the taxiing speed must be first decreased to zero and then increased again. Therefore, the aircraft thrust is not increased to 15,000 N, but it is directly increased to 85,000 N.
In summary, the taxiing time and fuel consumption of aircraft under taxiing conflicts existing are higher compared to those under unimpeded taxiing. Although the taxiing speed curve and thrust/braking ratio consistently change before the taxiing conflict, this may change the optimized taxiing scheme after taxiing conflict.
6.5. Comparison of Optimization Results in Airports with Different Altitudes
Different airport environments can influence the fuel consumption of aircraft for taxiing. Thus, the fuel flow coefficient of the aircraft was modified in this experiment with consideration of different environments, such as air pressure and temperature, in plateau airports compared to those of plain airports to analyze the optimization results of aircraft taxiways in these two types of airports.
In this section, the Lhasa Gonggar International Airport (ICAO: ZULS), Kunming Changshui International Airport (ICAO: ZPPP), and ZSPD were selected as the aircraft taxiing surfaces. Table 10 shows the environmental aircraft data.

Table 10.
Environmental parameters in three airports with different altitudes.
The fuel flows of Learjet35A, A320, and A333 under different taxiing states in ZULS, ZPPP, and ZSPD can be obtained by integrating the data in Table 9 into Equations (4), (5), and (6), respectively. Table 11 illustrates the results.

Table 11.
Fuel flow of aircraft under various taxiing states in different airports. (Unit: kg/s).
The taxiing experiment is implemented on sunny days in three airports. Specifically, the aircraft, taxiing speed, and acceleration of the aircraft are not influenced and equal. The Pareto solution sets of B738, A320, B777, A310, B747, and A340 in three airports with respect to taxiing time and fuel consumption were obtained through multi-objective optimization of taxiways (Figure 9).
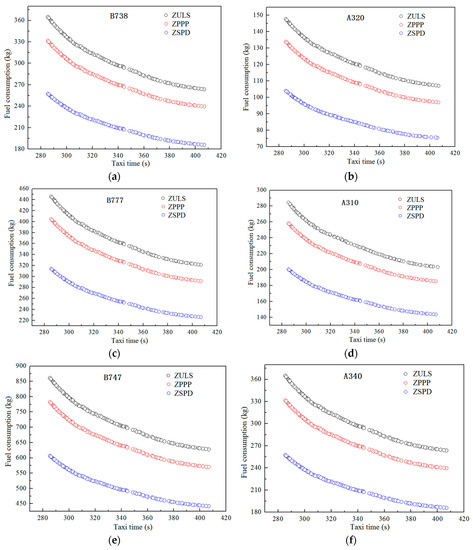
Figure 9.
Comparison of Pareto fronts for the optimization goals of different aircraft in various airports: (a) B738; (b) A320; (c) B777; (d) A310; (e) B747; and (f) A340.
When aircraft initiate taxiing in plateau and plain airports on sunny days, their taxiing speed and acceleration will not be influenced by the plateau’s environment. However, the thrust level of the engine is sensitive to environmental changes. Therefore, the taxiing time of different aircraft on various airports is generally equal. Figure 9 demonstrates that the aircraft fuel consumption in ZULS for taxiing under the same length is the highest, followed by the consumption in ZPPP and ZSPD.
The two end aircraft taxiing schemes for the Pareto curves in three airports were selected. Table 12 presents the data for the most time-saving and fuel-saving taxiing schemes.

Table 12.
Comparison of the optimized aircraft taxiway under two taxiing schemes (Unit: kg).
The figure shows that the fuel consumptions of B738 and A320 for the most time-saving taxiing in ZULS are 14.37 kg and 13.79 kg higher than those in ZPPP, and 48.47 kg and 43.72 kg higher than those in ZSPD. The fuel consumptions of B738 and A320 for the most fuel-saving taxiing in ZULS are 10.5 kg and 10.14 kg higher than those in ZPPP, and 35.06 kg and 31.67 kg higher than those in ZSPD.
The fuel consumptions of wide aircraft, namely, B777 and A310, for the most time-saving taxiing in ZULS are 41.33 kg and 26.12 kg higher than those in ZPPP, and 132.08 kg and 84.08 kg higher than those in ZSPD. Moreover, the fuel consumptions of B777 and A310 for the most fuel-saving taxiing in ZULS are 29.65 kg and 17.8 kg higher than those in ZPPP, and 95.09 kg and 59.46 kg higher than those in ZSPD.
The fuel consumptions of ultra-wide aircraft, such as B747 and A340, for the most time-saving taxiing in ZULS are 78.9 kg and 33.26 kg higher than those in ZPPP, and 254.75 kg and 107.39 kg higher than those in ZSPD. Furthermore, the fuel consumptions of B747 and A340 for the most fuel-saving taxiing in ZULS are 57.49 kg and 24.01 kg higher than those in ZPPP, and 185.65 kg and 77.71 kg higher than those in ZSPD.
In summary, the fuel consumption of different aircraft for taxiing in ZULS is 42% higher than that in ZSPD, and that in ZPPP is 29% higher than that in ZSPD. Therefore, the aircraft fuel consumption on taxiways with equal lengths at plateau airports is higher than that in plain airports. This variation is due to the increase in aircraft fuel flow under different taxiing states with an increment in altitude and a reduction of surface temperature and air pressure in airports.
7. Conclusions and Prospects
Surface operations in busy airports must adapt to the practical needs of taxiing to obtain multi-objective optimization results on taxiing time, fuel consumption, and pollutant emissions with consideration to conflict resolution and airport environmental taxiing states. In this study, taxiing waiting points have been added into the aircraft taxiway. The aircrafts’ influences on these waiting points based on the multi-objective optimization of taxiing time and fuel consumption have been calculated. The coefficients of the fuel flow and pollutant emissions of airports with different altitudes must be modified. The influences of altitude on the Pareto front of the multi-objective optimization for aircraft taxiing have been determined. Optimized taxiing schemes under different conditions have been obtained through a contrast analysis. These schemes will provide references to help airports to make relevant decisions.
Further studies can perfect airport taxiing optimization under different meteorological conditions. The effects of the type of taxiing conflict and the uncertainty of waiting time on multi-objective optimization will be explored further. Future studies should consider real-time weather conditions in the airport when studying multi-objective aircraft taxiing speed curves. For example, aircraft taxiing speed under low visibility or rainy or snowy days will decrease to maintain safe operating conditions under decreased ground frictional force. Further studies on aircraft taxiing should consider the types of aircraft conflict (e.g., crossing, head-on, and rear-end conflicts), the number of conflicts, the deceleration distance, and the uncertainty of waiting time in practical operations. In addition, the actual traffic conditions of the airport and the waiting time of the airport runway in the process of studying aircraft surface taxiing will also be investigated in future work.
Annotations
| Variables | Meanings |
| Type of aircraft (i = 1, 2, 3, 4, which are types A, B, C, and D of the aircraft, respectively) | |
| Taxiing state (j = 1, 2, 3, 4, which represents acceleration, uniform speed, idling, and turning) | |
| Speed curve of aircraft i | |
| Set of speed curves of aircraft i | |
| Taxiway marked with l | |
| Taxiing time (s) | |
| Fuel consumption (kg) | |
| HC emissions (g) | |
| CO emissions (g) | |
| Aircraft i weight categories (light, medium-weight, and heavy aircraft) | |
| Maximum taxiing speed (knot) | |
| Minimum taxiing speed (knot) | |
| Taxiing speed at turning (knot) | |
| Taxiing acceleration (m/s−2) | |
| Fuel flow of the aircraft in taxiing state j (kg/s) | |
| Fuel flow on seal level of aircraft in taxiing state j (kg/s) | |
| Ratio between the environmental pressure on the airport surface and the sea-level pressure under international standard atmospheric (ISA) conditions | |
| Ratio between the environmental temperature on the airport’s surface and at sea-level Temperature of the international standard atmosphere | |
| Environmental temperature of the airport’s surface () | |
| Environmental pressure of the airport’s surface (hPa) | |
| Emission index of pollutant k of the aircraft at the taxiing state j | |
| Emission indexof sea-level pollutant type of the aircraft under taxiing state j under ISA conditions | |
| Taxiing speed of aircraft on the airport’s surface (knot) | |
| Taxiing time under taxiing state j (s) | |
| Taxiing section s | |
| Taxiing time in taxiing section s (s) | |
| Thrust level (%) | |
| Fuel consumption for taxiing in section s (kg) | |
| Pollutant emission indices from taxiing in section s (g) |
Author Contributions
Conceptualization, M.Z.; methodology, M.Z.; software, Q.H. and H.L.; validation, S.L.; formal analysis, Q.H.; investigation, Q.H.; data curation, Q.H.; writing—original draft preparation, M.Z.; writing—review and editing, H.L.; visualization, S.L.; supervision, M.Z.; funding acquisition, M.Z.
Funding
This research was funded by the National Science Foundation of China, grant number No. U1633119, No. U1233101, and No. 71271113.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Fuel consumption and emission of the representative aircraft for taxiing at the speed of idling, uniform speed, and deceleration.
Table A1.
Fuel consumption and emission of the representative aircraft for taxiing at the speed of idling, uniform speed, and deceleration.
| Aircraft Models | Fuel Consumption and Pollutant Emissions | Turning | Idling | Uniform Speed | Acceleration |
|---|---|---|---|---|---|
| 35A | FUEL (kg/s) | 0.024 | 0.0184 | 0.0203 | 0.0277 |
| HC (g/kg fuel) | 20.04 | 22.0983 | 21.4122 | 20.0871 | |
| CO (g/kg fuel) | 58.6 | 63.3243 | 61.7496 | 55.4504 | |
| NOX (g/kg fuel) | 2.82 | 2.4183 | 2.5522 | 3.0878 | |
| A320 | FUEL (kg/s) | 0.1011 | 0.0763 | 0.0846 | 0.1176 |
| HC (g/kg fuel) | 1.4000 | 1.5304 | 1.4870 | 1.4030 | |
| CO (g/kg fuel) | 17.6 | 19.5696 | 18.913 | 16.287 | |
| NOX (g/kg fuel) | 4 | 3.4783 | 3.6522 | 4.3478 | |
| A333 | FUEL (kg/s) | 0.228 | 0.1633 | 0.1849 | 0.2711 |
| HC (g/kg fuel) | 9.37 | 10.5739 | 10.1726 | 9.3976 | |
| CO (g/kg fuel) | 42.67 | 48.0257 | 46.2404 | 39.0996 | |
| NOX (g/kg fuel) | 4.53 | 3.8283 | 4.0622 | 4.9978 |

Table A2.
Data sheet for different engines types.
Table A2.
Data sheet for different engines types.
| Type | Model | Engine Type | Number of Engines |
|---|---|---|---|
| Narrow aircraft | B738 | CFM56-7B26 | 2 |
| A320 | CFM56-5A1 | 2 | |
| Wide aircraft | B777 | Trent892 | 2 |
| A320 | CF6-80C2A2 | 2 | |
| Ultra-wide aircraft | B747 | RB211-524D4 | 4 |
| A340 | CFM56-5C4 | 4 |
Note: The original data source of different engines types was obtained from the BADA 3.15 release, Available online: https://ext.eurocontrol.int/bada (accessed on 2 November 2019).

Table A3.
The fuel flows of these aircraft types under different taxiing states.
Table A3.
The fuel flows of these aircraft types under different taxiing states.
| Model | Fuel Flows (kg/s) | |||
|---|---|---|---|---|
| Turning | Idling | Uniform Speed | Acceleration | |
| B738 | 0.113 | 0.0837 | 0.0934 | 0.1326 |
| A320 | 0.1011 | 0.0763 | 0.0846 | 0.1176 |
| B777 | 0.3 | 0.2087 | 0.239 | 0.361 |
| A320 | 0.189 | 0.138 | 0.155 | 0.233 |
| B747 | 0.3 | 0.2426 | 0.2617 | 0.3383 |
| A340 | 0.124 | 0.0898 | 0.1012 | 0.1468 |
References
- EUROCONTROL. Challenges of Growth 2013—Task 4: European Air Traffic in 2035. 2013. Available online: http://www.eurocontrol.int/sites/default/files/article/content/documents/official-documents/reports/201306-challenges-of-growth-2013-task-4.pdf (accessed on 2 November 2019).
- European Commission. Roadmap to a Single European Transport Area: Towards a Competitive and Resource Efficient Transport System. White Paper. 2011. Available online: http://ec.europa.eu/transport/themes/ strategies/2011_white_paper_en.htm (accessed on 2 November 2019).
- Atkin, J.A.D.; Burke, E.K.; Ravizza, S. The airport ground movement problem: Past & current research and future directions. In Proceedings of the International Conference on Research in Air Transportation, Budapest, Hungary, 1–4 June 2010; pp. 131–138. [Google Scholar]
- Bennell, J.A.; Mesgarpour, M.; Potts, C.N. Airport runway scheduling. Ann. Oper. Res. 2013, 204, 249–270. [Google Scholar] [CrossRef]
- Sölveling, G.; Clarke, J.-P. Scheduling of airport runway operations using stochastic branch and bound methods. Transp. Res. C Emerg. Tech. 2014, 45, 119–137. [Google Scholar] [CrossRef]
- Dell’Orco, M.; Marinelli, M.; Altieri, M.G. Solving the gate assignment problem through the fuzzy bee colony optimization. Transp. Res. C Emerg. Tech. 2017, 80, 424–438. [Google Scholar] [CrossRef]
- Chen, J.; Weiszer, M. Toward a more realistic, cost-effective and greener ground movement through active routing: A multi objective shortest path approach. Part I: Optimal speed profile generation. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1196–1209. [Google Scholar] [CrossRef]
- Honeywell. Electric Green Taxiing System. 2013. Available online: www.greentaxiing.com/resources/EGTS_Positioning_paper.pdf (accessed on 2 November 2019).
- Adler, N.; Martini, G.; Volta, N. Measuring the environmental efficiency of the global aviation fleet. Transp. Res. B Meth. 2013, 53, 82–100. [Google Scholar] [CrossRef]
- Joint Planning and Development Office. Concept of Operations for the Next Generation Air Transportation System; Version 3.2; Joint Planning and Development Office: Washington, DC, USA, 2010. Available online: http://jpe.jpdo.gov/ee/docs/conops/NextGen_ConOps;_v3_2.pdf (accessed on 2 November 2019).
- SESAR. European ATM Master Plan; SESAR: Brussels, Belgium, 2012; Available online: https://www.atmmasterplan.eu/download/29 (accessed on 2 November 2019).
- European Commission. Flightpath 2050, Europe’s Vision for Aviation. Report of the High Level Group on Aviation Research, Directorate-General for Research and Innovation, Directorate General for Mobility and Transport; European Commission: Luxemburg, 2011; Available online: https://www.acare4europe.org/sites/acare4europe.org/files/ document/ flightpath2050_final.pdf (accessed on 2 November 2019).
- Hao, L.; Ryerson, M.S.; Kang, L.; Hansen, M. Estimating fuel burn impacts of taxi-out delay with implications for gate-hold benefits. Transp. Res. C Emerg. Tech. 2017, 80, 454–466. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Advanced Surface Movement Guidance and Control Systems (A-SMGCS) Manual; ICAO: Montreal, QC, Canada, 2004; Available online: http://www.icao.int/Meetings/anconf12/Document%20Archive/9830_cons_en[1].pdf (accessed on 2 November 2019).
- Clare, G.L.; Richard, A.G. Optimisation of taxiway routing and runway scheduling. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1000–1013. [Google Scholar] [CrossRef]
- Chen, J.; Stewart, P. Planning aircraft taxiing trajectories via a multiobjective immune optimisation. In Proceedings of the Seventh International Conference on Natural Computation, Shanghai, China, 26–28 July 2011; pp. 2235–2240. [Google Scholar]
- Lesire, C. An iterative algorithm for planning of airport ground movement. In Proceedings of the 19th European Conference on Artificial Intelligence, Lisbon, Portugal, 16–20 August 2010; pp. 413–418. [Google Scholar]
- Atkin, J.A.D.; Burke, E.K.; Ravizza, S. A more realistic approach for airport ground movement optimisation with stand holding. In Proceedings of the 5th Multidisciplinary International Scheduling Conference, Phoenix, AZ, USA, 9–12 August 2011; pp. 1–15. [Google Scholar]
- Ravizza, S.; Atkin, J.A.D.; Burke, E.K. A more realistic approach for airport ground movement optimisation with stand holding. J. Sched. 2014, 17, 507–520. [Google Scholar] [CrossRef]
- Bakowski, D.L.; Hooey, B.L.; Foyle, D.C.; Wolter, C.A.; Cheng, L.W.S. NextGen surface trajectory-based operations: Contingency-hold clearances. In Proceedings of the IEEE/AIAA Digital Avionics Systems Conference, East Syracuse, NY, USA, 5–10 October 2013; pp. 1B6-1–1B6-11. [Google Scholar]
- Cheng, V.H.L.; Sweriduk, G.D. Trajectory design for aircraft taxi automation to benefit trajectory-based operations. In Proceedings of the 2009 7th Asian Control Conference, Hong Kong, China, 27–29 August 2009; pp. 99–104. [Google Scholar]
- Haus, S.; Sendobry, A.; Urvoy, C.; Klingauf, U. Control theoretic concept for intuitive guidance of pilots during taxiing. In Proceedings of the IEEE/AIAA 30th Digital Avionics Systems Conference, Seattle, WA, USA, 16–20 October 2011; pp. 6B3-6–6B3-14. [Google Scholar]
- Turgut, E.T.; Cavcar, M.; Usanmaz, O.; Yay, O.D.; Dogeroglu, T.; Armutlu, K. Investigating actual landing and takeoff operations for time-in-mode, fuel and emissions parameters on domestic routes in Turkey. Transp. Res. D Transp. Environ. 2017, 53, 249–262. [Google Scholar] [CrossRef]
- Khoo, H.L.; Teoh, L.E. A bi-objective dynamic programming approach for airline green fleet planning. Transp. Res. D Transp. Environ. 2014, 33, 166–185. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, T.; Yu, Y.; Chen, D.; Zhu, B. Scenario analysis of CO2 emissions from China’s civil aviation industry through 2030. Appl. Energy 2016, 175, 100–108. [Google Scholar] [CrossRef]
- Smeltink, J.; Soomer, M. An optimisation model for airport taxi scheduling. In Proceedings of the INFORMS Annual Meeting, Denver, CO, USA, 24–27 October 2004. [Google Scholar]
- Herrero, J.G.; Berlanga, A. Methods for operations planning in airport decision support systems. Appl. Intell. 2005, 22, 183–206. [Google Scholar] [CrossRef]
- Balakrishnan, H.; Jung, Y.C. A framework for coordinated surface operations planning at Dallas-Fort Worth International Airport. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Hilton Head, SC, USA, 20–23 August 2007. [Google Scholar]
- Roling, P.C.; Visser, H.G. Optimal airport surface traffic planning using mixed-integer linear programming. Int. J. Aerospace Eng. 2008, 1, 1–11. [Google Scholar] [CrossRef]
- Koeners, G.J.M.; Stout, E.P.; Rademaker, R.M. Improving taxi traffic flow by real-time runway sequence optimization using dynamic taxi route planning. In Proceedings of the 2011 IEEE/AIAA 30th Digital Avionics Systems Conference, Seattle, WA, USA, 16–20 October 2011. [Google Scholar]
- Ravizza, S.; Chen, J. The trade-off between taxi time and fuel consumption in airport ground movement. In Proceedings of the Advanced Systems for Public Transport, Santiago, Chile, 23–27 July 2012. [Google Scholar]
- Lee, H.; Balakrishnan, H. Optimization of airport taxiway operations at Detroit Metropolitan Airport (DTW). In Proceedings of the 10th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Fort Worth, TX, USA, 13–15 September 2010. [Google Scholar]
- Weiszer, M.; Chen, J. A heuristic approach to greener airport ground movement. In Proceedings of the IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014. [Google Scholar]
- Chen, J.; Weiszer, M.; Stewart, P. Optimal speed profile generation for airport ground movement with consideration of emissions. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems—(ITSC 2015), Las Palmas, Spain, 15–18 September 2015. [Google Scholar]
- Brownlee, A.E.I.; Weiszer, M.; Chen, J.; Ravizza, S.; Woodward, J.R.; Burke, E.K. A fuzzy approach to addressing uncertainty in Airport Ground Movement optimization. Transp. Res. C Emerg. 2018, 92, 150–175. [Google Scholar] [CrossRef]
- Booth, D.; Flynn, B.; Sultana, J. Airport Collaborative Decision Making (A-CDM) Implementation Manual. Version 5.0. 31 March 2017. Available online: https://www.eurocontrol.int/publication/airport-collaborative- decision-making-cdm-implementation-manual (accessed on 2 November 2019).
- International Civil Aviation Organization. Aircraft Engine Emissions; Annex-16-Vol-2-3rd-Edition; International Civil Aviation Organization: Montreal, QC, Canada, 2008; Available online: www.icao.int/environmental-protection/technology-stand ards_FR.aspx (accessed on 2 November 2019).
- Bakowski, D.L.; Foyle, D.C.; Hooey, B.L.; Kunkle, C.L.; Jordan, K.P. NextGen flight deck Surface Trajectory-Based Operations (STBO): Speed-based taxi clearances. In Proceedings of the Twelfth International Symposium on Aviation Psychology, Dayton, OH, USA, 2–5 May 2011; pp. 44–49. [Google Scholar]
- DuBois, D.; Paynter, G. Fuel flow method 2 for Estimating Aircraft Emissions; SAE Technical Paper 2006-01-1987. J. Aerospace 2006, 115, 1–14. [Google Scholar]
- Nikoleris, T.; Gupta, G.; Kistler, M. Detailed estimation of fuel consumption and emissions during aircraft taxi operations at Dallas/Fort Worth International Airport. Transp. Res. D Transp. Environ. 2011, 16, 302–308. [Google Scholar] [CrossRef]
- Alirezaei, M.; Niaki, S.T.A.; Niaki, A.A. A bi-objective hybrid optimization algorithm to reduce noise and data dimension in diabetes diagnosis using support vector machines. Expert Syst. Appl. 2019, 127, 47–57. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).