Efficient Energy Management in a Microgrid with Intermittent Renewable Energy and Storage Sources

Abstract

Substituting a single large power grid into various manageable microgrids is the emerging form for maintaining power systems. A microgrid is usually comprised of small units of renewable energy sources, battery storage, combined heat and power (CHP) plants and most importantly, an energy management system (EMS). An EMS is responsible for the core functioning of a microgrid, which includes establishing continuous and reliable communication among all distributed generation (DG) units and ensuring well-coordinated activities. This research focuses on improving the performance of EMS. The problem at hand is the optimal scheduling of the generation units and battery storage in a microgrid. Therefore, EMS should ensure that the power is shared among different sources following an imposed scenario to meet the load requirements, while the operational costs of the microgrid are kept as low as possible. This problem is formulated as an optimization problem. To solve this problem, this research proposes an enhanced version of the most valuable player algorithm (MVPA) which is a new metaheuristic optimization algorithm, inspired by actual sporting events. The obtained results are compared with numerous well-known optimization algorithms to validate the efficiency of the proposed EMS.

1. Introduction

The alarming rise in carbon emissions means production of clean energy is required urgently. The recent incorporation of both large and small renewable energy sources into the existing power system is a positive step towards decarbonizing our power generation, however, much effort is still required to address the challenges directly associated with widespread penetration of such energy sources. In addition to reducing carbon emissions, these efforts are primarily targeted to produce a sustainable energy supply.

Location-based renewable energy sources have naturally become an alternative power source within the microgrid, which is constituted of distributed generation (DG) units, storage devices, and loads. There is a tendency for the microgrid to operate in both islanded and grid-connected modes. Determining an optimal share of power produced by available DGs in a microgrid is a challenge and has remained one of the most interesting and important topics of research.

In literature, various performance attributes of microgrids were optimized using different optimization algorithms. Power generation scheduling was optimized in [1] using an artificial fish swarm algorithm (AFSA), whereas, in [2], day-a-head optimized scheduling was presented using a harmony search (HS) and differential evolution (DE) algorithms. Reference [3] solved the economic power dispatch using four algorithms, namely, the direct search method, particle swarm optimization (PSO), lambda logic, and lambda iteration. In reference [4], additive-increase-multiplicative-decrease algorithms were used to optimize power sharing among active DGs. In order to determine the optimal component sizing in a microgrid, the mixed integer linear programming (MILP) method has been used to model the microgrid components with consideration of demand response [5]. In another study [6], similar sizing problems of microgrid components were solved using a genetic algorithm (GA) and the energy management issue was formulated using MILP. In addition to component sizing, system configuration was optimized in [7] using the multi-objective PSO by taking into account production cost, reliability, and environmental impact. The studied system comprised of a diesel generator, solar panels, wind turbines, and battery storage. Several methods have also been used for optimizing multi variable problems of energy management systems (EMS) in microgrids [8,9,10,11,12,13]. Wang et al. [14] investigated EMS of a microgrid with multi period optimization problems using an MPI based PSO algorithm and concluded that the proposed algorithm could be effectively used to improve the operation time.

Four techniques were used in [15] to determine the optimized operational strategy for an entire day based on least operating cost and minimum carbon emissions. These techniques were a non-dominated sorting genetic algorithm (NSGA), multi-objective PSO, multi-objective uniform water cycle algorithm (WCA), and normal constraint algorithm. Reference [16] presented a real time EMS that had the tendency to optimally minimize carbon emissions and energy cost, and simultaneously maximized the power coming from renewable DGs using binary PSO. An improved binary PSO with double-structure coding was applied to optimize a microgrid operation [17]. In this research, the effectiveness of the proposed algorithm was verified based on the simulation results. Another real time EMS was also proposed by applying multi-objective PSO for an islanded microgrid [18]. Compared with a multi objective GA, the proposed algorithm creates faster computation. A multi-objective PSO algorithm was later modified to optimize the operation of the system with minimum energy consumption, cost, and emissions [19]. It was found that the proposed multi-objective PSO could be validated for multi variable EMS of a factory. The optimal power control strategy for a standalone microgrid was developed and presented in [20] where optimized gains of a proportional-integrator controller of inverter-based DGs using hybrid big bang-big crunch (BB–BC) algorithm were found.

With the aim of adjusting microgrid generation to energy demand, numerous technical studies have been carried out to improve energy management with penetration of renewable energy sources combined with energy storage devices in microgrids [21,22,23,24,25]. Alvarez et al. [26] conducted an optimization of micro sources in a DG microgrid in terms of emission and fuel consumption costs. This work showed a faster response of microgrid management with better micro source stability and global cost. Another study, [27], evaluated optimal energy management in an isolated microgrid with renewable energy sources (i.e., PV and wind power plants) using pumped-storage and demand response. Through this research, technical and economic performances of the system were significantly improved by implementing demand response and optimal scheduling of the pumped-storage. Kim et al. [28] evaluated the acceptability and stability of a hybrid microgrid system to provide power supply for Gasado Island in South Korea. It showed that the system is not only stable but also capable of predicting the electricity supply and demand, managing the batteries charge/discharge, and controlling the distributed generators with lower costs and higher renewable energy fraction. Meanwhile, a technical analysis of a hybrid system was performed for electricity shortage conditions caused by a disaster [29]. The hybrid system is off-grid and consists of conventional and renewable energy sources and energy storage system. As a result, the renewable energy sources can provide backup power supply in the absence of conventional energy sources during disaster. The authors in another study [30] analyzed optimal energy management of a renewable-based microgrid using a PSO algorithm combined with a primal-dual interior point and concluded that the proposed robust model effectively solved the microgrid energy management problems by minimizing operation costs and satisfying the PVs insolation limitation and the microgrid physical constraints.

In reference [31], a robust management system was proposed for a microgrid in the presence of high penetration of renewable DGs. This system tended to minimize the microgrid’s running and worst-case transaction costs, along with the utility of the dispatchable loads while considering the stochastic nature of DGs. Reference [32] presented a model for stochastic microgrid energy scheduling with the primary goal of minimizing anticipated running costs and power losses. Plug-in electric vehicles, storage devices, and DGs were taken into consideration while modeling the microgrid. In another study [33], several forecasting methods were applied to optimize the EMS of distributed energy resources. In reference [34], the charging and discharging rates of batteries were controlled to optimize energy management in a microgrid constituted of renewable energy sources and storage devices. For optimal energy management, a drop-based controller was utilized, whereas, for power distribution among charging stations, an aggregator was used. Ultimately the power was distributed among charging stations subjected to their droop participation. The Markov decision process (MDP) was used to formulate multi-energy systems scheduling in [35], where the decision space and large state of MDP were solved using a rollout algorithm. Wind power, batteries, and combined heat and power (CHP) were used to model a microgrid in grid connected mode. Reference [36] proposed a memory-based GA to minimize costs by optimally distributing power among DGs connected in a microgrid. An algorithm was implemented on the microgrid consisting of solar plants, wind plants, and CHP. Chen et al. [37] evaluated a mutual dependency of cogeneration units and proposed a direct search method to solve the CHP dispatch problem. A number of studies have been done to verify the proposed approach. Another study [38] analyzed the effect of distributed energy resources integration in an industrial microgrid and proposed a model with onsite generation, i.e., CHP and a wind turbine, which was applied to a manufacturing facility. In a recent study [39], optimization of energy, heat, and demand in a microgrid was conducted using a mathematical model based on MILP with the aim of minimizing the operational cost.

In this paper, we propose an efficient energy management system (EEMS) for the optimal scheduling of different sources in a microgrid, considering the intermittent behavior of renewable energy sources, with and without storage resources. The developed system can efficiently manage the energy under different scenarios. This EEMS uses an enhanced version of the most valuable player algorithm (EMVPA) to minimize the operating cost of the microgrid.

The remainder of this paper is organized as follows. The investigated microgrid is introduced in Section 2. The details of the energy management strategy are described in Section 3. The problem formulation for minimizing operating cost is presented in Section 4 and the optimization algorithms are proposed in Section 5. Results and discussion are provided in Section 6 and finally, conclusions are drawn in Section 7.

2. Description of the Microgrid

In this paper, a microgrid with a certain number of sources is considered, consisting of wind energy plants, solar PV plants, CHP, storage batteries and utility, as well as an EMS responsible for coordination of all components of the microgrid (Figure 1). The microgrid can be operated in grid-connected mode or disconnected (islanded) mode.

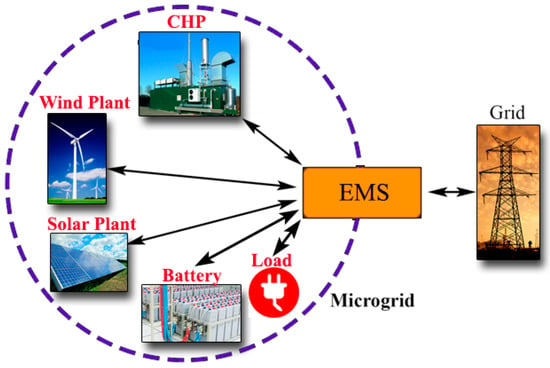
Figure 1. Microgrid representation.

3. Efficient Energy Management System (EEMS)

An EMS is required to coordinate the energy share among different sources of the microgrid based on the selected scenario. The word “efficient,” added to the EMS, demonstrates the proposed work uses EMVPA to make EMS operations more efficient in terms of running costs. The energy management strategy used in this study is represented by the flowchart given in Figure 2, which allows an operator to manage the microgrid using one scenario from the three defined scenarios. For all three scenarios, the main sources of energy are renewable sources. It is worth mentioning that, although three scenarios are investigated in this paper, more scenarios can be added to the EEMS. All proposed scenarios are described in the following subsections.

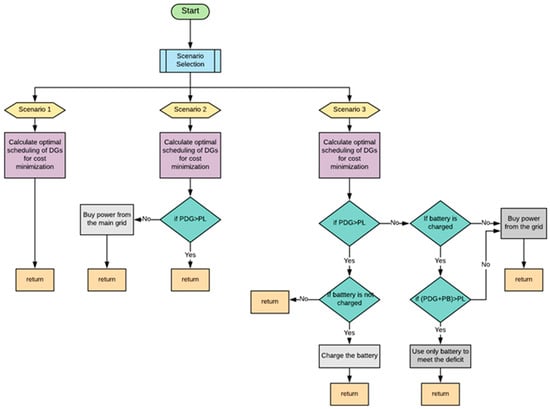
Figure 2. Flowchart of the proposed EMS of the microgrid.

3.1. Scenario 1

All DGs can only be operated within their respective minimum and maximum limits. Moreover, there is no power that can be transferred from the utility or the main grid. Thus, the microgrid operates in islanded mode.

3.2. Scenario 2

All DGs can work within their limits and the microgrid can buy limited power from the utility only when DGs cannot supply the requested load.

3.3. Scenario 3

The microgrid has the facility of storage batteries and all DGs can work within their limits. The microgrid can buy limited power from the utility only when DGs and battery cannot supply the requested load. As shown in Figure 2, it is pertinent that if the generated power from DGs is greater than the load, the surplus energy is used to charge the battery bank. In the case where the battery bank is fully charged, no extra power will be generated from the DGs. On the other hand, if the power generated by DGs is less than the requested load, the deficit of power is provided by the battery bank. If DGs and the battery bank cannot supply the load, the deficit of power is bought from the main grid.

4. Optimization Problem

As aforesaid, the role of the EMS is to optimally schedule the different sources of the microgrid based on the selected scenario for each hour in order to minimize the operating cost of the microgrid under some constraints. This can be formulated mathematically as an optimization problem which is described in the following subsections.

4.1. Objective Function

The objective function of the considered optimization problem can be approximated by a quadratic nonlinear function as follows [39]:

$${\mathrm{C}}_{\mathrm{i}}\left(\mathrm{t}\right)={\mathsf{\alpha }}_{\mathrm{i}}\times {\mathrm{P}}_{\mathrm{i}}{\left(\mathrm{t}\right)}^2+{\mathsf{\beta }}_{\mathrm{i}}\times {\mathrm{P}}_{\mathrm{i}}\left(\mathrm{t}\right)+{\mathsf{\gamma }}_{\mathrm{i}}$$

(1)

where, $\mathrm{i}$ denotes the number of DG units under consideration, $\mathrm{C}$ and $\mathrm{P}$ represent the cost in $ and power generated in MW on an hourly basis, respectively. DG technology and fuel cost are incorporated in coefficients $\mathsf{\alpha }$, $\mathsf{\beta }$, and $\mathsf{\gamma }$, where $\mathsf{\alpha }$, specifically, is used to introduce DG related nonlinearity.

4.2. Design Variables

For this optimization problem, power generated by each DG is taken as a design variable. A solution is initially proposed in a vector form containing all design variables and given to the optimizer to optimize the solution in upcoming iterations and find a vector that contains the optimally distributed power output from each generator. A solution vector x, for n wind energy plants, m PV plants and k CHP, is given in the following expression:

$$x=\left[{\mathrm{P}}_{\mathrm{wp}1},{\mathrm{P}}_{\mathrm{wp}2},\dots {\mathrm{P}}_{\mathrm{wpn}},{\mathrm{P}}_{\mathrm{sp}1},{\mathrm{P}}_{\mathrm{sp}2},\dots {\mathrm{P}}_{\mathrm{spm}},{\mathrm{P}}_{\mathrm{CHP}1},{\mathrm{P}}_{\mathrm{CHP}2},\dots {\mathrm{P}}_{\mathrm{CHPk}}\right]$$

(2)

where ${\mathrm{P}}_{\mathrm{wp}}$, ${\mathrm{P}}_{\mathrm{sp}}$, and ${\mathrm{P}}_{\mathrm{CHP}}$ represent the power from wind energy plants, solar PV plants and CHP, respectively.

4.3. Constraints

4.3.1. Power Balance

The power produced by the EEMS must be equal to the requested load at any instant. This can be represented by the following equation:

$${\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{DG}}}{\mathrm{P}}_{\mathrm{i}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{Battery}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{Grid}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{L}}\left(\mathrm{t}\right)$$

(3)

where ${\mathrm{P}}_{\mathrm{L}}\left(\mathrm{t}\right)$ is the total power required by the load at instant (t), ${\mathrm{P}}_{\mathrm{Battery}}\left(\mathrm{t}\right)$ is the power of storage batteries, and ${\mathrm{P}}_{\mathrm{Grid}}\left(\mathrm{t}\right)$ is the power from the grid at instant (t). It is worth to mention that, ${\mathrm{P}}_{\mathrm{Battery}} {\mathrm{and}\mathrm{P}}_{\mathrm{Grid}}$ depend on the selected scenario. For example, for Scenario 1, there is no storage device used and the microgrid is not allowed to buy power from the main grid. For Scenario 2, there is no battery; however, when the DGs cannot supply the requested load at a given time the deficit of power is bought from the grid. Finally, for Scenario 3, there are batteries (that can charge and discharge) and if there is deficit in accumulative power of DGs and battery, the power needed will be provided by the main grid.

4.3.2. Power Limits

Each DG source is limited by a maximum value and a minimum value that can vary from one instant to another. This constraint can be expressed as follows:

$${\mathrm{P}}_{\mathrm{i}\min }\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{i}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{i}\max }\left(\mathrm{t}\right)$$

(4)

where ${\mathrm{P}}_{\mathrm{i}\min }\left(\mathrm{t}\right)$ is the minimum value of power of i^th DG at instant (t) and ${\mathrm{P}}_{\mathrm{i}\max }\left(\mathrm{t}\right)$ is the maximum value of power of i^th DG at instant (t).

4.3.3. Battery Limits

The batteries are considered in this work as a secondary source of power. They can charge and discharge within a given range. Therefore, we can write the following constraint:

$${\mathrm{P}}_{\mathrm{Discharge}\min }\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{Battery}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{Charge}\max }\left(\mathrm{t}\right)$$

(5)

where ${\mathrm{P}}_{\mathrm{Discharge}\min }\left(\mathrm{t}\right)$ is the minimum discharging value allowed for the batteries at time (t) and ${\mathrm{P}}_{\mathrm{Charge}\max }\left(\mathrm{t}\right)$ is the maximum charging capacity of the batteries.

5. Optimization Algorithms

To solve the considered optimization problem, an enhanced version of the MVPA is developed. This transforms the EMS system into a more efficient one; i.e., EEMS. In the following two sections, the classical version of the MVPA and the enhanced version will be explained. It is worth explaining here that using an enhanced version of the MVPA, which is a modern metaheuristic, instead of any other classical method is motivated by the advantages of modern metaheuristics over classical methods. Among these advantages is their ability to adapt to any problem with no/or few modifications, which allows them to be easily applied to different scenarios.

5.1. Most Valuable Player Algorithm

The MVPA is a new metaheuristic optimization algorithm developed by Bouchekara [40], inspired by sports events. The main step in the MVPA is a population of players that compete individually to win the Most Valuable Player (MVP) trophy and collectively to win the championship. One important feature of the MVPA is that it has no internal parameter to tune. In [41], a comparative study was carried out between metaheuristic algorithms inspired by sports events including the MVPA. The MVPA has been ranked first for unimodal problems and equally ranked first with two other algorithms for multimodal problems. In reference [42] the MVPA was used for circular antenna arrays optimization to maximize sidelobe levels reduction.

The flowchart of the MVPA is shown in Figure 3a. The inputs needed by the MVPA are:

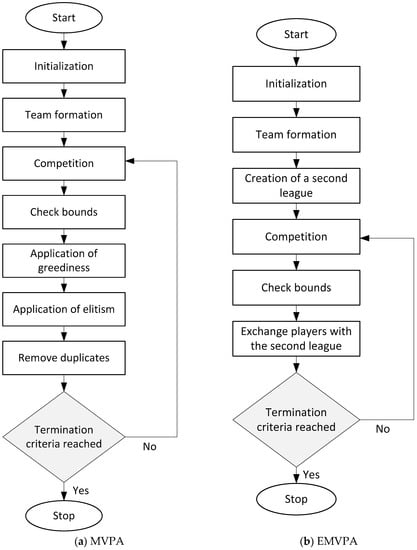
Figure 3. Flowchart of the MVPA and the EMVPA.

• The objective function (noted as ObjFunction) which can be a mathematical explicit function or a more complicated one;
• The dimension of the problem (noted as ProblemSize) which represents the number of design variables of the treated problem;
• The number of players which is equivalent to the population size in other population-based optimization algorithms (noted as PlayersSize);
• The number of teams in the league noted as (TeamsSize); and
• The maximum number of fixtures (noted as MaxNFix) which is equivalent to the maximum number of iterations in other optimization algorithms.

The main output of the MVPA is the best solution obtained for the treated problem i.e., the MVP. However, the other outputs can easily be obtained, for example, the value of the best objective function obtained or the evaluation of this last value during the optimization process.

After reading the inputs, the MVPA starts with the initialization step as shown in Figure 3a. In this first step the players (i.e., solutions) are spread out randomly within the search space. In the second step, the players are regrouped to form TeamsSize teams followed by the most important step for the MVPA, the competition step.

The pseudocode of the competition step is given below:

for i = 1: TeamsSize
Teams selection	${\mathrm{TEAM}}_{\mathrm{i}}=$ Select the team number i from the league’s teams
	${\mathrm{TEAM}}_{\mathrm{j}}=$ Randomly select another team j from the league’s teams where j ≠ i
Individual competition	$\begin{array}{cc}\hfill {\mathrm{TEAM}}_{\mathrm{i}}={\mathrm{TEAM}}_{\mathrm{i}}& +\mathrm{rand}\times \left({\mathrm{FranchisePlayer}}_{\mathrm{i}}-{\mathrm{TEAM}}_{\mathrm{i}}\right)\hfill \\ & +2\times \mathrm{rand}\times \left(\mathrm{MVP}-{\mathrm{TEAM}}_{\mathrm{i}}\right)\hfill \end{array}$
Collective competition	if${\mathrm{TEAM}}_{\mathrm{i}}\mathrm{wins}$ against ${\mathrm{TEAM}}_{\mathrm{j}}$
		${\mathrm{TEAM}}_{\mathrm{i}}={\mathrm{TEAM}}_{\mathrm{i}}+\mathrm{rand}\times \left({\mathrm{TEAM}}_{\mathrm{i}}-{\mathrm{FranchisePlayer}}_{\mathrm{j}}\right)$
	else
		${\mathrm{TEAM}}_{\mathrm{i}}={\mathrm{TEAM}}_{\mathrm{i}}+\mathrm{rand}\times \left({\mathrm{FranchisePlayer}}_{\mathrm{j}}-{\mathrm{TEAM}}_{\mathrm{i}}\right)$
	end if
end for

The competition step, as detailed in the pseudocode given above, starts with the selection of the first team ${\mathrm{TEAM}}_{\mathrm{i}}$ (all teams are selected one after another as for the first team) and the opponent team ${\mathrm{TEAM}}_{\mathrm{j}}$ which is selected randomly from the poll of teams where j ≠ i. In the individual competition phase, players compete and try individually to become their teams’ franchise players (the best player of their teams) and then to win the MVP trophy i.e., to become the league’s best player. In the collective competition phase, ${\mathrm{TEAM}}_{\mathrm{i}}$ plays against ${\mathrm{TEAM}}_{\mathrm{j}}$ and the players of ${\mathrm{TEAM}}_{\mathrm{i}}$ are updated based on the results of the game. Teams aim to win the championship.

After the competition step, the players are checked and if any player is outside the search space, it is brought back to the crossed bound. This step is called check bounds in the flowchart of Figure 3a. Then, the objective function values of the players are compared to their initial values. If a player improves in the competition step, he is kept, otherwise the initial player is kept. This is called the greediness step in the flowchart of Figure 3a. After that, the last two steps aim to apply elitism and then remove duplicate players, respectively. Finally, if a predefined stopping criterion (or more generally a set of predefined criteria) is met, the process stops otherwise returns to Step 3 and iterates again following the same steps.

5.2. Enhanced Most Valuable Player Algorithm

The flowchart of the EMVPA is shown in Figure 3b. The EMVPA has the same structure as the MVPA, however, for the EMVPA a second league is created and after each iteration the best players of this league are traded to teams in the first league while the worst players are moved to the second league. As can be seen from Figure 3b, the EMVPA starts with the initialization step followed by the team formation step described above. After that, a second league (smaller than the main league) is created. Then, once the competition and check-bound steps are finished, players are exchanged between the two leagues. In this step the worst players of the main league are moved to the second league while the best players of the second league are moved to the first. Finally, the algorithm iterates Steps 4 to 6 until the desired number of iterations is reached. It is worth mentioning that, steps such as the ‘application of greediness’, ‘application of elitism’ and ‘remove duplicates’ are removed in the enhanced version of the MVPA.

6. Results and Discussion

The performance of the EEMS based on the proposed EMVPA is tested using two different microgrid systems. The obtained results are then compared with the performance of EMS using the MVPA, PSO, GA, black hole (BH) algorithm, artificial bee colony (ABC), and electromagnetism-like mechanism (EM) algorithm in order to assess the performance of the proposed EEMS. In the simulation, each algorithm is run 30 times, and the best results of each algorithm are reported. All algorithms (except MVPA and EMVPA) are initialized with a population size of 50. For MVPA and EMVPA, PlayersSize = 100 and TeamsSize = 20. Moreover, the maximum number of iterations is set at 1000 for all algorithms and for all cases.

It must be noted that the developed codes and programs are run using MATLAB software on Core i7 @ 2.50 GHz, 8 GB RAM machine.

6.1. Microgrid #1

The first microgrid investigated in this paper is shown in Figure 4. This microgrid consists of a load area represented by the IEEE 37-bus test system, five DGs, a CHP, and a storage battery source.

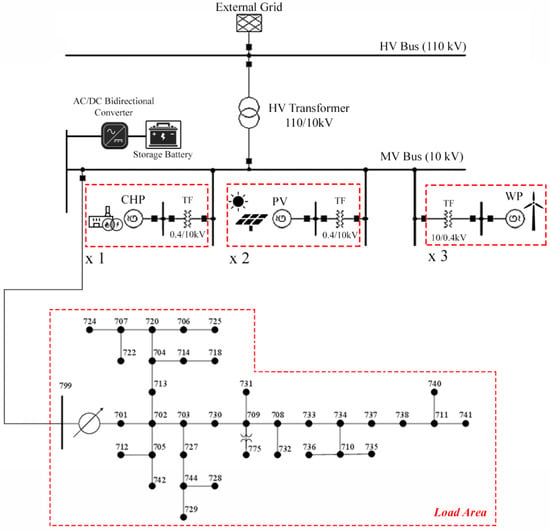
Figure 4. Schematic of power system with five DGs and IEEE 37-node test feeder.

The individual maximum capacities of CHP, each PV, and wind energy plant are 1000 kW, 250 kW, and 750 kW, respectively. The CHP can run at full capacity for the entire day, i.e., it can provide 1000 kW at any time, however, due to the intermittency of renewable energy sources, the power output from wind and PV plants is irregular. The power availability for each DG per hour in a running day is shown in Figure 5 [4]. The battery has a storage capacity of 300 kWh.

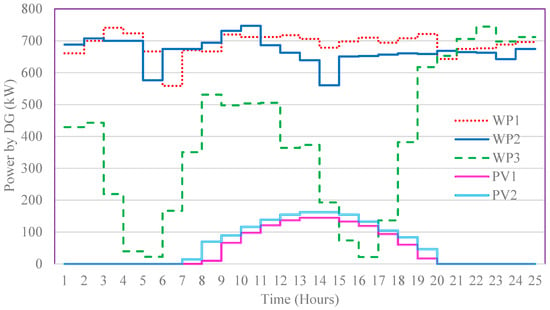
Figure 5. Hourly availability of power by intermittent DGs [4].

The load demand follows an hourly trend, given in Table 1 [4]. It can be noted that the load peaks between hour 18 and hour 23. The electricity price (from the main grid) is given in Table 1. Furthermore, the coefficients of the cost function of different DGs are tabulated in Table 2 [4]. These coefficients are based on the technology used for each DG.

Table 1. Load demand [4] and electricity price per hour.

Hour	Load (kW)	Electricity Price ($/kWh)
1	1471	0.043
2	1325	0.035
3	1263	0.026
4	1229	0.022
5	1229	0.022
6	1321	0.038
7	1509	0.043
8	1663	0.07
9	1657	0.28
10	1643	0.744
11	1643	0.744
12	1652	0.744
13	1666	0.28
14	1639	0.744
15	1642	0.372
16	1640	0.363
17	1676	0.112
18	1920	0.077
19	2214	0.065
20	2382	0.079
21	2382	0.235
22	2327	0.1
23	2174	0.056
24	1903	0.048

Table 2. Cost coefficients of DG [4].

Plant	WP1	WP2	WP3	PV1	PV2	CHP
α	0.0027	0.0028	0.0026	0.0055	0.0055	0.0083
β	17.83	17.54	17.23	29.3	29.58	75.73
γ	4.46	4.45	4.44	4.45	4.46	5.21

6.1.1. Case 1 (Scenario 1)

It is assumed that renewable energy sources will never run out and, therefore, the microgrid will never need to rely on battery storage, virtual power plants, or the utility grid. The optimization results for the first scenario are presented in Table 3. In this table, the first column represents the hour of the day, the second set of columns represent the power of each unit, the third set of columns represents the cost needed to generate the required power for each unit, and the last column represents the total cost of generating the required load at each hour.

Table 3. Optimal energy management (powers and costs) obtained by the EEMS using EMVPA for Case 1.

Hour	Power (kW)						Cost ($)						Total Cost ($)
	WP1	WP2	WP3	PV1	PV2	CHP	WP1	WP2	WP3	PV1	PV2	CHP
1	351	690	430	0	0	0	10.719	16.554	11.849	0	0	0	39.122
2	615	710	0	0	0	0	15.426	16.905	0	0	0	0	32.331
3	563	700	0	0	0	0	14.499	16.729	0	0	0	0	31.229
4	529	700	0	0	0	0	13.893	16.729	0	0	0	0	30.622
5	649	580	0	0	0	0	16.033	14.624	0	0	0	0	30.657
6	471	680	170	0	0	0	12.859	16.378	7.369	0	0	0	36.606
7	478	680	351	0	0	0	12.983	16.378	10.488	0	0	0	39.850
8	428	700	535	0	0	0	12.092	16.729	13.659	0	0	0	42.480
9	422	735	500	0	0	0	11.985	17.343	13.056	0	0	0	42.384
10	383	750	510	0	0	0	11.289	17.607	13.228	0	0	0	42.124
11	440	690	513	0	0	0	12.306	16.554	13.280	0	0	0	42.139
12	615	667	370	0	0	0	15.426	16.150	10.815	0	0	0	42.392
13	649	642	375	0	0	0	16.033	15.712	10.902	0	0	0	42.646
14	682	562	200	147	48	0	16.621	14.308	7.886	8.757	5.880	0	53.453
15	702	655	0	135	150	0	16.978	15.940	0	8.406	8.897	0	50.221
16	715	656	24.950	122	122.050	0	17.210	15.957	4.870	8.025	8.070	0	54.132
17	697	661	140	97	81	0	16.889	16.045	6.852	7.292	6.856	0	53.934
18	713	666	385	0	0	156	17.174	16.133	11.074	0	0	17.024	61.405
19	725	660	620	0	0	209	17.388	16.028	15.124	0	0	21.038	69.577
20	650	672	660	0	0	400	16.051	16.238	15.813	0	0	35.503	83.605
21	678	670	710	0	0	324	16.550	16.203	16.675	0	0	29.747	79.175
22	682	665	750	0	0	230	16.621	16.115	17.364	0	0	22.628	72.729
23	691	645	700	0	0	138	16.782	15.764	16.502	0	0	15.661	64.709
24	504	680	719	0	0	0	13.447	16.378	16.830	0	0	0	46.655

Figure 6 shows the optimal energy management among all DGs as optimized by the EMVPA, MVPA, PSO, GA, BH, ABC, and EM, over the course of 24 hours. Basically, these graphs indicate the power produced by each DG at a given hour. It can be noted that for all algorithms, the sum of power produced by all DGs equals the load demand, maintaining the load demand balance.

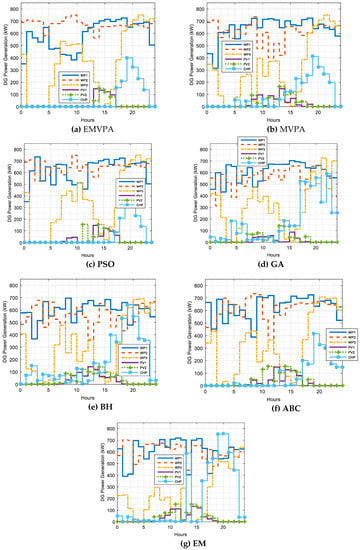
Figure 6. Optimal scheduling of DGs for Case 1 using tested algorithms.

The total costs per hour obtained by the EMS using different algorithms are given in detail in Table 4 which are also illustrated in Figure 7. The last row of this table gives the total cost for 24 hours. Total cost obtained using the EMVPA is $1184.18, which is the lowest among the tested algorithms. The second-best algorithm for Case 1 is PSO which gives a total cost of $1230.709, while the third algorithm, the ABC, gives a total cost of $1323.594. It can also be seen from Table 4 that the EMVPA achieved better results at any hour, which gives the minimum cost of EEMS, being the best power system scheduling solution at any instant.

Table 4. Total cost per hour obtained by the EMS using tested algorithms for Case 1.

	EMVPA	MVPA	PSO	GA	BH	ABC	EM
1	39.122	39.172	39.122	46.999	44.557	39.241	47.422
2	32.331	36.590	32.331	42.318	46.246	36.588	41.890
3	31.229	35.653	31.278	42.729	49.520	36.566	43.255
4	30.622	30.645	30.622	41.653	42	35.042	41.267
5	30.657	30.663	30.657	50.974	45.034	35.096	40.695
6	36.606	45.128	36.613	46.338	45.977	43.162	42.595
7	39.850	39.938	39.953	58.745	51.906	44.410	50.187
8	42.480	55.093	47.158	58.655	60.901	47.079	57.563
9	42.384	53.346	47.349	59.139	58.794	52.454	58.157
10	42.124	52.650	47.188	59.429	59.710	46.973	58.546
11	42.139	55.690	46.647	58.287	65.156	48.325	59.173
12	42.392	53.266	48.685	60.439	59.135	53.752	59.903
13	42.646	47.844	47.279	57.679	61.281	53.768	57.399
14	53.453	63.523	53.453	63.713	68.693	65.085	92.087
15	50.221	65.096	53.757	68.912	64.259	54.586	59.931
16	54.132	65.927	54.132	66.193	68.696	59.799	59.456
17	53.934	70.984	59.726	66.129	81.586	62.367	78.585
18	61.405	73.136	68.308	91.969	82.236	64.055	91.664
19	69.577	81.472	69.578	97.152	97.700	77.199	98.356
20	83.605	84.283	83.605	88.555	97.660	84.494	104.155
21	79.175	79.272	79.175	92.646	92.320	79.412	104.322
22	72.729	74.843	72.729	79.393	80.878	76.817	94.007
23	64.709	68.251	64.709	91.059	77.448	66.764	82.545
24	46.655	46.694	46.655	66.587	53.742	60.560	54.157
Total cost ($)	1184.177	1349.159	1230.709	1555.692	1555.435	1323.594	1577.317

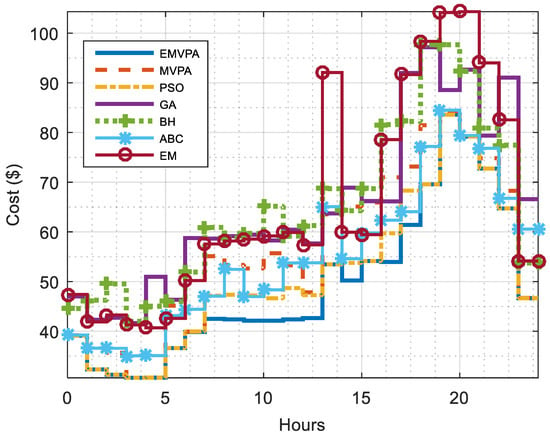
Figure 7. Total cost per hour obtained by the EMS using tested algorithms for Case 1.

6.1.2. Case 2 (Scenario 2)

The load given in Table 1 is assumed to be increased by 10% and the CHP is not operated. Table 5 provides the optimization results for this case. It can be seen that the EEMS buys power from the main grid only when there is a deficit of power (in hour 5 and hour 6, for instance). In such cases all DGs must run at their maximum capacity.

Table 5. Optimal energy management (powers and costs) obtained by the EEMS using EMVPA for Case 2.

Hour	Power (kW)						Cost ($)						Total Cost ($)
	WP1	WP2	WP3	PV1	PV2	Grid	WP1	WP2	WP3	PV1	PV2	Grid
1	498.100	690	430	0	0	0	13.342	16.554	11.849	0	0	0	41.745
2	302.500	710	445	0	0	0	9.854	16.905	12.108	0	0	0	38.866
3	689.300	700	0	0	0	0	16.752	16.729	0	0	0	0	33.481
4	651.900	700	0	0	0	0	16.085	16.729	0	0	0	0	32.814
5	670	580	21	0	0	80.900	16.407	14.624	4.802	0	0	1.554	35.833
6	560	680	170	0	0	43.100	14.446	16.378	7.369	0	0	1.412	38.193
7	628.900	680	351	0	0	0	15.674	16.378	10.488	0	0	0	42.541
8	594.300	700	535	0	0	0	15.057	16.729	13.659	0	0	0	45.445
9	587.700	735	500	0	0	0	14.940	17.343	13.056	0	0	0	45.339
10	547.300	750	510	0	0	0	14.219	17.607	13.228	0	0	0	45.054
11	604.300	690	513	0	0	0	15.236	16.554	13.280	0	0	0	45.069
12	720	667	370	60.200	0	0	17.299	16.150	10.815	6.214	0	0	50.479
13	710	642	375	105.600	0	0	17.121	15.712	10.902	7.544	0	0	51.278
14	682	562	200	147	166	45.900	16.621	14.308	7.886	8.757	9.370	29.668	56.943
15	702	655	75	135	155	84.200	16.978	15.940	5.732	8.406	9.045	27.212	56.101
16	715	656	25	122	135	151	17.210	15.957	4.871	8.025	8.453	47.606	54.516
17	697	661	140	97	110	138.600	16.889	16.045	6.852	7.292	7.714	13.469	54.792
18	713	666	385	62	86	200	17.174	16.133	11.074	6.267	7.004	13.334	57.652
19	725	660	620	20	50	360.400	17.388	16.028	15.124	5.036	5.939	20.363	59.514
20	650	672	660	0	0	638.200	16.051	16.238	15.813	0	0	43.991	48.102
21	678	670	710	0	0	562.200	16.550	16.203	16.675	0	0	114.987	49.428
22	682	665	750	0	0	462.700	16.621	16.115	17.364	0	0	40.260	50.101
23	691	645	700	0	0	355.400	16.782	15.764	16.502	0	0	17.269	49.049
24	694.300	680	719	0	0	0	16.841	16.378	16.830	0	0	0	50.049

The results obtained using the EMVPA are compared with the results optimized by the other algorithms as shown in Table 6 and Figure 8. The total cost obtained by the EEMS using the EMVPA is the lowest (equally with PSO) among the tested algorithms at $1132.384. The initial version of the MVPA ranks third at an operating cost of $1137.679.

Table 6. Total cost per hour obtained by the EMS using tested algorithms for Case 2.

	EMVPA	MVPA	PSO	GA	BH	ABC	EM
1	41.745	41.745	41.745	41.754	41.764	41.745	41.748
2	38.866	38.867	38.866	38.872	38.912	38.866	38.888
3	33.481	33.481	33.481	37.806	37.819	33.486	37.840
4	32.814	32.814	32.814	32.827	37.241	32.834	37.240
5	35.833	35.833	35.833	35.833	35.781	35.833	35.833
6	38.193	38.193	38.193	38.193	38.105	38.193	38.193
7	42.541	42.541	42.541	47.021	47.038	42.554	47.098
8	45.445	45.445	45.445	54.414	54.656	50.026	54.556
9	45.339	45.339	45.339	54.746	54.808	50.601	55.134
10	45.054	49.869	45.054	54.695	54.656	50.797	55.212
11	45.069	45.088	45.069	54.735	54.918	50.781	54.744
12	50.479	50.484	50.479	55.396	56.027	55.402	55.082
13	51.278	51.735	51.278	55.893	56.615	55.950	55.756
14	56.943	56.943	56.943	56.931	56.233	56.943	56.943
15	56.101	56.101	56.101	56.093	55.409	56.101	56.101
16	54.516	54.516	54.516	54.509	53.884	54.516	54.516
17	54.792	54.792	54.792	54.786	54.389	54.792	54.792
18	57.652	57.652	57.652	57.644	56.778	57.652	57.652
19	59.514	59.514	59.514	59.514	58.866	59.514	59.514
20	48.102	48.102	48.102	48.102	47.878	48.102	48.102
21	49.428	49.428	49.428	49.428	49.201	49.428	49.428
22	50.101	50.101	50.101	50.101	50.021	50.101	50.101
23	49.049	49.049	49.049	49.049	48.865	49.049	49.049
24	50.049	50.049	50.049	50.049	49.839	50.049	50.050
Total cost ($)	1132.384	1137.679	1132.384	1188.392	1189.702	1163.316	1193.572

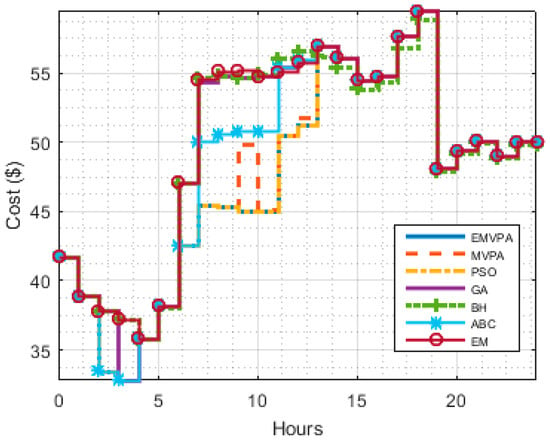
Figure 8. Total cost per hour obtained by the EMS using tested algorithms for Case 2.

6.1.3. Case 3 (Scenario 3)

The operating strategy of this case is identical to that of the case using Scenario 2 in the previous subsection. However, this case differs from Case 2 in that the storage capability is available. The optimization of the microgrid under Scenario 3 was completed and the results are provided in Table 7. It can be noted that when there is a surplus of power from the DGs, the battery is charged on an hourly basis, as for hour 1 and hour 2. However, the battery cannot exceed its maximum charging capacity. For this reason, the battery is no longer being charged in hour 3 and hour 4. Moreover, when there is a deficit of power from the DGs sources, in hour 6 for example, the battery is discharged and used as a second source of power after DGs. However, when the DGs and battery together cannot supply the load, the power is bought from the grid; hours 19 and 20 serve as an example for this situation.

Table 7. Optimal energy management (powers and costs) obtained by the EMS using EMVPA for Case 3.

Hour	Power (kW)							Cost ($)						Total Cost ($)
	WP1	WP2	WP3	PV1	PV2	Battery	Grid	WP1	WP2	WP3	PV1	PV2	Grid
1	665.0	690.0	430.0	0.0	0.0	0.0	0.0	16.318	16.554	11.849	0	0	0	44.721
2	435.6	710.0	445.0	0.0	0.0	166.9	0.0	12.227	16.905	12.108	0	0	0	41.240
3	689.3	700.0	0.0	0.0	0.0	300.0	0.0	16.752	16.729	0	0	0	0	33.481
4	651.9	700.0	0.0	0.0	0.0	300.0	0.0	16.085	16.729	0	0	0	0	32.814
5	670.0	580.0	21.0	0.0	0.0	300.0	0.0	16.407	14.624	4.802	0	0	0	35.833
6	560.0	680.0	170.0	0.0	0.0	219.1	0.0	14.446	16.378	7.369	0	0	0	38.193
7	672.0	680.0	351.0	0.0	16.0	176.0	0.0	16.443	16.378	10.488	0	4.933	0	48.243
8	659.2	700.0	535.0	0.0	0.0	235.1	0.0	16.215	16.729	13.659	0	0	0	46.603
9	587.7	735.0	500.0	0.0	0.0	300.0	0.0	14.940	17.343	13.056	0	0	0	45.339
10	547.3	750.0	510.0	0.0	0.0	300.0	0.0	14.219	17.607	13.228	0	0	0	45.054
11	604.3	690.0	513.0	0.0	0.0	300.0	0.0	15.236	16.554	13.280	0	0	0	45.069
12	720.0	667.0	370.0	60.2	0.0	300.0	0.0	17.299	16.150	10.815	6.214	0	0	50.479
13	710.0	642.0	375.0	105.6	0.0	300.0	0.0	17.121	15.712	10.902	7.544	0	0	51.278
14	682.0	562.0	200.0	147.0	166.0	300.0	0.0	16.621	14.308	7.886	8.757	9.370	0	56.943
15	702.0	655.0	75.0	135.0	155.0	254.1	0.0	16.978	15.940	5.732	8.406	9.045	0	56.101
16	715.0	656.0	25.0	122.0	135.0	169.9	0.0	17.210	15.957	4.871	8.025	8.453	0	54.516
17	697.0	661.0	140.0	97.0	110.0	18.9	119.7	16.889	16.045	6.852	7.292	7.714	11.632	54.792
18	713.0	666.0	385.0	62.0	86.0	0.0	200.0	17.174	16.133	11.074	6.267	7.004	13.334	57.652
19	725.0	660.0	620.0	20.0	50.0	0.0	360.4	17.388	16.028	15.124	5.036	5.939	20.363	59.514
20	650.0	672.0	660.0	0.0	0.0	0.0	638.2	16.051	16.238	15.813	0	0	43.991	48.102
21	678.0	670.0	710.0	0.0	0.0	0.0	562.2	16.550	16.203	16.675	0	0	114.987	49.428
22	682.0	665.0	750.0	0.0	0.0	0.0	462.7	16.621	16.115	17.364	0	0	40.260	50.101
23	691.0	645.0	700.0	0.0	0.0	0.0	355.4	16.782	15.764	16.502	0	0	17.269	49.049
24	700.0	680.0	719.0	0.0	0.0	0.0	0.0	16.942	16.378	16.830	0	0	0	50.151

The total costs per hour obtained by the EMS using the investigated algorithms are tabulated in Table 8 and sketched in Figure 9. The total cost obtained using the EMVPA is $1144.694, which is the lowest cost among the algorithms. The second-best algorithm for Case 3 is the PSO which gives a total cost of $1144.695, whilst the third algorithm is the MVPA, which has a total cost of $1154.013. It can also be seen from Table 8 that the EMVPA achieved better results than the tested algorithms at any hour.

Table 8. Total costs per hour obtained by the EMS using tested algorithms for Case 3.

	EMVPA	MVPA	PSO	GA	BH	ABC	EM
1	44.721	44.721	44.721	44.721	44.594	44.721	44.721
2	41.240	41.240	41.240	41.350	41.412	41.312	41.296
3	33.481	33.482	33.481	37.842	37.829	37.824	37.921
4	32.814	32.814	32.814	37.258	37.238	32.824	37.257
5	35.833	35.833	35.833	35.833	35.757	35.833	35.833
6	38.193	38.193	38.193	38.193	38.059	38.193	38.193
7	48.243	48.243	48.243	48.242	47.849	48.243	48.243
8	46.603	46.603	46.603	55.931	56.656	51.129	55.627
9	45.339	45.339	45.339	54.533	54.662	50.313	55.305
10	45.054	49.737	45.054	55.163	54.434	45.081	55.116
11	45.069	45.133	45.069	54.810	54.999	50.330	55.587
12	50.479	50.561	50.479	56.093	56.304	51.404	55.815
13	51.278	55.767	51.278	56.621	56.649	52.049	56.061
14	56.943	56.943	56.943	56.938	56.072	56.943	56.943
15	56.101	56.101	56.101	56.092	55.302	56.101	56.101
16	54.516	54.516	54.516	54.509	53.931	54.516	54.516
17	54.792	54.792	54.792	54.786	54.389	54.792	54.792
18	57.652	57.652	57.652	57.644	56.778	57.652	57.652
19	59.514	59.514	59.514	59.514	58.866	59.514	59.514
20	48.102	48.102	48.102	48.102	47.878	48.102	48.102
21	49.428	49.428	49.428	49.428	49.201	49.428	49.428
22	50.101	50.101	50.101	50.101	50.021	50.101	50.101
23	49.049	49.049	49.049	49.049	48.865	49.049	49.049
24	50.150	50.151	50.151	50.151	49.839	50.151	50.151
Total cost ($)	1144.694	1154.013	1144.695	1202.903	1197.586	1165.605	1203.325

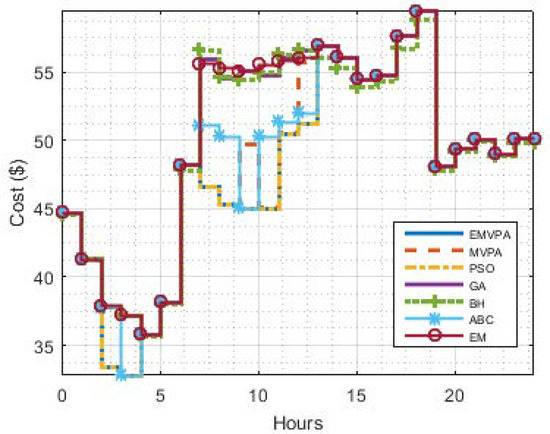
Figure 9. Total cost per hour obtained by the EMS using tested algorithms for Case 3.

6.2. Microgrid #2

To assess the performance of the proposed EEMS on a large-scale test system, a second microgrid is considered as shown in Figure 10. The microgrid consists of a load area represented by the 141-bus test system with 14 DGs, a CHP, and a storage battery source. The data used for the second system is given in Table 9 and Table 10.

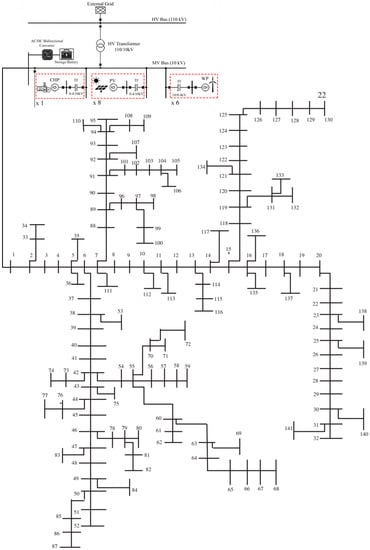
Figure 10. Schematic of power system with fourteen DGs and 141-node test feeder.

Table 9. Load demand [43] and electricity prices per hour.

Hour	Load (kW)	Electricity Price ($/kW h)
1	3482	0.043
2	2946	0.035
3	2761	0.026
4	2558	0.022
5	2541	0.022
6	2616	0.038
7	3635	0.043
8	4339	0.07
9	4748	0.28
10	5100	0.744
11	5231	0.744
12	5306	0.744
13	5454	0.28
14	5215	0.744
15	5363	0.372
16	5383	0.363
17	5198	0.112
18	5051	0.077
19	4496	0.065
20	5275	0.079
21	5479	0.235
22	5536	0.1
23	5370	0.056
24	4611	0.048

Table 10. Cost coefficients of DG.

Plant	WP1	WP2	WP3	WP4	WP5	WP6	PV1	PV2	PV3	PV4	PV5	PV6	PV7	PV8	CHP
α	0.0027	0.0028	0.0026	0.0028	0.0026	0.0026	0.0055	0.0055	0.0055	0.0055	0.0055	0.0055	0.0055	0.0055	0.0083
β	17.83	17.54	17.23	17.54	17.23	17.23	29.3	29.58	29.3	29.58	29.3	29.58	29.3	29.58	75.73
γ	4.46	4.45	4.44	4.45	4.44	4.44	4.45	4.46	4.45	4.46	4.45	4.46	4.45	4.46	5.21

Case 4 (Scenario 3)

This case simulates the operating strategy of Scenario 3 in Figure 2, as analyzed in Case 3 of microgrid #1. The optimization results obtained using the EMVPA are provided in detail in Table 11 and Table 12. It can be seen from Table 11 that when the capacity of the DGs is greater than the load, the battery is charged in hour 1 and hour 18. The grid is needed only when the DGs and battery cannot supply the requested power as given in hours 15, 16, and 17.

Table 11. Optimal energy management (powers) obtained by the EMS using EMVPA for Case 4.

Hour	WP1	WP2	WP3	WP4	WP5	WP6	PV1	PV2	PV3	PV4	PV5	PV6	PV7	PV8	CHP	Battery	Grid
1	665	689.972	430	690	690	430	0	0	0	0	0	0	0	0	187.028	0	0
2	0	710	437.592	648.137	705.271	445	0	0	0	0	0	0	0	0	0	300	0
3	661	700	0	700	700	0	0	0	0	0	0	0	0	0	0	300	0
4	458	700	0	700	700	0	0	0	0	0	0	0	0	0	0	300	0
5	670	579.350	0	580	580	0	0	0	0	0	0	0	0	0	131.650	300	0
6	406.007	679.993	170	680	680	0	0	0	0	0	0	0	0	0	0	300	0
7	672	672.772	317	679.755	680	351	0	14.855	0	15.973	0	0	0	0	231.646	300	0
8	668	700	535	700	700	535	10	72	0	72	0	0	0	0	347	300	0
9	723	735	496.003	733.011	735	499.993	57.667	91.517	0	0	0	16.097	0	91.964	568.749	300	0
10	715	750	506.635	750	749.441	510	99.480	117.569	0	118	41.036	110.046	19.780	117.904	495.109	300	0
11	674.770	689.972	513	690	689.985	513	123	142	123	142	123	0	100.213	142	565.060	300	0
12	720	667	370	667	667	370	140.897	144.450	139.038	156	140.996	156	141	0	826.619	300	0
13	710	642	375	642	642	375	149	166	149	166	149	166	149	160.826	813.174	300	0
14	682	562	200	562	562	200	147	166	147	166	147	166	147	166	1000	300	0
15	702	655	75	655	655	75	135	155	135	155	135	155	135	155	1000	105	281
16	715	656	25	656	656	25	122	135	122	135	122	135	122	135	1000	0	622
17	697	661	140	661	661	140	97	110	97	110	97	110	97	110	1000	0	410
18	713	666	385	666	666	385	62	86	62	86	62	86	62	86	1000	0	0
19	554.010	660	620	660	660	619.991	0	0	0	0	0	0	0	0	1000	22	0
20	650	672	660	672	672	660	0	0	0	0	0	0	0	0	1000	300	0
21	678	670	710	670	670	710	0	0	0	0	0	0	0	0	1000	11	360
22	682	665	750	665	665	750	0	0	0	0	0	0	0	0	1000	0	359
23	691	645	700	645	645	700	0	0	0	0	0	0	0	0	1000	0	344
24	700	680	719	680	680	719	0	0	0	0	0	0	0	0	733	0	0

Table 12. Optimal energy management (costs) obtained by the EMS using EMVPA for Case 4.

Hour	WP1	WP2	WP3	WP4	WP5	WP6	PV1	PV2	PV3	PV4	PV5	PV6	PV7	PV8	CHP	Grid	Total Cost ($)
1	16.318	16.553	11.849	16.554	16.554	11.849	0	0	0	0	0	0	0	0	19.374	0	109.052
2	0	16.905	11.980	15.819	16.822	12.108	0	0	0	0	0	0	0	0	0	0	73.634
3	16.247	16.729	0	16.729	16.729	0	0	0	0	0	0	0	0	0	0	0	66.435
4	12.627	16.729	0	16.729	16.729	0	0	0	0	0	0	0	0	0	0	0	62.815
5	16.407	14.613	0	14.624	14.624	0	0	0	0	0	0	0	0	0	15.180	0	75.448
6	11.700	16.378	7.369	16.378	16.378	0	0	0	0	0	0	0	0	0	0	0	68.204
7	16.443	16.252	9.902	16.374	16.378	10.488	0	4.899	0	4.932	0	0	0	0	22.753	0	118.422
8	16.372	16.729	13.659	16.729	16.729	13.659	4.743	6.590	0	6.590	0	0	0	0	31.489	0	143.289
9	17.353	17.343	12.987	17.309	17.343	13.056	6.140	7.167	0	0	0	4.936	0	7.180	48.284	0	169.097
10	17.210	17.607	13.170	17.607	17.597	13.228	7.365	7.938	0	7.951	5.652	7.715	5.030	7.948	42.707	0	188.722
11	16.492	16.553	13.280	16.554	16.554	13.280	8.054	8.660	8.054	8.660	8.054	0	7.386	8.660	48.005	0	198.247
12	17.299	16.150	10.815	16.150	16.150	10.815	8.578	8.733	8.524	9.075	8.581	9.075	8.581	0	67.816	0	216.344
13	17.121	15.712	10.902	15.712	15.712	10.902	8.816	9.370	8.816	9.370	8.816	9.370	8.816	9.217	66.797	0	225.449
14	16.621	14.308	7.886	14.308	14.308	7.886	8.757	9.370	8.757	9.370	8.757	9.370	8.757	9.370	80.948	0	228.778
15	16.978	15.940	5.732	15.940	15.940	5.732	8.406	9.045	8.406	9.045	8.406	9.045	8.406	9.045	80.948	90.814	317.827
16	17.210	15.957	4.871	15.957	15.957	4.871	8.025	8.453	8.025	8.453	8.025	8.453	8.025	8.453	80.948	196.098	417.782
17	16.889	16.045	6.852	16.045	16.045	6.852	7.292	7.714	7.292	7.714	7.292	7.714	7.292	7.714	80.948	39.844	259.545
18	17.174	16.133	11.074	16.133	16.133	11.074	6.267	7.004	6.267	7.004	6.267	7.004	6.267	7.004	80.948	0	221.751
19	14.339	16.028	15.124	16.028	16.028	15.123	0	0	0	0	0	0	0	0	80.948	0	173.617
20	16.051	16.238	15.813	16.238	16.238	15.813	0	0	0	0	0	0	0	0	80.948	0	177.339
21	16.550	16.203	16.675	16.203	16.203	16.675	0	0	0	0	0	0	0	0	80.948	73.631	253.087
22	16.621	16.115	17.364	16.115	16.115	17.364	0	0	0	0	0	0	0	0	80.948	31.237	211.880
23	16.782	15.764	16.502	15.764	15.764	16.502	0	0	0	0	0	0	0	0	80.948	16.715	194.743
24	16.942	16.378	16.830	16.378	16.378	16.830	0	0	0	0	0	0	0	0	60.725	0	160.462

The total costs obtained by the EMS using the investigated algorithms are shown in Table 13. A simple comparison between the different algorithms shows that the EMVPA has the lowest total cost of $ 3883.633 followed by the PSO and the ABC, which give $3940.981 and $3989.233, respectively. This result again demonstrates the superiority of the EEMS based on the EMVPA compared to the other algorithms.

Table 13. Total cost per hour obtained by the EMS using tested algorithms for Case 4.

	EMVPA	MVPA	PSO	GA	BH	ABC	EM
1	109.052	131.097	109.051	149.420	140.238	119.882	146.214
2	73.634	88.327	73.632	104.006	93.852	88.178	87.882
3	66.435	75.267	75.082	104.293	99.423	86.126	108.663
4	62.815	81.638	71.697	101.301	93.807	83.835	97.278
5	75.448	109.561	87.637	105.112	106.625	83.099	112.875
6	68.204	100.136	68.226	96.122	93.333	72.623	88.867
7	118.422	128.738	126.987	158.330	154.699	124.681	165.397
8	143.289	174.430	151.824	189.479	190.573	158.646	195.657
9	169.097	179.052	173.734	210.983	203.663	174.360	206.838
10	188.722	204.723	186.305	209.471	216.408	181.923	217.271
11	198.247	208.734	197.381	222.841	221.767	194.220	222.691
12	216.344	220.478	219.896	229.937	220.997	213.539	226.406
13	225.449	228.701	229.613	234.735	220.379	225.563	234.122
14	228.778	228.778	228.778	225.685	210.226	228.778	228.778
15	227.013	227.013	227.013	224.785	213.111	227.013	227.013
16	221.684	221.684	221.684	219.751	206.573	221.684	221.684
17	219.701	219.701	219.701	217.352	206.913	219.701	219.701
18	221.751	221.751	221.751	219.166	208.851	221.751	221.751
19	173.617	187.769	175.060	209.117	208.643	187.023	208.273
20	177.339	177.339	177.339	177.125	171.369	177.339	177.339
21	179.457	179.457	179.457	179.331	173.082	179.457	179.457
22	180.644	180.644	180.644	180.422	173.329	180.644	180.644
23	178.028	178.028	178.028	177.809	169.839	178.028	178.028
24	160.462	160.502	160.462	169.719	174.178	161.139	164.167
Total cost ($)	3883.633	4113.548	3940.981	4316.291	4171.878	3989.233	4316.997

6.3. Daily Cost Reduction Analysis

Table 14 presents the percentage of daily cost reduction obtained using EMVPA compared with the remaining algorithms. It can be observed from this table that the EMVPA presents high-cost reductions for Case 1 and Case 4 and moderate cost reductions for Case 2 and Case 3. The highest cost reduction percentage is obtained for Case 1 compared to the EM. For Case 2 and Case 3, the results of the EMVPA and the PSO are almost identical. These results confirm the superiority of the EMVPA compared with the other algorithms at optimizing the energy management of microgrids.

Table 14. Comparison of daily cost reduction using EMVPA with the other algorithms.

Case	MVPA	PSO	GA	BH	ABC	EM
Case 1	12.229%	3.781%	23.881%	23.868%	10.533%	24.925%
Case 2	0.465%	0.000%	4.713%	4.818%	2.659%	5.126%
Case 3	0.808%	0.000%	4.839%	4.417%	1.794%	4.872%
Case 4	5.589%	1.455%	10.024%	6.909%	2.647%	10.039%

Moreover, it is worth mentioning that, for microgrid #1 the calculation speed of the EMVPA is around 12 s per hour while for the calculation speed for microgrid #2 is around 23 s per hour.

7. Conclusions

In this paper, an EEMS based on an enhanced version of the most valuable player algorithm is proposed and developed to optimize the operation of a microgrid by minimizing the operating cost. The EEMS aims to schedule different sources of energy based on a selected scenario. In the first scenario, the power generated from DGs is always greater than the requested load. In the second scenario, the EEMS can buy energy from the grid only when the DGs cannot supply the requested load. In the last scenario, a battery storage is added to the microgrid, which is the second source of power after DGs, while the main grid is the last option. It is obvious that more scenarios can be added to the EEMS in the future.

In comparison to other optimization algorithms, the proposed EEMS using the EMVPA achieves better results and can determine the optimal scheduling of different DGs, battery storage, and the power needed from the grid based on the selected scenario. Moreover, four cases for two different microgrids were investigated. For Case 1, the daily cost reduction varies from 3.781% for the PSO (the second-best method after the EMVPA) to 24.925% for the EM (the worst method for this case). Likewise, for Case 2, it varies from 0% for the PSO to 5.126% for the EM. For Case 3, it varies from 0% for the PSO to 4.872% for the EM. Finally, for Case 4, the daily cost reduction varies from 1.455% for the PSO to 10.039% for the EM. Furthermore, it is found that the EEMS using the proposed EMVPA provides the most cost-effective solution for each hour ensuring its efficacy and robustness. Since energy markets are moving towards real-time pricing, such a modified approach is highly desirable to effectively address power-sharing problems.

The optimization results using the proposed method is expected to give an optimal energy management system strategy, which will assist energy practitioners in managing generation units and energy storage devices in renewable energy based microgrids. Furthermore, the results of this study may have implications for future implementation of microgrid projects and renewable energy resources development in general.

Further research is recommended in the following areas: Additional scenarios can be investigated and the influence of the efficiency of forecasting models can be assessed, while unbalanced microgrid systems can also be investigated. Also, uncertainty modeling of load demands and renewable generation can be included in these models.