rl4dtn: Q-Learning for Opportunistic Networks

Abstract

Opportunistic networks are highly stochastic networks supported by sporadic encounters between mobile devices. To route data efficiently, opportunistic-routing algorithms must capitalize on devices’ movement and data transmission patterns. This work proposes a routing method based on reinforcement learning, specifically Q-learning. As usual in routing algorithms, the objective is to select the best candidate devices to put forward once an encounter occurs. However, there is also the possibility of not forwarding if we know that a better candidate might be encountered in the future. This decision is not usually considered in learning schemes because there is no obvious way to represent the temporal evolution of the network. We propose a novel, distributed, and online method that allows learning both the network’s connectivity and its temporal evolution with the help of a temporal graph. This algorithm allows learning to skip forwarding opportunities to capitalize on future encounters. We show that explicitly representing the action for deferring forwarding increases the algorithm’s performance. The algorithm’s scalability is discussed and shown to perform well in a network of considerable size.

1. Introduction

Opportunistic networks (ONs) are networks supported by mobile devices that meet sporadically. As data can only be transmitted during encounters, nodes must carry it with them for potentially prolonged periods until an opportunity to pass on the data arises. Unlike a traditional data network, ONs are formed by multiple network partitions that change continuously, and data delivery depends on multiple hops that do not necessarily form an end-to-end path at any given moment.

1.1. Applications for Opportunistic Networks

These kinds of networks (sometimes called delay- or disruption-tolerant networks—DTNs) have multiple applications. For example, sensor networks are composed of widely distributed low-cost devices that collect environmental data. This application is an important component of smart cities and Internet of Things (IoT) research [1]. The networking component is tasked with collecting all the produced data to be processed. An ON can transmit data without depending on external infrastructure, sometimes under very adverse conditions [2].

Opportunism can be used in conventional networks to reduce the load on the infrastructure and better use network devices’ computational, storage and communication resources. Device2Device (D2D) functionality allows LTE network terminals, or smartphones, to download directly from neighboring terminals instead of doing it through the cellular network [3]. That can significantly reduce latency, power consumption, and infrastructure costs [4].

There are many applications wherein vehicles want to exchange information within a vehicle fleet: Cars could warn other vehicles of a dangerous event using a vehicular ad hoc network (VANET); A team of fire-fighting robots might coordinate tasks and provide communication infrastructure while searching for survivors in a building on fire; a swarm of UAVs could communicate to keep formation; etc.

1.2. Network Properties

In general, ONs are intended to support communications over Challenged Networks [5], which are described by the following properties:

Disconnection: Nodes can be outside other nodes’ range for long periods. This can happen for single nodes or groups.

Low duty cycle: Nodes can shut down network interfaces to save battery, only briefly coming online.

Limited resources: Nodes can have limited battery power supply and low computational resources, such as CPU and storage.

Low bandwith: Usually over wireless links, subject to high losses and latencies.

The characteristics mentioned above lead to the need for long queuing times, where messages must be held in buffers for minutes, hours, or days at a time, unlike the milliseconds usual in structured networks. Because of this, routing algorithms supporting ONs are called “carry-and-forward” algorithms.

ONs are usually highly stochastic systems. There are three main sources of randomness. In the first place, mobility. While there are ONs with deterministic behavior (e.g., orbiting spaceships [6]), most mobile devices do not exactly have repeating trajectories. Examples include service robots in a warehouse, cars in a city, or people in a building.

The second source of randomness is the generation of data to be transmitted. Data generation at the nodes is usually an external process outside the control of the network.

Finally, wireless communications are subject to interference from external devices and other environmental conditions.

1.3. Performance Metrics

As a result, ONs operate under conditions hostile to data delivery, and there exists the possibility that a message will be lost. Thus, the main performance metrics of an ON are delivery rate and latency distribution. The delivery rate is the fraction of emitted messages that reach the destination. The latency is the travel time of the delivered messages. Notice that latency is only computed over messages that reach the destination. Higher delivery rates frequently depend on higher latencies, as harder-to-deliver messages must be held in the network waiting to be delivered. Because links are supported by shared and limited mediums, typically wireless, the communication overhead is also important. Excessive communications utilization can lead to the degradation of the network and thus impact the performance. The number of transmissions also impacts directly power consumption, a scarce resource in many mobile applications.

1.4. Opportunistic Algorithms

Due to the wide variety of use cases, many algorithms are developed [7]. A defining property of an ON algorithm is whether it generates extra message copies. Forwarding protocols route a single copy of the message; Flooding protocols produce multiple replicas to increase the delivery rate at the cost of increased network overhead.

Two big classes of algorithms are stateless and stateful. The former is based on efficiently disseminating the copies of a message, so it is also known as “dissemination-based”. The later algorithms collect data on the ON behavior and attempt to use this knowledge to make more effective routing decisions. Many different techniques are used. Distance-vector style algorithms are popular, but more complex methods are also proposed.

We propose using machine learning (ML) techniques, specifically reinforcement learning (RL) and Q-learning, to solve the routing problem. As we will see below, multiple works use this approach. However, our proposal uses a particular way of modeling the network that captures more information from the network’s behavior. In our previous work [8], this model was applied for ML routing in ON; however, in that work, the training was performed offline using recorded traces. In this work, the ML process is performed online, and the model is built and maintained during the network’s lifetime. We show that the application of this network model improves the network’s performance compared to the conventional Q-learning application. It is also competitive with conventional protocols, especially regarding network overhead, as it does not depend on additional traffic for routing information.

2. Related Work

One of the simplest ON algorithms is Epidemic Routing [9], a stateless and flooding-based epidemic protocol wherein messages behave as contagious diseases, infecting new devices when they are met. This method achieves the highest possible delivery rate and the lowest latency possible at the cost of a massive load on the network, as every forwarding opportunity is taken, and every node ends up with a copy of every packet.

Various algorithms improve upon Epidemic Routing to reduce the network load. For example, BSW [10] is a version of Spray and Wait [11] which proposes the following method for controlling the propagation: first, messages have attached a “number of copies” attribute, a configuration parameter set at transmission time, which controls the total number of copies of the message in the network. Then, when an “infected” node meets a non-exposed one, half of the copies are handed over and half kept by the emitter. Once a copy count reaches 1, no more forwardings are performed until the message’s final destination is encountered.

Unlike BSW, which does not collect information on the network, PRoPHET [12] attempts to learn the best forwarders for different destinations. PRoPHET is based on the exchange of distance tables between nodes in a process conceptually similar to Distance Vector protocols. The main difference is that the distance is represented by a “predictability” or delivery probability. These predictability vectors are exchanged between nodes upon meeting. The predictability of a node as a target is reinforced when meeting it and is subject to exponential decay as time passes. Furthermore, it can be transitively reinforced: when node A meets node B, then A’s predictability values for nodes in B’s table are reinforced. This transitive reinforcement is affected by the B’s own predictability. The basic idea is that nodes encountered more frequently have higher predictability, as are nodes reachable through high-predictability nodes.

This process of learning better opportunistic routes can be attacked with other methods (for an overview of current algorithms, see [7]). We consider that machine learning techniques are a promising alternative for the following reasons:

• ML is very efficient at detecting and capitalizing on patterns, which are the basis of efficient ON routing.
• ML effectiveness frequently depends on the availability of training data, which an ON can provide, as every packet can be considered an instance of the routing problem.
• ONs are complex systems with different components –such as mobility, data generation, and wireless interference– that are difficult to model and characterize. One of the ML strengths is that it can be applied without a deep understanding of the system’s dynamics.

In this work, we will discuss the application of reinforcement learning to ON routing.

3. Reinforcement and Q-Learning in Routing

Reinforcement learning (RL) is a machine learning (ML) technique based on the exploration of the solution space by learning agents. These agents interact with the environment or state through actions that produce a reward. These rewards serve as feedback to inform the agent about the appropriateness of the action in the given scenario, allowing it to learn a policy to produce optimal behavior.

Designing an RL system consists of defining the 4-tuple $<S,A,P,R>$, where S and A are the sets of states and actions; $P:S\times A\to S$ is a transition matrix, potentially stochastic. S, A, and P define a Markov decision process (MDP) described as $s_{i+1}\leftarrow \delta (s_i,a_i)$, which can be either deterministic or not. $R:S\times A\times S\to \mathbb{R}$ is the reward function that assigns a state transition value. Rewards themselves can also be either deterministic or not.

Because the rewards are obtained from a single state transition, but the agent is expected to produce an effective sequence of actions, a mechanism to calculate a global reward V is also needed. Thus, the RL problem can be described as finding the optimum policy $\pi :S\to A$ to select the best action in a given state, as to maximize a cumulative reward $V^{\pi }:S\to \mathbb{R}$ where the S indicates the starting state for applying the policy $\pi$. The sequence of states evaluated by $V^{\pi }$ must be produced by iteratively evaluating $\delta$ with the available actions in each moment. The reward itself is usually computed as the discounted cumulative reward from the produced sequence of states, starting from a state $s_0$, as:

$$V^{\pi }\left(s_0\right)\to \sum _{i=0}^{\infty }{\gamma }^i{r}_i$$

(1)

where $0\le \gamma <1$ is a parameter that controls an exponential reduction in the weight given to instant rewards $r_i$ further from the starting state.

This problem is challenging because to evaluate $V^{\pi }$, the state sequence produced by $\delta$ and the resulting rewards must be known, which is not always possible. In particular, the state transitions caused by actions or the resulting rewards might be non-deterministic.

To overcome the difficulty of optimizing a policy for an unknown sequence of states, actions, and rewards, Q-learning [13] proposes using a particular evaluation function:

$$Q(s,a)\leftarrow r(s,a)+\gamma \underset{a^{\prime }}{max}Q(\delta (s,a),a^{\prime })$$

(2)

This function says that the evaluation of an action is the sum of the immediate reward and the best achievable evaluation from the action’s target state. Notice that this is a recursive definition and that both $r(s,a)$ and $\delta (s,a)$ can be observed as they are only evaluated once in the present state s (they are sampled).

This equation iteratively approximates the Q function and obtains the associated policy in the process. For this, a learning agent stores the learned $Q(s,a)$ values in a table. Then, it repeatedly evaluates policies in epochs. After selecting an action a in state s, it updates the Q as follows:

$$\begin{array}{cc}\hfill Q(s,a)& \leftarrow (1-\alpha )Q(s,a)\hfill \\ \hfill & +\alpha (r(s,a)+\gamma \underset{a^{\prime }}{max}Q(\delta (s,a),a^{\prime })\hfill \end{array}$$

(3)

where $\alpha$ is a learning parameter controlling the convergence speed. As all actions for all states are sampled repeatedly, the Q estimation converges to the value of Equation (2) [13]. During the system’s training, the optimal known policy is to select the highest valued action in any state. As usual in ML, a balance must be found between exploitation (using the highest valued actions) and exploration (evaluating alternate actions).

The fact that Q-learning correctly takes into account the future effect of actions, and provides a policy that does not depend on previous knowledge or domain model, made it very useful for attacking the problem of routing in dynamic networks [14,15].

The first and most influential application of Q-learning to routing is Q-routing [16]. As in most RL routing protocols, the learning agent is a network node, and the Q-learning is applied in a distributed manner where each node x maintains a $Q_x$ table. Q-routing introduced several design decisions that were later applied by many other algorithms. First, Q-routing reduces a distance metric instead of maximizing a reward; $Q_x(d,y)$ is defined as the node x’s estimation of the latency from node y to destination d. Furthermore, instead of exploring the solution space by sending data packets through sub-optimal paths, Q-learning introduced a separate channel for exchanging neighboring nodes’ best Q values. When a node needs to recompute its own Q table, it will request $T_y={min}_{z\in N_y}{Q}_y(d,z)$ from all neighbors. That makes the algorithm somewhat similar to classical Bellman–Ford. Finally, node x updates its table as:

$$Q_x(d,y)\leftarrow (1-\alpha )Q_x(d,y)+\alpha (q+s+T_y)$$

(4)

where q and s are the local queue and transmission times. Notice that because the Q value represents a latency that is not subject to discounting for further away nodes, $\gamma =1$ is used.

Q-learning-based routing has been adapted to various networks [17]. We will briefly mention some of the algorithms applied to ONs.

One of the most influential Q-learning ON routing is Delay Tolerant Reinforcement-Based (DTRB) [18]. DTRB is a flooding-based algorithm wherein messages are replicated, maximizing a reward computed by a dedicated distance-table gossiping algorithm.

In DTRB, nodes maintain two tables, a table with the distances to every known node in the network and a table of rewards for every known message destination node.

The distance stored in the first table is an estimation of the time needed to propagate a message to the target node. These temporal distance tables are maintained by exchanging time-stamped control messages. These messages flood information about the last time a given node was met in the network. Then, nodes use the time elapsed as a distance measure.

This learned distance value is then used to compute a reward used in a conventional Q-learning scheme (see Equation (5)). A node computes the one-hop reward R for a given neighbor as $e^{-k}$, where k is the time-distance measure stored in the distance table or 0 if the entry is older than a configuration parameter. Then, a Q practicability of delivery value is computed as an estimation of the future rewards after taking a particular action. The discount factor ${\gamma }_x$ is dynamic, getting smaller the faster that the neighborhood of x changes. This means that the algorithm favors nodes with low mobility.

$$Q_c(d,x)\leftarrow (1-\alpha )Q_c(d,x)+\alpha (R+{\gamma }_x\times \underset{y\in N_x}{max}{Q}_x(d,y))$$

(5)

The computed rewards are distributed in the same control messages mentioned and are subject to further exponential aging. Finally, messages are replicated to nodes with higher computed Q-values than their own.

The basic idea of the algorithm is to distribute a routing metric through control messages and then use it as the immediate reward in a Q-learning scheme. The resulting Q-values are used as an estimation of the global cost of an opportunistic delivery path.

An alternative is to integrate the routing metric within the Q-tables. For example, CARL-DTN [19] is a flooding protocol that uses Q-learning to learn a Q-value associated with every destination. Q-values are updated when nodes meet or go out of range. The Q-value combines the hop count with other node characteristics such as TTL, node popularity, or remaining power. This combination is achieved using a fuzzy logic controller (FLC).

The update function for node c when meeting node x, for destination d is:

$$\begin{array}{cc}\hfill Q_c(d,x)& \leftarrow (1-\alpha )Q_c(d,x)\hfill \\ \hfill & +\alpha (R(d,x)+\gamma ·FuzzTO·\underset{y\in N_x}{max}{Q}_x(d,y))\hfill \end{array}$$

(6)

where the immediate return $R(d,x)$ is an indicator function which returns 1 if the destination d is directly reachable through x, and otherwise 0. FuzzTO is a fuzzy transfer opportunity metric that combines the social characteristics of a node and its estimated ability to complete message forwarding. When a node becomes disconnected, the associated Q-value begins to decay exponentially.

In these protocols, the Q-learning process is decoupled from the data delivery, respecting the classical separation between routing and forwarding. These depend on exchanging routing data, and in this regard, they inherit the Q-routing property of being a combination of Q-learning and a conventional routing algorithm. As a side effect, routes with associated messaging are maintained for all nodes in the network, whether there is actual traffic through them or not. Furthermore, they are only usable with destination-based routing.

Other algorithms take a more direct approach to Q-learning. In FQLRP [20], each message is considered an agent, and the set of possible states is the set of network nodes. Therefore, the set of actions available to an agent is the set of neighboring nodes at a given moment. Then, the reward is computed as a function of the current node and its neighboring nodes’ attributes, such as available buffer space and remaining energy. The idea is that the rewards express the likelihood of a successful forwarding. A modification of the basic Q-learning scheme is that the candidate nodes are first filtered through a Fuzzy Logic-Based Instant Decision Evaluation.

All these protocols share in common that Q-learning is used to select a candidate node to replicate data to, but there is no explicit action to not copy. Q-values are computed for actions, and in the usual representation, the only actions considered are forwardings.

Furthermore, no explicit notion of time or sequencing is defined, using the simple exponential decay of Q-values to express the passing of time. This precludes the system from learning that it is better to avoid copying because there is probably a better opportunity in the future. It is important because many ONs have marked temporal patterns, such as the schedules of public transport systems, the workday and weekly mobility cycles of city inhabitants, or the migration patterns of wild animals. Integrating the notion of time and sequence in the learning system would allow capitalizing on those patterns. We will evaluate the gains of this representation in Section 6.

Finally, we want to mention a related but different concept to ON, the Opportunistic Routing. This term usually refers to the ability to take advantage of overheard messages in a broadcast medium. The Opportunistic Routing application is not restricted to ONs in the sense of networks whose devices encounter sporadically. In fact, most Opportunistic Routing research concentrates on ad hoc and mesh networks, which are connected networks, though with a potentially dynamic topology.

4. ON Model

We propose to apply Q-learning to a particular representation of the ON that we presented in [8]. In this model, a special Opportunistic Network Model (ONM) graph is built, which represents both the encounters between network devices and the temporal evolution of the network. Each network device is represented in this model by a set of graph nodes. Each node of this set captures the network device’s state at the moment of an encounter with another device. In the resulting graph, there are two classes of edges: “copy” edges that link nodes belonging to different devices and represent an opportunity to copy a message from one device to another during an encounter; and “time” edges link all the nodes that model a device through time.

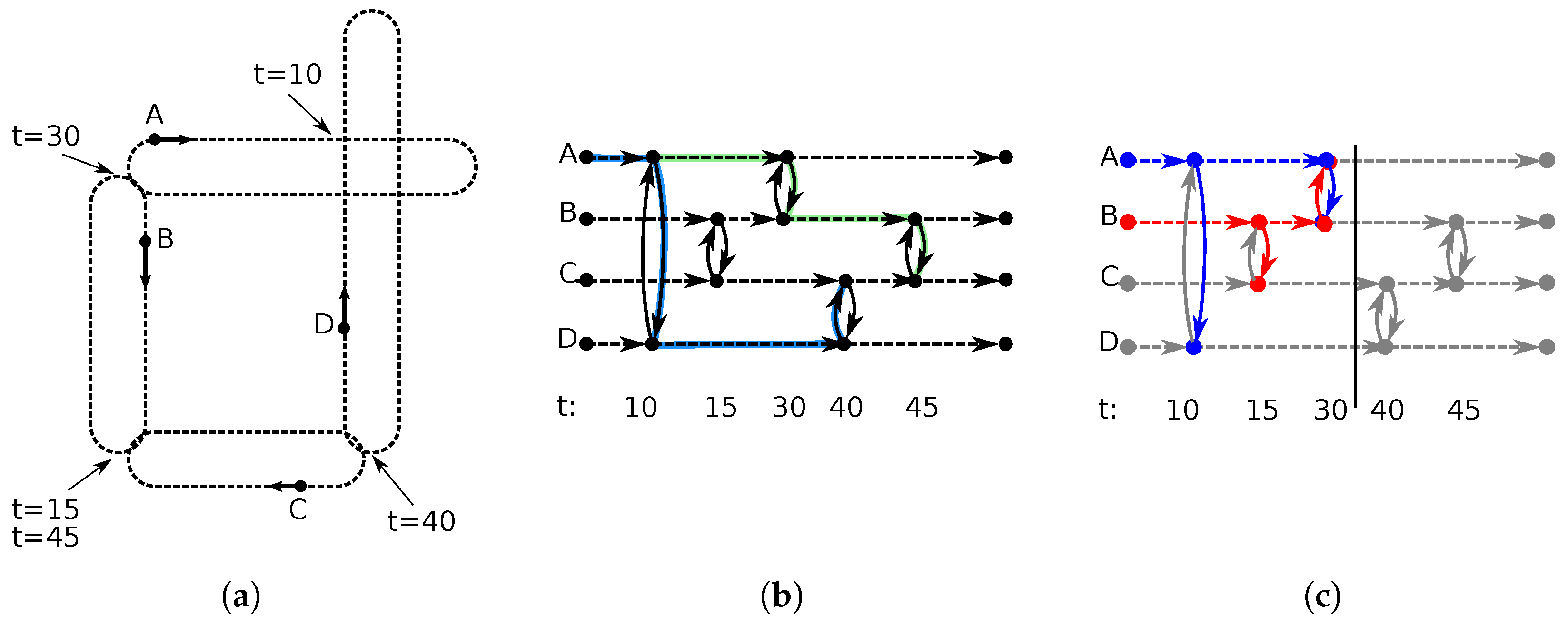
Figure 1a shows an example mobility scenario for four mobile devices, from A to D. The devices follow closed trajectories and meet at the points marked with arrows at the indicated times. In this example, devices B and C meet twice, at times 15 and 45.

The ONM graph that captures this scenario is shown in Figure 1b. Solid arrows represent encounters; dotted arrows represent time passing between encounters. The colored edges show two opportunistic paths between devices A and C.

Although this graph can be built from a complete trace of the mobility scenario, as described in [8] (useful for analyzing recorded scenarios or synthetic traces produced by simulators), in this work, the graph is built online, by the devices themselves, during the real-life scenario execution. In this case, each device builds a local view of the whole graph in a distributed manner, with only the edges it participates in. Figure 1c shows this process for devices A and B. Each device registers a local view of the graph as time passes and meetings occur. For example, in Figure 1c, the new nodes created at $t=30$ have corresponding identical pairs created in both participating devices. These duplicates will be merged if all the local views are consolidated in a single representation.

The online-build model captures the history of what happened and does not contain information on the future evolution of the network. To predict the future, in this work, we capitalize on the temporal patterns of many opportunistic networks, as seen in Section 6.

The pseudocode for the online graph construction is shown in Algorithm 1.

Algorithm 1: Distributed online ONM graph construction.

An important detail is that all the nodes associated with a single device have a single time edge, except for the last one, which has none. Furthermore, notice that time edges are added from the receiving node; this is once the edge has been “traversed”.

A path over the ONM graph represents a possible propagation trace of a message. A trajectory starting at a given node represents a new message emitted by the corresponding device at the indicated time. A message traversing a copy edge represents that the message is copied between two devices. To traverse a time edge, a message must be stored in the device’s buffer, surviving up to the destination node’s time.

In an ON, the order of encounters is critical for delivering a message. In Figure 1, the path A–D–C depends on nodes A and D encountering before D and C. This dependency is naturally represented in the ONM.

In this model, routing messages in an ON is equivalent to routing them in a static graph. Edges can have different costs associated, allowing great flexibility in the definition of optimality, as discussed in Section 5.

The model allows representing multiple simultaneous transfers if the underlying network supports them, in the form of multiple copy edges leaving or arriving at a single node. For example, a broadcast transmission would be represented by multiple copy edges leaving a single node, each reaching a different device in range. Furthermore, additional information can be stored in the graph to support learning algorithms and performance modeling. For example, nodes may have associated the location and remaining battery storage, and copy edges can be assigned radio propagation characteristics.

As mentioned before, many ON networks are not entirely random but exhibit patterns. These patterns manifest themselves in the ONM. For example, the closeness between devices reflects in more frequent copy edges, while periodic trajectories manifest as a recurrence of copy edges at specific times. This allows using the ONM as a base to apply ML techniques.

5. Algorithm

As seen in Section 2, ON Q-learning-based algorithms usually do not maintain an explicit, graph-based model of the network. More specifically, the passage of time is usually captured by a simple parameter-decay mechanism, which depends on ad hoc configuration parameters that must be selected and tuned separately, usually through simulation.

Our strategy uses an ONM as the representation of the network. The ONM is a graph, though not a connectivity one. Nevertheless, a path connecting nodes in ONM still represents a data trajectory connecting a source with a destination. A shortest-path algorithm with adequately chosen edge weights can be used to find an optimal delivery trajectory.

There are two main classes of problems wherein RL is used to find the shortest path in a graph. The first class of problems is, naturally, network routing (see Figure 2b), where the graph is the connectivity graph of the network [21]. In this representation, edges are network links, and nodes are network routers. Each graph node is an agent that makes forwarding decisions that collectively solve the routing of messages from sources to destinations. As each node is an agent, each node trains only for the available actions; this is forwarding to neighboring nodes.

The second class of problems is the robot navigation problem (see Figure 2a). In this case, the graph represents a map; for example, nodes are rooms, and edges are doors connecting rooms. The learning agent is a robot that must navigate through the map to reach a destination [15]. The agent has a policy to be trained, which dictates the next action (edge) to follow as it moves through the graph, like in a maze. Each graph node is a state in this representation, with a single Q-table attached to the single agent. The Q-table is trained by repeatedly moving through the map.

Neither of these two representations is well suited as a base for applying RL for opportunistic routing using ONM. The main problem is that the RL states coincide with the nodes from the underlying graph in both representations. As a result, though they differ in whom they consider an agent and thus how many Q-tables there are and where they are stored, the content of the Q-table is similar in both cases: it assigns a Q-value to a target graph node.

In the ONM graph representation, nodes and edges are not fixed beforehand. They are defined during the network’s lifetime and describe a single instance of the mobility scenario. Furthermore, each node is visited only once during this instance.

Thus, because the graph nodes are associated with a particular real-world instance of the network, and they are poor candidates for Q-learning actions and states, which must be usable through multiple learning episodes.

We propose rl4dtn an opportunistic routing algorithm based on applying Q-learning over an online-generated ONM graph (see Figure 3). The main characteristics are summed up in

Table 1. Reinforcement learning structure for rl4dtn algorithm.

Agent	Mobile device.
State	A (device, timeslot) pair, where the time is divided into set time slots.
Action	Connect two states, either on the same device (store data) or another (forward data).
Evaluation time	Encounter between devices (i.e., ONM node).
Q-Metric and task	Minimization of a distance metric.
Determinism	States and actions are non-deterministic.

.

5.1. States and Actions

In our approach, each network device is an agent and maintains the Q-table for all the associated system states and possible actions from its point of view.

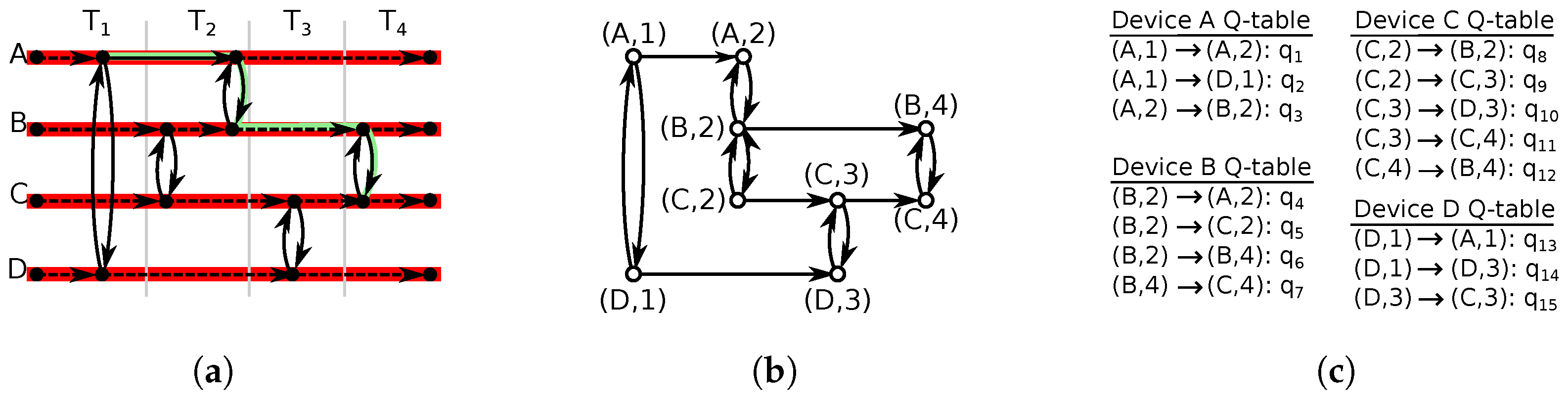
Because the optimum action to choose depends on the time at which the agent is, we divide the scenario’s duration into time slots (see Figure 3a) and then use each slot from every device as a potential state for the RL process. Thus, a state is defined by a pair $(networkdevice,timeslot)$, and actions are the possible state transitions (see Figure 3b). Notice that actions are not the edges from the ONM; ONM edges connect ONM nodes, which are defined by a device and an encounter time stamp. RL actions connect states defined by a device and a discretized time slot. The resulting Q-tables are shown in Figure 3c.

Paralleling the ONM edges, there are two possible classes of actions. In one, the destination of the state transition is a state associated with the same origin device but at a later time slot; this represents storing data between different time slots. In the other scenario, the destination is a state with a different device but in the same time slot; this represents a data-forwarding action.

Notice that the state space can be seen as the time discretization of the ONM graph; multiple graph nodes from a device that occur in the same time slot map to a single state. For example, in Figure 3a, there are two encounters by node B in time slot $T_2$. Both encounters are represented by the same state $(B,2)$ in Figure 3b.

Furthermore, an action can capture the effect of multiple ONM edges. For example, all encounters between a pair of devices that happened in the same time slot, each modeled by a separate ONM copy edge, are represented as the same action: forwarding between the involved devices in the given time slot.

Actions that connect subsequent states within the same device are called survival actions, the idea being that when the link exists, data have survived between time slots. Notice that a survival action is available on all states except for the last state associated with a device.

The Q-learning is performed each time a forwarding decision is made, this is on each ONM graph node. If there are multiple forwarding decision evaluations within a time slot, they all contribute to the computation of the time slot’s Q-value.

The time slot size is a configuration parameter for rl4dtn. In one extreme, when there is a single time slot that spans the whole mobility scenario, the rl4dtn model behaves as a single, static connectivity graph. In this case, there is a single forwarding action computed for connecting each pair of nodes, and there are no survival actions. The Q-value for the actions is computed from all the forwardings made through the scenario, and no temporal distribution of encounters is captured. As the number of slots increases, the number of nodes per state is reduced since the time slots become shorter, and thus fewer nodes share a slot. This means there are fewer Q-learning evaluations to update the state’s Q-value, while at the same time, the number of states increases. The result is a degradation of the system’s learning convergence. Because we want to capture changing mobility patterns through time, a balance must be reached for the optimum time slot size. We discuss this effect in more detail in Section 6.

An agent can perform multiple actions simultaneously, representing the generation of replicas of the routed message, with each copy later being routed independently. Thus, if we configure the protocol to choose a single action, rl4dtn behaves as forwarding algorithm. If multiple actions are allowed, the algorithm becomes flooding-based.

5.2. Q-Value and Rewards

As is usual in routing, the RL problem is posed as distance minimization instead of reward maximization. Furthermore, as usual in these cases, we fix the discount factor $\gamma =1$. The resulting Q-update function is shown in Equation (7).

$$Q_c(d,x)\leftarrow (1-\alpha )Q_c(d,x)+\alpha (R+\underset{y\in N_x}{min}{Q}_x(d,y))$$

(7)

The definition of the immediate cost R itself is flexible. For example,

Table 2. Immediate edge costs R for rl4dtn for various distance definitions.

	Time Edge	Copy Edge
Latency	$T_{dest}-T_{source}$	0
Hop count	0	1
Power consumption	0	$Pwr(source,dest)$

presents the immediate cost of edges under several distance metrics. The hop count metric minimizes the number of transmissions, while the latency attempts to deliver the data as fast as possible. The power consumption cost can be seen as a generalization of hop count, where the transmission cost is a function $Pwr$ of the distance between the nodes, the radio environment, message size, etc.

Notice that the immediate cost R used to update a Q-value is computed on every encounter or ONM graph edge. As a result, the instances of evaluation of a state–action pair and the values of R are non-deterministic.

In RL algorithms, the definition of when a message is considered delivered is under the control of the reward function, which is an arbitrary function. It can accommodate concepts such as multicast (deliver to a set of nodes), anycast (deliver to any of a set of nodes), or generalizations such as subscription-based delivery (deliver to nodes that request messages with specific properties).

5.3. Opportunistic Route Exploration

An essential part of the behavior of ML systems is exploration; rl4dtn explores the space of solutions by two mechanisms. The first is the standard $ϵ-greedy$ policy, where, at the action-selection time, there is a probability $ϵ$ of selecting a random action instead of the known best (the one with minimum associated Q-value).

The second exploration mechanism is to generate multiple message copies, where each one is routed independently. This replication is managed using Binary Spray and Focus (BSF) [22]. This is similar to the Binary Spray and Wait technique mentioned in Section 2, differing only in its behavior when the copies count reaches one. In BSW, this single copy is held locally and delivered only to the destination device if it is met directly. In BSF, this copy can be handed over to another device and then remain hopping from device to device until meeting the destination. Notice that if the emitting device sets the number of copies parameter to one, the algorithm behaves as a pure forwarding algorithm.

As usual in Q-learning, the exploration parameters can be reduced during the system’s lifetime, favoring exploration in the early stages and exploitation in later stages to improve performance and convergence.

The pseudocode for rl4dtn is shown in Algorithm 2. The entry point is on line 16, which is called on every encounter after updating the ONM model when a forwarding decision must be made (we assume we are handling a single message msg). For this purpose, a list of candidate destination states is built on lines 17–24. One of the candidates is the survival action (line 18). As mentioned before, this can be directly obtained from the rl4dtn model if already available from previous evaluations. If not, it can be a placeholder, as this action is known to exist. Besides the survival action, all copy actions are added to the list of candidates (line 19). If one of the neighboring agents is the target for the message, the message is delivered, and no further processing is made.

Once a list of candidates is built, line 25 selects a copy or survival target using the $ϵ-greedy$ selection function (lines 3–7). After this, line 26 updates the Q value. That is done on lines 8–18, applying Equation (7). In our case, line 12 computes immediate hop count costs from Table 2.

If the selected action was a forwarding, Binary spray and focus is used on lines 27–33 to either forward half message copies if there are more than one (line 28) or migrate the single available copy to the new device (line 31).

Algorithm 2: rl4dtn pseudocode.

As a baseline, we implemented a straightforward Q-learn algorithm not based on ONM. Unlike rl4dtn, only actions associated with forwarding are maintained (no survival actions), and forwarding is performed if the best candidate has a better Q-evaluation than its own. In Algorithm 2, this implies the removal of line 18, the condition on line 27, and the substitution of the action selection function on line 7. The message-copies handling is identical to rl4dtn. This allows us to evaluate the impact of using ONM to learn explicit actions for keeping messages. Any improvement from Q-learn to rl4dtn can be assigned to the use of the ONM model. Please, notice that the computational complexity of both algorithms is roughly equal. Both are evaluated in the same situations (at forwarding decisions), the only difference being that rl4dtn has one more transition to consider: the explicit storing action.

6. Simulation

We test the algorithms using the RioBuses dataset [23], which collects the GPS trajectories of buses in Rio de Janeiro, Brazil. It contains over 12,000 units, moving over 700 bus lines through November 2014. In this work, we down-sample the dataset to 1000 buses, which is still a large use-case for an ON [24]. We generate ten distinct down-sampled sets to produce statistics. Nevertheless, the ONM representation allows simulating the entire dataset, even using desktop-grade hardware [8].

We run the algorithm in a scenario where all units emit two messages, one at 00:00 and another at 12:00, directed to a single fixed collection point located in one of the city bus terminals. Successful delivery is achieved when a message arrives within the same day. Messages underway are removed every night at midnight, but the learned protocol parameters are kept.

To calibrate the algorithm parameters, we simulate the first seven days of the trace. The results are shown in Figure 4. The delivery rate is computed at the end of the corresponding day. The reduction in delivery rate on days 4 and 5 corresponds to the weekend, with reduced bus services (1 October 2014 was a Wednesday).

Figure 4a shows the impact of the $\alpha$ parameter on the learning process (see Equation (7)). The algorithm was configured with eight copies per message. The best learning is achieved with a very aggressive $\alpha =1.0$.

As described in Section 5, the Q-parameters are learned per time slot to allow for learning different patterns throughout the day. On the other hand, more slots mean fewer encounters per slot, which slows down learning. The impact of the number of time slots is shown in Figure 4b. It can be seen as the single-slot scenario learns fastest, as it considerably outperforms the alternatives at the end of the first day. Nevertheless, 6 or 12 slots finally catch up and outperform after day 3. Having 24 slots degrades performance, possibly because the number of encounters per slot is too small to sustain effective reinforcement learning.

In rl4dtn, reinforcement learning is performed by observing the propagation of data messages through the network. Thus, having multiple replicas of a message improves the learning process. Additionally, it improves the delivery rate, as it is enough for a single message copy to arrive for a successful delivery. This effect can be seen in Figure 4c. On the other hand, producing multiple copies of messages increases the data transmitted in the network. This effect will be discussed in Section 6.

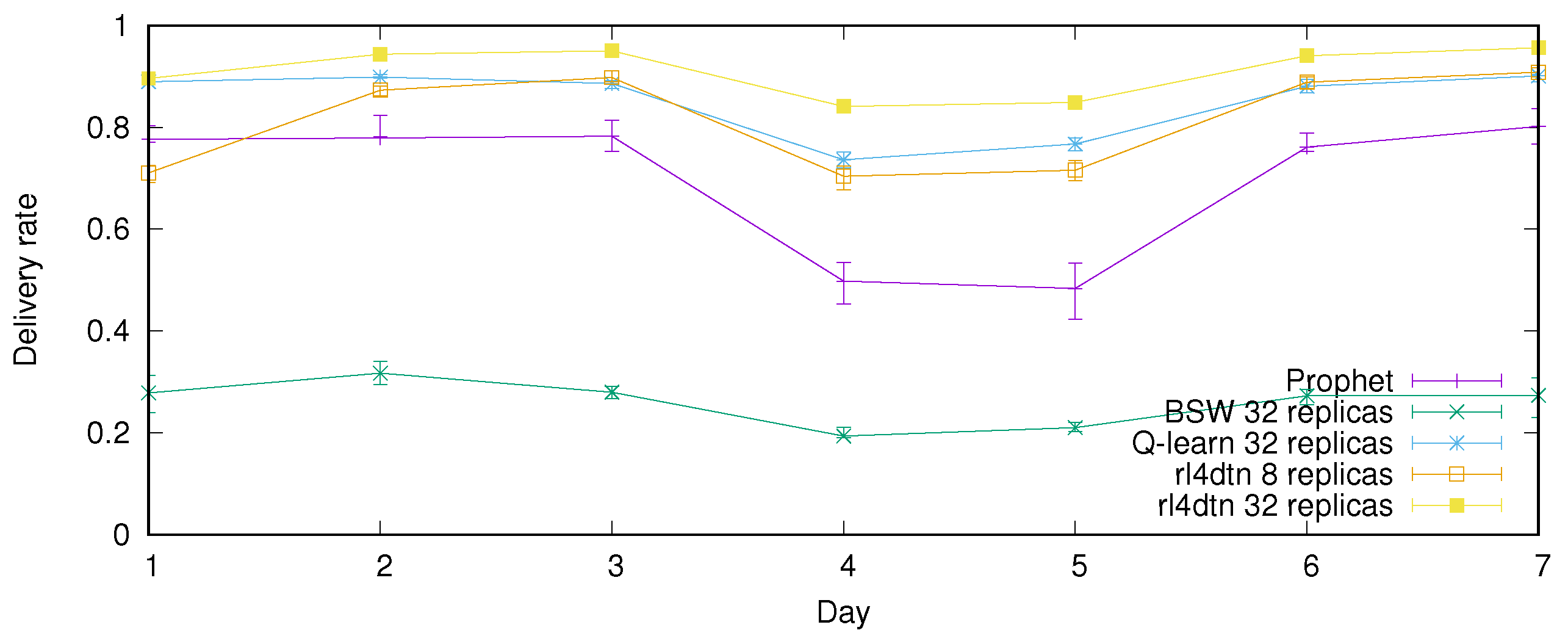
Figure 5 compares rl4dtn delivery performance with BSW, PRoPHET and the reference Q-learning protocol. The average over ten simulations with different buses samples is shown, with the corresponding interquartile range. The number of time slots used for rl4dtn and Q-learning is 6, the number of message copies is 8, and the $ϵ$ parameter driving the Q-learning exploration is set at 1.0 at the beginning and then reduces linearly to 0.5 on the last day.

BSW underperforms considerably. PRoPHET suffers the most from the reduction in mobility through the weekend.

It can be seen that rl4dtn offers a better delivery rate. Furthermore, the performance difference between Q-learn and ld4dtn shows the impact of using the ONM as a base for the learning process.

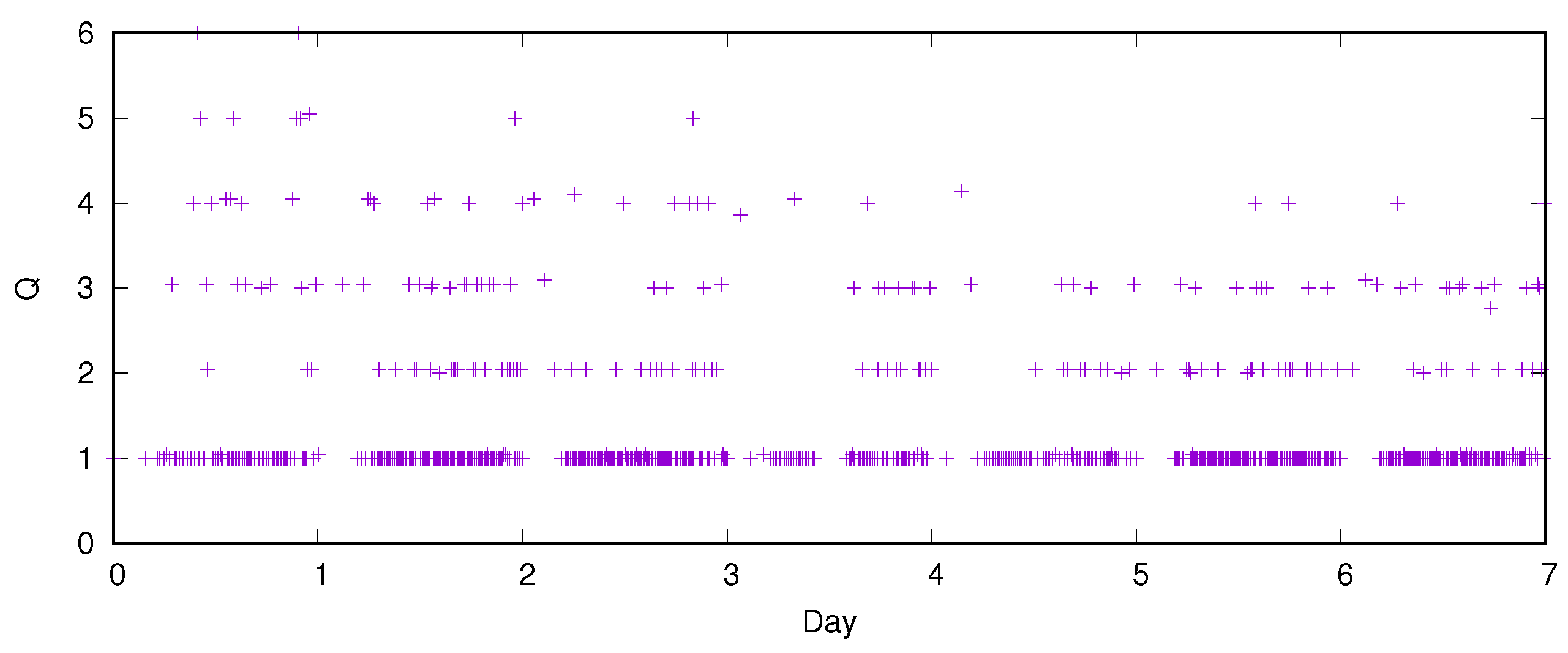
Figure 6 displays a 1:50 sample of the Q-values as they evolve through the system’s learning. This shows the convergence behavior of the Q-learning process. Notice that the Q-values estimate the cost of an opportunistic path; in our scenario, this cost is the hop count. It can be seen that the system starts with Q values up to 6, and from day three, it settles on many paths of one bus hop, considerably less but roughly similar paths of length 2 and 3, and very few of length 4. The gap with almost no deliveries in the early morning can be seen.

Figure 7 shows the latency histogram, which is the time between message generation and message arrival, for the messages emitted at 12:00 and successfully delivered. rl4dtn has a marked peak at around 2 h latency, while the other algorithms have a more indistinct behavior. Notice that two hours is a reasonable average trip duration, using bus lines, from anywhere in the Rio de Janeiro region to a given collection point. This suggests that rl4dtn finds more direct paths than the alternatives, which depend more on longer, more random journeys.

Traffic Efficiency

The traffic produced by an ON algorithm is an important metric, as it directly impacts power consumption. This traffic is produced by agents exchanging routing data and when forwarding messages.

Thus, the total traffic in the network is:

$$T_{tot}=E\times S_R+T\times S_M$$

(8)

where the parameters are shown in

Table 3. Data exchange parameters.

		BSW	PRoPHET	Q-Learn, rl4dtn
E	Number of encounters	From ONM graph (copy edges)
T	Number of message forwardings	From simulation
$S_M$	Size of message	1 KB + 4 B	1 KB	1 KB + 8 B + 4 B
$S_R$	Routing exchange size	0	1.000*8B	0

, assuming 1 KB messages and 1000 buses.

BSW does not attempt to learn from the network, and no routing information is exchanged. The only addition to the messages is the integer number of the number of copies.

PRoPHET exchanges a predictability vector during each encounter. This vector contains a floating-point predictability value for each device in the network. rl4dtn does not exchange routing data; in its place, a Q-value used to update a Q-table is retrieved from the destination when forwarding. Additionally, the messages have a copies-count integer.

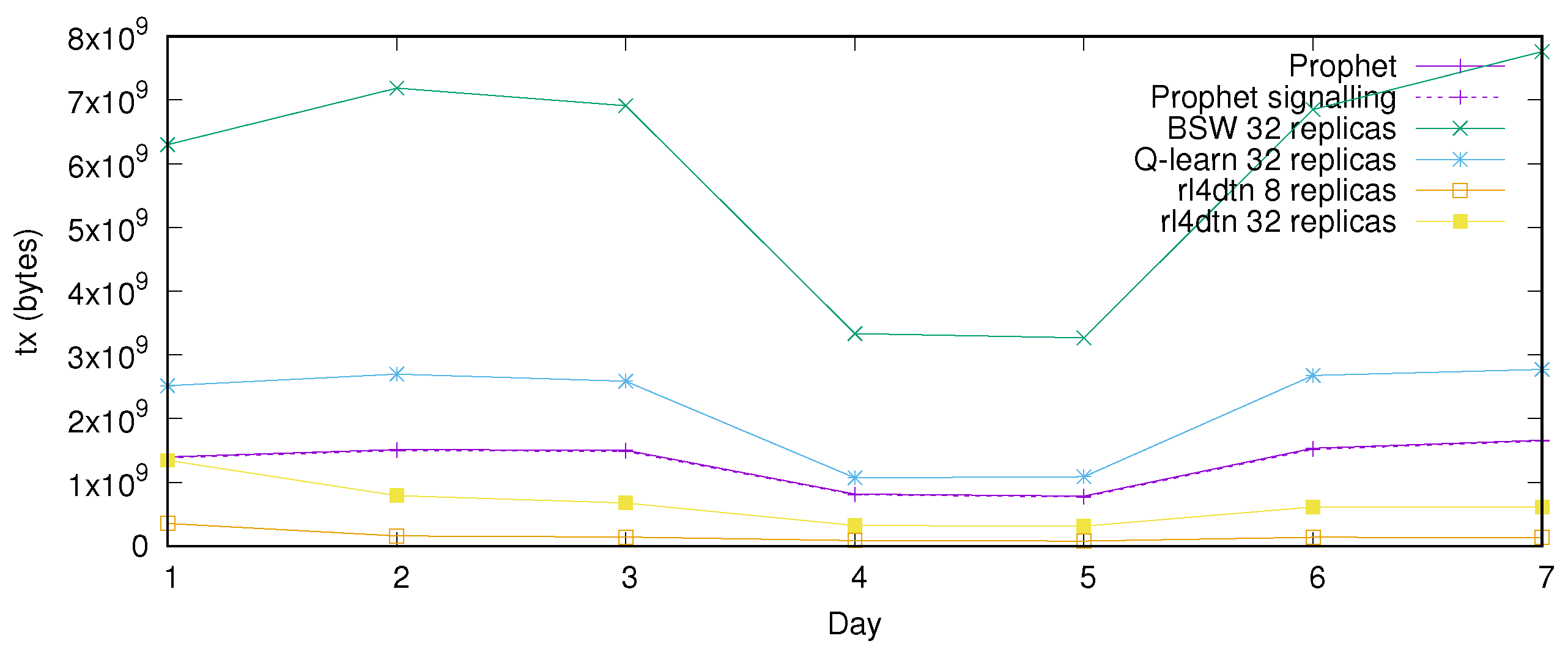
The total traffic produced in the network is shown in Figure 8. BSW has a very high transmission cost, despite not producing routing data. This is related to the fact that every transmission opportunity is taken, and the maximum allowable number of replications is produced. Nevertheless, the delivery rate is poor because the replication is made very aggressively following the message generation, not achieving adequate dissemination through the network. It can be seen that PRoPHET has a high traffic consumption, the vast majority of it being routing information and not data transmissions. This signaling grows with the number of encounters (vector exchanges) and devices in the network (vector size). Furthermore, it must be noted that a considerable part of the routing information exchange might not be of interest to the actual data flows in the network. Finally, rl4dtn achieves better delivery performance with a lower data overhead.

7. Conclusions and Future Work

We presented rl4dtn, an opportunistic networks routing algorithm based on Q-learning, that takes advantage of a particular opportunistic network model. This model captures the evolution of the network through time using a temporal graph. The network devices build and use this model in a distributed fashion during the network’s lifetime.

This work shows that this model allows our Q-learning-based method to outperform classic Q-learning approaches. By comparing rl4dtn with a conventional Q-learning algorithm, we show that the rl4dtn’s advantage comes from the fact that the learning mechanism feeds from temporal data. These temporal data allow learning from the temporal patterns in the distribution of encounters arising from the devices’ movement patterns. Temporal patterns are a defining characteristic of ONs, differentiating them from conventional networks.

At the same time, the resulting algorithm obtains a higher delivery rate with a considerably lower network overhead than representative ON routing algorithms; this is very important for networks with large numbers of devices where the routing data transmissions can represent a significant load.

Amongst the issues that need more attention, we point out that although the dataset used in this work is typical, more tests are needed as ONs cover a broad spectrum of mobility scenarios.

Another area of improvement is the management of time slots. In this work, the time-slot size is fixed and experimentally determined. A scheme can be devised where the system adjusts the slots dynamically and automatically without an explicit configuration. For example, the system could adjust the time-slot size to maintain a certain number of encounters per slot, enough to sustain effective Q-learning. As a result, for example, nighttime slots could be longer and peak-hour slots shorter.

In summary, the proposed routing algorithm builds on top of a previously presented network model, which allows it to outperform classic Q-learning approaches. It achieves higher delivery rates with lower network overhead than representative ON routing algorithms. There are several lines for improvement that must be explored.