Evolutionary Computation for Sparse Synthesis Optimization of CCAAs: An Enhanced Whale Optimization Algorithm Method

Abstract

Concentric circular antenna arrays (CCAAs) can obtain better performance than other antenna arrays. However, high overhead and excessive sidelobes still make its application difficult. In this paper, we consider the sparse synthesis optimization of CCAAs. Specifically, we aim to turn off a specific number of antennas while reducing the sidelobe of CCAAs. First, we formulate an optimization problem and present the solution space. Then, we propose a novel evolutionary method for solving the optimization problem. Our proposed method introduces hybrid solution initialization, hybrid crossover method, and hybrid update methods. Simulation results show the effectiveness of the proposed algorithm and the proposed improvement factors.

1. Introduction

With the rapid development of computer technology and wireless communication technology, increasing numbers of users are being connected to the network. However, due to the large number of users accessing 5G and 6G networks, a single common antenna often cannot provide sufficient network support for users. Increasing the transmission power of the antenna alone often cannot improve the network quality, and creates severe interference problems. In this case, using multiple antennas to form an antenna array and conduct beamforming can be seen as an effective technique to enhance wireless communication performance [1].

Specifically, multiple antennas can be controlled by a single controller and then emit the same electromagnetic wave towards the target. These electromagnetic waves are superimposed and canceled in free space to generate a beam pattern with a distribution of strengths and weaknesses [2]. We note that the direction with the strongest gain is called the mainlobe and the rest are called the sidelobes. By pointing the mainlobe to the target user, the power received by the target user can be greatly enhanced, thus strengthening the performance of the antenna system in long-range and high-speed scenarios.

The antennas can be distributed in different manners to form different antenna arrays. Common antenna arrays include linear antenna arrays, square antenna arrays, Yagi–Uda antenna arrays, etc. In recent years, concentric circular antenna arrays (CCAAs) [3] have received a lot of attention from researchers due to their unique advantages and inherent merits [4]. As shown in Figure 1, CCAAs consist of some concentric circular rings, and each ring contains a various number of antennas. Compared with other antenna arrays, CCAAs can perform 360-degree beam scanning to achieve more comprehensive coverage [5]. On the other hand, CCAAs can obtain relatively small sidelobes, thus reducing the interference signals.

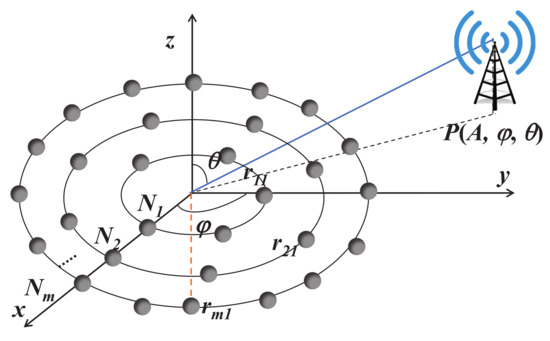
Figure 1. CCAA model.

In existing CCAAs, the excitation current weights of array elements are often set as uniform, as this scheme requires no further design and is easy to implement. However, these unoptimized and simple uniform CCAAs have some drawbacks that lead to their limited application in the real world. Specifically, CCAAs often contain a huge number of array elements which indeed effectively improve the transmission performance of CCAAs but cause a large overhead. Actually, in most scenarios, not all array elements need to be turned on. On the other hand, the sidelobes of uniform CCAAs are also difficult to suppress, which may generate a great deal of interference to the surrounding devices [6]. Therefore, some of the array elements of CCAAs can be turned off and some array elements can be assigned low excitation current weights, thereby completing the sparse synthesis optimization of CCAAs.

The existing methods for performing sparse synthesis are based on the following types of methods. Some work has utilized deterministic optimization methods to perform sparse synthesis of various antenna arrays, such as convex optimization methods to determine which antennas need to be turned off and optimize the excitation current accordingly. However, these methods often require the relaxation of certain key constraints, leading to a degradation of the optimization performance. Several works have employed evolutionary computation to perform sparse synthesis tasks. This is due to the fact that evolutionary computation is able to solve many NP-hard problems and does not require information about the gradient of the problem. Therefore, evolutionary computation can be seen as an effective method to perform the sparse synthesis optimization of CCAAs. For instance, references [7,8,9] considers using moth flame optimization, a teaching–learning-based optimization algorithm, and a cuckoo search algorithm to solve the sparse synthesis optimization of CCAAs and obtain suitable results.

Most of these methods only consider reducing the sidelobes or decreasing the number of active antennas as much as possible. However, aiming to keep the transmission power steady, there also is a requirement to reduce the maximum sidelobe level while switching off a fixed number of antennas. This requirement has been overlooked in the literature. Note that turning off a specific number of array elements of CCAAs while optimizing sidelobes is challenging because the structure of the decision variables will be changed. Different from these methods, we aim to turn off the specific number of antennas while reducing the sidelobe of CCAAs via a novel evolutionary algorithm in this work. Our contributions are summarized as follows.

• We formulate a novel optimization problem to turn off a specific number of antennas while reducing the sidelobes of CCAAs. The problem is challenging because it involves both binary and continuous decision variables and is an NP-hard problem.
• We propose an enhanced whale optimization algorithm (EWOA) to solve our formulated problem. EWOA introduces chaos theory and thereby proposes a novel hybrid solution initialization method. Moreover, we propose a hybrid solution crossover approach to balance the exploitation and exploration abilities of the EWOA. Finally, we propose a hybrid solution update method to handle the specific structure of the problem. After being enhanced, the proposed EWOA is more suitable and efficient in solving our considered problem and has a main difference from the conventional EWOA.
• We conduct extensive simulations to verify the performance of the proposed EWOA. The simulation results show that the proposed EWOA is effective and outperforms other peer algorithms. Moreover, the proposed improved factors are also evaluated and demonstrated.

The rest of the paper is organized as follows. In Section 2, we briefly present some existing works in terms of deterministic methods and evolutionary approaches. Moreover, Section 3 introduces the considered models and formulates our problem. In addition, we propose the EWOA and the corresponding improved factors in Section 4. Furthermore, Section 5 conducts the simulations. Finally, the paper is concluded in Section 6.

2. Related Works

In this work, we consider using an evolutionary algorithm to solve the antenna optimization problem. Thus, in this part, we briefly present some existing works in the fields of deterministic methods and evolutionary approaches.

2.1. Deterministic Methods

Some works use deterministic methods to determine the excitation current weights of array elements. For instance, Buttazzoni et al. [10] proposed an iterative algorithm for sparse antenna arrays which introduces a compressive sensing approach for transforming the original non-convex optimization problem into a convex problem. Moreover, the authors in [11] proposed a deterministic approach to the optimal power synthesis of mask-constrained shaped beams through the CCAAs. Additionally, Fan et al. [12] formulated a unified sparse array design framework for beam pattern synthesis based on this design metric. The authors in [13] discussed a novel technique for sparse array synthesis in which the synthesis strategy was based on a sparse forcing algorithm using an improvement of reweighted minimization. In [14], a novel analytical approach to the synthesis of linear sparse arrays with non-uniform amplitude excitation was presented and thoroughly discussed. Comisso et al. [15] presented an iterative algorithm for the synthesis of the 3D radiation pattern generated by an antenna array of arbitrary geometry. However, these methods often require a relaxation of certain key constraints, leading to a degradation of the optimization performance.

2.2. Evolutionary Computation Approaches

Some approaches have adopted various evolutionary computation approaches to perform sparse synthesis tasks. For example, the authors in [4] used three evolutionary optimization algorithms, quantum particle swarm optimization (QPSO), teaching–learning-based optimization (TLBO), and symbiotic organism search (SOS), to thin the CCAAs. Moreover, Dutta et al. [16] proposed an improved version of QPSO to minimize the SLLs of CCAAs, in which the array elements have been considered to be uniformly excited with unit excitation amplitude. In [7], the authors presented an accurate approach based on moth flame optimization (MFO) to solve the CCAA synthesis problem for achieving lower SLL. In addition, Ismaiel et al. [17] proposed an optimization method based on a comprehensive learning particle swarm optimizer (CLPSO) to reduce the SLL of CCAAs, in which the excitation current weights are considered. In [18], a method based on a combination of ant lion optimizer and sequential quadratic programming was proposed for concentric circular antenna array (CCAA) synthesis, in which excitation amplitudes of array elements were optimized for CCAAs with low maximum sidelobe level (MSL), narrow first null beamwidth (FNBW), and low dynamic range ratio (DRR). Challa et al. [19] presented an optimized CCAA of antennas based on biogeography-based optimization (BBO). In [20], the authors used a political optimizer (PO), which is a novel evolutionary algorithm, to reduce the SLL of the CCAA. However, most of these methods only consider reducing the sidelobes or decreasing the number of the activated antennas as much as possible and do not consider turning off the specific number of array elements of CCAAs while decreasing the sidelobes.

Different from these works, we consider turning off a specific number of antennas while reducing the sidelobe of CCAAs via a novel evolutionary algorithm in this work. The details of our model and problem are presented as follows.

3. Model and Problem

In this section, we first present our considered CCAA model. Then, we formulate our considered sparse synthesis optimization problem in CCAAs.

3.1. CCAA Models

We show CCAA models in Figure 1. As can be seen, CCAAs consist of some concentric circular rings, and each ring contains a various number of antennas. Moreover, we assume that each antenna element of CCAA is radiation isotropic. In addition, all the antenna elements of CCAA are controlled by a centralized process and these antennas are synchronized in terms of time, frequency, and initial phase. Furthermore, all the antenna elements are fixed and the relative positions cannot be changed.

In this case, the electromagnetic waves generated by all the array elements will be precisely superimposed at the receiver and offset in some directions. Intuitively, these antennas will generate a beam pattern that contains a mainlobe and some sidelobes [21]. Mathematically, we can use the array factor as the index to show the signal strength of the CCAA system. In CCAAs, the array factor is a complex function of the excitation current weights of array elements of CCAAs, which is shown as follows [22].

$$\begin{array}{cc}\hfill F(\theta ,\varphi )=& \hfill \sum _{m=1}^M\sum _{n=1}^{N_m}{I}_{mn}·e^{j\left[k{r}_{m}sin\left(\theta \right)cos\left(\varphi -{\varphi }_{mn}\right)\right]+{\gamma }_{mn}},\hfill \end{array}$$

(1)

where M is the number of concentric rings. Moreover, $N_m$ is the number of antennas of the mth concentric rings, where $m=1,2,\dots ,M$. Note that we use $N_T$ to denote the total number of antennas in the CCAA, which can be calculated as $N_L={\sum }_{m=1}^M{N}_m$. In addition, $k=2\pi /\lambda$m, where $\lambda$ is the wavelength. Additionally, $r_m$ is the radius of the mth circle with the value of $N_m{d}_m/2\pi$, wherein $d_m$ is the spacing between the elements on the mth concentric rings. Furthermore, $\theta$ and $\varphi$ are the zenith and azimuth angles, ${\theta }_0$ and ${\phi }_0$ are the directions of the mainlobe, and ${\varphi }_{mn}$ is the central angle of the nth antenna element of the mth concentric rings. The most important parameters of Equation (1) are $I_{mn}$ and ${\gamma }_{mn}$, where $I_{mn}$ is the excitation current weight of nth antenna element of the mth circle and ${\gamma }_{mn}$ is the initial phase of nth antenna element of the mth circle. We assume that the initial phase of all the antennas are synchronized, thus ${\gamma }_{mn}$ can be calculated as follows.

$$\begin{array}{c}\hfill {\gamma }_{mn}=-k{\gamma }_{m}sin\left({\theta }_0\right)cos({\phi }_0-{\phi }_{mn}).\end{array}$$

(2)

3.2. Inactivated or Activated Antenna Model

In this work, we aim to turn off a specific number of array elements in CCAAs while achieving some other optimization objective. Thus, we introduce our inactivated or activated antenna model in this section.

Specifically, we consider the use of a binary vector $\mathit{B}=\{b_1,b_2,\cdots ,b_{N_T}\}$ to denote the antenna’s inactivated or activated condition. As shown in Figure 2, we use 0 to indicate that the antenna is not turned on, and 1 to indicate that the antenna is turned on. Mathematically, this model can be expressed as follows.

$$b_l=\left\{\begin{array}{cc}0,& \mathrm{The}l\mathrm{th}\mathrm{antenna}\mathrm{is}\mathrm{turned}\mathrm{off},\\ 1,& \mathrm{The}l\mathrm{th}\mathrm{antenna}\mathrm{is}\mathrm{turned}\mathrm{on}.\end{array}\right.$$

(3)

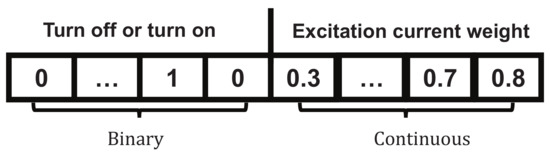
Figure 2. Inactivated or activated antenna model.

3.3. Sidelobe Suppression Model

As previously mentioned, the portion of the signal that is not the mainlobe belongs to the sidelobes. Therefore, it is difficult for us to evaluate the suppression of the sidelobes in a beam pattern. Generally speaking, we use the maximum sidelobe level (SLL) as a performance index to evaluate the suppression of the total sidelobes. This is because once the maximum SLL is suppressed, all the sidelobes will be suppressed. Mathematically, the calculation of the maximum SLL is as follows:

$$\begin{array}{c}\hfill f_{sll}\left(\mathit{I}\right)=\frac{\mathit{B}\left|AF\left({\theta }_{SLL}\right)\right|}{\left|AF\left({\theta }_{ML}\right)\right|},\end{array}$$

(4)

where $\mathit{I}=\{I_1,I_2,...,I_{N_T}\}$ is a vector denote the excitation current weights of the total antennas.

3.4. Optimization Problem

In this work, we aim to turn off a specific number of antennas while reducing the sidelobe of CCAAs. Based on the models and analyses above, we can carefully control $\mathit{B}$ and $\mathit{I}$ to optimize the maximum SLL. Specifically, our considered optimization problem can be expressed as follows:

$$\begin{array}{cc}\hfill \underset{\{B,I\}}{\min }& \hfill f=f_{sll}\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \hfill 0⩽I_l⩽1,\forall l\in N_T\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill & \hfill b_l=[0,1],\forall l\in N_T\hfill \end{array}$$

(5c)

We mention that our considered problem is a very complex optimization problem. Specifically, controlling the excitation current weights of antennas to minimize the maximum SLL is already an NP-hard problem. Our problem is more complicated than that, which means that our problem is also a complex NP-hard problem. Moreover, most existing works only consider optimizing the excitation current weights, which only have continuous decision variables. Likewise, there are also some works that only consider determining whether the antennas should be switched on or switched off, which only have binary decision variables. Different from these works, we consider both excitation current weight and antenna switched-on optimizations. Thus, our formulated problem involves both continuous and binary decision variables, which is difficult to solve with the existing methods. In this case, a powerful high-performance algorithm is urgently needed to solve our problem.

4. Proposed Algorithm

In this section, we aim to propose a novel and powerful algorithm to solve our considered problem. To this end, we introduce an evolutionary computation method and then enhance the algorithm, thereby achieving better objective values by controlling the decision variables of $\mathit{B}$ and $\mathit{I}$.

4.1. Overview of Evolutionary Computation

Evolutionary computation is a very popular advanced optimization method in recent years. Evolutionary computation refers to the rules and guidelines of nature, physics, and chemistry, so as to abstract important mathematical models with solution significance, thereby achieving the purpose of searching the solution space [23].

Specifically, most evolutionary computation algorithms generate a population in which each individual in the population is a solution to the problem to be solved. These individuals can be evaluated by an objective function, and the corresponding individuals with high objectives will have higher values. Individuals in the population are constantly updated in iteration, and individuals with high values can influence individuals with low values to update. In this way, through continuous iteration, the algorithm can continuously search for better solutions in the solution space.

Mathematically, we denote the population as P, in which $P=\{X_1,X_2,...,X_{N_{pop}}\}$, wherein $X_i$ is the ith solution of the population. Moreover, $X_i$ must be a feasible solution to the optimization problem shown in Equation (5), which can be denoted as $X_i=\{x_1,x_2,...,x_{N_{dim}}\}=\{{\mathit{B}}_i,{\mathit{I}}_i\}$.

4.2. Conventional Whale Optimization Algorithm

Among the various evolutionary computation algorithms, the whale optimization algorithm (WOA) is a recently proposed algorithm with high performance. In some engineering problems, WOA often achieves better performance than other algorithms. WOA considers th prey-encircling spiral bubble-net feeding maneuver, and the search for prey of the whale population. These models can be expressed as follows.

4.2.1. Encircling Prey

Whales can find prey and surround them. The WOA algorithm allows individuals other than other individuals to update their positions to approach the optimal position, which can be expressed as follows.

$$\begin{array}{c}\overrightarrow{D}=\left|\overrightarrow{C}·X^{*}\left(t\right)-X\left(t\right)\right|,\hfill \\ X(t+1)=X^{*}\left(t\right)-\overrightarrow{A}·\overrightarrow{D},\hfill \end{array}$$

(6)

where t indicates the iteration, $X^{*}$ is the position vector of the best solution of current population, and $\left|\right|$ is the absolute value operator. The coefficient vectors A and C can be calculated as follows.

$$\begin{array}{c}\overrightarrow{A}=2\overrightarrow{a}·r-\overrightarrow{a},\hfill \\ \overrightarrow{C}=2r,\hfill \end{array}$$

(7)

where a is a parameter that is linearly decreased from 2 to 0 through the iteration and r is a random number [0, 1].

4.2.2. Bubble-Net Attacking Method

The bubble-net attacking method contains two methods which are detailed as follows.

(i)

Shrinking encircling mechanism. This behavior is achieved by reducing the value of parameter a, and the details can be found in [24].

(ii)

Spiral updating position. WOA uses a helix-shaped movement of humpback whales to guide the update of the population, which can be shown as follows.

$$\begin{array}{c}\overrightarrow{D^{\prime }}=\left|X^{*}\left(t\right)-X\left(t\right)\right|,\hfill \\ X(t+1)=\overrightarrow{D^{\prime }}·e^{bl}·cos\left(2\pi l\right)+X^{*}\left(t\right),\hfill \end{array}$$

(8)

where $\overrightarrow{D^{\prime }}$ is the distance between the current whale and prey, b is a constant parameter, and l is random in [−1, 1].

4.2.3. Search for Prey

WOA develops a random selection method to enhance the exploration capabilities of the algorithm, as follows.

$$\begin{array}{c}\overrightarrow{D}=\left|\overrightarrow{C}·X_{\mathrm{rand}}-X\right|,\hfill \\ X(t+1)=X_{\mathrm{rand}}-\overrightarrow{A}·\overrightarrow{D},\hfill \end{array}$$

(9)

where $X_{rand}$ is a random position vector.

4.2.4. Shortcomings

Although WOA has many inherent advantages, there are still some flaws and urgent problems in WOA that are relevant to solving our problem. For example, the problem requires that the partial decision variables be binary, and the partial decision variables are continuous variables from 0 to 1. This makes our problem a very intractable mixed solution optimization problem, which poses a challenge to the solution of WOA. Second, the development ability and exploration ability required by WOA to solve different problems are not the same. These flaws prompted us to improve it and propose an improved version of WOA.

4.3. Proposed Enhanced Algorithm

In order to make WOA more able to solve our optimization problem, we propose an enhanced WOA (EWOA) in this part. The details and improved factors are shown as follows.

4.3.1. Hybrid Solution Initialization Method

The conventional WOA uses a stochastic number generator to generate the initial population. A generated initial population via this type has the following issues. First, this method will lead to a decrease in the performance of the initial solution, thereby reducing the convergence performance of the algorithm. Second, our problem is a mixed solution problem, and a stochastic number generator can only produce continuous solutions. Due to these reasons, we propose a hybrid solution update method in this part.

First, we generate the continuous part of the solution via chaos maps. Note that chaos maps are special mathematical structures that include periodic and stochastic continuous sequences. Because of their characteristics, they are often used in the improvement of initialization in evolutionary computation algorithms. Specifically, there are about 10 common chaotic maps, namely, Chebyshev, circle, Gauss/mouse, iterative, logistic, piecewise, sine, singer, sinusoidal, and tent. In this work, we select an iterative map to generate the continuous part of the solutions, which can be detailed as follows.

$$p_{q+1}=sin\left(\frac{c\pi }{p_q}\right),c=0.7,$$

(10)

where $p_q$ is the qth sequence of the iterative map. Then, the continuous part of a solution can be initialized as follows.

$$x_k=l{b}_k+p_q(u{b}_k-l{b}_k),$$

(11)

By using this method, the initial solution generated by the algorithm will have a more balanced performance, so the algorithm’s performance is better.

Second, we generate the binary part of the solution, which can be detailed as follows.

$$\mathit{B}={Rand}_{1,0}\left(N_{\mathrm{sel}},N_S-N_{\mathrm{sel}}\right),$$

(12)

where ${Rand}_{1,0}\left(a,b\right)$ can generate a vector combined with a ones and b zeros.

4.3.2. Hybrid Solution Crossover

We consider a crossover method to hybridize solutions to enhance the exploration ability of our proposed algorithm. Specifically, the best solution for the population often contains the most information and can guide all individuals to explore in a better direction. In each iteration, we select some individuals and use the crossover with the best solution to improve them. The details of this method are as follows. As with the proposed hybrid solution initialization method, this crossover method operates on different classes of solutions separately.

For the discrete part, we first find the discrete dimension which is different from the best solution and exchange information between the two. Subsequently, we judge whether the discrete part of the current individual satisfies the selected number of antennas. If the number is too large or too small, we invert the random selection solution from the individual until the number of antennas selected by the individual is appropriate.

For the continuous part, we make individuals exchange information with the best solution with half the probability. The pseudocode for this method is shown in Algorithm 1.

Algorithm 1: Hybrid Solution Crossover.

4.3.3. Hybrid Solution Update

In this section, we update the two parts of the hybrid solution separately. Specifically, the continuous solution part is still updated using the original WOA update method. For discrete solutions, we consider mutating and crossing them first. The method is specifically shown in Algorithm 2.

Algorithm 2: Hybrid Solution Update.

4.3.4. Main Steps and Complexity Analysis of EWOA

The main steps of the proposed EWOA can be shown in Algorithm 3. Moreover, the complexity of EWOA is examined. The calculation of the objective function value, which is considerably more difficult than other steps in our optimization problem, takes the longest. Thus, other steps can be skipped in this situation. As a result, when the maximum number of iterations and population size are denoted as $t_{max}$ and $N_{pop}$, respectively, the complexity of EWOA is $\mathcal{O}(t_{max}·N_{pop})$.

Algorithm 3: EWOA.

5. Simulations

In this section, we perform simulations to evaluate the performance of EWOA. First, we present our experimental setup, comparison algorithms, etc. Second, we present our optimization results. Third, we illustrate the effectiveness of the improvement factors.

5.1. Setups

In this work, we use a CCAA with 10 rings for the simulation. In this case, the total number of antenna elements in the CCAA is 440, and the number of elements per ring is $8\times$ m, where m is the number of turns. Furthermore, we aim to turn off one half of the antenna elements. Moreover, our used CPU was an 11th Gen Intel(R) Core(TM) i7-11700 @ 2.50 GHz with 16 GB of RAM.

In addition, we introduced some comparison algorithms for comparison, specifically, the dragonfly algorithm (DA) [25], conventional WOA [24], gray wolf optimization (GWO) [26], sine cosine algorithm (SCA) [27], and salp swarm algorithm (SSA) [28]. In this case, all algorithm populations were set to 50, and the number of iterations was set to 200. Note that these algorithms are both evolutionary algorithms, in which their computational complexities correspond to the times of fitness calculations. Thus, in this work, these algorithms have the same complexity which is $t_{max}\times N_{pop}$, i.e., $50\times 200$.

5.2. Simulation Results

We first evaluated the objective function values of different algorithms to solve our problem and give the average, maximum, and minimum values in Table 1. It can be seen that our proposed method is superior to all other comparison algorithms. The reason is that we have a better balance between exploration ability and exploitation ability. Moreover, as shown in Figure 3, we give the convergence curves of different algorithms. It can be seen that our algorithm’s convergence is the fastest. It can be seen that our proposed initial solution method can effectively speed up convergence. In addition, as shown in Table 2, we give the running time of different algorithms. It can be seen that the running time of all algorithms is similar, and our algorithm does not increase the running complexity of the algorithm. Furthermore, as shown in Figure 4, we provide the beam patterns of the CCAAs obtained by different algorithm. As can be seen, our proposed EWOA achieved the best beam pattern performance. For a more intuitive demonstration, we plot the structure of the optimized CCAAs in Figure 5. Specifically, the entire antenna array is the structure of the original CCAA. After being optimized by our algorithm, some antennas are switched off while the rest are also switched on.

Table 1. Statistical results of the objective values obtained by different approaches.

(DB)	AVE.	MAX.	MIN.
DA	−23.2598	−22.6900	−23.7409
GWO	−23.2644	−22.6404	−24.0011
SSA	−23.2434	−22.6982	−23.8245
WOA	−23.441	−22.8497	−24.0907
SCA	−21.2753	−20.1031	−22.3683
EWOA	−23.7883	−23.2147	−24.1995

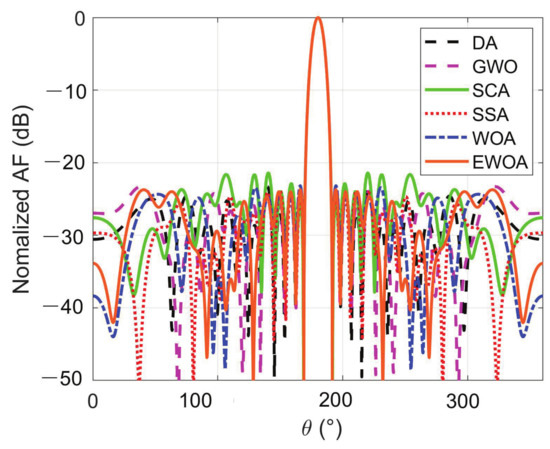
Figure 3. Beam patterns obtained by different algorithms.

Table 2. Statistical results of the running time obtained by different approaches.

(DB)	AVE.	MAX.	MIN.
DA	409.3217	520.8348	286.9482
GWO	271.8296	298.7387	232.12
SSA	273.4268	302.3688	222.1255
WOA	297.5742	312.5098	290.1445
SCA	254.5393	290.0058	189.7762
EWOA	313.075	250.7853	331.1821

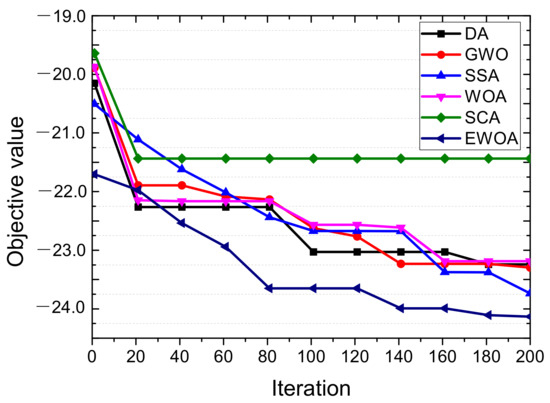
Figure 4. Convergence rates obtained by different algorithms.

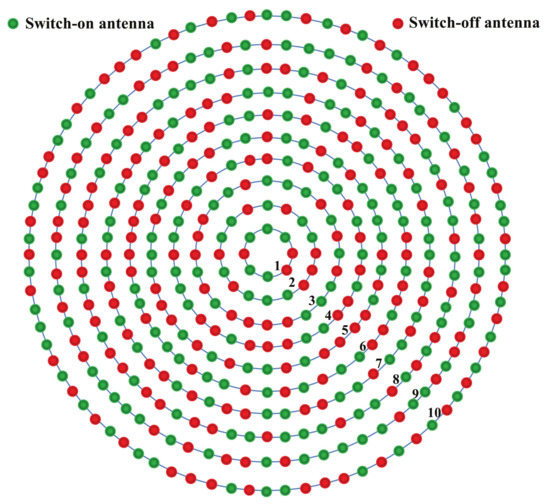
Figure 5. State of the CCAA.

On the other hand, we evaluated the impact of different improved factors on the algorithm. We considered different chaotic map-based initialization methods and proposed crossover methods. The optimization results and running time are shown in Table 3 and Table 4, respectively. It can be seen that our selected chaotic map has the best performance, and the proposed crossover method can also effectively improve the performance of the algorithm. In addition, these algorithms are all on the same running time, which means that there is no additional increase in the running time of the algorithm.

Table 3. Statistical results of the objective values obtained by different improved factors.

(DB)	AVE.	MAX.	MIN.
Chebyshev	−23.5074	−23.0789	−23.934
Circle	−23.4647	−23.0118	−23.8412
Guass/mouse	−23.4788	−22.9087	−24.0222
Iterative	−23.5758	−23.0417	−23.9682
Logistic	−23.4941	−22.5767	−23.9068
Piecewise	−23.4257	−22.7275	−23.8546
Sine	−23.4498	−22.8004	−24.0941
Singer	−23.4784	−22.9801	−23.9801
Sinusoidal	−23.508	−23.0097	−23.9226
Tent	−23.4395	−23.0049	−23.9017
Crossover	−23.7153	−23.1617	−24.2604
EWOA	−23.7883	−23.2147	−24.1995

Table 4. Statistical results of the running time obtained by different improved factors.

(s)	AVE.	MAX.	MIN.
Chebyshev	300.2103	311.8449	273.2599
Circle	300.4639	308.2679	264.3575
Guass/mouse	305.5025	321.2203	285.5261
Iterative	311.7976	337.1776	182.6852
Logistic	306.6116	323.0361	290.9548
Piecewise	306.8332	328.9165	279.5588
Sine	331.7841	340.0234	322.1776
Singer	333.9409	341.0207	314.4988
Sinusoidal	337.2349	350.9823	277.0756
Tent	336.8633	354.8735	274.9848
Crossover	302.2373	316.8397	243.6888
EWOA	313.075	331.1821	250.7853

Except for the considered scenario in our original submission, we further added examples: one involving a very low population within 440 antenna elements and another one involving smaller arrays of 100 elements with large and small populations. The corresponding simulation results are presented as follows. Specifically, Table 5 shows the simulation results obtained by different algorithms in the case with 10 populations and 440 elements. Moreover, Table 6 shows the simulation results obtained by different algorithms in the case with 50 populations and 120 elements. In addition, Table 7 shows the simulation results obtained by different algorithms in the case with 10 populations and 120 elements. As can be seen, our proposed algorithm also outperforms other compared algorithms in the three cases. The reason may be that we balance the exploration and exploitation abilities and can make our proposed algorithm more suitable for solving our optimization problem.

Table 5. Statistical results of the objective values obtained by different approach in the case with 10 populations and 440 elements.

(DB)	AVE.	MAX.	MIN.
DA	−22.492	−21.281	−23.5388
GWO	−22.7027	−21.8035	−23.5196
SSA	−22.7403	−22.0197	−23.8178
WOA	−22.7205	−21.647	−23.4629
SCA	−20.1068	−18.9223	−22.2253
EWOA	−23.0437	−22.5879	−23.6858

Table 6. Statistical results of the objective values obtained by different approach in the case with 50 populations and 120 elements.

(DB)	AVE.	MAX.	MIN.
DA	−8.73719	−8.39645	−9.46009
GWO	−9.05977	−8.16812	−9.57519
SSA	−8.99624	−8.71156	−9.36257
WOA	−9.09705	−8.32748	−9.47902
SCA	−8.91788	−8.3524	−9.36407
EWOA	−9.41423	−9.15111	−9.6363

Table 7. Statistical results of the objective values obtained by different approach in the case with 10 populations and 120 elements.

(DB)	AVE.	MAX.	MIN.
DA	−8.27269	−7.7332	−9.08744
GWO	−8.68996	−7.24128	−9.26944
SSA	−8.59402	−7.72822	−9.31861
WOA	−8.67264	−7.46379	−9.38475
SCA	−8.56307	−7.73576	−9.14937
EWOA	−9.1513	−8.67405	−9.45595

6. Conclusions

This paper considered the sparse synthesis optimization of CCAAs. We aimed to turn off a specific number of antennas while reducing the sidelobe of CCAAs. First, we formulated an optimization problem and presented the solution space. Then, we proposed an EWOA method for solving the optimization problem. EWOA introduced hybrid solution initialization, crossover, and update methods. Finally, we conducted simulations to show the effectiveness of the proposed EWOA and the proposed improvement factors.